Identification of Vibration Source Influence Intensity in Combine Harvesters Using Multivariate Regression Analysis
Abstract
1. Introduction
2. Materials and Methods
- Linear analysis, separately on each axis, based on the vibratory components corresponding to that axis;
- Linear analysis on all axes simultaneously;
- Nonlinear analysis, axis by axis;
- Multidirectional nonlinear analysis.
- It provides an accessible and interpretable analytical framework;
- There is no significant experimental evidence to justify the assumption of major nonlinearities in the transmission of vibrations from the source to the receiver in the analyzed configurations.
3. Results
3.1. C110H Combine
3.1.1. Case of Stationary Operating Mode
3.1.2. Case of Working Operating Mode
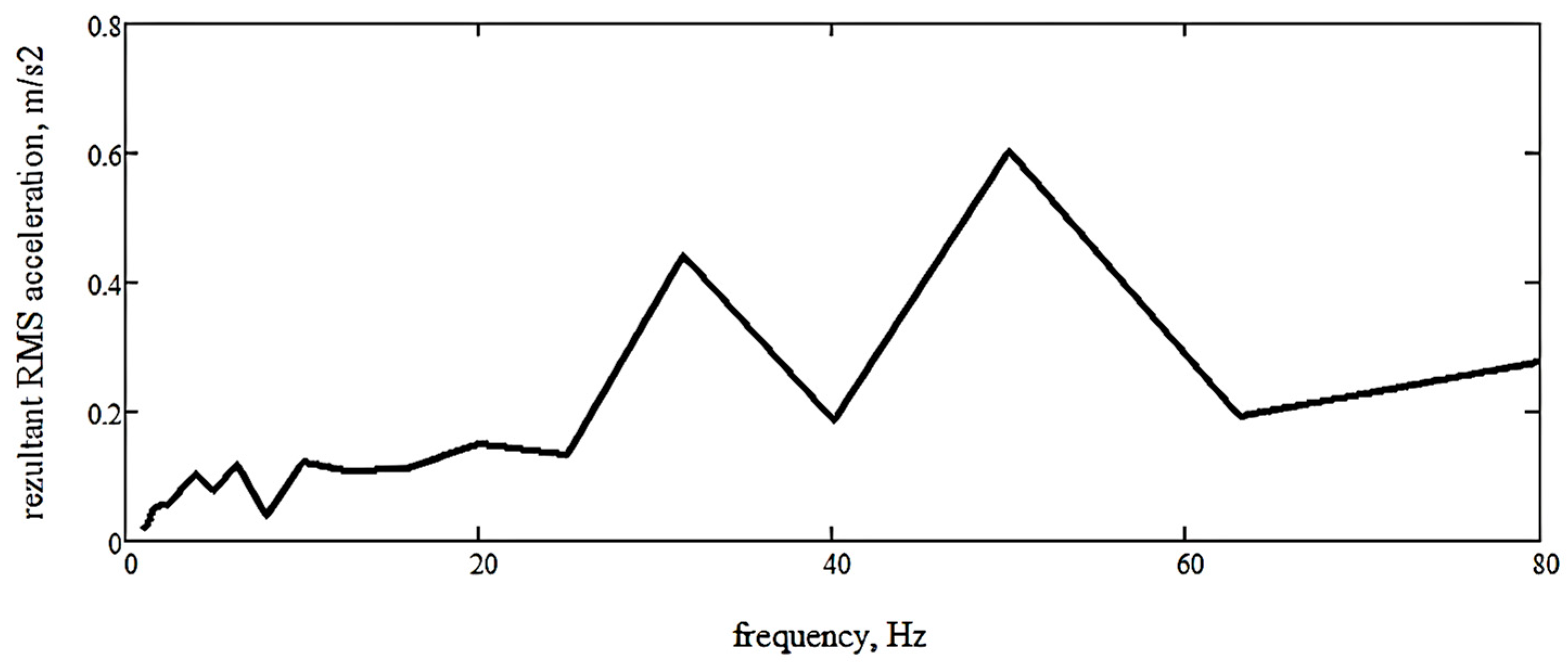
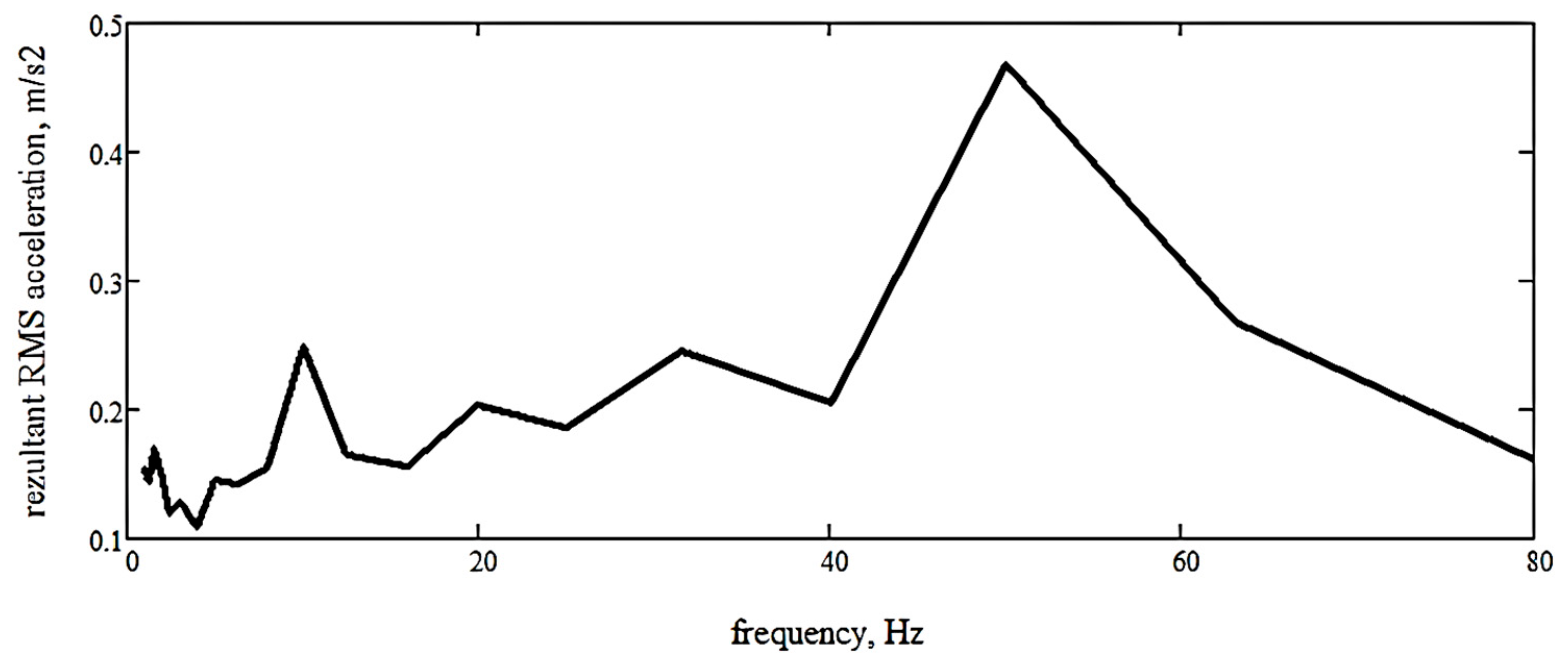
3.1.3. Identification of the Maximum RMS Resultant Acceleration at the Operator’s Seat
3.2. CASE IH Combine
3.2.1. Case of Stationary Operating Mode
3.2.2. Case of Working Operating Mode
3.2.3. Identification of the Maximum Resultant Accelerations at the Operator’s Seat
4. Possibilities for Ranking the Influences of the Combine’s Vibratory Components on the Operator’s Seat
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Ranking of Vibration Intensity at the Operator’s Seat
Appendix A.1.1. C110H Combine in Stationary Operating Mode
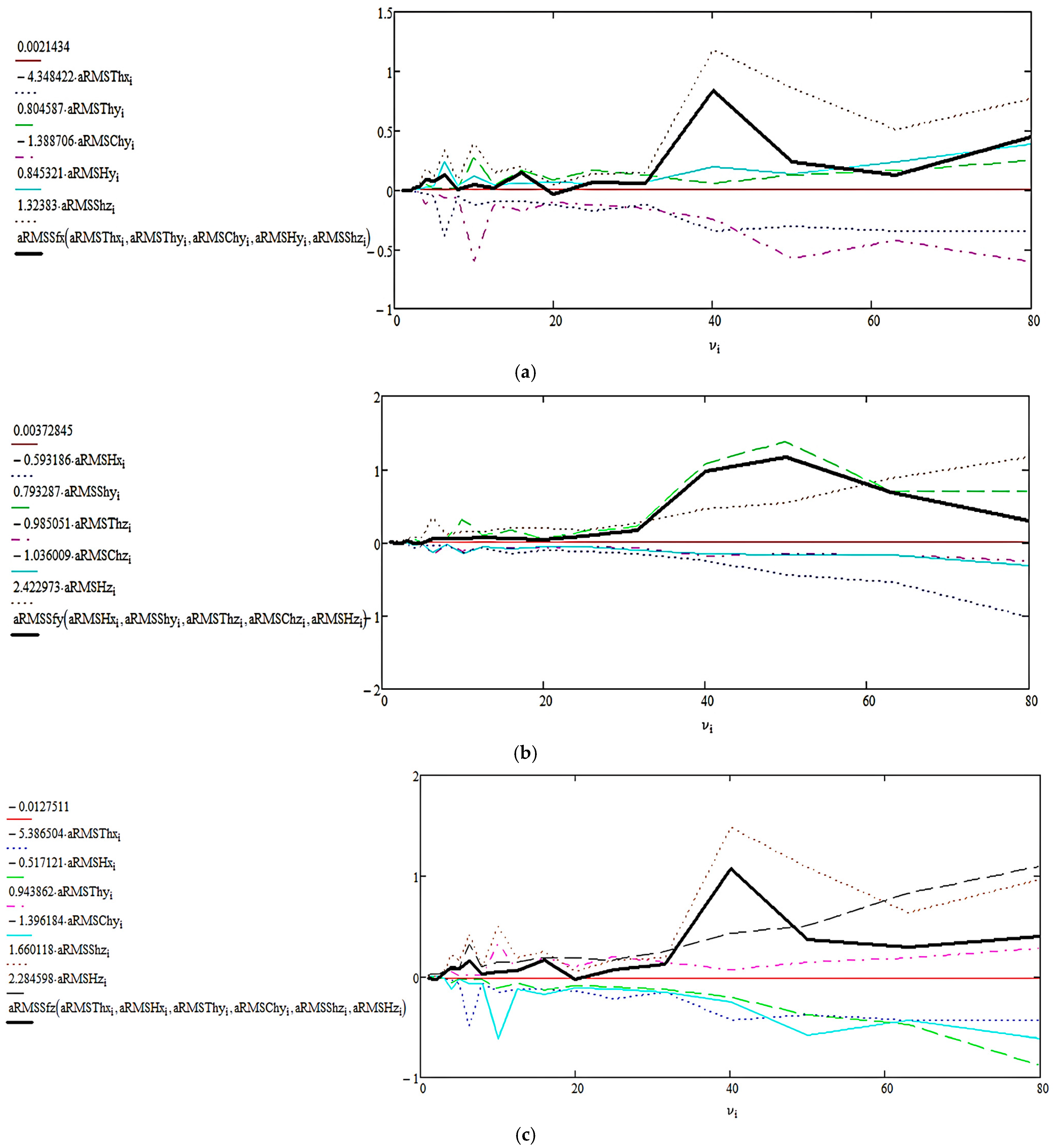
| Direction | Dominant Component |
|---|---|
| Ox | |
| Oy | |
| Oz |
Appendix A.1.2. C110H Combine in Working Operating Mode
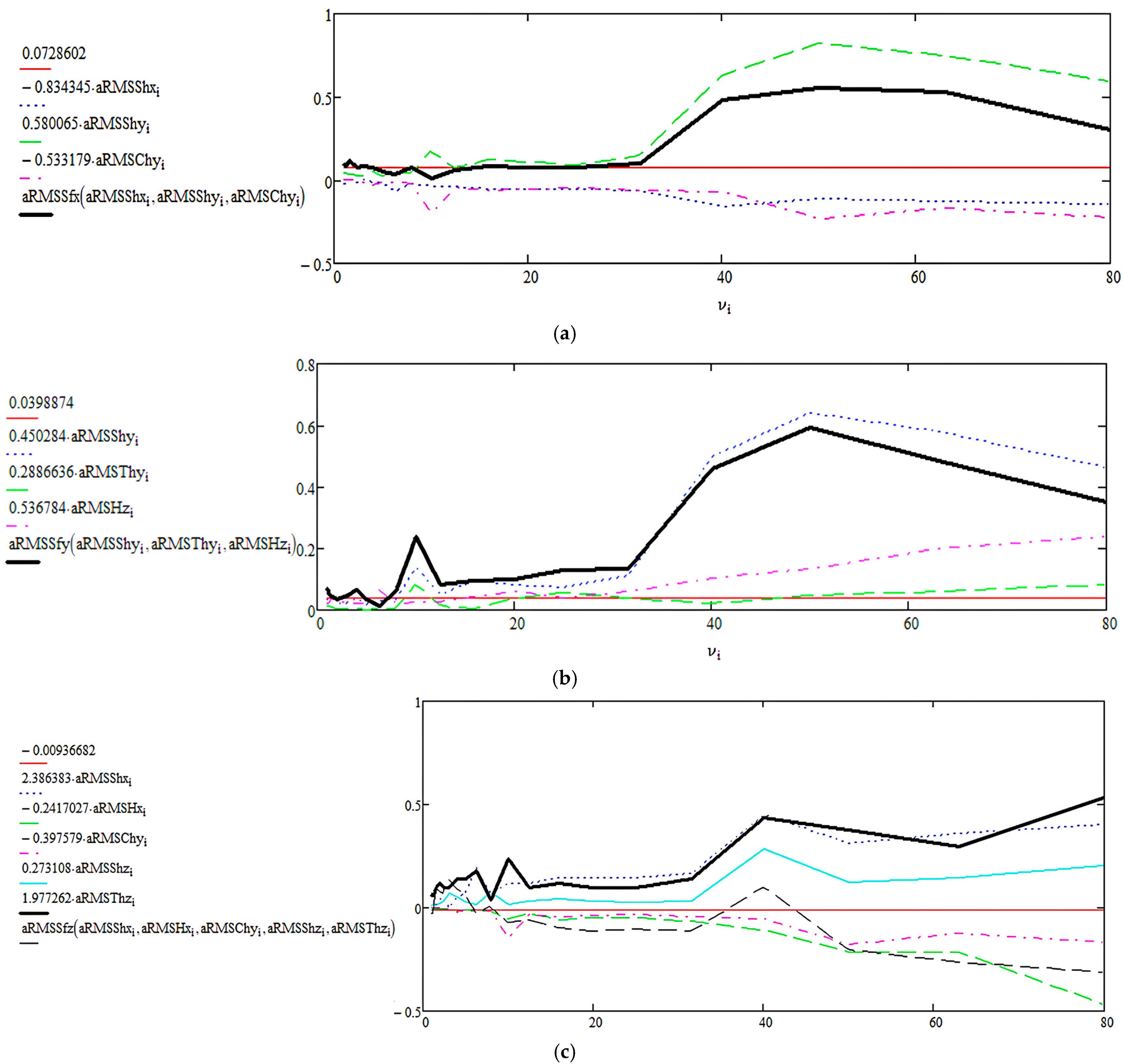
| Direction | Dominant Component |
|---|---|
| Ox | |
| Oy | |
| Oz |
Appendix A.1.3. CASE IH Combine in Stationary Operating Mode
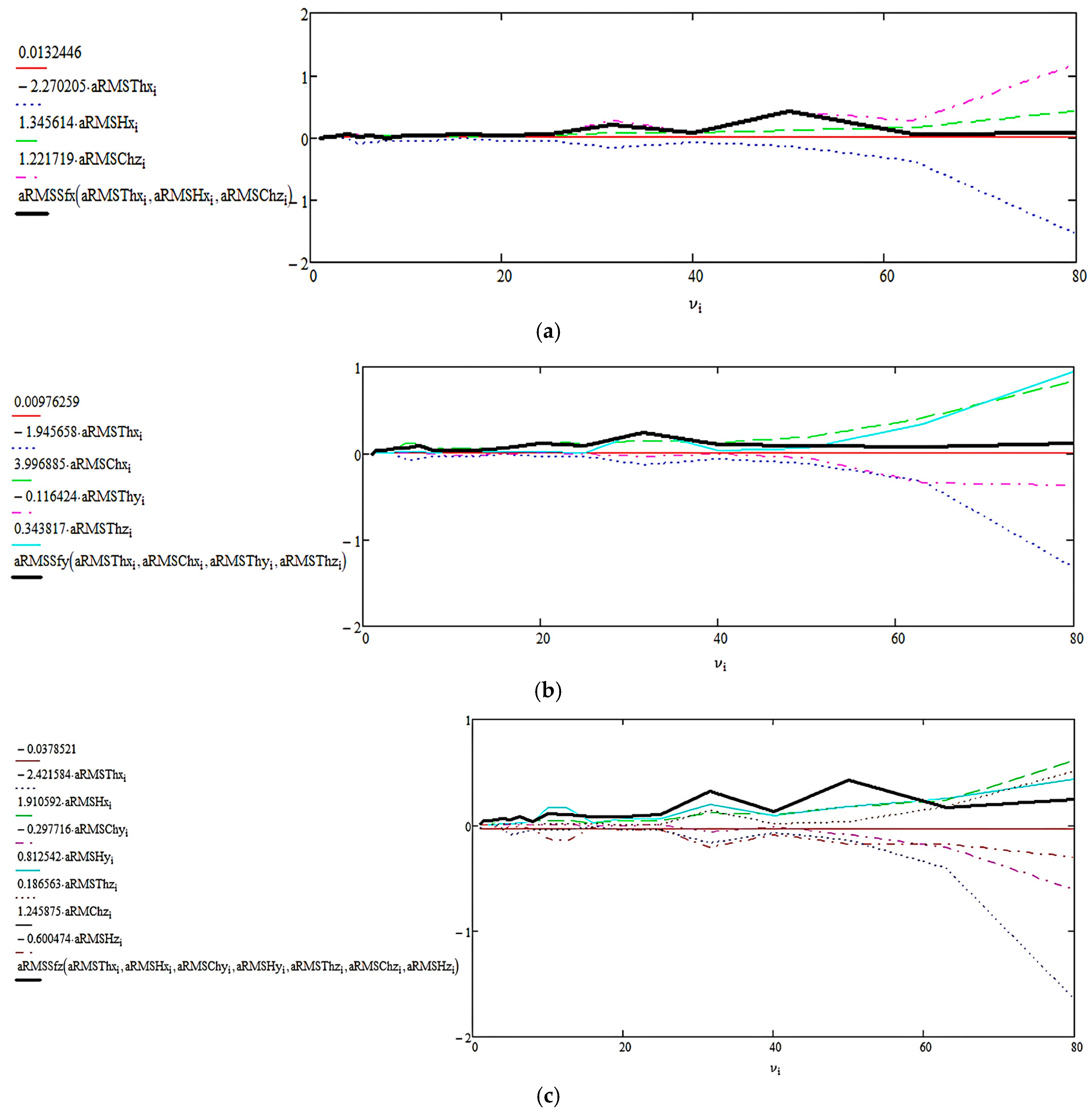
| Direction | Dominant Component |
|---|---|
| Ox | |
| Oy | |
| Oz |
Appendix A.1.4. CASE IH Combine in Working Operating Mode
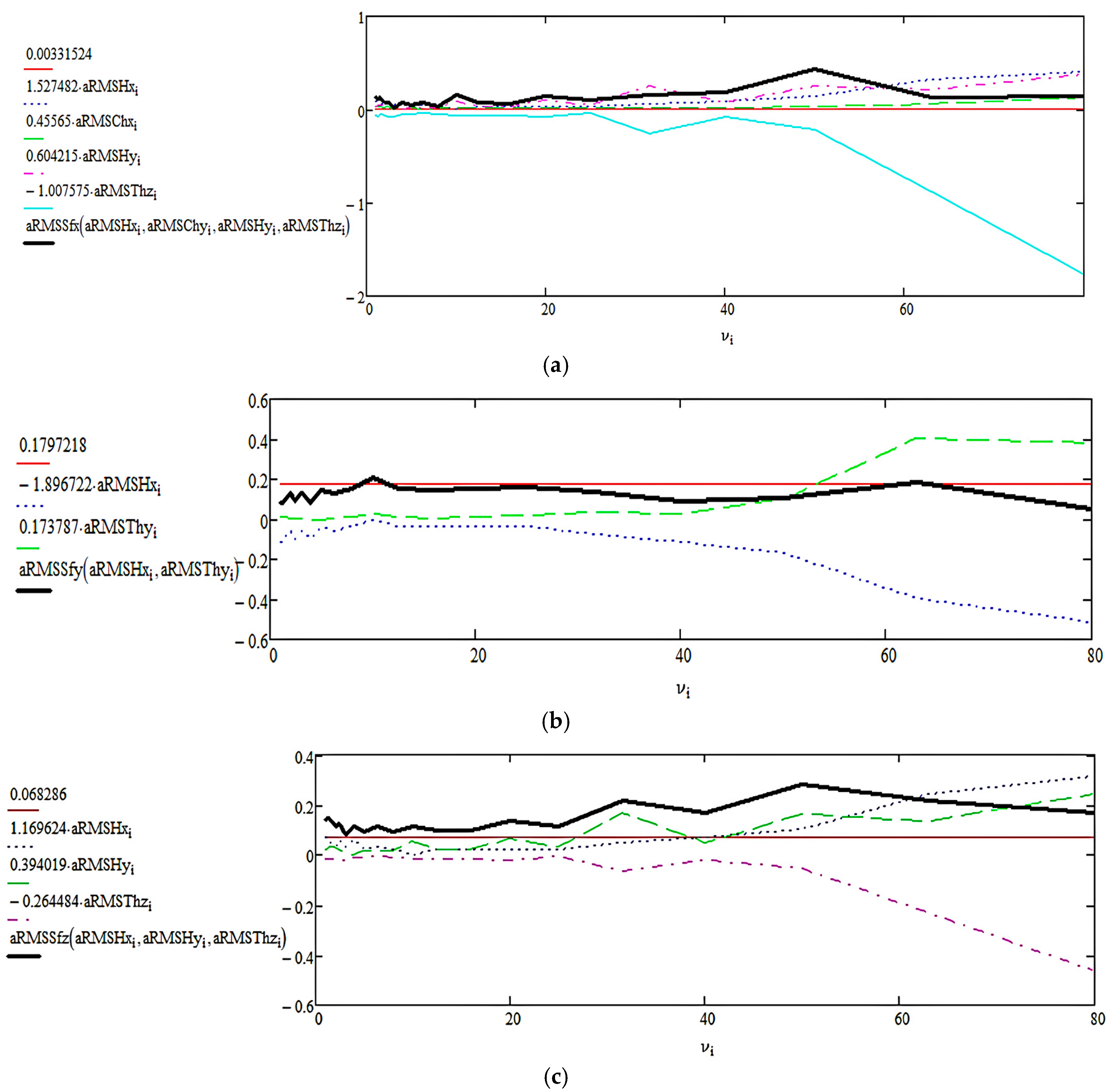
| Direction | Dominant Component |
|---|---|
| Ox | |
| Oy | |
| Oz |
References
- Chapra, S.C. Applied Numerical Methods with MATLAB for Engineers and Scientists, 3rd ed.; McGraw-Hill: New York, NY, USA, 2023. [Google Scholar]
- Zaharie, D. Nonlinear Regression Models (Course); West University of Timisoara: Timisoara, Romania, 2023. [Google Scholar]
- Freedman, D.A. Statistical Models: Theory and Practice; Cambridge University Press: Cambridge, UK, 2009; p. 26. [Google Scholar]
- Dimitriadou, S.; Nikolakopoulos, K.G. Multiple linear regression models with limited data for the prediction of reference evapotranspiration of the Peloponnese, Greece. Hydrology 2022, 9, 124. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, X. Combining variable selection and multiple linear regression for predicting soil nitrogen and organic carbon using NIR spectroscopy. Agronomy 2020, 12, 638. [Google Scholar] [CrossRef]
- Guan, T.; Alam, M.K.; Rao, M.B. Sample size calculations in simple linear regression. Entropy 2023, 25, 611. [Google Scholar] [CrossRef] [PubMed]
- Rencher, A.C.; Christensen, W.F. Methods of Multivariate Analysis, 3rd ed.; Wiley Series in Probability and Statistics; John Wiley & Sons: Hoboken, NJ, USA, 2012; p. 19. [Google Scholar]
- Yamauchi, A.; Imagawa, H.; Yokonishi, H.; Sakakibara, K.-I.; Tayama, N. Multivariate analysis of vocal fold vibrations on various voice disorders using high-speed digital imaging. Appl. Sci. 2021, 11, 6284. [Google Scholar] [CrossRef]
- Vulovic, M.; Prvulovic, S.; Tolmac, J.; Radisic, B.; Bajic, D.; Josimovic, M.; Sarenac, U.; Vulovic, S. Dynamic balancing and vibration analysis of rotor turbines: Methodologies and applications in predictive maintenance. Symmetry 2025, 17, 743. [Google Scholar] [CrossRef]
- Rehman, N.U.; Aftab, H. Multivariate variational mode decomposition. arXiv 2019, arXiv:1907.04509. [Google Scholar] [CrossRef]
- Frost, J. Multicollinearity in Regression Analysis: Problems, Detection and Remedies. Statistics by Jim. Available online: https://statisticsbyjim.com/regression/multicollinearity-in-regression-analysis/ (accessed on 24 February 2023).
- Lai, H.; Gao, X. Modified BIC criterion for model selection in linear mixed models. Mathematics 2023, 11, 2130. [Google Scholar] [CrossRef]
- Kim, W.; Jeon, J.; Jang, M.; Kim, S.; Lee, H.; Yoo, S.; Ahn, J. Developing a dynamic feature selection system (DFSS) for stock market prediction: Application to the Korean industry sectors. Appl. Sci. 2024, 14, 7314. [Google Scholar] [CrossRef]
- Piekutowska, M.; Niedbała, G.; Piskier, T.; Lenartowicz, T.; Pilarski, K.; Wojciechowski, T.; Pilarska, A.A.; Czechowska-Kosacka, A. The Application of Multiple Linear Regression and Artificial Neural Network Models for Yield Prediction of Very Early Potato Cultivars before Harvest. Agronomy 2021, 11, 885. [Google Scholar] [CrossRef]
- Lee, G.-C. A regression-based method for monthly electric load forecasting in South Korea. Energies 2024, 17, 5860. [Google Scholar] [CrossRef]
- Aldahmani, E.; Alzubi, A.; Iyiola, K. Demand forecasting in supply chain using uni-regression deep approximate forecasting model. Appl. Sci. 2024, 14, 8110. [Google Scholar] [CrossRef]
- Borrero, J.D.; Mariscal, J.; Vargas-Sánchez, A. A new predictive algorithm for time series forecasting based on Machine Learning techniques: Evidence for decision making in agriculture and tourism sectors. Stats 2022, 5, 1145–1158. [Google Scholar] [CrossRef]
- Lukman, A.F.; Kibria, B.M.G.; Nziku, C.K.; Amin, M.; Adewuyi, E.T.; Farghali, R. K-L estimator: Dealing with multicollinearity in the logistic regression model. Mathematics 2023, 11, 340. [Google Scholar] [CrossRef]
- Liang, R.; Liu, W.; Kaewunruen, S.; Zhang, H.; Wu, Z. Classification of external vibration sources data-driven models using hybrid CNNs and LSTMs. Struct. Control Health Monit. 2023, 2023, 1900447. [Google Scholar] [CrossRef]
- Wang, C. Load identification of acoustic and vibration sources following linear regression and least-squares of generalized matrix inverse method. J. Inf. Comput. Sci. 2014, 11, 3229–3239. [Google Scholar] [CrossRef]
- Li, S.M.; Jiang, X.X.; Lim, C.W. Research on Multi-Correlative Subsystems Analysis for Vibration Source Identification. In Vibration Engineering and Technology of Machinery; Sinha, J., Ed.; Mechanisms and Machine Science; Springer: Cham, Switzerland, 2015; Volume 23. [Google Scholar] [CrossRef]
- Fu, W.; Chen, H.; Kan, Z. Optimizing parameters on vibration breakshovel of radish harvester. Agric. Eng. 2011, 27, 46–50. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, X.; Li, J. Design and laboratory test of vibration excitation device for jujube harvester. In Proceedings of the 1st International Conference on New Materials, Machinery and Vehicle Engineering (NMMVE 2022); Volume 22: Advances in Transdisciplinary Engineering; Xu, J., Cai, Y., El Mansori, M., Eds.; IOS Press: Amsterdam, The Netherlands, 2022. [Google Scholar]
- Zhou, J.; Li, S.; Yang, D.; Zhong, J.; Mo, H.; Zhang, B.; Deng, X. Influence of sugarcane harvester cutterhead axial vibration on sugarcane ratoon cutting quality. Trans. Chin. Soc. Agric. Eng. 2017, 33, 16–24. [Google Scholar] [CrossRef]
- Al-Balhawi, A.; Zhang, B. Investigations of elastic vibration periods of tall reinforced concrete office buildings. Wind Struct. 2019, 29, 209–223. [Google Scholar] [CrossRef]
- Gao, R.; Yang, H.; Yang, Z. Evaluation of tractor driving vibrations fatigue based on multiple physiological parameters. PLoS ONE 2021, 16, e0254636. [Google Scholar] [CrossRef]
- Villibor, G.P.; Santos, F.L.; de Queiroz, D.M.; Guedes, D.M. Vibration levels and rear and front axles of a tractor in agricultural operations. Acta Sci. Technol. 2014, 36, 7–14. [Google Scholar] [CrossRef][Green Version]
- Periasamy, B.; Mishra, A.K. Statistical modelling of the blast design parameters influencing ground vibrations in a limestone quarry using design-expert. Arab. J. Geosci. 2023, 16, 571. [Google Scholar] [CrossRef]
- Cvetković, M.M.; Desai, R.; de Winkel, K.N.; Papaioannou, G.; Happee, R. Explaining human body responses in random vibration: Effect of motion direction, sitting posture, and anthropometry. arXiv 2023, arXiv:2306.12115. [Google Scholar] [CrossRef]
- Chen, F.; Li, S.; Zhang, Y.; Wang, J. Detection of the vibration signal from human vocal folds using a 94-GHz millimeter-wave radar. Sensors 2017, 17, 543. [Google Scholar] [CrossRef] [PubMed]
- Vien, B.S.; Chiu, W.K.; Russ, M.; Fitzgerald, M. Modal frequencies associations with musculoskeletal components of human legs for extracorporeal bone healing assessment based on a vibration analysis approach. Sensors 2022, 22, 670. [Google Scholar] [CrossRef]
- Nguyen, H.T.P.; Woo, Y.; Huynh, N.N.; Jeong, H. Scoring of human body-balance ability on wobble board based on the geometric solution. Appl. Sci. 2022, 12, 5967. [Google Scholar] [CrossRef]
- Chu, W.; Yang, H.-C.; Chang, S.-F. The effect of whole-body vibration training on biomarkers and health beliefs of prefrail older adults. Appl. Sci. 2021, 11, 3557. [Google Scholar] [CrossRef]
- Grigorjeva, T.; Luta, G.; Vilkas, A. Experimental study of vibrations in agricultural combines with respect to operator seat and frame dynamics. Agronomy 2023, 13, 488. [Google Scholar] [CrossRef]
- Gusiatnikov, V.I.; Kuznetsov, I.N. Analysis of the vibration load of agricultural machines with increased operating speeds. Machines 2022, 10, 181. [Google Scholar] [CrossRef]
- Malakhov, D.; Miroshnichenko, D. Finite Element dynamic analysis of harvester frame under multisource vibration loading. Sensors 2021, 21, 3893. [Google Scholar] [CrossRef]
- Benos, L.; Tsaopoulos, D.; Bochtis, D. A Review on Ergonomics in Agriculture. Part II: Mechanized Operations. Appl. Sci. 2020, 10, 3484. [Google Scholar] [CrossRef]
- Vitale, E.; Vella, F.; Matera, S.; Rizzo, G.C.; Rapisarda, L.; Roggio, F.; Musumeci, G.; Rapisarda, V.; Romano, E.; Filetti, V. Precision Agriculture: Assessment of Ergonomic Risks of Assisted Driving System. Appl. Sci. 2024, 14, 3738. [Google Scholar] [CrossRef]
- Barač, Z.; Jurić, M.; Plaščak, I.; Jurić, T.; Marković, M. Assessing Whole-Body Vibrations in an Agricultural Tractor Based on Selected Operational Parameters: A Machine Learning-Based Approach. AgriEngineering 2025, 7, 72. [Google Scholar] [CrossRef]
- Oncescu, T.A.; Persu, I.C.; Bostina, S.; Biris, S.S.; Vilceleanu, M.V.; Nenciu, F.; Matache, M.G.; Tarnita, D. Comparative Analysis of Vibration Impact on Operator Safety 2 for Diesel and Electric Agricultural Tractors. AgriEngineering 2025, 7, 40. [Google Scholar] [CrossRef]
- Oncescu, T.A.; Costea, I.M.; Burciu, S.C.; Rentea, C.A. Evaluation of the Dynamic Behavior and Vibrations of the Operator-Vehicle Assembly in Electric Agricultural Tractor Operations: A Simulation Approach for Sustainable Transport Systems. Systems 2025, 13, 710. [Google Scholar] [CrossRef]
- Cutini, M.; Brambilla, M.; Bisaglia, C. Whole-Body Vibration in Farming: Background Document for Creating a Simplified Procedure to Determine Agricultural Tractor Vibration Comfort. Agriculture 2017, 7, 84. [Google Scholar] [CrossRef]
- Jahanbakhshi, A.; Ghamari, B.; Heidarbeigi, K. Vibrations Analysis of Combine Harvester Seat in Time and Frequency Domain. J. Mech. Eng. Sci. 2020, 14, 639–654. [Google Scholar] [CrossRef]
- Marin, E.; Cârdei, P.; Vlăduț, V.; Biriş, S.S.; Ungureanu, N.; Bungescu, S.T.; Voicea, I.; Cujbescu, D.; Găgeanu, I.; Popa, L.D.; et al. Researches on the influence of the main vibration-generating components in grain harvesters on the operator’s comfort. Inmateh Agric. Eng. 2024, 74, 800–823. [Google Scholar] [CrossRef]
- ISO 2631-1:2001; Mechanical Vibration and Shock. Evaluation of Human Exposure. Part 1: General Requirements. Available online: https://e-standard.eu/en/standard/26040 (accessed on 27 August 2025).
- ISO 2631-5:2018; Mechanical Vibration and Shock. Evaluation of Human Exposure to Whole-Body Vibration. Part 5: Method for Evaluation of Vibration Containing Multiple Shocks. Available online: https://www.iso.org/standard/50905.html (accessed on 27 August 2025).
- StatsKingdom. Available online: https://www.statskingdom.com/ (accessed on 27 August 2025).
- Statology. ANOVA F-Value and p-Value Explained. Available online: https://www.statology.org/anova-f-value-p-value (accessed on 27 August 2025).
- Bing Search. F-statistic, Meaning. Available online: https://www.bing.com/search?q=F-ststistic%2C+meaning (accessed on 27 August 2025).
- Zondervan-Zwijnenburg, M.A.J.; van de Schoot, A.G.J.; Hoijtink, H.J.A. Testing ANOVA Replications by Means of the Prior Predictive p-Value. Meta-Psychology 2022, 6, MP.2019.1615. [Google Scholar] [CrossRef]
- Yao, Y.; Li, X.; Yang, Z.; Li, L.; Geng, D.; Huang, P.; Li, Y.; Song, Z. Vibration characteristics of corn combine harvester with the time-varying mass system under non-stationary random vibration. Agriculture 2022, 12, 1963. [Google Scholar] [CrossRef]
- Endaq Blog. Vibration Measurements: Vibration Analysis Basics. Available online: https://blog.endaq.com/vibration-measurements-vibration-analysis-basics (accessed on 27 August 2025).
- Buzdugan, G.; Fetcu, L.; Radeș, M. Mechanical Vibrations; Didactic and Pedagogical Publishing House: Bucharest, Romania, 1982. [Google Scholar]
- Chen, S.; Zhou, Y.; Tang, Z.; Lu, S. Modal vibration response of rice combine harvester frame under multi-source excitation. Biosyst. Eng. 2020, 194, 177–195. [Google Scholar] [CrossRef]
- Li, Y.; Tang, Z.; Ren, H.; Zhou, Y. Vibration Response of Combine Harvester Chassis Undergoing Multisource Excitation Force Distribution. Math. Probl. Eng. 2021, 2021, 8856094. [Google Scholar] [CrossRef]
- Pang, J.; Li, Y.; Ji, J.; Xu, L. Vibration excitation identification and control of the cutter of a combine harvester using triaxial accelerometers and partial coherence sorting. Biosystem. Eng. 2019, 185, 25–34. [Google Scholar] [CrossRef]



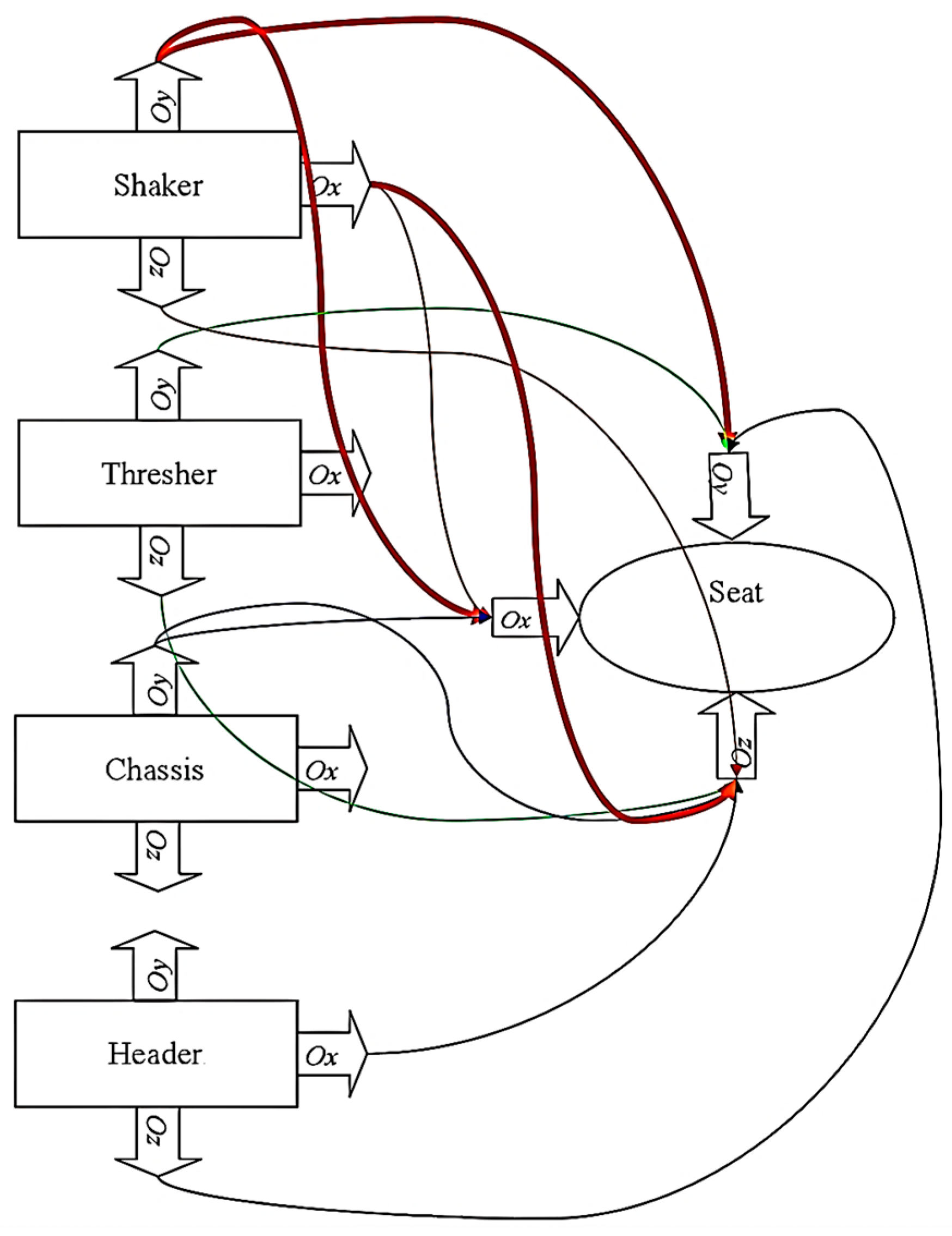
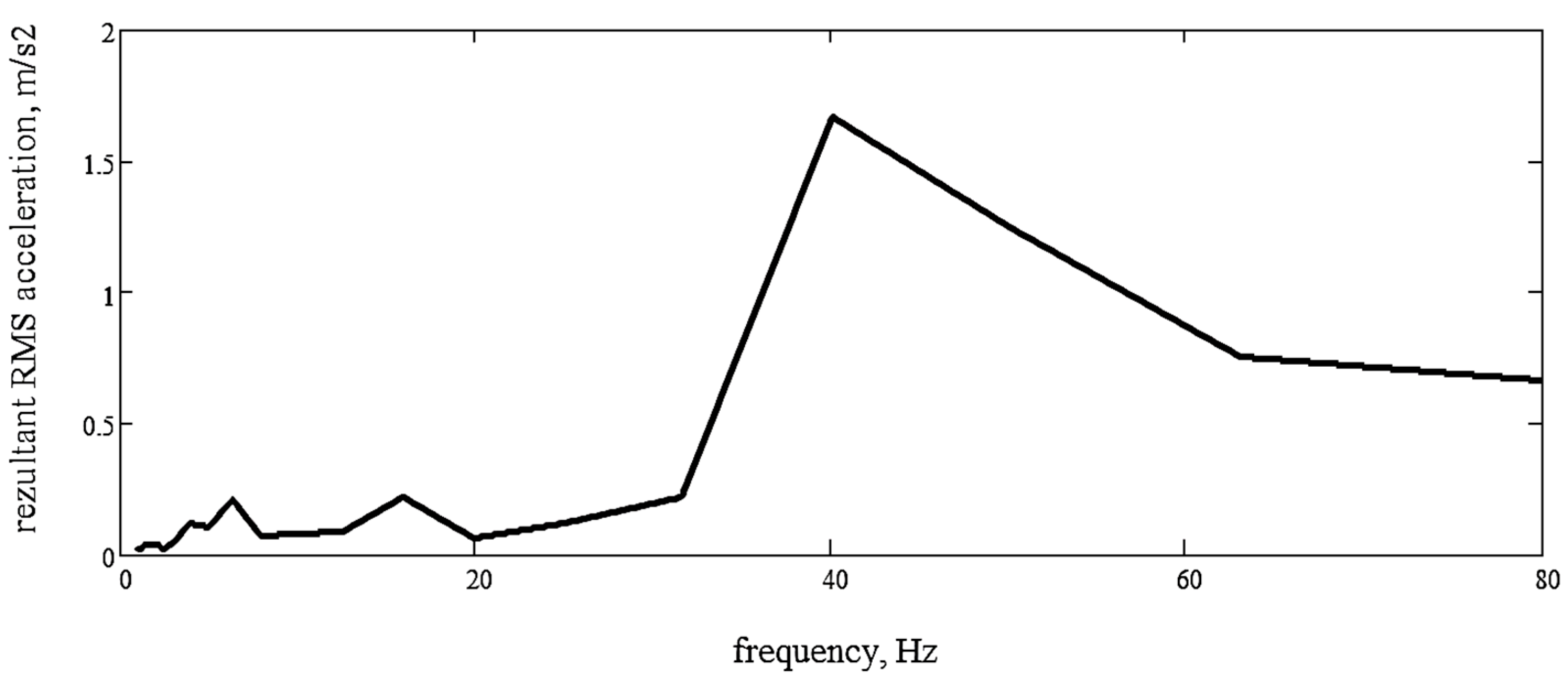
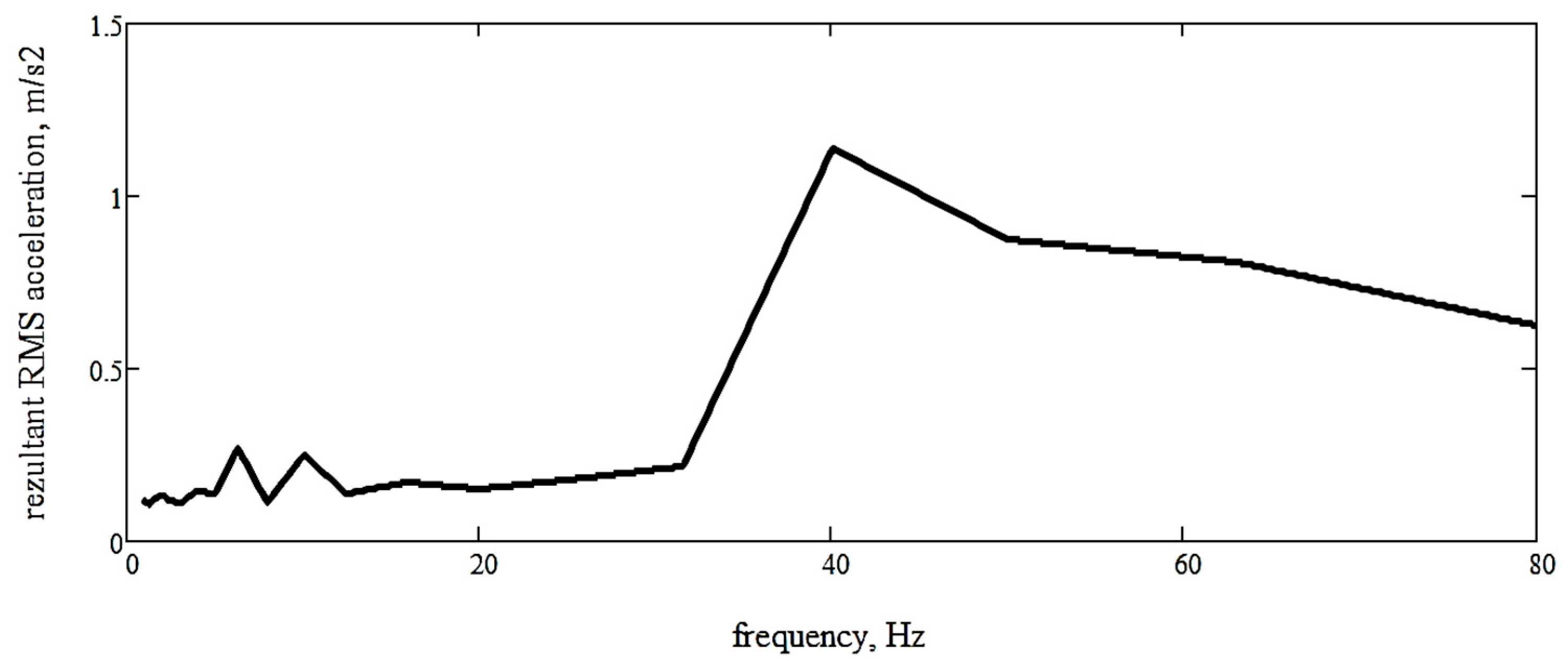

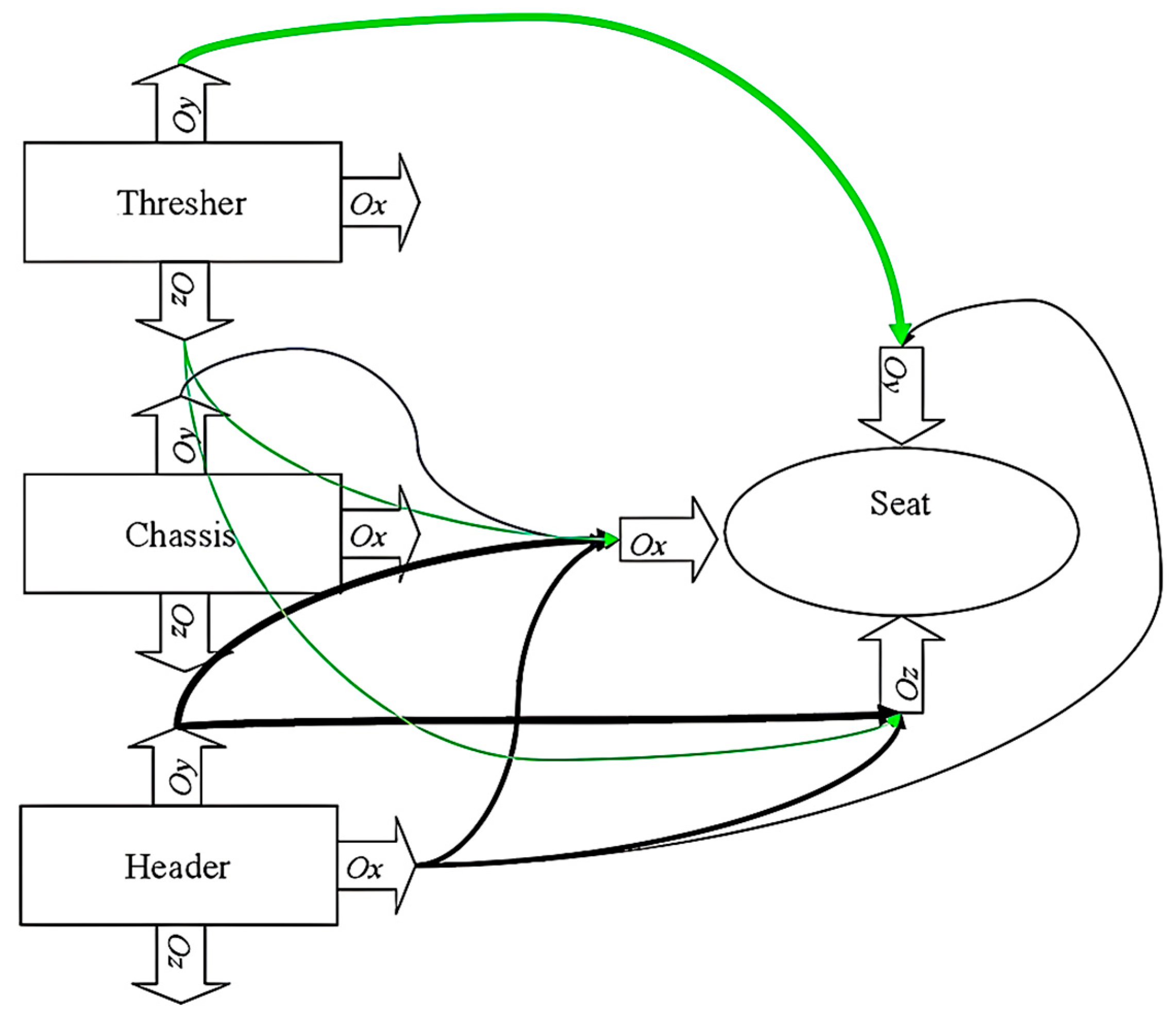
| No. | Notation | Definition |
|---|---|---|
| 1 | RMS acceleration component on the Ox axis at the straw walker | |
| 2 | RMS acceleration component on the Ox axis at the threshing mechanism | |
| 3 | RMS acceleration component on the Ox axis at the chassis | |
| 4 | RMS acceleration component on the Ox axis at the header | |
| 5 | RMS acceleration component on the Ox axis at the operator’s seat | |
| 6 | RMS acceleration component on the Oy axis at the straw walker | |
| 7 | RMS acceleration component on the Oy axis at the threshing mechanism | |
| 8 | RMS acceleration component on the Oy axis at the chassis | |
| 9 | RMS acceleration component on the Oy axis at the header | |
| 10 | RMS acceleration component on the Oy axis at the operator’s seat | |
| 11 | RMS acceleration component on the Oz axis at the straw walker | |
| 12 | RMS acceleration component on the Oz axis at the threshing mechanism | |
| 13 | RMS acceleration component on the Oz axis at the chassis | |
| 14 | RMS acceleration component on the Oz axis at the header | |
| 15 | RMS acceleration component on the Oz axis at the operator’s seat |
| Coefficient of Determination | C110 H Combine | CASE IH Combine | ||
|---|---|---|---|---|
| R2 | Equation (1) | 0.96 | Equation (8) | 0.98 |
| R2 | Equation (2) | 1.00 | Equation (9) | 0.69 |
| R2 | Equation (3) | 0.98 | Equation (10) | 0.99 |
| R2 | Equation (4) | 0.96 | Equation (11) | 0.85 |
| R2 | Equation (5) | 0.97 | Equation (12) | 0.31 |
| R2 | Equation (6) | 0.98 | Equation (13) | 0.58 |
| Direction | C110 H Combine | CASE IH Combine | ||
|---|---|---|---|---|
| Operating mode | Stationary | Working | Stationary | |
| Ox | ||||
| Oy | , | |||
| Oz | , | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cârdei, P.; Vlăduț, N.-V.; Biriș, S.-Ș.; Oncescu, T.-A.; Ungureanu, N.; Atanasov, A.Z.; Nenciu, F.; Matei, G.; Boruz, S.; Popa, L.-D.; et al. Identification of Vibration Source Influence Intensity in Combine Harvesters Using Multivariate Regression Analysis. Appl. Sci. 2025, 15, 10159. https://doi.org/10.3390/app151810159
Cârdei P, Vlăduț N-V, Biriș S-Ș, Oncescu T-A, Ungureanu N, Atanasov AZ, Nenciu F, Matei G, Boruz S, Popa L-D, et al. Identification of Vibration Source Influence Intensity in Combine Harvesters Using Multivariate Regression Analysis. Applied Sciences. 2025; 15(18):10159. https://doi.org/10.3390/app151810159
Chicago/Turabian StyleCârdei, Petru, Nicolae-Valentin Vlăduț, Sorin-Ștefan Biriș, Teofil-Alin Oncescu, Nicoleta Ungureanu, Atanas Zdravkov Atanasov, Florin Nenciu, Gheorghe Matei, Sorin Boruz, Lorena-Diana Popa, and et al. 2025. "Identification of Vibration Source Influence Intensity in Combine Harvesters Using Multivariate Regression Analysis" Applied Sciences 15, no. 18: 10159. https://doi.org/10.3390/app151810159
APA StyleCârdei, P., Vlăduț, N.-V., Biriș, S.-Ș., Oncescu, T.-A., Ungureanu, N., Atanasov, A. Z., Nenciu, F., Matei, G., Boruz, S., Popa, L.-D., Teliban, G.-C., Milea, O.-E., Dumitru, Ș., Tăbărașu, A.-M., Vanghele, N., Cismaru, M., Radu, C., & Isticioaia, S. (2025). Identification of Vibration Source Influence Intensity in Combine Harvesters Using Multivariate Regression Analysis. Applied Sciences, 15(18), 10159. https://doi.org/10.3390/app151810159








