Hybrid AI-Driven Computer-Aided Engineering Optimization: Large Language Models Versus Regression-Based Models Validated Through Finite-Element Analysis

Abstract

This study investigates the application potential of large language models (LLMs), particularly GPT-4o, in generating geometric parameter suggestions during the early stages of structural design. Design recommendations from the LLM are validated using a finite-element solver (FFE Plus solver), forming the core workflow of the proposed approach. To assess its effectiveness, the LLM’s performance is compared against traditional regression-based surrogate models, which serve as baseline references. A two-hole hanger bracket serves as the case study, evaluating prediction accuracy, data efficiency, generalization capability, and workflow complexity across three materials: 6061-T6, AISI 304, and AISI 1020. The key evaluation indicators include safety factor (SF) and Mass. The results show that the regression models offer high accuracy and interpretability but require extensive amounts of simulation data; in this study, each material required 252 samples to adequately cover the design space. In contrast, GPT-4o produced feasible design suggestions using only 18 initial samples, combining semantic prompting and finite-element analysis. Its prediction accuracy improved significantly with a small number of iterations, demonstrating superior data efficiency and cross-material adaptability. Overall, the findings suggest that, when paired with appropriate prompting strategies and validation mechanisms, LLMs hold great promise as an assistive tool in early-stage structural design optimization.

1. Introduction

In recent years, the rapid advancement of artificial intelligence (AI) technologies has progressively reshaped the paradigms of engineering design and computational decision-making. In particular, AI has emerged as a critical enabler of efficiency and innovation during the early stages of product development.

With the recent breakthroughs in generative AI, large language models (LLMs), such as GPT-4, have been widely adopted in natural language processing and technical knowledge retrieval. These models are now gradually being applied to engineering domains, including structural design, manufacturing workflows, and engineering education [1,2,3].

However, in contrast to conventional engineering tools grounded in numerical computation and physical modeling, the ability of LLMs to generate design suggestions that are both physically stable and relevant to real-world engineering applications remains largely unverified. This issue is particularly critical in high-precision tasks such as geometric parameter optimization and structural performance prediction, in which standardized evaluation protocols and practical application frameworks for LLM-generated outputs are still lacking [4,5,6].

To address these challenges, this study proposes a structured design recommendation framework based on LLMs and performs a systematic comparison with traditional regression-based surrogate modeling techniques. The proposed methodology integrates prompt engineering strategies [7,8], parameter space generation, finite-element analysis (FEA), and error-based validation to evaluate the predictive accuracy and implementation efficiency of LLMs in a computer-aided engineering (CAE) optimization context.

A dual-hole hanger bracket is selected as the case study and is characterized by three key geometric design parameters: thickness (Z), inner fillet radius (R), and rib angle (A). These parameters, respectively, influence global stiffness, stress distribution, and local reinforcement effectiveness.

To ensure material diversity and general applicability, three widely used engineering materials are considered, including 6061-T6 aluminum alloy, AISI 304 stainless steel, and AISI 1020 medium carbon steel. The LLM is tasked with generating design parameter sets based on semantic prompts, while a second-order regression model is constructed from multivariable polynomial fitting using FEA-generated data [9]. All suggested designs are verified through FEA to assess structural feasibility and quantify prediction error.

The main objective of this study is to examine whether LLMs, without reliance on explicit mathematical modeling or domain-specific training, can produce valid and physically meaningful design parameters. In addition, by comparing the results with those obtained from regression models, this research evaluates the accuracy, efficiency, and practical utility of LLM-based parameter recommendations. The findings aim to establish an intelligent design workflow that combines semantic inference with simulation-based validation, serving as a foundation for AI-assisted structural optimization in mechanical engineering.

While several recent studies, as reviewed in Section 2.2, have explored the use of LLMs for conceptual design generation or engineering question-answering, most applications remain limited to textual tasks or knowledge retrieval. However, these approaches often lack quantitative validation, physical consistency checks, or integration with simulation workflows. Moreover, few studies have systematically compared LLM-generated outputs with established engineering optimization methods such as regression-based surrogate modeling. Therefore, it remains unclear whether LLMs can perform valid parametric reasoning or produce structurally feasible designs in a simulation-driven context.

2. Literature Review

2.1. Applications and Comparisons of Various Optimization Approaches

In the early stages of mechanical design, selecting appropriate geometric parameters is a critical task that directly affects structural performance, product weight, and material utilization [10]. Traditionally, this process involves generating a large number of design combinations and validating each one through FEA to evaluate mechanical behaviors such as stress distribution and deformation, and the safety factor. Although effective, this brute-force or regression-based optimization approach often requires considerable computational resources and engineering effort, particularly when the design space contains multiple interacting variables.

To mitigate this computational burden, a variety of optimization strategies have been proposed. Regression-based surrogate models offer interpretable mathematical relationships and enable sensitivity analysis, yet their accuracy is constrained by training-sample quality and the assumption of smooth response surfaces. These models tend to struggle near the domain boundaries or in extrapolation scenarios, leading to biased predictions or poor generalization [11].

To overcome such limitations, advanced machine learning approaches have been introduced. Deep learning methods have shown potential in capturing complex, nonlinear relationships between design variables and structural performance metrics. For instance, integrating deep neural networks into structural optimization tasks enables end-to-end mappings from design inputs to performance outputs, with reduced reliance on extensive FEA [12]. Nevertheless, these models typically require substantial training data and lack interpretability.

Bayesian optimization represents another effective technique for design space exploration, especially in data-scarce scenarios. By modeling the objective function as a probabilistic distribution, the process systematically balances exploitation and exploration to efficiently locate optimal designs. Its iterative update mechanism enables adaptive sampling, making it particularly valuable when FEA evaluations are expensive [13]. This approach is frequently paired with Gaussian processes or neural networks for performance estimation.

Among evolutionary algorithms, the NSGA-II framework remains a widely adopted method for multi-objective optimization. It employs a fast non-dominated sorting mechanism and crowding distance calculations to preserve solution diversity, making it suitable for structural optimization tasks involving conflicting goals such as minimizing mass while maximizing safety [14]. Extensions of NSGA-II have also incorporated constraint-handling and surrogate-assisted evaluations to further enhance convergence in engineering applications.

The list of other notable contributions includes Kriging-based surrogate models, which interpolate simulation results using spatial correlation functions and are particularly useful in high-fidelity CAE environments. However, their performance diminishes in high-dimensional or noisy datasets [15]. Likewise, radial basis function (RBF) networks and support vector regression (SVR) have been explored as alternatives for surrogate modeling, each with their own trade-offs between flexibility, data requirements, and computational cost [16].

Recent studies have also emphasized the importance of hybrid frameworks that integrate traditional engineering knowledge with AI tools. These frameworks enable efficient design iteration while maintaining physical feasibility, particularly when combined with adaptive sampling strategies, dimensionality reduction techniques, or domain-specific constraints [17,18].

Overall, the selection of an appropriate optimization method depends on the complexity of the design task, available computational resources, and data characteristics.

2.2. Applications of Artificial Intelligence Tools in Engineering Domains

In recent years, LLMs, such as GPT-4, have shown increasing potential for the support of design optimization tasks [4]. Trained on extensive corpora of technical texts, LLMs possess semantic reasoning capabilities that allow them to interpret design objectives, constraints, and patterns expressed in engineering language. As a result, they can suggest feasible parameter combinations without explicitly solving physical equations [19,20,21]. A growing body of research has begun to explore AI-assisted design recommendation methods, demonstrating their potential to reduce iteration time and generate near-optimal solutions under given constraints [22,23,24].

Recent advancements have explored the role of LLMs within optimization workflows. EvoLLM shows that an LLM can act as an evolution strategy by reading ranked solution histories and proposing distribution updates through in-context prompting, and the reported results indicate zero-shot optimization on BBOB (Black-Box Optimization Benchmark) functions and small neuroevolution tasks, with better performance than random search and Gaussian Hill Climbing [25].

Within engineering and manufacturing workflows, systematic evaluations have reported that ChatGPT can assist conceptual and functional design tasks and early-stage ideation, though it requires verification for critical analysis and detailed technical design. These studies also underscore its sensitivity to prompt phrasing and emphasize the importance of careful integration into real-world engineering workflows [26].

Beyond design tasks, LLMs have been used to convert heterogeneous sensor webpages into FAIR-compliant tabular data and to retrieve relevant datasets via embedding-based similarity, with a case study showing high precision and mean reciprocal rank in a smart-farming scenario [27].

Multi-agent LLM frameworks have further demonstrated gains in complex reasoning and tool-use pipelines by coordinating planning, tool execution, and reflection agents, which supports their potential as assistants for engineering tasks that involve multi-step coordination and continuous feedback [28].

2.3. Prompt Engineering Strategies and Developments

As LLMs become increasingly integrated into engineering design workflows, prompt engineering has emerged as a critical 21st century skill for effectively guiding these models to produce contextually relevant and technically sound outputs. Instead of relying solely on algorithmic adjustments or model retraining, prompt engineering emphasizes human-in-the-loop strategies to frame queries, specify constraints, and iteratively refine responses [29]. This shift reflects a transformation from traditional tool operation to prompt-based reasoning, enabling engineers to translate domain knowledge into semantically precise instructions that LLMs can interpret and act upon.

Recent studies have introduced structured prompting frameworks that follow engineering logic. One example is the use of iterative prompting loops that progressively narrow the design space by incorporating previous outputs, constraint feedback, and domain-specific goals. This recursive approach allows dynamic refinement and semantic interpretation during parameter selection, helping LLMs mimic expert-like decision-making processes without explicit numerical analysis [30]. In addition, cognitive-science-inspired techniques such as chain-of-thought prompting and few-shot learning have proven effective for tasks requiring multi-step reasoning, trade-off evaluation, and conditional decision-making. These methods leverage the model’s internal representation capabilities to maintain coherence among variables and align outputs with optimization goals and physical feasibility [31].

Building on these advances, prompt engineering has been extended to complex scientific and medical reasoning tasks, demonstrating domain transferability and the importance of prompt structure. For example, few-shot chain-of-thought prompts have significantly improved the factual accuracy and reasoning quality of LLM outputs in biomedical diagnostics, emphasizing that structurally guided prompting plays a key role beyond general NLP tasks [32]. Similar approaches have been applied in robotics planning and scientific computing, where semantically clear prompts have enabled LLMs to navigate constraints and goals in technical contexts [33].

To further improve the applicability of LLMs in engineering domains, domain-aware prompt engineering has been emphasized as a means to bridge linguistic reasoning with real-world constraints. This involves crafting prompts that encode not only the semantic meaning but also the physical boundaries, safety constraints, and design trade-offs inherent in real-world systems. Such integration ensures that LLM outputs align with the practical requirements of engineering decision-making [34].

In summary, the optimization of engineering design has evolved through various methodologies, including traditional regression models, machine learning techniques, and evolutionary algorithms. Each approach presents different trade-offs in terms of design complexity, data requirements, and model interpretability. With the emergence of LLMs, both academia and industry have started to explore the potential of these models as novel tools used for design assistance. The models have demonstrated capabilities in semantic reasoning and parameter generation, particularly under data-scarce and complex design scenarios.

Recent studies have confirmed that, when guided by carefully crafted prompt engineering strategies, LLMs can effectively interpret design objectives and constraints expressed in engineering language and generate practically feasible parameter suggestions. This research focuses on evaluating the feasibility of applying LLMs to early-stage geometric parameter recommendation tasks and comparing their predictive accuracy, generalization ability, and application efficiency with those of traditional regression models. The literature review not only clarifies the development trends of various optimization methods but also underscores the critical role of prompt engineering in guiding LLM reasoning. This provides a solid theoretical foundation for the experimental design and model validation presented in the following sections.

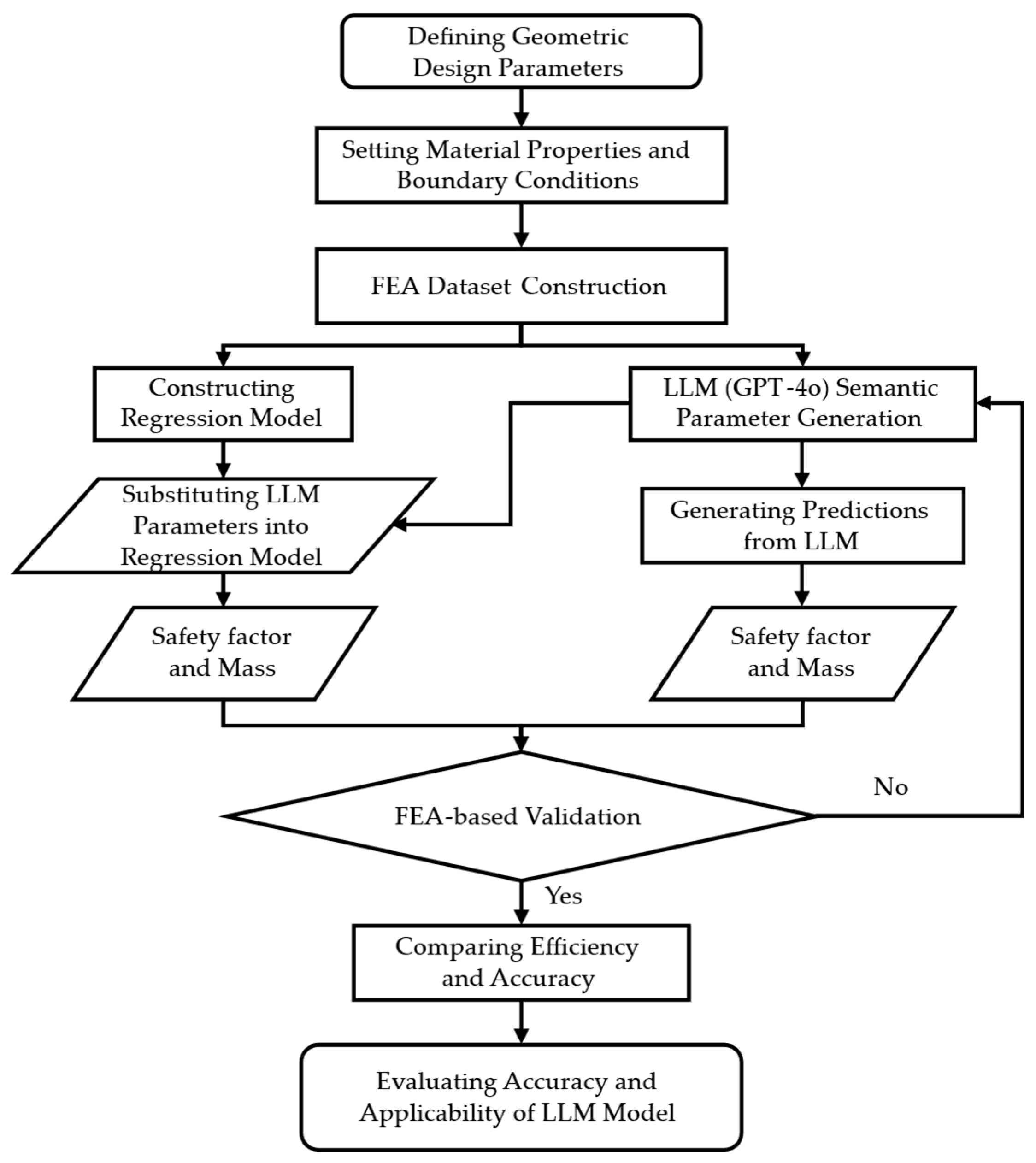
3. Methodology

This section outlines the core theoretical foundations adopted in this study, namely the FEA and the LLM (GPT-4o). Their underlying principles and application assumptions are discussed in the context of their respective roles within the proposed framework.

The FEA was employed to verify structural performance through numerical simulation, whereas the LLM was utilized to generate feasible geometric parameter sets based on semantic reasoning. These two techniques served distinct yet complementary functions: the FEA provided physics-based validation, and the LLM offered AI-assisted design suggestions. Together, they formed the basis for the integration of traditional regression modeling with artificial intelligence within the structural design optimization process.

3.1. Research Workflow

An integrated workflow combining FEA, a regression model, and an LLM (GPT-4o) was proposed to generate and validate geometric design recommendations. A dual-hole hanger bracket was adopted as the case study to demonstrate the proposed approach and assess its effectiveness in a structural optimization context. The overall research workflow is illustrated in Figure 1.

The workflow of this study begins with the definition of geometric design parameters, followed by the setting up of material properties and boundary conditions. These configurations are used to perform FEA via the FFE Plus solver to construct a dataset, which then serves as the foundation for both the training of regression models and the design of prompts for the LLM.

After both models are established, semantic parameter generation is performed using the LLM (GPT-4o). The recommended parameters are then simultaneously input into the trained regression model and the FEA simulation to predict the safety factor (SF) and Mass. Additionally, the LLM generates independent predictions based on the same input, which are subsequently cross-validated against the FEA results.

Finally, the design suggestions produced by the regression model and the LLM are compared and analyzed in terms of prediction accuracy and computational efficiency, in order to evaluate the feasibility and application potential of the LLM as an assistive tool in early-stage engineering design workflows.

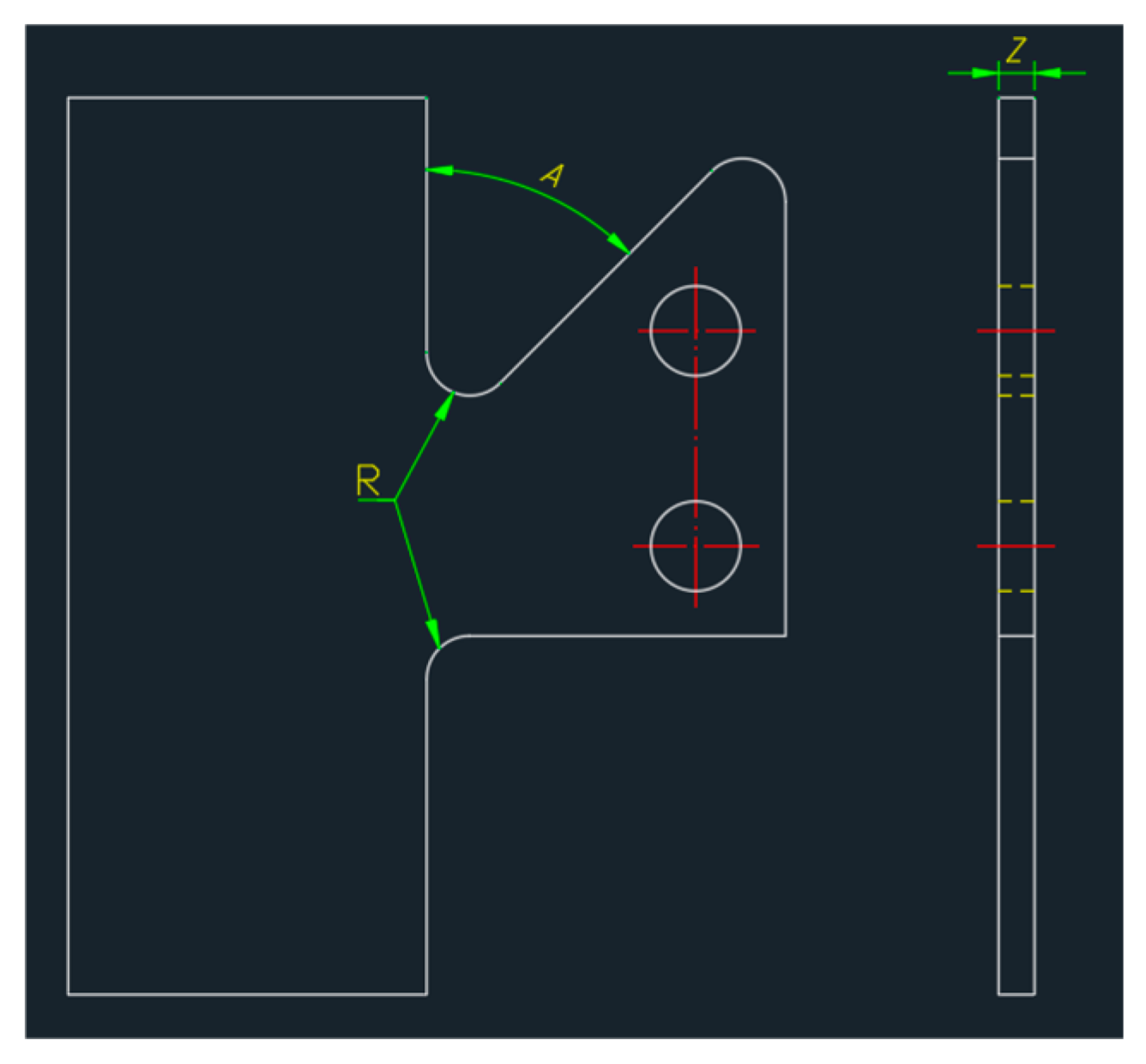
3.2. Geometric Dimensioning Parameter Definition

A two-hole hanger bracket was selected as the case study for implementing and validating the proposed workflow for generating and verifying structural dimensioning recommendations. Such brackets have been commonly used in mechanical fastening and load-bearing applications, due to their straightforward geometry, predictable structural behavior, and ease of parameterization, making them well-suited as benchmark models for CAE-based optimization studies.

Three key geometric design parameters, illustrated in Figure 2, were selected as the primary variables for analysis and model-driven recommendation:

• Thickness (Z, mm): Represents the plate thickness of the bracket body, serving as a key factor influencing load-carrying capacity and global stiffness. An increase in thickness generally improves structural strength and the safety factor but also results in greater mass, thereby creating a trade-off between strength and weight.
• Inner Fillet Radius (R, mm): Located at the junction between the bracket body and the reinforcement rib, this parameter affects stress concentration and distribution. A smaller radius may lead to sharp-corner effects and fatigue risks, while an excessively large radius can compromise geometric compactness and interfere with design constraints.
• Rib Angle (A, degrees): Defined as the angle between the reinforcement rib and the bracket body, this parameter determines the alignment of the rib relative to the primary load path. An appropriate rib angle contributes to directional stiffness, reduces bending moment eccentricity, and improves local load-transfer efficiency.

These three geometric variables form the core design space in this study and are utilized as input dimensions for the sample generation, FEA simulation using the FFE Plus solver, regression model training, and GPT-4o prompt construction

3.3. Finite-Element Analysis Setup

To support the evaluation and validation of both the regression model and the large language model (GPT-4o), a systematic simulation workflow based on FEA was implemented. The FEA setup emphasized simulation efficiency, reproducibility, and stability to ensure consistent and reliable outputs for comparative assessment.

All simulations were conducted using SolidWorks Simulation 2021, with the analysis type configured as linear static analysis under the assumptions of small deformations and linear elasticity. This configuration was considered appropriate for exploring the impacts of geometric parameter variations on structural responses such as stress, deformation, Mass, and SF.

To enhance computational throughput across large parameter sets, the FFE Plus iterative solver was selected as the core computation engine. Its efficiency in handling sparse systems and high-degree-of-freedom models made it particularly suitable for batch simulations involving multiple design combinations.

Meshing was performed using solid tetrahedral elements, supported by SolidWorks’ automated meshing functionality. Local mesh refinement was applied in regions with significant geometric transitions or anticipated stress concentrations, to ensure accurate resolution of structural responses.

All simulations were executed under uniform boundary conditions, loading scenarios, and solver precision parameters. This consistency across cases ensured data comparability and supported the development of a cohesive dataset for regression modeling and LLM-driven recommendation validation.

3.3.1. Linear Static Finite-Element Analysis: Theory and Assumptions

The FEA was adopted as the theoretical basis for the simulation of structural behavior under static loading conditions. Linear static analysis was applied to assess how geometric variations influenced stress distribution, deformation, Mass, and SF.

The linear static analysis was based on the assumptions of small deformations and linear elastic material behavior. It was governed by the following fundamental equation of equilibrium:

$$Ku=F$$

(1)

where $K$ is the global stiffness matrix assembled from the element stiffness matrices, $u$ is the nodal displacement vector, and $F$ is the external load vector.

The FEA simulations were conducted under the following assumptions:

(1)

The material is homogeneous, isotropic, and linearly elastic according to Hooke’s law.

(2)

Structural deformations remain within the small strain regime.

(3)

Geometric and contact nonlinearities are not considered.

(4)

All applied loads are static, with no inertial or time-dependent effects included.

In this study, the simulated case involves a single solid part without additional geometric or contact nonlinearities. Within the defined geometric dimensioning parameter range, all FEA results remained within the elastic regime, with no stress values exceeding the yield strength of the selected materials.

For example, considering the most conservative case, using AISI 304 stainless steel, which has the lowest yield strength (207 MPa) among the materials investigated, the maximum von Mises stress observed across the design space was 129.1 MPa, confirming that all deformations were elastic and the linear material assumption holds throughout the analysis.

3.3.2. FFE Plus Solver: Implementation and Applicability

To implement the FEA framework in practice, the FFE Plus solver within SolidWorks Simulation 2021 was selected as the core computational engine for all simulations. This iterative solver was optimized for linear static problems and was well-suited to large models because it was based on the conjugate gradient method and utilized preconditioning techniques, such as Jacobi and symmetric successive overrelaxation (SSOR), to accelerate convergence. The solver iteratively updated the displacement vector $u$ so that the residual $‖Ku-F‖$ converged within an acceptable tolerance.

Compared with direct solvers such as sparse LU decomposition, FFE Plus significantly reduces memory usage, making it suitable for large-scale models or problems involving high numbers of degrees of freedom. It also offers faster computation, particularly when solving sparse systems, and improves simulation throughput in repetitive tasks such as design parameter optimization or design of experiments (DOE). Furthermore, it integrates well with automatic meshing and local refinement features, enabling flexible and efficient preprocessing.

In this study, over 30 sets of geometric parameter combinations were analyzed to evaluate their effects on structural performance. Key variables included thickness (Z), inner fillet radius (R), and rib angle (A), which were assessed through outputs such as von Mises stress, deformation, Mass, and SF. The FEA results demonstrated strong consistency with expected physical behavior, supporting their use as validation references for regression models and LLM-based design recommendations.

However, it is important to note that FFE Plus is limited by the assumptions of linear elasticity and small deformations. The solver does not account for material nonlinearities, geometric nonlinearity, or contact behavior. As such, the simulation results are best suited for comparative studies and early-stage design evaluations, rather than final validation in nonlinear or complex loading scenarios.

3.3.3. Material Properties

The material properties used in the simulations are summarized in

Table 1. Table of material properties.

Material	Young’s Modulus (GPa)	Yield Strength (MPa)	Density (kg/m3)
AISI 1020	210	350	7870
6061-T6	69	275	2700
AISI 304	190	207	8000

, including elastic modulus, yield strength, and density. To investigate the influence of geometric design parameters on structural performance across varying material conditions, three commonly used engineering materials were selected: 6061-T6 aluminum alloy, AISI 304 stainless steel, and AISI 1020 medium carbon steel.

Each material was applied to all design samples under identical geometric and boundary conditions. This consistent setup ensured a reliable basis for evaluating the prediction accuracy and generalization capability of both the regression model and the LLM across different material types.

The rationale for material selection is as follows:

• AISI 1020 medium carbon steel is a heat-treatable material with high yield strength and stiffness. Representing traditional structural steels, it serves as a high-strength, high-density reference case for assessing performance under more demanding mechanical requirements.
• 6061-T6 aluminum alloy is a widely used lightweight material with high specific strength and excellent machinability. It is extensively applied in the transportation and consumer product industries. In this study, it represents a low-density material suitable for evaluating the trade-off between weight and strength.
• AISI 304 stainless steel offers moderate strength and good ductility. As a commonly used general-purpose structural material that does not require heat treatment, it provides a practical baseline for analyzing structural stiffness and SF behavior, particularly under mid-range density and stiffness conditions.

3.3.4. Boundary Conditions and Load Application

To simulate realistic usage scenarios in which the bracket supported suspended or tensile components, the upper and lower planes on the left side of the model were defined as fully fixed. This configuration emulated the connection to a rigid structure, such as a wall or supporting frame, with all translational and rotational degrees of freedom constrained.

Loading was applied through the two holes on the right side of the bracket, which served as the primary force application regions. Horizontal tensile forces of Fx₁ = +981 N and Fx₂ = −981 N were applied in opposite directions to simulate a symmetric tensile load. Additionally, equal vertical forces of Fy₁ = Fy₂ = −49.05 N were introduced to reflect realistic vertical loading conditions acting on both holes. This configuration ensured a balanced and representative stress state for evaluating the structural response under multiaxial loading, as shown in Figure 3.

These applied forces were derived from a practical use case developed within our university’s Computer-Aided Engineering course, in which the two-hole hanger bracket was used as a structural design project for students. The magnitudes of the loads were determined based on typical force estimates encountered in real-world structural mounting scenarios.

Prior to incorporating these loading conditions into the present study, preliminary finite-element simulations were performed to verify that, for all three candidate materials, the resulting stress distributions remained within the elastic regime. The verification confirmed that none of the maximum von Mises stress values exceeded the respective yield strength, thereby validating the assumption of linear elasticity. Overall, the selected loading configuration was both practically representative and analytically appropriate.

3.3.5. Mesh Generation and Convergence Analysis

To balance simulation accuracy and computational efficiency, all finite-element models in this study adopted the automatic mesh refinement functionality provided by SolidWorks Simulation. The blended curvature-based mesher option was enabled to increase element density in geometrically sensitive regions, such as sharp corners, fillets, and rib transition zones. This meshing strategy ensures stable stress resolution and accurately captures localized effects, thereby enhancing the reliability of structural response predictions.

Given the sensitivity of simulation results to geometric variations and the need for consistency across samples, a uniform meshing criterion was applied throughout. To verify mesh independence, a convergence study was conducted by fixing the geometry and material while progressively reducing the mesh size. The variation in maximum von Mises stress was monitored to assess the effect of element size. As shown in Figure 4, stress values stabilized once the mesh size was reduced below 1 mm, indicating convergence had been achieved.

Based on this analysis, a mesh size of 1 mm was selected as the standard configuration for all simulations. This choice provided a practical trade-off between solution accuracy and computational cost. All simulation cases converged successfully, with no element distortion or numerical instabilities observed, demonstrating the reliability and reproducibility of the adopted meshing strategy.

To ensure the robustness of the mesh convergence analysis, two representative geometric configurations were selected for detailed mesh sensitivity verification. These include the design space minimum configuration (Z = 3, R = 5, A = 45) and the maximum configuration (Z = 5, R = 8, A = 65), corresponding to the geometric extremes defined by the dimensional parameter boundaries.

Since the mesh generation was geometry-driven and the simulation results across all cases were governed by linear elasticity assumptions, the mesh convergence outcomes were consistent across all three materials (6061-T6 aluminum alloy, AISI 304 stainless steel, and AISI 1020 medium carbon steel).

3.3.6. Output Parameters and Data Acquisition

Within the optimization framework developed in this study, structural mass (Mass) was defined as the primary objective function. The optimization goal was to minimize mass in order to enhance material utilization and reduce overall structural cost. Mass values were automatically computed based on the geometric volume of the CAD model and the assigned material density, making it a straightforward and reliable output from the FEA.

In parallel, the safety factor (SF) was defined as a critical constraint to ensure that the structure operates within the elastic range under the applied design load. It is calculated as

$$SF={\displaystyle \frac{{\sigma }_{yield}}{{\sigma }_{von Mises}}}$$

(2)

where ${\sigma }_{yield}$ denotes the material yield strength and ${\sigma }_{von Mises}$ is the maximum equivalent stress obtained from the FEA simulation. In this study, a constraint condition of SF > 3 was imposed to ensure adequate structural safety.

In addition to these two key response variables, the maximum von Mises stress (MPa) and the maximum total deformation (mm) were recorded as supplementary outputs. These auxiliary parameters enable a more comprehensive evaluation of structural strength and stiffness, support physical plausibility checks, and provide the basis for subsequent error analysis and model verification.

3.4. Regression Model Construction and Validation

To establish a mathematical model capable of predicting structural response behavior and serving as a baseline for evaluating parameter recommendations from the LLM, a second-order polynomial regression model was constructed based on results from the FEA. The model was designed to predict two key response variables: Mass and SF.

3.4.1. Rationale for Using Second-Order Polynomial Regression

In this study, a second-order polynomial regression model was adopted as the baseline for comparison with the LLM, primarily due to its high interpretability. The quadratic expansion provides a clear mathematical formulation that explicitly represents the influence of geometric design parameters, including thickness (Z), fillet radius (R), and rib angle (A), on Mass and SF. It also reveals the relationships between independent and dependent variables, which helps establish a structured basis for comparison with the prompt engineering process used in the LLM. Furthermore, during the early stages of design, sensitivity analysis can be conducted by taking partial derivatives of the regression equation, allowing for a deeper investigation into the physical significance of each design variable.

Although more advanced machine learning models, such as random forests or neural networks, may yield higher predictive accuracy, they typically require large-scale data and result in reduced model transparency, making them less suitable for comparison with LLMs under low-data conditions.

Moreover, no additional feature engineering (e.g., reciprocal area, power-law terms) was performed, as the aim was to maintain a minimal and interpretable model structure while isolating the effects of core geometric variables.

3.4.2. Design of Training Samples and Data Generation

A full factorial design was adopted to generate a finite yet representative set of sample combinations within the predefined ranges of the three geometric dimensioning variables: thickness (Z), inner fillet radius (R), and rib angle (A). For each parameter combination, FEA was performed to compute the structural mass and maximum von Mises stress, from which the SF was derived and used as one of the model’s response outputs.

The design variable ranges were defined as follows: Z ∈ [3, 5] mm (step size: 1 mm), R ∈ [5, 8] mm (step size: 1 mm), and A ∈ [45°, 65°] (step size: 1°). This configuration yielded a total of 252 design samples, with the complete dataset provided in the Supplementary Materials. These ranges were selected based on prior engineering experience gained from structural bracket design projects conducted in our institution. The selected boundaries reflect dimensioning practices commonly adopted in small-scale mechanical components, where lightweight design and structural safety must be balanced.

Specifically, a thickness of 3–5 mm and a fillet radius of 5–8 mm are typically used in medium-load-bearing brackets, while a rib angle between 45° and 65° offers a trade-off between ease of manufacturing and effective stress distribution. These constraints also help to avoid geometries that could lead to stress singularities or violate the assumptions of linear elastic analysis.

All generated samples were simulated under consistent material properties, boundary conditions, and meshing parameters to ensure data uniformity and comparability for regression model training and validation.

3.4.3. Formulation of Regression Equations

The regression model was formulated as a full second-order polynomial, incorporating the main effects, quadratic terms, and two-way interaction terms of the three geometric design variables. The general form of the model can be expressed as

$$Y={\beta }_0+{\beta }_{1}Z+{\beta }_{2}R+{\beta }_{3}A+{\beta }_4{Z}^2+{\beta }_5{R}^2+{\beta }_6{A}^2+{\beta }_{7}ZR+{\beta }_{8}ZA+{\beta }_{9}RA$$

(3)

where $Y$ denotes the response variable, either the SF or Mass; $Z,R$, and $A$ represent the three geometric design variables; and ${\beta }_0$ to ${\beta }_9$ are the regression coefficients determined via the Ordinary Least Squares (OLS) method.

In this study, six regression equations were constructed in total, corresponding to the SF and Mass predictions for each of the three selected materials.

Model construction and statistical analysis were performed using IBM SPSS Statistics 26. All main variables, their squared terms, and their pairwise interactions were entered into the linear regression module. Both the Enter method and the Stepwise method were applied for model selection and validation. SPSS provided coefficient estimation, residual diagnostics, and statistical significance testing to assess model goodness-of-fit and parameter stability.

3.4.4. Evaluation of Regression Model Accuracy

To assess the predictive capability and robustness of the regression model across different geometric design parameter combinations, model diagnostics were conducted using IBM SPSS Statistics. The coefficient of determination (R²) was adopted as the primary evaluation metric, representing the proportion of variance in the response variable explained by the model. Values approaching 1 indicated a strong fit to the FEA validation results and correspondingly higher predictive accuracy.

To further verify the model’s practical applicability within the defined design space, several geometric parameter sets predicted by the regression model were re-evaluated using FEA conducted with the FFE Plus solver. The predicted response values were then compared against actual simulation outputs to quantify the prediction error. This process ensured that the regression model yielded not only statistically reliable predictions but also physically meaningful outputs. It also established a performance benchmark for subsequent comparison with the parameter recommendations generated by the LLM.

3.5. Prompt Engineering for GPT-4o

3.5.1. GPT-4o Framework and Application Assumptions

The training of GPT-4o is composed of two main stages. The first stage involves unsupervised pretraining on a large-scale corpus that includes web content, source code, mathematical documents, and multimodal data. The second stage applies reinforcement learning from human feedback (RLHF) to refine the model’s generation behavior, with the aim of aligning outputs more closely with user intent and ethical considerations [35].

During training, particular emphasis is placed on improving the model’s ability to interpret mathematical logic, cross-linguistic relationships, and domain-specific semantic structures, including those found in engineering contexts. Although GPT-4o has not been fine-tuned for engineering simulation tasks, it demonstrates reliable capabilities in areas such as architectural design, code generation, and the interpretation of structural semantics. As a result, it serves as a viable non-numerical knowledge source for generating design parameter suggestions in engineering applications.

3.5.2. LLM-Based Parameter Recommendation and Screening

To explore the potential of LLMs in recommending structural geometric parameters, the GPT-4o model developed by OpenAI was employed. GPT-4o is an autoregressive, multimodal language model with advanced semantic understanding and reasoning capabilities, capable of generating logically consistent recommendations based on natural language prompts.

In this study, GPT-4o was configured as a collaborative design assistant equipped with embedded structural engineering knowledge. Its task was to generate a set of geometric design variables, including thickness (Z), fillet radius (R), and rib angle (A), that satisfied both structural safety and mass minimization objectives under predefined constraints.

To facilitate post-processing, the results were required to be structured in a format that could be easily converted into CSV files. This ensured compatibility with batch FEA procedures and enhanced reproducibility and automation within the workflow.

After generation, all LLM-recommended parameter sets were validated through FEA simulations. Their performance was quantitatively compared with the predictions from the regression model to assess the accuracy, feasibility, and practical utility of LLM-based parameter generation in the early-stage structural optimization process.

3.5.3. Training Examples Provided to the LLM

In this study, a series of structured prompts were designed to guide the GPT-4o model in generating geometry-based structural design suggestions under conditions similar to a conventional computer-aided engineering (CAE) workflow. These prompts were sequentially organized to simulate a static analysis process, covering material specification, geometric dimensioning, boundary conditions, and load applications. The prompt sequence mimicked the typical setup–load–solve–evaluate cycle found in most commercial FEA platforms, allowing GPT-4o to emulate a decision-support assistant role within a virtual CAE workflow. The interaction process with the LLM was iterative, with each prompt building upon the context established by the previous step.

The prompt design was divided into the following stages:

(1)

Material Property Declaration:

The process began with the provision of basic material properties, including Young’s modulus (GPa), yield strength (MPa), and density (kg/m³), for three candidate materials. The design also included three geometric dimensioning parameters (Z, R, and A). At this stage, 18 samples of SF and Mass data obtained from the FFE Plus solver were shared with GPT-4o for reference. GPT-4o confirmed the input validity and requested additional setup details to proceed. The full prompt text used in this stage is provided in Appendix A.1.

(2)

Boundary Conditions and Load Application:

Next, GPT-4o was provided with detailed information about boundary constraints and applied loads. Upon receiving this information, GPT-4o autonomously outlined an analysis strategy, summarizing the key problem definitions, input parameters, and objectives, and initiated the design exploration process. The full prompt text used in this stage is provided in Appendix A.2.

(3)

Initial Optimization Request (Wide Design Space):

The first optimization task asked GPT-4o to generate a set of geometric parameters that minimize mass while maintaining an SF greater than 3. Although GPT-4o tended to return a subset of the previously provided data rather than generating truly novel solutions at this stage, this behavior was anticipated due to the wide parameter bounds defined in the initial setup. The full prompt text used in this stage is provided in Appendix A.3.

(4)

Search Space Refinement and Convergence:

To guide GPT-4o toward more targeted solutions, the design parameter ranges were narrowed in subsequent prompts. These refined prompts were intended to iteratively direct GPT-4o toward convergence. Each result was verified through FEA simulation and fed back into the prompt sequence, allowing GPT-4o to progressively improve its understanding of the design space. The full prompt text used in this stage is provided in Appendix A.4.

(5)

Material Substitution for Cross-Material Validation:

To assess the generalization ability of GPT-4o across different material conditions, additional prompts were issued to substitute for the base material (AISI 1020) with 6061-T6 aluminum alloy and AISI 304 stainless steel. This step allowed us to evaluate GPT-4o’s ability to adapt its design suggestions under altered physical constraints while maintaining semantic consistency with prior optimization goals. The full prompt text used in this stage is provided in Appendix A.5.

The above prompt design process illustrates the structure and application of the parameters used in the prompt-driven optimization workflow of this study, aiming to enhance its transparency and reproducibility. The complete verbatim prompts used for GPT-4o parameter generation are included in Appendix A for future reference and extension, while the GPT-4o Parameter Generation Summary is presented in

Table 2. GPT-4o Parameter Generation Summary.

Stage	Prompt Summary	Key Inputs	Output Purpose
1	Declare materials + parameter ranges	Material Properties, Z/R/A ranges	Establish LLM context
2	Provide boundary and load conditions	Fx, Fy, fixed constraints	Add physics to context
3	Request initial optimization	Wide range, SF > 3	First design suggestion
4	Restrict search space	Z/R/A refined	Force focused convergence
5	Cross-material prediction prompts	New material properties (e.g., 6061, 304), same constraints	Evaluate generalization with material substitution

.

3.5.4. Limitations of the LLM-Based Approach

The GPT-4o model has not been fine-tuned for specific engineering case studies, and its outputs are generated solely through language-based reasoning without any embedded physical computation mechanisms. As a result, all recommended parameters must be validated using CAE tools to confirm their physical feasibility and structural applicability.

In cross-material generalization scenarios, the accuracy of the generated recommendations may decrease due to the model’s limited ability to account for material-specific mechanical properties. This challenge highlights the need for further prompt refinement and contextual adaptation to improve reliability.

Moreover, the quality and relevance of the outputs are highly sensitive to the structure, clarity, and semantic specificity of the prompts. This underscores the importance of well-constructed and context-aware prompt design when applying LLMs in engineering optimization workflows.

3.6. Computational Setup

To ensure reproducibility and enable the performance evaluation of the finite-element simulations and model development process, all hardware and software configurations used in this study were documented in detail. The computational workflow consisted of two main components: (1) batch FEA performed using SolidWorks Simulation, and (2) parameter recommendation generation and data processing using the GPT-4o model.

All FEA simulations were executed on custom-built a single desktop workstation assembled for this study. The system included an ASUS TUF Gaming B560 motherboard, an Intel Core i5 11400F CPU with six cores and twelve threads; 64 gigabytes of DDR4 RAM from ADATA to support large-scale simulation batches and ensure computational stability; an MSI NVIDIA GeForce GTX 1060 graphics card with 6 gigabytes of memory, used primarily for visualization and model manipulation rather than solver acceleration; a 1 terabyte PCIe Gen3 solid-state drive (Kingston NV1 series) for data storage; and the Windows 11 Professional 64-bit operating system.

The simulation software utilized was SolidWorks Simulation 2021, configured in linear static analysis mode with the Fast Finite Element Plus (FFE Plus) iterative solver. On average, each simulation, including meshing, solving, and post-processing, required approximately 1 to 3 min, depending on the geometric complexity and material type of the model.

4. Results

This section presents a comparative evaluation of two modeling approaches used for geometric parameter recommendation in early-stage structural optimization. These include a traditional second-order polynomial regression model and an LLM (GPT 4o). The objective of this analysis is to assess the predictive accuracy, constraint satisfaction, and generalization capabilities of both models under various material conditions.

To ensure an unbiased comparison, both models were evaluated using independently generated parameter sets, which were subsequently validated through FEA. The evaluation focused on two key performance indicators: structural Mass and SF. For the regression model, performance was quantified not only by FEA validation but also by the coefficient of determination (R²), which reflects the model’s ability to fit the training data.

This section is organized into three parts. The first part (Section 4.1.) describes the derivation and statistical performance of the regression models. Section 4.2. presents the LLM-generated design recommendations and highlights the iterative prompt engineering process used to achieve convergence under design constraints. Section 4.3. compares the Mass and SF prediction errors from both models across three material types: AISI 1020, 6061 T6 aluminum alloy, and AISI 304 stainless steel. It also discusses model adaptability, training efficiency, and performance near the boundary of the design space.

4.1. Regression Model Derivation Results

Following model construction and coefficient estimation using IBM SPSS Statistics, the final regression equations were formulated for the prediction of the SF and structural mass (Mass). The models were derived as complete second-order polynomial expressions, incorporating main effects, quadratic terms, and two-way interactions of the geometric design variables: thickness (Z), fillet radius (R), and rib angle (A). The resulting equations are shown below.

These equations form the basis for subsequent comparisons with the parameter suggestions generated by the LLM, GPT-4o. Their predictive performance will be validated through the FFE Plus solver to assess accuracy, generalizability, and physical feasibility. In addition, the coefficient of determination (R²) is used to quantify the regression model’s explanatory power and overall goodness of fit.

4.1.1. Regression Model Derivation Results for AISI 1020

Equations (4) and (5) represent the polynomial regression models developed for AISI 1020, using a training dataset of 252 samples. Both models yielded coefficients of determination (R²) equal to 1.000, which is expected, given the deterministic nature of the FEA-generated data and the inclusion of all relevant second-order and interaction terms in the regression model. This result indicates a perfect fit to the training data. Further validation through FEA confirmed that the models achieved high prediction accuracy for both the SF and Mass. In addition, the ANOVA results indicated that both models were statistically significant: the SF model reported an F-value of 83,083.234 (p < 0.001), and the Mass model reported an F-value of 9,206,243.102 (p < 0.001). These results suggest that the independent variables collectively contribute significantly to predicting both response variables.

$${SF}_{AISI 1020}=10.59-3.585Z-0.259R-0.925A+0.025Z^2+0.001R^2-0.004A^2+0.072ZR+0.181ZA+0.017RA$$

(4)

$${Mass}_{AISI 1020}=-40.988+55.414Z+1.470R+0.305A+0Z^2-0.013R^2+0.034A^2+0.256ZR+0.110ZA-0.014RA$$

(5)

4.1.2. Regression Model Derivation Results for 6061-T6

Equations (6) and (7) represent the polynomial regression models developed for 6061-T6, using a training dataset of 252 samples. Both models yielded coefficients of determination (R²) equal to 1, which is expected, given the deterministic nature of the FEA-generated data and the inclusion of all relevant second-order and interaction terms in the regression model. This result indicates a perfect fit to the training data. Further validation through FEA confirmed that the models achieved high prediction accuracy for both the SF and Mass. In addition, the ANOVA results indicated that both models were statistically significant: the SF model reported an F-value of 82,094.028 (p < 0.001), and the Mass model reported an F-value of 9,038,568.985 (p < 0.001). These results suggest that the independent variables collectively contribute significantly to predicting both response variables.

$${SF}_{6061-T6}=8.362-2.816Z-0.205R-0.726A+0.019Z^2+0.001R^2-0.003A^2+0.057ZR+0.142ZA+0.013RA$$

(6)

$${Mass}_{6061-T6}=-14.087+19.016Z+0.504R+0.108A-0.001Z^2-0.004R^2+0.011A^2+0.088ZR+0.038ZA-0.005RA$$

(7)

4.1.3. Regression Model Derivation Results for AISI 304

Equations (8) and (9) represent the polynomial regression models developed for AISI 304, using a training dataset of 252 samples. Both models yielded coefficients of determination (R²) equal to 1.000, which is expected, given the deterministic nature of the FEA-generated data and the inclusion of all relevant second-order and interaction terms in the regression model. This result indicates a perfect fit to the training data. Further validation through FEA confirmed that the models achieved high prediction accuracy for both the SF and Mass. In addition, the ANOVA results indicated that both models were statistically significant: the SF model reported an F-value of 82,523.215 (p < 0.001), and the Mass model reported an F-value of 9,238,848.161 (p < 0.001). These results suggest that the independent variables collectively contribute significantly to predicting both response variables.

$${SF}_{AISI 304}=6.285-2.121Z-0.154R-0.552A+0.015Z^2+0.001R^2-0.002A^2+0.043ZR+0.107ZA+0.01RA$$

(8)

$${Mass}_{AISI 304}=-47.671+56.324Z+1.494R+0.311A+0Z^2-0.013R^2-0.035A^2+0.261ZR+0.112ZA-0.014RA$$

(9)

4.2. LLM-Based Design Recommendations

After the prompt engineering and iterative training process described in Section 3.5, GPT-4o successfully generated parameter combinations that satisfied the design objectives. In this study, convergence was defined as the achievement of parameter sets for which the predicted mass closely matched the FEA-validated mass, with minimal error, while maintaining an SF greater than 3. Once the LLM-generated suggestions met these criteria, the prompt refinement process was terminated.

It is important to note that only the FEA simulation data for AISI 1020 medium carbon steel were provided to GPT-4o as initial training references. For the other two materials, 6061-T6 aluminum alloy and AISI 304 stainless steel, the model was given only their material properties during the initial prediction stage. These properties included Young’s modulus, yield strength, and density. No initial FEA data were provided. FEA simulations were used exclusively in the subsequent validation and convergence phases. As a result, GPT-4o had to rely entirely on the semantic content of the prompts to interpret the mechanical context and infer appropriate geometric design suggestions. This prediction mechanism can be characterized as an application of semantic generalization, rather than a process based on direct numerical training.

4.2.1. LLM-Based Design Recommendations for AISI 1020

The initial prompt instructed the model to minimize structural mass while ensuring an SF greater than 3. To enhance the model’s sensitivity to design trade-offs and improve the quality of its recommendations, a set of 18 reference samples was first supplied as context (see

Table 3. FEA-based training dataset provided to the LLM for AISI 1020.

Sample Number	Thickness (mm)	Fillet Radius (mm)	Rib Angle (°)	Mass (g)	Safety Factor
C01	3	5	45	201.69	2.721
C02	3	5	60	214.21	5.779
C03	3	5	75	223.37	9.134
C04	3	10	45	204.26	4.663
C05	3	10	60	215.81	8.528
C06	3	10	75	224.44	9.658
C07	5	5	45	336.14	4.45
C08	5	5	60	357.01	9.417
C09	5	5	75	372.29	14.98
C10	5	10	45	340.44	7.755
C11	5	10	60	359.68	14.12
C12	5	10	75	374.07	16.16
C13	7	5	45	470.6	6.243
C14	7	5	60	499.81	13.29
C15	7	5	75	521.2	20.9
C16	7	10	45	476.62	10.83
C17	7	10	60	503.55	19.77
C18	7	10	75	523.7	22.9

). These samples covered a broad range of geometric configurations and their corresponding FEA performance outcomes.

Based on this reference set, GPT-4o was then instructed to generate new parameter combinations. The model produced Samples C19 through C25, as summarized in

Table 4. LLM-generated design parameters prior to FEA validation for AISI 1020.

Sample Number	Thickness (mm)	Fillet Radius (mm)	Rib Angle (°)	Mass (g)	Safety Factor
C19	3	5	55	210.57	4.7
C20	3	7	45	202.51	3.5
C21	3	6	60	214.44	6.3
C22	3	7	52	208.82	5
C23	3	7.5	58	213.51	6.6
C24	3	8	60	215.04	7.5
C25	3	7	65	217.94	8.1

. Although these outputs showed a gradual decrease in mass and appeared to approach more reasonable values, the associated safety factors were consistently much higher than required.

At this stage, no iterative validation with FEA had been conducted. According to the reference dataset established in this study, GPT-4o’s mass predictions tended to be more accurate, while the predictions for the safety factor exhibited lower accuracy. Therefore, the elevated safety factors may reflect overestimation by the model rather than actual over-engineering. This interpretation should thus be treated with caution.

To address this issue, the prompting strategy was revised by instructing GPT-4o to generate parameter sets that maintained the SF at a level slightly above 3 while minimizing mass. Under this updated instruction, the model generated Samples C26 through C28. Among them, Sample C28 (Z = 3 mm, R = 6.6 mm, A = 46°) demonstrated the best overall performance, achieving a mass of 203.32 g and an SF of 3.5. The prediction errors relative to the FEA results were 0.58% below the actual value for mass and 8.6% above the SF. Both indicators successfully met the design objectives (see

Table 5. Refined LLM-generated design parameters and FEA validation results for AISI 1020.

Sample Number	Thickness (mm)	Fillet Radius (mm)	Rib Angle (°)	Mass (g)	Safety Factor
C26 (Result of LLM generation)	3	6.8	54	210 (0.1%)	3.2 (40%)
C26 (Result of FEA)	3	6.8	54	210.33	5.4
C27 (Result of LLM generation)	3	6.6	50	205 (0.9%)	3.2 (27%)
C27 (Result of FEA)	3	6.6	50	206.99	4.4
C28 (Result of LLM generation)	3	6.6	46	204.5 (−0.58%)	3.2 (8.6%)
C28 (Result of FEA)	3	6.6	46	203.32	3.5

).

4.2.2. LLM-Based Design Recommendations for 6061-T6

To evaluate the generalization capability of the LLM in generating geometric parameter recommendations under different material conditions, additional case studies were conducted using 6061-T6 aluminum alloy and AISI 304 stainless steel. In these cases, no FEA-based training data were provided to the LLM during the recommendation process.

In the 6061-T6 aluminum alloy case, the initial recommendation (Sample C30) failed to meet the design requirement, with an SF of only 2.7. However, after three rounds of iterative semantic prompt adjustments, Sample C33 was successfully generated by the LLM, achieving an SF of 3.0 with only 3% error and maintaining a mass of 70 g with a prediction error of just 0.2%. These results indicated that the LLM was capable of adapting its recommendations to a lightweight and high-stiffness aluminum alloy scenario without relying on material-specific training data. The detailed performance comparison is summarized in

Table 6. Refined LLM-generated design parameters and FEA validation results for 6061-T6.

Sample Number	Thickness (mm)	Fillet Radius (mm)	Rib Angle (°)	Mass (g)	Safety Factor
C30 (Result of LLM generation)	3	7	45	200 (−65%)	3.2 (15%)
C30 (Result of FEA)	3	7	45	69.21	2.7
C31 (Result of LLM generation)	3	6.6	50	70.5 (0.3%)	3.2 (6%)
C31 (Result of FEA)	3	6.6	50	70.74	3.4
C32 (Result of LLM generation)	3	6.6	46	70.5 (−1.4%)	3.0 (6%)
C32 (Result of FEA)	3	6.6	46	69.49	2.8
C33 (Result of LLM generation)	3	6.6	48	70 (0.2%)	3.0 (3%)
C33 (Result of FEA)	3	6.6	48	70.14	3.1

.

4.2.3. LLM-Based Design Recommendations for AISI 304

In the AISI 304 stainless steel case, the initial recommendation (Sample C34) did not satisfy the design requirement, yielding an SF of only 2.3. After reconfiguration of the prompt, the LLM generated Sample C35 (Z = 4 mm, R = 7 mm, A = 60°), which achieved a predicted mass of 275 g with a prediction error of 0.7% and an SF of 3.2 with an error of −3%. These results demonstrated the model’s adaptability to materials with high density and high yield strength. The detailed performance comparison is provided in

Table 7. Refined LLM-generated design parameters and FEA validation results for AISI 304.

Sample Number	Thickness (mm)	Fillet Radius (mm)	Rib Angle (°)	Mass (g)	Safety Factor
C34 (Result of LLM generation)	3	7	60	210 (−1%)	3.0 (23%)
C34 (Result of FEA)	3	7	60	207.81	2.3
C35 (Result of LLM generation)	4	7	60	275 (0.7%)	3.2 (−3%)
C35 (Result of FEA)	4	7	60	277.08	3.1

.

4.3. Comparison of Mass and Safety Factor Prediction Errors

4.3.1. Error Comparison for AISI 1020

After substituting the C28 parameters recommended by the LLM (Z = 3, R = 6.6, A = 46) into the regression model (Equations (4) and (5)), the predicted mass was 203.2 g and the predicted SF was 3.53. When compared with the actual FEA simulation results (Mass = 203.32 g, SF = 3.5), the regression model demonstrated near-perfect predictive accuracy, with a negligible error of less than 0.1% for both outputs.

In contrast, the direct predictions generated by the LLM for the same parameter set yielded a mass of 204.5 g and an SF of 3.2. Compared with the actual FEA simulation results, the prediction errors were −0.58% for mass and 8.6% for the SF. A comparison of the predicted values and the corresponding FEA results is illustrated in Figure 5. Although the LLM’s predictions were less precise than those of the regression model, its recommendation still met the design criteria, achieving a mass deviation of only 1.3 g (0.6%) and satisfying the constraint of having an SF greater than 3.

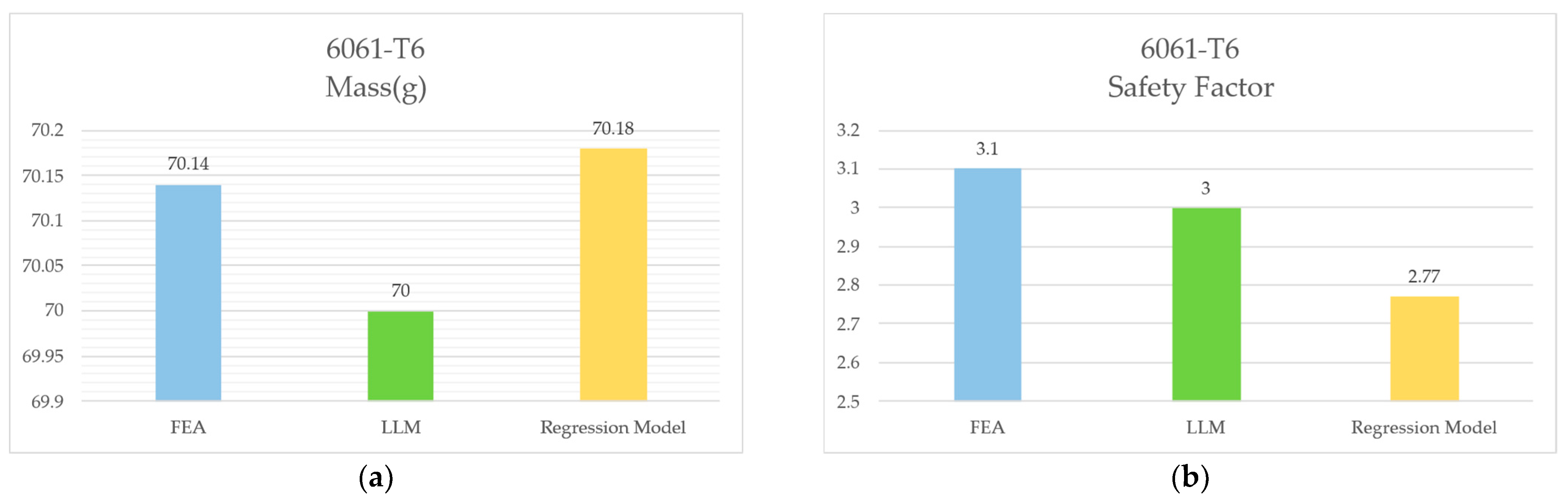
4.3.2. Error Comparison for 6061-T6

After substituting the C33 parameters recommended by the LLM (Z = 3, R = 6.6, A = 48) into the regression models (Equations (6) and (7)), the predicted mass was 70.18 g and the predicted SF was 2.77. Compared with the actual FEA simulation results (mass = 70.14 g, SF = 3.1), the regression model exhibited near-perfect predictive accuracy for mass, with an error of less than 0.1%. However, the SF prediction showed a significant error of approximately 11%, and the predicted value fell below the design constraint of SF > 3.

In contrast, the direct predictions generated by the LLM for the same parameter set yielded a mass of 70 g and an SF of 3. Compared with the actual FEA simulation results, the prediction errors were 0.2% for mass and 3.2% for the SF. A comparison of the predicted values and the corresponding FEA results is illustrated in Figure 6. Although the LLM prediction was slightly less accurate than the regression model in terms of mass, with a deviation of 0.18 g, the SF prediction was accurate and satisfied the design constraint of having an SF greater than 3.

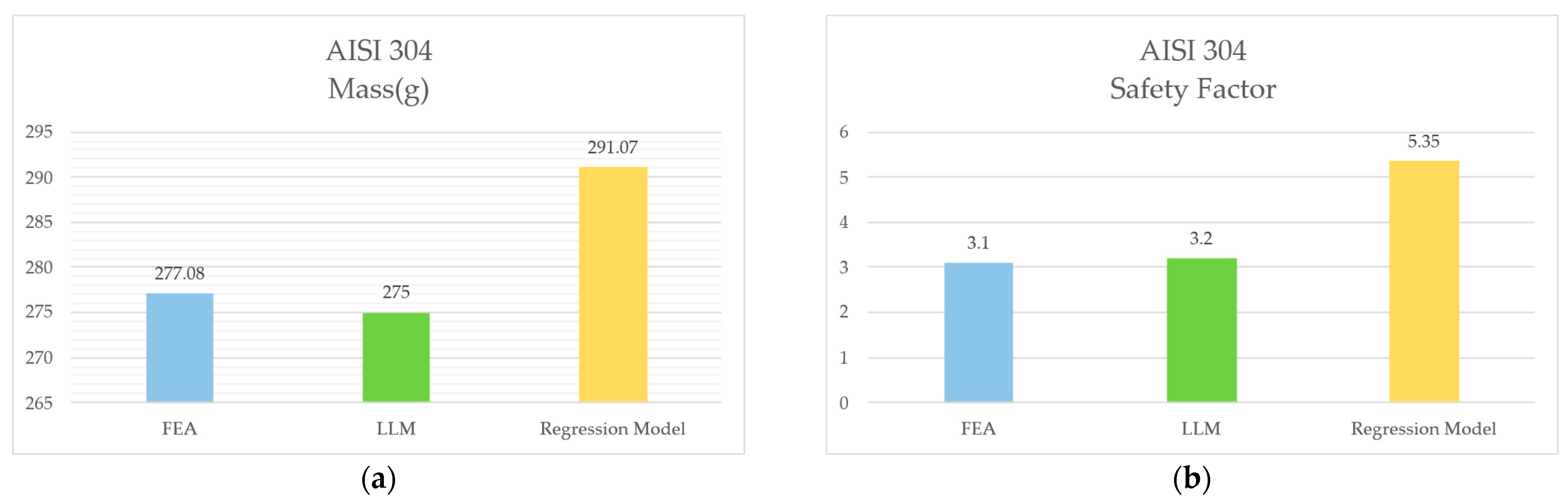
4.3.3. Error Comparison for AISI 304

After substituting the C35 parameters recommended by the LLM (Z = 4, R = 7, A = 60) into the regression models (Equations (8) and (9)), the predicted mass was 291.07 g and the predicted SF was 5.35. Compared with the actual FEA simulation results (mass = 277.08 g, SF = 3.1), the regression model exhibited a mass prediction error of −4.8%. Although the predicted SF satisfied the constraint of having an SF greater than 3, it showed a substantial deviation of approximately −42%.

In contrast, the direct predictions generated by the LLM for the same parameter set yielded a mass of 275 g and an SF of 3.2. The corresponding prediction errors relative to the FEA results were 0.7% for mass and −3% for the SF. A comparison of the predicted values and the corresponding FEA results is illustrated in Figure 7. While the mass predictions from both models differed by 16 g (approximately 5%), the LLM demonstrated significantly better accuracy in predicting the SF for this material.

This discrepancy indicates that although the regression model exhibits a high coefficient of determination (R² equal to 1), its predictive accuracy may decline when applied to parameter combinations with low sampling density or those located near the boundaries of the design space. This limitation highlights the importance of ensuring comprehensive coverage of training samples, as well as the potential advantages of incorporating physics-informed methods or adaptive sampling strategies in future regression-based surrogate models.

In contrast, the LLM consistently generated parameter recommendations that satisfied the safety factor constraint (SF > 3), likely due to repeated emphasis on this requirement in the prompt content. Furthermore, a clear trend can be observed across different material types. Since the initial recommendations were refined through iterative training involving FEA validation, the number of required iterations decreased significantly. For AISI 1020, the process involved 18 initial data points, seven prompt content refinements, and three rounds of FEA-integrated training, resulting in a total of 28 iterations. In comparison, only four FEA-integrated training rounds were required for 6061-T6, and merely two for AISI 304, with predictive accuracy improving accordingly. Overall, in this study, the LLM-based workflow required only about 27 FEA simulations across the three materials, compared with the 756 FEA simulations needed to construct the polynomial regression models, clearly demonstrating the substantial advantage of the LLM-based workflow in data efficiency. The prediction errors for AISI 1020 were −0.58% for mass and 8.6% for SF, while those for 6061-T6 were 0.2% and 3%, respectively. For AISI 304, the corresponding errors were 0.7% for mass and −3% for SF.

5. Discussion

5.1. Time Efficiency and Process Challenges of Modeling Approaches

When comparing the time efficiency of the two prediction methods, using only the number of required analysis samples as a benchmark cannot fully reflect the actual time consumed in building the entire prediction model. However, it still serves as a fundamental quantitative indicator.

For the regression-based approach, the most time-consuming task lies in constructing a complete simulation dataset and deriving the corresponding regression equations. In this study, polynomial regression models were established for both Mass and SF for three materials (AISI 1020, 6061-T6, and AISI 304). Each material required 252 FEA simulations for different design combinations, totaling 756 simulations. Each FEA simulation took approximately 2 min, resulting in a cumulative simulation time of nearly 25 h. Additionally, all simulation results needed to be imported into the statistical software IBM SPSS Statistics 26 to construct regression models and calculate the coefficients of determination, with six separate regression model derivations required in total.

As highlighted in Section 2.1, many prior studies have also pointed out a key limitation of database-driven prediction models: although they offer strong coupling between variables and performance metrics, the accuracy of their predictions can be compromised if the data coverage is not sufficiently broad. To enhance prediction precision, it is often necessary to further expand the scope and density of the database, especially when dealing with complex design spaces or multiple interacting parameters.

In contrast, the design suggestion mechanism based on LLMs required far fewer samples during the initial data construction phase. This study provided only 18 sample sets as model input. Across all three materials, the LLM-based workflow required approximately 27 FEA simulations in total, compared with the 756 simulations needed for the regression models, thereby quantitatively demonstrating its substantial advantage in data efficiency. However, the most time-consuming part of LLM-based model development was not data collection or analysis, but rather the iterative process of prompt engineering: designing, refining, and optimizing prompts. During the interactions with LLMs, hallucinations often occurred, with references to seemingly plausible but physically infeasible outputs. Numerous studies have discussed how to mitigate hallucination and assess whether the generated outputs fall into this category. Common strategies include guided prompt design, multi-turn semantic verification, human-in-the-loop feedback mechanisms, and cross-referencing with external knowledge bases [36,37,38,39].

To reduce the impact of hallucinations on design accuracy, this study adopted a manual process involving multiple rounds of prompt refinement and FEA validation to assess the reliability and feasibility of the model-generated suggestions. Although this human–machine interaction loop reduced the number of required samples, it still demanded substantial amounts of time for the manual verification and interpretation of results.

Overall, while regression models require significant numbers of simulations and statistical modeling steps, they offer interpretable and stable prediction outcomes. On the other hand, LLMs can quickly generate parameter suggestions with minimal data, but more time must be invested in prompt refinement and result verification. Therefore, when evaluating prediction efficiency, both the number of analysis samples and the labor-intensive verification process should be considered together.

5.2. Design Safety in AI-Driven Optimization

In addition to considerations of time efficiency and manual workload, the application of AI models in engineering design must also account for potential safety risks. In AI-driven optimization processes, design safety remains a critical concern. In traditional engineering workflows, human designers inherently consider user safety in order to ensure structural reliability and risk mitigation. Although safety issues were not directly encountered in the present study, prior research has highlighted the importance of integrating safety considerations into AI-driven design frameworks to address potential risks.

In safety-critical applications, it is essential to incorporate foundational engineering safety principles, such as safety margins, fail-safe mechanisms, and procedural safeguards, to enhance system robustness and fault tolerance [40]. Furthermore, when applying AI in domains with high safety requirements, human–AI interaction design must take into account user trust, model interpretability, and real-time feedback during operation [41,42]. Recent studies have proposed combining system modeling with prompt–agent co-design frameworks to enhance the transparency and multi-level validation of AI-generated decisions, particularly in safety reasoning tasks [43].

Building on these insights, future research should focus on developing prompt generation and validation pipelines with built-in safety assurance mechanisms. Such systems would help prevent risks associated with the “black-box” nature of AI decision-making. Especially in early-stage structural optimization, embedding safety-aware design strategies not only protects end-user safety but also ensures engineering performance and system reliability. These approaches are essential for improving the acceptability and practical value of AI tools in engineering design applications.

6. Conclusions

This study explored the application of LLMs, specifically, GPT-4o, in generating parameter recommendations during the early stages of structural design. A two-hole hanger bracket was used as a case study to compare the performance of LLMs with that of traditional regression-based surrogate models under identical FEA conditions. The comparison focused on prediction accuracy, data efficiency, generalization capability, and time cost. The main findings are summarized as follows:

• Prediction Accuracy: Both the regression model and GPT-4o demonstrated the ability to generate parameter suggestions that approached the target SF and Mass constraints. However, the regression model failed to meet the safety factor threshold (SF > 3) for the 6061-T6 material. In contrast, GPT-4o, although initially less accurate, showed improving performance attained through prompt refinement and iterative simulation. This adaptive behavior highlights its potential as a design assistant during early-stage exploration.
• Data Efficiency: The regression model required a substantial dataset (252 samples per material) to build reliable polynomial equations. In comparison, GPT-4o generated near-optimal suggestions using only 18 initial reference samples, supplemented by a few rounds of prompt engineering and simulation validation. This demonstrates its advantage in data-scarce environments. Overall, the LLM-based workflow required only about 27 FEA simulations for all three materials, compared with 756 for the regression models, thereby quantitatively demonstrating its substantial advantage in data efficiency, particularly in data-scarce environments.
• Generalization Capability: The regression model’s applicability to new materials was constrained by the coverage of its training dataset. Without retraining, its predictive power diminished for unseen materials. Conversely, GPT-4o maintained consistent performance across different materials—6061-T6 aluminum alloy, AISI 304 stainless steel, and AISI 1020 medium carbon steel—and exhibited reduced iteration requirements as more prompts were refined, showcasing strong semantic reasoning and cross-material adaptability.
• Process Complexity and Interpretability: While the LLM-based workflow significantly reduced sample requirements, it relied heavily on manual prompt iterations and FEA verification to suppress hallucinations. This process involved prompt adjustment, parameter translation, and simulation coordination, contributing to workflow complexity. The regression-based approach, despite requiring extensive simulations, followed a relatively straightforward and repetitive process, demanded lower domain expertise, and yielded interpretable mathematical models that facilitated design traceability.
• Numerical Function Construction: Unlike regression or surrogate models that rely on explicitly constructed numerical functions, LLMs offer a fundamentally different approach by generating design suggestions through semantic interpretation rather than direct numerical prediction. However, post-hoc FEA simulations remain essential to validate the physical feasibility of these suggestions. This workflow does not eliminate the need for numerical analysis altogether, but rather shifts it to the verification stage. In other words, an LLM does not predict SF or Mass values directly via learned equations, but proposes parameter combinations that are then evaluated through FEA validation. This distinction highlights the model’s semantic reasoning capabilities while acknowledging the continued importance of physical verification in engineering workflows.

In summary, LLMs show strong potential as AI-assisted tools for structural design, particularly in early-stage conceptual exploration. When combined with human expertise and automated validation mechanisms, LLMs can serve as efficient and adaptive alternatives to traditional optimization approaches, offering a promising direction for data-efficient, intelligent, and scalable engineering design workflows.

7. Future Perspectives

7.1. Toward LLM–CAE Workflow Automation

To address the manual effort and hallucination issues encountered in current LLM-based workflows, future research should explore the development of automated frameworks that tightly integrate LLMs with CAE tools via application programming interfaces (APIs). In this study, GPT-4o-generated design parameters were manually refined through multiple rounds of prompt engineering and validated using finite-element analysis (FEA) to ensure structural feasibility and safety. While this approach effectively suppressed hallucinations and improved the engineering applicability of LLM outputs, the overall process remained labor-intensive, limiting its scalability and practicality in real-world engineering workflows.

Recent studies have proposed using APIs to automate interactions between generative models and simulation tools [44,45,46], enabling real-time validation, feedback collection, and iterative optimization in a human–AI collaborative loop. Such systems could reduce manual intervention, accelerate the design cycle, and improve solution reliability. For less-experienced engineers working in early-stage structural optimization, automated validation mechanisms can further reduce operational errors and increase confidence in design outputs.

7.2. Statistical Benchmarking and Future Research Directions

In addition to workflow automation, future work should aim to establish standardized benchmarks for hallucination-related behavior in LLMs. By systematically recording invalid outputs and verification results, researchers can build a statistical foundation for evaluating LLM reliability in engineering tasks. This will allow future studies to go beyond point-wise validation and adopt large-scale sampling strategies, thereby enabling more robust statistical analyses (e.g., mean error, standard deviation) across multiple prediction trials.

Furthermore, as LLMs evolve, their application can be extended to more complex optimization tasks, such as multi-objective trade-offs, nonlinear constraints, or dynamic boundary conditions. The integration of LLMs with cloud-based CAE platforms also offers promising opportunities for cross-platform deployment, enabling scalable and collaborative design environments.