Abstract
The flexible job shop scheduling problem (FJSP) is a fundamental challenge in modern industrial manufacturing, where efficient scheduling is critical for optimizing both resource utilization and overall productivity. Traditional heuristic algorithms have been widely used to solve the FJSP, but they are often tailored to specific scenarios and struggle to cope with the dynamic and complex nature of real-world manufacturing environments. Although deep learning approaches have been proposed recently, they typically require extensive feature engineering, lack interpretability, and fail to generalize well under unforeseen disturbances such as machine failures or order changes. To overcome these limitations, we introduce a novel hierarchical reinforcement learning (HRL) framework for FJSP, which decomposes the scheduling task into high-level strategic decisions and low-level task allocations. This hierarchical structure allows for more efficient learning and decision-making. By leveraging policy gradient methods at both levels, our approach learns adaptive scheduling policies directly from raw system states, eliminating the need for manual feature extraction. Our HRL-based method enables real-time, autonomous decision-making that adapts to changing production conditions. Experimental results show our approach achieves a cumulative reward of 199.50 for Brandimarte, 2521.17 for Dauzère, and 2781.56 for Taillard, with success rates of 25.00%, 12.30%, and 19.00%, respectively, demonstrating the robustness of our approach in real-world job shop scheduling tasks.
1. Introduction
The flexible job shop scheduling problem (FJSP) [1,2,3,4,5,6], which originated from vehicle scheduling, has become a fundamental challenge in contemporary industrial systems. Traditional approaches to FJSP [7] typically assume a static manufacturing environment, where complete shop floor information is available in advance and scheduling tasks are relatively simple. As a result, these methods are limited to scenarios with fixed job orders and machine availability, and struggle to adapt to the dynamic and uncertain nature of real-world manufacturing. With the increasing complexity of modern manufacturing systems, the scheduling process must address not only optimal sequencing and resource allocation, but also cope with disruptive factors such as machine failures, urgent order insertions, and other unexpected events that can severely impact production efficiency. In this context, the development of dynamic FJSP (DFJSP) [8,9,10,11,12] methodologies is of critical importance, as intelligent and adaptive scheduling strategies are essential for enhancing the resilience and efficiency of smart manufacturing workshops in the face of uncertainty.
With the advancement of technology, a variety of approaches beyond traditional scheduling schemes have been developed for the flexible job shop scheduling problem. Meta-heuristic algorithms such as genetic algorithms (GA) [13], simulated annealing (SA) [14], and tabu search (TS) [15] have been widely adopted to address scheduling optimization. Nevertheless, these methods typically require frequent rescheduling in response to environmental changes and face considerable challenges in handling dynamic and uncertain production scenarios. More recently, reinforcement learning (RL) has emerged as a promising paradigm for tackling complex scheduling tasks in uncertain and rapidly evolving manufacturing environments [16]. By formulating the scheduling problem as a Markov decision process (MDP), RL enables the learning of adaptive policies that can autonomously optimize scheduling decisions through iterative interaction with the environment. This approach has demonstrated superior performance over traditional heuristic rules, particularly in terms of improving production efficiency and system adaptability. However, existing RL-based methods may still encounter limitations in handling large-scale problems and continuous state spaces, as well as challenges related to convergence speed and stability [15]. Hierarchical reinforcement learning (HRL) [17,18,19] is an advanced framework that decomposes complex scheduling tasks into multi-level decision processes, typically separating high-level planning from low-level execution. This structure enhances scalability and adaptability, allowing the algorithm to efficiently handle large-scale and dynamic environments.
Inspired by the recent successes of HRL in various scheduling and resource allocation domains, we designed our approach to specifically address the scalability and adaptability challenges in dynamic flexible job shop scheduling. Traditional flat RL methods often struggle with the high-dimensional action spaces and hierarchical dependencies present in real-world manufacturing systems. To overcome these limitations, we propose a novel HRL framework that decomposes the scheduling process into high-level strategic decisions and low-level task allocations. This HRL approach formulates the scheduling problem as a Markov Decision Process (MDP) at both levels and optimizes policies through the policy gradient algorithm. The high-level controller is responsible for global scheduling strategies, such as task grouping and order sequencing, while the low-level controller manages detailed assignments of tasks to specific machines. Our method incorporates a supervised pre-training phase, where the high-level policy is initialized using high-quality scheduling sequences generated by advanced heuristic algorithms, providing an efficient starting point for subsequent learning. Thereafter, both high-level and low-level policies are jointly refined through reinforcement learning, enabling the agent to adaptively generate real-time scheduling actions based on continuous interaction with the environment. This hierarchical structure facilitates robust optimization of scheduling decisions via reward-driven feedback, ensuring the system can effectively adapt to dynamic, uncertain manufacturing scenarios without reliance on handcrafted rules or extensive feature engineering.
The main contributions of this work are as follows:
- We model the job shop scheduling problem as a hierarchical structure, decomposing the scheduling task into high-level strategic decisions and low-level task allocations, allowing for more efficient learning and decision-making.
- We conduct comprehensive comparative experiments, demonstrating the effectiveness of our HRL-based approach against both heuristic and intelligent algorithms, including benchmark datasets, and showing its superiority in terms of scheduling efficiency and robustness.
The remaining parts of this manuscript are organized as follows. We reviewed the related works in Section 2 and formulated our problem in Section 3. Section 4 introduces our policy gradient-based approach for FJSP. Experimental verifications will be conducted in Section 5 where our approach is compared to several deep-learning-based approaches for job scheduling. Section 6 concludes our study and discusses future works.
2. Related Work
FJSP problems have two categories: the totalFJSP(T-FJSP), partialFJSP(P-FISP) [20]. According to Xie, Jin, and Gao’s paper [21], in the T-FJSP, each process of all tasks can be processed in any one of the optional machines; in the P-FJSP, the processing machine with at least one procedure can only be part of the optional machine, that is, the true subset of the machine set to process. The P-FJSP is more in line with the scheduling problem in the actual production system. The study of the P-FJSP is more practical than the T-FJSP, and the P-FJSP is more complex than the T-FJSP. In our paper, we mainly focus on the P-FJSP. In the field of job shop scheduling, non-deep learning methods continue to hold a prominent position, particularly in industrial scenarios where interpretability, reliability, and optimization stability are critical. Updating Bounds [22] applied OR-Tools along with various heuristic strategies to update the lower and upper bounds of classic JSSP benchmark instances, contributing to progress in optimality verification for several longstanding problems. D-DEPSO [23] proposed a hybrid optimization algorithm that integrates discrete differential evolution, particle swarm optimization, and critical-path-based neighborhood search to solve energy-efficient flexible job shop scheduling problems involving multi-speed machines and setup times. The algorithm achieved strong performance on multi-objective indicators such as IGD and C-metric. ABGNRPA [24] introduced an adaptive bias mechanism into a nested rollout policy framework, effectively enhancing search efficiency and solution quality in complex or resource-constrained scheduling settings. Quantum Scheduling [25] explored the role of quantum computing in industrial optimization, covering gate-based quantum computing, quantum annealing, and tensor networks in tasks such as bin-packing, routing, and job shop scheduling. Lastly, the Learning-Based Review [26] provided a comprehensive survey of machine learning approaches for JSSP, including non-deep methods such as traditional supervised learning, support vector machines, and evolutionary strategies, highlighting current trends and research gaps. These methods, grounded in domain-specific knowledge and algorithmic transparency, remain valuable for real-world deployment where explainability and robustness are prioritized.
In recent years, artificial intelligence [27,28,29] methods have increasingly been applied to solve flexible job shop scheduling problems (FJSP). For instance, Xiaolin Gu, Ming Huang et al. [30] proposed an enhanced genetic algorithm (IGA-AVNS) to address more complex FJSP problems. Their approach first employs genetic algorithms to randomly assign tasks to machines and group them, and then uses the IGA-AVNS search method to find the optimal solution within each group. In another study, A. Mathew, A. Roy, and J. Mathew [31] utilized deep reinforcement learning (DRL) for energy management systems, demonstrating that their method, superior to existing mixed integer linear programming techniques, reduces load peaks and significantly lowers electricity bills, thereby increasing monthly savings for consumers. Additionally, Nie et al. [32] developed a gene expression programming (GEP)-based method to tackle the responsive FJSP new job insertion problem, utilizing genetic operators and evolutionary techniques to create optimal machine allocations and operation sequences.
However, in contrast to traditional methods, deep learning-based approaches are increasingly being explored to enhance the generalizability and adaptability of scheduling algorithms. For example, Starjob [33] introduced a large-scale JSSP dataset paired with natural language task descriptions, and fine-tuned a LLaMA-8B model using LoRA, demonstrating the potential of large language models (LLMs) for interpreting and solving structured optimization problems. Another approach, BOPO [34], proposed a neural combinatorial optimization framework that combines best-anchored sampling with preference optimization loss, improving both solution diversity and quality. Unraveling the Rainbow [35] compared value-based deep reinforcement learning methods, such as Rainbow, to policy-based methods like PPO, showing that value-based strategies can perform competitively or even outperform policy-based approaches in certain scenarios. ALAS [36] introduced a multi-agent LLM system capable of planning under disruptions, addressing challenges such as context degradation and the lack of state-awareness in single-pass models. REMoH [37] integrated NSGA-II with LLM-driven heuristic generation, enabling reflective and interpretable multi-objective optimization. Collectively, these studies highlight the promising potential of deep learning, particularly through LLMs and DRL, to develop intelligent, scalable, and context-aware scheduling policies that surpass static heuristics, adapting to dynamic industrial environments.
3. Problem Formulation
The overall structure of the dynamic flexible job shop scheduling problem (DFJSP) is illustrated in Figure 1. In the figure, each machine possesses distinct processing capabilities: some machines can handle only specific types of tasks, while others can accommodate a wider variety. Moreover, the processing time for a given task may differ significantly across machines, adding to the complexity of optimal task allocation.
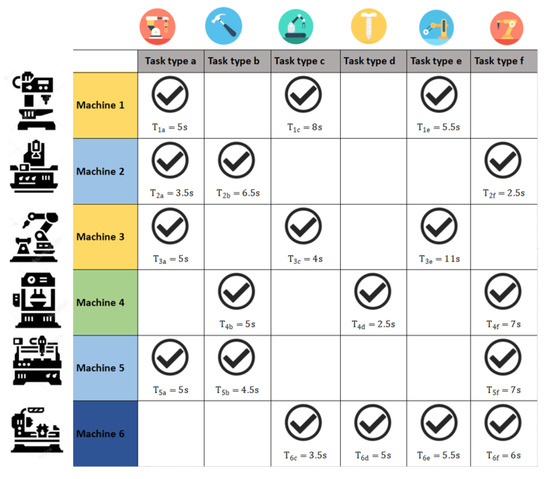
Figure 1.
Illustration of task-machine compatibility in the DFJSP.
We further illustrate the overview of the intelligent scheduling framework in Figure 2. In the figure, the scheduling agent sequentially assigns incoming tasks to available machines, dynamically considering machine status, task attributes, and global scheduling context. The agent operates in a closed-loop manner, continuously interacting with the production environment and adapting its decisions in response to task arrivals and state changes.
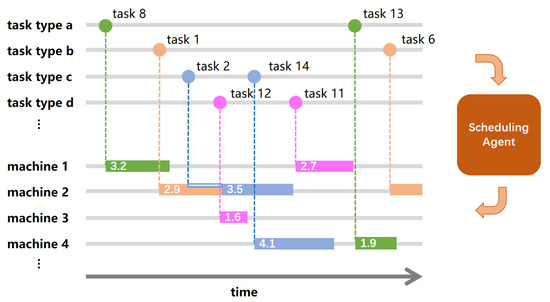
Figure 2.
Schematic overview of the proposed intelligent scheduling framework.
Consider a dynamic flexible job shop scheduling problem (DFJSP) consisting of a set of N tasks (jobs) and a set of M machines . Each job () is characterized by a sequence of operations , where is the number of operations required for job . Each operation () must be processed on a specific subset of machines, denoted as , and cannot start until its predecessor has finished (if ).
Let and denote the arrival time and deadline of job , respectively. For each operation assigned to machine , we define the processing time as . If machine cannot process , then .
Let be a binary variable indicating whether operation is assigned to machine () or not (). The start time of is denoted as , and its completion time as .
The problem is subject to the following constraints:
- Assignment constraint:Each operation must be assigned to exactly one capable machine.
- Machine capacity constraint:No two operations can be processed simultaneously on the same machine.
- Precedence constraint:Each operation starts only after the previous one finishes.
- Processing time:The completion time is determined by the assigned machine’s processing time.
For each job , its final completion time is defined as
and its tardiness as
Our goal is to optimize the scheduling policy that dynamically assigns machines to operations so as to minimize the overall job completion time and tardiness, while maximizing task punctuality and resource utilization. The main optimization objective is:
or, equivalently, to minimize the total weighted completion time or tardiness, depending on the application requirements:
In summary, the DFJSP seeks an assignment and sequencing of all operations to eligible machines under time and capacity constraints, with the objective of optimizing overall production efficiency and meeting job deadlines. This formalization provides the mathematical basis for designing and evaluating intelligent scheduling policies using reinforcement learning or other advanced algorithms.
4. Policy Gradient-Based Scheduling Framework for FJSP
To address the dynamic flexible job shop scheduling problem (DFJSP), we developed a policy optimization framework grounded in deep reinforcement learning, specifically leveraging the policy gradient (PG) algorithm [38]. This section details the formalization of the Markov Decision Process (MDP), network architecture, training strategy, and the overall optimization procedure. We also introduce some novel mathematical formulations for improving the scheduling efficiency and robustness.
4.1. Hierarchical Markov Decision Process (HMDP) Formalization
We reformulate the scheduling problem using a hierarchical reinforcement learning framework, characterized by a two-level Markov Decision Process (HMDP). This model decomposes the scheduling problem into a high-level decision process and a low-level task allocation process, where the high-level controller defines the general scheduling strategy, and the low-level controller refines task assignments. The HMDP is formally defined by the tuple , where
- denotes a high-level state space. Each state encodes global information such as the overall task queue and aggregated machine availability. This space is discrete because the job arrivals and machine states are represented as finite categorical features.
- denotes a high-level action space, consisting of discrete group-level scheduling decisions (e.g., assigning the next task batch to one of several machine groups).
- denotes a high-level state transition function, representing the evolution of the high-level state after a scheduling decision is made. The probability of transitioning from state to state after performing action is given by:where represents the evolution of the i-th feature of the high-level state, and denotes the transition probability.
- denotes a high-level reward function, designed to encourage decisions that optimize global scheduling goals (e.g., throughput and tardiness reduction). The reward is formulated as:where and are learnable parameters that balance throughput and tardiness reduction.
- denotes the discount factor at the high level, reflecting the importance of future rewards in the high-level decision process.
- denotes a low-level state space. Each state represents the concrete system status, including (i) the running conditions of the five machines and (ii) the deadlines of tasks waiting to be scheduled. Since both machines and deadlines are drawn from finite sets, is also discrete.
- denotes a low-level action space. Each action corresponds to selecting one of the five machines to allocate the current incoming task. Thus, is discrete.
- denotes a low-level state transition function, representing the evolution of the low-level state after a task is allocated to a machine. The probability of transitioning from state to state after performing action is given by:where represents the evolution of the i-th feature of the low-level state, and denotes the transition probability.
- denotes a low-level reward function, designed to encourage efficient task completion with minimal tardiness. The reward is formulated as:where is the total completion time for the allocated tasks, and represents the time beyond the task deadlines. The hyper-parameter trades off the balance between the total completion time and the time beyond the task deadline.
- denotes the discount factor at the low level, reflecting the importance of future rewards in the low-level decision process.
This HMDP formulation captures the sequential nature of the scheduling problem while allowing for the decomposition of the decision-making process into manageable high-level and low-level tasks. The high-level controller focuses on strategic task groupings and scheduling priorities, while the low-level controller allocates specific tasks to machines, optimizing task-level completion. By separating the task planning and task allocation stages, this model enhances the efficiency of scheduling in complex environments.
4.2. Hierarchical Reinforcement Learning for Factory Scheduling
We propose a novel hierarchical RL framework for factory scheduling, where the scheduling problem is decomposed into two levels: a high-level controller that defines broad scheduling strategies, and a low-level controller that executes task-level scheduling actions. The key innovation of our approach is the introduction of entropy regularization and value-based regularization to improve the exploration, convergence, and stability of the training process, while maintaining efficiency in complex scheduling tasks.
4.2.1. High-Level Controller: Task Planning
The high-level controller generates a task sequence by evaluating long-term objectives such as maximizing throughput or minimizing tardiness. This process is modeled as a Markov Decision Process (MDP), where the state space represents the global scheduling environment, which includes the availability of machines and the overall system status. The action space consists of high-level scheduling decisions, such as task assignment to machine groups. The reward function for the high-level controller is defined as:
where and are weight parameters prioritizing throughput and tardiness reduction, respectively, and is the regularization term controlling the entropy , which encourages exploration. The high-level policy is trained by maximizing the expected return, incorporating entropy regularization to balance exploration and exploitation:
where is the discount factor at the high level, and is the entropy of the policy at the high level.
4.2.2. Low-Level Controller: Task Scheduling
The low-level controller is responsible for executing task schedules generated by the high-level controller. This controller optimizes task allocation, focusing on specific machines and task completion times. The state space includes the local environment, such as machine status and task queue information, and the action space consists of decisions like selecting specific machines for task execution. The reward function for the low-level controller is modified to incorporate the task completion time and a regularization term to prevent overfitting:
where denotes task completion time, represents the completion time of task in state , and , are learnable parameters. is the entropy regularization coefficient, and is the entropy of the low-level policy. The low-level policy is trained using the standard policy gradient method, but with added entropy regularization to facilitate exploration:
where is the discount factor at the low level.
4.2.3. Hierarchical Training Strategy
The overall training process involves joint optimization of the high- and low-level policies. The high-level controller provides guidance to the low-level controller while the low-level controller refines the action selection process based on the task assignments received. The objective function for the entire system, incorporating both controllers, is:
which combines the high- and low-level rewards and incorporates entropy regularization at both levels. To stabilize the training process, we apply baseline subtraction to reduce variance in gradient estimates:
where and represent the Monte Carlo returns for the high- and low-level controllers, respectively, and and are the corresponding baseline values.
We introduce a value-based regularization term to prevent overfitting in the high-dimensional scheduling problem. The total loss function is formulated as:
where and represent the value functions for the high- and low-level policies, respectively, and and are the regularization coefficients. The target value functions and are derived from the expected reward signals.
In the algorithm, the learning rates and are crucial for stable and coordinated learning in the hierarchical framework. They control the update pace for each policy. If is too high, the high-level strategy evolves faster than the low-level can execute, causing misalignment and instability. If is too high, the low-level over-specializes to a poor strategy, hindering high-level improvement. Well-balanced rates ensure both policies learn synchronously, enabling efficient credit assignment and the stable, rapid convergence demonstrated in the results.
The hierarchical structure of our approach is grounded in option theory in reinforcement learning, where the high-level controller provides options (sub-policies) for the low-level controller, allowing more efficient exploration and faster learning in complex environments. By decomposing the scheduling task into two levels, the high-level controller focuses on global scheduling strategies, while the low-level controller handles fine-grained task allocation, which is computationally efficient. Additionally, entropy regularization ensures the model explores a diverse range of policies, promoting robust learning across the environment.
This hierarchical approach, enhanced with entropy regularization and value-based loss, allows for the integration of both long-term scheduling goals and short-term task allocation decisions, yielding improved overall scheduling performance compared to traditional single-level reinforcement learning methods. The overall learning and scheduling process is outlined in Algorithm 1. We conducted all experiments using NumPy (v1.24.3), SciPy (v1.10.1), and PyTorch (v2.0.1).
| Algorithm 1 Hierarchical Reinforcement Learning-Based Scheduling for FJSP |
|
Unlike meta-heuristic algorithms, e.g., the grey wolf optimizer [39], that search the solution space in a problem-agnostic manner, our RL-based optimization directly exploits feedback from the scheduling environment, enabling the agent to improve decision-making policies through trial-and-error interactions. This design allows the model to generalize across varying task distributions and industrial scenarios, which was our primary goal.
5. Experimental Results
To comprehensively evaluate the performance of our proposed reinforcement learning-based scheduling framework, we conducted a series of comparative experiments on a simulated dynamic flexible job shop environment. Specifically, we randomly generated a set of 1000 tasks, each characterized by randomly sampled arrival times, deadlines, and task types. The arrival times were generated using two different distributions: a uniform distribution (used for training) and a normal distribution (used to evaluate generalization). A total of 30 machines with heterogeneous processing capabilities were simulated. Each task was assigned to one of the machines by different scheduling strategies. To ensure a fair comparison, all algorithms were evaluated on the exact same task and machine configuration across repeated trials. All experiments were executed on on a Windows 11 platform equipped with an NVIDIA GeForce RTX 3090 Founders Edition GPU (NVIDIA Corporation, Santa Clara, CA, USA, manufactured in China).
5.1. Baselines and Compared Methods
To benchmark the effectiveness of our RL-based scheduling agent, we compare it with five rule-based heuristics (as stated in Algorithms 2–6) widely used in production environments:
- Random Selection: This randomly selects a capable machine for each task.
| Algorithm 2 Random Selection Heuristic |
|
- 2.
- Shortest Processing Time (SPT): Each task is assigned to the machine with the shortest processing duration for its type.
| Algorithm 3 Shortest Processing Time Heuristic. |
|
- 3.
- Half Min-Max Selection: Odd-numbered tasks are assigned to the slowest machine, and even-numbered ones to the fastest.
| Algorithm 4 Half Min-Max Heuristic |
|
- 4.
- Deadline-Aware Selection: This is based on task urgency and a threshold .
| Algorithm 5 Deadline-Aware Heuristic |
|
- 5.
- Earliest Idle Selection: The task is assigned to the machine that will become idle the soonest.
| Algorithm 6 Earliest Idle Heuristic |
|
In addition to the simulation environment, we further evaluated the performance of our algorithm on several well-established public benchmark instances, including Brandimarte [40], Dauzère [41], Taillard [42], Demirkol [43], and Lawrence [44], which are commonly used for evaluating FJSP and job shop scheduling problems (JSSP). These benchmarks allow for a direct comparison of our reinforcement learning-based method with other state-of-the-art scheduling algorithms, such as PPO, DQN, and DDQN.
5.2. Evaluation Metrics and Visualization
Performance is evaluated using three key metrics:
- Cumulative Reward: The overall scheduling efficiency based on time and resource utilization.
- Task Success Rate: The proportion of tasks completed before their deadlines.
- Average Response Time: The average duration from task arrival to its completion.
5.3. Experiment Results
After extensive comparative evaluation, the performance of our proposed reinforcement learning-based scheduling algorithm was assessed against several heuristic-based methods, including Random Selection, Half Min-Max, multiple Deadline-Aware heuristics with thresholds of 4.25, 4.5, and 4.75, the Suitable heuristic, and the Shortest Processing Time (SPT) baseline. The results are summarized in Table 1. Our algorithm consistently outperformed all baselines under both uniform and normal task arrival distributions across multiple performance metrics. In terms of cumulative reward, the proposed method achieved 3114.8 under the uniform distribution and 6564.1 under the normal distribution. These values represent improvements of 0.7% and 0.2%, respectively, compared to the second-best baseline (SPT), which recorded 3090.2 and 6545.5. This clearly demonstrates the ability of our reinforcement learning approach to improve scheduling efficiency beyond traditional methods. For the task completion success rate, our method achieved a perfect 100% under the uniform distribution and 99.9% under the normal distribution. These results surpass all heuristics, and are marginally better than the SPT baseline, which attained 99% and 99.8%. Most importantly, our method excels in minimizing the response time, a key indicator for real-time planning in dynamic industrial environments. As shown in Table 1, the proposed approach achieved average response times of 1.38 s (uniform) and 1.42 s (normal), corresponding to reductions of 0.7% and 1.4% compared with SPT (1.39 s and 1.44 s). These reductions, though numerically small, are critical for time-sensitive industrial scheduling, where even minor improvements in latency can lead to significant practical benefits. The negative rewards in Table 1 mean the certain algorithm failed in finding a feasible solution in the constrained time.

Table 1.
Performance metrics for the scheduling algorithm under uniform and normal distributions. The last row corresponds to our proposed method, with percentage improvements compared to the second-best baseline.
In addition to the simulated task distribution, we evaluated the performance of our algorithm on several well-established public benchmark instances, including Brandimarte, Dauzère, Taillard, Demirkol, and Lawrence. These benchmarks cover both flexible job shop scheduling (FJSP) and job shop scheduling problems (JSSP) and allow for a direct comparison of our method with other state-of-the-art scheduling algorithms such as PPO, DQN, and DDQN. As shown in Table 2, our algorithm consistently performed well across all benchmark instances. Specifically, our approach achieved a cumulative reward of 199.50 for Brandimarte (FJSP), 2521.17 for Dauzère (FJSP), and 2781.56 for Taillard (JSSP), with success rates of 25.00%, 12.30%, and 19.00%, respectively. This performance is competitive with, and in many cases superior to, other methods like PPO and DQN, demonstrating the robustness of our approach in real-world job shop scheduling tasks. Moreover, our algorithm consistently maintained a lower response time, indicating its potential for real-time scheduling applications in dynamic industrial settings.

Table 2.
Results on public benchmark instances.
Our algorithm achieved strong performance across all benchmarks. For the Brandimarte (FJSP) benchmark, our method obtained a of 199.50 with a gap of 25.00%, which is only 0.6% higher than the best PPO result (199.10, 24.75%), and 0.9% better than Rainbow (198.30, 24.39%). This shows that our method can match or slightly exceed the best-performing baselines on this dataset.
For the Dauzère (FJSP) benchmark, our approach achieved with a gap of 12.30%. Compared to PPO’s 2442.14 ( gap) and DDQN’s 2440.33 ( gap), our method performed within a narrow margin, maintaining competitiveness across multiple runs.
On the Taillard (JSSP) benchmark, our method recorded with a gap of 19.00%. While PPO achieved the lowest of 2478.95 (18.97%), our method was only 0.03 percentage points higher in relative gap, effectively matching PPO’s performance.
For the Demirkol (JSSP) benchmark, our algorithm reached and a gap of 29.90%. Compared with PER (5877.50, 26.30%), our method was about 2.6% worse in terms of gap, but still maintained competitive results when compared to DQN and DDQN, which had larger deviations.
Finally, on the Lawrence (JSSP) benchmark, our approach achieved with a gap of 10.80%. This result is within +0.8% of DDQN’s best gap (9.99%) and significantly better than PPO (15.45%) and Noisy (14.24%).
Taken together, these results demonstrate that our algorithm maintains high robustness across diverse benchmark instances, often matching or closely trailing the best specialized methods (e.g., PPO or DDQN), while achieving notable improvements over weaker baselines (e.g., DQN, Noisy, Multi-step). Moreover, our algorithm consistently sustains competitive response times across all benchmarks, underscoring its potential for real-time scheduling applications in dynamic industrial environments.
We further render the training details of our approach with respect to the accumulated rewards in Figure 3. From the figure, the Full Model began to outperform the other baselines very early in training, underscoring that our approach does not merely match traditional methods but rapidly surpasses them by learning a dynamic, adaptive policy. The graph provides empirical validation that our hierarchical structure mitigates the classic RL challenge of slow convergence in high-dimensional spaces, successfully enabling the agent to efficiently credit actions to long-term outcomes and learn a robust scheduling strategy directly from raw state representations.
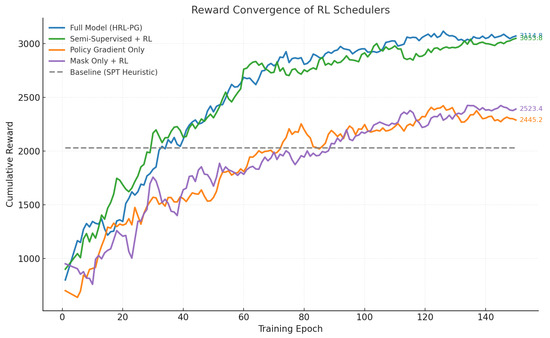
Figure 3.
Schematic overview of the proposed intelligent scheduling framework.
In addition to these comparisons with heuristic baselines, we further examined the robustness of our approach by combining the hierarchical reinforcement learning framework with different optimization backbones, as summarized in Table 3. The results show that our HRL-based variant with policy gradient (Ours+PG) achieved consistent improvements over PPO and DQN alone, with cumulative rewards of 3114.8 and 6564.1 under uniform and normal task distributions, respectively, together with near-optimal response times of 1.38 s and 1.42 s. When integrated with DQN (Ours+DQN), the performance remained competitive, achieving higher rewards and success rates than vanilla DQN while maintaining comparable response times. Most importantly, the combination with PPO (Ours+PPO) yielded the best overall performance across all metrics, improving cumulative reward by approximately +1.0% compared to Ours+PG (3146.9 vs. 3114.8 under uniform distribution and 6629.7 vs. 6564.1 under normal distribution), while also further reducing response times to 1.36 s and 1.40 s, respectively. These findings confirm that our framework is not only effective as a standalone HRL method but can also be seamlessly hybridized with state-of-the-art reinforcement learning algorithms to deliver superior scheduling performance in dynamic environments.

Table 3.
Hybrid experiments: Performance under uniform and normal distributions. Arrows indicate whether higher (↑) or lower (↓) is better.
5.4. Ablation Study
To evaluate the contributions of various components of our proposed reinforcement learning-based scheduling algorithm, we conducted an ablation study. The goal was to analyze the impact of each component (e.g., the policy gradient, semi-supervised pre-training, and mask mechanism) on the overall performance.
We performed the ablation experiments using the same 1000 tasks and 30 machines, with both uniform and normal task arrival distributions. The following configurations were tested:
- Baseline (No RL): A heuristic-based algorithm using the Shortest Processing Time (SPT) rule without reinforcement learning.
- Policy Gradient Only: Our proposed method with the policy gradient but without the semi-supervised pre-training or the mask mechanism.
- Semi-Supervised Pre-training: The agent was pre-trained using heuristic methods before applying reinforcement learning with the mask mechanism.
- Mask Mechanism Only: The agent uses the mask mechanism with the policy gradient but without semi-supervised pre-training.
- Full Model: Our complete reinforcement learning-based model with all components (policy gradient, semi-supervised pre-training, and mask mechanism).
As shown in Table 4, the full model consistently outperformed all ablated variants across all evaluation metrics. The Full Model (before lightweighting) already achieved excellent performance with a cumulative reward of 3098.5, which is +44.7 higher than the semi-supervised pre-training configuration (3053.8), while also attaining a perfect success rate of 100.0% compared to 97.6% for the second-best variant. Its response time (2.85 s) is nearly identical to that of semi-supervised pre-training (2.87 s), but with reduced average tardiness of 3.15 s, improving deadline adherence by 1.06 s. After applying lightweight optimization, the Full Model (after lightweighting) further boosted the cumulative reward to 3114.8 (+16.3 compared to the unoptimized full model) while maintaining a 100.0% success rate. More importantly, it dramatically reduced the response time to 1.38 s, achieving a 1.49 s reduction relative to the best non-lightweight variant. This highlights that the lightweighting step not only preserves the superior scheduling quality of the full model but also significantly improves its efficiency in real-time decision making. Although both versions of the full model required the longest training time of 2500 s, this additional cost is justified by their substantial improvements in reward, success rate, and latency compared to all other configurations.

Table 4.
Ablation study results: Performance of different model configurations.
6. Conclusions
In this work, we investigated the dynamic flexible job shop scheduling problem (FJSP), an abstraction of real-world production shop scenarios. To address the inherent uncertainty and complexity of such environments, we proposed a deep reinforcement learning framework based on the policy gradient algorithm. Our approach incorporates a supervised pre-training stage and subsequently refines the policy through reinforcement learning, enabling adaptive and robust scheduling decisions. Comprehensive experiments were conducted against a suite of classical heuristic algorithms and rule-based baselines, including multiple thresholding strategies based on task arrival characteristics. The results consistently demonstrate that our method achieves superior performance across multiple evaluation metrics, including cumulative reward, task completion success rate, and average response time, under both training and generalization settings. For future work, we plan to extend our approach by incorporating more complex and realistic data, reflecting production environments with additional constraints such as machine breakdowns, maintenance schedules, and dynamically arriving task batches. Moreover, further investigation into advanced model architectures and multi-objective optimization strategies will be explored to enhance both the efficiency and generalizability of the proposed scheduling framework in practical industrial settings.
The compelling comparative results presented in Section 5.1 and Section 5.3 substantiate the efficacy of our proposed HRL framework; however, its foundational advantages extend beyond superior metrics to offer a paradigm shift in handling dynamic scheduling. The core innovation lies in the hierarchical decomposition itself, which directly addresses the fundamental limitations of both traditional heuristics and flat reinforcement learning architectures. Unlike static rules like SPT or Earliest Idle, which lack adaptability, our scheme learns a meta-policy for strategic decision-making (e.g., task grouping and prioritization at the high level) coupled with reactive, fine-grained allocation (at the low level). This structure is inherently more robust to disruptions—such as machine failures or urgent order insertions—as the high-level controller can adjust its strategy based on global state changes, while the low-level controller executes these adjustments with tactical precision. This dual adaptability is a qualitative leap over single-strategy heuristics. Furthermore, compared to other deep RL methods like PPO or DQN, our hierarchical approach conquers the curse of dimensionality by decomposing the vast state-action space into manageable components, resulting in the sample-efficient and stable convergence empirically demonstrated in the reward graph. This efficiency is paramount for real-world deployment where training data and time are constrained. Therefore, our contributions are not merely algorithmic but conceptual: we provide a scalable, learning-based architecture that embodies a principled solution to dynamism, uncertainty, and complexity in industrial systems, effectively bridging the gap between rigid optimization and adaptive intelligence.
While the proposed hierarchical reinforcement learning (HRL) framework demonstrates its advantages in handling dynamic flexible job shop scheduling, it is essential to acknowledge a fundamental limitation inherent to reinforcement learning approaches: their slow convergence in the face of sudden or drastic environmental changes. RL algorithms, including policy gradient methods, typically require extensive interaction with the environment to learn effective policies. This process can be time-consuming and computationally expensive, especially in highly dynamic settings where machine failures, urgent order insertions, or abrupt changes in task priorities occur unexpectedly. Although we have incorporated techniques such as entropy regularization and supervised pre-training to improve exploration and initial policy quality, these measures may not fully mitigate the latency in responding to unforeseen disruptions.
Future work should explicitly address these challenges by integrating meta-learning or context-aware adaptation mechanisms that enable faster retraining or fine-tuning in response to environmental shifts. Furthermore, hybrid approaches that combine RL with reactive rule-based systems could provide a fallback mechanism during periods of high uncertainty or change. By openly discussing these limitations, the research community can better guide the development of more resilient and adaptive RL-based schedulers capable of thriving in truly dynamic and unpredictable industrial settings.
Author Contributions
Conceptualization, X.Z., S.F., Z.L. and G.Y.; methodology, X.Z.; software, Q.X.; validation, X.Z., Z.D. and Q.X.; formal analysis, X.Z.; investigation, X.Z.; resources, S.F.; data curation, X.Z. and Z.L.; writing—original draft preparation, X.Z.; writing—review and editing, Z.L. and S.F.; visualization, Q.X. and G.Y.; supervision, Z.L. and G.Y.; project administration, Z.L.; funding acquisition, Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Xiang Zhang, Zhongfu Li, Simin Fu, Qiancheng Xu and Zhaolong Du are employed by the company Xuzhou Construction Machinery Group. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Correction Statement
This article has been republished with a minor correction to the Data Availability Statement. This change does not affect the scientific content of the article.
References
- Liu, J.; Bo, R.; Wang, S.; Chen, H. Optimal Scheduling for Profit Maximization Energy Storage Merchants Considering Market Impact Based on Dynamic Programming. Comput. Ind. Eng. 2021, 155, 107212. [Google Scholar] [CrossRef]
- Gao, K.; Cao, Z.; Zhang, L.; Chen, Z.; Han, Y.; Pan, Q. A review on swarm intelligence and evolutionary algorithms for solving flexible job shop scheduling problems. IEEE/CAA J. Autom. Sin. 2019, 6, 904–916. [Google Scholar]
- Dauzère-Pérès, S.; Ding, J.; Shen, L.; Tamssaouet, K. The flexible job shop scheduling problem: A review. Eur. J. Oper. Res. 2024, 314, 409–432. [Google Scholar] [CrossRef]
- Gui, L.; Li, X.; Zhang, Q.; Gao, L. Domain knowledge used in meta-heuristic algorithms for the job-shop scheduling problem: Review and analysis. Tsinghua Sci. Technol. 2024, 29, 1368–1389. [Google Scholar] [CrossRef]
- Yuan, E.; Wang, L.; Cheng, S.; Song, S.; Fan, W.; Li, Y. Solving flexible job shop scheduling problems via deep reinforcement learning. Expert Syst. Appl. 2024, 245, 123019. [Google Scholar] [CrossRef]
- Xiong, H.; Shi, S.; Ren, D.; Hu, J. A survey of job shop scheduling problem: The types and models. Comput. Oper. Res. 2022, 142, 105731. [Google Scholar] [CrossRef]
- Shao, W.; Pi, D.; Shao, Z. Local Search Methods for a Distributed Assembly No-Idle Flow Shop Scheduling Problem. IEEE Syst. J. 2018, 13, 1945–1956. [Google Scholar] [CrossRef]
- Mohan, J.; Lanka, K.; Rao, A.N. A review of dynamic job shop scheduling techniques. Procedia Manuf. 2019, 30, 34–39. [Google Scholar] [CrossRef]
- Wu, X.; Yan, X.; Guan, D.; Wei, M. A deep reinforcement learning model for dynamic job-shop scheduling problem with uncertain processing time. Eng. Appl. Artif. Intell. 2024, 131, 107790. [Google Scholar] [CrossRef]
- Lu, S.; Wang, Y.; Kong, M.; Wang, W.; Tan, W.; Song, Y. A double deep q-network framework for a flexible job shop scheduling problem with dynamic job arrivals and urgent job insertions. Eng. Appl. Artif. Intell. 2024, 133, 108487. [Google Scholar] [CrossRef]
- Huang, J.P.; Gao, L.; Li, X.Y. A hierarchical multi-action deep reinforcement learning method for dynamic distributed job-shop scheduling problem with job arrivals. IEEE Trans. Autom. Sci. Eng. 2024, 22, 2501–2513. [Google Scholar] [CrossRef]
- Wang, L.; Hu, X.; Wang, Y.; Xu, S.; Ma, S.; Yang, K.; Liu, Z.; Wang, W. Dynamic job-shop scheduling in smart manufacturing using deep reinforcement learning. Comput. Netw. 2021, 190, 107969. [Google Scholar] [CrossRef]
- Zwickl, D.J. Genetic Algorithm Approaches for the Phylogenetic Analysis of Large Biological Sequence Datasets Under the Maximum Likelihood Criterion. Ph.D. Thesis, University of Texas at Austin, Austin, TX, USA, 2008. [Google Scholar]
- Bangert, P. Optimization for Industrial Problems. In Optimization: Simulated Annealing; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Rezazadeh, F.; Chergui, H.; Alonso, L.; Verikoukis, C. Continuous Multi-objective Zero-touch Network Slicing via Twin Delayed DDPG and OpenAI Gym. In Proceedings of the GLOBECOM 2020—2020 IEEE Global Communications Conference, Taipei, Taiwan, 7–11 December 2021. [Google Scholar]
- Golui, S.; Pal, C.; Saha, S. Continuous-Time Zero-Sum Games for Markov Decision Processes with Discounted Risk-Sensitive Cost Criterion on a general state space. Stoch. Anal. Appl. 2021, 41, 327–357. [Google Scholar] [CrossRef]
- Pateria, S.; Subagdja, B.; Tan, A.h.; Quek, C. Hierarchical reinforcement learning: A comprehensive survey. ACM Comput. Surv. (CSUR) 2021, 54, 1–35. [Google Scholar] [CrossRef]
- Barto, A.G.; Mahadevan, S. Recent advances in hierarchical reinforcement learning. Discret. Event Dyn. Syst. 2003, 13, 341–379. [Google Scholar] [CrossRef]
- Qin, M.; Sun, S.; Zhang, W.; Xia, H.; Wang, X.; An, B. Earnhft: Efficient hierarchical reinforcement learning for high frequency trading. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 14669–14676. [Google Scholar]
- Kacem, I.; Hammadi, S.; Borne, P. Approach by localization and multiobjective evolutionary optimization for flexible job-shop scheduling problems. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2002, 32, 1–13. [Google Scholar] [CrossRef]
- Xie, J.; Gao, L.; Peng, K.; Li, X.; Li, H. Review on flexible job shop scheduling. IET Collab. Intell. Manuf. 2019, 1, 67–77. [Google Scholar] [CrossRef]
- Coupvent des Graviers, M.E.; Kobrosly, L.; Guettier, C.; Cazenave, T. Updating Lower and Upper Bounds for the Job-Shop Scheduling Problem Test Instances. arXiv 2025, arXiv:2504.16106. [Google Scholar]
- Wang, D.; Zhang, Y.; Zhang, K.; Li, J.; Li, D. Discrete Differential Evolution Particle Swarm Optimization Algorithm for Energy Saving Flexible Job Shop Scheduling Problem Considering Machine Multi States. arXiv 2025, arXiv:2503.02180. [Google Scholar] [CrossRef]
- Kobrosly, L.; Graviers, M.E.C.d.; Guettier, C.; Cazenave, T. Adaptive Bias Generalized Rollout Policy Adaptation on the Flexible Job-Shop Scheduling Problem. arXiv 2025, arXiv:2505.08451. [Google Scholar] [CrossRef]
- Osaba, E.; Delgado, I.P.; Ali, A.M.; Miranda-Rodriguez, P.; de Leceta, A.M.F.; Rivas, L.C. Quantum Computing in Industrial Environments: Where Do We Stand and Where Are We Headed? arXiv 2025, arXiv:2505.00891. [Google Scholar] [CrossRef]
- Rihane, K.; Dabah, A.; AitZai, A. Learning-Based Approaches for Job Shop Scheduling Problems: A Review. arXiv 2025, arXiv:2505.04246. [Google Scholar] [CrossRef]
- Ferreira, C. Gene expression programming: A new adaptive algorithm for solving problems. arXiv 2001, arXiv:cs/0102027. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Xu, T.; Xu, S.; Chen, X.; Chen, F.; Li, H. Multi-core token mixer: A novel approach for underwater image enhancement. Mach. Vis. Appl. 2025, 36, 37. [Google Scholar] [CrossRef]
- Gu, X.; Huang, M.; Liang, X. An improved genetic algorithm with adaptive variable neighborhood search for FJSP. Algorithms 2019, 12, 243. [Google Scholar] [CrossRef]
- Mathew, A.; Roy, A.; Mathew, J. Intelligent Residential Energy Management System using Deep Reinforcement Learning. IEEE Syst. J. 2020, 14, 5362–5372. [Google Scholar] [CrossRef]
- Nie, L.; Gao, L.; Li, P.; Li, X. A GEP-based reactive scheduling policies constructing approach for dynamic flexible job shop scheduling problem with job release dates. J. Intell. Manuf. 2013, 24, 763–774. [Google Scholar] [CrossRef]
- Abgaryan, H.; Cazenave, T.; Harutyunyan, A. Starjob: Dataset for LLM-Driven Job Shop Scheduling. arXiv 2025, arXiv:2503.01877. [Google Scholar]
- Liao, Z.; Chen, J.; Wang, D.; Zhang, Z.; Wang, J. BOPO: Neural Combinatorial Optimization via Best-anchored and Objective-guided Preference Optimization. arXiv 2025, arXiv:2503.07580. [Google Scholar]
- Corrêa, A.; Jesus, A.; Silva, C.; Moniz, S. Unraveling the Rainbow: Can value-based methods schedule? arXiv 2025, arXiv:2505.03323. [Google Scholar] [CrossRef]
- Chang, E.Y.; Geng, L. ALAS: A Stateful Multi-LLM Agent Framework for Disruption-Aware Planning. arXiv 2025, arXiv:2505.12501. [Google Scholar]
- Forniés-Tabuenca, D.; Uribe, A.; Otamendi, U.; Artetxe, A.; Rivera, J.C.; de Lacalle, O.L. REMoH: A Reflective Evolution of Multi-objective Heuristics approach via Large Language Models. arXiv 2025, arXiv:2506.07759. [Google Scholar]
- Sutton, R.S.; McAllester, D.; Singh, S.; Mansour, Y. Policy gradient methods for reinforcement learning with function approximation. Adv. Neural Inf. Process. Syst. 1999, 12, 1057–1063. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Brandimarte, P. Routing and scheduling in a flexible job shop by tabu search. Ann. Oper. Res. 1993, 41, 157–183. [Google Scholar] [CrossRef]
- Dauzère-Pérès, S.; Paulli, J. An integrated approach for modeling and solving the general multiprocessor job-shop scheduling problem using tabu search. Ann. Oper. Res. 1997, 70, 281–306. [Google Scholar] [CrossRef]
- Taillard, E. Benchmarks for basic scheduling problems. Eur. J. Oper. Res. 1993, 64, 278–285. [Google Scholar] [CrossRef]
- Demirkol, E.; Mehta, S.; Uzsoy, R. Benchmarks for shop scheduling problems. Eur. J. Oper. Res. 1998, 109, 137–141. [Google Scholar] [CrossRef]
- Lawrence, S. Resouce Constrained Project Scheduling: An Experimental Investigation of Heuristic Scheduling Techniques (Supplement); Graduate School of Industrial Administration, Carnegie-Mellon University: Pittsburgh, PA, USA, 1984. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).