Evaluation of Multilevel Thresholding in Differentiating Various Small-Scale Crops Based on UAV Multispectral Imagery
Abstract
1. Introduction
2. Materials and Methods
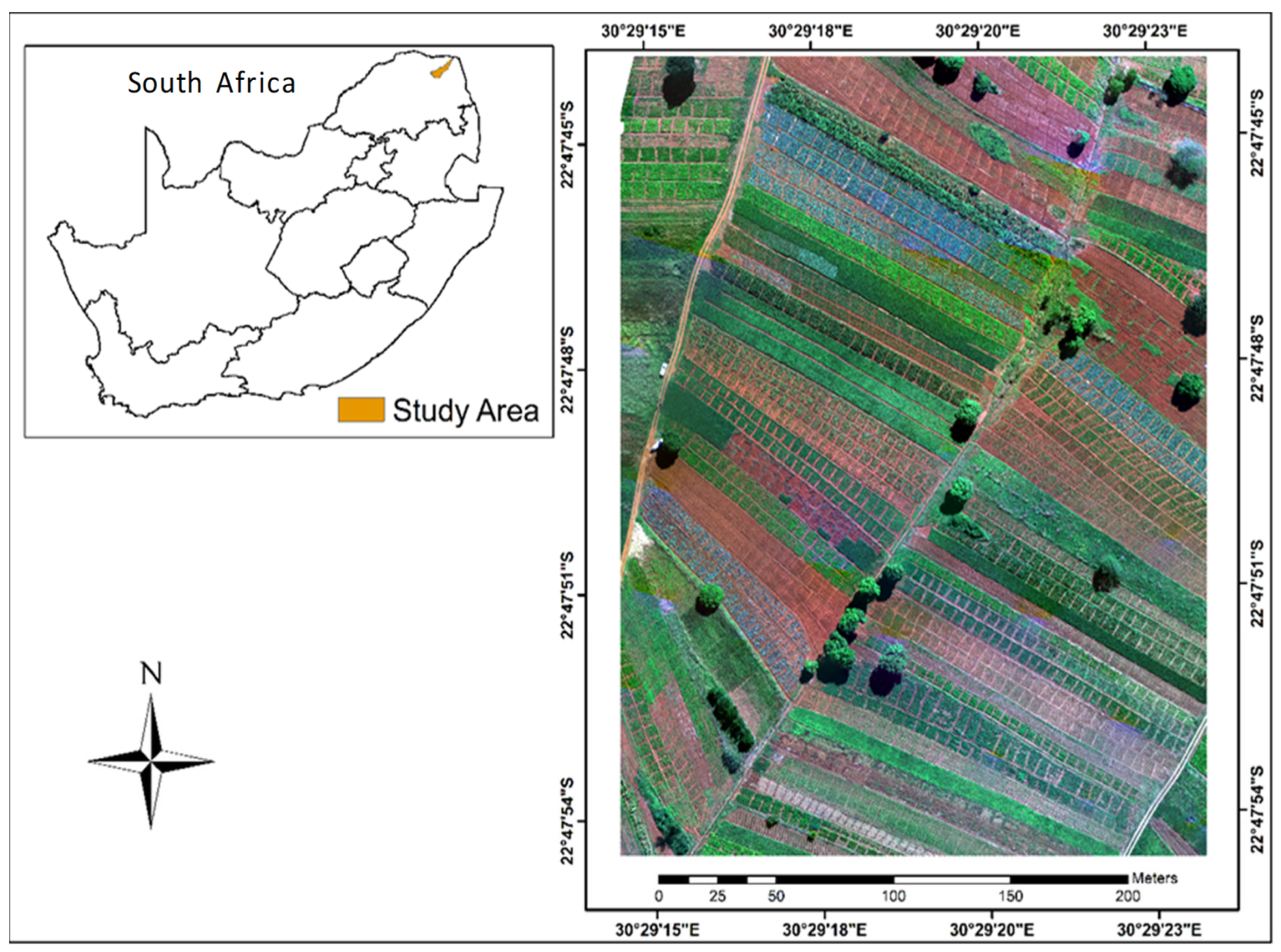
2.1. Study Area
2.2. Data Acquisition
2.2.1. UAV Multispectral Imagery
2.2.2. Field Spectrometry Data
2.3. UAV Imagery Preparation
2.4. Assessing Variability in the UAV Spectral Radiance Properties of Crops
2.5. Spectral Profiling of UAV Spectral Radiance Properties of Crops
2.6. Crop Spectral Reflectance Thresholding Selection
2.7. Multilevel Thresholding of Crop Types
2.8. Classification of Crops Using Machine Learning Algorithms
2.9. Classification Accuracy Assessment
3. Results
3.1. Identification of Crops Cultivated in the Study Site
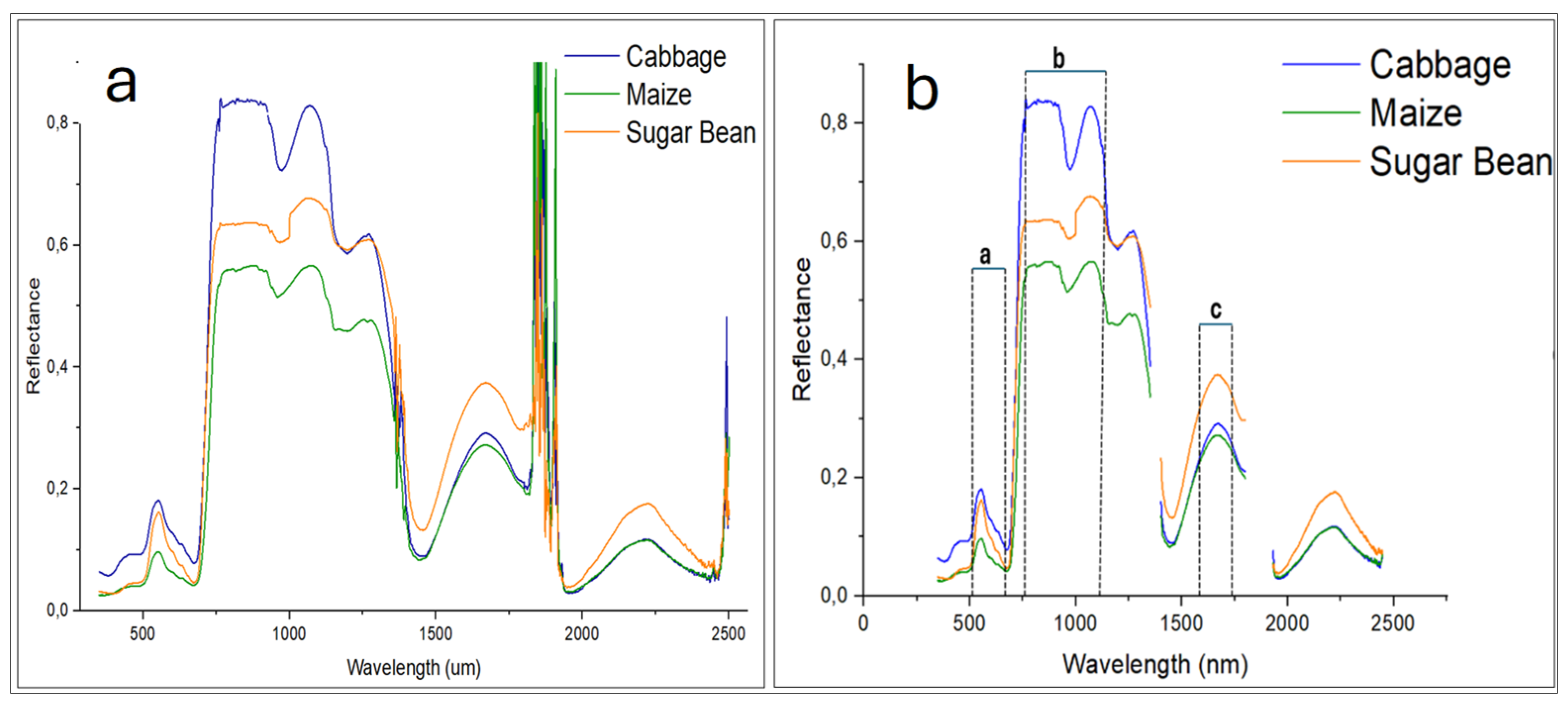
3.2. Spectral Characterization of Crops from UAV Imagery
3.3. Hyperspectral Reflectance Patterns of the Identified Crops
3.4. Reflectance Behavior of Maize Cultivars in ASD Spectral Regions Corresponding to the UAV Spectral Wavelengths
3.5. Reflectance , , and for the Surveyed Crops
3.6. Optimized Threshold Values Selected from 0.443 µm–0.507 µm and 0.533 µm–0.587 µm Wavelengths
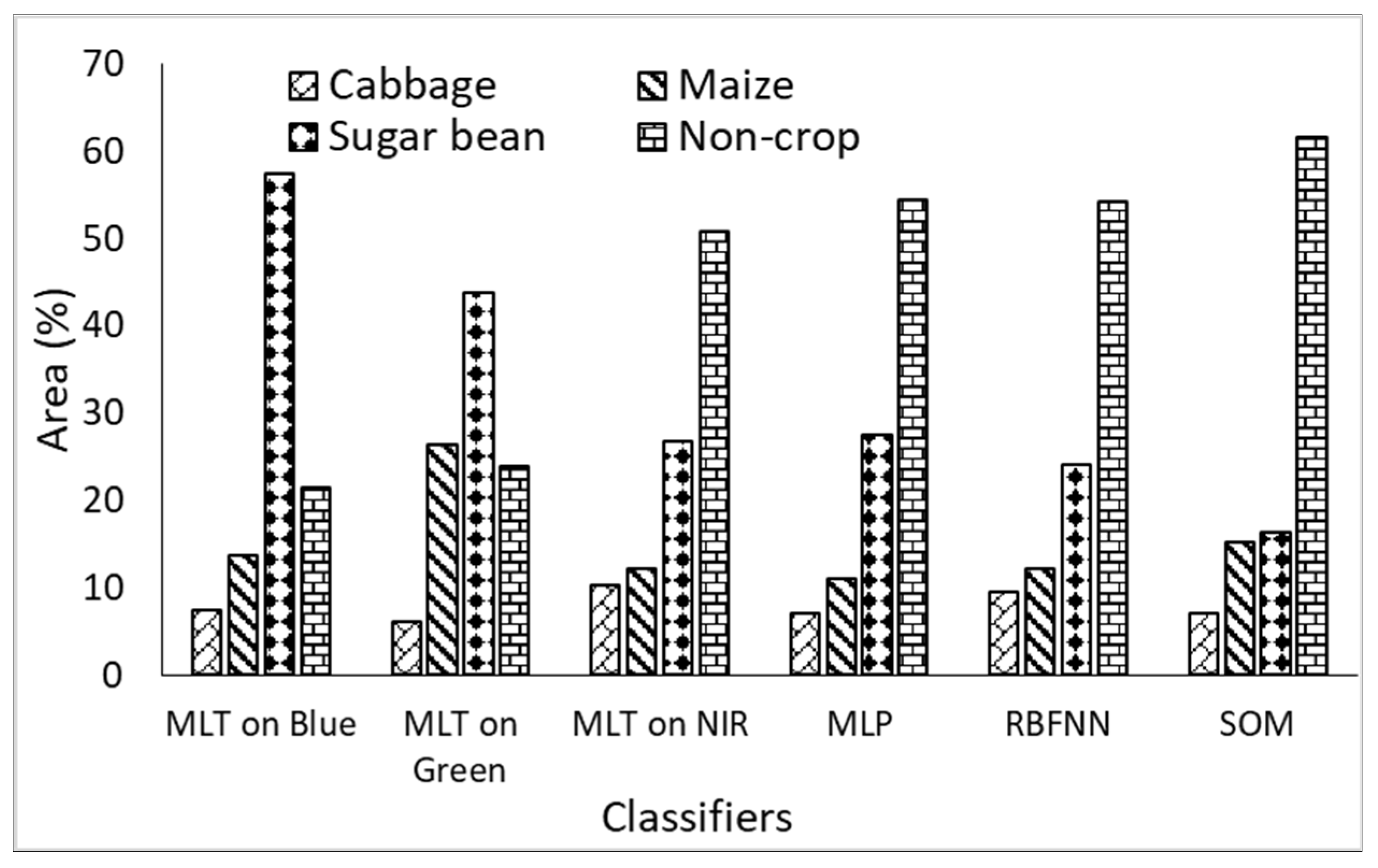
3.7. Area Determination of the Surveyed Crops
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Kwak, G.H.; Park, N.W. Impact of texture information on crop classification with machine learning and UAV images. Appl. Sci. 2019, 9, 643. [Google Scholar] [CrossRef]
- Zhao, H.; Meng, J.; Shi, T.; Zhang, X.; Wang, Y.; Luo, X.; Lin, Z.; You, X. Validating the Crop Identification Capability of the Spectral Variance at Key Stages (SVKS) Computed via an Object Self-Reference Combined Algorithm. Remote Sens. 2022, 14, 6390. [Google Scholar] [CrossRef]
- Delrue, J.; Bydekerke, L.; Eerens, H.; Gilliams, S.; Piccard, I.; Swinnen, E. Crop mapping in countries with small-scale farming: A case study for West Shewa, Ethiopia. Int. J. Remote Sens. 2013, 34, 2566–2582. [Google Scholar] [CrossRef]
- Omia, E.; Bae, H.; Park, E.; Kim, M.S.; Baek, I.; Kabenge, I.; Cho, B.K. Remote sensing in field crop monitoring: A comprehensive review of Sensor Systems, Data Analyses and Recent Advances. Remote Sens. 2023, 15, 354. [Google Scholar] [CrossRef]
- Meng, X.; Li, C.; Li, J.; Li, X.; Guo, F.; Xiao, Z. Yolov7-ma: Improved yolov7-based wheat head detection and counting. Remote Sens. 2023, 15, 3770. [Google Scholar] [CrossRef]
- Pareeth, S.; Karimi, P.; Shafiei, M.; De Fraiture, C. Mapping Agricultural Landuse Patterns from Time Series of Landsat 8 Using Random Forest Based Hierarchial Approach. Remote Sens. 2019, 11, 601. [Google Scholar] [CrossRef]
- Fang, H.; Wu, B.; Liu, H.; Huang, X. Using NOAA AVHRR and LandsatTM to estimate rice area year-by-year. Remote Sens. Tech. 1997, 12, 23–26. [Google Scholar]
- Serbin, G.; Hunt, E.R., Jr.; Daughtry, C.S.T.; McCarty, G.W.; Doraiswamy, P.C. An Improved ASTER Index for Remote Sensing of Crop Residue. Remote Sens. 2009, 1, 971–991. [Google Scholar] [CrossRef]
- Navarro, A.; Rolim, J.; Miguel, I.; Catalão, J.; Silva, J.; Painho, M.; Vekerdy, Z. Crop Monitoring Based on SPOT-5 Take-5 and Sentinel-1A Data for the Estimation of Crop Water Requirements. Remote Sens. 2016, 8, 525. [Google Scholar] [CrossRef]
- Bautista, S.A.; Fita, D.; Franch, B.; Castiñeira-Ibáñez, S.; Arizo, P.; Sánchez-Torres, M.J.; Becker-Reshef, I.; Uris, A.; Rubio, C. Crop Monitoring Strategy Based on Remote Sensing Data (Sentinel-2 and Planet), Study Case in a Rice Field after Applying Glycinebetaine. Agronomy 2022, 12, 708. [Google Scholar] [CrossRef]
- Mndela, Y.; Ndou, N.; Nyamugama, A. Irrigation Scheduling for Small-Scale Crops Based on Crop Water Content Patterns Derived from UAV Multispectral Imagery. Sustainability 2023, 15, 12034. [Google Scholar] [CrossRef]
- Delavarpour, N.; Koparan, C.; Nowatzki, J.; Bajwa, S.; Sun, X. A technical study on UAV characteristics for precision agriculture applications and associated practical challenges. Remote Sens. 2021, 13, 1204. [Google Scholar] [CrossRef]
- Devia, C.A.; Rojas, J.P.; Petro, E.; Martinez, C.; Mondragon, I.F.; Patiño, D.; Rebolledo, M.C.; Colorado, J. High-throughput biomass estimation in rice crops using UAV multispectral imagery. J. Intell. Robot. Syst. 2019, 96, 573–589. [Google Scholar] [CrossRef]
- Liu, L.; Liu, M.; Guo, Q.; Liu, D.; Peng, Y. MEMS Sensor Data Anomaly Detection for the UAV Flight Control Subsystem. In Proceedings of the 2018 IEEE SENSORS, New Delhi, India, 28–31 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Sona, G.; Passoni, D.; Pinto, L.; Pagliari, D.; Masseroni, D.; Ortuani, B.; Facchi, A. UAV multispectral survey to map soil and crop for precision farming applications. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 1023–1029. [Google Scholar] [CrossRef]
- Shin, J.; Cho, Y.; Lee, H.; Yoon, S.; Ahn, H.; Park, C.; Kim, T. An optimal image selection method to improve quality of relative radiometric calibration for UAV multispectral images. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 43, 493–498. [Google Scholar] [CrossRef]
- Li, M.; Zang, S.; Zhang, B.; Li, S.; Wu, C. A review of remote sensing image classification techniques: The role of spatio-contextual information. Eur. J. Remote Sens. 2014, 47, 389–411. [Google Scholar] [CrossRef]
- Verde, N.; Mallinis, G.; Tsakiri-Strati, M.; Georgiadis, C.; Patias, P. Assessment of Radiometric Resolution Impact on Remote Sensing Data Classification Accuracy. Remote Sens. 2018, 10, 1267. [Google Scholar] [CrossRef]
- Sisodia, P.S.; Tiwari, V.; Kumar, A. Analysis of supervised maximum likelihood classification for remote sensing image. In Proceedings of the International Conference on Recent Advances and Innovations in Engineering (ICRAIE-2014), Jaipur, India, 9–11 May 2014; IEEE: Piscataway, NJ, USA; pp. 1–4. [Google Scholar]
- Song, D.; Liu, B.; Li, X.; Chen, S.; Li, L.; Ma, M.; Zhang, Y. Hyperspectral data spectrum and texture band selection based on the subspace-rough set method. Int. J. Remote Sens. 2015, 36, 2113–2128. [Google Scholar] [CrossRef]
- Snevajs, H.; Charvat, K.; Onckelet, V.; Kvapil, J.; Zadrazil, F.; Kubickova, H.; Seidlova, J.; Batrlova, I. Crop detection using time series of sentinel-2 and sentinel-1 and existing land parcel information systems. Remote Sens. 2022, 14, 1095. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Kerner, H.; Nakalembe, C.; Becker-Reshef, I. Field-level crop type classification with k nearest neighbors: A baseline for a new Kenya smallholder dataset. arXiv 2020, arXiv:2004.03023. [Google Scholar] [CrossRef]
- Htitiou, A.; Boudhar, A.; Lebrini, Y.; Hadria, R.; Lionboui, H.; Elmansouri, L.; Tychon, B.; Benabdelouahab, T. The performance of random forest classification based on phenological metrics derived from Sentinel-2 and Landsat 8 to map crop cover in an irrigated semi-arid region. Remote Sens. Earth Syst. Sci. 2019, 2, 208–224. [Google Scholar] [CrossRef]
- Lago-Ferna’ndez, L.; Corbacho, F. Normality-based validation for crisp clustering. Pattern Recognit. 2010, 43, 782–795. [Google Scholar] [CrossRef]
- Cunnick, H.; Ramage, J.M.; Magness, D.; Peters, S.C. Mapping Fractional Vegetation Coverage across Wetland Classes of Sub-Arctic Peatlands Using Combined Partial Least Squares Regression and Multiple Endmember Spectral Unmixing. Remote Sens. 2023, 15, 1440. [Google Scholar] [CrossRef]
- Li, Z.; Chen, J.; Rahardja, S. Kernel-Based Nonlinear Spectral Unmixing with Dictionary Pruning. Remote Sens. 2019, 11, 529. [Google Scholar] [CrossRef]
- Bangira, T.; Alfieri, S.M.; Menenti, M.; van Niekerk, A.; Vekerdy, Z. A Spectral Unmixing Method with Ensemble Estimation of Endmembers: Application to Flood Mapping in the Caprivi Floodplain. Remote Sens. 2017, 9, 1013. [Google Scholar] [CrossRef]
- Ahmad, U.; Nasirahmadi, A.; Hensel, O.; Marino, S. Technology and data fusion methods to enhance site-specific crop monitoring. Agronomy 2022, 3, 555. [Google Scholar] [CrossRef]
- Shao, Y.; Lan, J. A Spectral Unmixing Method by Maximum Margin Criterion and Derivative Weights to Address Spectral Variability in Hyperspectral Imagery. Remote Sens. 2019, 11, 1045. [Google Scholar] [CrossRef]
- Heinz, D.C.; Chang, C. Fully constrained least squares linear spectral mixture analysis method for material quantification in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2002, 39, 529–545. [Google Scholar] [CrossRef]
- Zhan, Y.; Meng, Q.; Wang, C.; Li, J.; Li, D. Fractional vegetation cover estimation over large regions using GF-1 satellite data. Proc. Spie Int. Soc. Opt. Eng. 2014, 9260, 819–826. [Google Scholar]
- Chen, F.; Wang, K.; Tang, T.F. Spectral Unmixing Using a Sparse Multiple-Endmember Spectral Mixture Model. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5846–5861. [Google Scholar] [CrossRef]
- Averbuch, A.; Zheludev, M. Two linear unmixing algorithms to recognize targets using supervised classification and orthogonal rotation in airborne hyperspectral images. Remote Sens. 2012, 4, 532–560. [Google Scholar] [CrossRef]
- Zhao, D.; Eyre, J.X.; Wilkus, E.; de Voil, P.; Broad, I.; Rodriguez, D. 3D characterization of crop water use and the rooting system in field agronomic research. Comput. Electron. Agric. 2022, 202, 107409. [Google Scholar] [CrossRef]
- Li, S.; Li, F.; Gao, M.; Li, Z.; Leng, P.; Duan, S.; Ren, J. A new method for winter wheat mapping based on spectral reconstruction technology. Remote Sens. 2021, 13, 1810. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Chen, Y. Modifications of the Multi-Layer Perceptron for Hyperspectral Image Classification. Remote Sens. 2021, 13, 3547. [Google Scholar] [CrossRef]
- Tsoulos, I.G.; Varvaras, I.; Charilogis, V. RbfCon: Construct Radial Basis Function Neural Networks with Grammatical Evolution. Software 2024, 3, 549–568. [Google Scholar] [CrossRef]
- Fan, X.; Zhang, S.; Xue, X.; Jiang, R.; Fan, S.; Kou, H. An Improved Self-Organizing Map (SOM) Based on Virtual Winning Neurons. Symmetry 2025, 17, 449. [Google Scholar] [CrossRef]
- Jardim, S.; António, J.; Mora, C. Image thresholding approaches for medical image segmentation-short literature review. Procedia Comput. Sci. 2023, 219, 1485–1492. [Google Scholar] [CrossRef]
- Lu, T.; Wan, L.; Wang, L. Fine crop classification in high resolution remote sensing based on deep learning. Front. Environ. Sci. 2022, 10, 991173. [Google Scholar] [CrossRef]
- Zhao, H.; Chen, Z.; Jiang, H.; Jing, W.; Sun, L.; Feng, M. Evaluation of Three Deep Learning Models for Early Crop Classification Using Sentinel-1A Imagery Time Series—A Case Study in Zhanjiang, China. Remote Sens. 2019, 11, 2673. [Google Scholar] [CrossRef]
- Ewees, A.A.; Abualigah, L.; Yousri, D.; Sahlol, A.T.; Al-qaness, M.A.A.; Alshathri, S.; Elaziz, A. Modified Artificial Ecosystem-Based Optimization for Multilevel Thresholding Image Segmentation. Mathematics 2021, 9, 2363. [Google Scholar] [CrossRef]
- Hernández Molina, D.D.; Gulfo-Galaraga, J.M.; López-López, A.M.; Serpa-Imbett, C.M. Methods for estimating agricultural cropland yield based on the comparison of NDVI images analyzed by means of Image segmentation algorithms: A tool for spatial planning decisions. Ingeniare Rev. Chil. De Ing. 2023, 31, 24. Available online: https://www.scielo.cl/pdf/ingeniare/v31/0718-3305-ingeniare-31-24.pdf (accessed on 20 July 2025). [CrossRef]
- Hosny, K.M.; Khalid, A.M.; Hamza, H.M.; Mirjalili, S. Multilevel thresholding satellite image segmentation using chaotic coronavirus optimization algorithm with hybrid fitness function. Neural Comput. Appl. 2023, 35, 855–886. [Google Scholar] [CrossRef] [PubMed]
- Sharp, K.G.; Bell, J.R.; Pankratz, H.G.; Schultz, L.A.; Lucey, R.; Meyer, F.J.; Molthan, A.L. Modifying NISAR’s Cropland Area Algorithm to Map Cropland Extent Globally. Remote Sens. 2025, 17, 1094. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, A.; Vishwakarma, A. Multilevel Thresholding of Grayscale Complex Crop Images using Minimum Cross Entropy. In Proceedings of the 2023 10th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 23–24 March 2023; pp. 806–810. [Google Scholar] [CrossRef]
- Bangira, T.; Alfieri, S.M.; Menenti, M.; van Niekerk, A. Comparing Thresholding with Machine Learning Classifiers for Mapping Complex Water. Remote Sens. 2019, 11, 1351. [Google Scholar] [CrossRef]
- Kapur, J.N.; Sahoo, P.K.; Wong, A.K.C. A new method for gray-level picture thresholding using the entropy of the histogram. Comput. Vis. Graph. Image Process. 1985, 29, 273–285. [Google Scholar] [CrossRef]
- Wu, B.; Zhou, J.; Ji, X.; Yin, Y.; Shen, X. An ameliorated teaching–learning-based optimization algorithm-based study of image segmentation for multilevel thresholding using Kapur’s entropy and Otsu’s between class variance. Inf. Sci. 2020, 533, 72–107. [Google Scholar] [CrossRef]
- Eisham, Z.K.; Haque, M.M.; Rahman, M.S.; Nishat, M.M.; Faisal, F.; Islam, M.R. Chimp optimization algorithm in multilevel image thresholding and image clustering. Evol. Syst. 2023, 14, 605–648. [Google Scholar] [CrossRef]
- Akgün, A.; Eronat, A.H.; Türk, N. Comparing Different Satellite Image Classification Methods: An Application in Ayvalik District, Western Turkey. In Proceedings of the 20th ISPRS Congress Technical Commission IV, Istanbul, Turkey, 12–23 July 2004; pp. 1091–1097. Available online: http://www.isprs.org/proceedings/xxxv/congress/comm4/papers/505.pdf (accessed on 10 July 2025).
- Li, X.; Zou, Y. Multi-Level Thresholding Based on Composite Local Contour Shannon Entropy Under Multiscale Multiplication Transform. Entropy 2025, 27, 544. [Google Scholar] [CrossRef]
- Kang, X.; Hua, C. Multilevel thresholding image segmentation algorithm based on Mumford–Shah model. J. Intell. Syst. 2023, 32, 20220290. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Sumari, P.; Gandomi, A.H. A Novel Evolutionary Arithmetic Optimization Algorithm for Multilevel Thresholding Segmentation of COVID-19 CT Images. Processes 2021, 9, 1155. [Google Scholar] [CrossRef]
- Bao, X.; Jia, H.; Lang, C. Dragonfly Algorithm with Opposition-Based Learning for Multilevel Thresholding Color Image Segmentation. Symmetry 2019, 11, 716. [Google Scholar] [CrossRef]
- Levene, H. Robust testes for equality of variances. In Contributions to Probability and Statistics; Olkin, I., Ed.; MR0120709; Stanford University Press: Palo Alto, CA, USA, 1960; pp. 278–292. [Google Scholar]
- Tukey, J.W. Exploratory Data Analysis; Addison-Wesley: Reading, MA, USA, 1977; Volume 2. [Google Scholar]
- Bardet, J.-M.; Dimby, S.-F. A new non-parametric detector of univariate outliers for distributions with unbounded support. Extremes 2017, 20, 751–775. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, D.; Zhu, W.; Wang, L. Multi-Level Thresholding Image Segmentation Based on Improved Slime Mould Algorithm and Symmetric Cross-Entropy. Entropy 2023, 25, 178. [Google Scholar] [CrossRef] [PubMed]
- Almeida, L.B. Multilayer perceptrons. In Handbook of Neural Computatio; IOP Publishing Ltd.: Bristol, UK; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Powell, M.J.D. Radial basis functions for multivariate interpolation: A review. In IMA Conference on Algorithms for the Approximation of Functions and Data; RMCS: Shrivenham, UK, 1985; pp. 143–167. [Google Scholar]
- Duda, R.O.; Hart, P.E. Pattern Classification; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Kohonen, T. The Self-Organizing Map; IEEE: Piscataway, NJ, USA, 1990; Volume 78, pp. 1464–1480. [Google Scholar] [CrossRef]
- Kangas, J.; Kohonen, T.; Laaksonen, J. Variants of self-organizing maps. IEEE Trans. Neural Netw. 1990, 1, 93–99. [Google Scholar] [CrossRef] [PubMed]
- Cohen, J. A coefficient of agreement for nominal scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Li, M.; Shamshiri, R.R.; Weltzien, C.; Schirrmann, M. Crop Monitoring Using Sentinel-2 and UAV Multispectral Imagery: A Comparison Case Study in Northeastern Germany. Remote Sens. 2022, 14, 4426. [Google Scholar] [CrossRef]
- Vidican, R.; Mălinaș, A.; Ranta, O.; Moldovan, C.; Marian, O.; Ghețe, A.; Ghișe, C.R.; Popovici, F.; Cătunescu, G.M. Using Remote Sensing Vegetation Indices for the Discrimination and Monitoring of Agricultural Crops: A Critical Review. Agronomy 2023, 13, 3040. [Google Scholar] [CrossRef]
- Lin, Y.C.; Habib, A. Quality control and crop characterization framework for multi-temporal UAV LiDAR data over mechanized agricultural fields. Remote Sens. Environ. 2021, 256, 112299. [Google Scholar] [CrossRef]
- Ndou, N.; Thamaga, K.H.; Mndela, Y.; Nyamugama, A. Radiometric Compensation for Occluded Crops Imaged Using High-Spatial-Resolution Unmanned Aerial Vehicle System. Agriculture 2023, 13, 1598. [Google Scholar] [CrossRef]
- Baio, F.H.; Santana, D.C.; Teodoro, L.P.; Oliveira, I.C.; Gava, R.; de Oliveira, J.L.; Silva Junior, C.A.; Teodoro, P.E.; Shiratsuchi, L.S. Maize yield prediction with machine learning, spectral variables and irrigation management. Remote Sens. 2022, 15, 79. [Google Scholar] [CrossRef]
- Xue, J.; Su, B. Significant remote sensing vegetation indices: A review of developments and applications. J. Sens. 2017, 2017, 1353691. [Google Scholar] [CrossRef]
- Torres, R.M.; Yuen, P.W.T.; Yuan, C.; Piper, J.; McCullough, C.; Godfree, P. Spatial Spectral Band Selection for Enhanced Hyperspectral Remote Sensing Classification Applications. J. Imaging 2020, 6, 87. [Google Scholar] [CrossRef]
- Curran, P.J. Remote sensing of foliar chemistry. Remote Sens. Environ. 1989, 30, 271–278. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Mariotto, I.; Gumma, M.K.; Middleton, E.M.; Landis, D.R.; Huemmrich, K.F. Selection of hyperspectral narrowbands (HNBs) and composition of hyperspectral twoband vegetation indices (HVIs) for biophysical characterization and discrimination of crop types using field reflectance and Hyperion/EO-1 data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 427–439. [Google Scholar] [CrossRef]
- Potgieter, A.B.; Zhao, Y.; Zarco-Tejada, P.J.; Chenu, K.; Zhang, Y.; Porker, K.; Biddulph, B.; Dang, Y.P.; Neale, T.; Roosta, F.; et al. Evolution and application of digital technologies to predict crop type and crop phenology in agriculture. In Silico Plants 2021, 3, diab017. [Google Scholar] [CrossRef]
- Durañona Sosa, N.L.; Vázquez Noguera, J.L.; Cáceres Silva, J.J.; García Torres, M.; Legal-Ayala, H. RGB Inter-Channel Measures for Morphological Color Texture Characterization. Symmetry 2019, 11, 1190. [Google Scholar] [CrossRef]
- Miller, R.G., Jr. Jacknifing variances. Ann. Math. Statist. 1968, 39, 567–582. [Google Scholar] [CrossRef]
- Gastwirth, J.L.; Gel, Y.R.; Miao, W. The Impact of Levene’s Test of Equality of Variances on Statistical Theory and Practice. Stat. Sci. 2009, 24, 343–360. [Google Scholar] [CrossRef]
- Angulo, L.; Pamboukian, S. Spectral Behavior of Maize, Rice, Soy, and Oat Crops Using Multi-Spectral Images from Sentinel-2. In Proceedings of the 5th Brazilian Technology Symposium: Emerging Trends, Issues, and Challenges in the Brazilian Technology, Campinas, Brazil, 23–25 October 2018; Springer International Publishing: Cham, Switzerland, 2021; Volume 2, pp. 327–336. [Google Scholar]
- Zhao, D.; Raja Reddy, K.; Kakani, V.G.; Read, J.J.; Carter, G.A. Corn (Zea mays L.) growth, leaf pigment concentration, photosynthesis and leaf hyperspectral reflectance properties as affected by nitrogen supply. Plant Soil 2003, 257, 205–218. [Google Scholar] [CrossRef]
- Sudu, B.; Rong, G.; Guga, S.; Li, K.; Zhi, F.; Guo, Y.; Zhang, J.; Bao, Y. Retrieving SPAD values of summer maize using UAV hyperspectral data based on multiple machine learning algorithm. Remote Sens. 2022, 14, 5407. [Google Scholar] [CrossRef]
- Jumiawi, W.A.; El-Zaart, A. Otsu Thresholding model using heterogeneous mean filters for precise images segmentation. In Proceedings of the 2022 International Conference of Advanced Technology in Electronic and Electrical Engineering (ICATEEE), M’sila, Algeria, 26–27 November 2022; IEEE: Piscataway, NJ, USA; pp. 1–6. [Google Scholar]
- Mahmoud, E.; Alkhalaf, S.; Senjyu, T.; Furukakoi, M.; Hemeida, A.; Abozaid, A. GAAOA-Lévy: A hybrid metaheuristic for optimized multilevel thresholding in image segmentation. Sci. Rep. 2025, 15, 27232. [Google Scholar] [CrossRef] [PubMed]
- Houssein, E.H.; Mohamed, G.M.; Ibrahim, I.A.; Wazery, Y.M. An efficient multilevel image thresholding method based on improved heap-based optimizer. Sci. Rep. 2023, 13, 9094. [Google Scholar] [CrossRef] [PubMed]
- Komadina, A.; Martinić, M.; Groš, S.; Mihajlović, Z. Comparing Threshold Seletion Methods for Network Anomaly Detection. IEEE Access 2024, 12, 124943–124973. [Google Scholar] [CrossRef]
- Rodríguez-Esparza, E.; Zanella-Calzada, L.A.; Oliva, D.; Heidari, A.A.; Zaldivar, D.; Pérez-Cisneros, M.; Foong, L.K. An efficient Harris hawks-inspired image segmentation method. Expert Syst. Appl. 2020, 155, 113428. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, L.; Yu, F.; Heidari, A.A.; Wang, M.; Oliva, D.; Muhammad, K.; Chen, H. Ant colony optimization with horizontal and vertical crossover search: Fundamental visions for multi-threshold image segmentation. Expert Syst. Appl. 2020, 167, 114122. [Google Scholar] [CrossRef]
- Zhou, T.; Fu, H.; Sun, C.; Wang, S. Shadow Detection and Compensation from Remote Sensing Images under Complex Urban Conditions. Remote Sens. 2021, 13, 699. [Google Scholar] [CrossRef]
- Hlaing, S.H.; Khaing, A.S. Weed and crop segmentation and classification using area thresholding. IJRET Int. J. Res. Eng. Technol. 2014, 3, 375–382. Available online: https://scispace.com/pdf/weed-and-crop-segmentation-and-classification-using-area-2rnuyikbqa.pdf (accessed on 20 June 2025).
- Tufail, R.; Tassinari, P.; Torreggiani, D. Assessing feature extraction, selection, and classification combinations for crop mapping using Sentinel-2 time series: A case study in northern Italy. Remote Sens. Appl. Soc. Environ. 2025, 38, 101525. [Google Scholar] [CrossRef]
- Genc, L.; Inalpulat, M.; Kizil, U.; Mirik, M.; Smith, S.E.; Mendes, E. Determination of water stress with spectral reflectance on sweet corn (Zea mays L.) using classification tree (CT) analysis. Zemdirb.-Agric. 2013, 100, 81–90. [Google Scholar] [CrossRef]
- Aitkenhead, M.J.; Dyer, R. Improving Land-cover Classification Using Recognition Threshold Neural Networks. Photogramm. Eng. Remote Sens. 2007, 73, 413–421. [Google Scholar] [CrossRef][Green Version]
- Sun, Z.; Wang, D.; Zhong, G. A Review of Crop Classification Using Satellite-Based Polarimetric SAR Imagery. In Proceedings of the7th International Conference on Agro-geoinformatics (Agro-geoinformatics), Hangzhou, China, 6–9 August 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Ma, X.; Li, L.; Wu, Y. Deep-Learning-Based Method for the Identification of Typical Crops Using Dual-Polarimetric Synthetic Aperture Radar and High-Resolution Optical Images. Remote Sens. 2025, 17, 148. [Google Scholar] [CrossRef]




| Band Name | Center (µm) | Wavelength Range (µm) |
|---|---|---|
| Blue | 0.475 | 0.443–0.507 |
| Green | 0.560 | 0.533–0.587 |
| Red | 0.668 | 0.654–0.682 |
| Red Edge | 0.717 | 0.705–0.729 |
| Near-IR | 0.842 | 0.785–0.899 |
| MLP | RBFNN | SOM | |||
| We applied the MLP to differentiate crop types as follows: Network topology: We trained the MLP for crop type characterization using five (5) UAV spectral bands as input layer nodes and two (2) hidden layers, each of which had five (5) nodes, to improve the learning process. Training parameters: We used both automatic training and dynamic learning rates to train models. The learning rate was set to 0.01, with a 0.5 momentum factor and sigmoid constant of 1. Backpropagation training: We trained the MLP for crop type differentiation using Equation (12), adopted from Almeida [62]: | We applied the RBFNN algorithm to differentiate crop types as follows: Basis functions: We used the set of the basis functions (Equation (13)) proposed by Powell [63]: | We applied the SOM algorithm to differentiate crop types as follows: is the n-dimensional feature of SOM, the neuron in the output layer with minimum distance to the input feature vector (known as the winner) is then determined as follows: | |||
| (12) | (13) | (14) | |||
| , computed using Equation (18): | . RBFNN training: The training of RBFNN for classifying crops involved two steps. The number of hidden layers were determined through the deployment of an unsupervised k-means classifier, using Equation (16) proposed by Duda and Hart [64]: | ., according to Equations (17) and (19), such that | |||
| (15) | (16) | (17) | |||
| (18) | Then, centers of the RBFs were aligned with the centers of the clusters from the k-means results, using Equations (20) and (23): | (19) | |||
| was computed in Equation (12). The number of hidden layer nodes used in this study were estimated using Equation (13): | (20) | and is obtained by deploying Equation (22), adopted from Kohonen [65]: | |||
| (21) | denotes the number of radial basis functions: | (22) | |||
| denotes output layer nodes.), such that | (23) | Fine tuning: We applied fine tuning to optimize the decision boundaries between crop classes based on the training data. We used the learning vector quantization (LVQ) proposed by Kangas et al. [66]. If x is correctly classified, then | |||
| (24) | is the radial basis function, computed using Equation (26): | (25) | |||
| denotes the mean value of the measured values. | (26) | If x is incorrectly classified, then | |||
| . | (27) | ||||
| Otherwise | |||||
| (28) | |||||
| denotes a gain term, which decreases as time decreases. | |||||
| Blue | Green | Red | |||||||
| Cabbage | Maize | Sug. bean | Cabbage | Maize | Sug. bean | Cabbage | Maize | Sug. bean | |
| N | 200 | 200 | 200 | 200 | 200 | 200 | 200 | 200 | 200 |
| α | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 |
| μ | 0.34 | 0.45 | 0.36 | 0.42 | 0.62 | 0.49 | 0.25 | 0.33 | 0.25 |
| σ | 0.11 | 0.14 | 0.09 | 0.12 | 0.11 | 0.07 | 0.09 | 0.06 | 0.08 |
| Var. | 0.01 | 0.02 | 0.1 | 0.01 | 0.01 | 0.01 | 002 | 0.02 | 0.01 |
| Min. | 0.23 | 0.089 | 0.247 | 0.209 | 0.164 | 0.319 | 0.166 | 0.141 | 0.113 |
| Max. | 0.855 | 0.376 | 0.413 | 0.966 | 0.833 | 0.811 | 0.617 | 0.792 | 0.327 |
| p-value | <0.001 | <0.001 | <0.001 | ||||||
| Red edge | NIR | ||||||||
| Cabbage | Maize | Sug. bean | Cabbage | Maize | Sug. bean | ||||
| N | 200 | 200 | 200 | 200 | 200 | 200 | |||
| α | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | |||
| μ | 0.55 | 063 | 0.67 | 0.72 | 0.70 | 0.68 | |||
| σ | 0.11 | 0.09 | 0.12 | 0.06 | 0.11 | 0.11 | |||
| Var. | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | |||
| Min. | 0.37 | 0.15 | 0.46 | 0.41 | 0.341 | 0.46 | |||
| Max. | 0.94 | 0.88 | 0.89 | 0.93 | 0.91 | 0.92 | |||
| p-value | <0.001 | <0.001 | |||||||
| 0.443 µm–0.507 µm | 0.533 µm–0.587 µm | 0.654 µm–0.682 µm | |||||||
| Cabbage | Maize | Sug. bean | Cabbage | Maize | Sug. bean | Cabbage | Maize | Sug. bean | |
| N | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| α | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 |
| μ | 0.38 | 0.48 | 0.34 | 0.39 | 0.59 | 0.55 | 0.22 | 0.37 | 0.2 |
| σ | 0.12 | 0.12 | 0.05 | 0.09 | 0.12 | 0.09 | 0.06 | 0.12 | 0.03 |
| Var. | 0.01 | 0.01 | 0 | 0.01 | 0.01 | 0.01 | 0 | 0.02 | 0 |
| Min. | 0.2 | 0.21 | 0.23 | 0.22 | 0.36 | 0.36 | 0.12 | 0.16 | 0.12 |
| Max. | 0.85 | 0.83 | 0.47 | 0.98 | 0.87 | 0.85 | 0.58 | 0.8 | 0.34 |
| p-value | <0.001 | <0.001 | <0.001 | ||||||
| 0.705 µm–0.729 µm | 0.785 µm–0.899 µm | ||||||||
| Cabbage | Maize | Sug. bean | Cabbage | Maize | Sug. bean | ||||
| N | 100 | 100 | 100 | 100 | 100 | 100 | |||
| α | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | |||
| μ | 0.68 | 0.67 | 0.71 | 0.68 | 0.67 | 0.71 | |||
| σ | 0.09 | 0.07 | 0.08 | 0.09 | 0.07 | 0.08 | |||
| Var. | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | |||
| Min. | 0.41 | 0.45 | 0.46 | 0.41 | 0.45 | 0.46 | |||
| Max. | 0.97 | 0.85 | 0.95 | 0.97 | 0.85 | 0.95 | |||
| p-value | <0.001 | <0.001 | |||||||
| 0.443 µm–0.507 µm | 0.533 µm–0.587 µm | 0.785 µm–0.899 µm | |||||||
| Surveyed crops | |||||||||
| Cabbage | 0.33 | 0.43 | 0.1 | 0.18 | 0.25 | 0.07 | 0.62 | 0.75 | 0.13 |
| Maize | 0.5 | 0.68 | 0.18 | 0.29 | 0.44 | 0.17 | 0.63 | 0.72 | 0.09 |
| Sugar bean | 0.49 | 0.61 | 0.12 | 0.18 | 0.22 | 0.04 | 0.66 | 0.77 | 0.11 |
| 0.443 µm–0.507 µm | 0.533 µm–0.587 µm | 0.785 µm–0.899 µm | ||||
| Surveyed crops | ||||||
| Cabbage | 0.18 | 0.58 | 0.075 | 0.36 | 0.425 | 0.745 |
| Maize | 0.48 | 0.79 | 0.335 | 0.695 | 0.495 | 0.855 |
| Sugar bean | 0.55 | 0.95 | 0.12 | 0.28 | 0.645 | 0.935 |
| 0.443 µm–0.507 µm | 0.533 µm–0.587 µm | 0.785 µm–0.899 µm | |
| Cabbage–Maize | 0.53 | 0.348 | 0.62 |
| Maize–Sugar bean | 0.67 | 0.24 | 0.75 |
| Classifier | Overall Accuracy | KIA |
|---|---|---|
| MLT on Blue band | 0.435 | 0.372 |
| MLT on Green band | 0.333 | 0.307 |
| MLT on NIR | 0.496 | 0.488 |
| MLP | 0.594 | 0.531 |
| RBFNN | 0.662 | 0.616 |
| SOM | 0.643 | 0.659 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mfamana, S.; Ndou, N. Evaluation of Multilevel Thresholding in Differentiating Various Small-Scale Crops Based on UAV Multispectral Imagery. Appl. Sci. 2025, 15, 10056. https://doi.org/10.3390/app151810056
Mfamana S, Ndou N. Evaluation of Multilevel Thresholding in Differentiating Various Small-Scale Crops Based on UAV Multispectral Imagery. Applied Sciences. 2025; 15(18):10056. https://doi.org/10.3390/app151810056
Chicago/Turabian StyleMfamana, Sange, and Naledzani Ndou. 2025. "Evaluation of Multilevel Thresholding in Differentiating Various Small-Scale Crops Based on UAV Multispectral Imagery" Applied Sciences 15, no. 18: 10056. https://doi.org/10.3390/app151810056
APA StyleMfamana, S., & Ndou, N. (2025). Evaluation of Multilevel Thresholding in Differentiating Various Small-Scale Crops Based on UAV Multispectral Imagery. Applied Sciences, 15(18), 10056. https://doi.org/10.3390/app151810056






