Vibration Analysis of Variable-Thickness Multi-Layered Graphene Sheets

Abstract

This study investigates the vibrational characteristics of multi-layered graphene sheets with variable thickness (VTGSs) by using molecular dynamics (MD) simulations. It is aimed to determine how the natural frequencies and vibration damping ratios of variable-thickness graphene change with respect to temperature. Atomistic models for six distinct geometries (1L, 3LT, 3LTB, 5LT, 5LTB, and 9LTB) were generated to analyze the influence of structural design and temperature on their natural frequencies. The simulations were performed using the Large-Scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) with an AIREBO potential to represent interatomic carbon interactions. Natural frequencies of all atomistic models were extracted by applying the Fast Fourier Transform (FFT) method to the Velocity Autocorrelation Function (VACF) data obtained from the simulations. In addition, the analysis was conducted at three different temperatures: 250 K, 300 K, and 350 K. Key findings reveal that an increase in the number of graphene layers results in a decrease in the fundamental natural frequency due to the increased mass of the structure. Moreover, it was noted that natural frequencies decrease with increasing temperature. It is attributed to the reduction in structural rigidity at higher thermal energies. These results provide critical insights into how geometric and thermal variations affect the dynamic behavior of complex multi-layered graphene structures.

1. Introduction

Graphene, a two-dimensional material composed of a single layer of carbon atoms, has garnered significant attention in the scientific community due to its exceptional mechanical, electrical, and thermal properties [1,2,3,4]. These properties make graphene a promising candidate for a wide range of applications, including electronics, sensors, and energy storage devices [3,5]. One crucial aspect of graphene’s behavior is its vibration characteristics, which can provide insights into the material’s structural integrity and potential applications.

According to a review by Gibson et al. [6], three primary models are employed to investigate the vibrational behavior of carbon nanotubes (CNTs) and graphene: (a) Atomistic Methods: In the molecular dynamics (MD) approach, the material’s behavior is derived from the forces and energies between its constituent atoms. It treats atoms as discrete particles that interact with neighboring atoms within the material [7]. (b) Continuum Methods: In this approach, to simplify the analysis, an individual nanotube is defined as a discrete continuous beam or shell. The vibration equations of nanotubes are modeled using classical beam or shell vibration equations, such as the Euler–Bernoulli beam model. (c) Atomistic–Continuum (Hybrid) methods: The fundamental idea behind the hybrid models is to link the molecular properties derived from atomistic simulations to the macroscopic mechanical behavior described by solid mechanics, as in the FEM.

Upon reviewing the academic literature, it is evident that the mechanical and thermal properties of nanotubes have been the subject of intensive research, with a significant number of studies. However, studies on the vibrational properties of nanotubes have been comparatively limited in contrast to the focus on their other characteristics.

A comprehensive investigation of the energy, structural, mechanical, and vibrational properties of single-walled carbon nanotubes (SWNTs) through molecular mechanics and molecular dynamics methods was performed, employing an accurate interaction potential derived from quantum mechanics, presented in Ref. [8]. Zheng et al. [9] presented a comprehensive analysis of the vibrational characteristics of diamane nanosheets. Utilizing a dual-methodology approach, the study combines MD simulations with the Kirchhoff plate model to determine natural frequencies and modal shapes. Ansari et al. [10] conducted an analysis of the vibrational behavior of single-walled carbon nanocones (SWCNCs) by employing a molecular structural method and MD simulations. The investigation is focused on elucidating the influence of various parameters, including apex angle, length, and boundary conditions, on the natural frequencies of these nanostructures. Arash et al. [11] introduced an analysis of the free vibration characteristics of single-layered graphene sheets (SLGSs) and double-layered graphene sheets (DLGSs), utilizing a combined approach of nonlocal continuum theory and MD simulations. The research underscores the limitations inherent in classical elastic models when applied to nanoscale structures, thereby highlighting the necessity of employing nonlocal models for the accurate prediction of their vibrational behavior. The vibrational behavior of multi-walled carbon nanotubes (MWCNTs) embedded in an elastic medium, employing a model that incorporates the effect of intertube displacements, was analyzed by ref. [12]. Jalali et al. [13] investigated the influence of out-of-plane defects on the vibrational behavior of single-layered graphene sheets (SLGSs) by employing a dual approach that combines nonlocal elasticity theory with MD simulations. A key finding from both methodologies is that the presence of out-of-plane defects leads to an increase in the vibrational frequency of the graphene. Furthermore, the analysis demonstrates that while classical elasticity theory significantly overestimates these frequencies, the nonlocal model can be brought into good agreement with the MD simulation results when calibrated with an appropriate scale parameter. Seifoori et al. [14] simulated the impact behavior of multi-layered graphene sheets using a spring–mass analytical model that incorporates van der Waals (vdW) interactions alongside MD simulations. The analytical model is found to be in good agreement with the MD simulations, particularly for square and rectangular double-layered graphene. It was concluded that as the number of graphene layers increases, the resulting post-impact deflection and vibration are reduced due to the influence of vdW forces. Bedi et al. [15] studied the vibrational behavior of defective single-walled carbon nanotubes (SWCNTs) and graphene sheets using MD simulations. The simulations demonstrated that vacancy defects have a more pronounced effect on reducing the natural frequency compared to Stone–Wales defects. It was also concluded that the frequency decreases as the size of the structures increases, and that for SWCNTs, chirality does not have a considerable impact on the frequency. In a study conducted by Jiang et al. [16], the vibrational properties of graphene resonators containing vacancy defects are investigated using MD simulations. The simulations revealed that while the location of the defects has a negligible effect on the resonant frequency, an increase in the number of defects leads to a monotonic decrease in frequency and a corresponding monotonic increase in resonance amplitude. Mao et al. [17] investigated the vibrational characteristics of defective graphene sheets under tension using molecular dynamics. They considered perfect SLGSs, SLGSs with a single vacancy, SLGSs with low-concentration vacancies, and SLGSs with high-concentration vacancies. They observed that the frequencies of the SLGSs decreased as the vacancy concentration increased during the elastic stage. Similarly, in Ref. [18], the effects of different defect concentrations and positions on the vibration frequency of nanoribbons were investigated. It was demonstrated that both vacancy concentration and vacancy position have a certain effect on the vibration frequency of graphene nanoribbons. The study also highlighted that the trend of vibration frequency variation is similar for nanoribbons with similarly dispersed vacancies. Madani et al. [19] conducted a vibrational analysis of annular graphene sheets, achieved by determining a precise “nonlocal parameter” for the nonlocal plate theory through MD simulations. The research demonstrates that this parameter is dependent on the geometry of the graphene, such as its annular radii, and that by accurately defining it, the fidelity of the continuum model can be significantly enhanced. Huang et al. [20] employed MD simulations to investigate the influence of external factors—specifically morphology, tension, and vibration—on the wetting characteristics of graphene. The simulations demonstrate that an increase in vibrational amplitude coupled with a decrease in its period (i.e., higher frequency) also leads to the graphene becoming more hydrophobic. Rahman et al. [21] investigated the ripples that result from thermal agitation in graphene sheets of various sizes, employing MD simulations under different boundary conditions and temperatures. A primary finding of the research is that freely vibrating edges play a dominant role in dictating the shape and vibrational modes of the ripples and are capable of introducing new modes of vibration. Furthermore, it has been determined that as the size of the graphene increases, its natural vibrational frequency decreases, while the amplitude of the ripples increases. Cheng et al. [22] investigated the influence of vertical vibration on nanoscale friction by analyzing a diamond tip sliding on a two-layer graphene substrate via MD simulations. The research reveals that vibration has a dual, frequency-dependent influence on friction.

In this research paper, we investigate the vibration of graphene sheets with variable thickness using molecular dynamics simulations and Fast Fourier Transform analysis. The study of graphene sheets with variable thickness is particularly important as it reflects the practical scenarios where graphene may experience non-uniform stresses or deformations, leading to thickness variations across the material. Although a substantial body of research has been conducted on the dynamic behavior of uniform single-layer and multi-layer graphene sheets, there is a notable scarcity of studies focusing on variable-thickness graphene models. This constitutes a significant research gap, as such structures hold immense potential for the design and manufacturing of advanced nanomaterials and nanodevices. The non-uniform nature of these models necessitates a more sophisticated analysis that accounts for the variations in mass and stiffness distribution. In this context, the present study addresses this gap by conducting a comprehensive vibrational analysis of variable-thickness graphene sheets (VTGSs). Unlike prior work on uniform sheets, our analysis reveals how the non-uniform distribution of mass and stiffness profoundly influences the dynamic response of these structures. This approach not only provides a more complex and realistic structural analysis but also offers critical insights that are essential for future applications in nano-electromechanical systems and beyond. In this paper, we employ molecular dynamics simulations and Fast Fourier Transform analysis to determine the natural frequencies and damping ratios of six different VTGS models. The primary objective is to elucidate the distinct effects of both structural configuration and ambient temperature on the vibrational response, providing foundational knowledge for the design and application of advanced graphene-based nanodevices.

2. Methodology

As mentioned before, this study aimed to analyze the natural frequencies of variable-thickness graphene sheets (VTGSs). As a powerful computational resource for molecular dynamics simulations, the Large-Scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) [23] is instrumental in investigating nanoscale phenomena. It operates by numerically solving Newtonian equations of motion, wherein interatomic interactions dictate the trajectories of many atoms. In this study, all molecular dynamics simulations are carried out by using LAMMPS. As a classical molecular dynamics code, it remains under active development, with continuous incorporation of additional features and enhancements. Notably, the recent integration of the Reactive Bond Order (REBO) [24] many-body potential, a Tersoff/van der Waals hybrid potential, has enabled smoother transitions compared to those previously available within LAMMPS. In addition, the REBO potential also accounts for intramolecular van der Waals forces. Furthermore, the AIREBO (Adaptive Intermolecular Reactive Empirical Bond Order) potential was created to imitate interactions between carbon atoms by Brenner et al. [25,26]. It is a Tersoff-style bond order potential adding torsional and Lennard-Jones [27] interactions to the REBO (Reactive Empirical Bond Order) potential. The latest developed potential, AIREBO, was considered appropriate for use in these analyses.

The atomistic models are generated by using the molecular visualization program VMD (Visual Molecular Dynamics) [28]. The initial positions of the atoms for the VTGSs are provided using the Carbon Nanostructure Builder plugin in the VMD program. In this way, atomic models with six different geometries given in Figure 1 are obtained for the VTGSs.

Figure 1 presents six different graphene models, each with a distinct design. The labels 1L, 3LT, 3LTB, 5LT, 5LTB, and 9LTB correspond to the 1-layered, 3-layered, 3-symmetrically layered, 5-layered, 5-symmetrically layered, and 9-symmetrically layered graphene models, respectively. The dimension denoted as L is 10 nm, which serves as the width for all models. The single-layer (1L) model and the bottom or middle layers of the other models are square-shaped. Figure 1 illustrates how the dimensions of the remaining layers vary in relation to the length L.

After generating the atomistic models, clamped boundary conditions are applied by fixing four edges of variable-thickness graphene sheets. The graphene sheets are applied with an initial velocity profile to approximate the mode shape of the target resonant frequency through manual adjustment of the carbon atom coordinates. The target resonant frequency is the expected first mode shape for the general plates, and it is imitated as a velocity function for each atom as in Equation (1) [29].

$$\left|v_i\right|=[1-\cos ({\displaystyle \frac{2m\pi x_i}{L_x}})][1-\cos ({\displaystyle \frac{2n\pi y_i}{L_y}})]$$

(1)

Here, m and n are integer numbers and show the mode shape of graphene sheet/s (first shape mode: $m=1$ and $n=1$), $L_x$ and $L_y$ are the dimensions of graphene sheet/s, $v_i$ is the velocity of the ith atom. Following the imposition of appropriate boundary conditions by fixing the edge atoms, the VTGSs were permitted to undergo unconstrained vibration. The Velocity Autocorrelation Function (VACF), averaged over the group of atoms, was calculated by using the temporal evolution of the geometric center of the unrestrained atoms. The VACF data is recorded over a specified duration (approximately 1 ns), contingent upon the dimensions and boundary conditions of the respective VTGSs. Subsequently, vibration frequencies were determined via the Fast Fourier Transform (FFT) method. During this analysis, the equations of motion were integrated using the velocity-Verlet algorithm, with a fundamental time step of 1 fs implemented to ensure adequate conservation of energy. Temperature regulation of the system at 300 K was achieved through the application of the NVT ensemble (canonical ensemble, moles (N), volume (V), and temperature (T) are kept constant in the system) and NVE (microcanonical ensemble, constant particle (N), volume (V) and energy (E)) assumptions. The NVT ensemble is utilized during the initial driven vibration process, whereas the NVE ensemble is employed during the ongoing unconstrained vibration process.

To summarize, our methodology involves the following sequential steps:

1-

Atomistic Model Generation: The initial step involved the creation of six distinct atomistic models for VTGSs as given in Figure 1. This was accomplished using the Carbon Nanostructure Builder plugin within the VMD [28].

2-

Simulation Software and Interatomic Potential: All MD simulations were performed using LAMMPS, a well-established and robust simulation package. For modeling the interatomic carbon interactions, we selected the AIREBO potential.

3-

Boundary and Initial Conditions: To simulate a realistic scenario, clamped boundary conditions were applied by fixing the atoms on all four edges of the graphene sheets. To initiate the vibration, the system was not subjected to random thermal noise alone. Instead, an initial velocity profile, defined by Equation (1), was applied to the atoms to specifically excite a mode shape approximating the fundamental resonance mode. This is a crucial step to ensure that the fundamental frequency is prominently captured in the subsequent analysis.

4-

Simulation Protocol and System Evolution: The simulation was conducted in two main phases. An initial phase using the NVT (canonical) ensemble was employed to equilibrate the system at the target temperature (e.g., 300 K) and apply the initial driven vibration. Following this, the system was allowed to evolve under the NVE (microcanonical) ensemble, simulating an unconstrained, energy-conserving vibration. The integration of the equations of motion was performed using the velocity-Verlet algorithm with a time step of 1 fs to ensure numerical stability and energy conservation.

5-

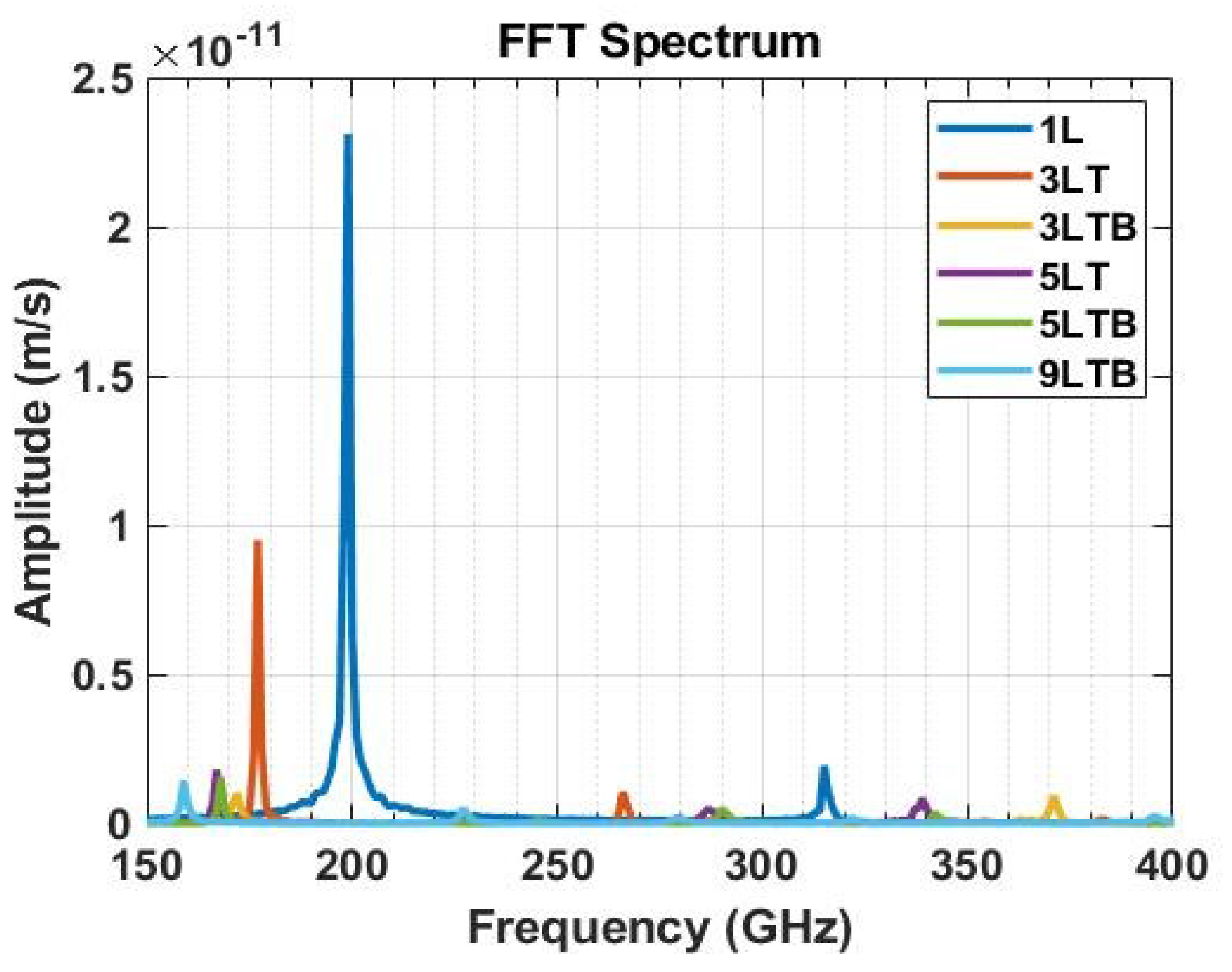
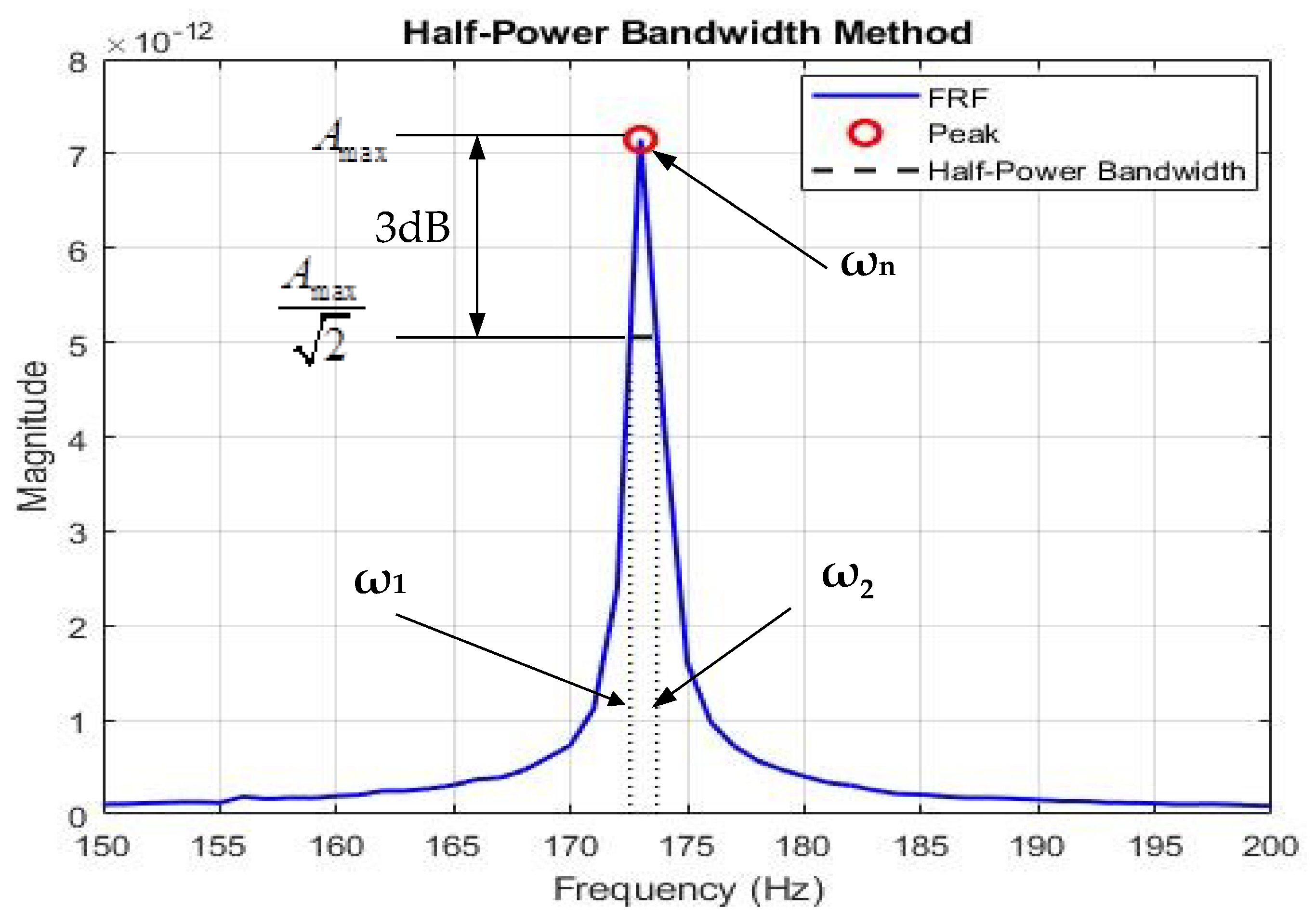
Data Acquisition and Analysis: During the NVE phase, VACF was recorded over a duration of approximately 1 ns. The natural frequencies of the structure were then extracted from this time-domain data by applying the FFT method, which converts the VACF into a VDOS spectrum. The peaks in this spectrum directly correspond to the natural frequencies of the system.

6-

Parametric Temperature Study: To investigate the influence of thermal effects, the entire simulation procedure described above was systematically repeated for three distinct temperatures: 250 K, 300 K, and 350 K.

3. Results and Discussion

The analyzed VTGSs show that structural modifications significantly change the frequencies of the atomistic model, as expected. As mentioned before, the Velocity Autocorrelation Function (VACF) data is collected during the unconstrained vibration section. After that, the collected data is processed by the Fast Fourier Transform (FFT) method. As a result of this process, the natural frequencies appear, and these natural frequencies are illustrated with Vibrational Density of States (VDOS) graphics, as given in Figure 2.

Figure 2 represents the FFT result of the 5LT model, and each peak point of the graph represents the natural frequency of the structure. The horizontal and vertical axes represent frequency (GHz) and Velocity Autocorrelation Function (VACF) amplitude, respectively. The first peak indicates the fundamental natural frequency of the 5LT model at 300 K, which is 168.0 GHz and highlighted in Figure 2.

The main problem of the vibration analysis by using molecular dynamics simulations is the undetermined mode shapes. Although the system is driven by the initial vibration, the interaction between atoms has a disruptive effect on the vibration. As a result of this effect, the mode shape is also distorted, and the obtained displacement vectors appear as a composition of all mode shapes. While FFT analysis is effective for identifying dominant frequencies, visualizing the corresponding mode shapes in a time-dependent MD simulation requires examining the structure’s displacement throughout its vibration. Figure 3 illustrates the dynamic nature of this dominant first mode shape for the 5LT model at 300 K. Figure 3a,b capture the structure at its approximate maximum displacements in opposing directions, effectively visualizing the oscillation and confirming the sustained dominance of the first mode shape during the unconstrained vibration.

The mode shapes obtained analytically were compared with the mode shapes from a molecular dynamics (MD) simulation for a (5LT) model using the Modal Assurance Criterion (MAC), as defined in Equation (2).

$$\mathrm{M}\mathrm{A}\mathrm{C}={\displaystyle \frac{{\left|{\left\{{\varphi }_A\right\}}_i^T{\left\{{\varphi }_B\right\}}_j\right|}^2}{\left({\left\{{\varphi }_B\right\}}_j^T{\left\{{\varphi }_B\right\}}_j\right)\left({\left\{{\varphi }_A\right\}}_i^T{\left\{{\varphi }_A\right\}}_i\right)}}$$

(2)

In Equation (2), ϕ_A and ϕ_B are the mode shape vectors to be compared. The subscripts i and j represent the relevant mode. The value approaches 1 as the two mode shape vectors become more linearly dependent and approaches 0 as they become more linearly independent. The mode shapes of the analytical model and the MD simulation model are given in Figure 4, and the calculated MAC value is 0.92.

The mode shapes shown in Figure 4 were found to have a high degree of similarity, with a correlation of 0.92 according to MAC.

The first natural frequencies of all VTGS models at different temperature values (250, 300, and 350 K) are given in

Table 1. Fundamental natural frequencies of VTGSs at different temperature values.

Model Name	Fundamental Frequency [GHz]
	250 K	300 K	350 K
1L	201	200 [11]	199
3LT	178	177	177
3LTB	173	172	172
5LT	169	168	167
5LTB	169	168	168
9LTB	160	160	159

.

For the 1L model in Table 1, the obtained natural frequency results were compared with the literature and found to be in good agreement. Following this comparison, similar molecular dynamics analyses were conducted for all other models. According to Table 1, as the number of layers with varying cross-sections increases, the natural frequencies decrease for all temperature values. In addition, a similar decreasing trend is observed for the natural frequency values obtained with increasing temperatures.

Figure 5, Figure 6 and Figure 7 comparatively present the Vibrational Density of States (VDOS) graphs for layered graphene structures with varying cross-sections under clamped boundary conditions. Their natural frequencies at three different simulation temperatures (250 K, 300 K, and 350 K) are shown as superimposed plots for each temperature. In this manner, the natural frequencies of six differently modeled layered graphene structures at the same simulation temperatures were determined, and the effects of these models on natural frequencies were investigated. The sampling rate, frequency bandwidth, frequency resolution, and sampling number are 10 × 10⁵ GHz, 0–5 × 10¹⁴ GHz, 1 GHz, and 500,001, respectively.

The horizontal axis in Figure 4, Figure 5 and Figure 6 illustrates the vibrational frequencies of the atoms within the system. Elevated amplitudes observed in these graphs signify a substantial presence or a high intensity of vibrational modes at the corresponding frequencies. This implies that the atomic movements at those specific frequencies are particularly energetic or dominant. Consequently, the high-amplitude peaks within these graphs are indicative of the prevailing vibrational modes at the given frequencies and correspond to the fundamental natural frequency values unique to each investigated model.

High-frequency peaks are correlated with interatomic bond stretching vibrations, while low-frequency peaks are associated with bending or lattice vibrations. An examination of Figure 4, Figure 5 and Figure 6 reveals that distinct natural frequencies were obtained for each model. The augmented mass of the graphene structure, resulting from an increased number of layers, led to a corresponding decrease in its natural frequencies. While an inverse relationship generally exists between layer count and natural frequencies, it is imperative to acknowledge that discrepancies in interlayer distance and van der Waals forces also exert an influence on the rigidity of the graphene structure.

In addition, the damping ratios (ζ) corresponding to the natural frequencies were calculated from the half-power points of the peaks in the frequency spectrum via the half-power bandwidth method given with Equation (3) and illustrated in Figure 8 [30]. The calculated damping ratios for each model and temperature are given in

Table 2. Damping ratios for obtained fundamental natural frequencies of VTGSs at different temperature values.

Model Name	Damping Ratio [%]
	250 K	300 K	350 K
1L	0.0016	0.0017	0.0024
3LT	0.0021	0.0042	0.0022
3LTB	0.0049	0.0027	0.0027
5LT	0.0049	0.0027	0.0027
5LTB	0.0024	0.0053	0.0024
9LTB	0.0047	0.0061	0.0031

.

$$\zeta ={\displaystyle \frac{{\omega }_2-{\omega }_1}{2{\omega }_n}}$$

(3)

In simulation studies conducted at different temperatures, significantly different damping ratios were obtained for both the same and different models. Consequently, it is not possible to make a definitive statement that the damping ratio decreases or increases with a rise or fall in temperature. While the damping ratio in some models shows a stable increasing trend with rising temperature (1L), it may decrease in another model (3LTB). In other models, an increase in temperature may cause the damping ratio to first increase slightly before decreasing as the temperature continues to rise (5LTB). This behavior is entirely dependent on the structure of the models under investigation, as a steady increase in the damping ratio is observed with rising temperature in the uniform 1L model.

Subsequently, the frequency variation with simulation temperature for each developed graphene model was investigated. In order to achieve this purpose, frequency spectra were obtained through analyses conducted at simulation temperatures of 250 K, 300 K, and 350 K. The frequency spectra acquired for each model are presented in Figure 9, Figure 10 and Figure 11.

Upon examining the graphs in Figure 9, Figure 10 and Figure 11, it is observed that the fundamental natural frequencies tend to decrease with increasing temperature. This phenomenon occurs because the elevated temperature enhances the atoms’ thermal energy, causing them to deviate more significantly from their average positions. This increased thermal motion, in turn, reduces the structure’s rigidity, leading to a decrease in its natural frequencies.

When the amplitude is high at a particular frequency, it means the system’s atoms are vibrating intensely at that frequency. Consequently, each atomistic model shows different behavior in this regard across varying temperatures, and the amplitudes of the dominant frequencies were observed distinctly for each temperature value. This is a common occurrence in molecular dynamics studies.

Furthermore, an increase in temperature leads to a broadening of the frequency peaks. This is attributed to the fact that higher temperatures result in more frequent interatomic interactions, thereby enhancing the vibrational damping effect. Additionally, at higher temperatures, changes in interatomic distances due to thermal expansion influenced bond forces, leading to slight shifts in natural frequencies. In this way, some peaks were observed to shift to lower frequencies (thermal softening), while others shifted to higher frequencies (thermal hardening).

4. Conclusions

In this study, the vibrational behavior of variable-thickness multi-layered graphene sheets (VTGSs) was comprehensively analyzed using molecular dynamics simulations. Six different atomistic models were developed to investigate how structural geometry and temperature influence the fundamental natural frequencies and the damping ratios under clamped boundary conditions. The AIREBO potential was employed, and the natural frequencies were determined by applying FFT analysis to the VACF data generated during unconstrained vibration. The damping ratios were calculated via the half-power bandwidth method.

The primary findings of this research are summarized as follows:

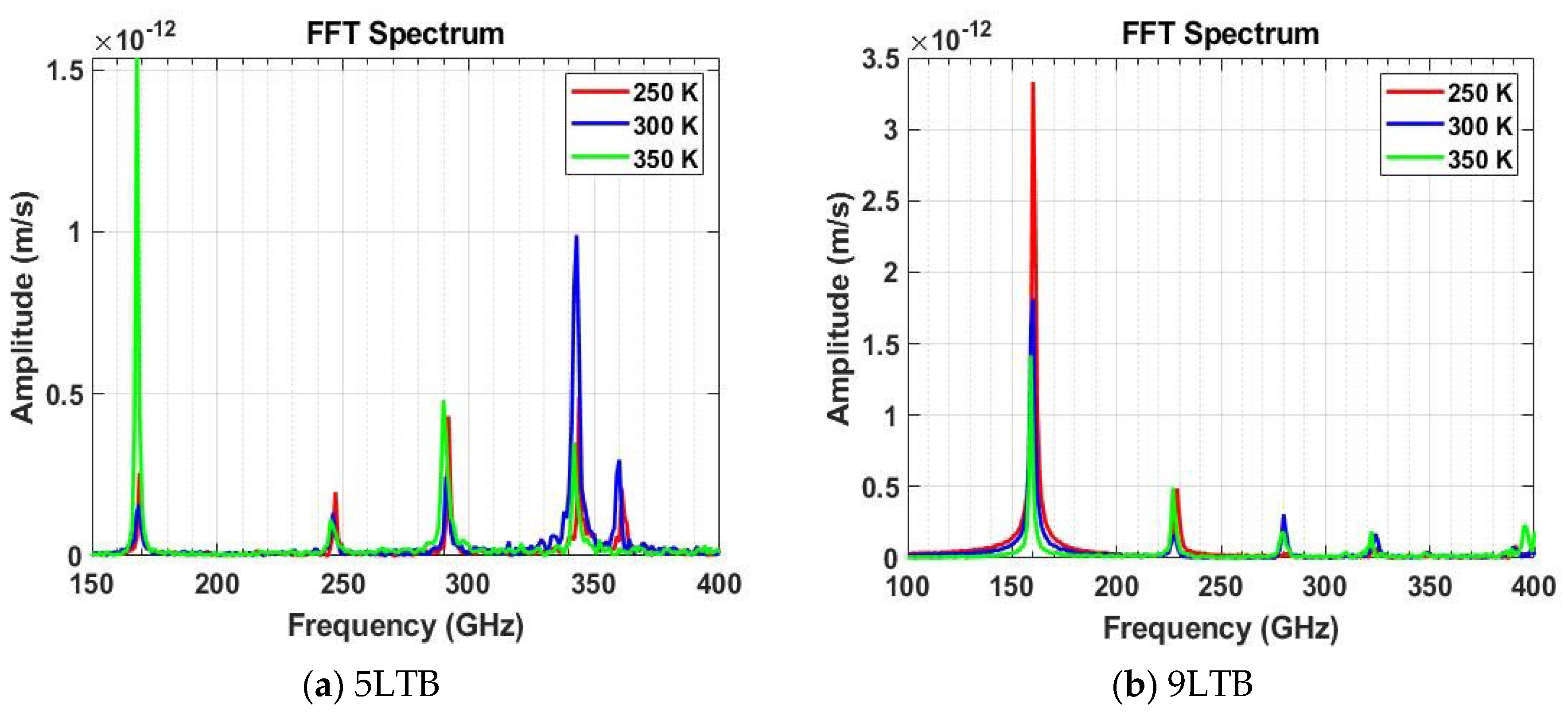
• The inverse relationship between the number of graphene layers and the natural frequency is a direct consequence of the increased mass. As the number of layers increases, the total mass of the nanostructure rises, while the stiffness—primarily determined by in-plane covalent bonds—does not increase proportionally. This alters the mass-to-stiffness ratio, resulting in a lower natural frequency. As described by fundamental vibration theory, a system’s natural frequency is proportional to the square root of its stiffness (k) over its mass (m). While adding layers increases both mass and stiffness (due to van der Waals forces), the increase in mass is the dominant factor, leading to a decrease in the overall natural frequency. This relationship is crucial for designing nanoresonators, as it enables precise frequency tuning by simply controlling the number of layers.
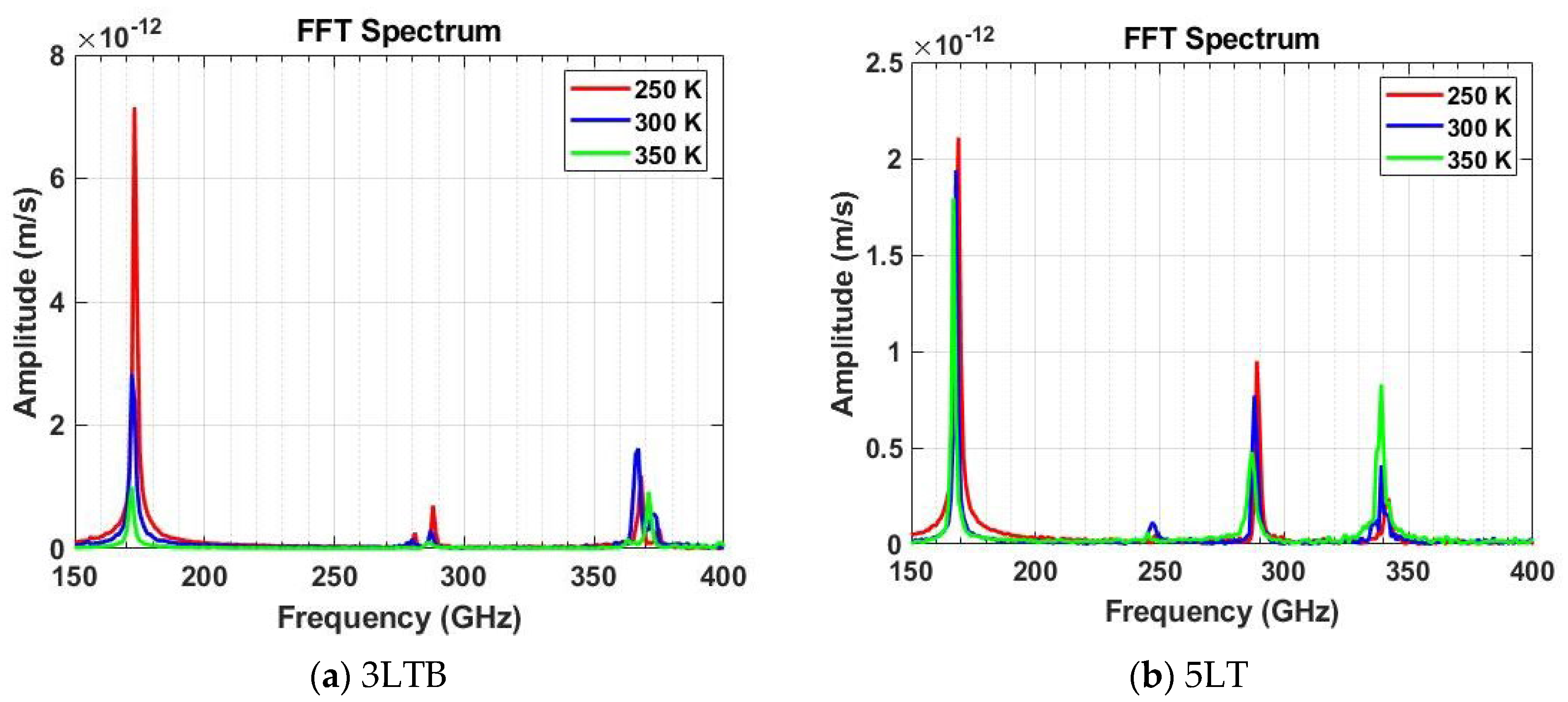
• It has been established that the vibrational response is significantly influenced by temperature. For all models, an increase in simulation temperature from 250 K to 350 K resulted in a relative decrease in the fundamental natural frequencies. This behavior is attributed to a reduction in the structure’s overall rigidity, which is a direct consequence of increased thermal motion causing atoms to deviate more from their equilibrium positions. This phenomenon is known as thermal softening. The rise in temperature increases the kinetic energy of the atoms, leading to larger-amplitude thermal vibrations. These increased vibrations alter the average bond lengths and angles between atoms, thereby reducing the material’s macroscopic elastic properties. As the temperature increases, the thermal motion of the atoms intensifies, which in turn reduces the material’s rigidity. Since the mass remains constant, the dominant effect on the frequency is the drop in rigidity, which ultimately lowers the natural frequency. This phenomenon highlights the potential for nanoresonators to be used as temperature sensors, where the frequency shift can serve as a highly sensitive measure of temperature.
• The frequency peaks were also observed to broaden at higher temperatures. It indicates an enhanced vibrational damping effect due to more frequent interatomic interactions.
• Simulation studies at varying temperatures showed no single trend for damping ratios; their behavior is highly dependent on the model’s structure. For example, while the damping ratio of the uniform 1L model steadily increased with rising temperature, it decreased in the 3LTB model and followed a more complex pattern of initial increase then decrease in the 5LTB model.

In conclusion, this study demonstrates that both the geometric arrangement of layers and the ambient temperature are critical parameters for the vibrational characteristics of variable-thickness multi-layered graphene. The detailed insights obtained from these simulations are essential for the future design and optimization of graphene-based nano-electromechanical systems, where precise frequency tuning is a fundamental requirement.