Development of Resource Map for Open-Loop Ground Source Heat Pump System Based on Heating and Cooling Experiments
Abstract
1. Introduction
2. Experimental Site and Methods
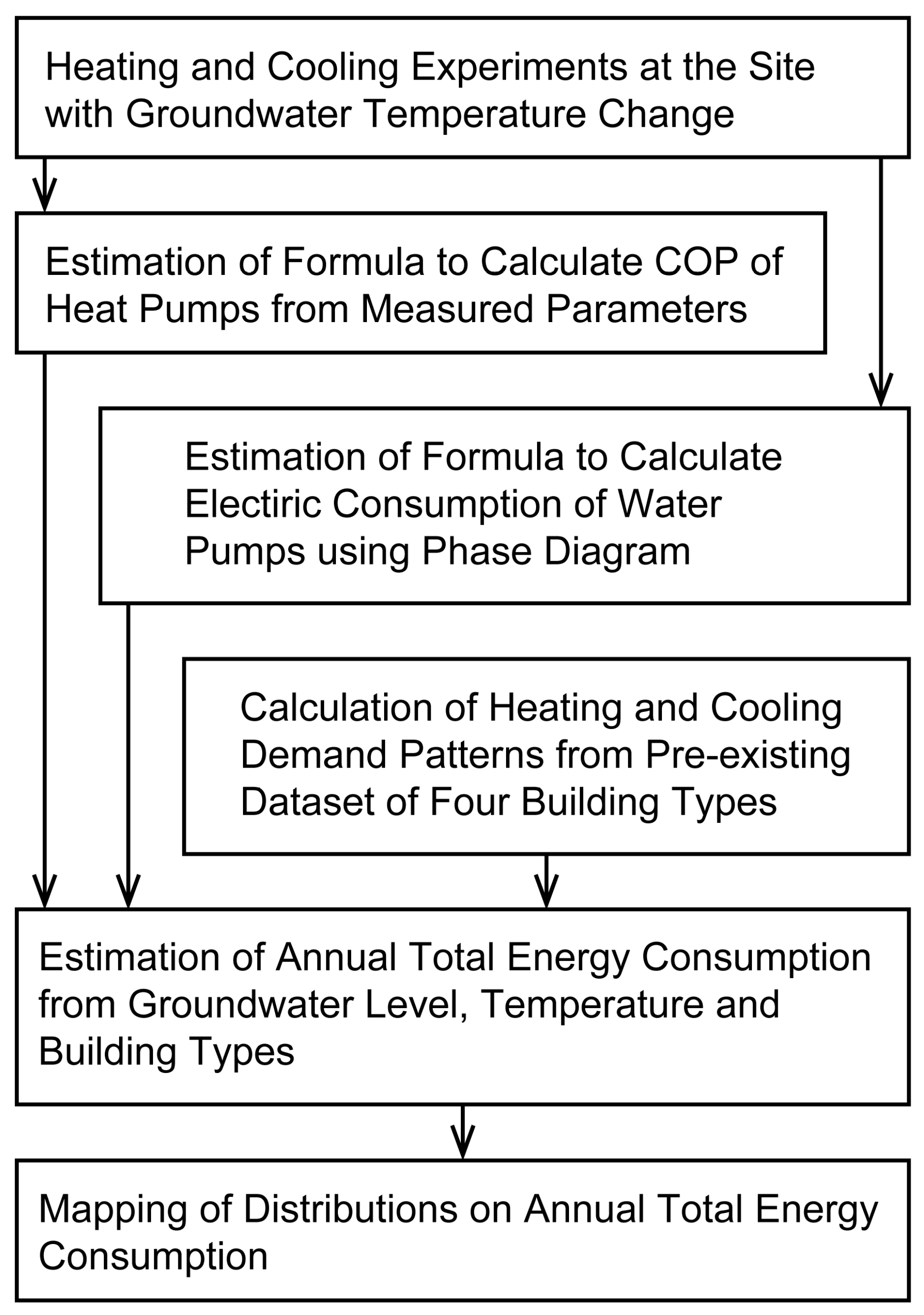
2.1. Methodological Overview
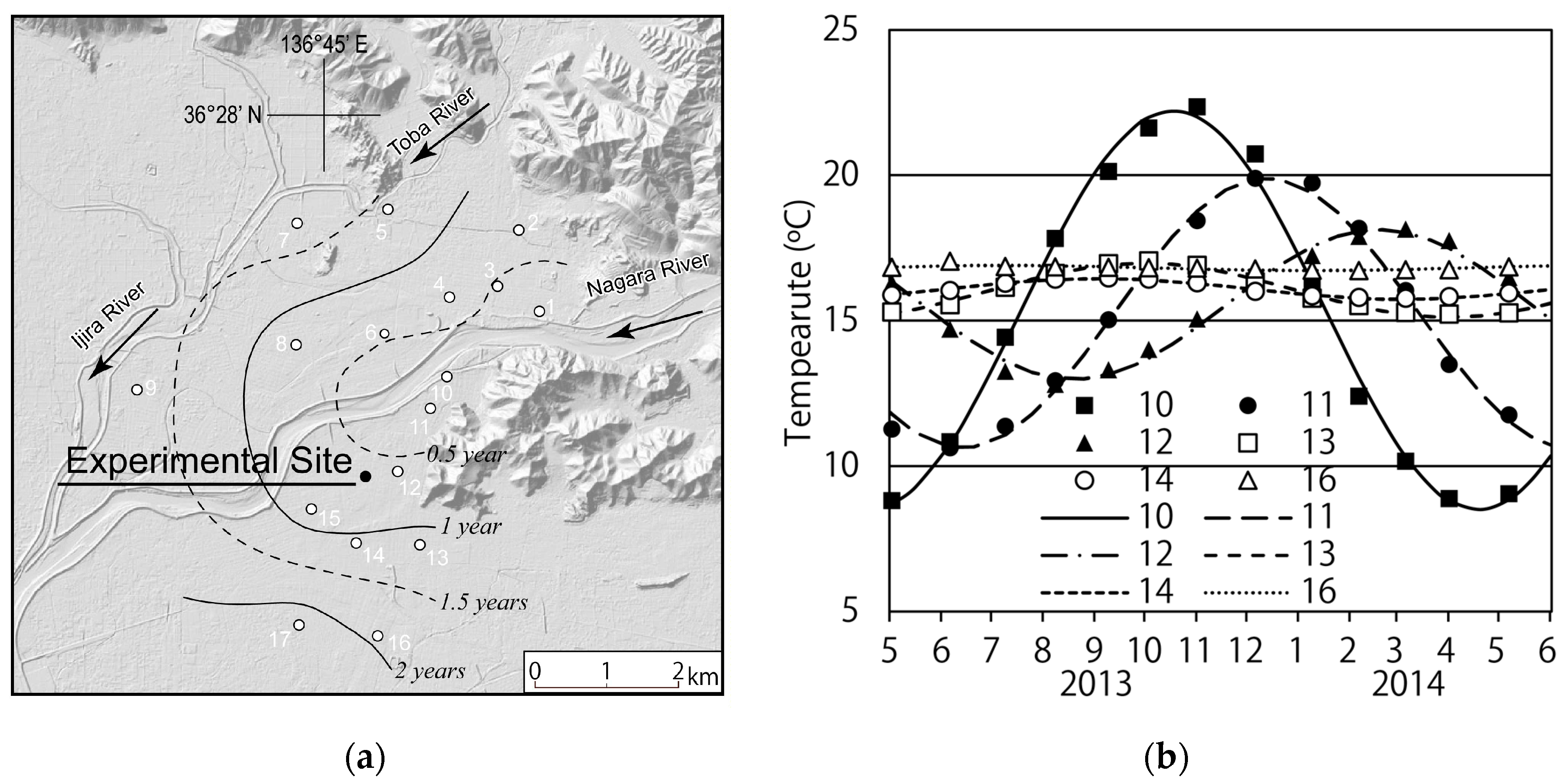
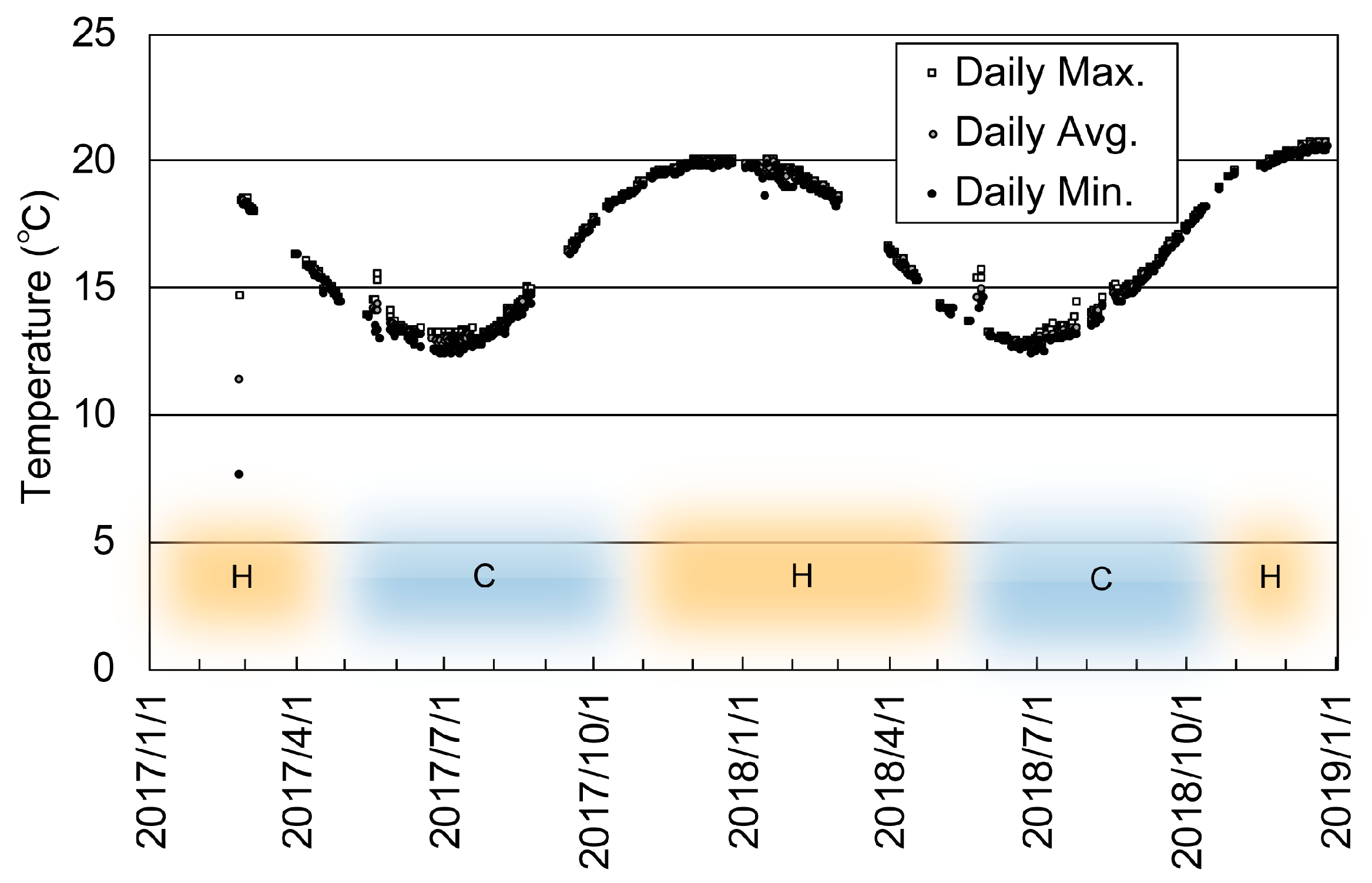
2.2. Site Characteristics
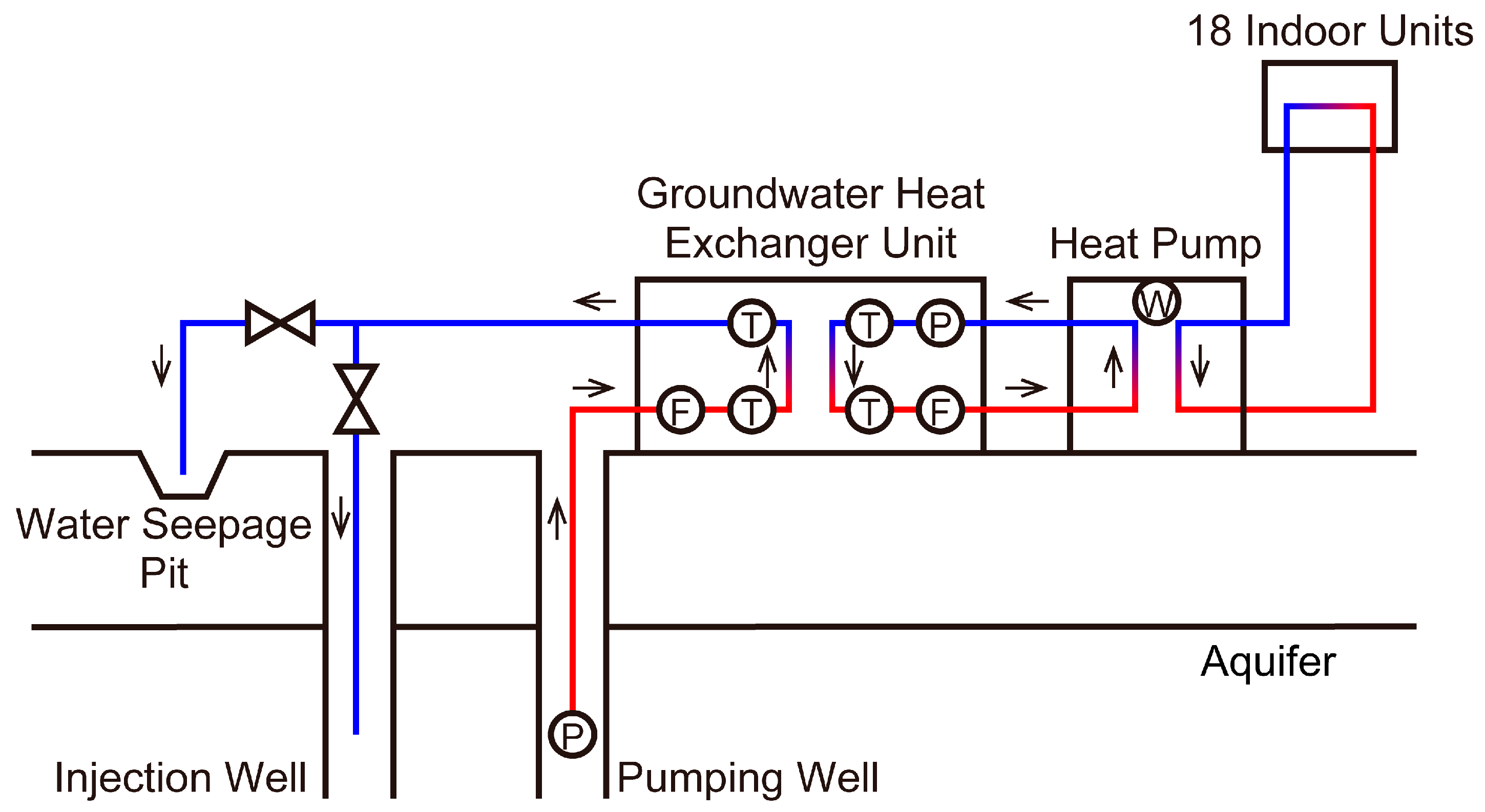
2.3. Experimental System
2.4. Estimation of Energy Consumption for Heat Pump and Groundwater Pump
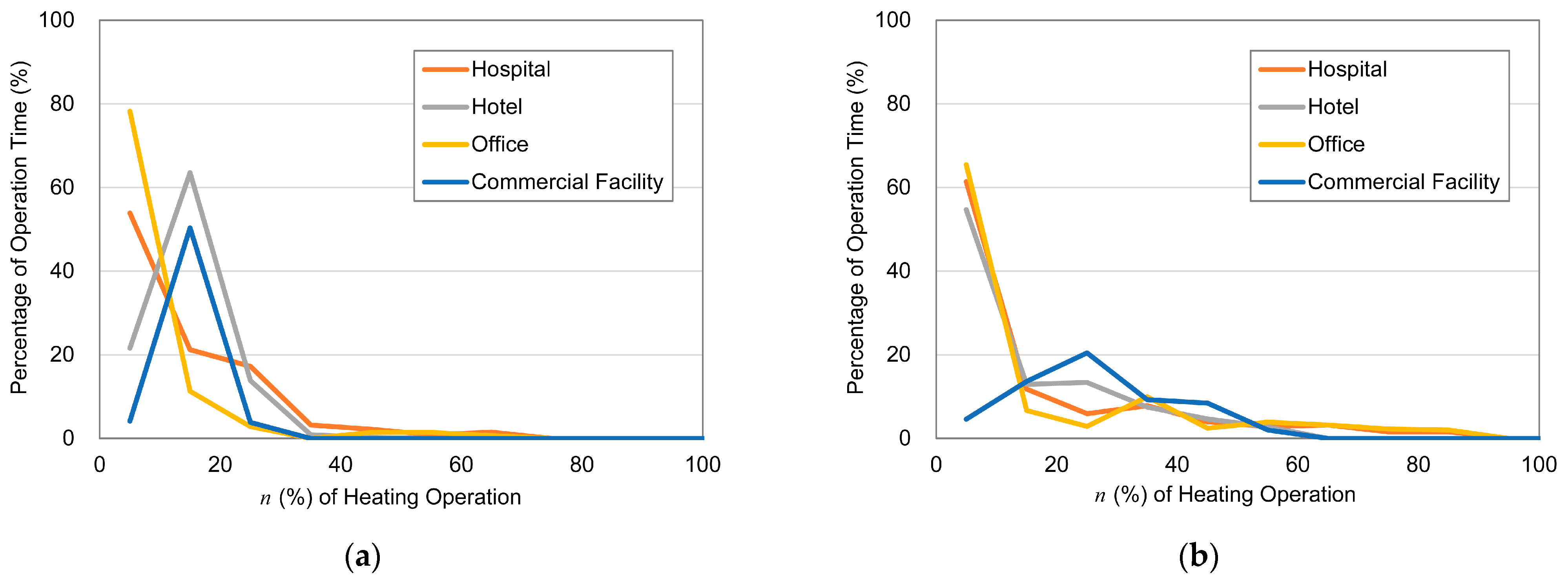
2.5. Heating and Cooling Demand Patterns
2.6. Mapping Annual Total Energy Consumption
3. Results
3.1. COP Estimated from Measured Parameters
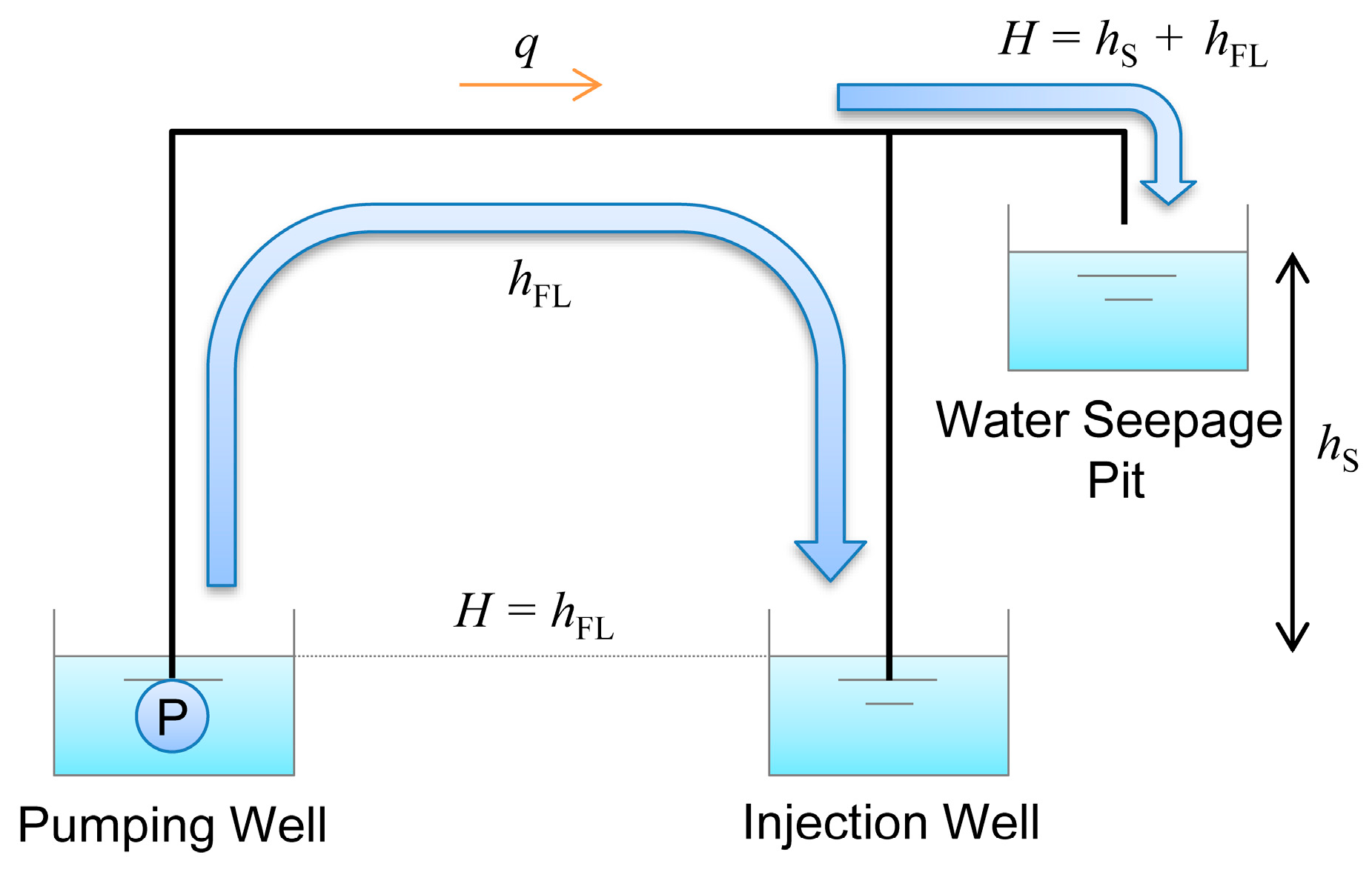
3.2. Energy Consumption of Groundwater Pump Estimated from Flow Rate and Total Dynamic Head
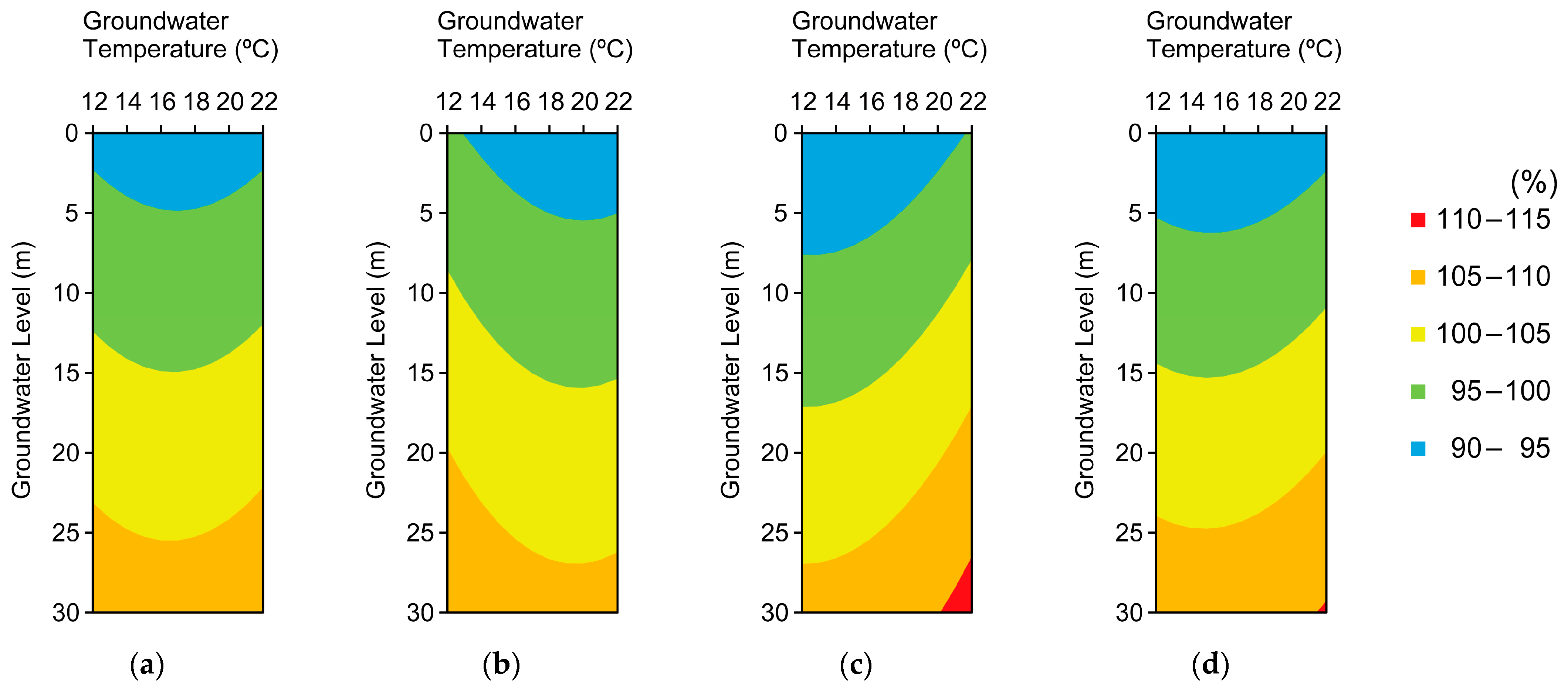
3.3. Effects of Groundwater Depth/Temperature/Building Type on Annual Total Energy Consumption
3.4. Resource Maps of Open-Loop GSHP Systems
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lund, J.W.; Toth, A.N. Direct Utilization of Geothermal Energy 2020 Worldwide Review. Geothermics 2021, 90, 101915. [Google Scholar] [CrossRef]
- Fujii, H.; Inatomi, T.; Itoi, R.; Uchida, Y. Development of Suitability Maps for Ground-Coupled Heat Pump Systems Using Groundwater and Heat Transport Models. Geothermics 2007, 36, 459–472. [Google Scholar] [CrossRef]
- Shrestha, G.; Bando, K.; Ishihara, T.; Fujino, T.; Isoishi, K.; Tomigashi, A.; Uchida, Y. Assessment of Installation Suitability of a Vertical Closed Loop Ground Source Heat Pump System in Regional Scale. Geothermics 2023, 113, 102766. [Google Scholar] [CrossRef]
- Kaneko, S.; Uchida, Y.; Shrestha, G.; Ishihara, T.; Yoshioka, M. Factors Affecting the Installation Potential of Ground Source Heat Pump Systems: A Comparative Study for the Sendai Plain and Aizu Basin, Japan. Energies 2018, 11, 2860. [Google Scholar] [CrossRef]
- Duque, J.; Moya, M.; Urresta, E.; Harnisth, K. Geospatial Assessment of Soil Thermal Conductivity for Geothermal Energy Systems in Ecuador. Geothermics 2025, 131, 103373. [Google Scholar] [CrossRef]
- Assouline, D.; Mohajeri, N.; Gudmundsson, A.; Scartezzini, J.-L. A Machine Learning Approach for Mapping the Very Shallow Theoretical Geothermal Potential. Geotherm. Energy 2019, 7, 19. [Google Scholar] [CrossRef]
- Galgaro, A.; Di Sipio, E.; Teza, G.; Destro, E.; De Carli, M.; Chiesa, S.; Zarrella, A.; Emmi, G.; Manzella, A. Empirical Modeling of Maps of Geo-Exchange Potential for Shallow Geothermal Energy at Regional Scale. Geothermics 2015, 57, 173–184. [Google Scholar] [CrossRef]
- Santilano, A.; Donato, A.; Galgaro, A.; Montanari, D.; Menghini, A.; Viezzoli, A.; Di Sipio, E.; Destro, E.; Manzella, A. An Integrated 3D Approach to Assess the Geothermal Heat-Exchange Potential: The Case Study of Western Sicily (Southern Italy). Renew. Energy 2016, 97, 611–624. [Google Scholar] [CrossRef]
- Walch, A.; Li, X.; Chambers, J.; Mohajeri, N.; Yilmaz, S.; Patel, M.; Scartezzini, J.L. Shallow Geothermal Energy Potential for Heating and Cooling of Buildings with Regeneration under Climate Change Scenarios. Energy 2022, 244, 123086. [Google Scholar] [CrossRef]
- Zhang, Y.; Choudhary, R.; Soga, K. Influence of GSHP System Design Parameters on the Geothermal Application Capacity and Electricity Consumption at City-Scale for Westminster, London. Energy Build. 2015, 106, 3–12. [Google Scholar] [CrossRef]
- Ohtani, T.; Ishihara, M.; Kojma, S. A Potential Installation of Groundwater Heat Pump Systems Inferred from Well Information in the Nobi Plain. J. Geotherm. Res. Soc. Jpn. 2008, 30, 121–129. [Google Scholar] [CrossRef]
- Nam, Y.; Ooka, R. Development of Potential Map for Ground and Groundwater Heat Pump Systems and the Application to Tokyo. Energy Build. 2011, 43, 677–685. [Google Scholar] [CrossRef]
- Abesser, C.; Lewis, M.A.; Marchant, A.P.; Hulbert, A.G. Mapping Suitability for Open-Loop Ground Source Heat Pump Systems: A Screening Tool for England and Wales, UK. Q. J. Eng. Geol. Hydrogeol. 2014, 47, 373–380. [Google Scholar] [CrossRef]
- Arola, T.; Eskola, L.; Hellen, J.; Korkka-Niemi, K. Mapping the Low Enthalpy Geothermal Potential of Shallow Quaternary Aquifers in Finland. Geotherm. Energy 2014, 2, 9. [Google Scholar] [CrossRef]
- Stemmle, R.; Hammer, V.; Blum, P.; Menberg, K. Potential of Low-Temperature Aquifer Thermal Energy Storage (LT-ATES) in Germany. Geotherm. Energy 2022, 10, 24. [Google Scholar] [CrossRef]
- Al-Madhlom, Q.; Al-Ansari, N.; Laue, J.; Nordell, B.; Hussain, H.M. Site Selection of Aquifer Thermal Energy Storage Systems in Shallow Groundwater Conditions. Water 2019, 11, 1393. [Google Scholar] [CrossRef]
- Stemmle, R.; Lee, H.; Blum, P.; Menberg, K. City-Scale Heating and Cooling with Aquifer Thermal Energy Storage (ATES). Geotherm. Energy 2024, 12, 2. [Google Scholar] [CrossRef]
- Todorov, O.; Alanne, K.; Virtanen, M.; Kosonen, R. Aquifer Thermal Energy Storage (ATES) for District Heating and Cooling: A Novel Modeling Approach Applied in a Case Study of a Finnish Urban District. Energies 2020, 13, 2478. [Google Scholar] [CrossRef]
- Luo, J.; Wang, H.; Zhang, H.; Yan, Z. A Geospatial Assessment of the Installation Potential of Shallow Geothermal Systems in a Graben Basin. Renew. Energy 2021, 165, 553–564. [Google Scholar] [CrossRef]
- Ohtani, T.; Mizuno, T.; Kohda, A. Underground Temperature Distribution and Spatial Suitability Assessment for Geothermal Heat Pumps in the Alluvial Fan of the Nagara River, Central Japan. J. Geotherm. Res. Soc. Japan 2019, 41, 121–133. [Google Scholar] [CrossRef]
- Society of Heating, Air-Conditioning and Sanitary Engineers of Japan. Planning, Design and Operation of City Gas Cogeneration; Society of Heating, Air-Conditioning and Sanitary Engineers of Japan: Tokyo, Japan, 2015. [Google Scholar]
- Sotoyama, Y. Intelligible Book of Pump Technologies; The Nikkan Kogyo Shimbun: Tokyo, Japan, 2016. [Google Scholar]
- Ohtani, T.; Mizuno, T.; Kouda, A.; Kojima, S. Seasonal Change of Underground Temperature and the Use of Geothermal in Gifu City, Japan. In Proceedings of the World Geothermal Congress 2015, Melbourne, VIC, Australia, 19–24 April 2015; pp. 19–25. [Google Scholar]
- Uchida, Y.; Sakura, Y. Subsurface Temperature Profiles in the Nobi Plain, Central Japan. Bull. Geol. Surv. Japan 1999, 50, 635–659. [Google Scholar]
- Uchida, Y.; Hayashi, T. Water Environment Map No. 4 “Nobi Plain” [CD-ROM]; Geological Survey of Japan, AIST: Tsukuba, Japan, 2004. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ohtani, T.; Soma, K.; Masaki, I. Development of Resource Map for Open-Loop Ground Source Heat Pump System Based on Heating and Cooling Experiments. Appl. Sci. 2025, 15, 9195. https://doi.org/10.3390/app15169195
Ohtani T, Soma K, Masaki I. Development of Resource Map for Open-Loop Ground Source Heat Pump System Based on Heating and Cooling Experiments. Applied Sciences. 2025; 15(16):9195. https://doi.org/10.3390/app15169195
Chicago/Turabian StyleOhtani, Tomoyuki, Koji Soma, and Ichiro Masaki. 2025. "Development of Resource Map for Open-Loop Ground Source Heat Pump System Based on Heating and Cooling Experiments" Applied Sciences 15, no. 16: 9195. https://doi.org/10.3390/app15169195
APA StyleOhtani, T., Soma, K., & Masaki, I. (2025). Development of Resource Map for Open-Loop Ground Source Heat Pump System Based on Heating and Cooling Experiments. Applied Sciences, 15(16), 9195. https://doi.org/10.3390/app15169195






