Study on the Stability Evaluation Index System for Rock Slope–Anchoring Systems
Abstract
1. Introduction
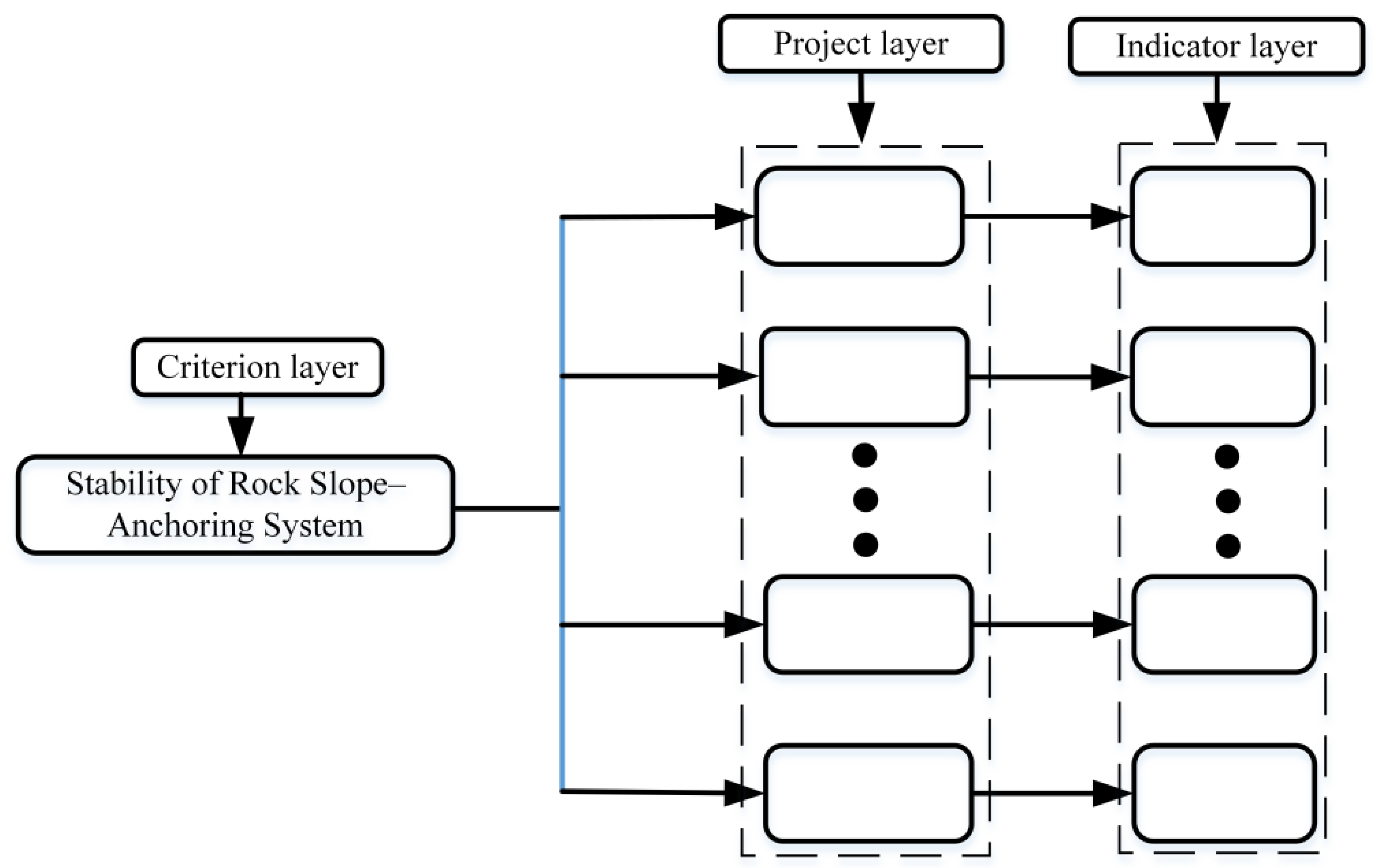
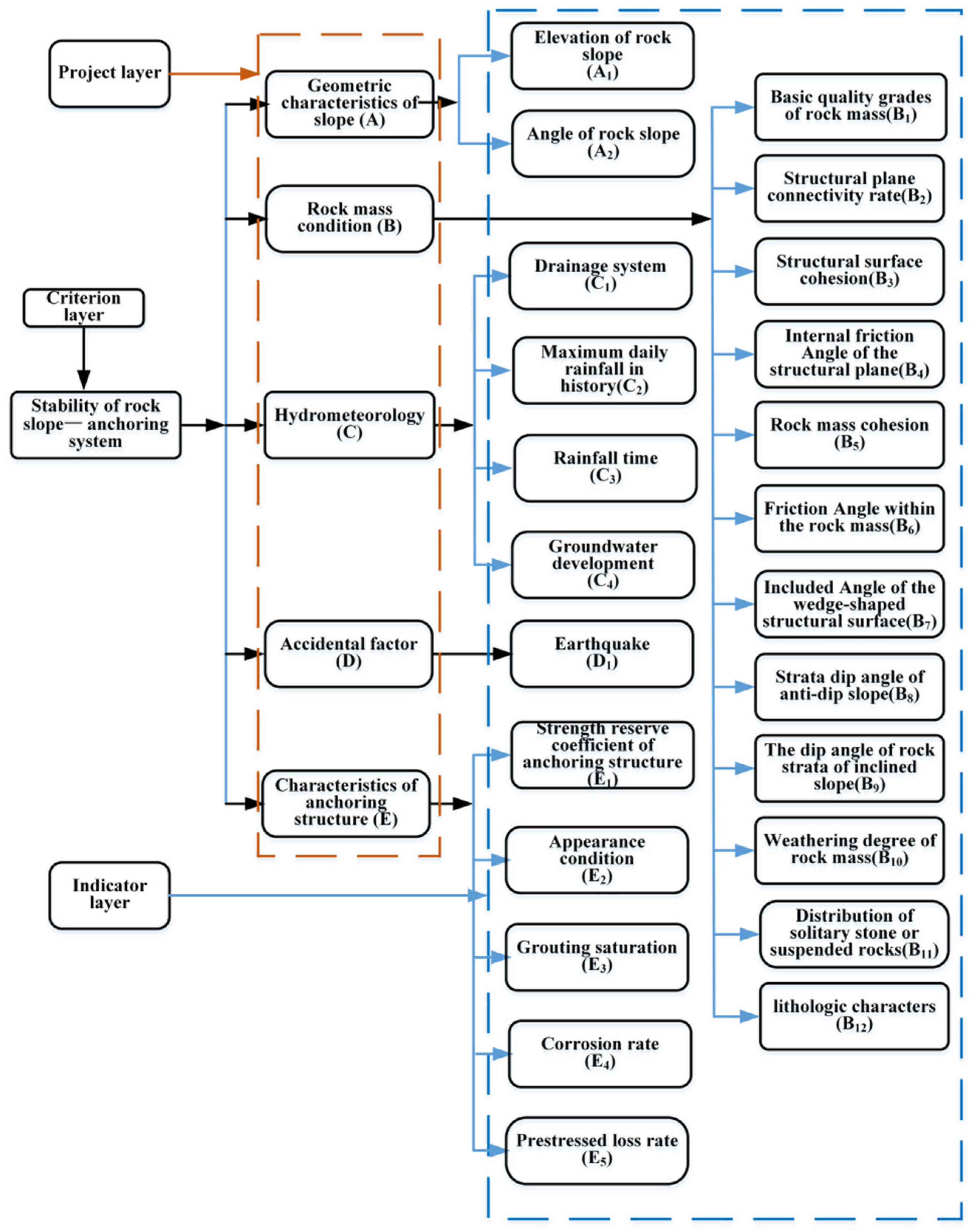
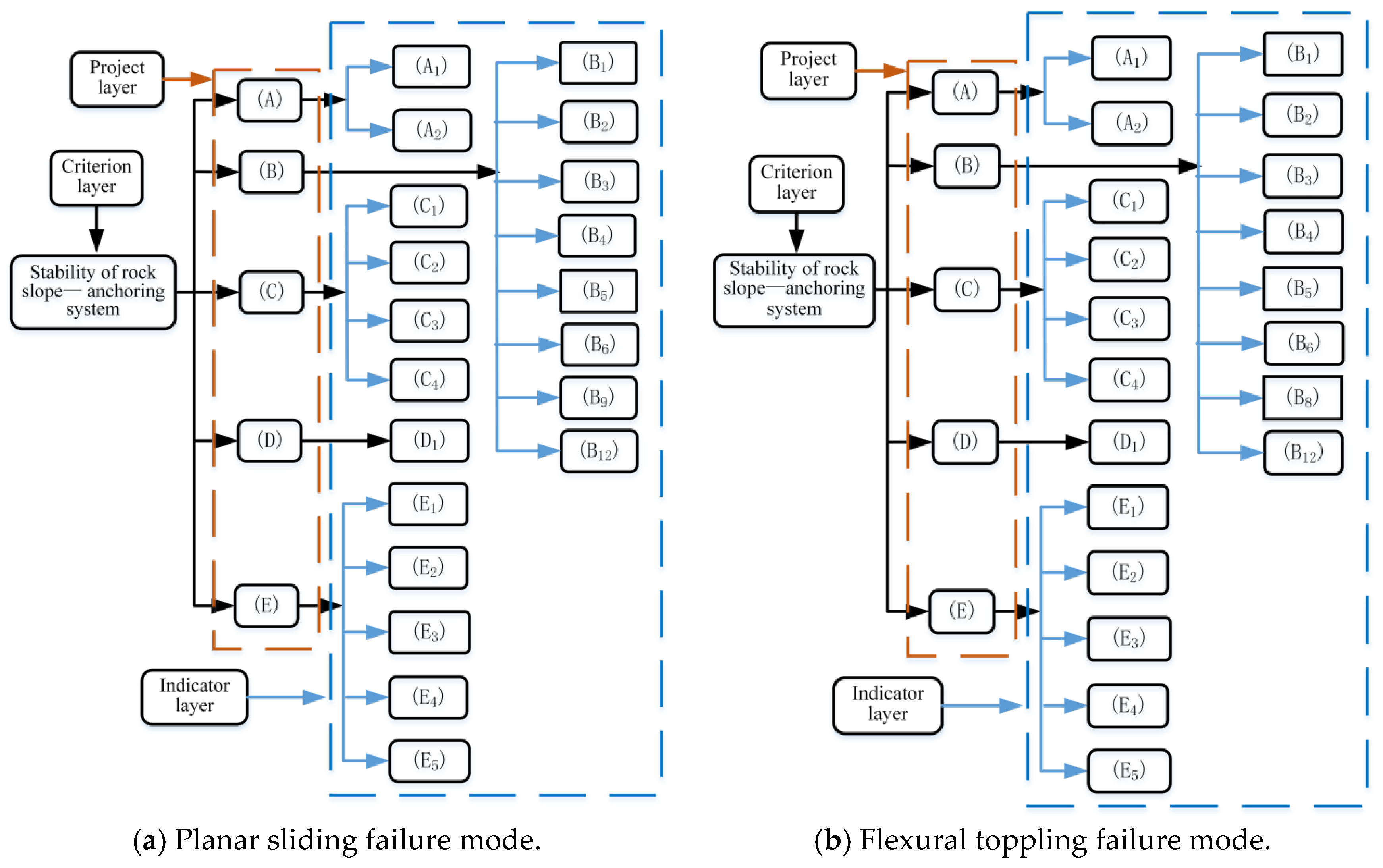
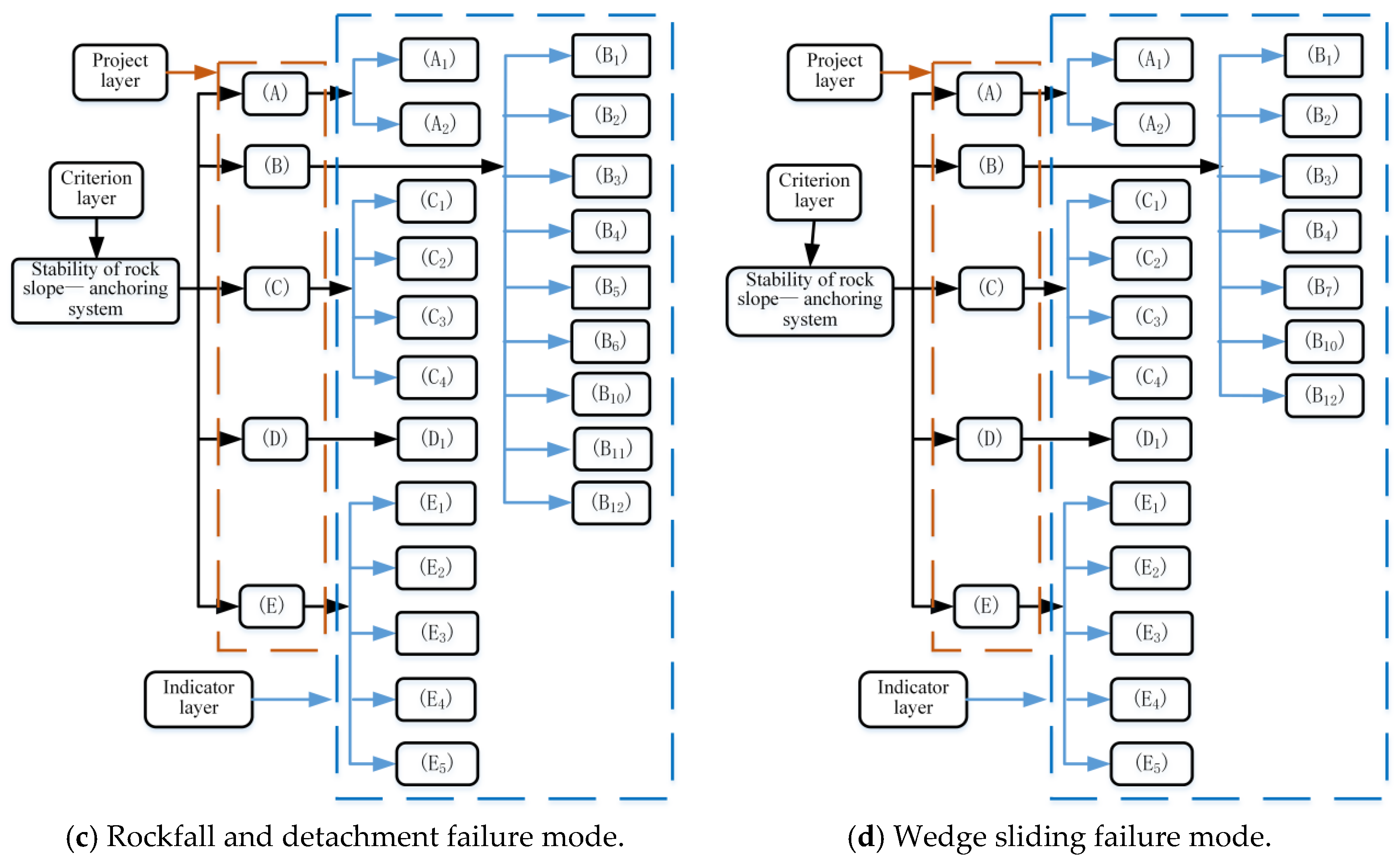
2. Hierarchical Analytic Structure of the Indicator System
2.1. Construction of the Hierarchical Analytical Structure for Rock Slope–Anchoring Systems
2.2. Indicator Selection
2.2.1. Preliminary Screening of Indicators
2.2.2. Indicator Screening
3. Grading Criteria
3.1. Classification of Indicators
3.2. Determination of Classification Criteria
3.2.1. Determination of Classification Criteria for Qualitative Indicators
3.2.2. Determination of Grading Standards for Quantitative Indicators
4. Validation of Classification Criteria
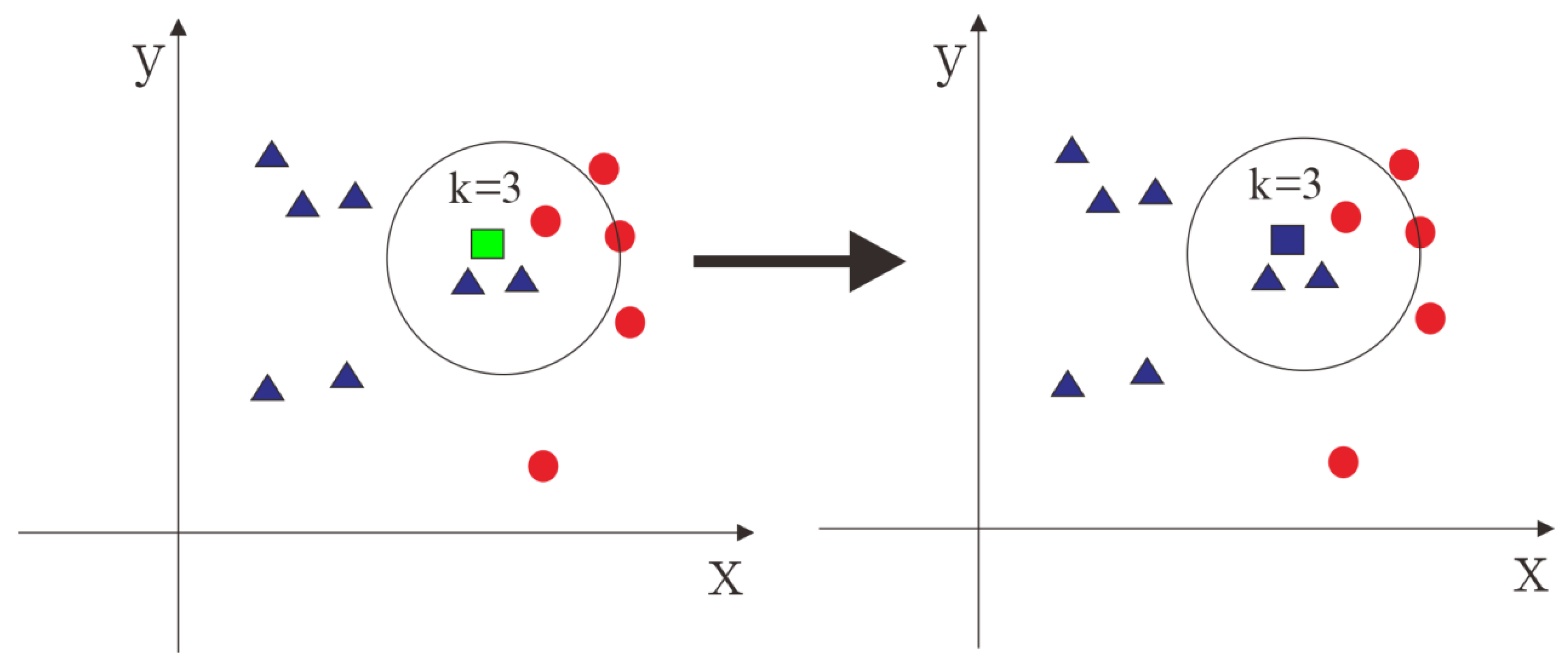
4.1. Basic Principle of the KNN Algorithm
4.2. Evaluation of the KNN Model
4.3. Implementation Procedure of the Rationality Test
4.4. Comparative Analysis of Grading Standard Determination Methods
5. Conclusions
6. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Du, Y.; Li, H.; Chicas, S.D.; Huo, L. Progress and perspectives of geotechnical anchor bolts on slope engineering in China. Front. Environ. Sci. 2022, 10, 928064. [Google Scholar] [CrossRef]
- Ding, W.; Wang, Z.; Huang, X.; Chen, L.; Zheng, Y. Influence of corrosion on anchoring bond behavior of jointed rock mass. KSCE J. Civ. Eng. 2022, 26, 1914–1928. [Google Scholar] [CrossRef]
- Pei, S.F.; Hao, W.F.; Fan, Y.L.; Chen, H.; Li, W.T. Operation condition of anchoring system in large-scale water conservancy and hydropower projects. J. Changjiang River Sci. Res. Inst. 2024, 41, 142–150. (In Chinese) [Google Scholar]
- Wen, L.; Huang, L.; Xiang, X.; Yang, X.Z.; Zhang, G.C. Research status and development trend of geotechnical anchorage technology in hydropower projects. Saf. Environ. Eng. 2023, 30, 35–45. (In Chinese) [Google Scholar]
- Lama, B.; Momayez, M. Review of non-destructive methods for rock bolts condition evaluation. Mining 2023, 3, 106–120. [Google Scholar] [CrossRef]
- Kang, H.; Yang, J.; Gao, F.; Li, J. Experimental Study on the Mechanical Behavior of Rock Bolts Subjected to Complex Static and Dynamic Loads. Rock Mech. Rock Eng. 2020, 53, 4993–5004. [Google Scholar] [CrossRef]
- Luga, E.; Periku, E. A pioneer in-situ investigation on the bearing capacity and failure causes of real scale fully grouted rockbolts. Constr. Build. Mater. 2021, 310, 124826. [Google Scholar] [CrossRef]
- Zheng, L.; Zuo, Q. Experimental study on the effect of water-induced deterioration on shear properties of bolted rock joints. Case Stud. Constr. Mater. 2024, 20, e03027. [Google Scholar] [CrossRef]
- Ullah, S.; Khan, M.U.; Rehman, G. A brief review of the slope stability analysis methods. Geol. Behav. 2020, 4, 73–77. [Google Scholar] [CrossRef]
- Koopialipoor, M.; Jahed Armaghani, D.; Hedayat, A.; Marto, A.; Gordan, B. Applying various hybrid intelligent systems to evaluate and predict slope stability under static and dynamic conditions. Soft Comput. 2019, 23, 5913–5929. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Taha, M.R.; Keawsawasvong, S.; Mirzaei, H.; Jebeli, M. An effective artificial intelligence approach for slope stability evaluation. IEEE Access 2022, 10, 5660–5671. [Google Scholar] [CrossRef]
- Asteris, P.G.; Rizal, F.I.M.; Koopialipoor, M.; Roussis, P.C.; Ferentinou, M.; Armaghani, D.J.; Gordan, B. Slope stability classification under seismic conditions using several tree-based intelligent techniques. Appl. Sci. 2022, 12, 1753. [Google Scholar] [CrossRef]
- Lin, S.; Zheng, H.; Han, C.; Han, B.; Li, W. Evaluation and prediction of slope stability using machine learning approaches. Front. Struct. Civ. Eng. 2021, 15, 821–833. [Google Scholar] [CrossRef]
- Lin, S.; Zheng, H.; Han, B.; Li, Y.; Han, C.; Li, W. Comparative performance of eight ensemble learning approaches for the development of models of slope stability prediction. Acta Geotech. 2022, 17, 1477–1502. [Google Scholar] [CrossRef]
- Qin, J.; Du, S.; Ye, J.; Yong, R. SVNN-ANFIS approach for stability evaluation of open-pit mine slopes. Expert Syst. Appl. 2022, 198, 116816. [Google Scholar] [CrossRef]
- Moayedi, H.; Tien Bui, D.; Kok Foong, L. Slope stability monitoring using novel remote sensing based fuzzy logic. Sensors 2019, 19, 4636. [Google Scholar] [CrossRef]
- Ahangari Nanehkaran, Y.; Pusatli, T.; Chengyong, J.; Chen, J.; Cemiloglu, A.; Azarafza, M.; Derakhshani, R. Application of machine learning techniques for the estimation of the safety factor in slope stability analysis. Water 2022, 14, 3743. [Google Scholar] [CrossRef]
- Bi, J.; Luo, X.; Zhang, H.; Shen, H. Stability analysis of complex rock slopes reinforced with prestressed anchor cables and anti-shear cavities. Bull. Eng. Geol. Environ. 2019, 78, 2027–2039. [Google Scholar] [CrossRef]
- Yan, M.; Xia, Y.; Liu, T.; Bowa, V.M. Limit analysis under seismic conditions of a slope reinforced with prestressed anchor cables. Comput. Geotech. 2019, 108, 226–233. [Google Scholar] [CrossRef]
- Chen, S.; Yang, Z.; Zhang, W.; Li, L.; Zheng, Y.; Yuan, Y. Numerical simulation of the stability of a cutting slope and study on its reinforcement scheme. Adv. Civ. Eng. 2022, 2022, 5306923. [Google Scholar] [CrossRef]
- Liu, Y.; Lai, J.; Xu, J. Study on slope monitoring and stability based on bolt–cable combined support. Buildings 2024, 14, 886. [Google Scholar] [CrossRef]
- Xia, P.; Zeng, B.; Pan, Y. Stability Evaluation Method for Rock Slope-Anchorage Systems Based on Genetic Algorithms and Discrete Element Analysis. Appl. Sci. 2025, 15, 5057. [Google Scholar] [CrossRef]
- Wang, L.; Sun, D.; Yao, Y.; Wu, L.; Xu, Y. Kinematic limit analysis of three-dimensional unsaturated soil slopes reinforced with a row of piles. Comput. Geotech. 2020, 120, 103428. [Google Scholar] [CrossRef]
- Guo, M.; Li, C.; Wang, S.; Yin, S.; Liu, S.; Ge, X. Vector-sum method for 2D slope stability analysis considering vector characteristics of force. Int. J. Geomech. 2019, 19, 04019058. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, W.; Zheng, H. Stability analysis of slopes using the vector sum numerical manifold method. Bull. Eng. Geol. Environ. 2021, 80, 345–352. [Google Scholar] [CrossRef]
- Bian, X.; Liu, J.; Nie, L.; Ma, S.; Tao, W.; Qiu, C.; Xu, G. Reliability evaluation of a high slope reinforced by anchor based on the stochastic finite-element method: Case study. Case Stud. Constr. Mater. 2023, 19, e02650. [Google Scholar] [CrossRef]
- Chen, J.F.; Du, C.C.; Peng, M.; Sun, R.; Zhao, F.; Shi, Z.M. System reliability analysis of a slope stabilized with anchor cables and piles under seismic loading. Acta Geotech. 2023, 18, 4493–4514. [Google Scholar] [CrossRef]
- Xia, P.; Hu, X.; Wu, S.; Ying, C.; Liu, C. Slope Stability Analysis Based on Group Decision Theory and Fuzzy Comprehensive Evaluation. J. Earth Sci. 2020, 31, 1121–1132. [Google Scholar] [CrossRef]
- Wang, G.; Zhao, B.; Wu, B.; Zhang, C.; Liu, W. Intelligent prediction of slope stability based on visual exploratory data analysis of 77 in situ cases. Int. J. Min. Sci. Technol. 2023, 33, 47–59. [Google Scholar] [CrossRef]
- Sardana, S.; Verma, A.K.; Verma, R.; Singh, T.N. Rock slope stability along road cut of Kulikawn to Saikhamakawn of Aizawl, Mizoram, India. Nat. Hazards 2019, 99, 753–767. [Google Scholar] [CrossRef]
- Sardana, S.; Verma, A.K.; Singh, A.; Laldinpuia. Comparative analysis of rockmass characterization techniques for the stability prediction of road cut slopes along NH-44A, Mizoram, India. Bull. Eng. Geol. Environ. 2019, 78, 5977–5989. [Google Scholar] [CrossRef]
- Jingwen, L.; Jiangang, Q.; Yuanming, D.; Xu, F.; Xiaoli, L. Safety Evaluation Method of Antifloating Anchor System Based on Comprehensive Weighting Method and Gray-Fuzzy Theory. Math. Probl. Eng. 2020, 2020, 3216948. [Google Scholar] [CrossRef]
- Zhu, H.; Xiang, Q.; Luo, B.; Du, Y.; Li, M. Evaluation of failure risk for prestressed anchor cables based on the AHP-ideal point method: An engineering application. Eng. Fail. Anal. 2022, 138, 106293. [Google Scholar] [CrossRef]
- Wang, J.; Cao, Q.; Mi, X.; Li, D. Research on safety evaluation of bolt support based on analytic hierarchy process-entropy weight method. E3S Web Conf. 2020, 213, 03019. [Google Scholar] [CrossRef]
- Wang, J.; Apel, D.B.; Xu, H.; Wei, C. Evaluation of the performance of yielding rockbolts during rockbursts using numerical modeling method. Int. J. Coal Sci. Technol. 2022, 9, 87. [Google Scholar] [CrossRef]
- Gaurav, K.; Kumar, R.; Mandal, P.K.; Das, A.J. Evaluation of a novel pyramidal design of rock bolt bearing plate using analytical, experimental, and numerical methods. Eng. Struct. 2023, 297, 116998. [Google Scholar] [CrossRef]
- Ye, W.; Ma, Y.; Qin, C.; Wang, H.; Li, C.; Ding, Z. Effects of degraded durability on the long-term stability of in-service slopes with reinforced concreted support structures. Sci. Rep. 2024, 14, 21297. [Google Scholar] [CrossRef] [PubMed]
- Skipochka, S.; Krukovskyi, O.; Serhiienko, S.; Krasovskyi, I. Non-destructive testing of rock bolt fastening as an element of monitoring the state of mine workings. Min. Miner. Depos. 2019, 16–23. [Google Scholar] [CrossRef]
- Zatar, W.; Xiao, F.; Chen, G.; Nghiem, H. Assessment of the Conditions of Anchor Bolts Grouted with Resin and Cement Through Impact-Echo Testing and Advanced Spectrum Analysis. Buildings 2025, 15, 399. [Google Scholar] [CrossRef]
- Skipochka, S.; Krukovskyi, O.; Serhiienko, V.; Krasovskyi, I. Physical modeling of the rock bolt interaction with the rock massif. E3S Web Conf. 2019, 123, 01002. [Google Scholar] [CrossRef]
- Yu, S.; Zhu, W.; Niu, L. Experimental and numerical evaluation on debonding of fully grouted rockbolt under pull-out loading. Int. J. Coal Sci. Technol. 2022, 9, 8. [Google Scholar] [CrossRef]
- Aghababaei, S.; Jalalifar, H. A field data-based approach for risk and relative efficiency assessment of rock bolt designs in underground coal mines. Research Square 2022. [Google Scholar] [CrossRef]
- Sun, H.; Liu, H.; Liu, X.; Ye, Z. Mechanical testing and numerical simulation of intelligent terminal structure of rockbolt used as a deformable support and for safety monitoring in rock engineering. Tunn. Undergr. Space Technol. 2024, 148, 105769. [Google Scholar] [CrossRef]
- Fuławka, K.; Pytel, W.; Szumny, M.; Mertuszka, P.; Pałac-Walko, B.; Hartlieb, P.; Jakić, M.; Nöger, M. Prototype of instrumented rock bolt for continuous monitoring of roof fall hazard in deep underground mines. Sensors 2022, 23, 154. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, S.; Entezam, S.; Jodeiri Shokri, B.; Mirzaghorbanali, A.; Nourizadeh, H.; Motallebiyan, A.; Entezam, A.; McDougall, K.; Karunasena, W.; Aziz, N. Predicting grout’s uniaxial compressive strength (UCS) for fully grouted rock bolting system by applying ensemble machine learning techniques. Neural Comput. Appl. 2024, 36, 18387–18412. [Google Scholar] [CrossRef]
- Hosseini, S.; Jodeiri Shokri, B.; Mirzaghorbanali, A.; Nourizadeh, H.; Entezam, S.; Motallebiyan, A.; Entezam, A.; McDougall, K.; Karunasena, W.; Aziz, N. Predicting axial-bearing capacity of fully grouted rock bolting systems by applying an ensemble system. Soft Comput. 2024, 28, 10491–10518. [Google Scholar] [CrossRef]
- Taheri, A.; Tani, K. Assessment of the Stability of Rock Slopes by the Slope Stability Rating Classification System. Rock Mech. Rock Eng. 2010, 43, 321–333. [Google Scholar] [CrossRef]
- Song, Y.; Xue, H.; Meng, X. Evaluation method of slope stability based on the Qslope system and BQ method. Bull. Eng. Geol. Environ. 2019, 78, 4865–4873. [Google Scholar] [CrossRef]
- Moses, D.; Tumelo, K.D.; Sugeng, W. Rock slope stability analysis by using integrated approach. World J. Eng. Technol. 2020, 8, 405–428. [Google Scholar] [CrossRef]
- Mazzoccola, D.F.; Hudson, J.A. A comprehensive method of rock mass characterization for indicating natural slope instability. Q. J. Eng. Geol. Hydrogeol. 1996, 29, 37–56. [Google Scholar] [CrossRef]
- Basahel, H.; Mitri, H. Probabilistic assessment of rock slopes stability using the response surface approach—A case study. Int. J. Min. Sci. Technol. 2019, 29, 357–370. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, C.; Liu, T.; Ren, Z. A new method of assessing the stability of anti-dip bedding rock slopes subjected to earthquake. Bull. Eng. Geol. Environ. 2021, 80, 3693–3710. [Google Scholar] [CrossRef]
- Aladejare, A.E.; Akeju, V.O. Design and sensitivity analysis of rock slope using Monte Carlo simulation. Geotech. Geol. Eng. 2020, 38, 573–585. [Google Scholar] [CrossRef]
- Azarafza, M.; Nanehkaran, Y.A.; Rajabion, L.; Akgün, H.; Rahnamarad, J.; Derakhshani, R.; Raoof, A. Application of the modified Q-slope classification system for sedimentary rock slope stability assessment in Iran. Eng. Geol. 2020, 264, 105349. [Google Scholar] [CrossRef]
- Ghafour, B.D. Rock Slope Stability Assessment for Some Locations Within Koisanjaq City, Kurdistan Region, Iraq. Iraqi Geol. J. 2025, 58, 134–148. [Google Scholar] [CrossRef]
- Kim, H.; Rehman, H.; Ali, W.; Naji, A.M.; Kim, J.J.; Kim, J.; Yoo, H. Classification of factors affecting the performance of fully grouted rock bolts with empirical classification systems. Appl. Sci. 2019, 9, 4781. [Google Scholar] [CrossRef]
- Frenelus, W.; Peng, H.; Zhang, J. An insight from rock bolts and potential factors influencing their durability and the long-term stability of deep rock tunnels. Sustainability 2022, 14, 10943. [Google Scholar] [CrossRef]
- Yi, W.; Wang, M.; Zhao, S.; Tong, J.; Liu, C. The effect of rock hardness and integrity on the failure mechanism of mortar bolt composite structure in a jointed rock mass. Eng. Fail. Anal. 2023, 143, 106831. [Google Scholar] [CrossRef]
- Han, W.; Luan, H.; Liu, C. Assessment of bolt reinforcement effect based on analytic hierarchy process. Geotech. Geol. Eng. 2019, 37, 803–812. [Google Scholar] [CrossRef]
- Lin, M.; Zhang, F.; Wang, W. Experimental Study on Durability and Bond Properties of GFRP Resin Bolts. Materials 2024, 17, 2814. [Google Scholar] [CrossRef]
- SL386-2007; Code for Design of Slopes in Hydraulic and Hydroelectric Engineering. China Water & Power Press: Beijing, China, 2007. (In Chinese)
- SL/T 212-2020; Technical Specification for Prestressed Anchoring in Hydraulic Engineering. China Water & Power Press: Beijing, China, 2020. (In Chinese)
- Wu, R. Study on the Mechanism of Rainfall-Induced Landslides. Master’s Thesis, Central South University, Changsha, China, 2013. (In Chinese). [Google Scholar]
- Institute of Water Resources and Hydropower Research. Handbook of Rock Mechanics Parameters; China Electric Power Press: Beijing, China, 1991. (In Chinese) [Google Scholar]


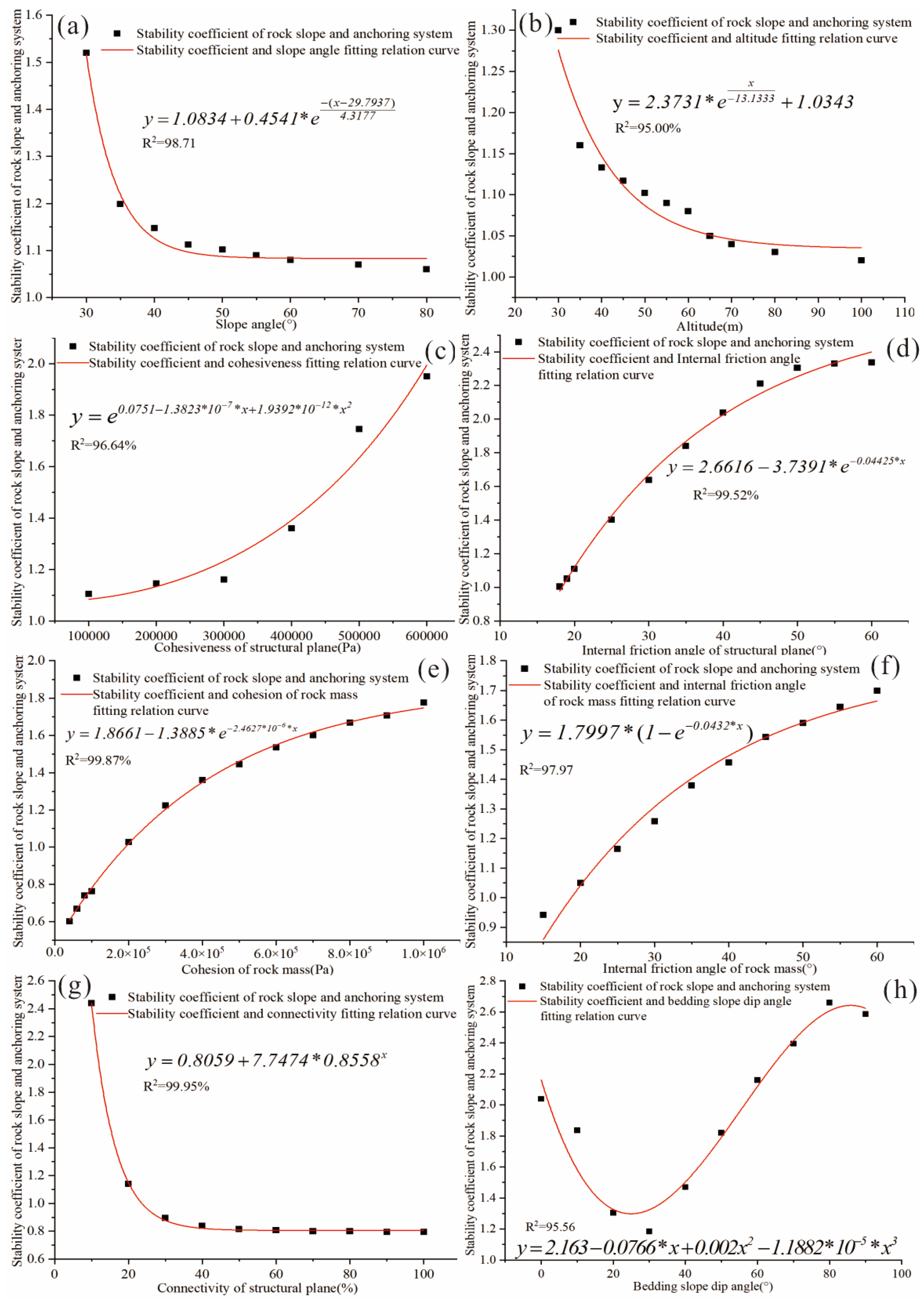
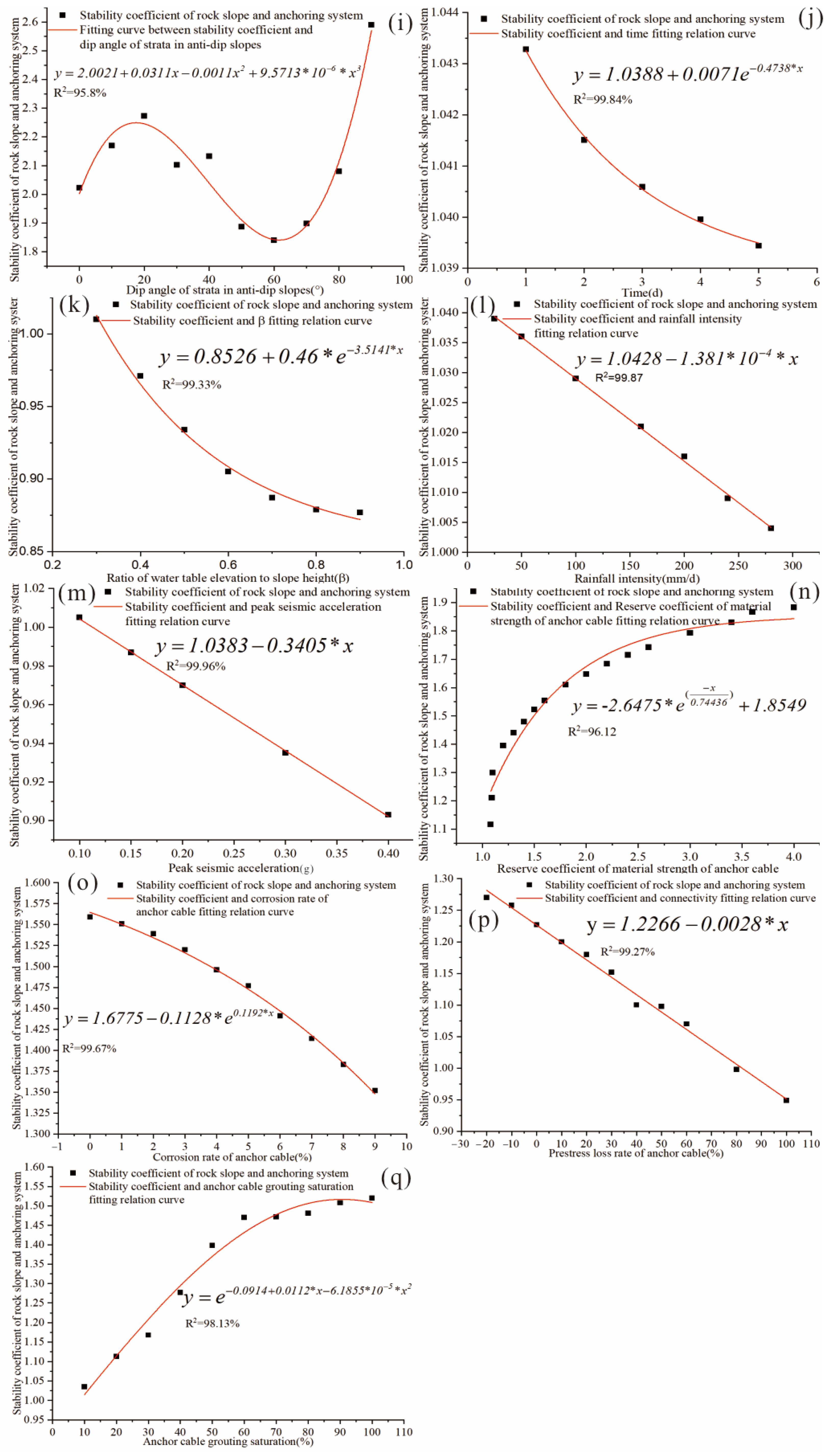
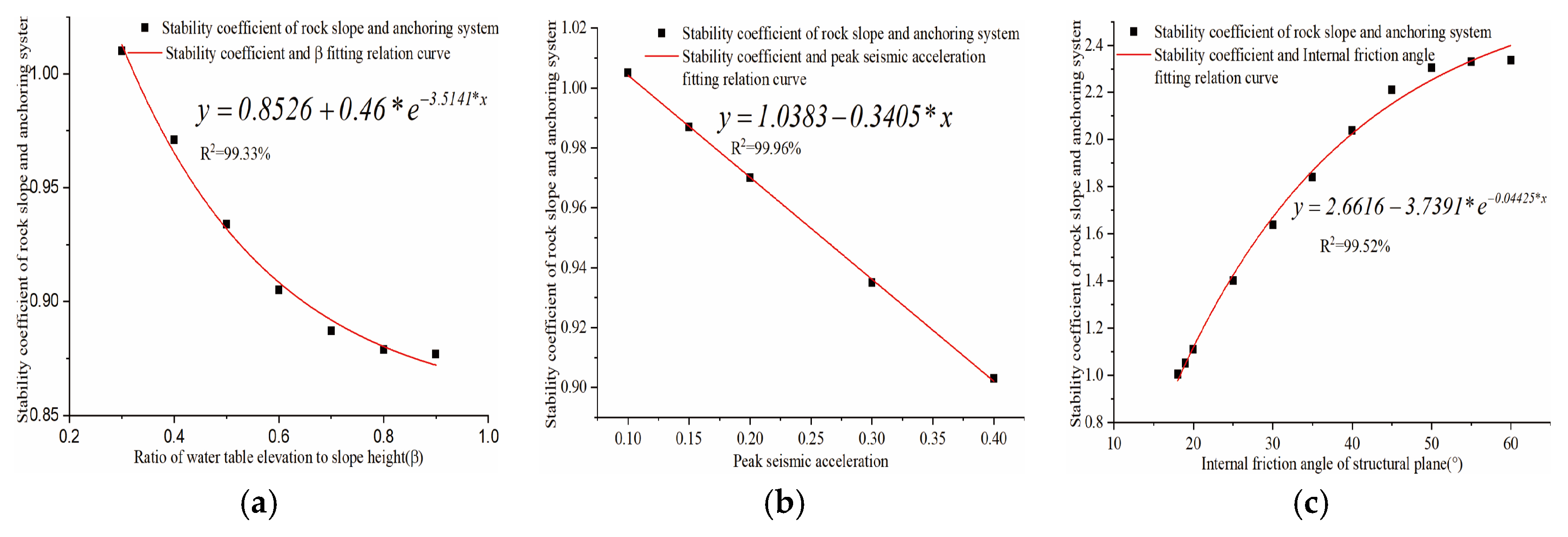

| Stability Evaluation Method | Description | Reference |
|---|---|---|
| Limit Equilibrium Method | Slope stability is evaluated by calculating the factor of safety (FoS) using limit equilibrium analysis, which is suitable for simple slope assessments. | Ullah [9] Bi [18] Yan [19] |
| Numerical Simulation Methods | Methods such as the Finite Element Method (FEM), Finite Difference Method (FDM), and Discrete Element Method (DEM) can be used to analyze the stress–strain behavior of complex slopes. | Ullah [9] Chen [20] Liu [21] Xia [22] |
| Artificial Intelligence Methods | Machine learning methods predict slope stability based on training data, making them suitable for large-scale data analysis. | Koopialipoor [10] |
| Limit Analysis Method | Plasticity theory is used to determine the conditions of slope failure, making this method suitable for investigating slope failure mechanisms. | Ullah [9] Wang [23] |
| Vector Sum Method | This method calculates the sliding direction and stability of slopes and is applicable in complex geological settings. | Ullah [9] Guo [24] Yang [25] |
| Reliability Theory | Reliability theory is applied to estimate the probability of failure in rock slopes, thereby enabling a probabilistic assessment of slope stability. | Bian [26] Chen [27] |
| Fuzzy Comprehensive Evaluation Method | The membership degree of each indicator is determined based on fuzzy set theory. According to the weights and membership degrees, fuzzy operations are applied to obtain the membership degree at the criterion level, thereby enabling the evaluation of slope stability. | Xia [28] |
| Stability Evaluation Method | Artificial Intelligence Algorithms | Reference |
|---|---|---|
| Slope Stability Evaluation Method Based on Artificial Intelligence Algorithms | Artificial Neural Network (ANN), Imperialist Competitive Algorithm (ICA), Genetic Algorithm (GA), Particle Swarm Optimisation (PSO), and Artificial Bee Colony (ABC). | Koopialipoor [10] |
| Artificial Neural Network (ANN) combined with an improved Sine Cosine Algorithm (SCA). | Khajehzadeh [11] | |
| Decision Tree (DT), Random Forest (RF), and AdaBoost. | Asteris [12] | |
| Support Vector Machine (SVM), Gradient Boosting Regression (GBR), and Bagging methods. | Lin [13] | |
| AdaBoost, Gradient Boosting Machine (GBM), Bagging, Extremely Randomized Trees (ET), Random Forest (RF), Histogram-Based Gradient Boosting (HistGB), Voting, and Stacking. | Lin [14] | |
| Single-Valued Neutrosophic Number (SVNN) and Adaptive Neuro-Fuzzy Inference System (ANFIS). | Qin [15] | |
| Neuro-Fuzzy (NF) systems integrated with Invasive Weed Optimization (IWO) and Elephant Herding Optimization (EHO). | Moayedi [16] | |
| Multilayer Perceptron (MLP), Support Vector Machine (SVM), k-Nearest Neighbors (k-NN), Decision Tree (DT), and Random Forest (RF). | Ahangari [17] | |
| Intelligent visual analysis utilizing methods such as Principal Component Analysis (PCA), Kernel PCA, Factor Analysis (FA), Independent Component Analysis (ICA), Non-negative Matrix Factorisation (NMF), and t-distributed Stochastic Neighbor Embedding (t-SNE). | Wang [29] |
| Non-Destructive Testing Technologies | Detection Objective | Reference |
|---|---|---|
| Ultrasonic Testing | Assess internal defects and corrosion level of rock bolt | Lama [5] Yu [41] |
| Fibre Optic Sensing Technology | Real-time monitoring of strain and deformation in rock bolt | Lama [5] |
| Piezoelectric Sensors | Dynamic response of rock bolt | Lama [5] |
| Electromagnetic Induction Technology | Evaluate metal loss in rock bolt | Lama [5] |
| Impact-Echo Method | Detect the integrity of rock bolt | Lama [5] Skipochka [38] Zatar [39] |
| Acoustic Emission Technology | Identify microcracks and damage in rock bolt | Lama [5] |
| Vibration Attenuation Measurement | The rock bolt fastening quality | Skipochka [38] |
| Indicator Category | Contents Included | Reference |
|---|---|---|
| Geomechanical Indicators | Uniaxial compressive strength, rock mass type, BQ (basic quality index of rock mass), friction angle of geomaterials, cohesion of geomaterials, unit weight of geomaterials, rock density, lithology, geomaterial type, dry density of rock mass, dip, dip direction and friction angle of dominant discontinuities, tensile strength of rock layers and shear strength of joints, depth of tensile fractures | Taheri [47]; Song [48]; Koopialipoor [10]; Khajehzadeh [11]; Asteris [12]; Lin [13]; Lin [14]; Qin [15]; Moayedi [16]; Ahangariet [17]; Wang [29]; Moses [49]; Mazzoccola [50]; Basahel [51]; Zheng [52]; Aladejare [53] |
| Topographic and Geometric Structure Indicators | Qslope (rock slope quality evaluation), slope angle, slope height, potential slip surface angle, elevation, slope aspect | Song [48]; Azarafza [54]; Ghafour [55]; Koopialipoor [10]; Khajehzadeh [11]; Asteris [12]; Lin [13]; Lin [14]; Qin [15]; Moayedi [16]; Ahangariet [17]; Wang [29] |
| Environmental and Dynamic Indicators | Peak ground acceleration, horizontal acceleration coefficient, pore water pressure, stream power index (SPI), topographic wetness index, direction of seismic inertial force, variation in water depth | Koopialipoor [10]; Khajehzadeh [11]; Asteris [12]; Lin [13]; Lin [14]; Qin [15]; Moayedi [16]; Mazzoccola [50]; Zheng [52]; Aladejare [53] |
| Comprehensive Safety Performance Indicators | BQ, Qslope, geological strength index (GSI), slope mass rating (SMR), continuous slope mass rating (CoSMR), Chinese slope mass rating (CSMR), failure approaching index (FAI) of anchoring structures | Song [48]; Azarafza [54]; Sardana [30]; Sardana [31]; Zhu [33] |
| Anchoring System Indicators | Rock mass integrity, influence of groundwater, properties of anchoring materials, prestress level, installation accuracy, grouting effectiveness, long-term stress variation, environmental impact, support parameters, quality of bolts and accessories, construction management and monitoring level, rock strength, development of joints, rebar type, grouting materials, borehole quality, grouting methods, groundwater flow, temperature variation, static load, dynamic impact, corrosion resistance and tensile strength of materials, grouting quality, anchoring depth, humidity, chemical erosion, stress redistribution, deformation control, rock hardness and integrity, compressive strength of grouting materials, rock mass classification, anchor rod diameter, number of bolts, excavation timing, layer characteristics, anchorage length, bolt type and construction technology, grouting quality, bolt type, installation angle, water–cement ratio of grout body, curing time and properties of grouting materials | Zhu [33]; Wang [34]; Kim [56]; Frenelus [57]; Yi [58]; Hosseini [45]; Han [59]; Luga [7]; Lin [60]; Hosseini [46] |
| Rock Slope Height | Cohesion of Rock Mass | Distribution of Isolated or Overhanging Rock Blocks | Earthquake |
|---|---|---|---|
| Rock Slope Angle | Internal Friction Angle of Rock Mass | Lithology | Strength Reserve Coefficient |
| Basic Quality Grade of Rock Mass | Included Angle of Discontinuities in Wedge Structure | Drainage System | Visual Condition |
| Connectivity of Discontinuities | Dip Angle of Adverse Bedding Plane | Rainfall Intensity | Grouting Saturation |
| Cohesion of Discontinuities | Dip Angle of Favorable Bedding Plane | Rainfall Duration | Corrosion Rate |
| Internal Friction Angle of Discontinuities | Degree of Weathering of Rock Mass | Groundwater Development | Prestress Loss Rate |
| P-wave Velocity of Rock Mass | Riverbank Erosion | Unit Weight of Rock | Gully Development |
| Jointing Degree (Fracturing Degree) | Slope Crest Load | Erosion Characteristics at Slope Angle | Surface Water |
| Fracture Density | Distance from River Influence | Elastic Modulus | In situ Stress |
| Criterion Layer | Project Layer | Indicator Layer | Unit or Evaluation Grade | Acquisition Method |
|---|---|---|---|---|
| Stability of Rock Slope–Anchoring System | Slope Geometrical Features | Slope Angle | ° | Surveying |
| Slope Height | m | Surveying | ||
| Hydro-meteorological Conditions | Drainage System | Excellent, Good, Fair, Poor, Very Poor | Site Investigation | |
| Historical Maximum Daily Rainfall | mm | Monitoring | ||
| Rainfall Duration | d | Monitoring | ||
| Groundwater Level Status | Ratio of Groundwater Level to Slope Height | Monitoring | ||
| Rock Mass Conditions | Basic Quality Grade of Rock Mass | I, II, III, IV, V | Testing | |
| Connectivity of Discontinuities | % | Site Investigation | ||
| Cohesion of Discontinuities | KPa | Testing | ||
| Internal Friction Angle of Discontinuities | ° | Testing | ||
| Rock Mass Cohesion | KPa | Testing | ||
| Rock Mass Internal Friction Angle | ° | Testing | ||
| Included Angle of Structural Planes | ° | Site Investigation | ||
| Dip Angle of Counter-Inclined Rock Strata | ° | Site Investigation | ||
| Dip Angle of Inclined Rock Strata | ° | Site Investigation | ||
| Degree of Weathering | Unweathered, Slightly Weathered, Moderately Weathered, Highly Weathered, Completely Weathered | Site Investigation | ||
| Distribution of Isolated or Suspended Rock Blocks | Site Investigation | |||
| Lithology | Hard, Medium Hard, Soft, Moderately Soft, Very Soft | Testing | ||
| Accidental Factors | Earthquake | I, II, III, IV, V | Monitoring | |
| Anchoring Structure Parameters | Strength Reserve Coefficient | % | Design | |
| Visual Condition | I, II, III, IV, V | Site Investigation | ||
| Grouting Saturation | % | Testing | ||
| Corrosion Degree of Anchor Cables | % | Testing | ||
| Prestress Loss Rate | % | Testing |
| Type | Indicator | ||
|---|---|---|---|
| Qualitative Indicators | Drainage System | Degree of Weathering | Lithology |
| Rock Mass Quality Grade | Distribution of Isolated or Overhanging Rock Blocks | Visual Condition | |
| Quantitative Indicators | Rock Slope Height | Internal Friction Angle of Rock | Groundwater Development |
| Rock Slope Angle | Interfacial Angle of Wedge-shaped Discontinuities | Seismic Activity | |
| Joint Connectivity Rate | Dip Angle of Adversely Dipping Discontinuities | Strength Reserve Coefficient | |
| Joint Cohesion | Dip Angle of Favorably Dipping Discontinuities | Grouting Saturation | |
| Joint Internal Friction Angle | Maximum Daily Historical Rainfall | Corrosion Rate | |
| Rock Cohesion | Rainfall Duration | Prestress Loss Rate | |
| Indicator | Grading Standard |
|---|---|
| Drainage System | Excellent, Good, Moderate, Poor, Very Poor |
| Basic Quality Grade of Rock Mass | I, II, III, IV, V |
| Degree of Weathering | Unweathered, Slightly Weathered, Moderately Weathered, Strongly Weathered, Completely Weathered |
| Distribution of Boulders or Overhanging Blocks | No signs of surface loosening; small overhanging blocks (0.01 < volume < 1 m3); some loosened surfaces and small overhanging blocks; several loosened surfaces and small overhanging blocks; potentially detached overhanging blocks (volume > 1 m3) |
| Lithology | Hard Rock, Moderately Hard Rock, Soft Rock, Rather Soft Rock, Very Soft Rock |
| Surface Appearance Condition | I, II, III, IV, V |
| Operating Conditions | Slope Stability Grade | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| Normal Operating Condition | 1.30~1.25 | 1.25~1.20 | 1.20~1.15 | 1.15~1.10 | 1.10~1.05 |
| Unusual Operating Condition I | 1.25~1.20 | 1.20~1.15 | 1.15~1.10 | 1.10~1.05 | |
| Unusual Operating ConditionII | 1.15~1.10 | 1.10~1.05 | 1.05~1.00 | ||
| Type | Shear Strength Parameters | Bulk Modulus (Pa) | Shear Modulus (Pa) | |
|---|---|---|---|---|
| C (Pa) | φ (°) | |||
| Rock Mass | 1 × 106 | 23.0 | 2 × 108 | 1 × 108 |
| Type | Shear Strength Parameters of Grouted Body | Stiffness of Grouted Body (Pa/m) | Perimeter of Grouted Body (m) | Cross-Sectional Area (m2) | Young’s Modulus | Yield Strength of Anchor Cable (Pa) | |
|---|---|---|---|---|---|---|---|
| C (Pa) | Φ (°) | ||||||
| Anchor Cable | 1.75 × 106 | 20 | 1.12 × 107 | 1.75 × 106 | 1.81 × 10−4 | 2 × 108 | 4000 |
| Type | Shear Strength Parameters | Saturated Water Content | Saturated Permeability Coefficient (m/d) | Density (kN/m3) | |
|---|---|---|---|---|---|
| C (Pa) | φ (°) | ||||
| Rock Mass | 30 × 106 | 28.0 | 0.38 | 0.579 | 20 |
| Type | Pullout Strength (kPa) | Tensile Strength (kN) | Bond Length (m) | Shear Strength (kN) | Bond Diameter (m) | Anchor Cable Spacing (m) | Safety Factor for Pullout Resistance | Safety Factor for Tensile Resistance | Safety Factor for Shear Resistance | Anchor Cable Length | Anchor Cable Angle |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Anchor Cable | 300 | 2000 | 13 | 0 | 0.383 | 4 | 4.5 | 2 | 1 | 25 | 45° |
| Indicator | Classification Interval | Stability Grade | Decision Attribute |
|---|---|---|---|
| Elevation of the Rock Slope–Anchoring System (m) | [0~3] | V | (Safe) |
| [3~7] | IV | (Basically Safe) | |
| [7~12] | III | (Potential Risk) | |
| [12~21] | II | (Unsafe) | |
| [21~100] | I | (Extremely Unsafe) | |
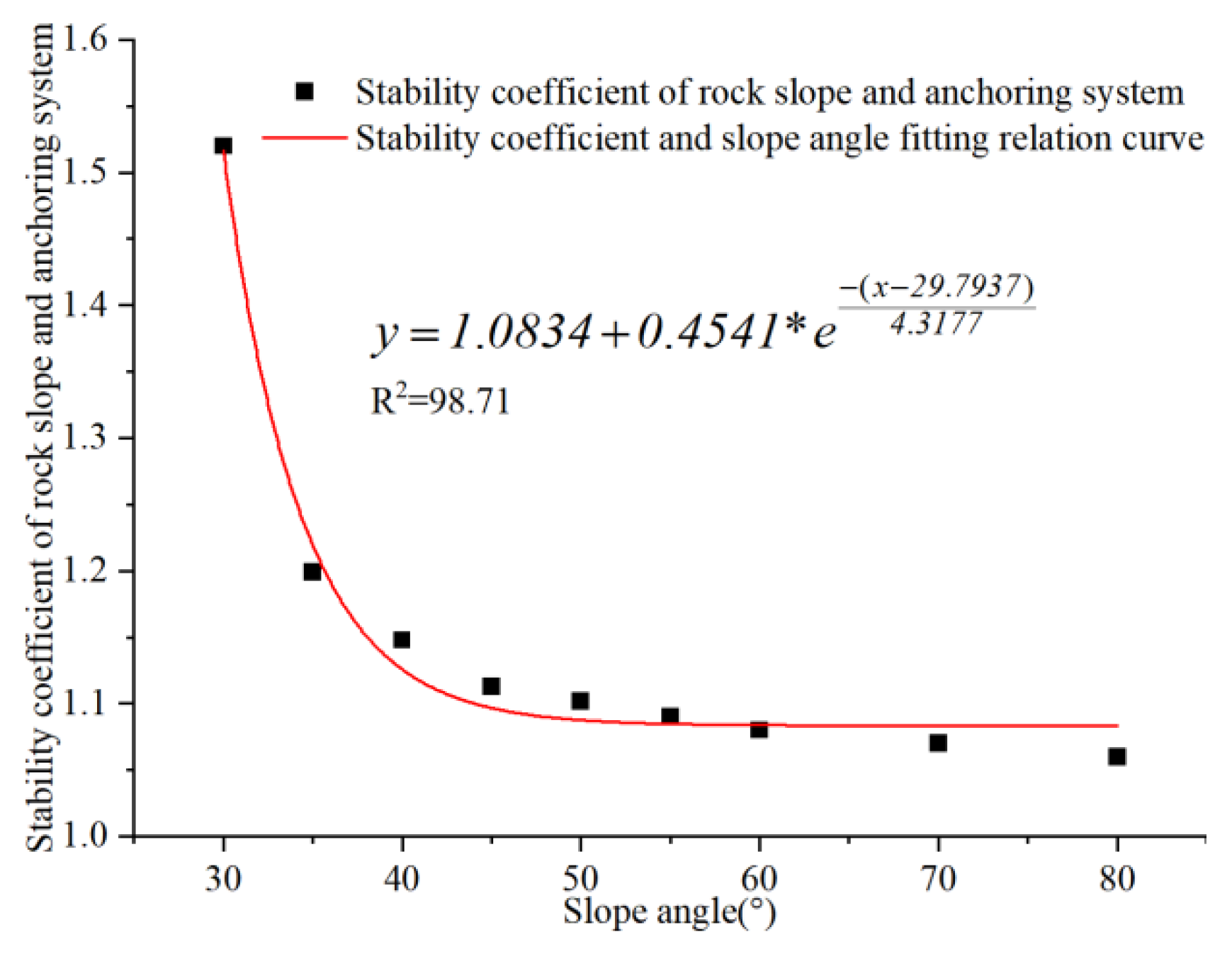
| Slope Angle of the Rock Slope–Anchoring System(°) | [30~31] | V | (Safe) |
| [31~32.2] | IV | (Basically Safe) | |
| [32.2~34] | III | (Potential Risk) | |
| [34~37] | II | (Unsafe) | |
| [37~80] | I | (Extremely Unsafe) |
| Rainfall Intensity (mm/d) | Q < 10 | 10 < Q < 25 | 25 < Q < 50 | 50 < Q < 100 | 100 < Q |
|---|---|---|---|---|---|
| Rainfall Intensity Classification | Light Rain | Moderate Rain | Heavy Rain | Rainstorm | Severe Rainstorm |
| Indicator | Classification Interval | Stability Grade | Decision Attribute |
|---|---|---|---|
| Rainfall Duration(d) | [0–0.4] | V | (Safe) |
| [0.4~0.9] | IV | (Basically Safe) | |
| [0.9~1.6] | III | (Potential Risk) | |
| [1.6~2.7] | II | (Unsafe) | |
| [2.7~5] | I | (Extremely Unsafe) | |
| Rainfall Intensity (mm/d) | [[0–30] | V | (Safe) |
| [30~60] | IV | (Basically Safe) | |
| [60~90] | III | (Potential Risk) | |
| [90~120] | II | (Unsafe) | |
| [120~150] | I | (Extremely Unsafe) | |
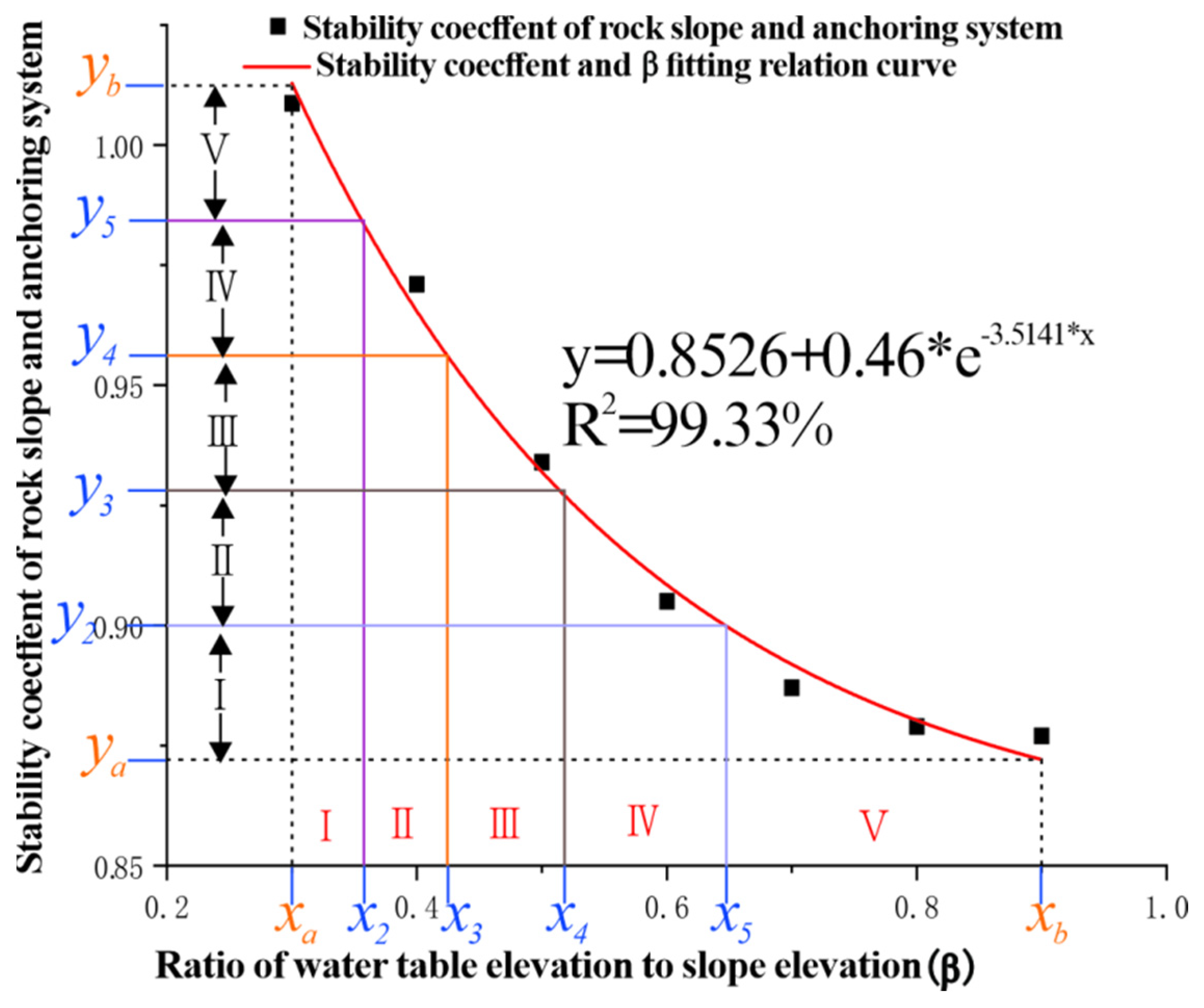
| Groundwater Development (Ratio of Groundwater Head to Slope Elevation) | [0–0.06] | V | (Safe) |
| [0.06~0.14] | IV | (Basically Safe) | |
| [0.14~0.24] | III | (Potential Risk) | |
| [0.24~0.41] | II | (Unsafe) | |
| [0.41~0.9] | I | (Extremely Unsafe) |
| Basic Seismic Intensity | 7 Degrees | 8 Degrees | 9 Degrees | ||
|---|---|---|---|---|---|
| Peak Ground Acceleration | 0.1 g | 0.15 g | 0.2 g | 0.3 g | 0.4 g |
| Comprehensive Horizontal Seismic Coefficient | 0.025 | 0.038 | 0.05 | 0.075 | 0.1 |
| Indicator | Classification Interval | Stability Grade | Decision Attribute |
|---|---|---|---|
| Peak Ground Acceleration (g) | [0–0.08] | V | (Safe) |
| [0.08~0.16] | IV | (Basically Safe) | |
| [0.16~0.24] | III | (Potential Risk) | |
| [0.24~0.32] | II | (Unsafe) | |
| [0.32~0.4] | I | (Extremely Unsafe) |
| Indicator | Value Range |
|---|---|
| Cohesion of Discontinuities | 10 kPa~600 kPa |
| Internal Friction Angle of Discontinuities | 10°~60° |
| Cohesion of Rock Mass | 0 kPa~4000 kPa |
| Internal Friction Angle of Rock Mass | 10°~70° |
| Connectivity Rate of Discontinuities | 10%~100% |
| Dip Angle of Rock Layers in Dip Slope | 0°~90° |
| Dip Angle of Rock Layers in Anti-dip Slope | 0°~90° |
| Intersection Angle of Discontinuities in Wedge Body | 20°~150° |
| Indicator | Classification Interval | Stability Grade | Decision Attribute |
|---|---|---|---|
| Joint cohesion (kPa) | [0–322.41] | I | (Extremely Unsafe) |
| [322.41~425.77] | II | (Unsafe) | |
| [425.77~498.01] | III | (Potential Risk) | |
| [498.01~554.1] | IV | (Basically Safe) | |
| [554.1~600] | V | (Safe) | |
| Joint internal friction angle (°) | [10–14.4] | I | (Extremely Unsafe) |
| [14.4~20] | II | (Unsafe) | |
| [20~27.3] | III | (Potential Risk) | |
| [27.3~38.2] | IV | (Basically Safe) | |
| [38.2~60] | V | (Safe) | |
| Joint connectivity rate (%) | [10–11.4] | V | (Safe) |
| [11.4~13.3] | IV | (Basically Safe) | |
| [13.3~15.9] | III | (Potential Risk) | |
| [15.9~20.3] | II | (Unsafe) | |
| [20.3~100] | I | (Extremely Unsafe) | |
| Dip angle of bedding planes in dip direction (°) | [69.56–88] * [88–90] | V | (Safe) |
| [60.35–69.56] * | IV | (Basically Safe) | |
| [51.87~60.35] * [0–3.6] | III | (Potential Risk) | |
| [42.65~51.87] * [3.6–9.34] | II | (Unsafe) | |
| [24.68–42.65] * [9.34–24.68] | I | (Extremely Unsafe) | |
| Dip angle of bedding planes in opposite direction (°) | [87.08–90] * | V | (Safe) |
| [83.68~87.08] * | IV | (Basically Safe) | |
| [79.49–83.68] * | III | (Potential Risk) | |
| [73.75–79.49] * [6.05–19] * | II | (Unsafe) | |
| [19–35.13] | I | (Extremely Unsafe) | |
| Rock mass cohesion (kPa) | [0–90.6] * | I | (Extremely Unsafe) |
| [90.6~207.4] * | II | (Unsafe) | |
| [207.4–372] * | III | (Potential Risk) | |
| [372–653.4] * | IV | (Basically Safe) | |
| [653.4–4000] * | V | (Safe) | |
| Rock mass internal friction angle (°) | [10–14.74] * | I | (Extremely Unsafe) |
| [14.74~20.7] * | II | (Unsafe) | |
| [20.7–28.75] * | III | (Potential Risk) | |
| [28.75–41.19] * | IV | (Basically Safe) | |
| [41.19–70] * | V | (Safe) | |
| Included angle of wedge-shaped structural planes (°) | [20–28.22] | V | (Safe) |
| [28.22~38.7] | IV | (Basically Safe) | |
| [38.7–53.18] | III | (Potential Risk) | |
| [53.18–76.77] | II | (Unsafe) | |
| [76.77–150] | I | (Extremely Unsafe) |
| Indicator | Classification Interval | Stability Grade | Decision Attribute |
|---|---|---|---|
| Strength Reserve Factor | [1–1.15] * | I | (Extremely Unsafe) |
| [1.15~1.35] * | II | (Unsafe) | |
| [1.35–1.61] * | III | (Potential Risk) | |
| [1.61–2.02] * | IV | (Basically Safe) | |
| [2.02–3] * | V | (Safe) | |
| Grouting Saturation (%) | [10–20] * | I | (Extremely Unsafe) |
| [20~30] * | II | (Unsafe) | |
| [30–42] * | III | (Potential Risk) | |
| [42–56] * | IV | (Basically Safe) | |
| [56–100] * | V | (Safe) | |
| Corrosion Rate (%) | [0–5.8] | V | (Safe) |
| [5.8~9.2] | IV | (Basically Safe) | |
| [9.2–11.6] | III | (Potential Risk) | |
| [11.6–13.5] | II | (Unsafe) | |
| [13.5–15] | I | (Extremely Unsafe) | |
| Prestress Loss Rate (%) | [[0–20] | V | (Safe) |
| [20~40] | IV | (Basically Safe) | |
| [[40–60] | III | (Potential Risk) | |
| [[60–80] | II | (Unsafe) | |
| [[80–100] | I | (Extremely Unsafe) |
| Indicator | Grading Criteria | Indicator | Grading Criteria | Indicator | Grading Criteria |
|---|---|---|---|---|---|
| Slope Height A1 (m) | [0~3] | Included angle of wedge-shaped structural planes B7 (°) | [20~28.22] | Rainfall Duration C3 (d) | [0~0.4] |
| [3~7] | [28.22~38.7] | [0.4~0.9] | |||
| [7~12] | [38.7–53.18] | [0.9~1.6] | |||
| [12~21] | [53.18–76.77] | [1.6~2.7] | |||
| [21~100] | [76.77–150] | [2.7~5] | |||
| Slope Angle A2 (°) | [30~31] | Dip angle of bedding planes in opposite direction B8 (°) | [87.08~90] | Groundwater Development C4(Ratio of Groundwater Head to Slope Elevation) | [0~0.06] |
| [31~32.2] | [83.68~87.08] * | [0.06~0.14] | |||
| [32.2~34] | [79.49~83.68] * | [0.14~0.24] | |||
| [34~37] | [73.75~79.49] * [6.05~19] * [19~35.13] | [0.24~0.41] | |||
| [37~80] | [0~6.05] * [35.13~58.14] | [0.41~0.9] | |||
| Basic Quality Grade of Rock Mass B1 | V | Dip angle of bedding planes in dip direction B9 (°) | [69.56~88] * [88~90] | Seismic Activity D1 (peak ground acceleration) | [0~0.08 g] |
| IV | [60.35~69.56] * | [0.08 g~0.16 g] | |||
| III | [51.87~60.35] * [0~3.6] | [0.16 g~0.24 g] | |||
| II | [42.65~51.87] * [3.6~9.34] | [0.24 g~0.32 g] | |||
| I | [24.68~42.65] * [9.34~24.68] | [0.32 g~0.4 g] | |||
| Discontinuity Connectivity Rate B2 (%) | [10~11.4] | Degree of Weathering B10 | Unweathered | Strength Reserve Factor E1 | [1~1.15] * |
| [11.4~13.3] | Slightly Weathered | [1.15~1.35] * | |||
| [13.3~15.9] | Moderately Weathered | [1.35~1.61] * | |||
| [15.9~20.3] | Strongly Weathered | [1.61~2.02] * | |||
| [20.3~100] | Completely Weathered | [2.02~3] * | |||
| Cohesion of Discontinuities B3 (KPa) | [0–322.41] | Distribution of Boulders or Overhanging Blocks B11 | No signs of surface loosening | Surface Appearance Condition E2 | V |
| [322.41~425.77] | Small overhanging blocks (0.01 < volume < 1 m3) | IV | |||
| [425.77~498.01] | Some loosened surfaces and small overhanging blocks | III | |||
| [498.01~554.1] | Several loosened surfaces and small overhanging blocks | II | |||
| [554.1~600] | Potentially detached overhanging blocks (volume > 1 m3) | I | |||
| Internal Friction Angle of Discontinuities B4 (°) | [10~14.4] | Lithology B12 | Hard Rock | Grouting Saturation E3 (%) | [10~20] * |
| [14.4~20] | Moderately Hard Rock | [20~30] * | |||
| [20~27.3] | Soft Rock | [30~42] * | |||
| [27.3~38.2] | Rather Soft Rock | [42~56] * | |||
| [38.2~60] | Very Soft Rock | [56~100] * | |||
| Rock Mass Cohesion B5 (KPa) | [0~90.6] * | Drainage System C1 | Excellent | Corrosion Rate E4 (%) | [0~5.8] |
| [90.6~207.4] * | Good | [5.8~9.2] | |||
| [207.4~372] * | Moderate | [9.2~11.6] | |||
| [372~653.4] * | Poor | [11.6~13.5] | |||
| [653.4~4000] * | Very Poor | [13.5~15] | |||
| Internal Friction Angle of Rock Mass B6 (°) | [10~14.74] * | Rainfall Intensity C2 (mm/d) | [0~30] | Prestress Loss Rate E5 (%) | [0~20] |
| [14.74~20.7] * | [30~60] | [20~40] | |||
| [20.7~28.75] * | [60~90] | [40~60] | |||
| [28.75~41.19] * | [90~120] | [60~80] | |||
| [41.19~70] * | [120~150] | [80~100] |
| Grading Standard Determination Method | Accuracy |
| Grading Standard Determination Method Based on Stability Influence Patterns | 75.3% |
| Equal Interval Grading Standard Determination Method | 65.2% |
| Difference | 10.1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, P.; Zeng, B.; Liu, J.; Pan, Y. Study on the Stability Evaluation Index System for Rock Slope–Anchoring Systems. Appl. Sci. 2025, 15, 9147. https://doi.org/10.3390/app15169147
Xia P, Zeng B, Liu J, Pan Y. Study on the Stability Evaluation Index System for Rock Slope–Anchoring Systems. Applied Sciences. 2025; 15(16):9147. https://doi.org/10.3390/app15169147
Chicago/Turabian StyleXia, Peng, Bowen Zeng, Jie Liu, and Yiheng Pan. 2025. "Study on the Stability Evaluation Index System for Rock Slope–Anchoring Systems" Applied Sciences 15, no. 16: 9147. https://doi.org/10.3390/app15169147
APA StyleXia, P., Zeng, B., Liu, J., & Pan, Y. (2025). Study on the Stability Evaluation Index System for Rock Slope–Anchoring Systems. Applied Sciences, 15(16), 9147. https://doi.org/10.3390/app15169147






