Axial Compression Behavior of Steel Angles with Double-Shear Splice Connections in Transmission Towers
Abstract
1. Introduction
2. Experimental Program
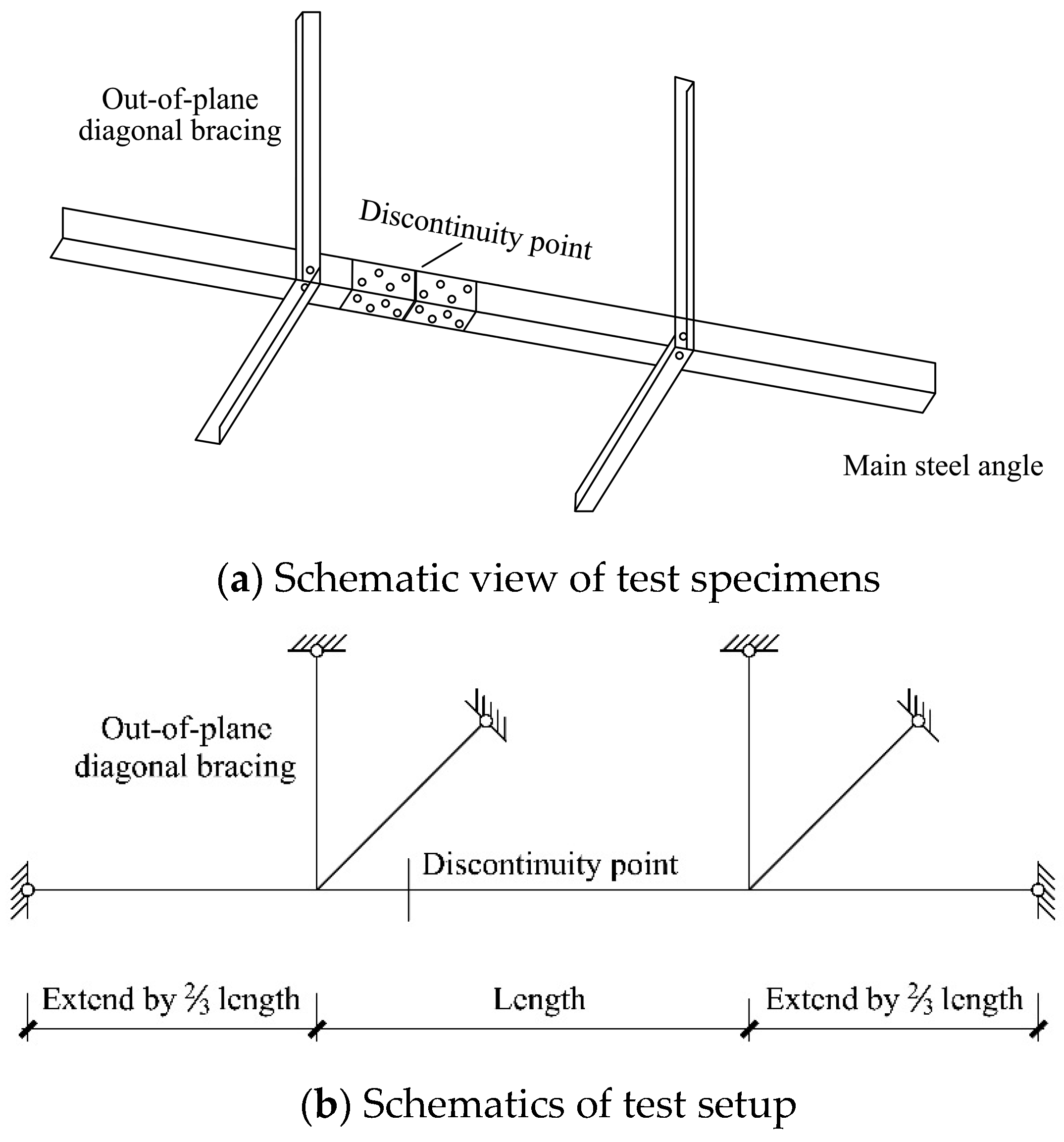
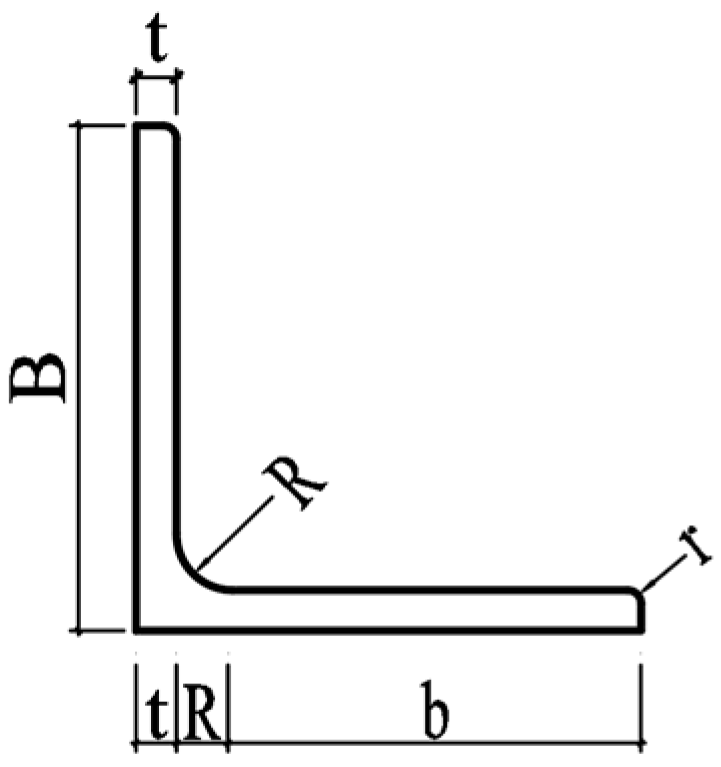
2.1. Specimen Design
2.2. Test Setup and Loading Procedures
2.3. Mechanical Properties of Steel Angles
3. Experimental Tests and Discussions
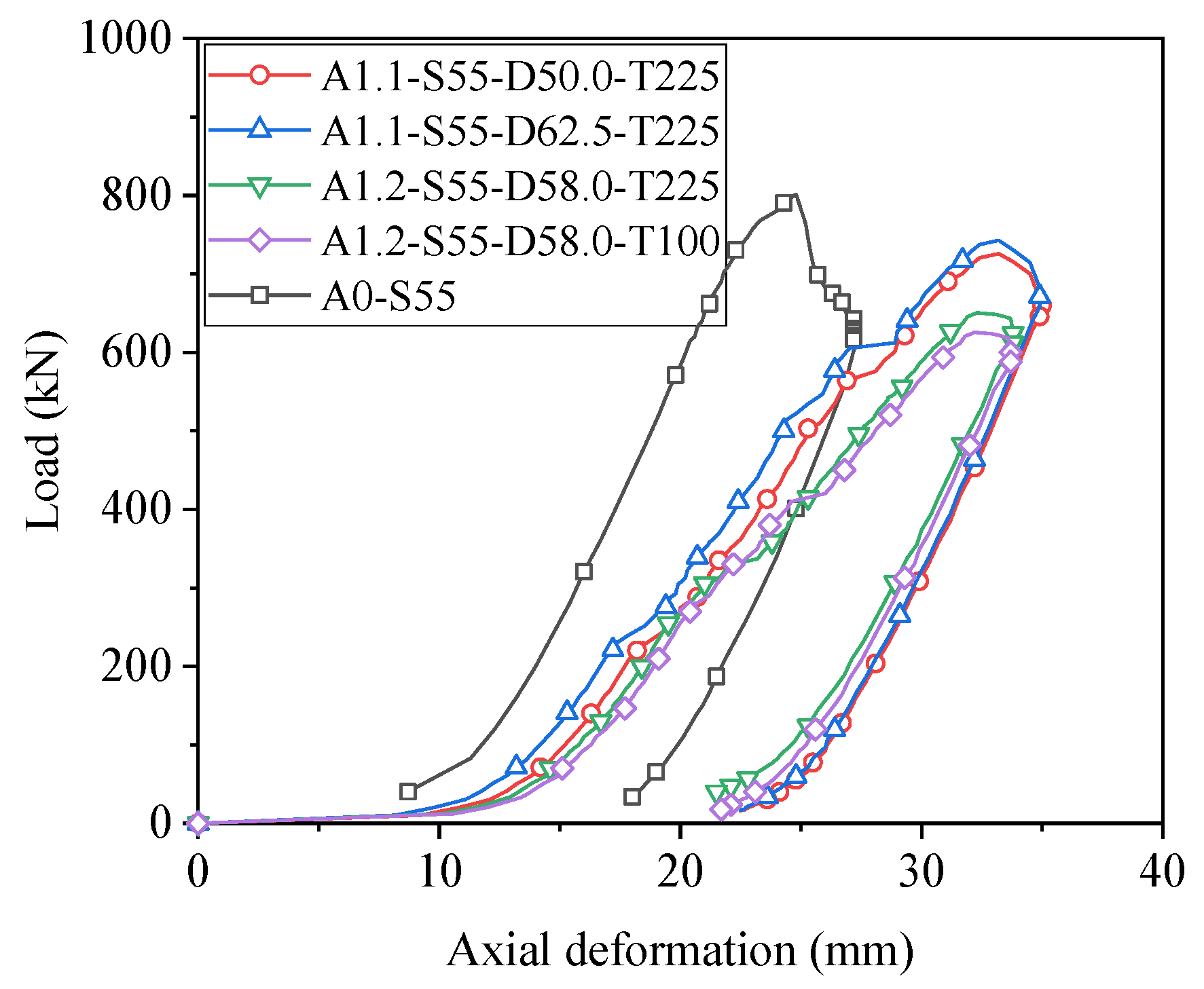
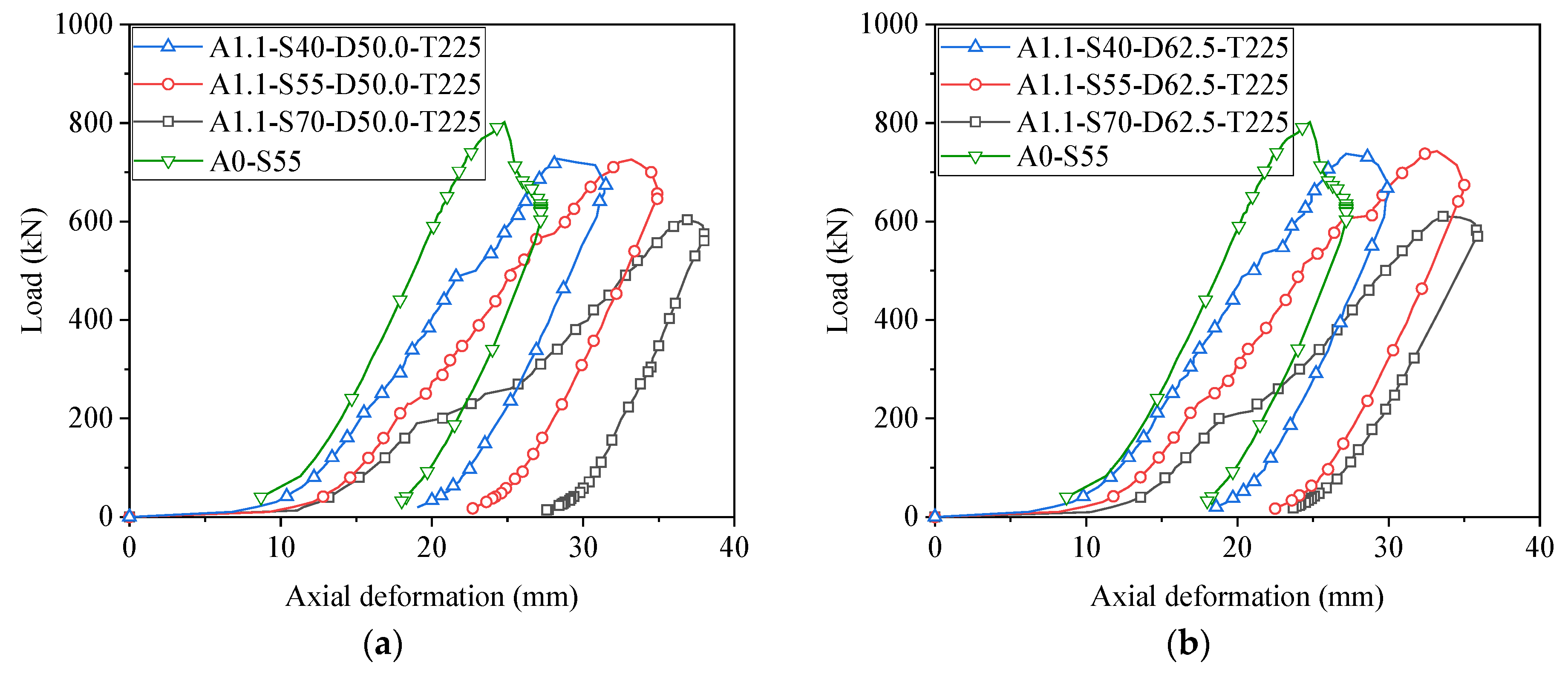
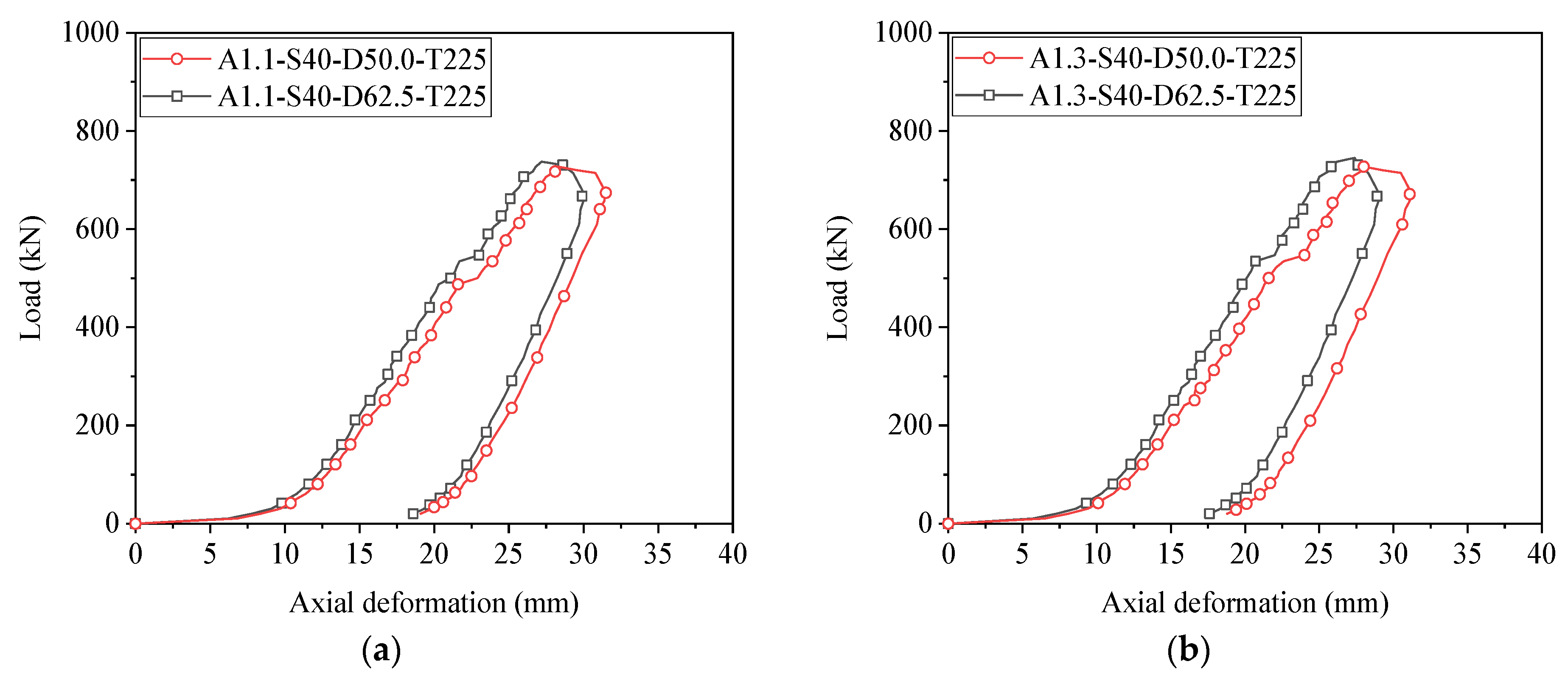
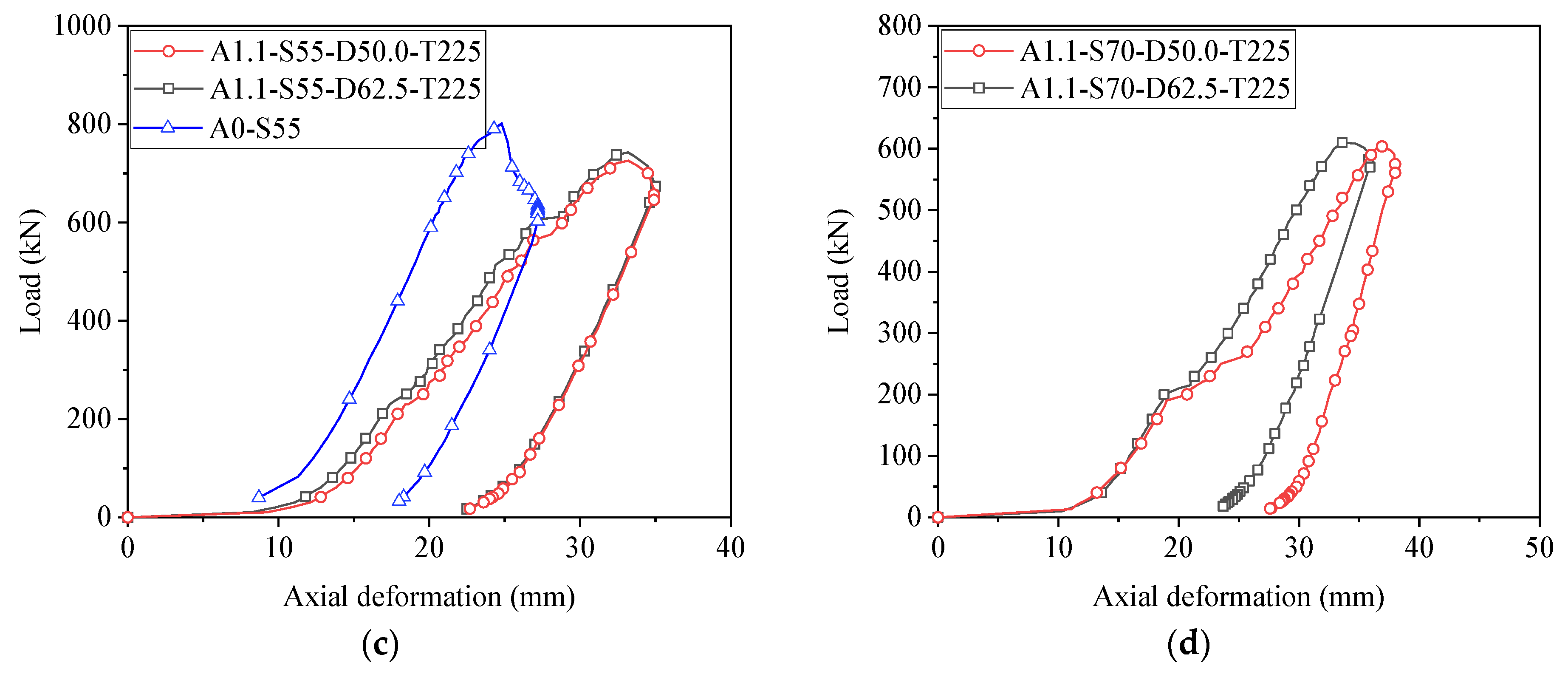
3.1. Load-Deformation Curves
3.2. Failure Modes of Steel Angles
3.3. Load-Deflection Curves
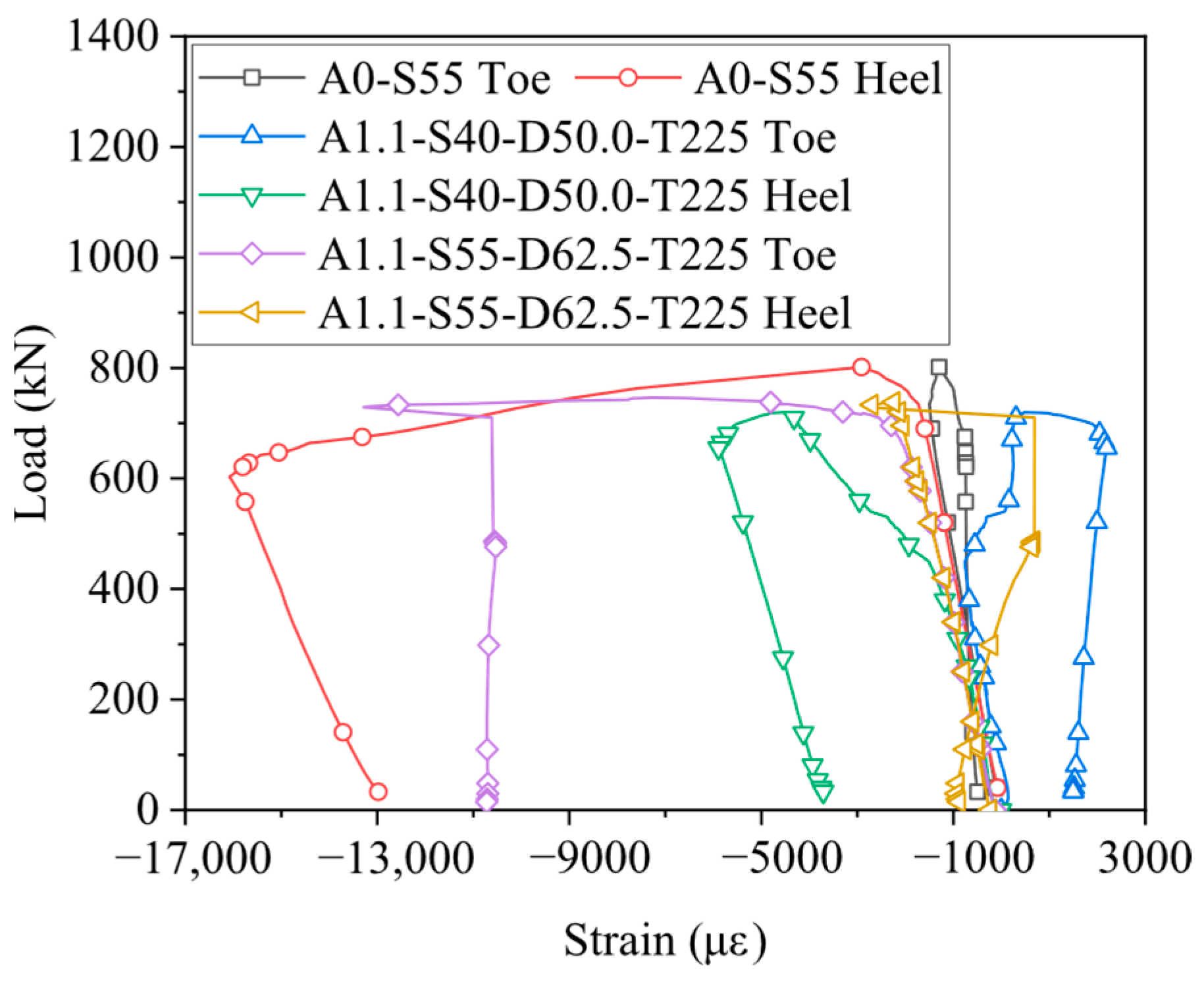
3.4. Load-Strain Curves
4. Discussion of Experimental Results
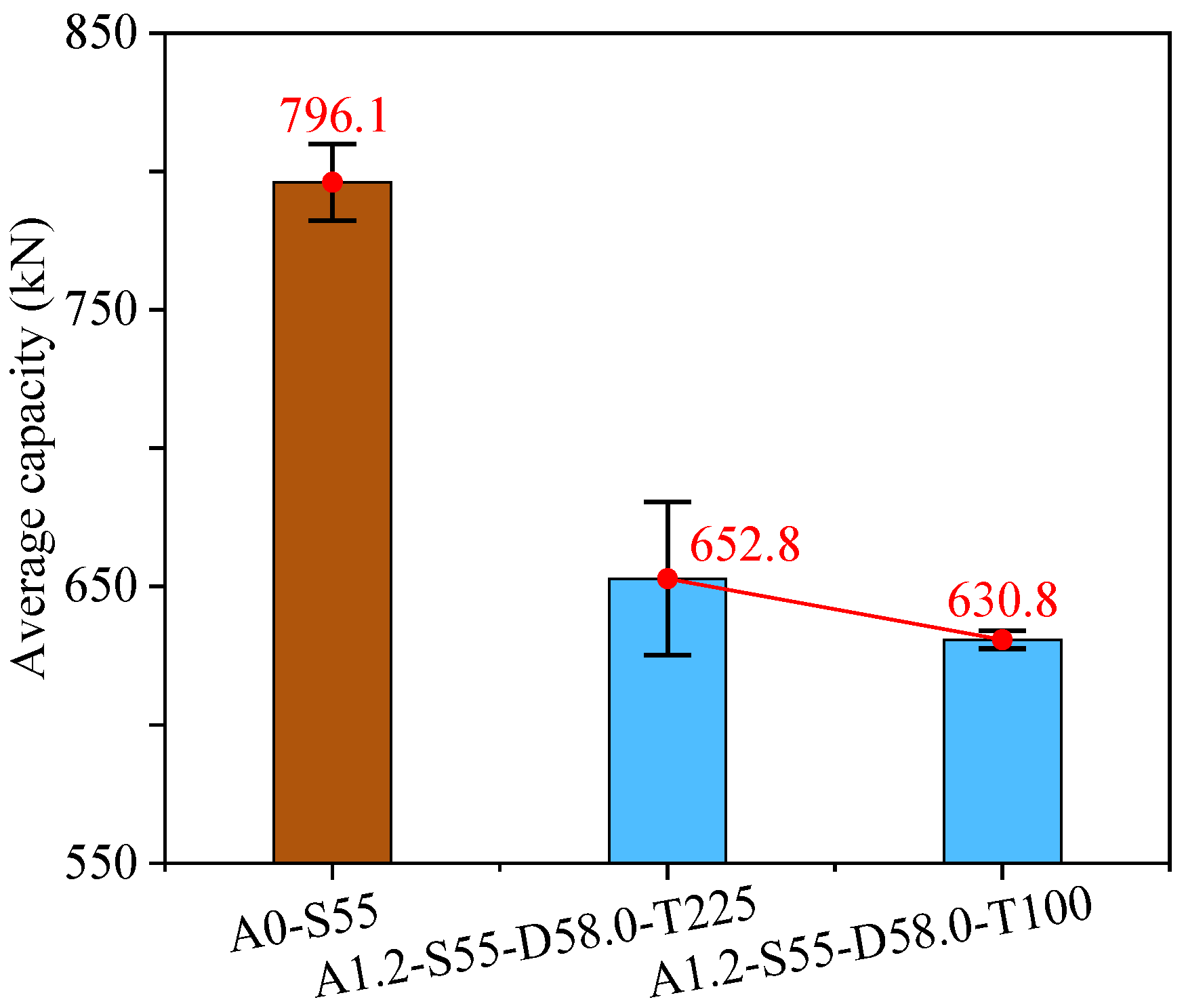
4.1. Effect of Splice Steel Ratio
4.2. Effect of Slenderness
4.3. Effect of Bolt Spacing
4.4. Effect of Torque for Bolting
5. Design Equations for Steel Angles in Compression
5.1. Calculation Methods in Chinese Design Codes
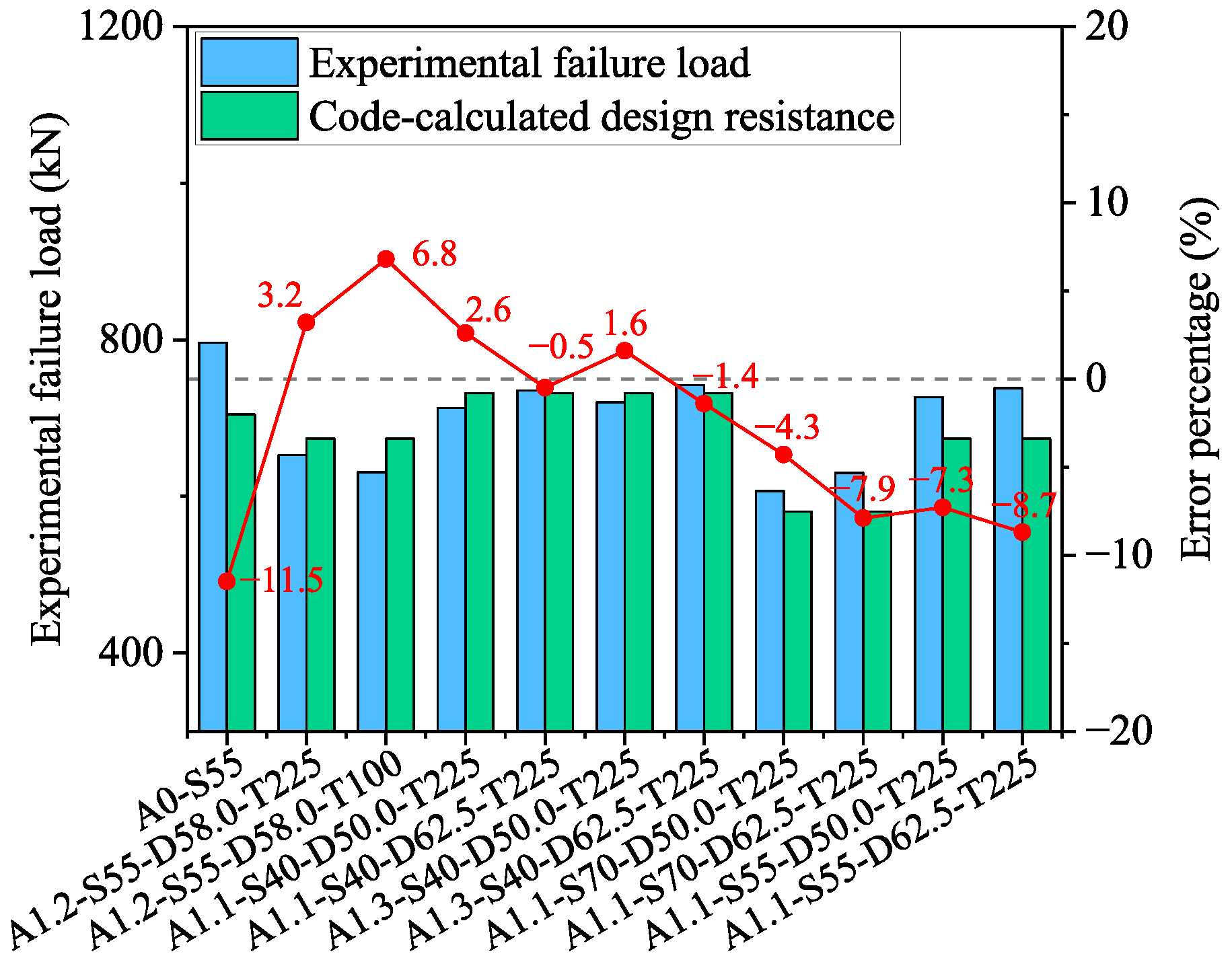
5.2. Comparison of Theoretical and Experimental Results
6. Conclusions
- The failure mode of the intact steel angle was flexural buckling under axial compression. For steel angles with double-shear splice connections, specimens with the same upper and lower sections of L125 × 10 exhibited flexural–torsional buckling and buckling of diagonal bracing at the connection. For steel angles with different upper and lower sections of L125 × 10 and L140 × 10, specimen A1.1-S55-D50.0-T225 exhibited the same failure mode as those with the same upper and lower angles, but specimen A1.1-S55-D62.5-T225 failed in flexural–torsional buckling.
- The load-deformation curves exhibited similar trends for specimens with different design parameters. Compared to intact specimens, spliced steel angles demonstrated a sudden increase in the axial deformation during initial loading due to the occurrence of bolt slippage at the connection. The load capacity of spliced steel angles was substantially lower than that of the intact specimens.
- Increasing the splice steel ratios from 1.1 to 1.3 showed a negligible effect on the load capacity of spliced steel angles. An increase in the slenderness from 40 to 70 significantly reduced the compressive load capacity. By increasing the bolt spacing, the ultimate load of steel angles increased, but the beneficial effect of a large bolt spacing decreases with increasing slenderness. Reducing the bolting torque from 225 N·m to 100 N·m had a minimal influence on load capacity.
- Experimental load capacities were compared with the calculated results using the design method for compressive steel angles in GB50017-2017 and DL/T 5154-2012. Comparisons between experimental and calculated load capacities revealed that the calculated value overestimates the ultimate load capacity of spliced angles in compression, indicating the need for revision of current design provisions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xie, Q.; Zhang, J. Experimental study on failure modes and retrofitting method of latticed transmission tower. Eng. Struct. 2021, 226, 111365. [Google Scholar] [CrossRef]
- Qiu, F.; Qiu, J.X.; Feng, H.; Wang, H.J.; Qian, H.L.; Jin, X.F.; Wang, K.Y.; Fan, F. Calculation method of stability bearing capacity of transmission tower angle steel considering semi-rigid constraint. Curved Layer. Struct. 2022, 9, 202–211. [Google Scholar] [CrossRef]
- Kettler, M.; Taras, A.; Unterweger, H. Member capacity of bolted steel angles in compression—Influence of realistic end supports. J. Constr. Steel Res. 2017, 130, 22–35. [Google Scholar] [CrossRef]
- Xu, J.J.; He, S.Y.; Cao, X.J.; Lu, Y.; Liu, X.Y.; Yan, X.Q. Analytical and numerical analysis of angle steel joints for conductors in lattice transmission towers. Case Stud. Constr. Mater. 2022, 17, e01592. [Google Scholar] [CrossRef]
- Qian, Y.; Huang, C.; Han, B.; Cheng, F.; Qiu, S.; Deng, H.; Duan, X.; Zheng, H.; Liu, Z.; Wu, J. Quantitative analysis of bolt loosening angle based on deep learning. Buildings 2024, 14, 163. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, H.J.; Yang, H.L.; Huang, X.; Zhu, L.; Guo, Y. Stability bearing capacity of equal-leg angle steel columns with end connection joints. J. Constr. Steel Res. 2024, 216, 108606. [Google Scholar] [CrossRef]
- Filipović, A.; Dobrić, J.; Baddoo, N.; Može, P. Experimental response of hot-rolled stainless steel angle columns. Thin Walled Struct. 2021, 163, 107659. [Google Scholar] [CrossRef]
- Huang, Z.L.; Liu, H.J.; Liu, H.Y.; Li, Z.L. Experimental study on stability behavior of equal-leg angle steel columns. Thin Walled Struct. 2021, 166, 108042. [Google Scholar] [CrossRef]
- Qu, S.; Guo, Y.; Sun, Q. Resistances of high-strength steel equal-leg-angle section columns eccentrically connected by one leg. J. Constr. Steel Res. 2022, 191, 107143. [Google Scholar] [CrossRef]
- Xu, Z.; Tong, G.; Zhang, L.; Guo, Y. Testing, modelling and design of aluminium alloy single-angle members connected by one leg under eccentric compression. Thin Walled Struct. 2023, 184, 110474. [Google Scholar] [CrossRef]
- Huang, X.; He, S.Y.; Liu, X.Y.; Han, D.G.; Pu, F.; Yan, H.Q.; Kang, S.B. Compression behaviour of Q355 steel equal-leg angles with simulated local defects at the mid-height. J. Constr. Steel Res. 2024, 217, 108673. [Google Scholar] [CrossRef]
- Tan, X.Z.; Song, Z.Y.; Jin, Y.; Zhang, X.; Zhao, J. Analysis of stability capacity of locally corroded single angle members under axial compression. J. Shandong Electr. Power Coll. 2022, 25, 13–19. [Google Scholar]
- Shi, G.; Liu, Z.; Ban, H.Y.; Zhang, Y.; Shi, Y.J.; Wang, Y.Q. Tests and finite element analysis on the local buckling of 420 MPa steel equal angle columns under axial compression. Steel Compos. Struct. 2012, 12, 31–51. [Google Scholar] [CrossRef]
- Shi, G.; Liu, Z.; Zhang, Y.; Shi, Y.J.; Wang, Y.Q. Study on the local buckling behavior of steel equal angle members under axial compression with the steel strength variation. In Sustainable Development of Urban Environment and Building Material, Pts 1–4; Li, H., Liu, Y.F., Guo, M., Zhang, R., Du, J., Eds.; Trans Tech Publications Ltd.: Durnten-Zurich, Switzerland, 2012; pp. 2430–2436. [Google Scholar]
- Shi, G.; Zhou, W.J.; Bai, Y.; Liu, Z. Local buckling of steel equal angle members with normal and high strengths. Int. J. Steel Struct. 2014, 14, 447–455. [Google Scholar] [CrossRef]
- Gusella, F.; Orlando, M.; Peterman, K. Stiffness and resistance of brace-to-upright joints with lipped channel braces assembled flange-to-flange. J. Constr. Steel Res. 2022, 193, 107258. [Google Scholar] [CrossRef]
- Roure, F.; Peköz, T.; Somalo, M.R.; Bonada, J.; Pastor, M.M.; Segura, A. Cross-aisle stiffness analysis of industrial welded cold-formed steel rack upright frames. Thin Walled Struct. 2019, 141, 332–344. [Google Scholar] [CrossRef]
- Yao, Y.F.; Huang, H.; Zhang, W.; Ye, Y.X.; Xin, L.; Liu, Y. Seismic performance of steel-PEC spliced frame beam. J. Constr. Steel Res. 2022, 197, 107456. [Google Scholar] [CrossRef]
- Yao, Y.F.; Zhou, L.Q.; Huang, H.; Chen, Z.; Ye, Y.X. Cyclic performance of novel composite beam-to-column connections with reduced beam section fuse elements. Structures 2023, 50, 842–858. [Google Scholar] [CrossRef]
- Mengelkoch, N.S.; Yura, J.A. Single-angle compression members loaded through one leg. In Proceedings of the Annual Stability Conference, Structural Stability Research Council, Seattle, WA, USA, 24–27 April 2002; pp. 201–218. [Google Scholar]
- Hu, F.F.; Gao, C.Z.; Jiang, W.Q.; Liu, S.X.; An, L.Q.; Gao, J.; Du, H.Y. Research on semi-rigid of bolted joint in main member of transmission tower. Steel Constr. (Chin. Engl.) 2018, 33, 83–87. [Google Scholar]
- Jiang, W.Q.; Wang, Z.Q.; McClure, G.; Wang, G.L.; Geng, J.D. Accurate modeling of joint effects in lattice transmission towers. Eng. Struct. 2011, 33, 1817–1827. [Google Scholar] [CrossRef]
- Gan, Y.D.; Deng, H.Z.; Li, C. Simplified joint-slippage model of bolted joint in lattice transmission tower. Structures 2021, 32, 1192–1206. [Google Scholar] [CrossRef]
- Yang, F.L.; Zhu, B.R.; Xing, H.J. The slip characteristics and parametric study of bolted connections for transmission towers. Eng. Mech. 2017, 34, 116–127. [Google Scholar]
- He, S.Y.; Ma, H.Y.; Yan, X.Q.; Jiang, R.; Xiao, Y.H. Study on uneven shear of double-clad shear connection joint bolts of transmission tower. J. Wuhan Univ. Technol. 2021, 43, 49–57. [Google Scholar]
- Taha, A.M.; Dabaon, M.A.; El-Boghdadi, M.H.; Hassanein, M.F. Experimental testing and evaluation of real-scale lap-splice bolted connections used in typical lattice steel transmission towers. Thin Walled Struct. 2022, 171, 108790. [Google Scholar] [CrossRef]
- Eom, T.S.; Yang, J.M.; Kim, D.K.; Lim, J.J.; Lee, S.H. Experimental investigation of bolted end-plate angle splice in encased composite columns. Eng. Struct. 2019, 190, 31–40. [Google Scholar] [CrossRef]
- Eom, T.S.; Cho, S.R.; Lim, J.J. Behavior of end plate connection for steel angles. Eng. Struct. 2022, 252, 113714. [Google Scholar] [CrossRef]
- Jiang, W.Q. Accurate Modeling of Structural Joint and Its Application in Lattice Transmission Tower Analysis. Ph.D. Thesis, North China Electric Power University, Beijing, China, 2011. [Google Scholar]
- Jiang, W.Q.; Chen, X.Y.; Liu, J.L.; Niu, Z.B.; Feng, L.Y.; An, L.Q. Study on bearing capacity of transmission tower main leg with bolted joints. Chin. J. Constr. Mach. 2021, 19, 471–476. [Google Scholar]
- Xue, S.D.; Wang, L.S.; Li, X.Y.; Zhou, Y. Finite element analysis of axial pressure stability bearing capacity of angle steel such as transmission tower. Build. Struct. 2023, 53, 1431–1435. [Google Scholar]
- Gao, F. Research on the Stability Capacity of the Equal Angle Steel Main Member in Transmission Tower Considering Middle Disconnected Joint. Master’s Thesis, Chongqing University, Chongqing, China, 2021. [Google Scholar]
- Qu, K.M. Experimental and Numerical Study on the Stability Capacity of Angle Column Connection Joints in Transmission Towers. Master’s Thesis, Chongqing University, Chongqing, China, 2021. [Google Scholar]
- DL/T 5486-2020; Technical Specification for the Design of Steel Supporting Structures of Overhead Transmission Line. National Energy Administration: Beijing, China, 2020.
- Li, J.; He, S.Y.; Li, Z.L.; Wang, R.; Pu, S.T.; Huang, X.; Yan, X.Q. Experimental Study on Axial Compression Behavior of Angle Steel Main Members with Double-Shear Splicing Joints. Prog. Steel Build. Struct. 2025, 27, 48–56. [Google Scholar]
- GB/T 2975-2018; Steel and Steel Products. Location and Preparation of Samples and Test Pieces for Mechanical Testing. Standardization Administration of China: Beijing, China, 2018.
- GB/T 228.1-2021; Metallic Materials. Tensile Testing. Part 1: Method of Test at Room Temperature. Standardization Administration of China: Beijing, China, 2021.
- GB 50017-2017; Standard for Design of Steel Structures. Standardization Administration of China: Beijing, China, 2017.
- DL/T 5154-2012; Technical Regulation of Design for Tower and Pole Structures of Overhead Transmission Line. National Energy Administration: Beijing, China, 2012.











| Specimen Designation | Main Angles | Inner Angle Steel | Outer Splice Plates | Slenderness | Length of Top Angle (mm) | Length of Bottom Angle (mm) | Splice Steel Ratio | Bolt Spacing (mm) | Bolt Torque (N·m) |
|---|---|---|---|---|---|---|---|---|---|
| A0-S55 | L125 × 10 | - | - | 55 | 1350 | - | - | - | |
| A1.2-S55-D58.0-T225 | L125 × 10 | L100 × 7 | −8 × 105 | 55 | 1260 | 1880 | 1.2 | 58.0 | 225 |
| A1.2-S55-D58.0-T100 | L125 × 10 | L100 × 7 | −8 × 105 | 55 | 1260 | 1800 | 1.2 | 58.0 | 100 |
| A1.1-S40-D50.0-T225 | L125 × 10 | L100 × 7 | −6 × 105 | 40 | 1020 | 1280 | 1.1 | 50.0 | 225 |
| A1.1-S40-D62.5-T225 | L125 × 10 | L100 × 7 | −6 × 105 | 40 | 1020 | 1280 | 1.1 | 62.5 | 225 |
| A1.3-S40-D50.0-T225 | L125 × 10 | L100 × 8 | −8 × 105 | 40 | 1020 | 1280 | 1.3 | 50.0 | 225 |
| A1.3-S40-D62.5-T225 | L125 × 10 | L100 × 8 | −8 × 105 | 40 | 1020 | 1280 | 1.3 | 62.5 | 225 |
| A1.1-S70-D50.0-T225 | L125 × 10 | L100 × 7 | −6 × 105 | 70 | 1515 | 2515 | 1.1 | 50.0 | 225 |
| A1.1-S70-D62.5-T225 | L125 × 10 | L100 × 7 | −6 × 105 | 70 | 1515 | 2515 | 1.1 | 62.5 | 225 |
| A1.1-S55-D50.0-T225 | L140 × 10 +L125 × 10 | L100 × 7 | −6 × 105 | 55 | 1260 | 1880 | 1.1 | 50.0 | 225 |
| A1.1-S55-D62.5-T225 | L140 × 10 +L125 × 10 | L100 × 7 | −6 × 105 | 55 | 1260 | 1800 | 1.1 | 62.5 | 225 |
| Steel Coupon | Yield Strength (MPa) | Ultimate Strength (MPa) | Yield Strain (%) | Elongation (%) | Elastic Modulus (MPa) |
|---|---|---|---|---|---|
| Main angle | 377.3 | 555.6 | 0.39 | 13.5 | 204,422.1 |
| Diagonal bracing | 391.4 | 563.4 | 0.40 | 14.7 | 202,798.5 |
| Splice steel 100 × 7 | 413.9 | 572.7 | 0.41 | 11.5 | 198,224.3 |
| Splice steel 100 × 8 | 392.6 | 562.1 | 0.40 | 14.8 | 201,097.9 |
| Specimen Designation | Splice Steel Ratio | Slenderness | Bolt Spacing | Failure Mode | Load Capacity (kN) | Average Capacity (kN) |
|---|---|---|---|---|---|---|
| A0-S55 | - | 55 | - | Flexural buckling of steel angles | 803.7 | 796.1 |
| 780.2 | ||||||
| 804.5 | ||||||
| A1.2-S55-D58.0-T225 | 1.2 | 55 | 58.0 | Flexural–torsional buckling of steel angles, Buckling of diagonal bracing at the connection | 684.5 | 652.8 |
| 640.5 | ||||||
| 633.5 | ||||||
| A1.2-S55-D58.0-T100 | 1.2 | 55 | 58.0 | Flexural–torsional buckling of steel angles, Buckling of diagonal bracing at the connection | 627.9 | 630.8 |
| 630.2 | ||||||
| 634.3 | ||||||
| A1.1-S40-D50.0-T225 | 1.1 | 40 | 50.0 | Flexural–torsional buckling of steel angles, Buckling of diagonal bracing at the connection | 720.4 | 712.9 |
| 717.3 | ||||||
| 701.0 | ||||||
| A1.1-S40-D62.5-T225 | 1.1 | 40 | 62.5 | Flexural–torsional buckling of steel angles, Buckling of diagonal bracing at the connection | 737.0 | 735.2 |
| 732.3 | ||||||
| 736.3 | ||||||
| A1.3-S40-D50.0-T225 | 1.3 | 40 | 50.0 | Flexural–torsional buckling of steel angles, Buckling of diagonal bracing at the connection | 708.5 | 720.1 |
| 721.1 | ||||||
| 730.6 | ||||||
| A1.3-S40-D62.5-T225 | 1.3 | 40 | 62.5 | Flexural–torsional buckling of steel angles, Buckling of diagonal bracing at the connection | 747.2 | 742.1 |
| 737.9 | ||||||
| 741.3 | ||||||
| A1.1-S70-D50.0-T225 | 1.1 | 70 | 50.0 | Flexural–torsional buckling of steel angles, Buckling of diagonal bracing at the connection | 603.7 | 606.7 |
| 610.5 | ||||||
| 605.8 | ||||||
| A1.1-S70-D62.5-T225 | 1.1 | 70 | 62.5 | Flexural–torsional buckling of steel angles, Buckling of diagonal bracing at the connection | 622.1 | 630.1 |
| 638.2 | ||||||
| A1.1-S55-D50.0-T225 | 1.1 | 55 | 50.0 | Flexural–torsional buckling of steel angles | 739.7 | 726.5 |
| Flexural–torsional buckling of steel angles, Buckling of diagonal bracing at the connection | 731.0 | |||||
| 708.9 | ||||||
| A1.1-S55-D62.5-T225 | 1.1 | 55 | 62.5 | Flexural–torsional buckling of steel angles | 742.2 | 738.1 |
| 727.8 | ||||||
| 744.4 |
| Side Bracing Connections | Schematic | Slenderness |
|---|---|---|
| Full overlap |  | Equation (2) |
| partial overlap |  | Equation (3) |
| Non-overlap |  | Equation (4) |
| Specimen Designation | Splice Steel Ration | Slenderness | Bolt Spacing (mm) | Experimental Failure Load (kN) | Code-Calculated Design Resistance (kN) | ||
|---|---|---|---|---|---|---|---|
| A0-S55 | - | 55 | - | 796.1 | 704.5 | 1.13 | −11.5% |
| A1.2-S55-D58.0-T225 | 1.2 | 55 | 58.0 | 652.8 | 673.6 | 0.97 | 3.2% |
| A1.2-S55-D58.0-T100 | 1.2 | 55 | 58.0 | 630.8 | 673.6 | 0.94 | 6.8% |
| A1.1-S40-D50.0-T225 | 1.1 | 40 | 50.0 | 712.9 | 731.6 | 0.97 | 2.6% |
| A1.1-S40-D62.5-T225 | 1.1 | 40 | 62.5 | 735.2 | 731.6 | 1.00 | −0.5% |
| A1.3-S40-D50.0-T225 | 1.3 | 40 | 50.0 | 720.1 | 731.6 | 0.98 | 1.6% |
| A1.3-S40-D62.5-T225 | 1.3 | 40 | 62.5 | 742.1 | 731.6 | 1.01 | −1.4% |
| A1.1-S70-D50.0-T225 | 1.1 | 70 | 50.0 | 606.7 | 580.4 | 1.05 | −4.3% |
| A1.1-S70-D62.5-T225 | 1.1 | 70 | 62.5 | 630.1 | 580.4 | 1.09 | −7.9% |
| A1.1-S55-D50.0-T225 | 1.1 | 55 | 50.0 | 726.5 | 673.6 | 1.08 | −7.3% |
| A1.1-S55-D62.5-T225 | 1.1 | 55 | 62.5 | 738.1 | 673.6 | 1.10 | −8.7% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, C.; Kang, S.-B.; Pei, L.-Y.; Zeng, G.-S.; Ma, H.-Y.; Han, D.-G.; He, S.-Y. Axial Compression Behavior of Steel Angles with Double-Shear Splice Connections in Transmission Towers. Appl. Sci. 2025, 15, 9140. https://doi.org/10.3390/app15169140
Xu C, Kang S-B, Pei L-Y, Zeng G-S, Ma H-Y, Han D-G, He S-Y. Axial Compression Behavior of Steel Angles with Double-Shear Splice Connections in Transmission Towers. Applied Sciences. 2025; 15(16):9140. https://doi.org/10.3390/app15169140
Chicago/Turabian StyleXu, Cheng, Shao-Bo Kang, Lu-Yao Pei, Gen-Sheng Zeng, Hai-Yun Ma, Da-Gang Han, and Song-Yang He. 2025. "Axial Compression Behavior of Steel Angles with Double-Shear Splice Connections in Transmission Towers" Applied Sciences 15, no. 16: 9140. https://doi.org/10.3390/app15169140
APA StyleXu, C., Kang, S.-B., Pei, L.-Y., Zeng, G.-S., Ma, H.-Y., Han, D.-G., & He, S.-Y. (2025). Axial Compression Behavior of Steel Angles with Double-Shear Splice Connections in Transmission Towers. Applied Sciences, 15(16), 9140. https://doi.org/10.3390/app15169140






