Atomistic Modeling of Microstructural Defect Evolution in Alloys Under Irradiation: A Comprehensive Review
Abstract
1. Introduction
1.1. The Grand Challenge of Materials in Extreme Environments
1.2. The Promise of Atomistic Modeling
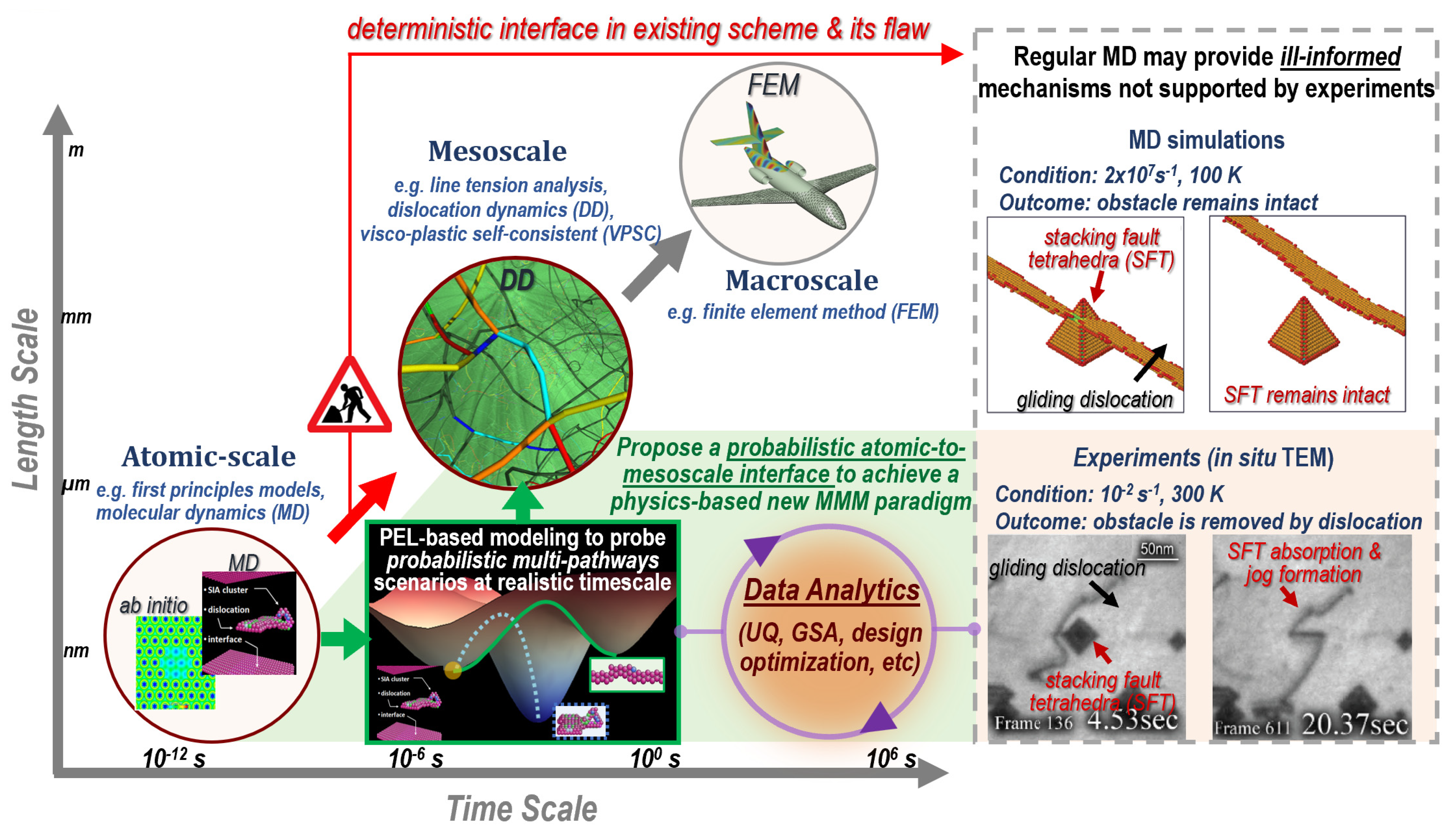
2. Methodological Advances: From Conventional MD to Long-Term Atomistic Modeling
2.1. Classical Molecular Dynamics (MD) in Irradiation Studies
2.2. Beyond Conventional MD: Probing Long-Timescale Kinetics
3. Atomistic Modeling on Point Defect Behavior
3.1. SIAs and Vacancies’ Dynamics in Different Crystalline Structures
3.1.1. BCC Metals
3.1.2. FCC Metals
3.1.3. HCP Metals
3.2. Effect of Chemical Complexity on Defect Behavior in Multi-Component Alloys
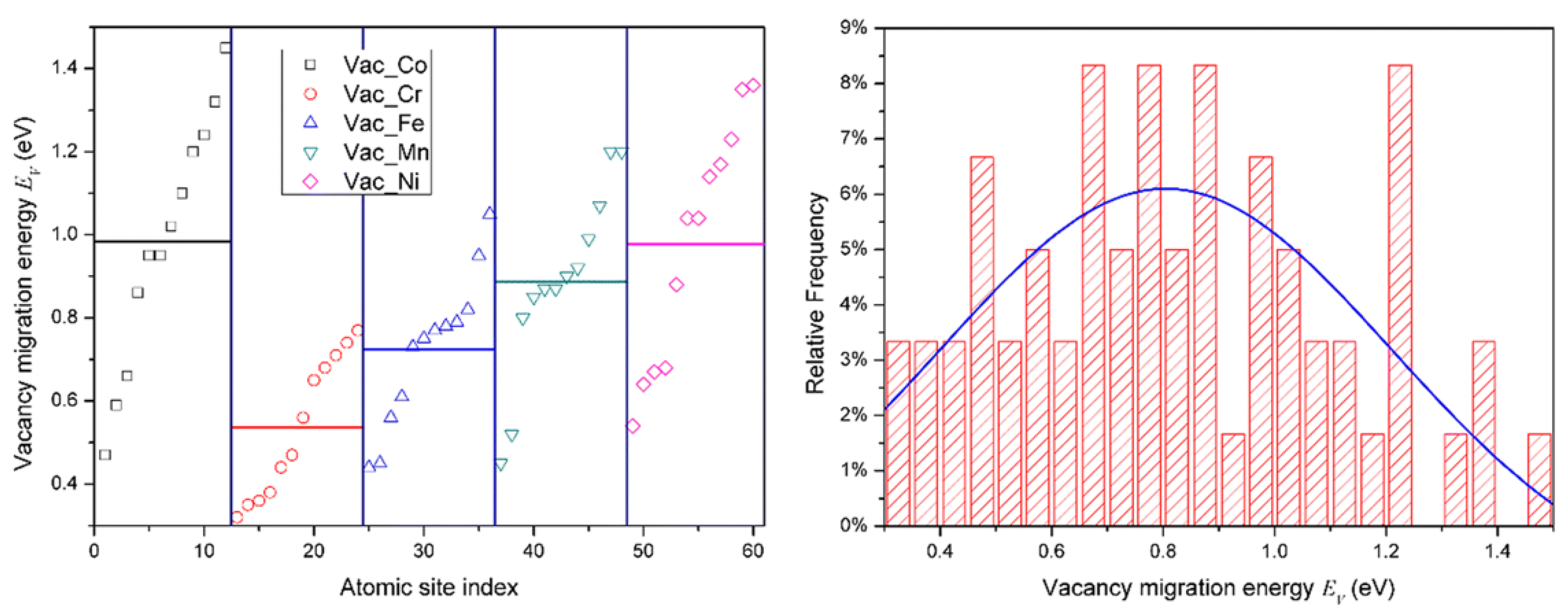
3.2.1. A Spectrum of Defect Energetics
3.2.2. Sluggish Diffusion and Complex Defect Transport
3.2.3. Enhanced Recombination and Reduced Damage Accumulation
4. Extended Defect Generation and Evolution Under Irradiation and Mechanical Loading
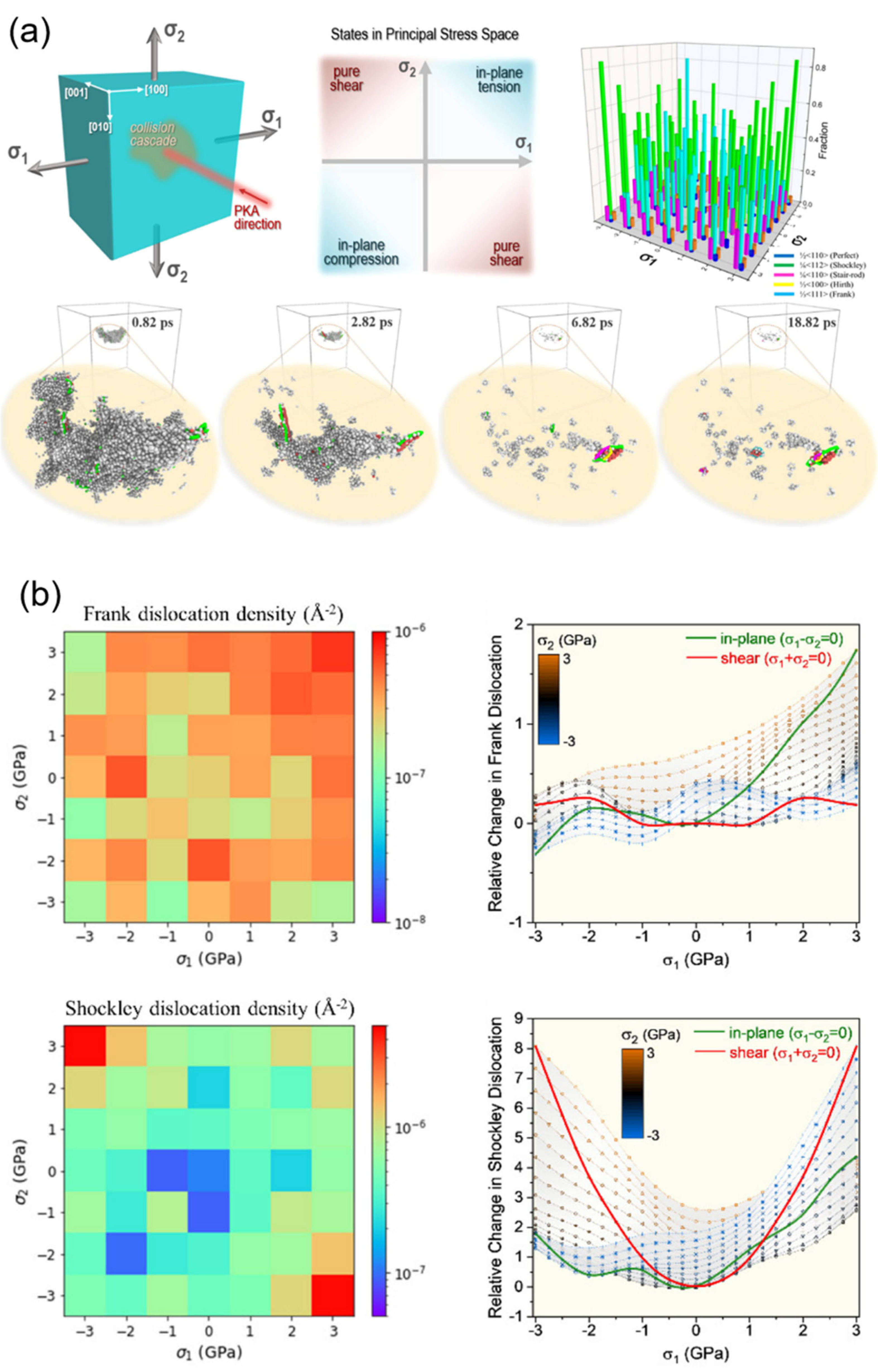
4.1. Stress Sensitivity of Irradiated Dislocation Loops
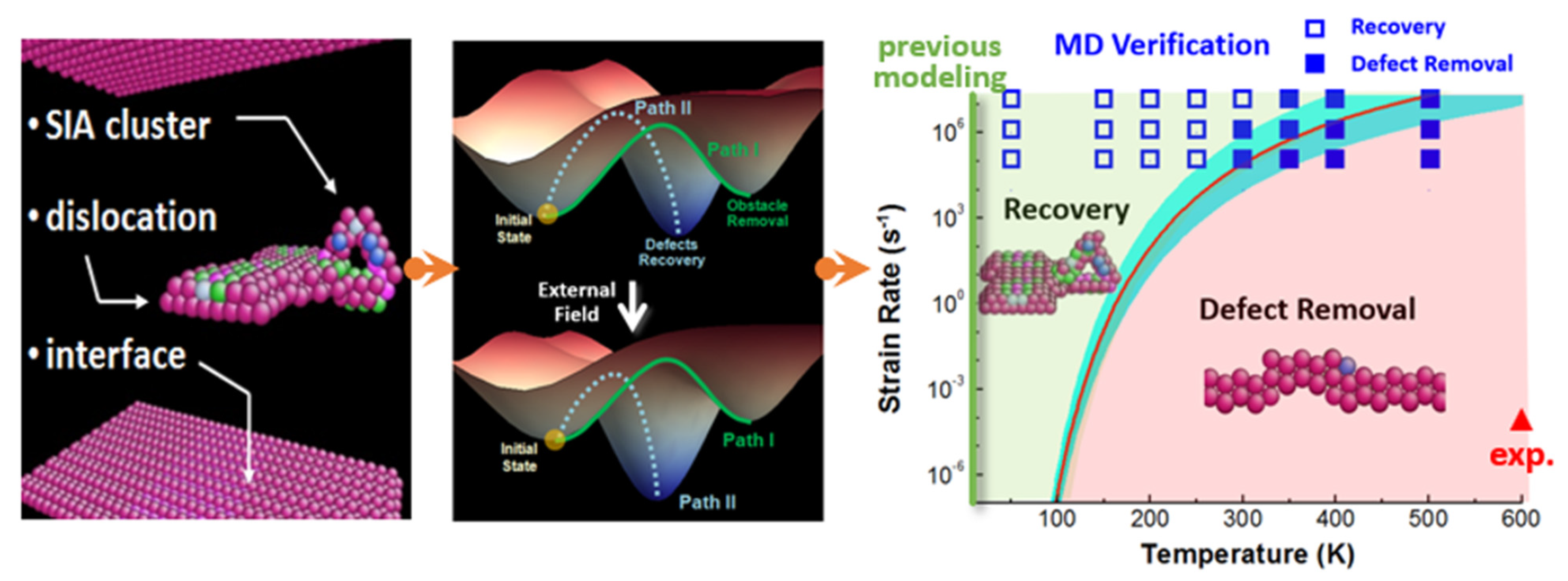
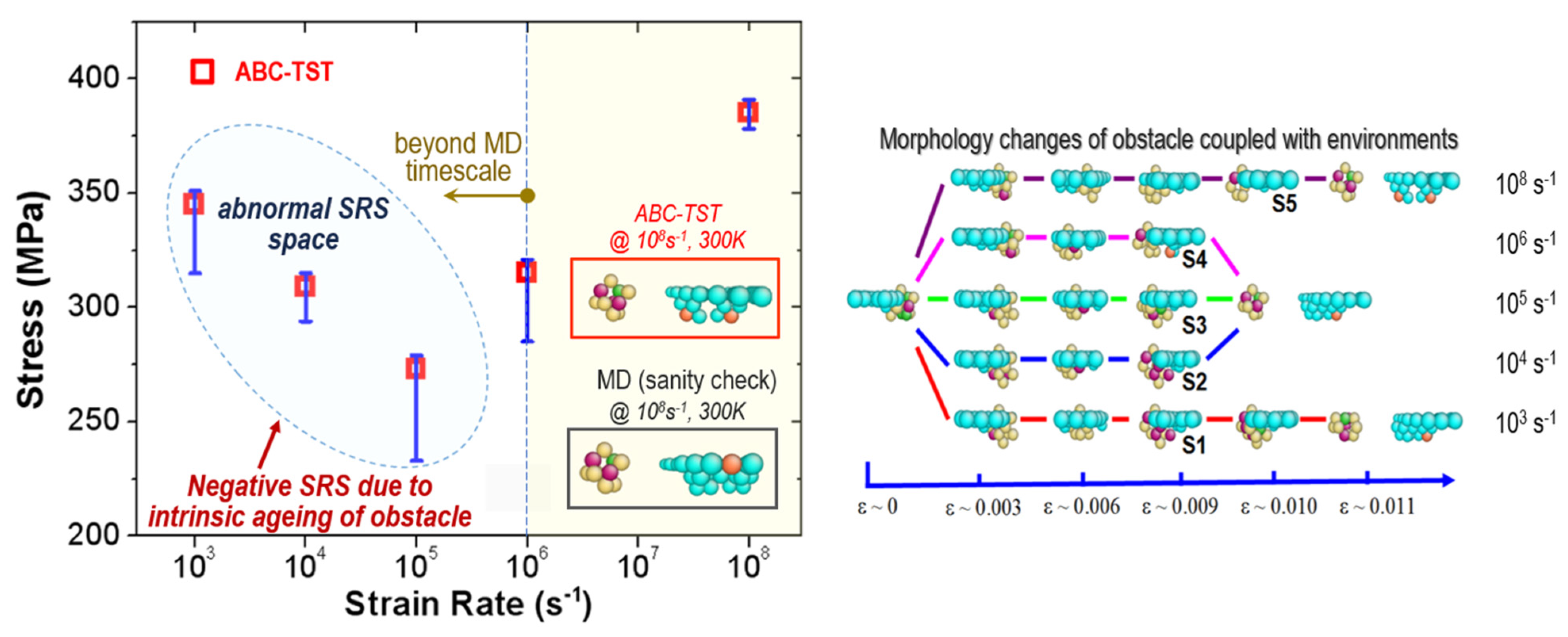
4.2. Dislocation–Obstacle Interaction Mechanisms at Various Thermomechanical Conditions
4.3. Grain Boundaries Under Extreme Environments
5. Accelerating Discovery with Data-Driven Methods and Machine Learning
5.1. Quantum-Accurate Machine Learning Interatomic Potentials (MLIPs)
5.2. AI-Driven Automation of Defect Identification and Analysis
5.3. Surrogate Modeling for Rapid PSP Exploration and Design
6. Concluding Remarks and Future Outlook
6.1. Summary of Key Advances and Insights
6.2. Outlook and Newly Emergent Fundamental Questions
Funding
Conflicts of Interest
References
- Zinkle, S.J.; Was, G.S. Materials challenges in nuclear energy. Acta Mater. 2013, 61, 735–758. [Google Scholar] [CrossRef]
- Zinkle, S.; Snead, L. Designing Radiation Resistance in Materials for Fusion Energy. Annu. Rev. Mater. Res. 2014, 44, 241–267. [Google Scholar] [CrossRef]
- Yvon, P.; Carré, F. Structural materials challenges for advanced reactor systems. J. Nucl. Mater. 2009, 385, 217–222. [Google Scholar] [CrossRef]
- Knaster, J.; Moeslang, A.; Muroga, T. Materials research for fusion. Nat. Phys. 2016, 12, 424–434. [Google Scholar] [CrossRef]
- Odette, G.R. On the status and prospects for nanostructured ferritic alloys for nuclear fission and fusion application with emphasis on the underlying science. Scr. Mater. 2018, 143, 142–148. [Google Scholar] [CrossRef]
- Fan, Y.; Kushima, A.; Yip, S.; Yildiz, B. Mechanism of Void Nucleation and Growth in bcc Fe: Atomistic Simulations at Experimental Time Scales. Phys. Rev. Lett. 2011, 106, 125501. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Cao, P. Long Time-Scale Atomistic Modeling and Simulation of Deformation and Flow in Solids. In Handbook of Materials Modeling: Applications: Current and Emerging Materials; Andreoni, W., Yip, S., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 1–27. [Google Scholar]
- Was, G.S. Materials degradation in fission reactors: Lessons learned of relevance to fusion reactor systems. J. Nucl. Mater. 2007, 367–370, 11–20. [Google Scholar] [CrossRef]
- Was, G.S. Fundamentals of Radiation Materials Science Metals and Alloys; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Odette, G.R.; Alinger, M.J.; Wirth, B.D. Recent Developments in Irradiation-Resistant Steels. Annu. Rev. Mater. Res. 2008, 38, 471–503. [Google Scholar] [CrossRef]
- Ardell, A.J.; Bellon, P. Radiation-induced solute segregation in metallic alloys. Curr. Opin. Solid State Mater. Sci. 2016, 20, 115–139. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, S.; Weber, W.J.; Nordlund, K.; Granberg, F.; Djurabekova, F. Atomic-level heterogeneity and defect dynamics in concentrated solid-solution alloys. Curr. Opin. Solid State Mater. Sci. 2017, 21, 221–237. [Google Scholar] [CrossRef]
- Zhang, X.; Hattar, K.; Chen, Y.; Shao, L.; Li, J.; Sun, C.; Yu, K.; Li, N.; Taheri, M.L.; Wang, H.; et al. Radiation damage in nanostructured materials. Prog. Mater. Sci. 2018, 96, 217–321. [Google Scholar] [CrossRef]
- Zhang, Y.; Egami, T.; Weber, W.J. Dissipation of radiation energy in concentrated solid-solution alloys: Unique defect properties and microstructural evolution. MRS Bull. 2019, 44, 798–811. [Google Scholar] [CrossRef]
- Gibson, J.B.; Goland, A.N.; Milgram, M.; Vineyard, G.H. Dynamics of Radiation Damage. Phys. Rev. B 1960, 120, 1229–1253. [Google Scholar] [CrossRef]
- Shibuta, Y.; Sakane, S.; Miyoshi, E.; Okita, S.; Takaki, T.; Ohno, M. Heterogeneity in homogeneous nucleation from billion-atom molecular dynamics simulation of solidification of pure metal. Nat. Commun. 2017, 8, 10. [Google Scholar] [CrossRef]
- Kadau, K.; Germann, T.C.; Lomdahl, P.S. Molecular Dynamics Comes of Age: 320 Billion Atom Simulation on BlueGene/L. Int. J. Mod. Phys. C 2006, 17, 1755–1761. [Google Scholar] [CrossRef]
- Zepeda-Ruiz, L.A.; Stukowski, A.; Oppelstrup, T.; Bulatov, V.V. Probing the limits of metal plasticity with molecular dynamics simulations. Nature 2017, 550, 492–495. [Google Scholar] [CrossRef]
- So/rensen, M.R.; Voter, A.F. Temperature-accelerated dynamics for simulation of infrequent events. J. Chem. Phys. 2000, 112, 9599–9606. [Google Scholar] [CrossRef]
- Perez, D.; Uberuaga, B.P.; Shim, Y.; Amar, J.G.; Voter, A.F. Chapter 4 Accelerated Molecular Dynamics Methods: Introduction and Recent Developments. In Annual Reports in Computational Chemistry; Wheeler, R.A., Ed.; Elsevier: Amsterdam, The Netherlands, 2009; pp. 79–98. [Google Scholar]
- Voter, A.F. A method for accelerating the molecular dynamics simulation of infrequent events. J. Chem. Phys. 1997, 106, 4665–4677. [Google Scholar] [CrossRef]
- Montalenti, F.; Voter, A.F. Applying Accelerated Molecular Dynamics to Crystal Growth. Phys. Status Solidi B 2001, 226, 21–27. [Google Scholar] [CrossRef]
- Voter, A.F.; Montalenti, F.; Germann, T.C. Extending the Time Scale in Atomistic Simulation of Materials. Annu. Rev. Mater. Res. 2002, 32, 321–346. [Google Scholar] [CrossRef]
- Henkelman, G.; Jónsson, H. A dimer method for finding saddle points on high dimensional potential surfaces using only first derivatives. J. Chem. Phys. 1999, 111, 7010–7022. [Google Scholar] [CrossRef]
- Heyden, A.; Bell, A.T.; Keil, F.J. Efficient methods for finding transition states in chemical reactions: Comparison of improved dimer method and partitioned rational function optimization method. J. Chem. Phys. 2005, 123, 224101. [Google Scholar] [CrossRef]
- Xu, H.; Osetsky, Y.N.; Stoller, R.E. Self-evolving atomistic kinetic Monte Carlo: Fundamentals and applications. J. Phys. Condens. Matter 2012, 24, 375402. [Google Scholar] [CrossRef]
- Barkema, G.T.; Mousseau, N. Event-Based Relaxation of Continuous Disordered Systems. Phys. Rev. Lett. 1996, 77, 4358–4361. [Google Scholar] [CrossRef] [PubMed]
- Mousseau, N.; Béland, L.K.; Brommer, P.; Joly, J.-F.; El-Mellouhi, F.; Machado-Charry, E.; Marinica, M.-C.; Pochet, P. The Activa-tion-Relaxation Technique: ART Nouveau and Kinetic ART. J. At. Mol. Opt. Phys. 2012, 2012, 14. [Google Scholar]
- Cancès, E.; Legoll, F.; Marinica, M.-C.; Minoukadeh, K.; Willaime, F. Some improvements of the activation-relaxation technique method for finding transition pathways on potential energy surfaces. J. Chem. Phys. 2009, 130, 114711. [Google Scholar] [CrossRef]
- Kushima, A.; Lin, X.; Li, J.; Eapen, J.; Mauro, J.C.; Qian, X.; Diep, P.; Yip, S. Computing the viscosity of supercooled liquids. J. Chem. Phys. 2009, 130, 224504. [Google Scholar] [CrossRef]
- Kushima, A.; Lin, X.; Li, J.; Qian, X.; Eapen, J.; Mauro, J.C.; Diep, P.; Yip, S. Computing the viscosity of supercooled liquids. II. Silica and strong-fragile crossover behavior. J. Chem. Phys. 2009, 131, 164505–164509. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Yip, S.; Yildiz, B. Autonomous basin climbing method with sampling of multiple transition pathways: Application to anisotropic diffusion of point defects in hcp Zr. J. Phys. Condens. Matter 2014, 26, 365402. [Google Scholar] [CrossRef]
- Yu, Y. Simulations of irradiation resistance and mechanical properties under irradiation of high-entropy alloy NiCoCrFe. Mater. Today Commun. 2022, 33, 104308. [Google Scholar] [CrossRef]
- Cheng, Z.; Sun, J.; Gao, X.; Wang, Y.; Cui, J.; Wang, T.; Chang, H. Irradiation effects in high-entropy alloys and their applications. J. Alloy. Compd. 2023, 930, 166768. [Google Scholar] [CrossRef]
- Cusentino, M.A.; Wood, M.A.; Dingreville, R. Compositional and structural origins of radiation damage mitigation in high-entropy alloys. J. Appl. Phys. 2020, 128, 125904. [Google Scholar] [CrossRef]
- Qian, L.; Bao, H.; Li, R.; Peng, Q. Atomistic insights of a chemical complexity effect on the irradiation resistance of high entropy alloys. Mater. Adv. 2022, 3, 1680–1686. [Google Scholar] [CrossRef]
- Mo, Y.; Liang, Y.; Guo, W.; Tian, Y.; Wan, Q. Atomistic simulation of chemical short-range order on the irradiation resistance of HfNbTaTiZr high entropy alloy. Int. J. Plast. 2024, 183, 104155. [Google Scholar] [CrossRef]
- Xu, Q.; Yuan, X.; Eckert, J.; Şopu, D. Crack-healing mechanisms in high-entropy alloys under ion irradiation. Acta Mater. 2024, 263, 119488. [Google Scholar] [CrossRef]
- Tung, C.-H.; Cheung, K.; Fan, Y.; Kushima, A.; So, K.P.; Chen, W.-R.; Yip, S. A perspective on soft matter molecular simulations: Deformation and flow at mesoscopic timescales. J. Appl. Phys. 2025, 137, 050902. [Google Scholar] [CrossRef]
- Fu, C.-C.; Torre, J.D.; Willaime, F.; Bocquet, J.-L.; Barbu, A. Multiscale modelling of defect kinetics in irradiated iron. Nat. Mater. 2005, 4, 68–74. [Google Scholar] [CrossRef]
- Yip, S.; Short, M.P. Multiscale materials modelling at the mesoscale. Nat. Mater. 2013, 12, 774–777. [Google Scholar] [CrossRef]
- Schmauder, S.; Schäfer, I. Multiscale Materials Modeling: Approaches to Full Multiscaling; De Gruyter: Berling, Germany, 2016. [Google Scholar]
- Fish, J.; Wagner, G.J.; Keten, S. Mesoscopic and multiscale modelling in materials. Nat. Mater. 2021, 20, 774–786. [Google Scholar] [CrossRef]
- Lin, P.D.; Nie, J.F.; Cui, W.D.; He, L.; Lu, Y.P.; Cui, S.G. A multiscale study on the microstructure and hardening models of the irra-diation defects on reactor pressure vessel steels: Modelling and experiment. J. Mater. Res. Technol. 2024, 30, 520–531. [Google Scholar] [CrossRef]
- Mohamed, S.; Po, G.; Lewis, R.; Nithiarasu, P. Multiscale computational study to predict the irradiation-induced change in engineering properties of fusion reactor materials. Nucl. Mater. Energy 2024, 39, 101647. [Google Scholar] [CrossRef]
- Calder, A.F.; Bacon, D.J.; Barashev, A.V.; Osetsky, Y.N. On the origin of large interstitial clusters in displacement cascades. Philos. Mag. 2010, 90, 863–884. [Google Scholar] [CrossRef]
- Zamora, R.J.; Uberuaga, B.P.; Perez, D.; Voter, A.F. The Modern Temperature-Accelerated Dynamics Approach. Annu. Rev. Chem. Biomol. Eng. 2016, 7, 87–110. [Google Scholar] [CrossRef] [PubMed]
- Plimpton, S.J.; Perez, D.; Voter, A.F. Parallel algorithms for hyperdynamics and local hyperdynamics. J. Chem. Phys. 2020, 153, 054116. [Google Scholar] [CrossRef]
- Fan, Y.; Iwashita, T.; Egami, T. How thermally activated deformation starts in metallic glass. Nat. Commun. 2014, 5, 5083. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Iwashita, T.; Egami, T. Evolution of elastic heterogeneity during aging in metallic glasses. Phys. Rev. E 2014, 89, 062313. [Google Scholar] [CrossRef]
- Fan, Y.; Iwashita, T.; Egami, T. Crossover from Localized to Cascade Relaxations in Metallic Glasses. Phys. Rev. Lett. 2015, 115, 045501. [Google Scholar] [CrossRef]
- Fan, Y.; Iwashita, T.; Egami, T. Energy landscape-driven non-equilibrium evolution of inherent structure in disordered material. Nat. Commun. 2017, 8, 15417. [Google Scholar] [CrossRef]
- Liu, C.; Yan, X.; Sharma, P.; Fan, Y. Unraveling the non-monotonic ageing of metallic glasses in the metastability-temperature space. Comput. Mater. Sci. 2020, 172, 109347. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, C.; Fan, Y.; Yang, Y.; Guan, P. Soft-Mode Parameter as an Indicator for the Activation Energy Spectra in Metallic Glass. J. Phys. Chem. Lett. 2020, 11, 2781–2787. [Google Scholar] [CrossRef]
- Liu, C.; Fan, Y. Emergent Fractal Energy Landscape as the Origin of Stress-Accelerated Dynamics in Amorphous Solids. Phys. Rev. Lett. 2021, 127, 215502. [Google Scholar] [CrossRef]
- Jiang, L.; Bai, Z.; Powers, M.; Fan, Y.; Zhang, W.; George, E.P.; Misra, A. Deformation mechanisms in crystalline-amorphous high-entropy composite multilayers. Mater. Sci. Eng. A 2022, 848, 143144. [Google Scholar] [CrossRef]
- Tung, C.-H.; Chang, S.-Y.; Bai, Z.; Fan, Y.; Yip, S.; Do, C.; Chen, W.-R. Data-Driven Insights into the Structural Essence of Plasticity in High-Entropy Alloys. JOM 2024, 76, 5755–5767. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Liu, C.; Hwang, J.; Fan, Y.; Wang, Y. Atomistically informed mesoscale modelling of deformation behavior of bulk metallic glasses. Acta Mater. 2024, 276, 120136. [Google Scholar] [CrossRef]
- Liu, C.; Guan, P.; Fan, Y. Correlating defects density in metallic glasses with the distribution of inherent structures in potential energy landscape. Acta Mater. 2018, 161, 295–301. [Google Scholar] [CrossRef]
- Malek, R.; Mousseau, N.; Barkema, G.T. Characterization of the Activation-Relaxation Technique: Recent Results on Models of Amorphous Silicon. Mat. Res. Soc. Symp. Proc. 2001, 677, AA8.4. [Google Scholar] [CrossRef]
- Valiquette, F.; Mousseau, N. Energy landscape of relaxed amorphous silicon. Phys. Rev. B 2003, 68, 125209. [Google Scholar] [CrossRef]
- Kallel, H.; Mousseau, N.; Schiettekatte, F. Evolution of the Potential-Energy Surface of Amorphous Silicon. Phys. Rev. Lett. 2010, 105, 045503. [Google Scholar] [CrossRef]
- Béland, L.K.; Brommer, P.; El-Mellouhi, F.; Joly, J.-F.; Mousseau, N. Kinetic activation-relaxation technique. Phys. Rev. E 2011, 84, 046704. [Google Scholar] [CrossRef] [PubMed]
- Joly, J.-F.; B’eland, L.K.; Brommer, P.; El-Mellouhi, F.; Mousseau, N. Optimization of the Kinetic Activation-Relaxation Technique, an Off-Lattice and Self-Learning Kinetic Monte-Carlo Method. J. Phys. Conf. Ser. 2012, 341, 012007. [Google Scholar] [CrossRef]
- Rodney, D.; Schuh, C. Distribution of Thermally Activated Plastic Events in a Flowing Glass. Phys. Rev. Lett. 2009, 102, 235503. [Google Scholar] [CrossRef]
- Cortés-Ortuño, D.; Wang, W.; Beg, M.; Pepper, R.A.; Bisotti, M.-A.; Carey, R.; Vousden, M.; Kluyver, T.; Hovorka, O.; Fangohr, H. Thermal stability and topological protection of skyrmions in nanotracks. Sci. Rep. 2017, 7, 4060. [Google Scholar] [CrossRef]
- Hayakawa, S.; Xu, H. Saddle point sampling using scaled normal coordinates. Comput. Mater. Sci. 2021, 200, 110785. [Google Scholar] [CrossRef]
- Fan, Y.; Kushima, A.; Yildiz, B. Unfaulting mechanism of trapped self-interstitial atom clusters in bcc Fe: A kinetic study based on the potential energy landscape. Phys. Rev. B 2010, 81, 104102. [Google Scholar] [CrossRef]
- Fan, Y.; Osetsky, Y.N.; Yip, S.; Yildiz, B. Onset Mechanism of Strain-Rate-Induced Flow Stress Upturn. Phys. Rev. Lett. 2012, 109, 135503. [Google Scholar] [CrossRef] [PubMed]
- Tang, X.-Z.; Guo, Y.-F.; Fan, Y.; Yip, S.; Yildiz, B. Interstitial emission at grain boundary in nanolayered alpha-Fe. Acta Mater. 2016, 105, 147–154. [Google Scholar] [CrossRef]
- Tang, X.-Z.; Guo, Y.-F.; Sun, L.; Fan, Y.; Yip, S.; Yildiz, B. Strain rate effect on dislocation climb mechanism via self-interstitials. Mater. Sci. Eng. A 2018, 713, 141–145. [Google Scholar] [CrossRef]
- Lau, T.T.; Kushima, A.; Yip, S. Atomistic Simulation of Creep in a Nanocrystal. Phys. Rev. Lett. 2010, 104, 175501. [Google Scholar] [CrossRef]
- Li, J.; Kushima, A.; Eapen, J.; Lin, X.; Qian, X.; Mauro, J.C.; Diep, P.; Yip, S.; Buehler, M. Computing the Viscosity of Supercooled Liquids: Markov Network Model. PLoS ONE 2011, 6, e17909. [Google Scholar] [CrossRef]
- Cao, P.; Dahmen, K.A.; Kushima, A.; Wright, W.J.; Park, H.S.; Short, M.P.; Yip, S. Nanomechanics of slip avalanches in amorphous plasticity. J. Mech. Phys. Solids 2018, 114, 158–171. [Google Scholar] [CrossRef]
- Li, X.-T.; Tang, X.-Z.; Fan, Y.; Guo, Y.-F. The interstitial emission mechanism in a vanadium-based alloy. J. Nucl. Mater. 2020, 533, 152121. [Google Scholar] [CrossRef]
- Li, Y.; Garner, F.A.; Hu, Z.; Shao, L. Void swelling in pure iron after sequential self-ion-irradiation at different energies: Effect of injected interstitials and additional damage in regions containing pre-existing voids. J. Nucl. Mater. 2024, 598, 155178. [Google Scholar] [CrossRef]
- Wang, S.; Wang, H.; Yi, X.; Tan, W.; Ge, L.; Sun, Y.; Guo, W.; Yang, Q.; Cheng, L.; Zhang, X.; et al. Damage recovery stages revisited: Thermal evolution of non-saturated and saturated displacement damage in heavy-ion irradiated tungsten. Acta Mater. 2024, 273, 119942. [Google Scholar] [CrossRef]
- Liski, A.; Lu, E.; Makkonen, I.; Chen, Z.; Mizohata, K.; Tuomisto, F. Migration and clustering of early-stage irradiation damage in vanadium. Phys. Rev. Mater. 2024, 8, 113602. [Google Scholar] [CrossRef]
- Liu, T.Y.; Demkowicz, M.J. Effect of grain boundaries and rigid inclusions on plasticity in nickel bicrystals containing helium bubbles and radiation-induced self-interstitial atom clusters. J. Nucl. Mater. 2024, 594, 155030. [Google Scholar] [CrossRef]
- Terentyev, D.A.; Klaver, T.P.C.; Olsson, P.; Marinica, M.-C.; Willaime, F.; Domain, C.; Malerba, L. Self-Trapped Interstitial-Type Defects in Iron. Phys. Rev. Lett. 2008, 100, 145503. [Google Scholar] [CrossRef] [PubMed]
- Takaki, S.; Fuss, J.; Kuglers, H.; Dedek, U.; Schultz, H. The resistivity recovery of high purity and carbon doped iron following low temperature electron irradiation. Radiat. Eff. 1983, 79, 87–122. [Google Scholar] [CrossRef]
- Nikolaev, A.L.; Arbuzov, V.L.; Davletshin, A.E. On the effect of impurities on resistivity recovery, short-range ordering, and defect migration in electron-irradiated concentrated Fe-Cr alloys. J. Phys. Condens. Matter 1997, 9, 4385–4402. [Google Scholar] [CrossRef]
- Nikolaev, A.L. Specificity of stage III in electron-irradiated Fe-Cr alloys. Philos. Mag. 2007, 87, 4847–4874. [Google Scholar] [CrossRef]
- Eldrup, M.; Singh, B. Accumulation of point defects and their complexes in irradiated metals as studied by the use of positron annihilation spectroscopy—A brief review. J. Nucl. Mater. 2003, 323, 346–353. [Google Scholar] [CrossRef]
- Wirth, B.D. How Does Radiation Damage Materials? Science 2007, 318, 923–924. [Google Scholar] [CrossRef]
- Bacon, D.; Osetsky, Y.; Stoller, R.; Voskoboinikov, R. MD description of damage production in displacement cascades in copper and α-iron. J. Nucl. Mater. 2003, 323, 152–162. [Google Scholar] [CrossRef]
- Osetsky, Y.N.; Bacon, D.J.; Serra, A.; Singh, B.N.; Golubov, S.I. One-dimensional atomic transport by clusters of self-interstitial atoms in iron and copper. Philos. Mag. 2003, 83, 61–91. [Google Scholar] [CrossRef]
- Matsukawa, Y.; Zinkle, S.J. One-Dimensional Fast Migration of Vacancy Clusters in Metals. Science 2007, 318, 959–962. [Google Scholar] [CrossRef] [PubMed]
- Matsukawa, Y.; Zinkle, S.J. Dynamic observation of the collapse process of a stacking fault tetrahedron by moving dislocations. J. Nucl. Mater. 2004, 329–333 Pt B, 919–923. [Google Scholar] [CrossRef]
- Uberuaga, B.P.; Hoagland, R.G.; Voter, A.F.; Valone, S.M. Direct Transformation of Vacancy Voids to Stacking Fault Tetrahedra. Phys. Rev. Lett. 2007, 99, 135501. [Google Scholar] [CrossRef]
- Wirth, B.D.; Bulatov, V.V.; de la Rubia, T.D. Dislocation-stacking fault tetrahedron interactions in Cu. J. Eng. Mater. Technol. 2002, 124, 329–334. [Google Scholar] [CrossRef]
- Osetsky, Y.N.; Rodney, D.; Bacon, D.J. Atomic-scale study of dislocation–stacking fault tetrahedron interactions. Part I: Mechanisms. Philos. Mag. 2006, 86, 2295–2313. [Google Scholar] [CrossRef]
- Samolyuk, G.D.; Golubov, S.I.; Osetskiy, Y.N.; Stoller, R.E. DFT Study Revises Interstitial Configurations in Hcp Zr; ORNL/TM-2011/516; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2011. [Google Scholar]
- Osetsky, Y.; Bacon, D.; de Diego, N. Anisotropy of point defect diffusion in alpha-zirconium. Metall. Mater. Trans. A 2002, 33, 777–782. [Google Scholar] [CrossRef]
- Golubov, S.I.; Barashev, A.; Stoller, R.E. On the Origin of Radiation Growth of hcp Crystals; ORNL/TM-2011/473; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2011. [Google Scholar]
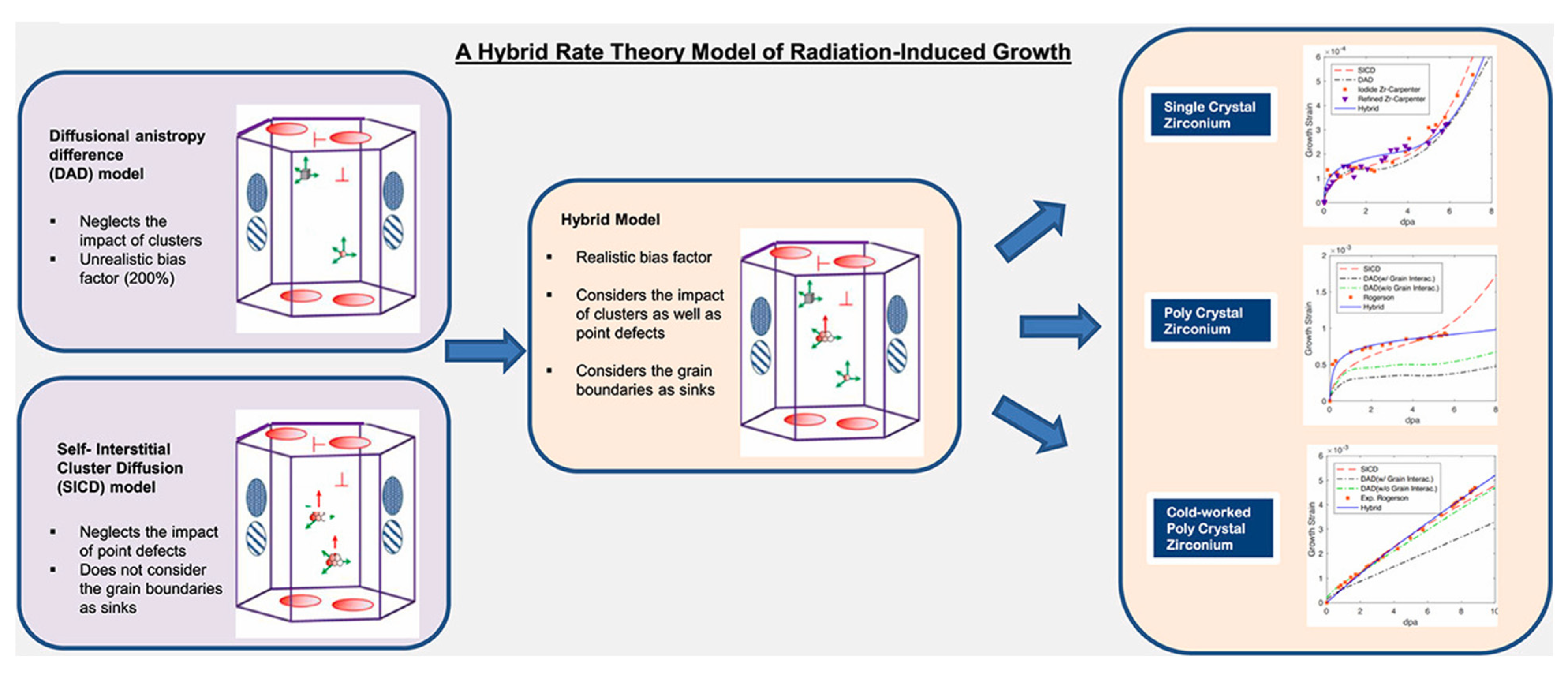
- Mohseni, M.; Saidi, P.; Dai, C.; Béland, L.K.; Welland, M.; Daymond, M.R. A hybrid rate theory model of radiation-induced growth. Acta Mater. 2024, 271, 119878. [Google Scholar] [CrossRef]
- Zhao, S.; Stocks, G.M.; Zhang, Y. Defect energetics of concentrated solid-solution alloys from ab initio calculations: Ni0.5Co0.5, Ni0.5Fe0.5, Ni0.8Fe0.2 and Ni0.8Cr0.2. Phys. Chem. Chem. Phys. 2016, 18, 24043–24056. [Google Scholar] [CrossRef]
- Zhao, S.; Egami, T.; Stocks, G.M.; Zhang, Y. Effect of d electrons on defect properties in equiatomic NiCoCr and NiCoFeCr concentrated solid solution alloys. Phys. Rev. Mater. 2018, 2, 013602. [Google Scholar] [CrossRef]
- Zhao, S. Effects of local elemental ordering on defect-grain boundary interactions in high-entropy alloys. J. Alloys Compd. 2021, 887, 161314. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, J.; Ma, S.; Xiong, Y.; Huang, S.; Kai, J.; Zhao, S. Revealing the crucial role of rough energy landscape on self-diffusion in high-entropy alloys based on machine learning and kinetic Monte Carlo. Acta Mater. 2022, 234, 118051. [Google Scholar] [CrossRef]
- Gao, C.; Wang, S.; Liu, X.; Singh, C.V. Defect energetics in an high-entropy alloy fcc CoCrFeMnNi. Mater. Adv. 2024, 5, 4231–4241. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, Z.; Xun, K.; Asta, M.; Ding, J.; Ma, E. Minimizing the diffusivity difference between vacancies and interstitials in multi-principal element alloys. Proc. Natl. Acad. Sci. USA 2024, 121, e2314248121. [Google Scholar] [CrossRef]
- Li, Y.; Du, J.-P.; Shinzato, S.; Ogata, S. Tunable interstitial and vacancy diffusivity by chemical ordering control in CrCoNi medium-entropy alloy. npj Comput. Mater. 2024, 10, 134. [Google Scholar] [CrossRef]
- Starikov, S.; Grigorev, P.; Drautz, R.; Divinski, S.V. Large-scale atomistic simulation of diffusion in refractory metals and alloys. Phys. Rev. Mater. 2024, 8, 043603. [Google Scholar] [CrossRef]
- Zhang, Y.; Stocks, G.M.; Jin, K.; Lu, C.; Bei, H.; Sales, B.C.; Wang, L.; Béland, L.K.; Stoller, R.E.; Samolyuk, G.D.; et al. Influence of chemical disorder on energy dissipation and defect evolution in concentrated solid solution alloys. Nat. Commun. 2015, 6, 8736. [Google Scholar] [CrossRef]
- Yang, T.; Li, C.; Zinkle, S.J.; Zhao, S.; Bei, H.; Zhang, Y. Irradiation responses and defect behavior of single-phase concentrated solid solution alloys. J. Mater. Res. 2018, 33, 3077–3091. [Google Scholar] [CrossRef]
- Lu, C.; Niu, L.; Chen, N.; Jin, K.; Yang, T.; Xiu, P.; Zhang, Y.; Gao, F.; Bei, H.; Shi, S.; et al. Enhancing radiation tolerance by controlling defect mobility and migration pathways in multicomponent single-phase alloys. Nat. Commun. 2016, 7, 13564. [Google Scholar] [CrossRef]
- Ullah, M.W.; Xue, H.; Velisa, G.; Jin, K.; Bei, H.; Weber, W.J.; Zhang, Y. Effects of chemical alternation on damage accumulation in concentrated solid-solution alloys. Sci. Rep. 2017, 7, 4146. [Google Scholar] [CrossRef]
- Osetsky, Y.; Bacon, D.; Serra, A.; Singh, B.; Golubov, S. Stability and mobility of defect clusters and dislocation loops in metals. J. Nucl. Mater. 2000, 276, 65–77. [Google Scholar] [CrossRef]
- Lin, P.; Cui, S.; Nie, J.; He, L.; Cui, W. Molecular Dynamics Simulations of Displacement Cascades in BCC-Fe: Effects of Dislocation, Dislocation Loop and Grain Boundary. Materials 2023, 16, 7497. [Google Scholar] [CrossRef] [PubMed]
- Yin, S.; Zuo, Y.; Abu-Odeh, A.; Zheng, H.; Li, X.-G.; Ding, J.; Ong, S.P.; Asta, M.; Ritchie, R.O. Atomistic simulations of dislocation mobility in refractory high-entropy alloys and the effect of chemical short-range order. Nat. Commun. 2021, 12, 4873. [Google Scholar] [CrossRef] [PubMed]
- Roy, A.; Nandipati, G.; Casella, A.M.; Senor, D.J.; Devanathan, R.; Soulami, A. A review of displacement cascade simulations using molecular dynamics emphasizing interatomic potentials for TPBAR components. npj Mater. Degrad. 2025, 9, 1. [Google Scholar] [CrossRef]
- He, M.; Yang, Y.; Gao, F.; Fan, Y. Stress sensitivity origin of extended defects production under coupled irradiation and mechanical loading. Acta Mater. 2023, 248, 118758. [Google Scholar] [CrossRef]
- Da Fonseca, D.; Mompiou, F.; Jourdan, T.; Crocombette, J.P.; Chartier, A.; Onimus, F. Evidence of dislocation loop preferential nu-cleation in irradiated aluminum under stress. Scr. Mater. 2023, 233, 115510. [Google Scholar] [CrossRef]
- Bakó, B.; Groma, I.; Györgyi, G.; Zimányi, G. Dislocation patterning: The role of climb in meso-scale simulations. Comput. Mater. Sci. 2006, 38, 22–28. [Google Scholar] [CrossRef]
- Martínez, E.; Senninger, O.; Caro, A.; Soisson, F.; Nastar, M.; Uberuaga, B.P. Role of Sink Density in Nonequilibrium Chemical Re-Distribution in Alloys. Phys. Rev. Lett. 2018, 120, 106101. [Google Scholar] [CrossRef]
- Schuler, T.; Nastar, M.; Soisson, F. Towards the modeling of the interplay between radiation induced segregation and sink mi-crostructure. J. Appl. Phys. 2022, 132, 080903. [Google Scholar] [CrossRef]
- Wu, B.; Bai, Z.; Misra, A.; Fan, Y. Atomistic mechanism and probability determination of the cutting of Guinier-Preston zones by edge dislocations in dilute Al-Cu alloys. Phys. Rev. Mater. 2020, 4, 020601. [Google Scholar] [CrossRef]
- Osetsky, Y.N.; Bacon, D.J. An atomic-level model for studying the dynamics of edge dislocations in metals. Model. Simul. Mater. Sci. Eng. 2003, 11, 427–446. [Google Scholar] [CrossRef]
- Rong, Z.; Osetsky, Y.N.; Bacon, D.J. A model for the dynamics of loop drag by a gliding dislocation. Philos. Mag. 2005, 85, 1473–1493. [Google Scholar] [CrossRef]
- Voskoboinikov, R.; Osetsky, Y.; Bacon, D. Interaction of edge dislocation with point defect clusters created in displacement cascades in α-zirconium. Mater. Sci. Eng. A 2005, 400–401, 49–53. [Google Scholar] [CrossRef]
- Voskoboynikov, R.; Osetsky, Y.; Bacon, D. Self-interstitial atom clusters as obstacles to glide of edge dislocations in α-zirconium. Mater. Sci. Eng. A 2005, 400–401, 54–58. [Google Scholar] [CrossRef]
- Bacon, D.J.; Osetsky, Y.N.; Rong, Z. Computer simulation of reactions between an edge dislocation and glissile self-interstitial clusters in iron. Philos. Mag. 2006, 86, 3921–3936. [Google Scholar] [CrossRef]
- Terentyev, D.; Malerba, L.; Bacon, D.J.; Osetsky, Y.N. The effect of temperature and strain rate on the interaction between an edge dislocation and an interstitial dislocation loop in α-iron. J. Phys. Condens. Matter 2007, 19, 456211. [Google Scholar] [CrossRef]
- Terentyev, D.; Grammatikopoulos, P.; Bacon, D.; Osetsky, Y.N. Simulation of the interaction between an edge dislocation and a <1 0 0> interstitial dislocation loop in α-iron. Acta Mater. 2008, 56, 5034–5046. [Google Scholar] [CrossRef]
- Bacon, D.J.; Osetsky, Y.N.; Rodney, D. Dislocation–Obstacle Interactions at the Atomic Level. In Dislocations in Solids; Hirth, J.P., Kubin, L., Eds.; Elsevier: Amsterdam, The Netherlands, 2009; pp. 1–90. [Google Scholar]
- Khater, H.; Bacon, D. Dislocation core structure and dynamics in two atomic models of α-zirconium. Acta Mater. 2010, 58, 2978–2987. [Google Scholar] [CrossRef]
- Monnet, G.; Osetsky, Y.; Bacon, D. Mesoscale thermodynamic analysis of atomic-scale dislocation–obstacle interactions simulated by molecular dynamics. Philos. Mag. 2010, 90, 1001–1018. [Google Scholar] [CrossRef]
- Terentyev, D.; Bacon, D.J.; Osetsky, Y.N. Reactions between a 1/2 <111> screw dislocation and <100> interstitial dislocation loops in alpha-iron modelled at atomic scale. Philos. Mag. 2010, 90, 1019–1033. [Google Scholar]
- Terentyev, D.; Osetsky, Y.; Bacon, D. Competing processes in reactions between an edge dislocation and dislocation loops in a body-centred cubic metal. Scr. Mater. 2010, 62, 697–700. [Google Scholar] [CrossRef]
- Osetsky, Y.N.; Matsukawa, Y.; Stoller, R.E.; Zinkle, S.J. On the features of dislocation–obstacle interaction in thin films: Large-scale atomistic simulation. Philos. Mag. Lett. 2006, 86, 511–519. [Google Scholar] [CrossRef]
- Onimus, F.; Monnet, I.; Béchade, J.; Prioul, C.; Pilvin, P. A statistical TEM investigation of dislocation channeling mechanism in neutron irradiated zirconium alloys. J. Nucl. Mater. 2004, 328, 165–179. [Google Scholar] [CrossRef]
- Fan, Y.; Osetskiy, Y.N.; Yip, S.; Yildiz, B. Mapping strain rate dependence of dislocation-defect interactions by atomistic simula-tions. Proc. Natl. Acad. Sci. USA 2013, 110, 17756–17761. [Google Scholar] [CrossRef]
- Bai, Z.; Fan, Y. Abnormal Strain Rate Sensitivity Driven by a Unit Dislocation-Obstacle Interaction in bcc Fe. Phys. Rev. Lett. 2018, 120, 125504. [Google Scholar] [CrossRef] [PubMed]
- Hull, D.; Bacon, D. Introduction to Dislocations, 5th ed.; Butterworth Heinemann: Oxford, UK, 2011. [Google Scholar]
- El-Awady, J.A. Unravelling the physics of size-dependent dislocation-mediated plasticity. Nat. Commun. 2015, 6, 5926. [Google Scholar] [CrossRef]
- Hussein, A.M.; Rao, S.I.; Uchic, M.D.; Dimiduk, D.M.; El-Awady, J.A. Microstructurally based cross-slip mechanisms and their effects on dislocation microstructure evolution in fcc crystals. Acta Mater. 2015, 85, 180–190. [Google Scholar] [CrossRef]
- Amodeo, R.J.; Ghoniem, N.M. Dislocation dynamics. I. A proposed methodology for deformation micromechanics. Phys. Rev. B 1990, 41, 6958–6967. [Google Scholar] [CrossRef]
- Bulatov, V.V.; Hsiung, L.L.; Tang, M.; Arsenlis, A.; Bartelt, M.C.; Cai, W.; Florando, J.N.; Hiratani, M.; Rhee, M.; Hommes, G.; et al. Dislocation multi-junctions and strain hardening. Nature 2006, 440, 1174–1178. [Google Scholar] [CrossRef]
- Brechet, Y.; Estrin, Y. On the influence of precipitation on the Portevin-Le Chatelier effect. Acta Met. Mater. 1995, 43, 955–963. [Google Scholar] [CrossRef]
- Dunlop, J.; Bréchet, Y.; Legras, L.; Estrin, Y. Dislocation density-based modelling of plastic deformation of Zircaloy-4. Mater. Sci. Eng. A 2007, 443, 77–86. [Google Scholar] [CrossRef]
- Lebyodkin, M.A.; Brechet, Y.; Estrin, Y.; Kubin, L.P. Statistics of the Catastrophic Slip Events in the Portevin–Le Châtelier Effect. Phys. Rev. Lett. 1995, 74, 4758–4761. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; McCormick, P.G.; Estrin, Y. The morphology of Portevin–Le Chatelier bands: Finite element simulation for Al–Mg–Si. Acta Mater. 2001, 49, 1087–1094. [Google Scholar] [CrossRef]
- Needleman, A.; Van der Giessen, E. Elasticity: Finite Element Modeling A2—Buschow, K.H. Jürgen. In Encyclopedia of Materials: Science and Technology, 2nd ed.; Cahn, R.W., Flemings, M.C., Ilschner, B., Kramer, E.J., Mahajan, S., Veyssière, P., Eds.; Elsevier: Oxford, UK, 2005; pp. 1–6. [Google Scholar]
- Gracie, R.; Ventura, G.; Belytschko, T. A new fast finite element method for dislocations based on interior discontinuities. Int. J. Numer. Methods Eng. 2007, 69, 423–441. [Google Scholar] [CrossRef]
- Tang, M.; Xu, G.; Cai, W.; Bulatov, V. Dislocation Image Stresses at Free Surfaces by the Finite Element Method. MRS Proc. 2003, 795, U2-4. [Google Scholar] [CrossRef]
- Zhong, Y.; Zhu, T. Simulating nanoindentation and predicting dislocation nucleation using interatomic potential finite element method. Comput. Methods Appl. Mech. Eng. 2008, 197, 3174–3181. [Google Scholar] [CrossRef]
- Lebensohn, R.A.; Hartley, C.S.; Tomé, C.N.; Castelnau, O. Modeling the mechanical response of polycrystals deforming by climb and glide. Philos. Mag. 2010, 90, 567–583. [Google Scholar] [CrossRef]
- Lebensohn, R.A.; Tomé, C.N.; Castañeda, P.P. Self-consistent modelling of the mechanical behaviour of viscoplastic polycrystals incorporating intragranular field fluctuations. Philos. Mag. 2007, 87, 4287–4322. [Google Scholar] [CrossRef]
- Subramanian, G.; Tomé, C.N. Progress Report on the Incorporation of Lower Lengthscales into Polycrystal Plasticity Models; LA-UR-12-25613; Los Alamos National Laboratory: Los Alamos, NM, USA, 2012. [Google Scholar]
- Turner, P.A.; Tomé, C.N.; Christodoulou, N.; Woo, C.H. A self-consistent model for polycrystals undergoing simultaneous irradiation and thermal creep. Philos. Mag. A 1999, 79, 2505–2524. [Google Scholar] [CrossRef]
- Kubin, L.P.; Canova, G.; Condat, M.; Devincre, B.; Pontikis, V.; Bréchet, Y. Dislocation Microstructures and Plastic Flow: A 3D Simulation. Solid State Phenom. 1992, 23–24, 455–472. [Google Scholar]
- Zbib, H.M.; Rhee, M.; Hirth, J.P. On plastic deformation and the dynamics of 3D dislocations. Int. J. Mech. Sci. 1998, 40, 113–127. [Google Scholar] [CrossRef]
- Schwarz, K.W. Simulation of dislocations on the mesoscopic scale. I. Methods and examples. J. Appl. Phys. 1999, 85, 108–119. [Google Scholar] [CrossRef]
- Ghoniem, N.M.; Tong, S.-H.; Sun, L.Z. Parametric dislocation dynamics: A thermodynamics-based approach to investigations of mesoscopic plastic deformation. Phys. Rev. B 2000, 61, 913–927. [Google Scholar] [CrossRef]
- Zbib, H.M.; de la Rubia, D.T. A multiscale model of plasticity. Int. J. Plast. 2002, 18, 1133–1163. [Google Scholar] [CrossRef]
- Weygand, D.; Friedman, L.H.; Van der Giessen, E.; Needleman, A. Aspects of boundary-value problem solutions with three-dimensional dislocation dynamics. Model. Simul. Mater. Sci. Eng. 2002, 10, 437–468. [Google Scholar] [CrossRef]
- Arsenlis, A.; Cai, W.; Tang, M.; Rhee, M.; Oppelstrup, T.; Hommes, G.; Pierce, T.G.; Bulatov, V.V. Enabling strain hardening simulations with dislocation dynamics. Model. Simul. Mater. Sci. Eng. 2007, 15, 553. [Google Scholar] [CrossRef]
- El-Awady, J.A.; Biner, S.B.; Ghoniem, N.M. A self-consistent boundary element, parametric dislocation dynamics formulation of plastic flow in finite volumes. J. Mech. Phys. Solids 2008, 56, 2019–2035. [Google Scholar] [CrossRef]
- Huang, Z.; Allison, J.E.; Misra, A. Interaction of Glide Dislocations with Extended Precipitates in Mg-Nd Alloys. Sci. Rep. 2018, 8, 3570. [Google Scholar] [CrossRef]
- Huang, Z.; Yang, C.; Qi, L.; Allison, J.E.; Misra, A. Dislocation pile-ups at β1 precipitate interfaces in Mg-rare earth (RE) alloys. Mater. Sci. Eng. A 2019, 742, 278–286. [Google Scholar] [CrossRef]
- Dezerald, L.; Rodney, D.; Clouet, E.; Ventelon, L.; Willaime, F. Plastic anisotropy and dislocation trajectory in BCC metals. Nat. Commun. 2016, 7, 11695. [Google Scholar] [CrossRef] [PubMed]
- Clouet, E.; Caillard, D.; Chaari, N.; Onimus, F.; Rodney, D. Dislocation locking versus easy glide in titanium and zirconium. Nat. Mater. 2015, 14, 931–936. [Google Scholar] [CrossRef]
- Ventelon, L.; Lüthi, B.; Clouet, E.; Proville, L.; Legrand, B.; Rodney, D.; Willaime, F. Dislocation core reconstruction induced by carbon segregation in bcc iron. Phys. Rev. B 2015, 91, 220102. [Google Scholar] [CrossRef]
- Dezerald, L.; Proville, L.; Ventelon, L.; Willaime, F.; Rodney, D. First-principles prediction of kink-pair activation enthalpy on screw dislocations in bcc transition metals: V, Nb, Ta, Mo, W, and Fe. Phys. Rev. B 2015, 91, 094105. [Google Scholar] [CrossRef]
- Chaari, N.; Clouet, E.; Rodney, D. First-Principles Study of Secondary Slip in Zirconium. Phys. Rev. Lett. 2014, 112, 075504. [Google Scholar] [CrossRef]
- Proville, L.; Rodney, D.; Marinica, M.-C. Quantum effect on thermally activated glide of dislocations. Nat. Mater. 2012, 11, 845–849. [Google Scholar] [CrossRef]
- Terentyev, D.; Bonny, G.; Domain, C.; Pasianot, R.C. Interaction of a ½ ⟨111⟩ screw dislocation with Cr precipitates in bcc Fe studied by molecular dynamics. Phys. Rev. B 2010, 81, 214106. [Google Scholar] [CrossRef]
- Rodney, D.; Martin, G. Dislocation Pinning by Small Interstitial Loops: A Molecular Dynamics Study. Phys. Rev. Lett. 1999, 82, 3272–3275. [Google Scholar] [CrossRef]
- Singh, C.V.; Warner, D.H. An Atomistic-Based Hierarchical Multiscale Examination of Age Hardening in an Al-Cu Alloy. Met. Mater. Trans. A 2013, 44, 2625–2644. [Google Scholar] [CrossRef]
- Christiann, J.W. Chapter 1—General Introduction. In The Theory of Transformations in Metals and Alloys; Christian, J.W., Ed.; Pergamon: Oxford, UK, 2002; pp. 1–22. [Google Scholar]
- Singh, C.; Warner, D. Mechanisms of Guinier–Preston zone hardening in the athermal limit. Acta Mater. 2010, 58, 5797–5805. [Google Scholar] [CrossRef]
- Singh, C.V. Multiscale modeling predictions of age hardening curves in Al-Cu alloys. In Multiscale Materials Modeling: Approaches to Full Multiscaling; Schmauder, S., Schäfer, I., Eds.; De Gruyter: Berlin, Germany, 2016; pp. 37–72. [Google Scholar]
- Verestek, W.; Prskalo, A.-P.; Hummel, M.; Binkele, P.; Schmauder, S. Molecular dynamics investigations of the strengthening of Al-Cu alloys during thermal ageing. Phys. Mesomech. 2017, 20, 291–304. [Google Scholar] [CrossRef]
- Krasnikov, V.S.; Mayer, A.E.; Pogorelko, V.V.; Latypov, F.T.; Ebel, A.A. Interaction of dislocation with GP zones or θ phase precipitates in aluminum: Atomistic simulations and dislocation dynamics. Int. J. Plast. 2019, in press. [Google Scholar] [CrossRef]
- Onimus, F.; Béchade, J.-L. A polycrystalline modeling of the mechanical behavior of neutron irradiated zirconium alloys. J. Nucl. Mater. 2009, 384, 163–174. [Google Scholar] [CrossRef]
- Van Swygenhoven, H.; Derlet, P.M. Chapter 81—Atomistic Simulations of Dislocations in FCC Metallic Nanocrystalline Materials. In Dislocations in Solids; Hirth, J.P., Kubin, L., Eds.; Elsevier: Amsterdam, The Netherlands, 2008; pp. 1–42. [Google Scholar]
- Hatano, T.; Matsui, H. Molecular dynamics investigation of dislocation pinning by a nanovoid in copper. Phys. Rev. B 2005, 72, 094105. [Google Scholar] [CrossRef]
- Hatano, T. Dynamics of a dislocation bypassing an impenetrable precipitate: The Hirsch mechanism revisited. Phys. Rev. B 2006, 74, 020102. [Google Scholar] [CrossRef]
- Monnet, G. Mechanical and energetical analysis of molecular dynamics simulations of dislocation–defect interactions. Acta Mater. 2007, 55, 5081–5088. [Google Scholar] [CrossRef]
- Dutta, A.; Bhattacharya, M.; Gayathri, N.; Das, G.; Barat, P. The mechanism of climb in dislocation–nanovoid interaction. Acta Mater. 2012, 60, 3789–3798. [Google Scholar] [CrossRef]
- Zhu, T.; Li, J.; Samanta, A.; Leach, A.; Gall, K. Temperature and Strain-Rate Dependence of Surface Dislocation Nucleation. Phys. Rev. Lett. 2008, 100, 025502. [Google Scholar] [CrossRef] [PubMed]
- Weinberger, C.R.; Jennings, A.T.; Kang, K.; Greer, J.R. Atomistic simulations and continuum modeling of dislocation nucleation and strength in gold nanowires. J. Mech. Phys. Solids 2012, 60, 84–103. [Google Scholar] [CrossRef]
- Bai, X.-M.; Voter, A.F.; Hoagland, R.G.; Nastasi, M.; Uberuaga, B.P. Efficient Annealing of Radiation Damage Near Grain Boundaries via Interstitial Emission. Science 2010, 327, 1631–1634. [Google Scholar] [CrossRef]
- Kenik, E. Radiation-induced segregation in irradiated Type 304 stainless steels. J. Nucl. Mater. 1992, 187, 239–246. [Google Scholar] [CrossRef]
- Radiguet, B.; Etienne, A.; Pareige, P.; Sauvage, X.; Valiev, R. Irradiation behavior of nanostructured 316 austenitic stainless steel. J. Mater. Sci. 2008, 43, 7338–7343. [Google Scholar] [CrossRef]
- Jiao, Z.; Was, G. Novel features of radiation-induced segregation and radiation-induced precipitation in austenitic stainless steels. Acta Mater. 2011, 59, 1220–1238. [Google Scholar] [CrossRef]
- He, M.-R.; Wang, S.; Shi, S.; Jin, K.; Bei, H.; Yasuda, K.; Matsumura, S.; Higashida, K.; Robertson, I.M. Mechanisms of radiation-induced segregation in CrFeCoNi-based single-phase concentrated solid solution alloys. Acta Mater. 2017, 126, 182–193. [Google Scholar] [CrossRef]
- Lu, C.; Yang, T.; Jin, K.; Gao, N.; Xiu, P.; Zhang, Y.; Gao, F.; Bei, H.; Weber, W.J.; Sun, K.; et al. Radiation-induced segregation on defect clusters in single-phase concentrated solid-solution alloys. Acta Mater. 2017, 127, 98–107. [Google Scholar] [CrossRef]
- Barr, C.M.; Nathaniel, J.E.; Unocic, K.A.; Liu, J.; Zhang, Y.; Wang, Y.; Taheri, M.L. Exploring radiation induced segregation mechanisms at grain boundaries in equiatomic CoCrFeNiMn high entropy alloy under heavy ion irradiation. Scr. Mater. 2018, 156, 80–84. [Google Scholar] [CrossRef]
- Lin, W.; Yeli, G.; Wang, G.; Lin, J.; Zhao, S.; Chen, D.; Liu, S.; Meng, F.; Li, Y.; He, F.; et al. He-enhanced heterogeneity of radiation-induced segregation in FeNiCoCr high-entropy alloy. J. Mater. Sci. Technol. 2022, 101, 226–233. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, D.; Weaver, J.; Gigax, J.; Wang, Y.; Mara, N.A.; Fensin, S.; Maloy, S.A.; Misra, A.; Li, N. Heavy ion irradiation effects on CrFeMnNi and AlCrFeMnNi high entropy alloys. J. Nucl. Mater. 2023, 574, 154163. [Google Scholar] [CrossRef]
- Patki, P.V.; Pownell, T.J.; Bazarbayev, Y.; Zhang, D.; Field, K.G.; Wharry, J.P. Systematic study of radiation-induced segregation in neutron-irradiated FeCrAl alloys. J. Nucl. Mater. 2023, 574, 154205. [Google Scholar] [CrossRef]
- Cantwell, P.R.; Tang, M.; Dillon, S.J.; Luo, J.; Rohrer, G.S.; Harmer, M.P. Grain boundary complexions. Acta Mater. 2014, 62, 1–48. [Google Scholar] [CrossRef]
- Raabe, D.; Herbig, M.; Sandlöbes, S.; Li, Y.; Tytko, D.; Kuzmina, M.; Ponge, D.; Choi, P.-P. Grain boundary segregation engineering in metallic alloys: A pathway to the design of interfaces. Curr. Opin. Solid State Mater. Sci. 2014, 18, 253–261. [Google Scholar] [CrossRef]
- Pan, Z.; Rupert, T.J. Spatial variation of short-range order in amorphous intergranular complexions. Comput. Mater. Sci. 2017, 131, 62–68. [Google Scholar] [CrossRef]
- Schuler, J.D.; Rupert, T.J. Materials selection rules for amorphous complexion formation in binary metallic alloys. Acta Mater. 2017, 140, 196–205. [Google Scholar] [CrossRef]
- Grigorian, C.M.; Rupert, T.J. Critical cooling rates for amorphous-to-ordered complexion transitions in Cu-rich nanocrystalline alloys. Acta Mater. 2021, 206, 116650. [Google Scholar] [CrossRef]
- Lei, T.; Shin, J.; Gianola, D.S.; Rupert, T.J. Bulk nanocrystalline Al alloys with hierarchical reinforcement structures via grain boundary segregation and complexion formation. Acta Mater. 2021, 221, 117394. [Google Scholar] [CrossRef]
- Wardini, J.L.; Grigorian, C.M.; Rupert, T.J. Amorphous complexions alter the tensile failure of nanocrystalline Cu-Zr alloys. Materialia 2021, 17, 101134. [Google Scholar] [CrossRef]
- Grigorian, C.M.; Rupert, T.J. Multi-principal element grain boundaries: Stabilizing nanocrystalline grains with thick amorphous complexions. J. Mater. Res. 2022, 37, 554–566. [Google Scholar] [CrossRef]
- Garg, P.; Rupert, T.J. Grain incompatibility determines the local structure of amorphous grain boundary complexions. Acta Mater. 2023, 244, 118599. [Google Scholar] [CrossRef]
- Bai, Z.; Balbus, G.H.; Gianola, D.S.; Fan, Y. Mapping the kinetic evolution of metastable grain boundaries under non-equilibrium processing. Acta Mater. 2020, 200, 328–337. [Google Scholar] [CrossRef]
- Wang, Y.; Ghaffari, B.; Taylor, C.; Lekakh, S.; Li, M.; Fan, Y. Predicting the energetics and kinetics of Cr atoms in Fe-Ni-Cr alloys via physics-based machine learning. Scr. Mater. 2021, 205, 114177. [Google Scholar] [CrossRef]
- Bai, Z.; Misra, A.; Fan, Y. Universal Trend in the dynamic relaxations of tilted metastable grain boundaries during ultrafast thermal cycle. Mater. Res. Lett. 2022, 10, 343–351. [Google Scholar] [CrossRef]
- Li, X.-T.; Tang, X.-Z.; Guo, Y.-F.; Li, H.; Fan, Y. Modulating grain boundary-mediated plasticity of high-entropy alloys via chemo-mechanical coupling. Acta Mater. 2023, 258, 119228. [Google Scholar] [CrossRef]
- Liu, C.; Wang, Y.; Wang, Y.; Islam, M.; Hwang, J.; Wang, Y.; Fan, Y. Concurrent prediction of metallic glasses’ global energy and internal structural heterogeneity by interpretable machine learning. Acta Mater. 2023, 259, 119281. [Google Scholar] [CrossRef]
- Wang, Y.; Ghaffari, B.; Taylor, C.; Lekakh, S.; Engler-Pinto, C.; Godlewski, L.; Huo, Y.; Li, M.; Fan, Y. Nonmonotonic effect of chemical heterogeneity on interfacial crack growth at high-angle grain boundaries in Fe-Ni-Cr alloys. Phys. Rev. Mater. 2023, 7, 073606. [Google Scholar] [CrossRef]
- He, M.; Wang, Y.; Fan, Y. Metastable grain boundaries: The roles of structural and chemical disorders in their energetics, non-equilibrium kinetic evolution, and mechanical behaviors. J. Phys. Condens. Matter 2024, 36, 343001. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Zhang, S.; Zhang, Z.; Liu, H.; Teng, Y.; Wang, H.; Gong, H.; Shang, Y.; Guo, B.; Fan, Y.; et al. Ox-ide-Metal Hybrid Glass Nanomembranes with Exceptional Thermal Stability. Nano Lett. 2024, 24, 14475–14483. [Google Scholar] [CrossRef]
- Fan, Y.; Yildiz, B.; Yip, S. Analogy between glass rheology and crystal plasticity: Yielding at high strain rate. Soft Matter 2013, 9, 9511–9514. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, Y. Incident Velocity Induced Nonmonotonic Aging of Vapor-Deposited Polymer Glasses. J. Phys. Chem. B 2020, 124, 5740–5745. [Google Scholar] [CrossRef]
- Egami, T.; Fan, Y.; Iwashita, T. Mechanical Deformation in Metallic Liquids and Glasses: From Atomic Bond-Breaking to Ava-lanches. In Avalanches in Functional Materials and Geophysics; Salje, E.K.H., Saxena, A., Planes, A., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 199–225. [Google Scholar]
- Islam, M.; Ortiz, G.C.; Wang, Y.; Wang, Y.; Yoo, G.-H.; Kim, J.Y.; Park, E.S.; Fan, Y.; Wang, Y.; Hwang, J. Unveiling the Formation Mechanism of Medium Range Ordering in Zr-based Bulk Metallic Glasses Using Angular Correlation Analysis of 4D-STEM. Microsc. Microanal. 2024, 30, ozae044.951. [Google Scholar] [CrossRef]
- Li, H.; Xiao, H.; Egami, T.; Fan, Y. Infinitely rugged intra-cage potential energy landscape in metallic glasses caused by many-body interaction. Mater. Today Phys. 2024, 49, 101582. [Google Scholar] [CrossRef]
- Zhang, H.; Srolovitz, D.J.; Douglas, J.F.; Warren, J.A. Grain boundaries exhibit the dynamics of glass-forming liquids. Proc. Natl. Acad. Sci. USA 2009, 106, 7735–7740. [Google Scholar] [CrossRef]
- Han, J.; Vitek, V.; Srolovitz, D.J. Grain-boundary metastability and its statistical properties. Acta Mater. 2016, 104, 259–273. [Google Scholar] [CrossRef]
- Sharp, T.A.; Thomas, S.L.; Cubuk, E.D.; Schoenholz, S.S.; Srolovitz, D.J.; Liu, A.J. Machine learning determination of atomic dynamics at grain boundaries. Proc. Natl. Acad. Sci. USA 2018, 115, 10943–10947. [Google Scholar] [CrossRef] [PubMed]
- Was, G.; Bruemmer, S. Effects of irradiation on intergranular stress corrosion cracking. J. Nucl. Mater. 1994, 216, 326–347. [Google Scholar] [CrossRef]
- He, M.-R.; Johnson, D.C.; Was, G.S.; Robertson, I.M. The role of grain boundary microchemistry in irradiation-assisted stress corrosion cracking of a Fe-13Cr-15Ni alloy. Acta Mater. 2017, 138, 61–71. [Google Scholar] [CrossRef]
- Was, G.S.; Bahn, C.B.; Busby, J.; Cui, B.; Farkas, D.; Gussev, M.; Rigen He, M.; Hesterberg, J.; Jiao, Z.; Johnson, D.; et al. How irradiation promotes inter-granular stress corrosion crack initiation. Prog. Mater. Sci. 2024, 143, 101255. [Google Scholar] [CrossRef]
- Simonen, E.; Jones, R.; Bruemmer, S. Radiation effects on grain boundary chemistry relevant to stress corrosion cracking of stainless steels. J. Nucl. Mater. 1992, 191–194, 1002–1006. [Google Scholar] [CrossRef]
- Was, G.S.; Andresen, P.L. 3—Mechanisms behind irradiation-assisted stress corrosion cracking. In Nuclear Corrosion; Ritter, S., Ed.; Woodhead Publishing: Sawston, UK, 2020; pp. 47–88. [Google Scholar]
- Johnson, D.; Kuhr, B.; Farkas, D.; Was, G. Quantitative linkage between the stress at dislocation channel—Grain boundary interaction sites and irradiation assisted stress corrosion crack initiation. Acta Mater. 2019, 170, 166–175. [Google Scholar] [CrossRef]
- Barr, C.M.; Chen, E.Y.; Nathaniel, J.E.; Lu, P.; Adams, D.P.; Dingreville, R.; Boyce, B.L.; Hattar, K.; Medlin, D.L. Irradiation-induced grain boundary facet motion: In situ observations and atomic-scale mechanisms. Sci. Adv. 2022, 8, eabn0900. [Google Scholar] [CrossRef]
- Jacobs, R.; Morgan, D.; Attarian, S.; Meng, J.; Shen, C.; Wu, Z.; Xie, C.Y.; Yang, J.H.; Artrith, N.; Blaiszik, B.; et al. A practical guide to machine learning inter-atomic potentials—Status and future. Curr. Opin. Solid State Mater. Sci. 2025, 35, 101214. [Google Scholar] [CrossRef]
- Mortazavi, B.; Zhuang, X.; Rabczuk, T.; Shapeev, A.V. Atomistic modeling of the mechanical properties: The rise of machine learning interatomic potentials. Mater. Horiz. 2023, 10, 1956–1968. [Google Scholar] [CrossRef] [PubMed]
- Mortazavi, B. Machine Learning Interatomic Potentials: Keys to First-Principles Multiscale Modeling. In Machine Learning in Modeling and Simulation: Methods and Applications; Rabczuk, T., Bathe, K.-J., Eds.; Springer International Publishing: Cham, Switzerland, 2023; pp. 427–451. [Google Scholar]
- Tian, L.; Fan, Y.; Li, L.; Mousseau, N. Identifying flow defects in amorphous alloys using machine learning outlier detection methods. Scr. Mater. 2020, 186, 185–189. [Google Scholar] [CrossRef]
- He, M.; Li, Y.; Ghaffari, B.; Huo, Y.; Godlewski, L.; Li, M.; Fan, Y. Machine learning-augmented modeling on the formation of Si-dominated non-β” early-stage precipitates in Al-Si-Mg alloys with Si supersaturation induced by non-equilibrium solidification. Acta Mater. 2025, 282, 120454. [Google Scholar] [CrossRef]
- Shen, M.; Li, G.; Wu, D.; Yaguchi, Y.; Haley, J.C.; Field, K.G.; Morgan, D. A deep learning based automatic defect analysis framework for in situ TEM ion irradiations. Comput. Mater. Sci. 2021, 197, 110560. [Google Scholar] [CrossRef]
- Guo, K.; Yang, Z.; Yu, C.-H.; Buehler, M.J. Artificial intelligence and machine learning in design of mechanical materials. Mater. Horiz. 2021, 8, 1153–1172. [Google Scholar] [CrossRef]
- Vasudevan, R.; Pilania, G.; Balachandran, P.V. Machine learning for materials design and discovery. J. Appl. Phys. 2021, 129, 070401. [Google Scholar] [CrossRef]
- Fan, Y.; Cao, P.; Iwashita, T.; Ding, J. Editorial: Modeling of structural and chemical disorders: From metallic glasses to high entropy alloys. Front. Mater. 2022, 9, 1006726. [Google Scholar] [CrossRef]
- Tung, C.-H.; Huang, G.; Bai, Z.; Fan, Y.; Chen, W.; Chang, S.-Y. Structural origin of plasticity in strained high-entropy alloy. arXiv 2020, arXiv:2005.07088. [Google Scholar] [CrossRef]
- Truskett, T.M.; Torquato, S.; Debenedetti, P.G. Towards a quantification of disorder in materials: Distinguishing equilibrium and glassy sphere packings. Phys. Rev. E 2000, 62, 993–1001. [Google Scholar] [CrossRef] [PubMed]
- Richard, D.; Ozawa, M.; Patinet, S.; Stanifer, E.; Shang, B.; Ridout, S.A.; Xu, B.; Zhang, G.; Morse, P.K.; Barrat, J.-L.; et al. Predicting plasticity in disordered solids from structural indicators. Phys. Rev. Mater. 2020, 4, 113609. [Google Scholar] [CrossRef]
- Cubuk, E.D.; Ivancic, R.J.S.; Schoenholz, S.S.; Strickland, D.J.; Basu, A.; Davidson, Z.S.; Fontaine, J.; Hor, J.L.; Huang, Y.-R.; Jiang, Y.; et al. Structure-property relationships from universal signatures of plasticity in disordered solids. Science 2017, 358, 1033–1037. [Google Scholar] [CrossRef] [PubMed]
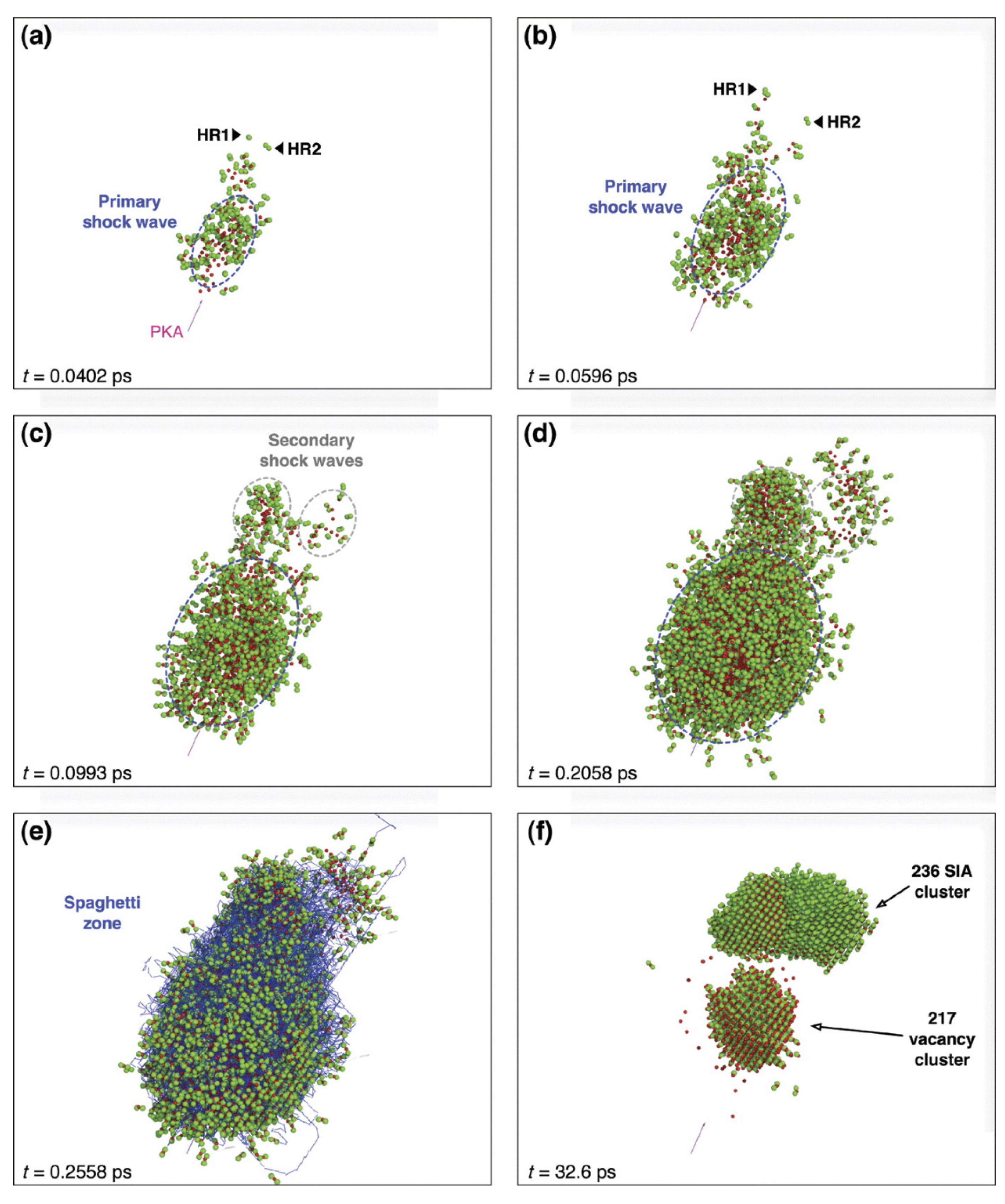
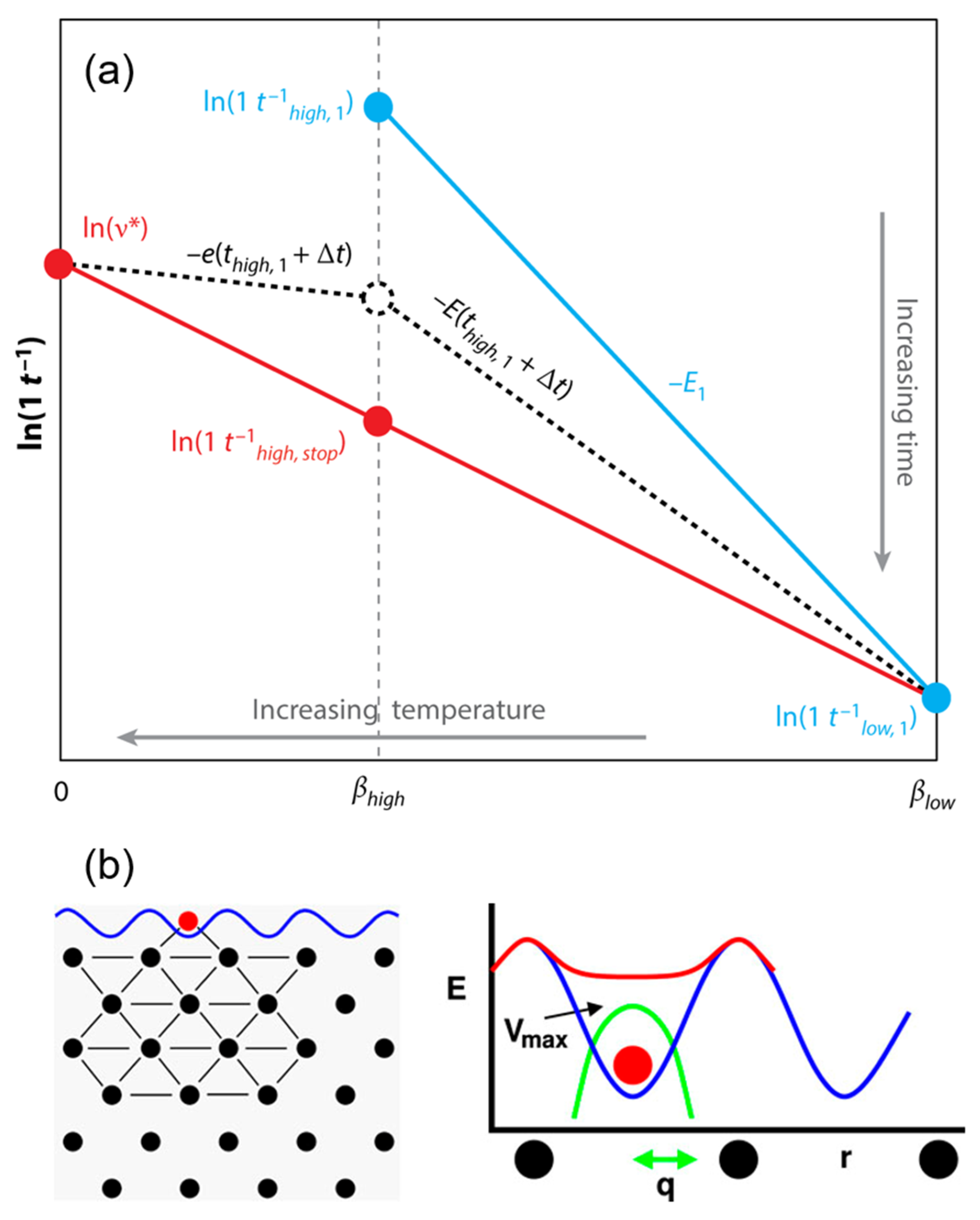
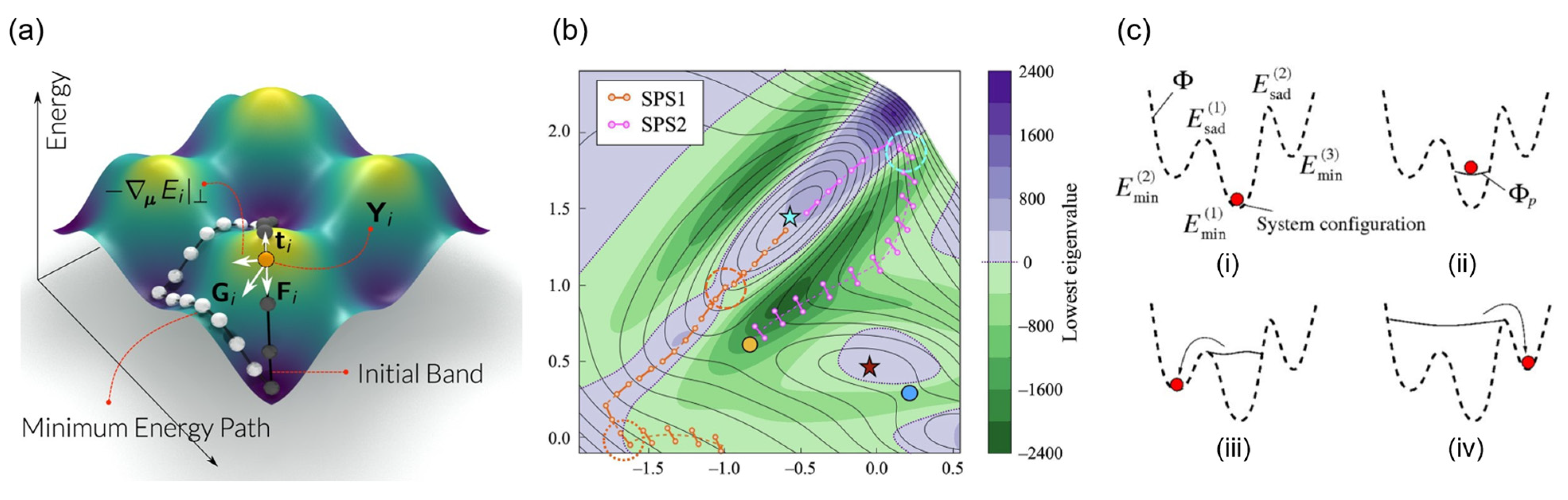
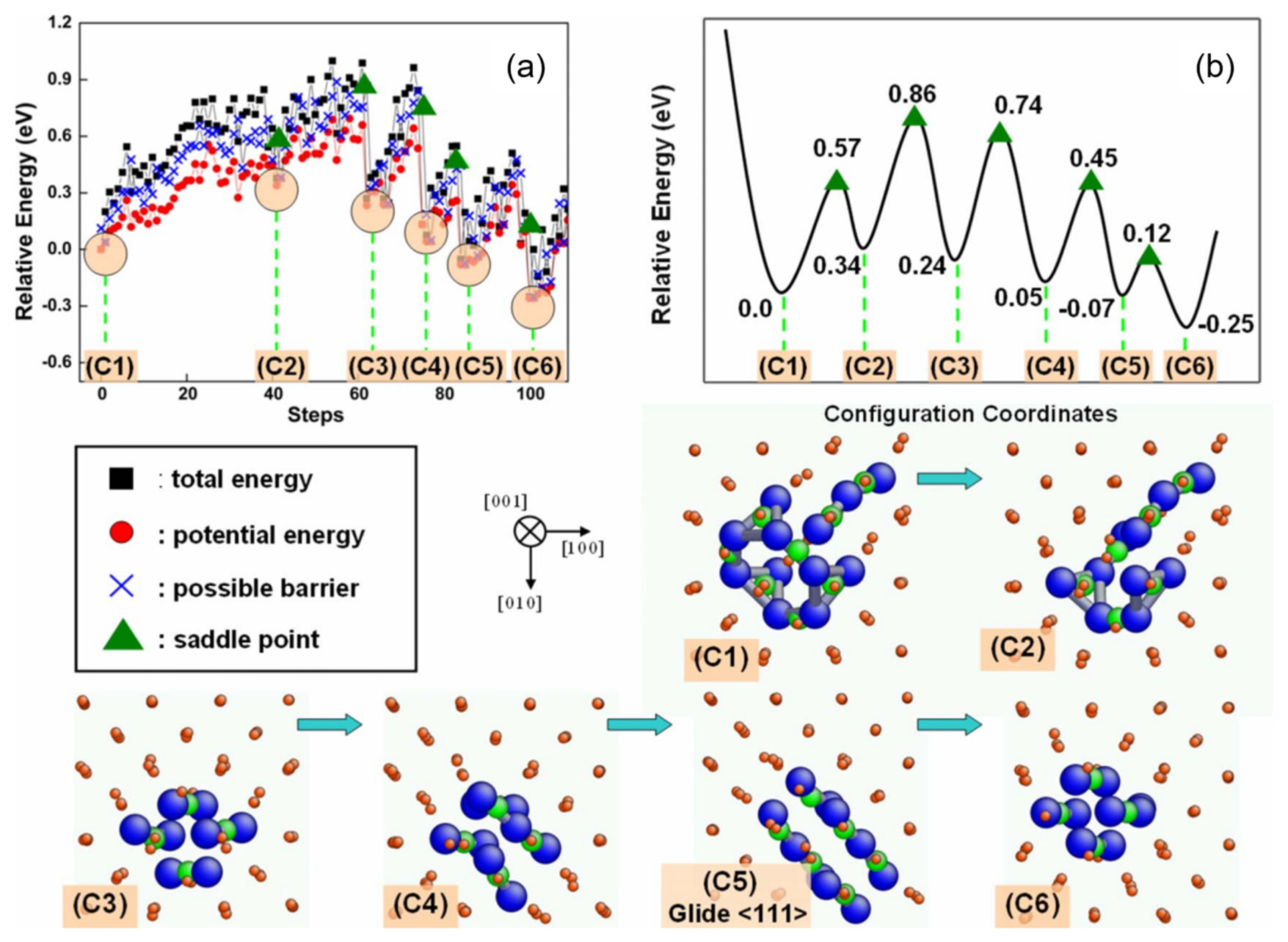
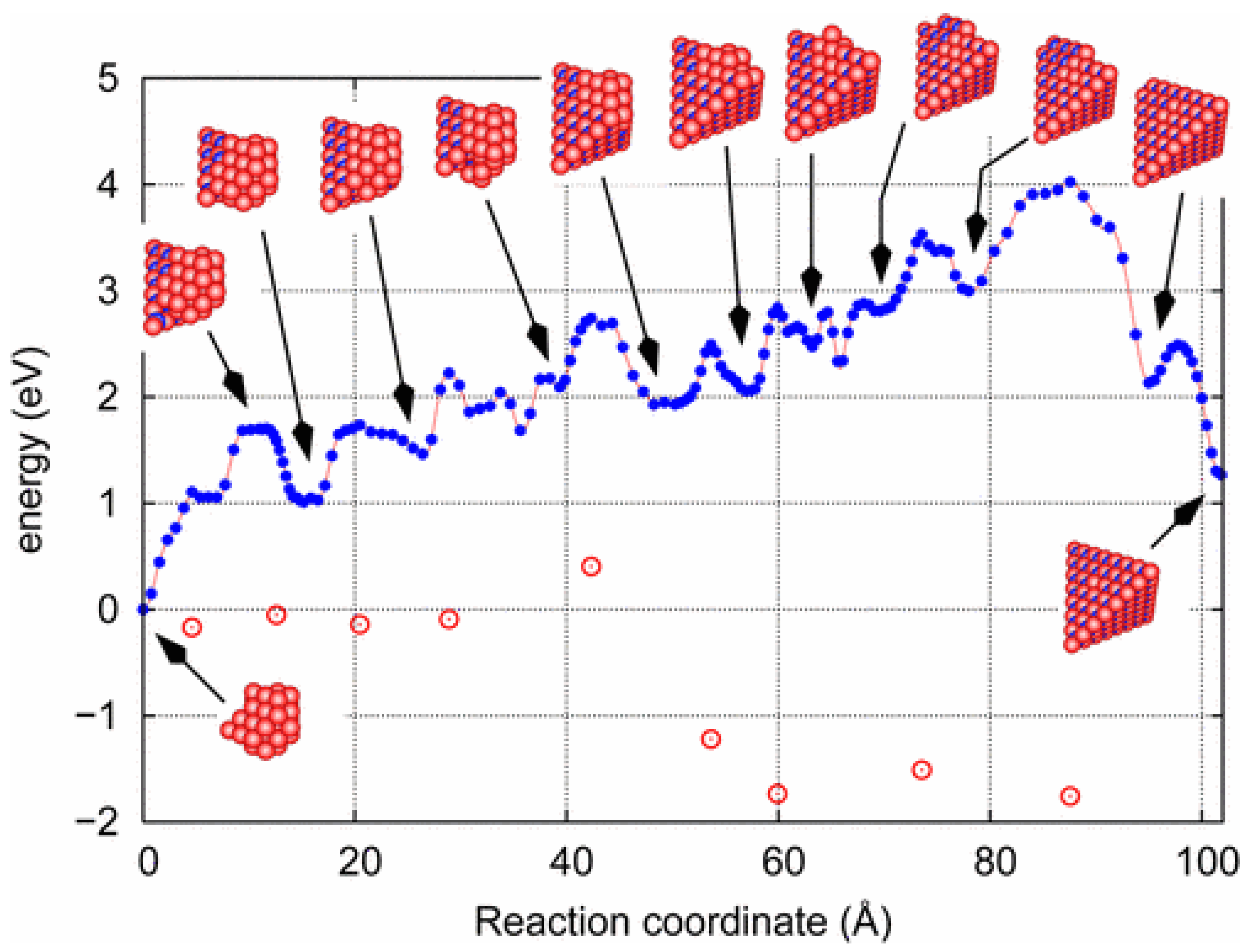
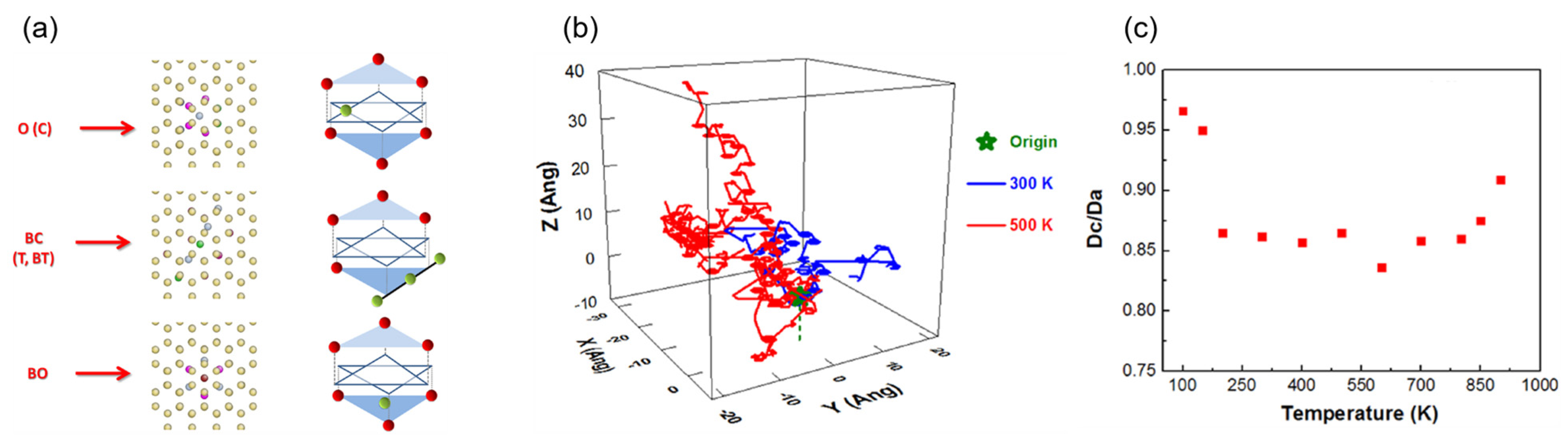

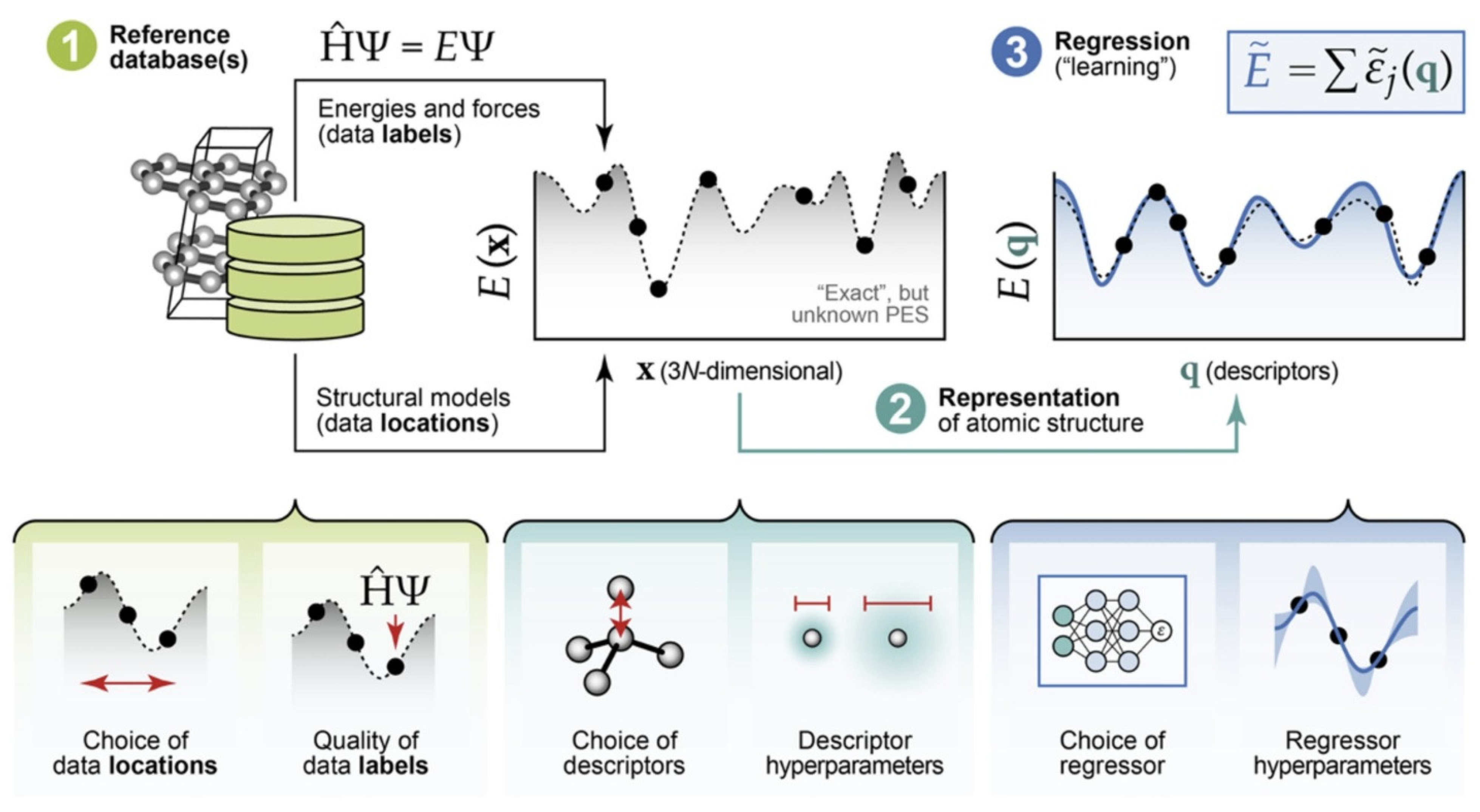
| Method | Primary Use Case | Key Advantage | Limitation/Scalability |
|---|---|---|---|
| Temp.-Accelerated Dynamics (TAD) | Accelerating rare events by manually increasing the temperature | Simulating long-time dynamics of a system in a single energy basin | Conceptually straightforward; extends MD time by leveraging high-T runs |
| Hyperdynamics | Accelerating rare events by modifying the potential energy surface | Boosts escape rates from energy wells without changing transition pathways | Requires the careful construction of a bias potential; also limited by the lowest barrier in the biased system |
| Nudged Elastic Band (NEB) | Finding the minimum energy path and saddle point between a known initial and the final state | Highly accurate for calculating the energy barrier of a specific, known mechanism | Requires a priori knowledge of the final state, making it unsuitable for discovering novel or complex mechanisms |
| Dimer Method | Finding a saddle point without knowing the final state | Proactively searches for an escape pathway from a given minimum | Relies on Hessian matrix calculations, which can be computationally expensive for large systems |
| Activation–Relaxation Technique (ART) | Exploring complex energy landscapes by finding multiple saddle points from a single minimum | Robustly samples the PEL to find a distribution of possible escape pathways | Can also be computationally demanding due to its reliance on the Hessian matrix |
| Autonomous Basin Climbing (ABC/ABC-E) | Systematically mapping reaction pathways and barriers without prior knowledge of mechanisms | Highly efficient as it avoids Hessian calculations; the ABC-E variant can find multiple competing pathways | The original ABC method tends to follow only the lowest-energy pathway, potentially missing other relevant mechanisms |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Y. Atomistic Modeling of Microstructural Defect Evolution in Alloys Under Irradiation: A Comprehensive Review. Appl. Sci. 2025, 15, 9110. https://doi.org/10.3390/app15169110
Fan Y. Atomistic Modeling of Microstructural Defect Evolution in Alloys Under Irradiation: A Comprehensive Review. Applied Sciences. 2025; 15(16):9110. https://doi.org/10.3390/app15169110
Chicago/Turabian StyleFan, Yue. 2025. "Atomistic Modeling of Microstructural Defect Evolution in Alloys Under Irradiation: A Comprehensive Review" Applied Sciences 15, no. 16: 9110. https://doi.org/10.3390/app15169110
APA StyleFan, Y. (2025). Atomistic Modeling of Microstructural Defect Evolution in Alloys Under Irradiation: A Comprehensive Review. Applied Sciences, 15(16), 9110. https://doi.org/10.3390/app15169110






