A Credibility-Based Self-Evolution Algorithm for Equipment Digital Twins Based on Multi-Layer Deep Koopman Operator

Abstract

In the context of Industry 4.0 and intelligent manufacturing, the scale and complexity of complex equipment systems are continuously increasing, making effective high-precision modeling, simulation, and prediction in the engineering field significant challenges. Digital twin technology, by establishing real-time connections between virtual models and physical systems, provides strong support for the real-time monitoring, optimization, and prediction of complex systems. However, traditional digital twin models face significant limitations when synchronizing with high-dimensional nonlinear and non-stationary dynamical systems due to the latter’s dynamic characteristics. To address this issue, we propose a multi-layer deep Koopman operator-based (MDK) credibility-based self-evolution algorithm for equipment digital twins. By constructing multiple time-scale embedding layers and combining deep neural networks for observability function learning, the algorithm effectively captures the dynamic features of complex nonlinear systems at different time scales, enabling their global dynamic modeling and precise analysis. Furthermore, to enhance the model’s adaptability, a trustworthiness-based evolution-triggering mechanism and an adaptive model fine-tuning algorithm are designed. When the digital twin model’s trustworthiness assessment indicates a decline in prediction accuracy, the evolution mechanism is automatically triggered to optimize and update the model with the fine-tuning algorithm to maintain its stability and robustness during dynamic evolution. The experimental results demonstrate that the proposed method achieves significant improvements in prediction accuracy within unmanned aerial vehicle (UAV) systems, showcasing its broad application potential in intelligent manufacturing and complex equipment systems.

1. Introduction

With the rapid advancements in Industry 4.0, the scale and complexity of modern equipment systems are continuously growing. This trend poses significant challenges to modeling, simulation, and prediction in engineering and science while simultaneously raising the expectations for the capabilities of these processes [1]. Traditional linear modeling methods exhibit notable limitations in addressing the nonlinear and non-stationary dynamic characteristics of complex systems, making them inadequate for high-precision predictions and real-time responsiveness [2]. Digital twin technology, as a cutting-edge system engineering tool, enables the real-time monitoring, prediction, and optimization of system states by synchronizing virtual models with physical systems [3]. However, traditional Digital twin models often struggle with limited prediction accuracy and adaptability when synchronizing with the dynamic evolution of complex nonlinear systems [4]. Ensuring the trustworthiness and evolutionary capability of these models, particularly under changes in system dynamics [5], has become a critical bottleneck in advancing Digital twin technology.

Complex equipment systems are characterized by highly nonlinear and multi-scale dynamic behavior, making their evolution inherently complex and difficult to predict. Traditional modeling approaches often lack the flexibility and adaptability required to address the multi-layered dynamics of such systems. These limitations make it difficult to adjust model structures in real time, preventing the accurate representation of global system behavior. Furthermore, current approaches often neglect the crucial aspect of model trustworthiness—the ability to reliably predict outcomes under significant changes in system states. Without trustworthiness assessments, models are prone to large errors during critical phases of system evolution, which can severely undermine their predictive and control capabilities.

To address these challenges, we propose a dynamic self-evolution algorithm for digital twins of complex equipment. Our approach leverages a multi-layer deep Koopman operator and incorporates a robust credible evaluation mechanism. First, the proposed algorithm uses a hierarchical Koopman operator framework to capture the multi-scale dynamic characteristics of systems across different time horizons, ensuring its ability to handle nonlinear evolution in complex systems. Second, a trustworthiness evaluation mechanism dynamically adjusts the model’s structure and parameters by monitoring system state changes, prediction errors, and sequence consistency in real time, thus ensuring model stability and adaptability during dynamic changes. By integrating trustworthiness evaluation, the algorithm can automatically trigger evolutionary processes when prediction accuracy deteriorates, thereby improving both precision and robustness across various evolutionary stages. The main contributions of this study are as follows:

(1) We establish a multi-timescale hierarchical embedding mechanism that leverages deep neural networks for the automatic learning of observation functions at each layer. By mapping raw system state sequences into multiple feature spaces, the proposed approach enables the simultaneous characterization of both short-term and long-term dynamic behaviors in complex equipment systems, thereby substantially enhancing overall modeling accuracy and predictive performance.

(2) We design a model credibility-based evolution-triggering mechanism and fine-tuning algorithm, introducing credibility evaluation metrics based on prediction error and sequence consistency. When prediction performance deteriorates or system dynamics undergo changes beyond the model’s adaptive range, the evolutionary fine-tuning process is automatically triggered, thus maintaining high reliability and adaptability.

(3) The effectiveness of the proposed MDK model is systematically validated using real flight datasets from an unmanned aerial vehicle (UAV) system. The experimental results demonstrate that the MDK model consistently outperforms traditional Koopman operator approaches, as well as mainstream sequence models such as long short-term memory (LSTM) networks and gated recurrent unit (GRU), achieving markedly superior prediction accuracy and stability.

2. Related Works

The modeling, simulation, and prediction of complex equipment systems have become increasingly vital in modern industry. To address the challenges posed by nonlinear dynamical systems, researchers have developed a range of approaches, including Digital twin technology, data-driven nonlinear modeling methods, and Koopman operator theory. While these techniques have shown outstanding performance in specific applications, they continue to face significant challenges and limitations when applied to high-dimensional, nonlinear, and dynamically evolving systems. In this section, we provide a comprehensive review and analysis of recent advancements in these fields, highlighting their strengths and identifying their limitations.

2.1. The Development of Digital Twin Technology

Digital twin technology has seen widespread adoption in recent years across domains such as intelligent manufacturing, aerospace, and smart transportation [6]. By creating digital models that mirror physical entities, Digital twin technology enables real-time system state monitoring and future behavior prediction based on current conditions. This approach not only improves operational efficiency but also minimizes downtime and failure rates through proactive fault prediction and health management [7,8].

In the domain of intelligent manufacturing, the application of digital twin technology has become increasingly sophisticated, particularly in areas such as process control and production optimization [9]. Recent studies have demonstrated that digital twin-driven intelligent manufacturing not only enhances lifecycle management and data integration capabilities but also leads to significant improvements in production efficiency and product quality [10]. The deep integration of emerging artificial intelligence technologies—including cloud computing, the Internet of Things, the Industrial Internet, and big data—with advanced manufacturing processes is enabling adaptive design and flexible production paradigms, thereby accelerating the shift toward highly automated and intelligent manufacturing systems.

Furthermore, some researchers have introduced digital twin frameworks based on large-scale models (such as generative AI) and self-supervised learning [11]. These frameworks are capable of autonomously optimizing system architectures, adjusting model parameters in response to environmental or data fluctuations, and performing real-time credibility assessments. Such capabilities provide effective support for the dynamic evolution of industrial systems, as well as robust decision making, in complex, real-world scenarios [12]. In addition, enabling technologies such as knowledge graphs, semantic modeling, and multi-agent collaboration have increasingly been incorporated into digital twin architectures, facilitating data interoperability across disparate systems and enabling reasoning over complex, multi-objective tasks [13]. Research efforts and practical deployments of digital twins are also expanding in the context of sustainability, including applications in green manufacturing, energy-efficient scheduling, and carbon emission reduction strategies [14].

Despite its strong potential across multiple fields, the implementation of Digital twin technology still faces significant technical challenges. The first challenge is the modeling of high-dimensional complex systems. Complex equipment systems often consist of multiple subsystems with intricate interactions, resulting in high dimensionality and nonlinearity that make it difficult for traditional modeling methods to accurately capture the system’s dynamic evolutionary behavior. Moreover, existing Digital twin technologies face issues with computational efficiency when processing real-time and high-dimensional data. Balancing predictive accuracy with real-time responsiveness remains a critical research topic in advancing Digital twin technology.

2.2. Nonlinear System Modeling Methods

Digital twin technology has emerged as a key support for intelligent operation, maintenance, and autonomous decision making in complex equipment systems, with continuous advancements in its theoretical frameworks. The dynamic evolution of such systems often exhibits pronounced nonlinearity, posing significant challenges to traditional linear modeling approaches, which are generally inadequate for high-precision description and prediction tasks [15]. Therefore, data-driven approaches to nonlinear system modeling have attracted growing interest from both academia and industry and now constitute a central theoretical foundation for digital twin implementation [16].

Data-driven deep learning methods currently represent the prevailing paradigm for nonlinear digital twin modeling. Neural network architectures such as Transformer, LSTM, and GRU have demonstrated considerable capability in high-dimensional nonlinear feature extraction, time-series prediction, and state recognition. For instance, Li et al. [17] combined LSTM and convolutional networks for equipment state identification and dynamic simulation, substantially improving the real-time decision-making capacity of digital twin systems. Guo et al. [18] developed a digital twin model employing a Transformer-LSTM structure, resulting in notable enhancements in the accuracy and robustness of nonlinear modeling for high-dimensional complex systems. Li et al. [19] introduced a graph neural network-based approach to large-scale system state modeling, along with neural architectures for multiphysics coupling, thereby advancing the ability of digital twins to characterize nonlinear dynamic phenomena.

Despite these advances, several challenges persist in nonlinear modeling, where a primary concern is the limited interpretability of many deep models. As data-driven models are typically constructed as “black boxes”, they often lack transparency regarding underlying system mechanisms, raising issues related to trustworthiness and explainability in digital twins [20]. Moreover, practical systems frequently involve multiphysics coupling and multi-scale dynamics, which further complicate the development of effective and accurate models [21]. Consequently, research attention has increasingly focused on enhancing the interpretability of deep learning models, aiming to shift nonlinear system modeling from “black-box” paradigms toward “gray-box” and even “white-box” approaches.

In this context, Koopman operator theory has attracted increasing attention. By mapping nonlinear dynamical systems to high-dimensional linear spaces, Koopman operator theory enables the transformation of inherently nonlinear problems into linearly analyzable and predictable forms in higher-dimensional settings [22]. This approach offers a promising avenue to address the interpretability limitations of conventional deep learning models while also supporting comprehensive global feature extraction and the modeling of complex coupled dynamical behaviors.

2.3. Koopman Operator Theory

In recent years, Koopman operator theory has garnered significant attention due to its ability to map nonlinear dynamical systems to linear representations in high-dimensional spaces, thereby offering a novel perspective for the modeling, prediction, and control of complex systems. Building upon this theoretical foundation, dynamic mode decomposition (DMD) and its various extensions have enabled the effective spatiotemporal separation and characterization of system dynamical modes. Kim et al. [23] has innovatively proposed an improved modeling method based on the Koopman operator framework. By integrating extended dynamic mode decomposition and genetic algorithms, this approach achieves global linear modeling and data-driven identification of gas turbine engine (GTE) dynamics, and further investigates parameter settings, prediction performance, as well as the underlying dynamic mechanisms under Koopman eigenfunctions. Xiao et al. [24] provided an in-depth review of the theoretical underpinnings, implementation strategies, and practical applications of DMD and its enhanced variants, highlighting its emergence as a key tool for the high-dimensional, data-driven analysis of dynamical systems.

Advances in deep learning have spurred the development of end-to-end neural network architectures approximating the Koopman operator, enabling the automated learning of embedded representations for complex systems and substantially improving modeling capability for high-dimensional and strongly nonlinear dynamics. For instance, Li et al. [25] proposed the Physics-Informed Koopman Neural Network (PIKN) approach, which integrates deep learning techniques with fundamental conservation laws in dynamical systems. Their results demonstrated notable improvements in both predictive accuracy and physical consistency for nonlinear system forecasting. Wang et al. [26] developed a Koopman operator learning model based on the Transformer architecture; experimental studies on large-scale nonlinear time-series datasets indicated that this approach is capable of capturing long-term dependencies and intricate dynamical patterns, thereby enhancing multi-step forecasting performance.

Despite these advancements, substantial challenges remain. Predominantly, current deep Koopman methods rely on single-layer or shallow embedding architectures, which typically constrain the model to capturing major dynamical features within a single observation space. This limitation hampers the expressive power of the learned feature space, often resulting in the loss of essential dynamic information and hindering the discrimination of dynamics across different scales or modalities—issues that are especially problematic in systems exhibiting multimodality, high complexity, and cross-scale interactions [27]. Additionally, the approximation of Koopman operators in shallow embeddings is susceptible to the inherent complexity of high-dimensional spaces, frequently leading to decreased model stability and incomplete coverage of the full dynamic spectrum in complex systems. Such limitations are particularly pronounced in engineering applications, where they impose constraints on the accuracy and reliability required for the state prediction and control of nonlinear systems [28].

3. Proposed Method

In complex equipment systems, nonlinear and multi-level dynamic characteristics make it challenging for traditional modeling and control methods to effectively address these complexities. To improve prediction accuracy and control performance, we propose a dynamic self-evolution algorithm for digital twins of complex equipment based on the multi-layer deep Koopman operator. The algorithm captures the system’s multi-level dynamic features by embedding the nonlinear dynamic behavior of the system into linear spaces across multiple time scales. Combined with a model evolution strategy, this enhances system robustness and stability.

3.1. Evolution Algorithm Based on Multi-Layer Deep Koopman Operator

3.1.1. Credibility-Based Self-Evolution Framework Based on MDK

Koopman operator theory offers a novel approach to analyzing nonlinear systems. By embedding nonlinear dynamical systems into a high-dimensional linear space, the Koopman operator can capture the global dynamic characteristics of a system. In this study, we extend the application of this operator by introducing a hierarchical structure to capture the multi-level dynamic evolution features of complex systems.

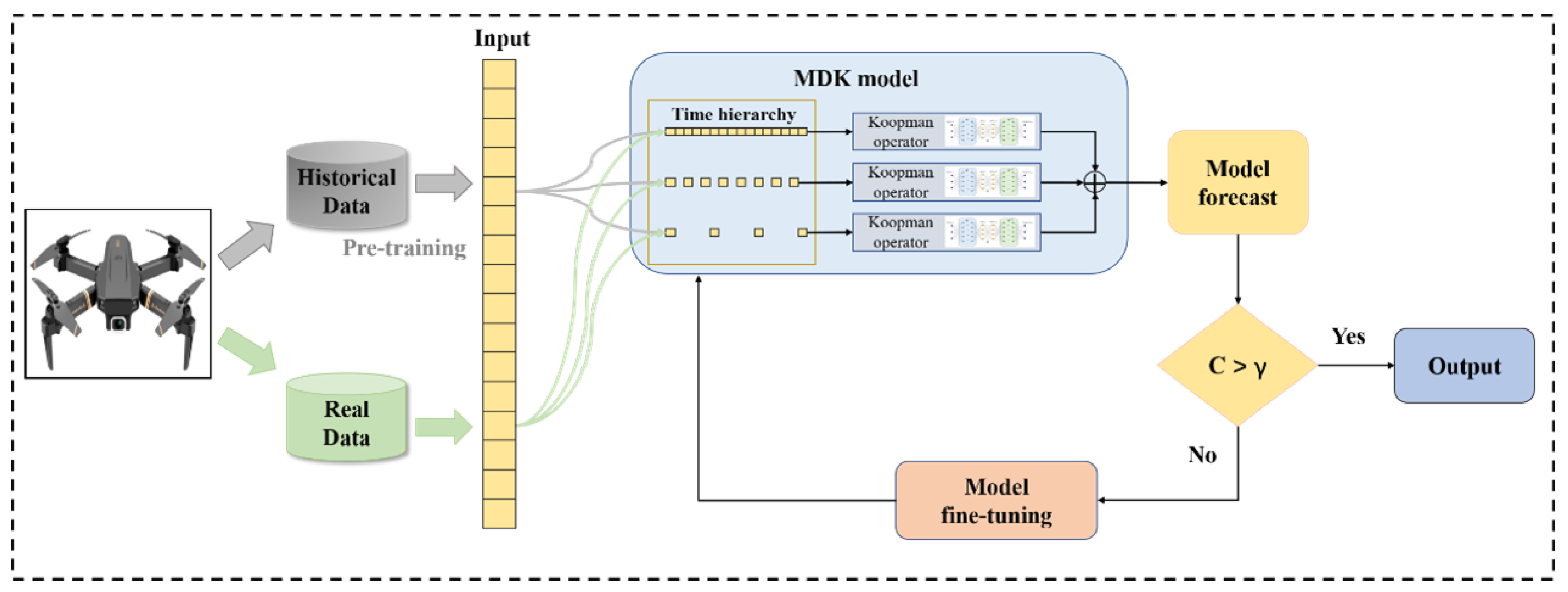
As illustrated in Figure 1, this study presents a credibility-based self-evolution framework designed for the dynamic modeling, prediction, and real-time credibility-based evolution of equipment digital twins based on the MDK model. The integration of hierarchical structures with deep learning techniques allows for the precise representation and adaptive adjustment of multi-scale dynamic features, ensuring efficient and stable predictive performance in dynamic environments.

In the model initialization phase, historical equipment data are used to pre-train the MDK model, laying the foundation for the Digital twin. During this stage, multi-scale feature spaces are constructed through hierarchical embeddings, where each space learns observables automatically by using deep neural networks; this process enables the MDK model to accurately capture the fundamental dynamic properties of the equipment system. By leveraging historical data, the pre-trained MDK model extracts nonlinear behavioral patterns of the system, establishing a solid basis for real-time prediction and subsequent evolution.

During operation, real-time data are integrated into the MDK model to update its inputs, enabling accurate predictions and simulations of the equipment’s current state. To ensure reliability and timeliness, the system conducts trustworthiness evaluations based on model outputs. The trustworthiness index, C, which combines prediction error and dynamic consistency, measures the deviation between model predictions and actual system states. When C exceeds a predefined threshold ($\gamma$), the predictions are deemed credible, allowing the system to directly utilize MDK model outputs for state prediction and decision making; conversely, when C falls below the threshold, it triggers the dynamic evolution mechanism, indicating the need for model adjustments.

The dynamic evolution mechanism fine-tunes and optimizes the MDK model to adapt to evolving system states, which involves adjusting model parameters using real-time data, refining observables, and optimizing the mapping relationships within the feature spaces. Specifically, by dynamically updating weights and embedding layer parameters, the MDK model can quickly adapt to changes in complex system dynamics, maintaining high prediction accuracy and robust system control. Adaptive learning rates and parameter smoothing mechanisms are incorporated to ensure stability during fine-tuning, preventing oscillations caused by over-adjustment.

By integrating trustworthiness evaluation with dynamic evolution mechanisms, the proposed MDK framework achieves two goals. First, it captures the multi-scale dynamic characteristics of complex equipment systems. Second, it ensures rapid and adaptive model evolution in response to significant changes in system states. This framework greatly enhances the predictive accuracy, real-time responsiveness, and stability of digital twins in complex environments, providing a robust and efficient solution for intelligent equipment management and optimization.

3.1.2. The Structure of the MDK Model

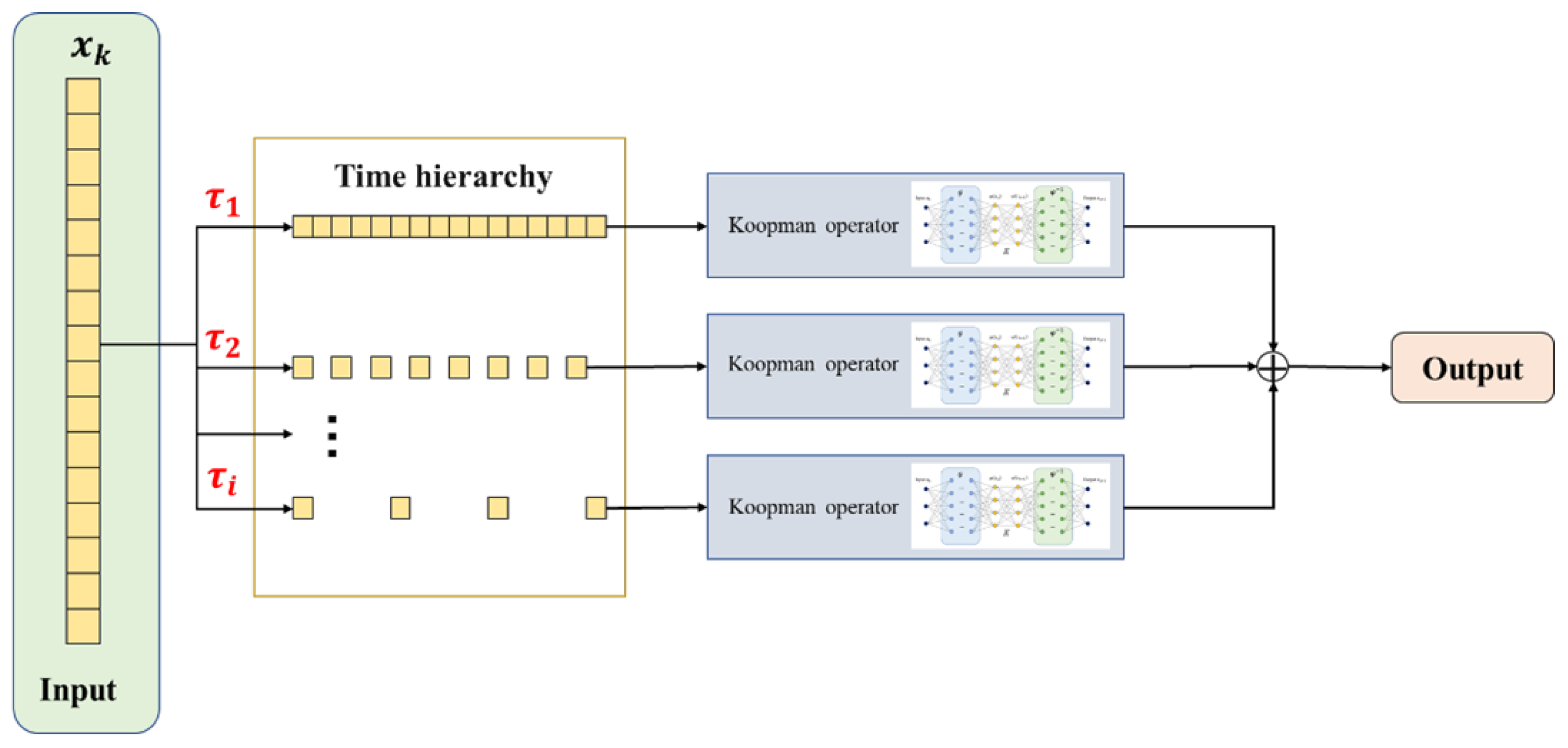
Under the Koopman operator framework, the dynamic behavior of a system is no longer dependent on traditional nonlinear equations but is instead described using a global linear operator K. However, the dynamic behavior of complex equipment systems often exhibits multi-level characteristics, making it difficult for a single-layer Koopman operator to accurately capture the global dynamics of the system. To address this issue, we propose the MDK model, as shown in Figure 2. The MDK model introduces multiple embedding layers to map system states into several feature spaces, enabling the simultaneous characterization of both the short-term dynamics and long-term evolution of the system. By incorporating deep neural networks to learn observables in each feature space, the MDK model effectively captures the multi-level characteristics and intrinsic patterns of complex dynamical systems. This capability provides strong support for the Digital twin modeling and evolution of complex equipment.

In the MDK model, multiple embedding layers are designed to fully capture the dynamic features of the system at different time scales, with each embedding layer adopting a distinct time-delay parameter. The size of the time-delay parameter directly impacts the feature extraction capability of each embedding layer: smaller time-delay parameters are more effective in capturing the system’s short-term dynamic variations, while larger time-delay parameters are used to describe the system’s long-term evolutionary behavior. Depending on the specific application scenario and data characteristics, there is a different i-th layer to describe the state evolution at its respective time scale. For state variable $X_t^i$, its time-delay embedding can be represented as

$$X_t^i=\left[x_t,x_{t-{\tau }_i},x_{t-2{\tau }_i},\cdots ,x_{t-⌊{\displaystyle \frac{N-1}{{\tau }_i}}⌋{\tau }_i}\right]$$

(1)

After the observables in the embedding spaces of all layers have been learned, they are combined linearly:

$${\phi }_{fused}\left(x\right)=\sum _{i=1}^M{w}_i·{\phi }_i\left(x\right)$$

(2)

Here, $w_i$ and ${\phi }_i\left(x\right)$ represent the weight coefficient and the observable function of the i-th layer, respectively. By adjusting the weight coefficients of each layer, the weighted fusion of features at different time scales can be performed, which improves the predictive accuracy of the global model.

3.1.3. The Structure of the Koopman Operator Autoencoder

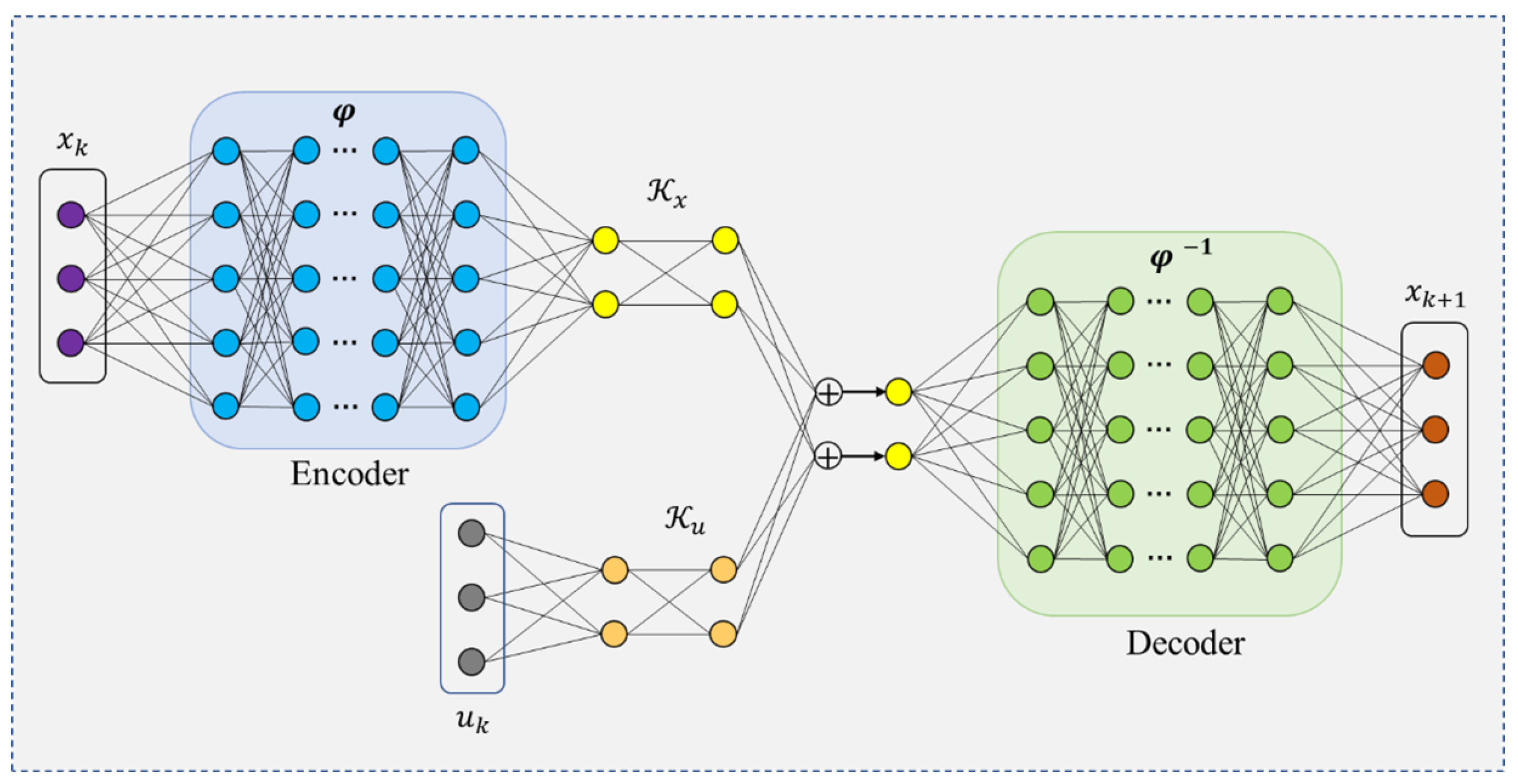
In this study, we denote by $x\left(k\right)\in R^n$ the state variable of a complex equipment system, whose evolution can be described by a nonlinear dynamic equation:

$$\dot{x}\left(k\right)=f(x\left(k\right),u\left(k\right),p\left(k\right))$$

(3)

Here, $u\left(k\right)$ represents the control input of the system, $p\left(k\right)$ represents the internal unmeasurable parameters of the system, and $f(·)$ is the nonlinear function describing the system dynamics.

Since the system has external input parameters, we divide the observables in the Koopman operator into two parts:

$$\phi (x,u)={\phi }_x(x,u)+{\phi }_u(x,u)$$

(4)

According to the Deep Koopman Affine with Control (DKAC) algorithm mentioned in the literature [29], we know that ${\phi }_x(x,u)={\phi }_x\left(x\right)$ and ${\phi }_u(x,u)=u$. Based on the system considered in this study, we designed the deep Koopman operator autoencoder network shown in Figure 3 and define the dynamics in the linear space as follows:

$$\phi \left(x_{k+1}\right)=K_x·\phi \left(x_k\right)+K_u·u_k$$

(5)

Here, $\phi :R^n⟶R^n$ represents the encoder network in the autoencoder structure.

According to Koopman operator theory, the following three loss functions are used during the training of each layer’s observation space.

• Reconstruction Loss

$$L_1={∥x_k-{\phi }^{-1}\left(\phi \left(x_k\right)\right)∥}_2^2$$

(6)

This is the most basic type of loss function, used to measure the difference between the system state predicted by the Koopman operator and the actual state.

B.

Linearization Loss

$$L_2={∥\phi \left(x_{k+1}\right)-K_x·\phi \left(x_k\right)+K_u·u_k∥}_2^2$$

(7)

The loss function can be defined as the error between the observed value under the Koopman operator and the observed value at the next time step. It ensures that the function transformed by the Koopman operator remains consistent with the evolution of the dynamical system.

C.

Prediction Loss

$$L_3={∥x_{k+1}-{\phi }^{-1}(K_x·\phi \left(x_k\right)+K_u·u_k)∥}_2^2$$

(8)

This loss function is used to ensure that no information is lost during the dimensionality reduction and reconstruction processes, allowing the model to capture more complex and uncertain dynamic features of the system, which improves the accuracy of the Koopman operator in the encoded space.

Finally, the loss function used to train the entire network is as follows:

$$L={\alpha }_1·L_1+{\alpha }_2·L_2+{\alpha }_3·L_3$$

(9)

Here, ${\alpha }_1$, ${\alpha }_2$, and ${\alpha }_3$ are weighting factors, each assigned a value of 1/3 in this study.

3.2. Credibility-Based Evolution-Triggering Mechanism

The dynamic evolution behavior of complex equipment systems is often characterized by high nonlinearity and uncertainty, making it difficult for a single model to maintain effective prediction and control across different stages of evolution [30,31]. To ensure that the model can consistently adapt to changes in system states, we propose a credibility-based evolution-triggering mechanism which periodically evaluates the model credibility value and automatically triggers model evolution when the credibility falls below a preset threshold, thereby maintaining the system’s prediction accuracy and stability.

The credibility of the model reflects the adaptability of the current model to the state of the system and its prediction performance [32]. To quantify credibility, this study incorporates both prediction error and sequence consistency, where the former measures the model’s short-term prediction accuracy, while the latter evaluates whether the model can maintain continuity and correctness in capturing the system’s dynamic behavior over a certain period.

Let $y\left(t\right)$ and $\widehat{y}\left(t\right)$ represent the time series of the actual output vector set and the predicted output vector set, respectively.

3.2.1. Prediction Error

The prediction error is a key indicator to evaluate the credibility of the model. The prediction error within a specific time window can be defined as

$$Error\left(t\right)={\displaystyle \frac{1}{N}}\sum _{i=0}^{N-1}∥y(t-i)-\widehat{y}(t-i)∥$$

(10)

Here, N is the length of the time window and $∥·∥$ represents the vector norm, where the Euclidean norm is typically used to calculate the difference. This error metric reflects the model’s prediction accuracy for the entire vector set $y\left(t\right)$ over a short period.

3.2.2. Sequence Consistency

In addition to the prediction error, sequence consistency is used to evaluate whether the model can accurately capture the system’s dynamic evolution trajectory over a long time period. This metric considers the trend of changes between the predicted output sequence and the actual output sequence. The consistency of sequence $S\left(t\right)$ can be calculated using the following formula:

$$S\left(t\right)=1-{\displaystyle \frac{1}{N-1}}\sum _{i=0}^{N-2}{\displaystyle \frac{∥(y(t-i)-y(t-i-1))-(\widehat{y}(t-i)-\widehat{y}(t-i-1))∥}{∥y(t-i)-y(t-i-1)∥}}$$

(11)

This formula measures the consistency between the trend of changes in the actual output vector set ($y\left(t\right)$) and the predicted output vector set ($\widehat{y}\left(t\right)$). The higher the sequence consistency, the more accurately the model captures the dynamic trajectory of the system.

3.2.3. Model Credibility Calculation

The overall credibility $C\left(t\right)$ of the model combines prediction error and sequence consistency metrics, calculated with a weighted average:

$$C\left(t\right)=\alpha ·(1-Error(t\left)\right)+(1-\alpha )·S\left(t\right)$$

(12)

Here, $\alpha$ is a weighting factor used to balance the contributions of prediction error and sequence consistency to model credibility. This weight can be adjusted based on the system’s sensitivity to short-term prediction accuracy or long-term evolution trends.

In this study, to balance the contribution of model prediction results and credibility assessment in the overall optimization objective, we set $\alpha$ to 0.5. The choice of $\alpha$ = 0.5 was primarily to prevent either component from exerting excessive influence on the results, thereby ensuring comprehensive and unbiased evaluation under the experimental conditions. In practice, the values of $\alpha$ can be selected based on the characteristics of different models and scenarios. When $\alpha$ approaches 0, the model places more emphasis on prediction accuracy, which is more suitable for stable or well-observed scenarios. When $\alpha$ approaches 1, the model focuses more on robustness, which is more appropriate for environments with high uncertainty or fluctuating data quality.

3.2.4. Evolution-Triggering Mechanism

The credibility-based triggering mechanism integrates the model prediction error, sequence consistency, and rate of system state changes. Serving as a preliminary decision-making module within the model fine-tuning algorithm, this mechanism continuously monitors the model’s real-time prediction error and sequence consistency to compute a comprehensive credibility metric. When the model’s real-time credibility ($C\left(t\right)$) falls below a predetermined threshold ($\gamma =C_{th}$), i.e., $C\left(t\right)<\gamma$, this indicates that the current model can no longer accurately reflect the actual dynamic evolution of the system. In such cases, the triggering mechanism automatically initiates the model evolution and fine-tuning processes.

The value of the credibility threshold ($\gamma$) is adjustable and may be determined based on the complexity of the system as well as the practical requirements for predictive accuracy and robustness. For complex systems characterized by rapid dynamics or stringent accuracy requirements, a higher threshold may be adopted to ensure that the model promptly and effectively adapts to changes in system states, thereby enhancing the reliability of prediction and decision-making outputs. In contrast, for systems exhibiting relatively stable dynamics or limited needs for frequent model updates, a lower triggering threshold may be utilized to curtail unnecessary computational expenditure and reduce the frequency of fine-tuning operations, thereby achieving an appropriate balance between real-time responsiveness and resource utilization.

3.3. Model Fine-Tuning Algorithm

In the modeling of complex equipment systems, optimizing network parameters is critical, especially when the system undergoes dynamic evolution or the model performs poorly. We propose an adaptive network parameter fine-tuning algorithm based on model credibility and prediction error. When the model credibility falls below a certain threshold, the algorithm dynamically adjusts network parameters based on prediction error, ensuring that the model adapts to the system’s dynamic evolution while maintaining high predictive performance. The specific credibility-based digital twin adaptive fine-tuning algorithm is shown in Algorithm 1.

Algorithm 1: Model confidence-based digital twin adaptive fine-tuning.

This fine-tuning algorithm leverages adaptive optimization based on model credibility and prediction error to dynamically adjust network parameters, ensuring accurate prediction and control performance during the system’s evolution phase in complex environments. The algorithm employs the Adam optimization method to update network weights and biases, combined with a dynamic learning rate and parameter smoothing mechanism to prevent drastic parameter fluctuations [33]. With this adaptive adjustment mechanism, the model can quickly recover performance when credibility decreases, thereby adapting to the evolution process of complex equipment systems.

The main steps of the algorithm are as follows.

• Initialize Network Parameters

Initialize the network parameters (${\theta }_0$), including weights and biases, and set the credibility threshold ($\gamma =C_{th}$).

B.

Monitor System States

Evaluate model credibility ($C\left(t\right)$) by considering prediction error ($Error\left(t\right)$) and sequence consistency ($S\left(t\right)$).

C.

Check Credibility Against the Threshold

If $C\left(t\right)>\gamma$, the network parameters remain unchanged; otherwise, proceed to the next step for parameter fine-tuning.

D.

Compute Gradients and Adjust Network Parameters

For the current prediction error ($Error\left(t\right)$), compute the gradient of loss function $LL\left(\theta \right)$ with respect to the network parameters ($\theta$), where $\theta$ includes weights and biases. The loss function is defined as the Mean Squared Error (MSE) of the prediction error:

$$LL\left(\theta \right)={\displaystyle \frac{1}{N}}\sum _{i=0}^{N-1}{∥y(t-i)-\widehat{y}(t-i;\theta )∥}^2$$

(13)

The gradient of the loss function with respect to the network parameters is

$${▽}_{\theta }LL\left(\theta \right)={\displaystyle \frac{\partial LL\left(\theta \right)}{\partial \theta }}$$

(14)

E.

Adjust Learning Rate

To prevent overly fast or slow adjustments, the learning rate ($\eta \left(t\right)$) is dynamically updated based on model credibility: higher credibility results in a smaller learning rate to avoid over-adjustment, while lower credibility increases the learning rate to rapidly improve model performance. The dynamic learning rate is updated as

$$\eta \left(t\right)={\eta }_0·{\displaystyle \frac{C_{th}}{C\left(t\right)+\epsilon }}$$

(15)

Here, ${\eta }_0$ is the initial learning rate, and $\epsilon$ is a small positive number to avoid division by zero.

F.

Update Network Parameters

Using the gradient and the dynamic learning rate, update the network parameters with gradient descent:

$$\theta (t+1)=\theta \left(t\right)-\eta \left(t\right)·{▽}_{\theta }LL\left(\theta \left(t\right)\right)$$

(16)

G.

Smooth Parameter Adjustment

After each parameter update, apply a parameter smoothing mechanism to prevent excessive adjustments that could lead to instability:

$$\theta (t+1)=\lambda ·\theta (t+1)+(1-\lambda )·\theta \left(t\right)$$

(17)

Here, $\lambda \in \left[0,1\right]$ is a smoothing factor that balances the updated parameters with the original parameters.

This adaptive fine-tuning mechanism ensures the model’s stability and adaptability, maintaining high predictive accuracy and robust performance during complex system evolution.

4. Experiments and Result Analysis

To validate the effectiveness of the proposed MDK model-based dynamic evolution algorithm for complex equipment digital twins, in this study, we selected a quadrotor UAV as the experimental subject. As a typical nonlinear complex system, the modeling and prediction of the flight attitude of a quadrotor UAV is a challenging problem. In this experiment, we evaluated the performance of the proposed algorithm by predicting the UAV’s flight attitude and verifying the modeling and prediction capabilities of the multi-layer deep Koopman operator dynamic evolution algorithm in complex nonlinear systems while also assessing the performance of the model evolution mechanism under dynamic changes.

4.1. Description of the Experiment

In this study, the experimental subject was a quadrotor UAV, a system characterized by high nonlinearity and multi-degree-of-freedom dynamic behavior. The flight of a quadrotor UAV is controlled by four motors, with each motor’s rotational speed determining the UAV’s flight attitude, which is typically described using Euler angles, including pitch, yaw, and roll angles. Variations in motor rotational speeds directly influence the UAV’s thrust and torque, which in turn affect its flight attitude and motion state. The UAV’s inertial position, representing its location in an inertial coordinate system during flight, is usually obtained with a GPS or Inertial Measurement Unit (IMU). Additionally, the body rate describes the UAV’s rotational speed relative to its own coordinate system, capturing the dynamic changes in attitude.

These parameters are critical to attitude prediction and control, and the accurate prediction and control of these variables will serve as key indicators for evaluating the performance of the algorithm. In the Digital twin model of the quadrotor UAV established in this study, the flight attitude of the UAV was observed. In this context, the model’s inputs consisted of the UAV’s current attitude information and the control information for the four motors, while the model output the attitude information for the next time step.

In the experimental setup, the MDK model utilized a three-layer fully connected multi-layer perceptron (MLP) for input embedding, with each layer comprising 64 nodes and employing the ReLU activation function; this structure mapped the original 10-dimensional sensor features into a higher-dimensional space, thereby enhancing the feature representation capacity necessary for effective Koopman operator modeling. Following each embedding layer, independent Koopman linear transformations were implemented to capture the multi-scale linear dynamics of the system, and after fusion, the outputs were passed through a two-layer decoder to recover the original state dimensionality. The detailed experimental parameter configurations are summarized in

Table 1. Hyperparameters of MDK.

Parameter	Value
Input embedding MLP	$10\ast 64\ast 64\ast 64$, ReLu()
Koopman layer	3, Linear(64,64)
Decoder	$192\ast 64\ast 10$, ReLu()
Dropout	0.2
Weight factor $\alpha$	0.5
Learning rate	0.001
Batch size	32
Smoothing factor $\lambda$	0.7
Optimizer	Adam

.

4.2. Data Preprocessing

In this experiment, we utilized a real flight dataset from the AscTec Pelican, a lightweight quadrotor UAV [34]. The total flight duration of the dataset is approximately 3 h and 50 min. The data were recorded by the UAV’s onboard computer and a Vicon motion capture system, encompassing several key flight parameters (10 dimensions), such as motor speeds, inertial positions, Euler angles, and body rates. All data were measured at a sampling frequency of 100 Hz, allowing for the capture of high-frequency dynamic changes during the UAV’s flight. Data collection was conducted over several days, with the UAV using batteries of varying performance levels and operating in different flight modes. Notably, motor degradation during flight added extra complexity to the model’s training and prediction processes.

In the Digital twin model of the quadrotor UAV established in this study, the length of the time series was determined by the size of the evolution time window, with a sensor sampling interval of 0.001 s. For the experiment, the first 60,001 flight data points from Dataset 1 were used as offline historical training data, while the last 26,001 flight data points from Dataset 1 were used as an online real-time data stream. Due to the temporal distance between the two datasets, along with differences in the UAV’s state (e.g., battery condition and motion fatigue) and flight modes, the Digital twin model had to dynamically evolve to accurately reflect the quadrotor’s flight dynamics.

4.3. Performance of Multi-Layer Koopman Operator

4.3.1. Comparison with Traditional Koopman Operator

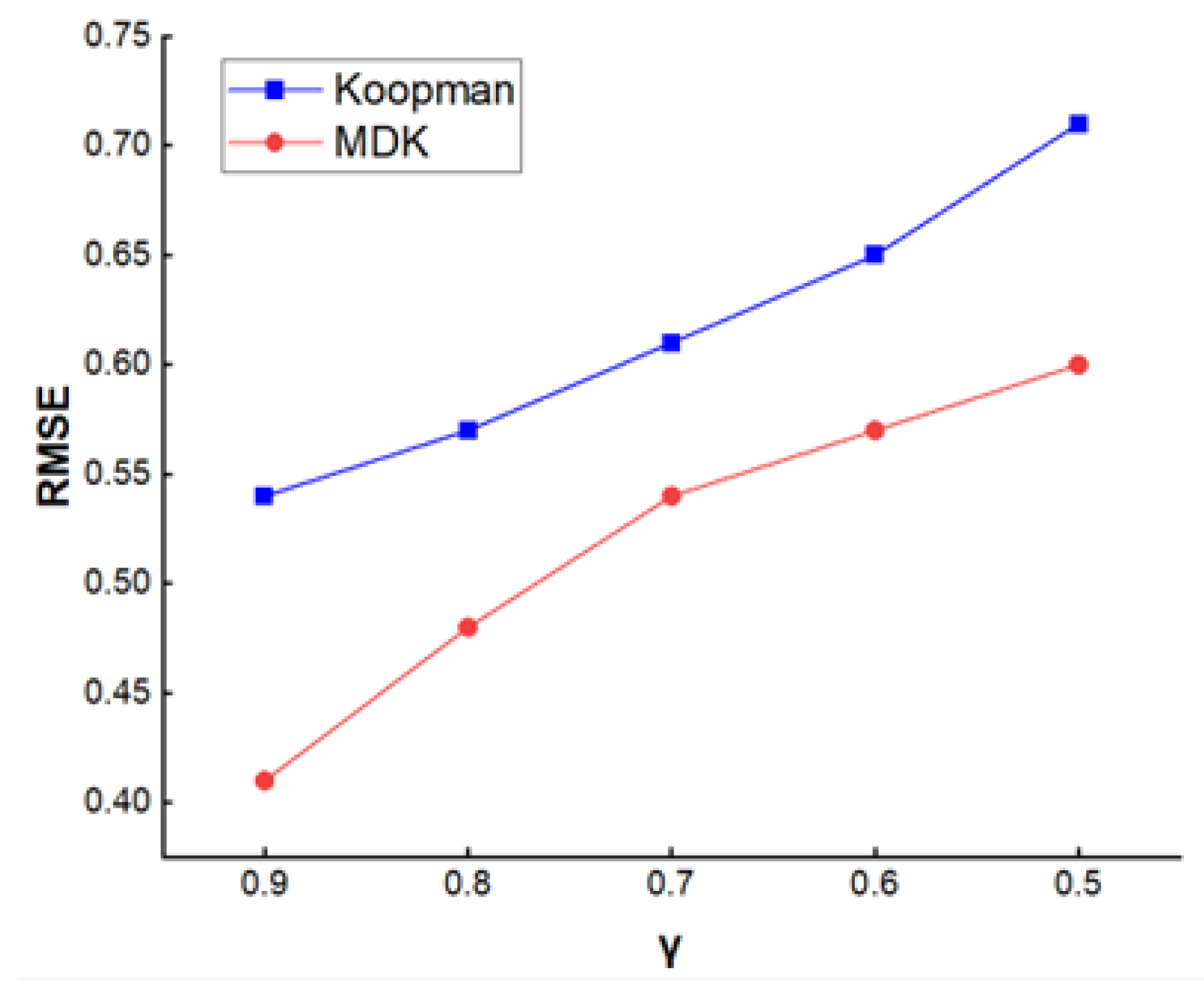
In this experiment, the prediction performance of the traditional Koopman operator and the MDK model was compared under different thresholds $\gamma$, primarily evaluated using the Root Mean Squared Error (RMSE) metric, where a smaller RMSE indicates higher prediction accuracy of the model. Thresholds of $\gamma =0.9, 0.8, 0.7, 0.6, 0.5$ were used to observe the performance of the different models, where $\gamma =C_{th}$.

From

Table 2. RMSE comparison between the MDK model and the traditional Koopman algorithm under different thresholds.

RMSE	$\mathit{\gamma }=0.9$	$\mathit{\gamma }=0.8$	$\mathit{\gamma }=0.7$	$\mathit{\gamma }=0.6$	$\mathit{\gamma }=0.5$
Koopman	0.52	0.57	0.61	0.65	0.71
MDK	0.41	0.48	0.54	0.57	0.60

, we can see that the MDK model outperforms the traditional Koopman operator across all thresholds, with its advantages being most significant at higher thresholds. At lower thresholds, although the errors of both models increase, the error increment for the MDK model is slower, demonstrating its better adaptability to the system’s dynamic evolution.

Meanwhile, as shown in Figure 4, at $\gamma =0.9$, the multi-layer Koopman operator achieves the lowest RMSE and the greatest performance improvement. Therefore, $\gamma =0.9$ was adopted for further study.

4.3.2. Comparison of Multi-Layer Koopman Operator with and Without Evolution Mechanism

This part of the experiment aimed to validate the effectiveness of the dynamic evolution mechanism of the established Digital twin model in improving its accurate mapping capability. During the experiment, all training data were normalized, and the entire model was trained offline using historical data. Subsequently, under the supervision of the credibility-based triggering mechanism, the proposed fine-tuning algorithm was employed to achieve the dynamic evolution of the Digital twin model on the real-time dataset. Meanwhile, the model credibility ($C\left(t\right)$), which comprehensively considers the error and consistency between the input and output sequences of the Digital twin model and the actual sampled sequences, was selected as the evolution-triggering condition.

First, $\gamma =0.9$ was set, and the impacts of the evolution mechanism and of its absence on the model’s RMSE value for different window sizes were compared. We conducted two groups of experiments: one with a Digital twin model featuring the dynamic evolution mechanism and the other without this mechanism. From Figure 5, we can see that adding the model credibility-based evolution mechanism improves performance for all window sizes compared with the algorithm without evolution. Moreover, the performance improvement is maximized when the window size is set to 80.

Next, we fixed the evolution window size to 80 and set the evolution-triggering threshold ($\gamma$) to 0.9. The experimental results show that the dynamically evolving Digital twin model achieved an average prediction accuracy RMSE of 0.4225 on the real-time dataset, while the Digital twin model without the dynamic evolution mechanism achieved an average RMSE of 0.5250 on the same dataset.

Among the UAV pose parameters, the three-axis spatial coordinates (x, y, z) not only represent the UAV’s position in space but are also closely related to its velocity and altitude variations. The slopes and inflection points of the spatial coordinate trajectories essentially capture changes in velocity and the effect of acceleration, while fluctuations along the z-axis directly correspond to variations in flight altitude. Furthermore, the attitude variables—pitch, roll, and yaw—are highly correlated with the evolution of the spatial position. For example, adjustments in pitch and roll are frequently accompanied by changes in altitude (z-axis), and variations in yaw primarily determine the direction of motion on the x–y plane.

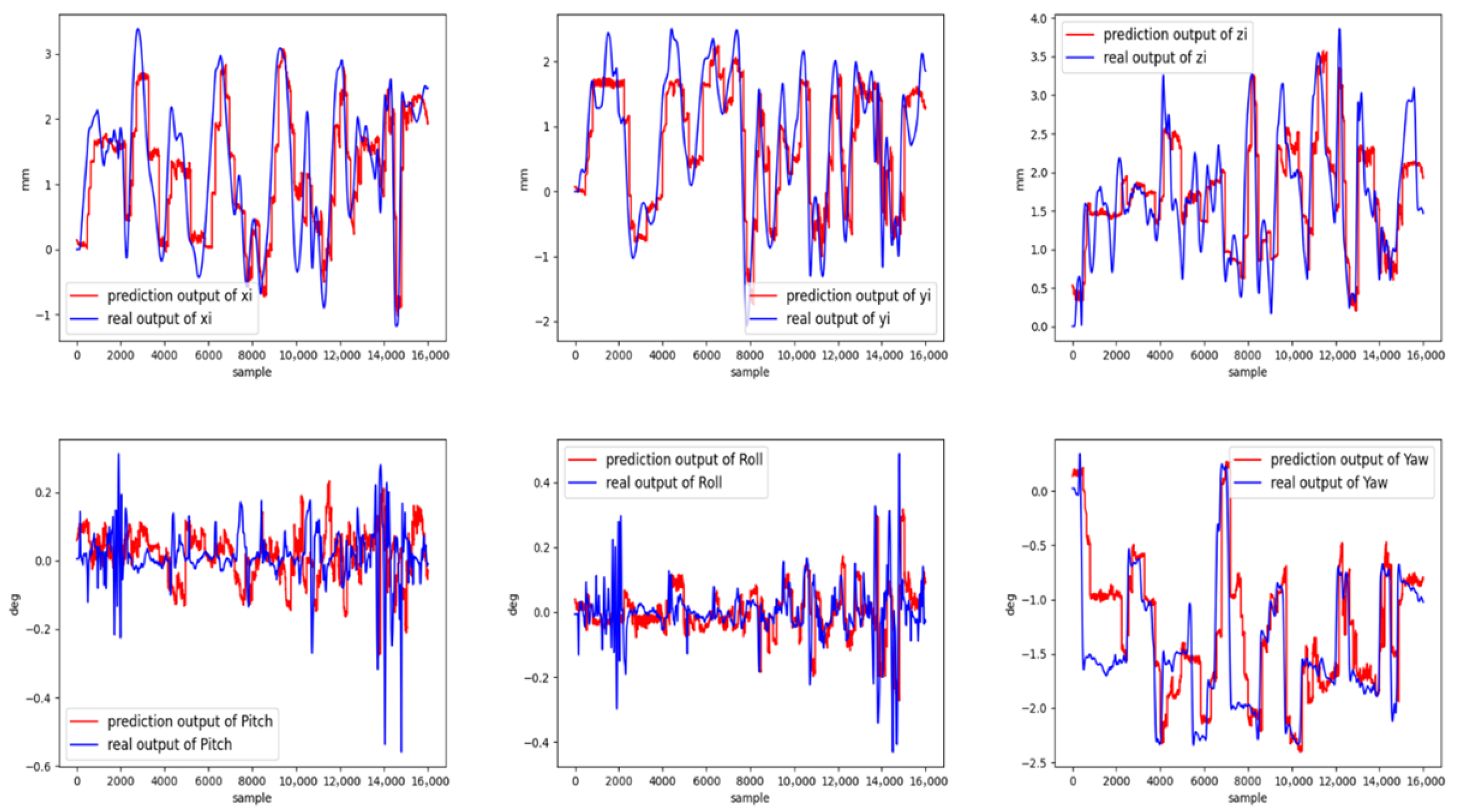
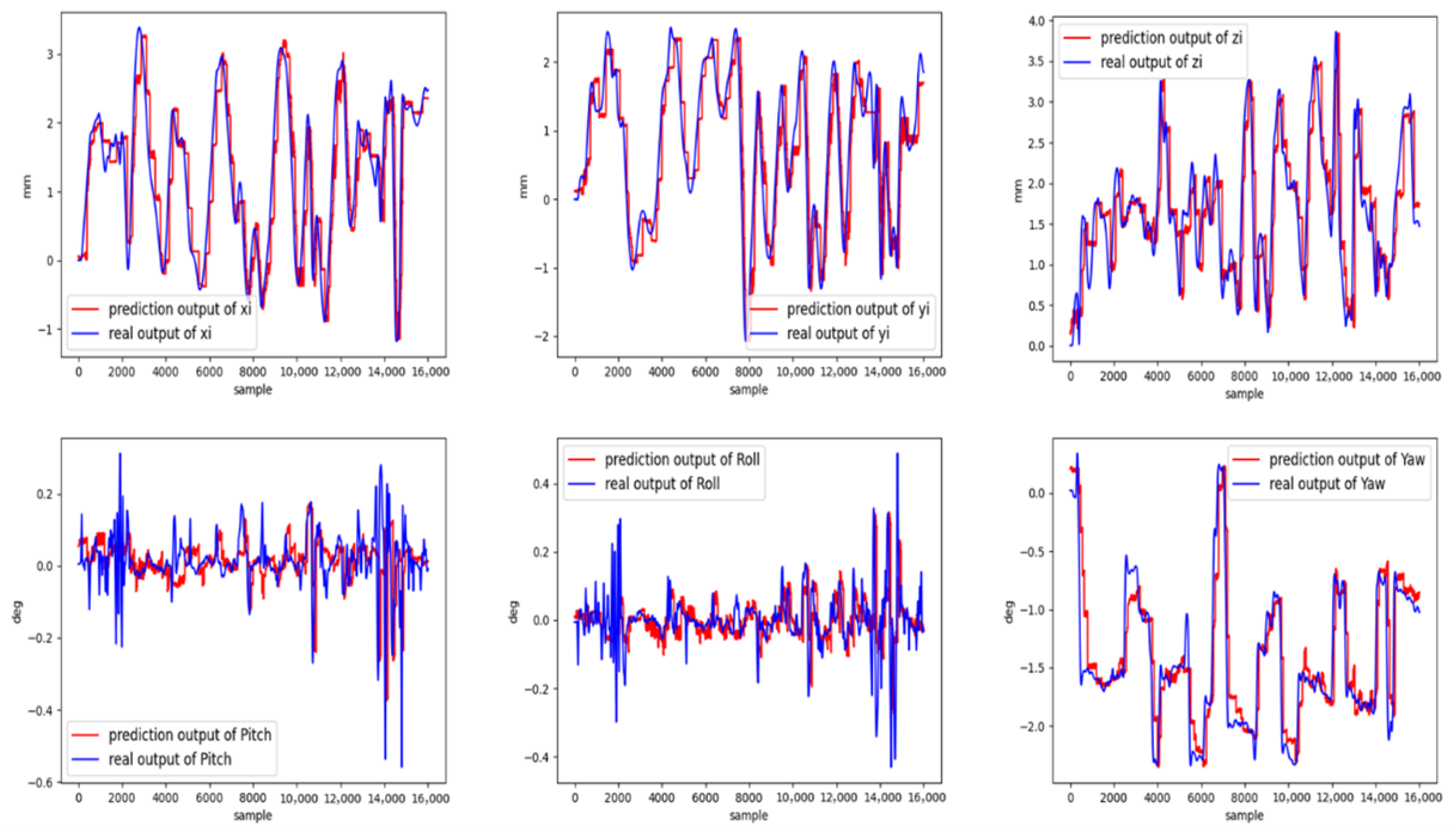
Figure 6 and Figure 7 present the predicted spatial coordinates (x, y, z) and attitude angles (pitch, roll, and yaw) for UAV flight under two settings, without and with the dynamic evolution mechanism, respectively. The comparison of these results demonstrates that incorporating the dynamic evolution mechanism substantially enhances model prediction performance.

In the absence of the dynamic evolution mechanism (Figure 6), the model is able to capture the overall trends of position and attitude; however, in segments characterized by rapid changes or strong system dynamics, there are significant discrepancies between predictions and measured data. In particular, during phases of rapid velocity or altitude change, the coupling between spatial and attitude predictions is inadequately represented, leading to observable prediction lag and errors. By contrast, after introducing the dynamic evolution mechanism (Figure 7), the model is capable of adaptively responding to temporal variations in the input data, yielding predictions that are consistently aligned with the true values across all six degrees of freedom. Sharp transitions in position and attitude, as well as coupled adjustments in speed and altitude, are closely tracked by the model, resulting in reduced lag and error. This improvement is most pronounced during periods of rapid dynamic change.

These results indicate that the dynamic evolution approach significantly improves the model’s ability to capture and model the intrinsic physical relationships between spatial coordinates and attitude angles, yielding predictions that more accurately reflect the actual UAV velocity, altitude, and attitude variations. Overall, the adoption of the evolution mechanism leads to a notable increase in the prediction accuracy.

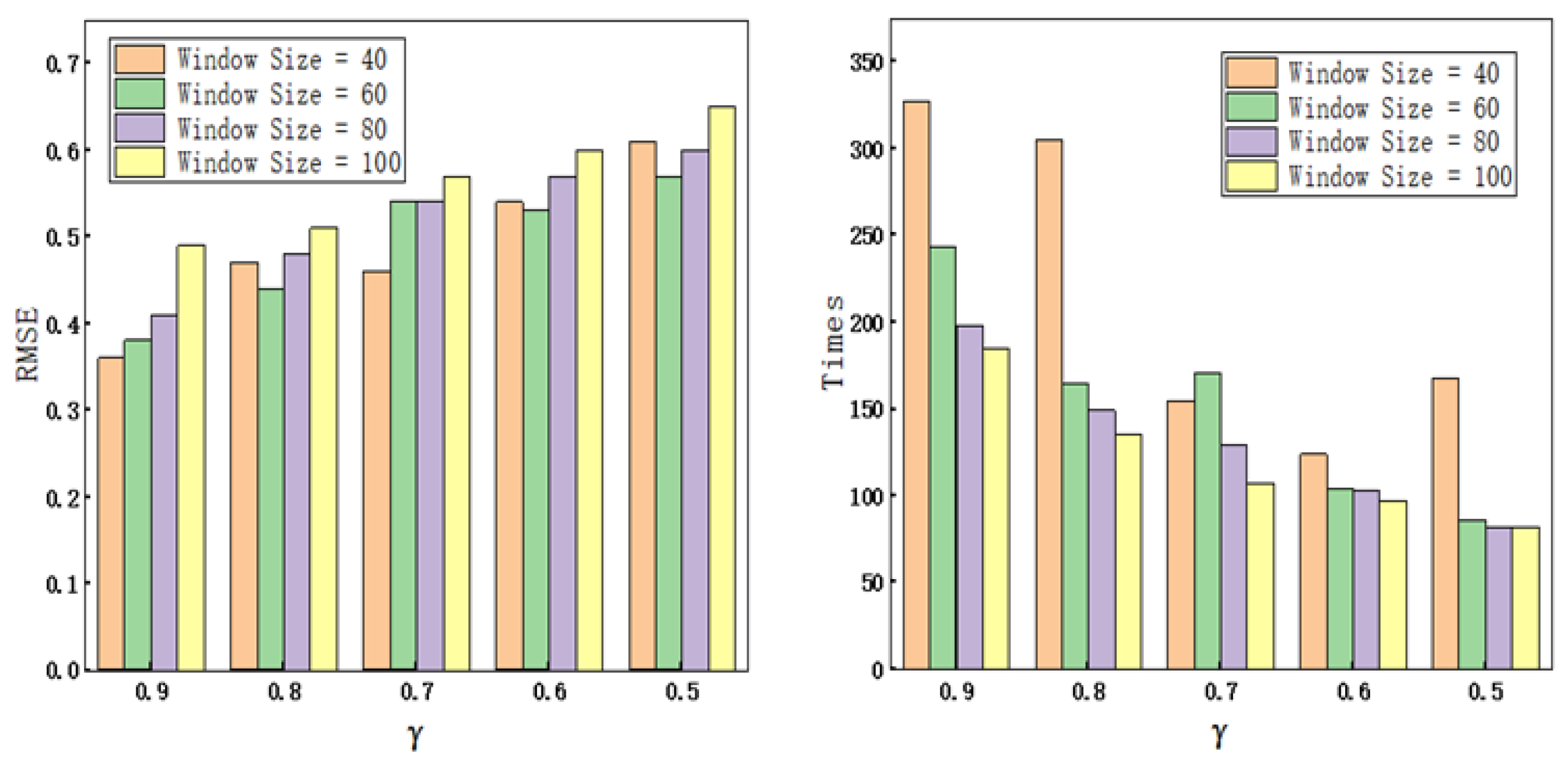
4.4. Evolution Results for Different Thresholds and Window Sizes

To analyze the impact of the evolution time window and event triggering threshold on the performance of Digital twin dynamic evolution, experiments were conducted with time window settings of $T_w=40, 60, 80, 100$ and the evolution-triggering thresholds of $\gamma =0.9, 0.8, 0.7, 0.6, 0.5$, respectively.

As shown in Figure 8, for the four evolution time windows, the number of evolution triggers gradually decreases as the triggering threshold decreases, while the model prediction accuracy (RMSE) gradually increases, which aligns with intuitive understanding. Therefore, in practical applications, a reasonable evolution-triggering threshold can be selected based on the required model credibility to achieve a balance among evolution computational cost, real-time performance, and prediction accuracy.

4.5. Comparison with Other Models

A series of comparative experiments were conducted to evaluate the effectiveness of the proposed algorithm. Five models, including MDK, were first pre-trained on the training set; based on the proposed framework, these trained models were subsequently applied to dynamic evolution tasks on the test set. To mitigate the impact of training uncertainty inherent in neural network models, each experimental group was tested 20 times on the dataset. The mean and standard deviation of the RMSE were calculated for each group to ensure the statistical significance of performance differences among models.

As presented in

Table 3. RMSE for different models with dynamic evolution.

Model	LSTM	GRU	Bi-LSTM	Bi-GRU	MDK
RMSE	0.4936 ± 0.0317	0.4529 ± 0.0268	0.4431 ± 0.0263	0.4415 ± 0.0382	0.4275 ± 0.0115

, MDK demonstrated the best performance when the dynamic evolution mechanism was introduced. The overall performance of the Bi-LSTM and Bi-GRU models was comparable, with both exceeding the performance of LSTM and GRU. These results are consistent with the enhanced feature extraction capabilities of the Bi-LSTM and Bi-GRU architectures.

In summary, the comparative experiments across multiple dimensions underscore the importance of dynamic evolution for digital twin models. Under equivalent conditions, MDK outperformed mainstream models in terms of both prediction accuracy and stability, further confirming the validity of the proposed approach.

5. Conclusions and Future Work

We propose a credibility-based self-evolving algorithm for equipment digital twins based on the MDK model and present comparative experiments on real-world datasets with several representative models. The experimental results demonstrate that the MDK model significantly enhances the predictive accuracy and adaptive evolution capability of digital twin systems, indicating strong potential for applications in dynamical system modeling, industrial process monitoring, and intelligent manufacturing. In particular, the MDK model outperforms conventional LSTM and GRU and their bidirectional variants in dynamically evolving environments, which validates its effectiveness in handling high-dimensional and time-varying complex systems.

Nonetheless, several limitations remain. First, while the adaptive capability of the MDK model is markedly improved, its performance relies on the availability of high-quality online data streams; therefore, the presence of significant noise or outliers in the data may affect model stability and credibility assessment. Second, the present experiments are mainly confined to structured time-series data; thus, the generalizability of the approach to other data types (e.g., graph-structured or unstructured data) and complex, multi-source heterogeneous systems requires further evaluation.

In the future, we will focus on the following directions: (1) enhancing the robustness of the model to improve its resilience to noise and anomalous conditions; (2) investigating methods for extension and transfer learning with multi-source heterogeneous data to increase generalizability across practical applications; and (3) exploring the deployment of the MDK model in broader domains, such as energy, healthcare, and intelligent transportation, to further examine its potential utility and boundary conditions.