A General Numerical Method to Calculate Cutter Profiles for Formed Milling of Helical Surfaces with Machinability Analysis

Abstract

Formed milling is one of the most commonly used methods for machining the helical surfaces of various screw rotors. The profile of a formed cutter is designed according to the profile of the helical surface, which is usually represented by discrete points. The most widely used analytical method is rather complex, and it is easy to obtain singular points. To obtain a reliable cutter profile and simplify the solution procedure, a general numerical method suited for rotors with an arbitrary tooth profile is proposed. The proposed method does not need to establish and solve the complex nonlinear contact equation and can determine the contact point accurately. Firstly, a series of intersection planes that are perpendicular to the revolving axis of the cutter is constructed. The searching of the contact points of the selected tooth curves with each intersection plane is achieved using the subdivision method. By this means, the plane–curve intersection is simplified to a straight line–curve intersection that can easily be solved via Newton iteration. Meanwhile, the machinability related to the profile of the formed cutter can also be analyzed. Two cutter profiles are used to validate the proposed method. The cutter profiles generated by the proposed method are compared with the profiles generated by the analytical method. The results indicate that the accuracy and computational efficiency increase significantly. Furthermore, the proposed method can also be applied to the design of formed grinding wheels.

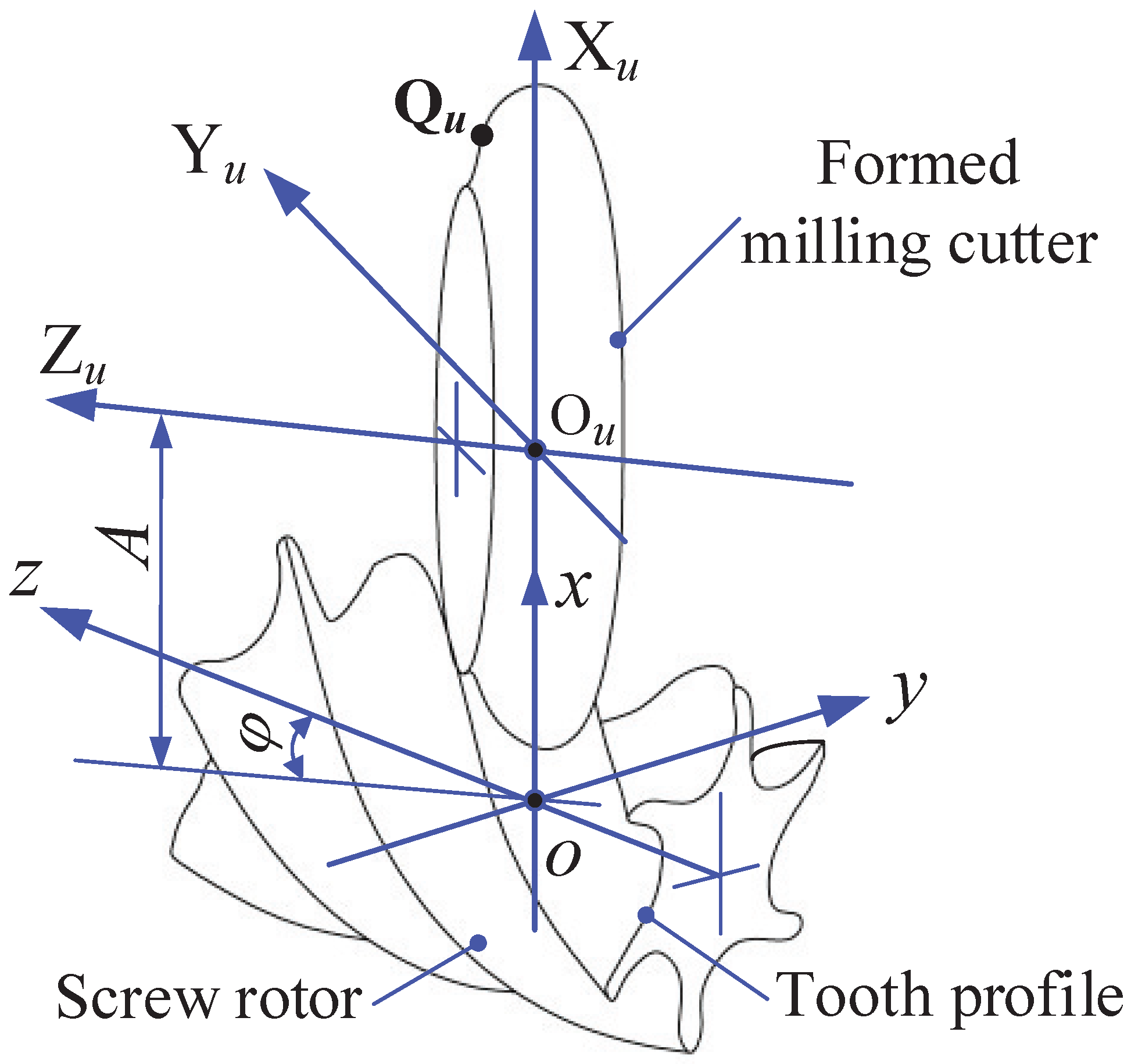
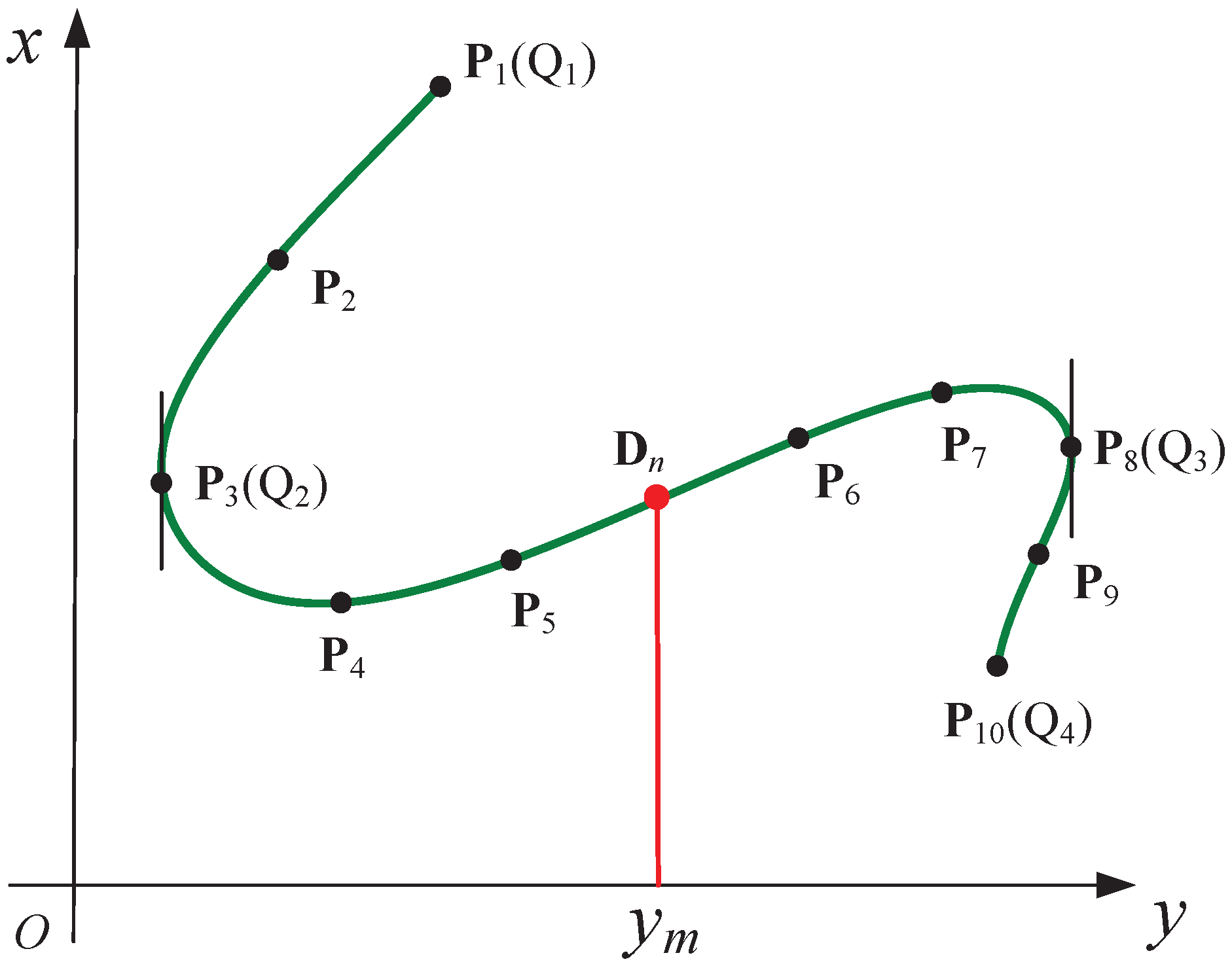
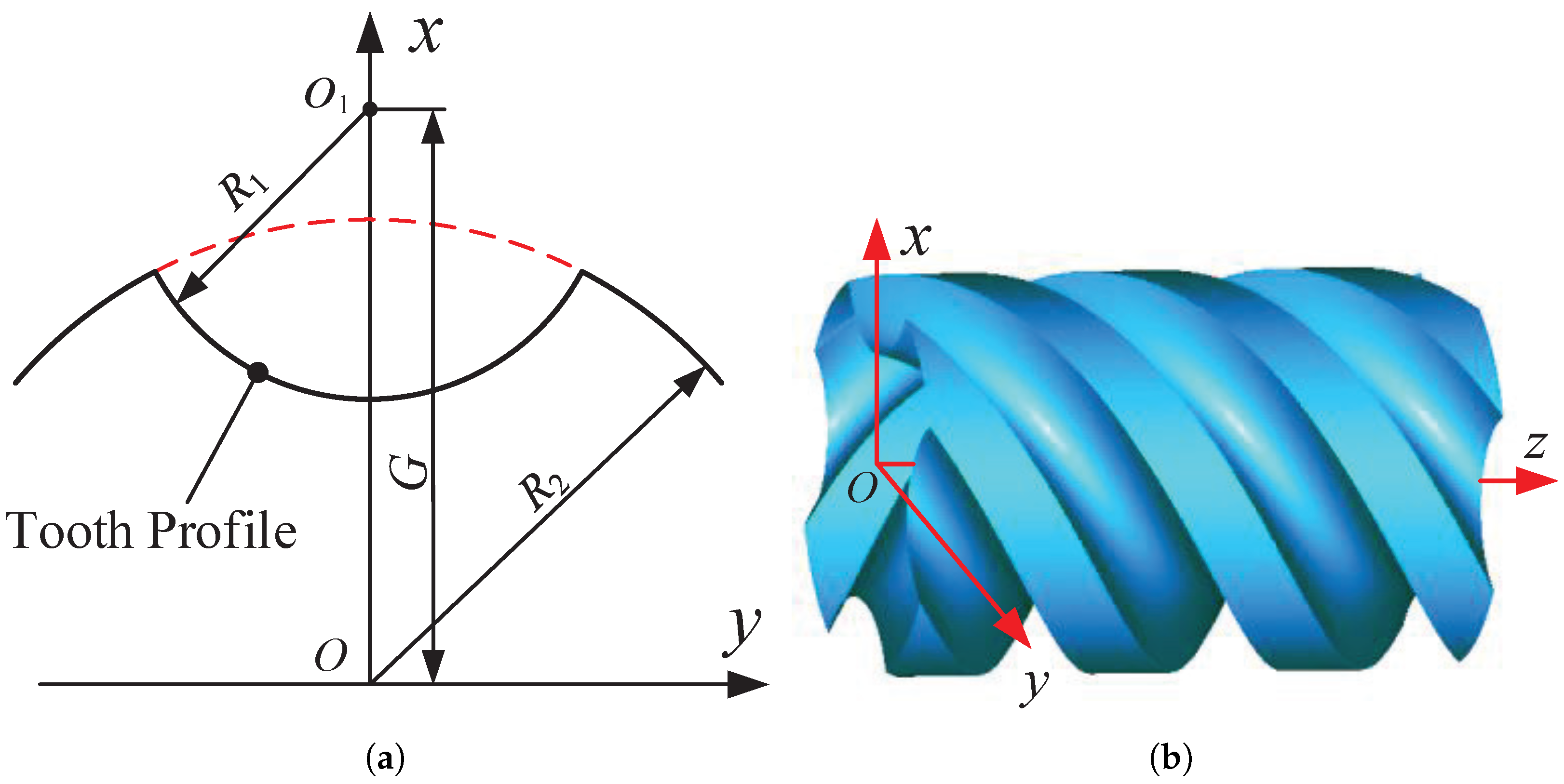
1. Introduction

Screw rotors are key components of screw kneaders, screw pumps and screw compressors [1,2,3]. To fully take the advantages of the rotors’ helical surfaces, these fluid machines are usually of simple structure, high reliability, and low energy consumption. Meanwhile, the tolerance requirements of the helical surfaces are strict. Large geometrical errors would degrade the product performances significantly. Compared with planer and cylinder surfaces, helical surfaces are much harder to be machined due to their complex geometries. The helical surfaces on screw rotors can be manufactured by milling, grinding, plastic forming, casting and additive manufacturing [4,5]. Currently, disc milling is commonly used for the mass production of screw rotors with the advantages of a simple tool trajectory, high machining efficiency and good machining consistency [6]. To achieve disc milling, the first problem to be solved is the robust and precise generation of the cutter profiles.

Traditionally, an analytical method was used for cutter profile design by solving the contact equation derived from the envelope theory of gearing [7,8,9]. The obtained cutter profile can theoretically be free of error when the tooth profile can be represented by a simple function [10]. However, tooth profiles are rarely expressed by a simple function but are commonly represented by discrete points [11]. In this case, these points should be fitted by parametric methods to determine their derivative values ahead of solving the contact equations [12]. The most common approach is to use a cubic spline to fit the rotor profile at the end planer, then build the contact equation according to the gearing enveloping theory, ultimately determining the contact line by solving the equation. A method for optimization of the installation angle and center distance was proposed by Liu [13] based on the solution of the contact-line equation using Matlab. Achmad fit the original rotor profile using a cubic spline in order to obtain the partial derivatives at each contact point [14]. Arifin also used a cubic spline to fit the rotor profile and to design the profile of whirling milling tools [15]. This method has also been used to optimize the position of inserts in a disk-type milling cutter for the formed milling of screw rotors [16]. Luu used constraints on the contact condition to generate the cutting-edge profile of an internal cylindrical skiving cutter [17]. Su built the contact-line equation according to the meshing relationship between the worm and formed grinding wheel and solved the equation by using the fsolve method in Matlab [18]. Li used the Newton–Raphson method to determine the points on the contact line between a formed grinding wheel and a helical gear [19]. However, the contact-line equation is usually nonlinear and must be built by a tedious derivation procedure; therefore, it should be solved by a complex algorithm.

The disadvantages of the analytical method can be summarized as follows [20]:

(1)

The process of establishing the contact equations is rather complex, and solving the nonlinear contact equation requires professional math skills.

(2)

Numerical instability easily occurs near singular points when solving the contact equations, which may lead to a faulty cutter profile.

(3)

The fitting error and the subsequently enlarged deviation error deteriorate the accuracy of the cutter profile, especially at the end points.

To simplify the cutter profile generation processes, several numerical methods have been developed. Sun et al proposed a cutter profile generation method based on the geometric requirement that the normal vector of the helical surface at the contact line must intersect with the revolving axis of the tool [21]. It also needs to solve a nonlinear equation to achieve a contact point. To avoid the solution of the nonlinear equations, one option is the minimum distance method, where a contact point is achieved on each of the helical curves [22]. Thus, the machinability of the helical surface is difficult to analyze. The computational accuracy is also subject to the point density generated on the helical curves. CAD approaches have the advantages of being intuitive and effective, as the machining process is considered a process of interference of the cutter with workpiece, with the interfered portion removed by the cutter [23,24,25]. The Boolean subtraction operation of the CAD approaches involves complex mathematics, and the tool surface is also required to be represented in the form of a mathematical equation. This process requires massive computations and is time consuming. The cutter designer should also be an expert in the advanced operation of the expensive software necessary to establish a 3D numerical model of the rotor. Meanwhile, the irregular distribution of triangular meshes at the intersection region between the tooth profile and cylinder significantly influences the computational accuracy [26]. The digital graphic scanning method was developed for the generation of the grinder profile, but its accuracy is limited by the smallest pixel size [27]. The obtained cutter profile is also discontinuous and needs to be smoothed by curve fitting.

Machinability analysis is necessary before the machining process due to the geometry complexity of screw rotors. The machinability related to the material of the cutter and rawpiece, the process parameters and the external environment could only be analyzed by conducting a milling or grinding experiment. Tao predicted the machining error of a screw rotor profile by analyzing the measurement results and then built a prediction model to determine the compensation values in order to improve the machining accuracy [28]. Jiang used the particle swarm algorithm to calculate the minimum total grinding curve length of a wheel disc in order to equilibrate its degree of wear [29]. Liu built a machining error influence model for the screw rotor profile considering the center distance, installation angle and grinding wheel wear [30]. An installation parameter optimization model for the machining of the screw rotors was also built by Liu in order to improve the machining performance [31]. A prediction model for the milling force was proposed by Wang based on the process kinematics and cutter workpiece engagement in order to reduce the error caused by cutting force [32]. The cutting interference is the most common machinability problem related to the cutter profile design and should be carefully examined. However, the traditional tool profile design method based on solving the contact equation is incapable of detecting the cutting interference directly. In that case, a subsequent manual checking or simulation of the three-dimensional mesh model of the cutter and the workpiece is needed [33]. This is a complex and time-consuming procedure, and the detection accuracy is limited by the precision of the three-dimensional model.

In order to simplify the procedure of formed milling cutter design for screw rotor profiles represented by either equations or discrete points, a general numerical method which does not rely on the contact line equation is proposed. Furthermore, the machinability related to the milling cutter design could be analyzed simultaneously. The rest of the paper is organized as follows. In Section 2, the numerical method for the formed cutting tool profile design is presented. In Section 3, two screw rotor profiles are used to verify the proposed method. In Section 4, machinability related to the cutter profile is discussed. Finally, the conclusions are drawn in Section 5.

2. Method for Cutter Profile Generation

2.1. Model of the Helical Surface

As shown in Figure 1, the helical surface is generally achieved by rotation transformation from the red line $C_0$, which is the initial tooth profile that is represented by discrete points. The helical surface, $\mathit{S}(\mathit{x},\mathit{y},\mathit{z})$, can be expressed as [12]

$$\left[\begin{array}{c}\mathit{x}\\ \mathit{y}\\ \mathit{z}\\ \mathbf{1}\end{array}\right]=\mathit{M}\left[\begin{array}{c}{\mathit{X}}_e\\ \begin{array}{c}{\mathit{Y}}_e\hfill \\ \mathbf{0}\hfill \end{array}\\ \mathbf{1}\end{array}\right]=\left[\begin{array}{cccc}cos\theta & -\epsilon sin\theta & 0& 0\\ \epsilon sin\theta & cos\theta & 0& 0\\ 0& 0& 1& H\theta /2\pi \\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}{\mathit{X}}_e\\ \begin{array}{c}{\mathit{Y}}_e\hfill \\ \mathbf{0}\hfill \end{array}\\ \mathbf{1}\end{array}\right]$$

(1)

where H is the lead of the helical surface, $\theta$ is the rotation angle of $C_0$ about the z axis, $\epsilon$ is the direction coefficient of rotation ($\epsilon =1$ for a right-hand screw rotor, $\epsilon =-1$ for a left-hand screw rotor), and ${\mathit{X}}_e={[x_{e,1},x_{e,2},\dots ,x_{e,m}]}_{1\times m}$, ${\mathit{Y}}_e={[y_{e,1},y_{e,2},\dots ,y_{e,m}]}_{1\times m}$ are point coordinates of $C_0$.

2.2. Coordinate Transformation of Cutter and Screw Rotor

Two coordinate systems are built on the formed milling cutter and the screw rotor respectively, namely the Cutter Coordinate system (CCS) that is represented by $O_u{X}_u{Y}_u{Z}_u$ and the Workpiece Coordinate System (WCS) that is represented by $oxyz$, as shown in Figure 2. The central axis of the milling cutter and screw rotor coincide with axis $Z_u$ and axis z, respectively. The coordinate transformation matrix between the CCS and WCS is shown below:

$$\left[\begin{array}{c}{X}_u\\ Y_u\\ Z_u\\ 1\end{array}\right]=\mathit{T}\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]=\left[\begin{array}{cccc}1& 0& 0& -A\\ 0& cos\phi & sin\phi & 0\\ 0& -sin\phi & cos\phi & 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$$

(2)

where, x, y, and z are the coordinates of a point in the WCS, $X_u$, $Y_u$, and $Z_u$ are the coordinates of the same point in the CCS, A is the spatial distance between axis $Z_u$ and axis z, and $\phi$ is the rotation angle between axis $Z_u$ and axis z.

2.3. The Process of Calculating the Formed Cutter Profile

The formed cutter profile is designed according to the screw rotor profile to be machined by computing the contact points between the two surfaces, as shown in Figure 3. Firstly, a group of intersection planes represented by ${\Gamma }_m$ is built along the axis $Z_u$. The normal vector of ${\Gamma }_m$ is parallel to the axis $Z_u$. $I_m$ is the intersection point between ${\Gamma }_m$ and $Z_u$. In that case, the contact point in ${\Gamma }_m$ should be the nearest point to $I_m$ on the intersection line between ${\Gamma }_m$ and the helical surface of the screw rotor.

Assume the coordinate value of $I_m$ in the CCS is $(0,0,Z_u)$, and $Z_u$ can be an arbitrary value within the computation range along the $Z_u$ axis. Its coordinate value in the WCS can be obtained by

$${\left[x_m,y_m,z_m,1\right]}^T={\mathit{T}}^{-1}{\left[0,0,{\mathrm{Z}}_u,1\right]}^T$$

(3)

The projection of ${\Gamma }_m$ in the $yoz$ plane is expressed as

$$ytan\phi -z+{\displaystyle \frac{Z_u}{cos\phi }}=0$$

(4)

The projection of an arbitrary contact point $D(x,y,z)$ on the intersection line between ${\Gamma }_m$ and the helical surface should be located on the line expressed by Equation (4). Its z value could be calculated by using Equation (4) according to its y value, and its x value can be calculated by searching the contact point between the normal of the $Y_u{O}_u{Z}_u$ plane in ${\Gamma }_m$ and the intersection line between ${\Gamma }_m$ and the helical surface. Then, the contact point $D^{*}(x^{*},y^{*},z^{*})$ can be calculated as

$$\left\{\begin{array}{c}\underset{x,y,z}{min}L(x,y,z)\hfill \\ L(x,y,z)=\sqrt{{(x-x_m)}^2+{(y-y_m)}^2+{(z-z_m)}^2}\hfill \end{array}\right.$$

(5)

Finally, the contact point on a formed cutter profile in ${\Gamma }_m$ is represented as

$$\left[Z_u,R_u\right]=\left[Z_u,L(x^{*},y^{*},z^{*})\right]$$

(6)

2.4. Searching the Contact Point Using Subdivision Method

The helical surface, S, is achieved by rotating and translating the initial tooth profile expressed by Equation (1) simultaneously. Thus, the intersection line between S and ${\Gamma }_m$ can be represented by a group of intersection points between a series of tooth profiles $\{C_0,C_1,\dots ,C_n\}$ and ${\Gamma }_m$. Based on the contact point computation principle, the searching process could be implemented in the rest of the intersecting planes. The detailed steps are as follows:

(1)

Dividing the computation range in the $Y_u$ direction into N sections with equal length. Thus, the nth intersection points between $C_n$ and ${\Gamma }_m$ in the $Y_u{O}_u{Z}_u$ plane can be denoted as $(0,Y_u,Z_u)$;

(2)

Calculating the coordinate values, $D_n(0,y_n,z_n)$, in the $yoz$ plane via Equation (2);

(3)

Calculating the rotating angle by ${\theta }_n=z_n/p$ and the coordinate values of the knot points and the control points of $C_n$ in the WCS via Equation (1);

(4)

Calculating the value of $x_n$ according to the method of Section 2.5;

(5)

Calculating the distance between the intersection point and the rotation center. Then, determining the minimum distance $L_{min}^k=min\left\{L_i\right\}$ and the corresponding index $i_{min}$. Judge $|Y_u^k\left(i_{min}\right)-Y_u^k(i_{min}+1)|\le {\epsilon }_b$, and go to step (7) if the criterion is satisfied; otherwise, go to step (6);

(6)

Inserting the subdivision points into the interval $[Y_u^k(i_{min}-1),Y_u^k\left(i_{min}\right)]$ and

$[Y_u^k\left(i_{min}\right),Y_u^k(i_{min}+1)]$, the inserted $Y_u$ coordinates for the next iteration are

$$\left\{\begin{array}{c}\begin{array}{c}{Y_u}^{k+1}\left(1\right)=Y_u^k(i_{min}-1),{Y_u}^{k+1}\left(3\right)=Y_u^k\left(i_{min}\right),{Y_u}^{k+1}\left(5\right)=Y_u^k(i_{min}+1)\hfill \\ {Y_u}^{k+1}\left(2\right)=Y_u^k(i_{min}-1)+{\displaystyle \frac{Y_u^k\left(i_{min}\right)-Y_u^k(i_{min}-1)}{2}}\hfill \\ {Y_u}^{k+1}\left(4\right)=Y_u^k\left(i_{min}\right)+{\displaystyle \frac{Y_u^k(i_{min}+1)-Y_u^k\left(i_{min}\right)}{2}}\hfill \end{array}\end{array}\right.$$

(7)

Then, go to step (2). It should be noted that the $Z_u$ coordinates of the new generated points are unchanged during the computation processes;

(7)

Calculating the coordinates of contact point ${\mathit{D}}^{*}$ within this intersection plane.

When searching the minimum distance point of the beginning or the end point of the sequence, the subdivision is only carried out within the boundary regions similarly with the above-mentioned processes.

2.5. Computing Intersection Point Between a Straight Line and a Cubic B-Spline

Generally, the tooth profile is represented by a group of discrete points, as shown in Figure 4. To obtain the coordinates of an intersection point, these points are interpolated using a cubic B-spline via the multiple knots technique at the boundary, and they can be expressed as [34]

$${\mathbf{P}}_i\left(u\right)={[x_i\left(u\right),y_i\left(u\right)]}^T=\sum _{j=0}^3{B}_{j,3}\left(u\right){\mathbf{V}}_{i+j},u\in [0,1]$$

(8)

where ${\mathbf{V}}_{\mathbf{i}}$, ${\mathbf{V}}_{\mathbf{i}+\mathbf{1}}$, ${\mathbf{V}}_{\mathbf{i}+\mathbf{2}}$, and ${\mathbf{V}}_{\mathbf{i}+\mathbf{3}}$ are the vertices of the characteristic polygon, and $B_{j,3}\left(u\right)$ represents the base functions of the cubic B-spline and can be written as

$$\left\{\begin{array}{c}\begin{array}{c}{B}_{0,3}\left(u\right)={\displaystyle \frac{1}{6}}{\left(1-u\right)}^3\hfill \\ B_{1,3}\left(u\right)={\displaystyle \frac{1}{6}}\left(3u^3-6u^2+4\right)\hfill \\ B_{2,3}\left(u\right)={\displaystyle \frac{1}{6}}\left(-3u^3+3u^2+3u+1\right)\hfill \\ B_{3,3}\left(u\right)={\displaystyle \frac{1}{6}}{u}^3\hfill \end{array}\end{array}\right.$$

(9)

Considering the complexity of the tooth profile, the spline needs to be divided according to the extreme points in the y coordinate direction as $Q_i(i=1,2,\dots ,n)$, and $n-1$ sections can be obtained. After that, the section number can be determined according to $Q_i\left(y\right)$. Considering $Q_i\left(y\right)$ can be sorted in either ascending order or descending order, if $y_m$ locates within the region of $[Q_i\left(y\right),Q_{i+1}\left(y\right)]$, it should satisfy the following criteria

$$\left|y_m-Q_i\left(y\right)\right|+\left|y_m-Q_{i+1}\left(y\right)\right|\le \left|Q_{i+1}\left(y\right)-Q_i\left(y\right)\right|+{\epsilon }_{inf}$$

(10)

where ${\epsilon }_{inf}$ is the infinitesimal value for the computation process.

Using the same procedure, the knot points of the region that $y_m$ locates in can also be determined. By using the multiple knots technique, a one-to-one relationship between the knot and the control points could be obtained. Thus, the control points for this section of the spline can be achieved by extracting the sequence of control points with the same index as the knot points. The parameter u of the intersection point should be satisfied with the following equation:

$$f\left(u\right)=y_m-\sum _{j=0}^3{B}_{j,3}\left(u\right){\mathbf{V}}_{i+j}\left(y\right)=0$$

(11)

where ${\mathbf{V}}_{\mathbf{i}+\mathbf{j}}\left(\mathbf{y}\right)$ denotes the y coordinate values of the corresponding control points.

This equation is a cubic polynomial equation, and u can be easily obtained by using the Newton iteration. The stop criterion is $|u_{k+1}-u_k|<{\epsilon }_a$, where k is the number of the iteration and ${\epsilon }_a$ is the threshold value. By substituting u into Equation (8), the x coordinate of $D_n$ can also be obtained.

2.6. Determine the Computation Range

The computation range along $Y_u$ and $Z_u$ should be determined as shown in Figure 5. The begin point and the end point of the tooth profile in the WCS are each denoted as $P_1(x_1,y_1,z_1)$ and $P_m(x_m,y_m,z_m)$. Then, the projection of the left boundary curve on $yoz$, $C_L$, can be generated as

$$f_L\left(\theta \right)={\left.\mathit{M}·{\left[x_1,y_1,z_1,1\right]}^T\right|}_{x=0}$$

(12)

The function of the projection line of the tool rotation axis on $yoz$ is

$$z=ytan\phi$$

(13)

By combining Equations (12) and (13), their cross-section point $P_b$ can be obtained. The coordinate values of $P_e$ can be obtained using the same procedure. Thus, the computation range in the tool rotation axis is

$$\left[Z_{min},Z_{\max }\right]={\displaystyle \frac{1}{cos\phi }}\left[P_b\left(y\right),P_e\left(y\right)\right]$$

(14)

The computation range in the $Y_u$ direction is related to the maximum radius of the cutter $R_m$, which has been unknown up to now, and the minimum radius of the cylinder $r_0$. To estimate $R_m$, the intersection curve between the $X_u{O}_u{Z}_u$ plane and the helical surface is computed firstly, which is also carried out by serching a group of intersection points between the $X_u{O}_u{Z}_u$ plane and a series of tooth profiles, as illustrated in Section 2.4. For an arbitrary intersection point $B_i(x_i,y_i,z_i)$, its distance to the cutter rotation axis is $R_i=A-x_i$, and the maximum value can be achieved as $r_m=max\left\{R_i\right\}$. This intersection curve is not the contact curve, so the maximum cutter radius should be no larger than $r_m$ to prevent over-cut, and $r_m$ is used to estimate the computation range of $Y_u$. A parallel plane of $yoz$ is constructed with an interval distance of $r_0$. The maximum and the minimum values of the Y coordinate in the CCS can be obtained by computing the intersection point of the maximum radius of the circle and the constructed plane as

$$\left[Y_{min},Y_{max}\right]=\left[-\sqrt{r_{\mathrm{m}}^2-{\left(A-r_0\right)}^2},+\sqrt{r_{\mathrm{m}}^2-{\left(A-r_0\right)}^2}\right]$$

(15)

3. Experiments and Discussion

The geometrical data of two screw rotors are used to generate the correspond formed cutter profiles by using the proposed numerical method. The first one has a helical surface with an arc tooth profile, which is represented by an equation of continuity. In that case, an error-free cutter profile can be obtained by using the analytical method. The cutter profile which is calculated by using the proposed numerical method is compared with the one that is calculated by using the analytical method in order to verify the computational accuracy of the proposed method. The second screw rotor has a helical surface which is represented by discrete points. The cutter profile is calculated to verify both the computational accuracy and the efficiency of the proposed numerical method.

3.1. Cutter Profile Generation for an Arc Tooth

The arc tooth profile used for veficication and its 3D model are shown Figure 6a and Figure 6b, respectively. The function of the tooth profile is

$$\left[x_0,y_0\right]=\left[G-Rcost,-Rsint\right]$$

(16)

The detailed geometry and the machining parameters are listed in

Table 1. Geometry and machining parameters of the helical surface with arc tooth.

Parameters	Value
Radius of the circular arc $R_1$	55.1 mm
Radius of the cylinder block $R_2$	111.69 mm
Distance between the rotor center and the circular arc center of tooth G	125 mm
Lead H	450 mm
Number of the teeth	4
Swivel angle $\phi$	31°
Distance rotor axis and the cutter axis A	200 mm

. To quantitatively evaluate the accuracy of the numerical method, the analytical method is also adopted to calculate the cutter profile where the contact equations were solved by use of the classical Levenberg–Marquardt algorithm [35].

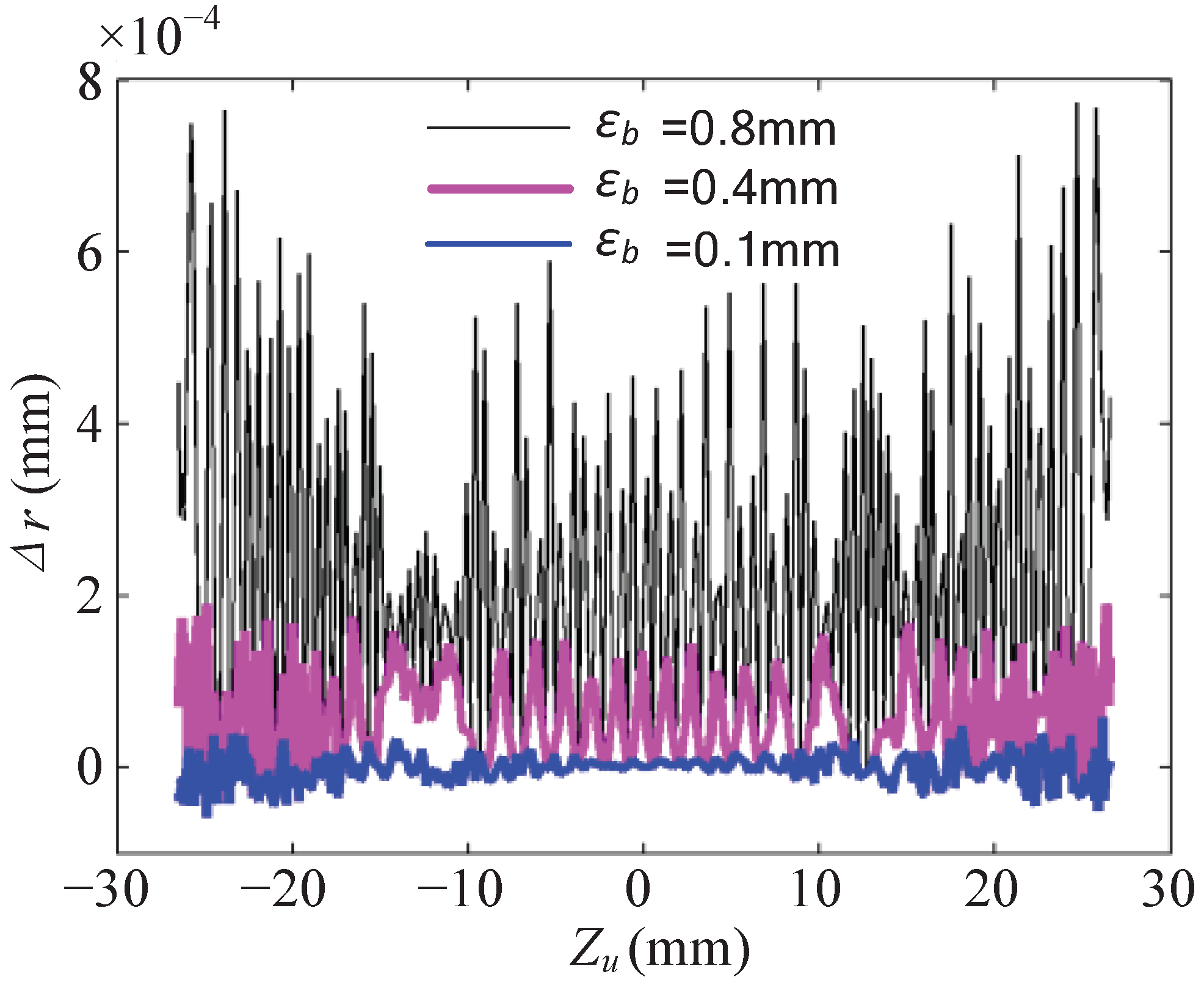
Based on the computation principle, when the tooth profile is given by discrete points, the cutter profile error generated by the proposed numerical method is only subjected to the interpolation error of the tooth profile, the computation accuracy of the intersection points between the spline and the intersection plane ${\epsilon }_a$, and the subdivision process to find the minimum distance point. For this case, ${\epsilon }_a$ is set to ${10}^{-8}$ mm; thus, its influence on the profile error of the cutter can be neglected. To reveal the relationship between the cutter profile error and the remaining two factors, three experimental schemes are carried out—namely, $S_1$, $S_2$ and $S_3$.

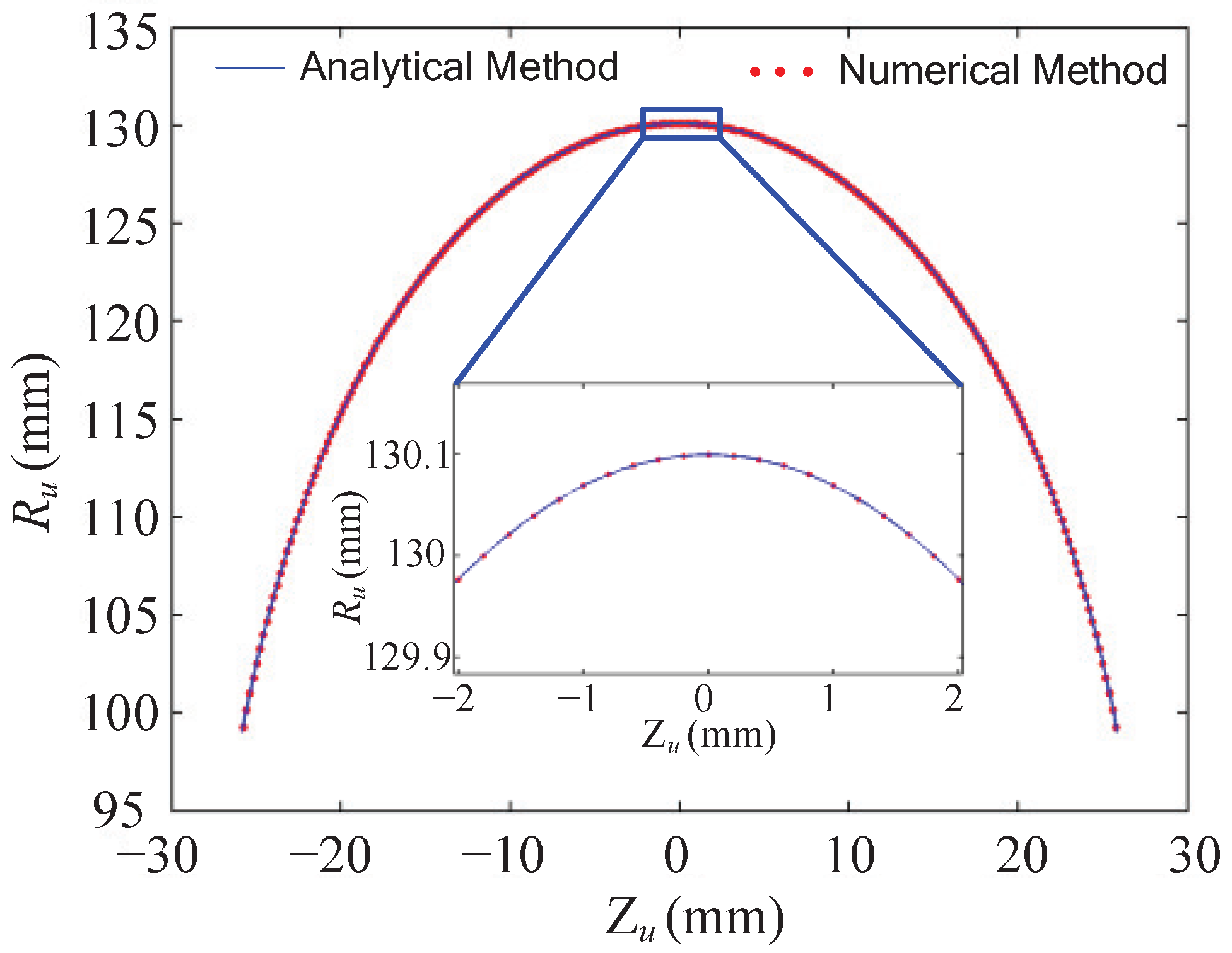
For $S_1$, points are sampled on the arc tooth profile with an equal angle of 0.01 rad. The threshold value of the subdivision is first set to ${\epsilon }_b=0.8$ mm. For ease of comparison, the $Z_u$ coordinates of the points of the cutter profile are generated in the same way as the ones that are used in the analytical method. The obtained cutter profiles are shown in Figure 7, where the result of the numerical method is well accordant with the result of the analytical method. The radius deviation is computed and shown in Figure 8. The maximum deviation (MD) is 0.7741 µm, and the root mean squares (RMS) value is 0.3111 µm. Then, the subdivision threshold value ${\epsilon }_b$ is set to 0.4 mm and 0.1 mm, respectively, and the deviations reduce significantly. For all of the above situations, the maximum deviations are within 1 µm, which indicates the high calculation precision of the proposed numerical method.

However, when ${\epsilon }_b$ is further decreased to 0.04 mm and 0.01 mm, the maximum deviation remained unchanged, as shown in

Table 2. Maximum profile deviations under different experimental schemes (µm).

${\mathit{\epsilon }}_{\mathit{b}}$ (mm)	0.8	0.4	0.1	0.04	0.01
$S_1$	0.7741	0.1896	0.0652	0.0558	0.0558
$S_2$	0.7737	0.1943	0.0131	0.0031	0.0016
$S_3$	0.8212	0.1934	0.0130	0.0026	0.0004

. As analyzed above, the error is most probably introduced by the B-spline interpolation. To verify this assumption, the experiment scheme, $S_2$, is carried out where the points are resampled on the arc tooth at an equal angle of 0.002 rad. The maximum deviations are also listed in Table 2. When ${\epsilon }_b=0.01$ mm, the maximum deviation value reduces to 0.0016 µm, which is far less than that in $S_1$.

For $S_3$, the intersection points are obtained not by the intersection of the interpolated B-spline curve and the straight line, but by combining the tooth function and the intersection planes, where no interpolation error exists. The maximum deviation reduces to 0.0004 µm at ${\epsilon }_b=0.01$ mm. The above results indicate that the proposed method can achieve an extremely high precision when the interpolation error is well controlled.

3.2. Cutter Profile Computation for the Point Represented Tooth Profile

The surface geometry and the machining parameters of the screw rotor are listed in

Table 3. Surface and the machining parameters of the rotor with point-represented tooth profile.

Parameters	Value
Lead H	450 mm
Number of the teeth	4
Swivel angle $\phi$	31°
Distance rotor axis and the cutter axis A	200 mm

. The tooth profile of this screw rotor is represented by discrete points, as shown in Figure 9a, where the point intervals are equal. The analytical method and the proposed numerical method are used to calculate the cutter profile according to the tooth profile, respectively. For easy comparison, the $Z_u$ coordinates of the points in the analytical method and the proposed numerical method are equal, and the number of points on the cutter profile is equal to the number of points on the tooth profile. Some of the coordinates of points on the tooth profile are listed in

Table A1. Tooth profile data of the rotor.

Number	x (mm)	y (mm)	Number	x (mm)	y (mm)
1	54.1090	48.7200	16	48.7772	42.5460
2	54.3630	48.3690	17	48.0891	42.1493
3	54.5590	47.9580	18	47.4190	41.7570
4	54.7370	47.2700	……	……	……
5	54.7470	46.7790	109	65.9914	−13.2746
6	54.6560	46.2640	110	66.5425	−13.9106
7	54.3290	45.5450	111	67.0876	−14.5497
8	53.9790	45.1170	112	67.6110	−15.2040
9	53.6100	44.8140	113	68.0180	−15.7386
10	53.1340	44.5580	114	68.4145	−16.2922
11	52.3888	44.2375	115	68.7810	−16.8550
12	51.6314	43.9128	116	69.2410	−17.9090
13	50.8768	43.5893	117	69.5650	−19.6360
14	50.1330	43.2700	118	69.5840	−20.4230
15	49.4426	42.9176	119	69.5180	−21.2100

. Some of the coordinates of points on the cutter profile generated by the analytical method are listed in

Table A2. Cutter profile obtained from the analytical method.

Number	${\mathit{Z}}_{\mathit{u}}$ (mm)	${\mathit{R}}_{\mathit{u}}$ (mm)	Number	${\mathit{Z}}_{\mathit{u}}$ (mm)	${\mathit{R}}_{\mathit{u}}$ (mm)
1	−36.3073	92.1070	16	−32.0739	106.9037
2	−36.0087	92.1088	17	−31.8269	107.9109
3	−35.6940	92.1900	18	−31.5446	109.0041
4	−35.2169	92.4427	……	……	……
5	−34.9141	92.7156	109	9.5635	95.1882
6	−34.6268	93.0853	110	9.9813	94.5182
7	−34.2803	93.7771	111	10.3929	93.8525
8	−34.0793	94.4505	112	10.8071	93.2068
9	−33.7651	96.1883	113	11.1413	92.6987
10	−33.0616	100.9608	114	11.4835	92.1979
11	−32.5698	104.1176	115	11.8301	91.7237
12	−32.2845	105.7557	116	12.4942	91.0528
13	−31.9882	107.3280	117	13.6221	90.3475
14	−32.0087	107.2747	118	14.1480	90.1410
15	−32.1703	106.4993	119	14.6862	90.0094

. Some of the coordinates of points on the cutter profile generated by the proposed numerical method are listed in

Table A3. Cutter profile obtained from the proposed numerical method.

Number	${\mathit{Z}}_{\mathit{u}}$ (mm)	${\mathit{R}}_{\mathit{u}}$ (mm)	Number	${\mathit{Z}}_{\mathit{u}}$ (mm)	${\mathit{R}}_{\mathit{u}}$ (mm)
1	−36.3073	92.0963	16	−31.9882	107.2591
2	−36.0087	92.1033	17	31.8269	107.9109
3	−35.6940	92.1900	18	−31.5446	109.0041
4	−35.2169	92.4427	……	……	……
5	−34.9141	92.7156	109	9.5635	95.1883
6	−34.6268	93.0853	110	9.9813	94.5182
7	−34.2803	93.7770	111	10.3929	93.8525
8	−34.0793	94.4480	112	10.8071	93.2068
9	−33.7651	96.1875	113	11.1413	92.6987
10	−33.0616	100.9583	114	11.4835	92.1979
11	−32.5698	104.1160	115	11.8301	91.7236
12	−32.2845	105.7552	116	12.4942	91.0526
13	−32.1703	106.3718	117	13.6221	90.3473
14	−32.0739	106.8808	118	14.1480	90.1418
15	−32.0087	107.1751	119	14.6862	90.0310

.

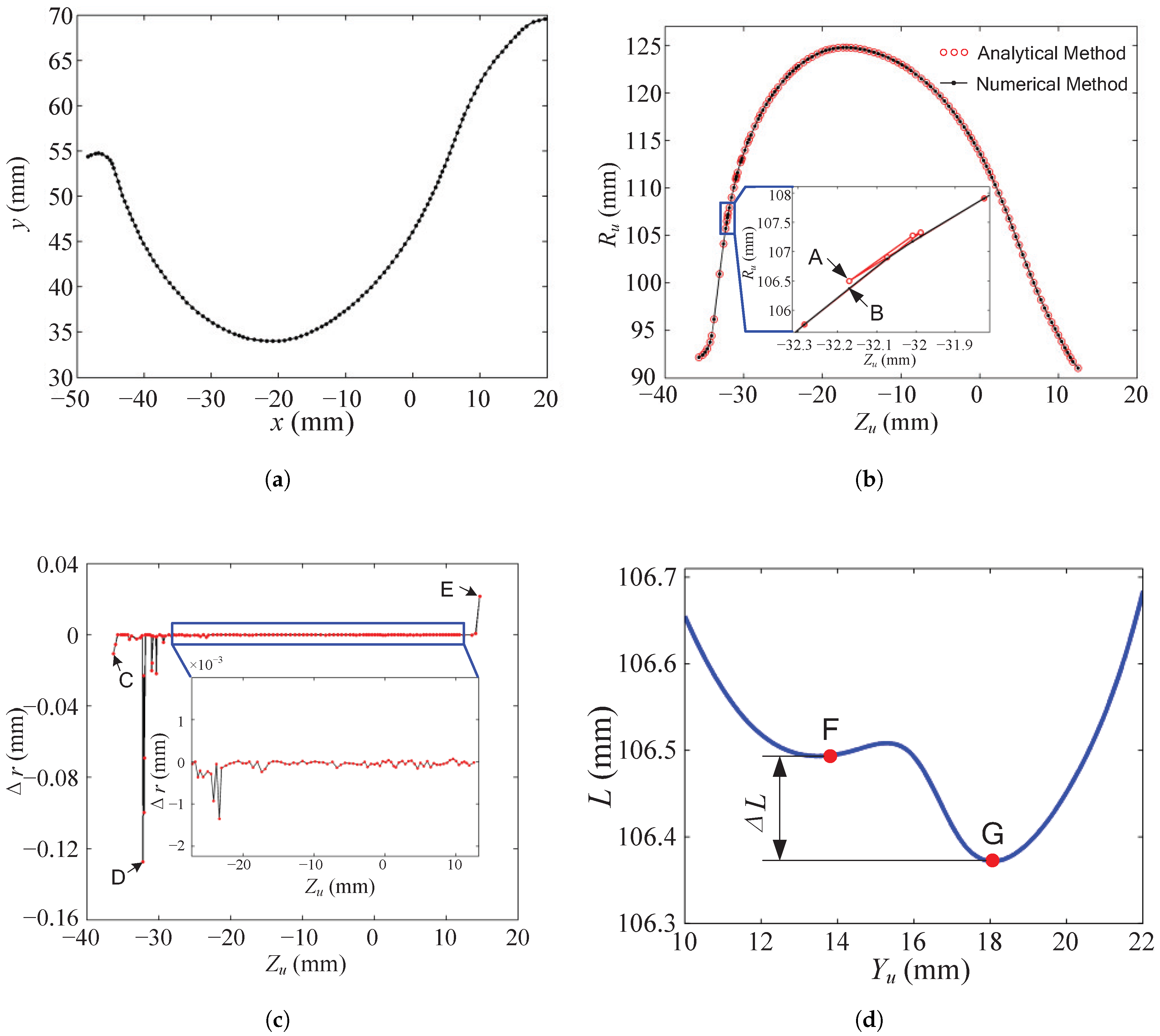
As shown in Figure 9b, the cutter profile is calculated using an analytical method by solving the contact equations [14]. The deviation value of each point is obtained by using cubic B-spline fitting with the multiple knots technique at the boundary. The result shows that the distribution of the points on the tool profile is no more uniform. In addition, there are several singular points, as shown in the enlarged part of this figure.

The profile of the cutter obtained by using the proposed numerical method is also shown in Figure 9b. Most of the profile obtained by using the analytical method closely coincides with the result of the proposed numerical method. However, at the enlarged portion, the numerical method obtains a smoother profile than the analytical method.

To further compare the two cutter profiles, the deviations of $R_u$ are computed as shown in Figure 9c. The computational precision and efficiency of the numerical method and the analytical method are listed in

Table 4. The precision and computational efficiency of numerical method and analytical method.

	Numerical Method	Analytical Method
Contact line equation	No need	Need
Derivative of contact line equation	No need	Need
Maximum error	$-0.00135$ mm	$-0.1275$ mm
Computation time of Matlab program	1.213 s	1.333 s

. The error of the numerical method is only $1.06\%$ of that of the analytical method. The computational time of the Matlab program for the numerical method is $9.00\%$ lower than that when using the analytical method. More importantly, the numerical method can be applied to any type of screw rotor profiles without building the contact line equation and taking its derivative, which is the most time-consuming operation of the analytical method.

The deviation curve is analyzed from three aspects:

(1)

The boundary points obtained by the analytical method, C and E, have large deviation values. This is because the derivative values are very sensitive to the boundary condition of the interpolation, and the derivative values significantly affect the solving of the contact equations.

(2)

The singular points obtained by the analytical method, including point D and the points nearby in Figure 9c, have even larger deviations. The maximum deviation value at the singular point A in Figure 9b is $-0.1275$ mm, which is not allowed for the machining of a screw rotor.

(3)

The deviation value of most points on the deviation curve, as shown in the expanded portion of Figure 9c, is within 1.5 µm. This indicates that the numerical method can reach as precise results as the analytical method under normal conditions.

The intersection curve where A is located is extracted and analyzed to figure out how the singular points occur when using the analytical method. The curve of distance from the intersection point to the rotation center is plotted in Figure 9d. The point G is the real global minimum point of the distance curve. The corresponding point on the distance curve of point A is F, which is a local minimum point obtained by the analytical method. The distance variation from F to G is $\Delta L=-0.1275$ mm, which is the same as the deviation value at point D in Figure 9c. Thus, the material near point A will be over-cut. The numerical method, on the other hand, obtained the real global minimum point.

4. Machinability Analysis

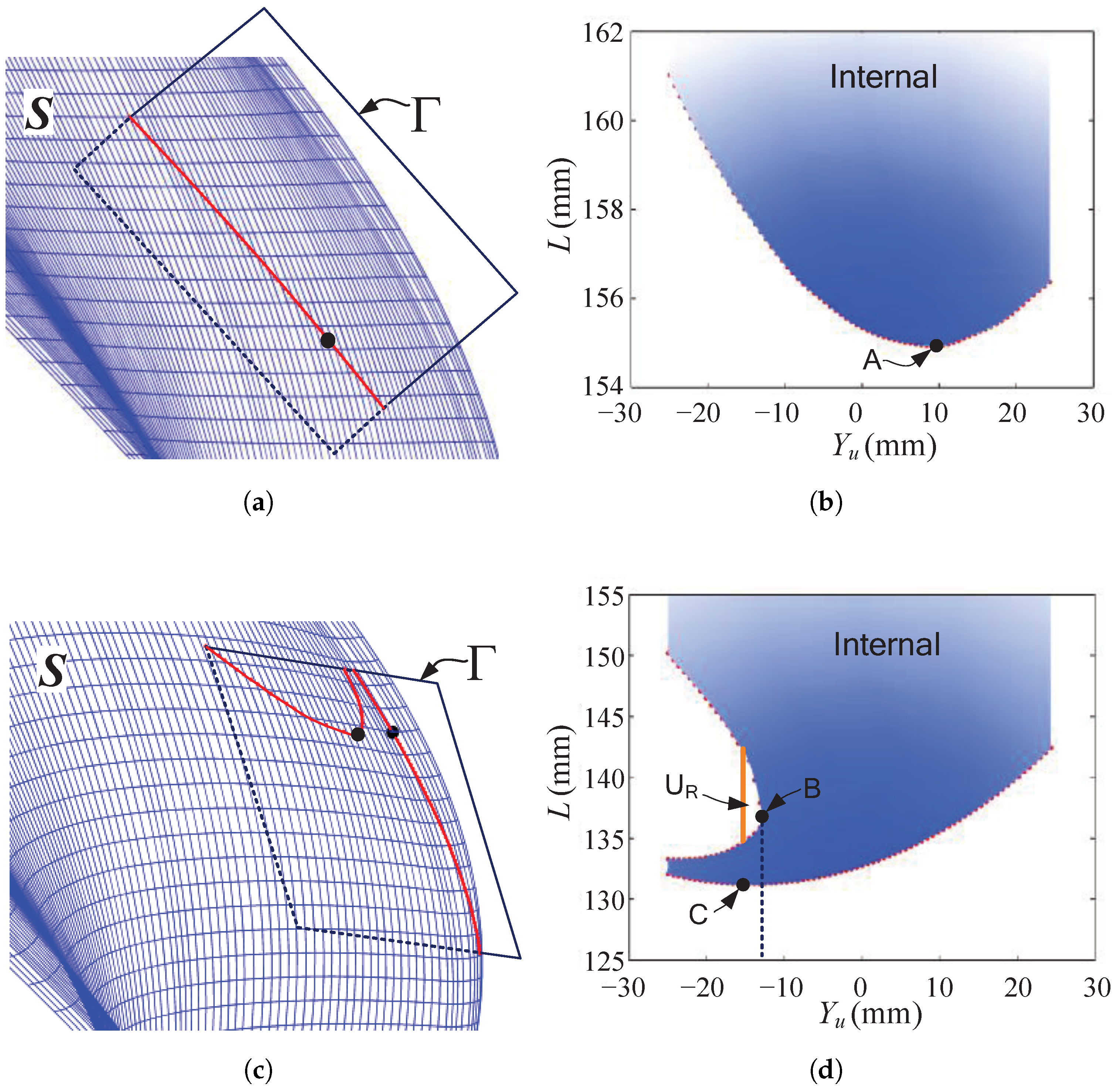
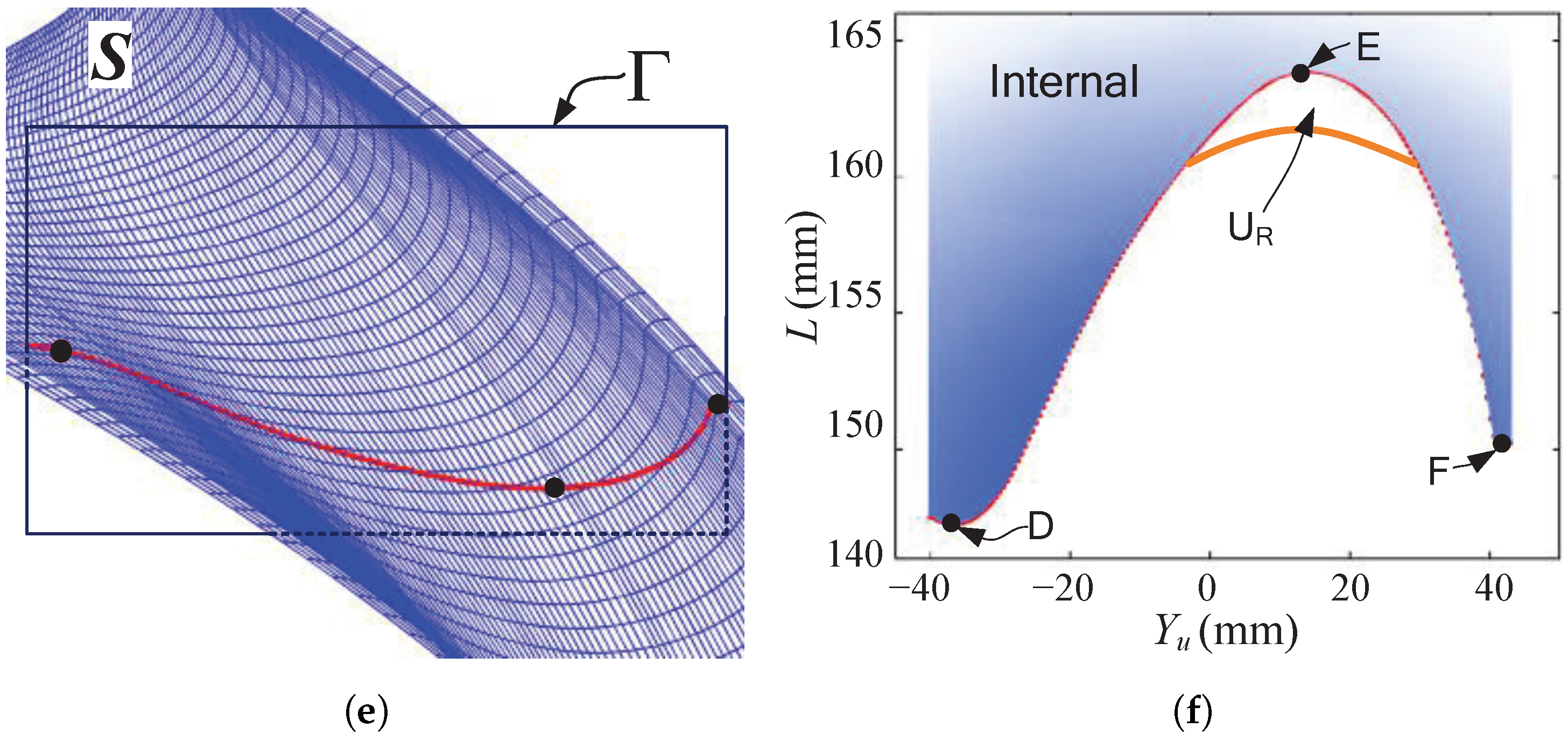
The machinability related to the cutter profile design is analyzed according to each of the intersection curves, as shown in Figure 10, where the intersection curves between the intersection planes and the helical surfaces are denoted along with the distance curve.

When the cutter is not interfering with the helical surface within the intersection plane, as shown by Figure 10a,b, the distance curve has a unique minimum point. The minimum value equals the radius of the cutter in this intersection plane. However, the intersection curve could be more complicated, as shown in Figure 10c, where two intersection curves are obtained. The distance curves also consist of two curves, as shown in Figure 10d. The point with the minimum distance can only exist on the lower curve. If C is the minimum point and C($Y_u$) < B($Y_u$), the block material above the point C, indicated by $U_R$, cannot be removed due to self-occlusion. Another interference problem case is shown in Figure 10e,f, which usually occurs when the radius of the cutter is larger than the minimum radius of the intersection curve. A global maximum point E exists on the distance curve, and the material near this region, $U_R$, cannot be removed. Otherwise, the cutter would interfere with the internal material of the desired surface.

The machinability analysis is carried out simultaneously with the cutter profile generation process by examining each of the intersection curves. The desired helical surface can be obtained when no interference occurs.

5. Conclusions

A general numerical method is proposed to design the formed milling cutters for the machining of various kinds of helical surfaces. A group of intersection planes are built in which contact points are searched via the subdivision method and the Newton iteration method. In that case, the cutter profile could be obtained without building and solving the nonlinear contact equation, and the problem of singularities can be prevented.

Two cutter profiles are designed to verify the proposed method. The results indicate that the computational accuracy and efficiency are significantly improved compared with the commonly used analytical method. Furthermore, the machinability related to the cutter profile design can be easily justified simultaneously with the contact point searching process.

The proposed method can also be used for the profile design of the formed grinding wheels. Future work will be devoted to the cutting process analysis related to the cutting force, process parameters, tool wear and error compensation.