Research on Performance Testing Methods for Electrical Equipment in High-Speed and Complex Environments: A Case Study on Roof Insulators of High-Speed Trains

Abstract

This paper proposes a rotating test method to address the limitations of high costs and the inability to replicate high-speed multiphase environments in icing wind tunnels and artificial climate chambers. The method simulates high-speed multiphase in an enclosed space using relative motion and duct regulation at a lower cost. Using the FQJG2-30/16-400 type roof insulator, the Eulerian–Eulerian and CFD (computational fluid dynamics) method was employed to compare the proposed rotating method with traditional linear airflow tests in wind–sand erosion and high-speed icing experiments. Results show maximum differences of 3.23% in the collision rate and 4.34% in the icing mass, indicating good consistency. Validation experiments in an artificial climate chamber further confirmed the feasibility of the rotating test method, with icing mass differences within 5–8%. This study provides a cost-effective approach for high-speed testing in multiphase environments.

1. Introduction

The operation of mechanical and electrical equipment at high speeds in complex environments is a very common working condition. Examples such as high-speed trains, airplanes, wind turbines, etc. operate at high speeds in environments with low temperatures, ice coverage, sand and dust, and salt fog over a long time. Therefore, their characteristics in a complex airflow field environment directly affect their stability and lifespan [1,2,3]. Taking high-speed rail as an example, long-term high-speed motion in sandy or low-temperature regions can lead to roof insulator material degradation and even flashover due to erosion and icing [4,5,6]. Similarly, wind turbine blades and high-speed aircraft also face similar issues, necessitating high speed multiphase testing to assess their long-term operational reliability [7,8,9].

Currently, wind tunnel and artificial climate chamber tests are widely used in the industry for the high-speed multiphase flow test [10,11]. The icing test is usually conducted in an ice wind tunnel. Ice wind tunnels can simulate low-temperature, high-humidity icing environments and have adjustable wind speeds. Liu et al. [12] and Zhang et al. [13] used ice wind tunnels to investigate the icing characteristics of offshore wind turbines blades. Guo [14] utilized a semi-open ice wind tunnel to study the icing characteristics of vertical-axis wind turbines in various environmental conditions. Malik et al. [15] investigated the water film backflow phenomena on aircraft wing surfaces under various powers of thermal de-icing systems using the ice wind tunnel at the University of Brunswick Institute of Technology. Han et al. [16] conducted icing tests on aircraft airfoils under normal and supercooled large droplets in the NRC-AIWT icing wind tunnel. Icing wind tunnel tests have provided the foundation for revealing icing mechanisms and have played a significant role in the study of de-icing for structures. However, wind tunnels are costly, functionally limited, and unable to create complex atmospheric environments test conditions internally. For instance, the ice wind tunnel can only conduct ice coverage tests, but cannot carry out other complex environmental tests.

Artificial climate chambers can simulate environments such as contamination and rain and support high-voltage testing, and they are widely used in research on erosion and contamination accumulation [17,18]. Fan [19] conducted glazed ice simulation experiments on insulators in an artificial climate chamber and studied the surface hydrophobicity and anti-icing performance. In addition, Wang [20] investigated the impact of contamination levels on the insulation of 220 kV composite insulators under minor icing conditions. Qiu [21] investigated the pollution flashover characteristics of 220 kV hollow porcelain insulators at different altitudes and contamination levels through artificial climate chamber tests. Zhang [22] investigated the aging of insulators eroded by sand in southern Xinjiang and explored the changes in surface roughness and elemental composition after aging from a microscopic perspective. Artificial climate chamber tests can simultaneously simulate multiphase flow and conduct energized tests. However, the existing artificial climate chambers were not designed for experiments involving high-speed airflow fields, and it is difficult to simulate high-speed airflow inside them, making them also unable to meet the requirements for high-speed multiphase tests.

To address the problem, this paper proposes a testing method based on a rotating reference frame. This method creates the required multiphase within the test space, then accelerates the sample to high speed through rotation. A designed duct is used to homogenize the flow field in the test section, thereby generating a high-speed uniform multiphase flow. This paper first presents the overall design scheme of the proposed method, and then attempts to prove the validity of this experimental method from the perspective of the flow field. The rotating reference frame method is used to solve the three-dimensional rotational flow field in this research. This method has been applied and the accuracy demonstrated in the study of rotating flow field characteristics in pump machinery [23], rotating wheel brake discs [24], helicopter rotors [25], and biological stirrers [26]. Subsequently, using high-speed rail roof insulators as the test objects, the equivalence of the rotating and linear airflow fields in collision and accumulation tests is compared through numerical simulation. Finally, icing tests on the insulator in an artificial climate chamber further validate the equivalence between the proposed and linear test methods.

2. Rotating High-Speed Multiphase Flow Generator

2.1. Flow-Field Uniformity Metrics

2.1.1. Uniformity of Flow Rate

Two primary metrics are used to evaluate velocity uniformity: velocity uniformity and the dynamic pressure coefficient. The velocity uniformity metric is defined as the root mean square value of the velocity deviation within the model region of the test section. The dynamic pressure coefficient, conversely, represents the average deviation of the dynamic pressure field within the same model region. Although their definitions differ, both metrics describe the uniformity of the velocity field. In this study, the dynamic pressure coefficient was selected to characterize the uniformity of the velocity field. The dynamic pressure coefficient at any point in the flow field is defined as the deviation of the local dynamic pressure from the average dynamic pressure value in the model region, expressed as follows:

$${\mu }_i=\left|{\displaystyle \frac{q_i}{q_{\mathrm{a}}}}-1\right|$$

(1)

where q_i denotes the dynamic pressure at a given point; q_a represents the average dynamic pressure value over the entire model region.

$$q_i={\displaystyle \frac{1}{2}}\rho v^2$$

(2)

Ideally, the dynamic pressure coefficient should be minimized. A value closer to zero indicates greater uniformity in the velocity field magnitude within the test section.

2.1.2. Uniformity of the Directional Field

The evaluation index for the uniformity of the flow field is primarily the airflow deviation angle. The airflow deviation angle refers to the angle at which the direction of the airflow at a given location deviates from the mainstream direction, reflecting the uniformity of the flow direction, which is mainly influenced by the transverse pressure gradient. The definition of the airflow deviation angle is as follows:

$${\beta }_i=\arctan \left({\displaystyle \frac{\sqrt{v_y^2+v_z^2}}{v_x}}\right)$$

(3)

where β_i denotes the flow deflection angle at a given point; v_x represents the velocity component along the x-axis (primary flow direction); v_y and v_z are the components along the y-axis and z-axis, respectively.

2.2. Test Space and Rotating Device

Figure 1 is the schematic diagram of the rotating device. An enclosed test space is formed inside the laboratory, and the high-speed rotating drive system is placed inside. The laboratory is designed to be sealed and heat-insulated to meet the requirements of low temperature and pressure tests, and a complex environment generation system installed to simulate various multiphase flows. The high-speed rotary drive system mainly comprises a self-balancing guide rail and slide system, a uniform-flow accelerating duct, and a high-speed drive system. The self-balancing guide rail and slide system supports the high-speed duct, it is the core of the high-speed motion platform, and it limits the rotating parts to only carry out high-speed circular motion along the guide rail. An automatic balancing device is installed on the opposite side of the duct to ensure the system’s stability at high-speed rotation. The asymmetric uniform-flow accelerating duct consists of contraction, test, and spread sections. It is fixed between the guide rails by two slides and is driven by the rotating direction and a connection rod to carry out high-speed circular motion on the guide rail. The primary work of this paper was to validate the equivalence of the proposed method and the apparatus in airflow testing.

2.3. Uniform-Flow Acceleration Duct

The multiphase flow test requires a uniform flow field. The generation of the flow field in this method is based on rotational motion. Different rotating radii of the test section airflow lead to different radial airflow velocities, affecting the test flow field quality. Within the symmetric duct structure of the test section, the airflow deflects radially outward, relative to the rotational motion. Consequently, the flow velocity at the outer radius of the rotating test section exceeds that at the inner radius. This phenomenon fundamentally arises from the asymmetry in the relative linear velocities induced by the rotation. To solve this problem, an asymmetric uniform-flow accelerating duct was designed to offset the deviation of the flow field in the test section by compensating the incoming flow, as shown in Figure 2.

In the XOY plane, the rotational motion results in a lower flow velocity in the lower half of the test section. To compensate for this discrepancy, the contraction section is designed with a larger opening in the lower half, allowing more airflow to enter the duct through this region. It is important to note that the duct is asymmetric only in the XOY cross-section (radial cross-section), while it remains axially symmetric in the XOZ cross-section (axial cross-section), as there is no velocity offset in the XOZ plane.

In Figure 2, L1, L2, and L3 correspond to the lengths of the contraction section, test section, and spread section, respectively. D11 and D12 denote the heights of the upper and lower regions of the contraction section in the XOY plane. Research indicates that the parameters primarily influencing the flow field quality in the test section are D11, D12. By conducting topology optimization of these three parameters with the flow field uniformity as the objective, their specific values are obtained as shown in

Table 1. Parameters before and after optimization.

	D11 (m)	D12 (m)	Dynamic Pressure Coefficient	Flow Deviation Angle
Original	0.5	0.5	0.0214	0.2011
Optimized	0.4	0.6	0.0134	0.1209

.

Using CFD methods, the parameters of the asymmetric duct were optimized. As illustrated in Figure 3, after optimization, the dynamic pressure coefficient in the test section decreased by 37.38%, and the flow deviation angle was reduced by 39.88%. The flow field uniformity now meets the experimental requirements. When specific values of 0.4 m and 0.6 m were assigned to D11 and D12, respectively, the axial dynamic pressure coefficient and flow deviation angle were minimized. With this configuration, the duct demonstrated the optimal flow uniformity.

3. Numerical Model and Methodology

3.1. Computational Domain and Mesh

The computations were performed using k-ε turbulence model, and employed a multiple reference frame (MRF) approach as shown in Figure 4. Data transfer between the inside and outside domains is achieved through interpolation. The diagrams of mesh generation are displayed in Figure 5, and the detailed information of boundary conditions and mesh setting are shown in

Table 2. Information of boundary conditions and mesh.

Boundary Conditions		Mesh Information
Items	Description	Items	Description
Inside domain	Rotates at 60 rpm about the Z-axis	Inside domain	tetrahedral elements, 0.1 m size
Outside domains	Remains stationary relative to the absolute coordinate system.	Outside domains	hexahedral elements, 0.5 m size
Duct and insulator walls	No-slip and stationery relative to adjacent cells.	Interfaces	topology share, 0.04 m size
Outside walls	No-slip and stationery to the absolute coordinate.	Duct wall boundary layers	5 boundary layers, 1.2 growth ratio, 0.0001 m first element height, 30 < y+ < 60
		Sphere body of influence (SBOI)	SBOI1: 0.04 m size SBOI2: 0.015 m size

. Figure 6 shows the grid independence verification results, confirming that the total number of 800 W grid partitions selected meets the calculation requirements. The final grid quality is shown in

Table 3. Mesh quality.

Quality Criterion	Warning Limit	Error (Failure) Limit	Worst
Maximum Aspect Ratio	Default (5)	Default (1000)	32.751
Minimum Cell Quality	Default (0.05)	Default (5 × 10−4)	0.047
Minimum Cell Quality	Default (0.05)	Default (5 × 10−3)	0.15
Maximum Skewness	Default (0.9)	Default (0.999)	0.85

.

3.2. Governing Equations of Airflow Field

The fluid in both the inside and outside computational domains satisfies the conservation of mass, momentum, and energy equations. Equations (1)–(3) represent the general form of these equations:

$${\displaystyle \frac{\partial \rho }{\partial t}}+\nabla ·\left(\rho \mathit{v}\right)=0$$

(4)

$${\displaystyle \frac{\partial }{\partial t}}(\rho \mathit{v})+\nabla ·\left(\rho \mathit{v}\mathit{v}\right)=-\nabla p+\nabla {\tau }^{ij}+\rho \mathit{g}$$

(5)

$${\displaystyle \frac{\partial \rho E}{\partial t}}+\mathbf{\nabla }\left(\rho \mathit{v}H\right)=\mathbf{\nabla }\cdot \left(\mathsf{\kappa }\left(\mathbf{\nabla }T\right)+v_i{\tau }^{ij}\right)+\rho \mathit{g}\mathit{v}$$

(6)

where t is the time; ρ is the fluid density; v is the velocity vector; τ^ij is the viscous stress tensor; g is the gravity acceleration; H is the total entropy of fluid; T is the fluid temperature; κ is the thermal conductivity; E is the material energy.

In the inside domain, the rotation of the reference frame must be considered. The velocity and acceleration transformation equations are given by Equations (4) and (5). Substituting Equations (4) and (5) into Equations (1)–(3) yields the control equations for the rotating flow field:

$$\mathit{v}=\omega \times \mathit{r}+{\mathit{v}}_r$$

(7)

$$\mathit{a}={\displaystyle \frac{d\mathit{v}}{dt}}=2\omega \times {\mathit{v}}_{\mathrm{r}}+\omega \times (\omega \times \mathit{r})+\alpha \times \mathit{r}+{\mathit{a}}_r$$

(8)

where v_r is the velocity vector under the rotating reference frame; ω is the angular velocity of the rotating reference frame; a and a_r are the angular acceleration under the stationary and rotating reference frame, respectively.

3.3. Governing Equations for the Parti Kelvin Phase

The Euler model is used to calculate the rotating multiphase flow due to its superior convergence performance in complex geometries. The test particles are assumed to be spheres without considering their deformation, phase change, and influence on air [27]. The Coriolis and centrifugal forces to the left of the momentum conservation equation represent rotational effects. The first term to the right of the momentum conservation equation represents resistance, and the second term represents external volumetric forces such as buoyancy and gravity. The resistance of the droplets plays a major role. The distribution of particles can be obtained by solving the continuity and momentum equations under the rotating reference frame:

$${\displaystyle \frac{\partial {\alpha }_{\mathrm{d}}{\rho }_{\mathrm{d}}}{\partial t}}+\nabla ·\left({\alpha }_{\mathrm{d}}{\rho }_{\mathrm{d}}{\mathit{v}}_{\mathrm{dr}}\right)=0$$

(9)

$$\begin{array}{c}{\displaystyle \frac{\partial }{\partial t}}({\alpha }_{\mathrm{d}}{\rho }_{\mathrm{d}}{\mathit{v}}_{\mathrm{d}})+\nabla ·\left({\alpha }_{\mathrm{d}}{\rho }_{\mathrm{d}}{\mathit{v}}_{\mathrm{dr}}{\mathit{v}}_{\mathrm{dr}}\right)+{\alpha }_{\mathrm{d}}{\rho }_{\mathrm{d}}(2\omega \times {\mathit{v}}_{\mathrm{dr}}+\omega \times (\omega \times r)+\alpha \times \mathit{r}+{\mathit{a}}_{\mathit{r}})\\ ={\displaystyle \frac{C_{D\mathrm{r}}{\mathrm{Re}}_{\mathrm{dr}}}{24K_{\mathrm{r}}}}{\alpha }_{\mathrm{d}}{\rho }_{\mathrm{d}}({\mathit{v}}_{\mathrm{ar}}-{\mathit{v}}_{\mathrm{dr}})+{\alpha }_d{\rho }_d(1-{\displaystyle \frac{\rho }{{\rho }_{\mathrm{d}}}}){\displaystyle \frac{1}{F{r}_r}}\end{array}$$

(10)

where subscripts a, d, and r represent the parameters of air phase, particle phase, and rotation, respectively; α is the volume fraction; C_D is the drag coefficient; Re_d is the Reynolds number of particles, K is the droplets inertial parameter. Fr_r is the external volumetric force, such as the interaction force of two-phase flow, etc. A source term is added to the momentum equation to introduce the Coriolis and centrifugal forces acting on the fluid in the rotating reference frame:

$$-2(\mathit{\omega }\times {\mathit{v}}_r)-\mathit{\omega }\times (\mathit{\omega }\times \mathit{r})$$

(11)

The empirical formula for the droplet resistance coefficient is the following:

$$\left\{\begin{array}{cc}{C}_{Dr}={\displaystyle \frac{24}{R{e}_{dr}}}\left(1+0.15{\mathrm{Re}}_{dr}^{0.687}\right)& R{e}_{dr}\le 1300\\ C_{Dr}=0.4& R{e}_{dr}>1300\end{array}\right.$$

(12)

4. Equivalence Analysis Between Rotational and Linear Testing Methods

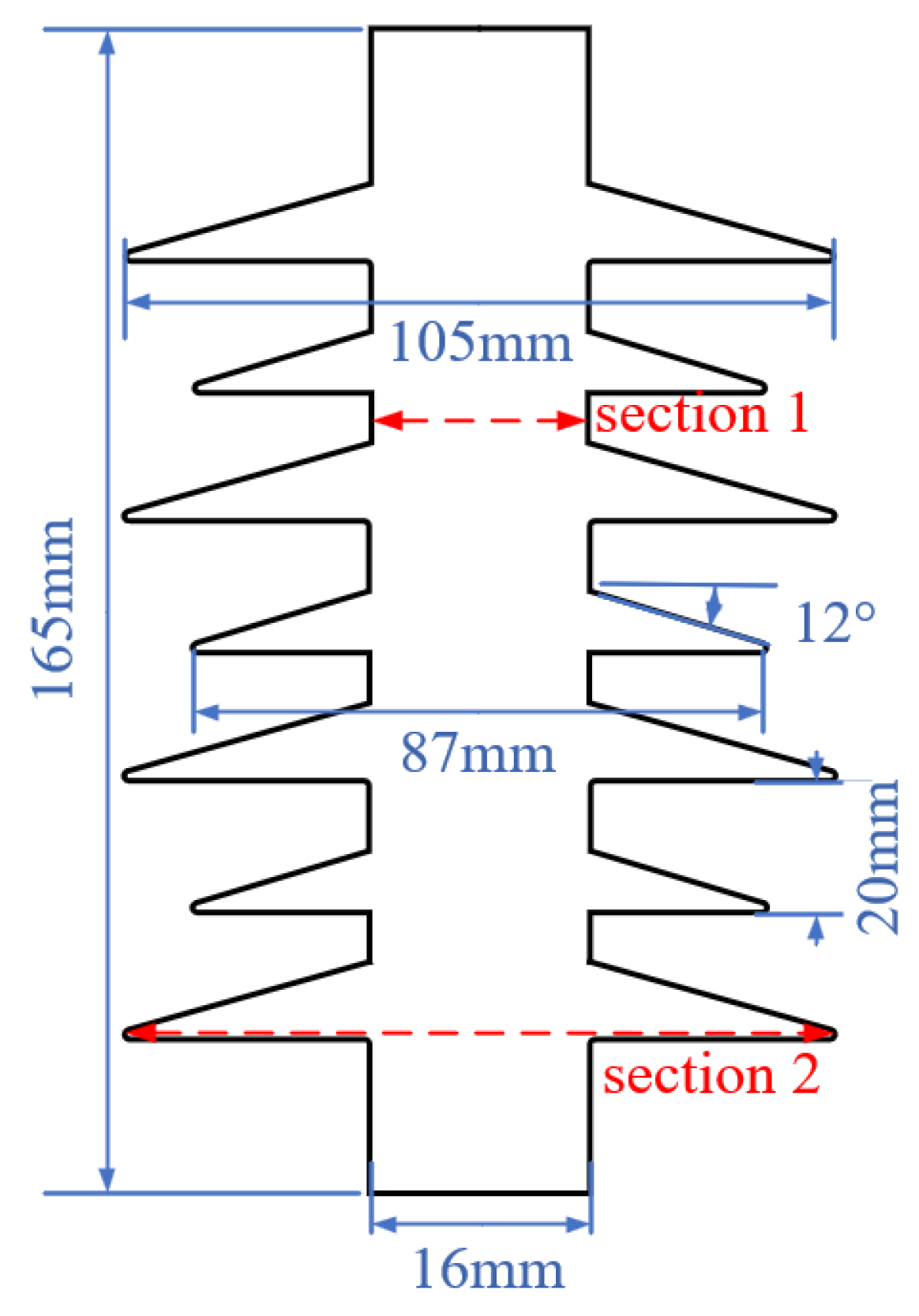
4.1. Test Insulator

Taking the roof insulator on a high-speed rail train as an example, the high-speed multiphase flow test can be divided into two types. The first is the particle collision test, which researches the collision process when the high-speed rail runs in rain, sandstorm, and haze areas. Another type is the particle accumulation test, which focuses on particle accumulation behavior, such as ice and pollution. This chapter verifies the equivalence between rotating and linear high-speed multiphase tests by simulating icing and sandstorm colliding with the insulators. The insulator was placed in the duct test section, and numerical simulations were used to research the similarities between the rotating and linear testing method.

Considering the wall effect, it should be noted that a 1/2 scale model (to avoid the wall effect) of the FQJG2-30/16-400 insulator was used in the study, with geometric parameters as shown in Figure 7. Geometric parameters of the duct in the following tests are shown in Table 1. The particle diameter d_m is 20 μm, the particle density ρ_d is 1000 kg/m³, and the particle volume mass ω_d is 0.6 g/m³.

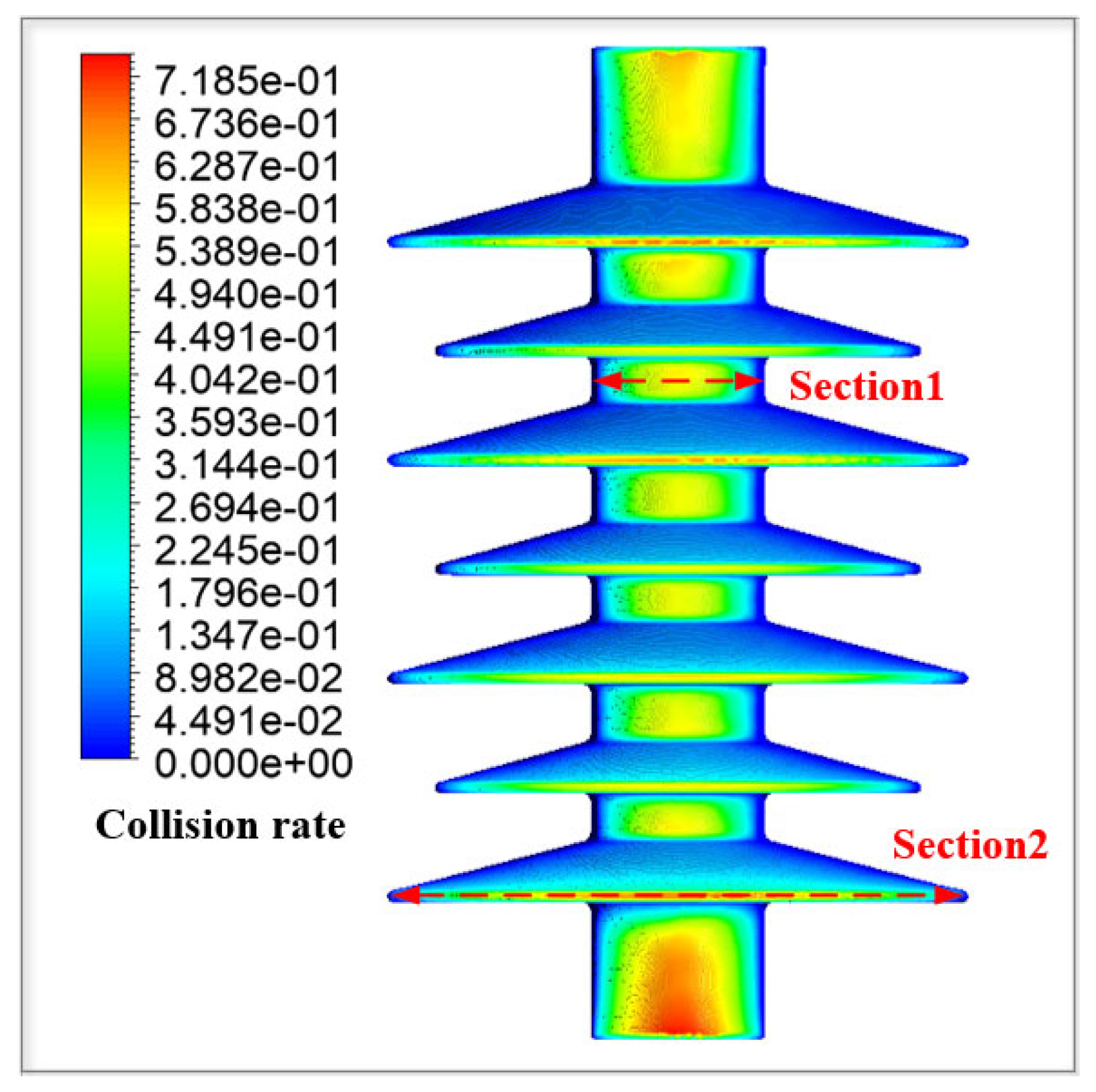
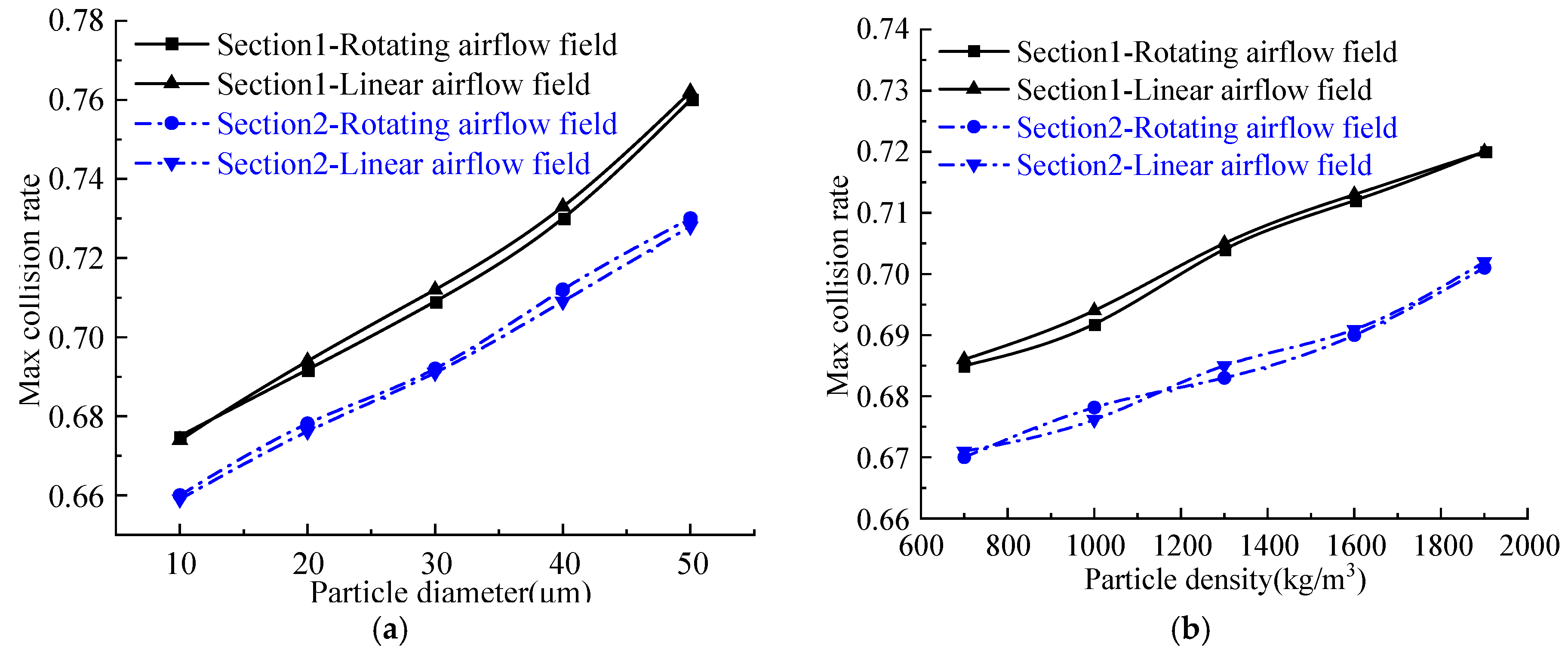
4.2. Equivalence on Collision Test

The continuous impact of high-speed particles can cause erosion on the surface of the insulators on the train roof, which affects their insulating properties and accelerates aging. Particle impact testing can be employed to investigate this erosive effect. Figure 8a presents the airflow velocity contour in the XOY plane in the test section of the rotating airflow test apparatus. As shown in the figure, after geometric optimization of the duct, the geometric structure exhibits an asymmetrical shape at the inlet; the inflow velocity in the test section reaches 67 m/s at a rotational radius of 6 m and a rotational speed of 60 rpm. Figure 8b presents the velocity distribution in the XOZ plane. Owing to the turbulence generated on both sides of the insulator, the velocities on both sides increase, with a greater increase observed on the upper and lower sides of the rod compared to the skirt region, leading to the maximum velocity in this area. Moreover, the velocity distribution in the far-field area of the test section is uniform. This indicates that the flow field obtained using the rotating test method meets the requirements.

Collision characteristics can be characterized by the local collision rate of particles on the surface; the local collision rate is defined as the ratio of the actual droplet collision rate on a differential surface element to the theoretical maximum droplet collision rate attainable on that same surface element. It serves as a dimensionless parameter characterizing the water collection capability of the differential surface, which is defined as follows:

$${\beta }_{\mathrm{p}}={\displaystyle \frac{a_d{\rho }_d({\mathit{v}}_{\mathit{d}}·{\mathit{n}}_{\mathbf{f}})}{{\omega }_d{V}_{\infty ,\mathrm{a}}}}$$

(13)

where v_d is the local particle velocity; n_f is the local normal direction vector.

Figure 9 illustrates the collision rate on the insulator surface under the rotating test method. As shown in the figure, particles primarily collide with the windward side of the insulator. The region with the highest impact rate is the central part of the insulator, particularly concentrated on the rod and the edges of the sheds, which is consistent with the actual situation.

To verify the equivalence of the collision rate results between the rotating test method and the traditional linear airflow test method, the collision rate of the insulator in the linear airflow field was calculated using the method described in [28]. The inlet velocity in the linear airflow field was taken as the average velocity at the inlet cross-section of the duct test section, which is 61.72 m/s, while the particle parameters were kept the same as those in the rotating test. The maximum collision rates at the rod center (Section 1 in Figure 9) and the shed edge (Section 2 in Figure 9) were compared between the rotating airflow field and the linear airflow field, with the results shown in Figure 10.

As shown in Figure 10, under the computational conditions where the two variables of particle diameter and density are changed while the other environmental parameters remain constant, the trend of the change in collision rate is approximately linear. The maximum collision rates at both sections increase with the particle diameter and density. This is because an increase in diameter and density enhances the particle mass, making it more difficult for the particles to follow the airflow around the insulator, thereby increasing the collision rate. Additionally, the figure reveals that the collision rates in the rotating and the straight airflow field are very close, with the maximum deviation in the data being only 3.23%. This indicates that the rotating airflow field exhibits good equivalence to the linear airflow field when conducting particle collision tests.

4.3. Equivalence on Accumulation Test

To study the equivalence of the accumulation test in the rotating airflow field using the example of ice accumulation on the insulator on the high-speed train roof, it is assumed that the ice type is rime ice. On defining the area of a local control surface as S, the particle mass Δm and the volume Δv accumulated on the local control surface within timestep Δt are as follows:

$$\Delta m=\Delta t{\beta }_p{\omega }_d{V}_{\infty ,\mathrm{a}}S$$

(14)

$$\Delta V=\Delta \mathrm{m}/{\beta }_{\mathrm{ice}}$$

(15)

where β_ice is the density of accumulated ice.

After obtaining the accumulated particle volume on the surface, the ice shape can be updated according to the normal growth rule, thereby obtaining the shape of the insulator after icing. The icing calculations were performed using FENSAP-ICE 2023 R1. A multi-step scheme was adopted for ice-shape iteration, with a temporal step of 5 min, a freestream velocity of 61.72 m s⁻¹ (identical to that in the collision test), an MVD of 20 µm, and an LWC of 0.6 g m⁻³. The icing calculation was performed on the test insulator in the rotating airflow field, and the ice shape on the insulator after 30 min is shown in Figure 11.

It was found that the icing primarily occurs on the windward side of the insulator and becomes more severe with increasing time. The regions with the most severe icing are the rod and the shed edges, which correspond to the higher collision rate areas in Figure 9. Moreover, the ice shapes obtained from the rotating and the linear airflow field are essentially consistent.

The inflow velocity in the linear airflow field is taken as the average velocity at the inlet of the duct test section, and the icing time is 30 min for all cases, with other parameters remaining unchanged. The mass of ice on the insulator under different particle diameters and volume masses in both the rotating and linear airflow fields are shown in Figure 12.

The figure shows that the icing mass on the insulator increases with the increase in particle diameter and volume mass. An increase in particle diameter leads to a higher collision rate, which results in a greater icing mass. Meanwhile, an increase in volume mass implies a higher concentration of particles in the air, meaning more particles reach the insulator surface per unit time, thereby causing an increase in the icing mass. Moreover, the icing mass calculated in the rotating airflow field is essentially the same as that in the linear airflow field, with the maximum difference being only 2.4%. This effectively demonstrates the good equivalence between the rotating and the linear airflow field when conducting accumulation tests.

5. Equivalence Study by Icing Experiment

5.1. Test Object and Facility

Icing tests on the FQJG2-30/16-400 roof insulator were conducted in an artificial climate chamber to verify the reliability of the computational results and the applicability of the rotating airflow field test. The climate chamber has a diameter of 7.8 m and a height of 11.8 m, with a temperature (degree Celsius) control range of −45 °C to 70 °C, a wind speed control range of 0 to 12 m/s, a humidity control range of 10% to 100%, and a median volume diameter (MVD) control range of supercooled water droplets from 20 μm to 500 μm.

The temperature and humidity measuring instruments used in the experiments have measurement errors of ±0.2 °C and ±1%, respectively; the anemometer has an error of ±0.1 m/s. The liquid water content (LWC) and MVD were measured using a rotating multi-conductor ice accretion probe.

The layout of the artificial climate chamber and the insulator arrangement is shown in Figure 13.

5.2. Test Procedures

The following procedures are used for this test:

(1)

Sample preprocessing: Before the test, the insulator is cleaned to remove surface grease and contaminants and then air-dried naturally.

(2)

Precooling: The insulator is placed in front of the air duct of the climate chamber and the refrigeration system turned on. When the temperature reaches the test value, the spraying system to start spraying is turned on.

(3)

Spraying system adjustment: The LWC is regulated by the tuning water pressure, while the MVD is controlled via air pressure adjustment (after water pressure stabilization). The nozzle opening is fine-tuned to optimize atomization. The parameters are maintained once the target LWC and MVD values are achieved.

(4)

Measurement of airflow velocity: The air duct system and fan power to control the airflow velocity is adjusted using a handheld anemometer to sample the airflow velocity at multiple horizontal and vertical positions at the windward side of the insulator and the average value taken.

(5)

Measurement of ice: The icing test lasts 60 min, keeping the temperature, wind speed, and water spray volume unchanged. The icing mass of the insulator is weighed every 10 min, and the local icing thickness measured by slicing after icing.

The icing test parameters are shown in

Table 4. Icing test parameters.

Test Group	Airflow Velocity (m/s)	Temperature (°C)	LWC (g/m3)	MVD (μm)
Test 1	15	−10	0.6	20
Test 2	10	−10	0.6	20
Test 3	15	−10	0.9	20
Test 4	15	−10	0.6	30

. Keeping the chamber temperature at –10 °C is suitable for forming rime icing. Each group of icing tests was repeated three times and the average of the results taken to avoid the influence of randomness.

5.3. Experiment Results

The climate chamber test and numerical simulation of the rotating method were carried out for the above four groups; the test and simulation results of the ice mass for all icing tests are shown in Figure 14. It is of note that the icing mass positively correlates with the icing time in the test and simulation results. The difference is largest at the beginning of the tests for all four groups, and the test results are smaller than the simulation result. The maximum difference appears at 11.4% when the icing time is 10 min in test 3; this is speculative due to the influence of the hydrophobicity of the silicone rubber material on the insulator surface. As the icing test progresses, the difference stabilizes between 5% and 8%. This shows that rotating airflow field equates well with the linear airflow field in the icing test.

6. Conclusions

This paper proposes a rotational high-speed airflow testing method for complex environments and preliminarily verified its consistency with the traditional linear airflow testing method. The main conclusions are as follows:

• Based on the principle of relative rotating motion, a test method is proposed to realize the test conditions of complex environments combining high-speed airflow.
• Numerical simulation shows that the collision and accumulation test results of the rotating airflow fields agree with the linear airflow field. The collision rate distribution and icing shape are basically the same. The maximum difference in the collision rate and the ice mass is 3.23% and 4.34%, respectively. It should be noted that the similarity conclusions presented herein are derived solely from comparative CFD results; their further validation will necessarily depend on forthcoming data obtained from an actual rotating test facility.
• It should be noted that this paper only verifies the feasibility of the proposed method in principle. Further research is needed to address practical engineering issues such as the duct wake effect and the stability of the rotating structure during high-speed rotation.