Design and Aerodynamic Analysis of Rigid Wing Sail of Unmanned Sailboat at Sea Based on CFD
Abstract
1. Introduction
2. Modeling of the Wing Sail
2.1. Model Development
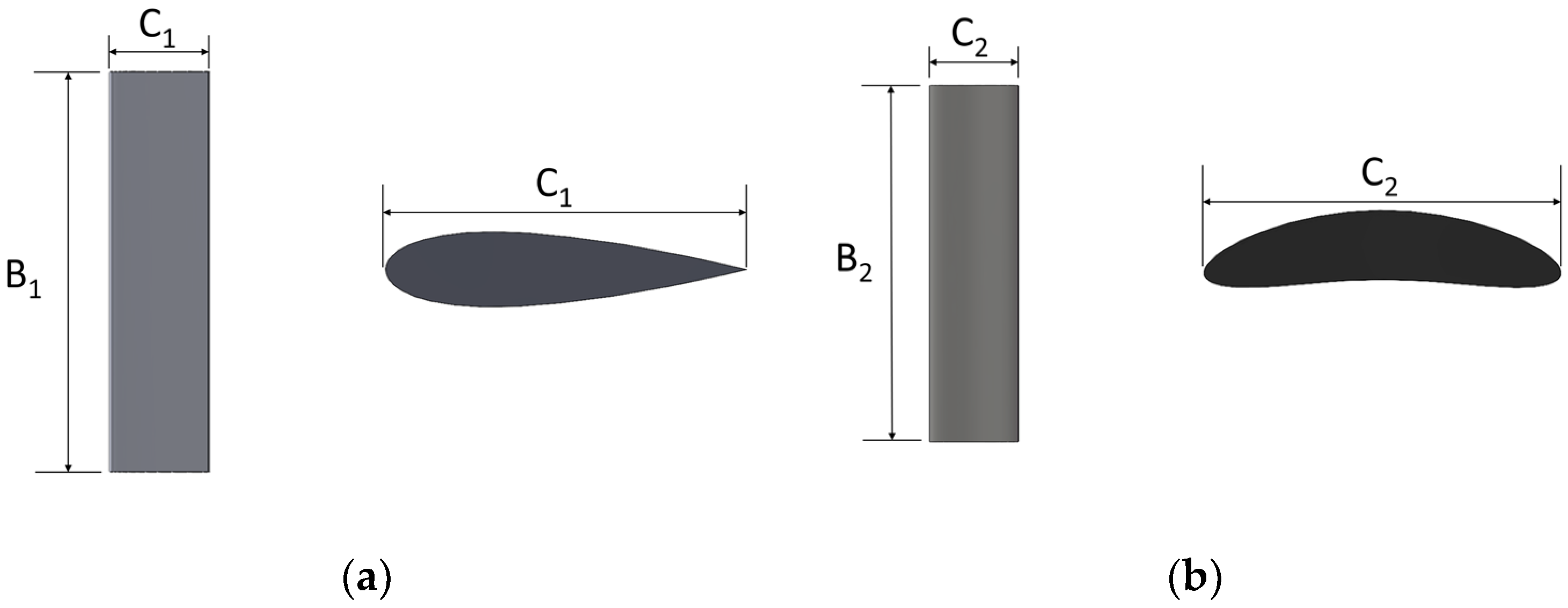
2.2. Definitions of Wing Sail Parameters
2.3. Development of the Simulation Model
3. Aerodynamic Analysis of the Wing Sail
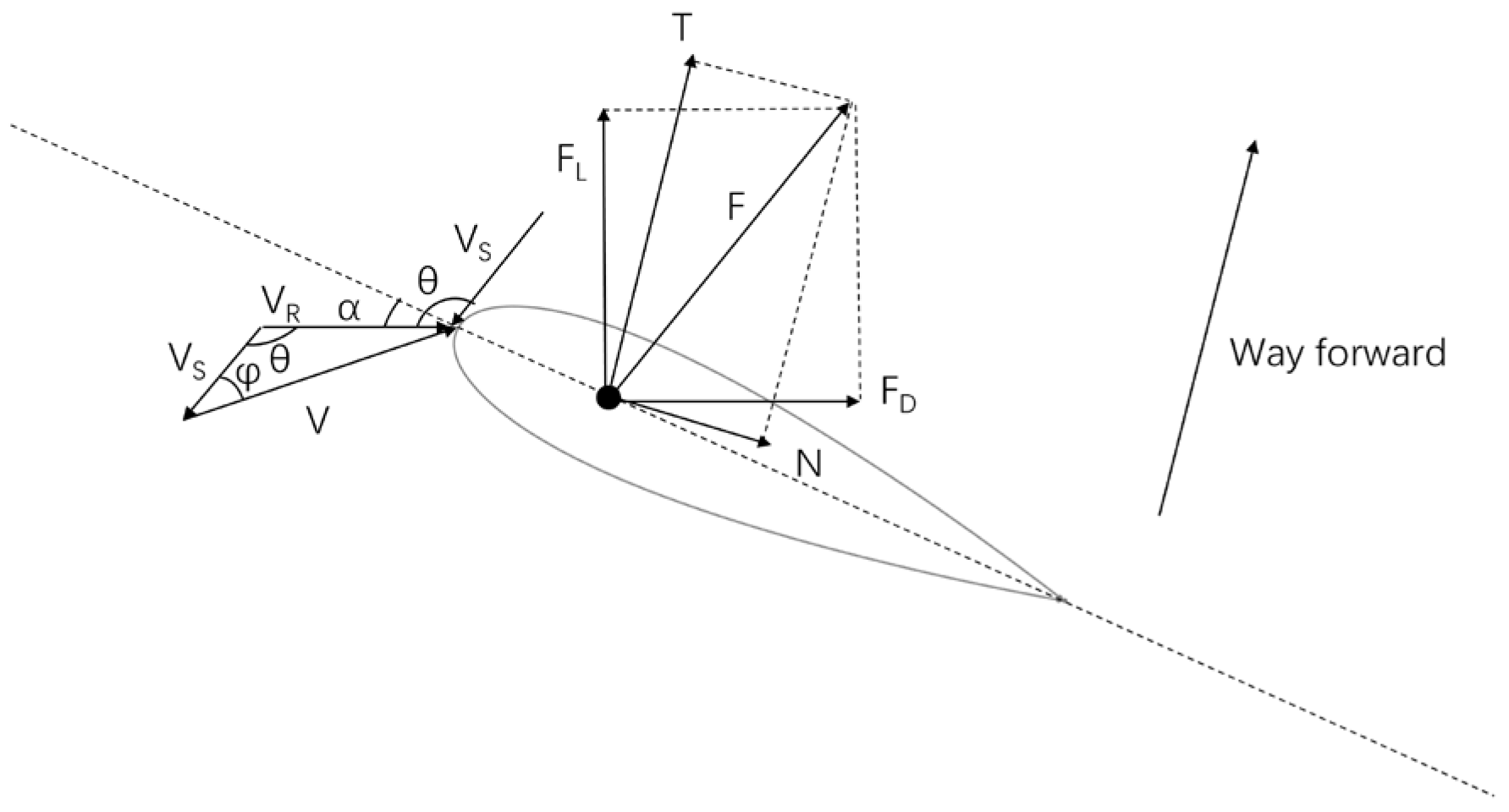
3.1. Principle of Forces Acting on the Wing Sail
3.2. Computational Method
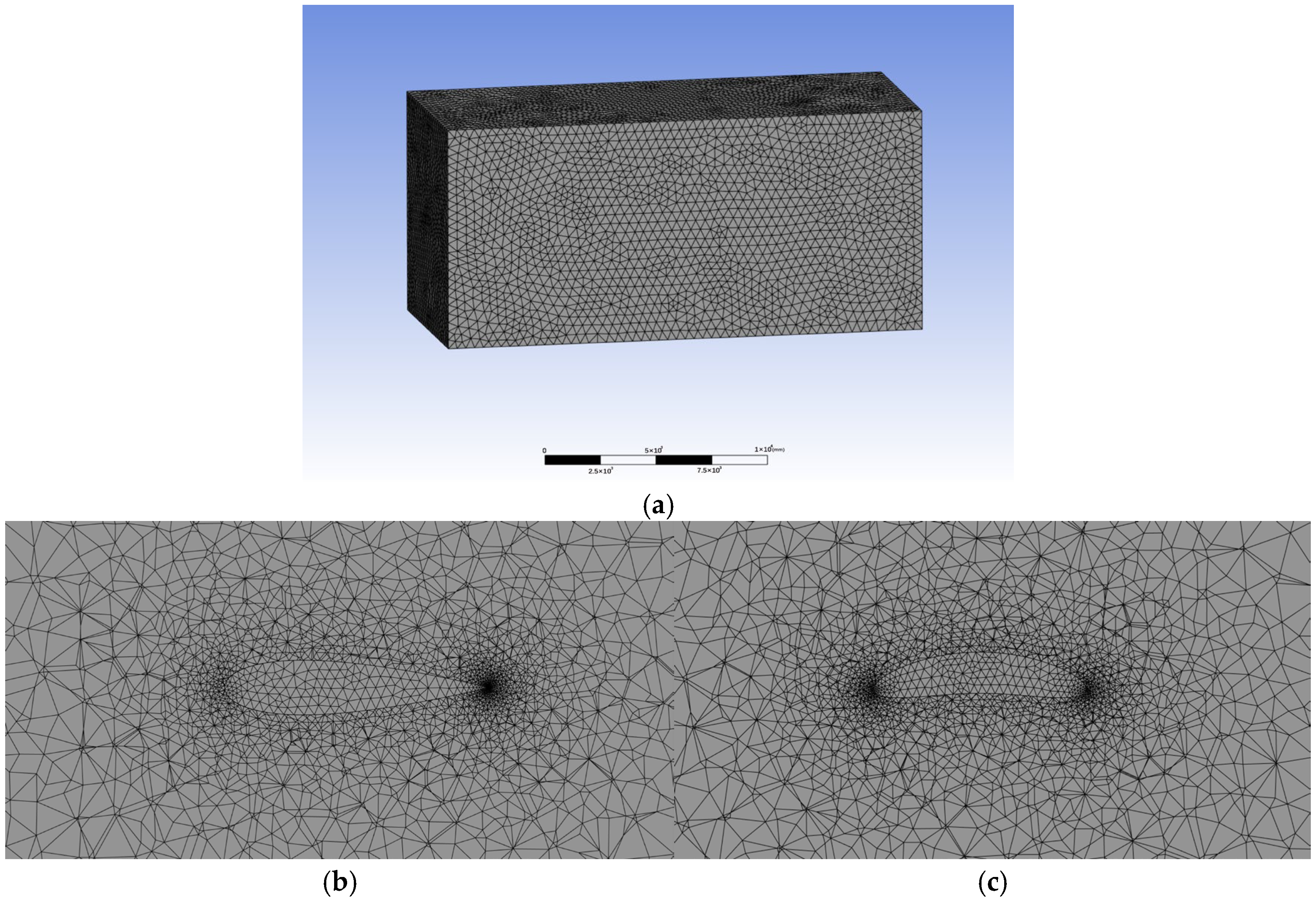
3.3. Meshing
4. Simulation and Analysis of the Rigid Wing Sail
4.1. Parameter Settings for Simulation
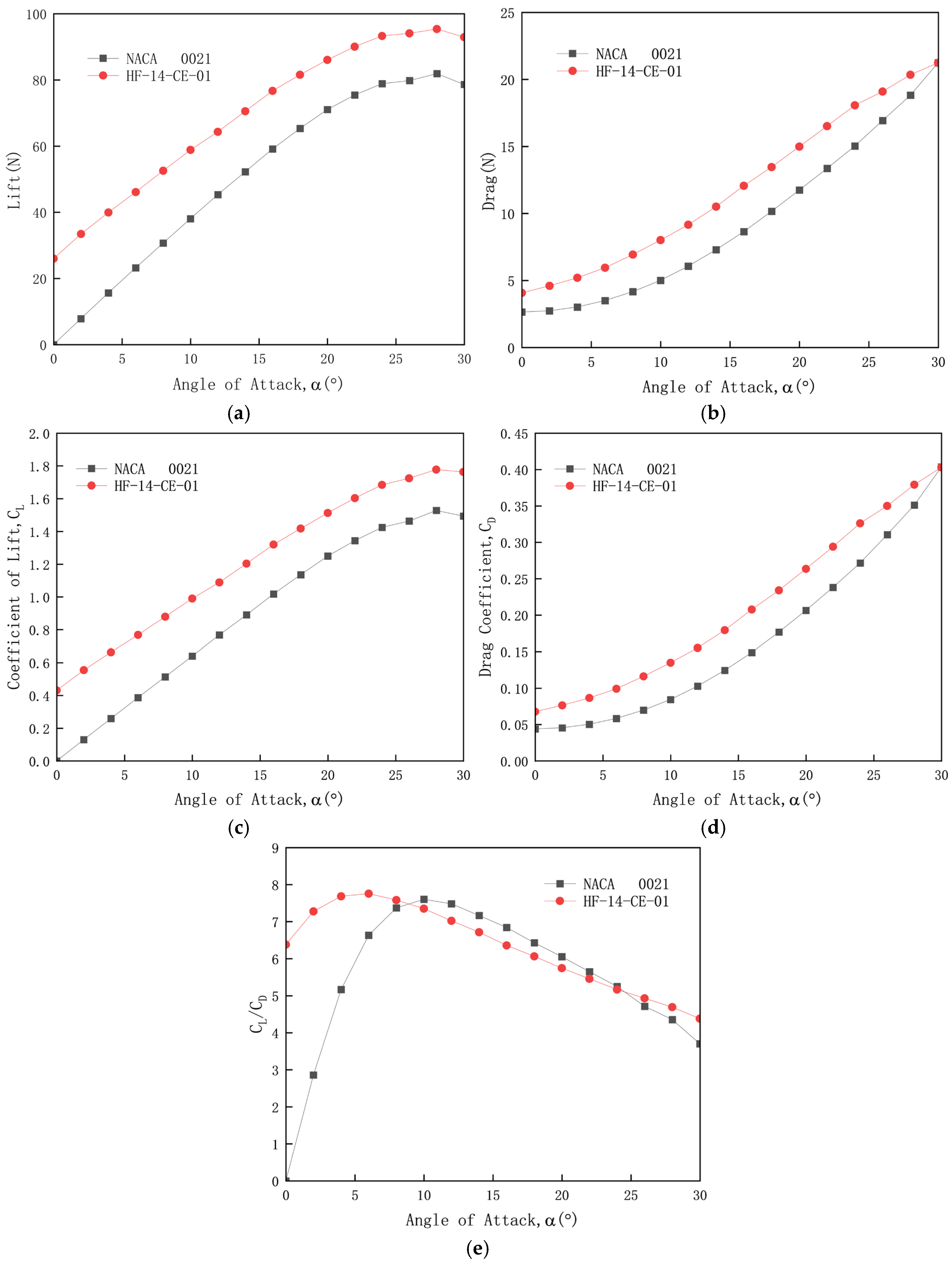
4.2. Comparative Analysis of Two Wing Sail Types
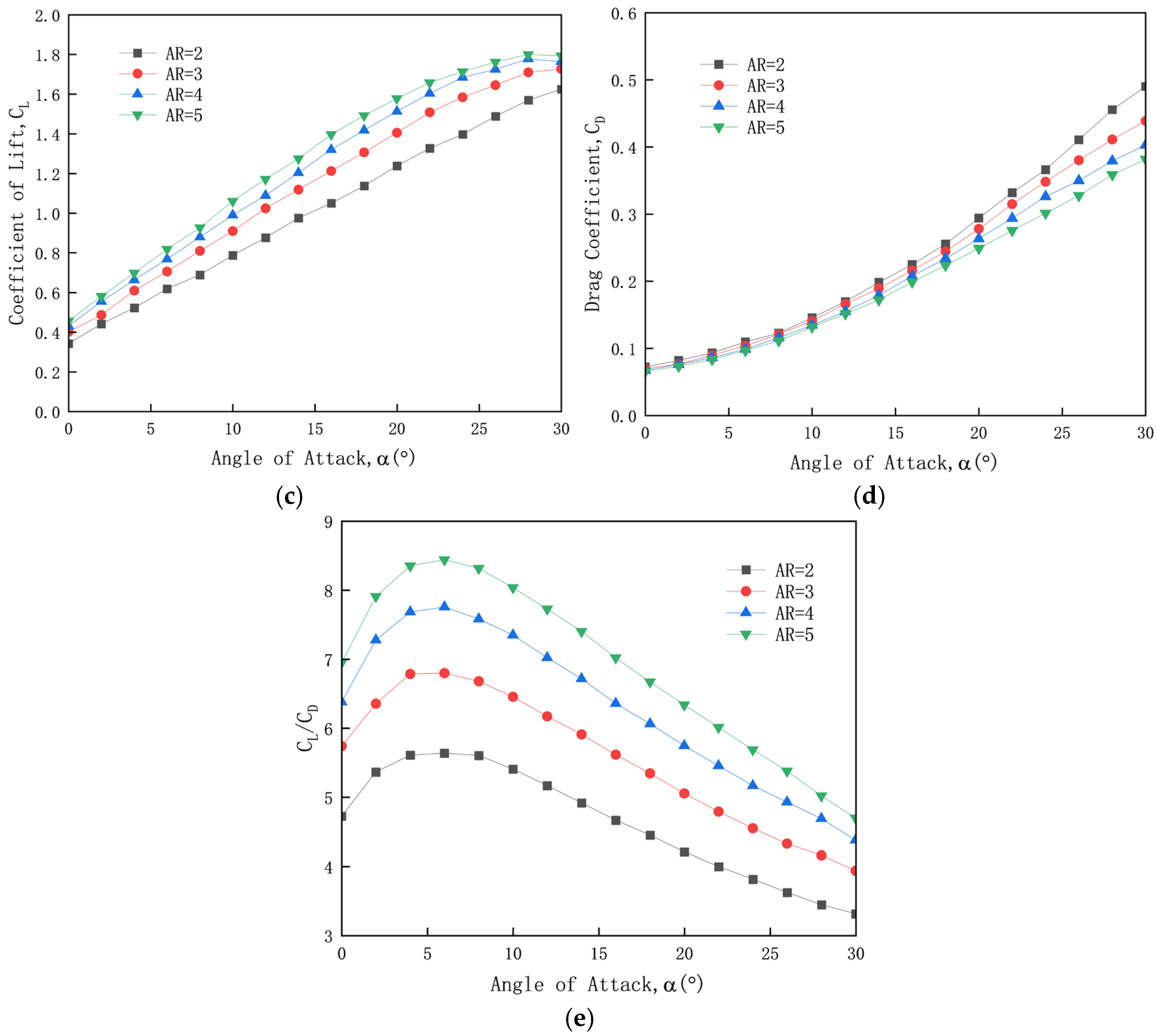
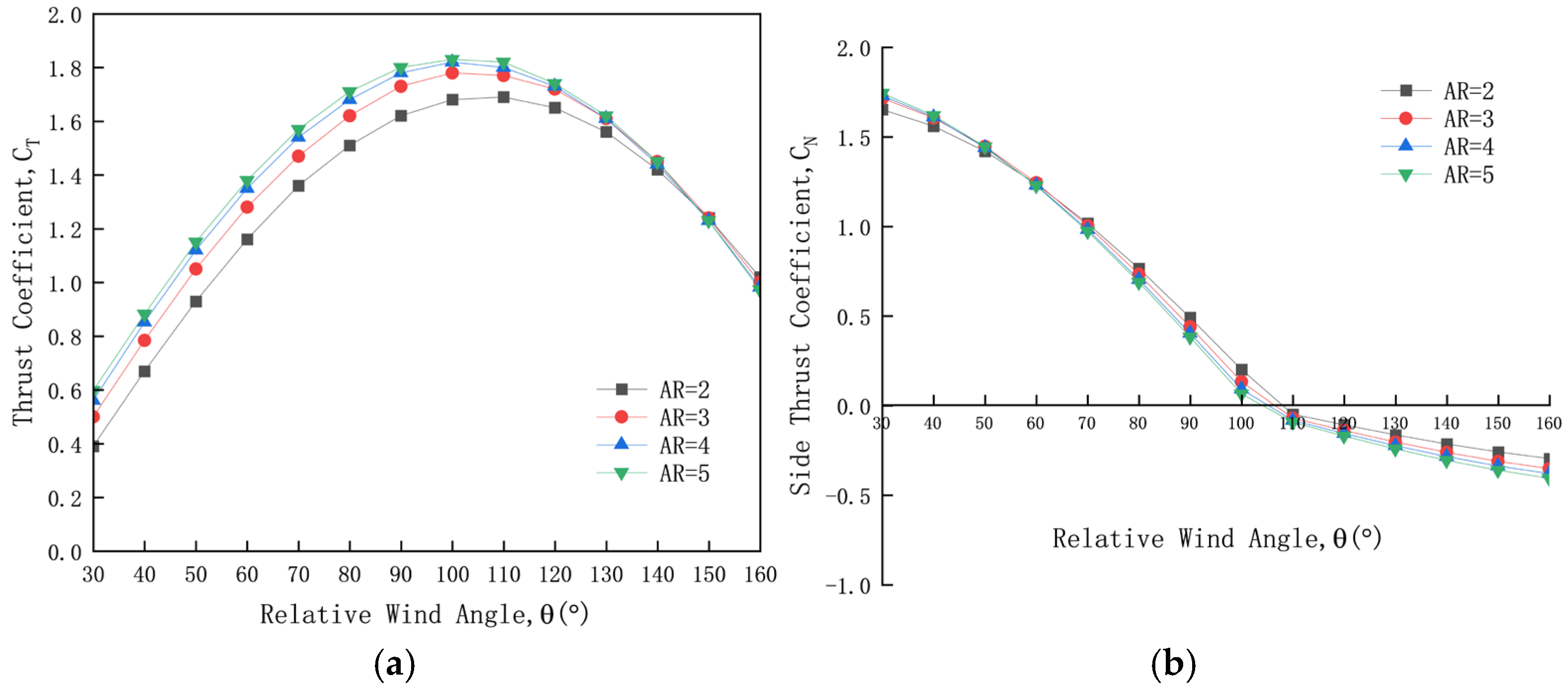
4.3. Impact of Aspect Ratio on the Aerodynamic Performance of Wing Sails
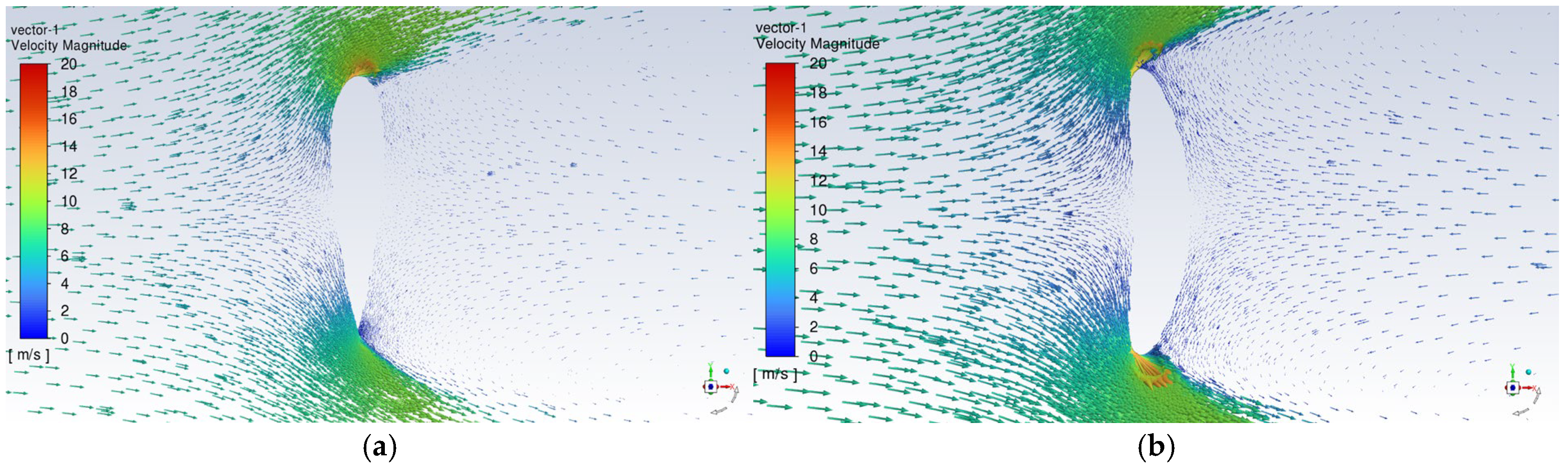
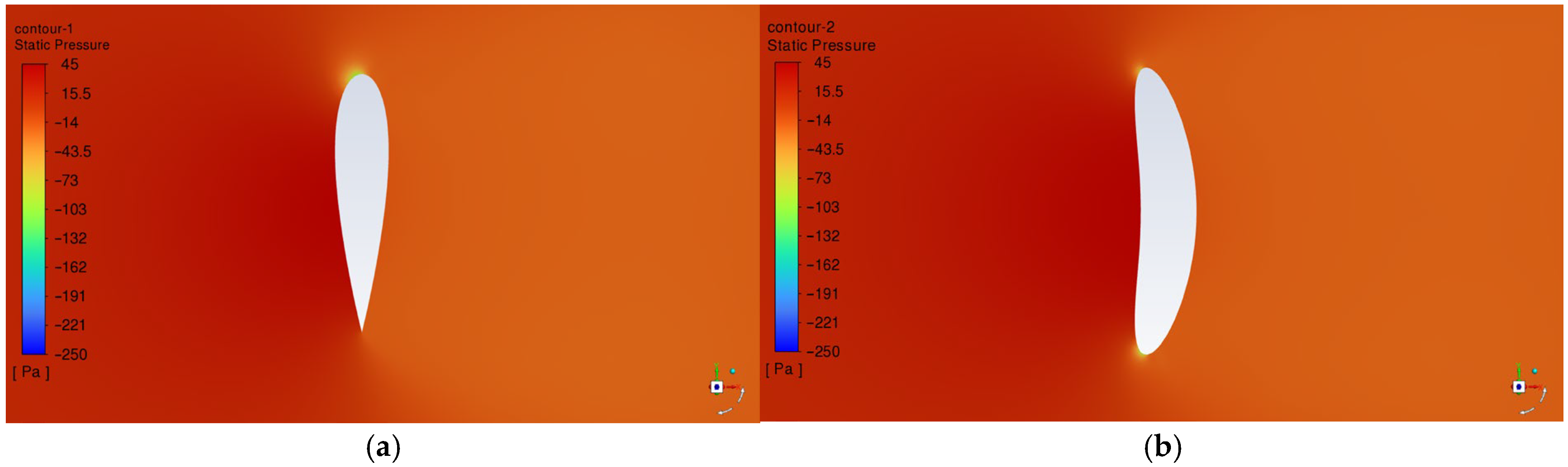
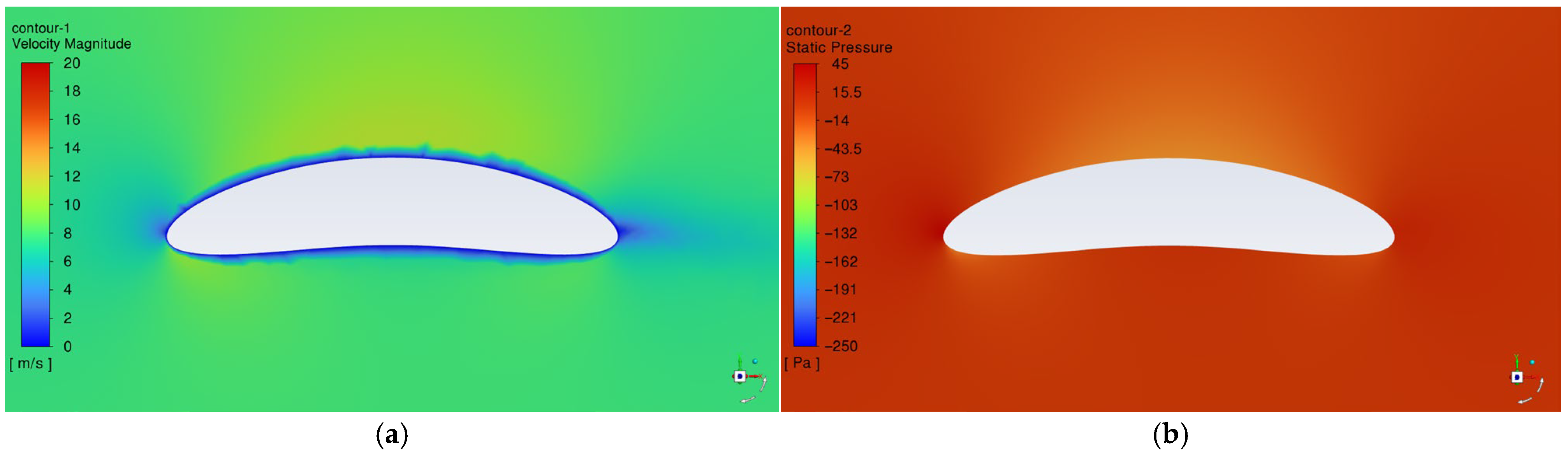
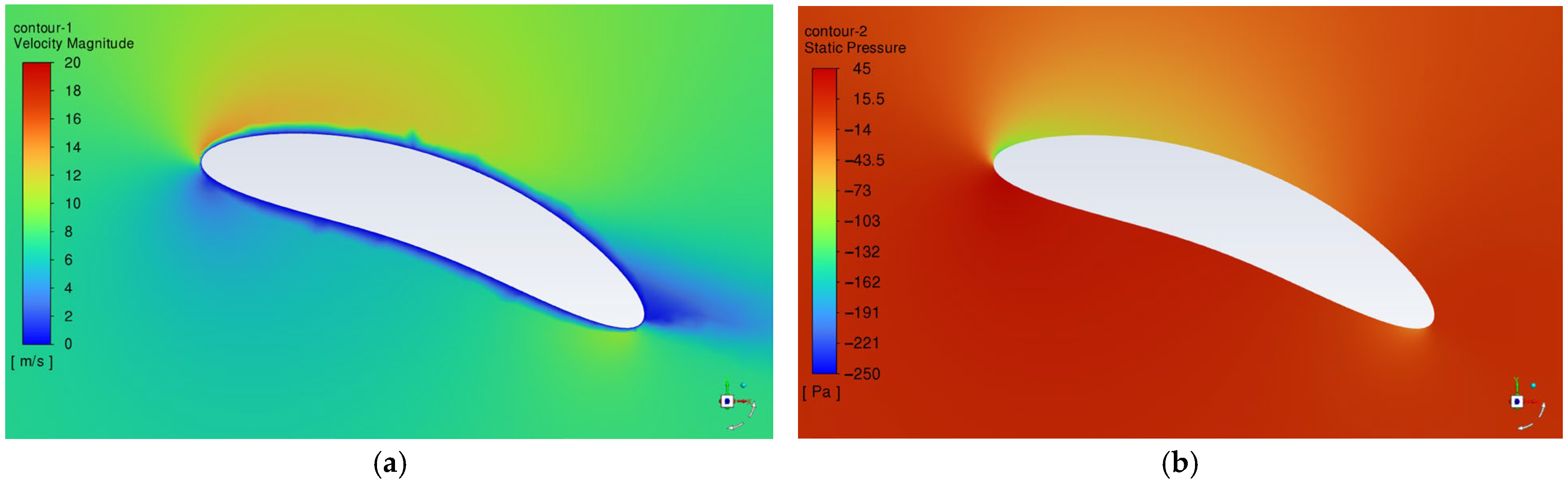
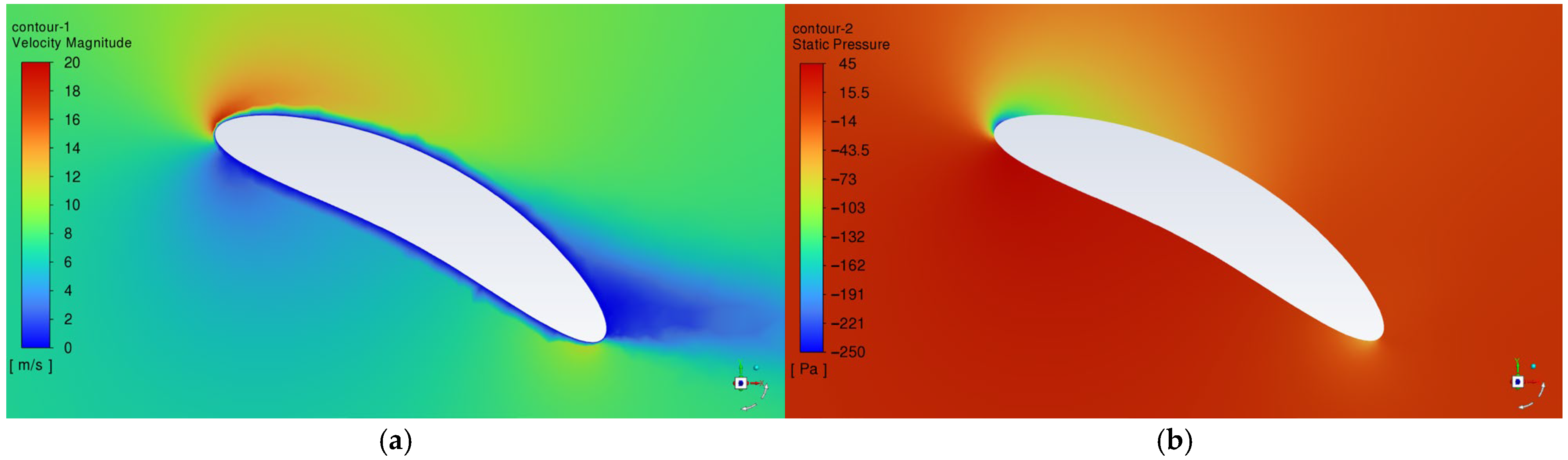
4.4. Speed and Static Pressure Distribution of the HF-14-CE-01 Wing Sail at Various Angles of Attack
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Unit | Meaning |
| C1 | mm | NACA 0021 chord length |
| C2 | mm | HF-14-CE-01 chord length |
| B1 | mm | NACA 0021 wingspan |
| B2 | mm | HF-14-CE-01 wingspan |
| AR | - | aspect ratio |
| P | N/m2 | pressure at a certain point in the fluid |
| ρ | kg/m3 | fluid density |
| v | m/s | flow velocity of the fluid at that point |
| g | m/s2 | acceleration due to gravity |
| h | m | height of the point |
| c | - | constant |
| V | m/s | true wind speed |
| VS | m/s | wind brought to the wing sail by the sailboat |
| VR | m/s | vector sum of V and VS |
| α | ° | angle of attack |
| φ | ° | wind direction angle |
| θ | ° | relative wind direction angle |
| FD | N | drag |
| FL | N | lift |
| F | N | resultant force |
| T | N | thrust |
| N | N | side thrust |
| CL | - | lift coefficient |
| CD | - | drag coefficient |
| CT | - | thrust coefficient |
| CN | - | side thrust coefficient |
| AS | m2 | projected area of the wing sail |
| - | direction in the three-dimensional coordinate system | |
| - | direction in the three-dimensional coordinate system | |
| m/s | direction in the three-dimensional coordinate system | |
| m/s | direction in the three-dimensional coordinate system | |
| Pa·s | dynamic viscosity of the fluid | |
| N | mass force | |
| m2/s2 | turbulent kinetic energy | |
| S−1 | specific dissipation rate | |
| Pk | - | generation term for turbulent kinetic energy |
| kg/(m·s) | eddy viscosity coefficient | |
| - | balance coefficient between turbulent kinetic energy and specific dissipation rate | |
| - | low Reynolds number correction factor | |
| CL/CD | - | lift/drag ratio |
References
- Qin, H.; Xiang, K.; Cao, X.; Qi, B.; Huang, X.; Wang, Y. Optimization design and experimental verification of unmanned sailboat sails. Phys. Fluids 2025, 37. [Google Scholar] [CrossRef]
- Sun, Z.; Feng, A.; Yu, J.; Zhao, W.; Huang, Y. Development of autonomous sailboat sails and future perspectives: A review. Renew. Sustain. Energy Rev. 2025, 207, 114918. [Google Scholar] [CrossRef]
- Chiodi, A.M.; Zhang, C.; Cokelet, E.D.; Yang, Q.; Mordy, C.W.; Gentemann, C.L.; Cross, J.N.; Lawrence-Slavas, N.; Meinig, C.; Steele, M.; et al. Exploring the Pacific Arctic seasonal ice zone with saildrone USVs. Front. Mar. Sci. 2021, 8, 640690. [Google Scholar] [CrossRef]
- Fer, I.; Peddie, D. Near surface oceanographic measurements using the SailBuoy. In Proceedings of the 2013 MTS/IEEE OCEANS-Bergen, Bergen, Norway, 10–13 June 2013; IEEE: New York, NY, USA, 2013; pp. 1–15. [Google Scholar]
- Ouchi, K.; Uzawa, K.; Kanai, A. Huge hard wing sails for the propulsor of next generation sailing vessel. In Proceedings of the Second International Symposium on Marine Propulsors, Hamburg, Germany, 17 June 2011. [Google Scholar]
- Viola, I.M.; Biancolini, M.E.; Sacher, M.; Cella, U. A CFD-based wing sail optimisation method coupled to a VPP. In Proceedings of the 5th High Performance Yacht Design Conference, Auckland, New Zealand, 9–11 March 2015. [Google Scholar]
- Atkinson, G.M. Analysis of lift, drag and CX polar graph for a 3D segment rigid sail using CFD analysis. J. Mar. Eng. Technol. 2019, 18, 36–45. [Google Scholar] [CrossRef]
- Chen, Z.; Cai, W.; Zeng, Q. A numerical study on the thrust and interaction of a three-sail wind-assisted propulsion system. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Hamburg, Germany, 5–10 June 2022; American Society of Mechanical Engineers: New York, NY, USA, 2022; Volume 85925, p. V007T08A056. [Google Scholar]
- Zhu, H.; Yao, H.-D.; Thies, F.; Ringsberg, J.W.; Ramne, B. Propulsive performance of a rigid wingsail with crescent-shaped profiles. Ocean. Eng. 2023, 285, 115349. [Google Scholar] [CrossRef]
- Ives, R.; Bassey, E.; Hamad, F.A. Investigation of the flow around an aircraft wing of section NACA 2412 utilising ANSYS fluent. INCAS Bull. 2018, 10, 95–104. [Google Scholar] [CrossRef]
- Guo, H.; Li, G.; Zou, Z. Numerical simulation of the flow around NACA0018 airfoil at high incidences by using RANS and DES methods. J. Mar. Sci. Eng. 2022, 10, 847. [Google Scholar] [CrossRef]
- Hewitt, P.G. Bernoulli’s principle. Sci. Teach. 2004, 71, 51. [Google Scholar]
- Tinoco, V.; Malheiro, B.; Silva, M.F. Design, modeling, and simulation of a wing sail land yacht. Appl. Sci. 2021, 11, 2760. [Google Scholar] [CrossRef]
- bin Mohamed Nadzri, M.A.A.; Ahmed, Y.A. Feasibility study of wing sail technology for commercial ship. J. Mek. 2021, 44, 26–45. [Google Scholar]
- Mi, B.; Yu, J. A New Grid-Slat Fusion Device to Improve the Take-Off and Landing Performance of Amphibious Seaplanes. J. Mar. Sci. Eng. 2024, 12, 2303. [Google Scholar] [CrossRef]
- Li, D.; Zhang, Y.; Li, P.; Dai, J.; Li, G. Aerodynamic performance of a new double-flap wing sail. Pol. Marit. Res. 2019, 26, 61–68. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, S.; Xie, T.; Zhang, Z.; Zhang, Y.; Lin, W.; Jiang, K.; Wang, T. Parameter Identification of an Unmanned Sailboat Combining Experiments and Numerical Analysis. J. Mar. Sci. Eng. 2024, 12, 2226. [Google Scholar] [CrossRef]
- Kleinstreuer, C. Modern Fluid Dynamics; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Kajishima, T.; Taira, K. Reynolds-averaged navier–stokes equations. In Computational Fluid Dynamics: Incompressible Turbulent Flows; Springer International Publishing: Cham, Germany, 2016; pp. 237–268. [Google Scholar]
- Łukaszewicz, G.; Kalita, P. Navier–stokes equations. Adv. Mech. Math. 2016, 34, 11–39. [Google Scholar]
- Matyushenko, A.A.; Garbaruk, A.V. Adjustment of the k-ω SST turbulence model for prediction of airfoil characteristics near stall. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2016; Volume 769, p. 012082. [Google Scholar]
- Zhao, M.; Wan, D.; Gao, Y. Comparative study of different turbulence models for cavitational flows around NACA0012 hydrofoil. J. Mar. Sci. Eng. 2021, 9, 742. [Google Scholar] [CrossRef]
- Liu, J.; Jiang, Z.; Du, L.; Lv, Z.; Cui, H.; Li, X.; Liang, G. Hydrodynamic and Vibroacoustic Simulation Analysis of the Main Float in an Acoustic Submerged Buoy System. J. Mar. Sci. Eng. 2025, 13, 1254. [Google Scholar] [CrossRef]
- Golshan, R.; Tejada-Martínez, A.E.; Juha, M.; Bazilevs, Y. Large-eddy simulation with near-wall modeling using weakly enforced no-slip boundary conditions. Comput. Fluids 2015, 118, 172–181. [Google Scholar] [CrossRef]
- Katz, A.; Sankaran, V. Mesh quality effects on the accuracy of CFD solutions on unstructured meshes. J. Comput. Phys. 2011, 230, 7670–7686. [Google Scholar] [CrossRef]
- Tipsuwan, Y.; Sanposh, P.; Techajaroonjit, N. Overview and control strategies of autonomous sailboats—A survey. Ocean. Eng. 2023, 281, 114879. [Google Scholar] [CrossRef]
- Kuang, L.; Li, H.; Su, X.; Song, X.; Wang, Z.; Zhang, Y.; Ma, W. Effect of chord length ratio on aerodynamic performance of two-element wing sail. Ocean. Eng. 2023, 287, 115946. [Google Scholar] [CrossRef]
- Li, Y.; Hu, J.; Zhao, Q.; Pan, Z.; Ma, Z. Hydrodynamic performance of autonomous underwater gliders with active twin undulatory wings of different aspect ratios. J. Mar. Sci. Eng. 2020, 8, 476. [Google Scholar] [CrossRef]
- Burgers, P. Dimensionally and Physically Proper Lift, Drag, and Thrust-Related Numbers as Figures of Merit: Normalized Lift, Drag, and Thrust, η L, η D, and η T. J. Aerosp. Eng. 2017, 30, 04016091. [Google Scholar] [CrossRef]
- Yasuda, A.; Taniguchi, T.; Katayama, T. Numerical Investigation of Aerodynamic Interactions between Rigid Sails Attached to Ship. J. Mar. Sci. Eng. 2024, 12, 1425. [Google Scholar] [CrossRef]
- Wu, C.H.; Chen, J.Z.; Lo, Y.L.; Fu, C.-L. Numerical and Experimental Studies on the Aerodynamics of NACA64 and DU40 Airfoils at Low Reynolds Numbers. Appl. Sci. 2023, 13, 1478. [Google Scholar] [CrossRef]



| Number of Meshes | Lift Coefficient CL | Drag Coefficient CD |
|---|---|---|
| 6 × 105 | 1.140 | 0.178 |
| 9 × 105 | 1.137 | 0.177 |
| 13.5 × 105 | 1.138 | 0.177 |
| Number of Meshes | Lift Coefficient CL | Drag Coefficient CD |
|---|---|---|
| 5.5 × 105 | 1.420 | 0.239 |
| 8.3 × 105 | 1.411 | 0.233 |
| 12.3 × 105 | 1.406 | 0.231 |
| Flow field velocity | 8 m/s |
| Angle of attack α | 0°, 2°, 4°, 6°, 8°, 10°, 12°, 14°, 16°, 18°, 20°, 22°, 24°, 26°, 28°, and 30° |
| Viscous equation | SST k-ω |
| Fluid domain material | Atmosphere |
| Calculated reference area | The projected area of the mainsail in the Y direction |
| Calculated reference length | 0.62 m |
| Solution method | Second-order SIMPLEC algorithm |
| Reporting definitions | Lift, drag, lift coefficient, and drag coefficient |
| Number of iterations | 103 |
| Angle of Attack | Lift Coefficient of the 3D Segment Rigid Sail | Drag Coefficient of the 3D Segment Rigid Sail | Lift Coefficient of the HF-14-CE-01 Wing Sail | Drag Coefficient of the HF-14-CE-01 Wing Sail |
|---|---|---|---|---|
| 0° | 0.45 | 0.06 | 0.31 | 0.06 |
| 10° | 1.02 | 0.13 | 0.71 | 0.16 |
| 20° | 1.55 | 0.26 | 1.05 | 0.34 |
| 30° | 1.80 | 0.37 | 1.34 | 0.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, C.; Tian, C.; Wang, H.; Ding, T. Design and Aerodynamic Analysis of Rigid Wing Sail of Unmanned Sailboat at Sea Based on CFD. Appl. Sci. 2025, 15, 9052. https://doi.org/10.3390/app15169052
Xu C, Tian C, Wang H, Ding T. Design and Aerodynamic Analysis of Rigid Wing Sail of Unmanned Sailboat at Sea Based on CFD. Applied Sciences. 2025; 15(16):9052. https://doi.org/10.3390/app15169052
Chicago/Turabian StyleXu, Changbin, Cunwei Tian, Huimin Wang, and Tianci Ding. 2025. "Design and Aerodynamic Analysis of Rigid Wing Sail of Unmanned Sailboat at Sea Based on CFD" Applied Sciences 15, no. 16: 9052. https://doi.org/10.3390/app15169052
APA StyleXu, C., Tian, C., Wang, H., & Ding, T. (2025). Design and Aerodynamic Analysis of Rigid Wing Sail of Unmanned Sailboat at Sea Based on CFD. Applied Sciences, 15(16), 9052. https://doi.org/10.3390/app15169052





