Machine Learning-Based Fracture Failure Analysis and Structural Optimization of Adhesive Joints
Abstract
1. Introduction
2. Analysis of the Tensile Fracture Failure of Single-Lap Joints
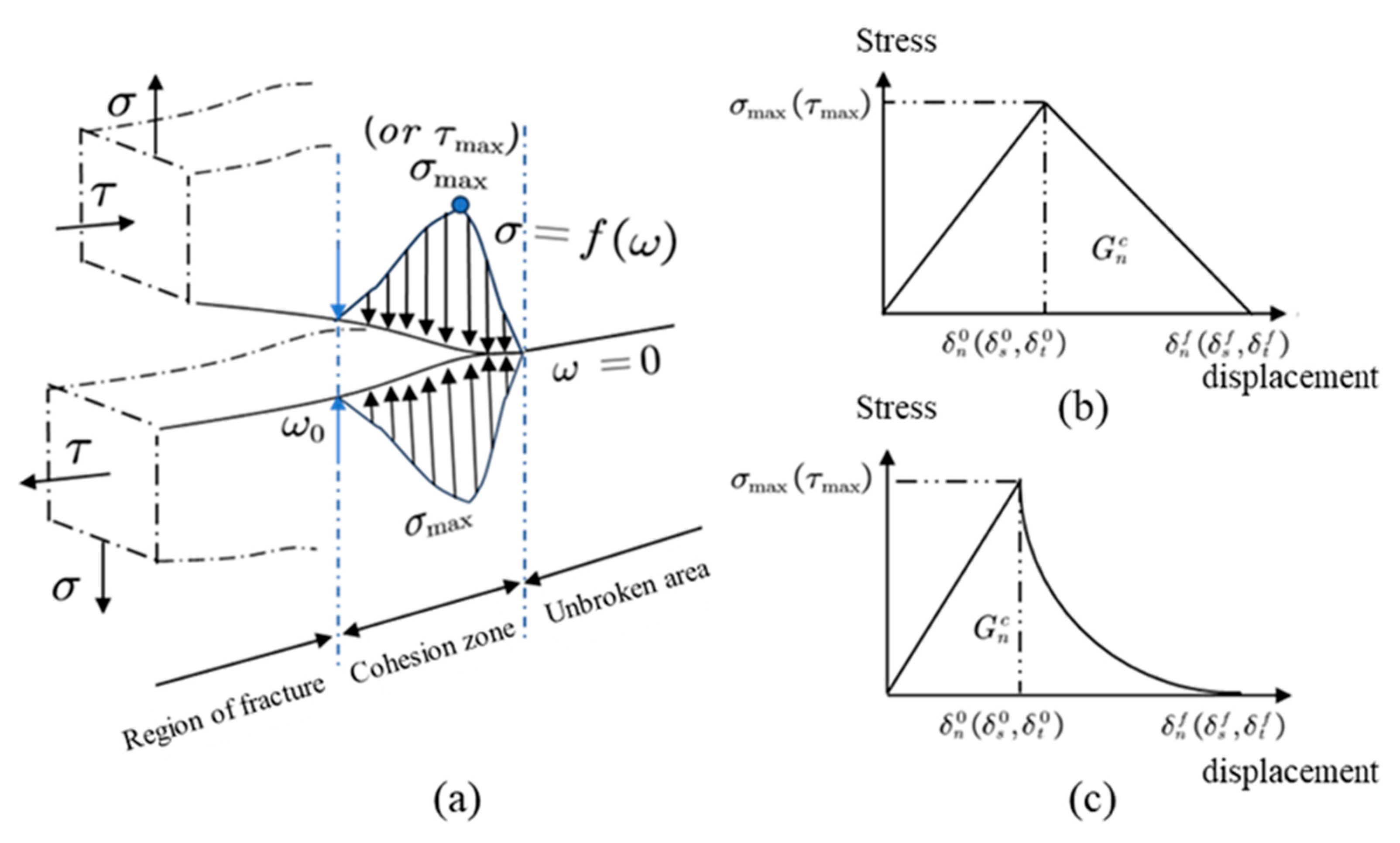
2.1. Adhesive Failure Analysis Based on the CZM Cohesion Model
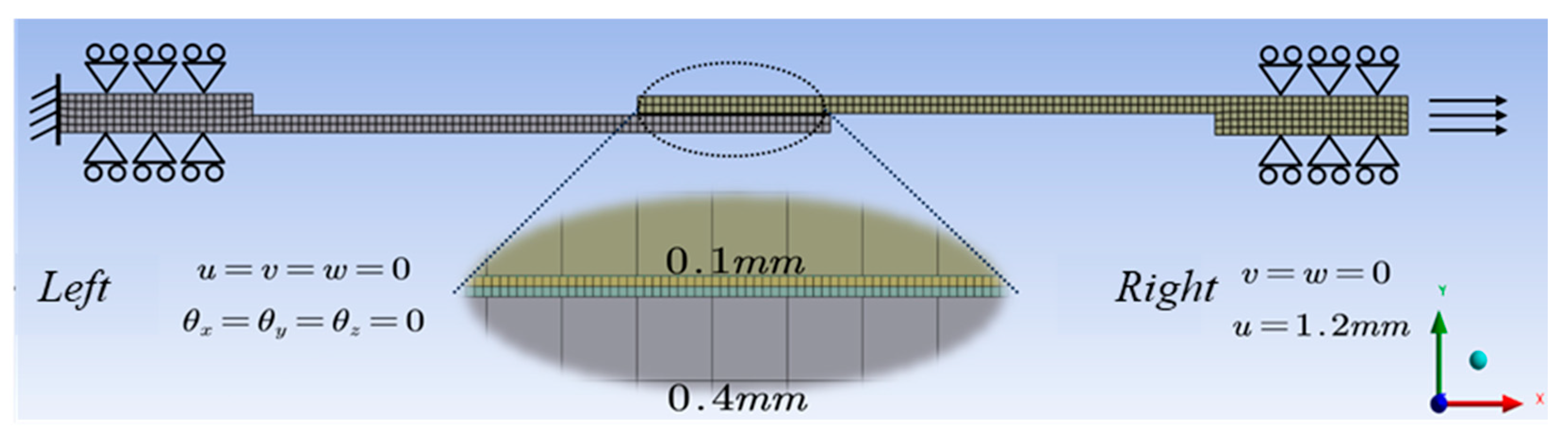
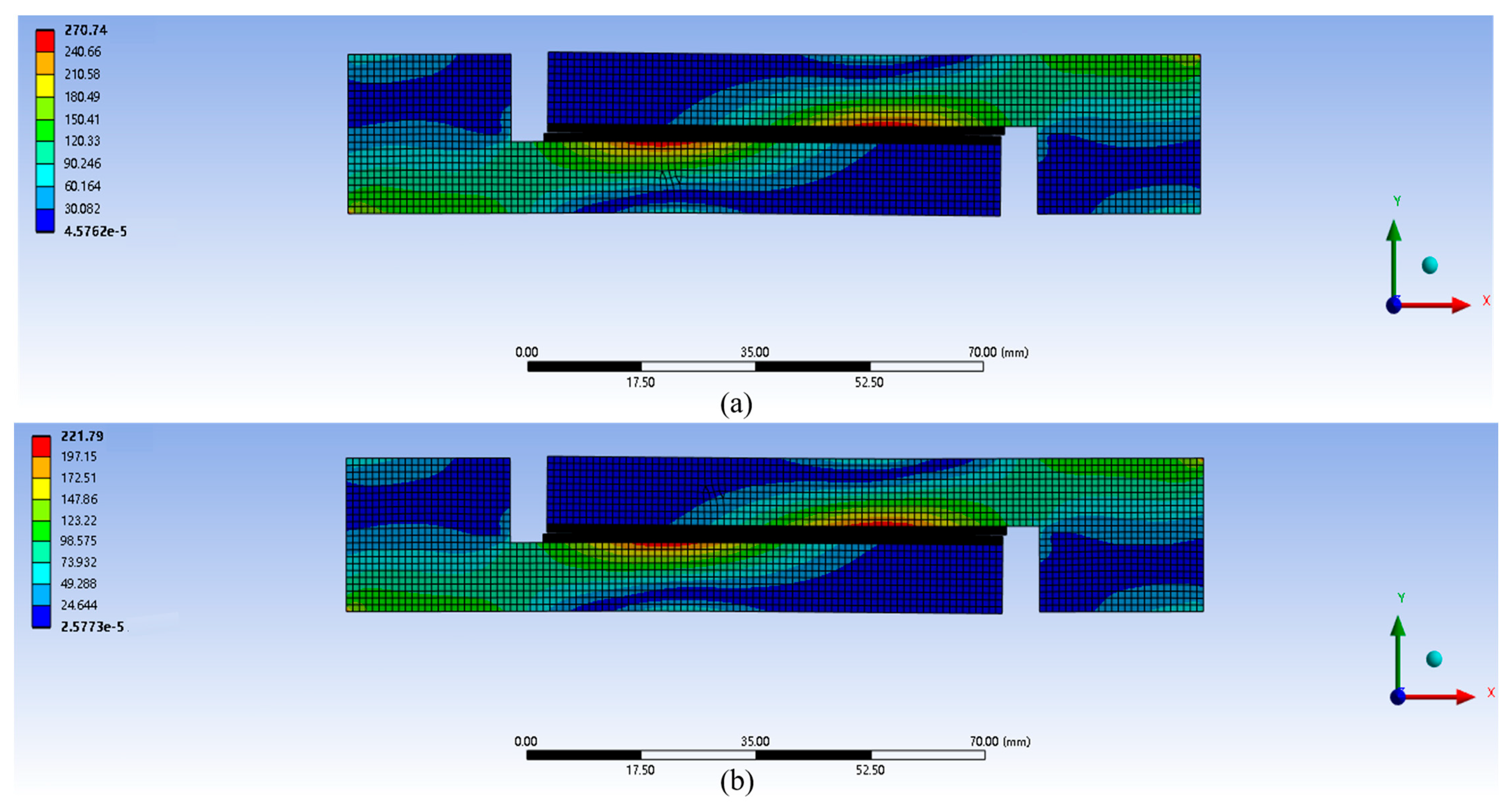
2.2. Finite Element Simulation of the Failure of Single-Lap Joint Due to Tensile Fracture
3. The Joint Strength Is Based on Research on Deep Neural Network Machine Learning
3.1. Data Sampling and Preprocessing
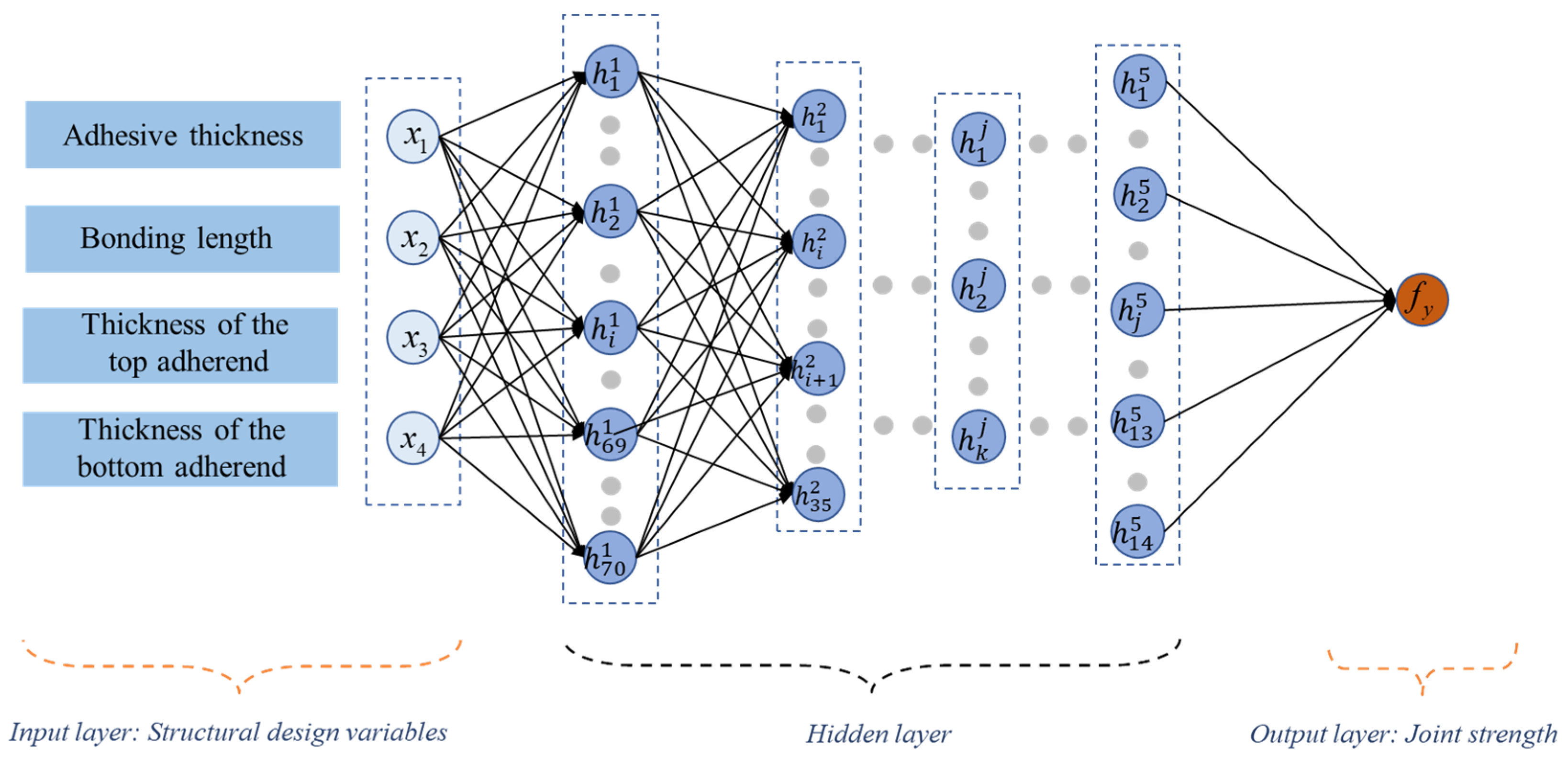
3.2. Construction and Training of Machine Learning Models
4. Single-Lap Joint Based on Structural Optimization Design of DNN Model and Genetic Algorithm
4.1. Single-Objective Optimization Research
4.2. Multi-Objective Optimization Research
5. Results and Discussion
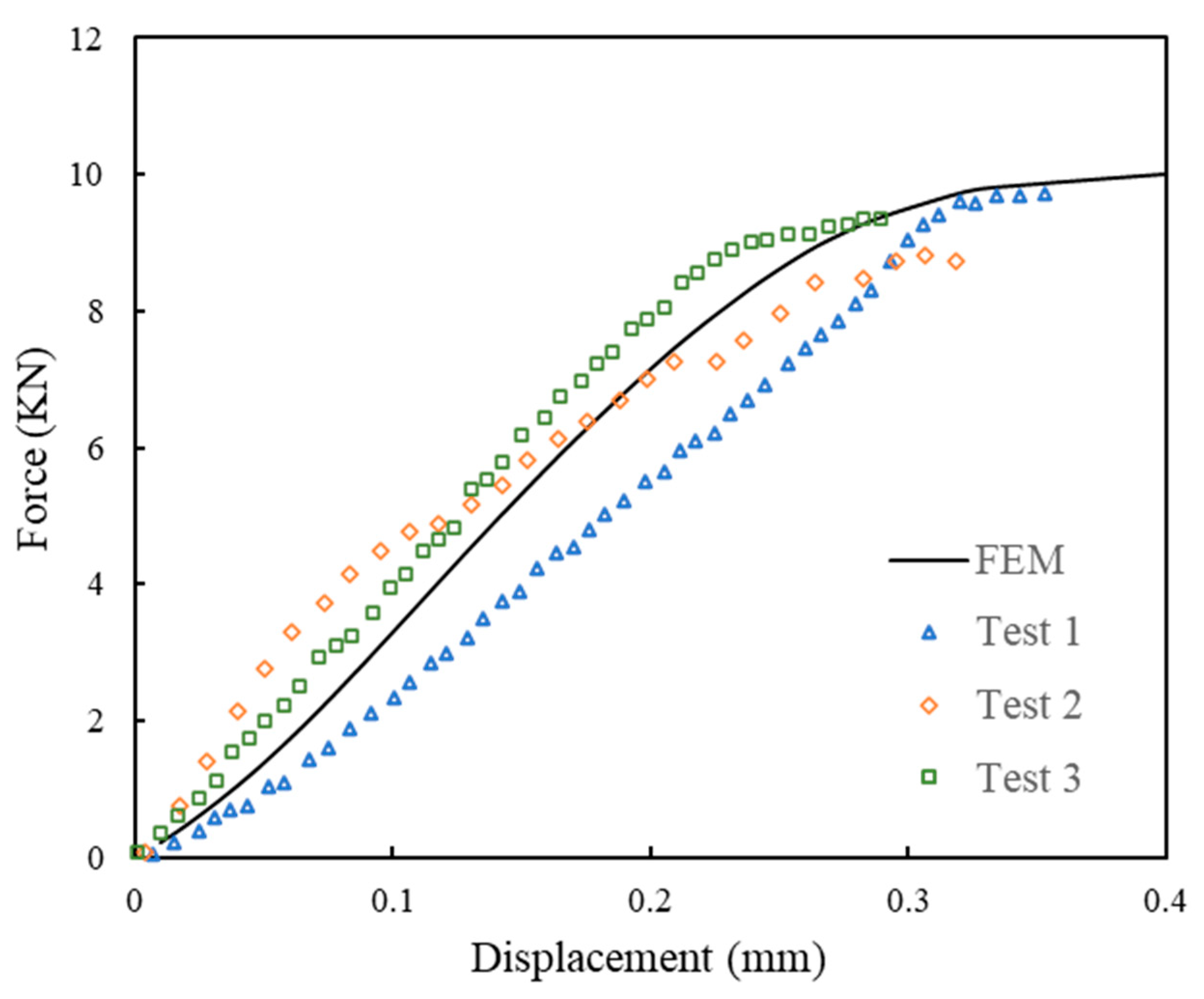
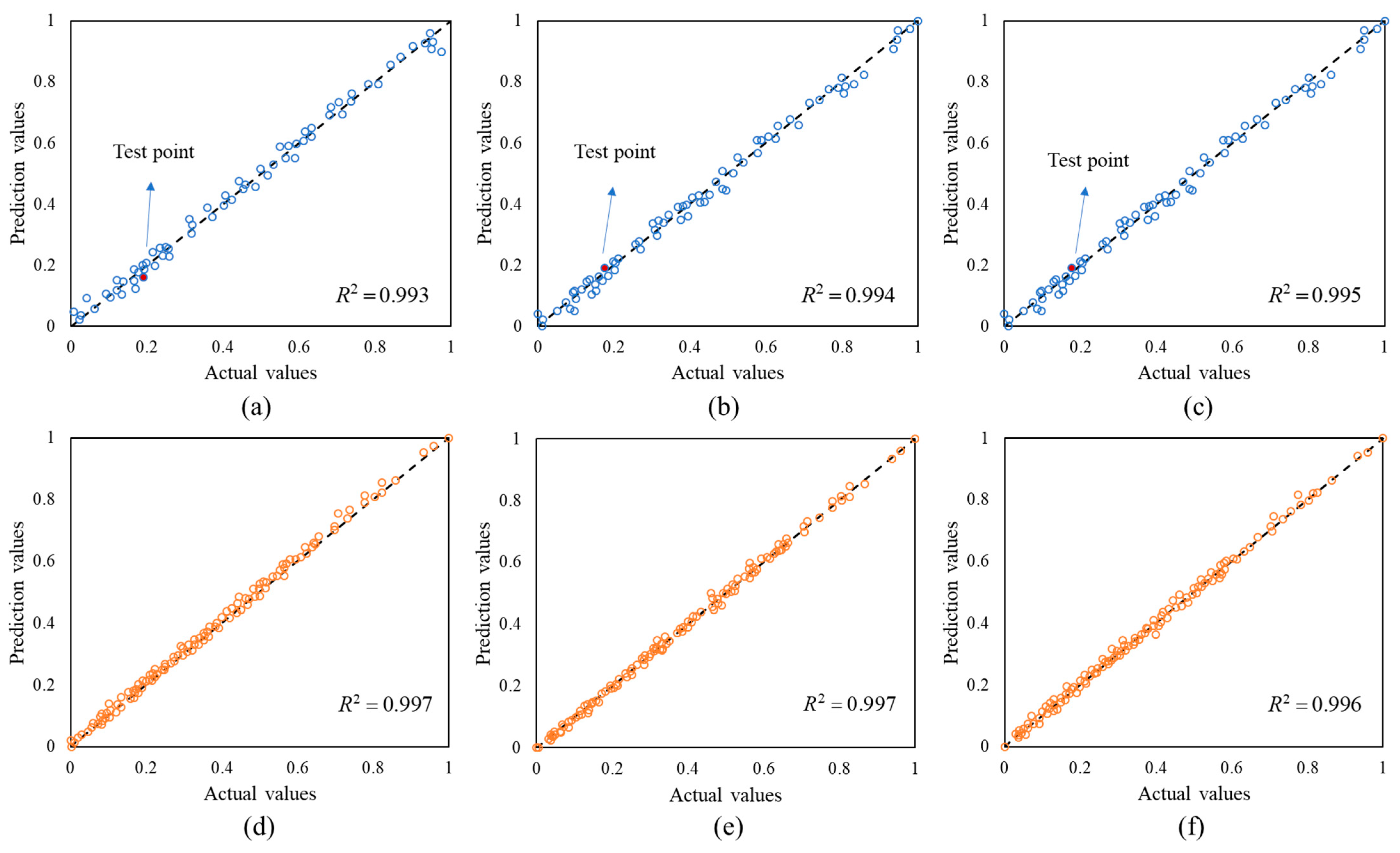
5.1. Verification of Finite Element Results and Accuracy Analysis of ML
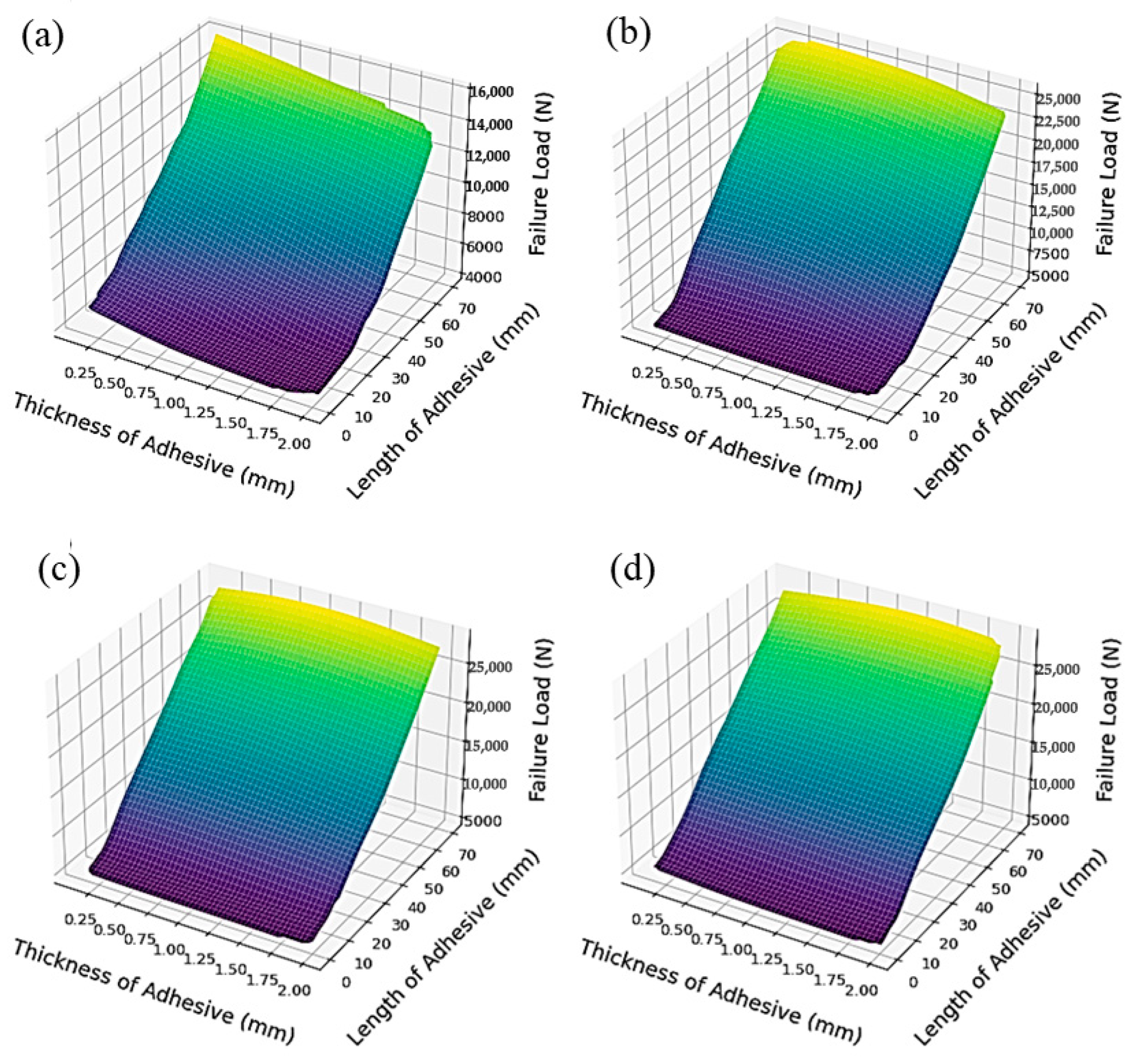
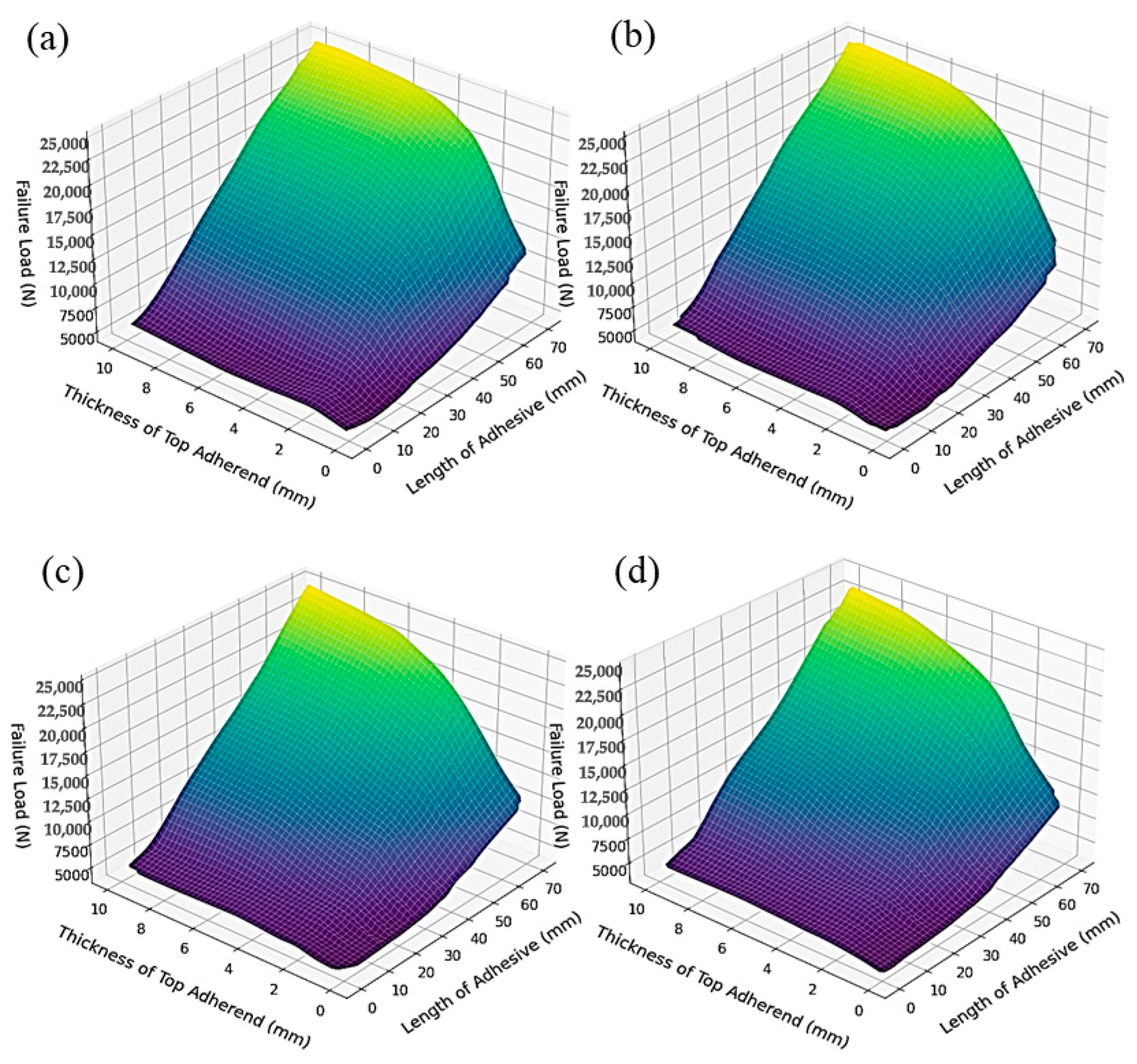
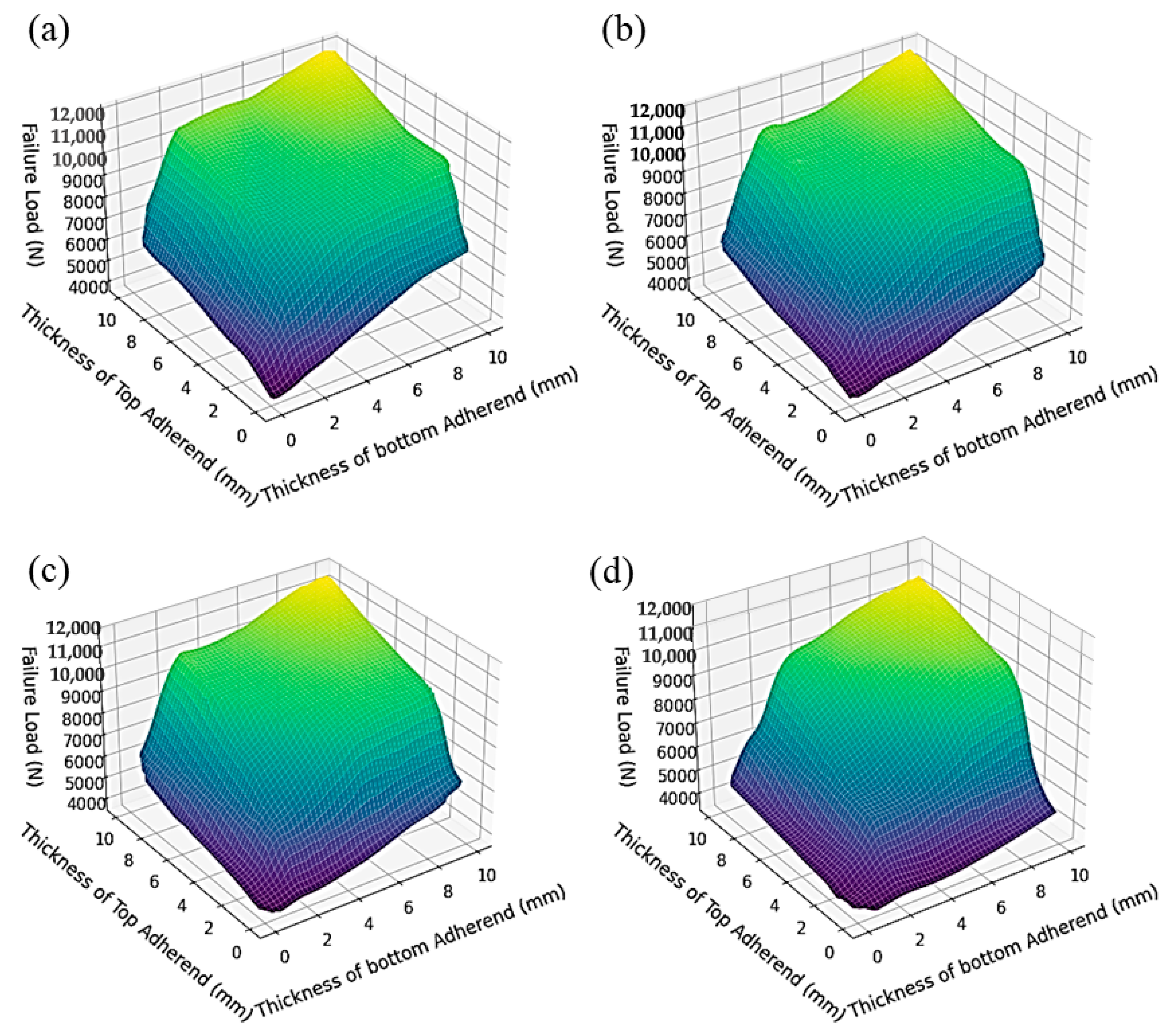
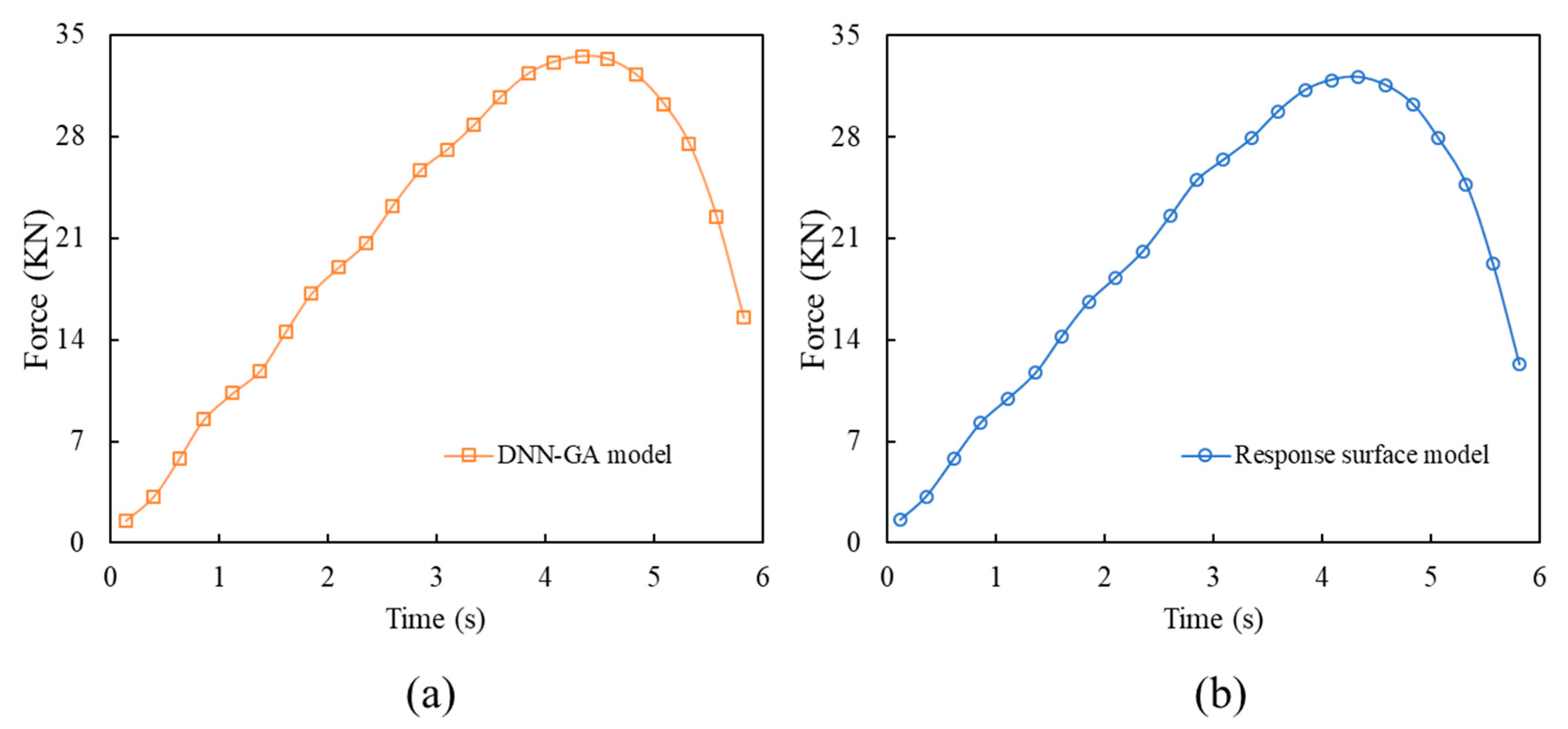
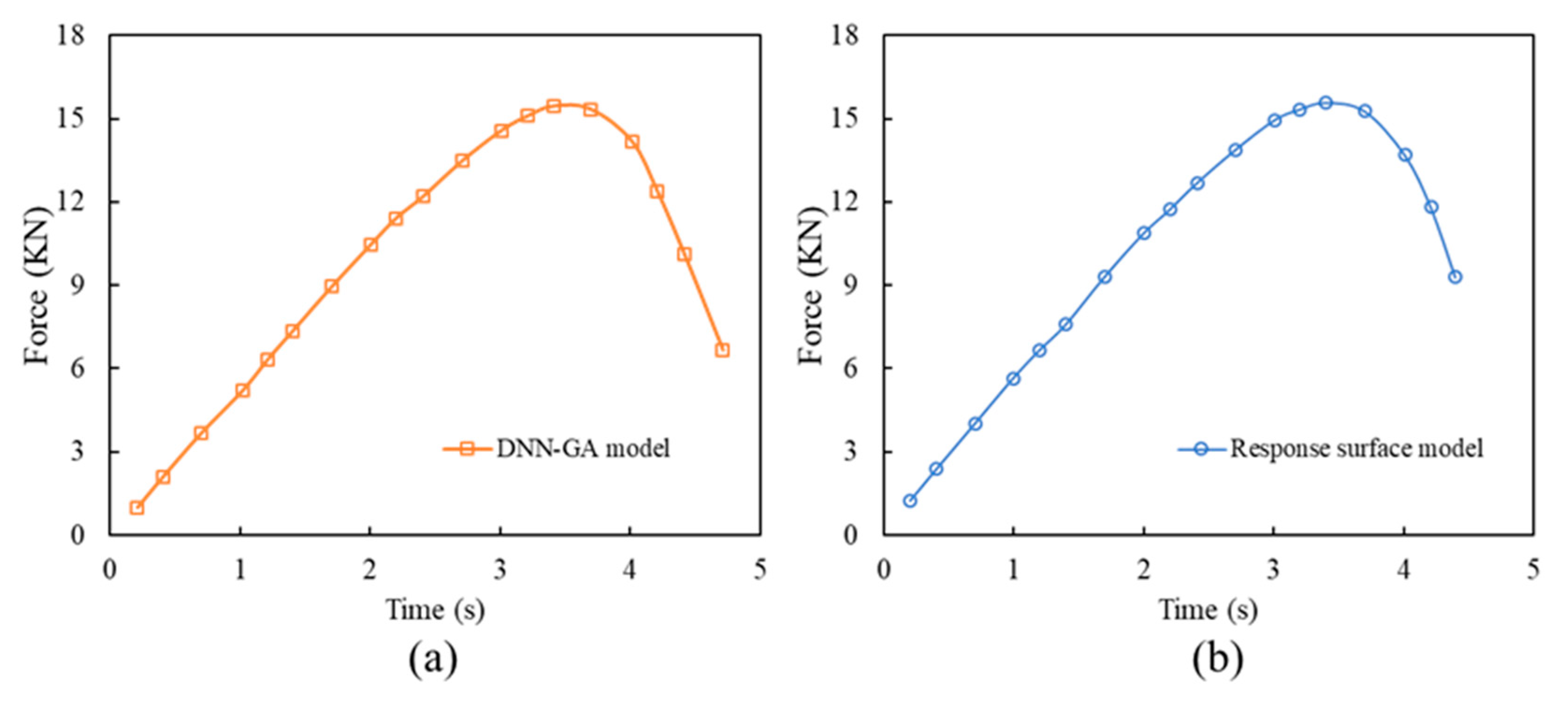
5.2. ML Response Surface Result Analysis
5.3. Analysis of Structural Optimization Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Beevers, A.; Steidler, S.M.; Durodola, J.; Coackley, M. Analysis of stiffness of adhesive joints in car bodies. J. Mater. Process. Technol. 2001, 118, 95–100. [Google Scholar] [CrossRef]
- Scarselli, G.; Corcione, C.; Nicassio, F.; Maffezzoli, A. Adhesive joints with improved mechanical properties for aerospace applications. Int. J. Adhes. Adhes. 2017, 75, 174–180. [Google Scholar] [CrossRef]
- Goland, M.; Reissner, E. The Stresses in Cemented Joints. J. Appl. Mech. 1944, 11, A17–A27. [Google Scholar] [CrossRef]
- Hart-Smith, L.J. Adhesive-Bonded Single-Lap Joints; Report NASA [74]CR-112236; NASA Langley Research Center: Hampton, VA, USA, 1973.
- Zhao, B.; Lu, Z.-H.; Lu, Y.-N. Closed-form solutions for elastic stress–strain analysis in unbalanced adhesive single-lap joints considering adherend deformations and bond thickness. Int. J. Adhes. Adhes. 2011, 31, 434–445. [Google Scholar] [CrossRef]
- Zhao, B.; Lu, Z.-H.; Lu, Y.-N. Two-dimensional analytical solution of elastic stresses for balanced single-lap joints—Variational method. Int. J. Adhes. Adhes. 2014, 49, 115–126. [Google Scholar] [CrossRef]
- Chen, D.; Cheng, S. An Analysis of Adhesive-Bonded Single-Lap Joints. J. Appl. Mech. 1983, 50, 109–115. [Google Scholar] [CrossRef]
- Cheng, S.; Chen, D.; Shi, Y. Analysis of Adhesive-Bonded Joints with Nonidentical Adherends. J. Eng. Mech. 1991, 117, 605–623. [Google Scholar] [CrossRef]
- Arenas, J.M.; Narbón, J.J.; Alía, C. Optimum adhesive thickness in structural adhesives joints using statistical techniques based on Weibull distribution. Int. J. Adhes. Adhes. 2010, 30, 160–165. [Google Scholar] [CrossRef]
- Öz, Ö.; Özer, H. An experimental investigation on the failure loads of the mono and bi-adhesive joints. J. Adhes. Sci. Technol. 2017, 31, 2251–2270. [Google Scholar] [CrossRef]
- Bendemra, H.; Compston, P.; Crothers, P.J. Optimisation study of tapered scarf and stepped-lap joints in composite repair patches. Compos. Struct. 2015, 130, 1–8. [Google Scholar] [CrossRef]
- Sülü, İ.Y. Mechanical behavior of composite parts adhesively jointed with the insert double-lap joint under tensile load. Weld. World 2018, 62, 403–413. [Google Scholar] [CrossRef]
- Gong, B.; Li, H. A couple Voronoi-RBSM modeling strategy for RC structures. Struct. Eng. Mech. 2024, 91, 239–250. [Google Scholar]
- Xu, H.; Cui, X.; Liu, Y.; Xu, Y.; Ling, X.; Li, Y. Effect of Fastening System Failure on the Micromechanical Properties of Railway Ballast Bed. KSCE J. Civ. Eng. 2025, 29, 100233. [Google Scholar] [CrossRef]
- Cao, L.; Lu, R.; Dou, Z.; Zheng, M.; Han, X.; Hao, Y.; Zhang, L.; Zhang, J.; Liu, B.; Li, X. Understanding the influence of high-strength submicron precipitate on the fracture performance of additively-manufactured aluminum alloy. Int. J. Plast. 2025, 188, 104306. [Google Scholar] [CrossRef]
- Gao, J.; Wang, S.; Zhang, C.; Chen, R.; Zhang, Y.; Zhang, Y.; Mu, R. Energy-based multi-axial fatigue prediction for tubular structures under non-proportional loading. Int. J. Fatigue 2025, 197, 108897. [Google Scholar] [CrossRef]
- Gu, Z.; Liu, Y.; Hughes, D.J.; Ye, J.; Hou, X. A parametric study of adhesive bonded joints with composite material using black-box and grey-box machine learning methods: Deep neuron networks and genetic programming. Compos. Part B Eng. 2021, 217, 108894. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Z.; Jing, X.; Yang, Z.; Xu, W. Optimization of multistage femtosecond laser drilling process using machine learning coupled with molecular dynamics. Opt. Laser Technol. 2022, 156, 108442. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, S.; Zhang, Y.; Wang, C.; Zhang, S.; Yang, Z.; Xu, W. Optimization of low-power femtosecond laser trepan drilling by machine learning and a high-throughput multi-objective genetic algorithm. Opt. Laser Technol. 2022, 148, 107688. [Google Scholar] [CrossRef]
- Mashrei, M.A.; Seracino, R.; Rahman, M.S. Application of artificial neural networks to predict the bond strength of FRP-to-concrete joints. Constr. Build. Mater. 2013, 40, 812–821. [Google Scholar] [CrossRef]
- Rangaswamy, H.; Sogalad, I.; Basavarajappa, S.; Acharya, S.; Patel, G.C.M. Experimental analysis and prediction of strength of adhesive-bonded single-lap composite joints: Taguchi and artificial neural network approaches. SN Appl. Sci. 2020, 2, 1055. [Google Scholar] [CrossRef]
- Wang, Z.; Li, J.; Yuan, Y.; Zhang, S.; Hu, W.; Ma, J.; Tan, J. Digital-twin-enabled online wrinkling monitoring of metal tube bending manufacturing: A multi-fidelity approach using forward-convolution-GAN. Appl. Soft Comput. 2025, 171, 112684. [Google Scholar] [CrossRef]
- Cevik, A.; Arslan, M.H.; Köroğlu, M.A. Genetic-programming-based modeling of RC beam torsional strength. KSCE J. Civ. Eng. 2010, 14, 371–384. [Google Scholar] [CrossRef]
- Pala, M. Genetic programming-based formulation for distortional buckling stress of cold-formed steel members. J. Constr. Steel Res. 2008, 64, 1495–1504. [Google Scholar] [CrossRef]
- Ravandi, E.G.; Rahmannejad, R.; Monfared, A.E.F.; Ravandi, E.G. Application of numerical modeling and genetic programming to estimate rock mass modulus of deformation. Int. J. Min. Sci. Technol. 2013, 23, 733–737. [Google Scholar] [CrossRef]
- Feng, X.; Zhao, J.; Kita, E. Genetic Algorithm-based Optimization of Deep Neural Network Ensemble. Rev. Socionetwork Strateg. 2021, 15, 27–47. [Google Scholar] [CrossRef]
- Al-Mosawe, A.; Kalfat, R.; Al-Mahaidi, R. Strength of Cfrp-steel double strap joints under impact loads using genetic programming. Compos. Struct. 2017, 160, 1205–1211. [Google Scholar] [CrossRef]
- Elices, M.; Guinea, G.V.; Gómez, J.; Planas, J. The cohesive zone model: Advantages, limitations and challenges. Eng. Fract. Mech. 2002, 69, 137–163. [Google Scholar] [CrossRef]
- Needleman, A. An analysis of decohesion along an imperfect interface. Int. J. Fract. 1990, 42, 21–40. [Google Scholar] [CrossRef]
- Reedy, E.D.; Guess, T.R. Comparison of butt tensile strength data with interface corner stress intensity factor prediction. Int. J. Solids Struct. 1993, 30, 2929–2936. [Google Scholar] [CrossRef]
- Irwin, G.R.; Paris, P.C. Chapter 1—Fundamental Aspects of Crack Growth and Fracture. In Engineering Fundamentals and Environmental Effects; Liebowitz, H., Ed.; Academic Press: Cambridge, MA, USA, 1971; pp. 1–46. [Google Scholar]
- Kanani, A.Y.; Wang, X.-E.; Hou, X.; Rennie, A.E.W.; Ye, J. Analysis of failure mechanisms of adhesive joints modified by a novel additive manufacturing-assisted method. Eng. Struct. 2023, 277, 115428. [Google Scholar] [CrossRef]
- Olsson Anders, M.J.; Sandberg Göran, E. Latin Hypercube Sampling for Stochastic Finite Element Analysis. J. Eng. Mech. 2002, 128, 121–125. [Google Scholar] [CrossRef]

| Parametric Variables | Lower Limit | Upper Limit |
|---|---|---|
| Bonding length, La (mm) | 10 | 70 |
| Thickness of the top adherent, T1 (mm) | 1 | 10 |
| Thickness of the bottom adherent, T2 (mm) | 1 | 10 |
| Adhesive thickness, t (mm) | 0.1 | 4 |
| Materials | Young Modulus (GPa) | Poisson’s Ratio |
|---|---|---|
| Al 6082T6 | 70.00 | 0.30 |
| Araldite 2015 | 1.85 | 0.33 |
| Adhesive Name | Tensile Breaking Strength | Shear Failure Strength | Tensile Toughness | Shear Toughness |
|---|---|---|---|---|
| Araldite 2015 | 21.63 (MPa) | 17.90 (MPa) | 0.43 (J/mm2) | 4.7 (J/mm2) |
| Model | GA Optimization | Response Surface Optimization |
|---|---|---|
| Adhesive thickness (mm) | 1.12505 | 1.25978 |
| Bonding length (mm) | 69.9685 | 70 |
| Thickness of the top adherent (mm) | 9.85702 | 10 |
| Thickness of the bottom adherent (mm) | 9.88717 | 10 |
| Adhesive thickness (mm) | 1.12505 | 1.25978 |
| Model | GA Optimization | Response Surface Optimization |
|---|---|---|
| Predicted value (N) | 33,103 | 33,564 |
| Verification value (N) | 33,603 | 32,332 |
| Error | 1.49% | 3.81% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Gu, Z.; Sun, M.; Guo, C.; Ding, X. Machine Learning-Based Fracture Failure Analysis and Structural Optimization of Adhesive Joints. Appl. Sci. 2025, 15, 9041. https://doi.org/10.3390/app15169041
Liu Y, Gu Z, Sun M, Guo C, Ding X. Machine Learning-Based Fracture Failure Analysis and Structural Optimization of Adhesive Joints. Applied Sciences. 2025; 15(16):9041. https://doi.org/10.3390/app15169041
Chicago/Turabian StyleLiu, Yalong, Zewen Gu, Mingze Sun, Claire Guo, and Xiaoxuan Ding. 2025. "Machine Learning-Based Fracture Failure Analysis and Structural Optimization of Adhesive Joints" Applied Sciences 15, no. 16: 9041. https://doi.org/10.3390/app15169041
APA StyleLiu, Y., Gu, Z., Sun, M., Guo, C., & Ding, X. (2025). Machine Learning-Based Fracture Failure Analysis and Structural Optimization of Adhesive Joints. Applied Sciences, 15(16), 9041. https://doi.org/10.3390/app15169041






