Modeling Relative Permeability-Resistivity Relationships from Seepage Experiment Laws
Abstract
Featured Application
Abstract
1. Introduction
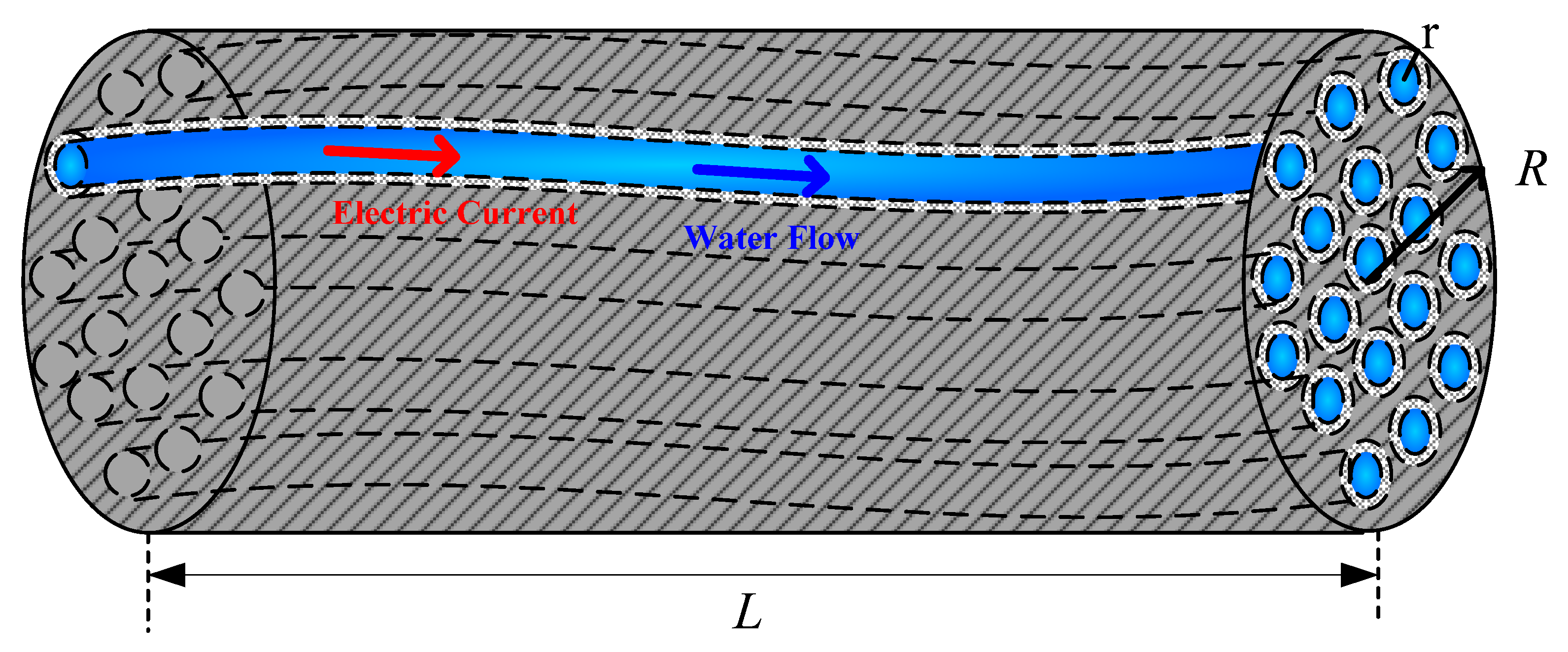
2. Experimental Design and Measurement
3. Research on Experimental Rules
3.1. Research on Empirical Laws of Water Relative Permeability
3.1.1. Effects of Pore Structure
3.1.2. Effect of Shale Content
3.2. Research on Empirical Laws of Oil Relative Permeability
3.2.1. Effects of Pore Structure
3.2.2. Effect of Shale Content
4. Modeling
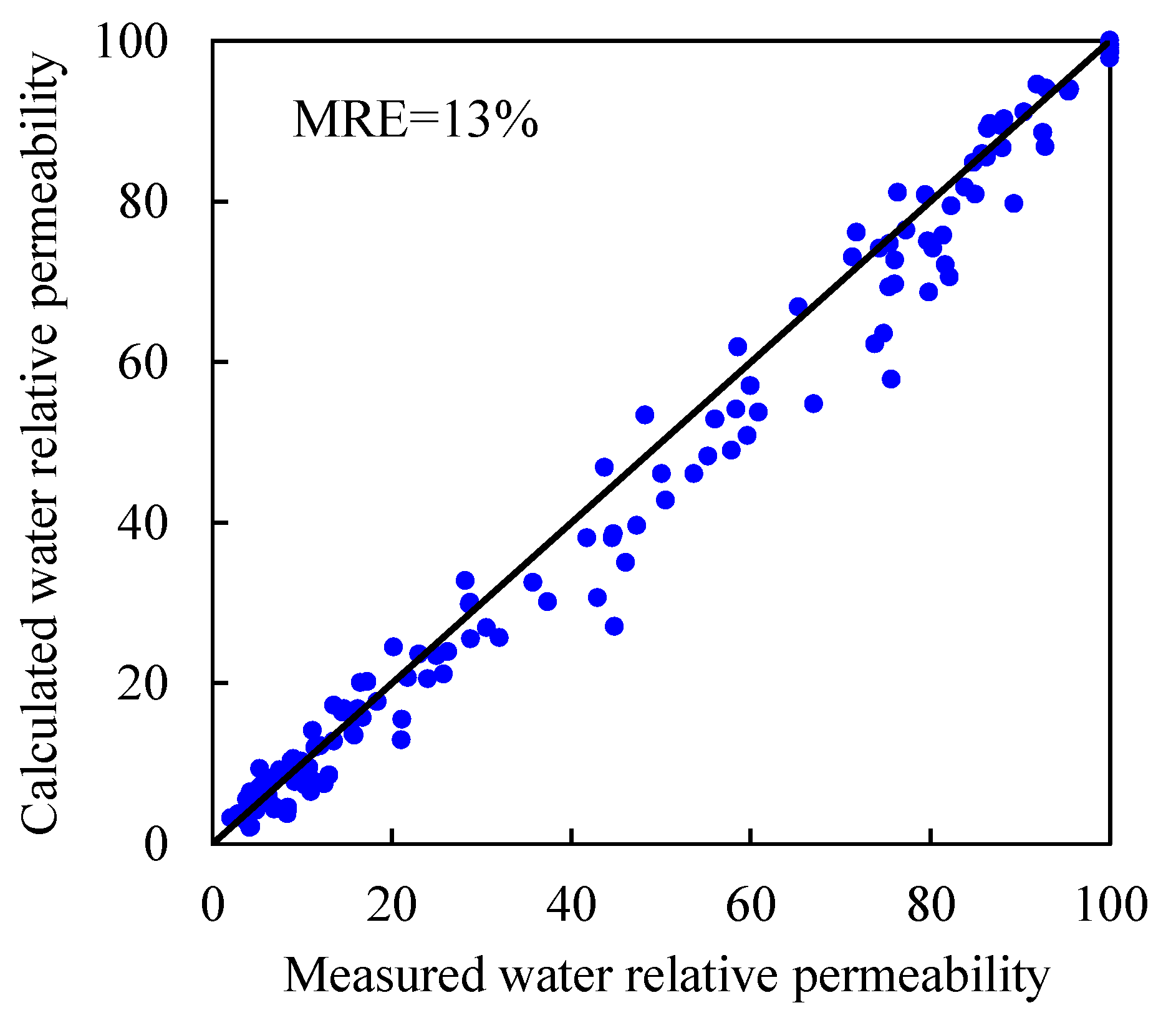
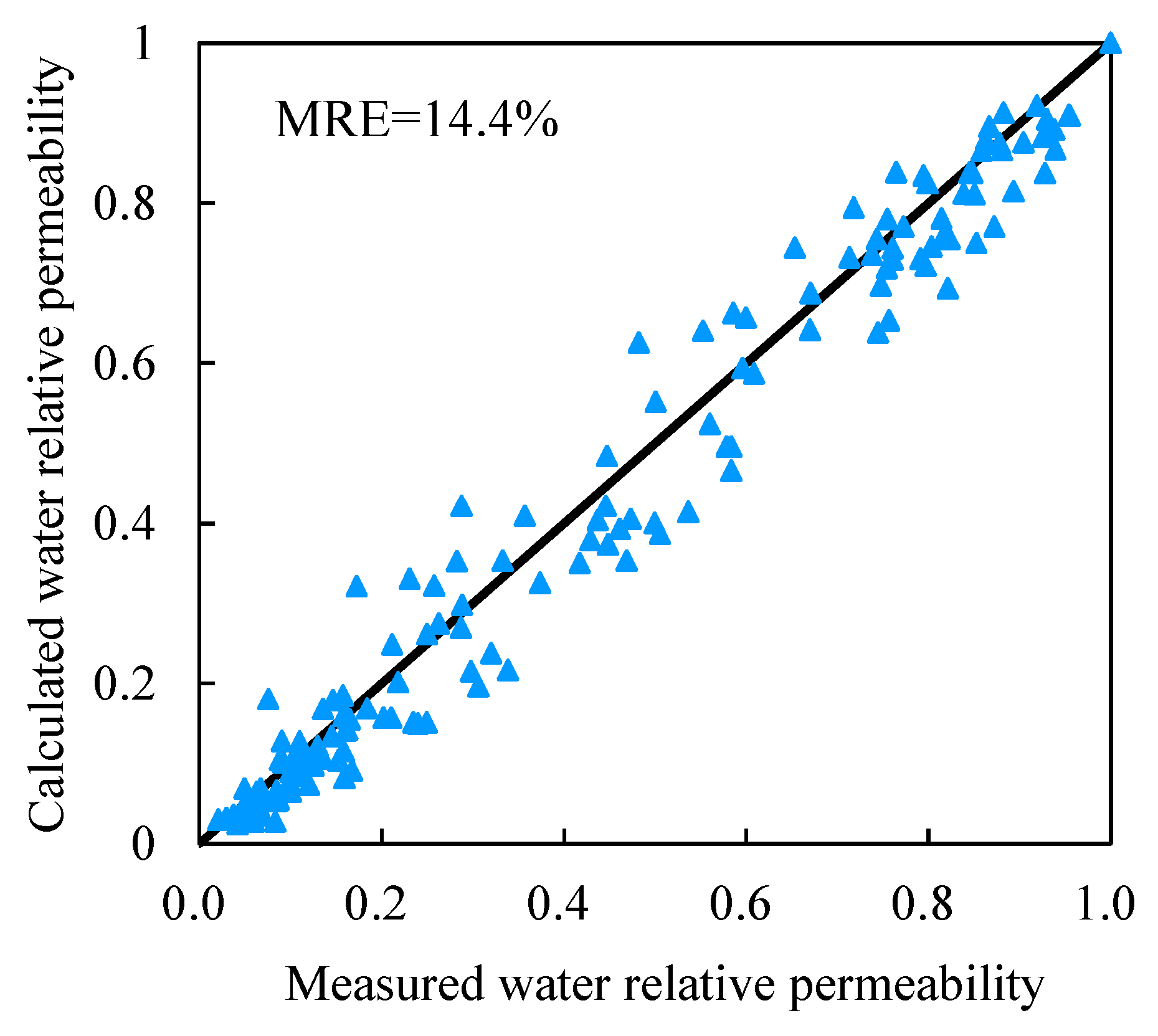
4.1. Relationship Model Between Water Relative Permeability and Resistivity
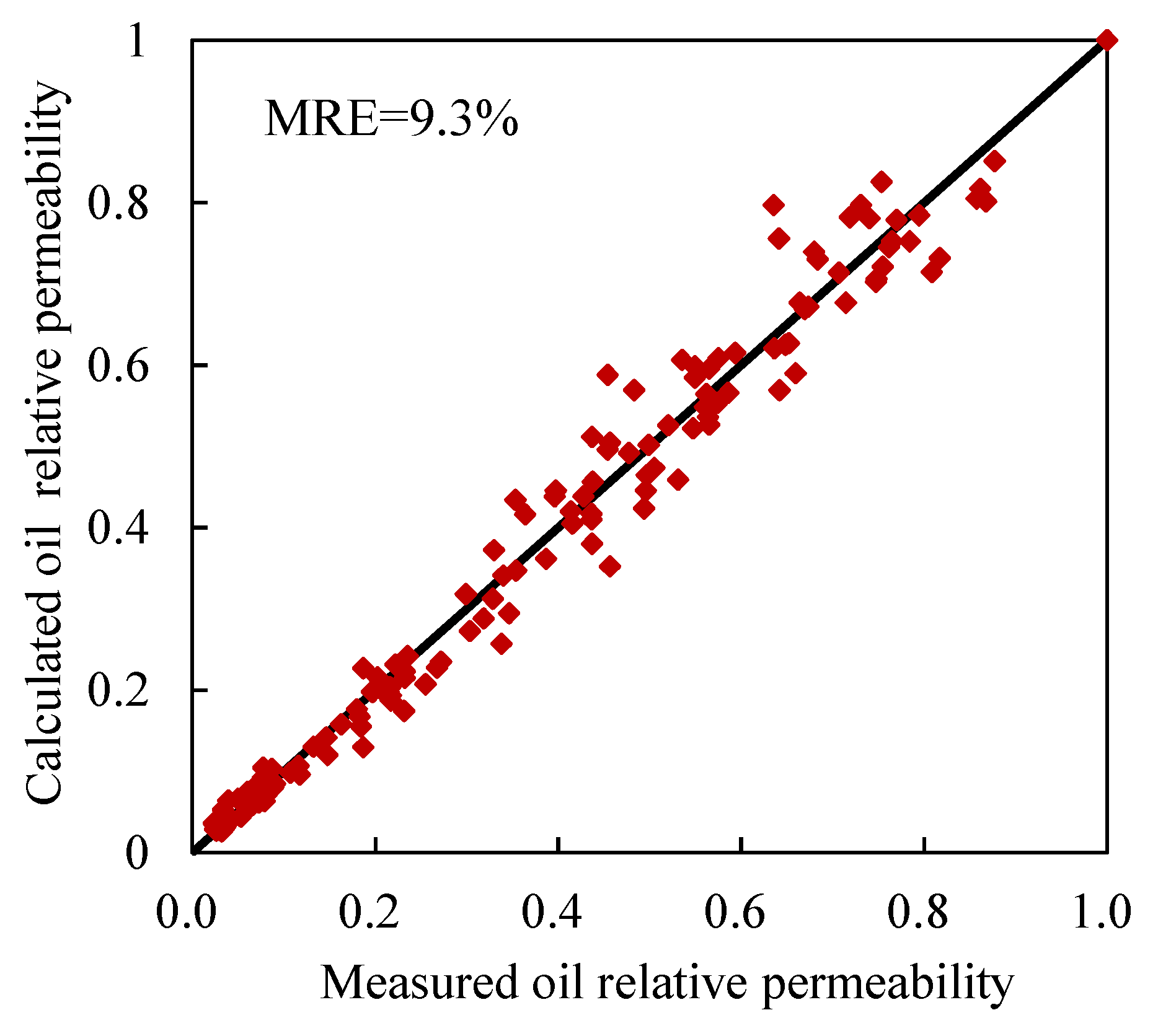
4.2. Relationship Model Between Oil Relative Permeability and Resistivity
4.3. Analysis and Evaluation Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, J.; Sun, W.; Shi, L.; Wang, X.; Liu, Z.; Teng, T. New Method for Productivity Prediction with Resistivity Logging Data. Well Logging Technol. 2021, 45, 411–415. [Google Scholar]
- Zheng, Y.; Shi, X.; Yue, B.; Zhang, B. A method for permeability evaluation based on relative permeability experiments and pressure mobility. Pet. Sci. Bull. 2024, 9, 563–573. [Google Scholar]
- Song, Y.; Liu, Y.; Tang, X.; Zhang, Z. Evaluation Method of Total Organic Carbon Content in Shale Based on Stacking Algorithm Ensemble Learning. Well Logging Technol. 2024, 48, 163–178. [Google Scholar]
- Zhou, Y.; Luo, S.; Mu, Y.; Lei, L.; Chen, L.; Lin, W. A New Method for Fluid Identification of Low-Contrast Oil Layers in the Western Margin of Ordos Basin. Well Logging Technol. 2024, 48, 117–126. [Google Scholar]
- Bai, S.; Wan, J.; Cheng, D.; Li, G.; Zhao, J.; Yang, L.; Wang, M. Study of relationship between petrophysical experimental parameters: Capillary pressure, NMR τ2 distribution, resistivity index, relative permeability. J. Chengdu Univ. Technol. (Sci. Technol. Ed.) 2014, 41, 483–491. [Google Scholar]
- Li, K. Interrelationship between Resistivity Index, Capillary Pressure and Relative Permeability. Transp. Porous Media 2011, 88, 385–398. [Google Scholar] [CrossRef]
- Dernaika, M.; Kalam, M.; Basioni, M.; Skjæveland, S. Hysteresis of Capillary Pressure, Resistivity Index and Relative Permeability in Different Carbonate Rock Types. Petrophysics 2012, 53, 316–332. [Google Scholar]
- Hou, B.; Cui, P.; Liang, W.; Wang, X.; Wang, Q. Correlation analysis between the capillary pressure and resistivity of the reservoir rock based on the rock-electric test. Pet. Geol. Oilfield Dev. Daqing 2022, 41, 75–82. [Google Scholar]
- Ma, D.; Wu, H.; Zeng, M. A new method for estimating relative permeability with resistivity data. Oil Gas Geol. 2015, 36, 695–700. [Google Scholar]
- Hu, W.; Yang, S.; Liu, G.; Wang, Z.; Wang, P.; Lie, H. A New Correction Method for Oil-Water Relative Permeability Curve on the Basis of Resistivity and Water Saturation Relationship. Transp. Porous Media 2015, 109, 527–540. [Google Scholar] [CrossRef]
- Pei, J. Model for Estimating Relative Permeability Based on Resistivity Index. Well Logging Technol. 2015, 39, 685–688. [Google Scholar]
- Wang, Y.; Pan, B.; Guo, Y. Relationship between relative permeability and electrical parameters of tight sandstone reservoirs. World Geol. 2017, 36, 1277–1283. [Google Scholar]
- MA, D.; Liu, C.; Xu, H.; Liu, B.; Tang, T. A new method for calculating relative permeability of polymer flooding based on core-electrical parameters. J. China Univ. Pet. (Ed. Nat. Sci.) 2017, 41, 118–123. [Google Scholar]
- Kolesnikov, B.; Arushanyan, R. The percolation model of relative conductivities and phase permeabilities. J. Phys. Conf. Ser. 2022, 2150, 012005. [Google Scholar] [CrossRef]
- Song, Y.; Wang, H.; Tang, X.; Deng, X.; Liu, Y. Relationship Between Oil-water Relative Permeability and Resistivity of Shaly Rock Based on the Similarity Between Water Flow and Electric Current. Well Logging Technol. 2015, 39, 543–549. [Google Scholar]
- Li, K. A New Method for Calculating Two-Phase Relative Permeability from Resistivity Data in Porous Media. Transp. Porous Media 2008, 74, 21–33. [Google Scholar] [CrossRef]
- Li, K.; Shapiro, M.; Horne, R.; Stanford, U.; Ma, S.; Hajari, A.; Mudhhi, M. In-situ Estimation of Relative Permeability from Resistivity Measurements. In Proceedings of the CPS/SPE International Oil & Gas Conference and Exhibition, Beijing, China, 8–10 June 2010. [Google Scholar]
- Li, H.; Fan, Z.; Xie, Y.; Gong, X.; Hao, B.; Sun, L.; Lei, X.; Yan, J. Characterization method of pore throat structure in dense sandstone based on NMR and CMP experiments. Bull. Geol. Sci. Technol. 2025, 44, 25–35. [Google Scholar]
- Lu, Y.; Liu, Z.; Liao, X.; Li, C.; Li, Y. Automatic classification of pore structures of low-permeability sandstones based on self-organizing-map neural network algorithm. Bull. Geol. Sci. Technol. 2024, 43, 318–330. [Google Scholar]
- Tian, J.; Wang, L.; Sima, L.; Fang, S.; Liu, H. Characterization of reservoir properties and pore structure based on micro-resistivity imaging logging: Porosity spectrum, permeability spectrum, and equivalent capillary pressure curve. Pet. Explor. Dev. 2023, 50, 553–561. [Google Scholar] [CrossRef]
- Pairoys, F.; Al–Zoukani, A.; Keskin, A. Correlation between Resistivity and Petrophysical Parameters of a Carbonate Rock During Two–Phase Flow Displacements. In Proceedings of the SPE Saudi Arabia Section Technical Symposium and Exhibition, Al–Khobar, Saudi Arabia, 19–22 May 2013. [Google Scholar]
- Shi, Y.; Meng, H.; Liu, T.; Zhang, H.; Wang, C. Evaluation of Relative Permeability from Resistivity Data for Fractal Porous Media. Petrophysics 2020, 61, 303–317. [Google Scholar] [CrossRef]
- Guo, Y.; Pan, B.; Liu, W. A research on the relationship between resistivity index and relative permeability at different measurement conditions based on the pore structure. Environ. Fluid Mech. 2016, 16, 1129–1141. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, X.; Hu, Y.; Li, J.; Su, J. Relationship between Rock Resistivity Increasing Coefficient and Water Saturation Based on Phase Percolation Analysis. Well Logging Technol. 2016, 40, 137–141. [Google Scholar]
- Zhao, D.; Hou, J.; Wang, X.; Liu, Y.; Chen, Y.; Zhang, Z. Controlling mechanism of pore-throat structure of different litholacies on gas-water relative permeability characteristics of tight sandstone gas reservoir: A case study of the Lower Shihezi Formation in the Well J72 block of the Dongsheng Gas Field, Ordos Basin. Bull. Geol. Sci. Technol. 2023, 42, 163–174. [Google Scholar]
- Ma, D.; Liu, C.; Cheng, C. New Relationship between Resistivity Index and Relative Permeability. J. Energy Resour. Technol. 2015, 137, 1–7. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, L.; Liu, Y.; Ma, K.; Luo, X. Effect of Displacement Pressure Gradient on Oil–Water Relative Permeability: Experiment, Correction Method, and Numerical Simulation. Processes 2024, 12, 330. [Google Scholar] [CrossRef]
- Song, Y.; Zhou, Y.; Tang, X.; Fu, J.; Hou, L. Method for Determination of Permeability of Shaly Sand Formation with Low Porosity and Permeability Based on Efficient Flow Pore. Prog. Geophys. 2016, 31, 327–333. (In Chinese) [Google Scholar]
- Ma, D.; Zhang, K.; Hu, J.; Li, H.; Ma, L.; Tang, T. Correlation between relative permeability, capillary pressure and resistivity index. Oil Gas Geol. 2019, 40, 190–195. [Google Scholar]
- Guo, Z. Experimental Study on Relationship Between Oil-Water Relative Permeability and Resistivity of Matrix-Conducting Shaly Rock. Ph.D. Thesis, Northeast Petroleum University, Heilongjiang, China, 2019. [Google Scholar]
- Song, Y.; Jiang, Y.; Song, Y.; Zhang, Y. Experimental Research on the Influencing Factors of m and n of Low Resistivity Oil Reservoirs in Southern Gulong Area. J. Jilin Univ. (Earth Sci. Ed.) 2014, 44, 704–714. [Google Scholar]
- Li, J.; Gao, C.; Zhao, B.; Cheng, X. Permeability Upscaling Conversion Based on Reservoir Classification. Processes 2024, 12, 1653. [Google Scholar] [CrossRef]
- Li, Z.; Mo, X. Study on the electric property of shaly sand and its interpretation method. J. Geosci. Res. Northeast Asia 1999, 2, 110–114. [Google Scholar]
- Mo, X.; He, D.; Li, Z.; Wen, X.; Li, G. The Application of Three—water Conduction Model in the Interpretation of Low—Resistivity Reservoir. J. Chang. Univ. Sci. Technol. 2001, 31, 92–95. [Google Scholar]

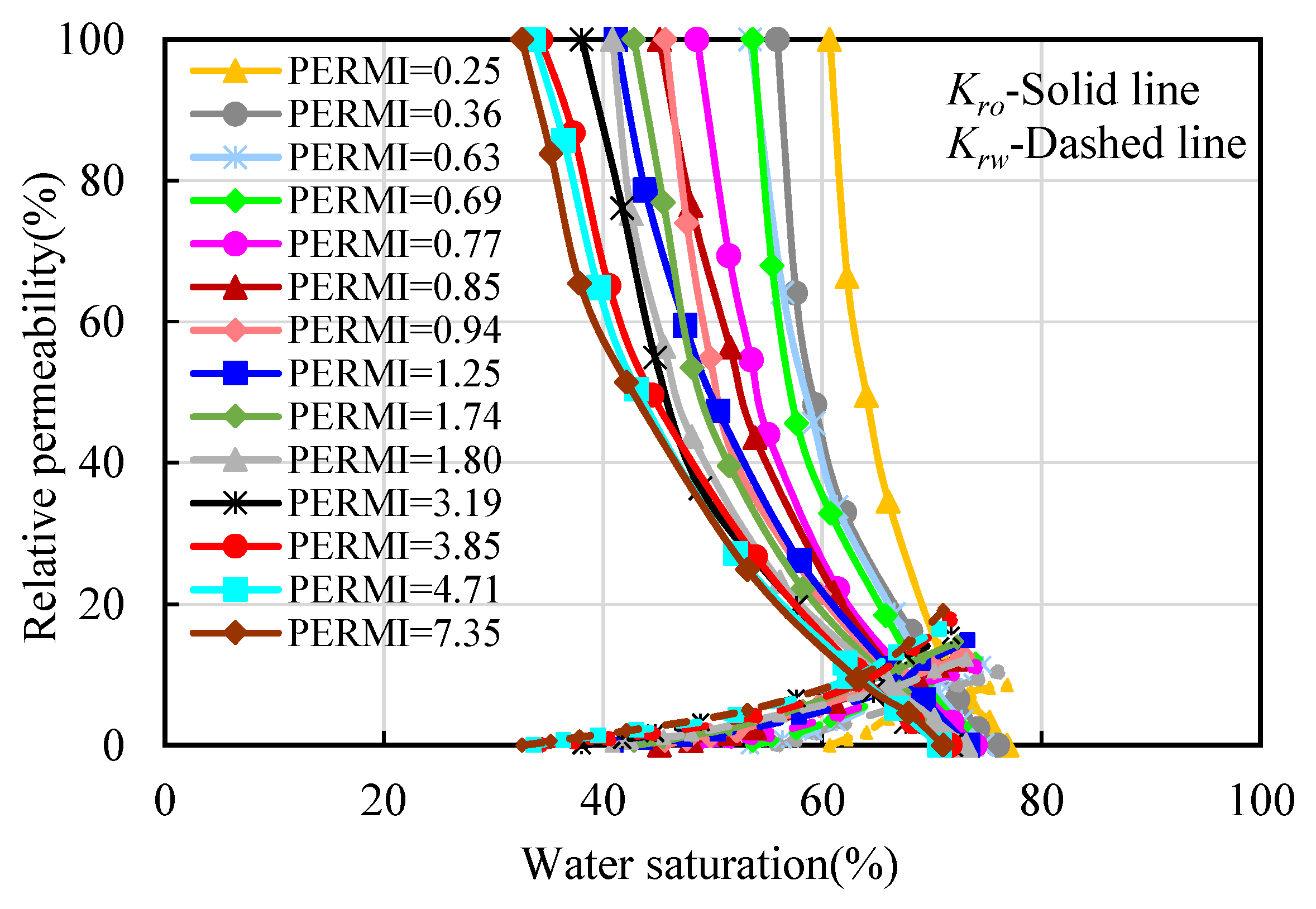

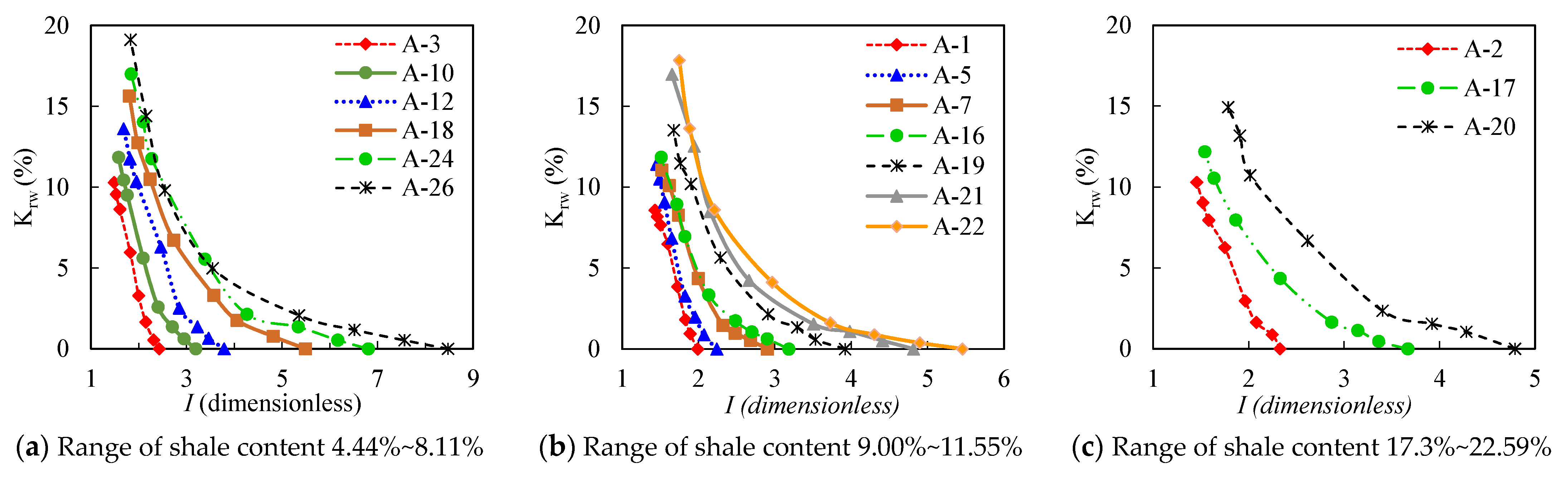
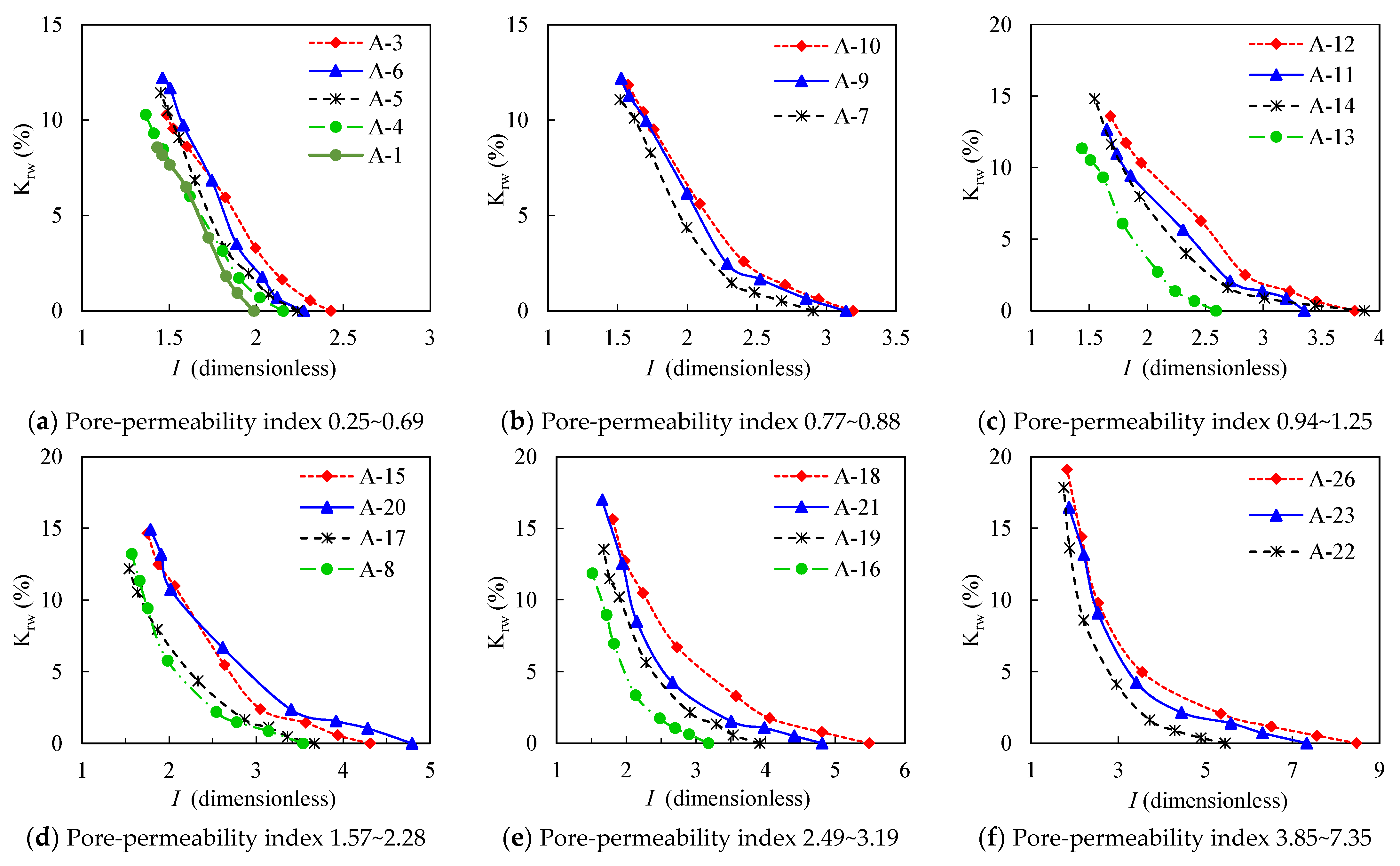

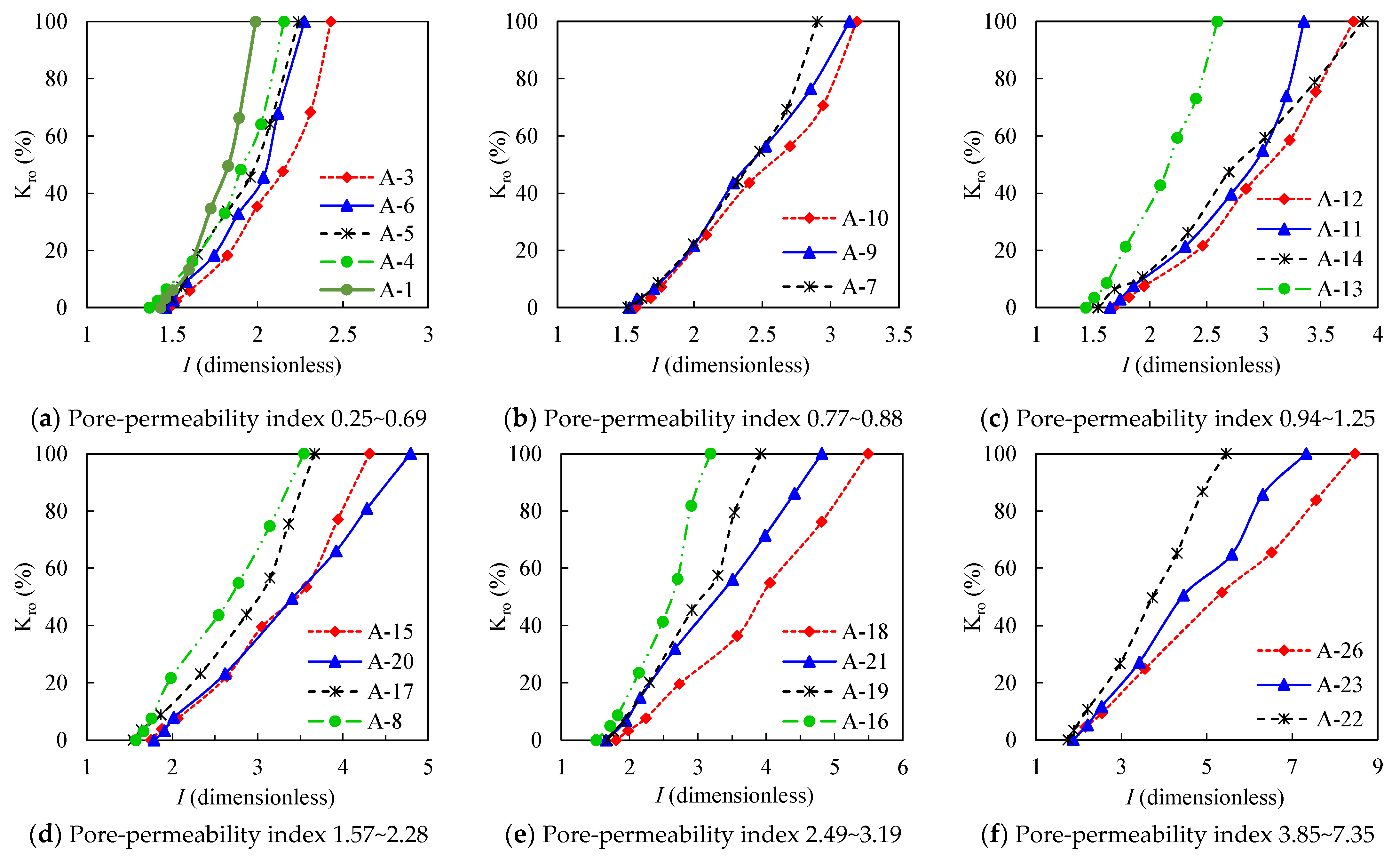




| Numbering | Core Sample | Porosity | Permeability | Shale Content | Irreducible Water Saturation | Pore Permeability Composite Index |
|---|---|---|---|---|---|---|
| (%) | (mD) | (%) | (%) | |||
| 1 | A-1 | 13.9 | 0.9 | 10.00 | 60.7 | 0.25 |
| 2 | A-4 | 18.9 | 2.5 | 10.00 | 55.9 | 0.36 |
| 3 | A-2 | 15.7 | 3.9 | 17.84 | 52.0 | 0.50 |
| 4 | A-3 | 17.3 | 4.8 | 5.30 | 51.7 | 0.53 |
| 5 | A-5 | 13.8 | 5.5 | 9.15 | 53.4 | 0.63 |
| 6 | A-6 | 17.4 | 8.3 | 6.20 | 53.7 | 0.69 |
| 7 | A-7 | 21.6 | 12.8 | 10.90 | 48.6 | 0.77 |
| 8 | A-9 | 24.5 | 17.9 | 8.58 | 45.1 | 0.85 |
| 9 | A-10 | 17.9 | 13.8 | 6.03 | 43.4 | 0.88 |
| 10 | A-11 | 18.0 | 16.1 | 12.70 | 45.7 | 0.94 |
| 11 | A-12 | 19.3 | 22.1 | 7.66 | 42.1 | 1.07 |
| 12 | A-13 | 19.2 | 23.5 | 14.17 | 50.8 | 1.11 |
| 13 | A-14 | 20.4 | 31.6 | 13.32 | 41.2 | 1.25 |
| 14 | A-8 | 22.2 | 54.7 | 29.20 | 43.0 | 1.57 |
| 15 | A-15 | 23.6 | 71.2 | 9.30 | 42.8 | 1.74 |
| 16 | A-16 | 17.6 | 56.4 | 11.55 | 44.2 | 1.79 |
| 17 | A-17 | 16.9 | 54.6 | 22.59 | 40.9 | 1.80 |
| 18 | A-20 | 17.1 | 89.0 | 17.29 | 40.3 | 2.28 |
| 19 | A-19 | 23.9 | 147.8 | 9.71 | 41.3 | 2.49 |
| 20 | A-21 | 25.5 | 245.5 | 9.00 | 39.0 | 3.10 |
| 21 | A-18 | 24.3 | 248.0 | 8.11 | 38.1 | 3.19 |
| 22 | A-22 | 23.4 | 346.4 | 11.55 | 34.3 | 3.85 |
| 23 | A-23 | 21.9 | 485.1 | 8.25 | 33.7 | 4.71 |
| 24 | A-24 | 26.9 | 606.7 | 4.96 | 34.8 | 4.75 |
| 25 | A-25 | 24.7 | 571.5 | 3.81 | 35.4 | 4.81 |
| 26 | A-26 | 25.5 | 1377.5 | 4.44 | 32.6 | 7.35 |
| Core Sample | Resistivity of Water-Saturated Rock Sample | Water Saturation | Oil Relative Permeability | Water Relative Permeability | Resistivity of Rock Sample | Resistivity Index |
|---|---|---|---|---|---|---|
| (Ω·m) | (%) | (%) | (%) | (Ω·m) | (Dimensionless) | |
| A-1 | 28.1 | 60.7 | 100.00 | 0.00 | 55.75 | 1.99 |
| 62.3 | 66.36 | 0.94 | 53.05 | 1.89 | ||
| 64.0 | 49.55 | 1.81 | 51.25 | 1.83 | ||
| 66.0 | 34.63 | 3.84 | 48.40 | 1.73 | ||
| 70.7 | 13.25 | 6.48 | 44.79 | 1.60 | ||
| 73.5 | 6.17 | 7.65 | 42.17 | 1.50 | ||
| 75.3 | 3.26 | 8.18 | 40.94 | 1.46 | ||
| 76.9 | 0.00 | 8.57 | 40.16 | 1.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Z.; Zhao, Y.; Liu, Z.; Fan, Q.; Guo, S. Modeling Relative Permeability-Resistivity Relationships from Seepage Experiment Laws. Appl. Sci. 2025, 15, 8963. https://doi.org/10.3390/app15168963
Guo Z, Zhao Y, Liu Z, Fan Q, Guo S. Modeling Relative Permeability-Resistivity Relationships from Seepage Experiment Laws. Applied Sciences. 2025; 15(16):8963. https://doi.org/10.3390/app15168963
Chicago/Turabian StyleGuo, Zhihua, Yang Zhao, Zongli Liu, Qi Fan, and Shuwen Guo. 2025. "Modeling Relative Permeability-Resistivity Relationships from Seepage Experiment Laws" Applied Sciences 15, no. 16: 8963. https://doi.org/10.3390/app15168963
APA StyleGuo, Z., Zhao, Y., Liu, Z., Fan, Q., & Guo, S. (2025). Modeling Relative Permeability-Resistivity Relationships from Seepage Experiment Laws. Applied Sciences, 15(16), 8963. https://doi.org/10.3390/app15168963






