Joint Spectral–Spatial Representation Learning for Unsupervised Hyperspectral Image Clustering

Abstract

Hyperspectral image (HSI) clustering has attracted significant attention due to its broad applications in agricultural monitoring, environmental protection, and other fields. However, the integration of high-dimensional spectral and spatial information remains a major challenge, often resulting in unstable clustering and poor generalization under noisy or redundant conditions. To address these challenges, we propose a Joint Spectral–Spatial Representation Learning (JSRL) framework for robust hyperspectral image clustering. We first perform spectral clustering to generate pseudo-labels and guide a residual Graph Attention Network (GAT) that jointly refines pixel-level spectral and spatial features. We then aggregate pixels into superpixels and employ a Variational Graph Autoencoder (VGAE) to learn structure-aware representations, further optimized via a quantum-behaved particle swarm optimization (QPSO) strategy. This hierarchical architecture not only mitigates spectral redundancy and reinforces spatial coherence, but also enables more robust and generalizable clustering across diverse HSI scenarios. Extensive experiments on multiple benchmark HSI datasets demonstrate that JSRL consistently achieves state-of-the-art performance, highlighting its robustness and generalization capability across diverse clustering scenarios.

1. Introduction

Hyperspectral imaging (HSI) technology, which can capture spectral information of ground objects across hundreds of contiguous narrow bands, has become an important means of identifying subtle material differences on the Earth’s surface in the field of remote sensing, yet its unsupervised analysis remains highly challenging because of spectral redundancy and spatial complexity. It plays a critical role in various application scenarios such as precision agriculture [1,2,3,4,5], environmental monitoring, and urban planning [6,7,8,9,10]. In recent years, with the continuous advancement of imaging devices and the significant reduction in data acquisition costs, HSI data has become increasingly accessible, leading to the rapid accumulation of large-scale unlabeled hyperspectral images. However, such unlabeled data cannot be directly used in supervised learning, which severely limits the deep mining of hyperspectral information and its practical value. Therefore, how to effectively explore the internal structure of HSI data without relying on manual annotations has become a key research issue [11,12].

In this context, hyperspectral image clustering, as a typical unsupervised learning paradigm, has gradually emerged as an important direction for addressing this problem due to its ability to automatically discover potential categories and reveal spatial semantic structures. Traditional clustering algorithms typically treat each pixel in a hyperspectral image as an independent point, ignoring the spatial correlations between neighboring pixels. This often leads to fragmentation of spatially coherent regions and the loss of critical local structural information [13,14]. In contrast, graph neural networks (GNNs) can naturally integrate spectral and spatial information, model complex pixel relationships, and require relatively less labeled data [6].

Building on these observations, recent research has increasingly focused on combining traditional clustering heuristics [1] (e.g., K-means) with deep learning techniques. The former provides rapid, unsupervised initial partitioning, which serves as a “weak supervision” signal for the latter. Deep models then refine these initial results by learning expressive representations that capture nonlinear relationships and enhance clustering performance. This iterative optimization strategy effectively mitigates the limitations posed by scarce annotations and significantly improves clustering accuracy and robustness in large-scale HSI scenarios [15,16].

Despite these notable advances, existing methods still face challenges such as high spectral dimensionality, redundancy, noise, and insufficient integration of spatial priors. While several approaches attempt to address these issues individually, they often overlook the synergy between local representation refinement and global structural modeling. Moreover, the decoupling of clustering and representation learning stages can lead to sub-optimal feature alignment, especially in complex HSI scenes.

To this end, we propose a Joint Spectral–Spatial Representation Learning (JSRL) framework for robust HSI clustering. JSRL adopts a hierarchical two-stage pipeline that progressively captures both fine-grained pixel-level features and global structural dependencies. In the first stage, we perform unsupervised spectral clustering to generate pseudo-labels, which guide a residual Graph Attention Network (GAT) for learning refined spectral-spatial representations. In the second stage, we aggregate pixels into superpixels and construct a region-level graph, where a Variational Graph Autoencoder (VGAE) captures latent structural relationships. To further optimize the global topology, we apply a Quantum-behaved Particle Swarm Optimization (QPSO) strategy to fine-tune the learned embeddings. This framework jointly integrates pseudo-supervision, local context refinement, and global structure modeling, effectively mitigating spectral redundancy, enhancing spatial consistency, and improving clustering generalization.

Our main contributions are as follows:

• We propose JSRL, a novel hierarchical clustering framework that unifies pixel-level pseudo-supervision and superpixel-level structural modeling to effectively capture both local spectral–spatial patterns and global contextual dependencies.
• We design a two-stage learning pipeline where residual GATs are used for context-aware refinement of pixel-wise representations, and a VGAE-QPSO module is introduced to learn and optimize structure-aware embeddings at the region level.
• Extensive experiments on three benchmark hyperspectral datasets demonstrate that JSRL consistently outperforms existing state-of-the-art clustering methods in terms of accuracy, robustness, and generalization under varying data conditions.

2. Related Works

Hyperspectral image (HSI) clustering has been extensively studied through a variety of approaches, which can be broadly categorized into: (1) traditional clustering methods and (2) representation learning-based methods. While traditional methods provide intuitive clustering priors, they often struggle with the high dimensionality and complex spatial patterns inherent in HSI data. Consequently, recent research has increasingly focused on learning-based approaches that aim to improve feature representation and clustering robustness.

2.1. Traditional Clustering Methods

Traditional HSI clustering methods mainly include centroid-based, density-based, bio-inspired, and graph-based approaches. Centroid-based algorithms, such as K-means [17], assign pixels to clusters by minimizing intra-cluster spectral distances. Although simple and efficient, these methods are highly sensitive to initialization and noise and fail to exploit spatial context, resulting in fragmented clusters [13,18,19]. Density-based methods like DBSCAN [20] and Density Peak Clustering [21] detect clusters based on data density, offering robustness to outliers [22]. However, their effectiveness diminishes on high-dimensional HSI data due to difficulty in estimating appropriate density thresholds. Bio-inspired algorithms, such as genetic algorithms and particle swarm optimization [23], provide global search capabilities to avoid local optima. Yet, these methods are typically computationally expensive and sensitive to hyperparameter settings [13]. Graph-based methods construct affinity graphs where each node corresponds to a pixel, and edges encode similarity. Sparse Subspace Clustering [24] and Low-Rank Representation [25] are popular for their ability to capture global data structure. However, their scalability is limited by high computational cost. Efficient variants using anchor graphs [26] or superpixel segmentation [27] reduce complexity but still suffer from insufficient spectral-spatial fusion and sensitivity to noise. In summary, although traditional clustering methods lay a solid foundation for HSI analysis, their limited ability to handle high-dimensional spectral redundancy, spatial correlation, and data heterogeneity motivates the exploration of more advanced, learning-based approaches.

2.2. Deep Representation Learning-Based Methods

The advent of deep learning has enabled powerful representation learning techniques that automatically extract meaningful spectral–spatial features for HSI clustering in an end-to-end manner. Early convolutional neural network (CNN) architectures [6] exploit local spatial continuity and have shown effectiveness in feature extraction. However, CNNs generally struggle to model non-local dependencies and complex spectral variations. Subspace learning approaches [28] aim to embed high-dimensional spectral data into compact latent spaces, improving efficiency and feature compactness. Nevertheless, they often overlook the spatial consistency among neighboring pixels, limiting their representational power. To overcome limitations of handcrafted priors and supervision scarcity, self-supervised and contrastive learning methods [29,30] have been introduced to enhance feature discriminability without requiring manual annotations. While promising, these approaches depend heavily on the quality of pseudo-labels or augmentation strategies, which are difficult to design for complex HSI datasets. More recently, graph neural networks have emerged as a powerful paradigm to jointly model spectral similarity and spatial topology via edge-weighted message passing. Methods incorporating residual Graph Attention Networks [31] or spectral-spatial co-attention mechanisms have achieved improved clustering performance by effectively fusing local and global contextual information. Despite these advances, most existing approaches focus on either pixel-level feature refinement or treat clustering and representation learning as separate stages, which restricts their ability to capture multi-scale structural dependencies comprehensively. Some recent work has increasingly adopted graph contrastive objectives to bolster unsupervised feature learning. Qi et al. [32] introduce SPGCC, which designs semantic-invariant augmentations at the superpixel level and achieves state-of-the-art gains on Indian Pines and Salinas. To further reduce model complexity, Yang et al. [33] propose S²GCL, a lightweight MLP-based framework that removes data augmentation entirely yet maintains competitive accuracy on four public datasets. Complementarily, Wang et al. [34] present MLGSC, a multi-level subspace contrastive scheme that unifies local–global graph representations and reports OA above 99% on Pavia University. These approaches highlight the trend toward contrastive, graph-centric representation learning, but they all rely on fixed affinity graphs, whereas our JSRL jointly optimizes the graph topology during training.

These limitations underscore the need for a unified and scalable framework that integrates local spectral-spatial refinement with global structural modeling. Motivated by this, we propose the Joint Spectral-Spatial Representation Learning (JSRL) framework, which hierarchically combines weak supervision, residual graph modeling, and global topology optimization to address the core challenges of Hyperspectral image clustering.

3. Methodology

3.1. Overview

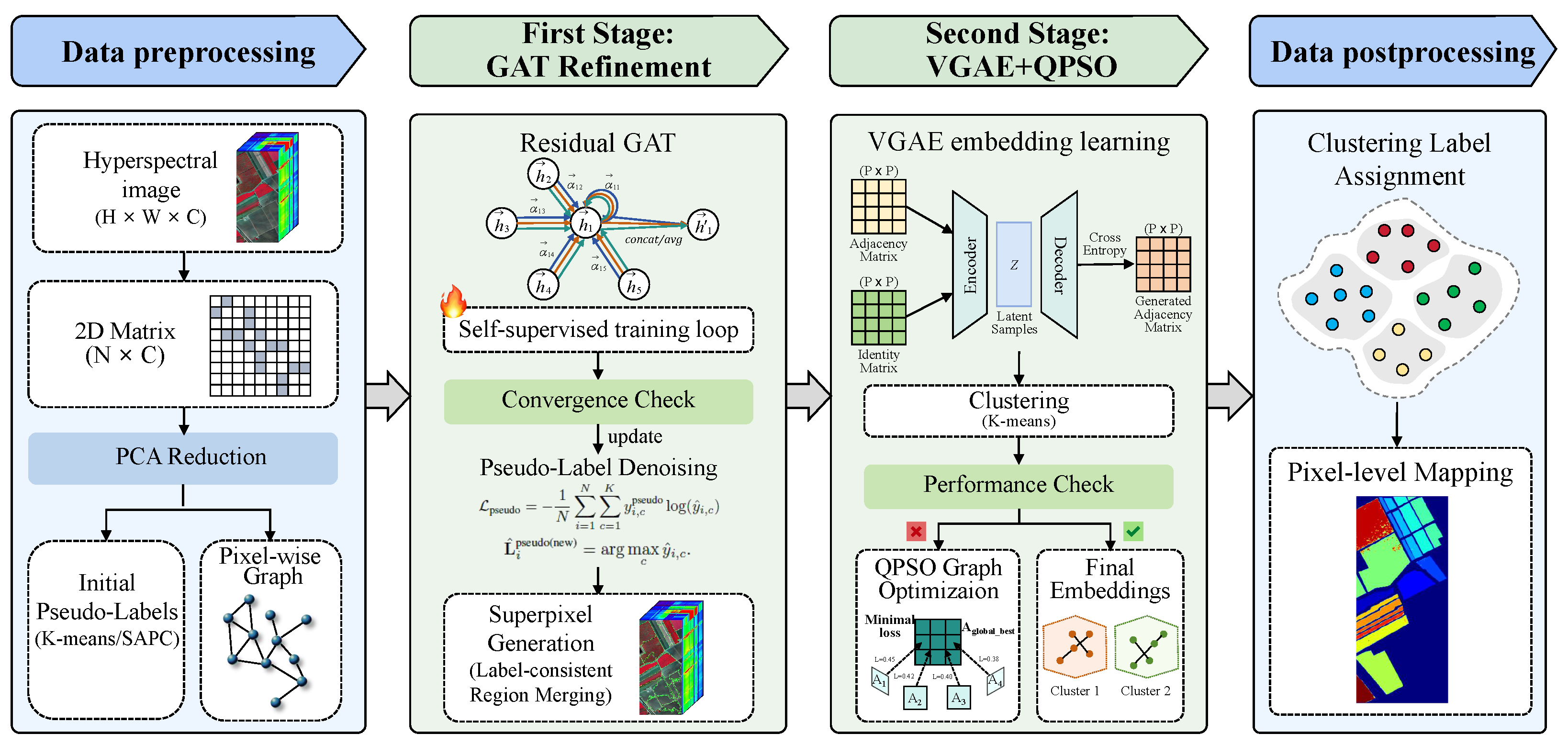
HSI clustering remains a challenging task due to the high spectral dimensionality, redundancy among bands, and the scarcity of labeled data. These factors often result in noisy feature representations, ambiguous cluster boundaries, and unstable clustering outcomes. To address these challenges, we propose a Joint Spectral–Spatial Representation Learning (JSRL) framework that hierarchically integrates pseudo-supervised pixel-level refinement and structure-aware global modeling for robust and generalizable clustering. As illustrated in Figure 1, our approach proceeds in two stages. The first stage obtains context-aware spectral-spatial pixel embeddings guided by pseudo-labels derived from unsupervised clustering on PCA-reduced features. A residual Graph Attention Network (GAT) refines these embeddings by aggregating local neighborhood information, enhancing feature robustness and discrimination. The second stage aggregates refined pixel features into superpixels to build a spatial adjacency graph. A Variational Graph Autoencoder (VGAE) encodes the graph topology into latent embeddings, which are further optimized via Quantum-behaved Particle Swarm Optimization (QPSO) to improve cluster separability. Finally, fused representations combining topology-aware embeddings and superpixel features are clustered to generate the final labels. This hierarchical design effectively combines pseudo-supervision, local spectral-spatial context, and global topological structure, enabling stable clustering performance across diverse HSI datasets.

3.2. Spectral Feature Compression and Pseudo-Label Initialization

Direct clustering of raw hyperspectral pixels is hindered by the curse of dimensionality and the substantial redundancy among spectral bands, which not only inflates computational cost but also amplifies noise and overfitting risk. To obtain a compact and denoised representation, we first perform dimensionality reduction using Principal Component Analysis (PCA), a linear technique well-suited for HSI data due to its robustness, interpretability, and efficiency.

Formally, given a hyperspectral image $\mathrm{HSI}\in {\mathbb{R}}^{H\times W\times C}$, where H and W denote spatial dimensions and C is the number of spectral bands, we reshape it into a two-dimensional matrix:

$$\mathbf{X}\in {\mathbb{R}}^{N\times C},N=H\times W,$$

(1)

where each row corresponds to the spectral vector of a single pixel. To reduce spectral redundancy and noise, we apply Principal Component Analysis (PCA), a linear dimensionality reduction technique well-suited for hyperspectral data due to its interpretability and computational efficiency:

$${\mathbf{X}}_{\mathrm{PCA}}={\mathrm{PCA}}_{C^{\prime }}\left(\mathbf{X}\right),C^{\prime }\ll C,$$

(2)

where $C^{\prime }$ is chosen to retain a high proportion (e.g., 95–99%) of the total spectral variance. The resulting low-dimensional representation ${\mathbf{X}}_{\mathrm{PCA}}$ is both compact and more robust to noise, facilitating subsequent clustering.

In the absence of ground-truth labels, we utilize unsupervised clustering to obtain initial pseudo-labels. Rather than relying solely on spectral similarity, we adopt Spatially Adaptive Probabilistic Clustering (SAPC), which incorporates spatial priors into a probabilistic clustering framework to improve label smoothness and local consistency:

$${\hat{\mathbf{L}}}^{\mathrm{pseudo}}=\mathrm{SAPC}({\mathbf{X}}_{\mathrm{PCA}},K),$$

(3)

where K denotes the number of clusters. SAPC ensures that pixels within spatially adjacent regions with similar spectral signatures are more likely to share the same label, mitigating the fragmentation problem of purely spectral-based methods. The resulting pseudo-labels provide a coarse but informative initialization for the GAT-based refinement stage, enabling spatial context to be gradually infused into the learned representations.

3.3. Pixel-Level Representation Refinement via Residual GAT

To incorporate spatial context into spectral features and enhance pixel-wise clustering, given the PCA-reduced spectral features and the initial pseudo-labels ${\hat{\mathbf{L}}}^{\mathrm{pseudo}}$ from SAPC, we model the hyperspectral image as a graph and iteratively refine pseudo-labels via a residual Graph Attention Network (GAT) under self-supervision.

Each pixel i is represented as a graph node with an initial feature vector formed by concatenating its PCA-reduced spectral vector ${\mathbf{x}}_i\in {\mathbb{R}}^{C^{\prime }}$ and its normalized spatial coordinate ${\mathbf{c}}_i=[r_i/H,c_i/W]$:

$${\mathbf{h}}_i^{\left(0\right)}=[{\mathbf{x}}_i\parallel {\mathbf{c}}_i]\in {\mathbb{R}}^{C^{\prime }+2}.$$

(4)

An undirected graph $G=(\mathcal{V},\mathcal{E})$ is constructed by connecting spatially adjacent and spectrally similar pixels. Specifically, an edge is formed between pixels i and j if they are within each other’s k-nearest neighbors in the image plane and satisfy the condition:

$${\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel }_2<{\tau }_s,$$

(5)

where ${\tau }_s$ is a spectral similarity threshold. The resulting binary adjacency matrix ${\mathbf{A}}_{\mathrm{pixel}}$ is symmetrically normalized to ensure numerical stability:

$$\hat{\mathbf{A}}={\mathbf{D}}^{-1/2}{\mathbf{A}}_{\mathrm{pixel}}{\mathbf{D}}^{-1/2},$$

(6)

where $\mathbf{D}$ is the degree matrix of ${\mathbf{A}}_{\mathrm{pixel}}$.

Based on the constructed graph, we apply a multi-layer residual GAT to refine node features by aggregating neighborhood context. At the l-th layer, the feature of node i is updated as follows:

$${\mathbf{h}}_i^{(l+1)}=\sigma \left(\sum _{a=1}^{N_a}\sum _{j\in {\mathcal{N}}_i}{\alpha }_{ij}^{\left(a\right)}{\mathbf{W}}^{\left(a\right)}{\mathbf{h}}_j^{\left(l\right)}\right)+{\mathbf{h}}_i^{\left(l\right)},$$

(7)

where $N_a$ is the number of attention heads, ${\alpha }_{ij}^{\left(a\right)}$ denotes the learned attention coefficient from node j to i in head a, ${\mathbf{W}}^{\left(a\right)}$ is a projection matrix, and $\sigma (·)$ is a non-linear activation function (e.g., ReLU). The residual connection stabilizes training and preserves original information.

Without access to ground-truth labels, we train the GAT in a self-supervised fashion to predict the pseudo-labels ${\hat{\mathbf{L}}}^{\mathrm{pseudo}}$ generated by SAPC. The training objective is the standard cross-entropy loss:

$${\mathcal{L}}_{\mathrm{pseudo}}=-{\displaystyle \frac{1}{N}}\sum _{i=1}^N\sum _{c=1}^K{y}_{i,c}^{\mathrm{pseudo}}log{\hat{y}}_{i,c},$$

(8)

where $y_{i,c}^{\mathrm{pseudo}}=1$ if pixel i belongs to cluster c, and ${\hat{y}}_{i,c}$ is the GAT-predicted probability.

After each training iteration, pseudo-labels are updated as follows:

$${\hat{L}}_i^{\mathrm{new}}=arg\underset{c}{max}{\hat{y}}_{i,c}.$$

(9)

The resulting pseudo-labels $\tilde{\mathbf{L}}$ incorporate both spectral discrimination and spatial consistency, forming a robust foundation for the subsequent superpixel-level clustering and topological graph modeling.

Intuitively, the residual Graph Attention Network can be viewed as a learned edge-aware filter: each pixel first listens to its immediate neighborhood through attention-weighted aggregation, then adds this contextual message back to its own feature via a skip connection, much like sharpening an image with information from surrounding pixels. This mechanism jointly promotes spectral discrimination and local spatial coherence while keeping the original signal intact.

3.4. Superpixel-Level Clustering and Graph Optimization

To preserve meaningful spectral–spatial information, we adopt a superpixel-based strategy that aggregates pixel-level features into spatially coherent regions, effectively reducing data complexity.

Based on the refined pixel-level pseudo-labels $\tilde{\mathbf{L}}$, we first generate superpixels by merging spatially connected pixels sharing the same label. For each superpixel $s\in \mathcal{S}$, a representative feature vector ${\mathbf{f}}_s$ is extracted by averaging the original spectral features and normalized spatial coordinates of its constituent pixels:

$${\mathbf{f}}_s=\left[{\displaystyle \frac{1}{|S_s|}}\sum _{i\in S_s}{\mathbf{x}}_i^{\mathrm{orig}}\parallel {\displaystyle \frac{1}{|S_s|}}\sum _{i\in S_s}{\mathbf{c}}_i\right],$$

(10)

where ${\mathbf{x}}_i^{\mathrm{orig}}\in {\mathbb{R}}^C$ is the spectral vector, and ${\mathbf{c}}_i=[r_i/H,c_i/W]\in {\mathbb{R}}^2$ is the spatial coordinate. To ensure numerical stability, we further normalize or project the aggregated features using PCA. Small superpixels below a threshold $T_s$ are merged into their nearest larger neighbors to ensure compact and balanced graph nodes.

We then construct a superpixel-level graph $G_S=(\mathcal{S},{\mathcal{E}}_S)$, where nodes represent superpixels and edges link spatially adjacent superpixels with similar spectral features. An edge is formed between superpixels $s_i$ and $s_j$ if they share a boundary and satisfy ${\parallel {\mathbf{f}}_{s_i}-{\mathbf{f}}_{s_j}\parallel }_2<{\tau }_s$, where ${\tau }_s$ is a spectral similarity threshold. The resulting binary adjacency matrix ${\mathbf{A}}_{\mathrm{superpixel}}\in {\{0,1\}}^{\left|\mathcal{S}\right|\times \left|\mathcal{S}\right|}$ encodes spatial and spectral connectivity.

To capture high-level graph structure, we adopt a Variational Graph Autoencoder (VGAE) [35] to encode each node into a latent representation $\mathbf{Z}\in {\mathbb{R}}^{\left|\mathcal{S}\right|\times d}$, which reconstructs adjacency via

$${\mathcal{L}}_{\mathrm{rec}}={∥{\mathbf{A}}_{\mathrm{superpixel}}-{\hat{\mathbf{A}}}_{\mathrm{superpixel}}∥}_F^2,{\hat{\mathbf{A}}}_{\mathrm{superpixel}}=\sigma \left(\mathbf{Z}{\mathbf{Z}}^{\top }\right),$$

(11)

where $\sigma (·)$ is the sigmoid activation. However, the manually constructed adjacency matrix ${\mathbf{A}}_{\mathrm{superpixel}}$ may still suffer from threshold sensitivity and noisy connectivity. To alleviate this, we introduce a topology refinement step using Quantum-behaved Particle Swarm Optimization (QPSO), which seeks an optimized adjacency matrix that enhances the reconstruction ability of VGAE while maintaining sparsity:

$${\mathcal{L}}_{\mathrm{QPSO}}={\mathcal{L}}_{\mathrm{rec}}+\lambda {\parallel {\mathbf{A}}_{\mathrm{superpixel}}\parallel }_1,$$

(12)

where $\lambda$ controls the trade-off between reconstruction accuracy and connectivity sparsity.

This joint modeling and refinement pipeline results in a topology-aware embedding space $\mathbf{Z}$, which encodes compact, structure-preserving representations suitable for final clustering. Compared to traditional clustering on raw spectral features, our approach yields more stable clusters by exploiting multi-scale contextual and topological cues.

Think of the VGAE encoder as compressing the superpixel graph into an “interactive map”: superpixels that look alike (similar spectra) and live next door (share a boundary) are placed close together, whereas dissimilar or distant regions are mapped farther apart. The decoder then attempts to redraw the road network (edges) from these coordinates; if two superpixels end up far apart on the map, it assigns a low connection probability. Minimizing the reconstruction loss therefore yields a latent space that faithfully preserves spectral–spatial structure while filtering out noise.

3.5. Quantum-Driven Optimization of Superpixel Graph Structures

Although the superpixel graph provides a compact and spatially coherent abstraction of the hyperspectral scene, the initial adjacency matrix ${\mathbf{A}}_{\mathrm{superpixel}}$ is typically constructed via hand-crafted criteria, relying on fixed thresholds of spectral similarity and spatial adjacency. This heuristic construction may lead to sub-optimal graph topology that fails to accurately reflect the intrinsic structural relationships between regions.

To address this issue, we propose a quantum-inspired optimization strategy based on Quantum-behaved Particle Swarm Optimization (QPSO). QPSO enables a data-driven refinement of the graph structure by iteratively updating candidate adjacency matrices in a high-dimensional latent space. The goal is to discover an optimized graph topology that facilitates accurate reconstruction and meaningful representation learning via a Variational Graph Autoencoder (VGAE).

Formally, each particle in the QPSO swarm represents a candidate adjacency matrix ${\mathbf{A}}^{\left(p\right)}$. For each particle p, a VGAE is trained to encode node features into latent embeddings ${\mathbf{Z}}^{\left(p\right)}\in {\mathbb{R}}^{\left|\mathcal{S}\right|\times d}$, and the reconstruction loss is defined as follows:

$${\mathcal{L}}_{\mathrm{rec}}^{\left(p\right)}={∥{\mathbf{A}}^{\left(p\right)}-{\hat{\mathbf{A}}}^{\left(p\right)}∥}_F^2,{\hat{\mathbf{A}}}^{\left(p\right)}=\sigma \left({\mathbf{Z}}^{\left(p\right)}{{\mathbf{Z}}^{\left(p\right)}}^{\top }\right),$$

(13)

where $\sigma (·)$ denotes the sigmoid activation function. To encourage sparsity and reduce over-connectivity, we impose an ${\ell }_1$-norm regularization, resulting in the total optimization objective:

$${\mathcal{L}}^{\left(p\right)}={\mathcal{L}}_{\mathrm{rec}}^{\left(p\right)}+\lambda {∥{\mathbf{A}}^{\left(p\right)}∥}_1,$$

(14)

where $\lambda$ controls the balance between structure fidelity and sparsity.

The QPSO algorithm iteratively updates each ${\mathbf{A}}^{\left(p\right)}$ by sampling from a quantum potential field centered around the global best adjacency matrix ${\mathbf{A}}_{\mathrm{gbest}}$. Compared to conventional PSO, QPSO allows more diverse exploration in non-convex search spaces and alleviates the risk of premature convergence. The optimization process terminates when the global loss stagnates or a maximum number of iterations is reached.

Upon convergence, the optimized adjacency matrix ${\mathbf{A}}_{\mathrm{opt}}$ is used to retrain the VGAE, yielding refined latent embeddings $\mathbf{Z}$. These embeddings are then concatenated with the spectral–spatial descriptors ${\mathbf{f}}_s^{\mathrm{processed}}$ of each superpixel to form the final representation:

$${\mathbf{f}}_s^{\mathrm{final}}=\left[{\mathbf{Z}}_s\parallel {\mathbf{f}}_s^{\mathrm{processed}}\right].$$

(15)

K-means is then applied to the fused features $\left\{{\mathbf{f}}_s^{\mathrm{final}}\right\}$ to generate the final cluster assignments ${\hat{\mathbf{L}}}^{\mathrm{final}}$.

The success of this optimization process fundamentally relies on the quality of the initial superpixel generation. The preceding residual GAT module ensures that each superpixel aggregates pixels with coherent spectral-spatial semantics, providing a strong prior for region-level modeling. This hierarchical pipeline—combining pixel-wise refinement, superpixel aggregation, and quantum-driven graph optimization—enables progressive enhancement of representation quality and clustering robustness.

Quantum-behaved Particle Swarm Optimisation (QPSO) can be pictured as a flock of candidate adjacency matrices “flying” through the search space. Each particle proposes a slightly rewired graph; after a short VGAE training session, we measure how well that graph can be reconstructed and how sparse it remains. The best-performing particle pulls the rest of the flock towards promising regions, while random quantum jumps maintain exploration. Iterations continue until the overall loss change becomes negligible, producing an adjacency matrix that reflects the scene topology yet avoids spurious connections.

4. Experiments

To comprehensively validate the effectiveness and generality of our proposed JSRL framework, we conduct extensive experiments on three widely used hyperspectral image datasets: Salinas, Pavia University, and Pavia Center. These datasets encompass diverse spectral and spatial characteristics, providing a robust testbed for evaluating clustering methods.

4.1. Datasets and Implementation Details

We evaluate JSRL on three widely-used hyperspectral datasets with diverse spectral and spatial characteristics. All datasets are preprocessed by removing noisy bands (e.g., water absorption), followed by normalization and PCA to retain 99% spectral energy. Salinas (AVIRIS sensor) contains $512\times 217$ pixels, 204 bands, and 16 agricultural classes. Pavia University and Pavia Center (ROSIS sensor) include $610\times 340$ and $1096\times 715$ pixels with 103 and 102 bands retained, respectively, each containing 9 urban classes.

In JSRL, the minimum superpixel size $T_{\min }$ is set to 20, and $k=10$ is used for graph construction. Both GAT and VGAE are trained for 200 epochs with a learning rate of 0.001. Experiments are run on a CPU with 16 GB RAM, and all results are averaged over 10 runs for reliability.

4.2. Evaluation Metrics and Compared Methods

To comprehensively evaluate clustering performance, we adopt there widely used metrics: Overall Accuracy (ACC), Normalized Mutual Information (NMI), and Adjusted Rand Index (ARI). Together, these metrics provide a multifaceted assessment of clustering quality by measuring label agreement with ground truth (ACC,) and cluster compactness and separation (NMI, ARI). This comprehensive evaluation ensures a robust and fair comparison of different clustering methods under various criteria.

We benchmark our proposed JSRL framework against a diverse set of conventional and state-of-the-art clustering approaches. Classical methods include K-means [17] and FCM [36], which serve as strong baselines for spectral clustering. In addition, we compare with more recent graph- and superpixel-based algorithms such as FSCAG [37], SGCNR [38], NCSC [39], SGLSC [40], and S³AGC [41], which exploit spatial and spectral contextual information for improved clustering. Furthermore, we utilize SAPC [42] as a base pseudo-label generator, leveraging its ability to produce initial superpixel-level cluster assignments. Our JSRL framework then refines these pseudo-labels through hierarchical spectral–spatial representation learning, enabling more accurate and semantically consistent clustering results.

4.3. Experimental Results

Table 1. Clustering performance comparison of different methods on three HSI datasets (%). The best results per metric are highlighted in bold.

Dataset	Metric	Method
		K-Means	FCM	FSCAG	SGCNR	NCSC	SGLSC	S3AGC	Ours
Salinas	ACC	64.56	60.65	65.90	62.24	74.97	76.64	74.65	79.39
	NMI	72.75	70.72	74.12	71.24	81.76	83.88	78.36	82.43
	ARI	53.92	47.61	54.44	49.78	66.50	65.53	60.95	68.40
Pavia Univ.	ACC	53.70	52.63	52.88	50.19	43.92	62.45	53.75	66.53
	NMI	53.21	52.91	55.88	50.68	43.55	54.10	49.02	58.51
	ARI	32.55	31.67	33.06	29.82	29.05	50.63	33.84	45.10
Pavia Center	ACC	72.36	70.44	72.75	74.53	65.84	82.04	85.48	93.75
	NMI	69.95	69.89	73.39	69.02	59.59	76.51	79.37	89.88
	ARI	76.69	76.81	80.57	75.94	72.55	87.07	88.04	95.02

shows the quantitative clustering results of our JSRL framework and several state-of-the-art baselines on three hyperspectral datasets: Salinas, Pavia University, and Pavia Center. Across all datasets and metrics—Accuracy (ACC), Normalized Mutual Information (NMI), and Adjusted Rand Index (ARI)—JSRL consistently outperforms competing methods, demonstrating strong robustness and generalization. On the Salinas dataset, JSRL achieves the highest ACC of 79.39%, surpassing baselines like NCSC (74.97%) and SGLSC (76.64%). Despite the greater challenge of Pavia University due to lower inter-class variance, JSRL still leads with ACC of 66.53% and NMI of 58.51%. On Pavia Center, which has clearer spatial boundaries, JSRL attains an ACC of 93.75% and ARI of 95.02%, significantly improving over prior results. These gains come from JSRL’s hierarchical design. Unlike methods treating pixels independently or relying on fixed superpixel boundaries, JSRL refines pseudo-labels from lightweight base clusterers (e.g., K-means, SAPC [42]) via a two-stage process. Pixel-wise GAT enhances spectral–spatial features, while superpixel-level VGAE with QPSO jointly optimizes global cluster structure, boosting semantic coherence and separability. 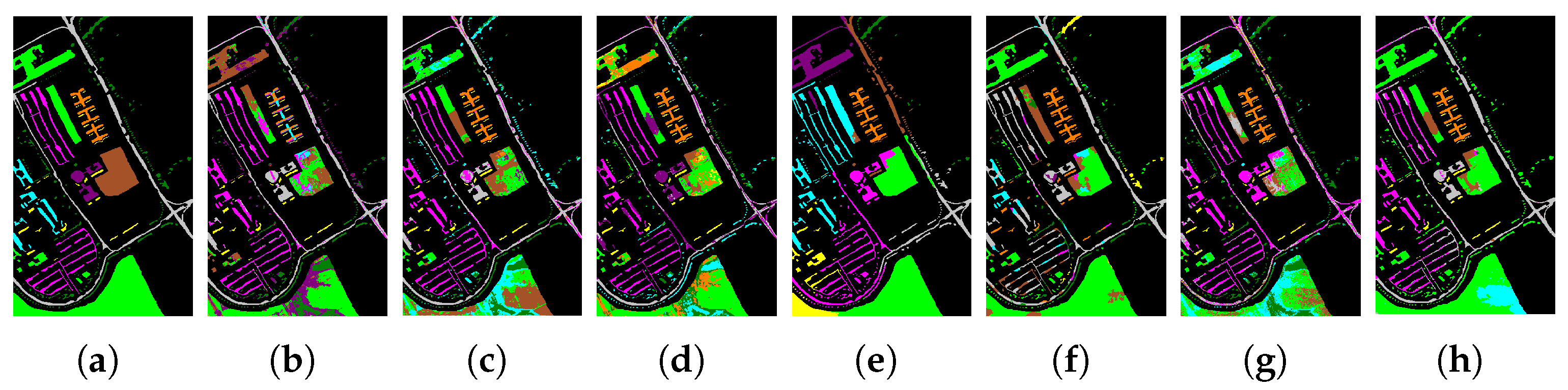Figure 2, Figure 3 and Figure 4 illustrate the visual clustering results on the Salinas, Pavia University, and Pavia Center datasets, respectively. Across all three datasets, the proposed JSRL method consistently produces more coherent segmentation maps with clearer region boundaries and fewer fragmented regions compared to competing approaches. In particular, on the Pavia Center dataset, JSRL yields significantly cleaner structures, which aligns with its superior performance in quantitative metrics. These visual results further demonstrate JSRL’s ability to effectively capture the intrinsic spectral–spatial structure of hyperspectral data. Taken together, the quantitative and qualitative results jointly validate the robustness and effectiveness of the proposed JSRL framework for hyperspectral image clustering.

4.4. Ablation Results

To further understand the contribution of each JSRL component, we conduct an ablation study by removing GAT, VGAE, and QPSO modules, respectively.

Table 2. Ablation study (%) of JSRL components across datasets. Best results per column are in bold.

Method	Salinas			Pavia Univ.			Pavia Center
	ACC	NMI	ARI	ACC	NMI	ARI	ACC	NMI	ARI
Ours	79.39	82.43	68.40	66.53	58.51	45.10	93.75	90.88	97.43
Ours (w/o GAT)	75.03	78.23	64.56	62.21	54.64	40.21	90.02	88.20	94.23
Ours (w/o VGAE)	76.46	79.30	65.50	64.30	56.28	42.56	92.24	89.71	95.36
Ours (w/o QPSO)	77.06	80.51	66.75	65.54	57.53	43.72	93.12	90.58	96.46

summarizes the ablation study of our JSRL framework across three hyperspectral image datasets. The results show that removing the GAT module consistently leads to the most significant performance degradation across all datasets (e.g., ACC drops from 79.39% to 75.03% on Salinas), underscoring its vital role in refining pixel-level representations via attention-based spectral–spatial aggregation. Eliminating the VGAE component also causes notable drops (e.g., ARI from 45.10% to 42.56% on Pavia University), confirming the importance of structure-aware encoding in modeling global topology. While the performance decline from removing QPSO is relatively modest, it is consistent across metrics and datasets, highlighting the benefit of graph structure refinement in boosting clustering separability. Overall, the ablation results validate that GAT, VGAE, and QPSO each play a distinct yet complementary role, and their integration is crucial for the effectiveness and generalizability of our spectral–spatial clustering framework.

4.5. Parameter Sensitivity and Runtime Results

For the hyperparameter study, we examine three key hyperparameters: the QPSO sparsity weight $\lambda$, the number of residual GAT layers L, and the latent dimension d of VGAE. Each factor is swept while the others are fixed to their default values ($\lambda =1$, $L=3$, $d=32$).

Table 3. Parameter sensitivity of JSRL on the Pavia Center dataset (ACC %). Each row varies a single factor; other parameters are kept at their defaults.

QPSO sparsity weight λ
$\lambda$	0.1	0.5	1.0	2.0	5.0	10.0	20.0
ACC (%)	87.92	91.33	93.75	92.64	91.83	89.46	84.75
Number of GAT layers $\mathit{L}$
L	1	2	3	4	5	6	8
ACC (%)	88.54	90.77	93.75	92.57	92.55	92.33	91.98
Latent dimension $\mathit{d}$ of VGAE
d	16	32	64	128	192	256	384
ACC (%)	91.04	93.75	92.65	92.76	92.69	92.44	92.11

shows that JSRL is robust: accuracy varies by less than 3 percentage points across all tested settings and remains within $\pm 1.0\%$ of the peak when $\lambda \in [0.5,2.0]$, $L\ge 2$, and $d\ge 32$. These observations justify the default configuration adopted throughout the paper and indicate a low risk of over-tuning.

We benchmark the wall-clock time required to cluster three benchmark scenes on a single NVIDIA RTX 3080 (CUDA 12, 16 GB RAM).

Table 4. Wall-clock runtime (seconds) of JSRL and ablated variants.

Variant	Salinas	PaviaU	PaviaC
JSRL (full)	38	66	71
– QPSO	29	49	54
– VGAE	24	39	43
– Residual GAT	30	52	58

reports averages over three runs. The full JSRL pipeline finishes the Salinas scene in 38 s, Pavia University in 66 s, and Pavia Center in 71 s. Removing the Quantum-behaved Particle Swarm Optimization (–QPSO) eliminates the graph-refinement loop and reduces runtime by roughly one-third, while omitting the Variational Graph Auto-Encoder (–VGAE) further shortens training time. In contrast, discarding the residual Graph Attention Network (–GAT) yields only modest savings, because the model still executes two forward passes per epoch for feature normalization. These figures show the following: (i) VGAE training accounts for 40% of total time; (ii) QPSO adds a controllable overhead (25%) that can be parallelized; (iii) The complete JSRL remains practical—under 1 min—for city-scale HSI scenes, while the memory footprint never exceeds 1.8 GB.

5. Conclusions

We present a hierarchical Joint Spectral–Spatial Representation Learning (JSRL) framework for hyperspectral image clustering that effectively addresses challenges of high spectral dimensionality, redundancy, and limited labeled data. By integrating pseudo-supervised pixel-level feature refinement via a residual Graph Attention Network with global topology-aware modeling through a Variational Graph Autoencoder, our method robustly captures both local spectral–spatial context and global structural information. The introduction of Quantum-behaved Particle Swarm Optimization further enhances graph topology optimization, improving cluster separability. Extensive experiments demonstrate that JSRL achieves stable and superior clustering performance across multiple hyperspectral datasets, highlighting its potential as a scalable and generalizable solution for unsupervised HSI analysis.

Despite the encouraging results, the present JSRL framework still exhibits several limitations that merit further study:

Computational footprint. Although QPSO accelerates graph optimization relative to exhaustive search, the two-stage training (GAT + VGAE) is still ≈1.8× slower than lightweight spectral–spatial CNN baselines on a single CPU. Future work will explore surrogate-model acceleration and mixed-precision training.

Sensitivity to graph-construction hyperparameters. Performance declines when the superpixel size $T_{min}$ or the k-nearest-neighbor radius is badly tuned for scenes with extreme object-scale variability. We are investigating Bayesian optimization and meta-learning schemes to auto-tune these parameters online.

Over-segmentation in highly textured regions. The residual GAT occasionally produces fragmented clusters where local contrast is very high, leading to superfluous boundaries. Adaptive attention radii or texture-aware regularizers may mitigate this issue.

These observations not only delineate the current boundaries of JSRL but also chart clear directions for subsequent research and optimization.