Synthetic Aperture Radar (SAR) Data Compression Based on Cosine Similarity of Point Clouds
Abstract
1. Introduction
2. Materials and Methods
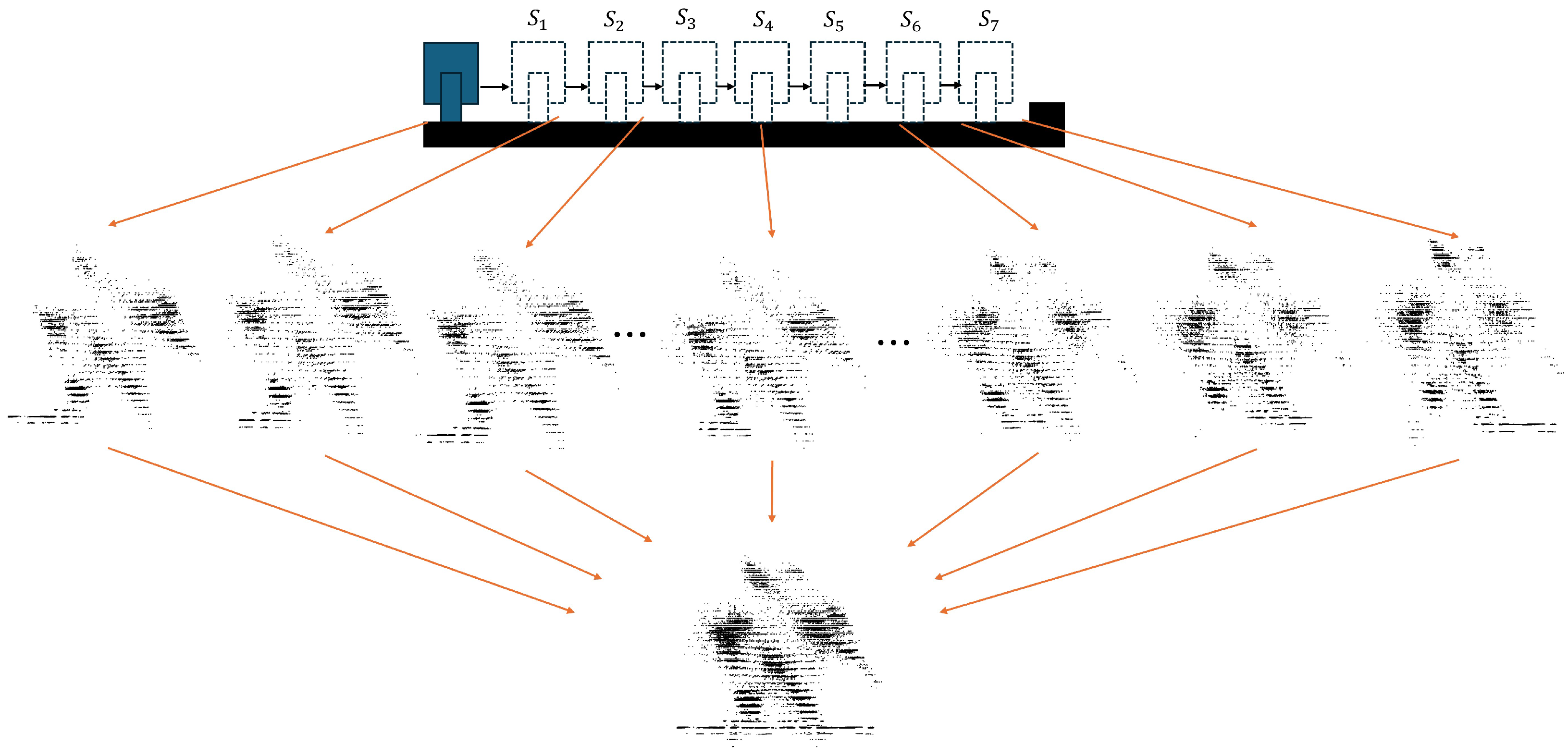
2.1. FMCW-Based SAR System and Point Cloud Generation
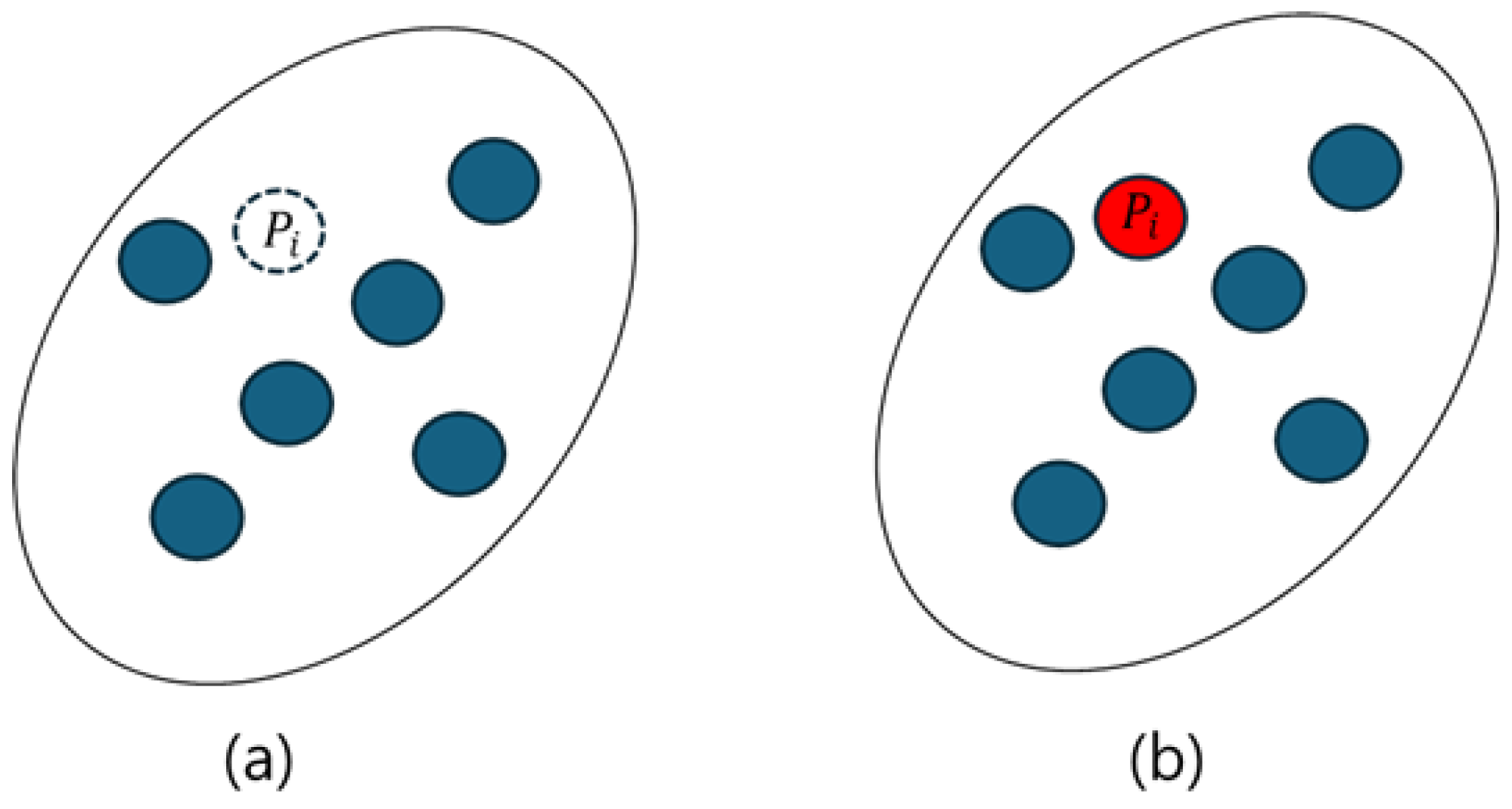
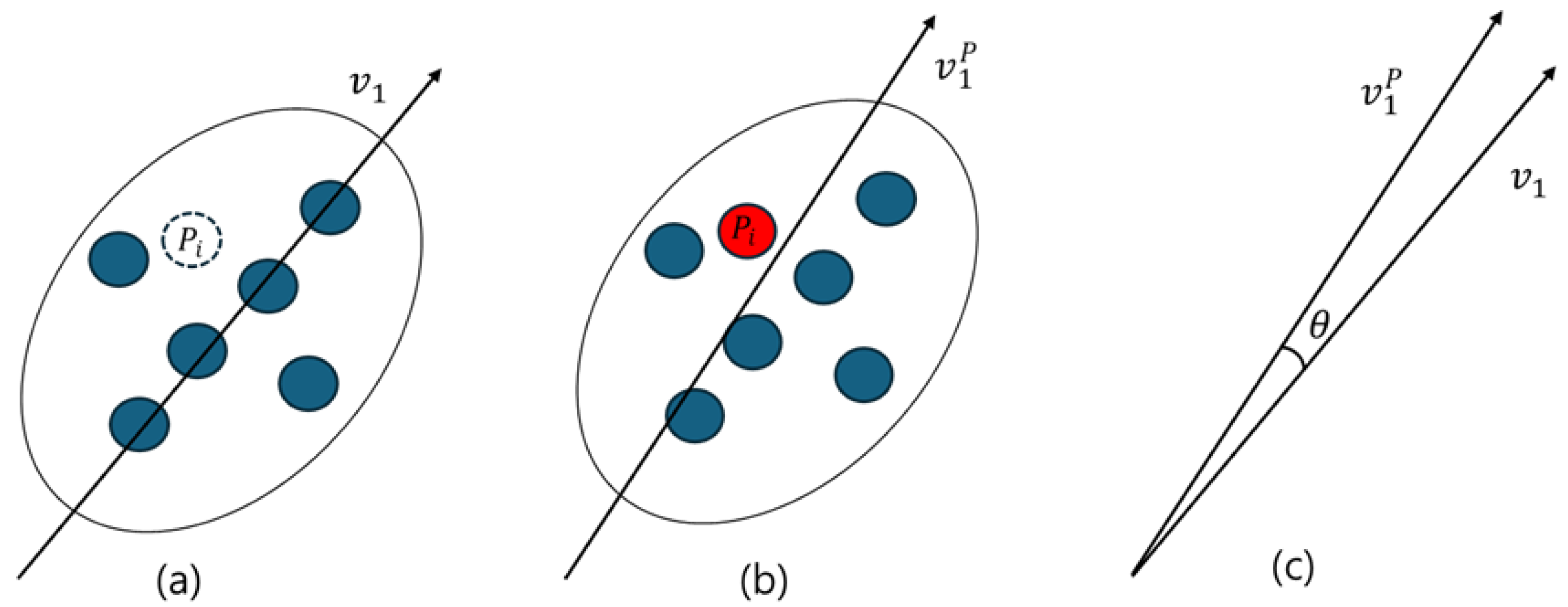
2.2. Novel Point Cloud Compression Based on Cosine Similarity
3. Discussion
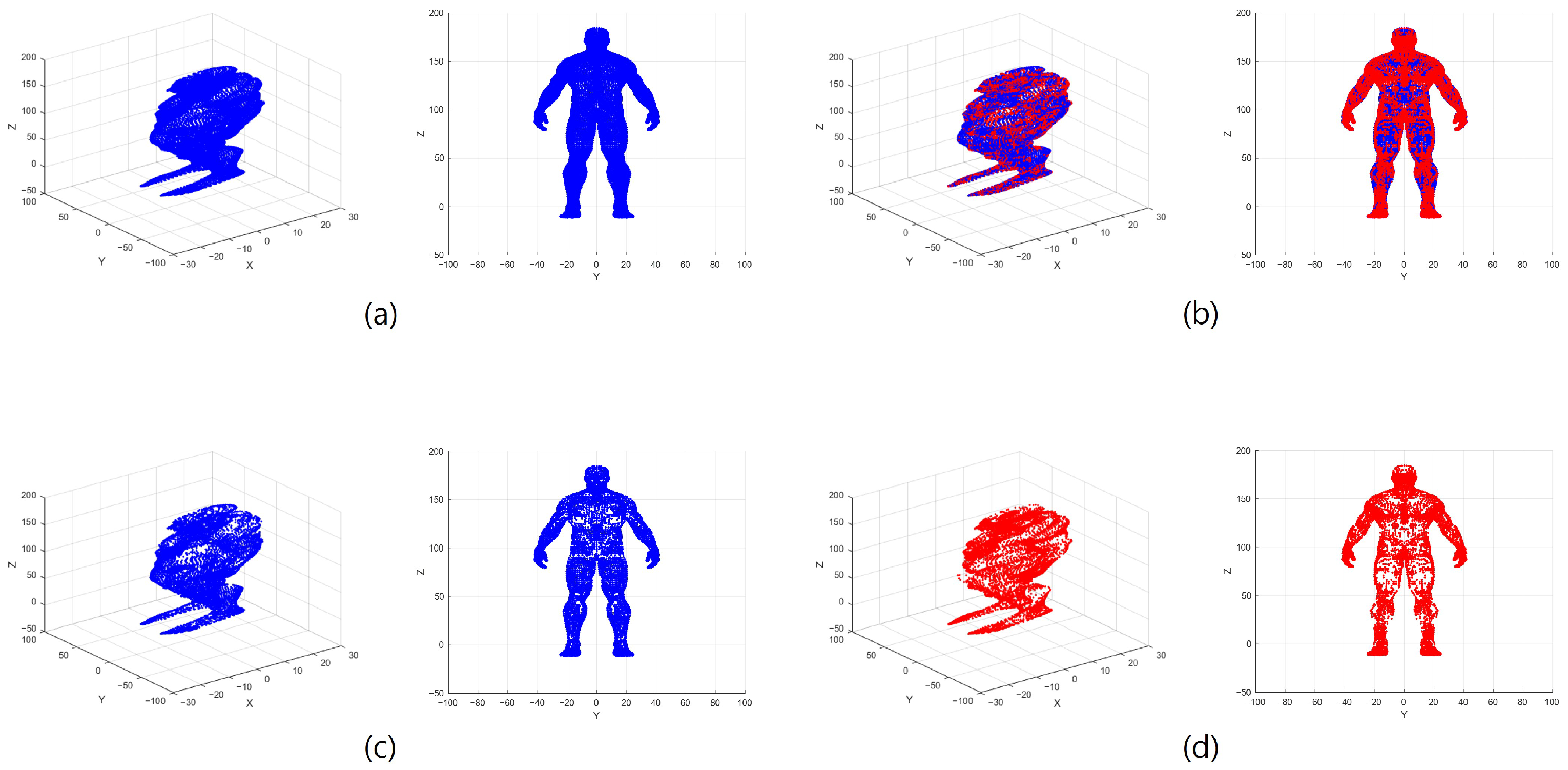
4. Experimental Results
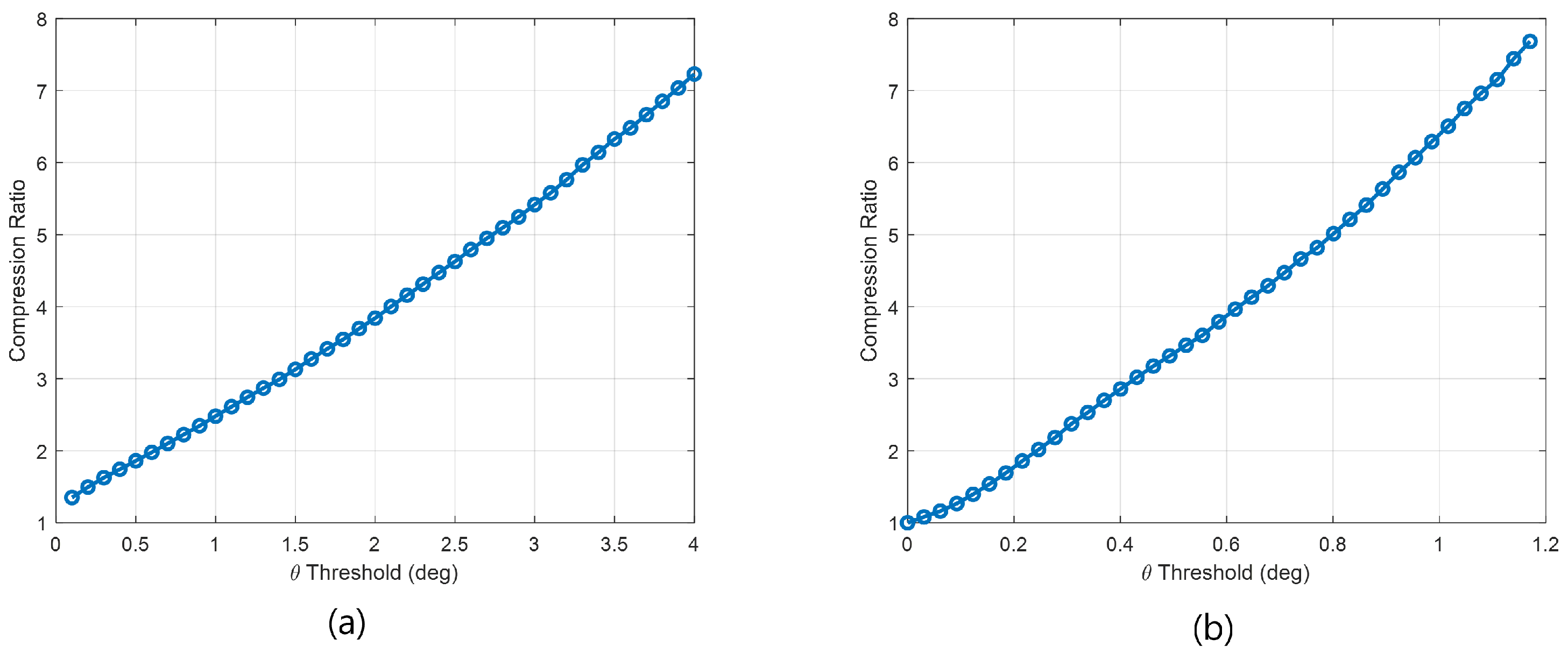
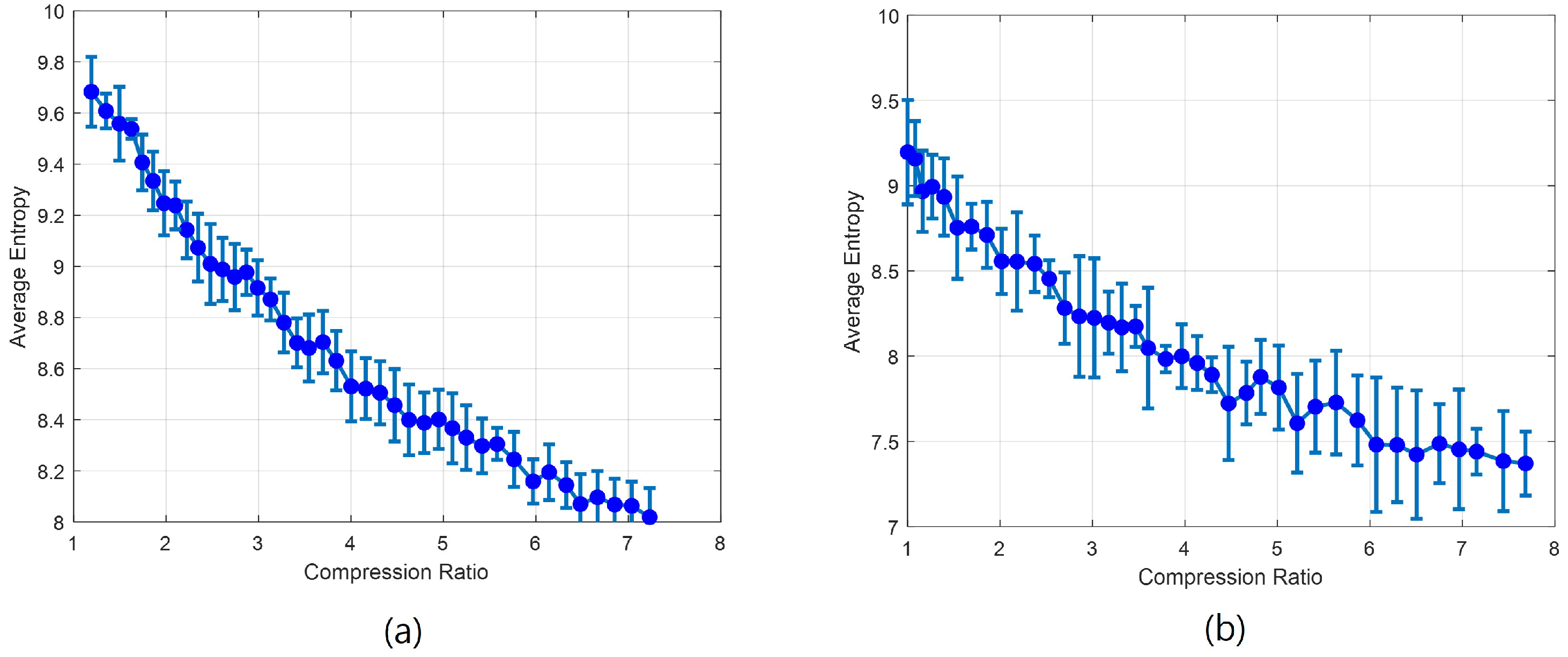
4.1. Entropy-Based Compression Performance
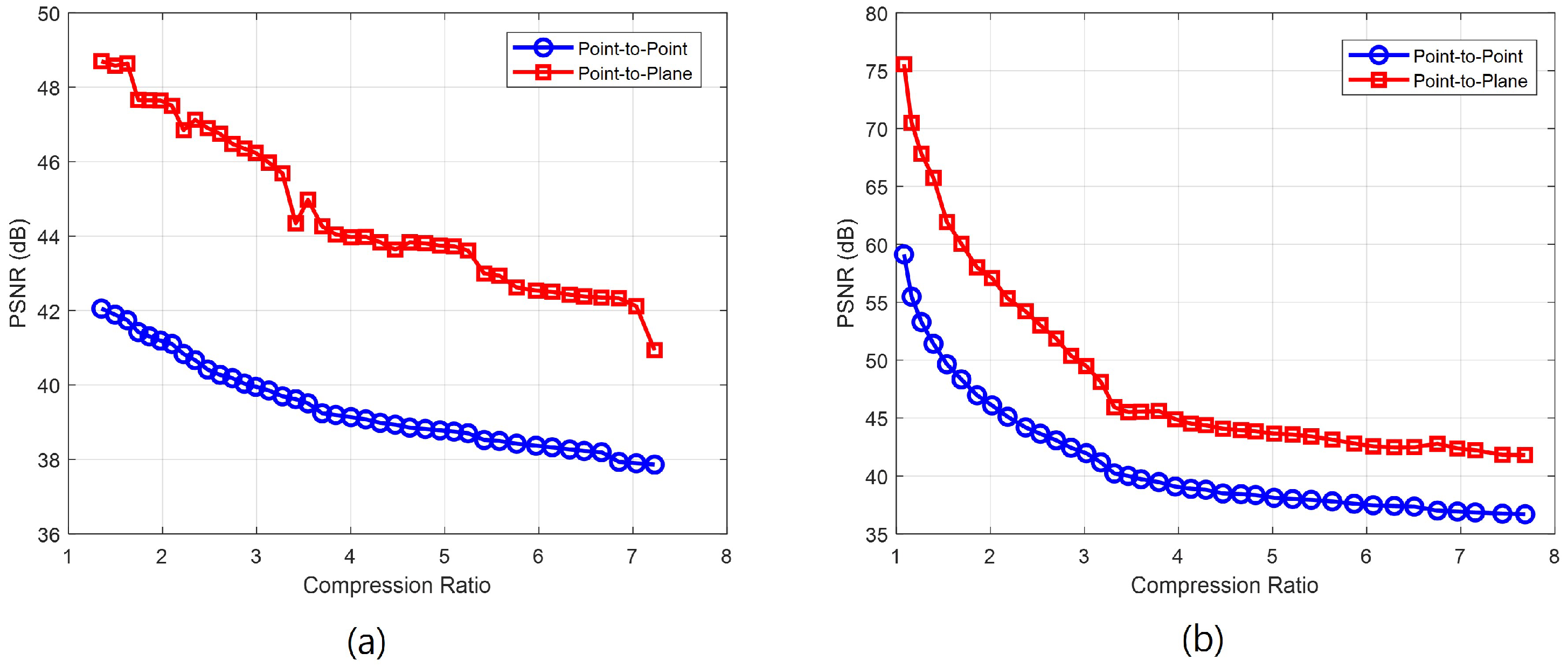
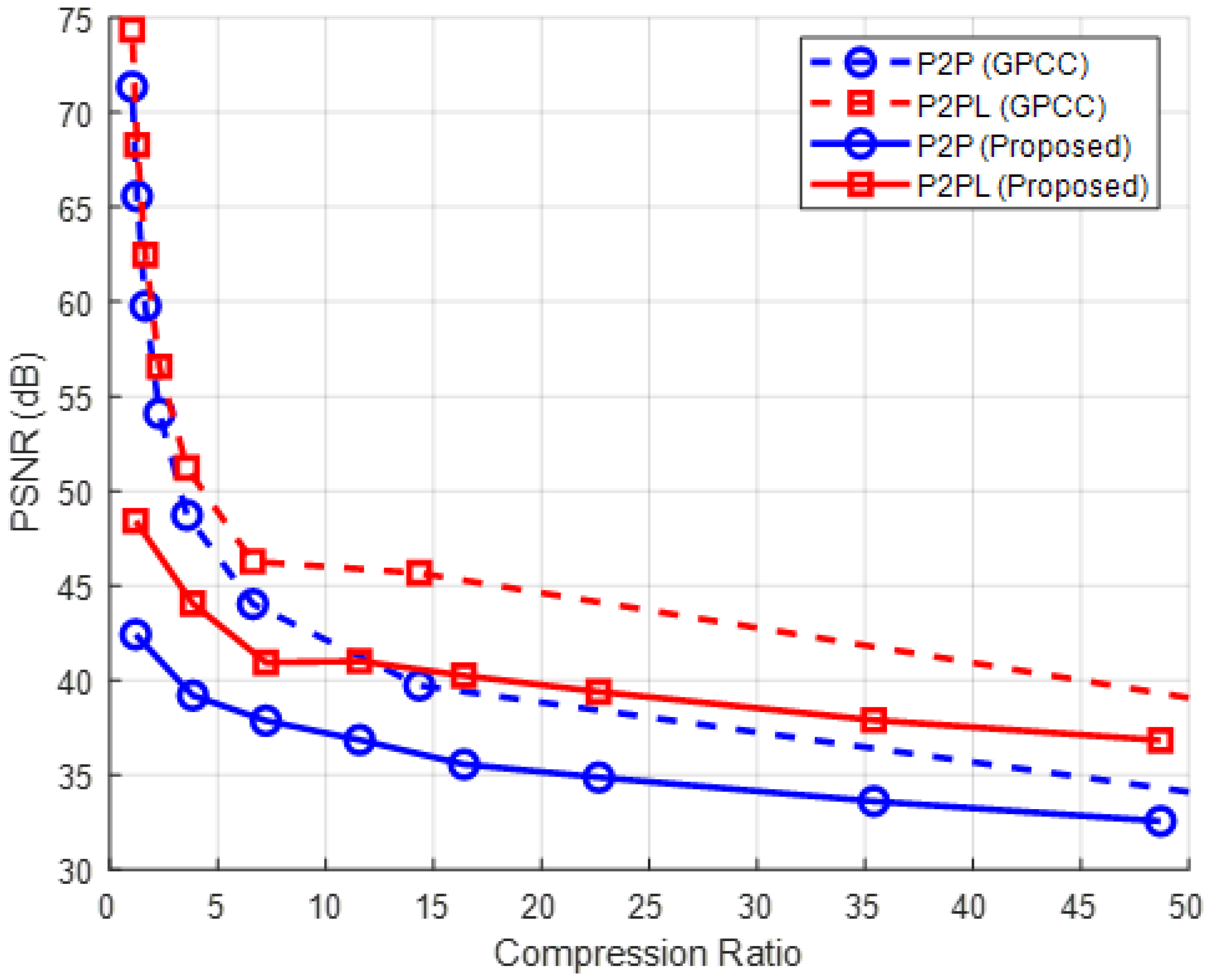
4.2. PSNR-Based Compression Performance
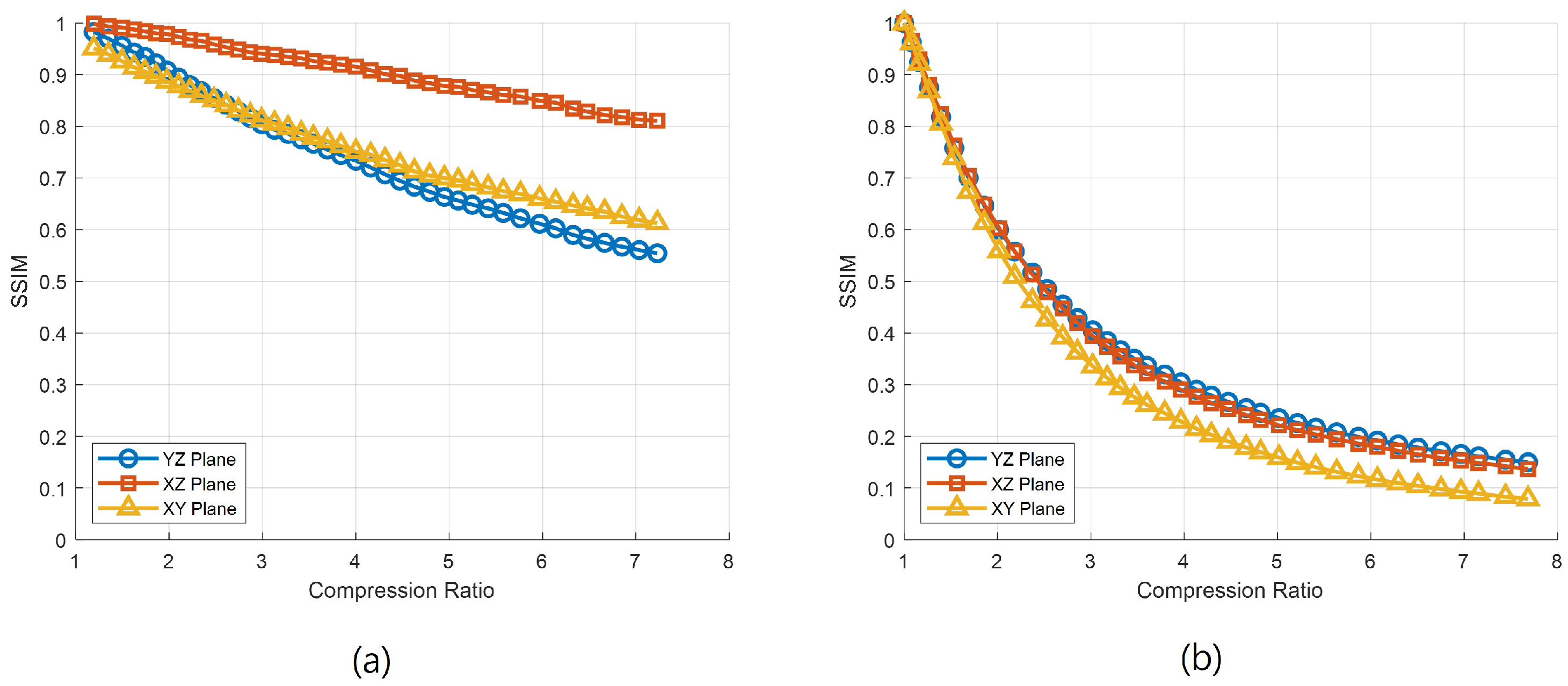
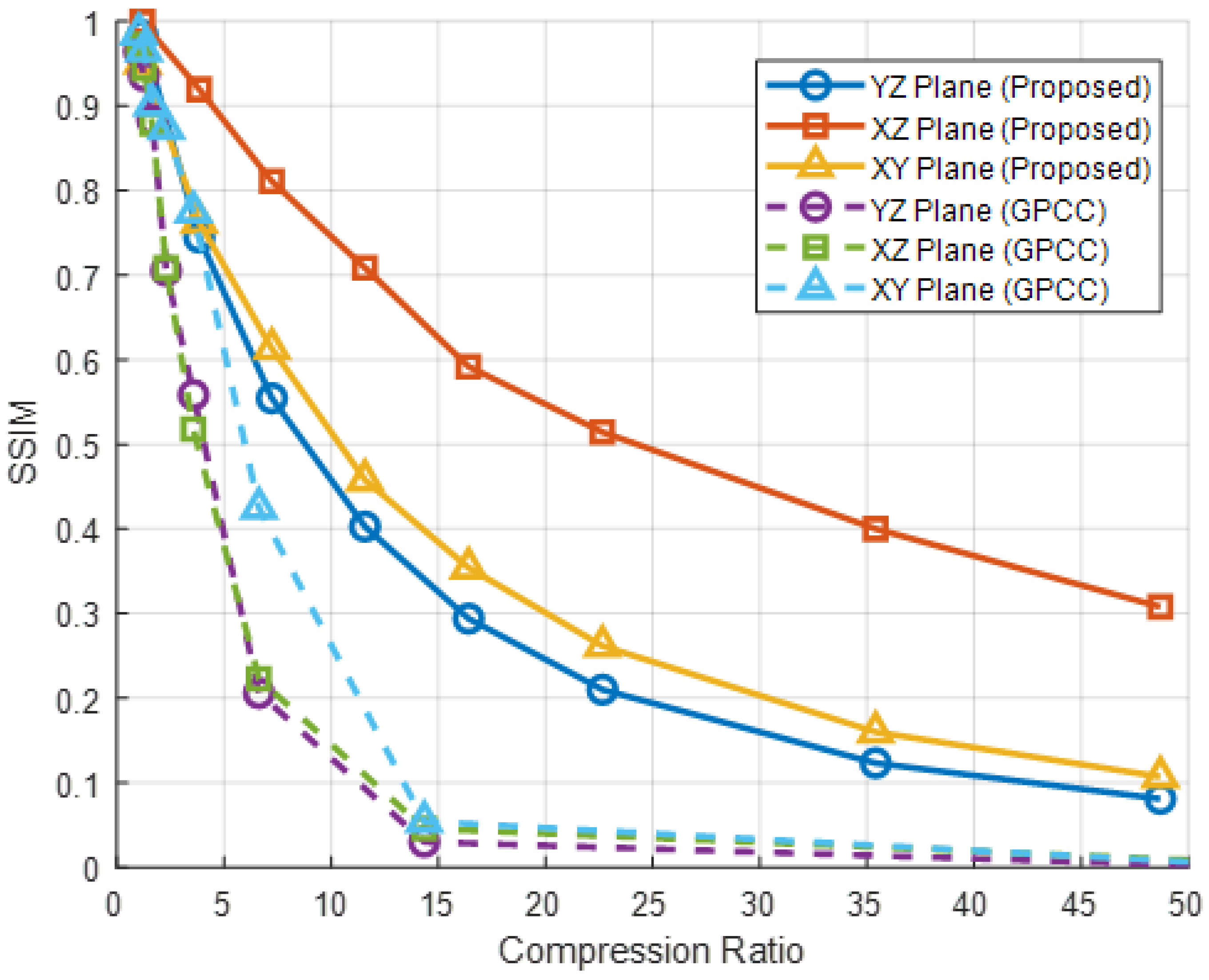
4.3. SSIM-Based Compression Performance
4.4. Comparison of Point Cloud Compression Performance: Proposed Method vs. G-PCC
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Otepka, J.; Ghuffar, S.; Waldhauser, C.; Hochreiter, R.; Pfeifer, N. Georeferenced Point Clouds: A Survey of Features and Point Cloud Management. ISPRS Int. J. Geo-Inf. 2013, 2, 1038–1065. [Google Scholar] [CrossRef]
- Chen, S.; Liu, B.; Feng, C.; Vallespi-Gonzalez, C.; Wellington, C. 3D Point Cloud Processing and Learning for Autonomous Driving: Impacting Map Creation, Localization, and Perception. IEEE Signal Process. Mag. 2021, 38, 68–86. [Google Scholar] [CrossRef]
- Cheng, Y.; Liu, Y. Person Reidentification Based on Automotive Radar Point Clouds. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5101913. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, J.; Jiang, G. Spatial and Temporal Awareness Network for Semantic Segmentation on Automotive Radar Point Cloud. IEEE Trans. Intell. Veh. 2024, 9, 3520–3530. [Google Scholar] [CrossRef]
- Cheng, Y.; Su, J.; Jiang, M.; Liu, Y. A Novel Radar Point Cloud Generation Method for Robot Environment Perception. IEEE Trans. Robot. 2022, 38, 3754–3773. [Google Scholar] [CrossRef]
- Sturm, C.; Wiesbeck, W. Waveform Design and Signal Processing Aspects for Fusion of Wireless Communications and Radar Sensing. Proc. IEEE 2011, 99, 1236–1259. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P.; Zheng, X. Signal Synthesis and Receiver Design for MIMO Radar Imaging. IEEE Trans. Signal Process. 2008, 56, 3959–3968. [Google Scholar] [CrossRef]
- Brown, W.M.; Porcello, L.J. An Introduction to Synthetic-Aperture Radar. IEEE Spectr. 1969, 6, 52–62. [Google Scholar] [CrossRef]
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A Tutorial on Synthetic Aperture Radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef]
- Garcia, D.C.; Fonseca, T.A.; Ferreira, R.U.; de Queiroz, R.L. Geometry Coding for Dynamic Voxelized Point Clouds Using Octrees and Multiple Contexts. IEEE Trans. Image Process. 2020, 29, 313–322. [Google Scholar] [CrossRef]
- Liu, H.; Yuan, H.; Liu, Q.; Hou, J.; Zeng, H.; Kwong, S. A Hybrid Compression Framework for Color Attributes of Static 3D Point Clouds. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 1564–1577. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, H.; Liu, H.; Ma, Z. Lossy Point Cloud Geometry Compression via End-to-End Learning. IEEE Trans. Circuits Syst. Video Technol. 2021, 31, 4909–4923. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Quach, M.; Valenzise, G.; Duhamel, P. Lossless Coding of Point Cloud Geometry Using a Deep Generative Model. IEEE Trans. Circuits Syst. Video Technol. 2021, 31, 4617–4629. [Google Scholar] [CrossRef]
- Li, D.; Ma, K.; Wang, J.; Li, G. Hierarchical Prior-Based Super Resolution for Point Cloud Geometry Compression. IEEE Trans. Image Process. 2024, 33, 1965–1976. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Rhee, S.; Kwon, H.; Kim, K. LiDAR Point Cloud Compression by Vertically Placed Objects Based on Global Motion Prediction. IEEE Access 2022, 10, 15298–15310. [Google Scholar] [CrossRef]
- Sheng, X.; Li, L.; Liu, D.; Xiong, Z. Attribute Artifacts Removal for Geometry-Based Point Cloud Compression. IEEE Trans. Image Process. 2022, 31, 3399–3413. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, P.; Wang, M.; Chen, P.; Wang, S.; Kwong, S. Geometric Prior Based Deep Human Point Cloud Geometry Compression. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 8794–8807. [Google Scholar] [CrossRef]
- Jung, C.; Yoo, Y.; Kim, H.-W.; Shin, H.-C. Detecting Sleep-Related Breathing Disorders Using FMCW Radar. J. Electromagn. Eng. Sci. 2023, 23, 437–445. [Google Scholar] [CrossRef]
- Yoo, Y.-K.; Jung, C.-W.; Shin, H.-C. Unsupervised Detection of Multiple Sleep Stages Using a Single FMCW Radar. Appl. Sci. 2023, 13, 4468. [Google Scholar] [CrossRef]
- Marin, R.; Melzi, S.; Castellani, U.; Rodolà, E. FARM: Functional Automatic Registration Method for 3D Human Bodies. arXiv 2019, arXiv:1807.10517. [Google Scholar] [CrossRef]
- Loper, M.; Mahmood, N.; Romero, J.; Pons-Moll, G.; Black, M.J. SMPL: A Skinned Multi-Person Linear Model. ACM Trans. Graph. 2015, 34, 248:1–248:16. [Google Scholar] [CrossRef]
- Tian, D.; Ochimizu, H.; Feng, C.; Cohen, R.; Vetro, A. Geometric Distortion Metrics for Point Cloud Compression. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 346–350. [Google Scholar]





| Parameter | Value |
|---|---|
| Center Frequency () | 79 GHz |
| Chirp Duration () | 256 µs |
| Sampling Frequency () | 4 MHz |
| Number of Channels () | 192 (12 Tx × 16 Rx) |
| Number of Chirps () | 32 |
| Number of Samples () | 1024 |
| Chirp Interval | 0.05 Section (20 fps) |
| Bandwidth (SR/MR) | 3.0 GHz/2.2 GHz |
| Range Resolution (SR) | 0.05 m (≈5 cm) |
| Range Resolution (MR) | 0.068 m (≈6.8 cm) |
| Azimuth Field of View (FOV) | ±45° |
| Elevation Field of View (FOV) | ±15° |
| Condition | 5 mm/s | 10 mm/s | 15 mm/s | 20 mm/s |
|---|---|---|---|---|
| Scan Time (s) | 160 | 80 | 55 | 40 |
| Scan Count | 1600 | 800 | 550 | 400 |
| Item | SAR-Based Data | SHREC’19 Mesh Data |
|---|---|---|
| Total Number of Points () | 32,964 points | 27,061 points |
| Number of Removed Points | 16,295 points (49.44%) | 13,774 points (50.89%) |
| Preserved Key Points () | 16,669 points (50.56%) | 13,287 points (49.11%) |
| Average Structural Angle () | ||
| Selected Threshold () | ||
| Compression Ratio (CR) | Approx. 2.0:1 | Approx. 2.0:1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.-B.; Lee, H.-H.; Shin, H.-C. Synthetic Aperture Radar (SAR) Data Compression Based on Cosine Similarity of Point Clouds. Appl. Sci. 2025, 15, 8925. https://doi.org/10.3390/app15168925
Kim Y-B, Lee H-H, Shin H-C. Synthetic Aperture Radar (SAR) Data Compression Based on Cosine Similarity of Point Clouds. Applied Sciences. 2025; 15(16):8925. https://doi.org/10.3390/app15168925
Chicago/Turabian StyleKim, Yong-Beum, Hak-Hoon Lee, and Hyun-Chool Shin. 2025. "Synthetic Aperture Radar (SAR) Data Compression Based on Cosine Similarity of Point Clouds" Applied Sciences 15, no. 16: 8925. https://doi.org/10.3390/app15168925
APA StyleKim, Y.-B., Lee, H.-H., & Shin, H.-C. (2025). Synthetic Aperture Radar (SAR) Data Compression Based on Cosine Similarity of Point Clouds. Applied Sciences, 15(16), 8925. https://doi.org/10.3390/app15168925






