A Recursive Truncated Taylor Expansion Downward Continuation Method for Geomagnetic Field

Abstract

In aeromagnetic detection and geomagnetic navigation, the reference geomagnetic maps usually need to be continued to different altitudes. Traditionally, the geomagnetic field upward continuation is stable. Nevertheless, the downward continuation is instable near the magnetic source and sensitive to the high-frequency noise. To address the problem, this article proposes a recursive truncated Taylor expansion (RTTE) downward continuation method for geomagnetic field. This method models the geomagnetic field in the vertical direction. The coefficients of the model are calculated based on the harmonicity of the geomagnetic field to ensure stability; a recursive process is implemented to extend its effect under a large continuation distance. To demonstrate the effectiveness of the proposed method, this paper compares the effects of the traditional Landweber iteration method and the proposed method using simulation data and real measured data. Under real measurement conditions, the MAE and RMSE of the proposed RTTE method are 0.1878 nT and 0.3184 nT, respectively, representing a reduction of 90.33% and 95.75% compared to the Landweber iteration method. The results show that the proposed RTTE method significantly improves the continuation accuracy compared with traditional methods, providing support for geomagnetic navigation and aeromagnetic exploration.

1. Introduction

Geomagnetic maps are essential in geomagnetic navigation, aerospace magnetic detection, etc. [1]. In aeromagnetic detection, geomagnetic reference maps are typically established at higher flight altitudes, while actual detection mission occurs at lower altitudes [2]. This altitude difference can introduce significant errors when using reference maps directly for target detection, necessitating the vertical continuation of the geomagnetic reference map. Geomagnetic field continuation estimates unmeasured altitude plane geomagnetic data from measured altitude plane data, essential for the geomagnetic field construction, geomagnetic matching navigation, and magnetic exploration [3,4].

In geophysics, potential field continuation is a key mathematical method, divided into upward and downward continuation. Upward continuation, inferring higher-altitude geomagnetic data from lower-altitude data, is a well-posed problem with a stable solution [5]. Downward continuation, inferring lower-altitude data from higher-altitude observations, is an ill-posed inverse problem of upward continuation [6].

An important approach to downward continuation is through the frequency domain. Primarily, the downward continuation uses an inverse operator in frequency domain of the upward continuation [7]. Nevertheless, its value at high frequencies increases exponentially, and the high-frequency noise of the data is amplified. Then the iterative method constructs an approximate mapping for the frequency-domain downward continuation operator to avoid the amplification of high-frequency noise [8,9]. As the number of iterations increases, the approximate mapping operator approaches the original downward continuation operator, and the high-frequency amplification effect re-emerges [10]. In order to solve the problem of high-frequency amplification, the integral iteration method [11], the Landweber iteration method [12], and Tikhonov iterative method [13] offer iterative approaches for downward continuation by improving the error correction terms in the iterative process. However, these methods still suffer from poor noise resistance, excessive iterations, and sensitive regularization parameters [14].

Spatial-domain downward continuation offers an alternative that bypasses the high-frequency instabilities inherent to frequency-domain operators. The prevailing framework employs a polynomial continuation structure derived from a Taylor expansion of the spatial field. The key point is estimating its high-order vertical derivatives [15]. Fedi and Florio first solved these via enhanced horizontal derivative method [16]. Zhang iteratively patched the downward continuation field using the residual of upward continuation [17]. Yin studies regularized the Taylor expansion in the wavenumber domain [18]. The same year, a mean-value-theorem reformulation is implemented to solve the derivatives [19]. Wang uses intermediate-plane prior information to refine intermediate steps for continuation [20]. These strategies improve the model or the iterative correction, but all remain limited by finite original data just on the single plane and the accuracy for large continuation steps is not optimal.

In this paper, we propose a recursive truncated Taylor expansion (RTTE) downward continuation method to implement downward continuation. In this method, the Taylor expansion of the potential field is performed in vertical direction, which establishes the analytical structure for using data from different altitude. Then, the reference plane is upward continued for data supplementation, and each order derivative of the Taylor expansion is calculated. And the downward continuation is implemented by vary small steps recursively, rather than a big jump to ensure the effectiveness on a large continuation distance. Thereby, the potential field continuation along the vertical line is realized. Simulation and measured data are used to validate the proposed method. The results show that the proposed method is more stable and effective in achieving downward continuation near the magnetic source compared to traditional methods.

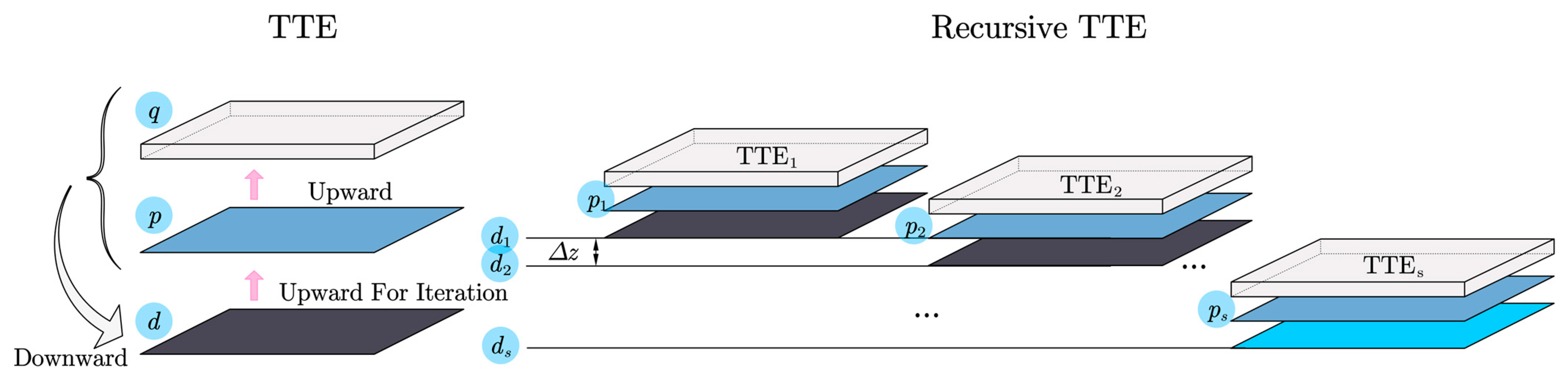
2. Recursive Truncated Taylor Expansion Downward Continuation

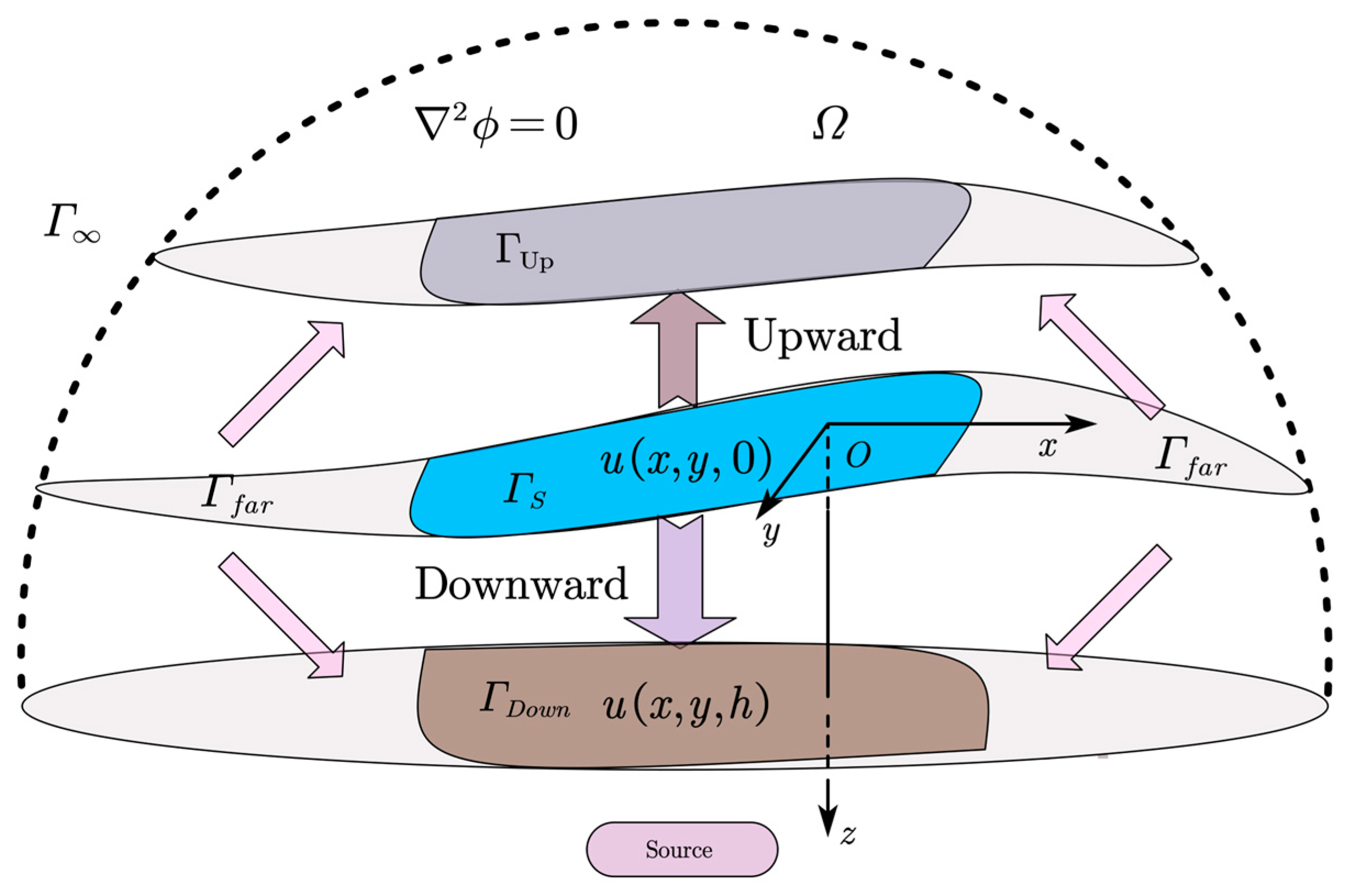
2.1. Basic Theory

Geomagnetic continuation theory covers upward and downward continuation, with a schematic diagram provided in Figure 1. Upward continuation can be solved using the Laplace equation. Downward continuation, as its inverse problem, is ill-posed. Typically, the downward continuation operator is derived from upward continuation integral equation.

In geomagnetic continuation, ${\mathrm{\Gamma }}_S$, ${\mathrm{\Gamma }}_{Up}$, and ${\mathrm{\Gamma }}_{\mathrm{Down}}$ denote the actual observation plane, upward continuation plane, and downward continuation plane. ${\mathrm{\Gamma }}_{\infty }$ represents the infinite boundary. ${\mathrm{\Gamma }}_{far}$ is the distant region extending outward from the observation plane. Together, ${\mathrm{\Gamma }}_S$, ${\mathrm{\Gamma }}_{\infty }$, and ${\mathrm{\Gamma }}_{far}$ form a closed surface enclosing a region $\mathrm{\Omega }$, within which the target continuation plane lies.

The coordinate system is established based on a local rectangular coordinate system using the North-East-Down (NED) reference frame. The origin is located at the center of the observation plane. Classical field theory shows that in source-free space $\mathrm{\Omega }$, upward potential field continuation is a boundary value problem of the Laplace equation, as in Equation (1) [21].

$$\left\{\begin{array}{cc}{\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}+{\displaystyle \frac{{\partial }^{2}u}{\partial y^2}}+{\displaystyle \frac{{\partial }^{2}u}{\partial z^2}}=0,& (x,y,z)\in \mathrm{\Omega },\\ u=u(x,y,z),& (x,y,z)\in {\mathrm{\Gamma }}_S,\\ u=0,& (x,y,z)\in {\mathrm{\Gamma }}_{\infty },\end{array}\right.$$

(1)

where $u$ is the magnetic field value within the closed region $\mathrm{\Omega }$ and its boundary. From the equation, we know that the magnetic field $u$ within the region $\mathrm{\Omega }$ is harmonic. According to the uniqueness theorem of electromagnetic field, once the harmonic field at the boundaries are known, the harmonic field at any spatial position within the region $\mathrm{\Omega }$ can be uniquely determined.

The partial differential equation is solved using Green’s second formula to calculate the geomagnetic values within the potential field region $\mathrm{\Omega }$, yielding the upward continuation integral formula [22].

$$u(x,y,-h)={\displaystyle \frac{h}{2\pi }}{\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }\frac{u(\xi ,\eta ,0)}{{[{(x-\xi )}^2+{(y-\eta )}^2+h^2]}^{\frac{3}{2}}}}}d\xi d\eta .$$

(2)

In the formula, h is the continuation altitude, $u(x,y,-h)$ is the magnetic field on the target plane ${\mathrm{\Gamma }}_{Up}$, and $u(x,y,0)$ is the magnetic field on the observation plane ${\mathrm{\Gamma }}_S$. The geomagnetic upward continuation integral equation yields a stable solution.

The downward continuation is the inverse problem of the upward continuation, which implies that solving an integral equation is required. Since the integral equation mentioned above can be expressed in convolution form, the calculation can be accelerated in the spatial frequency domain.

$$U_{-h}(k_x,k_y)=U_0(k_x,k_y)e^{-h\sqrt{k_x^2+k_y^2}},$$

(3)

In the equation, $k_x$ and $k_y$ represents the wavenumbers in the spatial frequency domain. $U_{-h}(k_x,k_y)$ and $U_0(k_x,k_y)$ represent the two dimensional Fourier transform of $u(x,y,-h)$ and $u(x,y,0)$, respectively. $e^{-h\sqrt{k_x^2+k_y^2}}$ is the frequency domain upward continuation operator. The downward continuation operator $H_{down}(k_x,k_y)$ is counted as the reciprocal of the upward continuation operator $H_{up}(k_x,k_y)$.

$$H_{down}={\displaystyle \frac{1}{H_{up}}}={\displaystyle \frac{1}{e^{-h\sqrt{k_x^2+k_y^2}}}}=e^{h\sqrt{k_x^2+k_y^2}}.$$

(4)

In the equation, we can know that when $k_x$ and $k_y$ becomes larger, the operator $H_{up}$ becomes smaller, while the operator $H_{down}$ becomes greater. Therefore, the high-frequency information is prone to disturbance when the map is downward continued. Traditionally, the Landweber iteration method is employed to solve the ill-posed inverse problems [12]. Nevertheless, the iteration method fail to step out the traditional operator structure, which does solve the problem effectively.

2.2. Proposed Method

In this study, we propose a recursive truncated Taylor expansion (RTTE) method to obtain stable downward continuation. Using Taylor expansion of vertical geomagnetic fields at single plane coordinates and fitting high order derivatives in space, it constructs downward continued geomagnetic maps.

The Taylor expansion of the magnetic map plane $u=u(x,y,z)$ on the observation plane $u_p=u(x,y,0)$ at vertical direction is given as follows:

$$u=u_p+{\displaystyle \sum _{j=1}^{\infty }\frac{1}{j!}\frac{{\partial }^j{u}_p}{\partial z^j}{(z-z_p)}^j},$$

(5)

where $u=u(x,y,z)$ is any geomagnetic plane of continuation in space and $z_p$ is defined as the altitude of the zero plane.

The key point for deriving the target plane is to solve the high order derivatives. The crux of high-order Taylor downward continuation is the paucity of data along the vertical, which thwarts accurate derivative estimation. Conventional practice fills the missing altitudes plane by implicitly treating the entire horizontal plane as a proxy. It transfers Equation (5) to frequency domain for solution. This global substitution inherits the high-frequency errors of the reference plane and soon demands extra regularization to remain stable.

Departing from this frequency-domain method, we instead augment the vertical profile directly. The upward continuation is implemented to supply additional data points while its inherent low-pass filter suppresses high-wavenumber noise. Rather than fitting derivatives to the full 2-D plane, we estimate them along a single vertical string, as illustrated in Figure 2.

In practical computations, it is necessary to truncate the Taylor series and construct a truncated Taylor series continuation model. For an nth-order truncation, it is required to solve for the nth-order derivatives. To derive each order derivative, the upward continuation is implemented from the observation plane $p$ to the upward continuation plane $q_i(i=1,\dots ,n)$, as illustrated in Figure 2.

We set the altitude of the $q_i$ as $i\Delta z$, where the $\Delta z=z_{q_1}-z_p$ is the altitude interval between two upward continuation plane. Then we can obtain the equation of each upward continuation plane with truncated Taylor series to t-order:

$$u_q=u_p+{\displaystyle \sum _{j=1}^t\frac{1}{j!}\frac{{\partial }^j{u}_p}{\partial z^j}{(z_q-z_p)}^j}.$$

(6)

Equation (6) describes the vertical spatial distribution of the geomagnetic field at different altitudes for a single coordinate point in the plane. Specifically, for a single point on the observation plane p and its corresponding point on the upward continuation plane $q_1\dots q_n$, a magnetic function related to altitude $z$ is formed in the vertical direction. As for the vertical line m, truncate the Taylor series to the t-order and express Equation (6) in matrix form as follows:

$$Y_m=A_m{X}_m,$$

(7)

$$Y_m={\left[\begin{array}{c}{u}_{q_1}^m-u_p^m\\ ⋮\\ u_{q_n}^m-u_p^m\end{array}\right]}_{n\times 1},A_m={\left[\begin{array}{ccc}\Delta z& \dots & {\displaystyle \frac{1}{t!}}\Delta z^t\\ ⋮& \ddots & ⋮\\ n\Delta z& \dots & {\displaystyle \frac{1}{t!}}{n}^t\Delta z^t\end{array}\right]}_{n\times t},X_m={\left[\begin{array}{c}{\displaystyle \frac{\partial u_p}{\partial z}}\\ ⋮\\ {\displaystyle \frac{{\partial }^t{u}_p}{\partial z^t}}\end{array}\right]}_{t\times 1},$$

where $Y_m$ is the observation data, $A_m$ is the structure matrix, and $X_m$ is the coefficient vector of derivatives of all orders.

When $n\ge t$, Equation (7) can be solved by the least squares method, yielding

$$X_m={({A_m}^T{A}_m)}^{-1}{A_m}^T{Y}_m.$$

(8)

For the convenience of calculation, the number of upward continuation plane n is set to be equal to the truncated order t of Taylor expansion. Equations (6) and (7) detail the solving process for the derivatives at an individual vertical line. By traversing all points on the reference plane, the derivatives at all vertical lines can be obtained. Based on these, downward continuation is performed using Moritz’s analytical continuation theory for potential fields [23]. As shown in Figure 3, plane $d$ is the downward continuation plane.

At the downward continuation plane $d$ and upward continuation plane, respectively:

$$\begin{array}{l}{u}_d=u_p+{\displaystyle \sum _{j=1}^{\infty }\frac{1}{j!}\frac{{\partial }^j{u}_p}{\partial z^j}}{(\Delta z_{dp})}^j,\\ u_q=u_p+{\displaystyle \sum _{j=1}^{\infty }\frac{1}{j!}\frac{{\partial }^j{u}_p}{\partial z^j}}{(\Delta z_{qp})}^j,\end{array}$$

(9)

In the equations, $\Delta z_{dp}=z_d-z_p$ represents the altitude interval between the plane $p$ and $d$, and $\Delta z_{qp}=z_q-z_p$ represents the altitude interval between the plane $p$ and $q$. ${\displaystyle \frac{{\partial }^j{u}_p}{\partial z^j}}$ is the all order derivatives of the geomagnetic field obtained from Equation (8).

Set $\Delta z_{qp}=-\Delta z_{dp}$ and sum Equations (9), then rearrange to obtain the following:

$$\begin{array}{c}{u}_d=2u_p-u_q+{\displaystyle \frac{2}{2!}}\Delta z_{dp}^2{\displaystyle \frac{{\partial }^2{u}_p}{\partial z^2}}+{\displaystyle \frac{2}{4!}}\Delta z_{dp}^4{\displaystyle \frac{{\partial }^4{u}_p}{\partial z^4}}+\dots =2u_p-u_q+R_t(z_{dp}),\\ R_t(z_{dp})=\left\{\begin{array}{ll}{\displaystyle \sum _{j=1}^{(t-1)/2}\frac{2}{(2j)!}\Delta z_{dp}^{2j}\frac{{\partial }^{2j}{u}_p}{\partial z^{2j}},}\hfill & \mathrm{if}t\mathrm{is}\mathrm{odd},\hfill \\ {\displaystyle \sum _{j=1}^{t/2}\frac{2}{(2j)!}\Delta z_{dp}^{2j}\frac{{\partial }^{2j}{u}_p}{\partial z^{2j}}},\hfill & \mathrm{if}t\mathrm{is}\mathrm{even},\hfill \end{array}\right.\end{array}$$

(10)

The residual term $R_t(z_{dp})$ of the downward continuation correction can be calculated using Equation (8).

Equations (5)–(10) describe the basic principles of carrying out a process of truncated Taylor expansion (TTE). The TTE iteration is illustrated in Figure 4. Upward continuation from the reference plane supplies supplementary data layers. With these and the reference plane, vertical derivatives of all required orders are computed, followed by downward continuation. The resulting plane is then upward-continued back to the reference altitude for comparison. If the residual or iteration times are not met, the truncation order and the number of supplementary layers are adjusted, and downward continuation is repeated. Otherwise, the optimal continuation plane is accepted.

Theoretically, the order of the derivatives of a vertical geomagnetic line should be extended to positive infinity, i.e., $t\to +\infty$, and having more upward continuation planes can ensure Equation (8) is well-posed. However, in practice, higher derivative order t induces polynomial oscillations and degrades continuation accuracy. Under low orders, accuracy can be improved by iteratively increasing the layer number n of supplementary data. However, this raises computational cost.

The truncated Taylor expansion (TTE) achieves one-step downward continuation yet loses accuracy when the continuation distance is large-step. To overcome this large-step instability, we adopt the RTTE scheme. This method decomposes the large step into a sequence of smaller TTE steps. This maintains a low truncation order t while markedly extending the reliable continuation range for large distances. The recursive algorithm diagram is shown in Figure 5.

The RTTE is based on the harmonic field, which states the smoothness of the spatial distribution of the geomagnetic field and is more suitable for small altitude intervals. Therefore, in a process of RTTE, a small altitude interval $\Delta z$ is set and the observation plane is continued downward by a $\Delta z$ altitude. The newly continued plane is regarded as the observation plane, and then the RTTE is applied again by a $\Delta z$ altitude. Step by step, the target plane is thus obtained.

Meanwhile, to ensure the truncation of Taylor expansion is reasonable, the downward continuation plane needs to be continued upward back to the known observation plane for comparison. If the difference exceeds the default threshold or is not optimal, it indicates the truncated order t of the derivative terms is not suitable to the downward altitude step. Then, increase or decrease the order by one and repeat the calculations until the difference is optimal and increase the layer number n of the supplementary data, ensuring the computational accuracy is acceptable.

The steps of the RTTE method are summarized as follows:

(a)

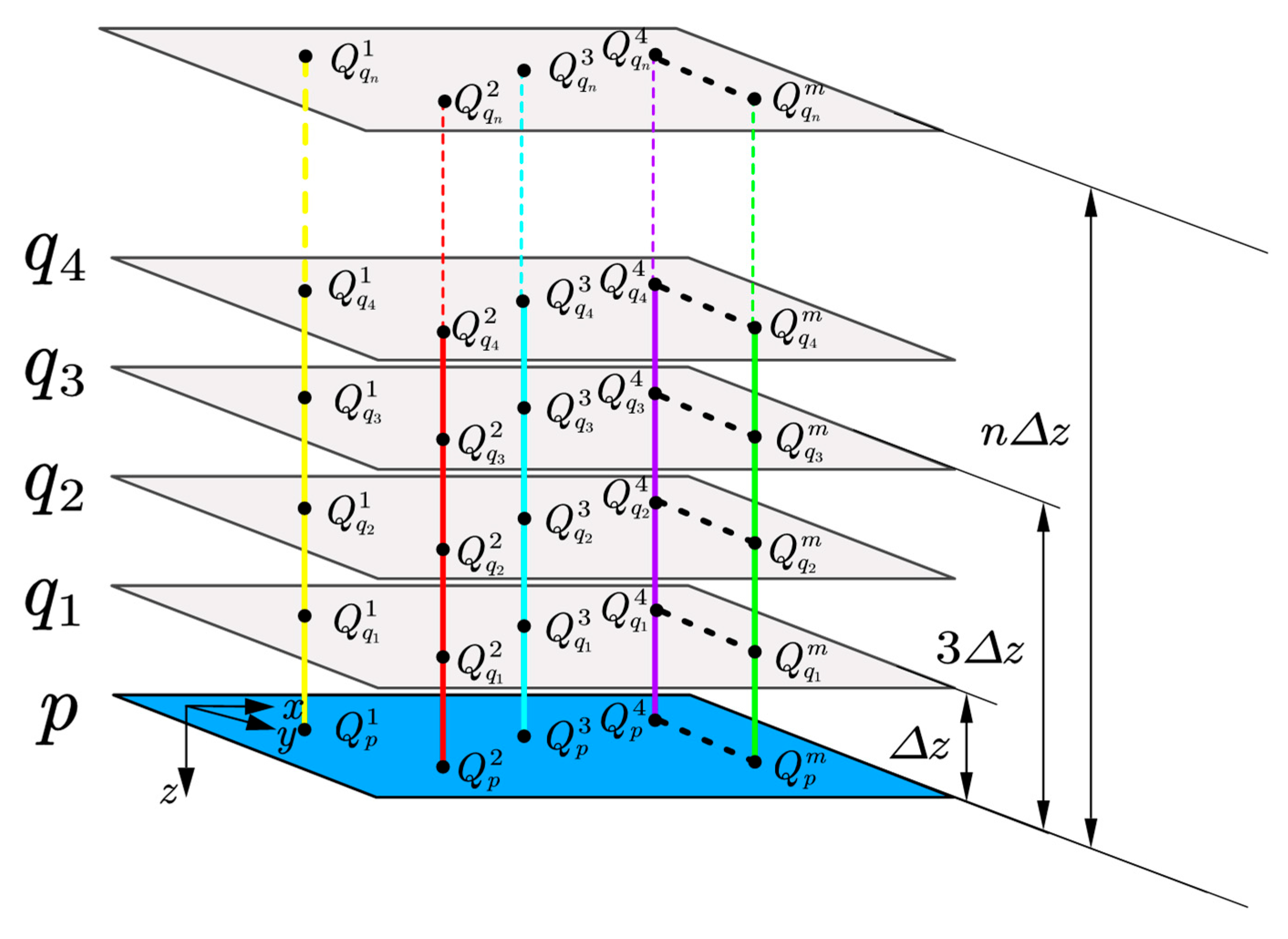
The geomagnetic space is constructed by multiple vertical lines. Each line’s magnetic field values form a function $u=f(z)$, with altitude z as the independent variable and magnetic field u as the dependent variable. This function can be expanded using a Taylor series as in Equation (5).

(b)

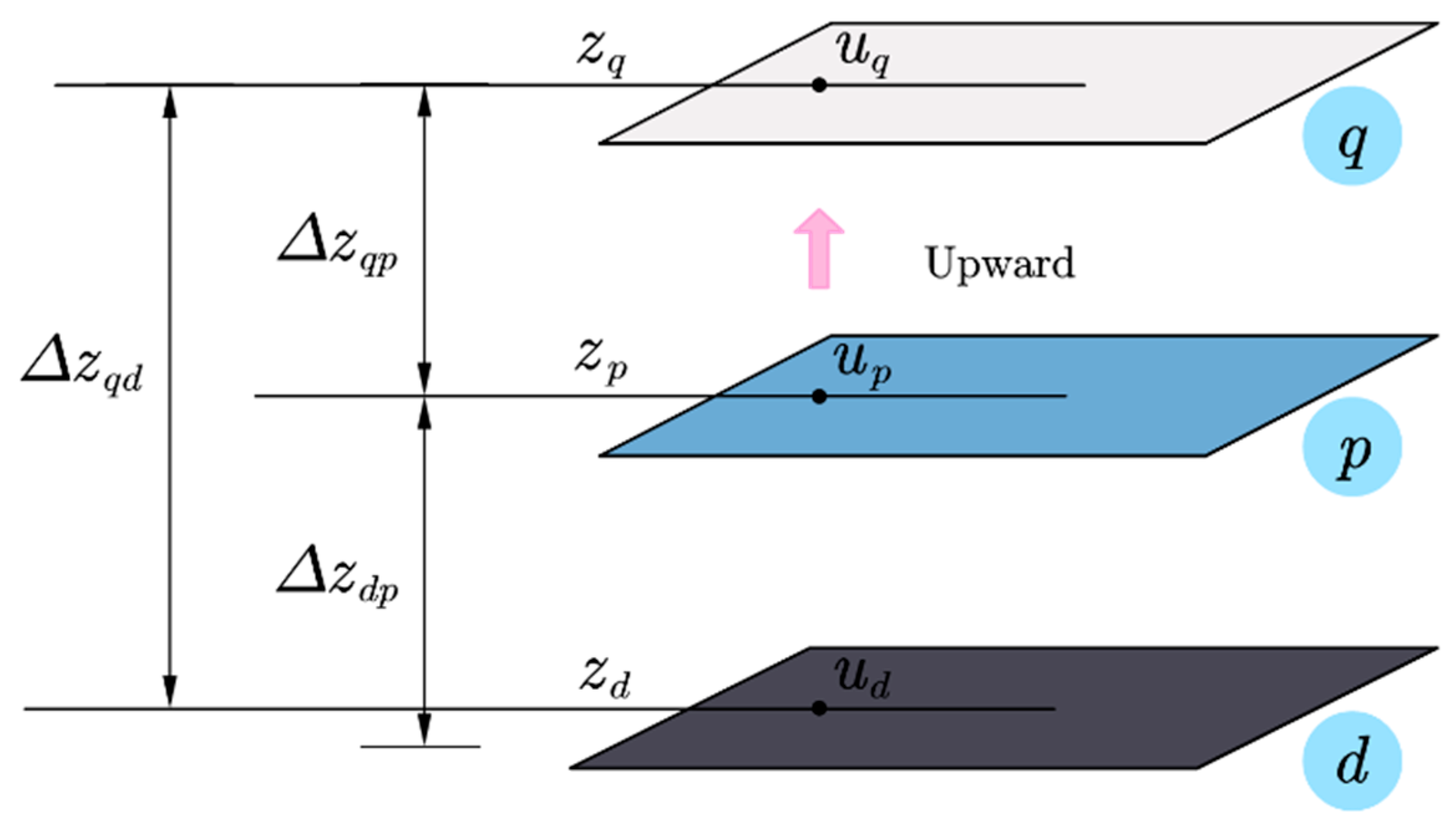
As upward continuation is a well-posed problem, use Equation (3) to perform spectral upward continuation of the known observation plane to supply data on vertical lines. Downward continuation is transformed into a process of downward extrapolation of the vertical magnetic field function $u=f(z)$ based on the known values on the vertical lines.

(c)

The values of the each order of derivatives on every vertical line can be calculated using Equation (8). The initial truncated order t of derivatives is set to $t_0=3$.

(d)

Using Equation (10), each order derivative terms obtained are used for the downward continuation of magnetic field by small step $\Delta z$.

(e)

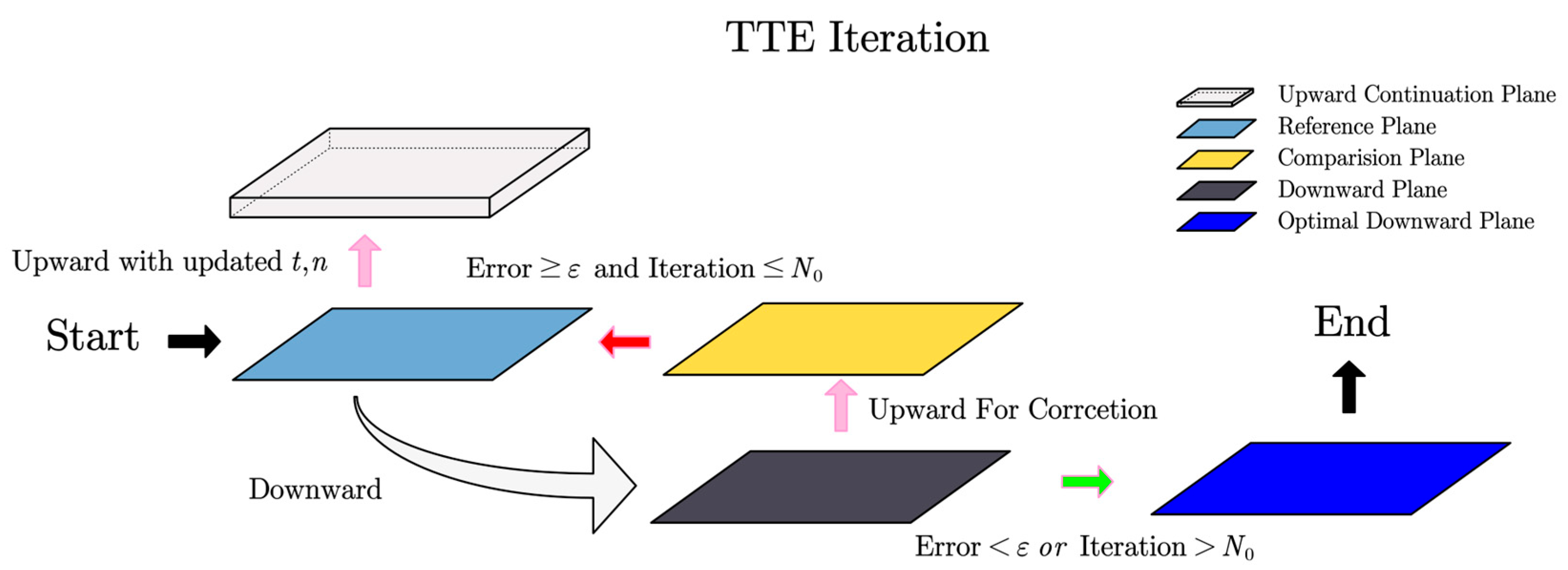
The downward continuation geomagnetic plane then is continued upward back to the observation plane for comparison. The truncated order t and the layer number n of the supplementary data can be optimized though repeating the step (b)–(e).

(f)

The optimal downward continuation plane $d_i$ by small step $\Delta z$ is seen as the new observation plane $p_{i+1}$. And the downward continuation step (b)–(f) is implemented again until to the target plane.

In summary, unlike traditional methods that treat the downward continuation of geomagnetic field only in frequency domain, our recursive truncated Taylor expansion (RTTE) method models the vertical spatial distribution of geomagnetic field on a vertical line as a function in harmonic field. This model is fitted using vertical derivatives as parameters. Our method transforms the downward continuation into a fitting and extrapolation process based on the reference and upward continuation geomagnetic maps, with iterative truncated order of derivatives and the layer number of the supplementary data. And the method solves the big step problem by implementing the small step downward continuation recursively. Thus, it inherently avoids the problem of amplifying noise in the high-frequency area in the downward continuation.

3. Experimental Verification

To verify the effectiveness of the RTTE, the simulation and measured data of the geomagnetic field are selected. In the simulation data, the shallow and deep sources of the geomagnetic field are selected as the environment. The former, from shallow sources, has a small regional distribution, generates a high gradient magnetic field, and represents high frequency data components. The latter, from deep seated magnetic substances, has a wide spatial distribution, generates a small gradient magnetic field, and corresponds to low frequency data components. Furthermore, the real measured data from the Kluane Lake West Aeromagnetic Survey [24] are chosen for practical verification.

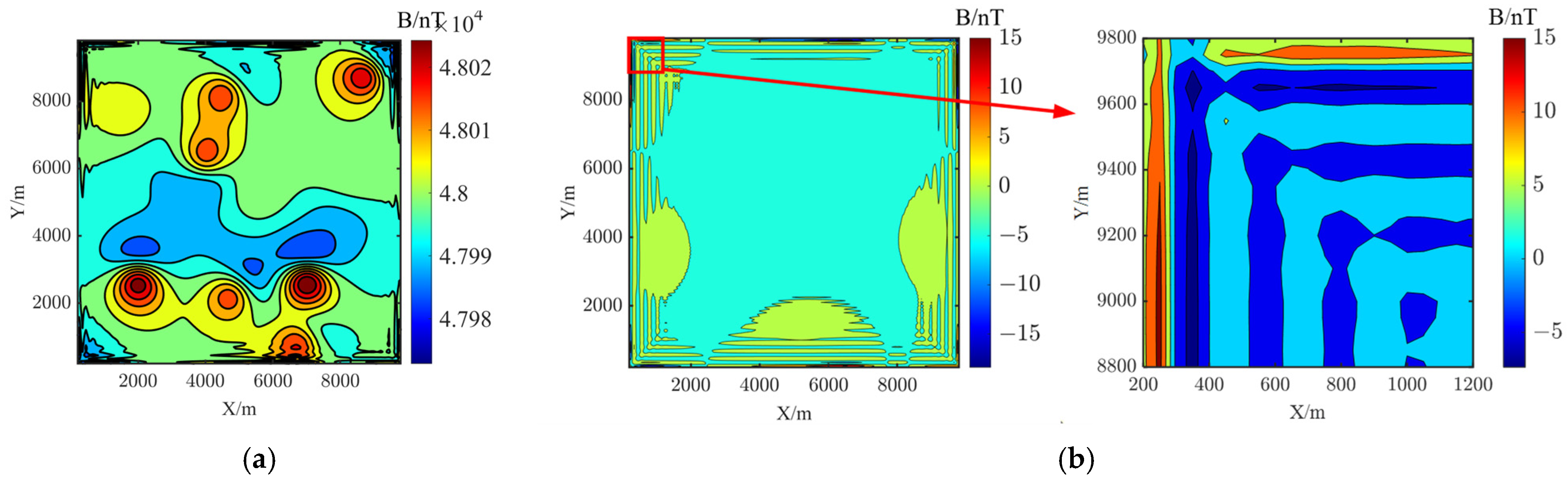
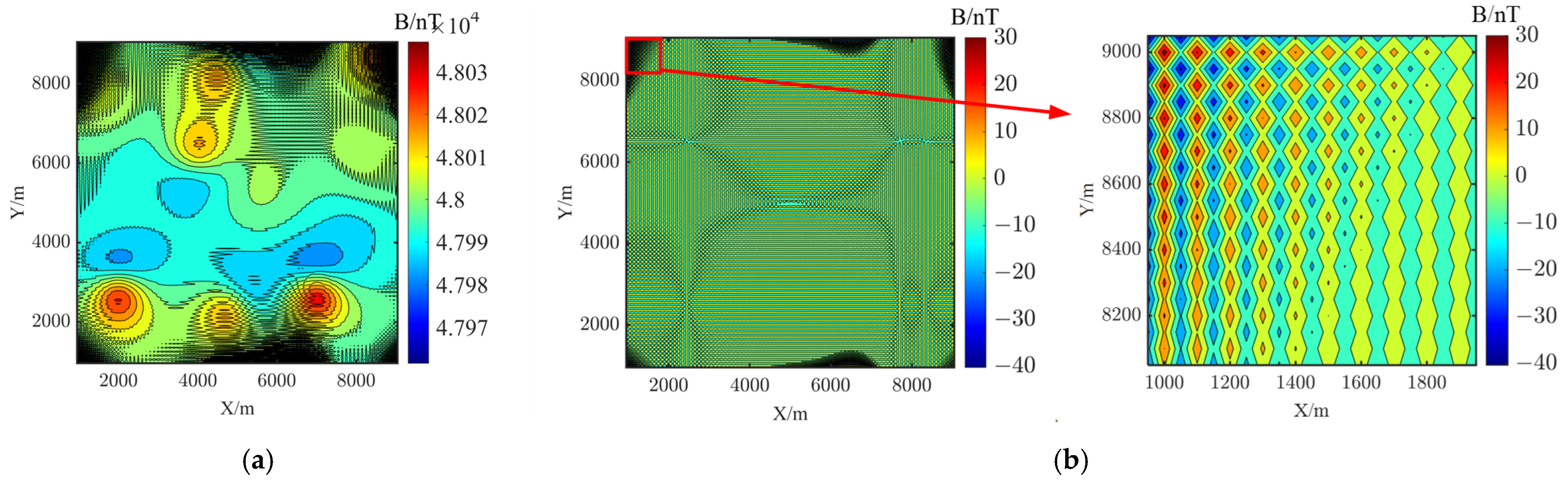
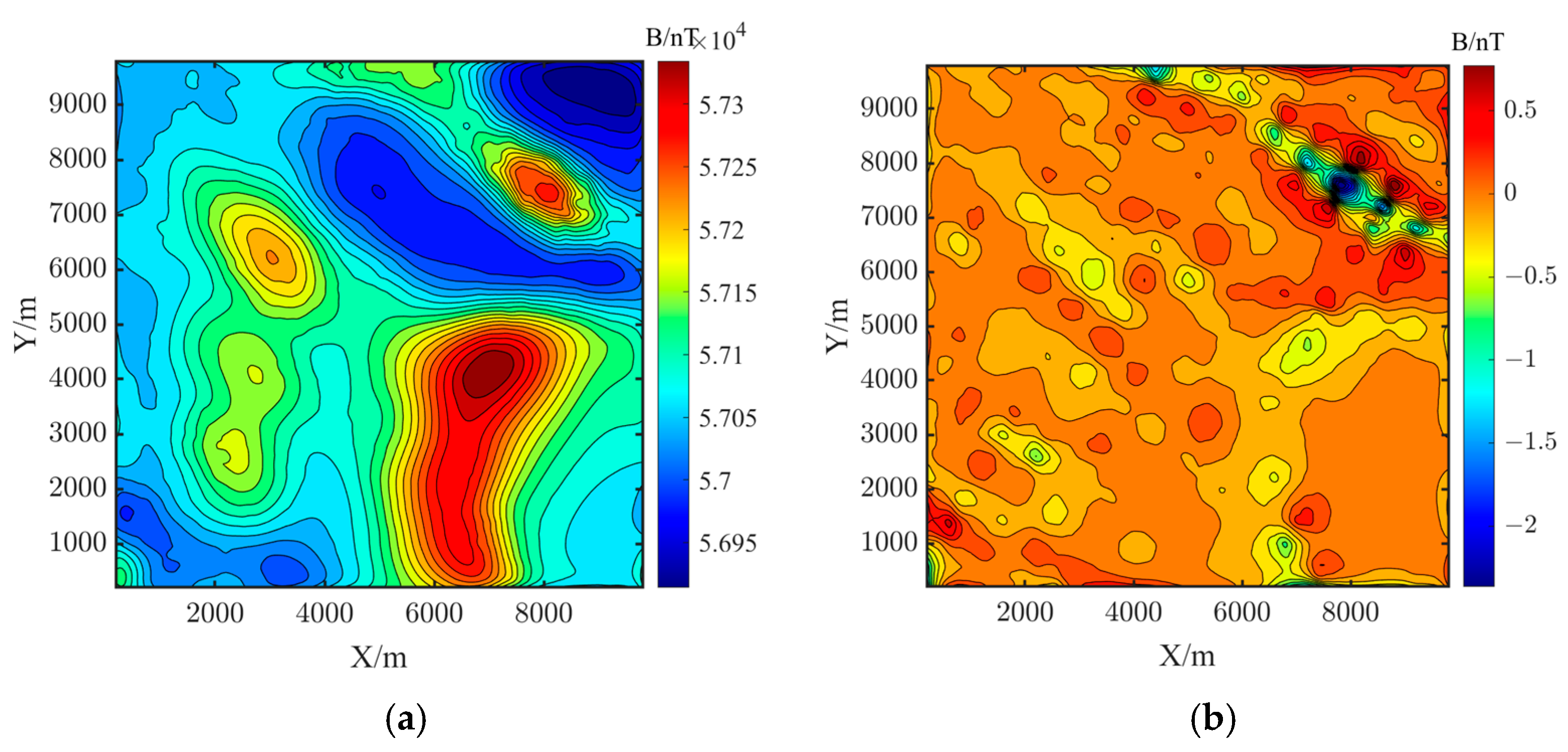
3.1. Simulation Geomagnetic Data Verification

As for shallow and deep sources (

Table 1. Simulation model for shallow sources simulation geomagnetic data.

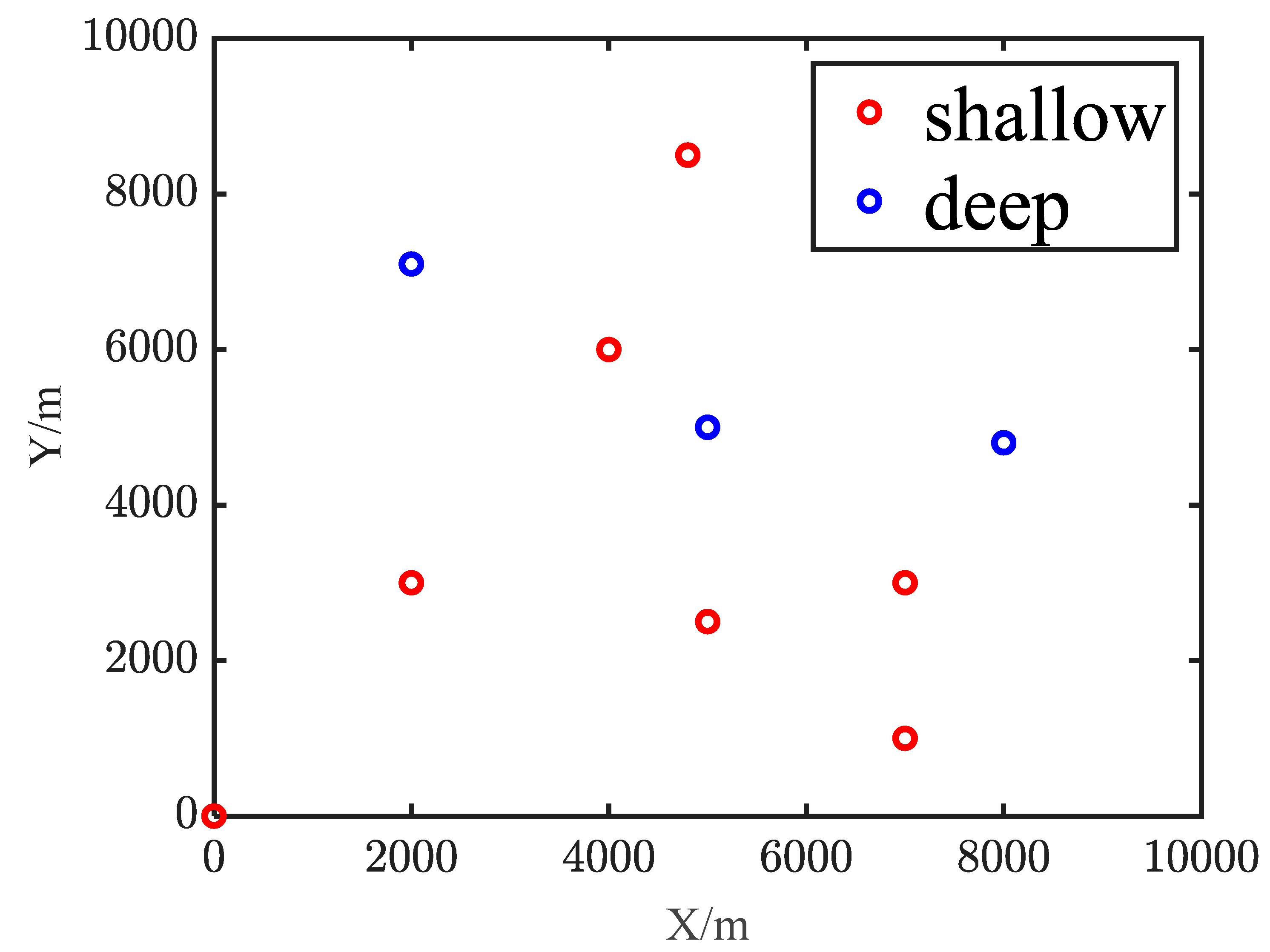
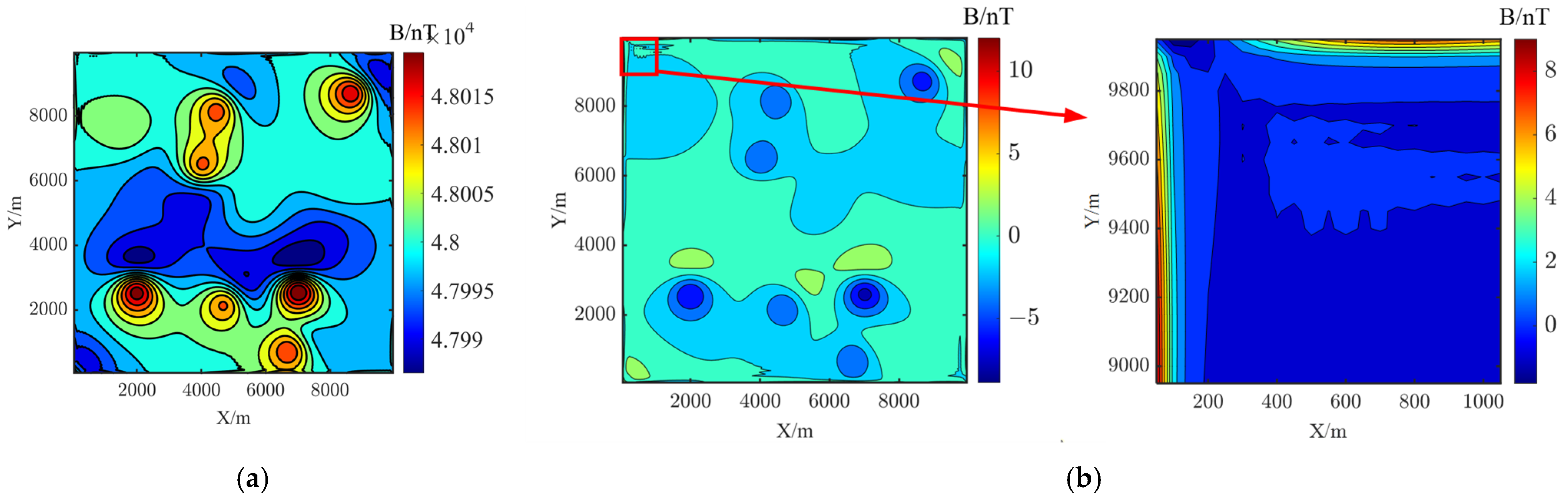
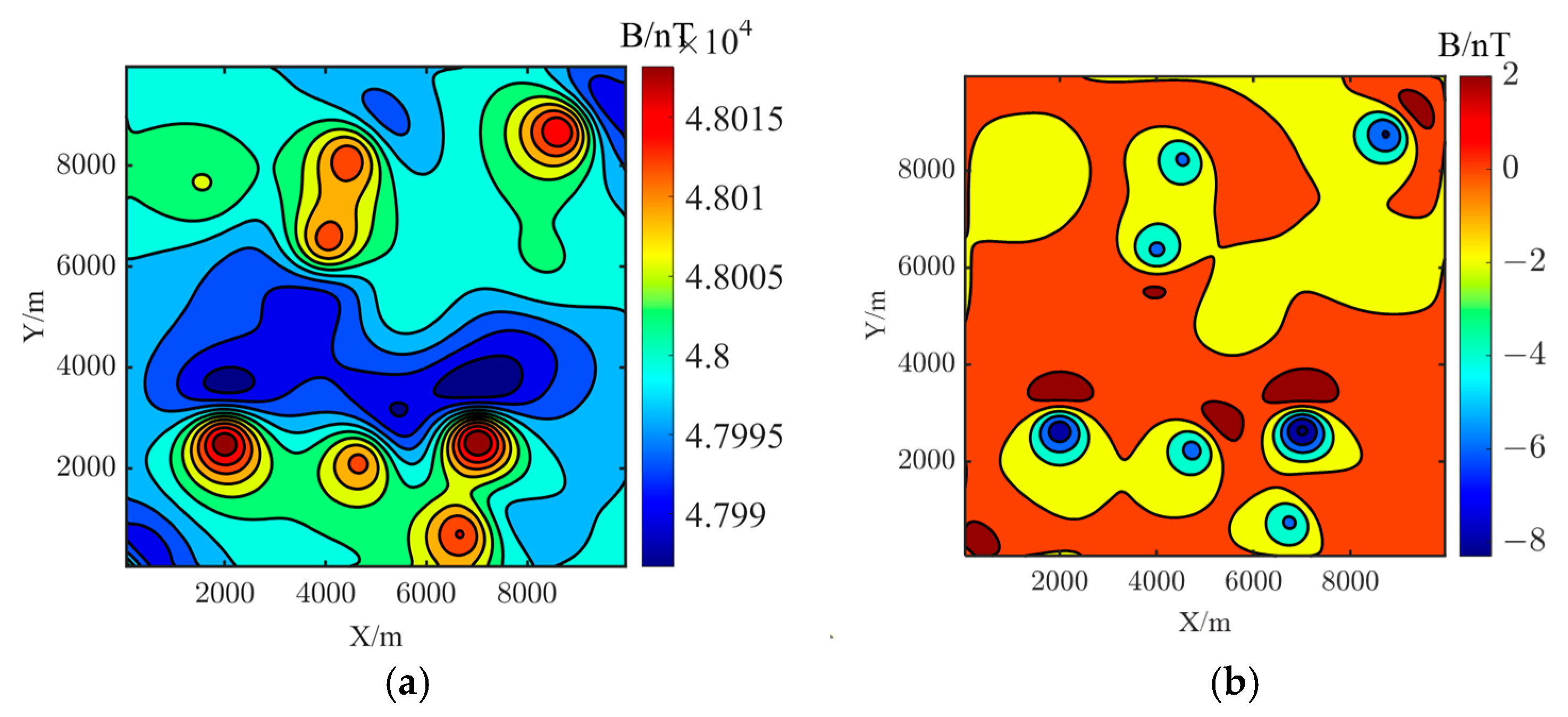
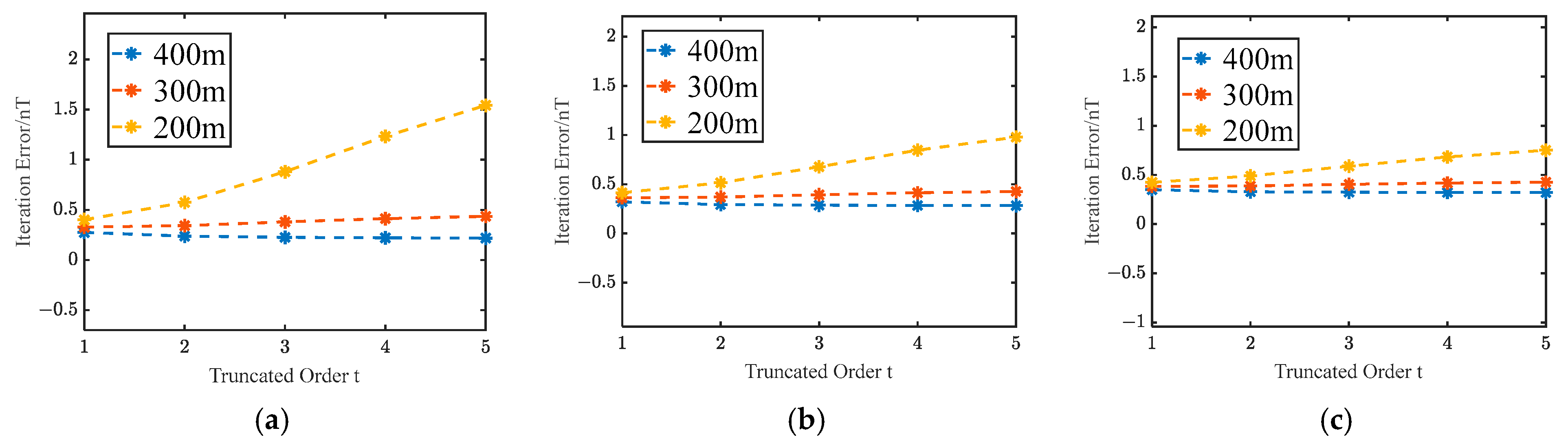
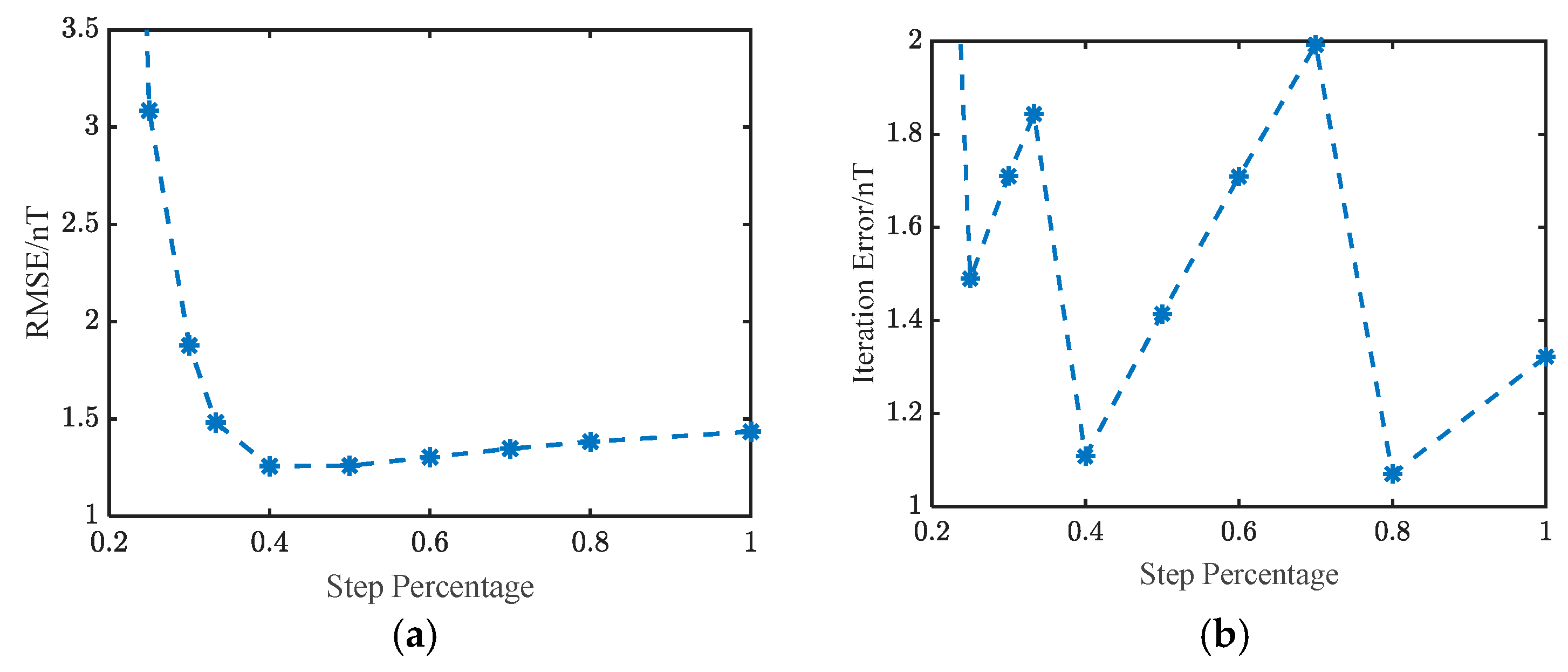
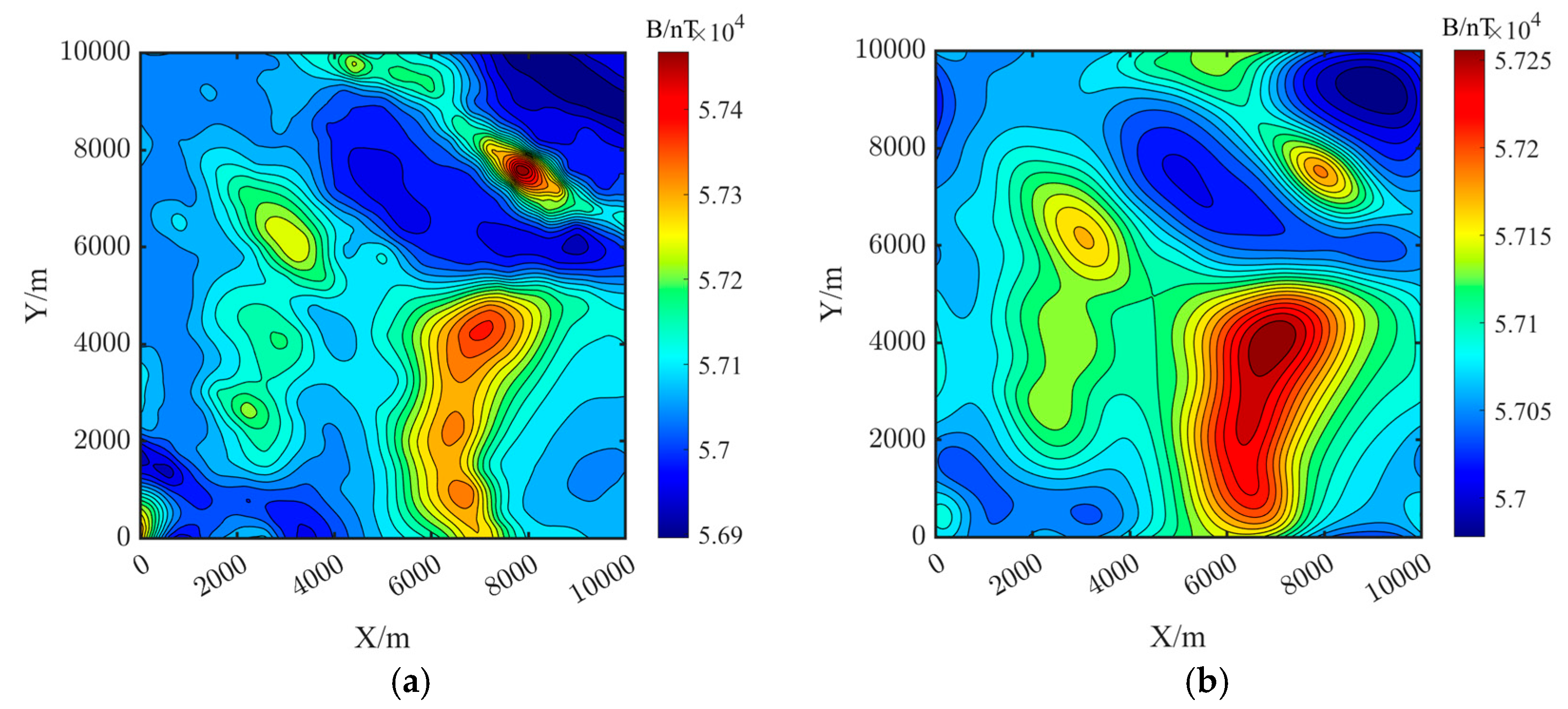
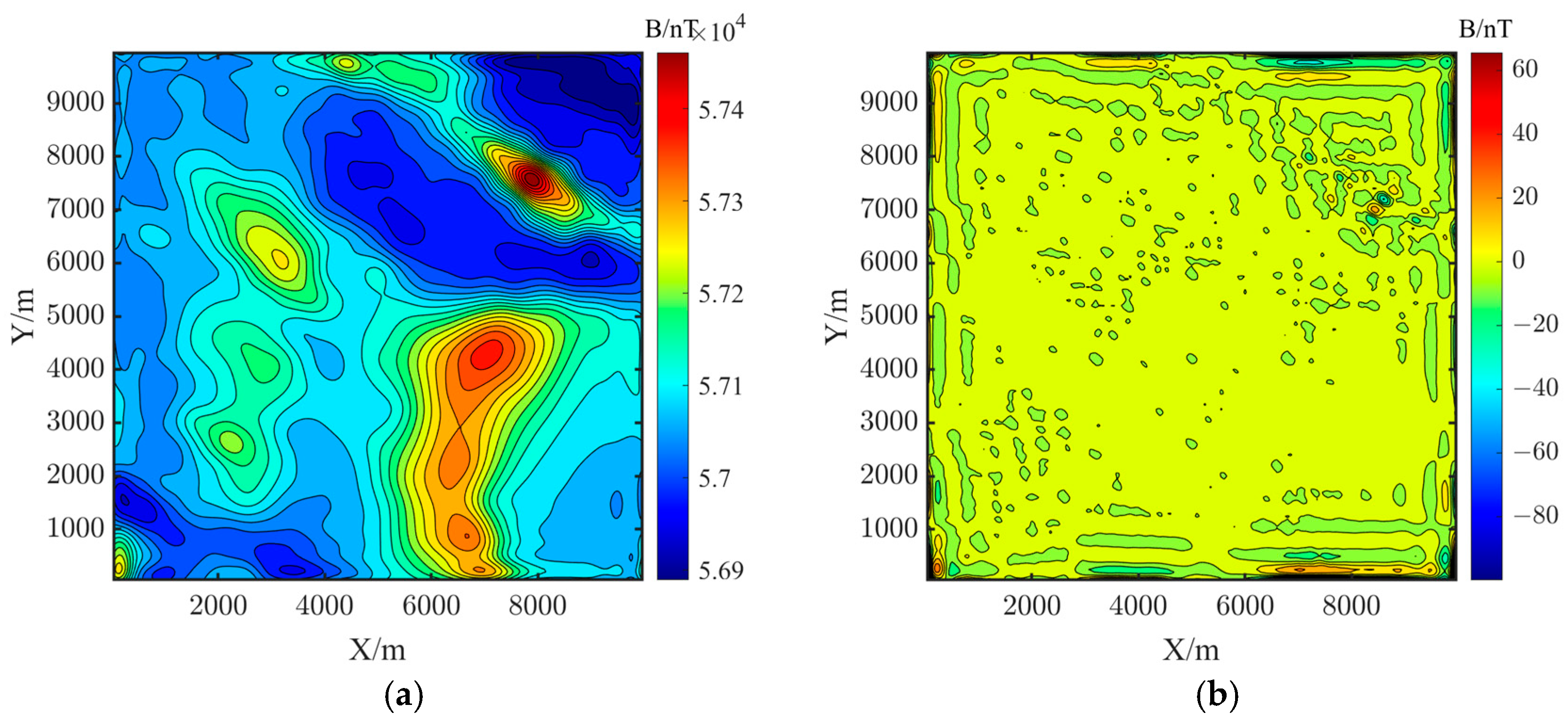
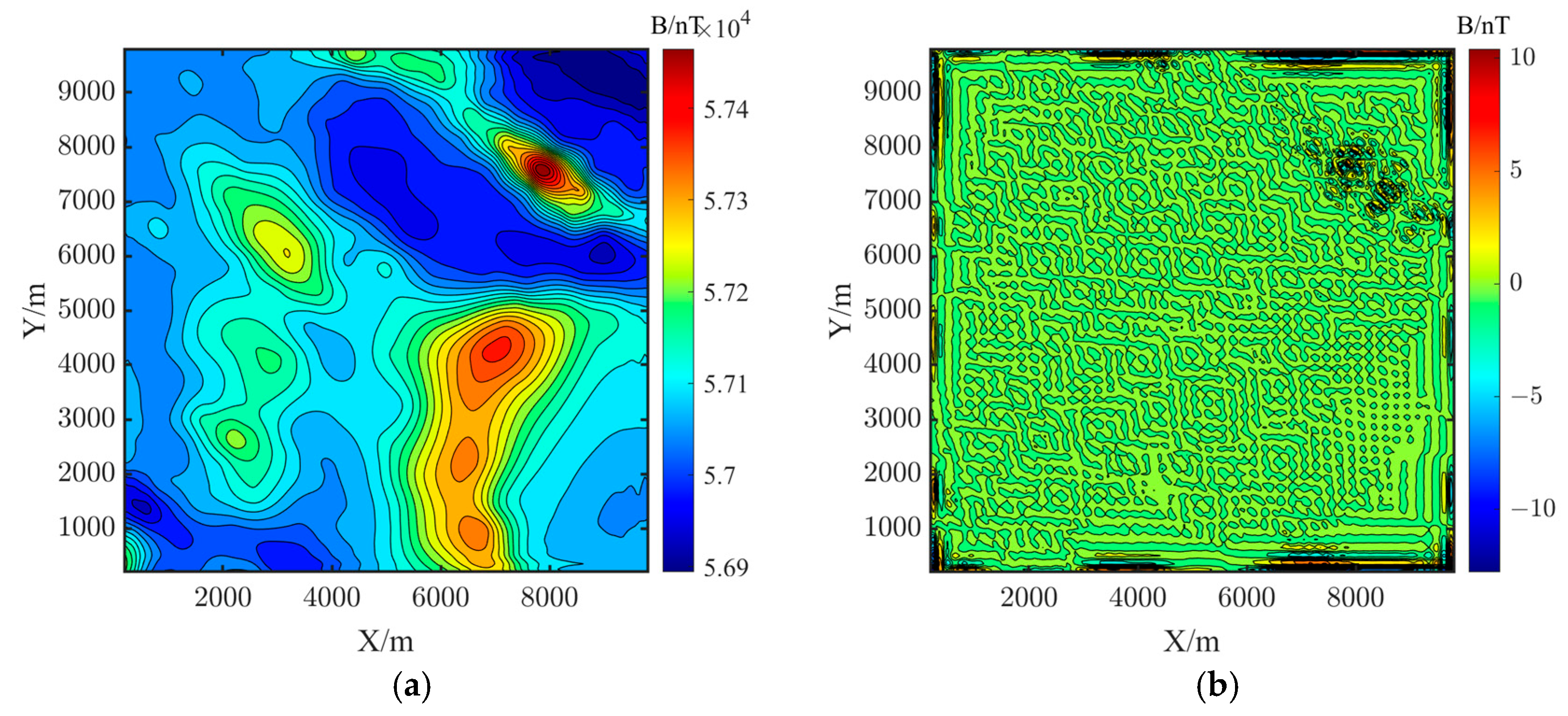
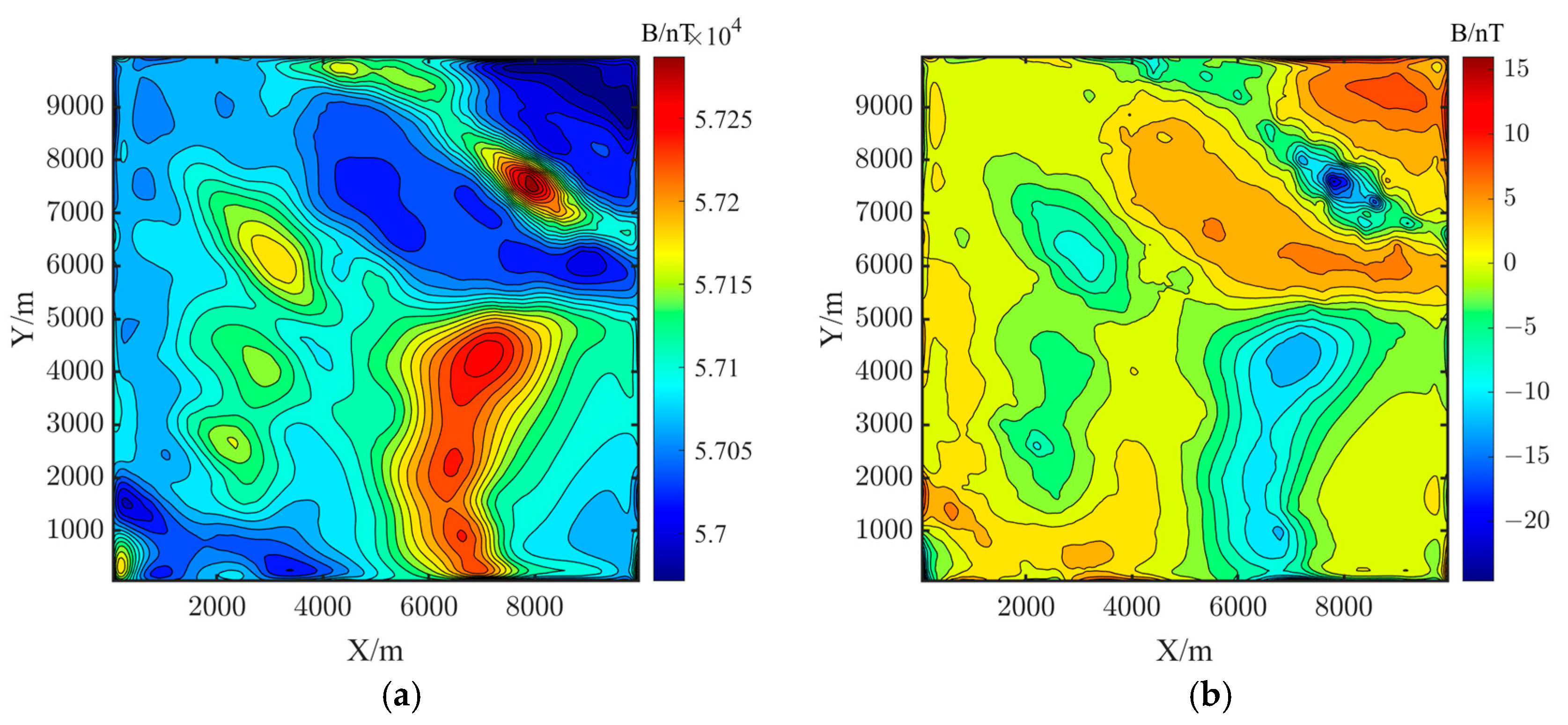
Number	Location			Sphere Radius/m	Magnetic Susceptibility/A/m
	x/m	y/m	z/m
1	0	0	−200	90	100
2	2000	3000	−200	95	100
3	4800	8500	−200	80	100
4	7000	3000	−200	100	100
5	4000	6000	−200	80	100
6	5000	2500	−200	83	100
7	7000	1000	−200	80	100
8	9000	9000	−200	90	100
9	5000	5000	−500	100	100
10	8000	4800	−500	100	100
11	2000	7100	−500	100	70

), a model with a burial depth of 200 m and 500 m is used. The model employs a composite configuration of spherical sources [25]. The composite configuration of spherical source is shown in Figure 6. Simulated geomagnetic maps at flight altitudes z = 200 m (Figure 7a) and z = 500 m (Figure 7b) serve as ground truth. The Landweber iteration [12], iterative Tikhonov regularization downward continuation (ITRDC) [13], truncated Taylor series iterative downward continuation (TTSIDC) [17] and the RTTE method are applied to downward continue the geomagnetic map from z = 500 m to 200 m. The continued map is compared with the z = 200 m ground truth map to obtain downward continuation errors, with results shown in Figure 8, Figure 9, Figure 10 and Figure 11.

To verify the accuracy of the methods, the mean absolute error (MAE) and root-mean-square error (RMSE) are chosen as the evaluation index, where the $u_i$ is the real magnetic field value and ${\hat{u}}_i$ is the estimated magnetic field value. N represents the number of the evaluated point on the map.

$$\begin{array}{l}\mathrm{MAE}={\displaystyle \frac{1}{N}}{\displaystyle {\displaystyle \sum }_{\mathrm{i}=1}^N}\left|u_i-{\hat{u}}_i\right|,\\ \mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{N}}{\displaystyle {\displaystyle \sum }_{\mathrm{i}=1}^N}{\left(u_i-{\hat{u}}_i\right)}^2}.\end{array}$$

(11)

The continuation results show that the RTTE method yields good continuation results for regions near the main magnetic source, nearly matching the ground truth except for boundary oscillations. The Landweber iteration method causes severe Gibbs effect at boundaries and Ringing effect at regions near the main magnetic source, leading to oscillatory distortions around the magnetic source.

Meanwhile, the error map Figure 8b, Figure 9b, Figure 10b and Figure 11b clearly show the error distribution. The Landweber iteration method generates continuation errors over 15 nT at the edge while the RTTE method matches the ground truth. However, the RTTE method and Landweber method has similar errors in low gradient and smooth region. The total plane’s MAE and RMSE of the RTTE method are lower than the Landweber iteration method’s (

Table 2. Comparison of downward continuation results for simulation data using different methods.

	MAE/nT	RMSE/nT
Landweber Iteration	1.7474	7.3740
ITRDC	1.4534	3.3050
TTSIDC	0.7717	1.2252
RTTE	0.3814	0.7192

), with MAE reduced by 78.2% and RMSE by 90.3%, proving the effectiveness of the RTTE method.

In the continuation simulations, the small step size is set to 100, the initial truncation order is t = 3 and the initial number of supplementary layers is 10. Upward continuation is performed over the equally spaced depths 10–100 m (one small step), yielding ten layers. Intermediate downward continuation planes were placed at 400 m, 300 m, and 200 m. The relationships among truncation order, number of supplementary layers, and iterative error for each layer are shown in Figure 12 and Figure 13.

Figure 12 shows that when few supplementary layers are upward continued, a lower truncation order yields better downward continuation accuracy. Conversely, higher orders demand a proportionally larger number n of upward-continued layers to maintain accuracy. Meanwhile, Figure 13 reveals that for a fixed low order of derivatives the gain in accuracy saturates as n increases. Exceeding this limit, further layers no longer improve the result. To surmount the accuracy ceiling, the truncation order must be raised.

Starting from t = 3 and n = 10, we implement the downward continuation with varying step lengths and record the RMSE of the final continuation surface and the iteration error is calculated as the sum of errors of all steps. As shown in Figure 14, the RTTE method improves accuracy when the large step is split into smaller ones. However, excessively small steps accumulate error. Hence the step size must be selected adaptively during iteration. For fixed t and n, the iteration error exhibits a clear zigzag, indicating that not all parameters are the optimal. From the result, we can see that smaller steps can have superior effect than just one step. Any further refinement of other step sizes requires re-tuning t and n.

3.2. Measured Geomagnetic Data Verification

To verify the practical effectiveness of RTTE method, we use measured aeromagnetic data from the Kluane Lake West Aeromagnetic Survey [26]. The survey dataset provides only a single-level geomagnetic measurement acquired at a fixed altitude above ground, lacking multi-level coverage. To validate the proposed method, the measured data were first upward-continued by 400 m to generate a synthetic reference plane. Figure 15a shows the measured data, and Figure 15b displays the upward continued geomagnetic map after continuing it 400 m upward using the upward continuation method.

The continued geomagnetic maps and error distribution using Landweber iteration, ITRDC, TTSIDC and the RTTE method are shown in Figure 16, Figure 17, Figure 18 and Figure 19. Both methods effectively process the measured data. However, as shown in

Table 3. Comparison of downward continuation results for real measured data using different methods.

	MAE/nT	RMSE/nT
Landweber Iteration	1.9419	7.4978
ITRDC	1.2399	5.8319
TTSIDC	3.0562	4.1886
RTTE	0.1878	0.3184

, the RTTE method improves continuation accuracy over Landweber iteration, reducing the mean absolute error by 90.9% and the root mean square error by 93.2%.

After simulation and measured data verification, the results confirm that the proposed method significantly enhances continuation accuracy by reducing the MAE and RMSE, thus validating the effectiveness of the RTTE method for downward continuation of geomagnetic maps.

4. Discussion

Our results demonstrate that RTTE outperforms single-step TTE in accuracy. This advantage arises because recursive small steps suppress polynomial oscillations inherent to high-order derivatives. Compared with the TTSIDC or the ITRDC, RTTE achieves similar RMS errors without tuning an explicit regularization parameter.

Figure 13 shows that low truncation orders (t ≤ 3) require fewer supplementary layers (n ≈ 6–8) to converge, whereas higher orders demand a near-linear increase in n. Figure 13c reveals a saturation effect: when t = 1, once n exceeds ~8, additional layers yield diminishing returns unless t is simultaneously increased. These observations suggest a practical tuning rule: raise t only after n has been optimized and the error plateau is reached.

The spherical composite model employed here simplifies real geological heterogeneity, which may amplify errors in rugged terrain. Moreover, the validation relies on data upward-continued 400 m from a single flight level. This smoothing potentially underestimates short-wavelength errors. Additionally, RTTE is computationally intensive because the number of recursive steps scales inversely with the step length and to achieve the optimal parameter n and t may cost a lot when t is great. Finally, when dealing with higher-order derivatives with the supplementary data, the regularization method could be incorporated into the model for more precise results and faster calculation.

5. Conclusions

In this paper, we proposed a recursive truncated Taylor expansion downward continuation method for geomagnetic field. The method improves the Taylor expansion derivative solver by introducing supplementary data at multiple altitudes, iteratively optimizes the truncation order and the number of supplementary layers, and decomposes a large downward-continuation step into several smaller recursive steps. The simulation data and real measured data verification indicate that the proposed method can enhance the downward continuation accuracy and the stability of continuation results. This study offers more precise geomagnetic data for aeromagnetic exploration and introduces new techniques for geomagnetic data processing. Future work will focus on optimizing the iteration and recursion of the method to solve the singularity at higher-order derivatives and exploring its potential in other geophysical data processing fields and projects.