Modeling Marshaling Yard Processes with M/Hypo_K/1/m Queuing Model Under Failure Conditions

Abstract

This study presents a comprehensive analysis of the M/Hypo_K/1/m queuing model to evaluate the performance of marshaling yards in freight rail classification systems. The model effectively captures the complex, multi-phase nature of service and repair processes by incorporating hypo-exponential probability distributions. The marshaling yard is modeled as a finite-capacity, single-server queue subject to potential server failures, reflecting real-world disruptions. Two complementary methodological frameworks are employed: a mathematical model based on continuous-time Markov chains (CTMCs) and a simulation model constructed using Colored Petri Nets (CPNs). In the analytical approach, both service time and repair time follow hypo-exponential distributions, which are used to approximate the gamma distribution. The simulation model built in CPN Tools allows for dynamic visualization and performance evaluation. In the CPN model, we applied a gamma distribution, which allowed us to evaluate the accuracy of the approximation implemented in the analytical model. The result indicated that utilization of the marshaling yard in primary shunting was approximately 23.81%, and with secondary shunting, 22.53%. The study output proves that the hypo-exponential distribution is able to approximate the gamma distribution. This dual-framework approach, combining analytics with simulation, provides a deeper understanding of system behavior, supporting data-driven decisions for capacity planning, failure mitigation, and operational optimization in freight rail networks.

1. Introduction

Railway transport has remained a key mode of freight transportation, primarily due to its high capacity, energy efficiency, and relative safety. In freight rail operations, trains are not typically fixed between set origins and destinations; instead, they are assembled daily based on customer demand through a process known as train classification. This classification typically takes place at dedicated facilities called marshaling yards, where railcars from different origins and with various destinations are sorted and reassembled [1].

A marshaling yard, also known as a classification or shunting yard, serves as a critical hub for the rail freight network. It enables the systematic disassembly and reconfiguration of trains to ensure cargo delivery across destinations [2]. The core operations involve primary shunting, where inbound trains are moved to a hump or flat switching track, disconnected, and sorted onto classification tracks [3]. Secondary shunting occurs at intermediate stations or terminals to reorganize, detach, or attach railcars, often for loading/unloading or adjusting train configurations for local deliveries. For example, from an industrial site, secondary shunting may involve moving specific wagons to loading docks while the rest of the train remains stationary [4].

Given rising freight volumes and limited rail infrastructure expansion, marshaling yards are increasingly acting as operational hubs in rail networks [5]. Yard congestion and high railcar dwell times often dominate total transit times and limit mainlines [6,7]. Optimizing yard operations is therefore critical for enhancing network fluidity, reducing idle times, and meeting delivery timetables. Studies affirm that improving yard performance reduces operational costs and increases asset utilization and service reliability [2].

Marshaling yard processes have been extensively modeled using two main approaches: queueing theory and simulation models. Queueing theory offers analytical tools to evaluate system performance; for example, M/G/1 and M/Cox2/1/m models have been applied to account for multi-phase operations and limited capacity [8,9]. In parallel, the simulation approach, particularly discrete event simulation (DES) and Colored Petri Nets (CPNs), allows for the detailed modeling of complex interactions [10].

Research works [11,12,13] show that optimizing the marshaling yard process can reduce railcar dwell time, improve asset utilization, and enhance service reliability. As stated, when the marshaling yard optimizes rail cars, they are available for new assignments, boosting network fluidity and reducing train idle time. This capability allows it to accommodate more trains, which in turn reduces bottlenecks that slow down the entire rail freight. Moreover, it reduces operating costs and can better meet delivery timetables to gain the trust of the customer.

There have been studies on the marshaling yard operations topic of interest in railway logistics and operations research for decades. Early work mainly focused on the development of heuristic and rule-based approaches to train classification. In the 1980s, the pioneering work by Ref. [14] introduced network-based optimization strategies for blocking freight cars by their destination. Similarly, Ref. [15] also contributed by modeling the classification process in the form of car blocking sequences. These initial studies mainly focused on the deterministic, which lacked the stochastic nature of train arrival.

In the 1990s or early 2000s, advances in algorithmic modeling and simulation tools facilitated a more dynamic representation of marshaling yard operations. For example, Ref. [16] developed a stochastic model for train and car movement using open queuing network theory. In the 2010s, optimization-driven frameworks for marshaling yard control emerged, and some works such as Ref. [17] introduce multistage train classification algorithms that optimize classification decisions and reduce re-handling and classification costs. These works are often considered deterministic or partially stochastic conditions, and while they improved operational precision, they did not fully address system-level uncertainty in arrival and service time.

More recently, researchers have introduced stochastic queuing models that incorporate real-world characteristics such as the limited capacity of the system, variable service times, and partial failure. The work of Ref. [18] modeled entire railway stations and yards using a multi-phase queuing system using a batch Markovian Arrival Process (BMAP). Their study showed how queuing network structures with routing and finite buffers could accurately represent real yard performance. In addition, simulation-queuing hybrid models have emerged to capture the nonlinear effects of arrival variability. Notably, Ref. [7] investigated the volume fluctuations in hump yard performance using discrete event simulation coupled with regression analysis. Their findings showed that increased variance in inbound train schedules significantly affected on-time departure and truck utilization, confirming the sensitivity of yard performance to stochastic input patterns.

In this article, it is assumed that requests for primary shunting are considered to be trains of wagons that must be served in the system, and all requests for secondary shunting are assumed to be failures. This is because primary shunting is the main function of the marshaling yard, and during secondary shunting, the hump is occupied and is not able to fulfill its main function. Note that although secondary shunting seems counterintuitive, as it is part of marshaling yard operations, it often corresponds with the interruption of the shunting process, as it is treated as reclassification. We considered secondary shunting as a failure, as it has an impact on the marshaling yard performance rather than mechanical or equipment failure.

The main objective of this paper is to model the marshaling yard using a finite capacity single-server queuing model subject to failure by applying a hypo-exponential probability distribution of the service and repair time. We applied a hypo-exponential probability distribution, even though the actual process follows a gamma probability distribution. This approach was chosen because it can effectively approximate gamma distributions under certain conditions while offering analytical tractability and computational advantages.

In recent decades, there has been a significant increase in interest in the generalization of probability distributions. In the fields of probability and statistics, exponential distributions are commonly used to model the time intervals between events in processes characterized by the memoryless property. However, these models frequently oversimplify complex systems that involve multiple phases or stages, each with varying rates. The hypo-exponential distribution addresses this limitation by summing K independent exponential random variables, each possessing a distinct rate parameter—see, for example [19,20,21]. The hypo-exponential distribution can be a generalization of an Erlang distribution of probability—the main difference lies in the fact that the Erlang distribution of probability has the same rate parameters for all its exponentially distributed phases. This distribution plays a significant role in stochastic and probabilistic theory due to its flexibility and applicability in various fields, including queuing theory, transport management systems, telecommunications, and economics.

This distribution has been extensively studied in various scholarly publications. For example, Refs. [22,23,24] model hypo-exponential distribution by generalizing the exponential distribution to analyze the performance of the system. The authors observe that when the failure of the system is more frequent, it should not be neglected in modeling and simulation to show the real behavior of the system. The work applied a hypo-exponential probability distribution in which each independent phase has a distinct rate. Similarly, Refs. [22,25] applied a hypo-exponential probability distribution to analyze the performance of the queueing system. To mention another example, Refs. [26,27] state the contribution and application of the hypo-exponential distribution in science and engineering. They mentioned that the hypo-exponential distribution is the sum of $K>2$ independent exponential random variables. A sequence of exponential phases using an Erlang K distribution can model random variables with less variability than an exponential distribution while retaining its mathematical properties. For a given mean μ, choosing K phases with a rate of $\mu$ each achieves the desired value. However, its coefficient of variation is restricted to ${\displaystyle \frac{1}{\sqrt{K}}}$. This limitation can be addressed by mixing two Erlang distributions, as discussed in [22], or modifying the phase-type representation, allowing each phase i to have a different exponential parameter ${\mu }_i$, leading to hypo-exponential distribution [28].

Much academic work focuses on applying a traditional queuing model that focuses on exponential inter-arrival and service distribution; however, the real-world system involves a phase where the rate varies from one stage to the other, and the classical exponential probability distribution, which assumes that the rate is the same across the phase, fails to represent the real system, which leads to inappropriate representation and prediction of the performance of the system. Hypo-exponential probability distribution is a powerful tool for modeling processes that have multiple phases. It allows engineers and researchers to analyze complex systems, providing insights into performance, reliability, and efficiency using its flexibility. Hypo-exponential distribution can serve as an effective approximation for the gamma distribution through either a fixed approximation approach or a smoothed hypo-exponential approximation method, as presented in [21].

This study applies simulation modeling techniques to evaluate the performance of a marshaling yard represented by a queueing system, where service and repair times are modeled using a gamma distribution. The aim is to compare these simulation results with those obtained from the hypo-exponential approximation result of the mathematical model. Prior work such as [29] analyzed the classification yards using simulation with exponentially distributed inter-arrival times and Erlang distributed service and repair times, while Ref. [30] developed a model focusing on hump operations.

This article is the continuation of Ref. [29], which considered primary and secondary shunting by extending previous models by incorporating hypo-exponential service and repair time distributions using the approximated method of the gamma distribution. This approach captures phase-type behavior and variability more accurately than conventional Erlang or exponential models. Consequently, the proposed model offers greater realism and flexibility, enhancing its applicability to real-world yard operations. In addition to this, this study makes a meaningful contribution to the railway systems modeling literature, improving both analytical depth and practical relevance.

Structurally, Section 2 outlines the materials and methods, including general assumptions (Section 2.1), steady-state mathematical analysis (Section 2.2), and the simulation model built using Colored Petri Nets (Section 2.3). The results and discussions are presented in Section 3, followed by conclusions drawn in Section 4.

2. Materials and Methods

2.1. General Concept

Modeling service or repair times using hypo-exponential probability distribution means a sum of K independent exponential distributions of probability with different rates ${\mu }_i$ for $i = 1,\dots ,K$. This type of probability distribution can be modeled using the method of phases, where each phase follows an exponential distribution. The mean value of the distribution is given by the sum of the reciprocals of the rates:

$$EX={\displaystyle \sum }_{i=1}^K{\displaystyle \frac{1}{{\mu }_i}}$$

(1)

It is possible to calculate the variance, DX, and the squared coefficient of variation $C^2\left(X\right)$, which is defined as follows:

$$DX={\sum }_{i=1}^K{\displaystyle \frac{1}{{\mu }_i^2}},$$

(2)

$$C^2\left(X\right)={\displaystyle \frac{{\sum }_{i}1/{\mu }_i^2}{{\left({\sum }_i\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${\mu }_i$}\right.\right)}^2}}.$$

(3)

Furthermore, it is important to note that the coefficient of variation should never be greater than 1—see Ref. [30].

In the modeled system, some random variables are gamma-distributed, and we try to find a way to approximate the gamma distribution to use the method of phases. One possible way is to use approximation via hypo-exponential distribution, as provided in the article [21]. The article provides an approximation of the gamma distribution via a so-called fixed hypo-exponential approximation method, which can match the first two moments of the gamma distribution.

In the analytical model, the gamma distribution used for modeling service and repair times is approximated using a hypo-exponential distribution. This is carried out by matching the first two moments (mean and variance) of the gamma distribution. To prove the validity of this approximation, the theoretical mean and variance of the gamma distribution were matched to the mean and variance of the hypo-exponential distribution, and we demonstrated that the simulations differed negligibly from those using the original gamma process. The approximation allows for analytical tractability while preserving the fundamental variability structure of the original gamma process.

Let us assume that the data follow a gamma probability distribution defined by a shape parameter $\alpha >2$ and the scale parameter $\theta$. The fixed hypo-exponential approximation method is well established [21] and assumes that such a gamma probability distribution can be approximated by a sum of K exponential distributions of probability, where $K=\left[\alpha \right]+1$ and $\left[\alpha \right]$ is an integer part of the shape parameter $\alpha$. It holds for the rates ${\mu }_i$ of individual exponential distributions [22]:

$${\mu }_i={\displaystyle \frac{K}{\alpha ·\theta }} \mathrm{for} i=1,\dots ,K-2$$

(4)

$${\mu }_{K-1}={\left[{\displaystyle \frac{\alpha ·\theta }{K}} \left(1+\sqrt{{\displaystyle \frac{K}{2\alpha }}\left(n-\alpha \right)}\right)\right]}^{-1}$$

(5)

$${\mu }_K={\left[{\displaystyle \frac{\alpha ·\theta }{K}} \left(1-\sqrt{{\displaystyle \frac{K}{2\alpha }}\left(n-\alpha \right)}\right)\right]}^{-1}$$

(6)

2.2. Mathematical Model

In this part, we are going to discuss the mathematical representation of the hump freight rail classification process using queueing theory under a steady state. The system can be modeled as a single-server queueing model subject to failures. In such a system, primary shunting represents customer service and secondary shunting represents failures of the system.

To ensure both analytical traceability and simulation validity, we adopt the following assumptions:

• Arrival process: Individual requests for primary shunting (trains of wagons waiting on arrival tracks after finishing their preparation for the classification process) will be called customers. Let the customer input process be the Poisson process with the parameter λ. This means that the inter-arrival times are exponentially distributed, with the mean inter-arrival time equal to $1/\lambda$;
• Service mechanism: The hump classification process will be considered as customer service. Service times are assumed to follow the hypo-exponential distribution of probability, which consists of n exponential phases with rates ${\mu }_p$ for $p=1,\dots ,n$;
• Shunting logic: Primary and secondary shunting operations are modeled separately by assuming the non-preemptive priority of secondary shunting over primary shunting;
• Failure and repair: During secondary shunting, we will refer to these occurrences as server failures, since both the hump and the arrival track are occupied. In this study, secondary shunting is modeled as a failure event due to its operational impact. Modeling it as a failure allows for the use of established failure repair queuing models, improving analytical traceability while accurately representing real-world disruption, and it aligns with prior studies on operational breakdown in freight yards. To clearly state that secondary shunting, such as trains coming from an industry site, considered a system failure as the hump, is not providing for primary shunting. This allows us to adopt the following assumption. We assume that the time intervals between failures follow an exponential distribution with the parameter η. Consequently, the time required for repairs follows a hypo-exponential distribution, with a sequence of s independent exponential phases, each with its rate ${\zeta }_r$ for $r=1,\dots ,s$. If a failure occurs while a customer is being serviced, the service will continue without interruption. Once the service is complete, the repair process can begin. That means we apply so called non-preemptive priority for failures of the system;
• System capacity: As the queueing system is finite, the number of tracks in the reception siding is equal to m, but since it was mentioned that in case of primary shunting, and also secondary shunting, an arrival track is occupied, we will consider that the capacity of the queue is equal to $m-1$.

  Table 1. Summary of mathematical symbols and their definitions.

  Symbol	Definition
  λ	Arrival rate—the rate at which customers (trains of wagons requesting primary shunting) enter the system
  n	The number of service phases
  ${\mathit{\mu }}_{\mathit{p}}$	Service rates for individual phases of service, where $p=1,\dots ,n$
  η	Failure rate—the rate at which system failures occur
  s	The number of repair phases
  ${\mathit{\zeta }}_{\mathit{r}}$	Repair rates for individual phases of repair, where $r=1,\dots ,s$
  m	System capacity—the total number of customers the system can accommodate
  F	System state—operational condition of the system (e.g., functioning or failed)
  k	Number of customers—current number of customers in the system
  ${\mathit{P}}_{\mathit{k},\mathit{p}/\mathit{r},\mathit{f}}$	Steady-state probability that the system has k customers at phase p (service) or r (repair) in state f
  ES	Expected number of customers in the service
  EL	Expected number of customers in the queue
  EK	Expected number of customers in the system (service + queue)
  EF	Expected number of failed servers (under repair)

  summarizes the notation used in the mathematical model.

The study focuses on the analysis of the following associated random variables that are necessary to define individual system states:

• The random variable K represents the number of customers in the system; the variable takes its value from the set $\left\{0,1,\dots ,m\right\}$;
• The random variables P and R represent the individual phases of service and repair, respectively, which take a value from the set $\left\{0,1,\dots ,n\right\}$ and $\left\{0,1,\dots ,s\right\}$. Please note that for the state, when the system is empty, both variables are equal to 0;
• The last random variable F takes the value from the set $\left\{0,1,2\right\}$ with the following meaning. When the variable F is 0, there is no failure in the system; that is, in our case, there is no need for secondary shunting. If the variable F is equal to 1, the failure of the system is waiting for repair (a request for secondary shunting is waiting). In this case, we should realize that secondary shunting must wait because the classification of an inbound freight train is being carried out. Finally, when the variable F is equal to 2, the system failure is being repaired. In this case, secondary shunting is taking place.

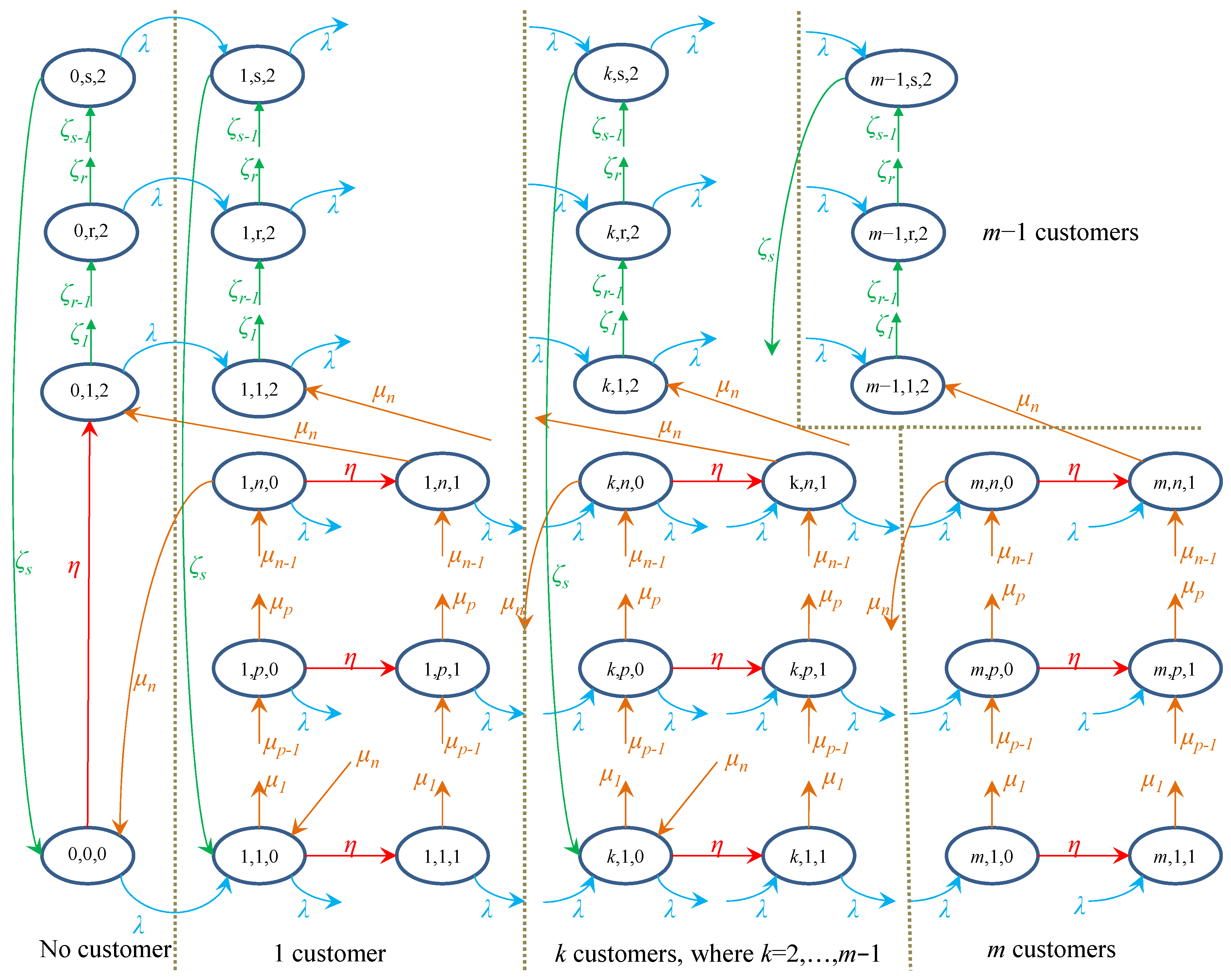
Based on these facts, we can represent the system as a triplet (k, p/r, f), which can describe each possible state of the system. Let us represent the mathematical model in a transition diagram—see Figure 1.

Based on the transition diagram, a linear equation system with $2mn+sm+1$ unknown steady-state probabilities of individual system states can be set up. However, using the three-dimensional state notation (k, p/r, f) presented in Figure 1 is not suitable for calculations in MATLAB software version R2021b, which can be used to solve the equation system. Therefore, an alternative state description had to be defined:

• States (k, p, f), where k ranges from 1 to m, p ranges from 1 to n, and f ranges from 0 to 1, can be expressed by a one-dimensional notation $fmn+\left(p-1\right)·m+k$ (resulting in $2mn$ states);
• States (k, r, 2), where k ranges from 0 to $m-1$ and r ranges from 1 to s, will be labeled using the formula $2mn+\left(r-1\right)·m+k+1$ (resulting in $ms$ states);
• The state (0, 0, 0) will be represented as $2mn+ms+1$.

Based on this one-dimensional state notation, the linear equation system can be defined in the following form:

$$\left(\lambda +\eta \right)·P_{2mn+ms+1}={\mu }_n·P_{\left(n-1\right)m+1}+{\zeta }_s·P_{2mn+\left(s-1\right)m+1}$$

(7)

$$\left(\lambda +{\mu }_1+\eta \right)·P_1=\lambda ·P_{2mn+ms+1}+{\mu }_n·P_{\left(n-1\right)m+2}+{\zeta }_s·P_{2mn+\left(s-1\right)m+2}$$

(8)

$$\left(\lambda +{\mu }_1+\eta \right)·P_k=\lambda ·P_{k-1}+{\mu }_n·P_{\left(n-1\right)m+k+1}+{\zeta }_s·P_{2mn+\left(s-1\right)m+k+1} \mathrm{for} k=2,\dots ,m-1$$

(9)

$$\left({\mu }_1+\eta \right)·P_m=\lambda ·P_{m-1}$$

(10)

$$\left(\lambda +{\mu }_1\right)·P_{mn+1}=\eta ·P_1$$

(11)

$$\left(\lambda +{\mu }_1\right)·P_{mn+k}=\lambda ·P_{mn+k-1}+\eta ·P_k \mathrm{for} k=2,\dots ,m-1$$

(12)

$${\mu }_1·P_{mn+m}=\lambda ·P_{mn+m-1}+\eta ·P_m$$

(13)

$$\left(\lambda +{\mu }_p+\eta \right)·P_{\left(p-1\right)m+1}={\mu }_{p-1}·P_{\left(p-2\right)m+1} \mathrm{for} p=2,\dots ,n$$

(14)

$$\left(\lambda +{\mu }_p+\eta \right)·P_{\left(p-1\right)m+k}=\lambda ·P_{\left(p-1\right)m+k-1}+{\mu }_{p-1}·P_{\left(p-2\right)m+k} \mathrm{for} k=2,\dots ,m-1 \mathrm{and} p=2,\dots ,n$$

(15)

$$\left({\mu }_p+\eta \right)·P_{\left(p-1\right)m+m}=\lambda ·P_{\left(p-1\right)m+m-1}+{\mu }_{p-1}·P_{\left(p-2\right)m+m} \mathrm{for} p=2,\dots ,n$$

(16)

$$\left(\lambda +{\mu }_p\right)·P_{mn+\left(p-1\right)m+1}={\mu }_{p-1}·P_{mn+\left(p-2\right)m+1}+\eta ·P_{\left(p-1\right)m+1} \mathrm{for} p=2,\dots ,n$$

(17)

$$\begin{array}{c}\left(\lambda +{\mu }_p\right)·P_{mn+\left(p-1\right)m+k}=\lambda ·P_{mn+\left(p-1\right)m+k-1}+{\mu }_{p-1}·P_{mn+\left(p-2\right)m+k}+\eta ·P_{\left(p-1\right)m+k} \mathrm{for} k=2,\dots ,m-1\\ \mathrm{and} p=2,\dots ,n\end{array}$$

(18)

$${\mu }_p·P_{mn+\left(p-1\right)m+m}=\lambda ·P_{mn+\left(p-1\right)m+m-1}+{\mu }_{p-1}·P_{mn+\left(p-2\right)m+m}+\eta ·P_{\left(p-1\right)m+m} \mathrm{for} p=2,\dots ,n$$

(19)

$$\left(\lambda +{\zeta }_1\right)·P_{2mn+1}={\mu }_n·P_{mn+\left(n-1\right)m+1}+\eta ·P_{2mn+ms+1}$$

(20)

$$\left(\lambda +{\zeta }_1\right)·P_{2mn+k+1}=\lambda ·P_{2mn+k}+{\mu }_n·P_{mn+\left(n-1\right)m+k+1} \mathrm{for} k=1,\dots ,m-2$$

(21)

$${\zeta }_1·P_{2mn+m}=\lambda ·P_{2mn+m-1}+{\mu }_n·P_{mn+\left(n-1\right)m+m}$$

(22)

$$\left(\lambda +{\zeta }_r\right)·P_{2mn+\left(r-1\right)m+1}={\zeta }_{r-1}·P_{2mn+\left(r-2\right)m+1} \mathrm{for} r=2,\dots ,s$$

(23)

$$\begin{array}{c}\left(\lambda +{\zeta }_r\right)·P_{2mn+\left(r-1\right)m+k+1}=\lambda ·P_{2mn+\left(r-1\right)m+k}+{\zeta }_{r-1}·P_{2mn+\left(r-2\right)m+k+1} \mathrm{for} k=1,\dots ,m-2 \mathrm{and}\\ r=2,\dots ,s\end{array}$$

(24)

$${\zeta }_r·P_{2mn+\left(r-1\right)m+m}=\lambda ·P_{2mn+\left(r-1\right)m+m-1}+{\zeta }_{r-1}·P_{2mn+\left(r-2\right)m+m} \mathrm{for} r=2,\dots ,s$$

(25)

Upon solving the equation system (7)–(25), it becomes essential to implement a normalization equation to address the linear dependency present among the equations. This step is critical for ensuring that the results are distinct and meaningful. The normalization equation can be articulated as follows:

$$P_{2mn+ms+1}+{\sum }_{k=1}^m{\sum }_{p=1}^n{\sum }_{f=0}^1{P}_{fmn+\left(p-1\right)·m+k}+{\sum }_{k=0}^{m-1}{\sum }_{r=1}^s{P}_{2mn+\left(r-1\right)·m+k+1 }=1.$$

(26)

Based on knowledge of the stationary-state probabilities, we can calculate the system performance using the following performance indicators. The mean number of customers (requests for primary shunting) found in service ES can be calculated using the following formula:

$$ES={\displaystyle \sum }_{k=1}^m{\displaystyle \sum }_{p=1}^n{\displaystyle \sum }_{f=0}^1{P}_{fmn+\left(p-1\right)·m+k}$$

(27)

For the mean number of customers (requests for primary shunting) waiting in the queue EL, the following holds:

$$EL={\displaystyle \sum }_{k=2}^m{\displaystyle \sum }_{p=1}^n{\displaystyle \sum }_{f=0}^1\left(k-1\right)·P_{fmn+\left(p-1\right)·m+k}+{\displaystyle \sum }_{k=1}^{m-1}{\displaystyle \sum }_{r=1}^{s}k·P_{2mn+\left(r-1\right)·m+k+1}$$

(28)

The mean number of customers (requests for primary shunting) found in the system is the sum of ES and EL:

$$EK=ES+EL={\sum }_{k=1}^m{\sum }_{p=1}^n{\sum }_{f=0}^{1}k·P_{fmn+\left(p-1\right)·m+k}+{\sum }_{k=1}^{m-1}{\sum }_{r=1}^{s}k·P_{2mn+\left(r-1\right)·m+k+1}.$$

(29)

The mean number of service disruptions corresponding to the probability that the system is under failure (secondary shunting is in progress) is as follows:

$$EF={\displaystyle \sum }_{k=0}^{m-1}{\displaystyle \sum }_{r=1}^s{P}_{2mn+\left(r-1\right)·m+k+1}$$

(30)

2.3. Colored Petri Net Simulation Model

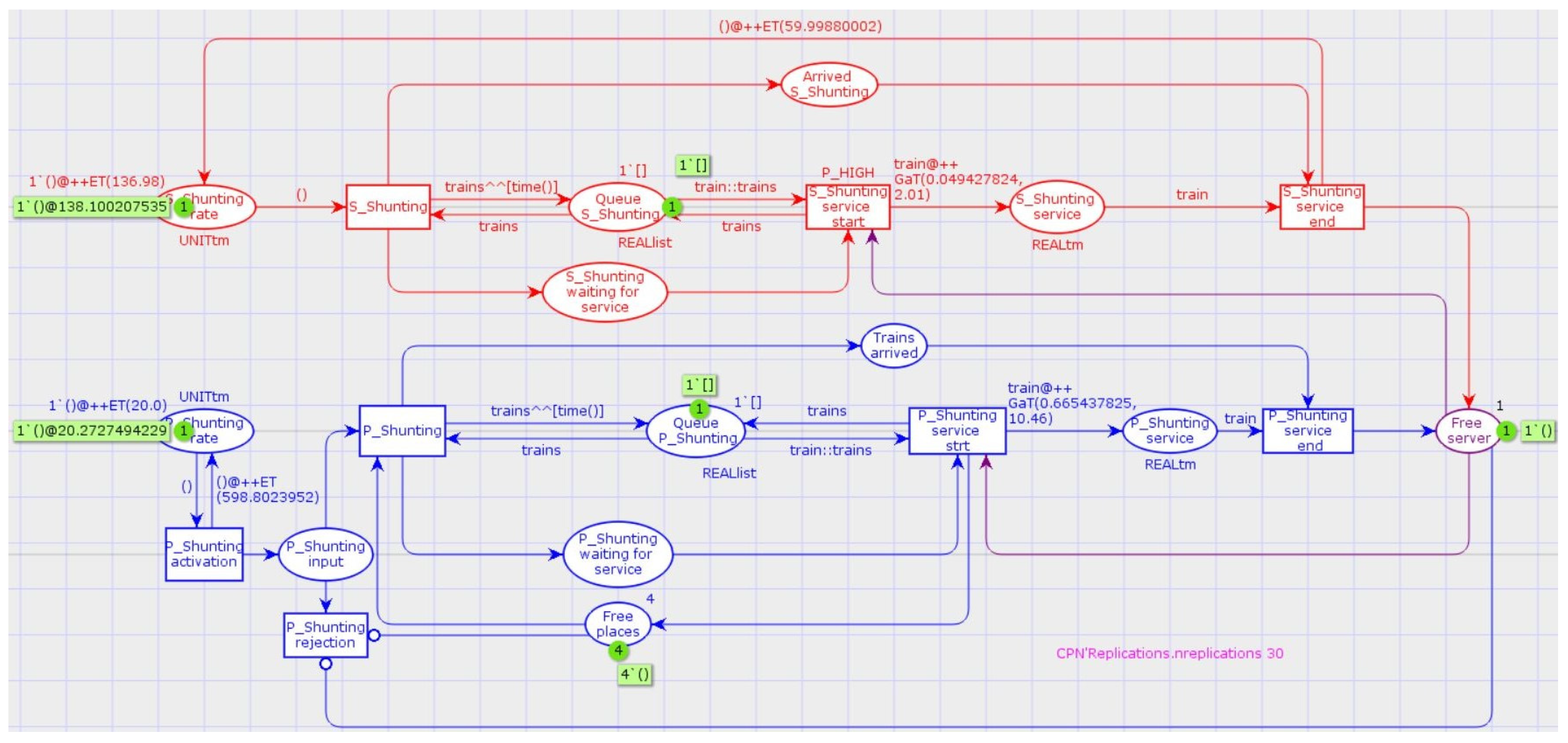
A Colored Petri Net model based on the M/Ga/1/m queueing system, which incorporates non-preemptive priority failures within the service line, was created to validate the results derived from the mathematical model created using hypo-exponential probability distribution by applying the fixed approximation method. Colored Petri Nets (CPNs) are a comprehensive tool for creating, modifying, simulating, and analyzing system performance metrics [31]. The model was created using CPN Tools version 4.0.1 (https://cpntools.org/2018/01/15/windows/) accessed on 19 May 2023. Before representing and simulating the marshaling yard, first we declared the following color sets, variables, and functions, which are the main components of the Petri Nets model, to work and obtain the desired output (see

Table 2. Declarations and monitoring functions of the simulation model.

Declaration	Meaning
Color set
Coloset UNIT = unit	This color set comprises a single unit, represented by ()
Coloset UNITtm = unit timed	It is a unit color set with a timestamp
Coloset REAL = real	A real number token
Coloset REALtm= real timed	Represents a timed real number applied to model a time delay
Coloset REALlist = list REAL	A list of real numbers
Variables
Var trains: REALlist	This variable is a list of real values, e.g., service times of multiple trains
Var trains: REAL	Represents a single value
Function
Fun ET(EX) = exponential (1.0/EX)	Generates a random value from an exponential distribution with mean EX
Fun GaT(l,k) = gamma(l,k)	Returns a random value from a Gamma distribution with shape k and rate l
Monitoring function
ES_S_Shunting	Expected (average) number of trains of wagons in service during secondary shunting
ES_P_Shunting	Expected (average) number of trains of wagons in service during primary shunting
EL_S_Shunting	Expected queue length during secondary shunting
EL_P_Shunting	Expected queue length during primary shunting
EK_S_Shunting	Expected total number of trains of wagons in the system during secondary shunting
EK_P_Shunting	Expected total number of trains of wagons in the system during primary shunting
EW_S_Shunting	Expected waiting time in secondary shunting
EW_P_Shunting	Expected waiting time in primary shunting
ET_S_Shunting	Expected total time in the system during secondary shunting
ET_P_Shunting	Expected total time in the system during primary shunting

):

• Color sets are represented using ‘UNIT’, ‘UNITtm’, ‘REALtm’, and ‘REALlist’, some of which are predefined by the programmer, and others are defined by the user;
• The variables are represented using ‘trains’ and ‘train’.

Figure 2 shows the simulation model with the initial marking. The model consists of 10 places, 9 transitions, arcs, and their inscriptions. In this simulation model, we applied a gamma distribution to generate the desired values of the random variables during simulation to validate the analytical model, which was modeled using a fixed approximation method, and we used the function ‘fun GaT (l,k) = gamma (l,k)’. In this function, l is the rate parameter and k is the shape parameter, as the Gamma distribution of probability is defined in CPN Tools by these two parameters. Please note that the Gamma distribution can be defined by the scale parameter instead of the rate parameter as well—it holds that the rate parameter is a reciprocal value of the scale parameter. Let us take into account that in this model, we used ‘P_Shunting’ and ‘S_Shunting’, which represented primary and secondary shunting, respectively. As we discussed earlier in this document, secondary shunting is considered a failure of the system.

We can describe the simulation model in more detail. The place ‘P_Shunting rate’ connected with the transition ‘P_Shunting activation’ represents the input flow of the trains of wagons into the system. The place ‘P_Shunting input’ indicates the arrival of trains of wagons into the system, which is the place used to decide whether the customer enters the queue through the transition ‘P_Shunting’ or is rejected through the transition ‘P_Shunting rejection’. The customer is rejected only when there is no free place in the queue and the server is busy—this is ensured by means of inhibition arcs ending in the transition ‘P_Shunting rejection’. The customer is waiting for the service in the place ‘Queue P_Shunting’. The transition ‘P_Shunting service strt’ allows for the start of the service. The service and the end of the service are represented using the place ‘P_Shunting service’ and the transition ‘P_Shunting service end’, respectively.

In addition to this, the failure of the system is represented using the place ‘S_Shunting rate’. Failures enter the system via the transition ‘S_Shunting’. The place ‘Queue S_Shunting’ models the waiting for the failure to be repaired. By firing the transition ‘S_Shunting service start’, the repair process is started; for the transition, the higher priority (‘P_HIGH’) is set up. This is because the place ‘Free server’ is a common input place for the transitions ‘P_Shunting service strt’ and ‘S_Shunting service start’, and thanks to the higher priority of the transition ‘S_Shunting service start’, the non-preemptive priority is modeled. The place ‘S_Shunting service’ indicates the ongoing service of the server.

Please note that trains of wagons waiting in the queue (the place ‘Queue P_Shunting’) and the failure of the system waiting to be repaired (the place ‘Queue S_Shunting’) are not represented by individual tokens but by a list of real values—the color set assigned to both places is ‘REALlist’. The list contains real values, where each value represents the simulation time when a customer or a failure has entered the system. To monitor the number of trains of wagons or failures in the queue and the system, some auxiliary places were created:

• The place ‘P_Shunting waiting for service’ enables the monitoring of the number of trains of wagons waiting in the queue;
• The place ‘Trains arrived’ was defined to monitor the number of trains of wagons found in the system;
• Via the place ‘S_Shunting waiting for service’, the number of failures waiting for repair is monitored;
• The place ‘Arrived S_Shunting’ monitors the number of failures under repair in the system.

For the model to work properly, we created additional auxiliary places such as ‘Free places’ and ‘Free server’ to represent the number of free places in the queue and to indicate that the server is available, respectively. Time durations of individual processes are modeled via initial markings of corresponding places or arc expressions of corresponding arcs. In addition to the function ‘GaT (l,k)’, which generates values of the Gamma probability distribution, the function ‘fun ET (EX) = exponential (1.0/EX)’ is used—the function generates values coming from the exponential distribution of probability with the mean value EX to model customer inter-arrival times and times between failures.

To measure the performance of the system, we used several monitoring functions. The most important performance measures that enable the comparison of simulation results with the results of the mathematical model are the following functions:

• The mean number of trains of wagons in the service ES is estimated using the monitoring function ‘ES_P_Shunting’ connected with the place ‘P_Shunting service‘;
• The monitoring function ‘EL_P_Shunting’ linked with the place ‘P_Shunting waiting for service’ helps us to estimate the mean number of trains of wagons in the queue EL;
• The monitoring function ‘ES_S_Shunting’, associated with the place ‘S_Shunting service’, measures the mean number of service disruptions (EF);
• The mean number of trains of wagons in the system (EK) is estimated by means of the monitoring function ‘EK-P_Shunting’, which is associated with the place ‘Trains arrived’.

Finally, we applied a breakpoint function to terminate the simulation at time 31,536,000 s, which is the conversion of 365 days. To execute the simulation, we run 30 independent experiments using the defined auxiliary text ‘CPN’Replications.replications 30′.

3. Results and Discussion

To evaluate the operational performance of the marshaling yard in Ostrava, two distinct stochastic models were developed. These models simulate the dynamics of both primary and secondary shunting processes in freight rail transport. Experimental analysis was conducted on both models to quantify system performance metrics such as the following:

• The average number of trains of wagons in service (ES);
• The average queue length (EL);
• The total number of trains of wagons in the system (EK);
• The average number of failed servers (EF).

This dual-model framework enables a comprehensive assessment of operational efficiency and provides insights into critical bottlenecks and potential areas for optimization.

In this study, we utilized empirical data on inter-arrival times, service durations, times between failures, and repair times, all of which are critical parameters for accurately modeling the dynamics of a marshaling yard system. The datasets were derived from a comprehensive analysis of operational documentation provided by the marshaling yard in Ostrava, which outlines the full procedural workflow of yard operations. To have a better understanding of the nature of the marshaling yard process, various probability distributions were tested for each type of random variable based on empirical data. A basic statistical summary of the data is presented in

Table 3. Data fitting for Ostrava marshaling yard.

Random Variable	Inter-Arrival Times	Service Times	Times to Failure	Repair Times
Sample average [min]	65.77	15.72	136.98	40.58
Sample variance [min2]	2761.50	23.62	10,046.05	821.05
Probability distribution	Exponential	Gamma	Exponential	Gamma
Shape parameter [-]	-	10.46	-	2.01
Scale parameter [min]	65.77	1.50	136.98	20.23

, indicating that for inter-arrival times and times to failure, the exponential distribution is found to be an adequate fit;; however, service and repair times are more flexible and needed due to the observed variability of the data. In the mathematical model, these can be approximated using hypo-exponential distributions, which allow for multiple phases and are better suited to capturing underlying variability. Please note that the Pearson’s chi-squared test was performed for all the datasets presented in the table to test hypotheses about corresponding probability distributions; in all cases, the p-value was greater than 0.05, so it is possible to fit our data based on the probability distributions.

Based on the above empirical data source, we approximated using the fixed hypo-exponential method through the equations mentioned in Section 2, from Equations (1)–(6). As summarized in

Table 4. Approximation method.

Service Times—Parameters	Service Times—Used Values	Repair Times—Parameters	Repair Times—Used Values
n	11	s	3
${\mathit{\mu }}_{\mathit{i}}$$\mathrm{for} \mathit{i}=\mathbf{1},\dots \mathbf{9}$ [min−1]	0.70	${\zeta }_1$ [min−1]	0.07
${\mathit{\mu }}_{\mathbf{10}}$ [min−1]	1.50	${\zeta }_2$ [min−1]	0.54
${\mathit{\mu }}_{\mathbf{11}}$ [min−1]	0.46	${\zeta }_3$ [min−1]	0.04
EX [min]	15.72	EX [min]	40.58
DX [min2]	23.62	DX [min2]	821.08

, the collected data served as the basis for calibrating our queuing model. In particular, service and repair times were approximated using the corresponding values of the sample average and sample variance to ensure consistency with observed real-world variability. To reflect the multi-phase nature of these processes, the queuing system was modeled using a hypo-exponential distribution, which offers enhanced flexibility in capturing diverse service and recovery durations compared to simpler exponential models.

Using the input data in

Table 5. Summary of the values of the input parameters.

Parameter	Unit	Value
Arrival rate λ	min−1	0.015
Number of service phases n	-	11
Service rate ${\mu }_1$ up to ${\mu }_9$	min−1	0.700
Service rate ${\mu }_{10}$	min−1	1.500
Service rate ${\mu }_{11}$	min−1	0.460
Failure rate η	min−1	0.007
Number of repair phases s	-	3
Repair rate ${\zeta }_1$	min−1	0.074
Repair rate ${\zeta }_2$	min−1	0.540
Repair rate ${\zeta }_3$	min−1	0.040
Capacity of the system m	-	5

, we developed a steady-state analysis of the queuing system in MATLAB and ran 30 simulation replications using a Colored Petri Net (CPN) model and the data presented in Table 3. The simulation model outcomes were compared to analytical results and presented with 95% confidence intervals, as shown in

Table 6. Performance results obtained from analytical and simulation outputs.

Performance Measure	Simulation Model			Analytical Result
	Average	Lower Bound	Upper Bound
ES	0.2382	0.2375	0.2387	0.2381
EF	0.2253	0.2242	0.2262	0.2253
EL	0.2115	0.2099	0.2134	0.2113
EK	0.4497	0.4473	0.45204	0.4494

. A 95% two-sided confidence interval was calculated for each indicator, indicated by the lower and upper bounds. This interval allows us to assess the mathematical result that falls within these bounds.

The results indicate a high degree of alignment between analytical and simulation outputs, confirming the robustness of the proposed models. Consequently, performance indicators are considered reliable for accurately assessing system performance:

• The utilization rate of the marshaling yard in primary shunting was approximately 23.81%, as indicated by ES;
• In secondary shunting, the server failure utilization reached 22.53%, as shown by EF;
• The average queue length was minimal (EL = 0.2113), suggesting low congestion within the system;
• The total number of trains of wagons in the system remained stable at approximately 0.4494, reflecting efficient throughput.

These findings highlight the yard’s moderate load levels, but also point to latent inefficiencies in secondary shunting that may benefit from process redesign or resource reallocation. The results showed that the hypo-exponential approximation provides a good result, as the analytical result falls within the boundaries of the 95% confidence interval of the simulation output. In addition to this, we matched the first two moments of the gamma distribution with hypo-exponential representation and confirmed the accuracy, as the performance metrics such as ES, EF, EL, and EK have less than 1% deviation when using hypo-exponential approximation and a true gamma input. This indicates that the approximation has promising results for representing the gamma distribution within acceptable bounds.

In addition to the aforementioned experiments, we conducted further experiments to evaluate system performance by systematically varying the arrival rate λ. Specifically, we examined arrival rates spanning from λ = 0.1000 min⁻¹ down to λ = 0.0067 min⁻¹ to observe their impact on key performance metrics.

The findings presented in

Table 7. Performance of the system with varying arrival rates.

Arrival Rate	Performance Measure
	ES			EL			EK			EF
	Lower Bound	Upper Bound	Analytical	Lower Bound	Upper Bound	Analytical	Lower Bound	Upper Bound	Analytical	Lower Bound	Upper Bound	Analytical
0.1000	0.7769	0.7810	0.7790	3.2446	3.2882	3.2664	4.0257	4.0649	4.0453	0.2169	0.2189	0.2179
0.0500	0.6632	0.6666	0.6649	1.6991	1.7219	1.7105	2.3644	2.3864	2.3754	0.2183	0.2205	0.2194
0.0333	0.4972	0.4998	0.4985	0.8399	0.8511	0.8455	1.3377	1.3501	1.3439	0.2206	0.2228	0.2217
0.0250	0.3843	0.3863	0.3853	0.4946	0.5010	0.4978	0.8790	0.8872	0.8831	0.2222	0.2244	0.2233
0.0200	0.3106	0.3122	0.3114	0.3326	0.3368	0.3347	0.6432	0.6492	0.6462	0.2232	0.2254	0.2243
0.0167	0.2601	0.2613	0.2607	0.2440	0.2472	0.2456	0.5039	0.5087	0.5063	0.2239	0.2261	0.2250
0.0152	0.2375	0.2387	0.2381	0.2099	0.2134	0.2113	0.4473	0.4520	0.4494	0.2242	0.2262	0.2253
0.0143	0.2233	0.2245	0.2239	0.1899	0.1925	0.1912	0.4132	0.4170	0.4151	0.2244	0.2266	0.2255
0.0125	0.1956	0.1966	0.1961	0.1542	0.1562	0.1552	0.3496	0.3530	0.3513	0.2248	0.2270	0.2259
0.0111	0.1740	0.1748	0.1744	0.1291	0.1307	0.1299	0.3029	0.3059	0.3044	0.2251	0.2273	0.2262
0.0100	0.1566	0.1574	0.1570	0.1107	0.1121	0.1114	0.2671	0.2697	0.2684	0.2253	0.2275	0.2264
0.0091	0.1424	0.1432	0.1428	0.0966	0.0978	0.0972	0.2388	0.2412	0.2400	0.2255	0.2277	0.2266
0.0083	0.1305	0.1313	0.1309	0.0855	0.0867	0.0861	0.2159	0.2181	0.2170	0.2257	0.2279	0.2268
0.0077	0.1205	0.1213	0.1209	0.0767	0.0777	0.0772	0.1970	0.1990	0.1980	0.2258	0.2280	0.2269
0.0071	0.1119	0.1125	0.1122	0.0694	0.0704	0.0699	0.1812	0.1830	0.1821	0.2259	0.2281	0.2270
0.0067	0.1045	0.1051	0.1048	0.0634	0.0642	0.0638	0.1678	0.1694	0.1686	0.2260	0.2282	0.2271

reveal a clear relationship between the arrival rate and key performance metrics in the system. Specifically, as the arrival rate (λ) decreases, there is a corresponding decline in the mean number of customers in service (ES), the mean number of customers in the queue (EL), and the mean number of customers in the system (EK). In contrast, a reduction in the arrival rate leads to an increase in the mean number of broken servers (EF).

This phenomenon suggests that decreased arrival rates result in lower train congestion within marshaling yards, which facilitates an uptick in secondary shunting operations due to diminished occupancy at the hump by primary shunting activities. Fewer trains in primary shunting operations allow the marshaling yard to better accommodate trains transitioning from secondary shunting. Ultimately, the data indicates a direct correlation between the arrival rate and the performance metrics (ES, EL, and EK), while highlighting an inverse relationship with the number of broken servers (EF).

These findings align with queueing theory principles, where lower arrival rates typically reduce congestion in the system, leading to fewer trains of wagons in service, in the queue, and overall in the system. However, the increase in broken lines (EF) occurs at lower arrival rates.

We can observe that the analytical output and simulation results summarized in the above table indicate a high degree of alignment. The relative error remains below 0.1% for ES, EL, and EK, and EF is effectively zero. These small discrepancies can be attributed to simulation randomness and numerical rounding in mathematical computations. The result affirms the correctness of the analytical model under the assumed system dynamics. Nonetheless, we acknowledge that the real-world marshaling yards may exhibit additional complexities such as phase-type arrivals, mechanical and infrastructure failure, and transit behavior, which are abstracted in this model. Therefore, while the analytical framework is highly accurate for the modeled assumptions, simulation remains a valuable complementary tool when extending the model to more complex or realistic yard operations.

4. Conclusions

In this paper, we introduced the M/Hypo_K/1/m queuing system subject to failure to evaluate the performance of marshaling yards in the classification of freight rail operations, using hypo-exponential probability distributions to capture the complexities inherent in the system. The analysis delves into the operational dynamics of the marshaling yard by examining two distinct modes of shunting carried out over the hump. The primary shunting operation concentrates on the systematic sorting and classification of incoming trains based on various criteria, such as cargo type and destination, while the secondary shunting operations are aimed at managing the reorganization of railcars to optimize train assembly and improve overall throughput.

To rigorously model this intricate process, we represent it as a finite single-server queuing system, which accommodates the reality of potential server failures that could disrupt operations. This model description allows for the consideration of multiple factors, such as the arrival rates of incoming trains, service rates of the sorting operations, and the finite capacity constraints of the yard.

The proposed two models demonstrate potential applicability and flexibility for representing the complex nature of marshaling yards. In pursuit of a comprehensive analysis, we developed two frameworks. The first framework is a mathematical model grounded in Markov processes, which provided insights into steady-state behavior and performance metrics. The mathematical model was solved using MATLAB to obtain the stationary probabilities of system states. The second simulation technique was modeled using Petri Nets, enabling us to visualize and simulate the queuing system of the marshaling yard to validate the mathematical output. The results indicated counterintuitive dynamics, such as increased secondary shunting under lower arrival rates. The findings support the use of hypo-exponential approximations for modeling service and repair times in marshaling yards, with the results showing an average queue length of 0.2113 and overall system utilization of 0.4634. These quantitative gains substantiate our decision to adopt more flexible service and repair time distributions. These results have practical implications for scheduling and capacity planning in the rail network.

Although the models have promising output for the performance of the system, we can point out the limitations of the model. As we can observe in the development of both models, they are highly abstracted, meaning that the models are simple and do not have a detailed description of the system. In addition to this, the models’ input parameters are limited, such as trains, system capacity, and a single service point, which ignores the number of people and technologies applied to facilitate the operational process. Although the models considered the secondary shunting as faulty, they did not consider mechanical and equipment failure. However, the designed models have the capability to analyze and predict the performance of marshaling yard operations.

The current study provides an analytical traceability model for marshaling yard operations under failure conditions using M/Hypo_K/1/m, which could be a springboard for future work to extend both the theoretical depth and practical applicability of this work. First, the assumption of exponentially distributed inter-arrival and failure times, although convenient for analytical modeling, may not fully capture the complexity of real yard dynamics. Future work could consider more general phase-type or semi-Markov arrival processes, such as the BMAP (Batch Markovian Arrival Process), which have been shown to better model non-Poisson input patterns observed in large-scale yards [16,20]. Extending the current model to a BMAP/Hypo_K/1/m system would allow for the more accurate estimation of congestion and queuing delays under bursty or correlated arrivals.

Second, while the study introduced a hypo-exponential repair process, further research could explore state-dependent repair mechanisms. In real-world operations, repair durations and re-shunting efforts may vary depending on yard congestion, crew availability, or the nature of failure. Incorporating such context-dependent repair rates could enhance the model’s predictive power and realism.

Third, the model applied in this study is limited to a single setting. In practice, large marshaling yards operate with parallel classification tracks, where incoming trains may be routed dynamically. Extending the model to a multi-server finite-capacity system like M/Hypo_K/c/m, with routing decisions, would better represent large-scale systems.

Fourth, this study treated secondary shunting as a form of system failure, which is not mechanical or infrastructure failure. Further research could explore how combining predictive with dynamic resequencing heuristics could both parameterize the Coxian-phase-type distribution to capture the multi-phase nature of service and repair, which could quantitatively reduce the congestion of the yard.