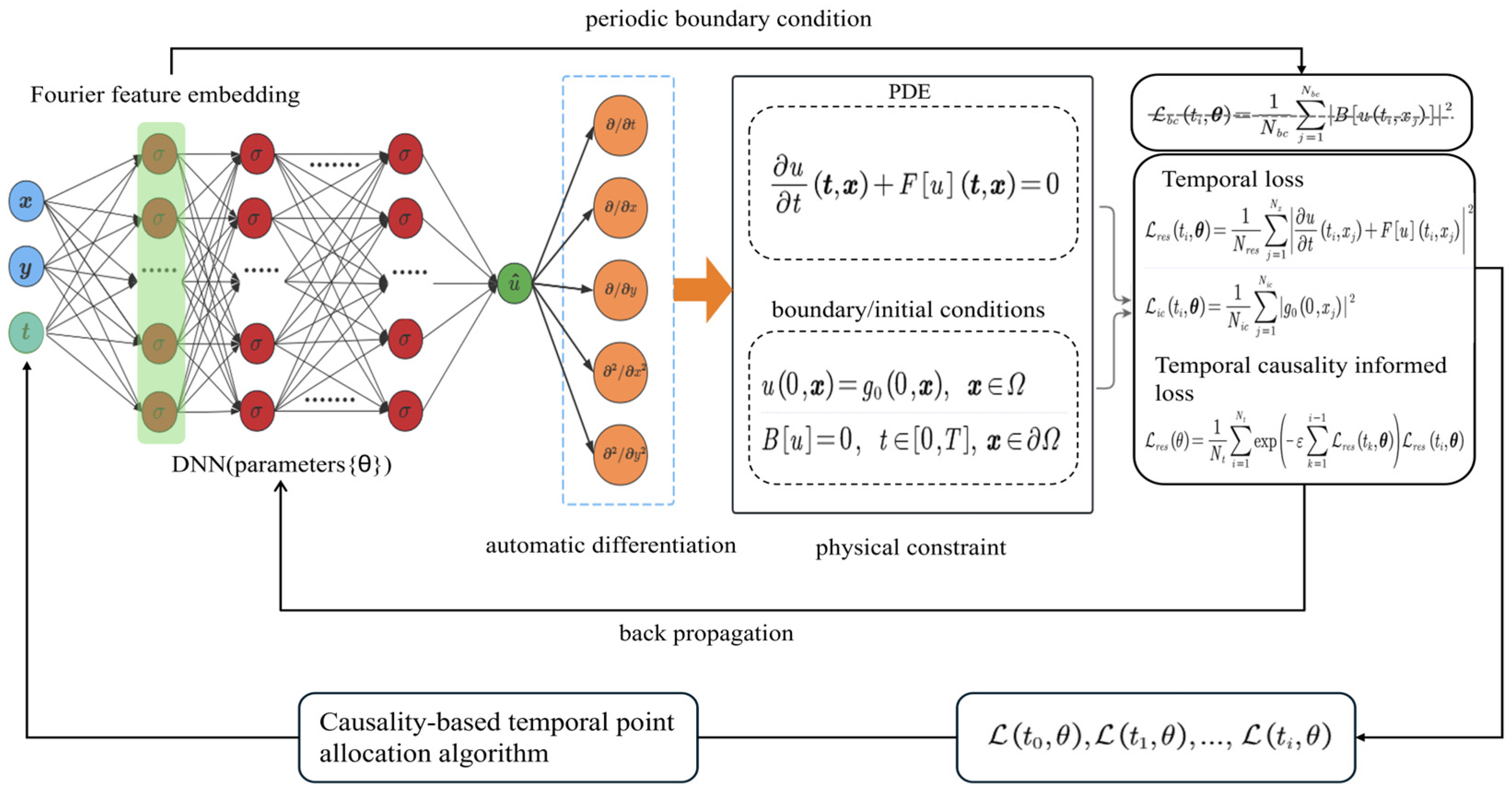
Figure 1.
Causal PINN framework for time-dependent problems with periodic boundary conditions in space.
Figure 1.
Causal PINN framework for time-dependent problems with periodic boundary conditions in space.
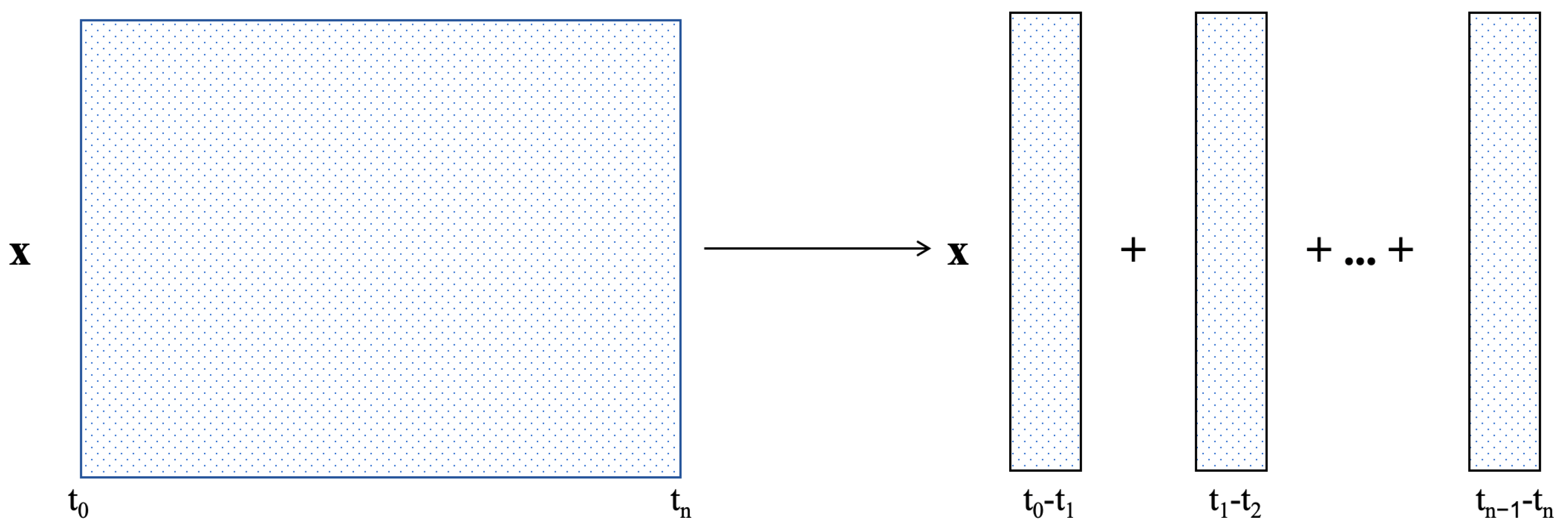
Figure 2.
Time-marching framework.
Figure 2.
Time-marching framework.
Figure 3.
Causality-based temporal point allocation algorithm combined with time marching. After the division of the entire temporal domain, a fixed number of temporal points are allocated to each local time subinterval. Take the first subinterval as an example for illustration. The time division point marks the separation where the residual loss is within the predefined threshold, and the temporal sampling is dynamically concentrated on the region after this point.
Figure 3.
Causality-based temporal point allocation algorithm combined with time marching. After the division of the entire temporal domain, a fixed number of temporal points are allocated to each local time subinterval. Take the first subinterval as an example for illustration. The time division point marks the separation where the residual loss is within the predefined threshold, and the temporal sampling is dynamically concentrated on the region after this point.
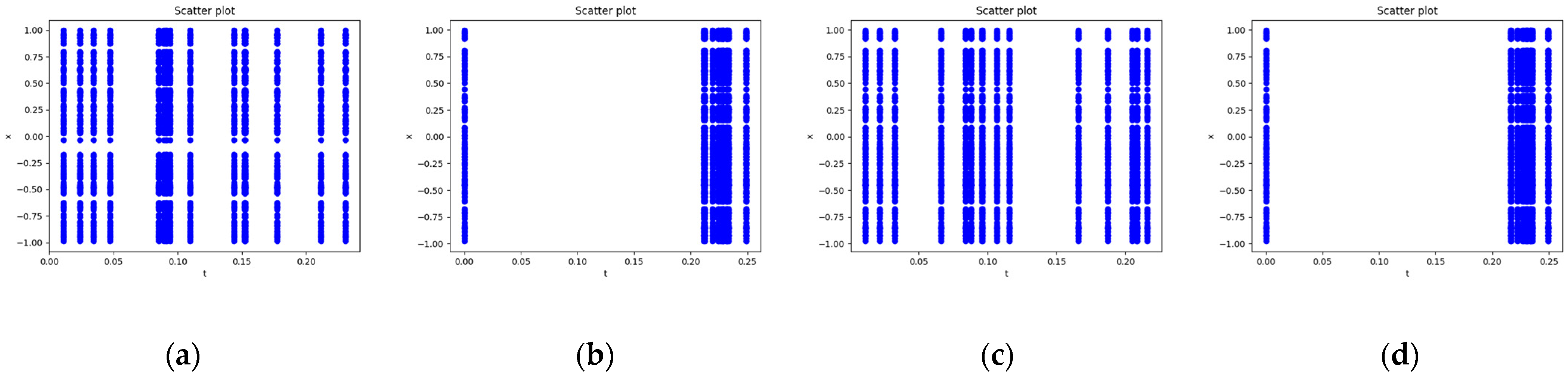
Figure 4.
Schematic diagram of time point allocation by the causality-based temporal point allocation algorithm. Take the first time subinterval as an example. (a) Initial random sampling of temporal points. (b) Redistribution of temporal sampling points toward regions with larger residuals (the latter portion). (c) Further adjustment after the residuals at all points except the first one fail to satisfy the criterion. (d) Redistribution of temporal sampling points toward the latter portion again.
Figure 4.
Schematic diagram of time point allocation by the causality-based temporal point allocation algorithm. Take the first time subinterval as an example. (a) Initial random sampling of temporal points. (b) Redistribution of temporal sampling points toward regions with larger residuals (the latter portion). (c) Further adjustment after the residuals at all points except the first one fail to satisfy the criterion. (d) Redistribution of temporal sampling points toward the latter portion again.
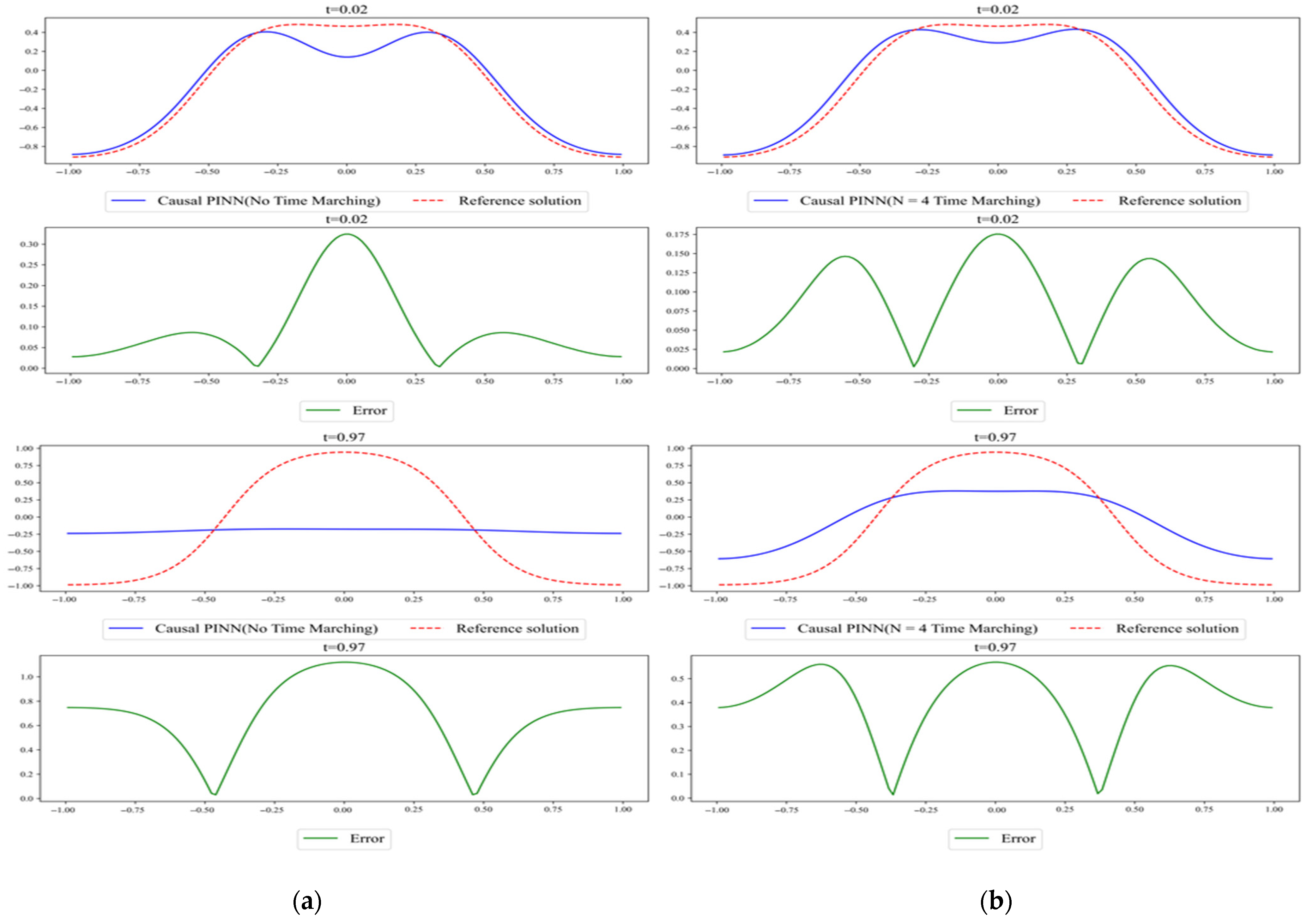
Figure 5.
Comparison of the results predicted by (a) Causal PINN with no time marching and (b) Causal PINN with N = 4 time marching. The reference solution was obtained with Chebfun.
Figure 5.
Comparison of the results predicted by (a) Causal PINN with no time marching and (b) Causal PINN with N = 4 time marching. The reference solution was obtained with Chebfun.
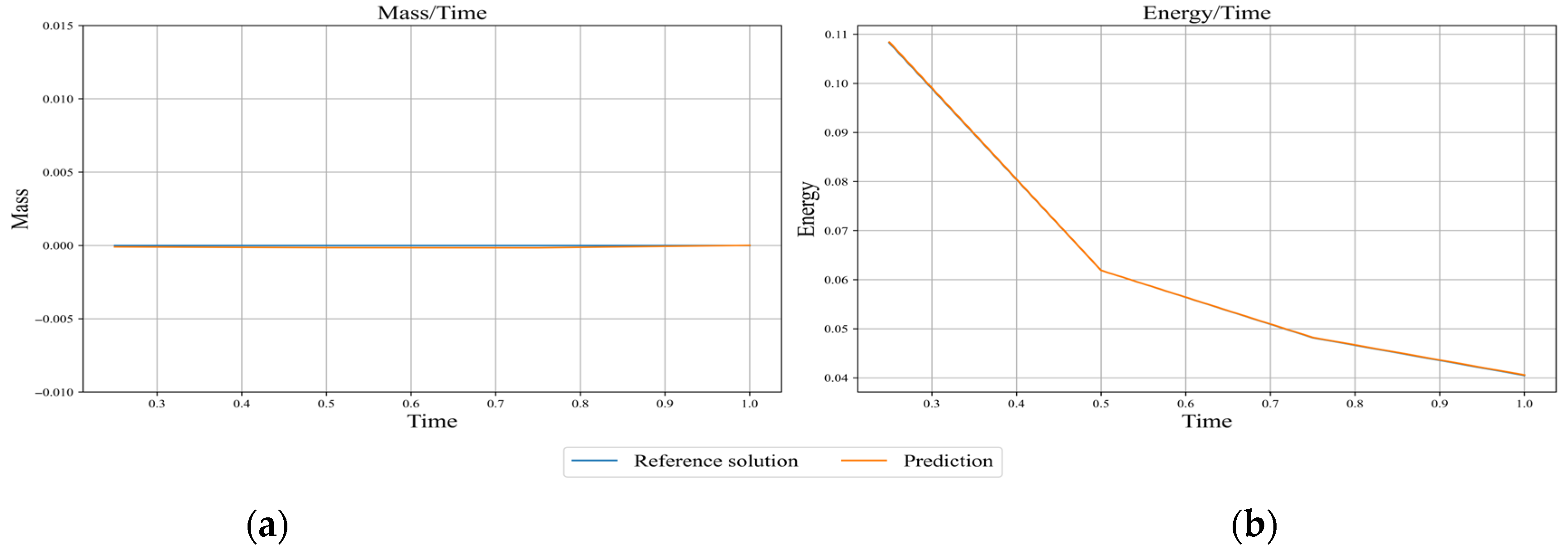
Figure 6.
Comparison of the (a) mass and (b) energy evolution between Causal PINN with no time marching and Causal PINN with N = 4 time marching. The reference represents the solution obtained with Chebfun. Mass is computed using Equation (25), and energy is computed using Equation (15).
Figure 6.
Comparison of the (a) mass and (b) energy evolution between Causal PINN with no time marching and Causal PINN with N = 4 time marching. The reference represents the solution obtained with Chebfun. Mass is computed using Equation (25), and energy is computed using Equation (15).
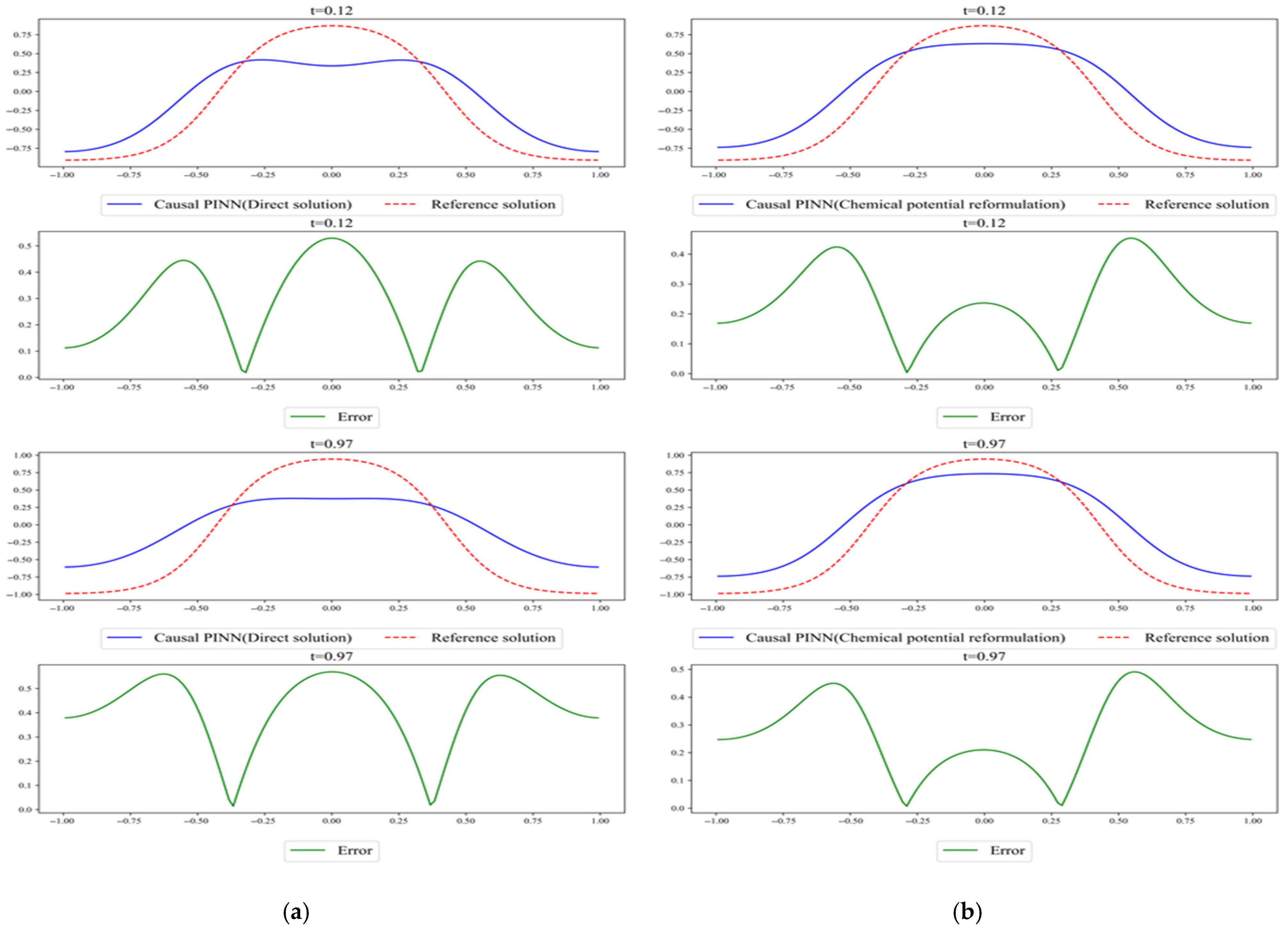
Figure 7.
Comparison of the results predicted by (a) direct solution and (b) chemical potential reformulation. The reference solution was obtained using Chebfun.
Figure 7.
Comparison of the results predicted by (a) direct solution and (b) chemical potential reformulation. The reference solution was obtained using Chebfun.
Figure 8.
Comparison of the (a) mass and (b) energy evolution between direct solution and chemical potential reformulation. Reference represents the solution obtained using Chebfun. Both sets of experiments were performed using a time-marching framework with N = 4. Mass is computed using Equation (25), and energy is computed using Equation (15).
Figure 8.
Comparison of the (a) mass and (b) energy evolution between direct solution and chemical potential reformulation. Reference represents the solution obtained using Chebfun. Both sets of experiments were performed using a time-marching framework with N = 4. Mass is computed using Equation (25), and energy is computed using Equation (15).
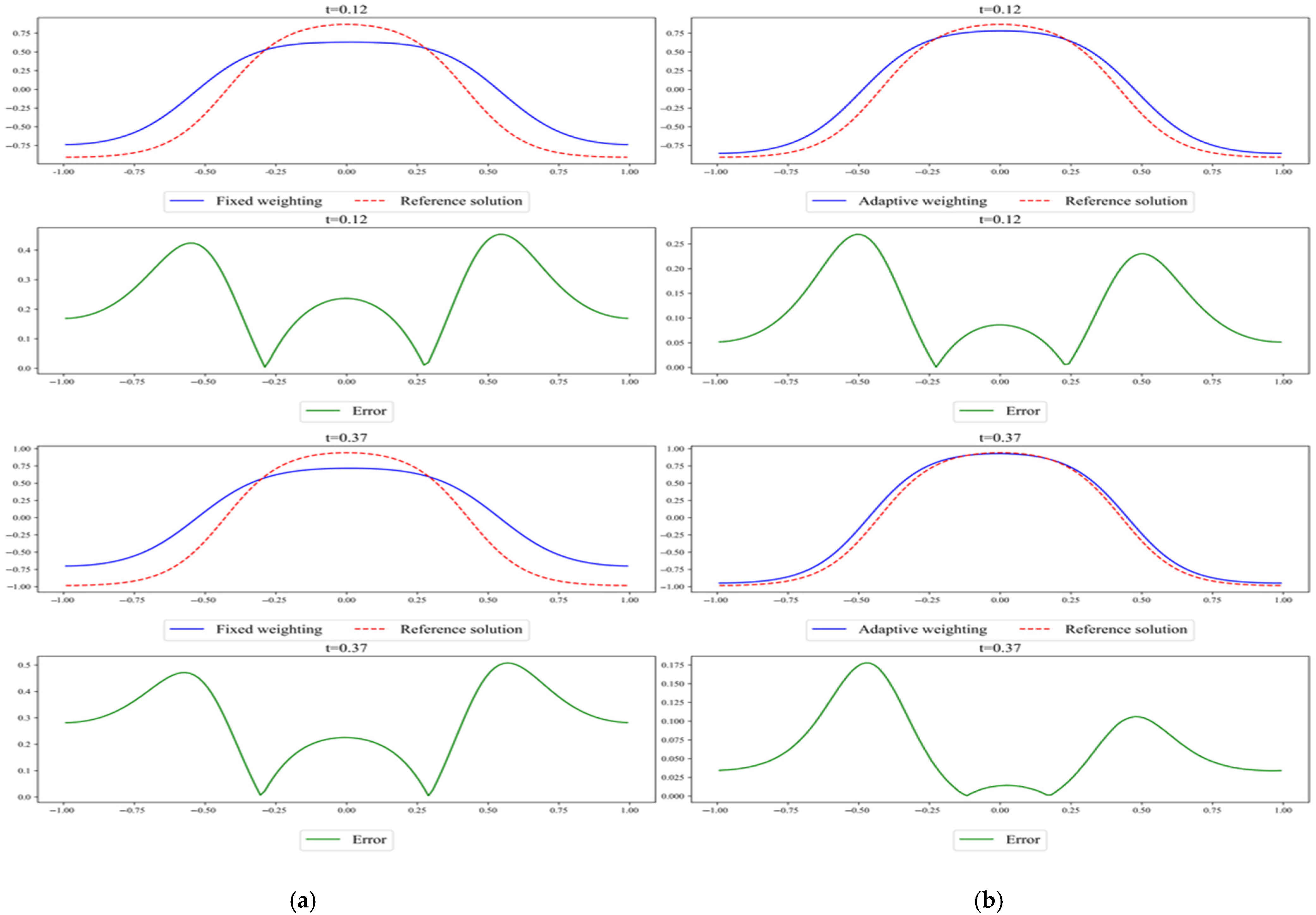
Figure 9.
Comparison of the results predicted via (a) fixed weighting and (b) adaptive weighting. Both use the time-marching and chemical potential formulation. The reference solution was obtained using Chebfun.
Figure 9.
Comparison of the results predicted via (a) fixed weighting and (b) adaptive weighting. Both use the time-marching and chemical potential formulation. The reference solution was obtained using Chebfun.
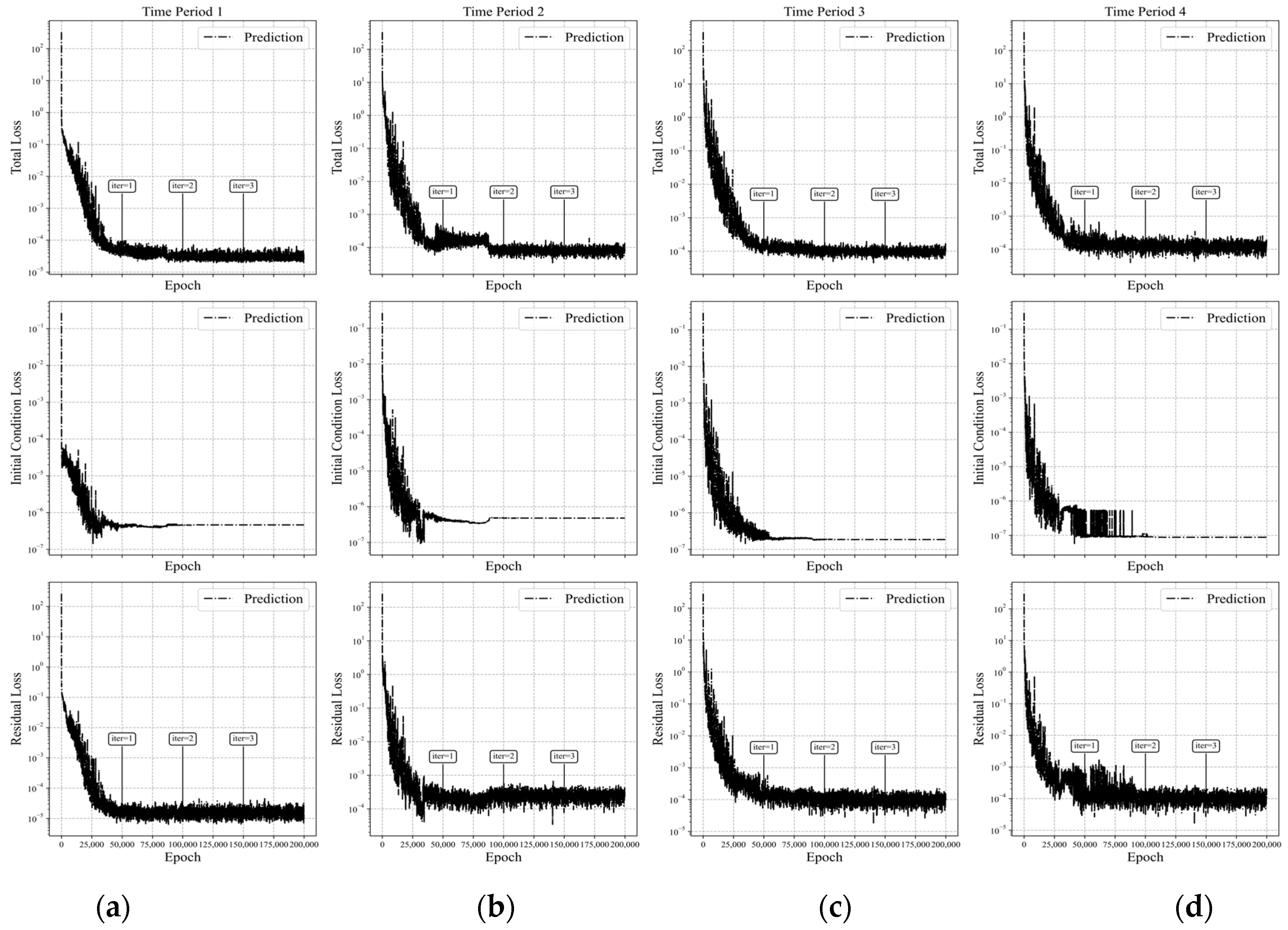
Figure 10.
Comparison of the loss curves between fixed weighting and adaptive weighting for Case 1 across four time-marching periods. (Time periods 1–4 correspond to intervals (a) [0, 0.25], (b) [0.25, 0.5], (c) [0.5, 0.75], and (d) [0.75, 1.0], respectively).
Figure 10.
Comparison of the loss curves between fixed weighting and adaptive weighting for Case 1 across four time-marching periods. (Time periods 1–4 correspond to intervals (a) [0, 0.25], (b) [0.25, 0.5], (c) [0.5, 0.75], and (d) [0.75, 1.0], respectively).
Figure 11.
Comparison of the results predicted for Case 1 using (a) adaptive weighting and (b) APM-PINN and their corresponding absolute error compared with the reference solution obtained using Chebfun. In the figure, the error is significantly lower with the introduction of the causality-based temporal point allocation algorithm compared to that without using it.
Figure 11.
Comparison of the results predicted for Case 1 using (a) adaptive weighting and (b) APM-PINN and their corresponding absolute error compared with the reference solution obtained using Chebfun. In the figure, the error is significantly lower with the introduction of the causality-based temporal point allocation algorithm compared to that without using it.
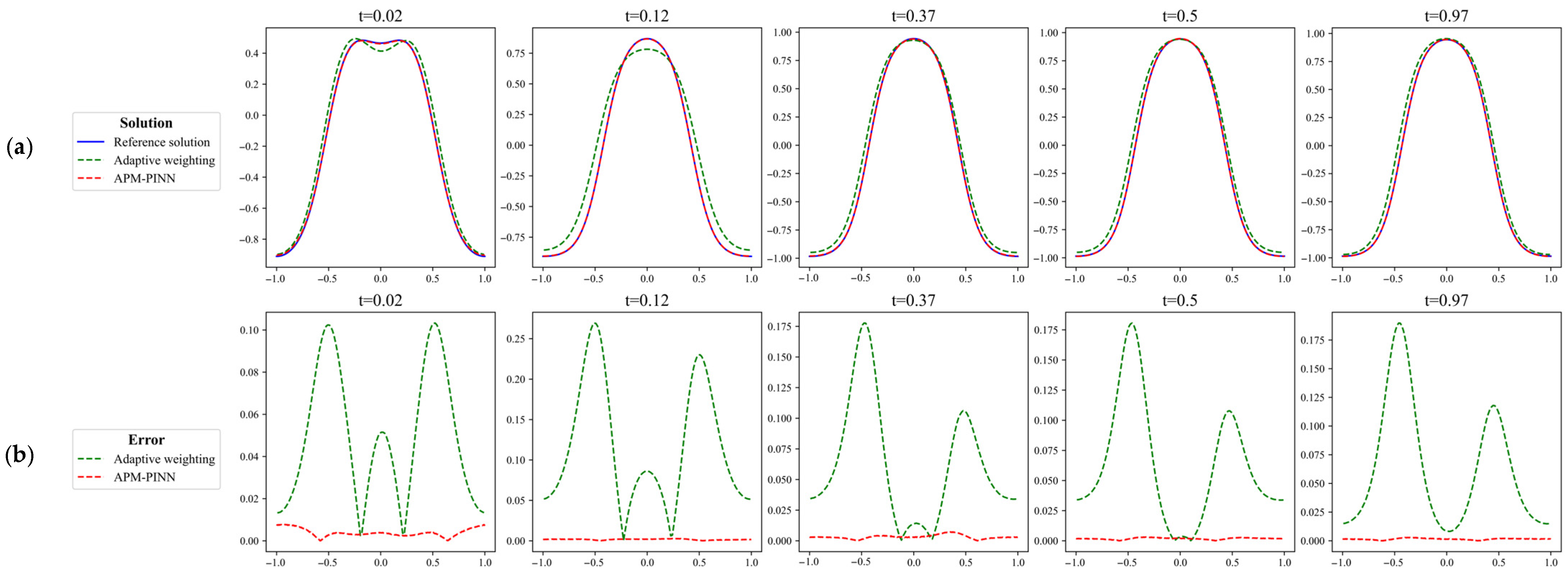
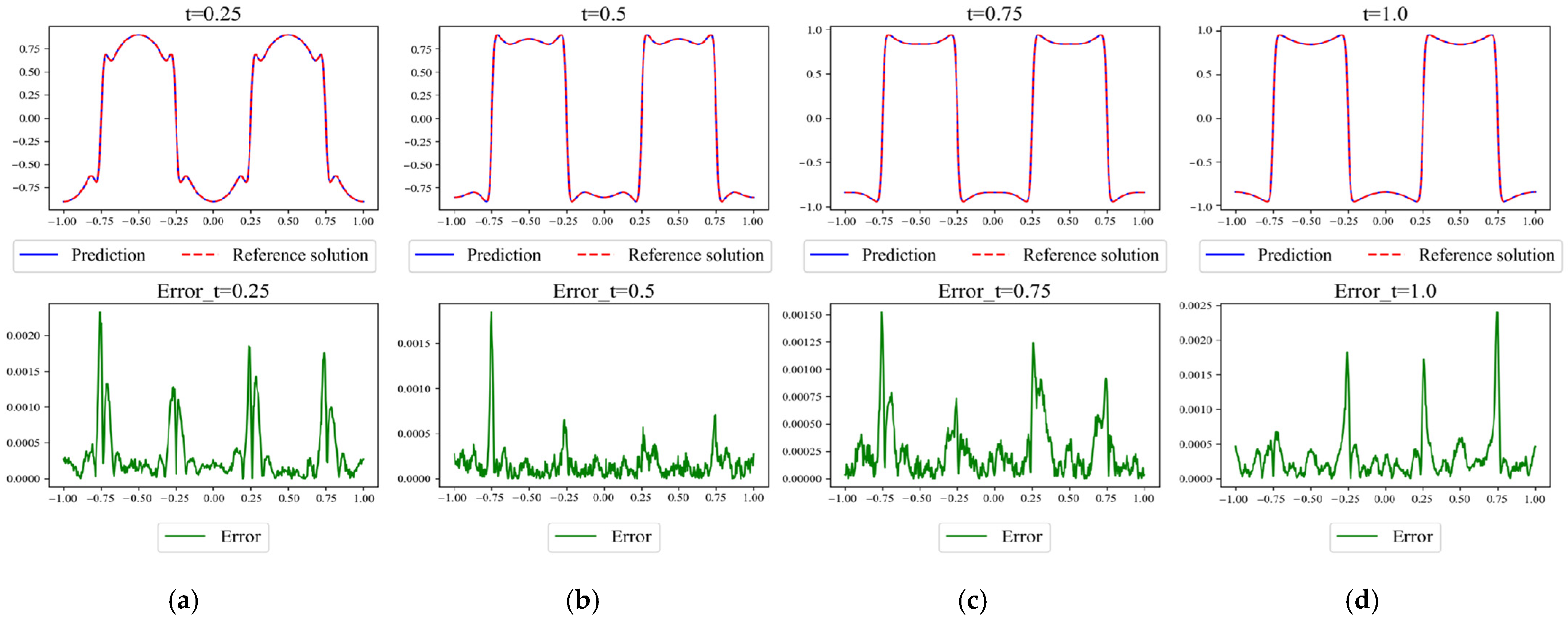
Figure 12.
Results of APM-PINN for Case 1 and the corresponding absolute error compared with the reference solution obtained using Chebfun. The snapshots at several key time points ((a) 0.02, (b) 0.12, (c) 0.37, (d) 0.5, (e) 0.97) are shown here, and the highest orders of magnitude of the error are all 10−3.
Figure 12.
Results of APM-PINN for Case 1 and the corresponding absolute error compared with the reference solution obtained using Chebfun. The snapshots at several key time points ((a) 0.02, (b) 0.12, (c) 0.37, (d) 0.5, (e) 0.97) are shown here, and the highest orders of magnitude of the error are all 10−3.
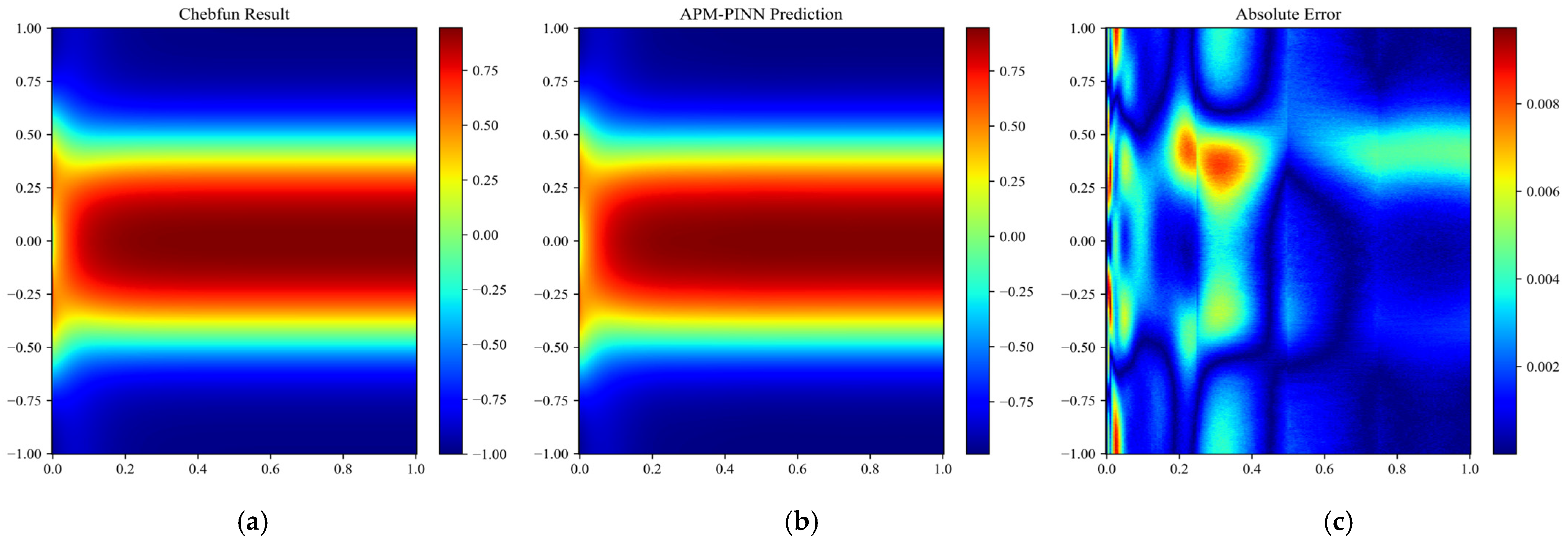
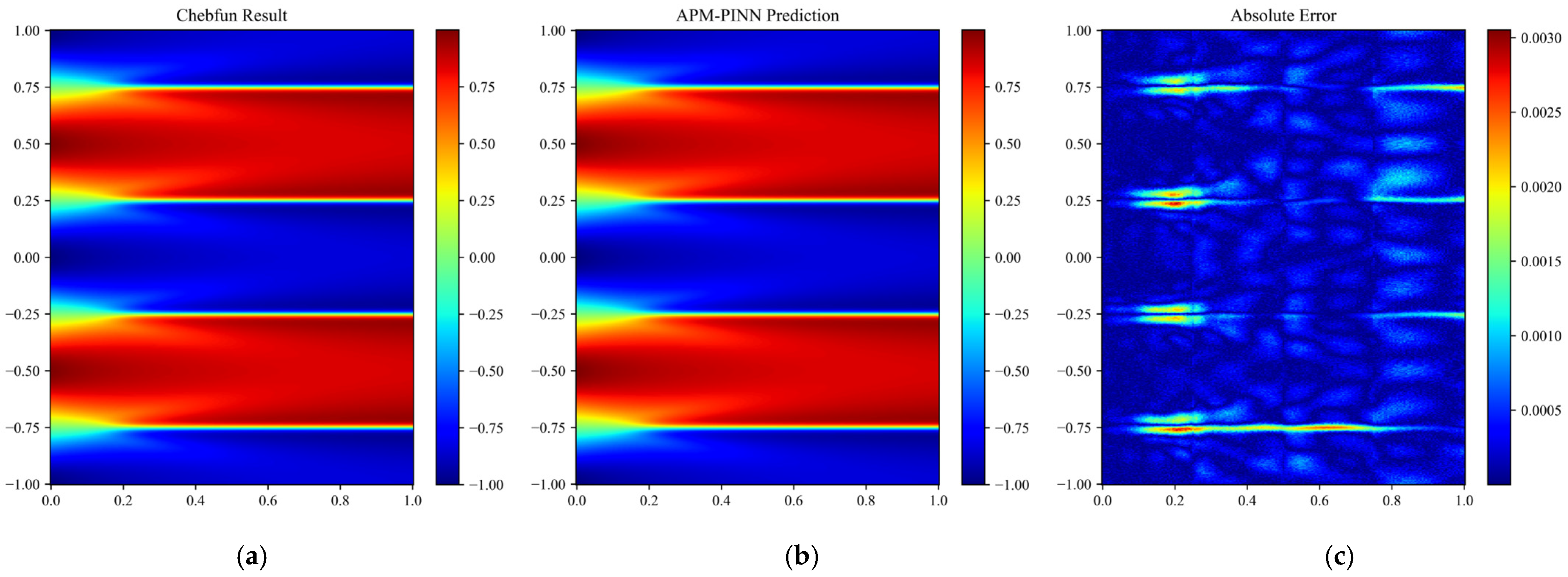
Figure 13.
Results obtained for Case 1 over the entire domain using (a) APM-PINN and (b) the reference solution. The absolute error is shown in (c).
Figure 13.
Results obtained for Case 1 over the entire domain using (a) APM-PINN and (b) the reference solution. The absolute error is shown in (c).
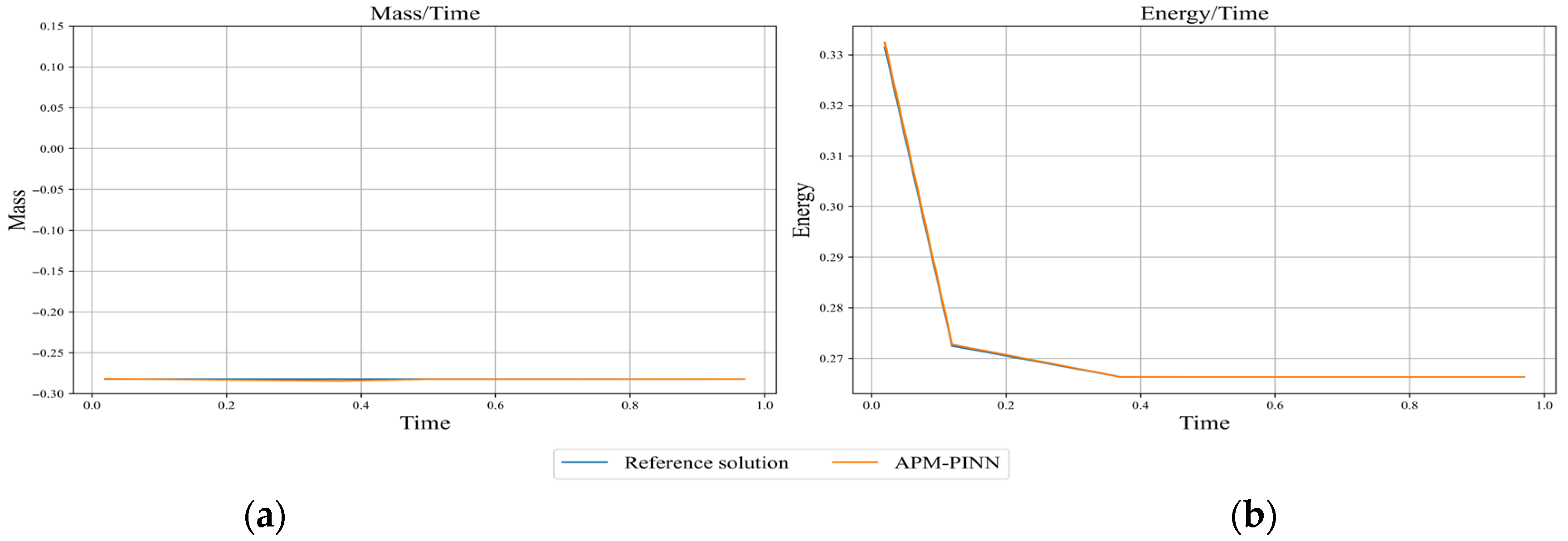
Figure 14.
Comparison of the evolutions of (a) mass and (b) energy from APM-PINN with those from the reference solution obtained with Chebfun. Mass is computed using Equation (25), and energy is computed using Equation (15).
Figure 14.
Comparison of the evolutions of (a) mass and (b) energy from APM-PINN with those from the reference solution obtained with Chebfun. Mass is computed using Equation (25), and energy is computed using Equation (15).
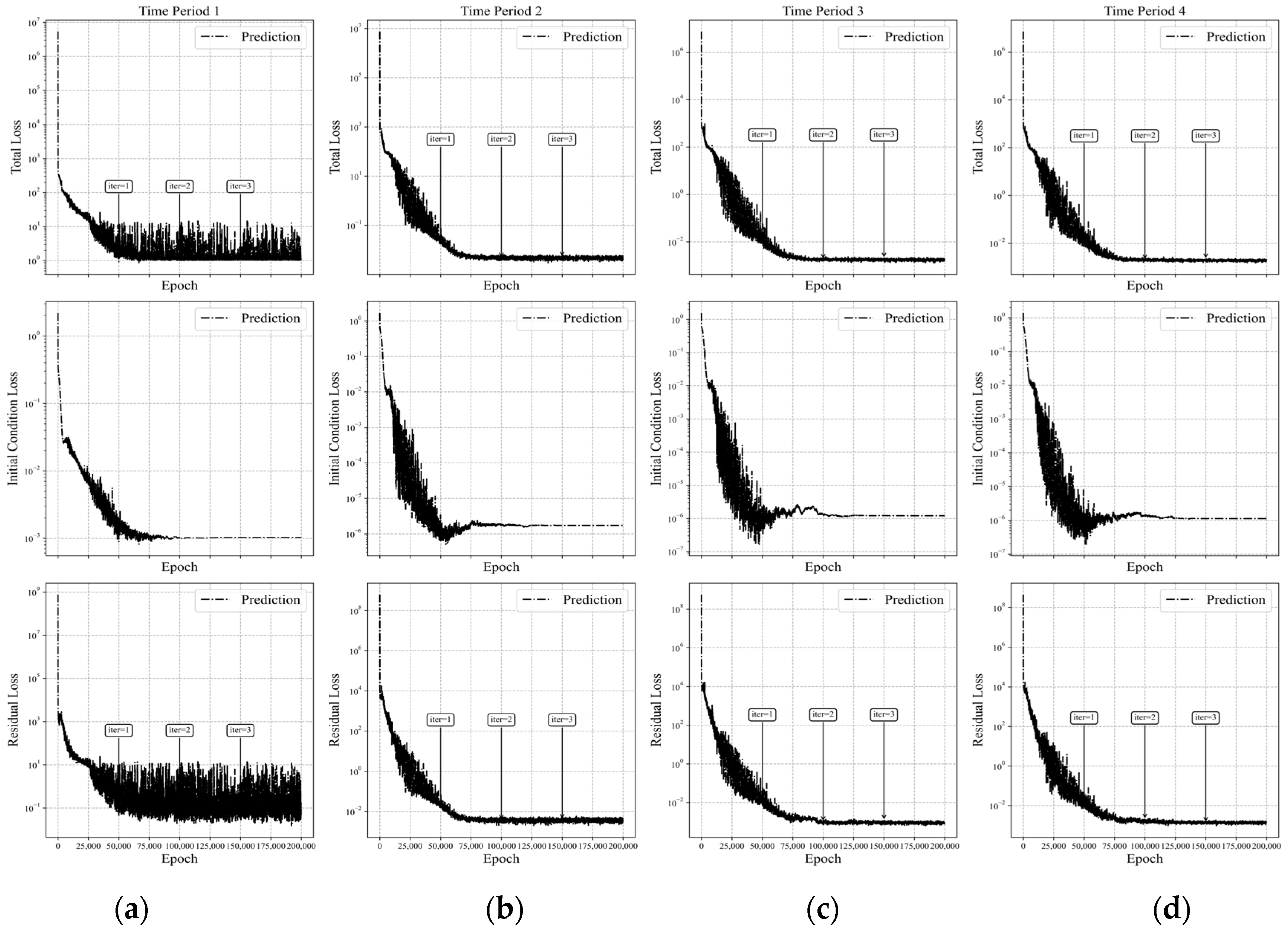
Figure 15.
Loss curves of APM-PINN for Case 1 across four time-marching periods. (Time periods 1–4 correspond to intervals (a) [0, 0.25], (b) [0.25, 0.5], (c) [0.5, 0.75], and (d) [0.75, 1.0], respectively.) The first row shows the total loss in the 4 time periods of training, the second row shows the initial condition loss, and the third row shows the residual loss.
Figure 15.
Loss curves of APM-PINN for Case 1 across four time-marching periods. (Time periods 1–4 correspond to intervals (a) [0, 0.25], (b) [0.25, 0.5], (c) [0.5, 0.75], and (d) [0.75, 1.0], respectively.) The first row shows the total loss in the 4 time periods of training, the second row shows the initial condition loss, and the third row shows the residual loss.
Figure 16.
Results of APM-PINN for Case 2 and corresponding absolute error compared with reference solution obtained using Chebfun. The snapshots at several key time points ((a) 0.25, (b) 0.50, (c) 0.75, (d) 1.0) are shown here, and the highest orders of magnitude of the error are all 10−3.
Figure 16.
Results of APM-PINN for Case 2 and corresponding absolute error compared with reference solution obtained using Chebfun. The snapshots at several key time points ((a) 0.25, (b) 0.50, (c) 0.75, (d) 1.0) are shown here, and the highest orders of magnitude of the error are all 10−3.
Figure 17.
Results for Case 2 over the entire domain obtained with (a) APM-PINN and (b) the reference solution. The absolute error is shown in (c).
Figure 17.
Results for Case 2 over the entire domain obtained with (a) APM-PINN and (b) the reference solution. The absolute error is shown in (c).
Figure 18.
Comparison of the evolutions of (a) mass and (b) energy obtained for APM-PINN with those from the solution obtained using Chebfun. Mass is computed using Equation (25), and energy is computed using Equation (15).
Figure 18.
Comparison of the evolutions of (a) mass and (b) energy obtained for APM-PINN with those from the solution obtained using Chebfun. Mass is computed using Equation (25), and energy is computed using Equation (15).
Figure 19.
Loss curves of APM-PINN for Case 2 across four time-marching periods. (Time Periods 1–4 correspond to intervals (a) [0, 0.25], (b) [0.25, 0.5], (c) [0.5, 0.75], and (d) [0.75, 1.0], respectively.) The first row shows the total loss during the 4 time periods of training, the second row shows the initial condition loss, and the third row shows the residual loss.
Figure 19.
Loss curves of APM-PINN for Case 2 across four time-marching periods. (Time Periods 1–4 correspond to intervals (a) [0, 0.25], (b) [0.25, 0.5], (c) [0.5, 0.75], and (d) [0.75, 1.0], respectively.) The first row shows the total loss during the 4 time periods of training, the second row shows the initial condition loss, and the third row shows the residual loss.
Table 1.
Comparison of the relative error between Causal PINN with and without time marching.
Table 1.
Comparison of the relative error between Causal PINN with and without time marching.
| Time | Error (N = 1) | Error (N = 4) |
|---|
| 0.02 | 0.2260 | 0.1765 |
| 0.12 | 0.6680 | 0.4558 |
| 0.37 | 0.8882 | 0.5367 |
| 0.5 | 0.9213 | 0.5388 |
| 0.97 | 0.9583 | 0.5633 |
Table 2.
Comparison of the relative error between direct solution and chemical potential reformulation (both using Causal PINN with four time-marching steps).
Table 2.
Comparison of the relative error between direct solution and chemical potential reformulation (both using Causal PINN with four time-marching steps).
| Time | Error (Direct) | Error (Chemical Potential) |
|---|
| 0.02 | 0.1765 | 0.1437 |
| 0.12 | 0.4558 | 0.3795 |
| 0.37 | 0.5367 | 0.4084 |
| 0.5 | 0.5388 | 0.4000 |
| 0.97 | 0.5633 | 0.3828 |
Table 3.
Comparison of the relative error between fixed weighting and adaptive weighting (both using Causal PINN with time marching).
Table 3.
Comparison of the relative error between fixed weighting and adaptive weighting (both using Causal PINN with time marching).
| Time | Error (Fixed Weighting) | Error (Adaptive Weighting) |
|---|
| 0.02 | 0.1437 | 0.1020 |
| 0.12 | 0.3795 | 0.1948 |
| 0.37 | 0.4084 | 0.1022 |
| 0.5 | 0.4000 | 0.1037 |
| 0.97 | 0.3828 | 0.1069 |
Table 4.
Relative errors of APM-PINN for Case 1 at t = 0.02, 0.12, 0.37, 0.5, and 0.97.
Table 4.
Relative errors of APM-PINN for Case 1 at t = 0.02, 0.12, 0.37, 0.5, and 0.97.
| Time | Error |
|---|
| 0.02 | 0.007499 |
| 0.12 | 0.002452 |
| 0.37 | 0.004565 |
| 0.5 | 0.002475 |
| 0.97 | 0.002097 |
Table 5.
Comparison of overall relative
errors for Case 1 using different PINN methods, including the Standard-PINNs, bc-PINN, TCAS-PINN, and APM-PINN, with varying numbers of neurons and training points [
44,
49]. For APM-PINN, N = 4 time marching was used and the number of points is for one time interval. The results of APM-PINN are obtained from five runs with different network initializations, and the mean value and standard deviation are given.
Table 5.
Comparison of overall relative
errors for Case 1 using different PINN methods, including the Standard-PINNs, bc-PINN, TCAS-PINN, and APM-PINN, with varying numbers of neurons and training points [
44,
49]. For APM-PINN, N = 4 time marching was used and the number of points is for one time interval. The results of APM-PINN are obtained from five runs with different network initializations, and the mean value and standard deviation are given.
| Method | Number of Neurons | Number of Points | Relative Error |
|---|
| Standard-PINNs | 4 × 128 | 1000 | 1.025 |
| bc-PINN | 4 × 200 | 20,000 | 0.03600 |
| TCAS-PINN | 4 × 128 | 1000 | 0.004568 |
| APM-PINN | 4 × 64 | 16 × 128 | 0.005005 ± 0.001416 |
Table 6.
Relative errors of APM-PINN for Case 2 at t = 0.25, 0.50, 0.75, and 1.0.
Table 6.
Relative errors of APM-PINN for Case 2 at t = 0.25, 0.50, 0.75, and 1.0.
| Time | Error |
|---|
| 0.25 | 0.0006993 |
| 0.5 | 0.0003035 |
| 0.75 | 0.0004053 |
| 1.0 | 0.0005116 |
Table 7.
Comparison of the overall relative error for Case 2 using different PINN methods, including the improved PINNs in [
48] and the present APM-PINN, with different numbers of neurons and training points. For APM-PINN, N = 4 time marching was used and the number of points is for one time interval. Note that “-” means the information is not found in the original paper. The results of APM-PINN are obtained from five runs with different network initializations, and the mean value and standard deviation are given.
Table 7.
Comparison of the overall relative error for Case 2 using different PINN methods, including the improved PINNs in [
48] and the present APM-PINN, with different numbers of neurons and training points. For APM-PINN, N = 4 time marching was used and the number of points is for one time interval. Note that “-” means the information is not found in the original paper. The results of APM-PINN are obtained from five runs with different network initializations, and the mean value and standard deviation are given.
| Method | Number of Neurons | Number of Points | Relative Error |
|---|
| Improved PINNs | 6 × 128 | - | 0.00951 |
| APM-PINN | 4 × 64 | 16 × 128 | 0.0005886 ± 0.00008482 |
Table 8.
Comparison of the relative
errors of three methods for Case 1, TCAS-PINN, APM-PINN, and Standard-PINN, with varying numbers of neurons and training points [
48]. Note that the results presented for TCAS-PINN and Standard-PINN are from [
44]. For APM-PINN, N = 4 time marching was used and the number of points is for one time interval.
Table 8.
Comparison of the relative
errors of three methods for Case 1, TCAS-PINN, APM-PINN, and Standard-PINN, with varying numbers of neurons and training points [
48]. Note that the results presented for TCAS-PINN and Standard-PINN are from [
44]. For APM-PINN, N = 4 time marching was used and the number of points is for one time interval.
| Method | Number of Neurons | Number of Points | Error |
|---|
| APM-PINN | 4 × 64 | 8 × 128 | 0.016341 |
| 4 × 64 | 16 × 128 | 0.003203 |
| 4 × 64 | 32 × 128 | 0.002907 |
| TCAS-PINN | 4 × 128 | 1000 | 0.004568 |
| 4 × 128 | 2000 | 0.004447 |
| 4 × 128 | 3000 | 0.004393 |
| Standard-PINN | 4 × 128 | 1000 | 1.025 |
| 4 × 128 | 2000 | 1.031 |
| 4 × 128 | 3000 | 1.020 |
Table 9.
Comparison of the relative errors of APM-PINN with different numbers of time intervals for Case 1. The neuron number is fixed at 4 × 64 and the number of points per interval is fixed at 16 × 128.
Table 9.
Comparison of the relative errors of APM-PINN with different numbers of time intervals for Case 1. The neuron number is fixed at 4 × 64 and the number of points per interval is fixed at 16 × 128.
| Method | Number of Points | Number of Time Intervals | Error
|
|---|
| APM-PINN | 16 × 128 | 4 | 0.003203 |
| 16 × 128 | 8 | 0.005293 |
| 16 × 128 | 16 | 0.005490 |
Table 10.
Comparison of the relative errors with different values for the threshold_factor in the causality-based temporal point allocation algorithm. N = 4 time marching is used, and the number of points is fixed at 16 × 128. The ratio of the number of temporal sampling points in the first and second half of the time interval for the redistribution (triggered by the condition “t_divided == t[0]”) is fixed at 2/1.
Table 10.
Comparison of the relative errors with different values for the threshold_factor in the causality-based temporal point allocation algorithm. N = 4 time marching is used, and the number of points is fixed at 16 × 128. The ratio of the number of temporal sampling points in the first and second half of the time interval for the redistribution (triggered by the condition “t_divided == t[0]”) is fixed at 2/1.
| Method | Threshold_Factor | Ratio | Relative Error |
|---|
| APM-PINN | 1.1 | 2/1 | 0.006953 |
| 1.3 | 2/1 | 0.004864 |
| 1.5 | 2/1 | 0.008437 |
Table 11.
Comparison of the relative errors with different temporal point redistributions (triggered by the condition “t_divided == t[0]”) in the causality-based temporal point allocation algorithm. N = 4 time marching is used, and the number of points is fixed at 16 × 128. The value of the threshold_factor is fixed at 1.3. The ratio denotes that for the number of temporal sampling points in the first and second half of the time interval for the redistribution.
Table 11.
Comparison of the relative errors with different temporal point redistributions (triggered by the condition “t_divided == t[0]”) in the causality-based temporal point allocation algorithm. N = 4 time marching is used, and the number of points is fixed at 16 × 128. The value of the threshold_factor is fixed at 1.3. The ratio denotes that for the number of temporal sampling points in the first and second half of the time interval for the redistribution.
| Method | Threshold_Factor | Ratio | Relative Error |
|---|
| APM-PINN | 1.3 | 3/1 | 0.01045 |
| 1.3 | 2/1 | 0.004864 |
| 1.3 | 1/1 | 0.005623 |