Concurrent Validity and Reliability of Chronojump Photocell in the Acceleration Phase of Linear Speed Test
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Procedure
2.3. Instruments
2.4. Statistical Analysis
2.4.1. Agreement Between Devices
2.4.2. Reliability
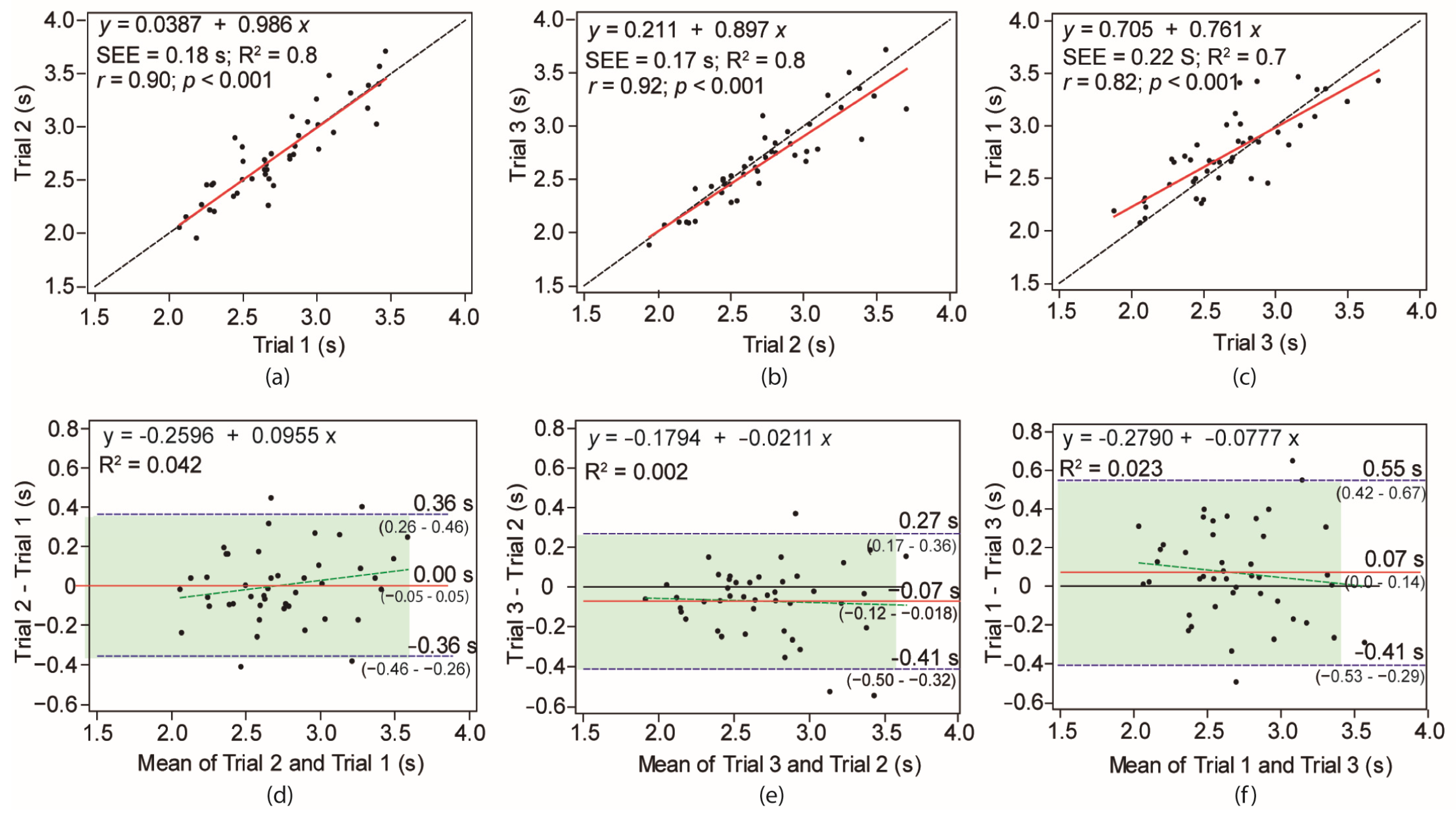
3. Results
4. Discussion
Limitations and Future Research
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| COD | Change of direction |
| FAT | Fully automatic systems |
| GPS | Global position systems |
| LPS | Local position systems |
| ICC | Intraclass correlations coefficient |
| CV | Coefficient of variation |
| SEM | Standard error of the measure |
| WMA | World Medical Association |
| PC | Personal computer |
| ID | Identity |
| ES | Effect size |
| LoA | Limits of agreement |
| CCC | Lin’s concordance index |
| rs | Spearman’s bivariate correlation |
| SEE | Standard error of estimate |
| SWC | Smallest worthwhile change |
| SDC | Smallest detectable change |
| Sd | Standard deviation of the difference of the values |
| ρ | Precision factor in the Lin’s concordance index |
| Cb | Accuracy factor in the Lin’s concordance index |
| CI | Confidence intervals at 95% |
| p | Probability at 95% |
| R2 | Coefficient of determination |
| U-CI | Upper confidence intervals at 95% |
| L-CI | Lower confidence intervals at 95% |
References
- Currell, K.; Jeukendrup, A.E. Validity, Reliability and Sensitivity of Measures of Sporting Performance. Sports Med. 2008, 38, 297–316. [Google Scholar] [CrossRef]
- Cronin, J.B.; Hansen, K.T. Strength and Power Predictors of Sports Speed. J. Strength. Cond. Res. 2005, 19, 349–357. [Google Scholar] [CrossRef]
- Miller, J.; Comfort, P.; McMahon, J. Laboratory Manual for Strength and Conditioning, 1st ed.; Taylor and Francis, Ed.; Routledge: New York, NY, USA, 2023; ISBN 9781003186762. [Google Scholar]
- Horníková, H.; Zemková, E. Relationship between Physical Factors and Change of Direction Speed in Team Sports. Appl. Sci. 2021, 11, 655. [Google Scholar] [CrossRef]
- Freitas, T.T.; Pereira, L.A.; Alcaraz, P.E.; Comyns, T.M.; Azevedo, P.H.S.M.; Loturco, I. Change-of-Direction Ability, Linear Sprint Speed, and Sprint Momentum in Elite Female Athletes: Differences between Three Different Team Sports. J. Strength. Cond. Res. 2022, 36, 262–267. [Google Scholar] [CrossRef]
- Altmann, S.; Ringhof, S.; Neumann, R.; Woll, A.; Rumpf, M.C. Validity and Reliability of Speed Tests Used in Soccer: A Systematic Review. PLoS ONE 2019, 14, e0220982. [Google Scholar] [CrossRef]
- Haugen, T.; Buchheit, M. Sprint Running Performance Monitoring: Methodological and Practical Considerations. Sports Med. 2016, 46, 641–656. [Google Scholar] [CrossRef] [PubMed]
- Multhuaptff, W.; Fernández-Peña, E.; Moreno-Villanueva, A.; Soler-López, A.; Rico-González, M.; Manuel Clemente, F.; Bravo-Cucci, S.; Pino-Ortega, J. Concurrent-Validity and Reliability of Photocells in Sport: A Systematic Review. J. Hum. Kinet. 2023, 92, 53–71. [Google Scholar] [CrossRef] [PubMed]
- Haugen, T.A.; Tønnessen, E.; Seiler, S.K. The Difference Is in the Start: Impact of Timing and Start Procedure on Sprint Running Performance. J. Strength. Cond. Res. 2012, 26, 473–479. [Google Scholar] [CrossRef] [PubMed]
- Thron, M.; Düking, P.; Ruf, L.; Härtel, S.; Woll, A.; Altmann, S. Assessing Anaerobic Speed Reserve: A Systematic Review on the Validity and Reliability of Methods to Determine Maximal Aerobic Speed and Maximal Sprinting Speed in Running-Based Sports. PLoS ONE 2024, 19, e0296866. [Google Scholar] [CrossRef] [PubMed]
- Simperingham, K.D.; Cronin, J.B.; Ross, A. Advances in Sprint Acceleration Profiling for Field-Based Team-Sport Athletes: Utility, Reliability, Validity and Limitations. Sports Med. 2016, 46, 1619–1645. [Google Scholar] [CrossRef]
- Healy, R.; Kenny, I.C.; Harrison, A.J. Profiling Elite Male 100-m Sprint Performance: The Role of Maximum Velocity and Relative Acceleration. J. Sport. Health Sci. 2022, 11, 75–84. [Google Scholar] [CrossRef] [PubMed]
- Schulze, E.; Julian, R.; Skorski, S. The Accuracy of a Low-Cost GPS System during Football-Specific Movements. J. Sports Sci. Med. 2021, 20, 126–132. [Google Scholar] [CrossRef]
- Fischer-Sonderegger, K.; Taube, W.; Rumo, M.; Tschopp, M. How Far from the Gold Standard? Comparing the Accuracy of a Local Position Measurement (LPM) System and a 15 Hz GPS to a Laser for Measuring Acceleration and Running Speed during Team Sports. PLoS ONE 2021, 16, e0250549. [Google Scholar] [CrossRef]
- Earp, J.E.; Newton, R.U. Advances in Electronic Timing Systems: Considerations for Selecting an Appropriate Timing System. J. Strength. Cond. Res. 2012, 26, 1245–1248. [Google Scholar] [CrossRef]
- Hopkins, W.G. Measures of Reliability in Sports Medicine and Science. Sports Med. 2000, 30, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Altmann, S.; Hoffmann, M.; Kurz, G.; Neumann, R.; Woll, A.; Haertel, S. Different Starting Distances Affect 5-m Sprint Times. J. Strength. Cond. Res. 2015, 29, 2361–2366. [Google Scholar] [CrossRef]
- Yeadon, M.R.; Kato, T.; Kerwin, D.G. Measuring Running Speed Using Photocells. J. Sports Sci. 1999, 17, 249–257. [Google Scholar] [CrossRef]
- Cronin, J.B.; Templeton, R. Timing Light Height Afects Sprint Times. J. Strength. Cond. Res. 2008, 22, 318–320. [Google Scholar] [CrossRef]
- Shalfawi, S.A.I.; Enoksen, E.; Tønnessen, E.; Ingebrigtsen, J. Assessing Test-Retest Reliability of the Portable Brower Speed Trap Ii Testing System. Kinesiology 2012, 44, 24–30. [Google Scholar]
- Bastida Castillo, A.; Gómez Carmona, C.D.; Pino Ortega, J.; de la Cruz Sánchez, E. Validity of an Inertial System to Measure Sprint Time and Sport Task Time: A Proposal for the Integration of Photocells in an Inertial System. Int. J. Perform. Anal. Sport. 2017, 17, 600–608. [Google Scholar] [CrossRef]
- Altmann, S.; Spielmann, M.; Engel, F.A.; Neumann, R.; Ringhof, S.; Oriwol, D.; Haertel, S. Validity of Single-Beam Timing Lights at Different Heights. J. Strength. Cond. Res. 2017, 31, 1994–1999. [Google Scholar] [CrossRef]
- Bond, C.W.; Willaert, E.M.; Noonan, B.C. Comparison of Three Timing Systems: Reliability and Best Practice Recommendations in Timing Short-Duration Sprints. J. Strength. Cond. Res. 2017, 31, 1062–1071. [Google Scholar] [CrossRef]
- Haugen, T.A.; Tønnessen, E.; Svendsen, I.S.; Seiler, S. Sprint Time Differences between Single- and Dual-Beam Timing Systems. J. Strength. Cond. Res. 2014, 28, 2376–2379. [Google Scholar] [CrossRef]
- Thapa, R.K.; Sarmah, B.; Singh, T.; Kushwah, G.S.; Akyildiz, Z.; Ramirez-Campillo, R. Test-Retest Reliability and Comparison of Single- and Dual-Beam Photocell Timing System with Video-Based Applications to Measure Linear and Change of Direction Sprint Times. Proc. Inst. Mech. Eng. Part P J. Sports Eng. Technol. 2023, 30, 17543371231203440. [Google Scholar] [CrossRef]
- Bataller-Cervero, A.V.; Gutierrez, H.; Derentería, J.; Piedrafita, E.; Marcén, N.; Valero-Campo, C.; Lapuente, M.; Berzosa, C. Validity and Reliability of a 10 Hz GPS for Assessing Variable and Mean Running Speed. J. Hum. Kinet. 2019, 67, 17–24. [Google Scholar] [CrossRef] [PubMed]
- Vachon, A.; Berryman, N.; Mujika, I.; Paquet, J.B.; Monnet, T.; Bosquet, L. Reliability of a Repeated High-Intensity Effort Test for Elite Rugby Union Players. Sports 2020, 8, 72. [Google Scholar] [CrossRef] [PubMed]
- Moreno-Azze, A.; López-Plaza, D.; Alacid, F.; Falcón-Miguel, D. Validity and Reliability of an IOS Mobile Application for Measuring Change of Direction Across Health, Performance, and School Sports Contexts. Appl. Sci. 2025, 15, 1891. [Google Scholar] [CrossRef]
- Hopkins, A.G.; Marshall, S.W.; Batterham, A.M.; Hanin, J. Progressive Statistics for Studies in Sports Medicine and Exercise Science. Med. Sci. Sports Exerc. 2009, 41, 3–12. [Google Scholar] [CrossRef]
- Altmann, S.; Spielmann, M.; Engel, F.A.; Ringhof, S.; Oriwol, D.; Härtel, S.; Neumann, R. Accuracy of Single Beam Timing Lights for Determining Velocities in a Flying 20-m Sprint: Does Timing Light Height Matter? J. Hum. Sport. Exerc. 2018, 13, 601–610. [Google Scholar] [CrossRef]
- Tomczak, M.; Tomczak, E. The Need to Report Effect Size Estimates Revisited. An Overview of Some Recommended Measures of Effect Size. Trends Sport. Sci. 2014, 1, 19–25. Available online: https://www.wbc.poznan.pl/publication/413565 (accessed on 1 May 2025).
- Lin, L.; Hedayat, A.S.; Sinha, B.; Yang, M. Statistical Methods in Assessing Agreement: Models, Issues, and Tools. J. Am. Stat. Assoc. 2002, 97, 257–270. [Google Scholar] [CrossRef]
- McBride, G.B. A Proposal for Strength-of-Agreement Criteria for Lin’s Concordance Correlation Coefficient. NIWA Client. Rep. 2005, HAM2005, 307–310. [Google Scholar]
- Hopkins, W.G. Spreadsheets for Analysis of Validity and Reliability. Sportscience 2015, 19, 36–45. Available online: https://go.gale.com/ps/i.do?p=AONE&sw=w&issn=11749210&v=2.1&it=r&id=GALE%7CA562004416&sid=googleScholar&linkaccess=abs&userGroupName=anon%7E8659cdc2&aty=open-web-entry (accessed on 1 May 2025).
- Passing, H.; Bablok, W. Comparison of Several Regression Procedures for Method Comparison Studies and Determination of Sample Sizes. Application of Linear Regression Procedures for Method Comparison Studies in Clinical Chemistry, Part II. J. Clin. Chem. Clin. Biochem. 1984, 22, 431–445. [Google Scholar] [CrossRef] [PubMed]
- Koo, T.K.; Li, M.Y. A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef] [PubMed]
- Portney, L.G. Foundations of Clinical Research: Applications to Evidence-Based Practice, 4th ed.; F.A. Davis: Philadelphia, PA, USA, 2020; ISBN 9780803661134. [Google Scholar]
- Atkinson, G.; Nevill, A.M. Statistical Methods for Assessing Measurement Error (Reliability) in Variables Relevant to Sports Medicine. Sports Med. 1998, 26, 217–238. [Google Scholar] [CrossRef]
- Sašek, M.; Miras-Moreno, S.; García-Ramos, A.; Cvjetičanin, O.; Šarabon, N.; Kavčič, I.; Smajla, D. The Concurrent Validity and Reliability of a Global Positioning System for Measuring Maximum Sprinting Speed and Split Times of Linear and Curvilinear Sprint Tests. Appl. Sci. 2024, 14, 6116. [Google Scholar] [CrossRef]
- Marco-Contreras, L.A.; Bataller-Cervero, A.V.; Gutiérrez, H.; Sánchez-Sabaté, J.; Berzosa, C. Analysis of the Validity and Reliability of the Photo Finish® Smartphone App to Measure Sprint Time. Sensors 2024, 24, 6719. [Google Scholar] [CrossRef]
- Smith, T.B.; Hopkins, W.G.; Lowe, T.E. Are There Useful Physiological or Psychological Markers for Monitoring Overload Training in Elite Rowers? Int. J. Sports Physiol. Perform. 2011, 6, 469–484. [Google Scholar] [CrossRef][Green Version]
- Hunter, S.K.; Senefeld, J.W.; Hunter, S.K.; Senefeld, J.W.; Physiol, J. Sex Differences in Human Performance. J. Physiol. 2024, 602, 4129–4156. [Google Scholar] [CrossRef]
- Manouras, N.; Batatolis, C.; Ioakimidis, P.; Karatrantou, K.; Gerodimos, V. The Reliability of Linear Speed with and without Ball Possession of Pubertal Soccer Players. J. Funct. Morphol. Kinesiol. 2023, 8, 147. [Google Scholar] [CrossRef] [PubMed]

| Chronojump (s) (95% CI) | Witty (s) (95% CI) | Difference (s) (95% CI) | ES (g) (95% CI) | CCC (95% CI) | CCC (ρ) | CCC (Cb) |
|---|---|---|---|---|---|---|
| 2.342 | 2.390 | 0.046 * | 0.11 | 0.983 | 0.988 | 0.995 |
| (2.299 to 2.385) | (2.347 to 2.433) | (0.038 to 0.053) | (0.09 to 0.13) | (0.988 to 0.995) |
| Absolute Reliability | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Chronojump | Witty | |||||||||||
| 2-1 | 3-2 | 1-3 | Mean | L-CI | U-CI | 2-1 | 3-2 | 1-3 | Mean | L-CI | U-CI | |
| Change in mean (s) | 0.00 | −0.07 | 0.07 | − | − | − | 0.02 | −0.03 | 0.01 | − | − | − |
| SEM (s) | 0.13 | 0.12 | 0.17 | 0.14 | 1.29 | 2.01 | 0.15 | 0.11 | 0.19 | 0.15 | ||
| SDC (s) | 0.36 | 0.34 | 0.48 | 0.40 | 0.35 | 0.46 | 0.41 | 0.31 | 0.52 | 0.42 | 0.37 | 0.49 |
| SWC (s) | 0.08 | 0.08 | 0.07 | 0.08 | 0.05 | 0.09 | 0.07 | 0.08 | 0.07 | 0.07 | 0.05 | 0.09 |
| Relative Reliability | ||||||||||||
| Chronojump | Witty | |||||||||||
| 2-1 | 3-2 | 1-3 | Mean | L-CI | U-CI | 2-1 | 3-2 | 1-3 | Mean | L-CI | U-CI | |
| ICC | 0.90 | 0.92 | 0.82 | 0.88 | 0.81 | 0.93 | 0.85 | 0.93 | 0.78 | 0.85 | 0.77 | 0.91 |
| CV | 0.22 | 0.21 | 0.26 | 0.23 | − | − | 0.23 | 0.20 | 0.26 | 0.23 | − | − |
| Standardized SEM | 0.34 | 0.31 | 0.48 | 0.36 | 0.31 | 0.41 | 0.43 | 0.29 | 0.55 | 0.39 | 0.35 | 0.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villalón-Gasch, L.; Jimenez-Olmedo, J.M.; Penichet-Tomas, A.; Sebastia-Amat, S. Concurrent Validity and Reliability of Chronojump Photocell in the Acceleration Phase of Linear Speed Test. Appl. Sci. 2025, 15, 8852. https://doi.org/10.3390/app15168852
Villalón-Gasch L, Jimenez-Olmedo JM, Penichet-Tomas A, Sebastia-Amat S. Concurrent Validity and Reliability of Chronojump Photocell in the Acceleration Phase of Linear Speed Test. Applied Sciences. 2025; 15(16):8852. https://doi.org/10.3390/app15168852
Chicago/Turabian StyleVillalón-Gasch, Lamberto, Jose M. Jimenez-Olmedo, Alfonso Penichet-Tomas, and Sergio Sebastia-Amat. 2025. "Concurrent Validity and Reliability of Chronojump Photocell in the Acceleration Phase of Linear Speed Test" Applied Sciences 15, no. 16: 8852. https://doi.org/10.3390/app15168852
APA StyleVillalón-Gasch, L., Jimenez-Olmedo, J. M., Penichet-Tomas, A., & Sebastia-Amat, S. (2025). Concurrent Validity and Reliability of Chronojump Photocell in the Acceleration Phase of Linear Speed Test. Applied Sciences, 15(16), 8852. https://doi.org/10.3390/app15168852









