Study on Seismic Response of Segmented Utility Tunnels Crossing Ground Fissures
Abstract
1. Introduction
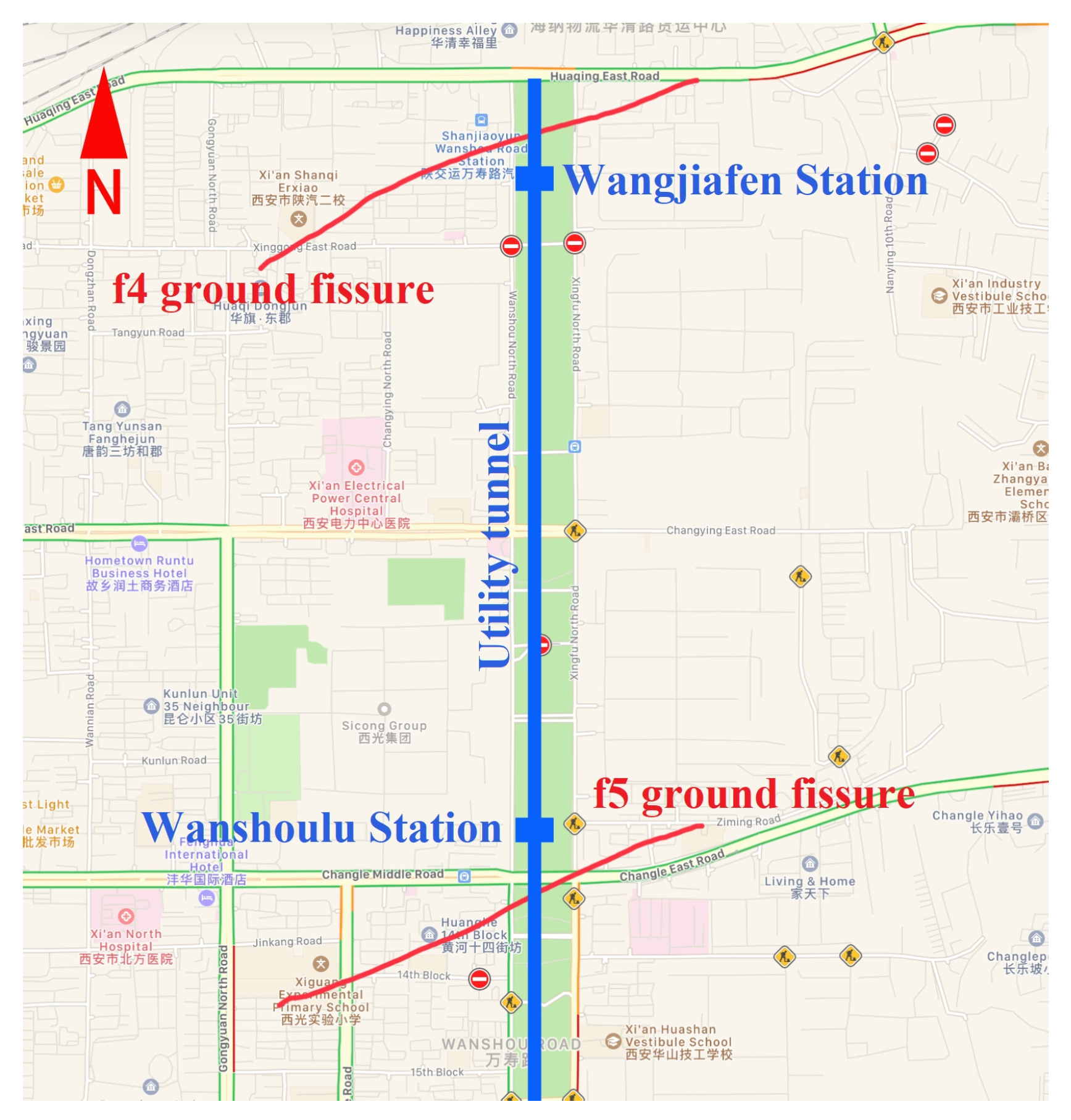
2. Project Overview
3. Finite Element Modeling
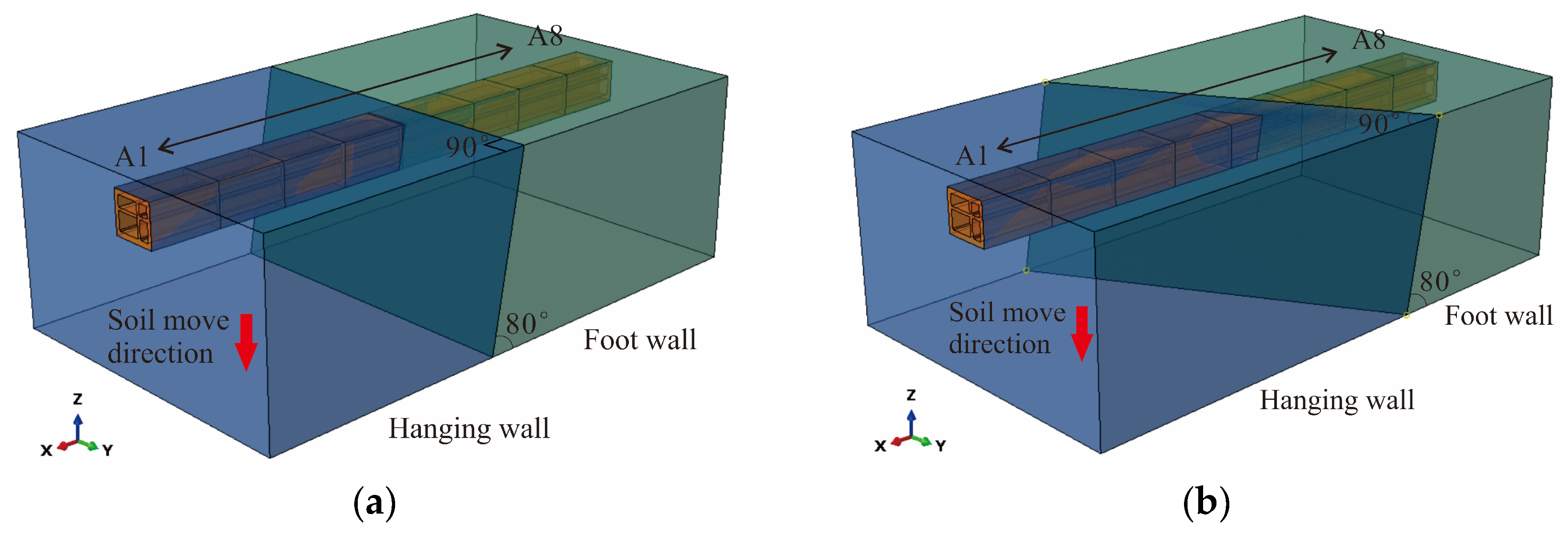
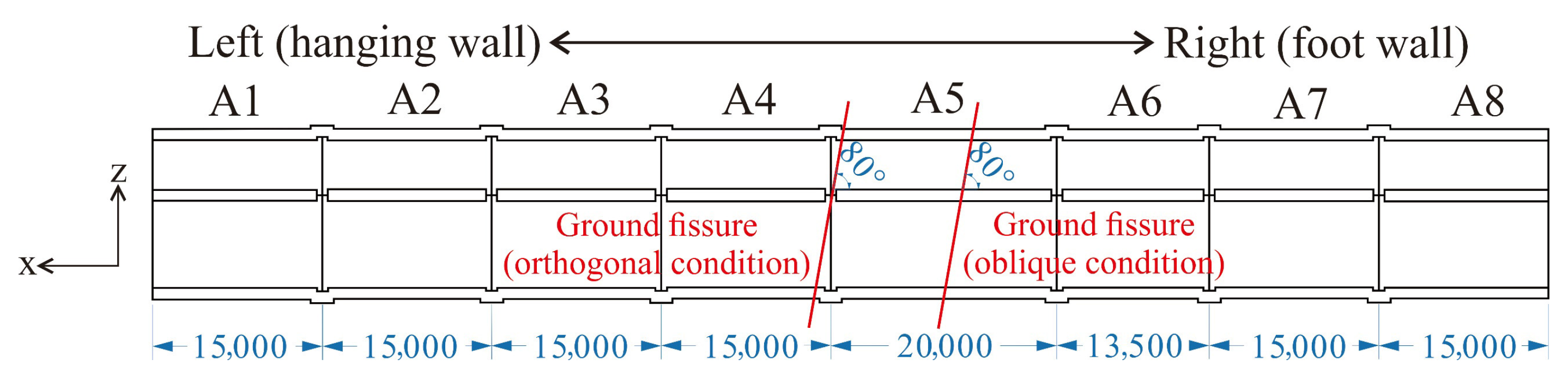
3.1. Model Establishment
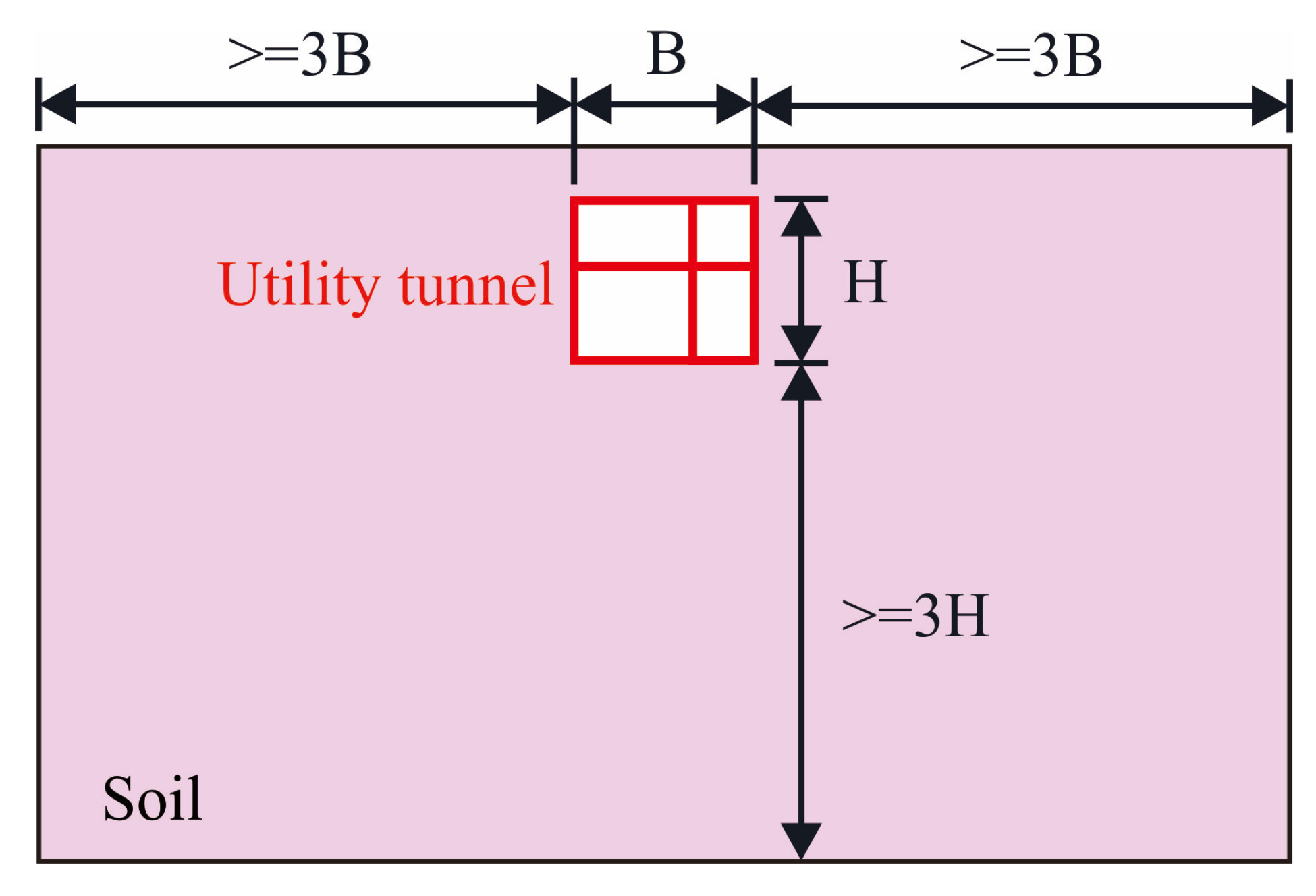
- Lateral soil coverage extending ≥ 3D (where D represents tunnel width) on both sides.
- Vertical embedment depth measuring ≥ 3H (where H denotes tunnel height) below the invert.
- The boundary conditions on the length direction should be consistent.
- When the length of the longitudinal boundary condition exceeds 100 m, the influence of the boundary condition on the tunnel can be ignored.
3.2. Material Constitutive
3.3. Contact and Boundary Conditions
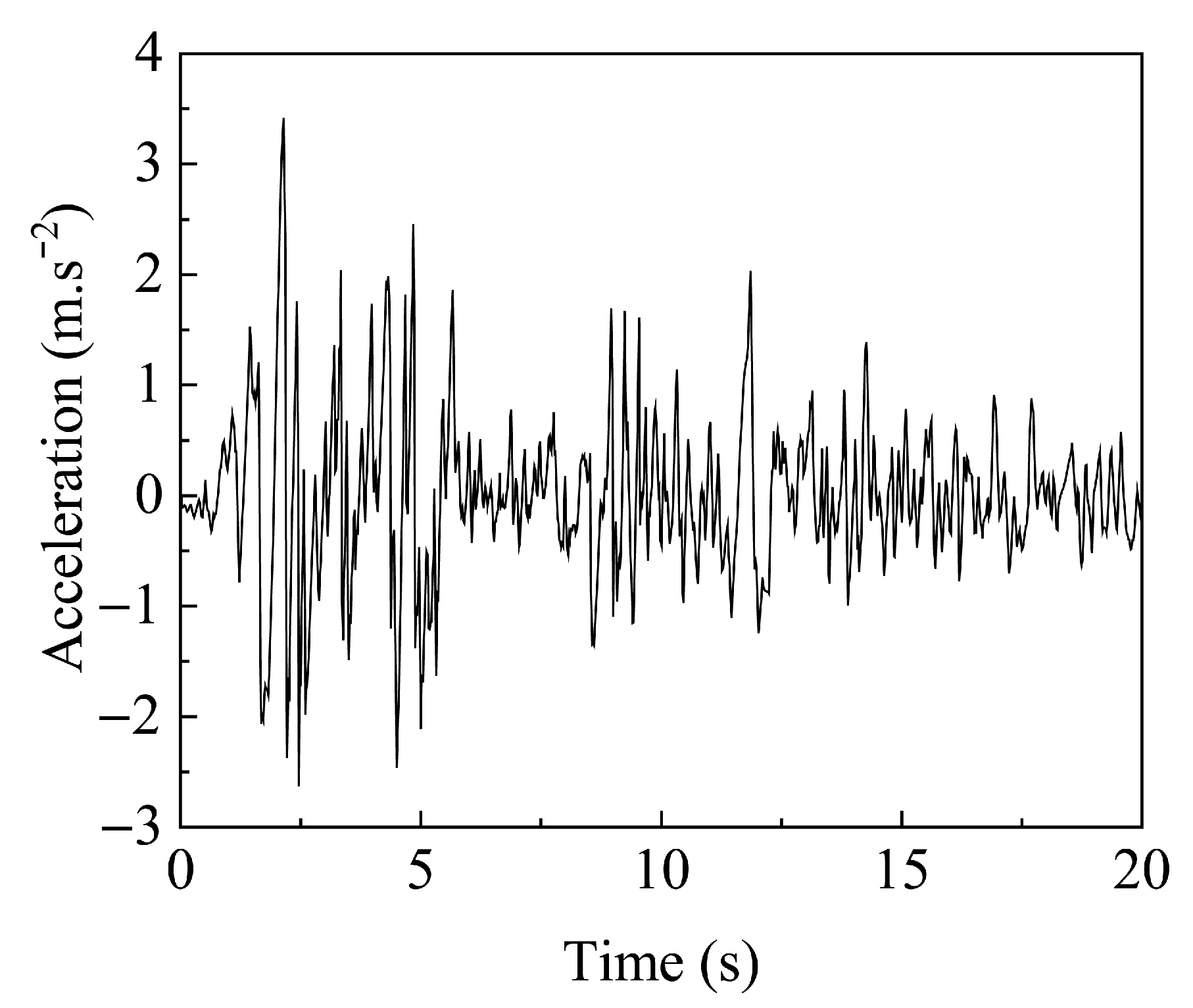
3.4. Seismic Waves
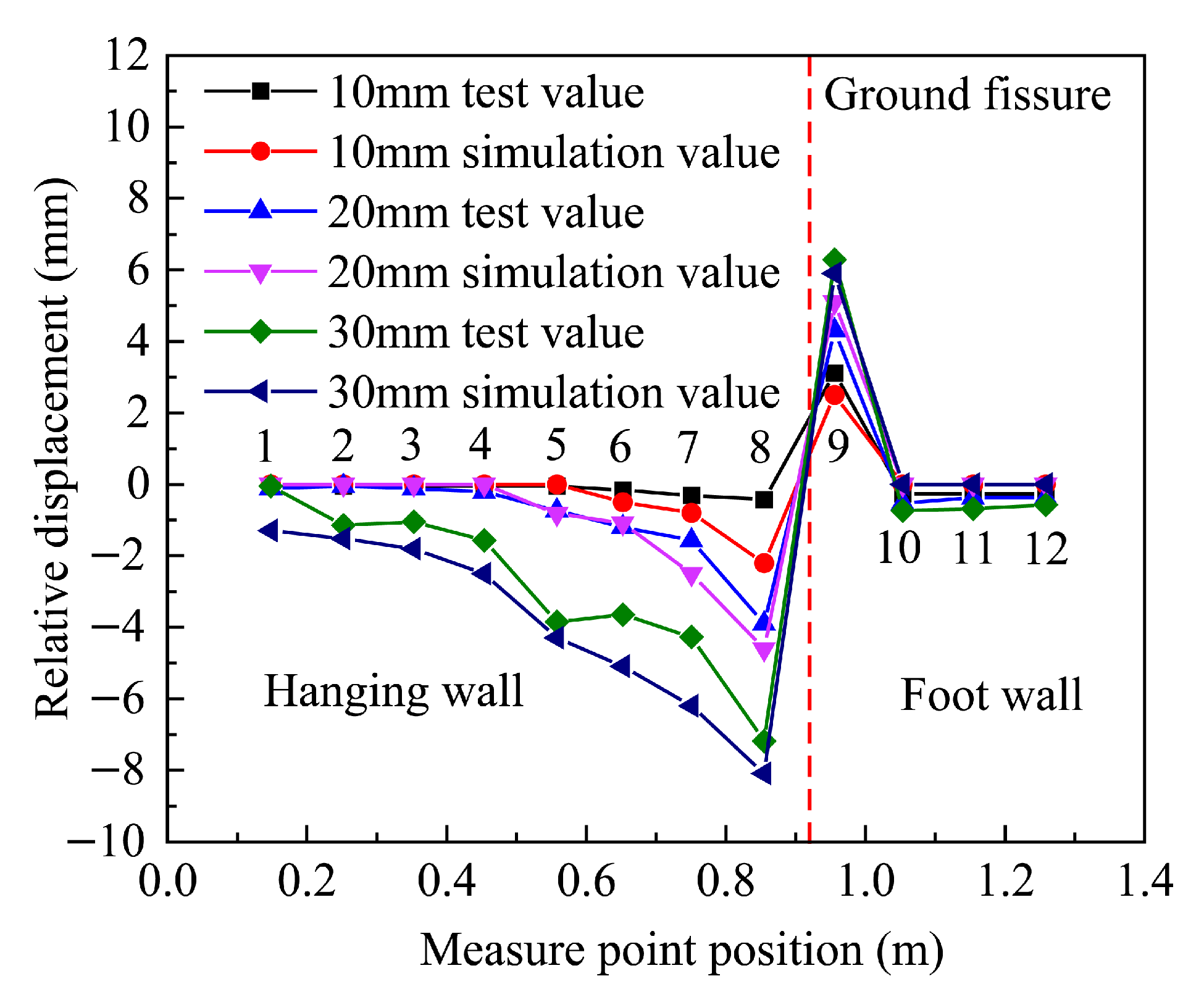
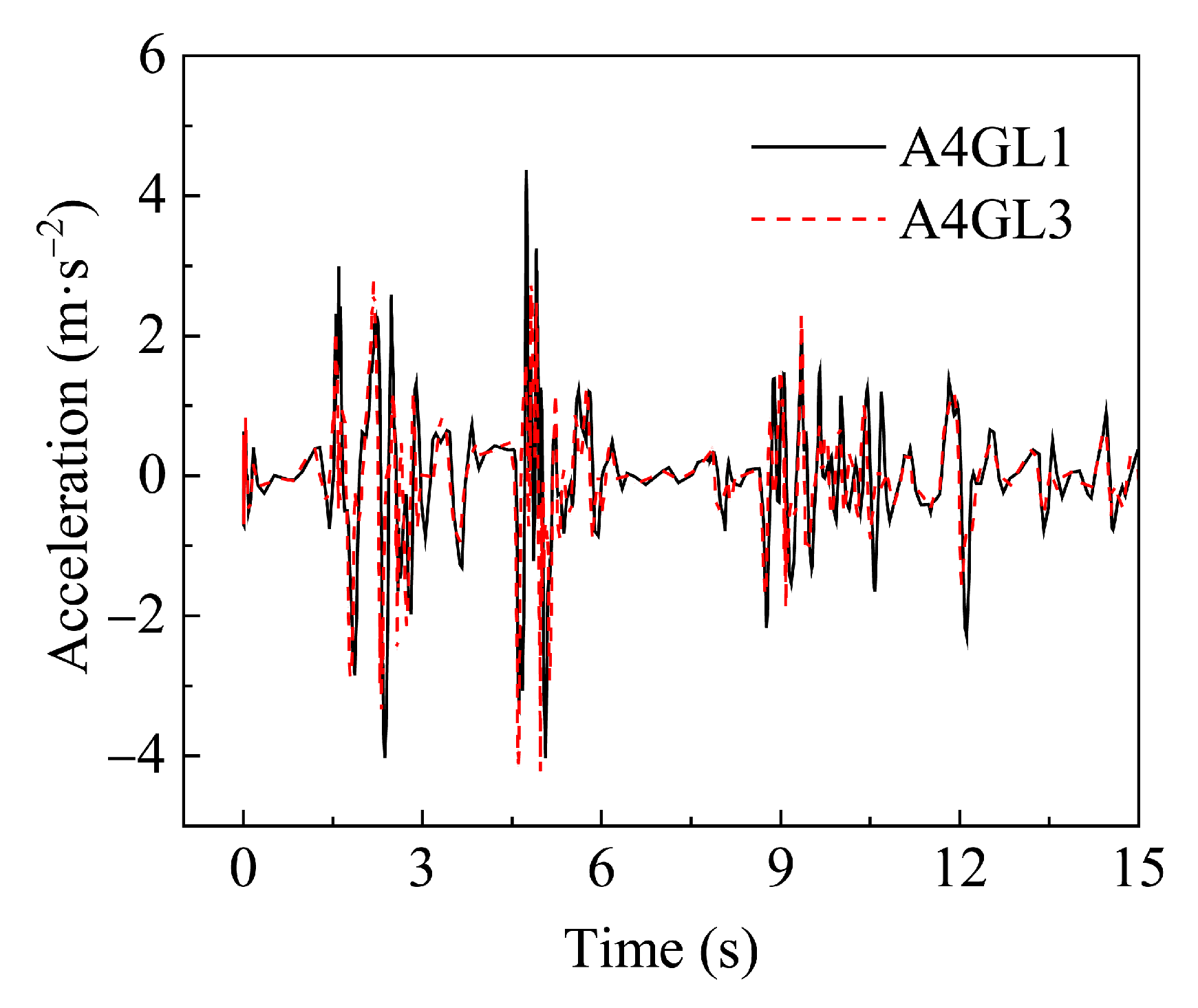
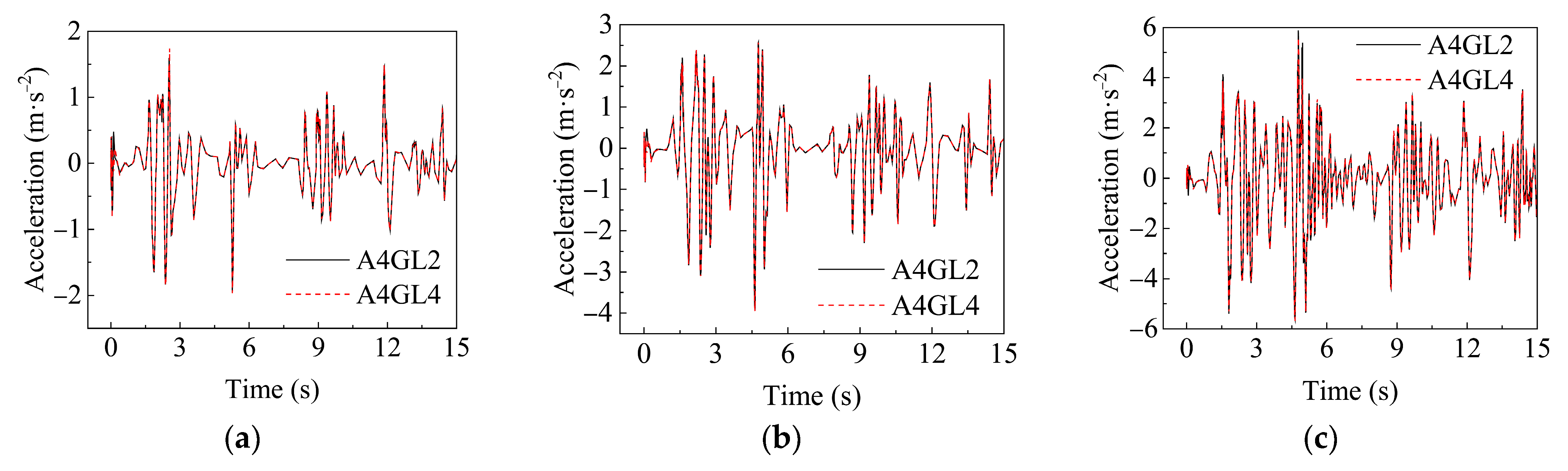
3.5. Model Verification
4. Results and Discussions
4.1. Soil Acceleration Analysis
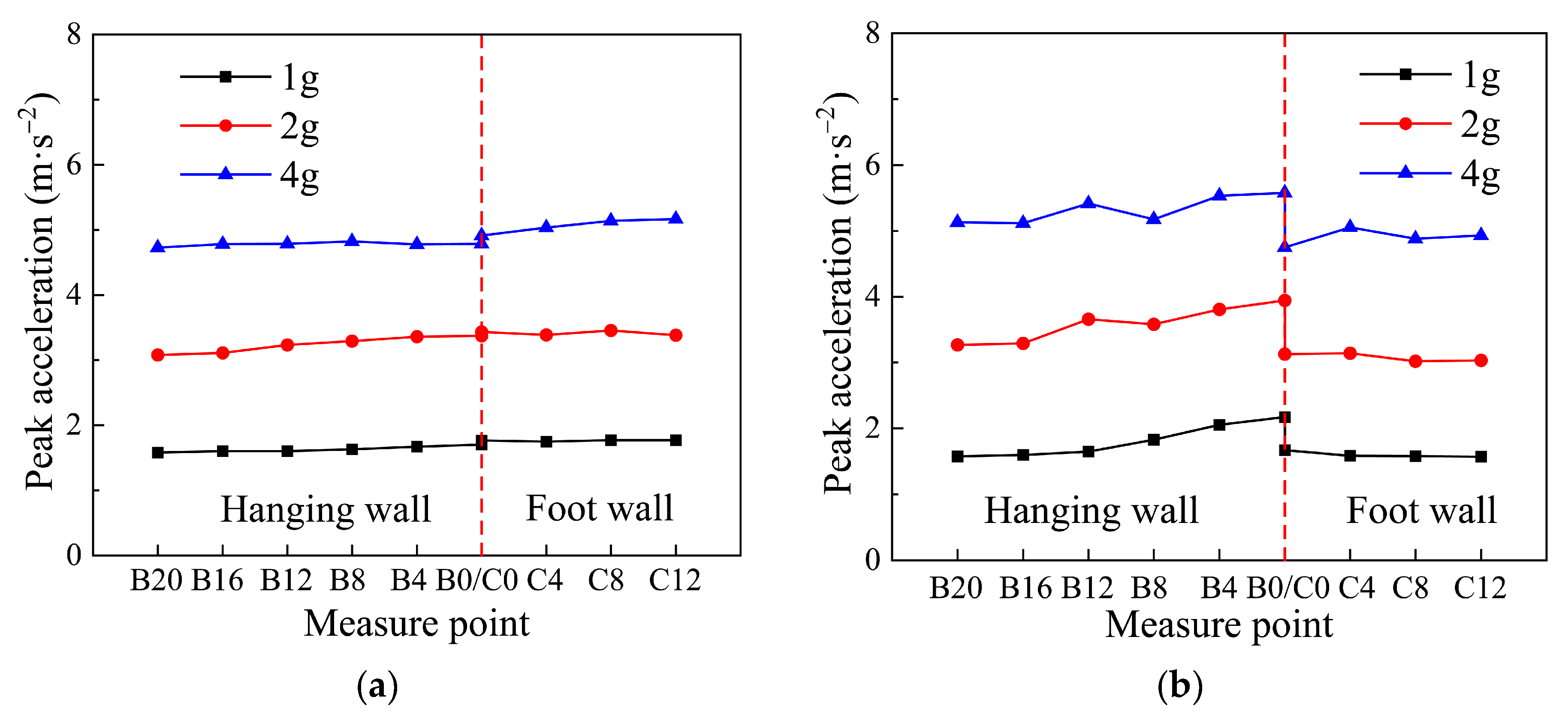
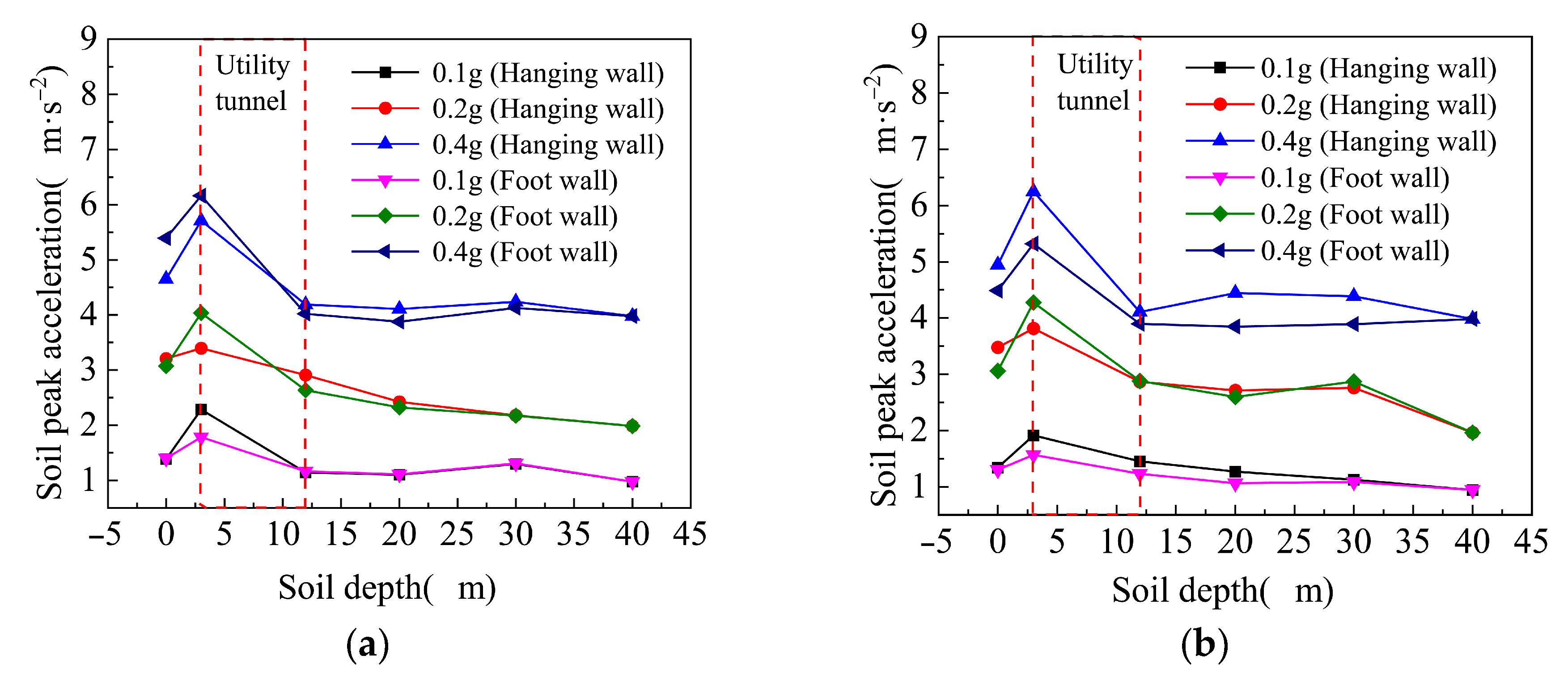
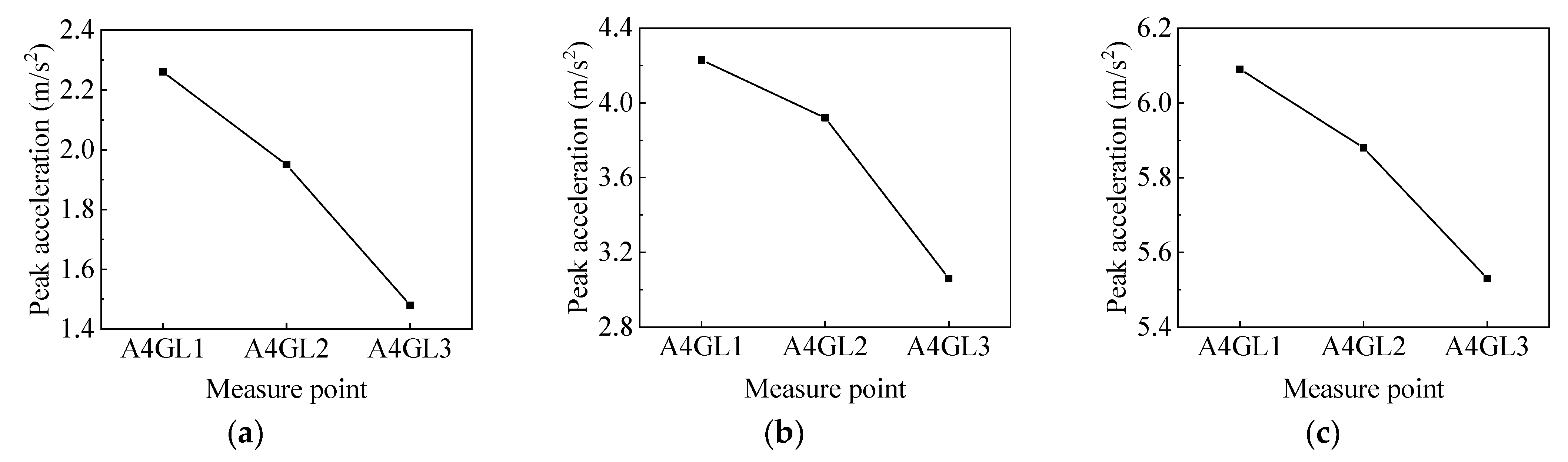
4.1.1. Peak Acceleration of Soil Surface
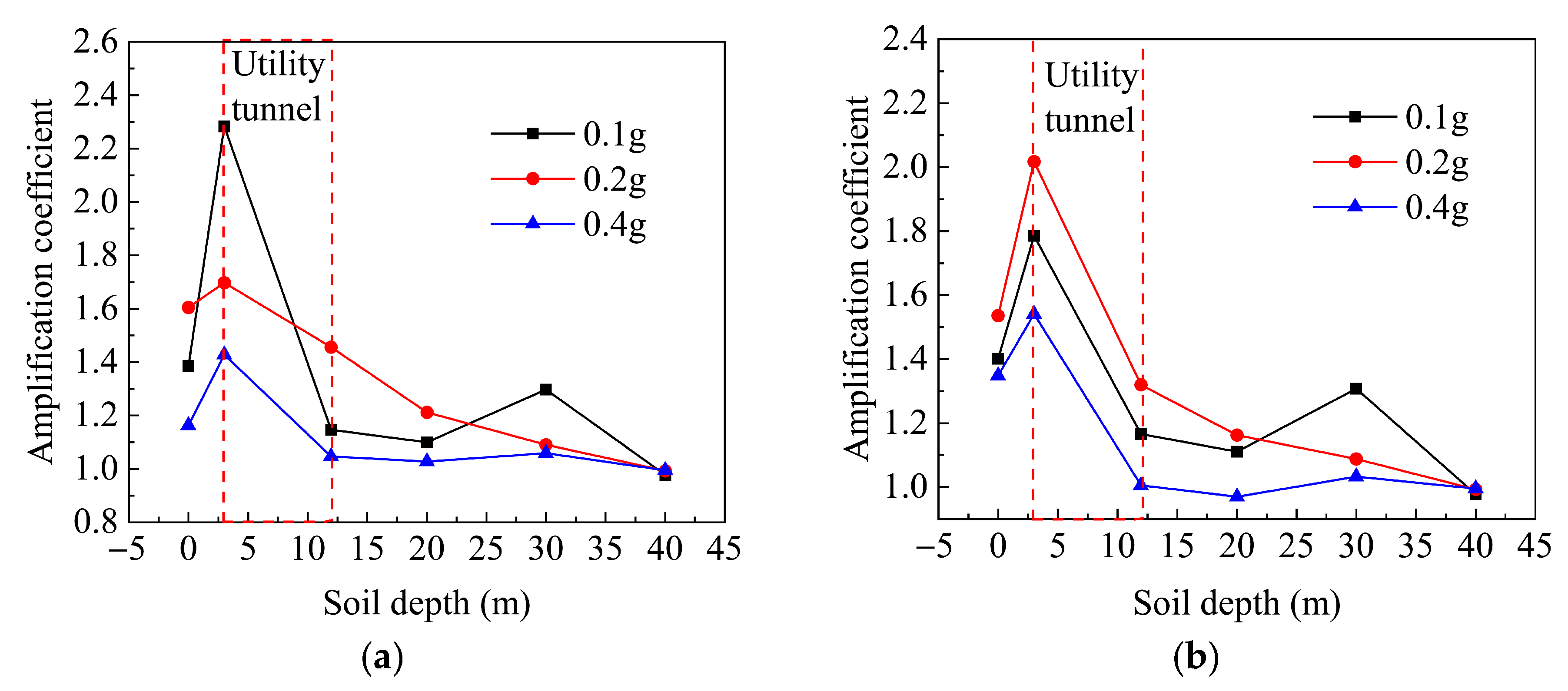
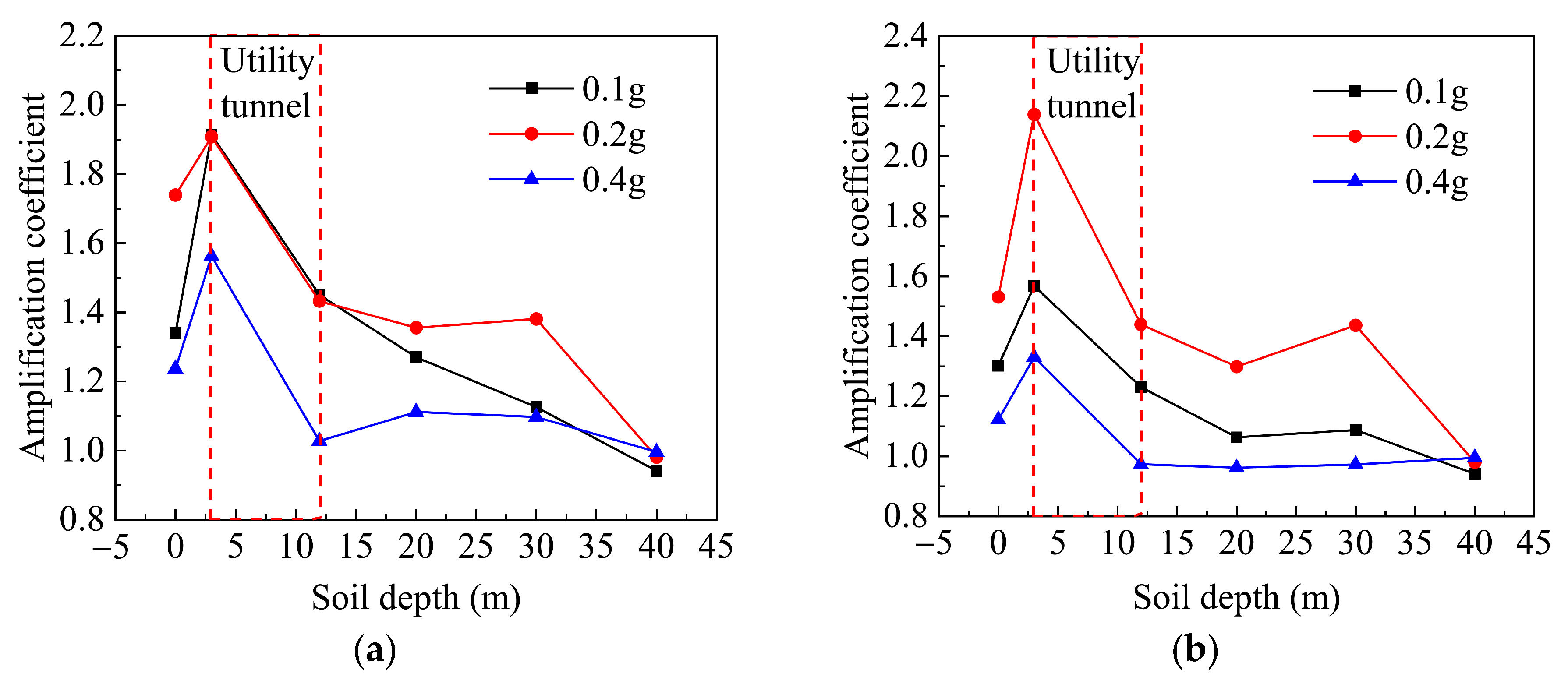
4.1.2. Soil Acceleration Amplification Coefficient
4.2. Tunnel Acceleration Analysis
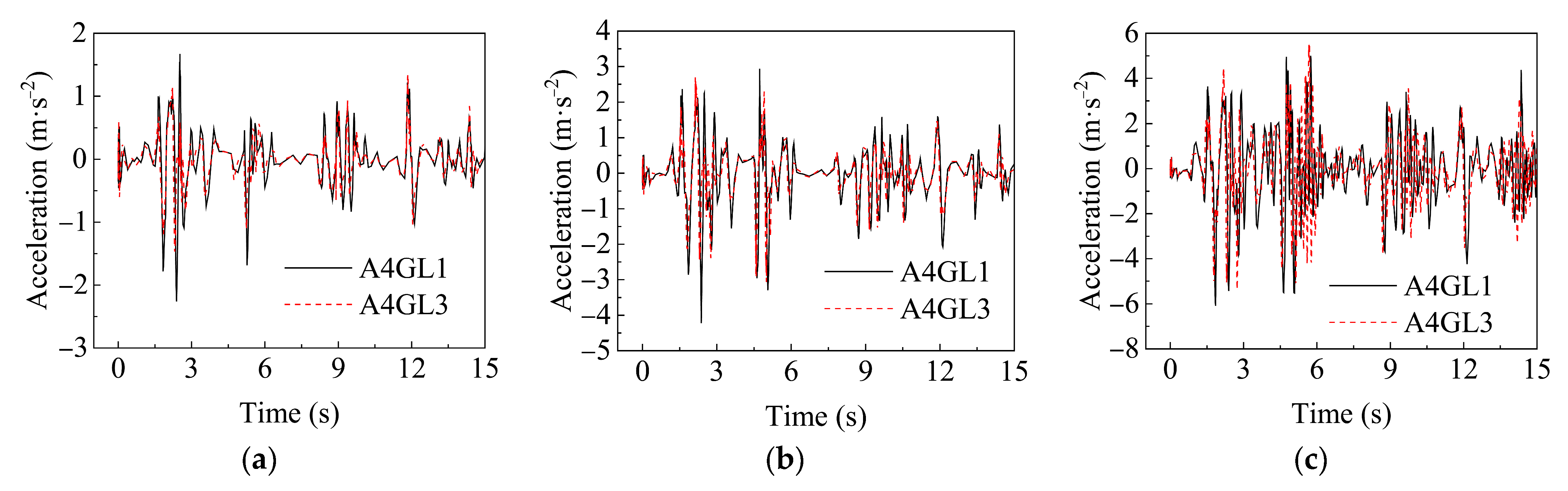
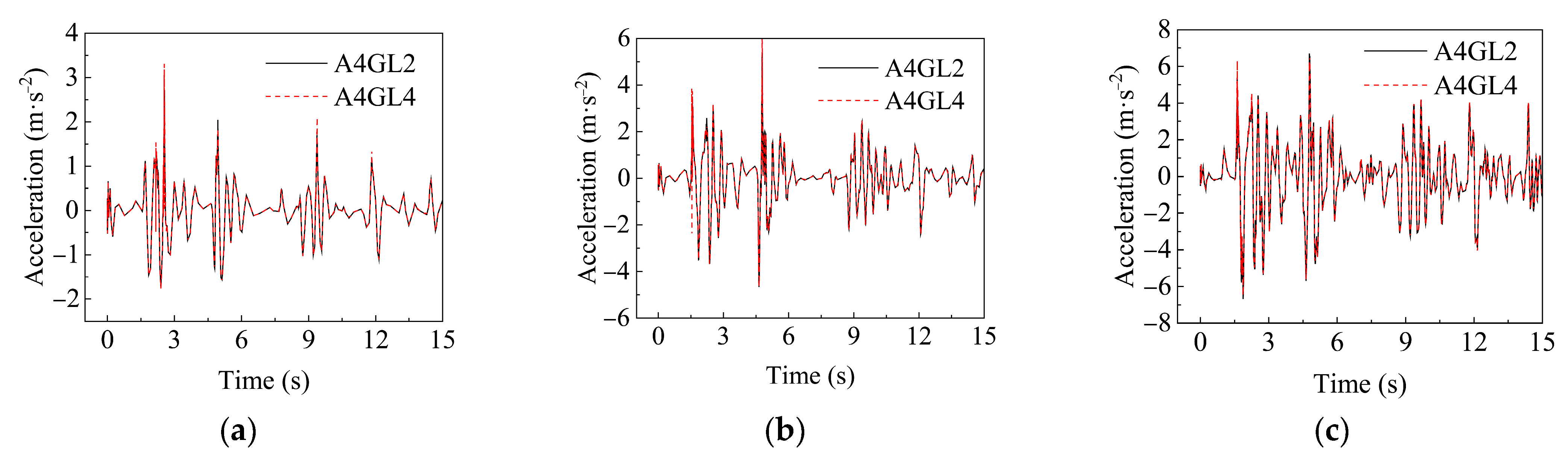
4.2.1. Acceleration–Time History Analysis of Tunnel Under Orthogonal Condition
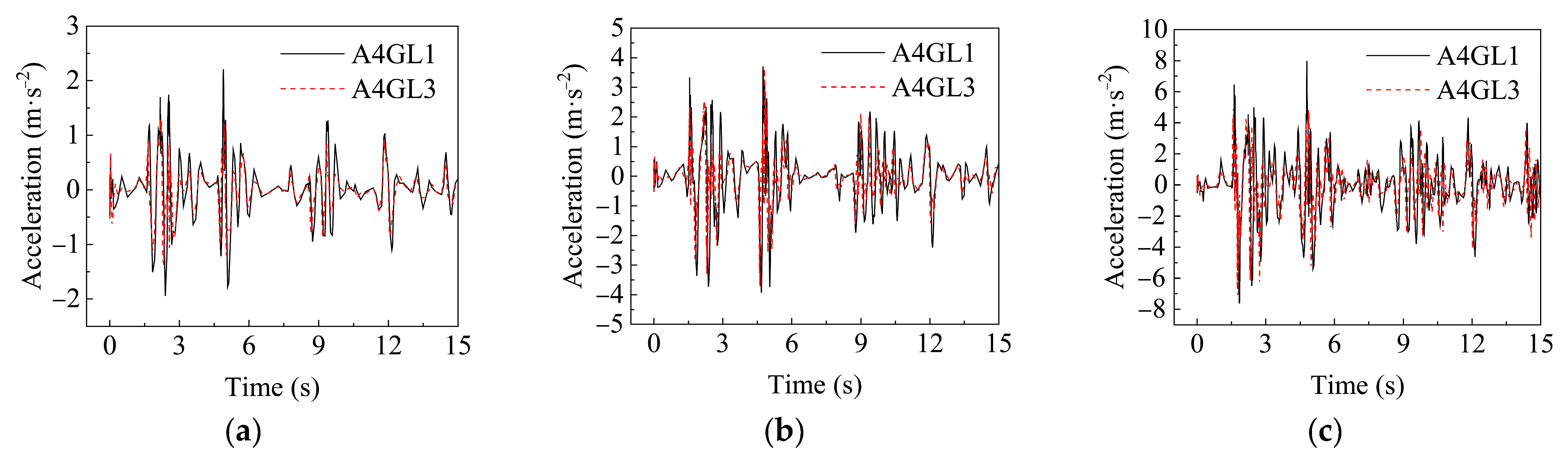
4.2.2. Acceleration–Time History Analysis of Tunnel Under Oblique Condition
4.3. Tunnel Displacement Analysis
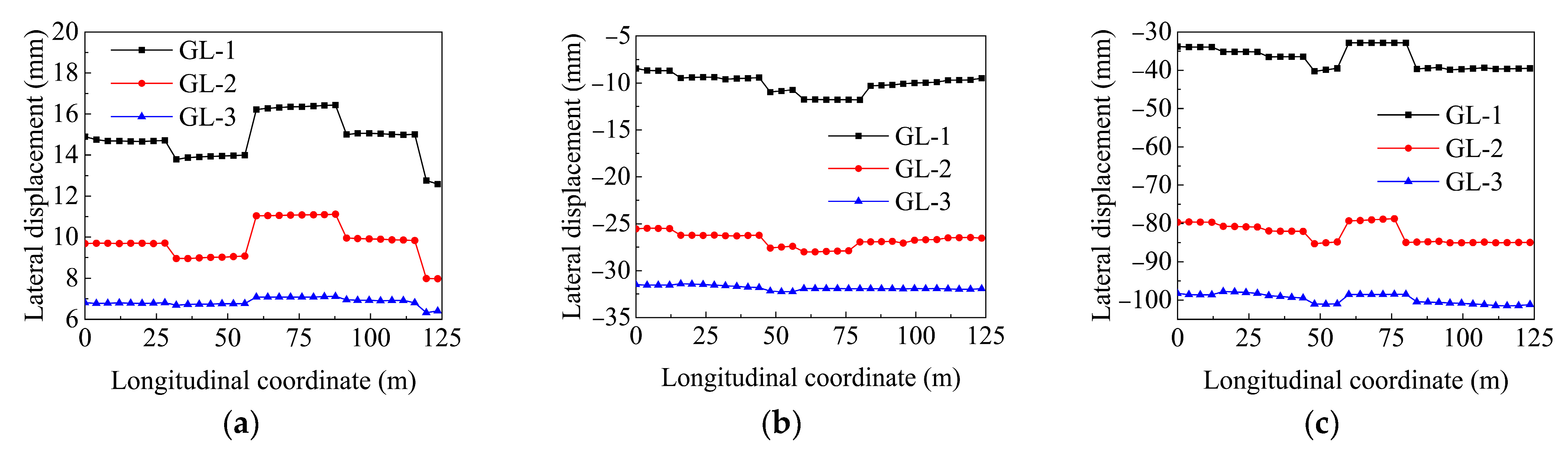
4.3.1. Lateral Displacement of Tunnel Under Orthogonal Condition
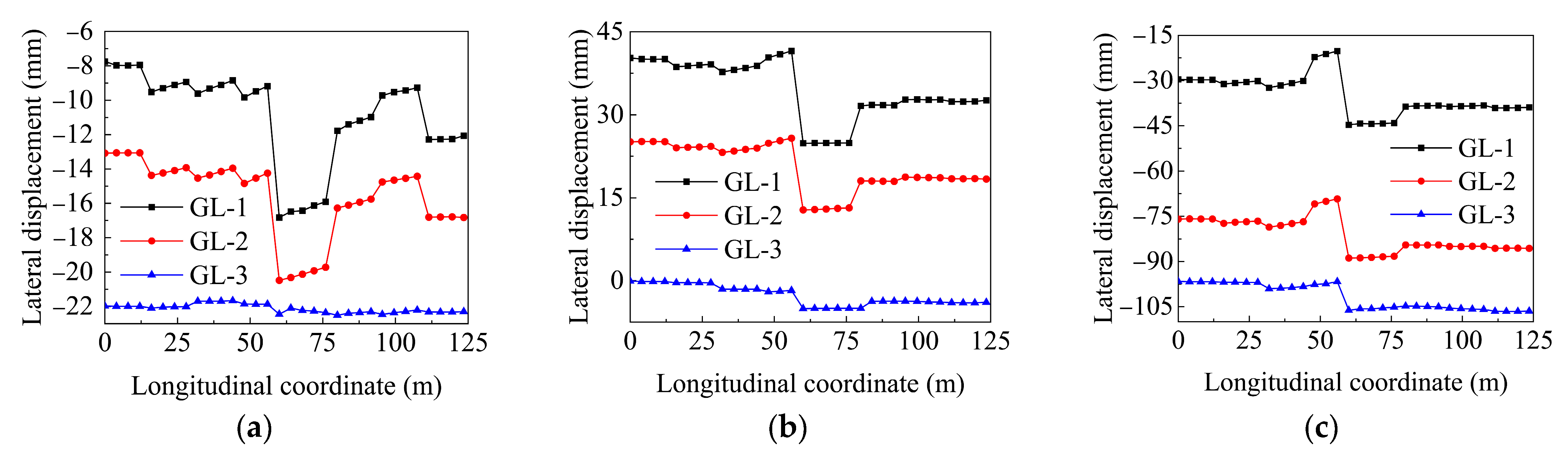
4.3.2. Lateral Displacemen Analysis of Tunnel Under Orthogonal Condition
4.4. Seismic Analysis and Design of Segmented Utility Tunnels
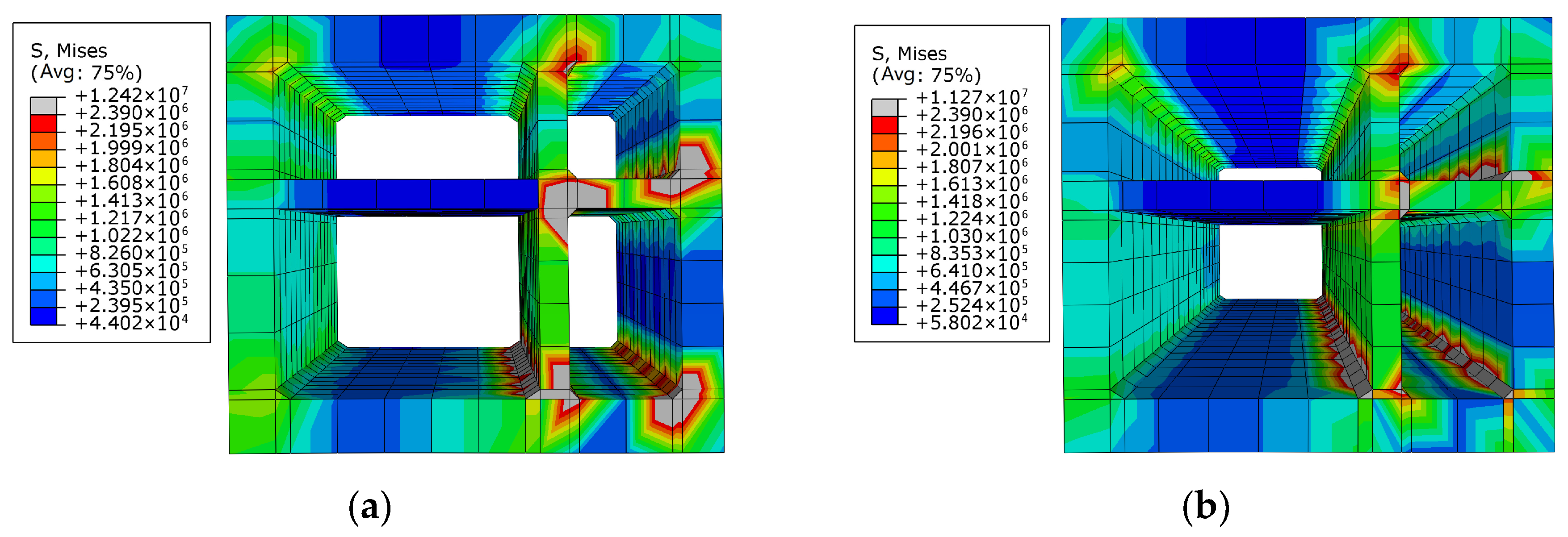
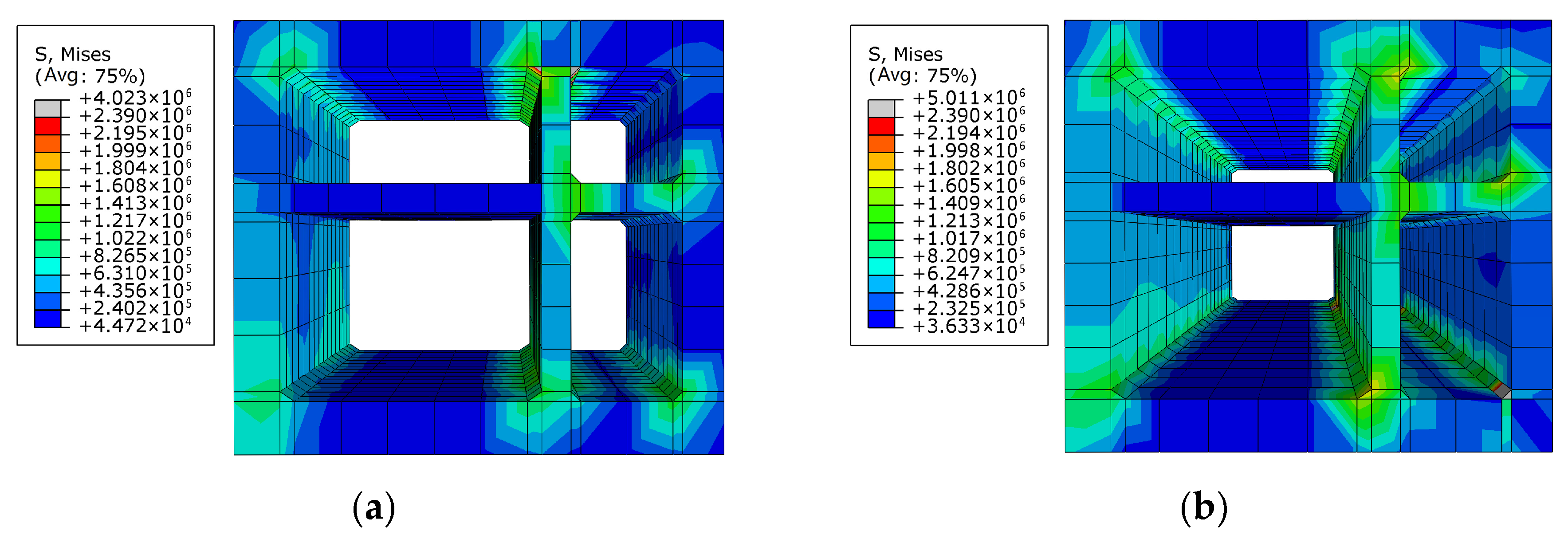
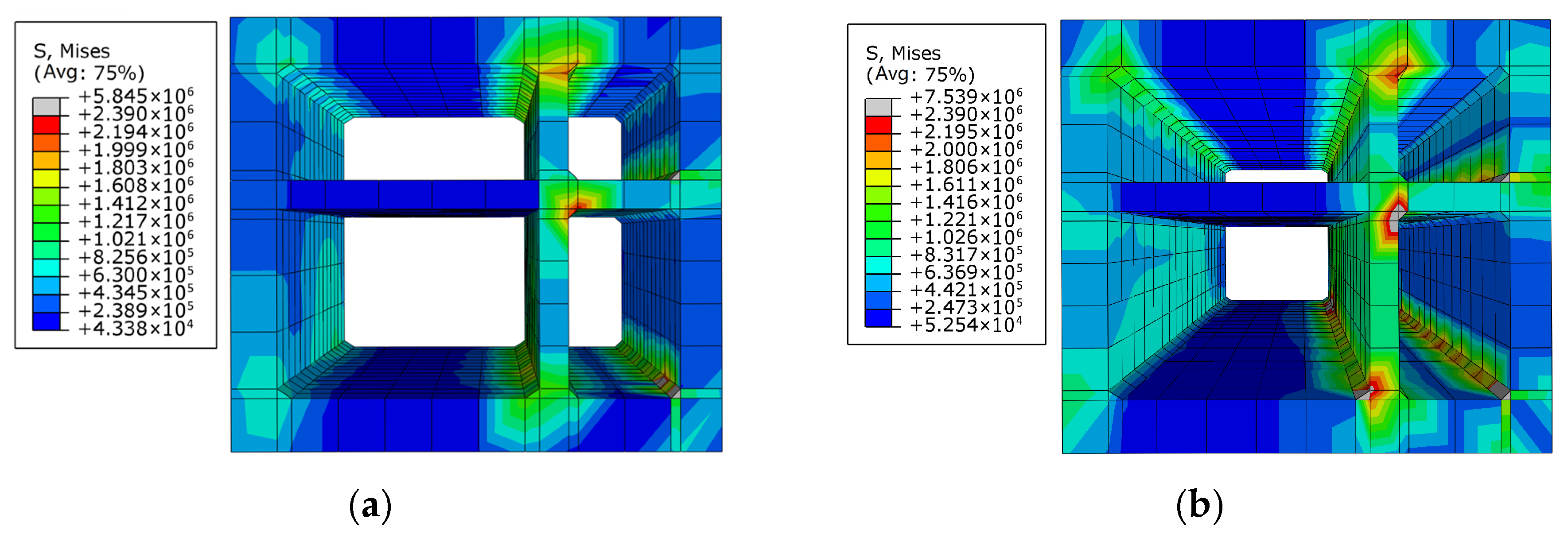
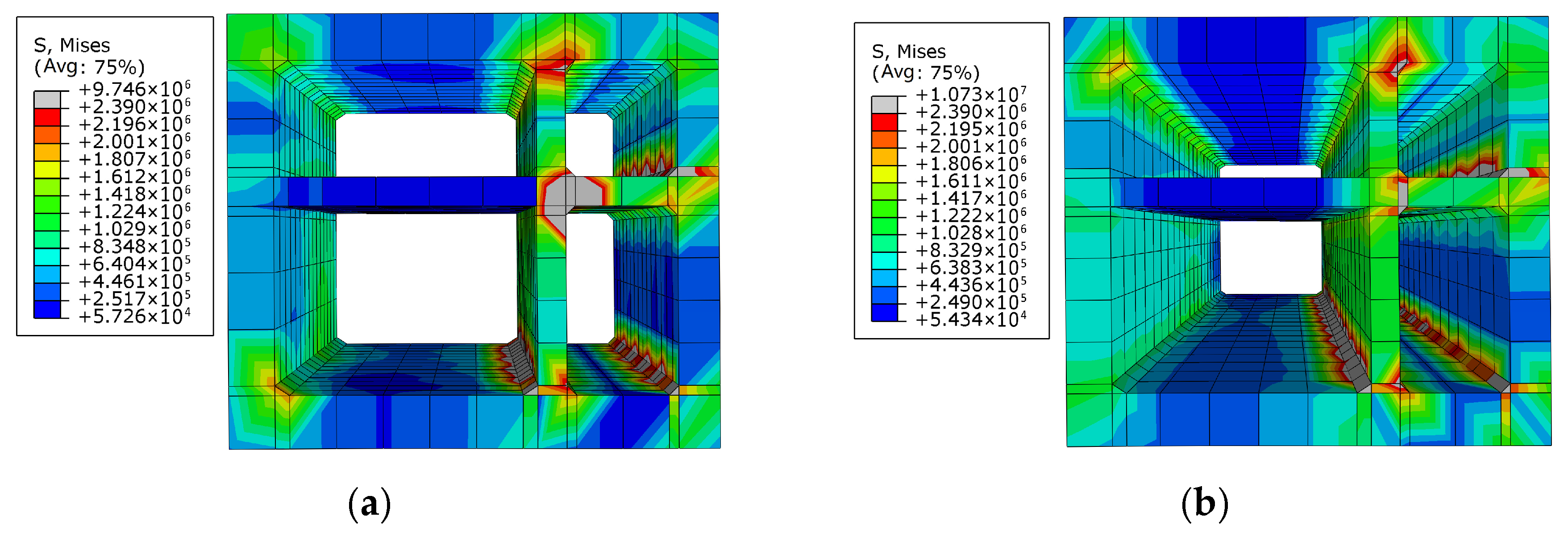
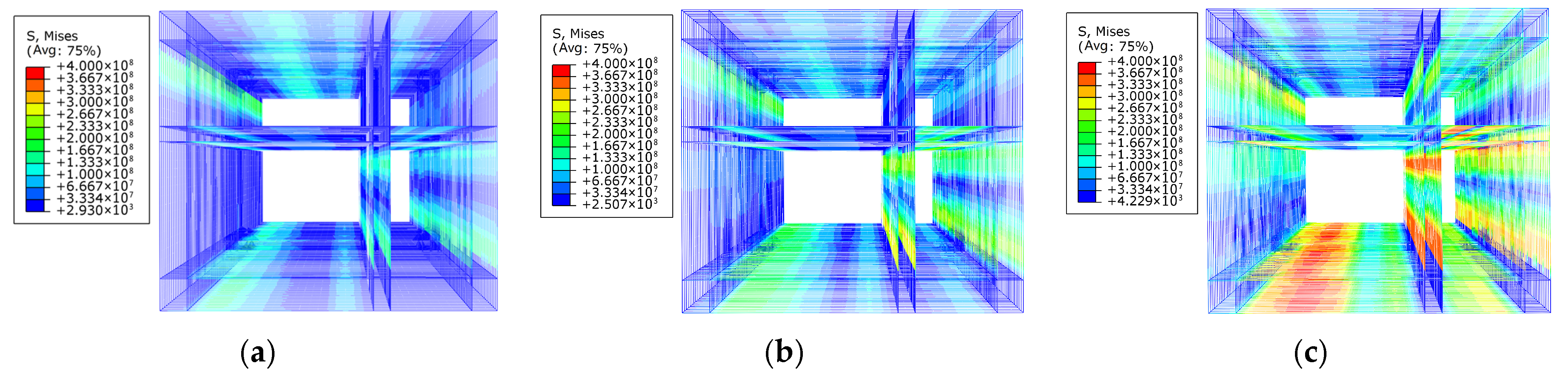
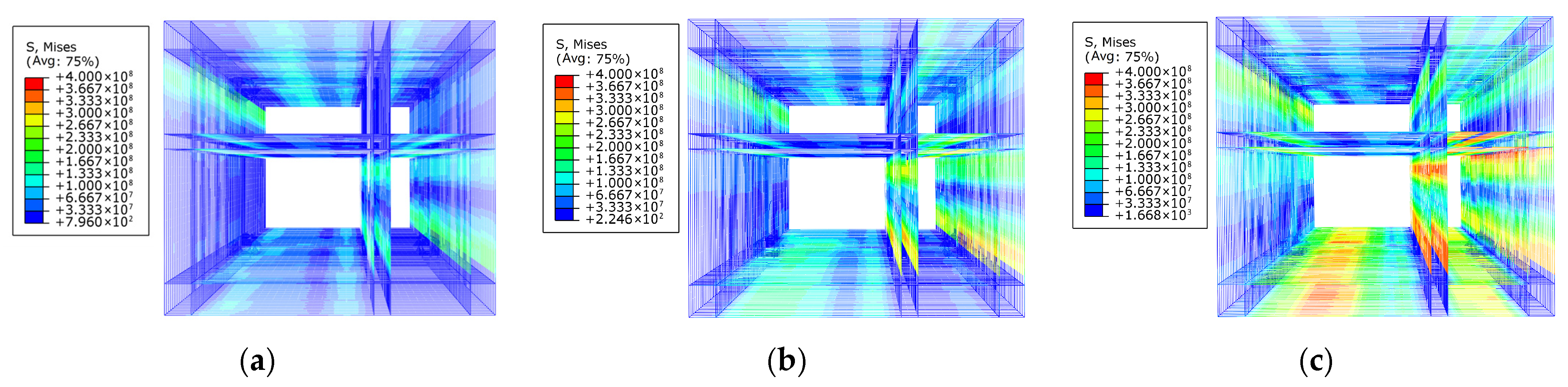
4.5. Damage Analysis of Tunnel
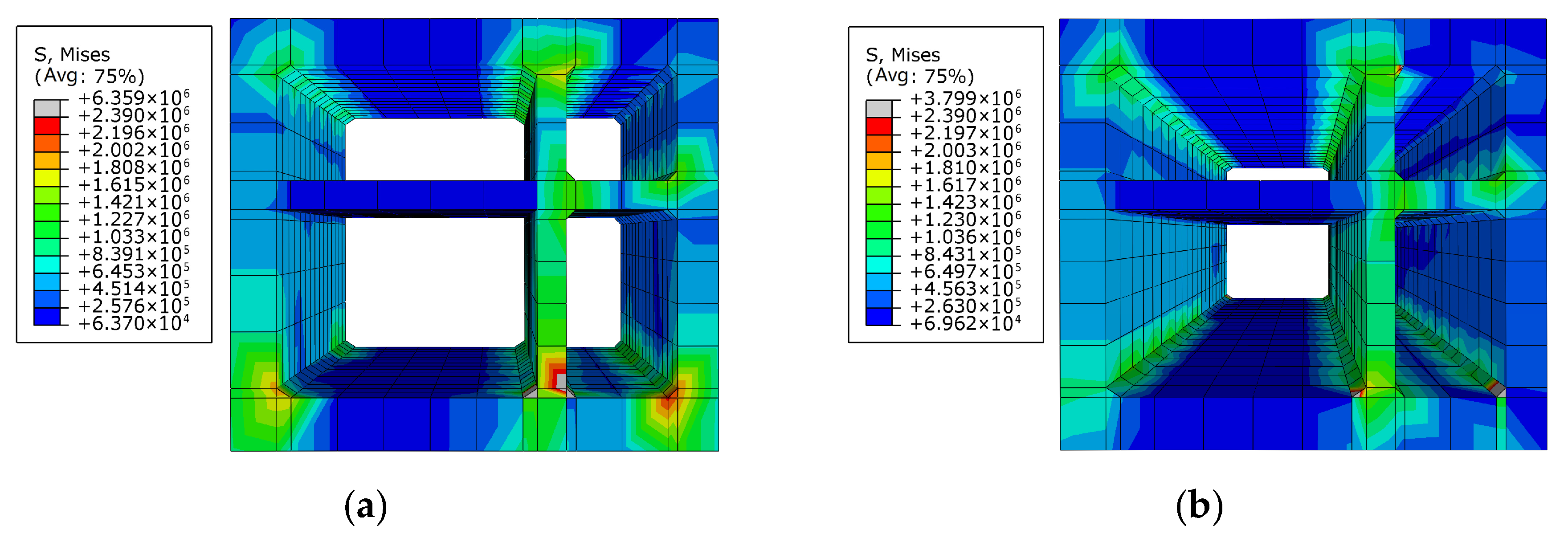
4.5.1. Concrete Damage of Tunnel Under Orthogonal Conditions
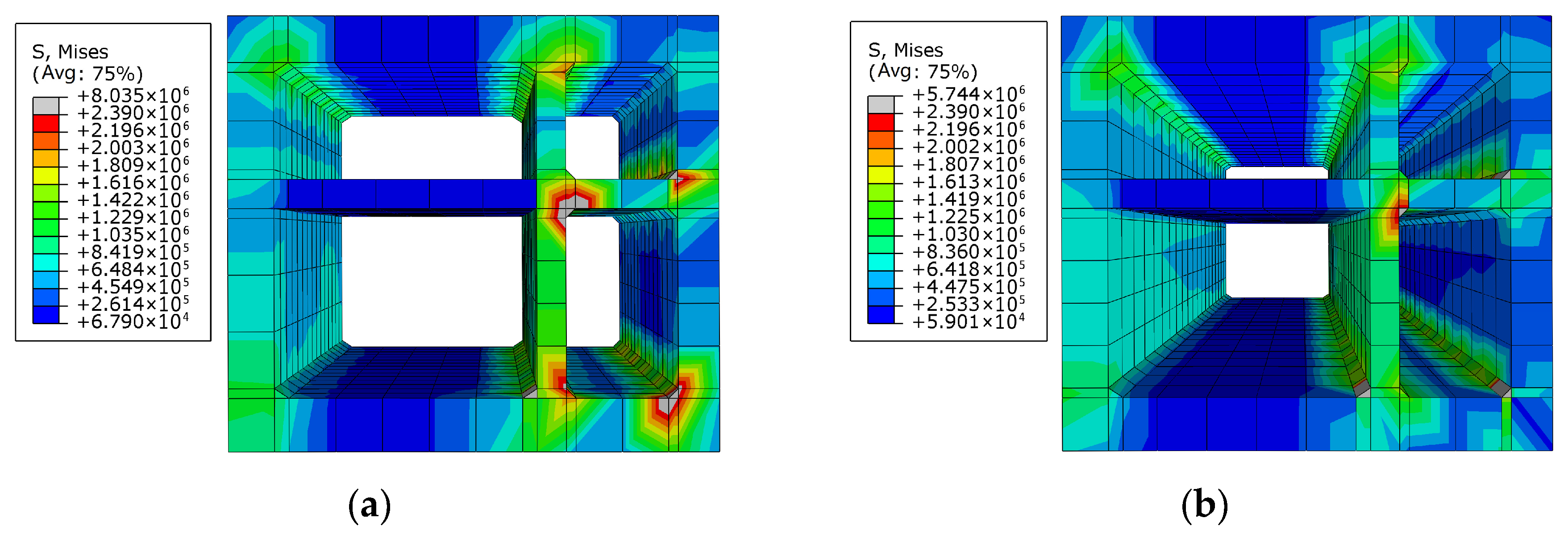
4.5.2. Concrete Damage of Tunnel Under Oblique Conditions
4.6. Analysis of Steel Bar Stress
5. Conclusions
- (1)
- Under oblique conditions, the peak accelerations of both the soil and tunnel were larger than that under orthogonal conditions, indicating that the oblique angle between the tunnel and the ground fissure will aggravate the influence of seismic action. When the soil is under both orthogonal and oblique conditions, the amplification coefficient will decrease with the increasing of soil depth. Therefore, under the action of an earthquake, the shallower the buried depth, the more dangerous the underground structure is.
- (2)
- The maximum differential displacement between tunnel sections (e.g., A4–A5) under oblique seismic input was found to exceed 20 mm under 0.4 g acceleration. Based on these results, it is suggested that an allowable differential displacement threshold is 15 mm for segmented utility tunnels crossing active fissures under rare earthquakes, considering structural integrity and waterproofing constraints.
- (3)
- The acceleration–time curves of the segmented utility tunnel under uniform seismic excitation at the same height basically coincide, while the curves of the tunnel roof and floor have obvious differences, and the peak acceleration of the tunnel roof is larger than that of the floor.
- (4)
- The segmented utility tunnel is more prone to damage when the tunnel crosses the ground fissure obliquely. Both the lateral displacement difference between the tunnel sections and the tunnel shear angle were greater than those under orthogonal conditions when the tunnel crosses the ground fissure obliquely. In addition, it is recommended that the shear angle limit should be calculated separately in different conditions when the utility tunnel is subjected to frequent earthquakes, and the shear angel limit can select the same value under the action of rare earthquake. The maximum shear angle observed was approximately 1/116 under 0.4 g. For frequent earthquakes, the shear angle of 1/200 may serve as a preliminary limit to prevent joint damage.
- (5)
- Concrete damage of the tunnel mainly appeared at the haunches of the right warehouse (which is smaller than the left warehouse), and there is also a great probability of steel bar yielding in these areas. However, in addition to the haunches of the smaller warehouse, the steel bar at the floor of the larger warehouse is also subjected to high stress. Therefore, attention should be paid to the strength design of the above positions. Stress concentration consistently occurred in the right warehouse haunch and the floor of the left warehouse. Therefore, a minimum longitudinal reinforcement ratio in those critical regions is 1.0%, which is above the general code requirement for seismic zones (0.6%).
- (6)
- Under the most severe seismic conditions (0.4 g oblique), the maximum lateral displacement difference between tunnel sections reached 24.4 mm, and the maximum shear angle was 1/116. The peak stress in concrete reached 5.8 MPa, exceeding the C40 tensile limit, and the steel stress peaked at 375 MPa near the right haunch, indicating local yielding. These values support the need for targeted reinforcement in high-risk zones such as tunnel joints and sidewall haunches.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Canto-Perello, J.; Curiel-Esparza, J. An analysis of utility tunnel viability in urban areas. Civ. Eng. Environ. Syst. 2006, 23, 11–19. [Google Scholar] [CrossRef]
- Hu, Y.; Li, Z.; He, J.; Huang, Z. Experimental study on seismic performance of prefabricated joints of underground utility tunnel. IOP Conf. Ser. Earth Environ. Sci. 2019, 267, 042109. [Google Scholar] [CrossRef]
- Jiang, L. State-of-the-art of seismic response of utility tunnel. Appl. Mech. Mater. 2013, 353–356, 2202–2205. [Google Scholar] [CrossRef]
- Datta, T.K.; Mashaly, E.A. Seismic response of buried submarine pipelines. J. Energy Resour. Technol. 1988, 110, 208–218. [Google Scholar] [CrossRef]
- Sharma, S.; Judd, W.R. Underground opening damage from earthquakes. Eng. Geol. 1991, 30, 263–276. [Google Scholar] [CrossRef]
- Yan, K.M.; Zhang, J.J.; Wang, Z.J.; Liao, W.M.; Wu, Z.J. Seismic response of deep buried pipeline under non-uniform excitations from large scale shaking table test. Soil Dyn. Earthq. Eng. 2018, 113, 180–192. [Google Scholar] [CrossRef]
- Wijewickreme, D.; Karimian, H.; Honegger, D. Response of buried steel pipelines subjected to relative axial soil movement. Can. Geotech. J. 2009, 46, 735–752. [Google Scholar] [CrossRef]
- Peng, J.B.; Chen, L.W.; Huang, Q.B.; Men, Y.M.; Fan, W.; Yan, J.K. Physical simulation of ground fissures triggered by underground fault activity. Eng. Geol. 2013, 155, 19–30. [Google Scholar] [CrossRef]
- Zhang, D.; Hu, Z.P.; Lu, G.G.; Wang, R.; Ren, X. Calculation of the vertical strata load of utility tunnel crossing ground fissure zone. Shock Vib. 2020, 2020, 8877016. [Google Scholar] [CrossRef]
- Yan, Y.; Qiu, J.; Huang, Q.; Wang, Z.; Xie, Y.; Liu, T. Ground fissure geology in Xi’an and failure mitigation measures for utility tunnel system due to geohazard. Arab. J. Geosci. 2021, 14, 1243. [Google Scholar] [CrossRef]
- Hashash, Y.M.A.; Hook, J.J.; Schmidt, B.; Yao, J.I.C. Seismic design and analysis of underground structures. Tunn. Undergr. Space Technol. 2001, 16, 247–293. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, Z.; Chen, J.; Bobet, A.; Zhao, M.; Yuan, Y. Analytical solution for longitudinal seismic response of tunnels liners with sharp stiffness transition. Tunn. Undergr. Space Technol. 2018, 77, 103–114. [Google Scholar] [CrossRef]
- Yu, H.; Cai, C.; Bobet, A.; Zhao, X.; Yuan, Y. Analytical solution for longitudinal bending stiffness of shield tunnels. Tunn. Undergr. Space Technol. 2019, 83, 27–34. [Google Scholar] [CrossRef]
- Chen, J.; Shi, X.; Li, J. Shaking table test of utility tunnel under non-uniform earthquake wave excitation. Soil Dyn. Earthq. Eng. 2010, 30, 1400–1416. [Google Scholar] [CrossRef]
- Wang, Z.Z.; Jiang, Y.J.; Zhu, C.A.; Sun, T.C. Shaking table tests of tunnel linings in progressive states of damage. Tunn. Undergr. Space Technol. 2015, 50, 109–117. [Google Scholar] [CrossRef]
- Yu, H.; Yan, X.; Bobet, A.; Yuan, Y.; Xu, G.; Su, Q. Multi-point shaking table test of a long tunnel subjected to non-uniform seismic loadings. Bull. Earthq. Eng. 2017, 16, 1041–1059. [Google Scholar] [CrossRef]
- Darli, C.M.; Tang, A.; Huang, D.; Zhang, J. Large scale shaking table model test and analysis on seismic response of utility tunnel in non-homogeneous soil. Earthq. Eng. Eng. Vib. 2021, 20, 505–515. [Google Scholar] [CrossRef]
- Jiang, L.; Chen, J.; Li, J. Seismic response of underground utility tunnels: Shaking table testing and FEM analysis. Earthq. Eng. Eng. Vib. 2010, 9, 555–567. [Google Scholar] [CrossRef]
- Cilingir, U.; Madabhushi, S.P.G. Effect of depth on the seismic response of square tunnels. Soils Found. 2011, 51, 449–457. [Google Scholar] [CrossRef]
- Baziar, M.H.; Moghadam, M.R.; Kim, D.S.; Choo, Y.W. Effect of underground tunnel on the ground surface acceleration. Tunn. Undergr. Space Technol. 2014, 44, 10–22. [Google Scholar] [CrossRef]
- Tsinidis, G.; Pitilakis, K.; Madabhushi, G.; Heron, C. Dynamic response of flexible square tunnels: Centrifuge testing and validation of existing design methodologies. Géotechnique 2015, 65, 401–417. [Google Scholar] [CrossRef]
- Tsinidis, G.; Pitilakis, K.; Madabhushi, G. On the dynamic response of square tunnels in sand. Eng. Struct. 2016, 125, 419–437. [Google Scholar] [CrossRef]
- Duan, X.; Dong, Q.; Ye, W. Experimental study on seismic performance of prefabricated utility tunnel. Adv. Civ. Eng. 2019, 2019, 8968260. [Google Scholar] [CrossRef]
- Zhang, J.; Yuan, Y.; Yu, H. Shaking table tests on discrepant response of shaft-tunnel junction in soil under transverse excitations. Soil Dyn. Earthq. Eng. 2019, 120, 345–359. [Google Scholar] [CrossRef]
- Ding, X.; Feng, L.; Wang, C.; Chen, Z.; Han, L. Shaking table testing of the seismic response of a utility tunnel with a joint connection. Soil Dyn. Earthq. Eng. 2020, 133, 106133. [Google Scholar] [CrossRef]
- Li, D.; Liang, J.; Dong, B.; Ba, Z. A multi-scale model for longitudinal seismic design of prefabricated utility tunnel based on multi-point constraints. Structures 2024, 62, 106176. [Google Scholar] [CrossRef]
- Huang, Z.; Feng, Y.; Tang, A.; Liu, Q. Influence of oblique incidence of p-waves on seismic response of prefabricated utility tunnels considering joints. Soil Dyn. Earthq. Eng. 2023, 167, 107797. [Google Scholar] [CrossRef]
- Li, D.; Liang, J.; Gan, M.; Zhao, H. A shell-spring model for longitudinal seismic design of underground cross utility tunnels. Eng. Mech. 2025, 42, 144–155. [Google Scholar] [CrossRef]
- Liang, J.; Zhou, Y.; Li, D.; Zhao, H. Longitudinal seismic analysis of underground cross precast utility tunnels. J. Earthq. Eng. Eng. Vib. 2023, 43, 182–189. [Google Scholar]
- Li, J.; Zhong, Z.; Han, C.; Li, G.; Shen, J. Seismic performance assessment of underground utility tunnel and internal pipeline considering effects of tunnel joints. Jpn. Geotech. Soc. Spec. Publ. 2024, 10, 710–714. [Google Scholar] [CrossRef]
- Qu, J. Dynamic Response of Utility Tunnel under the Effect of Oblique Incidence of Ground Motions. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2017. [Google Scholar]
- DBJ61-6-2006; Xi’an Ground Fissure Site Investigation and Engineering Design Specification. Shanxi Provincial Construction Press: Xi’an, China, 2006.
- GB 50010-2010; Code for Design of Concrete Structures. China Architecture and Building Press: Beijing, China, 2010.
- Zhu, L. Study on the Harm of Ground Fissures on Integrated Pipe Gallery in Loess Area. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2018. [Google Scholar]
- Xiong, Z.; Chen, X.; Gao, P.; Wei, J.; Huang, Y. Study on simulation of dynamic response of the structure crossing ground fissure in high-intensity of earthquake. J. Xi’an Univ. Archit. Technol. 2016, 48, 783–789. [Google Scholar] [CrossRef]
- Xiong, Z.; Zhang, C.; Huo, X. Shaking table tests on acceleration response of ground fissure site. Chin. J. Geotech. Eng. 2018, 40, 520–526. [Google Scholar] [CrossRef]
- Huang, Q.; Peng, J.; Fan, W. Metro tunnel hazards induced by active ground fissures in Xi’an and relevant control measures. Chin. J. Geotech. Eng. 2009, 31, 781–788. [Google Scholar] [CrossRef]
- Huang, H.; Qian, H.; Wu, C. Setback distance for seismic fortification and avoidance of structures in ground fissure sites. China Earthq. Eng. J. 2018, 40, 536–545. [Google Scholar] [CrossRef]
- Gu, Y.; Liu, J.; Du, Y. 3D consistent viscous-spring artificial boundary and viscous-spring boundary element. Eng. Mech. 2007, 24, 31–37. [Google Scholar] [CrossRef]
- Meng, H.; Chen, J.; Li, J. Shaking table test of soil-pipe dynamic interaction under non-uniform earthquake wave excitation. Chin. J. Undergr. Space Eng. 2008, 4, 852–859. [Google Scholar] [CrossRef]
- GB 50223-2008; Standard for Classification of Seismic Protection of Building Constructions. China Architecture & Building Press: Beijing, China, 2008.
- Li, K. Study on the Soil-Metro Tunnels Interactions in Ground Fissures Area. Ph.D. Thesis, Chang’an University, Xi’an, China, 2012. [Google Scholar]
- Huang, Q.; Peng, J.; Deng, Y. Design parameters of Xi’an metro line 2 tunnel passing through active ground fissure zones. Rock Soil Mech. 2010, 31, 2882–2888. [Google Scholar] [CrossRef]
- GB50011-2010; Seismic Design Code of Building. China Construction Industry Press: Beijing, China, 2016.

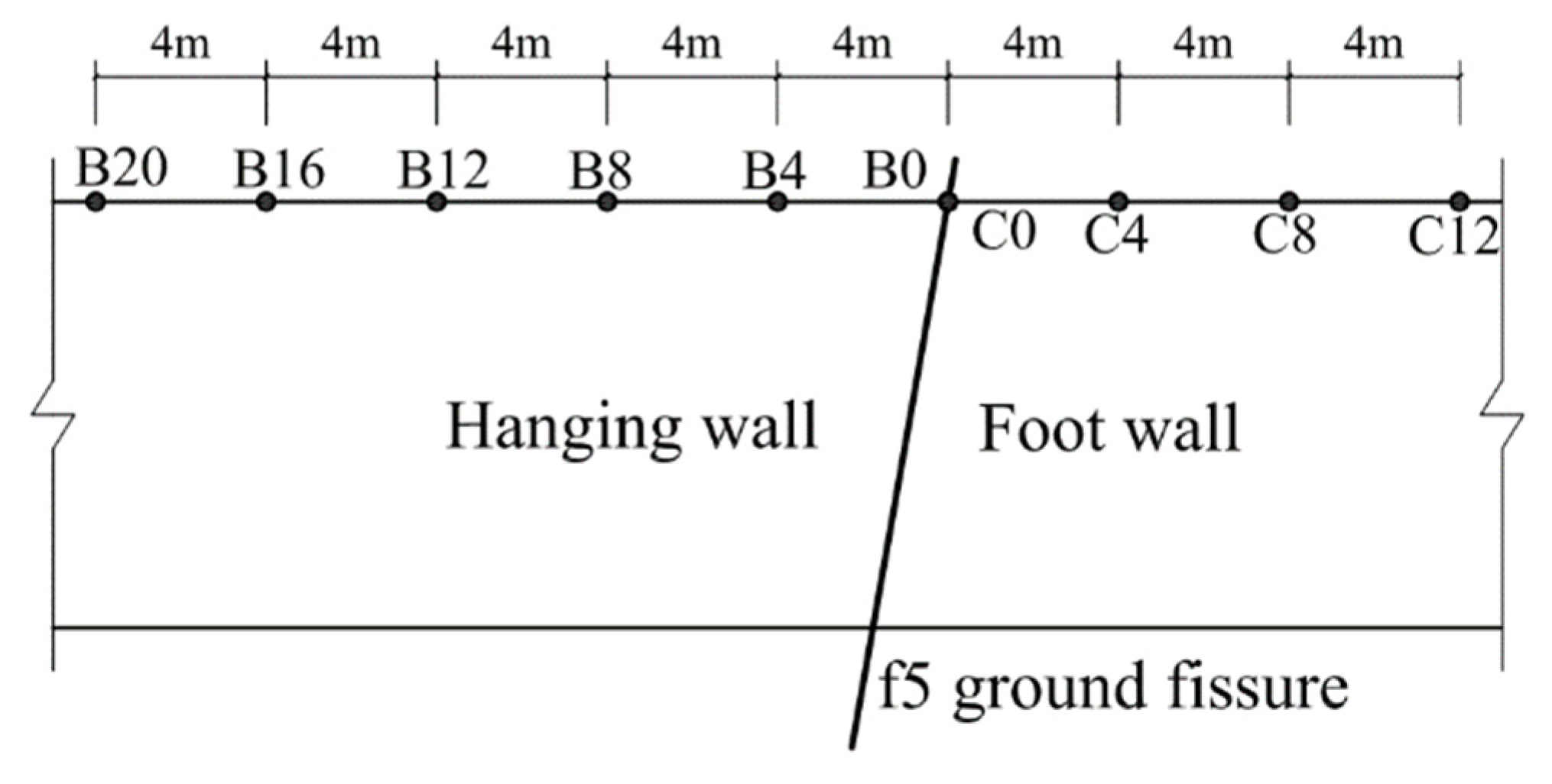

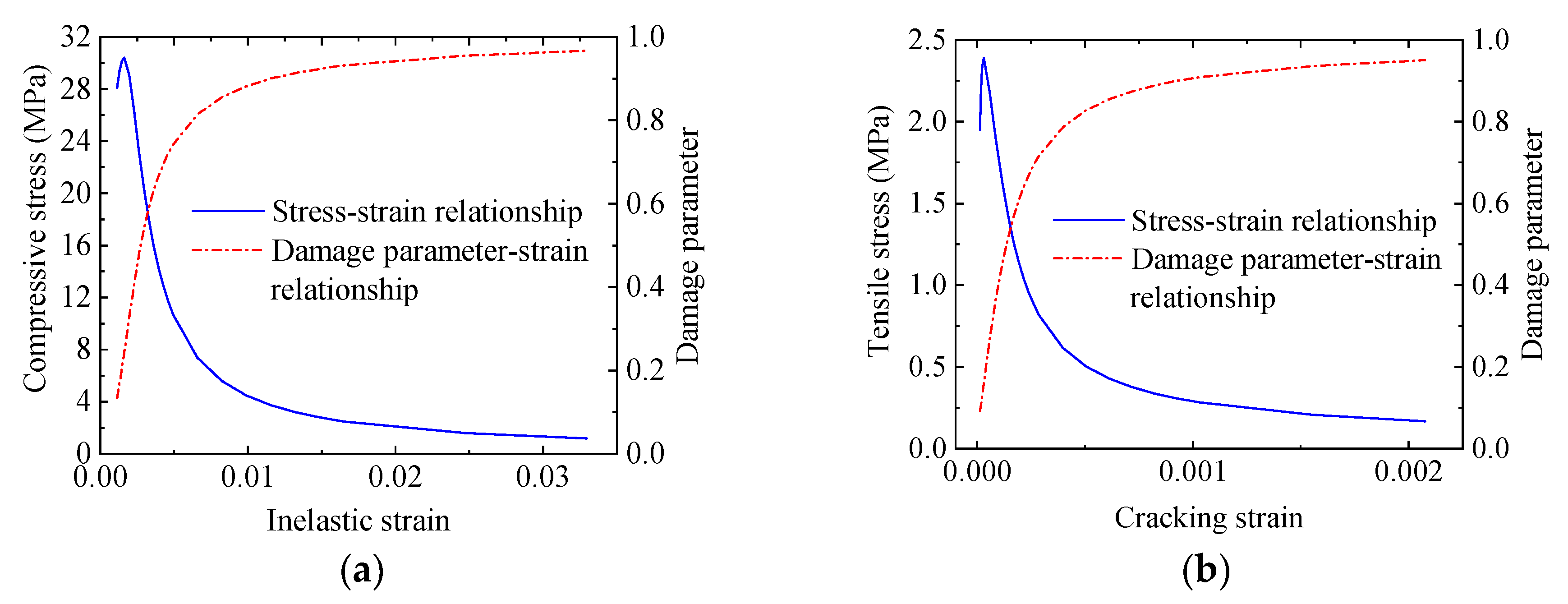
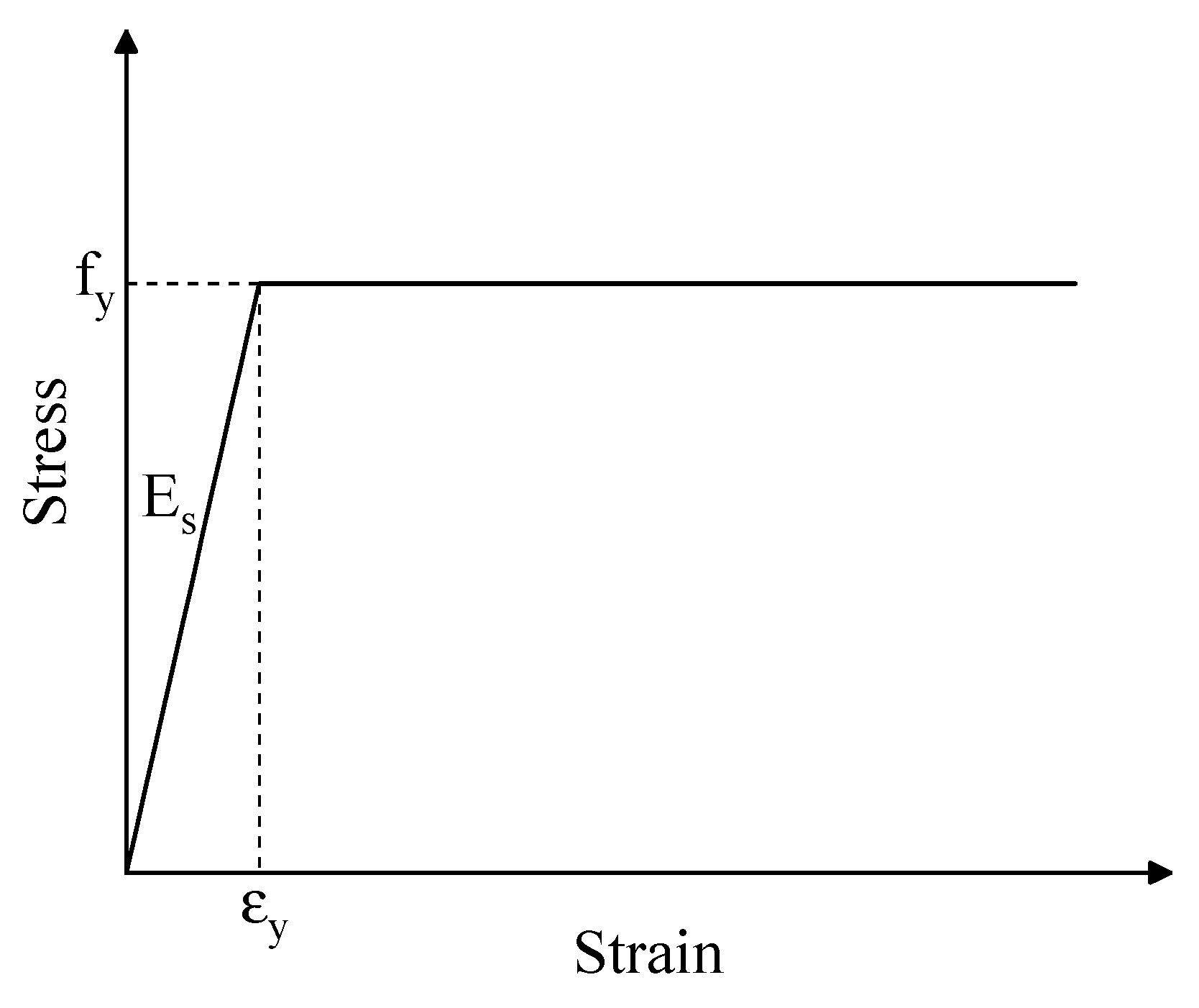
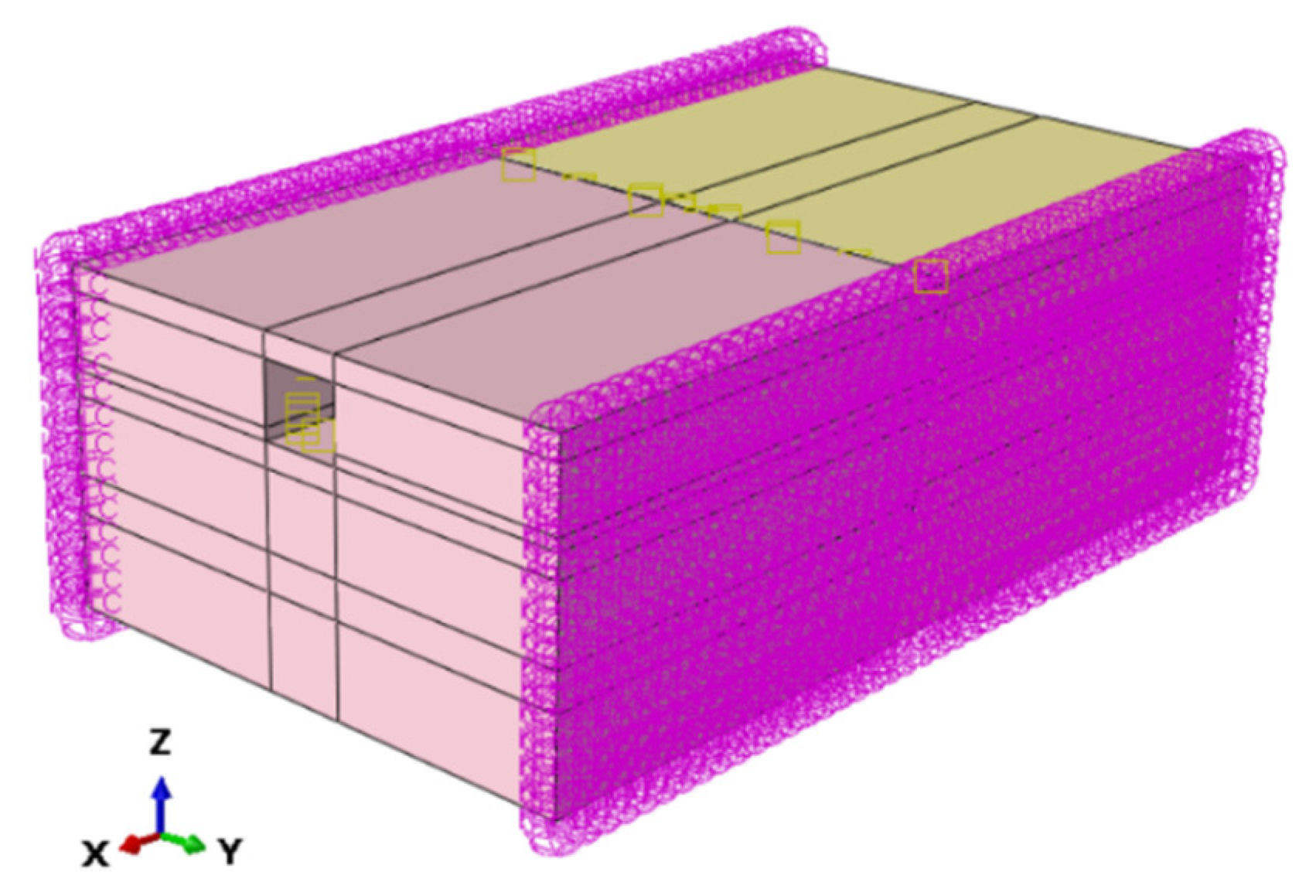


| Soil Layer | Soil Depth (m) | Soil Thickness (m) | Staggered Distance Between Hanging Wall and Foot Wall (m) | ||
|---|---|---|---|---|---|
| Foot Wall | Hanging Wall | Foot Wall | Hanging Wall | ||
| 3 | 3 | 3 | 3 | 0 | |
| 10 | 10.5 | 7 | 7.5 | 0.5 | |
| 13.7 | 14.9 | 3.7 | 4.4 | 0.7 | |
| 22.6 | 24.1 | 8.9 | 9.2 | 0.3 | |
| 26.6 | 28.7 | 4 | 4.6 | 0.6 | |
| 40 | 40 | 13.4 | 11.3 | N/A | |
| Soil Layer | Density (kg·m−3) | Shear Modulus (MPa) | Poisson’s Ratio | Internal Friction Angle (°) | Dilation Angle (°) | Cohesion (MPa) | S-Wave Velocity (m·s−1) | P-Wave Velocity (m·s−1) |
|---|---|---|---|---|---|---|---|---|
| 1755 | 35.80 | 0.34 | 21.2 | 9.2 | 0.0256 | 142.84 | 290.07 | |
| 1630 | 305.81 | 0.29 | 38.7 | 9.3 | 0.0371 | 433.14 | 901.46 | |
| 1710 | 330.03 | 0.30 | 42.8 | 11 | 0.0785 | 439.32 | 913.12 | |
| 1660 | 421.79 | 0.31 | 41.3 | 10.3 | 0.0293 | 504.07 | 978.24 | |
| 1730 | 440.00 | 0.29 | 42.8 | 11 | 0.1047 | 504.32 | 999.05 | |
| 1800 | 489.75 | 0.30 | 43.5 | 11.3 | 0.0493 | 526.39 | 1012.3 |
| Source | Moisture Content (%) | Bulk Density (kN·m−3) | Cohesion (MPa) | Internal Friction Angle (°) | Compression Modulus (MPa) |
|---|---|---|---|---|---|
| Prototype soil | 20.00 | 18.20 | 0.033 | 19.00 | 9.20 |
| Simulated soil | 8.90 | 21.50 | 0.00235 | 21.00 | 0.51 |
| Height (mm) | Diameter (mm) | Maximum Load (kN) | Compression Modulus (MPa) | Tensile Strength (MPa) | Height (mm) |
|---|---|---|---|---|---|
| 30.01 | 12.35 | 10.36 | 2.46 | 86.56 | 30.01 |
| Working Condition | Measure Point | Input Accelerations | ||
|---|---|---|---|---|
| 0.1 g | 0.2 g | 0.4 g | ||
| Orthogonal condition | A4GL1 | 15.4 | −11.0 | −39.0 |
| A4GL2 | 9.8 | −27.9 | −85.4 | |
| A4GL3 | 8.2 | −30.8 | −99.8 | |
| A4GL4 | 9.8 | −28.0 | 27.3 | |
| A5GL1 | 13.0 | −11.8 | −33.1 | |
| A5GL2 | 8.0 | −27.7 | −78.7 | |
| A5GL3 | 7.0 | −31.7 | −97.9 | |
| A5GL4 | 8.0 | −28.8 | −79.0 | |
| Oblique condition | A4GL1 | −8.4 | 43.2 | −18.3 |
| A4GL2 | −13.8 | 27.6 | −65.3 | |
| A4GL3 | −21.3 | −1.9 | −95.3 | |
| A4GL4 | −13.5 | 27.3 | −65.3 | |
| A5GL1 | −16.6 | 26.2 | −45.4 | |
| A5GL2 | −19.7 | 13.3 | −86.0 | |
| A5GL3 | −22.8 | −4.8 | −106.4 | |
| A5GL4 | −19.8 | 13.3 | −87.3 | |
| Tunnel Section | Working Condition | Input Acceleration | ||
|---|---|---|---|---|
| 0.1 g | 0.2 g | 0.4 g | ||
| A4 | Orthogonal condition | 0.00081 | 0.00221 | 0.00679 |
| Oblique condition | 0.00144 | 0.00503 | 0.00859 | |
| A5 | Orthogonal condition | 0.00067 | 0.00222 | 0.00723 |
| Oblique condition | 0.00069 | 0.00346 | 0.00680 | |
| Working Condition | Input Accelerations | ||
|---|---|---|---|
| 0.1 g | 0.2 g | 0.4 g | |
| Orthogonal condition | 1.8 | −0.2 | −6.7 |
| Oblique condition | 5.9 | 14.2 | 20.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nian, Y.; Liu, X.; Guo, M.; Feng, Z.; Zeng, J.; Huang, H. Study on Seismic Response of Segmented Utility Tunnels Crossing Ground Fissures. Appl. Sci. 2025, 15, 8845. https://doi.org/10.3390/app15168845
Nian Y, Liu X, Guo M, Feng Z, Zeng J, Huang H. Study on Seismic Response of Segmented Utility Tunnels Crossing Ground Fissures. Applied Sciences. 2025; 15(16):8845. https://doi.org/10.3390/app15168845
Chicago/Turabian StyleNian, Youyou, Xiaoxiao Liu, Mengxue Guo, Zhibin Feng, Jie Zeng, and Hua Huang. 2025. "Study on Seismic Response of Segmented Utility Tunnels Crossing Ground Fissures" Applied Sciences 15, no. 16: 8845. https://doi.org/10.3390/app15168845
APA StyleNian, Y., Liu, X., Guo, M., Feng, Z., Zeng, J., & Huang, H. (2025). Study on Seismic Response of Segmented Utility Tunnels Crossing Ground Fissures. Applied Sciences, 15(16), 8845. https://doi.org/10.3390/app15168845








