Stress Development in Droplet Impact Analysis of Rain Erosion Damage on Wind Turbine Blades: A Review of Liquid-to-Solid Contact Conditions
Abstract
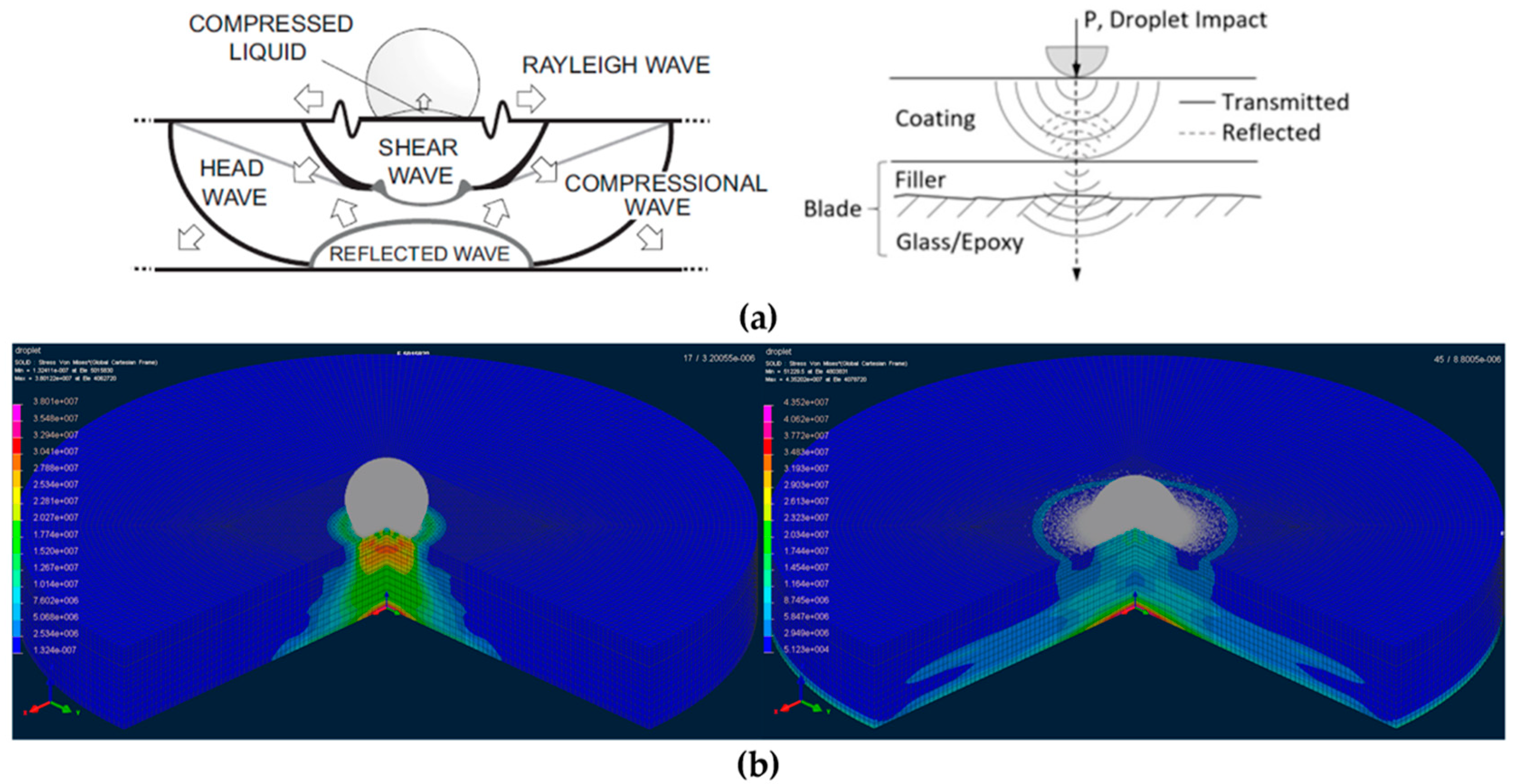
1. Introduction
2. Numerical Modelling Techniques
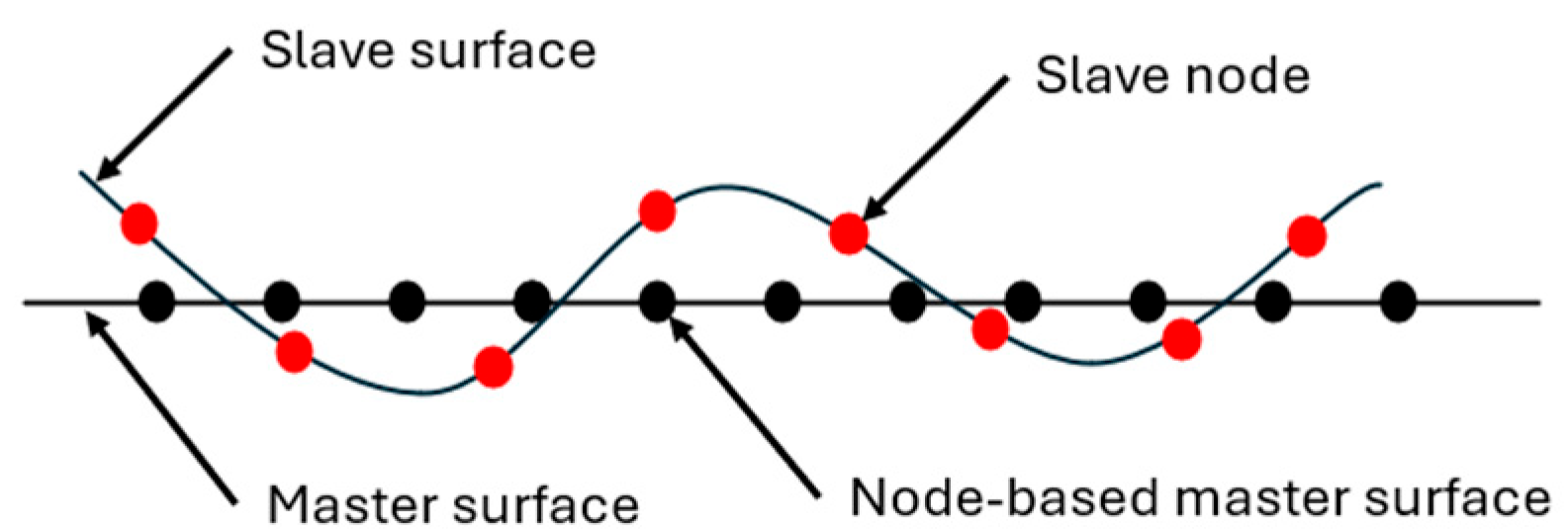
3. Contacts
4. Results and Discussion
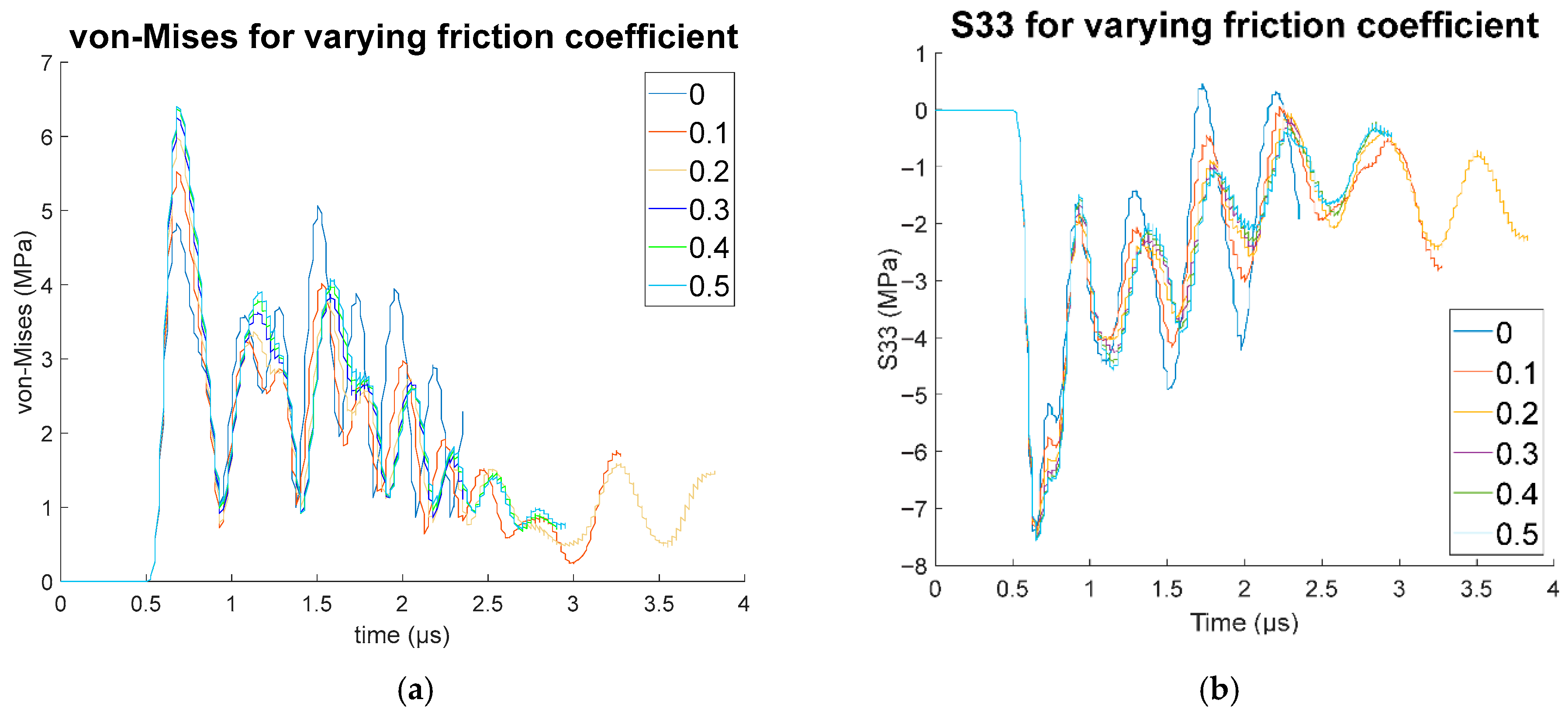
4.1. Effect of Friction
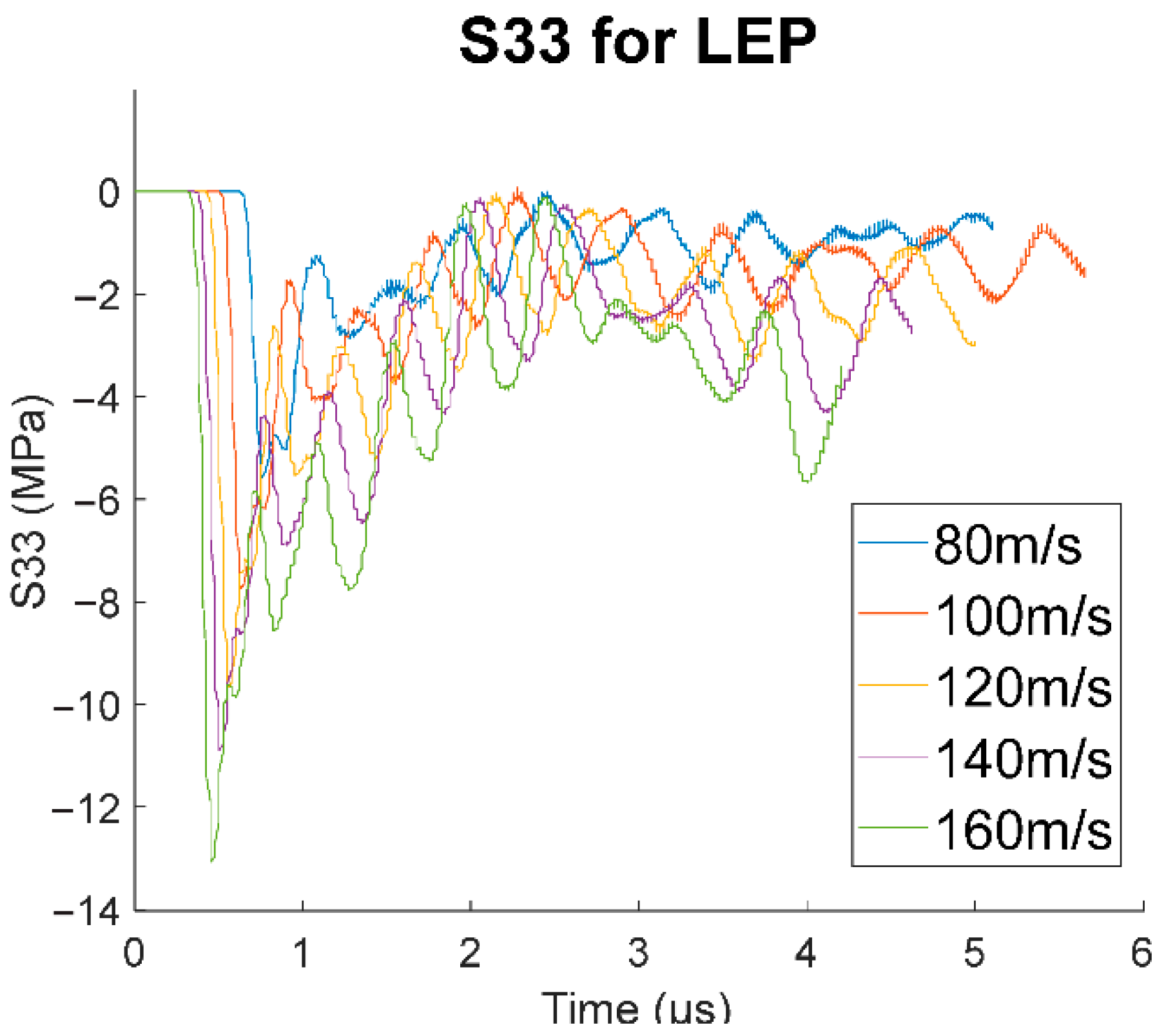
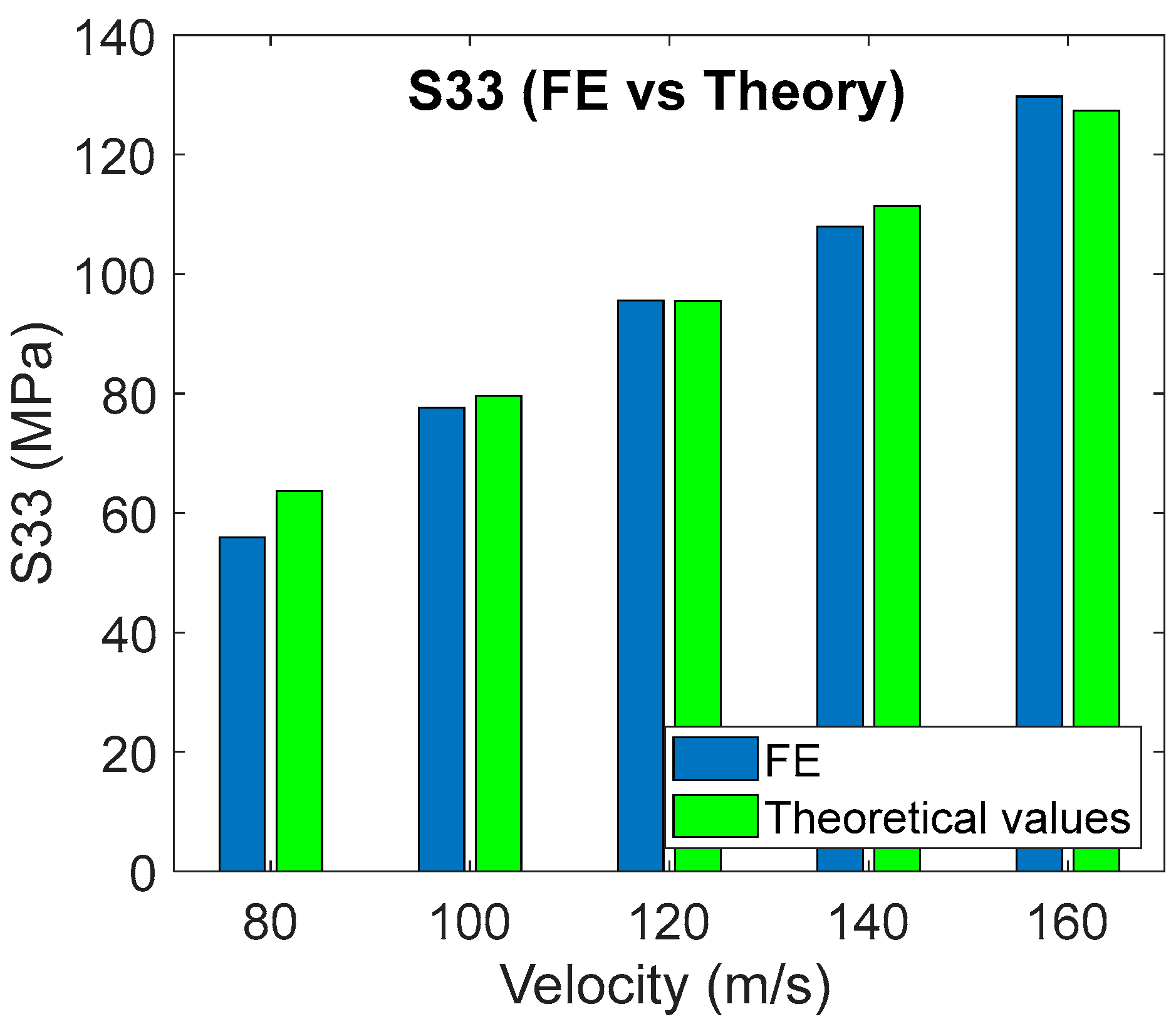
4.2. Effect of Impact Velocity
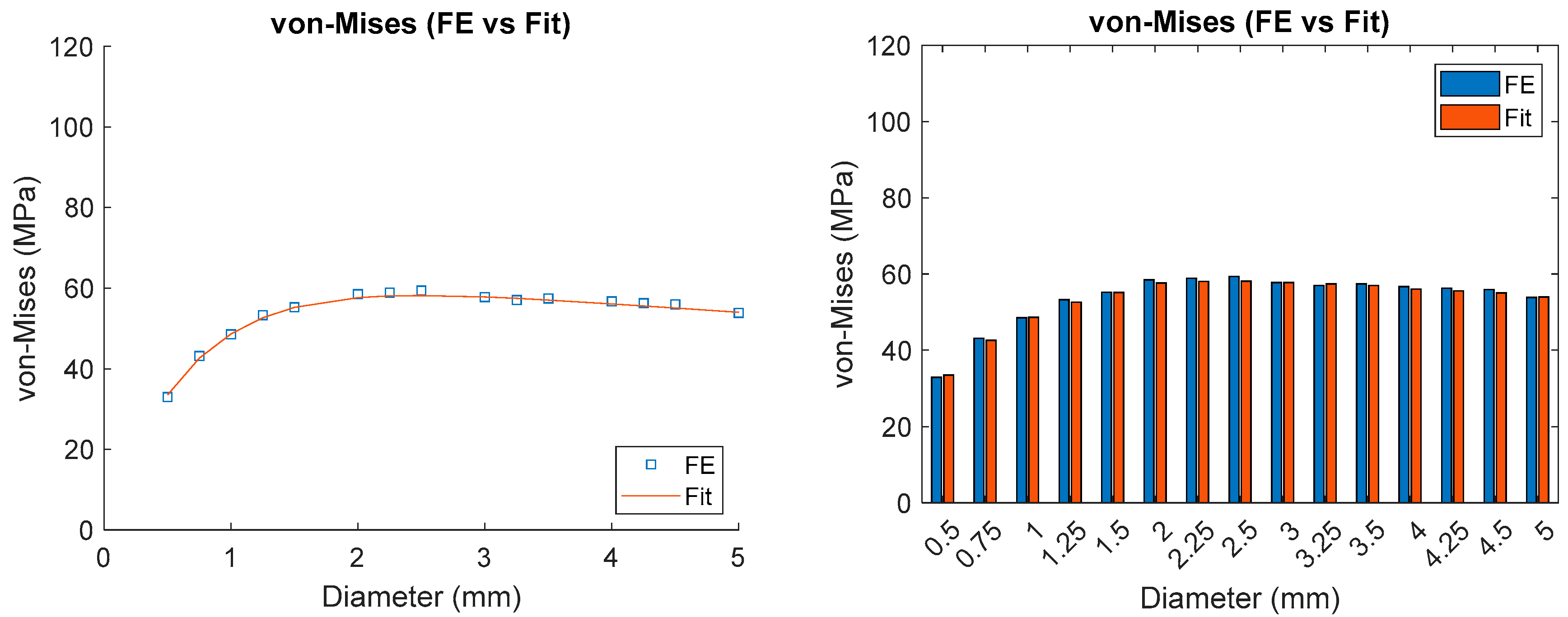
4.3. Effect of Droplet Diameter
4.4. Discussion on Simulation Results for Varying Droplet Diameter
- von Mises stress exponential relation:
- S33 exponential relation:
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Katsaprakakis, D.A.; Papadakis, N.; Ntintakis, I. A comprehensive analysis of wind turbine blade damage. Energies 2021, 14, 5974. [Google Scholar] [CrossRef]
- Mishnaevsky, L., Jr.; Tempelis, A.; Kuthe, N.; Mahajan, P. Recent developments in the protection of wind turbine blades against leading edge erosion: Materials solutions and predictive modelling. Renew. Energy 2023, 215, 118966. [Google Scholar] [CrossRef]
- Mishnaevsky, L., Jr.; Hasager, C.B.; Bak, C.; Tilg, A.M.; Bech, J.I.; Rad, S.D.; Fæster, S. Leading edge erosion of wind turbine blades: Understanding, prevention and protection. Renew. Energy 2021, 169, 953–969. [Google Scholar] [CrossRef]
- Wiser, R.; Bolinger, M.; Hoen, B.; Millstein, D.; Rand, J.; Barbose, G.; Darghouth, N.; Gorman, W.; Jeong, S.; O’Shaughnessy, E.; et al. Land-Based Wind Market Report: 2023 Edition; LBL Publications, U.S Department of Energy: Washington, DC, USA, 2023. [Google Scholar]
- Keegan, M.H.; Nash, D.H.; Stack, M.M. On erosion issues associated with the leading edge of wind turbine blades. J. Phys. D Appl. Phys. 2013, 46, 383001. [Google Scholar] [CrossRef]
- Wiser, R.; Jenni, K.; Seel, J.; Baker, E.; Hand, M.; Lantz, E.; Smith, A. Forecasting Wind Energy Costs and Cost Drivers: The Views of the World’s Leading Experts. 2016. Available online: https://escholarship.org/uc/item/0s43r9w4 (accessed on 15 July 2025).
- Sareen, A.; Sapre, C.A.; Selig, M.S. Effects of leading edge erosion on wind turbine blade performance. Wind. Energy 2014, 17, 1531–1542. [Google Scholar] [CrossRef]
- Elgendi, M.; AlMallahi, M.; Abdelkhalig, A.; Selim, Y. A review of wind turbines in complex terrain. Int. J. Thermofluids 2023, 17, 100289. [Google Scholar] [CrossRef]
- Gao, C.; Zhu, S.; An, N.; Na, H.; You, H.; Gao, C. Comprehensive comparison of multiple renewable power generation methods: A combination analysis of life cycle assessment and ecological footprint. Renew. Sustain. Energy Rev. 2021, 147, 111255. [Google Scholar] [CrossRef]
- Pugh, K.; Rasool, G.; Stack, M.M. Raindrop erosion of composite ma-terials: Some views on the effect of bending stress on erosion mechanisms. J. Bio-Tribo-Corros. 2019, 5, 1–12. [Google Scholar] [CrossRef]
- Slot, H.M.; Gelinck, E.R.M.; Rentrop, C.; Van Der Heide, E. Leading edge erosion of coated wind turbine blades: Review of coating life models. Renew. Energy 2015, 80, 837–848. [Google Scholar] [CrossRef]
- Bhong, M.; Khan, T.K.; Devade, K.; Krishna, B.V.; Sura, S.; Eftikhaar, H.K.; Thethi, H.P.; Gupta, N. Review of composite materials and applications. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Keegan, M.H. Wind Turbine Blade Leading Edge Erosion: An Investigation of Rain Droplet and Hailstone Impact Induced Damage Mechanisms. Ph.D. Thesis, University of Strathclyde, Glasgow, UK, 2014. [Google Scholar]
- Herring, R.; Dyer, K.; Martin, F.; Ward, C. The increasing importance of leading edge erosion and a review of existing protection solutions. Renew. Sustain. Energy Rev. 2019, 115, 109382. [Google Scholar] [CrossRef]
- Mishnaevsky, L., Jr. Repair of wind turbine blades: Review of methods and related computational mechanics prob-lems. Renew. Energy 2019, 140, 828–839. [Google Scholar] [CrossRef]
- Bech, J.I.; Hasager, C.B.; Bak, C. Extending the life of wind turbine blade leading edges by reducing the tip speed during extreme precipitation events. Wind. Energy Sci. 2018, 3, 729–748. [Google Scholar] [CrossRef]
- Ansari, Q.M.; Sánchez, F.; Doménech-Ballester, L.; Young, T.M. Evaluation of offshore wind turbine leading edge protection coating failure mode under rain erosion. Procedia Struct. Integr. 2024, 52, 122–132. [Google Scholar] [CrossRef]
- Brøndsted, P.; Lilholt, H.; Lystrup, A. Composite Materials for wind Turbine blades. Annu. Rev. Mater. Res. 2005, 35, 505–553. [Google Scholar] [CrossRef]
- Li, R.; Ninokata, H.; Mori, M. A numerical study of impact force caused by liquid droplet impingement onto a rigid wall. Prog. Nucl. Energy 2011, 53, 881–885. [Google Scholar] [CrossRef]
- Papi, F.; Balduzzi, F.; Ferrara, G.; Bianchini, A. Uncertainty quantification on the effects of rain-induced erosion on annual energy production and performance of a Multi-MW wind turbine. Renew. Energy 2021, 165, 701–715. [Google Scholar] [CrossRef]
- Langel, C.M.; Chow, R.C.; Van Dam, C.P.; Maniaci, D.C. RANS Based Methodology for Predicting the Influence of Leading Edge Erosion on Airfoil Performance (No. SAND-2017-11289); Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2017. [Google Scholar]
- Gohardani, O. Impact of erosion testing aspects on current and future flight conditions. Prog. Aerosp. Sci. 2011, 47, 280–303. [Google Scholar] [CrossRef]
- Domenech, L.; Renau, J.; Šakalytė, A.; Sánchez, F. Top coating anti-erosion performance analysis in wind turbine blades depending on relative acoustic impedance. Part 1: Modelling approach. Coatings 2020, 10, 685. [Google Scholar] [CrossRef]
- Keegan, M.H.; Nash, D.; Stack, M. Modelling rain drop impact on offshore wind turbine blades. In Proceedings of the TURBO EXPO 2012 GT2012, Copenhagen, Denmark, 11–15 June 2012. [Google Scholar]
- Nassiri, A.; Chini, G.; Vivek, A.; Daehn, G.; Kinsey, B. Arbitrary Lagrangian–Eulerian finite element simulation and experimental investigation of wavy interfacial morphology during high velocity impact welding. Mater. Des. 2015, 88, 345–358. [Google Scholar] [CrossRef]
- Macek, R.W.; Silling, S.A. Peridynamics via finite element analysis. Finite Elem. Anal. Des. 2007, 43, 1169–1178. [Google Scholar] [CrossRef]
- Bartolomé, L.; Teuwen, J. Prospective challenges in the experimentation of the rain erosion on the leading edge of wind turbine blades. Wind. Energy 2019, 22, 140–151. [Google Scholar] [CrossRef]
- Verma, A.S.; Castro, S.G.; Jiang, Z.; Teuwen, J.J. Numerical investigation of rain droplet impact on offshore wind turbine blades under different rainfall conditions: A parametric study. Compos. Struct. 2020, 241, 112096. [Google Scholar] [CrossRef]
- Elhadi Ibrahim, M.; Medraj, M. Water droplet erosion of wind turbine blades: Mechanics, testing, modeling and future perspectives. Materials 2019, 13, 157. [Google Scholar] [CrossRef] [PubMed]
- O’Carroll, A. Correlation of Mechanical Properties to Rain Erosion Resistance of Polymeric Materials. 2018. Available online: https://researchrepository.ul.ie/articles/thesis/Correlation_of_mechanical_properties_to_rain_erosion_resistance_of_polymeric_materials/19809898?file=35261017 (accessed on 22 May 2025).
- Mesh Tie Constraints. Available online: https://abaqus-docs.mit.edu/2017/English/SIMACAECSTRefMap/simacst-c-tiedconstraint.htm (accessed on 21 February 2025).
- ABAQUS, Inc. ABAQUS/Explicit: Advanced Topics. 2005. Available online: http://ftp.demec.ufpr.br/disciplinas/TM738/l7-connections.pdf (accessed on 27 July 2025).
- McHale, G.; Gao, N.; Wells, G.G.; Barrio-Zhang, H.; Ledesma-Aguilar, R. Friction coefficients for droplets on solids: The Liquid–Solid Amontons’ Laws. Langmuir 2022, 38, 4425–4433. [Google Scholar] [CrossRef]
- Doagou-Rad, S.; Mishnaevsky, L. Rain erosion of wind turbine blades: Computational analysis of parameters con-trolling the surface degradation. Meccanica 2020, 55, 725–743. [Google Scholar] [CrossRef]
- Bech, J.I.; Johansen, N.F.J.; Madsen, M.B.; Hannesdóttir, Á.; Hasager, C.B. Experimental study on the effect of drop size in rain erosion test and on lifetime prediction of wind turbine blades. Renew. Energy 2022, 197, 776–789. [Google Scholar] [CrossRef]
- Zhang, Y.; Pan, G.; Zhang, Y.; Haeri, S. A multi-physics peridynamics-DEM-IB-CLBM framework for the prediction of erosive impact of solid particles in viscous fluids. Comput. Methods Appl. Mech. Eng. 2019, 352, 675–690. [Google Scholar] [CrossRef]





| Layers | Properties | ||
|---|---|---|---|
| Density ρ (kg/m3) | Young’s Modulus E (GPa) | Poisson’s Ratio ν | |
| LEP (Gelcoat Epon E862 Epoxy) | 1150 | 2.5 | 0.4 |
| Filler | 1452.8 | 8 | 0.3 |
| Aluminium (Al) | 2820 | 70 | 0.3 |
| Properties GFRP | |
|---|---|
| Density ρ (kg/m3) | 1864 |
| Young’s modulus E11 (GPa) | 44.87 |
| Young’s modulus E22 (GPa) | 12.13 |
| Young’s modulus E33 (GPa) | 12.13 |
| Poisson’s ratio ν12 | 0.3 |
| Poisson’s ratio ν13 | 0.3 |
| Poisson’s ratio ν23 | 0.5 |
| Shear modulus G12 (GPa) | 3.38 |
| Shear modulus G13 (GPa) | 3.38 |
| Shear modulus G23 (GPa) | 3.38 |
| Friction Coefficient | WALL Time (s) |
|---|---|
| 0 | 509 |
| 0.1 | 452 |
| 0.2 | 437 |
| 0.3 | 411 |
| 0.4 | 412 |
| 0.5 | 416 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oddo, Q.L.; Ansari, Q.M.; Sánchez, F.; Mishnaevsky, L., Jr.; Young, T.M. Stress Development in Droplet Impact Analysis of Rain Erosion Damage on Wind Turbine Blades: A Review of Liquid-to-Solid Contact Conditions. Appl. Sci. 2025, 15, 8682. https://doi.org/10.3390/app15158682
Oddo QL, Ansari QM, Sánchez F, Mishnaevsky L Jr., Young TM. Stress Development in Droplet Impact Analysis of Rain Erosion Damage on Wind Turbine Blades: A Review of Liquid-to-Solid Contact Conditions. Applied Sciences. 2025; 15(15):8682. https://doi.org/10.3390/app15158682
Chicago/Turabian StyleOddo, Quentin Laplace, Quaiyum M. Ansari, Fernando Sánchez, Leon Mishnaevsky, Jr., and Trevor M. Young. 2025. "Stress Development in Droplet Impact Analysis of Rain Erosion Damage on Wind Turbine Blades: A Review of Liquid-to-Solid Contact Conditions" Applied Sciences 15, no. 15: 8682. https://doi.org/10.3390/app15158682
APA StyleOddo, Q. L., Ansari, Q. M., Sánchez, F., Mishnaevsky, L., Jr., & Young, T. M. (2025). Stress Development in Droplet Impact Analysis of Rain Erosion Damage on Wind Turbine Blades: A Review of Liquid-to-Solid Contact Conditions. Applied Sciences, 15(15), 8682. https://doi.org/10.3390/app15158682








