Dehazing Algorithm Based on Joint Polarimetric Transmittance Estimation via Multi-Scale Segmentation and Fusion
Abstract
1. Introduction
2. Correlation Theory
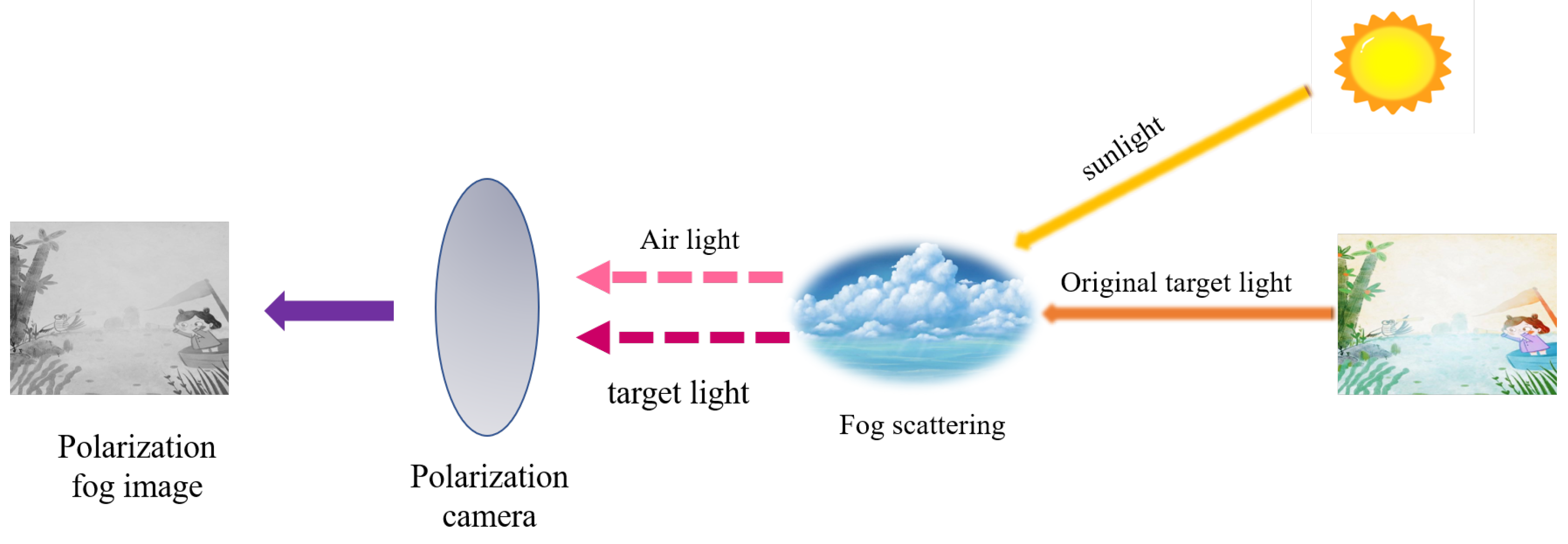
2.1. Atmospherical Scattering Model
- Attenuated target radiance: Light reflected from the target that is weakened through scattering and absorption by suspended particles in the atmosphere.
- Atmospheric light: Ambient light scattered by fog droplets, which dominates under dense haze conditions.
2.2. Stokes Vector
2.3. Transmittance Estimation
3. Experiment and Results
3.1. Data Preprocessing
- Demultiplexing the raw images into distinct polarization-direction components via the polarization unit array.
- Calculating light intensity values and DoP using Equation (5).
3.2. Determine the Atmospheric Light Intensity Value at Infinity
3.3. Boundary Constraints Based on Non Sky Region Light Intensity Values
3.4. Calculate Transmittance
3.5. Calculate Target Light
4. Result Analysis
5. Conclusions and Prospect
- This method depends on selecting sky regions to estimate the atmospheric polarization degree () and atmospheric light intensity at infinity (). For sky-free images, we are forced to rely on empirical priors for estimation, which may introduce significant estimation errors in specific scenarios.
- This approach heavily relies on the accuracy of image segmentation and fusion. In certain scenarios, visibly unnatural boundaries may emerge during segmentation and fusion, or inaccurate region classification may occur, leading to distorted boundaries. Future enhancements may involve employing semantic segmentation and salient object detection methodologies to further improve segmentation diversity and accuracy, thereby strengthening the algorithm’s robustness.
- There is still room for optimization in determining the boundary values of the target light in this article in order to make the estimation of transmittance more accurate and the dehazing effect better.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ancuti, C.O.; Ancuti, C.; Timofte, R.; Vleeschouwer, C.D. I-HAZE: A dehazing benchmark with real hazy and haze-free indoor images. arXiv 2018, arXiv:1804.05091. [Google Scholar] [CrossRef]
- Singh, D.; Chahar, V. A Comprehensive Review of Computational Dehazing Techniques. Arch. Comput. Methods Eng. 2018, 26, 1395–1413. [Google Scholar] [CrossRef]
- Yeh, C.H.; Kang, L.W.; Lee, M.S.; Lin, C.Y. Haze effect removal from image via haze density estimation in optical model. Opt. Express 2013, 21, 27127–27141. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Wang, X.; Chen, M.; Liu, S.; Zhou, X.; Shao, Z.; Liu, P. Thin cloud removal from single satellite images. Opt. Express 2014, 22, 618–632. [Google Scholar] [CrossRef]
- He, K.; Sun, J.; Tang, X. Single Image Haze Removal Using Dark Channel Prior. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 2341–2353. [Google Scholar] [CrossRef]
- Lee, S.; Yun, S.; Nam, J.H.; Won, C.; Jung, S.W. A review on dark channel prior based image dehazing algorithms. EURASIP J. Image Video Process. 2016, 2016, 4. [Google Scholar] [CrossRef]
- Li, Z.X.; Wang, Y.L.; Peng, C.; Peng, Y. Laplace dark channel attenuation-based single image defogging in ocean scenes. Multim. Tools Appl. 2023, 82, 21535–21559. [Google Scholar] [CrossRef]
- Wang, S.; Yang, T.; Sun, W.; Lu, X.; Fan, D. Adaptive Bright and Dark Channel Combined with Defogging Algorithm Based on Depth of Field. J. Sens. 2022, 2022. [Google Scholar] [CrossRef]
- Fang, Z.; Wu, Q.; Huang, D.; Guan, D. An Improved DCP-Based Image Defogging Algorithm Combined with Adaptive Fusion Strategy. Math. Probl. Eng. 2021, 2021. [Google Scholar] [CrossRef]
- Ancuti, C.; Ancuti, C.O.; Haber, T.; Bekaert, P. Enhancing underwater images and videos by fusion. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 81–88. [Google Scholar] [CrossRef]
- Chen, T.; Liu, M.; Gao, T.; Cheng, P.; Mei, S.; Li, Y. A Fusion-Based Defogging Algorithm. Remote Sens. 2022, 14, 425. [Google Scholar] [CrossRef]
- He, S.; Chen, Z.; Wang, F.; Wang, M. Integrated image defogging network based on improved atmospheric scattering model and attention feature fusion. Earth Sci. Inform. 2021, 14, 2037–2048. [Google Scholar] [CrossRef]
- Cai, B.; Xu, X.; Jia, K.; Qing, C.; Tao, D. DehazeNet: An End-to-End System for Single Image Haze Removal. IEEE Trans. Image Process. 2016, 25, 5187–5198. [Google Scholar] [CrossRef]
- Zhang, H.; Patel, V.M. Densely Connected Pyramid Dehazing Network. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3194–3203. [Google Scholar] [CrossRef]
- Kumar, R.; Kaushik, B.K.; Raman, B.; Sharma, G. A Hybrid Dehazing Method and its Hardware Implementation for Image Sensors. IEEE Sens. J. 2021, 21, 25931–25940. [Google Scholar] [CrossRef]
- Li, Z.X.; Wang, Y.L.; Peng, C. MIDNet: A Weakly Supervised Multipath Interaction Network for Image Defogging. In Proceedings of the 2024 36TH Chinese Control and Decision Conference, CCDC, Xi’an, China, 25–27 May 2024. [Google Scholar] [CrossRef]
- Song, Y.; Zhao, J.; Shang, C. A multi-stage feature fusion defogging network based on the attention mechanism. J. Supercomput. 2024, 80, 4577–4599. [Google Scholar] [CrossRef]
- Ma, T.; Zhou, J.; Zhang, L.; Fan, C.; Sun, B.; Xue, R. Image Dehazing With Polarization Boundary Constraints of Transmission. IEEE Sens. J. 2024, 24, 12971–12984. [Google Scholar] [CrossRef]
- Liu, S.; Li, H.; Zhao, J.; Liu, J.; Zhu, Y.; Zhang, Z. Atmospheric Light Estimation Using Polarization Degree Gradient for Image Dehazing. Sensors 2024, 24, 3137. [Google Scholar] [CrossRef] [PubMed]
- Ma, R.; Zhang, Z.; Zhang, S.; Wang, Z.; Liu, S. A Polarization-Based Method for Maritime Image Dehazing. Appl. Sci. 2024, 14, 4234. [Google Scholar] [CrossRef]
- Schechner, Y.; Narasimhan, S.; Nayar, S. Instant dehazing of images using polarization. In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. CVPR 2001, Kauai, HI, USA, 8–14 December 2001; Volume 1, pp. I–I. [Google Scholar] [CrossRef]
- Liang, J.; Ren, L.; Ju, H.; Qu, E.; Wang, Y. Visibility enhancement of hazy images based on a universal polarimetric imaging method. J. Appl. Phys. 2014, 116, 173107. [Google Scholar] [CrossRef]
- Liang, J.; Ren, L.; Qu, E.; Hu, B.; Wang, Y. Method for enhancing visibility of hazy images based on polarimetric imaging. Photon. Res. 2014, 2, 38–44. [Google Scholar] [CrossRef]
- Liang, J.; Ren, L.; Ju, H.; Qu, E. Polarimetric dehazing method for dense haze removal based on distribution analysis of angle of polarization. Opt. Express 2015, 23, 26146–26157. [Google Scholar] [CrossRef] [PubMed]
- Liang, J.; Zhang, W.; Ren, L.; Ju, H.; Qu, E. Polarimetric dehazing method for visibility improvement based on visible and infrared image fusion. Appl. Opt. 2016, 55, 8221–8226. [Google Scholar] [CrossRef]
- Teurnier, B.L.; Tullio, A.; Boffety, M. Enhancing the robustness of underwater dehazing by jointly using polarization and the dark channel prior. Appl. Opt. 2025, 64, 5195–5205. [Google Scholar] [CrossRef]
- Fang, S.; Xia, X.; Huo, X.; Chen, C. Image dehazing using polarization effects of objects and airlight. Opt. Express 2014, 22, 19523–19537. [Google Scholar] [CrossRef]
- Sun, C.; Ding, Z.; Ma, L. Optimized method for polarization-based image dehazing. Heliyon 2023, 9, e15849. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.; Bae, J.; Kim, J. Natural hdr image tone mapping based on retinex. IEEE Trans. Consum. Electron. 2011, 57, 1807–1814. [Google Scholar] [CrossRef]
- McCartney, E.J. Optics of the Atmosphere: Scattering by Molecules and Particles; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1976. [Google Scholar]
- Di Zenzo, S. A note on the gradient of a multi-image. Comput. Vision Graph. Image Process. 1986, 33, 116–125. [Google Scholar] [CrossRef]
- Chang, D.C.; Wu, W.R. Image contrast enhancement based on a histogram transformation of local standard deviation. IEEE Trans. Med. Imaging 1998, 17, 518–531. [Google Scholar] [CrossRef]
- Horé, A.; Ziou, D. Image Quality Metrics: PSNR vs. SSIM. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 2366–2369. [Google Scholar] [CrossRef]






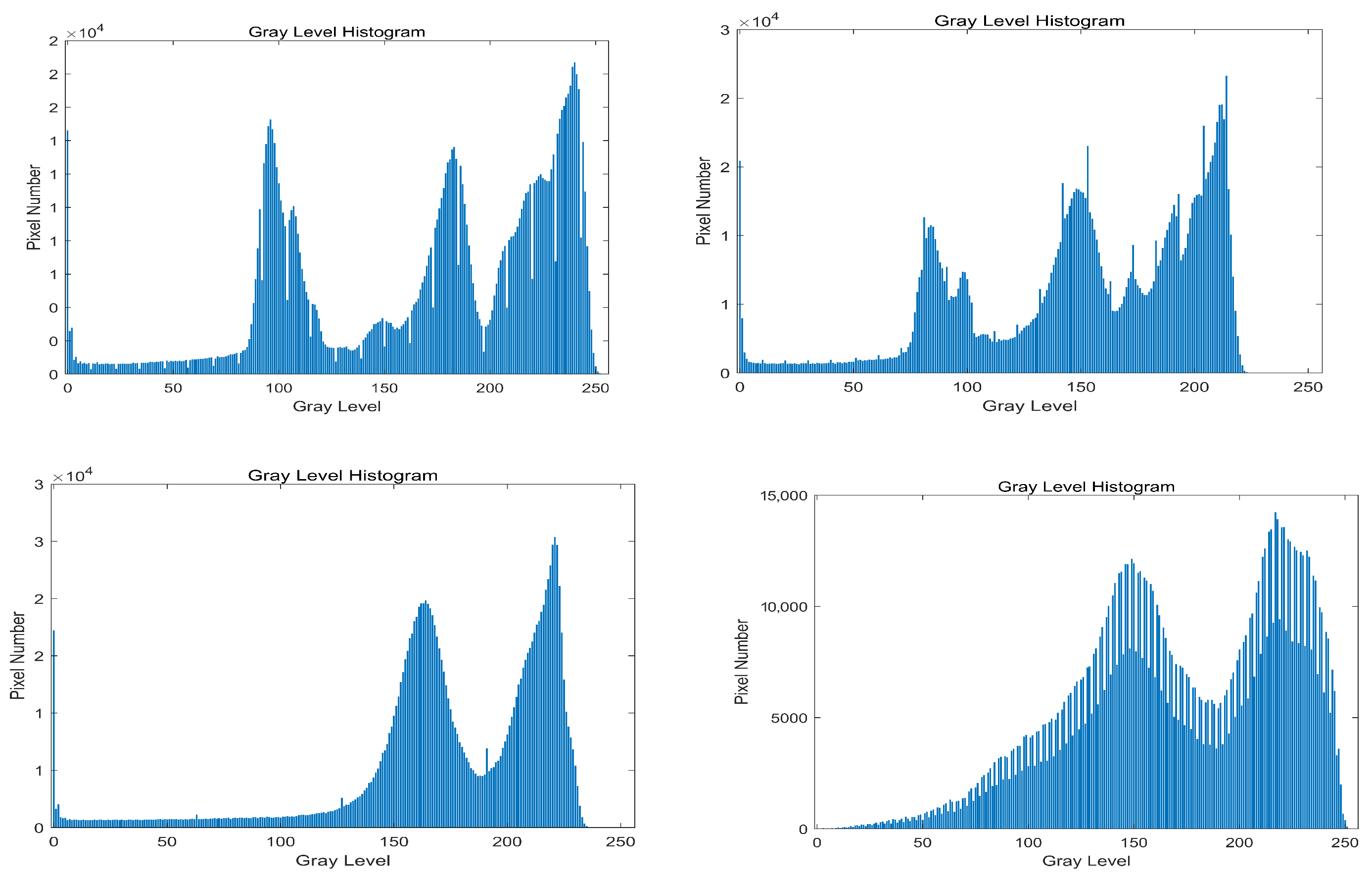
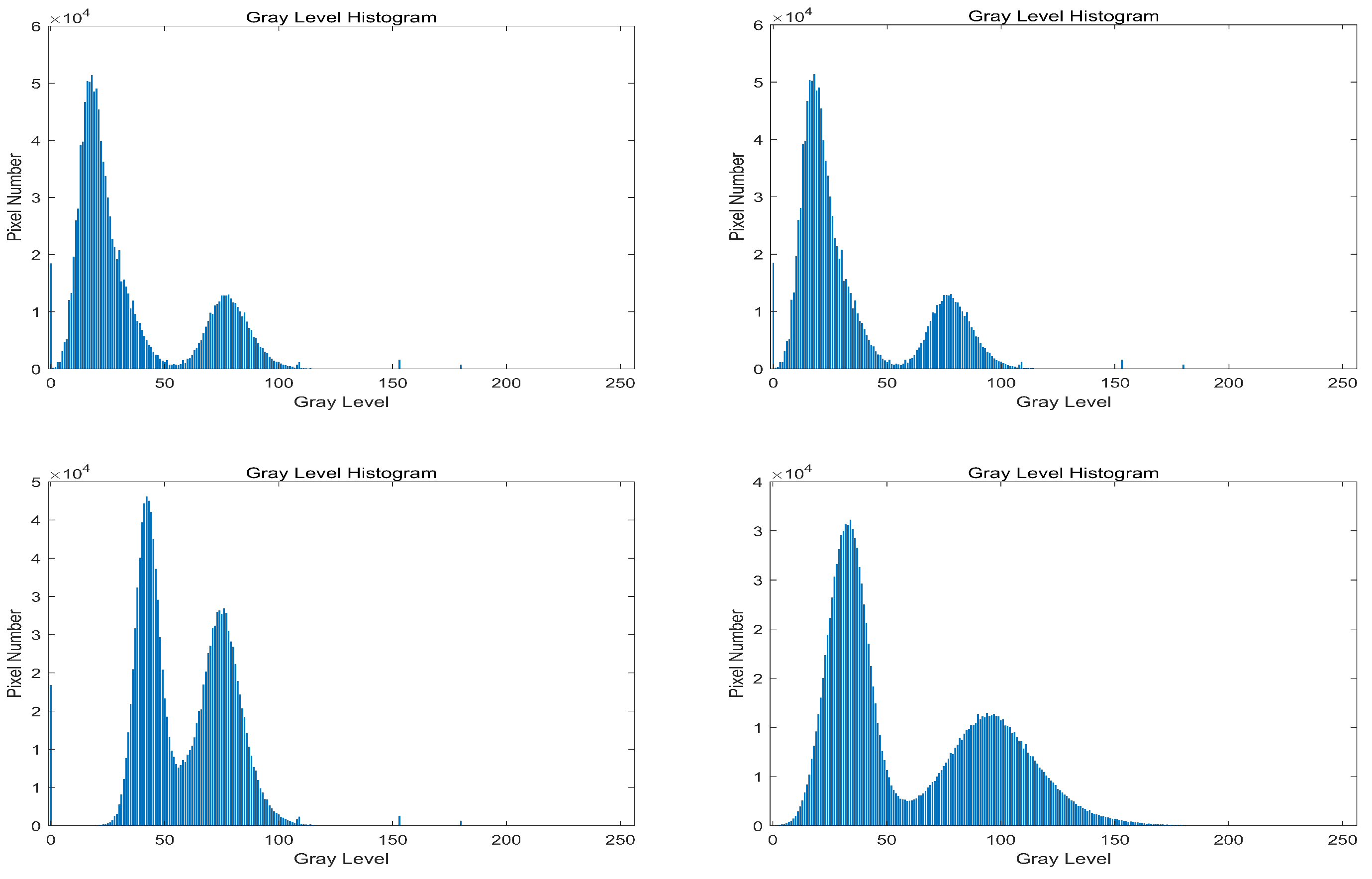







| Algorithm | Information Entropy | Average Gradient | Standard Deviation | SSMI | |
|---|---|---|---|---|---|
| Scenario 1 | Equalization | 7.0618 | 21.0541 | 74.7433 | 0.7938 |
| Tradional | 6.0503 | 22.6988 | 57.5973 | 0.2491 | |
| Ours | 7.2803 | 23.8238 | 37.6737 | 0.7959 | |
| Scenario 2 | Equalization | 7.0639 | 23.7906 | 74.8634 | 0.8125 |
| Tradional | 6.5632 | 18.6107 | 58.9985 | 0.4558 | |
| Ours | 6.8527 | 16.3776 | 18.7265 | 0.8884 | |
| Scenario 3 | Equalization | 6.6994 | 37.9909 | 75.0269 | 0.6617 |
| Tradional | 6.2549 | 24.9865 | 66.4276 | 0.4091 | |
| Ours | 7.0238 | 29.5858 | 28.8814 | 0.813691 | |
| Scenario 4 | Equalization | 7.2683 | 26.6495 | 73.8097 | 0.7970 |
| Tradional | 6.2721 | 18.7083 | 57.7610 | 0.6676 | |
| Ours | 6.7742 | 21.8333 | 12.0983 | 0.9191 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Zhang, Z.; Cao, X. Dehazing Algorithm Based on Joint Polarimetric Transmittance Estimation via Multi-Scale Segmentation and Fusion. Appl. Sci. 2025, 15, 8632. https://doi.org/10.3390/app15158632
Wang Z, Zhang Z, Cao X. Dehazing Algorithm Based on Joint Polarimetric Transmittance Estimation via Multi-Scale Segmentation and Fusion. Applied Sciences. 2025; 15(15):8632. https://doi.org/10.3390/app15158632
Chicago/Turabian StyleWang, Zhen, Zhenduo Zhang, and Xueying Cao. 2025. "Dehazing Algorithm Based on Joint Polarimetric Transmittance Estimation via Multi-Scale Segmentation and Fusion" Applied Sciences 15, no. 15: 8632. https://doi.org/10.3390/app15158632
APA StyleWang, Z., Zhang, Z., & Cao, X. (2025). Dehazing Algorithm Based on Joint Polarimetric Transmittance Estimation via Multi-Scale Segmentation and Fusion. Applied Sciences, 15(15), 8632. https://doi.org/10.3390/app15158632






