A Contribution of Shortest Paths Algorithms to the NetworkX Python Library

Abstract

NetworkX is a free Python library for graphs and networks and is used in many applications and projects to find the shortest path in path planning scenarios. For dense graphs, the library provides the Floyd–Warshall algorithm for shortest paths and the A* (“A-Star”) algorithm for shortest paths and path lengths. However, several extensions have been proposed to improve the A*, but they are not included in the library. In this context, this paper presents a set of implementations improving the A*, such as the IDA*, D* Lite, SMA*, Bidirectional A* and RTA*. The goal or challenge is to address the limitations of the A* in specific scenarios, such as searching for an optimal path repeatedly or when confronted with memory limitations, as exemplified by the NetworkX library. To do this, we first review the literature of the usage and general application of NetworkX in different domains of applicability and then explore their usage in a shortest path context. By reviewing and validating the usage of A* and extensions in Python using the NetworkX framework, the implementations were submitted to the network environment validation and passed the tests. We have also done the benchmarking of the A*, comparing it with the new ones, and concluded the better efficiency of the A* extensions in tri-objective scenario parameters (length, cost and toll). Despite the extensive utilisation of A* and its notable efficacy in identifying optimal paths, its performance is suboptimal in specific scenarios, such as when confronted with memory constraints and dynamic environments. Almost every algorithm outperformed or matched the A* in the fields that were developed to have an advantage, demonstrating the quality and robustness of the implemented algorithms. As a contribution and to foster further research in this shortest path specific context field, the dataset and Python code of the algorithms are available in a GitHub opensource repository.

1. Introduction

Shortest path problems have been studied in the last few decades to compute the shortest path in graph theory scenarios [1,2,3,4,5,6,7]. However, this topic continues to be applied and actively researched in recent years [8,9], especially in the context of graph theory [10] and graph visualization [11,12,13]. In parallel, several tools have been presented and studied to compute the shortest path in the graph theory as well as to analyse and visualize the networks, in particular using free or opensource tools [14,15].

NetworkX Library (NetworkX Library: https://networkx.org (accessed on 15 April 2025)) is a Python library that provides a handle for the creation and manipulation of graphs and networks. It is written in Python 3.11, and its source code is opensource. It was created by Aric Hagberg, Dan Schult and Pieter Swart [16], and over time with the contribution of other software developers. Being supported by some research centres, the first release version was published on 8 January 2020, and the current release version is the 3.4.2 published on 21 October 2024. For graph visualizations, many free and opensource tools have been studied [12,13,17], with NetworkX as one of the most promising options. It provides tools, a programming interface and a development environment for the creation, manipulation and study of the structure, dynamics and functions of complex networks, such as data structures for graphs, digraphs, multigraphs and standard graph algorithms, as well as network structures and analysis measures for complex network problems or representations. The library has been successfully used in many works and projects for graph or network visualization and analysis purposes, such as those presented in [17,18,19,20].

Actually, the NetworkX library includes algorithms to compute the shortest paths and path lengths between nodes in a graph as undirected and directed graphs. It includes the basic algorithm to compute shortest paths in a graph and shortest path algorithms for weighted and unweighted graphs, as well as for dense graphs [21]. The first set is oriented to compute all the shortest simple paths in the graph and the advanced set is centred on computing the shortest path lengths from a source to all reachable nodes for unweighted graphs. For the weighted graphs, it provides the implementation of the Dijkstra algorithm [22,23], Bellman-Ford path [24,25] and Jonhson path [26]. For dense graphs, the library provides the Floyd–Warshall algorithm [27,28] for shortest paths and the A* (“A star”) algorithm [29] for shortest paths and path lengths. Besides the potentiality of the library in other domains and the code availability for different graph types and methods or algorithms, it presents a limitation of extensions or improvements of the A* (Hart et al. 1968) [29], such as the Bidirectional A* [30], IDA* [31], SMA* [32], Dynamic A* [33], D* Lite [34] and RTAA* [35], among others.

The objective of this work is centred on the lack of algorithm diversity in the field of shortest path and path finding available within the NetworkX platform. The goal or challenge is to address the limitations of the A* in specific scenarios, such as searching for an optimal path repeatedly or when confronted with memory limitations, as exemplified by the library. In this sense, using the NetworkX code framework, we implemented D* Lite, Bidirectional A*, IDA*, SMA* and RTAA*, which have been submitted to network environment validation and passed the tests. We tested using a general graph scenario with tri-objective scenario parameters (length, cost and toll) to find a shortest path between an origin and a destination. We have performed the benchmarking of the A*, comparing it with the new ones, and compared their performance in terms of cost of the path found, search time, memory used and recalculation time for dynamic algorithms. To foster further research the dataset and the code of the algorithms are available on the GitHub 2.48.1 at: https://github.com/migcruzz/Testing_NetworkX_Algorithms.git (accessed on 3 June 2025) opensource repository.

The document is structured as follows. Section 2 presents the literature review on NetworkX usage. Section 3 presents the foundations of the implemented algorithms, and Section 4 presents the experimental results and discussion. Finally, Section 5 presents the conclusions and future work, followed by the references that supported this work.

2. Literature Review

Based on free and opensource tools, several tools have been presented over the last few decades for graph visualization as well as for representing scenarios of shortest path problems. With promising results, the NetworkX library, created by Aric Hagberg, Dan Schult and Pieter Swart [16], has been explored and improved, especially for network analysis and visualization, as well as for shortest path problems using classic algorithms, as compiled and published in research papers and in published books [34,35,36].

Analysing the literature review of the usage and exploration of NetworkX, the main use is centred on network analysis, such as the works of Abdelhamid et al. (2012) [37], Pacer (2015) [38], Gharibi et al. (2018) [39], Yan et al. (2019) [40], Boeing, G. (2020) [17], Bontonou et al. (2021) [18], Gao et al. (2022) [19] and Uribe et al. (2023) [20].

However, besides the main usage and exploration in graph and network analysis as well as in visualization, NetworkX has also been applied and explored in shortest path problems, particularly in both undirected and directed graphs with weighted and unweighted constraints between nodes in the graphs, as well as in scenarios involving dense graphs.

In the context of path search, path planning or route planning, there are several well-known algorithms. Dijkstra’s algorithm [22,41] is a method used to find the shortest path from one node to another in a graph that only has positive weights. In 1968, Hart et al. (1968) [29] presented a study that, with a formal basis for the heuristic determination of minimum cost paths, introduced the A* algorithm. The main difference between Dijkstra’s algorithm and A* is the use of a heuristic estimate function. This function estimates, for any node, the remaining distance to the destination. Dijkstra may be regarded as an instance of A* where the heuristic estimate function is identically zero (function ≡ 0) [30]. However, as A* has shown limitations when applied to more complex problems, improved variants have emerged to achieve faster registration results and increase efficiency.

Consequently, several studies and extensions have been presented [21,31,32,41,42,43,44], particularly in terms of performance time and memory usage.

Korf (1985) [31] and Partha (1989) [45] are two examples of those who started the research of analysing the memory constraints in heuristic search. Iterative Deepening A-Star (IDA*) was presented by Korf in 1985 and addresses the memory problem by combining depth first search with incrementally increasing f-cost limits and allowing for an optimal search without the need to maintain every node in the memory. Other studies have followed this limitation. Simplified Memory-bounded A* (SMA*) [32,46] is a shortest path algorithm that is based on the A* algorithm. The difference between SMA* and A* is that SMA* uses a bounded memory, while A* might need exponential memory. Dynamic A* (D*) [33,34] tries to deal with dynamic obstacles by updating edge weights in real time. D* maintains a list of nodes used to propagate information about changes of the cost function during the search of the path. D* Lite [33] implements the same behaviour of D* using an incremental heuristic search algorithm, i.e., it incrementally repairs solution paths when changes occur, promoting fast replanning. Anytime Repairing A* (ARA*) [47,48], by using a flexible time cost, returns a valid solution to a search path problem, even if it is interrupted before it ends, generating a non-optimal solution before progressively optimizing the solution for the search problem. Lifelong Planning A* (LPA*) [49,50] adapts the search process to changes in the graph without the need for recomputation. It updates the distance-from-start estimates calculated in the previous search during the current search, correcting only those that have become inconsistent in order to maintain shortest-path optimality. LPA* is able to reduce the number of nodes that need to be analysed by reusing information from previous calculations.

Bidirectional A* [51,52,53] runs two simultaneous heuristics searches: one forward from the initial state to a node n (goal), and one backward from the goal to the start, stopping when the two meet. Learning Real-time A* (LRTA*) [35,54] produces feasible paths any time during its execution and minimum length paths if run to completion. Real-time Adaptive A* (RTAA*) [55,56] executes the behaviour of A* with limited lookahead, defining a trade-off between optimality and computational cost.

Several studies have applied A* in different scenarios. Zeng & Church (2009) [57] explored A* in a scenario of real road networks. Rodríguez Puentes and Lazo-Cortés (2013) [58] explored shortest path finding problem(s), applying a proposed algorithm alongside Dijkstra’s and A* in a Geographic Information System scenario. Zhaoxing, (2019) [59] introduced a hybrid approach, A-Star+IDA*, as a simple hybrid search algorithm. Cadieux et al. (2020) [60] presented a Python algorithm for shortest-path in the context of river networks, exploring the multiple single-source weighted Dijkstra shortest path calculations. Tao et al. (2020) [61], using the Dijkstra algorithm, presented a study by finding minimum-weight link-disjoint paths with a few common nodes by building an integer linear programming model and designing a fast algorithm by using the techniques of augmenting paths and splitting nodes. Foead et al. (2021) [42] presented a systematic review of the A* algorithm and proposed the HPA-star algorithm, an extension to the A* with a faster runtime at the cost of not always finding the optimal path. Junshu (2021) [62] explored Dynamic A* to enhance dynamic path planning for unmanned vehicles used in epidemic prevention and disinfection tasks. Pardede et al. (2022) [43] presented a similar review but applied the A* and Dijkstra in game development. They also presented the Theta* algorithm, an extension of A*, to game development, designed for any-angle pathfinding, which allows direct line-of-sight between nodes, producing smoother, more realistic paths instead of restricting movement to the grid’s edges in a matrix representation. Anbaroğlu et al. (2022) [63], using a computationally reproducible approach to Dijkstra’s shortest path algorithm, developed an online education material to enable a researcher or analyst to understand how Dijkstra’s algorithm works. Lee at al. (2023) [64] explored LRTA* in the context of real-time path planning for controllable UAVs by employing subgoals through goal-conditioned reinforcement learning. Silva et al. (2023) [65] presented an application study to promote inclusive mobility through a multi-objective approach in a real city scenario involving bi-objective and tri-objective optimization. Schichler (2024) [66] proposed a cost-effective approach to smooth A* path planning for autonomous vehicles.

Haeupler et al. (2024) [67] explored Dijkstra and GyeongTaek et al. (2023) [68] explored LRTA* in the context of real-time path planning for controllable UAVs by employing subgoals through goal-conditioned reinforcement learning using an internal data structure to demonstrate that their proposal guarantees universal optimality for the problem of ordering vertices by distance from the source vertex. Muthuvel et al. (2025) [44] explored Q-learning algorithms in combination with the Dijkstra and A* algorithms. The hybrid approach can manage complex scenarios and guarantee optimal performance, even in a range of conditions in a road network scenario accounting for variables such as road conditions, length-to-width ratio and traffic conditions.

Another relevant point identified during the literature review is the availability of some algorithm’s implementations in open-source repositories such as GitHub. In our research, we identified the following repositories and Python implementations of A* extensions for path planning using a representation as graphs, namely, REP 1 [68], with implementations of several A* algorithm extensions, and the pgrouting.org project also provides some implementations of A* and Bidirectional A*. Another project is pymoo.org [69], which focuses on Multi-objective Optimization in Python.

3. Foundations

The Shortest Path Problem (SPP) consists of determining a path between a beginning (source) location and an end (target) location, such that the distance is minimum compared to alternatives. These alternatives are represented by a graph with several paths to be evaluated, which represents a computational challenge. In the following sections, we will briefly describe the algorithms used in this work, along with their corresponding pseudocode and some improvements in terms of research.

3.1. A-Star

The A* or “A-Star” (Hart, 1968) [29], a variant of the Dijkstra (Dijkstra, 1959) [22], is a well know algorithm [32,42,43]. It evaluates nodes by combining g(n), the cost reach node (or actual cost), and h(n), the cost to get from that node to the goal (or estimated cost), given by the formula f(n) = g(n)+ h(n), where f(n) represents the estimated total cost of the cheapest solution path passing through node n. Since g(n) gives the path cost from the start node to node n, and h(n) is the estimated cost of the cheapest path from n to the goal, f(n) estimates the cost of the cheapest solution through n. Thus, as the objective is to try to find the cheapest solution, a reasonable thing to try first is the node with the lowest value of g(n) + h(n). It turns out that this strategy is more than just reasonable. Provided that the heuristic function h(n) satisfies certain conditions, A* search is both complete and optimal. The algorithm is identical to uniform cost search, except that A* uses g(n) + h(n) instead of g(n).

The A* algorithm combines the strengths of two other algorithms: Dijkstra’s algorithm, tries to find the shortest path to all nodes from a single source node, and the greedy best-first search, and explores the node that appears to be closest to the goal, based on a heuristic function. The general A* process can be described by the following Algorithm 1:

Algorithm 1. A* algorithm pseudocode [29,44].

As we described in the literature review section, several studies have explored A* and have evidenced some limitations. For example, although the A* algorithm may find a path much quicker than uninformed search, it does not ensure that the result will be the shortest path [42]. Given the challenge in the definition of the heuristic function of the A* algorithm, many heuristic functions have been studied [70] and developed. One of the common heuristic functions in pathfinding is heuristic distance, such as diagonal distance, Manhattan distance and others [42]. Other studies [21,31,32,33,43,44,51,71] have extended the A* formalism with other heuristics and methods.

3.2. Iterative-Deepening-A* (IDA*)

In order to reduce the memory requirements of the A* algorithm, Korf (1985) [31] presented Iterative-Deepening-A* (IDA*), observing that A* stores all the nodes it generates in the open or closed lists, and hence is severely space-limited in practice. In contrast, IDA* requires space that is only linear in the maximum search depth, and it is often faster than A* because it incurs less overhead per node. IDA* combines features of iterative deepening depth-first search and is also referred to as a memory-efficient version of A*, as it requires significantly less memory while still ensuring optimal pathfinding. In this sense, by following a depth-first search, IDA* does not store most previously generated nodes. The main overhead of IDA* is not the initial iterations but rather from re-expansions during the same iteration of the same states via different paths, called duplicate nodes, in graphs with cycles. In other words, the main difference between IDA* and standard iterative deepening is that the cutoff used is the f-cost (g + h) rather than the depth. At each iteration, the cutoff value is the smallest f-cost of any node that exceeded the cutoff on the previous iteration [32]. The IDA* uses a heuristic function called F-score, which is used to estimate the cost of reaching the goal state from a given state, which is a combination of two other heuristic functions, g(n) and h(n). It is used to determine the order in which the algorithm expands nodes in the search tree, and thus it plays an important role in how quickly the algorithm finds a solution. A lower F-score indicates that a node is closer to the goal state and will be expanded before a node with a higher F-score. The general process of the IDA* can be described as follows in Algorithm 2:

Algorithm 2. IDA* algorithm pseudocode [31].

IDA* was the first widely used optimal, memory-bounded heuristic search algorithm, and many variants have since been developed. Manzini, G. (1995) [72] explored the Bidirectional perimeter search algorithm, known as BIDA*. Zhaoxing and Korf. (2019) [59] presented a simple hybrid search algorithm with the combination of A* and IDA*. The main goal is to run A* until memory is almost exhausted, then execute IDA* starting from the frontier nodes, which are the nodes open at the end of the A* phase.

Regarding this algorithm, it is important to mention that the original version of the implementation is presented in a recursive form. However, the same algorithm can be implemented with the same characteristics and functionalities in a non-recursive form. In this project, we started by following the recursive approach using the Python programming language. However, there was a limitation in the processing of Python scripts with a limit of 1000 iterations that blocked the execution when this value was exceeded. To overcome this limitation, we implemented the IDA* algorithm with the same objectives and functionalities, but without implementing the recursive form.

3.3. Dynamic A-Star (D*) and D* Lite

The D* or “Dynamic A-Star” algorithm presented by Stentz A. (1994) [33] is an informed incremental search algorithm. D* maintains a list of nodes used to propagate information about changes of the cost function during the search of the path. In contrast to canonical A*, which follows the path from start to finish, D* begins by searching backwards from the goal node. It works by iteratively selecting a node from a called OPEN list, evaluating it, and then propagates the node’s changes to all the neighbouring nodes and places them on the OPEN list. The algorithm distinguishes between current cost (important at the time of collection) and minimum costs (important for the sorts of the OPEN list). Another particularity is that the function which returns the minimum cost is always the lowest cost to the current point since it is the first entry of the OPEN list.

Koening and Likhachev (2002) [34] presented D* Lite, reformulating the strategy between the goal and the current position of an object, changing the search direction compared to A* and D* by fixing the target coordinate and by only considering a changing starting point through time. With this strategy, D* Lite increases the search efficiency, attaining a fast-replanning task.

Setiawan et al. (2014) [73] presented an experimental comparison of A* and D* Lite in the context of path planning for differential drive automated guided vehicles. The simulation and experimental results showed that, in general, D* Lite can plan the shorter path with faster computation time compared to A*. However, there are some cases when D* Lite is less effective than A* and so depends on the requirements of the system or context environment and variables.

Le et al. (2017) [74] presented an improvement to D* Lite, in particular for environments where the effect of changes is costly. They proposed the setting of a threshold on the ratio of the traversed path length to the total path length. An and Than (2018) [75] also explored D* Lite as a search-based planning method in robotics and autonomous systems.

More recently, Algarín-Pinto et al. (2023) [76] adapted D* Lite to improve guidance, navigation and control of a tail-actuated underwater vehicle in unknown environments. They presented promising results in terms of effectiveness by adding a waypoint tracking controller to correct the vehicle’s swimming performance inside three scenarios when the planner does not consider broader free spaces for replanning and in two scenarios where the vehicle passes too close to obstacles inside hallways.

Algorithm 3 presents the pseudo code of D* Lite.

Algorithm 3. D* Lite algorithm pseudocode [34,74].

3.4. Simplified Memory Bounded A* (SMA*)

With the objective of using a bounded memory, Simplified Memory Bounded A* (SMA*) [32,46] was proposed as a variant of shortest path based on A*. The difference is that nodes with the highest f-cost are pruned from the queue when there is no more available memory. Because those nodes are deleted, simple memory bounded A* must remember the f-cost of the best forgotten child of the parent node. When it seems that all explored paths are worse than such a forgotten path, the path is regenerated [32]. The general process execution (Algorithm 4) starts with the root node and adds nodes to the tree based on their costs, utilizing the available memory efficiently. If the memory limit is exceeded, it removes nodes while maintaining the lowest cost path.

Algorithm 4. SMA* algorithm pseudocode [32].

Lovinger and Zhang (2017) [46] proposed an enhancement of SMA*, providing a new open list, a simplified implementation, and a culling heuristic function that improves search performance through a priori knowledge of the search space.

3.5. Bidirectional A*

Pijls and Post (2009) [30,51] presented a new bidirectional search algorithm with shortened postprocessing with a balanced heuristic estimation approach in order to quickly provide a feasible approximation to the solution compared with the A* algorithm, which uses a non-balanced straightforward heuristic. The pseudo code of Bidirectional A* is described in Algorithm 5.

Algorithm 5. Bidirectional A* algorithm [30].

Nannicini et al. (2008) [52] presented a bidirectional search on time-dependent graphs based on restricting the scope of a time-dependent A* search. They applied this bidirectional search on a time dependent road network, where the backward search is used to limit the set of nodes that must be explored by the forward search. The authors argue that their approach can significantly decrease computational times. Rios and Chaimowicz (2011) [77] presented PNBA*, a Parallel Bidirectional Heuristic Search Algorithm, that combines the benefits of bidirectional search and parallel execution in the development of an efficient A*. Sharma et al. (2020) [53] presented an approach for parallelizing the Bidirectional A* algorithm, modifying it to make use of priority queues to break down the algorithm in its serial form and then using the GPU calculation capabilities to calculate the heuristic function and using it to identify the actual path.

3.6. Real-Time Adaptive A* (RTAA*)

Bulitko and Lee (2006) [35] explained that real-time search methods are suited for tasks in which the agent is interacting with an initially unknown environment in real time. In such simultaneous planning and learning problems, the agent is required to select its actions in a limited amount of time, while perceiving only a local part of the environment centred at the agent’s current location. Real-time heuristic search agents select actions using a limited lookahead search, evaluating the frontier states with a heuristic function [35].

The Real-time Adaptive A* (RTAA*) algorithm, proposed by Koening and Likhachev (2006) [55], is a real-time heuristic search method that chooses its local search spaces in a very fine-grained way in which the main idea is to update the heuristics of all states in the local search space very quickly and to save the heuristics to speed up future A* searches. As in A*, the merit of a node n is f(n) = g(n) + h(n). However, unlike A*, the interpretation of g(n) in RTA* is the actual distance of a node n from the current state of the problem solver, rather than from the original initial state. The key difference between RTA* and A* is that, in RTA*, the merit of every node is measured relative to the current position of the problem solver, and the initial state is irrelevant. RTA* is simply a best-first search given this slightly different cost function.

In parallel studies in real-time search methods, Learning Real-time A* (LRTA*) [35] produces feasible paths any time during its execution and minimum length paths if allowed to run to completion [54]. Howlett et al. (2006) [54] applied the LRTA* in the context of a path planner for unmanned air vehicle target sensing, which resulted in a planner that produces short-distance paths in acceptably short running times.

The pseudo code of the RTAA* is presented in Algorithm 6.

Algorithm 6. Real-time Adaptive A* (RTAA*) algorithm pseudocode [54].

Hernández et al. (2011) [56] presented an approach of RTAA* that incorporates depression avoidance, in other words, a strategy to prevent the algorithm from getting trapped in heuristic depressions, which are bounded regions in the search space where the heuristic values are significantly lower than those on the surrounding boundary, in problems with limited time constraints. Erra and Caggianese (2012) [78] presented Graphics Processing Unit (GPU) multiagent path planning for the RTA* algorithm to allow massively parallel, real-time execution.

4. Materials and Methods

4.1. Context and Dataset

In the context of pathfinding and the Shortest Path Problem (SPP) using graph-based analysis, our goal is to find the shortest and most efficient paths between vertices in a road network while accounting for variables such as the road length, cost and toll. In other words, we adopted tri-objective scenario parameters (length, cost and toll) to identify more accurate and efficient routes from an origin to a destination on a road map represented as a graph-based representation. To simulate a realistic scenario, we used a benchmarking dataset commonly referenced in research articles, namely the European cities dataset. This dataset consists of 120 records, each representing a connection between two cities. For each connection node, we consider three variables: toll, fuel (in litters) and distance (in kilometres).

Figure 1 presents an example of the dataset used during the tests.

In addition, we added a column (“W” or “combined_cost”) representing a linear combination of the three cost variables that calculated the total cost based on weights attributed to each variable: 30% to toll price, 20% to fuel cost and 50% to distance between the nodes. The formula is defined as:

W = 0.30 * Toll + 0.20 * Fuel + 0.5 * Distance

(1)

The additional column “W” has the objective to be the variable used in the shortest path algorithms between nodes of the graph network. The graph used to test and evaluate the precision, execution time and resources usage of each algorithm was generated from a dataset in CSV format containing toll prices, fuel costs and distances between multiple European cities. The data from the CSV file was processed using Python’s Pandas library and NetworkX graph methods. To create a graph that translated all the cities into nodes, with unified cost assigned to each edge, we used the weighted linear combination expression (Equation (1)) to represent the cost between cities. As a result, we created the test graph with 40 nodes corresponding to cities and 120 edges corresponding to all the connections between cities. Figure 2 presents an illustration in a graph-based representation that maps a subset of the dataset.

4.2. Computational Environment and Methodology Process

In terms of computational settings, the algorithms were executed on an Apple M3 chip (4.05 GHz) with 16 Gb of RAM and the macOS Sequoia 15.4.1 operating system. The algorithms were fully developed and tested using the Python programming language (version 3.11.9). All implementations of the algorithms were submitted to the NetworkX environment validation process through the official GitHub framework, and all tests were successfully passed, as detailed in the Appendix A, Appendix B, Appendix C, Appendix D and Appendix E.

The development methodology followed was based on the pseudocode and descriptions from the original research papers for each algorithm. The validation process ensured correct integration with the NetworkX framework, confirming the accuracy and robustness of the implementations (see Appendix A, Appendix B, Appendix C, Appendix D and Appendix E).

4.3. NetworkX Framework Integration

In order to integrate the developed algorithms within the technical architecture of the NetworkX platform, we began by developing the algorithms independently, to be integrated later into the library. After the initial algorithm versions were developed, the code was then transferred and integrated into the NetworkX source code, where we followed the contribution guidelines provided in the official Contributor Guide document.

The development process began by forking the NetworkX repository and, then cloning the library source code into the local machines. Then, we added the upstream main branch, and a virtual Python environment was created for development, using the “pip”-based venv environment. It was also necessary to install pre-commit checks to fulfil the code formatting guidelines.

After finishing the code integration with the source code, the whole project was tested using pytest to check for potential problems that could fail afterwards on the pull-request checks. Once the local tests were successfully passed, the code was pushed into the forked repository, where it was then submitted as a pull request to the NetworkX official repository. Upon submission, a set of continuous integration services were triggered to verify that the code adhered to quality standards and passed all required tests.

Contributor Guide document found on: https://github.com/networkx/networkx/blob/679191810fc962e282b606622c90355f2e6f58ad/CONTRIBUTING.rst (accessed on 19 May 2025).

5. Experiments and Results

5.1. Results of Algorithms Tests

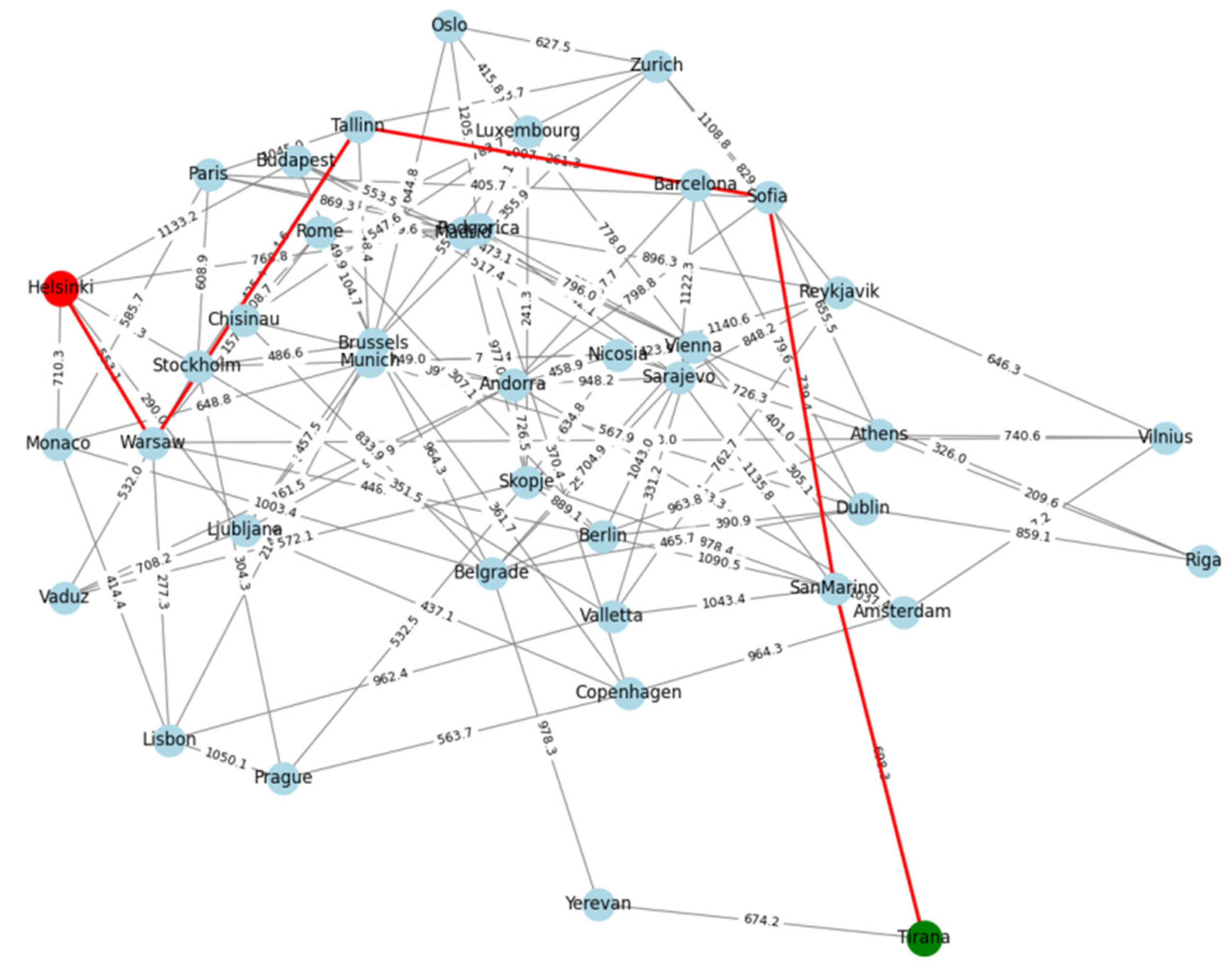
Using the previously defined city connections graph, all the algorithms were executed using the same origin and destination, one at a time and using the same machine resources and graph data. We began by running the already existing and implemented A* algorithm in NetworkX to establish a benchmark to test and compare the results of the developed algorithms. Figure 3 illustrates the optimal path identified by the A* algorithm (red line) in comparison with the other implemented algorithms.

The following subsections present the results obtained from executing all the developed algorithms, each compared against the A* benchmark to evaluate their real-time performance.

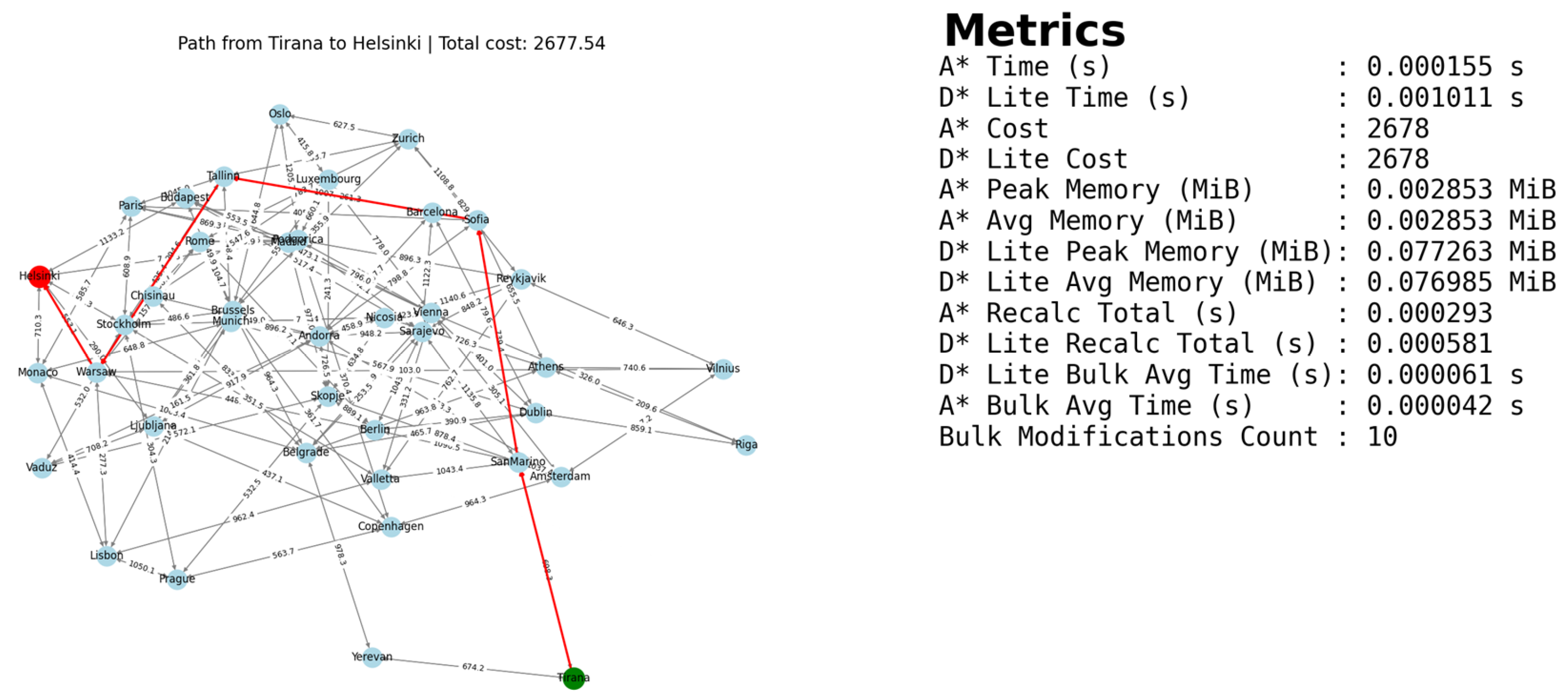
5.1.1. D* Lite Algorithm

Figure 4 presents the optimal path found between Tirana and Helsinki using the D* Lite algorithm, along with the performance metrics compared to the benchmark of the A* algorithm.

By analysing the result of the comparison run, we were able to conclude that the D* Lite is marginally slower than the A* while finding the same optimal path. However, the D* uses significantly more memory compared to A*. These results were somewhat expected since D* is designed for larger graphs with real-time graph changes, not static scenarios like the test case; its additional capabilities do not provide a clear advantage and may introduce overhead.

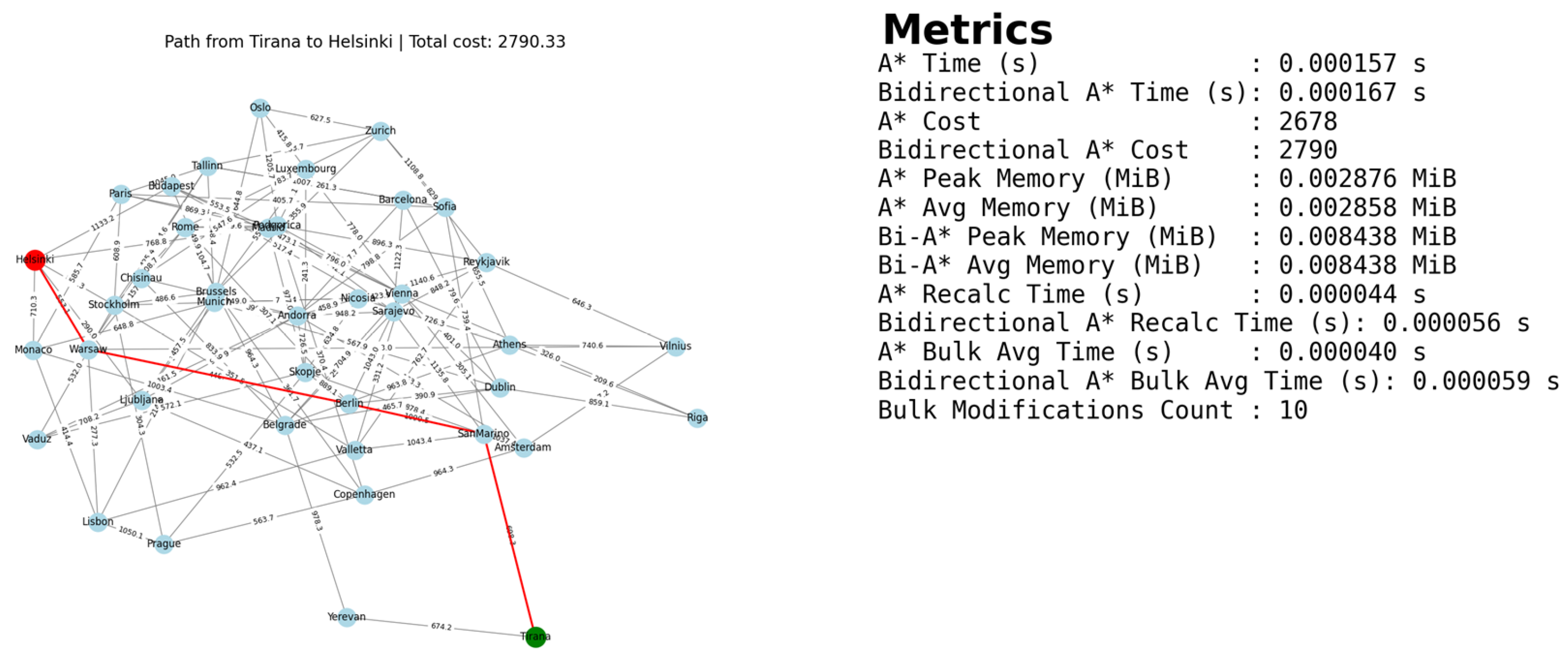
5.1.2. Bidirectional A* Algorithm

Figure 5 presents the results obtained from execution of the bidirectional A* algorithm, including its metrics.

Bidirectional A* required almost as much time as the A* algorithm. However, the optimal path found was slightly more expensive than the one found by A* and it also used more memory. In the remaining benchmarks, Bidirectional A* very closely resembles the A* capabilities. Since this algorithm is best suited for larger and more complex graphs, the results are consistent with what was expected.

5.1.3. IDA* Algorithm

The results of the execution of the IDA* algorithm, presented in Figure 6, show that the algorithm was able to find the same cost optimal path as A* while taking marginally more time to compute the result. On the other hand, it used less memory in peak times and even less in terms of average usage. Also, recalculation times were significantly slower as IDA* is not well-suited for graph recalculations but rather to find optimal paths with relatively high speed but consuming less memory.

5.1.4. RTAA* Algorithm

Results and metrics of the execution of the RTAA* algorithm are presented in Figure 7.

Real Time Adaptative A* required slightly more time to find the path when compared to A* and produced an optimal path with a higher overall cost, while also using more memory. These results are consistent with the algorithm characteristics, since the tests were focused on a static and small graph environment, which goes against the capabilities of the RTAA* algorithm since no real time adaptations were made.

5.1.5. SMA* Algorithm

As shown in Figure 8, the SMA* algorithm was able to find the same optimal path as A*, but with significantly less execution time and using less memory than A* and even outperforming IDA* in terms of memory usage. Additionally, SMA* demonstrates a good recalculation time compared to both algorithms, being only slightly slower than A* and faster than IDA*, even though the algorithm is not focused on recalculations but rather on optimizing memory use. In terms of amount of memory that can be utilised, the SMA* algorithm imposes a limit, which can be particularly advantageous for devices with limited memory resources.

5.2. Analysis and Discussion

Following the foundations, context and dataset described in previous sections, we conducted a benchmarking of the A* algorithm in comparison with five newly implemented algorithms in the NetworkX library, within tri-objective scenario parameters (distance, cost and toll).

After the various simulations using the different algorithms, we observed that some algorithms have advantages over others depending on the metrics. For example, and according to the graphs and metrics shown in the previous section, with regards to determining the optimal path between an origin and a destination (between Tirana and Helsinki cities), we achieved the following results in terms of algorithm performance, summarised in

Table 1. Comparison between the algorithms’ performances.

Algorithm	Time	Total Cost	Peak Memory	Avg. Memory	Recalculation Time	Bulk Average Time
A*	0.16 ms 1	2678	2.88 Kb 2	2.86 Kb 2	0.04 ms 1	0.04 ms 1
D* Lite	1.01 ms 1	2678	77.26 Kb 2	76.99 Kb 2	0.58 ms 1	0.06 ms 1
Bidirectional A*	0.17 ms 1	2790	8.44 Kb 2	8.44 Kb 2	0.06 ms 1	0.06 ms 1
IDA*	14.13 ms 1	2678	2.64 Kb 2	2.59 Kb 2	12.56 ms 1	3.48 ms 1
RTAA*	0.22 ms 1	3485	6.58 Kb 2	6.58 Kb 2	0.11 ms 1	0.09 ms 1
SMA*	0.08 ms 1	2678	2.57 Kb 2	2.57 Kb 2	0.06 ms 1	0.05 ms 1

¹ Time units converted from seconds to milliseconds for better visualization. ² Memory units converted from Megabits to Kilobits for better visualization.

.

From the table and simulation results, and considering the overall metrics of each algorithm, it is noticeable that the A* algorithm and the SMA* algorithm demonstrated a good overall performance, although SMA* showed an overall good performance, demonstrating competitive results in comparison to all the other implemented algorithms. Nevertheless, almost all other algorithms were able to perform equally well, in particular in the metrics related to the characteristics where they were specifically developed to have an advantage, highlighting the implementation quality and robustness of the implemented algorithms.

Regarding the D* Lite and RTAA* algorithms that were developed for handling larger graphs and faster recalculation times on path changes during execution, these algorithms are more complex than the rest of the variants. Considering the small size of the test graph and the absence of path changes during executions, these algorithms were not able to fully leverage their advantages, thus justifying the worse results in certain fields when compared to the A* algorithm benchmark.

The IDA* algorithm is designed to enhance memory utilisation through the implementation of a depth-first search strategy and is relevant in scenarios where a graph contains numerous branches, potentially resulting in devices with insufficient memory to accommodate all branches.

The D*-Lite algorithm has been developed to address the limitations of the A* algorithm when searching for a given path that involves the reuse of parts of a previous path and is relevant in the context of large graphs, where the D*-Lite algorithm has been shown to enhance performance.

The SMA* algorithm imposes a limit on the amount of memory that can be utilised, which renders it particularly advantageous for devices with limited memory resources. Bidirectional A* aims to reduce the time taken to search for a given path by searching in both directions, whereas A* only searches from the source. The RTAA* aims to determine a given path faster than A*, and although it is not the optimal solution it returns a result according to certain limits imposed by its parameters, such as the search depth of a given node.

Despite the extensive utilisation of the A* algorithm and its notable efficacy in identifying optimal paths, its performance is suboptimal in specific scenarios, such as when confronted with memory constraints and dynamic environments. For instance, A* can become less efficient on large graphs with thousands of nodes because it needs to store and manage cost values and search paths for many nodes. This can lead to increased memory consumption and longer processing times, depending on the data structures used.

With this simulation in a specific context, we tried to demonstrate that the A* and the developed extensions address the challenges of solving shortest path problems. The integration of new algorithms into NetworkX has the objective of allowing use of the library in a more broader range of problems, namely when confronted with memory constraints and dynamic environments.

It is important to note that the scope of this work is centred on integrating and testing already defined algorithms, specifically D* Lite, Bidirectional A*, IDA*, SMA* and RTAA*, within the NetworkX library. Also, regarding the specific context of the dataset used in the simulations that allowed us to test the efficiency of the A* extensions in a tri-objective parameter scenario.

It is worth mentioning that the objective of this work was not to create new algorithms but to enhance the NetworkX library with implementations of known algorithms, thereby supporting future research and development in graph-based pathfinding and optimisation in complex, real-world scenarios.

6. Conclusions and Future Work

This paper presents a set of implementations of algorithms that improve the A* algorithm, including IDA*, D* Lite, SMA*, Bidirectional A* and RTA*, that have been integrated in the Python library NetworkX. By reviewing and validating the usage of these A* algorithm extensions and the implementations in Python within the NetworkX framework, the implementations have been submitted to the network environment validation and passed the tests. Benchmarking was also preformed using a tri-objective scenario (length, cost and toll in a road network), in order to compare A* with the implemented extensions and assess their efficiency.

We concluded that each algorithm developed had its own approach of finding the optimal path, which showed their respective advantages and disadvantages. Considering the objectives and functionalities of each algorithm, we can conclude that the A* and SMA* algorithms demonstrated the best overall general performance, being competitive in comparison to all the other algorithms implemented. Nevertheless, all algorithms were able to find good solutions for the test case, and some implementations were able to perform better or equally as good as the A* algorithm in specific metrics, highlighting the implementation quality and robustness of the implemented algorithms. In particular, the D* Lite and Real Time Adaptative A* (RTAA*) algorithms, which were developed for handling larger graphs and faster recalculation times on path changes during execution, are more complex than the other implementations. Considering the relatively small dimension of the test graph and absence of path changes during executions, these algorithms were not able to fully demonstrate their advantage, which explains their lower performance in some metrics when compared to the A* algorithm benchmark.

Furthermore, NetworkX is a Python library direcly targeted for graphs with small to medium dimensions, and the Python programming language is based on a more developer-friendly and readable syntax, which makes it slower than other languages and does not allow for micro-optimisations such as, for example, the C++ language. These factors limited the ability of more advanced algorithms like the D* Lite and RTAA* algorithms to reflect their full performance and key advantages.

All the implementations have been submitted to network environment validation, having successfully passed the tests. The source code of the algorithms is available on the GitHub opensource repository in order to foster future research and development in graph-based pathfinding and optimisation in complex, real-world scenarios.

Future directions for this research may include incorporating other A* extension algorithms, such as Lifelong Planning A* (LPA*), Anytime D* and Learning Real-time A* (LRTA*). It will also be important to test the algorithms in larger and more complex benchmarking datasets to assess their performance in different types of graph topologies and domain-specific constraints.