Unpacking Performance Variability in Deep Reinforcement Learning: The Role of Observation Space Divergence

Abstract

Deep Reinforcement Learning (DRL) algorithms often exhibit significant performance variability across different training runs, even with identical settings. This paper investigates the hypothesis that a key contributor to this variability is the divergence in the observation spaces explored by individual learning agents. We conducted an empirical study using Proximal Policy Optimization (PPO) agents trained on eight Atari environments. We analyzed the collected agent trajectories by qualitatively visualizing and quantitatively measuring the divergence in their explored observation spaces. Furthermore, we cross-evaluated the learned actor and value networks, measuring the average absolute TD-error, the RMSE of value estimates, and the KL divergence between policies to assess their functional similarity. We also conducted experiments where agents were trained from identical network initializations to isolate the source of this divergence. Our findings reveal a strong correlation: environments with low-performance variance (e.g., Freeway) showed high similarity in explored observation spaces and learned networks across agents. Conversely, environments with high-performance variability (e.g., Boxing, Qbert) demonstrated significant divergence in both explored states and network functionalities. This pattern persisted even when agents started with identical network weights. These results suggest that differences in experiential trajectories, driven by the stochasticity of agent–environment interactions, lead to specialized agent policies and value functions, thereby contributing substantially to the observed inconsistencies in DRL performance.

1. Introduction

Deep reinforcement learning (DRL) has demonstrated an extraordinary ability to solve high-dimensional decision-making problems, from Atari video games [1] to the board game Go [2]. Among modern on-policy methods, Proximal Policy Optimization (PPO) [3] has emerged as a de facto baseline due to its empirical performance and implementation simplicity, and it remains the algorithm of choice in a wide range of recent studies. Yet, a persistent challenge plagues the field. Despite identical hyperparameters and training budgets, independent runs of the same DRL algorithm can yield markedly different returns [4], complicating the fair evaluation and deployment of new methods.

Existing research has identified several key sources contributing to this performance variability. One line of inquiry has focused on the profound impact of implementation details. Foundational work by Henderson et al. [4] demonstrated that differences in codebases, hyperparameter settings, and even random seeds could lead to drastically different outcomes. This was further emphasized by Engstrom et al. [5], who showed that seemingly minor code-level decisions—such as the choice of activation function or the order of operations—can alter performance by orders of magnitude. Another perspective has examined the dynamics of the training process itself. Bjorck et al. [6] provided evidence that much of this variability originates early in training, as a few “outlier” runs drift onto low-reward trajectories and never recover. This aligns with the work by Jang et al. [7], which explored how entropy-aware initialization can foster more effective exploration from the outset, thereby preventing early stagnation. A third approach has delved into the internal mechanics of the learning agent. For instance, Moalla et al. [8] recently established a connection between performance instability in PPO and internal “representation collapse,” where the network learns insufficiently diverse features, leading to trust issues in policy updates.

While these studies provide crucial insights into implementation, training dynamics, and internal representations, a complementary perspective remains less explored: the divergence in the observation space that each agent actually experiences. RL agents learn from the specific trajectories of states and rewards they encounter. If two agents, due to chance events early in training, begin to explore different regions of the state space, they are effectively training on different datasets. This can lead them to converge to substantially different—and unequally performing—policies. This paper investigates the hypothesis that this divergence in lived experience is a primary cause of performance variability. Unlike prior work focused on implementation choices or internal network states [8], we aim to directly quantify the differences in state visitation distributions among independently trained agents. And while studies like [6,7] identify that runs diverge, we characterize how they diverge in terms of the states they encounter and explicitly link this to the functional dissimilarity of the resulting policies.

In this work, we perform a controlled empirical study of five PPO agents, each trained with an independent random seed, across eight Atari environments—Alien, Boxing, Breakout, Enduro, Freeway, KungFuMaster, Pong, and Qbert—using the Arcade Learning Environment [9] and Gymnasium [10]. Training five independent PPO agents per game yields a spectrum of outcomes, from highly successful to comparatively poor policies. We then ask the following: Do higher-performing agents encounter a broader or different set of states than lower-performing agents? And do such differences manifest in the learned representations of the actor (policy) and critic (value function) networks? To answer these questions, we employ a range of analysis techniques. First, we visualize and quantify each agent’s observation distribution using dimensionality-reduction methods and statistical measures of dispersion and similarity. Second, we cross-evaluate the learned actor and value networks, applying them to states experienced by other agents to assess functional differences. Our findings reveal a clear correlation between divergence in explored observation spaces, dissimilarity of the learned networks, and variance in achieved performance across agents within each environment.

The remainder of this paper is organized as follows. Section 2 details our methodology. Section 3 presents the experimental results, featuring analyses of observation space characteristics and the discrepancies observed in actor–critic networks. In Section 4, we discuss the implications of our findings. Finally, Section 5 concludes the paper by outlining potential avenues for future research.

2. Methodology

To investigate the relationship between observation space divergence, network differences, and performance variability, a series of experiments were conducted using PPO agents trained on eight Atari environments. For this investigation, we specifically selected Proximal Policy Optimization (PPO) and the Atari 2600 benchmark suite. PPO was chosen due to its status as a robust, high-performing, and widely adopted baseline algorithm in the DRL community, making our findings on its variability highly relevant. The Atari suite, via the Arcade Learning Environment, offers a diverse collection of environments with varying complexities and reward structures. This diversity is crucial for our study, as it allows us to systematically compare the divergence phenomenon in games known to produce both highly consistent and highly variable performance outcomes.

2.1. Experimental Setup

All experiments were conducted on a workstation with the following specifications:

• Hardware: Intel(R) Core(TM) i7-14700K (28 cores), 128 GB RAM.
• Software: Python 3.10.16, along with key scientific computing libraries including NumPy 2.2.3, Pandas 2.2.3, SciPy 1.15.3, and Scikit-learn 1.7.0.

2.2. Training Environment and Agents

We trained five independent PPO agents for each of the eight Atari environments shown in Figure 1: Alien, Boxing, Breakout, Enduro, Freeway, KungFuMaster (KFM), Pong, and Qbert. The training was conducted using the Stable-Baselines3 [11], and the agents used the PPO hyperparameters for Atari games as released in the RL Baselines3 Zoo [12]. Each agent within an environment was trained from scratch, with the only source of variation being the random seeds.

2.3. Data Collection

After the training phase concluded for all agents, each of the five converged agents per environment was rolled out for 30 episodes. The performance, measured as the average reward over 30 evaluation episodes, was recorded for each agent. During these rollouts, at each step t, a tuple containing the current observation ($o_t$), the received reward ($r_t$), the value estimate from the agent’s own critic ($v_t=V_{\varphi }\left(o_t\right)$), and the action logits from the agent’s own actor (${\mathrm{action}\_\mathrm{logits}}_t={\pi }_{\theta }\left(o_t\right)$) was collected and stored. This process generated a dataset of trajectories specific to each agent’s learned policy.

2.4. Analysis of Observation Space

The collected observation data was analyzed to characterize the extent and nature of exploration by each agent and to compare observation distributions across agents.

2.4.1. Visualization

To qualitatively assess the similarity of explored observation spaces, the high-dimensional observation data (raw pixel frames) was visualized in a 2D space using t-SNE. For each environment, observations from all five agents were combined. From each agent’s collected observations, 5000 frames were randomly subsampled. These observations were then flattened into vectors before being projected into two dimensions using t-SNE. The perplexity hyperparameter for t-SNE was set to 30, a choice informed by a trustworthiness analysis (presented in Section 3.5) to ensure high-quality embeddings. The resulting scatter plots were color-coded by agent ID to reveal patterns of overlap and separation.

2.4.2. Single-Agent Observation Dispersion

To quantify the diversity of observations encountered by each individual agent, a multi-step process was employed:

• Data Loading and Preprocessing: For each agent, its collected observations over 30 episodes were loaded, and then 5000 frames were subsampled and flattened into vectors.
• Dimensionality Reduction and Denoising: Principal Component Analysis (PCA) was applied to reduce the dimensionality of the flattened observations to 50 dimensions. This step serves to denoise and compress the data, focusing on the directions of highest variance, which can lead to more robust and meaningful clustering in the subsequent step. Working with high-dimensional raw pixel data directly for clustering can be computationally expensive and sensitive to noise; PCA mitigates these issues by capturing the most salient features.
• State Space Discretization via Clustering: The PCA-transformed features from all agents within an environment were pooled together. K-means clustering was then performed on this pooled set of features to define a common set of discrete state categories. To assess the sensitivity of our metrics to the granularity of discretization, we performed this step with K values of 50, 100, and 200. The results for K = 100 are presented in the main analysis, with K = 50 and K = 200 used for comparison.
• Occupancy Histogram Generation: For each agent, an occupancy histogram (probability distribution, $p\left(c\right)$) over the K clusters was computed.
• Dispersion Metrics Calculation: Based on this probability distribution $p\left(c\right)$ (where c is a cluster index), the following metrics were calculated:
  • Entropy (H(p)): Measures the uncertainty or diversity of the visited clusters. Higher entropy indicates that an agent visits a wider range of distinct state categories more uniformly.

    $$H\left(p\right)=-\sum _{c}p\left(c\right)logp\left(c\right).$$

    (1)
  • Effective Support Size (${\mathit{N}}_{\mathit{eff}}$): Estimates the number of effectively visited clusters, providing an interpretable scale for diversity.

    $$N_{eff}=exp\left(H\left(p\right)\right).$$

    (2)
  • Coverage Ratio (Cov): The proportion of the K-defined clusters that were visited at least once.

    $$\mathrm{Cov}={\displaystyle \frac{\left|\{c\mid p(c)>0\}\right|}{K}}.$$

    (3)
  • Gini–Simpson Index (G): Measures diversity, with values closer to 1 indicating higher diversity (i.e., probabilities are spread out more evenly across many clusters).

    $$G=1-\sum _{c}p{\left(c\right)}^2.$$

    (4)

2.4.3. Pairwise Observation Distribution Comparison

To quantify the similarity between observation distributions of pairs of agents, the following metrics were computed. The cluster definitions and the individual agent occupancy histograms (e.g., $p_i\left(c\right)$ and $p_j\left(c\right)$) used for these pairwise comparisons are established and computed according to the procedures detailed in Section 2.4.2.

• Pairwise Total Variation (TV) Distance: For each pair of agents $(i,j)$, the TV distance between their cluster occupancy histograms $p_i\left(c\right)$ and $p_j\left(c\right)$ was calculated. This ranges from 0 (identical) to 1 (disjoint).

  $$TV(i,j)={\displaystyle \frac{1}{2}}\sum _c\left|p_i\left(c\right)-p_j\left(c\right)\right|.$$

  (5)
• Pairwise Maximum Mean Discrepancy (MMD): MMD was computed between the PCA-reduced feature sets of each pair of agents using a Gaussian kernel [13]. The kernel bandwidth sigma was set using the median heuristic. MMD is a statistical test for determining whether two samples are drawn from the same distribution, and its magnitude provides a measure of their dissimilarity. It operates directly on the feature representations rather than relying on the explicit cluster histograms.

  $$MMD(i,j)=\sqrt{{\mathbb{E}}_{x,x^{\prime }\sim P_i}\left[K(x,x^{\prime })\right]-2{\mathbb{E}}_{x\sim P_i,y\sim P_j}\left[K(x,y)\right]+{\mathbb{E}}_{y,y^{\prime }\sim P_j}\left[K(y,y^{\prime })\right]},$$

  (6)

  where K is a positive-definite kernel. We choose a Gaussian kernel $K(x,y)=exp(-|x-y{|}^2/2{\sigma }^2)$. The kernel bandwidth $\sigma$ is set to the median pairwise distance among all states in the combined dataset (median heuristic), which provides a reasonable scale. MMD is essentially a distance in reproducing kernel Hilbert space and is 0 iff the two distributions are identical (for characteristic kernels).

2.5. Analysis of Actor and Value Network Differences

To assess how the differences in explored observation spaces translate to differences in the learned actor and value networks, a cross-evaluation methodology was employed. For each pair of agents $(i,j)$ within an environment, the observations collected by agent i during its rollouts were used as input to the actor and value networks of agent j. The following metrics were calculated:

• Absolute TD-Error: The absolute TD-error was computed over agent i’s trajectory data using agent j’s value network, measuring how well agent j’s value function generalizes to agent i’s experiences.

  $${TD}_{i\to j}(s_t,r_t,s_{t+1})={\displaystyle \frac{1}{\left|{\mathcal{D}}_i\right|}}\sum _{(s_t,r_t,s_{t+1})\in {\mathcal{D}}_i}\left|r_t+\gamma V_{{\varphi }_j}\left(s_{t+1}\right)-V_{{\varphi }_j}\left(s_t\right)\right|.$$

  (7)
• Root Mean Squared Error (RMSE) of Value Estimates: For each state $s_t$ in agent i’s trajectory, the value estimated by agent i’s critic, $V_{{\varphi }_i}\left(s_t\right)$, was compared to the value predicted by agent j’s critic, $V_{{\varphi }_j}\left(s_t\right)$. This directly measures how different the output of the two value functions is on states that agent i visits.

  $${RMSE}_{i\to j}=\sqrt{{\displaystyle \frac{1}{\left|{\mathcal{D}}_i\right|}}\sum _{s_t\in {\mathcal{D}}_i}{\left(V_{{\varphi }_i}\left(s_t\right)-V_{{\varphi }_j}\left(s_t\right)\right)}^2}.$$

  (8)
• Kullback–Leibler Divergence (KLD) of Action Logits: For each state $s_t$ in agent i’s trajectory, KLD was computed using the action probability distributions (derived from the logits) produced by agent i’s actor, ${\pi }_{{\theta }_i}(·\mid s_t)$, and agent j’s actor, ${\pi }_{{\theta }_j}(·\mid s_t)$. This quantifies the policy divergence by comparing the action probability distributions from agent i’s actor and agent j’s actor for states in agent i’s trajectory.

  $${KLD}_{i\to j}={\displaystyle \frac{1}{\left|{\mathcal{D}}_i\right|}}\sum _{s_t\in {\mathcal{D}}_i}{D}_{\mathrm{KL}}\left({\pi }_{{\theta }_i}(·\mid s_t)\parallel {\pi }_{{\theta }_j}(·\mid s_t)\right).$$

  (9)

These metrics were computed for all 5 × 5 agent pairings in each of the eight environments, resulting in matrices that reveal the extent of network generalization and similarity.

2.6. Trained Agents with Identically Initialized Networks

To further investigate the sources of performance variability, we conducted an additional experiment. For four of the eight environments—Boxing and Qbert (high-performance variance), Alien (medium variance), and Freeway (low variance)—we trained five new agents starting from the same initial network weights. The only source of variation in these runs was the stochasticity inherent in the agent–environment interaction loop (e.g., action sampling, environment responses). This setup allows us to determine whether different weight initializations primarily drive performance divergence or if it emerges naturally from the training process itself. These agents were then analyzed using the same data collection and analysis pipeline described above.

3. Results

3.1. Performance Variation Across Agents and Environments

As detailed in

Table 1. Performance of trained agents (mean and standard deviation of rewards).

Task	#1	#2	#3	#4	#5
Alien	1394.33 (448.74)	1135.67 (491.36)	971.00 (509.41)	903.33 (257.38)	824.00 (255.94)
Boxing	99.73 (0.81)	99.10 (0.70)	99.03 (1.14)	93.47 (3.20)	92.10 (4.55)
Breakout	343.60 (90.93)	312.03 (114.54)	171.80 (174.42)	106.20 (143.42)	41.20 (19.39)
Enduro	874.20 (170.43)	862.67 (143.47)	771.20 (198.16)	711.13 (164.85)	700.93 (203.18)
Freeway	22.03 (1.62)	21.37 (1.33)	21.30 (1.51)	21.27 (1.31)	21.27 (1.34)
KFM	37,453.33 (7052.74)	34,853.33 (6008.42)	28,180.00 (7171.30)	22,820.00 (7527.79)	3600.00 (0.00)
Pong	21.00 (0.00)	21.00 (0.00)	20.80 (0.40)	19.83 (0.37)	19.33 (3.73)
Qbert	4050.00 (0.00)	4050.00 (0.00)	4050.00 (0.00)	2008.33 (1553.87)	1116.67 (977.84)

, the five PPO agents trained independently in each of the eight environments achieved markedly different final scores. The agents are consistently listed from #1 (highest score) to #5 (lowest score). The performance gap between the best and worst agents varied dramatically across environments.

Environments such as Freeway and Pong showed high consistency. In Freeway, scores were tightly clustered between 21.27 and 22.03, a minimal difference. In contrast, other environments displayed extreme variability. In KFM, the top agent scored 37,453, while the lowest-scoring agent achieved only 3600. Breakout also showed a massive spread, from 343.6 down to 41.2. Boxing and Qbert demonstrated significant, though less extreme, variance. This wide range of performance disparities provides a strong basis for investigating the correlation with observation space divergence.

Table 2. Collected data size from trained agents (mean and standard deviation of episode length).

Task	#1	#2	#3	#4	#5
Alien	856.57 (80.35)	731.37 (155.80)	711.17 (183.88)	699.20 (124.09)	746.60 (113.81)
Boxing	286.17 (21.92)	667.27 (46.83)	949.33 (29.09)	1163.43 (93.63)	1111.53 (68.38)
Breakout	17,244.43 (11,941.62)	22,010.73 (9967.87)	22,905.47 (9143.04)	23,686.77 (8433.69)	25,257.17 (6501.71)
Enduro	11,198.40 (1819.96)	11,753.43 (2229.88)	9535.17 (2540.15)	9534.53 (2057.03)	10,422.03 (2539.81)
Freeway	2044.43 (2.54)	2044.07 (2.26)	2044.20 (2.30)	2044.37 (1.89)	2044.23 (1.67)
KFM	3482.80 (788.32)	3866.47 (448.77)	3037.83 (595.05)	4139.97 (553.75)	1099.23 (2.54)
Pong	1684.03 (20.47)	1679.57 (26.72)	1688.63 (23.34)	2707.00 (302.06)	1794.80 (85.39)
Qbert	622.70 (1.90)	618.43 (6.15)	623.37 (7.86)	796.10 (111.40)	773.87 (52.29)

shows the mean episode lengths, which often correlate inversely with performance (e.g., in Boxing, higher-scoring agents have shorter episodes).

3.2. Qualitative Analysis of Observation Space via t-SNE

The t-SNE visualizations in Figure 2 and Figure 3 provide a qualitative view of the explored state manifolds, color-coded by an agent. The degree of overlap and separation between agent distributions varies significantly across games, correlating strongly with performance variance.

• Low-Variance Environments (Freeway, Enduro): In Freeway, the agent observations are thoroughly intermingled, forming a dense, homogeneous cloud with ring-like structures. This indicates that all agents explore nearly identical state spaces, consistent with their minimal performance variance. Enduro shows a similar pattern of high overlap, with points from all agents mixed together within several large clusters.
• High-Variance Environments (Boxing, Qbert, KFM, Breakout): These environments show clear signs of divergent exploration. In Boxing, agents form highly distinct clusters; for example, agent #1 (blue) and agent #3 (green) occupy almost completely separate regions. In Qbert, agents trace out unique, winding paths with little overlap, suggesting highly specialized policies. In KFM, the lowest-performing agent #5 (purple) forms tight, isolated clusters, while the higher-performing agents explore a much larger, albeit still differentiated, central region. Breakout shows less distinct clustering, but agents still carve out visibly different trajectories.
• Moderate-Variance Environments (Alien, Pong): These games represent an intermediate case. Alien agents share a large central cluster but also have unique “tendrils” of exploration. Pong agents form a series of concentric rings, but some agents are more confined to inner rings while others explore the outer regions more, and some agents (e.g., #5, purple) have more diffuse distributions.

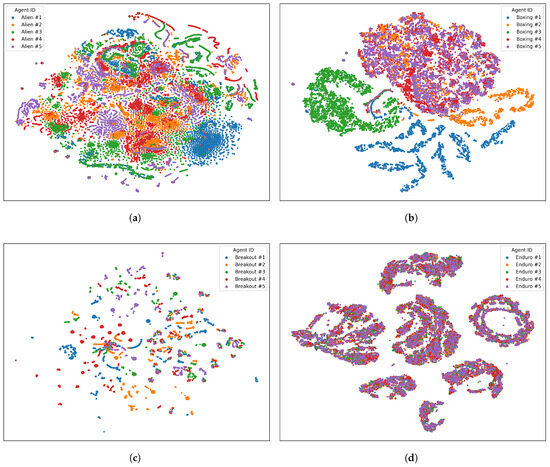
Figure 2. Qualitative t-SNE analysis of observation space representations from five distinct agents in four Atari games: (a) Alien, (b) Boxing, (c) Breakout, and (d) Enduro.

Figure 2. Qualitative t-SNE analysis of observation space representations from five distinct agents in four Atari games: (a) Alien, (b) Boxing, (c) Breakout, and (d) Enduro.

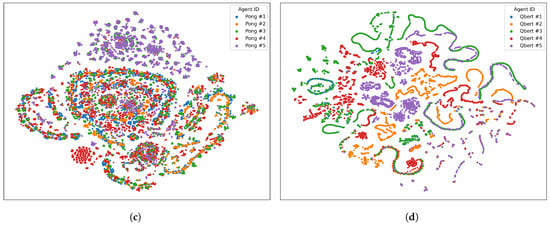
Figure 3. Qualitative t-SNE analysis of observation space representations from five distinct agents in four Atari games: (a) Freeway, (b) KungFuMaster, (c) Pong, and (d) Qbert.

Figure 3. Qualitative t-SNE analysis of observation space representations from five distinct agents in four Atari games: (a) Freeway, (b) KungFuMaster, (c) Pong, and (d) Qbert.

3.3. Quantitative Analysis of Observation Space

3.3.1. Single-Agent Observation Dispersion

The dispersion metrics in

Table 3. Single agent dispersion statistics (K = 100).

Agent	H	${\mathit{N}}_{\mathit{eff}}$	$\mathbf{Cov}$	G
Alien #1	3.41	30.33	0.52	0.95
Alien #2	3.75	42.70	0.76	0.97
Alien #3	3.77	43.17	0.75	0.97
Alien #4	3.39	29.81	0.70	0.94
Alien #5	3.60	36.62	0.60	0.96
Boxing #1	3.12	22.58	0.38	0.95
Boxing #2	3.77	43.52	0.70	0.97
Boxing #3	2.82	16.78	0.26	0.94
Boxing #4	3.80	44.92	0.63	0.97
Boxing #5	3.90	49.29	0.62	0.98
Breakout #1	2.90	18.14	0.50	0.88
Breakout #2	2.79	16.21	0.51	0.87
Breakout #3	2.73	15.40	0.45	0.87
Breakout #4	2.86	17.54	0.52	0.88
Breakout #5	2.73	15.38	0.38	0.88
Enduro #1	4.43	84.01	0.98	0.99
Enduro #2	4.39	80.82	0.99	0.99
Enduro #3	4.42	82.96	1.00	0.99
Enduro #4	4.44	84.72	0.98	0.99
Enduro #5	4.40	81.72	0.99	0.99
Freeway #1	4.55	94.51	1.00	0.99
Freeway #2	4.54	94.09	1.00	0.99
Freeway #3	4.54	93.84	1.00	0.99
Freeway #4	4.54	94.05	1.00	0.99
Freeway #5	4.54	94.00	1.00	0.99
KFM #1	4.26	70.70	0.96	0.98
KFM #2	4.24	69.09	0.90	0.98
KFM #3	4.31	74.49	0.95	0.98
KFM #4	4.26	70.71	0.93	0.98
KFM #5	3.52	33.74	0.53	0.96
Pong #1	4.15	63.51	0.74	0.98
Pong #2	3.99	54.04	0.69	0.98
Pong #3	4.45	85.65	1.00	0.99
Pong #4	4.10	60.40	0.88	0.98
Pong #5	3.91	49.71	0.93	0.97
Qbert #1	3.48	32.55	0.54	0.95
Qbert #2	3.19	24.36	0.45	0.94
Qbert #3	3.49	32.73	0.54	0.95
Qbert #4	2.98	19.69	0.45	0.92
Qbert #5	3.15	23.38	0.54	0.94

H: entropy, N_eff: effective support size, Cov: Coverage Ratio, G: Gini–Simpson Index.

(calculated with K = 100 clusters) quantify the t-SNE visualizations. In Freeway and Enduro, all five agents exhibit consistently high entropy (H), effective support size ($N_{eff}$), and coverage ($\mathrm{Cov}$), indicating they all explore the state space broadly and similarly. For example, all Freeway agents cover nearly 100% of the defined clusters. In high-variance games, these metrics exhibit significant differences between agents. In KFM, the lowest-performing agent (#5) has a much lower entropy (3.52) and effective size (33.74) compared to the others (H > 4.2, $N_{eff}$ > 69), quantitatively confirming its limited exploration seen in the t-SNE plot. In Boxing, there is no simple correlation between performance and dispersion (e.g., agent #3 has the lowest dispersion, while agent #1 has moderate dispersion), suggesting that the quality and uniqueness of the explored region, not just its size, are critical. In Qbert, the top three agents (which all achieved the max score) have higher dispersion than the lower-performing agents #4 and #5.

3.3.2. Pairwise Observation Distribution Comparison

The Pairwise Total Variation (TV) distance (

Table 4. Pairwise Total Variation (TV) distance between agent observation distributions.

	Alien #1	Alien #2	Alien #3	Alien #4	Alien #5
Alien #1	0.000	0.854	0.512	0.857	0.869
Alien #2	0.854	0.000	0.767	0.684	0.500
Alien #3	0.512	0.767	0.000	0.783	0.809
Alien #4	0.857	0.684	0.783	0.000	0.671
Alien #5	0.869	0.500	0.809	0.671	0.000
	Boxing #1	Boxing #2	Boxing #3	Boxing #4	Boxing #5
Boxing #1	0.000	0.959	0.936	0.979	0.985
Boxing #2	0.959	0.000	0.971	0.673	0.565
Boxing #3	0.936	0.971	0.000	0.979	0.984
Boxing #4	0.979	0.673	0.979	0.000	0.252
Boxing #5	0.985	0.565	0.984	0.252	0.000
	Breakout #1	Breakout #2	Breakout #3	Breakout #4	Breakout #5
Breakout #1	0.000	0.809	0.861	0.845	0.890
Breakout #2	0.809	0.000	0.879	0.843	0.905
Breakout #3	0.861	0.879	0.000	0.782	0.783
Breakout #4	0.845	0.843	0.782	0.000	0.792
Breakout #5	0.890	0.905	0.783	0.792	0.000
	Enduro #1	Enduro #2	Enduro #3	Enduro #4	Enduro #5
Enduro #1	0.000	0.146	0.123	0.130	0.135
Enduro #2	0.146	0.000	0.143	0.141	0.125
Enduro #3	0.123	0.143	0.000	0.135	0.124
Enduro #4	0.130	0.141	0.135	0.000	0.135
Enduro #5	0.135	0.125	0.124	0.135	0.000
	Freeway #1	Freeway #2	Freeway #3	Freeway #4	Freeway #5
Freeway #1	0.000	0.064	0.072	0.075	0.069
Freeway #2	0.064	0.000	0.066	0.071	0.072
Freeway #3	0.072	0.066	0.000	0.070	0.076
Freeway #4	0.075	0.071	0.070	0.000	0.067
Freeway #5	0.069	0.072	0.076	0.067	0.000
	KFM #1	KFM #2	KFM #3	KFM #4	KFM #5
KFM #1	0.000	0.206	0.227	0.210	0.779
KFM #2	0.206	0.000	0.205	0.165	0.818
KFM #3	0.227	0.205	0.000	0.235	0.711
KFM #4	0.210	0.165	0.235	0.000	0.794
KFM #5	0.779	0.818	0.711	0.794	0.000
	Pong #1	Pong #2	Pong #3	Pong #4	Pong #5
Pong #1	0.000	0.204	0.324	0.288	0.796
Pong #2	0.204	0.000	0.372	0.355	0.824
Pong #3	0.324	0.372	0.000	0.316	0.582
Pong #4	0.288	0.355	0.316	0.000	0.742
Pong #5	0.796	0.824	0.582	0.742	0.000
	Qbert #1	Qbert #2	Qbert #3	Qbert #4	Qbert #5
Qbert #1	0.000	0.831	0.084	0.698	0.782
Qbert #2	0.831	0.000	0.830	0.878	0.897
Qbert #3	0.084	0.830	0.000	0.736	0.781
Qbert #4	0.698	0.878	0.736	0.000	0.882
Qbert #5	0.782	0.897	0.781	0.882	0.000

) and Maximum Mean Discrepancy (MMD) (

Table 5. Pairwise Maximum Mean Discrepancy (MMD) between agent observation distributions.

	Alien #1	Alien #2	Alien #3	Alien #4	Alien #5
Alien #1	0.000	0.323	0.205	0.329	0.354
Alien #2	0.323	0.000	0.273	0.243	0.180
Alien #3	0.205	0.273	0.000	0.285	0.278
Alien #4	0.329	0.243	0.285	0.000	0.237
Alien #5	0.354	0.180	0.278	0.237	0.000
	Boxing #1	Boxing #2	Boxing #3	Boxing #4	Boxing #5
Boxing #1	0.000	0.476	0.557	0.542	0.536
Boxing #2	0.476	0.000	0.363	0.219	0.195
Boxing #3	0.557	0.363	0.000	0.437	0.430
Boxing #4	0.542	0.219	0.437	0.000	0.074
Boxing #5	0.536	0.195	0.430	0.074	0.000
	Breakout #1	Breakout #2	Breakout #3	Breakout #4	Breakout #5
Breakout #1	0.000	0.288	0.352	0.295	0.361
Breakout #2	0.288	0.000	0.418	0.332	0.434
Breakout #3	0.352	0.418	0.000	0.220	0.209
Breakout #4	0.295	0.332	0.220	0.000	0.213
Breakout #5	0.361	0.434	0.209	0.213	0.000
	Enduro #1	Enduro #2	Enduro #3	Enduro #4	Enduro #5
Enduro #1	0.000	0.023	0.017	0.020	0.021
Enduro #2	0.023	0.000	0.023	0.023	0.015
Enduro #3	0.017	0.023	0.000	0.019	0.014
Enduro #4	0.020	0.023	0.019	0.000	0.019
Enduro #5	0.021	0.015	0.014	0.019	0.000
	Freeway #1	Freeway #2	Freeway #3	Freeway #4	Freeway #5
Freeway #1	0.000	0.011	0.013	0.014	0.013
Freeway #2	0.011	0.000	0.012	0.011	0.011
Freeway #3	0.013	0.012	0.000	0.010	0.013
Freeway #4	0.014	0.011	0.010	0.000	0.012
Freeway #5	0.013	0.011	0.013	0.012	0.000
	KFM #1	KFM #2	KFM #3	KFM #4	KFM #5
KFM #1	0.000	0.067	0.060	0.078	0.315
KFM #2	0.067	0.000	0.076	0.078	0.334
KFM #3	0.060	0.076	0.000	0.098	0.282
KFM #4	0.078	0.078	0.098	0.000	0.317
KFM #5	0.315	0.334	0.282	0.317	0.000
	Pong #1	Pong #2	Pong #3	Pong #4	Pong #5
Pong #1	0.000	0.113	0.137	0.114	0.476
Pong #2	0.113	0.000	0.152	0.120	0.485
Pong #3	0.137	0.152	0.000	0.119	0.358
Pong #4	0.114	0.120	0.119	0.000	0.444
Pong #5	0.476	0.485	0.358	0.444	0.000
	Qbert #1	Qbert #2	Qbert #3	Qbert #4	Qbert #5
Qbert #1	0.000	0.225	0.013	0.156	0.225
Qbert #2	0.225	0.000	0.225	0.272	0.255
Qbert #3	0.013	0.225	0.000	0.159	0.225
Qbert #4	0.156	0.272	0.159	0.000	0.255
Qbert #5	0.225	0.255	0.225	0.255	0.000

) confirm the qualitative findings.

• Freeway and Enduro show extremely low TV distances (mostly <0.1 for Freeway, <0.15 for Enduro) and MMD values (mostly <0.015 for Freeway, <0.025 for Enduro), confirming that all agents have statistically very similar observation distributions.
• Boxing, Qbert, and KFM show very high TV distances, often approaching 1.0, indicating that many agent pairs explore almost entirely different sets of state clusters. For instance, the TV distance between Qbert #1 and Qbert #2 is 0.831. In KFM, the low-performing agent #5 has TV distances > 0.7 against all other agents. The MMD values are correspondingly high, quantitatively demonstrating the stark divergence in exploration.

3.3.3. Sensitivity to Cluster Number K

To ensure our findings were not an artifact of the chosen cluster number (K = 100), we repeated the analysis for K = 50 and K = 200. While the absolute values of the dispersion and TV distance metrics changed with K (as expected), the relative trends remained consistent. For instance, across all values of K, Freeway and Enduro agents consistently showed high, uniform dispersion and low pairwise TV distances. Conversely, Boxing and Qbert agents consistently exhibited significant differences in dispersion and high pairwise TV distances. This indicates that our core conclusion—that performance variance correlates with observation space divergence—is robust to the specific granularity of state space discretization. The complete tables for this sensitivity analysis, which confirm these trends, are provided in the Appendix A.

3.4. Analysis of Actor and Value Network Differences

Cross-evaluation of the learned networks (

Table 6. Mean and standard deviation of absolute TD-error (value eetwork cross-evaluation).

	Alien #1	Alien #2	Alien #3	Alien #4	Alien #5
Alien #1	5.062 (13.643)	4.566 (20.929)	4.126 (21.149)	3.962 (21.101)	4.096 (21.242)
Alien #2	4.426 (19.533)	4.855 (18.012)	3.631 (19.554)	3.677 (19.447)	3.610 (19.559)
Alien #3	5.524 (15.813)	4.156 (14.448)	3.414 (14.492)	3.787 (14.483)	3.670 (14.567)
Alien #4	4.288 (11.267)	4.177 (11.085)	3.442 (10.821)	3.929 (8.413)	3.775 (10.457)
Alien #5	3.610 (11.117)	4.304 (11.979)	2.804 (10.900)	3.355 (11.073)	3.093 (10.593)
	Boxing #1	Boxing #2	Boxing #3	Boxing #4	Boxing #5
Boxing #1	0.302 (0.318)	0.596 (0.555)	0.492 (0.563)	0.482 (0.543)	0.389 (0.516)
Boxing #2	0.806 (0.756)	0.278 (0.281)	0.398 (0.519)	0.282 (0.443)	0.239 (0.415)
Boxing #3	0.887 (0.785)	0.937 (0.802)	0.211 (0.220)	0.578 (0.571)	0.425 (0.512)
Boxing #4	0.780 (0.640)	0.375 (0.342)	0.339 (0.327)	0.165 (0.211)	0.181 (0.227)
Boxing #5	0.777 (0.683)	0.395 (0.384)	0.352 (0.376)	0.202 (0.274)	0.178 (0.245)
	Breakout #1	Breakout #2	Breakout #3	Breakout #4	Breakout #5
Breakout #1	0.492 (4.030)	0.496 (4.823)	0.360 (1.212)	0.510 (1.231)	0.510 (2.710)
Breakout #2	0.299 (3.824)	0.331 (4.800)	0.173 (0.858)	0.165 (0.635)	0.224 (2.645)
Breakout #3	0.273 (4.810)	0.283 (5.625)	0.126 (0.699)	0.098 (0.758)	0.110 (2.346)
Breakout #4	0.406 (4.518)	0.527 (5.628)	0.488 (0.842)	0.213 (0.868)	0.313 (2.500)
Breakout #5	0.275 (4.896)	0.324 (5.904)	0.125 (0.808)	0.108 (0.819)	0.117 (2.402)
	Enduro #1	Enduro #2	Enduro #3	Enduro #4	Enduro #5
Enduro #1	0.365 (0.556)	0.375 (0.543)	0.362 (0.535)	0.384 (0.544)	0.369 (0.516)
Enduro #2	0.362 (0.556)	0.368 (0.541)	0.356 (0.534)	0.383 (0.548)	0.365 (0.513)
Enduro #3	0.346 (0.524)	0.358 (0.520)	0.341 (0.504)	0.366 (0.518)	0.354 (0.496)
Enduro #4	0.365 (0.569)	0.377 (0.559)	0.362 (0.545)	0.380 (0.551)	0.369 (0.530)
Enduro #5	0.358 (0.530)	0.366 (0.521)	0.351 (0.509)	0.376 (0.527)	0.357 (0.493)
	Freeway #1	Freeway #2	Freeway #3	Freeway #4	Freeway #5
Freeway #1	0.014 (0.018)	0.015 (0.019)	0.014 (0.018)	0.014 (0.017)	0.011 (0.018)
Freeway #2	0.014 (0.019)	0.015 (0.019)	0.014 (0.018)	0.014 (0.018)	0.011 (0.019)
Freeway #3	0.015 (0.019)	0.015 (0.019)	0.014 (0.019)	0.014 (0.018)	0.011 (0.018)
Freeway #4	0.014 (0.018)	0.015 (0.018)	0.014 (0.018)	0.014 (0.017)	0.011 (0.017)
Freeway #5	0.015 (0.019)	0.015 (0.019)	0.014 (0.018)	0.015 (0.018)	0.012 (0.019)
	KFM #1	KFM #2	KFM #3	KFM #4	KFM #5
KFM #1	21.380 (40.486)	21.578 (39.371)	21.223 (38.835)	20.854 (37.581)	22.033 (40.885)
KFM #2	21.788 (41.577)	21.903 (40.504)	21.573 (40.012)	21.547 (38.781)	22.244 (41.771)
KFM #3	20.385 (37.923)	20.541 (37.465)	20.302 (35.906)	19.908 (34.719)	20.512 (37.669)
KFM #4	21.799 (41.559)	21.873 (40.700)	21.747 (40.639)	21.488 (39.138)	22.458 (42.314)
KFM #5	14.926 (28.450)	15.255 (32.852)	15.377 (28.981)	14.786 (28.030)	15.571 (30.718)
	Pong #1	Pong #2	Pong #3	Pong #4	Pong #5
Pong #1	0.005 (0.005)	0.013 (0.033)	0.068 (0.144)	0.123 (0.153)	0.116 (0.118)
Pong #2	0.011 (0.043)	0.007 (0.008)	0.063 (0.146)	0.114 (0.156)	0.111 (0.119)
Pong #3	0.054 (0.190)	0.067 (0.227)	0.011 (0.011)	0.126 (0.163)	0.089 (0.098)
Pong #4	0.104 (0.162)	0.125 (0.218)	0.089 (0.121)	0.017 (0.024)	0.119 (0.152)
Pong #5	0.063 (0.184)	0.087 (0.249)	0.048 (0.107)	0.129 (0.175)	0.028 (0.027)
	Qbert #1	Qbert #2	Qbert #3	Qbert #4	Qbert #5
Qbert #1	13.459 (40.799)	17.428 (68.259)	21.169 (48.023)	18.693 (48.216)	23.974 (63.322)
Qbert #2	21.006 (76.693)	21.924 (55.678)	19.646 (69.327)	19.100 (87.946)	22.719 (68.507)
Qbert #3	12.338 (38.798)	16.137 (66.068)	18.025 (44.184)	17.672 (47.846)	22.270 (63.021)
Qbert #4	14.591 (65.426)	9.250 (41.167)	22.122 (53.370)	12.973 (45.607)	17.736 (42.792)
Qbert #5	5.782 (21.723)	30.517 (78.335)	15.457 (31.070)	5.923 (24.812)	19.779 (43.431)

,

Table 7. RMSE of value predictions (value network cross-evaluation).

	Alien #1	Alien #2	Alien #3	Alien #4	Alien #5
Alien #1	0.000	144.577	113.062	144.116	142.873
Alien #2	94.272	0.000	94.082	100.405	91.038
Alien #3	98.369	50.567	0.000	50.526	49.087
Alien #4	60.747	54.165	57.083	0.000	57.330
Alien #5	58.614	46.007	56.287	53.889	0.000
	Boxing #1	Boxing #2	Boxing #3	Boxing #4	Boxing #5
Boxing #1	0.000	14.821	17.998	18.625	18.874
Boxing #2	5.238	0.000	6.008	5.078	5.472
Boxing #3	11.721	2.514	0.000	1.814	2.654
Boxing #4	8.454	3.326	1.733	0.000	0.778
Boxing #5	8.926	4.008	1.320	0.633	0.000
	Breakout #1	Breakout #2	Breakout #3	Breakout #4	Breakout #5
Breakout #1	0.000	13.209	13.732	7.988	9.830
Breakout #2	9.126	0.000	5.545	6.682	7.023
Breakout #3	6.973	5.874	0.000	3.001	4.424
Breakout #4	6.980	7.435	3.630	0.000	4.300
Breakout #5	9.928	12.507	4.670	6.514	0.000
	Enduro #1	Enduro #2	Enduro #3	Enduro #4	Enduro #5
Enduro #1	0.000	0.660	0.832	0.761	1.004
Enduro #2	0.651	0.000	0.775	0.695	0.920
Enduro #3	0.796	0.749	0.000	0.651	0.750
Enduro #4	0.712	0.694	0.634	0.000	0.698
Enduro #5	1.007	0.927	0.791	0.747	0.000
	Freeway #1	Freeway #2	Freeway #3	Freeway #4	Freeway #5
Freeway #1	0.000	0.023	0.028	0.030	0.069
Freeway #2	0.022	0.000	0.026	0.031	0.068
Freeway #3	0.027	0.027	0.000	0.028	0.061
Freeway #4	0.030	0.030	0.028	0.000	0.056
Freeway #5	0.063	0.068	0.061	0.058	0.000
	KFM #1	KFM #2	KFM #3	KFM #4	KFM #5
KFM #1	0.000	41.427	71.822	74.515	99.879
KFM #2	40.641	0.000	69.775	57.753	96.297
KFM #3	75.014	68.594	0.000	43.661	48.528
KFM #4	83.364	63.393	47.948	0.000	77.542
KFM #5	61.220	43.578	40.010	51.762	0.000
	Pong #1	Pong #2	Pong #3	Pong #4	Pong #5
Pong #1	0.000	0.101	0.366	0.818	0.874
Pong #2	0.187	0.000	0.371	0.786	0.877
Pong #3	0.392	0.355	0.000	0.757	0.773
Pong #4	0.677	0.487	0.391	0.000	0.631
Pong #5	0.414	0.465	0.361	0.647	0.000
	Qbert #1	Qbert #2	Qbert #3	Qbert #4	Qbert #5
Qbert #1	0.000	593.532	80.419	145.879	397.322
Qbert #2	502.554	0.000	469.197	522.818	380.142
Qbert #3	76.790	569.957	0.000	110.466	364.446
Qbert #4	251.197	296.141	151.877	0.000	227.688
Qbert #5	244.059	293.804	158.743	250.996	0.000

and

Table 8. Mean and standard deviation of KL divergence of action logits (actor network cross-evaluation).

	Alien #1	Alien #2	Alien #3	Alien #4	Alien #5
Alien #1	0.000	3.640 (2.879)	2.441 (3.047)	3.451 (2.731)	4.730 (4.081)
Alien #2	3.251 (3.140)	0.000	2.253 (2.433)	2.831 (2.740)	2.213 (2.185)
Alien #3	2.105 (2.308)	2.308 (2.391)	0.000	3.250 (2.959)	4.702 (4.060)
Alien #4	2.916 (2.809)	2.705 (3.039)	2.899 (3.103)	0.000	3.208 (3.014)
Alien #5	3.262 (3.063)	2.092 (2.352)	3.758 (4.141)	2.801 (2.476)	0.000
	Boxing #1	Boxing #2	Boxing #3	Boxing #4	Boxing #5
Boxing #1	0.000	9.609 (4.661)	6.428 (4.556)	6.798 (3.950)	4.989 (3.495)
Boxing #2	10.185 (7.840)	0.000	6.217 (5.017)	4.573 (5.023)	4.514 (5.009)
Boxing #3	12.033 (8.884)	7.685 (5.039)	0.000	6.610 (3.730)	6.582 (4.077)
Boxing #4	10.883 (7.330)	5.016 (4.726)	5.804 (3.565)	0.000	2.552 (3.602)
Boxing #5	10.436 (7.049)	4.731 (4.573)	5.519 (3.862)	1.836 (2.045)	0.000
	Breakout #1	Breakout #2	Breakout #3	Breakout #4	Breakout #5
Breakout #1	0.000	0.496 (0.975)	1.798 (2.181)	0.602 (1.265)	1.297 (1.968)
Breakout #2	1.065 (1.537)	0.000	0.782 (0.929)	0.469 (0.818)	1.656 (1.960)
Breakout #3	0.423 (0.759)	0.457 (0.577)	0.000	0.243 (0.917)	0.363 (0.681)
Breakout #4	0.968 (1.415)	0.631 (1.055)	0.667 (0.937)	0.000	0.991 (1.439)
Breakout #5	0.367 (0.828)	0.426 (0.576)	0.163 (0.644)	0.187 (0.803)	0.000
	Enduro #1	Enduro #2	Enduro #3	Enduro #4	Enduro #5
Enduro #1	0.000	0.709 (0.862)	0.688 (0.775)	0.668 (0.863)	0.790 (0.881)
Enduro #2	0.737 (0.840)	0.000	0.732 (0.854)	0.685 (0.822)	0.760 (0.902)
Enduro #3	0.679 (0.810)	0.752 (0.998)	0.000	0.642 (1.018)	0.646 (0.953)
Enduro #4	0.657 (0.828)	0.667 (0.834)	0.649 (0.807)	0.000	0.682 (0.968)
Enduro #5	0.782 (0.839)	0.735 (0.883)	0.630 (0.686)	0.676 (0.806)	0.000
	Freeway #1	Freeway #2	Freeway #3	Freeway #4	Freeway #5
Freeway #1	0.000	0.002 (0.000)	0.000 (0.000)	0.003 (0.000)	0.124 (0.005)
Freeway #2	0.001 (0.000)	0.000	0.001 (0.000)	0.003 (0.000)	0.109 (0.004)
Freeway #3	0.000 (0.000)	0.001 (0.000)	0.000	0.002 (0.001)	0.108 (0.013)
Freeway #4	0.002 (0.000)	0.002 (0.000)	0.002 (0.000)	0.000	0.040 (0.001)
Freeway #5	0.008 (0.000)	0.007 (0.000)	0.007 (0.001)	0.003 (0.000)	0.000
	KFM #1	KFM #2	KFM #3	KFM #4	KFM #5
KFM #1	0.000	0.042 (0.022)	0.035 (0.036)	0.051 (0.073)	0.042 (0.025)
KFM #2	0.043 (0.030)	0.000	0.039 (0.021)	0.022 (0.029)	0.088 (0.032)
KFM #3	0.039 (0.038)	0.045 (0.027)	0.000	0.039 (0.037)	0.037 (0.030)
KFM #4	0.060 (0.111)	0.024 (0.037)	0.046 (0.052)	0.000	0.093 (0.103)
KFM #5	0.080 (0.031)	0.142 (0.055)	0.034 (0.027)	0.064 (0.050)	0.000
	Pong #1	Pong #2	Pong #3	Pong #4	Pong #5
Pong #1	0.000	0.983 (1.202)	0.924 (1.483)	5.373 (5.521)	2.513 (2.894)
Pong #2	0.713 (0.800)	0.000	0.960 (1.497)	6.800 (6.938)	2.327 (2.432)
Pong #3	1.027 (1.653)	1.376 (1.828)	0.000	4.076 (4.804)	2.049 (2.235)
Pong #4	1.650 (1.814)	2.251 (2.687)	1.427 (1.864)	0.000	1.853 (2.703)
Pong #5	1.336 (1.880)	1.838 (2.165)	1.093 (1.477)	3.119 (3.791)	0.000
	Qbert #1	Qbert #2	Qbert #3	Qbert #4	Qbert #5
Qbert #1	0.000	0.805 (1.399)	0.108 (0.174)	0.690 (0.972)	0.221 (0.469)
Qbert #2	0.876 (1.184)	0.000	1.133 (2.091)	0.622 (0.968)	0.702 (0.856)
Qbert #3	0.118 (0.216)	0.723 (1.425)	0.000	0.753 (1.209)	0.201 (0.462)
Qbert #4	0.688 (1.396)	0.991 (1.908)	0.696 (1.486)	0.000	0.548 (0.970)
Qbert #5	0.525 (0.832)	0.749 (1.153)	0.322 (0.729)	0.508 (0.734)	0.000

) shows that divergence in observation space corresponds to functional divergence in the actor and value networks.

• For Freeway and Enduro, the off-diagonal values in the TD-error, RMSE, and KLD tables are very low, often close to the diagonal (self-evaluation) values. This means any agent’s networks can accurately predict values and replicate policies for states experienced by any other agent, indicating functional convergence.
• For Boxing, Qbert, and KFM, the off-diagonal values are substantially high. The KLD values in Boxing are frequently above 5.0, and the RMSE values in Qbert can be in the hundreds. This signifies that the agents have learned profoundly different policies and value functions that are highly specialized to their own unique experiences and do not generalize to those of their peers.

This provides strong evidence that when agents see different things, they learn to do other things, and their internal models of the world (value functions) become incompatible.

3.5. Analysis of Methodology Choices

3.5.1. Trustworthiness of t-SNE

To validate our choice of perplexity 30 for the t-SNE visualizations, we computed the trustworthiness metric for a range of perplexity values. Trustworthiness measures how well the local structure of the original high-dimensional data is preserved in the low-dimensional embedding. As shown in

Table 9. Trustworthiness scores of t-SNE embeddings across varying perplexity values. Columns denote different perplexity settings, and cell entries are the corresponding trustworthiness metrics, with the highest score highlighted in bold.

Task	5	10	30	50	200
Alien	0.9122	0.9166	0.9092	0.9063	0.8992
Boxing	0.9966	0.9984	0.9985	0.9984	0.9979
Breakout	0.9731	0.9865	0.9893	0.9880	0.9916
Enduro	0.9954	0.9965	0.9969	0.9968	0.9966
Freeway	0.9976	0.9995	0.9998	0.9997	0.9995
KFM	0.9958	0.9975	0.9967	0.9963	0.9951
Pong	0.9897	0.9959	0.9959	0.9959	0.9946
Qbert	0.9870	0.9994	0.9996	0.9995	0.9993

, a perplexity of 30 consistently yields high trustworthiness scores across most environments, indicating a reliable visualization.

3.5.2. Computation Time

Our analysis pipeline is computationally efficient. As shown in

Table 10. Mean and standard deviation of computation time (seconds) for PCA and K-means with K = 50, 100, and 200.

Task	PCA	K-Means
		50	100	200
Alien	12.516 (0.415)	0.133 (0.007)	0.546 (0.135)	0.871 (0.334)
Boxing	12.448 (0.411)	0.137 (0.006)	0.445 (0.172)	0.718 (0.346)
Breakout	13.845 (1.255)	0.111 (0.006)	0.443 (0.151)	0.777 (0.409)
Enduro	12.514 (0.469)	0.124 (0.003)	0.537 (0.136)	0.905 (0.202)
Freeway	12.169 (0.471)	0.125 (0.004)	0.465 (0.150)	0.552 (0.372)
KFM	12.568 (0.509)	0.119 (0.002)	0.542 (0.037)	0.917 (0.254)
Pong	11.910 (0.447)	0.146 (0.021)	0.350 (0.178)	0.403 (0.297)
Qbert	12.170 (0.527)	0.112 (0.005)	0.434 (0.145)	0.676 (0.369)

, PCA and K-means clustering take only a few seconds to a minute on the subsampled data. The main bottleneck is memory; increasing the number of samples per agent beyond 5000 becomes challenging, highlighting a limitation for even more fine-grained analyses on standard hardware.

3.6. Impact of Identical Network Initialization

To test whether performance variability stems solely from different random initializations or from the training process itself, we ran experiments where all five agents in an environment started with the same network weights. The results show that performance variance, while sometimes reduced, remains substantial in high-variance environments (

Table 11. Performance of trained agents with identically initialized networks (mean and standard deviation of rewards).

Task	#1	#2	#3	#4	#5
Alien	1456.00 (1065.92)	1079.33 (211.80)	1075.00 (425.80)	1070.33 (325.79)	916.33 (631.83)
Boxing	100.00 (0.00)	93.77 (2.50)	93.77 (2.60)	93.03 (4.53)	90.97 (3.43)
Freeway	21.43 (1.31)	21.33 (1.35)	21.30 (1.37)	21.27 (1.29)	21.13 (1.12)
Qbert	4050.00 (0.00)	4010.00 (48.99)	958.33 (221.11)	873.33 (44.22)	800.00 (0.00)

). In Boxing, scores still ranged from 100 down to 90.97. In Qbert, the gap was even larger, from 4050 down to 800. In contrast, Freeway remained highly consistent. Crucially, the observation space and network divergence metrics for these agents mirrored the results from the randomly initialized experiments. For instance, in high-variance environments like Boxing and Qbert, the single-agent dispersion statistics showed considerable spread between agents, unlike in Freeway where all agents explored consistently (

Table 12. Single agent dispersion statistics of trained agents with identically initialized networks.

Agent	H	${\mathit{N}}_{\mathit{eff}}$	$\mathbf{Cov}$	G
Alien #1	3.84	46.55	0.66	0.97
Alien #2	3.46	31.88	0.77	0.93
Alien #3	3.42	30.48	0.60	0.95
Alien #4	3.71	40.69	0.76	0.97
Alien #5	3.72	41.14	0.77	0.96
Boxing #1	2.77	15.89	0.28	0.92
Boxing #2	3.35	28.45	0.49	0.96
Boxing #3	3.83	46.28	0.65	0.98
Boxing #4	3.04	20.84	0.40	0.95
Boxing #5	3.82	45.46	0.67	0.97
Freeway #1	4.55	94.53	0.99	0.99
Freeway #2	4.54	93.97	1.00	0.99
Freeway #3	4.54	93.89	1.00	0.99
Freeway #4	4.54	93.80	1.00	0.99
Freeway #5	4.55	94.28	1.00	0.99
Qbert #1	3.08	21.82	0.43	0.93
Qbert #2	3.29	26.77	0.47	0.94
Qbert #3	2.92	18.46	0.31	0.93
Qbert #4	2.93	18.74	0.38	0.92
Qbert #5	3.04	20.90	0.37	0.93

). This divergence in experience led to functionally different networks; the cross-agent absolute TD-error was substantial in high-variance games but negligible in Freeway (

Table 13. Mean and standard deviation of absolute TD-error for agents with identically initialized networks (value network cross-evaluation).

	Alien #1	Alien #2	Alien #3	Alien #4	Alien #5
Alien #1	7.938 (34.771)	5.529 (40.785)	5.497 (40.223)	4.728 (40.526)	4.891 (40.635)
Alien #2	5.081 (17.172)	4.217 (8.028)	4.382 (16.863)	4.026 (14.063)	5.109 (11.535)
Alien #3	4.118 (14.219)	3.482 (14.628)	4.185 (13.904)	3.327 (14.711)	3.784 (14.777)
Alien #4	4.507 (17.851)	4.143 (17.104)	4.017 (17.549)	4.390 (17.833)	4.850 (19.507)
Alien #5	4.544 (16.142)	3.611 (15.878)	4.308 (16.030)	3.650 (15.803)	3.995 (15.891)
	Boxing #1	Boxing #2	Boxing #3	Boxing #4	Boxing #5
Boxing #1	0.036 (0.036)	0.570 (0.795)	0.554 (0.762)	0.598 (0.676)	0.516 (0.650)
Boxing #2	0.908 (0.858)	0.173 (0.213)	0.279 (0.313)	0.435 (0.370)	0.319 (0.327)
Boxing #3	1.336 (1.549)	0.241 (0.321)	0.221 (0.275)	0.455 (0.440)	0.247 (0.308)
Boxing #4	0.770 (0.727)	0.277 (0.332)	0.301 (0.339)	0.174 (0.216)	0.273 (0.293)
Boxing #5	1.171 (1.296)	0.257 (0.342)	0.245 (0.320)	0.425 (0.418)	0.215 (0.274)
	Freeway #1	Freeway #2	Freeway #3	Freeway #4	Freeway #5
Freeway #1	0.015 (0.018)	0.015 (0.018)	0.017 (0.019)	0.016 (0.019)	0.012 (0.019)
Freeway #2	0.015 (0.018)	0.015 (0.018)	0.016 (0.019)	0.016 (0.019)	0.012 (0.018)
Freeway #3	0.015 (0.018)	0.014 (0.017)	0.016 (0.018)	0.016 (0.019)	0.011 (0.018)
Freeway #4	0.014 (0.018)	0.014 (0.016)	0.016 (0.018)	0.016 (0.018)	0.011 (0.017)
Freeway #5	0.014 (0.018)	0.014 (0.017)	0.016 (0.018)	0.016 (0.018)	0.011 (0.017)
	Qbert #1	Qbert #2	Qbert #3	Qbert #4	Qbert #5
Qbert #1	17.643 (43.687)	23.649 (65.018)	28.110 (86.530)	16.074 (66.547)	22.951 (88.250)
Qbert #2	14.553 (36.225)	16.889 (54.559)	24.112 (85.800)	10.127 (61.133)	17.677 (83.162)
Qbert #3	11.549 (25.748)	7.513 (22.826)	2.730 (11.624)	8.916 (31.148)	7.016 (30.265)
Qbert #4	22.447 (27.629)	14.627 (23.644)	16.403 (22.565)	9.976 (23.709)	9.516 (15.295)
Qbert #5	21.291 (50.213)	15.357 (41.226)	14.825 (24.857)	21.417 (66.445)	3.444 (6.031)

). This pattern of divergence is also confirmed by the high pairwise dissimilarity (high TV and MMD values, see

Table 14. Pairwise TV distance for agents with identically initialized networks.

	Alien #1	Alien #2	Alien #3	Alien #4	Alien #5
Alien #1	0.000	0.619	0.822	0.643	0.718
Alien #2	0.619	0.000	0.774	0.700	0.638
Alien #3	0.822	0.774	0.000	0.757	0.740
Alien #4	0.643	0.700	0.757	0.000	0.613
Alien #5	0.718	0.638	0.740	0.613	0.000
	Boxing #1	Boxing #2	Boxing #3	Boxing #4	Boxing #5
Boxing #1	0.000	0.929	0.929	0.973	0.933
Boxing #2	0.929	0.000	0.773	0.979	0.850
Boxing #3	0.929	0.773	0.000	0.974	0.289
Boxing #4	0.973	0.979	0.974	0.000	0.972
Boxing #5	0.933	0.850	0.289	0.972	0.000
	Freeway #1	Freeway #2	Freeway #3	Freeway #4	Freeway #5
Freeway #1	0.000	0.065	0.072	0.074	0.074
Freeway #2	0.065	0.000	0.067	0.068	0.072
Freeway #3	0.072	0.067	0.000	0.075	0.079
Freeway #4	0.074	0.068	0.075	0.000	0.072
Freeway #5	0.074	0.072	0.079	0.072	0.000
	Qbert #1	Qbert #2	Qbert #3	Qbert #4	Qbert #5
Qbert #1	0.000	0.758	0.916	0.898	0.879
Qbert #2	0.758	0.000	0.895	0.730	0.713
Qbert #3	0.916	0.895	0.000	0.903	0.891
Qbert #4	0.898	0.730	0.903	0.000	0.777
Qbert #5	0.879	0.713	0.891	0.777	0.000

and

Table 15. Pairwise MMD for agents with identically initialized networks.

	Alien #1	Alien #2	Alien #3	Alien #4	Alien #5
Alien #1	0.000	0.215	0.348	0.250	0.291
Alien #2	0.215	0.000	0.328	0.229	0.226
Alien #3	0.348	0.328	0.000	0.291	0.264
Alien #4	0.250	0.229	0.291	0.000	0.163
Alien #5	0.291	0.226	0.264	0.163	0.000
	Boxing #1	Boxing #2	Boxing #3	Boxing #4	Boxing #5
Boxing #1	0.000	0.553	0.538	0.559	0.544
Boxing #2	0.553	0.000	0.225	0.463	0.277
Boxing #3	0.538	0.225	0.000	0.441	0.095
Boxing #4	0.559	0.463	0.441	0.000	0.442
Boxing #5	0.544	0.277	0.095	0.442	0.000
	Freeway #1	Freeway #2	Freeway #3	Freeway #4	Freeway #5
Freeway #1	0.000	0.011	0.011	0.012	0.011
Freeway #2	0.011	0.000	0.011	0.012	0.010
Freeway #3	0.011	0.011	0.000	0.012	0.011
Freeway #4	0.012	0.012	0.012	0.000	0.013
Freeway #5	0.011	0.010	0.011	0.013	0.000
	Qbert #1	Qbert #2	Qbert #3	Qbert #4	Qbert #5
Qbert #1	0.000	0.194	0.375	0.322	0.275
Qbert #2	0.194	0.000	0.322	0.266	0.241
Qbert #3	0.375	0.322	0.000	0.278	0.313
Qbert #4	0.322	0.266	0.278	0.000	0.232
Qbert #5	0.275	0.241	0.313	0.232	0.000

) and network error metrics (high RMSE and KLD values, see

Table 16. RMSE of value predictions for agents with identically initialized networks (value network cross-evaluation).

	Alien #1	Alien #2	Alien #3	Alien #4	Alien #5
Alien #1	0.000	211.413	205.393	209.773	206.833
Alien #2	105.855	0.000	107.732	95.769	74.780
Alien #3	81.813	81.002	0.000	88.808	93.255
Alien #4	57.325	61.768	70.915	0.000	38.993
Alien #5	28.692	27.610	31.997	22.099	0.000
	Boxing #1	Boxing #2	Boxing #3	Boxing #4	Boxing #5
Boxing #1	0.000	26.277	25.232	25.964	25.476
Boxing #2	11.259	0.000	1.045	1.054	1.270
Boxing #3	13.332	1.433	0.000	1.671	0.544
Boxing #4	7.830	1.270	1.111	0.000	0.837
Boxing #5	11.726	1.829	0.761	2.079	0.000
	Freeway #1	Freeway #2	Freeway #3	Freeway #4	Freeway #5
Freeway #1	0.000	0.043	0.029	0.028	0.062
Freeway #2	0.042	0.000	0.039	0.039	0.041
Freeway #3	0.028	0.038	0.000	0.025	0.058
Freeway #4	0.026	0.038	0.024	0.000	0.060
Freeway #5	0.054	0.039	0.057	0.057	0.000
	Qbert #1	Qbert #2	Qbert #3	Qbert #4	Qbert #5
Qbert #1	0.000	381.729	477.101	518.526	554.895
Qbert #2	126.572	0.000	316.792	288.990	303.697
Qbert #3	129.170	109.197	0.000	125.973	115.177
Qbert #4	73.667	62.259	64.624	0.000	55.432
Qbert #5	299.573	496.026	144.667	541.692	0.000

and

Table 17. Average and standard deviation of KLD for agents with identically initialized networks (actor network cross-evaluation).

	Alien #1	Alien #2	Alien #3	Alien #4	Alien #5
Alien #1	0.000 (0.000)	2.588 (2.449)	3.184 (2.705)	2.074 (2.055)	3.578 (3.203)
Alien #2	3.646 (3.635)	0.000 (0.000)	3.365 (3.147)	2.009 (1.851)	2.290 (2.735)
Alien #3	3.841 (4.202)	3.185 (2.868)	0.000 (0.000)	3.947 (3.600)	3.666 (3.621)
Alien #4	2.905 (3.664)	1.577 (1.444)	3.203 (2.997)	0.000 (0.000)	2.232 (2.240)
Alien #5	3.798 (4.947)	1.728 (1.823)	3.778 (3.648)	3.017 (2.609)	0.000 (0.000)
	Boxing #1	Boxing #2	Boxing #3	Boxing #4	Boxing #5
Boxing #1	0.000 (0.000)	7.752 (5.730)	10.043 (6.436)	8.779 (5.299)	8.894 (5.835)
Boxing #2	6.039 (4.752)	0.000 (0.000)	7.312 (6.168)	5.546 (3.896)	6.794 (5.672)
Boxing #3	3.554 (4.251)	5.966 (5.001)	0.000 (0.000)	5.373 (3.457)	3.883 (5.556)
Boxing #4	5.014 (4.029)	3.505 (2.186)	7.819 (6.909)	0.000 (0.000)	10.088 (8.279)
Boxing #5	4.304 (4.144)	6.278 (5.051)	4.308 (5.592)	4.978 (2.780)	0.000 (0.000)
	Freeway #1	Freeway #2	Freeway #3	Freeway #4	Freeway #5
Freeway #1	0.000 (0.000)	0.010 (0.000)	0.001 (0.000)	0.000 (0.000)	0.148 (0.006)
Freeway #2	0.005 (0.000)	0.000 (0.000)	0.002 (0.000)	0.004 (0.000)	0.014 (0.001)
Freeway #3	0.001 (0.001)	0.004 (0.000)	0.000 (0.000)	0.001 (0.000)	0.086 (0.003)
Freeway #4	0.000 (0.000)	0.009 (0.000)	0.001 (0.000)	0.000 (0.000)	0.139 (0.005)
Freeway #5	0.007 (0.000)	0.001 (0.000)	0.004 (0.000)	0.007 (0.000)	0.000 (0.000)
	Qbert #1	Qbert #2	Qbert #3	Qbert #4	Qbert #5
Qbert #1	0.000 (0.000)	0.643 (1.246)	1.834 (3.214)	0.868 (1.672)	0.542 (1.135)
Qbert #2	1.124 (2.864)	0.000 (0.000)	1.687 (2.995)	0.492 (0.626)	0.472 (0.528)
Qbert #3	1.913 (4.283)	1.331 (2.403)	0.000 (0.000)	1.230 (2.116)	1.176 (2.075)
Qbert #4	1.016 (1.841)	0.441 (0.436)	1.276 (2.430)	0.000 (0.000)	0.376 (0.582)
Qbert #5	1.452 (2.305)	0.608 (0.704)	1.498 (2.852)	0.359 (0.546)	0.000 (0.000)

). The key finding is that the stochasticity of the agent–environment interaction loop itself is a powerful driver of divergence. Even from an identical starting point, chance exploration events can set agents on different learning pathways from which they do not recover, leading to the same pattern of specialized, non-transferable policies and significant performance gaps.

4. Discussion

The results from our expanded study across eight Atari games provide compelling and robust evidence that divergence in explored observation spaces is a primary driver of performance variability in DRL. Our analysis indicates that the degree of this divergence is not random but is strongly tied to the intrinsic characteristics of the environment itself. The Freeway environment serves as a crucial control case. The consistent performance of Freeway agents is tightly linked to their consistent exploration patterns. All agents are guided through a similar, comprehensive set of experiences, which leads to the development of functionally equivalent policies and value functions. In stark contrast, high-variance environments like Boxing, Breakout, KFM, and Qbert reveal the consequences of divergent exploration. In these more complex settings, agents can and do find different niches within the state space. The t-SNE plots and quantitative metrics show that agents often specialize in distinct sub-regions, becoming experts in local areas while remaining naive about others. This specialization is path-dependent; early stochastic events steer an agent toward a particular trajectory, and the actor–critic learning loop reinforces this direction. An agent’s value network becomes more accurate for its frequented states, which in turn biases its policy to continue visiting them. This creates a feedback loop that amplifies initial small differences into significant chasms in both experience and capability.

4.1. Environment Characteristics and Their Impact on Divergence

The consistent patterns of divergence and stability observed across the eight Atari games can be primarily attributed to their intrinsic mechanics and objectives. By categorizing the environments, we can provide more targeted guidance for future DRL applications.

4.1.1. Low-Divergence Environments: Structured and Convergent

Environments that foster low divergence and stable performance, such as Freeway, Pong, and Enduro, often share characteristics like a clear, singular objective and a functionally narrow state space that guides agents toward a single dominant strategy.

• In Freeway, the goal is simple and monotonic: move up. There are no complex sub-tasks or branching strategic paths. This structure naturally channels all agents toward the same optimal behavior, leading to highly overlapping observation spaces and consistent performance.
• Pong is a purely reactive game where the optimal policy is to mirror the ball’s vertical movement. The simplicity and deterministic nature of this strategy mean there is little room for meaningful strategic variation to emerge.
• Enduro, while more complex visually, is also driven by a primary objective of continuous forward progress and overtaking. The core gameplay loop does not contain significant strategic “bottlenecks” that could send agents down wildly different learning paths.

In these games, the path to high rewards is straightforward, causing all agent trajectories and policies to converge. For real-world problems with similar characteristics (e.g., simple process optimization), we can expect DRL training to be relatively stable and reproducible.

4.1.2. High-Divergence Environments: Strategic Bottlenecks and Divergent Policies

Conversely, environments prone to high divergences, such as Qbert, Boxing, KFM, and Breakout, often feature strategic bottlenecks, multiple viable strategies, or complex state dependencies that amplify the effects of stochasticity.

• Boxing is a highly interactive, opponent-dependent game. An agent might learn an aggressive rushing strategy, while another learns a defensive, counter-punching style. These are two distinct but viable approaches that lead to entirely different patterns of interaction, creating separate clusters in the observation space and varied performance outcomes.
• Qbert and KFM contain significant exploration challenges and “bottlenecks.” In KFM, an agent that fails to learn how to defeat a specific enemy type will be trapped in early-level states, while an agent that succeeds will unlock a vast new region of the observation space. This creates a sharp bifurcation in experience and performance. Similarly, the unique board structure in Qbert presents many locally optimal paths, causing agents to specialize in different sections of the pyramid.
• Breakout is a classic example of an environment with a critical strategic bottleneck: learning to tunnel the ball behind the brick wall. Agents that discover this strategy enter a new, high-scoring phase of the game with a completely different set of observations. Agents that fail to discover it remain trapped in a low-scoring, repetitive gameplay loop, leading to extreme performance variance.

4.2. Potential Applications of Observation Space Divergence Analysis

The observation space divergence analysis presented in this study extends beyond understanding the problem of performance variability in DRL; it can be directly utilized to devise solutions for improving evaluation performance in practical applications. Specifically, the findings of this research can be applied to ensemble methods—a widely used technique for surpassing the performance of single agents [14]—from two perspectives.

First, for improving evaluation performance via ensemble methods. When ensembling N agents to boost performance, a novel approach can be explored beyond conventional techniques, such as majority voting, simple averaging, or weighted sums based on rewards. Specifically, one could employ a weighted sum based on the similarity between the representation of the current observation and the observation space representation of each agent in the ensemble. This method would give priority to the actions of agents whose experiences are most similar to the current situation, thereby potentially leading to more sophisticated and higher performance.

Second, for analyzing why ensemble effectiveness varies across environments. Our findings provide insight into predicting whether an ensemble will be effective in a given environment. For instance, in an environment like Freeway, where all agents explore a highly similar observation space, we can predict that the benefit of ensembling will be minimal because the individual agent policies are already convergent. In contrast, in an environment like Boxing, where agents learn distinct strategies (e.g., aggressive vs. defensive) resulting in clearly separated observation spaces, we can anticipate a significant performance boost from ensembling, as combining their different specializations would be highly complementary. This provides a practical guideline for determining where to focus limited computational resources when constructing ensembles.

4.3. General Implications and Study Limitations

The most significant finding is from the identical initialization experiment. The persistence of high-performance variance and observation space divergence in games like Boxing and Qbert, even when starting from the same network weights, demonstrates that the problem is not merely one of poor initialization. The stochastic nature of the RL interaction process itself is sufficient to drive agents onto divergent paths. This suggests that achieving reproducible performance in complex environments requires more than just fixing random seeds; it may require fundamentally new approaches to guide exploration or to make learning more robust to variations in experience.

Our comprehensive set of metrics—from visual t-SNE to quantitative measures of dispersion (entropy, TV distance, MMD) and network function (TD-error, RMSE, KLD)—presents a unified narrative. When agents see different things (high TV/MMD), their understanding of the world diverges (high-value RMSE), and their resulting behaviors diverge (high policy KLD). This work highlights that reporting only the mean and standard deviation of final scores can obscure the rich and varied behaviors that contribute to those scores. A deeper analysis of the underlying state visitation distributions is crucial for a comprehensive understanding of DRL algorithm behavior.

We acknowledge that the empirical results of our study focus on the PPO algorithm within the Atari domain. This deliberate choice of scope enabled a deep and multifaceted analysis of the divergence phenomenon. However, it is reasonable to question how these findings generalize to other algorithms and environments. We hypothesize that the core mechanism—stochastic agent–environment interactions leading to divergent experiential trajectories and specialized policies—is a fundamental aspect of the reinforcement learning process and is not unique to PPO. For instance, off-policy algorithms like DQN or SAC, which utilize a replay buffer, might exhibit different dynamics. A replay buffer could mitigate divergence by averaging experiences across different trajectories. Conversely, it could also exacerbate the issue if certain types of “lucky” trajectories become overrepresented early in training. Similarly, extending this analysis to domains with continuous action spaces, such as robotics tasks in MuJoCo, or environments with sparser rewards, represents an important next step. Exploring how the structure of the state space and the nature of the reward function influence the degree of observation divergence is a compelling avenue for future research.

5. Conclusions and Future Works

This paper investigated the role of observation space divergence as a contributing factor to performance variability in deep reinforcement learning. Through a series of experiments on PPO agents across eight Atari environments, we demonstrated a strong link between the similarity of states explored by different agents, the functional similarity of their learned networks, and the consistency of their final performance. The key findings include the following:

• We expanded the analysis to eight Atari games, confirming that environments with low variance in performance (e.g., Freeway, Enduro) exhibit highly similar state space exploration across agents. In contrast, high-variance environments (e.g., Boxing, KFM, Qbert) show significant divergence.
• Cross-evaluation of actor and value networks confirmed that agents with divergent observation distributions learn functionally different networks that do not generalize well to each other’s experiences.
• A new experiment with identically initialized networks revealed that performance variability and observation space divergence persist even without different initial weights, highlighting that stochasticity in the agent–environment interaction is a primary source of this divergence.
• Our analysis was shown to be robust to the choice of the number of clusters (K) used for state discretization, and the computational cost of the analysis pipeline was found to be modest.

This work highlights the importance of examining not only the performance levels achieved but also how agents attain them. Building on this foundational analysis in PPO and Atari, future research should extend this investigation in several key directions:

• Temporal and Causal Analysis: Study the evolution of observation space differences during the training process. Analyzing the temporal relationship between when divergence occurs and when agent performance begins to vary would help establish a more direct causal link and better explain the dynamic nature of performance fluctuations.
• Systematic Component Analysis: Conduct a comparative analysis of how different DRL components influence exploration behavior and performance variability. This includes systematically varying hyperparameters, network architectures, and regularization techniques to understand their impact on the observation space distribution of trained agents.
• Broadening Algorithmic and Environmental Scope: Apply this analysis pipeline to a broader range of algorithms, including other on-policy variants and prominent off-policy algorithms (e.g., SAC, DQN), to determine how mechanisms like replay buffers affect divergence. Furthermore, expanding the study to other domains, such as continuous control benchmarks or environments with sparse rewards, is crucial to test the generality of our findings.
• Developing Mitigation Strategies: Based on the insights from a component-level analysis, develop and benchmark novel exploration or regularization methods specifically designed to reduce undesirable trajectory divergence, promote more consistent learning outcomes, and directly mitigate DRL performance variability.
• Theoretical Foundations: Work towards proposing a theoretical framework that can interpret these diverse experimental results, providing a more formal understanding of the relationship between stochastic exploration, state space coverage, and performance instability in DRL.