Natural Frequency of Monopile Supported Offshore Wind Turbine Structures Under Long-Term Cyclic Loading
Abstract
1. Introduction
2. Numerical Modelling
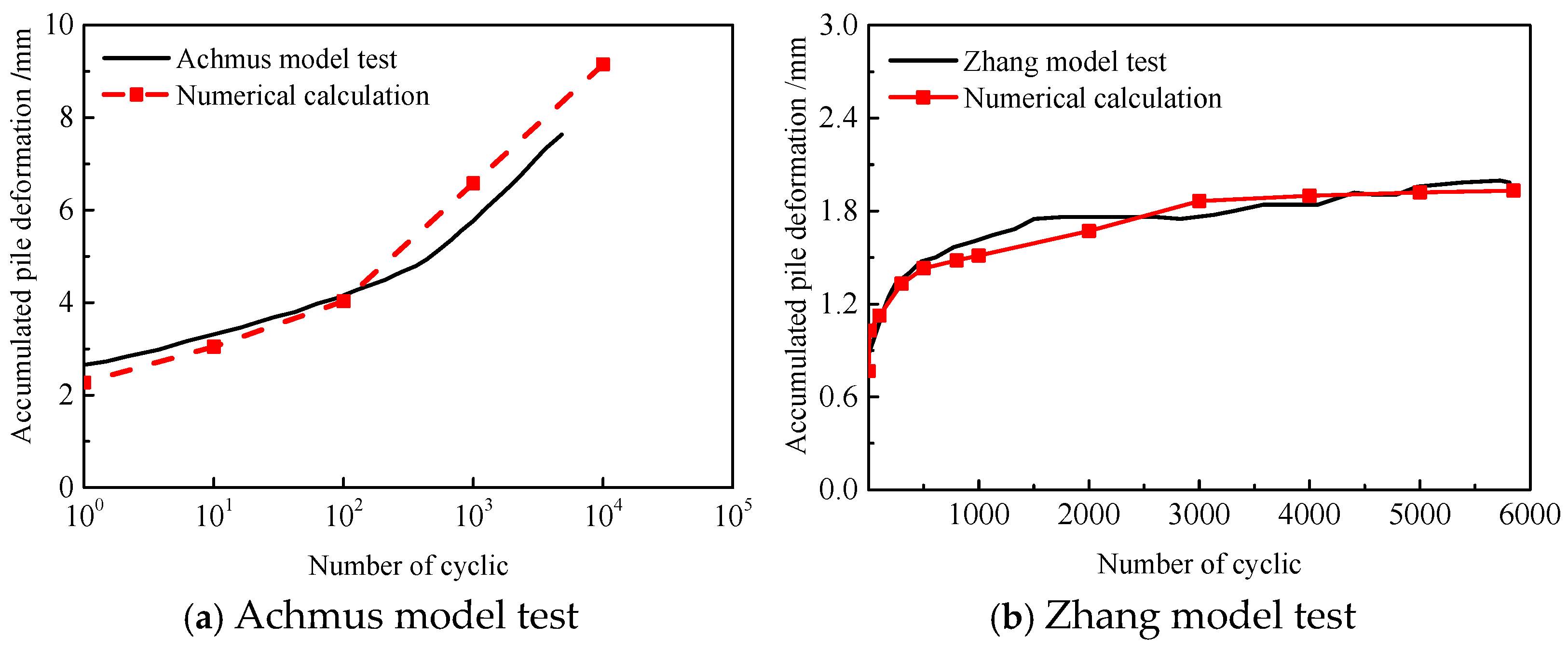
2.1. Validation of the Basic Model
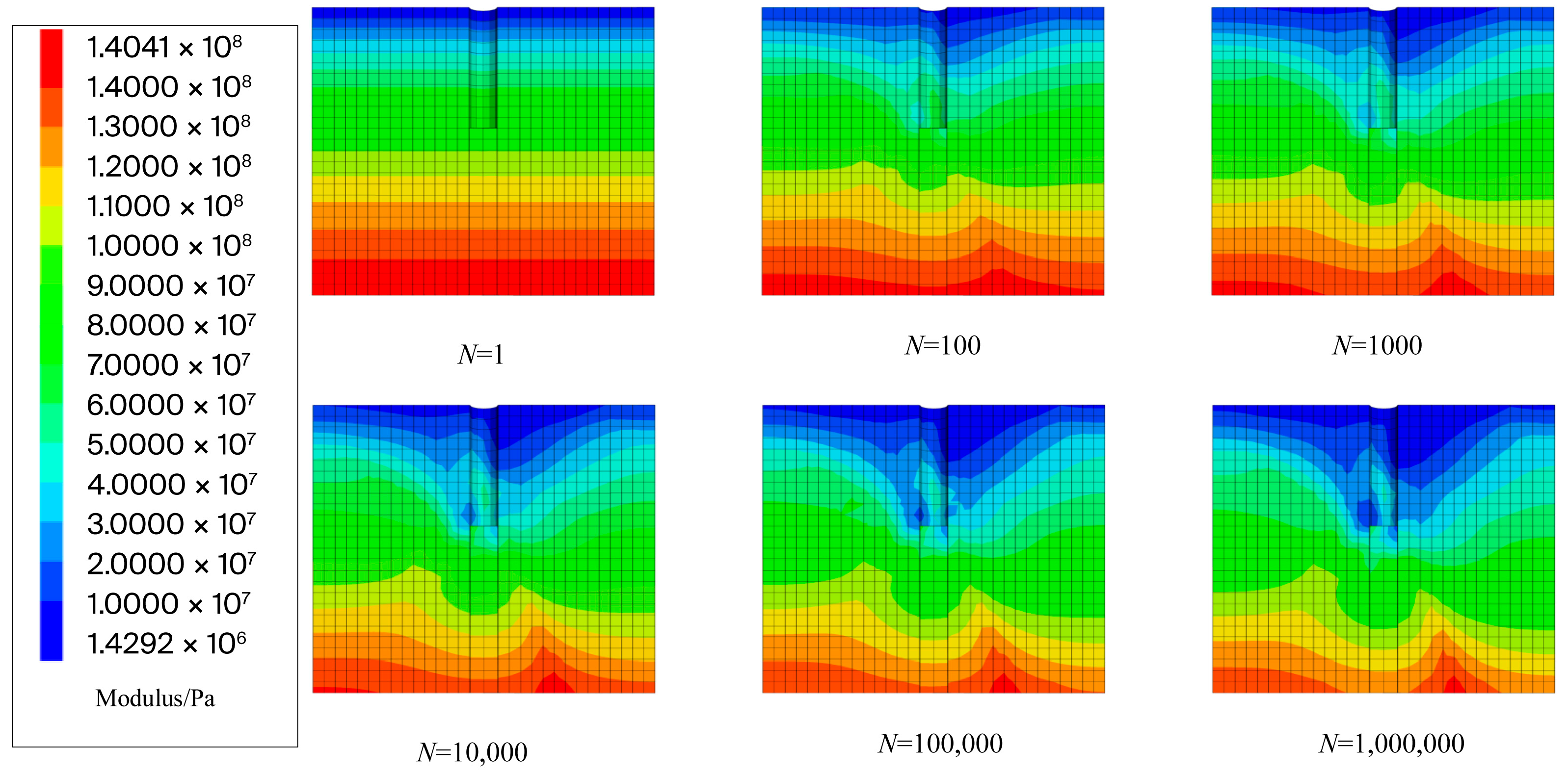
2.2. Soil Degradation Stiffness Model
3. Effect of Cyclic Loading
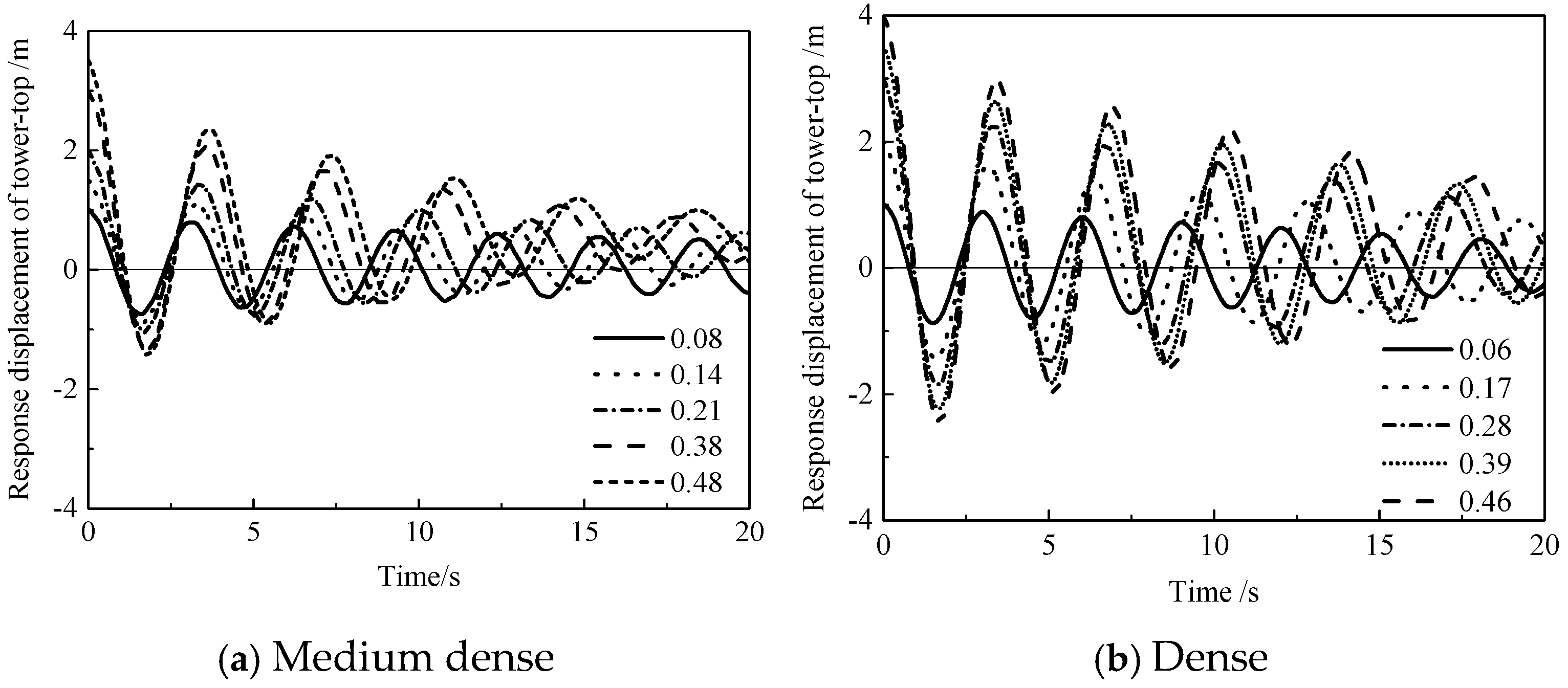
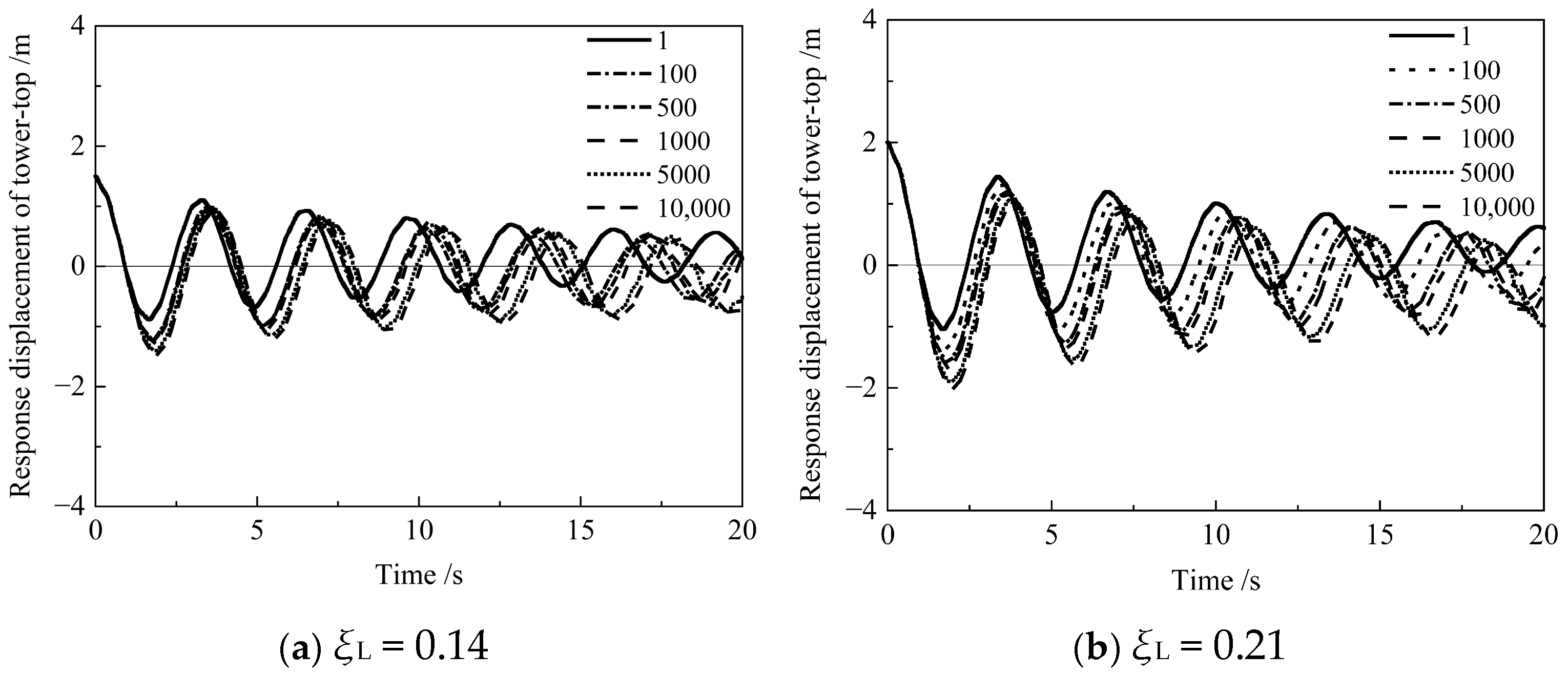
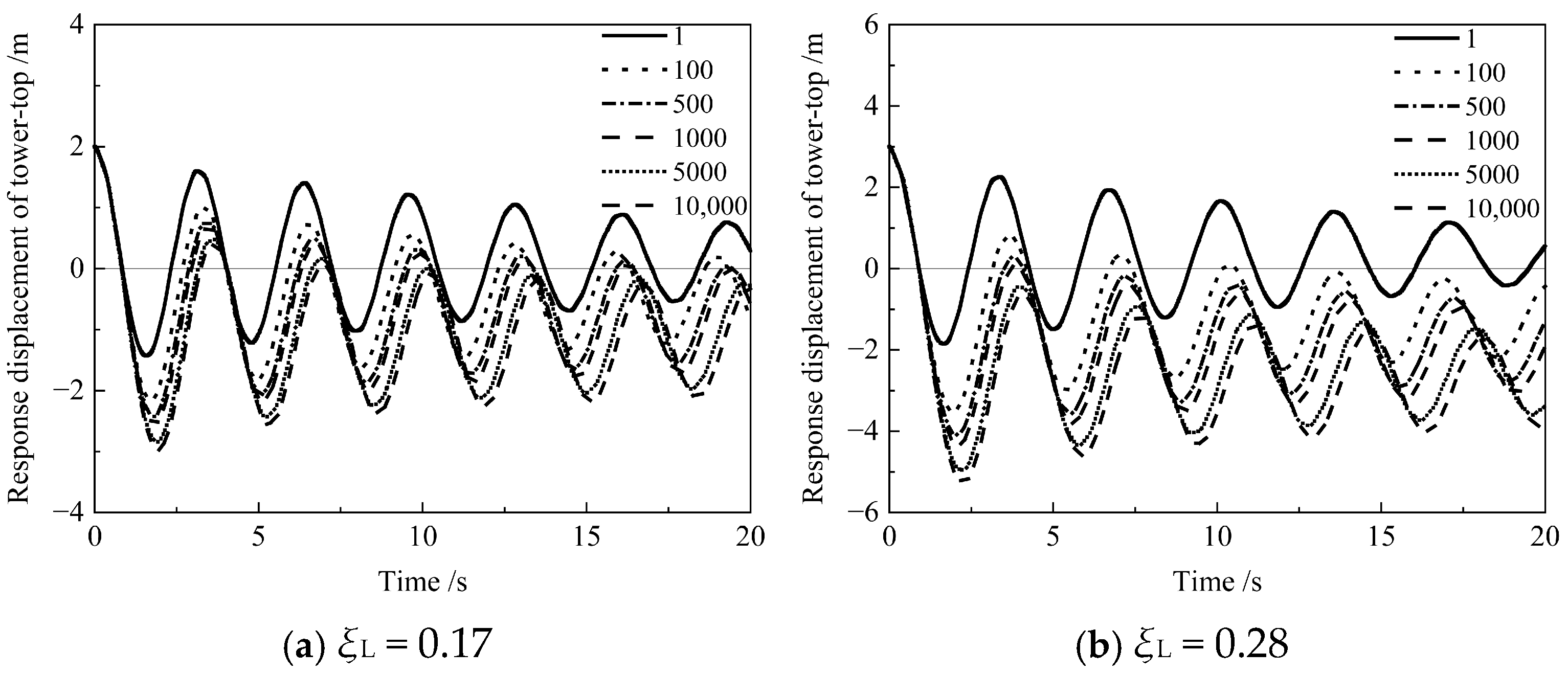
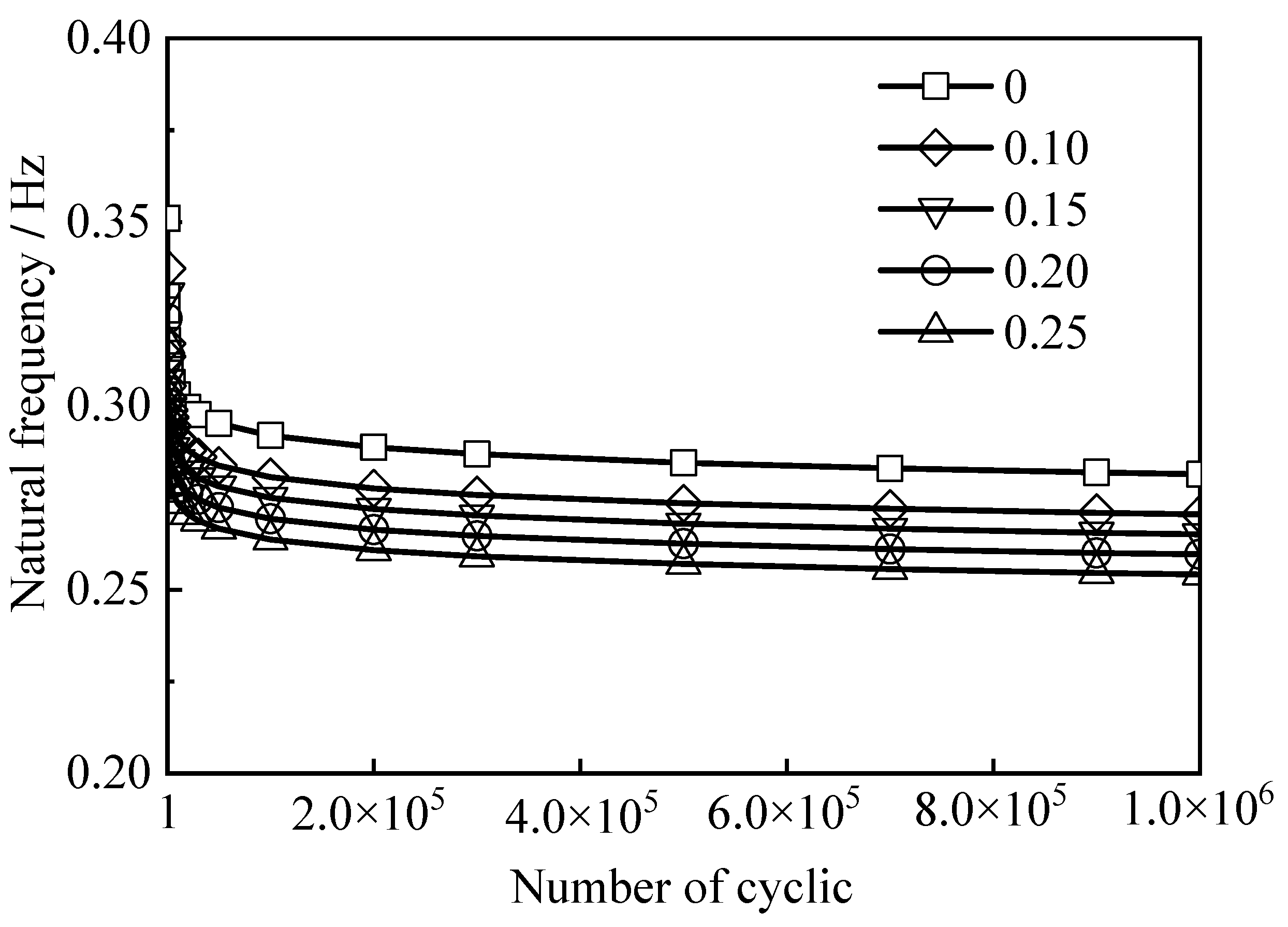
3.1. Amplitude of Cyclic Loading
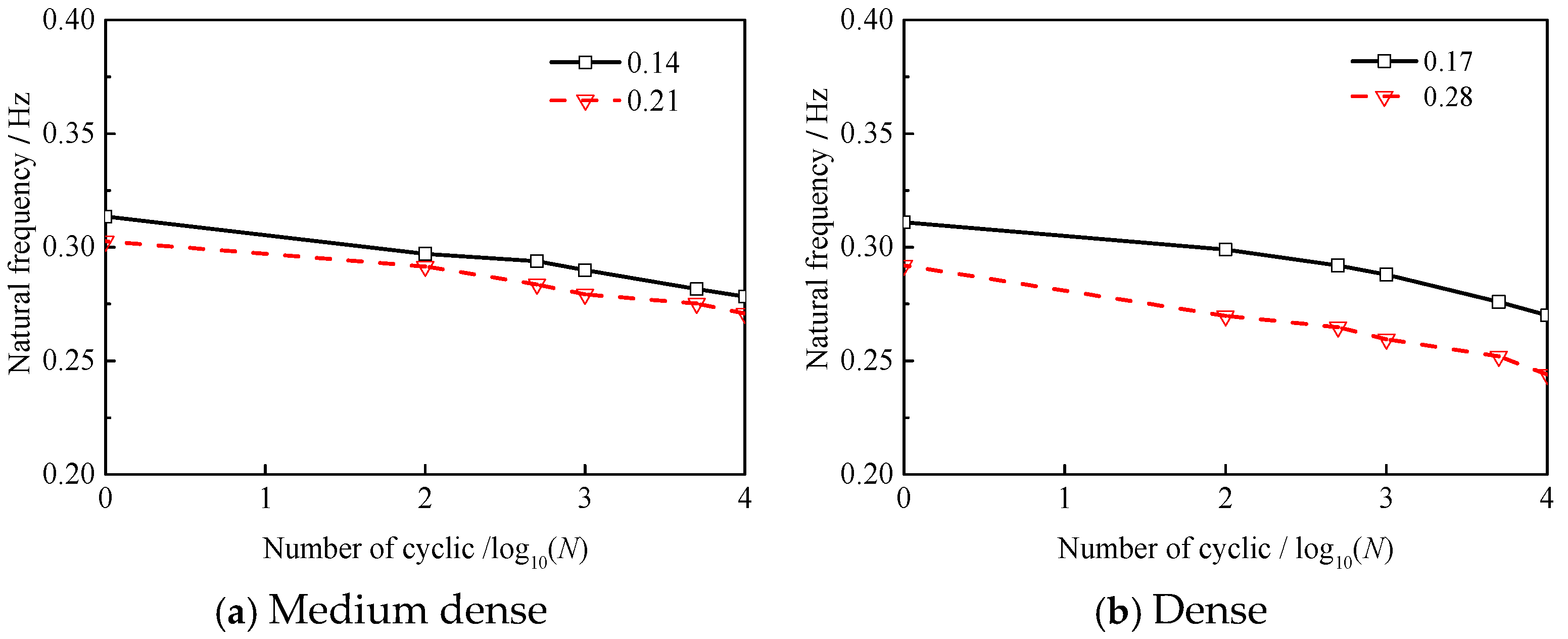
3.2. Number of Cyclic Loading
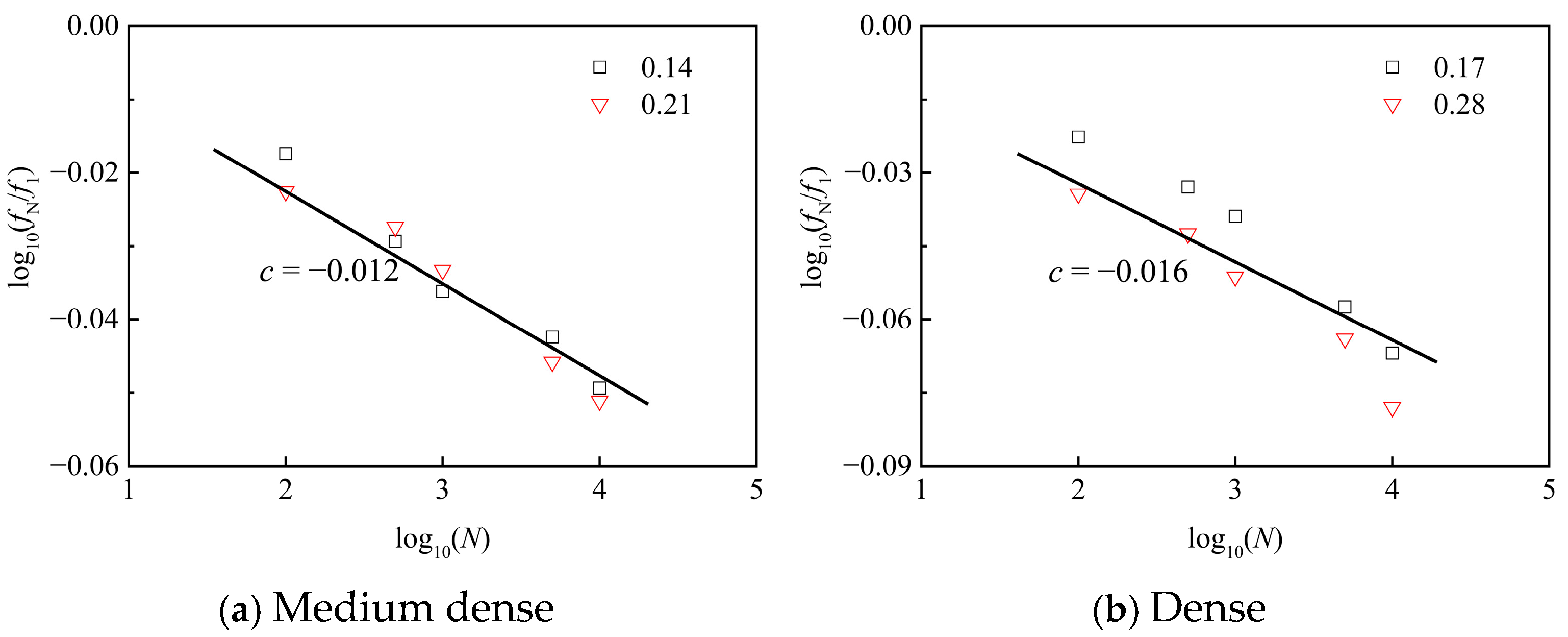
4. Simplified Calculation Method
4.1. Development of the Simplified Method
4.2. Evaluation of the Long-Term Natural Frequency
5. Conclusions
- (1)
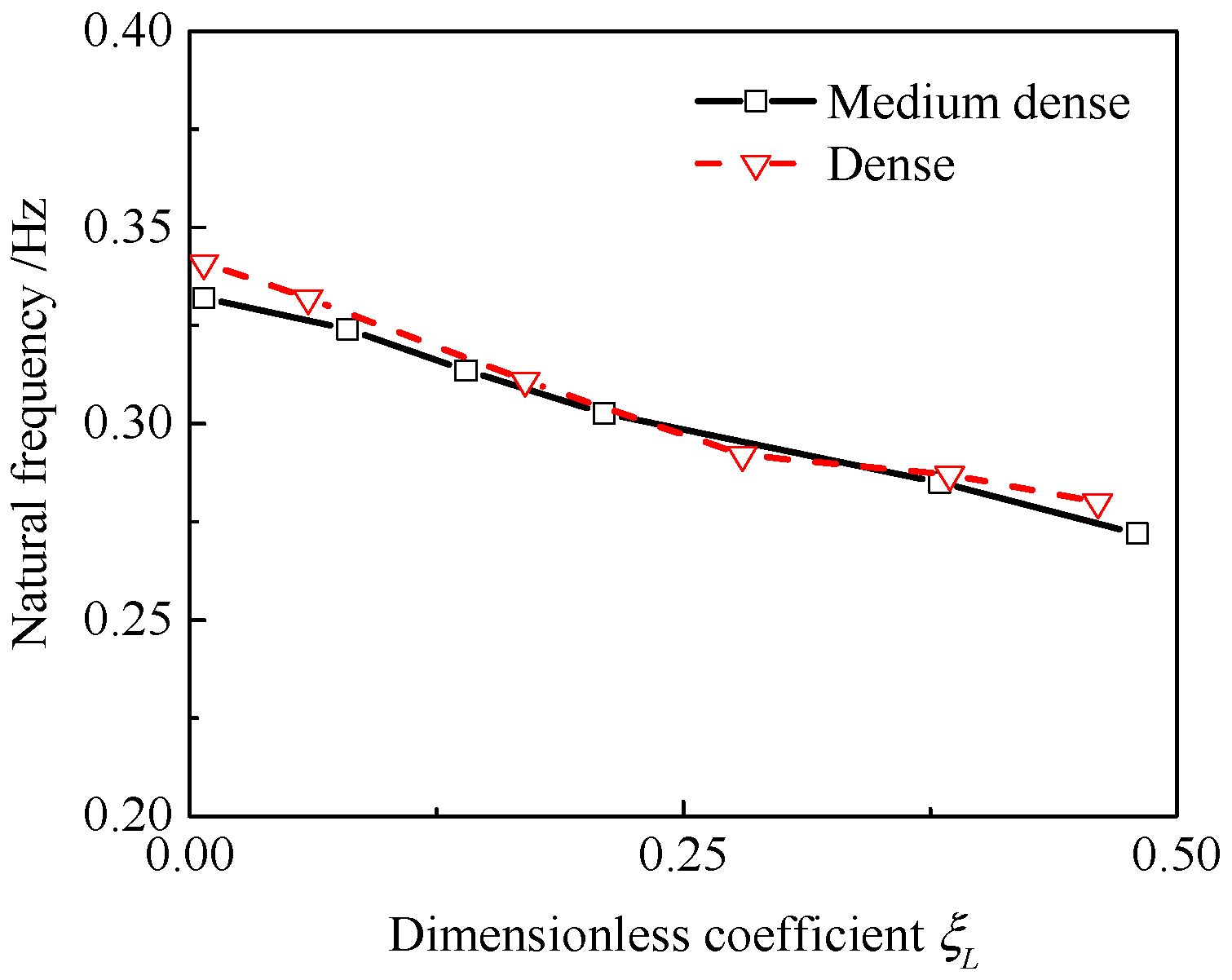
- The natural frequency of monopile-supported offshore wind turbines decreases linearly as cyclic loading amplitude rises. In early cyclic loading stages, this frequency drops sharply with more cycles. Later, it barely changes with additional cycles, stabilizing at a constant value.
- (2)
- The long-term cyclic loading would make the natural frequency of the wind turbine structures reduction effect. In an effort to ensure the sustained and secure operation of the offshore wind turbine over the long run, the natural frequency specified in the design of the structural system should lean towards 3P.
- (3)
- This simplified method is developed by the numerical results. Furthermore, this method allows for the rapid acquisition of the offshore wind turbine’s natural frequency, but soil layer is a homogeneous sandy soil, and pore-pressure is simplified, so the universality application of the simplified method needs to be further verified for complex soil layer. However, in the absence of monitoring data of the natural frequency, the proposed simplified method can provide some initial assessment in terms of frequency calculation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Initial elastic modulus of the soil | |
| Coefficients determined by the function of relative density of sand | |
| Atmosphere Pressure | |
| Minimum principal stress of the soil | |
| Coefficients defined via the sand’s relative density function | |
| Coefficient of soil pressure at rest | |
| Soil depth | |
| Natural bulk density of soil | |
| Soil secant modulus after Nth cycle | |
| Soil secant modulus under after first cyclic | |
| Number of cyclic | |
| Proportional parameters of exponential degradation function | |
| Parameters of exponential degradation function | |
| Cyclic stress ratio | |
| Maximum principal stress in the cyclic stress state | |
| Maximum principal stress in the static failure state | |
| Characteristic cyclic stress ratio | |
| Cyclic stress ratio of soil under loading conditions | |
| Cyclic stress ratio of soil under initial stress state | |
| Dimensionless coefficient of the cyclic loading | |
| Cyclic horizontal displacement amplitude of the pile at the mud surface | |
| Ultimate horizontal displacement of the pile at the mud surface | |
| Natural frequency under the dimensionless coefficient | |
| Cyclic loading | |
| Natural frequency when soil surrounding the pile is elastic | |
| First-cycle vibrational characteristics in monopile-supported offshore wind turbines | |
| Natural frequency in the Nth cyclic | |
| Cyclic loading amplitude’s influence coefficient on natural frequency | |
| Influence coefficient of cyclic loading cycles on natural frequency | |
| Wind turbine and blade | |
| Mass of the tower structure | |
| Tower height | |
| Flexural rigidity of the tower structure | |
| Frequency of wind turbine structures considering the stiffness degradation effect of soil | |
| Influence factors of the rotation foundation stiffness | |
| Influence factors of the lateral foundation stiffness | |
| Natural frequency | |
| Influence coefficient of the horizontal stiffness | |
| Influence coefficient of the rotational stiffness | |
| Influence coefficient of the coupled stiffness | |
| Horizontal stiffness | |
| Rotational stiffness | |
| Modulus of Inertia |
References
- Det Norske Veritas. DNV-OS-J101, Design of Offshore Wind Turbine Structures; DNV Press: Oslo, Norway, 2014. [Google Scholar]
- Liu, H.; Kaynia, A.M. Characteristics of cyclic undrained model SANISAND-MSu and their effects on response of monopiles for offshore wind structures. Geotechnique 2023, 73, 16. [Google Scholar] [CrossRef]
- Zaaijer, M.B. Foundation modelling to assess dynamic behaviour of offshore wind turbines. Appl. Ocean Res. 2006, 28, 45–57. [Google Scholar] [CrossRef]
- Byrne, B. Foundation Design for Offshore Wind Turbines; Géotechnique Lecture; University of Oxford: London, UK, 2011. [Google Scholar]
- Bhattacharya, S.; Adhikari, S. Experimental validation of soil–structure interaction of offshore wind turbines. Soil Dyn. Earthq. Eng. 2011, 31, 805–816. [Google Scholar] [CrossRef]
- Arany, L.; Bhattacharya, S.; Macdonald, J.H.; Hogan, S.J. Closed form solution of Eigen frequency of monopile supported offshore wind turbines in deeper waters incorporating stiffness of substructure and SSI. Soil Dyn. Earthq. Eng. 2016, 83, 18–32. [Google Scholar] [CrossRef]
- Andersen, L.; Vahdatirad, M.; Sichani, M.; Sørensen, J. Natural frequencies of wind turbines on monopile foundations in clayey soils—A probabilistic approach. Comput. Geotech. 2012, 43, 1–11. [Google Scholar] [CrossRef]
- Darvishi-Alamouti, S.; Bahaari, M.; Moradi, M. Natural frequency of offshore wind turbines on rigid and flexible monopiles in cohesionless soils with linear stiffness distribution. Appl. Ocean Research. 2017, 68, 91–102. [Google Scholar] [CrossRef]
- Yu, Z.L.; Amdahl, J. A Rayleigh-Ritz solution for high order natural frequencies and eigenmodes of monopile supported offshore wind turbines considering tapered towers and soil pile interactions. Mar. Structur. 2023, 92, 103485. [Google Scholar] [CrossRef]
- Schaumann, P.; Lochte-Holtgreven, S.; Steppeler, S. Special fatigue aspects in support structures of offshore wind turbines. Mater. Sci. Eng. Technol. 2011, 42, 1075–1081. [Google Scholar] [CrossRef]
- Shi, S.; Zhai, E.; Xu, C.; Iqbal, K.; Sun, Y.; Wang, S. Influence of Pile-Soil Interaction on Dynamic Properties and Response of Offshore Wind Turbine with Monopile Foundation in Sand Site. Appl. Ocean. Res. 2022, 126, 103279. [Google Scholar] [CrossRef]
- Bakhti, R.; Benahmed, B.; Laib, A. Finite Element Investigation of Offshore Wind Turbines Natural Frequency with Monopile Foundations System. J. Vib. Eng. Technol. 2023, 12, 2437–2449. [Google Scholar] [CrossRef]
- Achmus, M.; Kuo, Y.S.; Abdel-Rahman, K. Behavior of monopile foundations under cyclic lateral load. Comput. Geotech. 2009, 36, 725–735. [Google Scholar] [CrossRef]
- Chong, S. Numerical simulation of offshore foundations subjected to repetitive loads. Ocean Eng. 2017, 142, 470–477. [Google Scholar] [CrossRef]
- Chong, S.; Pasten, C. Numerical study on long-term monopile foundation response. Mar. Georesour. Geotechnol. 2018, 36, 190–196. [Google Scholar] [CrossRef]
- Cuéllar, P.; Mira, P.; Pastor, M.; Merodo, J.A.F.; Baeßler, M.; Rücker, W. A numerical model for the transient analysis of offshore foundations under cyclic loading. Comput. Geotech. 2014, 59, 75–86. [Google Scholar] [CrossRef]
- Cuéllar, P. Pile Foundations for Offshore Wind Turbines: Numerical and Experimental Investigations on the Behaviour Under Short-Term and Long-Term Cyclic Loading. Ph.D. Thesis, Technischen Universitt Berlin, Berlin, Germany, 2011. [Google Scholar]
- Li, J.; Guan, D.; Chiew, Y.-M.; Zhang, J.; Zhao, J. Temporal evolution of soil deformations around monopile foundations subjected to cyclic lateral loading. Ocean Eng. 2020, 217, 107893. [Google Scholar] [CrossRef]
- Zaaijer, M.B. Design Methods for Offshore Wind Turbines at Exposed Sites. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2002. [Google Scholar]
- Lombardi, D.; Bhattacharya, S.; Wood, D.M. Dynamic soil-structure interaction of monopile supported wind turbines in cohesive soil. Soil Dyn. Earthq. Eng. 2013, 49, 165–180. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Cox, J.A.; Lombardi, D.; Wood, D.M. Dynamics of offshore wind turbines supported on two foundations. ICE Proc. Geotech. Eng. 2013, 166, 159–169. [Google Scholar] [CrossRef]
- Carswell, W.; Arwade, S.; DeGroot, D.; Myers, A. Natural frequency degradation and permanent accumulated rotation for offshore wind turbine monopiles in clay. Renew Energy 2016, 97, 319–330. [Google Scholar] [CrossRef]
- Arany, L.; Bhattacharya, S.; Macdonald, J.; Hogan, S.J. Design of monopiles for offshore wind turbines in 10 steps. Soil Dyn. Earthq. Eng. 2017, 92, 126–152. [Google Scholar] [CrossRef]
- Wang, W.; Li, X.; Zhao, H.; Wang, B.; Li, Y. Vibration control of a pentapod offshore wind turbine under combined seismic wind and wave loads using multiple tuned mass damper. Appl. Ocean Res. 2020, 103, 102254. [Google Scholar] [CrossRef]
- Janbu, N. Soil compressibility as determined by oedometer and triaxial tests. In Proceedings of the 3rd European Conference on Soil Mechanics and Foundation Engineering, Wiesbaden, Germany, 15–18 October 1963. [Google Scholar]
- Duncan, J.; Chang, C. Nonlinear analysis of stress and strain in soils. J. Soil Mech. Found. Div. ASCE 1970, 96, 1629–1653. [Google Scholar] [CrossRef]
- Ma, H.; Yang, J.; Chen, L. Numerical analysis of the long-term performance of offshore wind turbines supported by monopiles. Ocean Eng. 2017, 136, 94–105. [Google Scholar] [CrossRef]
- Shirzadeh, R.; Weijtjens, W.; Guillaume, P.; Devriendt, C. The dynamics of an offshore wind turbine in parked conditions: A comparison between simulations and measurements. Wind Energy 2015, 18, 1685–1702. [Google Scholar] [CrossRef]
- Little, R.L.; Briaud, J.L. Full Scale Cyclic Lateral Load Tests on Six Single Piles in Sand; Department of Civil Engineering Texas A & M University: College Station, TX, USA, 1988. [Google Scholar]
- Long, J.H.; Vanneste, G. Effects of Cyclic Lateral Loads on Piles in Sand. J. Geotech. Eng. 1994, 120, 225–244. [Google Scholar] [CrossRef]
- Huurman, M. Development of traffic induced permanent strain in concrete block pavements. Heron 1996, 41, 29–52. [Google Scholar]
- Depina, I.; Hue Le, T.M.; Eiksund, G.; Benz, T. Behavior of cyclically loaded monopile foundations for offshore wind turbines in heterogeneous sands. Comput. Geotech. 2015, 65, 266–277. [Google Scholar] [CrossRef]
- Kuo, Y.S.; Achmus, M.; Abdel-Rahman, K. Minimum embedded length of cyclic horizontally loaded monopiles. J. Geotech. Geoenviron. Eng. 2011, 138, 357–363. [Google Scholar] [CrossRef]
- Kuo, Y.S.; Martin, A.; Khalid, A.R. Estimation of lateral deformation of monopile foundations by use of cyclic triaxial tests. Chin. J. Geotech. Eng. 2009, 31, 1729–1734. [Google Scholar] [CrossRef]
- Zhang, J.M.; Zhang, C.R.; Zhang, K. Model tests on large-diameter single pile under cyclic lateral loads in sand. Rock Soil Mech. 2021, 42, 783–789. [Google Scholar] [CrossRef]
- Luo, R.; Yang, M.; Li, W. Numerical study of diameter effect on accumulated deformation of laterally loaded monopiles in sand. Eur. J. Environ. Civ. Eng. 2018, 24, 2440–2452. [Google Scholar] [CrossRef]
- Ahmed, S.S.; Hawlader, B. Numerical Analysis of Large-Diameter Monopiles in Dense Sand Supporting Offshore Wind Turbines. Int. J. Geomech. 2016, 16, 04016018. [Google Scholar] [CrossRef]
- Zhu, B.; Byrne, B.W.; Houlsby, G.T. Long-term lateral cyclic response of suction caisson foundations in sand. J. Geotech. Geoenviron. Eng. ASCE 2013, 139, 73–83. [Google Scholar] [CrossRef]
- Nikitas, G.; Arany, L.; Aingaran, S.; Vimalan, J.; Bhattacharya, S. Predicting long term performance of offshore wind turbines using cyclic simple shear apparatus. Soil Dyn. Earthq. Eng. 2017, 92, 678–683. [Google Scholar] [CrossRef]
- Barari, A.; Bagheri, M.; Rouainia, M.; Ibsen, L. Deformation mechanisms for offshore monopile foundations accounting for cyclic mobility effects. Soil Dyn. Earthq. Eng. 2017, 97, 439–453. [Google Scholar] [CrossRef]
- Ward, I.P. Natural frequency analysis of offshore wind turbine monopiles. ICE Eng. Comput. Mech. 2016, 169, 196–208. [Google Scholar] [CrossRef]
- Amar Bouzid, D.; Bhattacharya, S.; Otsmane, L. Assessment of natural frequency of installed offshore wind turbines using nonlinear finite element model considering soil-monopile interaction. J. Rock Mech. Geotech. Eng. 2018, 10, 333–346. [Google Scholar] [CrossRef]
- Prendergast, L.J.; Gavin, K.; Doherty, P. An investigation into the effect of scour on the natural frequency of an offshore wind turbine. Ocean Eng. 2015, 101, 1–11. [Google Scholar] [CrossRef]
- Yi, J.H.; Kim, S.B.; Yoon, G.L.; Andersen, L.V. Natural frequency of bottom-fixed offshore wind turbines considering pile-soil-interaction with material uncertainties and scouring depth. Wind Struct. 2015, 21, 625–639. [Google Scholar] [CrossRef]
- Vught, J.H. Considerations on the Dynamics of Support Structures for an Offshore Wind Energy Converter. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2000. [Google Scholar]
- Arany, L.; Bhattacharya, S.; Adhikari, S.; Hogan, S.; Macdonald, J. An analytical model to predict the natural frequency of offshore wind turbines on three-spring flexible foundations using two different beam models. Soil Dyn. Earthq. Eng. 2015, 74, 40–45. [Google Scholar] [CrossRef]

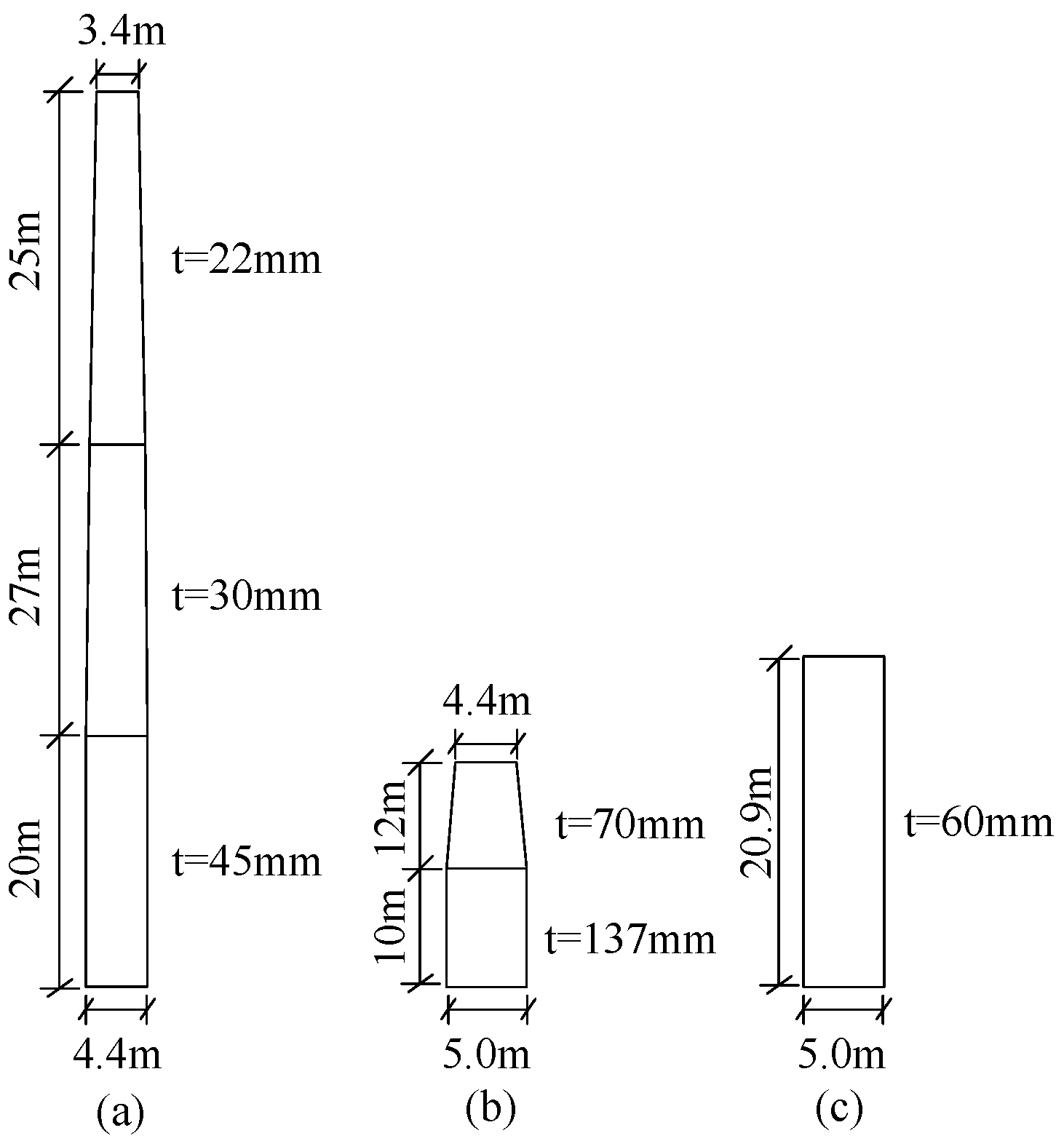
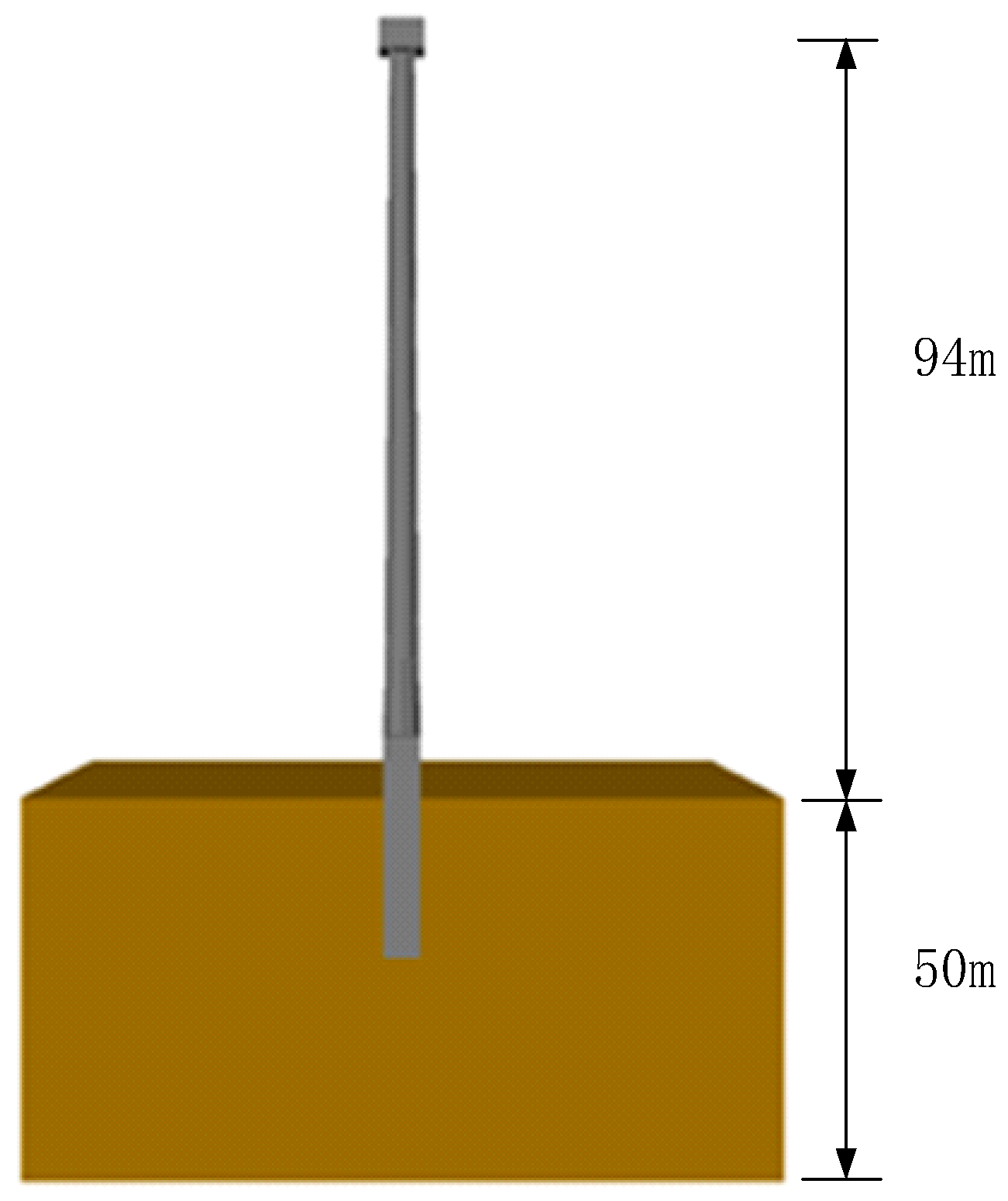
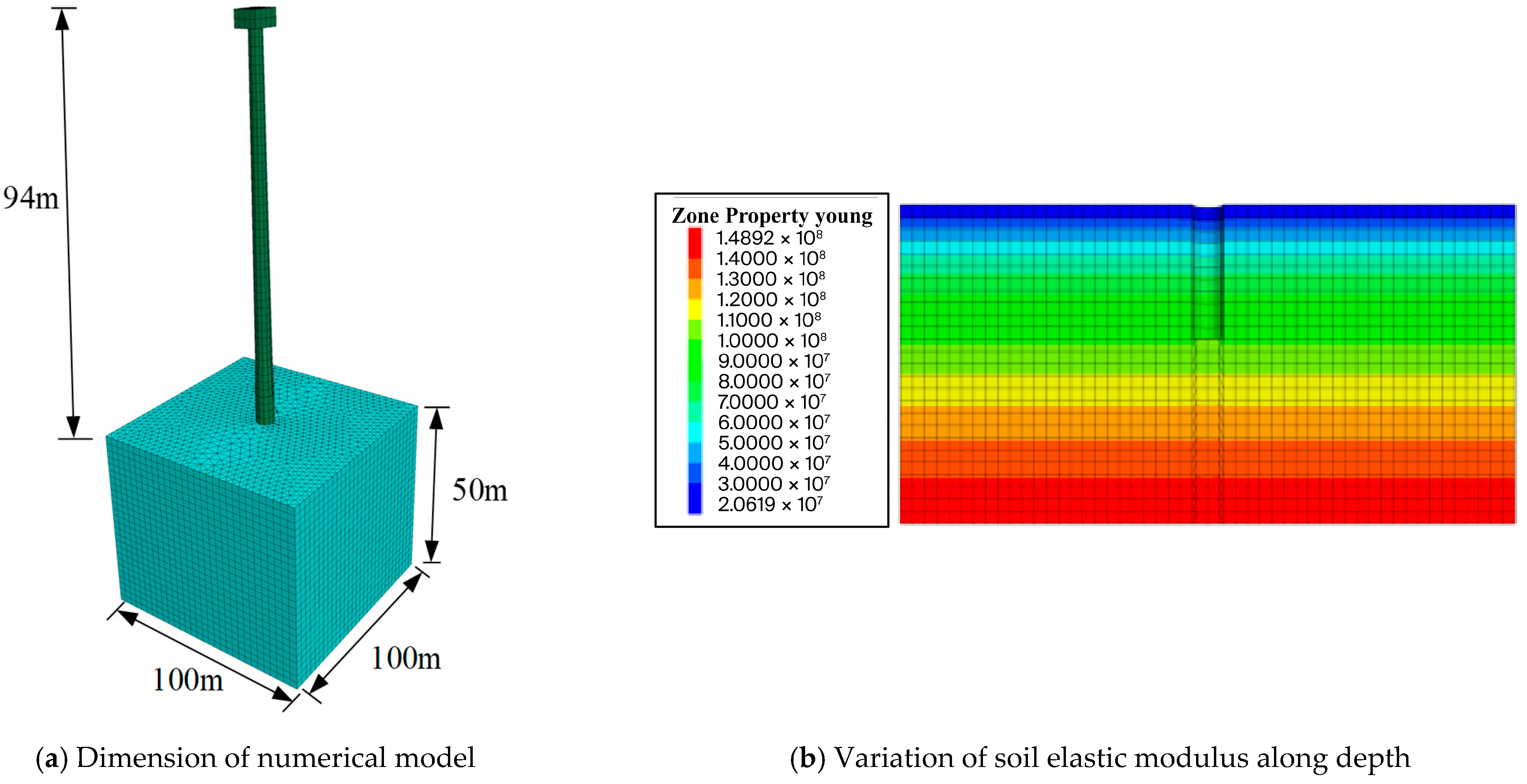

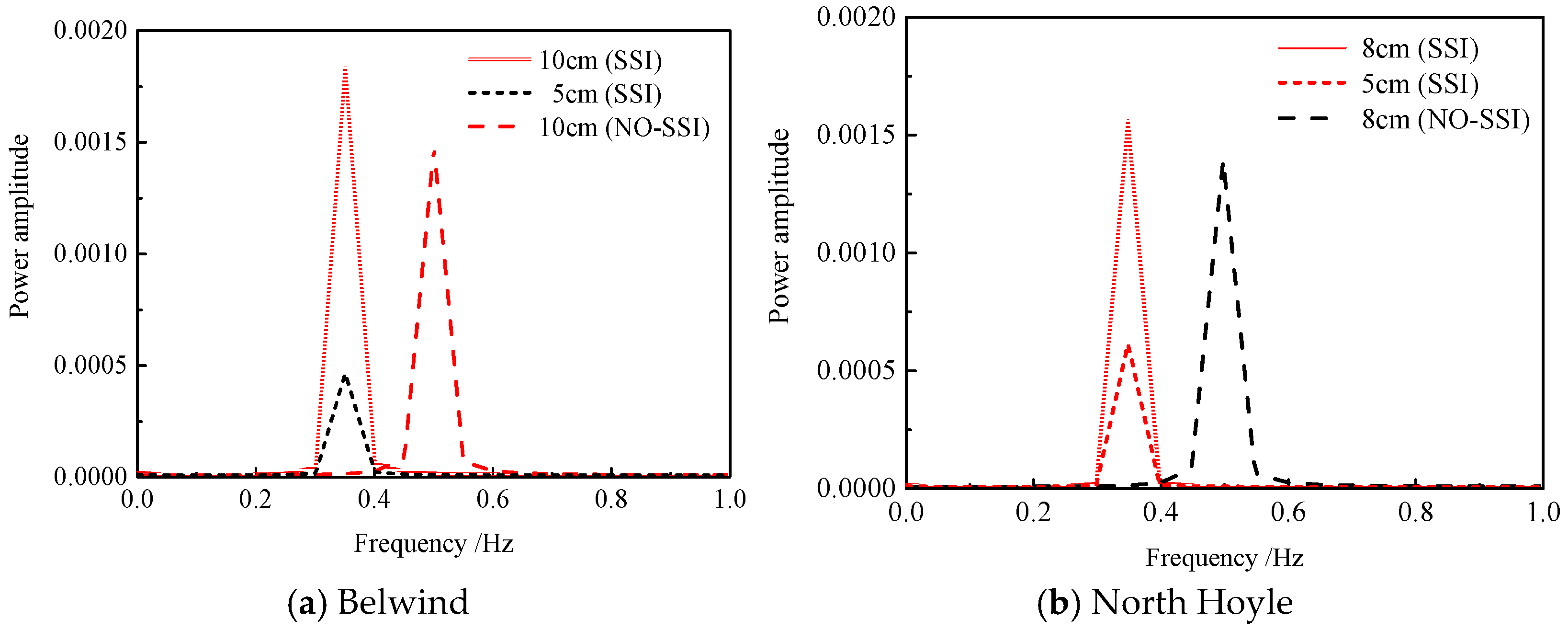

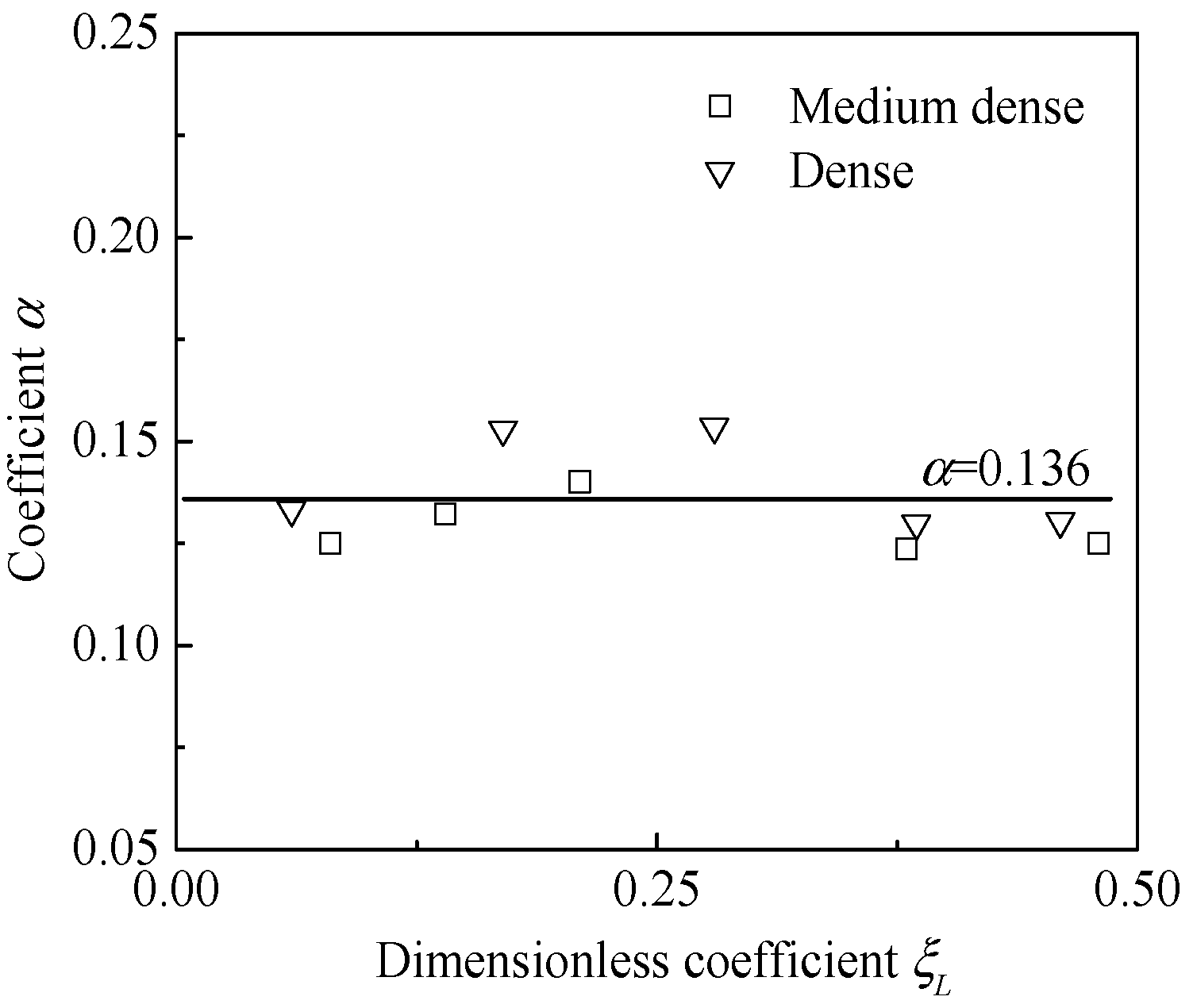
| Wind Power Plant Name | Measured Frequency/Hz | Calculated Frequency/Hz | Error | ||
|---|---|---|---|---|---|
| NO-SSI | SSI | NO-SSI | SSI | ||
| Belwind | 0.361 | 0.502 | 0.353 | 39% | 2.2% |
| North Hoyle | 0.350 | 0.494 | 0.349 | 41% | 0.3% |
| OWT Dimension and Foundation Stiffness | Symbol/Unit | Value |
|---|---|---|
| Top mass | mt/ton | 234.5 |
| Tower mass | mT/ton | 260 |
| Tower height | LT/m | 67.3 |
| Tower bottom diameter | Db/m | 5 |
| Tower top diameter | Dt/m | 3 |
| Tower wall thickness | tT/mm | 41 |
| Young’s modulus of tower material | E/GPa | 210 |
| Monopile diameter | Dp/m | 6 |
| Monopile wall thickness | tp/mm | 80 |
| Lateral stiffness | KL/GN·m−1 | 1.53 |
| Rock stiffness | KR/ GN m·rad−1 | 205.72 |
| Coupling stiffness | KLR/GN | −13.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, R.; Yang, H.; Sun, Y.; Zou, J.; Sun, B.; Xu, J. Natural Frequency of Monopile Supported Offshore Wind Turbine Structures Under Long-Term Cyclic Loading. Appl. Sci. 2025, 15, 8143. https://doi.org/10.3390/app15158143
Chen R, Yang H, Sun Y, Zou J, Sun B, Xu J. Natural Frequency of Monopile Supported Offshore Wind Turbine Structures Under Long-Term Cyclic Loading. Applied Sciences. 2025; 15(15):8143. https://doi.org/10.3390/app15158143
Chicago/Turabian StyleChen, Rong, Haitao Yang, Yilong Sun, Jinglong Zou, Boyan Sun, and Jialin Xu. 2025. "Natural Frequency of Monopile Supported Offshore Wind Turbine Structures Under Long-Term Cyclic Loading" Applied Sciences 15, no. 15: 8143. https://doi.org/10.3390/app15158143
APA StyleChen, R., Yang, H., Sun, Y., Zou, J., Sun, B., & Xu, J. (2025). Natural Frequency of Monopile Supported Offshore Wind Turbine Structures Under Long-Term Cyclic Loading. Applied Sciences, 15(15), 8143. https://doi.org/10.3390/app15158143






