A Probability Integral Parameter Inversion Method Integrating a Selection-Weighted Iterative Robust Genetic Algorithm
Abstract
1. Introduction
2. Methods
2.1. The PIM Prediction Model
2.2. Construction and Solution of Conditional Equations
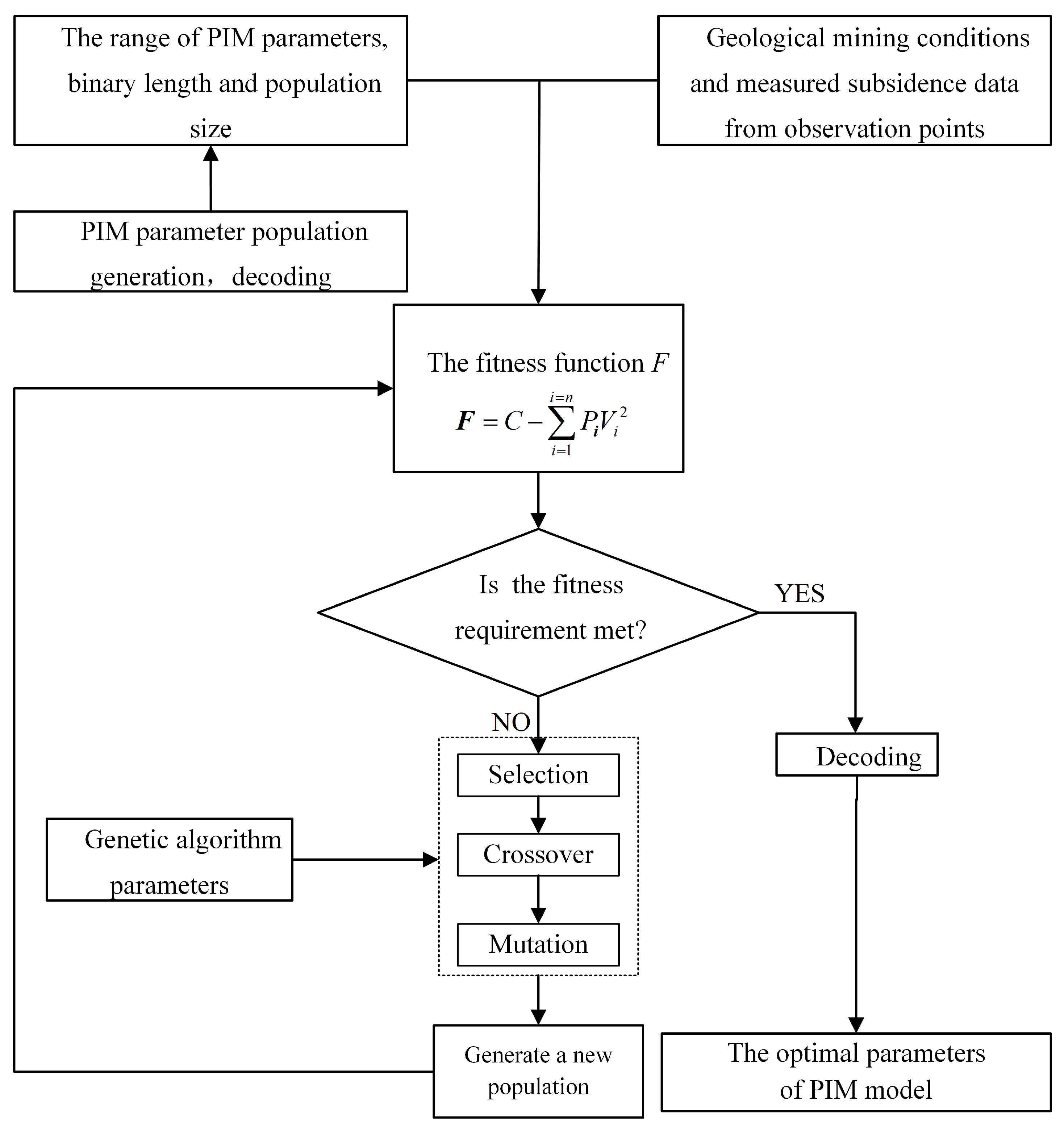
2.3. Prediction Parameters of PIM Solution Based on Robust Genetic Algorithm
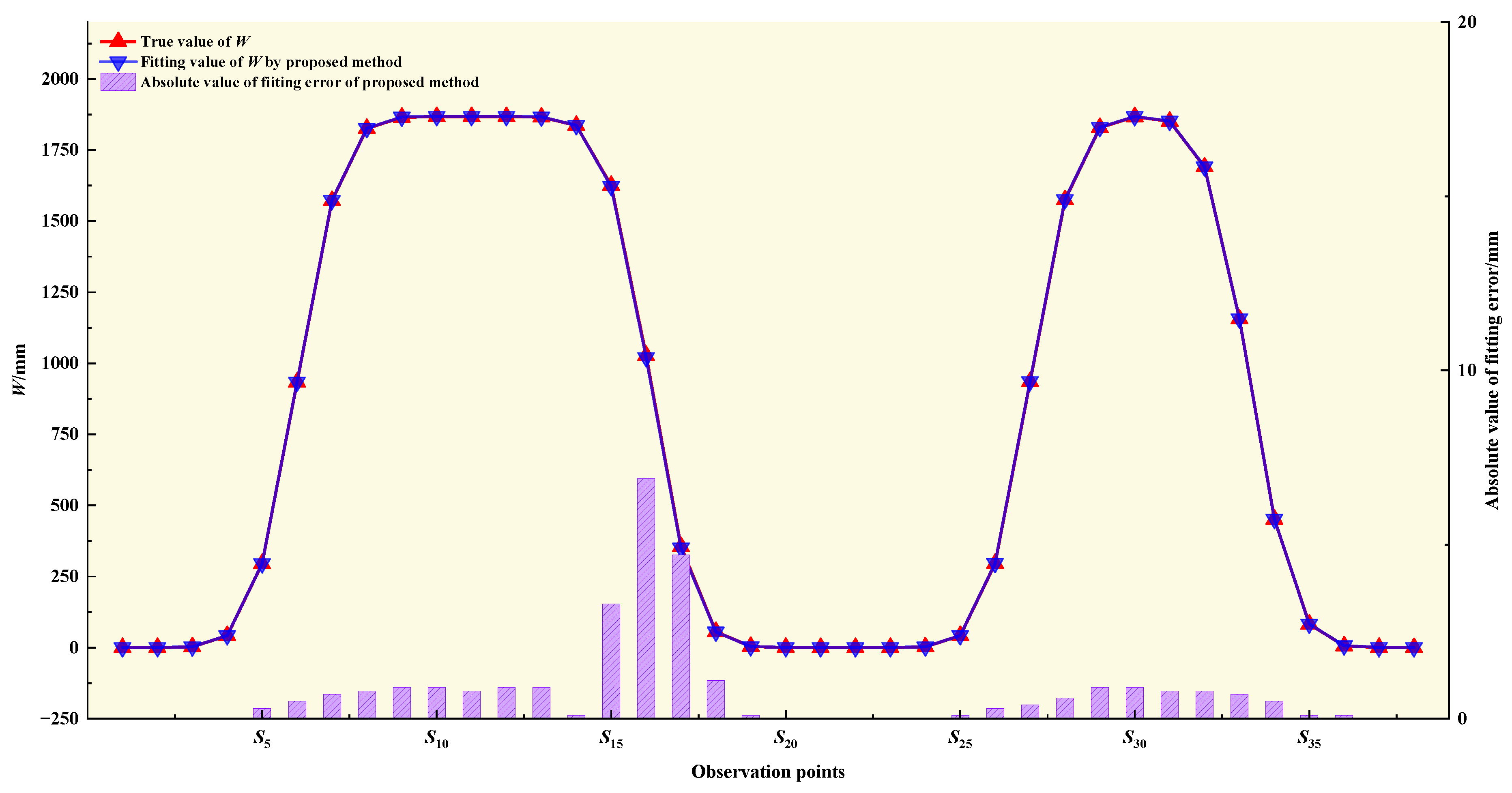
3. Simulated Experiment
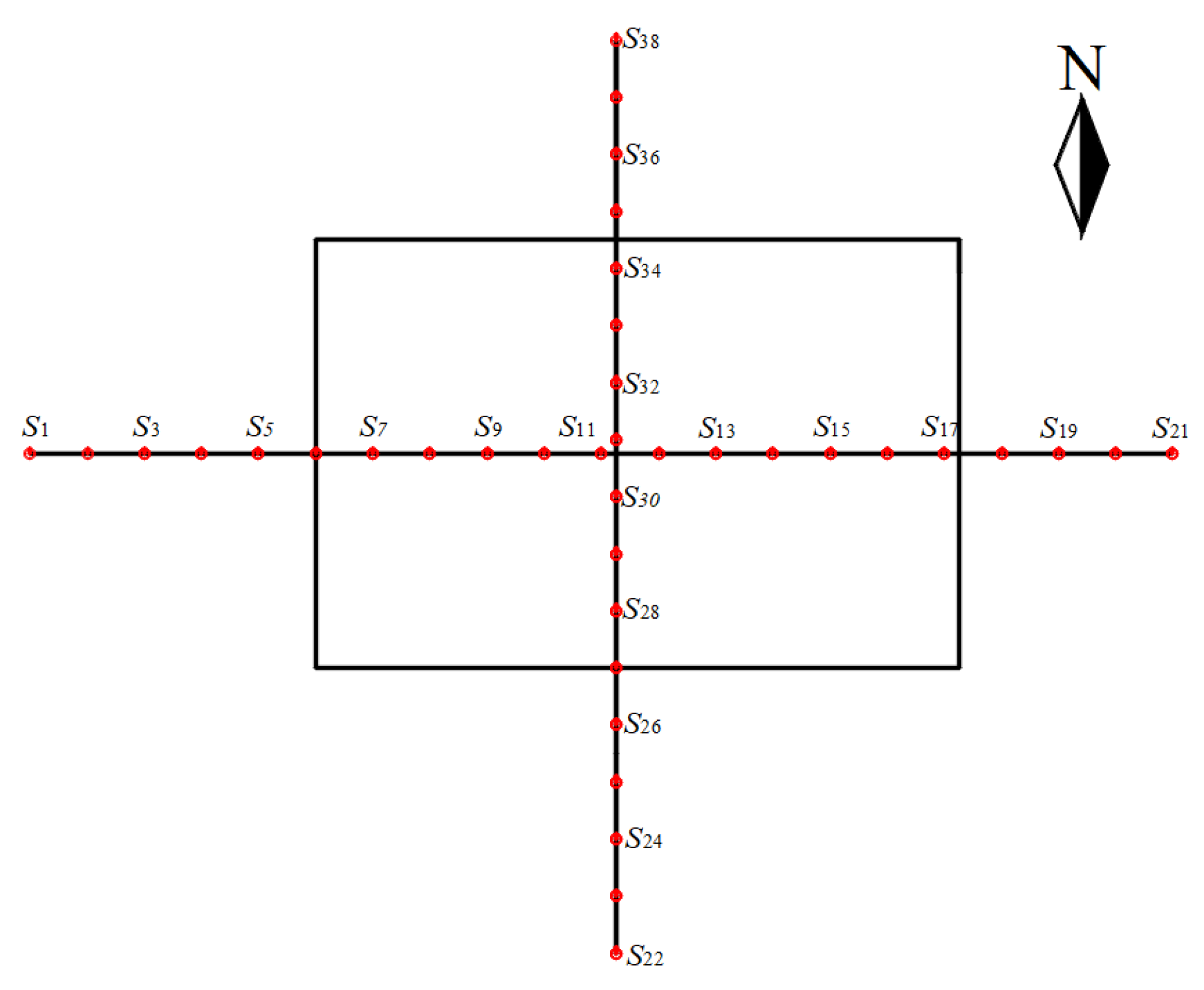
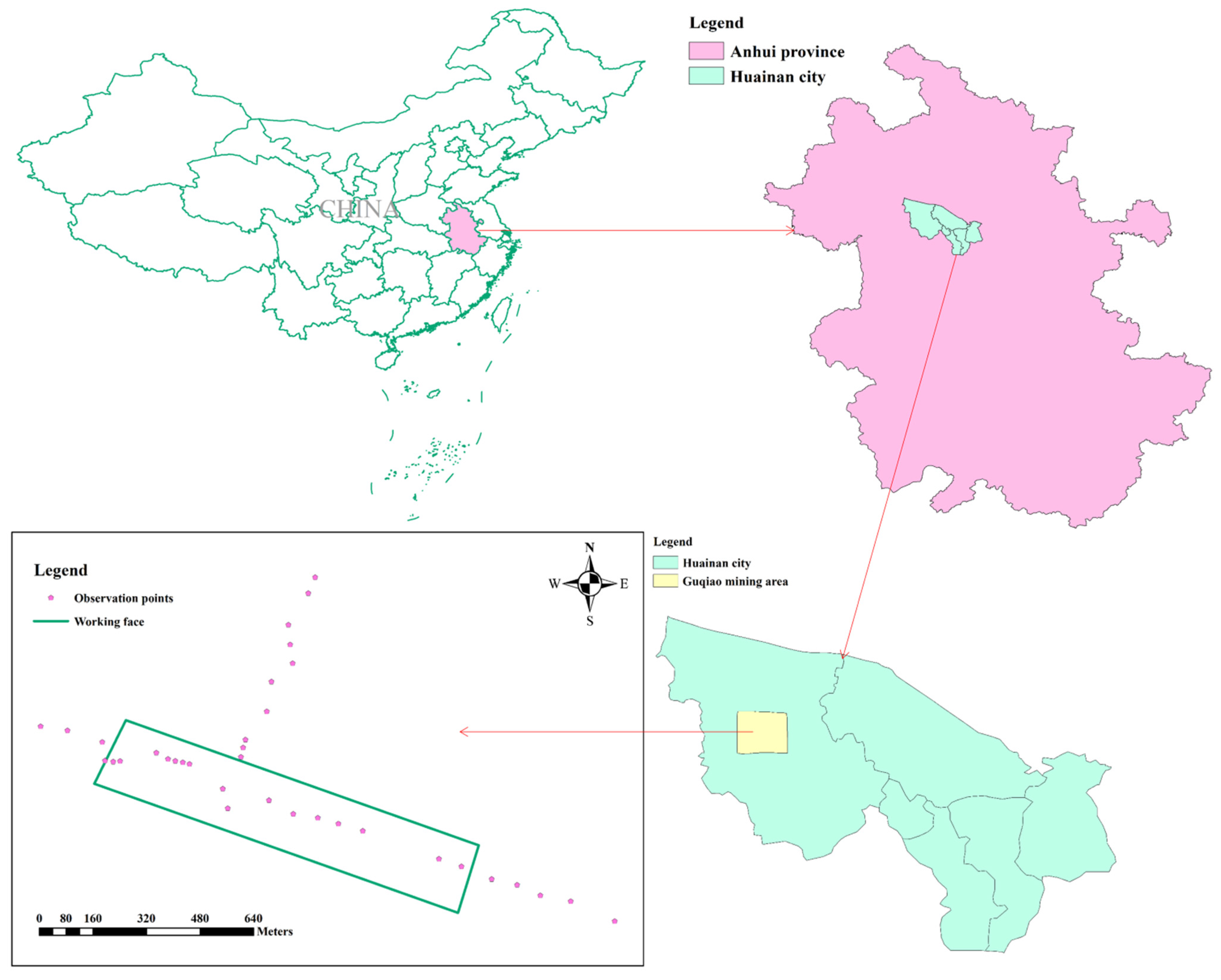
3.1. A Brief Introduction to the Mining Working Face
3.2. Overview of Data for Simulated Experimental Geological Mining Conditions
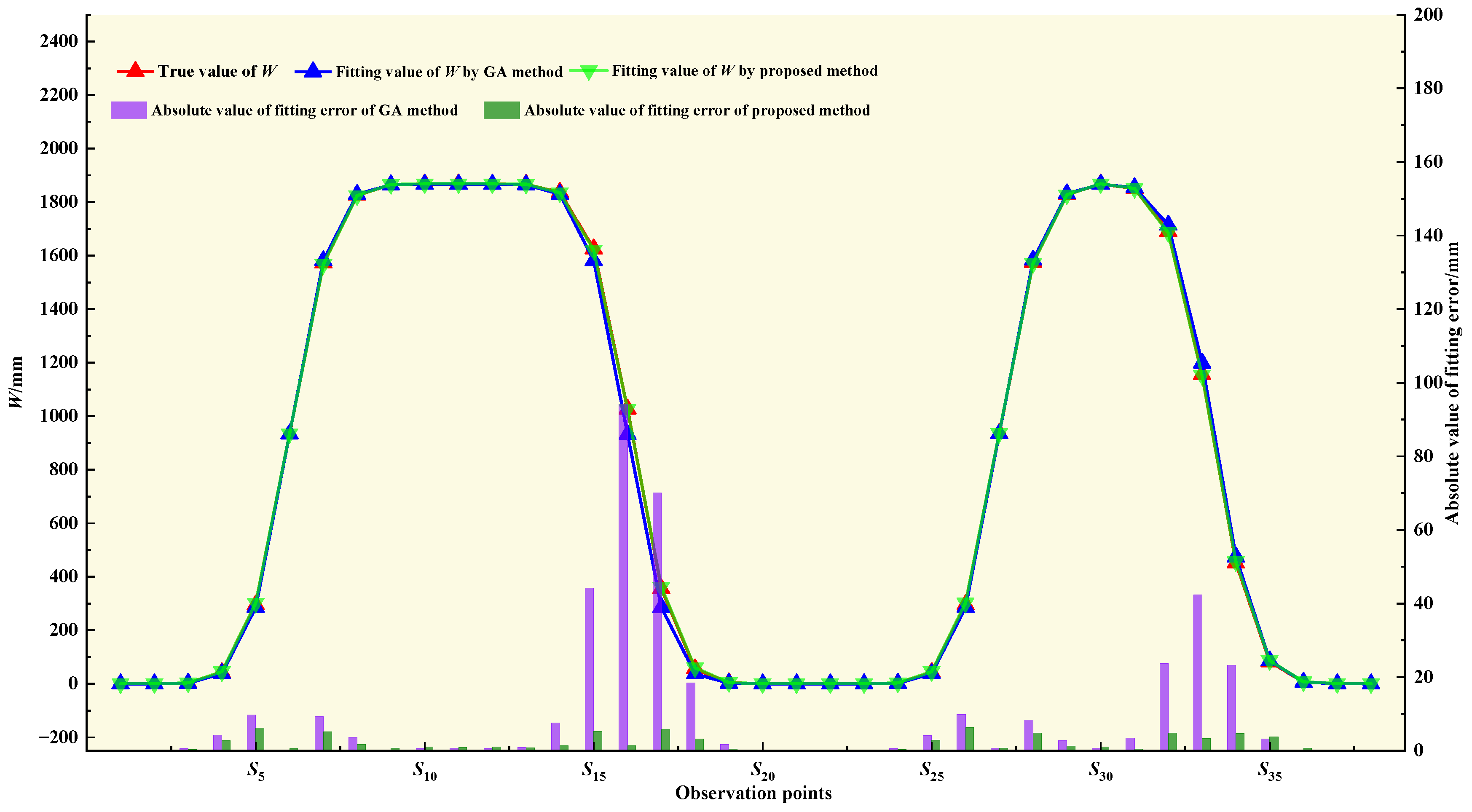
3.3. Simulation Application Experiment and Results
4. 1312(1) Working Face Experiment
4.1. A Brief Introduction to the 1312(1) Working Face
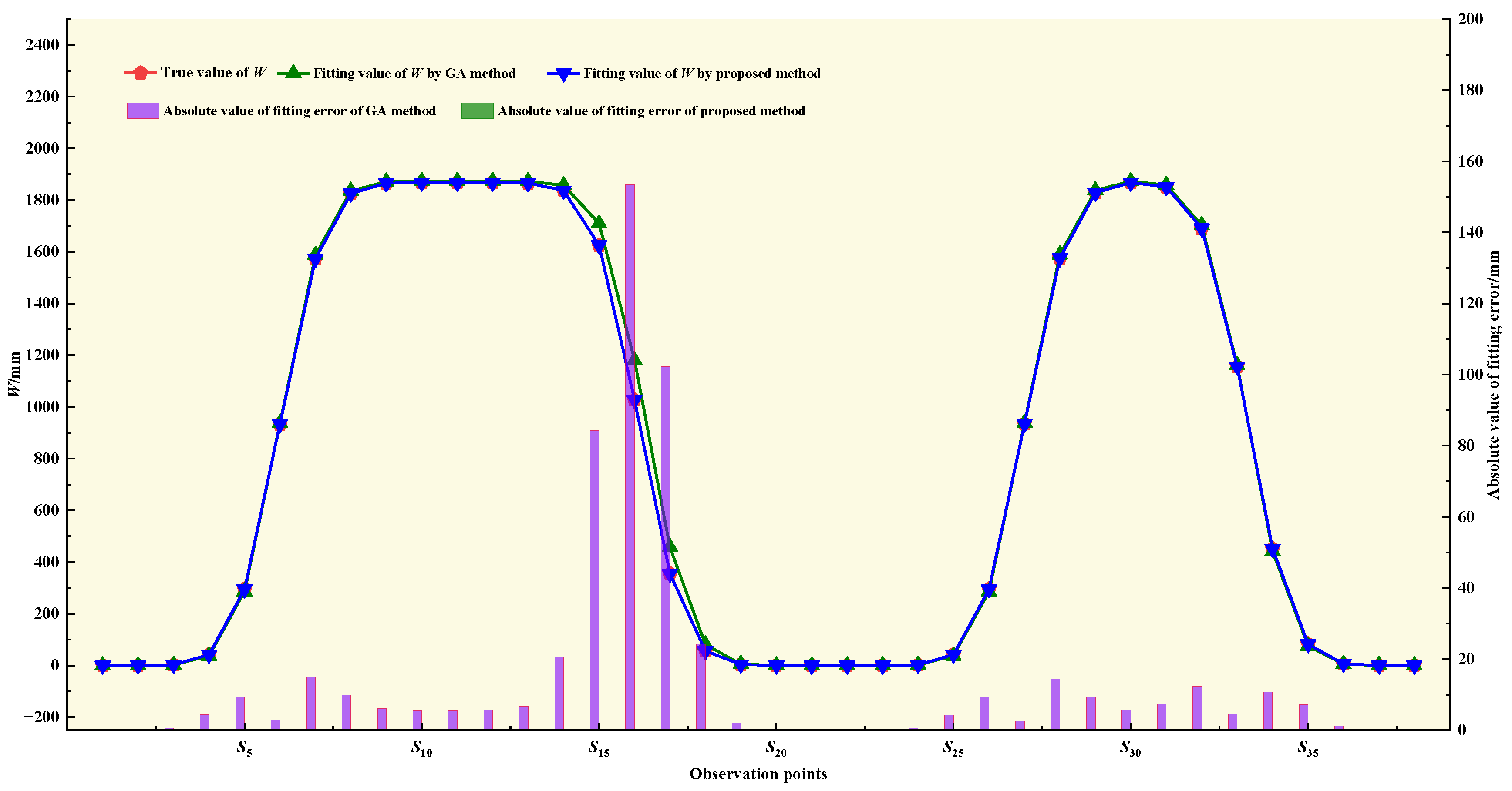
4.2. Engineering Application Experiments and Results
5. Discussion
5.1. The Impact of Changes in k Value on the Proposed Method
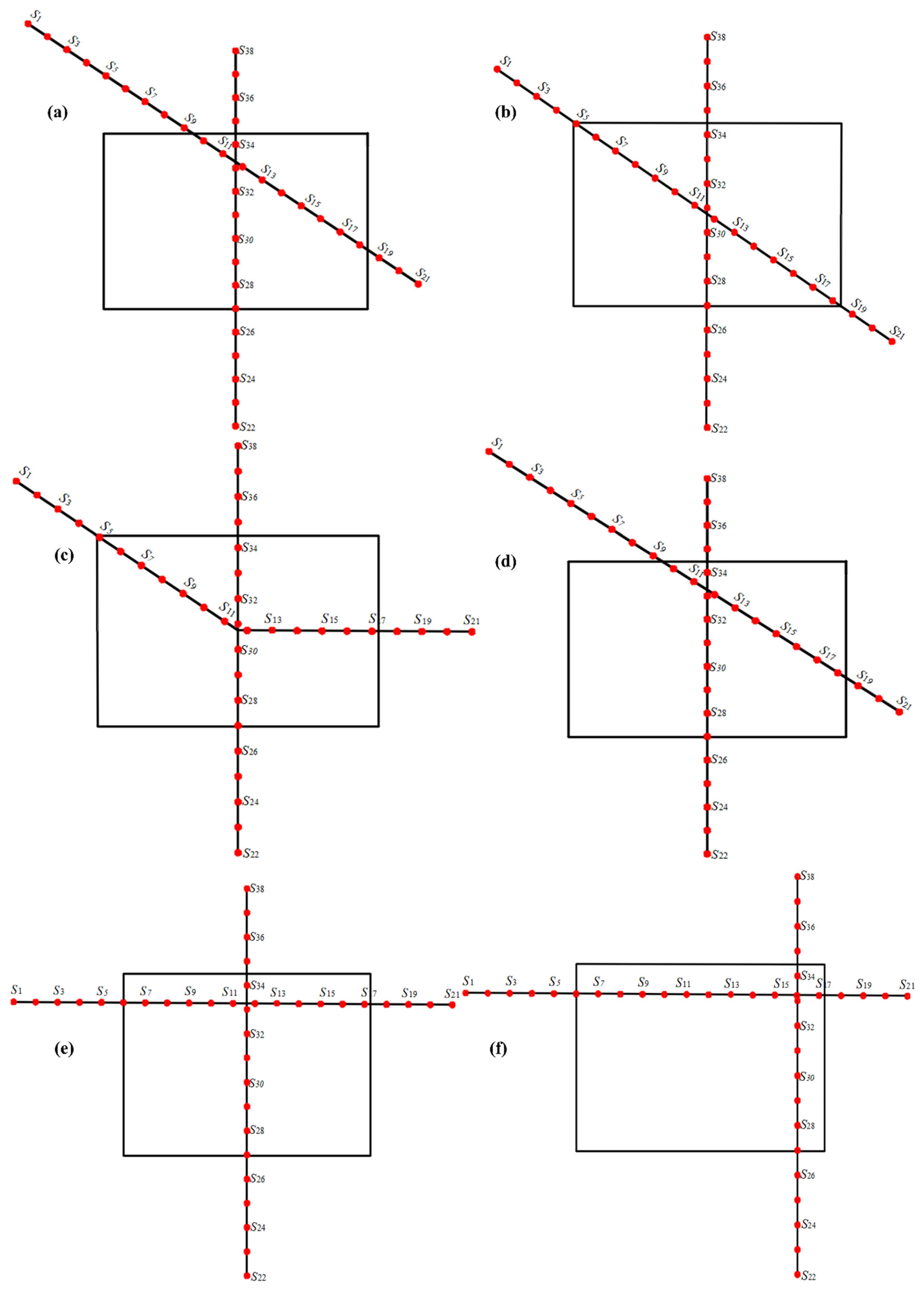
5.2. The Influence of Different Layout Forms of Survey Lines on Parameter Inversion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbol | Meaning |
| Wmax | maximum subsidence value |
| subsidence value of the strike section of the coal mining working face | |
| subsidence value of the trend profile of the coal mining working face | |
| ds, dt | length and width of unit mining |
| M | thickness of the mining face in a coal mine |
| q | subsidence coefficient |
| α | inclination angle of the coal seam |
| (x,y) | coordinates at any point on the surface |
| H | average mining depth of the working surface |
| Tanβ | main influence tangent |
| θ | greatest subsidence angle |
| D1 | length of inclination of working face |
| D3 | length of strike of working face |
| S1, S2, S3, and S4 | upper, lower, left, and right inflection point offsets of the working face, respectively |
| B = [q,tan β,θ,S1,S2,S3,S4] | estimated parameter for subsidence using probability integration method |
| G = [m,H,x,y,α,D3,D1] | geological and mining condition parameter of the working face |
| difference between the true value and the fitted value | |
| measured subsidence value | |
| predicted subsidence value | |
| Vmin | minimum residual sum of squares after adding weights |
| Pi | weight of the i-th observation value |
| j | total number of observed values |
References
- Chai, H.; Xu, H.; Hu, J.; Geng, S.; Guan, P.; Ding, Y.; Zhao, Y.; Xu, M.; Chen, L. Application of a Variable Weight Time Function Combined Model in Surface Subsidence Prediction in Goaf Area: A Case Study in China. Appl. Sci. 2024, 14, 1748. [Google Scholar] [CrossRef]
- Zhou, D.W.; Wu, K.; Chen, R.L.; Li, L. GPS/terrestrial 3D laser scanner combined monitoring technology for coal mining subsidence: A case study of a coal mining area in Hebei, China. Nat. Hazards 2014, 70, 1197–1208. [Google Scholar] [CrossRef]
- Lei, M.; Zhang, T.; Shi, J.; Yu, J. InSAR-CTPIM-Based 3D Deformation Prediction in Coal Mining Areas of the Baisha Reservoir, China. Appl. Sci. 2024, 14, 5199. [Google Scholar] [CrossRef]
- He, M.; Wang, Q.; Wu, Q. Innovation and future of mining rock mechanics. J. Rock Mech. Geotech. Eng. 2021, 13, 1–21. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, H.; Yang, X.; Shen, Y. Influence analysis of between subsidence and structure evolution in overburden rock under mining. J. China Coal Soc. 2019, 44, 9–17. [Google Scholar]
- Fan, H.; Lu, L.; Yao, Y. Method combining probability integration model and a small baseline subset for time series monitoring of mining subsidence. Remote Sens. 2018, 10, 1444. [Google Scholar] [CrossRef]
- Li, H.Z.; Guo, G.L.; Zha, J.F.; Wang, T.; Chen, Y.; Yuan, Y.; Huo, W. A new method of regional mining subsidence control for sustainable development in coal areas. Sustainability 2023, 15, 7100. [Google Scholar] [CrossRef]
- Hou, Z.X.; Yang, K.M.; Li, Y.R.; Gao, W.; Wang, S.; Ding, X.M.; Li, Y.X. Dynamic prediction model of mining subsidence combined with D-InSAR technical parameter inversion. Environ. Earth Sci. 2022, 81, 307. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, P.; Ji, X.; Li, Y. Prediction of surface subsidence in Gequan coal mine based on probability integral and numerical simulation. Acad. J. Eng. Technol. Sci. 2024, 7, 8–15. [Google Scholar] [CrossRef]
- Zhang, L.L.; Cheng, H.; Yao, Z.S.; Wang, X.J. Application of the improved Knothe time function model in the prediction of ground mining subsidence: A case study from Heze City, Shandong Province, China. Appl. Sci. 2020, 10, 3147. [Google Scholar] [CrossRef]
- Kim, Y.; Lee, S.S. Application of Artificial Neural Networks in Assessing Mining Subsidence Risk. Appl. Sci. 2020, 10, 1302. [Google Scholar] [CrossRef]
- Guo, W.B.; Deng, K.Z.; Zou, Y.F. Artificial Neural Network Model for Predicting Parameters of Probability-Integral Method. J. China Univ. Min. Technol. 2004, 33, 322–326. [Google Scholar]
- Shen, Z.; Xu, L.J.; Liu, X.P.; Qin, C.C.; Wang, Z.B. PIM parameters prediction model optimization based on machine learning methods. Bull. Surv. Mapp. 2016, 10, 35–38. [Google Scholar]
- Yu, N.F.; Yang, H.C. Optimal selection of prediction parameters for probability-integral method using particle swarm optimization and BP neural network. Sci. Surv. Mapp. 2008, 33, 78–80. [Google Scholar]
- LV, W.C.; Huang, H.; Chi, S.S.; Han, B.W. Neural network optimization algorithm for the prediction parameters of PIM. Sci. Surv. Mapp. 2019, 44, 35–41. [Google Scholar]
- Li, P.X.; Tan, Z.X.; Yan, L.L.; Deng, K.Z. Calculation method of probability integration method parameters based on Support vector machine. J. China Coal Soc. 2010, 35, 1247–1251. [Google Scholar]
- Wang, Z.S.; Deng, K.Z. Parameters identification of PIM based on multi-scale kernel partial least squares regression method. Chin. J. Rock Mech. Eng. 2011, 2, 3863–3870. [Google Scholar]
- Yang, J.; Liu, C.; Wang, B. BFGS method based inversion of parameters in probability integral model. J. China Coal Soc. 2019, 44, 3058–3068. [Google Scholar]
- Zha, J.F.; Feng, W.K.; Zhu, X.J. Research on Parameters Inversion in PIM by Genetic Algorithm. J. Min. Saf. Eng. 2011, 28, 655–659. [Google Scholar]
- Bo, H.Z.; Lu, G.H.; Li, H.Z.; Guo, G.L.; Li, Y.W. Development of a Dynamic Prediction Model for Underground Coal-Mining-Induced Ground Subsidence Based on the Hook Function. Remote Sens. 2024, 16, 377. [Google Scholar] [CrossRef]
- Chen, Y.; Tao, Q.X.; Liu, G.L.; Wang, L.Y.; Wang, F.Y. Detailed mining subsidence monitoring combined with InSAR and PIM. Chin. J. Geophys. Chin. Ed. 2021, 64, 3554–3566. [Google Scholar]
- Zhang, X.Y.; Tian, Y.P.; Zhang, X.F.; Bai, M.D.; Zhang, Z.T. Use of multiple regression models for predicting the formation of bromoform and dibromochloromethane during ballast water treatment based on an advanced oxidation process. Environ. Pollut. 2019, 254, 113028. [Google Scholar] [CrossRef] [PubMed]
- Bian, H.F.; Yang, H.C.; Zhang, S.B. Research on intelligent optimization for predicting parameters of probability-integral method. J. Min. Saf. Eng. 2013, 30, 385–389. [Google Scholar]
- Fan, H.D.; Cheng, D.; Deng, K.Z.; Chen, B.Q.; Zhu, C.G. Subsidence monitoring using D-InSAR and probability integral prediction modelling in deep mining areas. Surv. Rev. 2015, 47, 438–445. [Google Scholar] [CrossRef]
- Wang, Q.C.; Li, J.; Guo, G.L. Study on analogy analysis on prediction of surface subsidence parameters in mining area of Chongqing City. Coal Sci. Technol. 2018, 46, 196–202. [Google Scholar]
- Li, H.; Zheng, J.; Xue, L.; Zhao, X.; Lei, X.Q.; Gong, X. Inversion of Subsidence Parameters and Prediction of Surface Dynamics under Insufficient Mining. J. Min. Sci. 2023, 59, 693–704. [Google Scholar] [CrossRef]
- Wei, T.; Guo, G.L.; Li, H.Z.; Wang, L.; Yang, X.S.; Wang, Y.Z. Fusing Minimal Unit Probability Integration Method and Optimized Quantum Annealing for Spatial Location of Coal Goafs. KSCE J. Civ. Eng. 2023, 26, 2381–2391. [Google Scholar] [CrossRef]
- Wang, R.; Hao, K.R.; Chen, L.; Wang, T.; Jiang, C.L. A novel hybrid particle swarm optimization using adaptive strategy. Inf. Sci. 2021, 579, 231–250. [Google Scholar] [CrossRef]
- Shao, P.; Wu, Z.J.; Peng, H.; Wang, Y.L.; Li, G.Q. An Adaptive Particle Swarm Optimization Using Hybrid Strategy. Commun. Comput. Inf. Sci. 2018, 874, 26–39. [Google Scholar]
- Wang, L.; Jiang, C.; Wei, T.; Li, N.; Chi, S.S.; Zha, J.F.; Fang, S.Y. Robust Estimation of Angular Parameters of the Surface Moving Basin Boundary Induced by Coal Mining: A Case of Huainan Mining Area. KSCE J. Civ. Eng. 2020, 24, 266–277. [Google Scholar] [CrossRef]
- Wang, F.W.; Zhou, S.J.; Zhou, Q.; Lu, P.H. Comparisons between three methods in initial residuals problem of selecting weight iteration method. Sci. Surv. Mapp. 2015, 40, 18–21. [Google Scholar] [CrossRef]
- Li, H.J.; Tang, S.H.; Huang, J. Discussion for the selection of constant in selecting weight iteration method in robust estimation. Sci. Surv. Mapp. 2006, 31, 70–71+76+51. [Google Scholar]

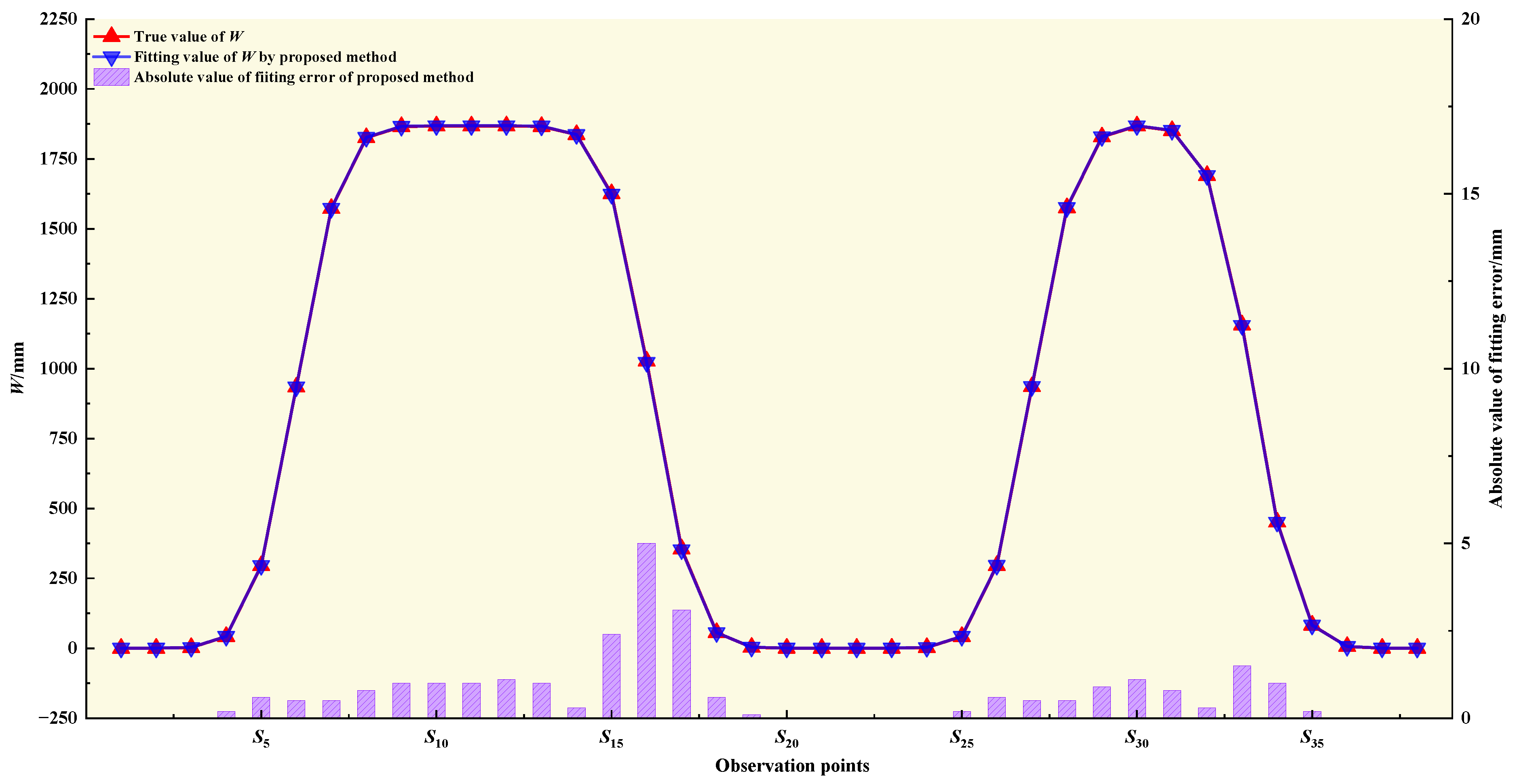
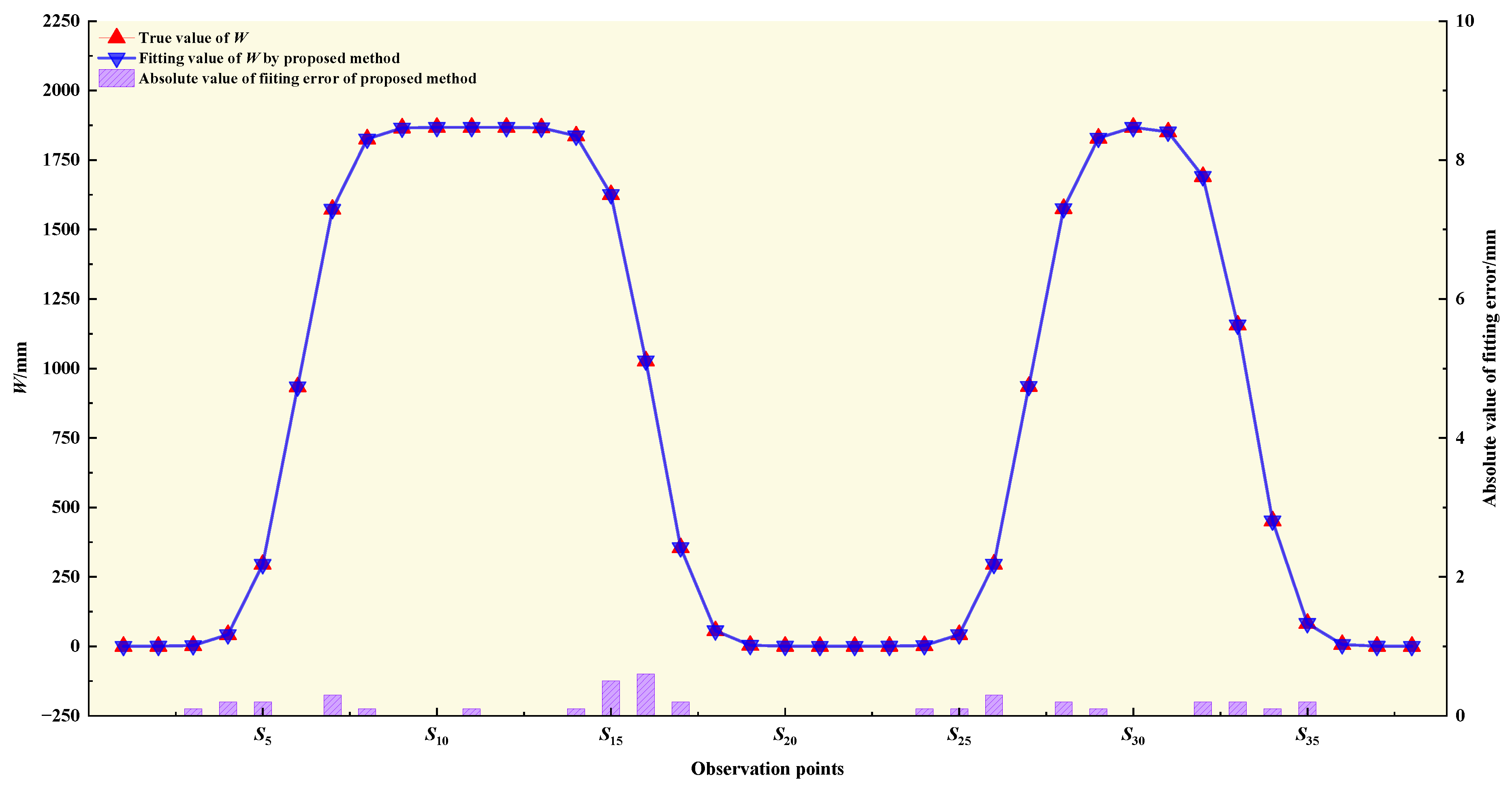
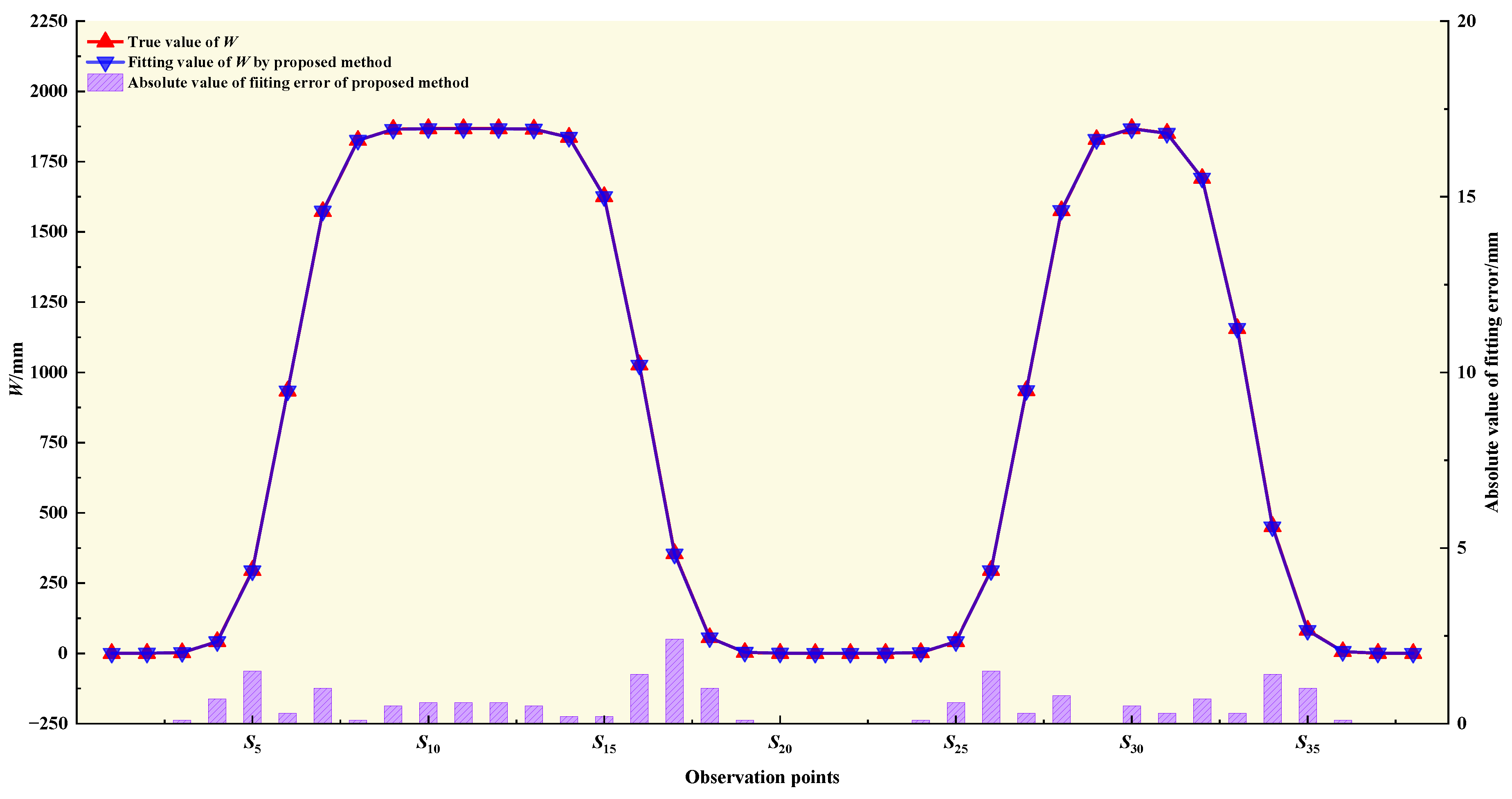
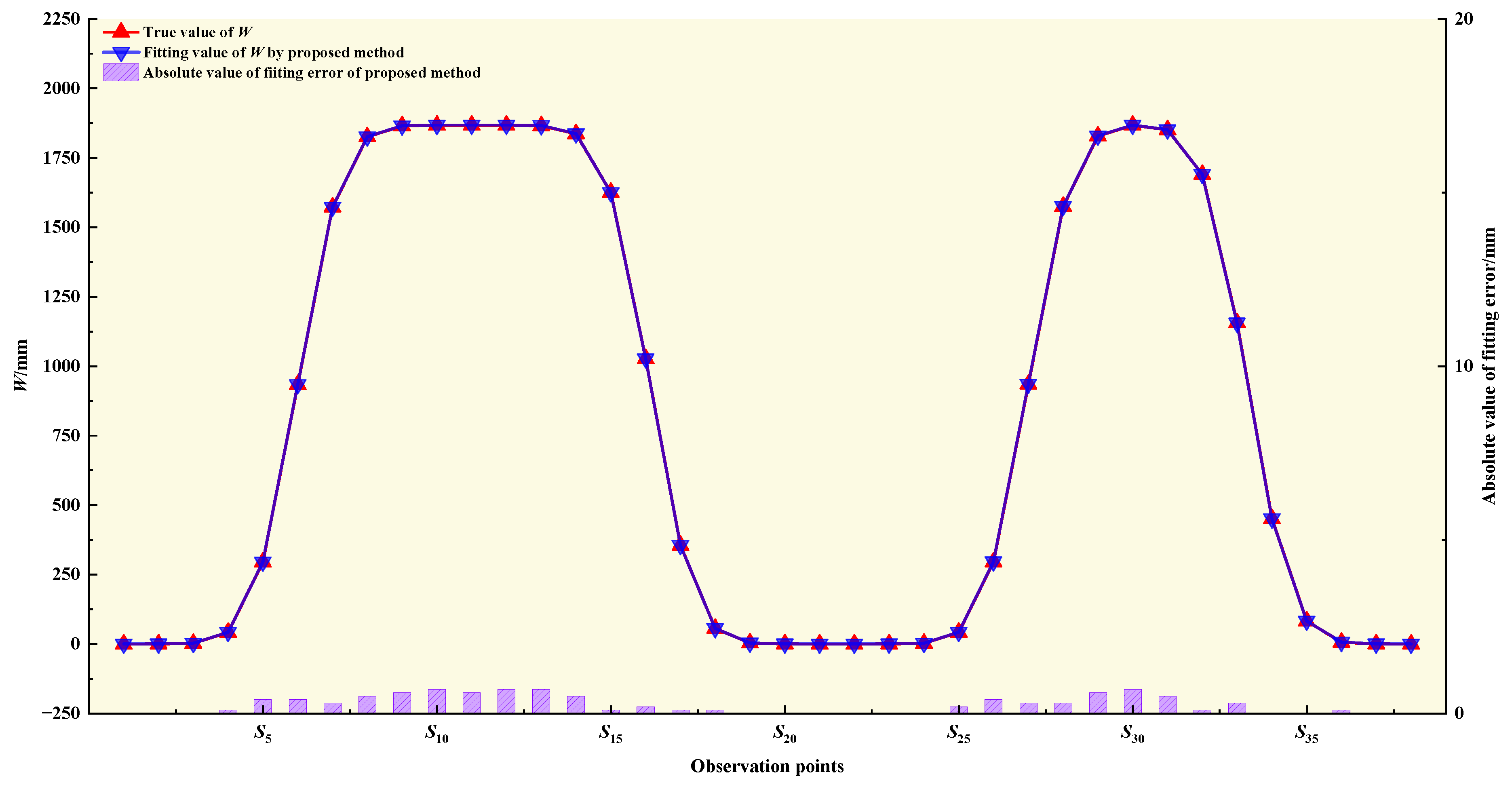

| Parameter | Design Value | Plan 1 | Plan 2 | Plan 3 | ||||
|---|---|---|---|---|---|---|---|---|
| GA Method | Proposed Method | GA Method | Proposed Method | GA Method | Proposed Method | |||
| q | IV | 0.64 | 0.6395 | 0.6405 | 0.6417 | 0.6400 | 0.6600 | 0.6403 |
| RE | 0.08% | 0.09% | 0.26% | 0.00% | 3.12% | 0.04% | ||
| tan β | IV | 1.5 | 1.5322 | 1.4804 | 1.5339 | 1.5000 | 1.4171 | 1.5013 |
| RE | 2.15% | 1.31% | 2.26% | 0.00% | 5.52% | 0.09% | ||
| θ/° | IV | 86.5 | 1.5322 | 85.5932 | 85.2471 | 85.9763 | 85.5607 | 85.6825 |
| RE | 2.15% | 1.05% | 1.45% | 0.61% | 1.09% | 0.95% | ||
| S1/m | IV | 45 | 49.9317 | 45.2301 | 39.7648 | 44.8008 | 47.2286 | 45.1187 |
| RE | 10.96% | 0.51% | 11.63% | 0.44% | 4.95% | 0.26% | ||
| S2/m | IV | 45 | 50.1448 | 44.8294 | 34.3203 | 45.1991 | 47.0186 | 45.5513 |
| RE | 11.43% | 0.38% | 23.73% | 0.44% | 4.49% | 1.23% | ||
| S3/m | IV | 45 | 44.3203 | 44.9171 | 45.7279 | 45.5575 | 46.5879 | 46.2037 |
| RE | 1.51% | 0.18% | 1.62% | 1.24% | 3.53% | 2.67% | ||
| S4/m | IV | 45 | 44.3203 | 47.0725 | 47.1754 | 45.4753 | 49.7983 | 45.3857 |
| RE | 1.51% | 4.61% | 4.83% | 1.06% | 10.66% | 0.86% | ||
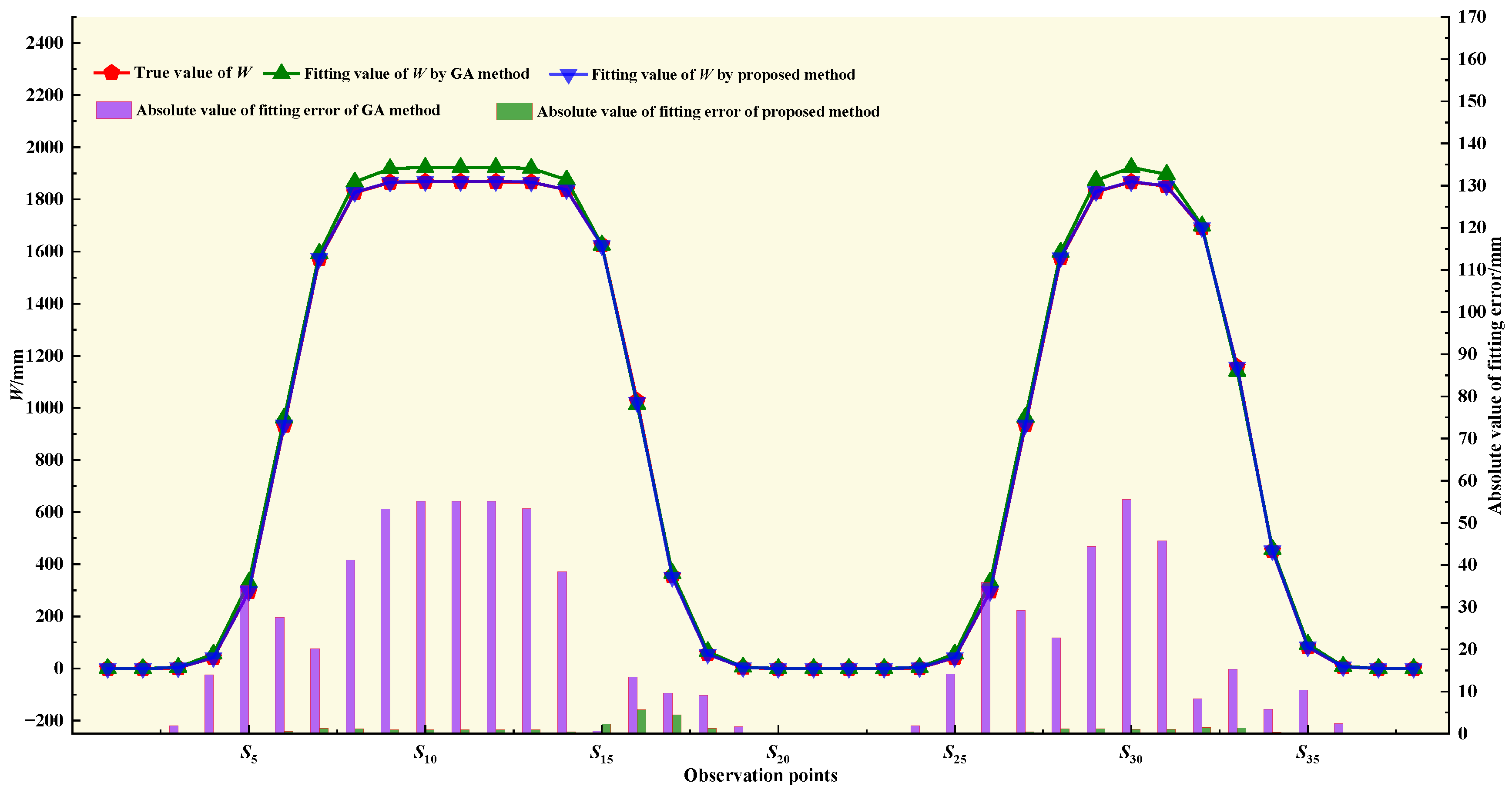
| RMSE/mm | 22.5 | 2.8 | 33.8 | 1.7 | 28.7 | 1.4 | ||
| Parameter | Reference Value | Engineering Application Plan 1 | Engineering Application Plan 2 | |||
|---|---|---|---|---|---|---|
| GA Method | Proposed Method | GA Method | Proposed Method | |||
| q | IV | 1.2672 | 1.5533 | 1.2404 | 1.3798 | 1.2889 |
| RE | 17.94% | 34.47% | 27.10% | 31.91% | ||
| tan β | IV | 1.8928 | 1.6547 | 1.8700 | 1.9113 | 1.8721 |
| RE | 12.58% | 1.20% | 0.98% | 1.09% | ||
| θ/° | IV | 86.5266 | 87.4652 | 85.3094 | 86.8843 | 85.5449 |
| RE | 1.08% | 1.41% | 0.41% | 1.13% | ||
| S1/m | IV | 14.0062 | 36.5795 | 17.0370 | 43.2282 | 23.7842 |
| RE | 161.17% | 21.64% | 208.64% | 69.81% | ||
| S2/m | IV | 44.5606 | 52.0727 | 42.7824 | 26.5384 | 34.7214 |
| RE | 16.86% | 3.99% | 40.44% | 22.08% | ||
| S3/m | IV | −2.9398 | 10.6886 | 15.6669 | −11.2751 | 9.6938 |
| RE | 463.58% | 632.92% | 283.53% | 429.74% | ||
| S4/m | IV | 6.2964 | 3.3455 | −21.3161 | 21.0065 | −4.0305 |
| RE | 46.87% | 438.54% | 233.63% | 164.01% | ||
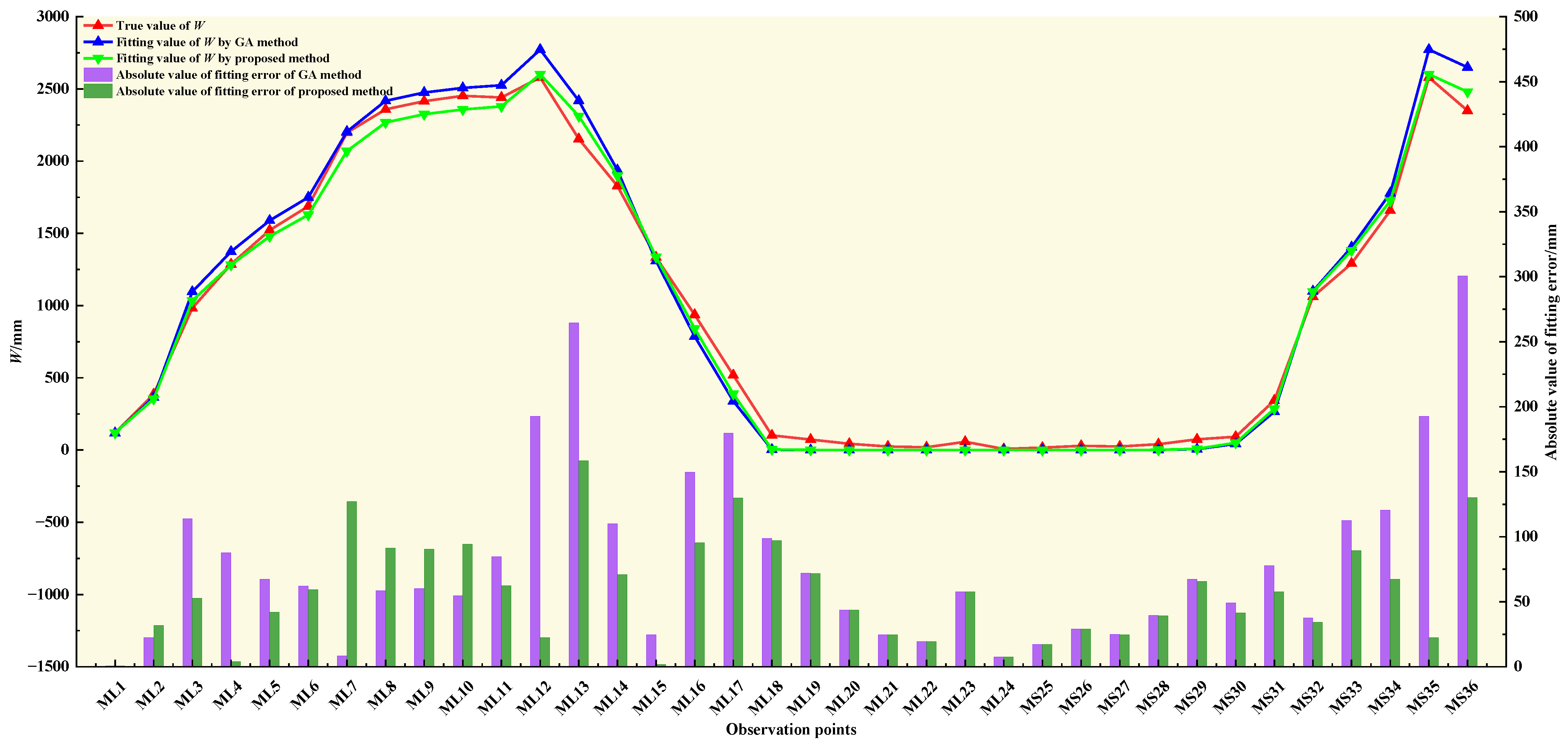
| RMSE/mm | 69.7 | 101.2 | 76.8 | 107.3 | 69.8 | |
| Parameter | q | tan β | θ/° | S1/m | S2/m | S3/m | S4/m | RMSE/mm | |
|---|---|---|---|---|---|---|---|---|---|
| k | Design value | 0.6400 | 1.5000 | 86.5000 | 45.0000 | 45.0000 | 45.0000 | 45.0000 | |
| k = 10 | IV | 0.6405 | 1.6011 | 85.6798 | 44.0935 | 46.3629 | 45.2836 | 46.2499 | 15.2 |
| RE | 0.08% | 6.74% | −0.95% | −2.01% | 3.03% | 0.63% | 2.78% | ||
| k = 1 | IV | 0.6400 | 1.5101 | 85.8538 | 44.4956 | 45.7281 | 46.7030 | 44.5848 | 1.6 |
| RE | 0.00% | 0.67% | −0.75% | −1.12% | 1.62% | 3.78% | −0.92% | ||
| k = 0.1 | IV | 0.6403 | 1.5013 | 85.6825 | 45.1187 | 45.5513 | 46.2037 | 45.3857 | 1.4 |
| RE | 0.04% | 0.09% | 0.95% | 0.26% | 1.23% | 2.67% | 0.86% | ||
| k = 0.01 | IV | 0.6414 | 1.5363 | 85.1924 | 45.4640 | 43.7179 | 45.9748 | 46.3232 | 7.5 |
| RE | 0.22% | 2.42% | −1.51% | 1.03% | −2.85% | 2.17% | 2.94% | ||
| k = 0.001 | IV | 0.6407 | 1.5794 | 86.0870 | 44.7540 | 44.0796 | 45.0884 | 44.7858 | 12.9 |
| RE | 0.11% | 5.29% | −0.48% | −0.55% | −2.05% | 0.20% | −0.48% | ||
| Parameter | q | tan β | θ/° | S1/m | S2/m | S3/m | S4/m | RMSE/mm | |
|---|---|---|---|---|---|---|---|---|---|
| k | Design value | 0.6400 | 1.5000 | 86.5000 | 45.0000 | 45.0000 | 45.0000 | 45.0000 | |
| k = 10 | IV | 0.6404 | 1.6268 | 86.0113 | 46.1155 | 45.3005 | 43.8490 | 47.2080 | 18.8 |
| RE | 0.06% | 8.45% | −0.56% | 2.48% | 0.67% | −2.56% | 4.91% | ||
| k = 1 | IV | 0.6444 | 1.5001 | 85.3051 | 44.8297 | 44.3856 | 43.7977 | 47.5408 | 9.2 |
| RE | 0.69% | 0.01% | −1.38% | −0.38% | −1.37% | −2.67% | 5.65% | ||
| k = 0.1 | IV | 0.6405 | 1.4804 | 85.5932 | 45.2301 | 44.8294 | 44.9171 | 47.0725 | 2.8 |
| RE | 0.09% | 1.31% | 1.05% | 0.51% | 0.38% | 0.18% | 4.61% | ||
| k = 0.01 | IV | 0.6390 | 1.5257 | 85.2503 | 43.8192 | 45.1534 | 46.4601 | 46.0842 | 3.9 |
| RE | −0.15% | 1.71% | −1.44% | −2.62% | 0.34% | 3.24% | 2.41% | ||
| k = 0.001 | IV | 0.6368 | 1.5205 | 85.6139 | 43.0816 | 46.2739 | 47.1941 | 44.4129 | 4.8 |
| RE | −0.50% | 1.37% | −1.02% | −4.26% | 2.83% | 4.88% | −1.30% | ||
| Parameter | q | tan β | θ/° | S1/m | S2/m | S3/m | S4/m | RMSE/mm | |
|---|---|---|---|---|---|---|---|---|---|
| k | Design value | 0.6400 | 1.5000 | 86.5000 | 45.0000 | 45.0000 | 45.0000 | 45.0000 | |
| k = 10 | IV | 0.6505 | 1.5557 | 85.7074 | 42.4913 | 45.6933 | 44.8361 | 44.8234 | 25.8 |
| RE | 1.64% | 3.72% | −0.92% | −5.57% | 1.54% | −0.36% | −0.39% | ||
| k = 1 | IV | 0.6427 | 1.5000 | 85.4679 | 43.9696 | 46.1892 | 46.7253 | 45.0778 | 5.0 |
| RE | 0.42% | 0.00% | −1.19% | −2.29% | 2.64% | 3.83% | 0.17% | ||
| k = 0.1 | IV | 0.6400 | 1.5000 | 85.9763 | 44.8008 | 45.1991 | 45.5575 | 45.4753 | 1.7 |
| RE | 0.00% | 0.00% | 0.61% | 0.44% | 0.44% | 1.24% | 1.06% | ||
| k = 0.01 | IV | 0.6407 | 1.5314 | 86.1272 | 44.4732 | 46.4933 | 43.4665 | 46.6973 | 5.8 |
| RE | 0.11% | 2.09% | −0.43% | −1.17% | 3.32% | −3.41% | 3.77% | ||
| k = 0.001 | IV | 0.6399 | 1.5000 | 85.1070 | 44.6436 | 45.1770 | 45.0159 | 46.3817 | 2.8 |
| RE | −0.01% | 0.00% | −1.61% | −0.79% | 0.39% | 0.04% | 3.07% | ||
| Parameter | q | tan β | θ/° | S1/m | S2/m | S3/m | S4/m | RMSE/mm | |
|---|---|---|---|---|---|---|---|---|---|
| Plan | Design value | 0.6400 | 1.5000 | 86.5000 | 45.0000 | 45.0000 | 45.0000 | 45.0000 | |
| Layout Plan 1 | IV | 0.6403 | 1.4982 | 84.7213 | 44.4317 | 46.8088 | 45.4997 | 48.2903 | 1.2 |
| RE | 0.05% | 0.12% | 2.06% | 1.26% | 4.02% | 1.11% | 7.31% | ||
| Layout Plan 2 | IV | 0.6400 | 1.5008 | 84.4382 | 46.1015 | 43.8334 | 43.5677 | 50.5812 | 0.2 |
| RE | 0.00% | 0.05% | 2.38% | 2.45% | 2.59% | 3.18% | 12.40% | ||
| Layout Plan 3 | IV | 0.6398 | 1.5048 | 84.9745 | 43.9372 | 46.2053 | 46.0874 | 46.9935 | 0.8 |
| RE | 0.03% | 0.32% | 1.76% | 2.36% | 2.68% | 2.42% | 4.43% | ||
| Layout Plan 4 | IV | 0.6402 | 1.4991 | 85.2291 | 41.6217 | 48.4276 | 44.1853 | 48.4487 | 0.4 |
| RE | 0.03% | 0.06% | 1.47% | 7.51% | 7.62% | 1.81% | 7.66% | ||
| Layout Plan 5 | IV | 0.6403 | 1.4996 | 85.3239 | 46.7982 | 43.9935 | 49.2968 | 43.0575 | 1.6 |
| RE | 0.05% | 0.03% | 1.36% | 4.00% | 2.24% | 9.55% | 4.32% | ||
| Layout Plan 6 | IV | 0.6128 | 1.5080 | 85.9702 | 39.7584 | 45.5032 | 40.3865 | 45.9748 | 45.0 |
| RE | 4.25% | 0.53% | 0.61% | 11.65% | 1.12% | 10.25% | 2.17% | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, C.; Liu, W.; Wang, L.; Zhu, X.; Tan, H. A Probability Integral Parameter Inversion Method Integrating a Selection-Weighted Iterative Robust Genetic Algorithm. Appl. Sci. 2025, 15, 8102. https://doi.org/10.3390/app15148102
Jiang C, Liu W, Wang L, Zhu X, Tan H. A Probability Integral Parameter Inversion Method Integrating a Selection-Weighted Iterative Robust Genetic Algorithm. Applied Sciences. 2025; 15(14):8102. https://doi.org/10.3390/app15148102
Chicago/Turabian StyleJiang, Chuang, Wei Liu, Lei Wang, Xu Zhu, and Hao Tan. 2025. "A Probability Integral Parameter Inversion Method Integrating a Selection-Weighted Iterative Robust Genetic Algorithm" Applied Sciences 15, no. 14: 8102. https://doi.org/10.3390/app15148102
APA StyleJiang, C., Liu, W., Wang, L., Zhu, X., & Tan, H. (2025). A Probability Integral Parameter Inversion Method Integrating a Selection-Weighted Iterative Robust Genetic Algorithm. Applied Sciences, 15(14), 8102. https://doi.org/10.3390/app15148102





