Abstract
Recent advances in sensor technology, data acquisition, and signal processing have enabled the development of data-driven structural health monitoring (SHM) strategies, offering a powerful alternative or complement to traditional model-based approaches. These approaches rely on damage-sensitive features (DSFs) extracted from vibration measurements. This study introduces an innovative, unsupervised learning framework leveraging transmissibility functions (TFs) as DSFs due to their local sensitivity to changes in dynamic behavior and their ability to operate without requiring input excitation measurements—an advantage in civil engineering applications where such data are often difficult to obtain. The novelty lies in the use of sequential sensor pairings based on structural connectivity to construct TFs that maximize damage sensitivity, combined with one-class classification algorithms for automatic damage detection and a damage index for spatial localization within sensor resolution. The method is evaluated through numerical simulations with noise-contaminated data and experimental tests on a masonry arch bridge model subjected to progressive damage. The numerical study shows detection accuracy above 90% with one-class support vector machine (OCSVM) and correct localization across all damage scenarios. Experimental findings further confirm the proposed approach’s localization capability, especially as damage severity increases, aligning well with observed damage progression. These results demonstrate the method’s practical potential for real-world SHM applications.
1. Introduction
Structural Health Monitoring (SHM) addresses a broad spectrum of infrastructure-related issues, including the detection, localization, and quantification of structural damage, as well as the prediction of the remaining service life of the structural system. Modern SHM systems typically consist of transducers networked through data acquisition and transmission systems that collect specific sets of measurements. With the advent of low-cost, high-performance sensors, smart transducers, and even smart materials, setting up densely deployed sensor networks has become economically viable, facilitating access to large volumes of vibration data.
To make informed decisions with the measured vibration data, SHM employs both model-based and data-driven techniques [1,2]. Among data-driven methods, vibration-based approaches are particularly attractive due to their ability to detect subtle changes in dynamic response. Meanwhile, alternative data modalities such as vision-based methods have also gained attention, especially with the rise of deep learning [3,4,5], although these lie outside the scope of the present study.
Model-based approaches, on the other hand, rely on the assumption that structural responses can be accurately simulated using numerical models, such as finite element models. However, developing these accurate numerical models, especially for large-scale structures, is a resource-intensive process that demands significant computational power and human expertise. The complexity and extensive data requirements further complicate this task. Even with all the investment in developing and validating a numerical model, the assumptions and simplifications inherent in modeling can introduce inaccuracies, potentially undermining the damage detection process.
To address these limitations, non-model-based approaches utilize damage indicators directly derived from measured data, avoiding the need for detailed physical models. These methods fit data analysis models to the measured input and/or output response data and then extract features that are sensitive to variations caused by damage. They are scalable, adaptable to changing conditions, and efficiently process large datasets. Within these non-model-based approaches, input-output methods offer greater accuracy but face challenges in measuring excitation forces, and the requirement for controlled input imposes significant limitations in real-world applications. In contrast, output-only methods, which rely solely on response data, bypass these constraints, making them more suitable for real-world monitoring of civil engineering systems. Approaches such as operational modal analysis, principal component analysis, independent component analysis, correlation analysis, time series analysis, and wavelet analysis have been proposed within this output-only category.
In output-only techniques for assessing structural integrity, commonly selected features include modal parameters [6,7,8,9,10,11,12,13,14] and parameters derived from statistical time series models, such as autoregressive (AR) model coefficients or residual errors when comparing monitored data with model predictions [15,16,17,18,19,20,21,22,23,24]. While these features are conceptually sound, each presents limitations or challenges requiring careful consideration. Modal parameters, for example, are global properties of the system; however, structural damage does not always impact global dynamic characteristics, especially in lower modes of vibration, potentially making modal properties insensitive to certain types of damage. Furthermore, environmental factors such as temperature, moisture, and measurement noise may alter modal characteristics to a degree comparable to damage effects, thereby masking damage indicators. While modal frequencies lack the capability to localize damage, mode shapes or mode shape curvatures are introduced to fulfill this role, as they can provide spatial information about damage locations. However, these features require measurements from a large number of sensor arrays to ensure completeness and highly accurate estimations for reliable results. In fact, all the aforementioned limitations of modal parameters as damage features require, first and foremost, the extraction of these parameters from sensor data using modal identification algorithms, increasing the computational cost. Similarly, features derived from statistical time series models, such as those AR models, are sensitive to noise, which can compromise detection accuracy in low-damage scenarios. Selecting the correct model and model order introduces additional computational complexity, which can hinder the use of these features in practical applications.
In contrast, transmissibility functions (TFs) paired with anomaly detection algorithms effectively address many of these limitations. Fundamentally, a transmissibility function represents the frequency-dependent ratio of the output response (e.g., acceleration) at one point on a structure to the output response at another point, when the structure is subjected to excitation. Unlike frequency response functions (FRFs), which require knowledge of the input force, TFs are derived solely from response measurements. This inherent characteristic, combined with their ability to capture damage-sensitive information across a broad frequency range, enhances robustness and detection reliability by reducing reliance on global system properties. The potential of TFs for damage detection has been explored in several foundational studies.
Early analytical and foundational studies laid the groundwork for transmissibility function (TF) concepts. Chesne and Deramaeker [25] provided the mathematical basis of TFs and analyzed their relationship with mechanical properties of mass-spring systems. Zhou et al. [26] introduced transmissibility coherence and proposed a damage index based on this feature to detect and estimate damage severity. Li et al. [27] extended the concept by proposing power spectral density transmissibility within a model-update framework. Zhu et al. [28] investigated damage sensitivities of TFs on lumped mass models and offered a procedure suitable for large-scale structures with limited sensors. Zhou et al. [29,30] contributed with clustering and dimensionality reduction techniques combined with TFs to reduce computational costs, demonstrating growing recognition of TFs as valuable damage-sensitive features.
In parallel, data-driven and machine learning-based approaches utilizing TFs have emerged. Yan et al. [31] reviewed TF fundamentals within system identification, focusing on operational modal analysis and model updating. Nguyen et al. [32] applied TFs as inputs to artificial neural networks for damage detection in simulated bridge data. Liu et al. [33] proposed integrating TF-based datasets with deep learning models using one-dimensional convolutional neural networks. Cheng and Cigada [34] provided analytical insights into TF mechanisms for damage localization, emphasizing their flexibility. Han et al. [35] developed damage detection methods based on TFs employing different distance metrics.
More recent advances focus on integration with model reduction, finite element updating, and specific application domains. Luo et al. [36,37] enhanced damage detection accuracy by coupling TFs with system equivalent reduction expansion processes and proposing a weighted transmissibility assurance criterion. Wu et al. [38] applied TFs for debonding detection and localization in concrete pavements. Li et al. [39] offered a comprehensive review of TF-based diagnostics for beam-like structures. Zou et al. [40] combined time-domain TFs with empirical mode decomposition for finite element model updating and damage localization. Dziedziech et al. [41] introduced a wavelet-based TF approach for detecting abrupt damage in buildings. Wang and Ding [42] developed a damage indicator based on response difference transmissibility. Markogiannaki et al. [43] and Izadi and Efsandiari [44] used TFs with finite element model updating to improve detection accuracy. Most recently, Meggitt and McGee [45] explored structural invariance concepts that enable TFs to locate damage in complex structures.
In the broader context of structural health monitoring, data-driven approaches play a pivotal role in advancing automated damage detection systems. By leveraging the selected damage-detecting features, these systems enable the shift from “on-schedule” to “on-demand” maintenance, allowing for more efficient and responsive decision-making. According to Rytter’s [46] classification of the damage identification problem, the first step in this process is detecting the presence of damage. At this initial level, the task typically involves one-class classification (OCC) algorithms, which are well-suited for identifying deviations from normal conditions based on these key features, making them essential for the early stages of SHM automation.
The OCC problem is a special type of classification issue where only data from one-class, the target class, is available. In the context of SHM, “damage detection” aligns with OCC, as baseline (positive) data from the undamaged structural state is readily available. However, potential damage scenarios, for which no training data exists, are numerous. With limited or no data from the damaged (negative) state, the classification boundary can only be defined using available positive data. The goal in OCC is to establish a boundary around the positive class that maximizes the inclusion of positive data while minimizing the acceptance of outliers or “negative” data [47].
Based on the model of the classifier, Khan and Madden [48] categorize OCC techniques into three types: density-based, boundary-based, and reconstruction-based. Density-based methods, such as the Gaussian, mixture of Gaussians, local outlier factor (LOF), and Parzen density methods, estimate the probability density function of the underlying distribution of the training target data points and determine whether the test data comes from the same distribution. The challenges associated with this approach are the selection of appropriate models and the well-sampled high number of training data requirements. In boundary-based methods, such as the one-class support vector machine model (OCSVM), a closed border or smooth boundary around the target data is built by introducing kernel tricks, with the task of optimizing the enclosed volume. Any test data outside the border of the boundary is considered an outlier. Boundary-based methods require fewer data samples compared to density-based methods for similar performance; however, in these models, optimizing the boundary poses a modeling challenge. In reconstruction-based methods, a model like an autoencoder is trained using the target class data, and then the test data showing a sufficiently large reconstruction error or not complying with the training data are pointed out as outliers. The k-means clustering-based classifier and auto-encoder or multi-layer perceptron (MLP) methods are the most widely used reconstruction-based models. In ensemble-based one-class classification, a combination of multiple one-class classifiers is utilized collectively to benefit from each for improved accuracy. They calculate a mixture value of novelty scores by summarizing multiple novelty scores of individually computed one-class classifiers. Ensemble-based OCC methods include tree-based methods, such as isolation forest (iForest), and clustering-based ensemble methods.
In this paper, a model-free, transmissibility-based methodology for structural damage assessment is proposed, addressing both detection and localization tasks using only measured data. The motivation stems from the practical challenges faced in civil engineering SHM, such as limited access to input excitation data, the complexity of modeling large-scale or historic structures, and the need for reliable damage-sensitive features that do not require prior knowledge of damage scenarios. To overcome these limitations, the damage detection problem is formulated as a One-Class Classification (OCC) task, where normalized transmissibility differences serve as the damage-sensitive features. Unlike previous studies that rely on labeled damage data or finite element models, this framework operates in an unsupervised manner using data solely from the undamaged condition. A key contribution of this study lies in the integration of transmissibility-based features with a comparative evaluation of multiple OCC techniques, a combination that has not been systematically explored in the literature. Furthermore, a direct performance comparison is conducted with a modal flexibility-based approach, demonstrating the superior sensitivity of the proposed method to local stiffness changes under noisy and constrained sensor conditions. The methodology is validated on a scaled model of a historic masonry arch bridge, highlighting its applicability to complex structures where idealized assumptions often fail, thereby contributing toward the practical implementation of data-driven damage localization strategies.
The remainder of the paper is organized as follows. A brief background on the fundamentals of transmissibility functions is provided, followed by a discussion of OCC techniques that exploit offline learning principles for damage detection. Next, a damage localization scheme is presented, formulating a localization index to identify maximum transmissibility differences across a range of frequencies. The subsequent sections offer verification of the proposed methodology, featuring numerical simulations conducted on a fixed-fixed beam and experimental data collected from a masonry arch bridge model. Finally, the paper concludes with a summary of the proposed methodology, highlighting its strengths and challenges.
2. Transmissibility Function
The equation of motion of a multi degree-of-freedom (DOF) system subjected to forced vibration is governed by the following differential equation:
where M, C, K are the mass, damping and stiffness matrices and are the displacement, velocity and acceleration responses, respectively. Assuming harmonic excitation forces, the response in the frequency domain as a function of the excitation, can be expressed as:
where , the frequency response function is defined as:
Focusing on two sets of coordinates i and j and partitioning the respective parts of the above expression, for a single excitation force applied at coordinate k, one can write
Eliminating , one gets
The local transmissibility between the two coordinates i and j, in reference to input location k, can be defined using two responses directly as:
The most commonly used approach to estimate transmissibility is through power spectral density functions, G:
Equation (8) is the ratio of the response cross spectral densities between coordinates i and j, defining how vibration is transmitted between these coordinates as a function of frequency. It should be noted that G becomes an auto spectrum when k = i or k = j and in that case, it will be analogous to coherence in frequency response functions. It should also be noted that the applied force does not necessarily need to be harmonic. Although the derivation assumed harmonic forces to relate two response spectra of like variables, the expressions still remain valid for other types of excitation including impulse and random loads [49].
The local TF obtained in this manner depends only on the location of the input excitation and does not require the input to be measured. Any change in the structural properties will clearly be reflected in the TF, which is expected to be quite sensitive to even local damage, as it characterizes the vibration response across-small sections of the structure. Among possible loading (unmeasured) conditions that can be implemented when using TF for damage detection, a potential alternative with practical significance is to use a single input moved to different points on the structure. For each excitation location, a transmissibility matrix of size , elements of which are functions of frequency can be formed for all combinations of outputs between location pairs.
The selection of appropriate features as damage indicators is essential, not only for reducing the dimensionality of the original dataset but also for eliminating the unrelated variables to ensure the success of the proposed methodology. To ‘close-in’ on the damaged region, typically the two successive pairs of coordinates are selected, and the transmissibilities corresponding to the two adjacent coordinates along the structure are interrogated. This corresponds to the first-upper diagonal of the matrix with entries .
Furthermore, to limit the dependence of the TF outside the domain enclosed by the output coordinates, the input location is also arranged such that it is collocated with one of the output coordinates. In this study, the excitation is always applied at the latter DOF in the selected pair (excitation at DOF i + 1 for the transmissibility ), following a consistent directional pairing. As a result, the transmissibility functions used are not symmetric, and their directionality reflects the excitation-measurement configuration. This selection is both theoretically motivated and practically consistent with a decentralized sensing strategy. Hence, with these two criteria imposed on the selection, the number of transmissibility functions retained as damage detection features reduces to to for an N-DOF system. With input location indicated as the superscript, the vector of selected features for damage detection as a function of frequency are defined as .
Although such a procedure requires impact testing across multiple locations to generate comprehensive TFs, impact testing can often be implemented with minimal disruption to the structure’s normal operations. For certain domain-specific applications, such as a metro tunnel structure discussed by Feng et al. [50], a sequential excitation and measurement scheme is quite feasible. Also, mobile sensing systems which navigate throughout the structure [28,51], may enable the use of these algorithms for autonomous damage detection. Nevertheless, it is acknowledged that impact testing may not always be practical, particularly for large or operationally sensitive structures. Future research could explore alternative excitation sources, such as ambient vibrations or operational loads, to derive transmissibility functions. This would increase the applicability of the proposed methodology in real-world SHM scenarios.
3. Damage Detection and Localization Scheme
In most transmissibility-based techniques using unlabeled data, the detection aspect of the damage identification problem is often bypassed, with the focus placed on a damage index that reflects transmissibility changes relative to an undamaged baseline for damage localization. In the relatively few studies that explicitly tackle the damage detection problem, distance measures are the most commonly applied metrics. Techniques like Euclidean distance [52] and Mahalanobis distance [26,29,30], coupled with deterministic threshold values, have been used to differentiate damaged states from baseline conditions. An alternative approach, similar to the modal assurance criterion (MAC) in modal analysis, was also proposed by Maia et al. [53], based on correlations of transmissibility functions for damage detection.
Other techniques, such as outlier analysis using the Monte Carlo method or threshold determination based on training data [54,55] for a specific significance level, as well as statistical process control using control charts [56], have also been employed to detect damage. However, these methods often rely on deterministic thresholds or assume Gaussian distributions for the selected features. These assumptions can limit both their computational efficiency and reliability when applied to complex, real-world scenarios. In contrast, the unsupervised one-class learning approach proposed in this study removes these constraints, enabling a fully data-driven framework. This allows for more flexible detection, as the system can adapt to a broader range of damage types without the need for pre-labeled data or assumptions about specific feature distributions.
Building on the core principles of unsupervised one-class learning, the proposed methodology for damage diagnosis is implemented in two stages: training and inspection. The first stage of training includes a learning process with the features built from the data corresponding to the undamaged or baseline state of the structure, while the second stage of inspection refers to the evaluation of data corresponding to the unknown structural state that attempts to classify it as an ‘outlier’ or ‘belonging’ to the trained class.
Damage detection is based on tracking the difference in amplitudes of the transmissibility functions selected as the DSFs. The selected transmissibility functions, or more specifically, the sum of the amplitudes of the transmissibility over the frequency range of interest, are tracked for detecting anomalies in the data patterns as an indication of structural changes. Hence, DSF is expressed as:
where , N is the number of sensors, and is the frequency band of interest.
For each consecutive sensor combination, this normalized measure compares the two states not only through the peaks at certain frequencies but over a specific frequency range which helps reduce the effect of noise and enhance damage detection accuracy. Subsequently, the outlier estimation methods developed can be implemented to distinguish the dataset belonging to the healthy state (‘normal’) from that belonging to the damaged state (‘outlier’).
The local outlier factor (LOF) is an algorithm based on the concept of the local density that is well-suited for this purpose. Instead of comparing the density of an observation with respect to the entire data distribution, LOF compares it to its neighbors. Outliers are defined as points with significantly lower density than their neighbors [57]. The algorithm utilizes the nearest neighbor search starting by calculating the distance between data point p and all other observations using a selected distance measure, , such as Euclidean, Manhattan or Minkowski. The kth closest point (k-nearest neighbor) and the associated distance are determined. This allows for assigning the reachability distance as:
The local reachability density (LRD) is calculated as the reciprocal of the average reachability distance using:
where Nk(p) represents the k-nearest neighbors of observation p and is the number of observations in Nk(p).
Finally, the LOF of observation p is computed as the average density ratio of the observation to its neighbors:
For normal observations, the LOF values are less than or close to 1, indicating that the local reachability density of an observation is higher than or similar to that of its neighbors. A local outlier factor value greater than 1 indicates an anomaly.
Similar to LOF, k-means relies on similarity of the data distribution. While designed specifically for partitioning the data into k-clusters, it can be adapted for OCC with a minor modification. By setting the number of clusters to one and using the ‘normal’ observations as belonging to this cluster, the centroid of this cluster is calculated. A distance measure (Euclidean) to this centroid can then be defined, allowing for the classification of new observations based on a user-specified threshold where those larger than the threshold are identified as outliers.
By taking a boundary-based approach, OCSVM aims to create a decision boundary that encloses most of the training samples. This transformation facilitates finding a clear decision boundary. In this new space, the origin typically represents the outlier class, separate from the remaining data points, which represent the target class. The algorithm then identifies a maximum-margin hyperplane—a decision surface with the largest possible margin—that divides most of the data points (target class) from the origin (outliers). This hyperplane allows for classifying new data points as belonging to the target class or being potential outliers.
The maximum-margin hyperplane with a normal vector w, is determined through solving the following optimization problem [58]:
subject to
where xi are the training examples belonging to one-class, are the slack variables introduced to relax the constraints and allow some error during training, ν is the regularization coefficient between 0 and 1 providing an upper-bound for the ratio of outliers among all training data and is the offset (or threshold).
In contrast to detecting anomalies by effectively profiling normal observations, iForest explicitly uses isolation for finding anomalies [59]. It leverages the fact that the anomalies are fewer than the normal observations and have different attribute values. The algorithm employs a tree structure, where anomalies are isolated closer to the root, while normal instances reside deeper in the tree. Within the tree structure, each internal node represents a feature and a split value, and each leaf node indicates an isolated data point. Since anomalies are rare, they require fewer splits to be isolated from the majority of normal data points. The algorithm measures the average distance it takes to isolate each data point. The points with the shorter path distances, indicating faster isolation within the tree structure are identified as anomalies.
Each of the one-class algorithms discussed above presents distinct advantages and limitations. LOF is effective for detecting local anomalies in non-uniform data distributions but requires careful tuning of neighborhood size. k-means clustering offers simplicity and efficiency for anomaly detection but relies on predefined cluster numbers and assumptions about data structure. iForest efficiently identifies anomalies in high-dimensional datasets by isolating data points, though it may struggle with complex local structures. Finally, OCSVM provides a robust, data-distribution-independent decision boundary, but its performance depends on kernel selection and parameter tuning.
After detecting damage, data from various locations within the structural system must be integrated to facilitate localization through relative comparison. To achieve this, local TF information at each frequency is analyzed. More specifically, the local TF with the largest difference is identified at each frequency and the count of occurrences are updated until the entire frequency range is covered. The localization decision is based on the maximum number of occurrences over the frequency range of interest. The sensor pair that is recorded most frequently with maximum occurrence (nmax) is isolated, and the region between the respective sensors is marked as a potential damage location. The method of counting occurrences allows for emphasizing the shape-wise shift in the local TF due to damage, enhancing the reliability of damage localization.
The localization index (DI) is defined as a normalized count by dividing this value by the total number of spectral lines. The normalization of the counts with the number of frequencies in the band of interest facilitates a clearer interpretation of the results. This process bounds the index to a maximum of 1, which occurs when the same local TF exhibits the highest difference between the tested and intact states across all frequencies in the range.
Table 1 displays the steps of the methodology employed for damage identification methodology at each phase. The initial training phase includes collecting repeated measurements at the baseline state of the structure to build a training dataset for the selected DSFs. Using this dataset, OCC models are developed. The monitoring phase begins with data collected from an unknown state of the system. DSF vectors extracted from this state are tested against the developed models for damage detection. Finally, the localization stage employs a data fusion approach integrating sensor information deployed throughout the structure to identify the potentially damaged region.

Table 1.
Damage detection methodology.
4. Numerical Simulations
The simulation example features a fixed-fixed beam modeled with ten nodes and eight identical lumped masses, as shown in Figure 1. The flexural rigidity, EI for the beam is taken as 5.1752 × 105 kN.m2 so that the fundamental frequency is 1 Hz in the undamaged state. Sensors measuring acceleration in the vertical direction are assumed to be present at each of the lumped mass locations. Viscous dissipation is included in the form of proportional damping with a magnitude of 5% of critical.
Figure 1.
Simulated structure with sensor locations.
Data for the baseline state, necessary for initial training and subsequent testing, is generated using the finite element model of the beam by assigning an initial velocity at each sensor location, one at a time. Acceleration measurements are simulated at these positions with a sampling time of 0.01 s, over a 30-s period. This data is then contaminated with varying levels of noise, randomly distributed within the range of 3% to 5%. The resulting signal pool includes 120 sets of acceleration measurements utilized to compute the transmissibility functions and extract the DSFs as defined in Equation (7). From this pool, the first 20 sets are used to train the classification model, while the remaining 100 sets are reserved for validation.
Damage states for testing are simulated by introducing a 20% reduction in flexural stiffness at each segment between the sensor locations, one at a time. Given the sensor arrangement, this results in seven different damage cases, each with a different damaged element. Acceleration measurements are then simulated and contaminated in the same manner with again 100 simulations conducted for each damage scenario. This process leads to a total of 700 sets of simulated damaged data for the beam.
The natural frequencies of the system associated with these damage cases, as well as the baseline state, are displayed in Table 2. Table 3, which lists the changes in natural frequencies across the inflicted damage scenarios, indicates that the most significant frequency change is less than 2%. This makes the proposed approach more attractive than alternative methods that employ identified modal parameters as DSFs.

Table 2.
Natural frequencies of the system for the baseline and the damaged states.

Table 3.
Percent change in the frequencies with damage.
Damage localization potential of the proposed methodology is demonstrated first with the noise-free data in Figure 2 and Figure 3. Figure 2 compares the extracted transmissibilities through the processing of this data for the baseline state and a selected damage scenario while Figure 3 presents the damage localization results for all damage cases. As can be seen in this figure, for all damage scenarios, the damaged member can be singled out with the damage index (DI > 0.9) under noise-free conditions.
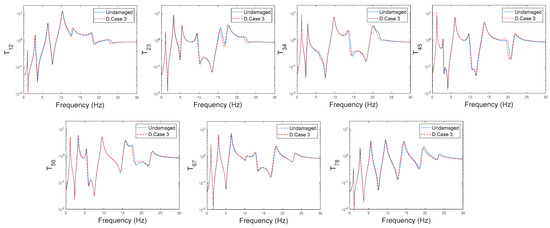
Figure 2.
Transmissibilities between successive coordinates: Baseline state versus Damage Case3 (No measurement noise).
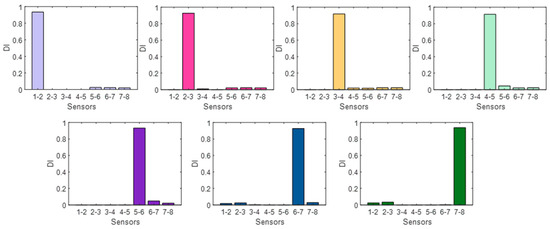
Figure 3.
Localization of Damage for the Damage Cases 1–7: No measurement noise.
Next, the proposed approach was tested with the noise-polluted data. The classification algorithms used for anomaly detection, including OCSVM, iForest and LOF require certain amount of historical data to train the model for the baseline (healthy system). DSFs extracted from the first 20 simulations out of the total of 120 generated for the baseline state were utilized to train these models, while the remaining 100 simulations were reserved for validation. For comparison purposes, the k-means clustering algorithm was applied to the entire dataset, which included both baseline and damage cases. The number of clusters was set to two to evaluate whether the extracted DSFs could naturally separate into distinct healthy and damaged groups based on similarity, without the use of any label information. Since k-means is an unsupervised method and does not involve an explicit training phase, it does not conform to the OCC framework. Therefore, it was included purely as a baseline clustering method to provide additional perspective on the separability of the DSFs in an unlabeled context.
The results of the classification for all four models used in this study are listed in the form of a confusion matrix in Table 4. The ‘true positive’ (actual damaged) side of the matrix shows very satisfactory performance across the models, with one notable exception. The performance of the iForest algorithm is rather unstable; while it accurately predicts the state of the system for some damage cases, its prediction accuracy is significantly lower for others. This variability in iForest’s performance may be attributed to its sensitivity to the distribution of the input features and the random nature of its tree construction, which relies on sub-sampling small portions of the dataset to build each isolation tree. In particular, damage scenarios with low-severity effects or overlapping DSF characteristics (e.g., Damage Cases 4 and 6) may limit its ability to effectively isolate anomalies. Furthermore, the presence of noise in the DSFs may affect the algorithm’s consistency in distinguishing between healthy and damaged states.

Table 4.
Confusion matrix data for classification of the 700 damaged and 100 healthy simulation cases.
In contrast, both the OCSVM and LOF algorithms exhibit very similar performance bordering on perfection. They miss only a few classifications in a single case. Meanwhile, the k-means algorithm demonstrates excellent true-positive predictions without exceptions. The performance across all models seems consistently high on the ‘true negative’ side of the matrix, suggesting that all are equally suited for the task. Focusing on the safety-critical aspect of the damage detection problem, where predicting an actual damaged case as undamaged (false negative) is of greater concern than raising a false alarm for an undamaged state, the k-means algorithm displays the best performance.
Following the detection stage, damage localization results utilizing the proposed index for the simulation cases are obtained and visually summarized in the box plot given in Figure 4 for comparison. It is noteworthy that for all the damage scenarios, the correct location has been identified, with the index reaching its peak at the truly damaged segment. However, unlike the noise-free case where DI fluctuates around 0.9, the median value for the normalized DI is around 0.3 for the noisy data. Nevertheless, it still leads to correct localization by identifying the damaged member with the highest DI, while the index for the remaining members remain clustered around 0.1. The only exception to this clear distinction between two clusters is D.Case 6, for which a few misclassifications occurred in the previous stage of damage detection. DI for the segment between sensors 7–8 has deviated from those of the remaining undamaged segments, albeit still lower than the truly damaged segment.The sensor locations in this model-free approach serve as discrete measurement points, analogous to finite elements that represent structural behavior in a model. The choice of sensor placement significantly influences the resolution of damage localization. By employing denser sensor arrangements, resolution can be enhanced, leading to more refined and accurate identification of damage. However, denser sensors may complicate data analysis due to the larger volume of data to process, potentially increasing computational demands. Additionally, while more sensors can enhance resolution, they may also amplify the effects of measurement noise, making it more challenging to distinguish between true damage and noise. Therefore, a careful balance must be achieved between sensor density and the overall complexity of the analysis.
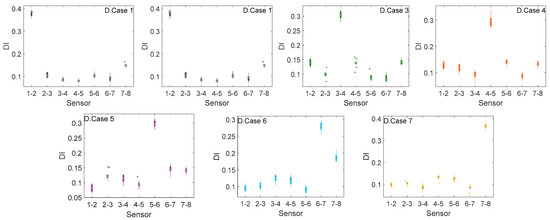
Figure 4.
Localization of Damage for the Damage Cases 1–7.
5. Case Study: Progressive Damage of a Masonry Arch Bridge Model
To assess the applicability and adaptability of the proposed methodology to real engineering structures, data collected from an experimental study conducted at the Materials Lab of the Civil Engineering Department at Istanbul Technical University is presented. The test specimen comprises a ¼-scale model of a specific span of the Uzunköprü bridge, a historical Ottoman bridge, dating back to the 15th Century, located over the Ergene River in Edirne, Turkey. The model features an arch ring with a span of 1.73 m and a rise of 0.94 m. It has an overall width of 1.4 m, encompassing both the spandrel walls and the fill. A reinforced concrete slab, 10 cm thick, with plan dimensions of 3.20 × 1.55 m, served as the foundation for the bridge model. Figure 5a,b display the photo of the bridge and the sketch of the test specimen.
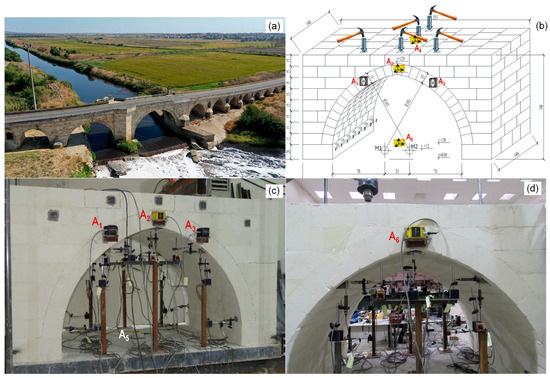
Figure 5.
(a) Uzunkopru Bridge, Edirne, Turkey, (b) sketch of the test specimen with accelerometer arrangement and impact locations, (c) front view, (d) back view of the test specimen.
As part of an extensive experimental campaign investigating the collapse of this arch bridge, vibration testing was conducted to monitor its structural health. Impact tests were performed, and acceleration data were collected at both the initial baseline and various damage stages of the specimen. Progressive damage states were simulated by incrementally increasing the vertical load applied at the quarter length of the specimen in three stages, up to a collapse load of 70 kN. The first stage (DS 1) involved loading up to 30 kN, the second stage (DS 2) up to 60 kN and the final stage reached the ultimate load of 70 kN. Each stage included three repetitions of loading-unloading cycles, with impact tests conducted after the third cycle of unloading to monitor the structural response. A total of six accelerometers were used to collect acceleration measurements: four triaxial units (A2, A4, A6 mounted on the structure; A5 mounted on the foundation to capture baseline motion) and two unidirectional units (A1, A3) mounted on the structure. The experimental setup is illustrated in Figure 5c,d. The arrangement of the accelerometers and the impact locations are indicated on the sketch, along with the geometric features of the specimen. Acceleration data were recorded with a sampling frequency of 1000 Hz (sampling interval of 0.001 s) to capture the dynamic response of the structure over a wide frequency range.
While the beam model served as a simplified, controlled validation platform for demonstrating the fundamental capabilities of the proposed damage detection methodology under idealized conditions, the masonry arch bridge test provided a more demanding proof-of-concept in a complex, real-world structure. This setup introduced additional challenges such as discontinuities, material heterogeneity, and nonlinear boundary effects that are absent in the beam model. The intent was not to replicate the mechanical behavior of the beam but to assess how well the transmissibility-based approach generalizes to practical applications under realistic conditions.
Figure 6 shows the load-displacement curves recorded during the static testing and the observed cracks when loading the specimen to the first 30 kN (DS 1) and then to 60 kN (DS 2). The damage observed during the first loading step of 30 kN included a vertical crack in the spandrel wall joint originating from the keystone extending to the upper edge as well as initiation of longitudinal cracking between the extrados and the wall. The longitudinal cracking that occurred between the voussoirs was measured to be around 1 mm, as shown in Figure 6c. Upon unloading the specimen, there was no significant permanent deformation observed at this load level. Damage observed at the end of the second load-unload cycles, which reached 60 kN, is shown in Figure 6d,e. The longitudinal cracks propagated and reached 3–4 mm around the keystone. At this stage, transverse cracking in the arch barrel initiated and the formation of the first plastic hinge began.
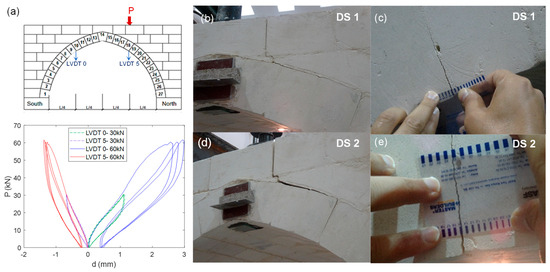
Figure 6.
(a) Load-displacement curves, (b) Initiation of the hinge, (c) cracking around on the wall and extrados during loading up to 30 kN (DS 1), (d) plastic hinge formation, (e) propagation of cracks during loading up to 60 kN (DS 2).
In the final stage of loading, as the load increased to 70 kN, a pronounced separation around the keystone occurred, along with the formation of hinges at the arch ring and at the abutment level, leading to large displacements beneath the loading beam. Loading was terminated after the second load-unload cycle, marking the announcement of collapse. Figure 7 displays the load-displacement curves and photos of the observed damage following the final load-unload cycle. Further details of the collapse investigation can be found in [60].
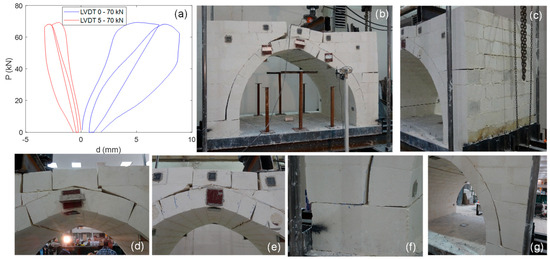
Figure 7.
(a) Load-displacement curves, (b) collapse at 70 kN, (c) side view, (d–e) keystone: frontside, (d), backside, (e), (f–g) springing point: frontside (f), backside (g).
The acceleration responses in the vertical direction (A1, A2, A3, A4, A6) due to impacts in the same direction were recorded. Specifically, A5 records the acceleration at the foundation level, and it is subtracted from the other measurements to account for baseline motion. This adjustment ensures that the measured responses reflect the system’s dynamic behavior more accurately, isolating the effects of the structural components from the foundation motion. The processed data are then used to identify the transmissibilities between the sensor pairs, which provide valuable insight into the structural integrity by revealing variations in response patterns across different locations. In this study, transmissibility functions were computed over the 0–400 Hz frequency range to ensure broad spectral coverage while maintaining a high signal-to-noise ratio. Figure 8 illustrates the transmissibility functions calculated for the different sensor pairs, highlighting the impact of structural changes on the system’s dynamic response.
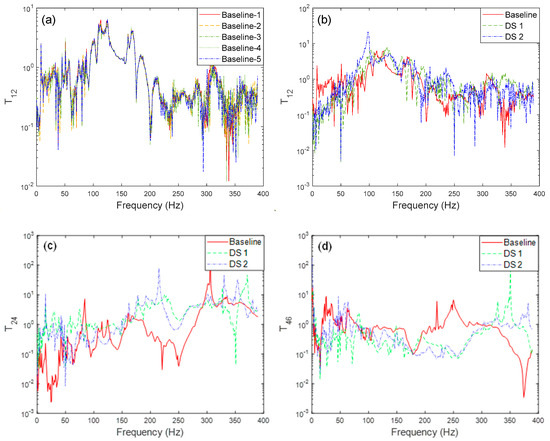
Figure 8.
Local transmissibility functions: (a) Baseline repetitions, (b–d) comparison of baseline and post load–unload states.
Since the number of training data was limited to five, OCSVM was preferred over the other learning models, and classification task was completed with the trained OCSVM. With the DSFs extracted from the impact tests that were conducted after loading the specimen to 30 kN (DS 1) and 60 kN (DS 2), test data was classified as ‘not-belonging’ to the trained state in both cases. To visualize this damage decision with OCSVM, DSFs were projected onto 2-D space using principal component analysis (PCA). Figure 9 presents the principal components of the training data, test data, and the decision boundary. As shown in this 2-D representation, even at a loading level of up to 30 kN (DS 1), the proposed method successfully detected damage.
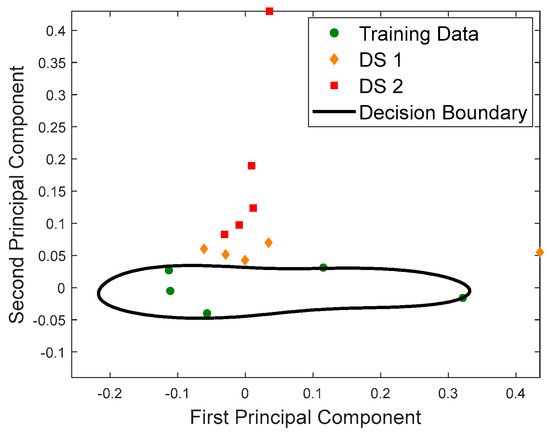
Figure 9.
Principal components of the DSFs for the training and testing data with the OCSVM decision boundary.
Acceleration responses recorded in the vertical direction due to vertical impacts were processed for damage localization, as this orientation is the only practical one for in-field bridge testing. The transmissibility-based damage index (DI) was then formulated along two orthogonal axes, separately: (i) longitudinal (spanwise)—using T12 and T23 to distinguish between regions A1–A2 and A2–A3—and (ii) lateral (widthwise)—using T24 and T46 to distinguish between regions A2–A4 and A4–A6. By comparing DI values in these two directions, one can identify not only where along the span the damage is, but also how far it has propagated through the depth of the arch. The localization results obtained with these two sets of localization index are displayed in Figure 9.
Examining the damage localization index along the span (Figure 10a), at the DS-1 loading level (30 kN), the damage index produced similar values for both regions A1–A2 and A2–A3. Although plastic hinge formation had initiated at the loaded side (A2–A3), there was also noticeable separation between the spandrel walls and the arch ring on either side of the bridge. This widespread separation introduced global changes in the system’s dynamic properties, affecting both sensor regions similarly. As a result, the damage index could not distinctly localize the damage at this load level. However, as the load increased and hinge formation was completed at DS-2 (60 kN), accompanied by the propagation of cracks, the index successfully identified the correct damaged region (A2–A3), where localized stiffness loss dominated the dynamic response.
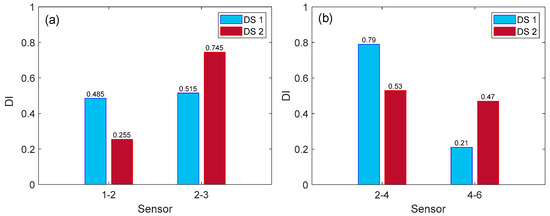
Figure 10.
Damage localization index along (a) the longitudinal axis (spanwise) and (b) the lateral axis (widthwise).
In the lateral direction (Figure 10b), at DS-1, cracks primarily formed on the front face of the arch. By comparing transmissibility-based index values between the front face and midsection (A2–A4) and between the midsection and back face (A4–A6), the damage index clearly pinpointed the affected side. As the load increased further to DS-2 and shear and tension cracks propagated through the arch’s depth, the back face was also damaged. Consequently, the damage index values across these lateral regions converged, reflecting a more uniformly distributed damage state through the arch’s thickness. This behavior is consistent with typical masonry arch bridge failure modes, where damage initiates on the loaded face and progresses inward with increasing severity.
6. Comparative Performance Evaluation with a Modal Flexibility-Based Damage Detection Approach
To evaluate the performance of the proposed transmissibility-based machine learning strategy, a comparative analysis was performed using a well-established modal flexibility-based damage detection method using the same datasets presented in the previous sections. This section presents a brief overview of the modal flexibility-based approach and the results of both the numerical simulations and the experimental studies, focusing on the accuracy, sensitivity, and damage localization capability.
Modal flexibility has been widely adopted in structural health monitoring due to its higher sensitivity to stiffness reductions, particularly in the lower modes [61,62,63,64,65,66,67,68]. As highlighted in prior studies, natural frequency-based methods often lack sensitivity to minor or localized damage, as the frequency shifts caused by such damage typically fall within the range of estimation uncertainty. Mode shape-based methods, while offering somewhat improved sensitivity, face limitations due to the challenges of accurate mode pairing and matching, especially in noisy or complex systems. Furthermore, localized damage does not always induce distinct or spatially localized changes in mode shapes, limiting their effectiveness for reliable damage localization.
The flexibility matrix is computed using:
where Φ is the mass-normalized mode shape matrix and contains the squared natural frequencies.
In practical applications, especially in experimental or operational scenarios where input excitation is unknown, the extracted mode shapes are not mass-normalized but instead arbitrarily scaled. That is,
Despite this, for damage localization purposes, relative changes in the diagonal entries of the flexibility matrix remain meaningful as long as the same set of modes and consistent scaling are applied across undamaged and damaged states.
It is important to note that modal flexibility-based methods require several critical preprocessing and system identification steps before damage detection can be performed. In this study, the modal parameters were identified using the Eigenvalue Realization Algorithm (ERA), a time-domain system identification technique that constructs the system’s state-space model from impulse response functions or free-decay responses. ERA provides estimates of natural frequencies and corresponding mode shapes, which can be subsequently used to form the flexibility matrix. In this approach, impulse response functions serve as inputs to the ERA, and multiple runs must be conducted to ensure mode stability and mitigate the effects of noise. Additionally, selecting the appropriate model order for constructing the system matrix and discriminating between physical system modes and spurious modes require careful evaluation and engineering judgment. To ensure comparability between structural states, consistent mode selection across undamaged and damaged conditions is essential. Moreover, the effects of modal truncation on the synthesized flexibility matrices must be carefully considered since it limits the capability for detecting localized and subtle damage. These additional steps introduce further user-dependent decisions, making it challenging to automate the entire process and potentially affecting the robustness of the damage identification outcome.
The first comparison was performed on the numerical case study of the fixed-fixed beam. The modal frequencies identified using the ERA are listed in Table 5. A comparison with the exact values provided in Table 2 shows excellent agreement, with frequency identification errors remaining below 1%. Similarly, the mode shapes were identified with very high accuracy, achieving a minimum Modal Assurance Criterion (MAC) value of 0.9998 between the exact and the identified mode shapes.

Table 5.
Modal frequencies identified by ERA.
Following the formulation given in Equation (13), the flexibility matrix was computed, and the relative changes in its diagonal entries were calculated for all damage cases. These values were then normalized with respect to the largest value to obtain the damage index, denoted as . The resulting damage indices for all damage cases are presented in Figure 11.
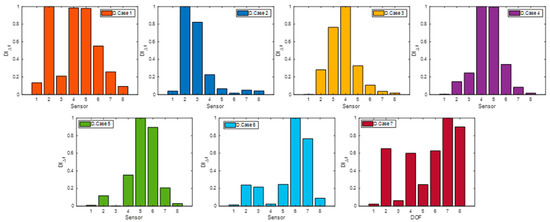
Figure 11.
Damage localization for the fixed-fixed beam using the flexibility-based approach.
It is clear from this figure that although the true damage location appears among the potential damage locations, the modal flexibility-based approach fails to isolate it as distinctly as the proposed transmissibility-based method especially for D. Case 1 and D. Case 7. It should be emphasized that in this numerical case, no modal truncation was applied, and issues such as mode selection and pairing for consistency, mode switching, missing or closely-spaced modes were not present. Therefore, a straightforward application of the modal flexibility-based approach was possible, yet its damage localization performance still remained inferior to that of the transmissibility-based strategy.
The next comparison was conducted using the experimental dataset from the arch structure, where the preprocessing stage required significant user interaction and engineering judgment, particularly for modal identification. Impulse response functions obtained from vertical acceleration measurements (A1, A2, A3, A4, A6) served as inputs to the ERA, and multiple runs of the algorithm were performed using the impact test data to reliably identify the true system modes. Figure 12 illustrates a representative example of this process in the form of stabilization diagrams, which plot the identified frequencies against varying system orders. Stable, physically meaningful modes were selected based on their consistent appearance across increasing model orders, while unstable or spurious modes were systematically eliminated. In addition, multiple impact tests were used to identify mode shapes separately for each run, and the MAC values between these identified shapes were computed. Mode shapes exhibiting consistently high MAC values across different runs were considered repeatable and reliable, further supporting the validity of the selected modes. Table 6 summarizes the modal parameters for the consistent modes selected across the baseline and the two damaged states, after loading to 30 kN and 60 kN.
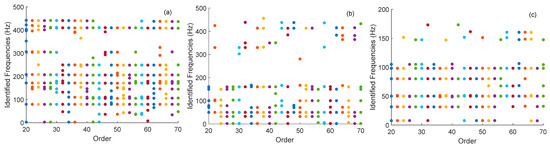
Figure 12.
Stabilization diagram for the identified natural frequencies from impact excitation at A1: (a) Baseline, (b) DS 1, (c) DS 2. Each color represents the set of frequency values obtained for a certain system order.

Table 6.
Modal frequencies identified by ERA.
Using these identified modes, flexibility matrices for both the undamaged and damaged states were synthesized, and the damage indices were computed based on the relative changes in the diagonal entries of the flexibility matrix, following the same procedure as in the numerical case. Figure 13 presents the computed damage indices for these cases. Based on this figure, the flexibility-based approach initially misidentifies the region around sensor 1 as the potential damage location, leading to a mislocalization in the first damage case (DS1). However, with an increased load and progression of damage in DS2, the method improves and correctly locates the damage around sensor 2.
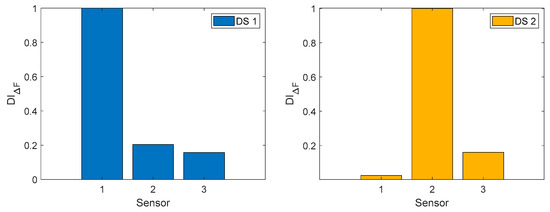
Figure 13.
Damage localization for the experimental arch using the flexibility-based approach.
The comparison between the flexibility- and transmissibility-based approaches highlights the advantages of the transmissibility-based method, particularly in detecting and localizing early-stage and distributed damage. In the arch bridge test, the flexibility-based method misidentified the damage location in the first damage case (DS1), where cracks initiated not only at the primary hinge formation zone but also with separations along the spandrel walls on both sides of the crown. These distributed damage patterns reduced the sensitivity of the flexibility-based method, which relies on global stiffness changes. In contrast, the transmissibility-based method, by capturing localized dynamic deviations between consecutive sensors, was able to more reliably indicate damage progression, even when cracks appeared asymmetrically. This effectiveness is further supported by its broader frequency range (0–400 Hz), which captures higher-order dynamics beyond the ~200 Hz limit of the flexibility-based approach, allowing for richer and more damage-sensitive features. In DS2, although both methods identified the damage zone between sensors 2 and 3, the flexibility-based method showed a sharper peak due to normalization (index values of 1.00, 0.17, and 0.01 for sensors 2–4), whereas the transmissibility-based approach exhibited a more gradual distribution (indices of 0.72 and 0.21 for sensor pairs 2–3 and 3–4). While this could suggest finer localization from the flexibility index, such sharpness results from the way each metric is scaled and should be interpreted accordingly. The performance of the transmissibility-based method further improved as the load increased and damage became more clearly localized in DS2.
Similar trends were observed in the numerical study, where—despite ideal conditions without modal truncation, mode switching, or pairing issues—the flexibility-based method still failed to localize certain damage cases as effectively as the transmissibility-based strategy. In addition to its accuracy, the transmissibility-based method requires significantly less data preprocessing and eliminates the need for complex modal identification procedures, including mode selection and issues like truncated, missing, or closely spaced modes. By removing user interaction and subjective decisions, it becomes far more suitable for automated, robust implementations, especially in noisy, operational, or variable environments where flexibility-based approaches often struggle.
7. Conclusions
This study introduced a purely response-based methodology for structural damage detection and localization by leveraging transmissibility functions combined with unsupervised machine learning techniques. Unlike traditional model-based methods, the proposed approach requires only response measurements from the baseline (undamaged) state, eliminating the need for excitation input or analytical modeling. The damage detection phase is implemented through a one-class classification model trained on baseline transmissibility amplitudes, while localization is achieved by evaluating frequency-wise sensor-pair differences and identifying the most affected pair.
The methodology was validated using both numerical simulations and experimental data. Simulations on a fixed–fixed beam subjected to progressive damage demonstrated high sensitivity to local stiffness reductions, even under realistic noise levels. Experimental validation was performed on a scaled masonry arch bridge model, where structural and material complexities more closely reflect real-world applications. The proposed transmissibility-based approach successfully detected early-stage damage and provided meaningful localization results based on frequency-domain data fusion.
In comparison with the modal flexibility method—which relies on mode shapes derived from system identification—the transmissibility-based framework offered several advantages. It captured dynamic changes across a broad frequency band, thereby improving sensitivity to damage near localized regions. While the flexibility-based method showed sharper localization peaks in some cases due to normalization, it required manual mode selection and extensive preprocessing. In contrast, the transmissibility approach is less sensitive to such subjective steps and better suited for automation.
The main contribution of this study lies in demonstrating that transmissibility-based learning, when combined with unsupervised classification, can provide an effective and scalable framework for structural health monitoring. Its application to a complex laboratory-scale structure marks a significant step beyond previous studies, which often focus on idealized systems or rely on supervised methods. The approach also supports the use of baseline-only data, which is particularly relevant for existing structures where damage-state data are not available.
Practical considerations, such as the need for impact testing across multiple locations, may pose challenges in terms of accessibility and testing duration, especially in large or operationally sensitive structures. Nevertheless, advancements in mobile sensing systems and automated data acquisition offer promising opportunities to streamline this process. Furthermore, the use of alternative excitation sources—such as ambient vibrations or operational loads—could eliminate the need for active input, thereby increasing the adaptability of the proposed approach to field conditions. Although the current methodology relies on repeated baseline measurements, future research may focus on real-time data acquisition and adaptive algorithms capable of continuously updating the baseline model, enhancing the feasibility of real-time structural health monitoring. Moreover, while the sensor configuration in this study was based on the expected damage locations and the structural characteristics of the test model, future work may focus on a comprehensive sensitivity analysis of sensor placement to derive generalized guidelines applicable to various structural systems.
Author Contributions
Conceptualization, O.G. and B.G.; Methodology, B.G.; Software, B.G.; Validation, O.G. and B.G.; Formal analysis, O.G. and B.G.; Investigation, O.G. and B.G.; Resources, O.G. and B.G.; Data curation, O.G.; Writing—original draft, O.G. and B.G.; Writing—review & editing, O.G. and B.G.; Visualization, B.G.; Supervision, O.G.; Project administration, O.G.; Funding acquisition, O.G. and B.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been supported by the Scientific Research Projects (BAP) of Istanbul Technical University under Project No MGA-2024-45495. The funding for the experimental part of the study was provided by the Scientific and Technological Research Council of Turkey (TUBITAK) under project number 114M305 and by the General Directorate of Highways (KGM) under protocol number KGM/TK-10.
Data Availability Statement
The data that support the findings of this study are available on request from the corresponding author upon reasonable request.
Conflicts of Interest
The first author is the owner and manager of the company MiTek Mitigation Technologies A.S., established within 1773 ITU Technopark. The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Avci, O.; Abdeljaber, O.; Kiranyaz, S.; Hussein, M.; Gabbouj, M.; Inman, D.J. A review of vibration-based damage detection in civil structures: From traditional methods to machine learning and deep learning applications. Mech. Syst. Signal Process. 2021, 147, 107077. [Google Scholar] [CrossRef]
- Wang, Z.; Cha, Y.J. Unsupervised machine and deep learning methods for structural damage detection: A comparative study. Eng. Rep. 2025, 7, e12551. [Google Scholar] [CrossRef]
- Azimi, M.; Eslamlou, A.D.; Pekcan, G. Data-driven structural health monitoring and damage detection through deep learning: State-of-the-art review. Sensors 2020, 20, 2778. [Google Scholar] [CrossRef] [PubMed]
- Beyene, D.A.; Maru, M.B.; Kim, T.; Park, S.; Park, S. Unsupervised domain adaptation-based crack segmentation using transformer network. J. Build. Eng. 2023, 80, 107889. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, C. Generative adversarial network based on domain adaptation for crack segmentation in shadow environments. Comput. Aided Civ. Infrastruct. Eng. 2025, 1–17. [Google Scholar] [CrossRef]
- Yuen, K.V.; Lam, H.F. On the complexity of artificial neural networks for smart structures monitoring. Eng. Struct. 2006, 28, 977–984. [Google Scholar] [CrossRef]
- Lee, J.; Kim, S. Structural damage detection in the frequency domain using neural networks. J. Intell. Mater. Syst. Struct. 2007, 18, 785–792. [Google Scholar] [CrossRef]
- Lam, H.F.; Ng, C.T. The selection of pattern features for structural damage detection using an extended Bayesian ANN algorithm. Eng. Struct. 2008, 30, 2762–2770. [Google Scholar] [CrossRef]
- Mehrjoo, M.; Khaji, N.; Moharrami, H.; Bahreininejad, A. Damage detection of truss bridge joints using artificial neural networks. Expert Syst. Appl. 2008, 35, 1122–1131. [Google Scholar] [CrossRef]
- Cury, A.; Crémona, C. Pattern recognition of structural behaviors based on learning algorithms and symbolic data concepts. Struct. Control Health Monit. 2012, 19, 161–186. [Google Scholar] [CrossRef]
- Goh, L.D.; Bakhary, N.; Rahman, A.A.; Ahmad, B.H. Prediction of unmeasured mode shape using artificial neural network for damage detection. J. Teknol. 2013, 61, 57–66. [Google Scholar] [CrossRef][Green Version]
- Zhou, X.T.; Ni, Y.Q.; Zhang, F.L. Damage localization of cable-supported bridges using modal frequency data and probabilistic neural network. Math. Probl. Eng. 2014, 2014, 837963. [Google Scholar] [CrossRef]
- Hakim, S.J.S.; Razak, H.A.; Ravanfar, S.A. Fault diagnosis on beam-like structures from modal parameters using artificial neural networks. Measurement 2015, 76, 45–61. [Google Scholar] [CrossRef]
- Betti, M.; Facchini, L.; Biagini, P. Damage detection on a three-storey steel frame using artificial neural networks and genetic algorithms. Meccanica 2015, 50, 875–886. [Google Scholar] [CrossRef]
- Krishnan Nair, K.; Kiremidjian, A.S. Time series based structural damage detection algorithm using Gaussian mixtures modeling. J. Dyn. Syst. Meas. Control. 2007, 129, 285–293. [Google Scholar] [CrossRef]
- Carden, E.P.; Brownjohn, J.M. ARMA modelled time-series classification for structural health monitoring of civil infrastructure. Mech. Syst. Signal Process. 2008, 22, 295–314. [Google Scholar] [CrossRef]
- Gul, M.; Catbas, F.N. Statistical pattern recognition for structural health monitoring using time series modeling: Theory and experimental verifications. Mech. Syst. Signal Process. 2009, 23, 2192–2204. [Google Scholar] [CrossRef]
- de Lautour, O.R.; Omenzetter, P. Damage classification and estimation in experimental structures using time series analysis and pattern recognition. Mech. Syst. Signal Process. 2010, 24, 1556–1569. [Google Scholar] [CrossRef]
- Figueiredo, E.; Park, G.; Farrar, C.R.; Worden, K.; Figueiras, J. Machine learning algorithms for damage detection under operational and environmental variability. Struct. Health Monit. 2011, 10, 559–572. [Google Scholar] [CrossRef]
- Ay, A.M.; Wang, Y. Structural damage identification based on self-fitting ARMAX model and multi-sensor data fusion. Struct. Health Monit. 2014, 13, 445–460. [Google Scholar] [CrossRef]
- Santos, A.; Figueiredo, E.; Silva, M.F.M.; Sales, C.S.; Costa, J.C.W.A. Machine learning algorithms for damage detection: Kernel-based approaches. J. Sound Vib. 2016, 363, 584–599. [Google Scholar] [CrossRef]
- Goi, Y.; Kim, C.W. Damage detection of a truss bridge utilizing a damage indicator from multivariate autoregressive model. J. Civ. Struct. Health Monit. 2017, 7, 153–162. [Google Scholar] [CrossRef]
- Krishnan, M.; Bhowmik, B.; Hazra, B.; Pakrashi, V. Real-time damage detection using recursive principal components and time-varying auto-regressive modeling. Mech. Syst. Signal Process. 2018, 101, 549–574. [Google Scholar] [CrossRef]
- Gunes, B. One-class machine learning approach for localized damage detection. J. Civ. Struct. Health Monit. 2022, 12, 1115–1131. [Google Scholar] [CrossRef]
- Chesne, S.; Deraemaeker, A. Damage localization using transmissibility functions: A critical review. Mech. Syst. Signal Process. 2013, 38, 569–584. [Google Scholar] [CrossRef]
- Zhou, Y.L.; Figueiredo, E.; Maia, N.; Perera, R. Damage detection and quantification using transmissibility coherence analysis. Shock Vib. 2015, 2015, 290714. [Google Scholar] [CrossRef]
- Li, J.; Hao, H.; Lo, J.V. Structural damage identification with power spectral density transmissibility: Numerical and experimental studies. Smart Struct. Syst. 2015, 15, 15–40. [Google Scholar] [CrossRef]
- Zhu, D.; Yi, X.; Wang, Y. A local excitation and measurement approach for decentralized damage detection using transmissibility functions. Struct. Control Health Monit. 2016, 23, 487–502. [Google Scholar] [CrossRef]
- Zhou, Y.L.; Maia, N.M.; Sampaio, R.P.; Wahab, M.A. Structural damage detection using transmissibility together with hierarchical clustering analysis and similarity measure. Struct. Health Monit. 2017, 16, 711–731. [Google Scholar] [CrossRef]
- Zhou, Y.L.; Maia, N.M.; Wahab, M.A. Damage detection using transmissibility compressed by principal component analysis enhanced with distance measure. J. Vib. Control 2018, 24, 2001–2019. [Google Scholar] [CrossRef]
- Yan, W.J.; Zhao, M.Y.; Sun, Q.; Ren, W.X. Transmissibility-based system identification for structural health monitoring: Fundamentals, approaches, and applications. Mech. Syst. Signal Process. 2019, 117, 453–482. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Bui, T.T.; De Roeck, G.; Wahab, M.A. Damage detection in Ca-Non Bridge using transmissibility and artificial neural networks. Struct. Eng. Mech. 2019, 71, 175–183. [Google Scholar]
- Liu, T.; Xu, H.; Ragulskis, M.; Cao, M.; Ostachowicz, W. A data-driven damage identification framework based on transmissibility function datasets and one-dimensional convolutional neural networks: Verification on a structural health monitoring benchmark structure. Sensors 2020, 20, 1059. [Google Scholar] [CrossRef]
- Cheng, L.; Cigada, A. An analytical perspective about structural damage identification based on transmissibility function. Struct. Health Monit. 2020, 19, 142–155. [Google Scholar] [CrossRef]
- Han, J.; Zhang, H.; Hou, Z. Several damage indices based on transmissibility for application in structural damage detection. In Experimental Vibration Analysis for Civil Structures; CRC Press: Boca Raton, FL, USA, 2020; pp. 193–202. [Google Scholar]
- Luo, Z.; Liu, H.; Yu, L. A multi-state strategy for structural damage detection using sensitivity of weighted transmissibility function. Int. J. Struct. Stab. Dyn. 2021, 21, 2150144. [Google Scholar] [CrossRef]
- Luo, Z.; Liu, H.; Yu, L. Weighted transmissibility assurance criterion for structural damage detection. J. Aerosp. Eng. 2021, 34, 04021016. [Google Scholar] [CrossRef]
- Wu, D.; Zeng, M.; Zhao, H.; Wang, Y.; Du, Y. Detection and localization of debonding beneath concrete pavement using transmissibility function analysis. Mech. Syst. Signal Process. 2021, 159, 107802. [Google Scholar] [CrossRef]
- Li, Q.; Liao, M.; Jing, X. Transmissibility function-based fault diagnosis methods for beam-like engineering structures: A review of theory and properties. Nonlinear Dyn. 2021, 106, 2131–2163. [Google Scholar] [CrossRef]
- Zou, Y.; Lu, X.; Yang, J.; Wang, T.; He, X. Structural damage identification based on transmissibility. Sensors 2022, 22, 393. [Google Scholar] [CrossRef]
- Dziedziech, K.; Staszewski, W.J.; Mendrok, K.; Basu, B. Wavelet-based transmissibility for structural damage detection. Materials 2022, 15, 2722. [Google Scholar] [CrossRef]
- Wang, Z.; Ding, L. Structural damage detection and localization using response difference transmissibility. J. Shanghai Jiaotong Univ. 2022, 29, 1126–1138. [Google Scholar] [CrossRef]
- Markogiannaki, O.; Arailopoulos, A.; Giagopoulos, D.; Papadimitriou, C. Vibration-based damage localization and quantification framework of large-scale truss structures. Struct. Health Monit. 2023, 22, 1376–1398. [Google Scholar] [CrossRef]
- Izadi, A.; Esfandiari, A. Structural damage identification by a sensitivity-based finite element model updating method using transmissibility function data. Ships Offshore Struct. 2023, 18, 1415–1428. [Google Scholar] [CrossRef]
- Meggitt, J.W.; McGee, R.C. On the limitations of transmissibility functions for damage localisation: The influence of completeness. Struct. Health Monit. 2024, 23, 3674–3686. [Google Scholar] [CrossRef]
- Rytter, A. Vibrational Based Inspection of Civil Engineering Structures. Ph.D. Thesis, Aalborg University, Aalborg, Denmark, 1993. [Google Scholar]
- Alam, S.; Sonbhadra, S.K.; Agarwal, S.; Nagabhushan, P. One-class support vector classifiers: A survey. Knowl. Based Syst. 2020, 196, 105754. [Google Scholar] [CrossRef]
- Khan, S.S.; Madden, M.G. One-class classification: Taxonomy of study and review of techniques. Knowl. Eng. Rev. 2014, 29, 345–374. [Google Scholar] [CrossRef]
- Fontul, M.; Ribeiro, A.M.R.; Silva, J.M.M.; Maia, N.M.M. Transmissibility matrix in harmonic and random processes. Shock. Vib. 2004, 11, 563–571. [Google Scholar] [CrossRef]
- Feng, L.; Yi, X.; Zhu, D.; Xie, X.; Wang, Y. Damage detection of metro tunnel structure through transmissibility function and cross-correlation analysis using local excitation and measurement. Mech. Syst. Signal Process. 2015, 60, 59–74. [Google Scholar] [CrossRef]
- Yi, X.; Zhu, D.; Wang, Y.; Guo, J.; Lee, K.M. Embedded transmissibility function analysis for damage detection in a mobile sensor network. In Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2010; SPIE: Bellingham, WA, USA, 2010; Volume 7647, pp. 700–708. [Google Scholar]
- Surace, C.; Worden, K. Novelty detection in a changing environment: A negative selection approach. Mech. Syst. Signal Process. 2010, 24, 1114–1128. [Google Scholar] [CrossRef]
- Maia, N.M.; Almeida, R.A.; Urgueira, A.P.; Sampaio, R.P. Damage detection and quantification using transmissibility. Mech. Syst. Signal Process. 2011, 25, 2475–2483. [Google Scholar] [CrossRef]
- Worden, K.; Manson, G.; Fieller, N.R. Damage detection using outlier analysis. J. Sound Vib. 2000, 229, 647–667. [Google Scholar] [CrossRef]
- Santos, A.; Silva, M.; Santos, R.; Figueiredo, E.; Maia, N.; Costa, J.C. Output-only structural damage detection based on transmissibility measurements and kernel principal component analysis. J. Commun. Inf. Syst. 2019, 34, 64–75. [Google Scholar] [CrossRef]
- Kullaa, J.; Heine, T. Feature comparison in structural health monitoring of a vehicle crane. Shock. Vib. 2008, 15, 207–215. [Google Scholar] [CrossRef]
- Pokrajac, D.; Lazarevic, A.; Latecki, L.J. Incremental local outlier detection for data streams. In Proceedings of the 2007 IEEE Symposium on Computational Intelligence and Data Mining, Honolulu, HI, USA, 1 March–5 April 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 504–515. [Google Scholar]
- Schölkopf, B.; Williamson, R.C.; Smola, A.; Shawe-Taylor, J.; Platt, J. Support vector method for novelty detection. In Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2000; pp. 582–588. [Google Scholar]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation forest. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 413–422. [Google Scholar]
- Mentese, V.G.; Gunes, O.; Celik, O.C.; Gunes, B.; Avsin, A.; Yaz, M. Experimental collapse investigation and nonlinear modeling of a single-span stone masonry arch bridge. Eng. Fail. Anal. 2023, 152, 107520. [Google Scholar] [CrossRef]
- Bernal, D.; Gunes, B. Damage localization in output-only systems: A flexibility based approach. In Proceedings of the Proc. Of the International Modal Analysis Conference (IMAC) XX, Los Angeles, CA, USA, 4–7 February 2002; Volume 4753, pp. 1185–1191. [Google Scholar]
- Duan, Z.; Yan, G.; Ou, J.; Spencer, B.F. Damage detection in ambient vibration using proportional flexibility matrix with incomplete measured DOFs. Struct. Control Health Monit. 2007, 14, 186–196. [Google Scholar] [CrossRef]
- Catbas, F.N.; Gul, M.; Burkett, J.L. Conceptual damage-sensitive features for structural health monitoring: Laboratory and field demonstrations. Mech. Syst. Signal Process. 2008, 22, 1650–1669. [Google Scholar] [CrossRef]
- Koo, K.Y.; Lee, J.J.; Yun, C.B.; Kim, J.T. Damage detection in beam-like structures using deflections obtained by modal flexibility matrices. Smart Struct. Syst. 2008, 4, 605–628. [Google Scholar] [CrossRef]
- Sung, S.H.; Koo, K.Y.; Jung, H.Y.; Jung, H.J. Damage-induced deflection approach for damage localization and quantification of shear buildings: Validation on a full-scale shear building. Smart Mater. Struct. 2012, 21, 115013. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, J.C.; Guo, S.L.; Wu, Z.S. Flexibility-based structural damage detection with unknown mass for IASC-ASCE benchmark studies. Eng. Struct. 2013, 48, 486–496. [Google Scholar] [CrossRef]
- Bernagozzi, G.; Ventura, C.E.; Allahdadian, S.; Kaya, Y.; Landi, L.; Diotallevi, P.P. Output-only damage diagnosis for plan-symmetric buildings with asymmetric damage using modal flexibility-based deflections. Eng. Struct. 2020, 207, 110015. [Google Scholar] [CrossRef]
- Le, N.T.; Nguyen, A.; Thambiratnam, D.P.; Chan, T.H.T.; Khuc, T. Locating and quantifying damage in beam-like structures using modal flexibility-based deflection changes. Int. J. Struct. Stab. Dyn. 2020, 20, 2042008. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).