Filtering Process to Optimize the Technical Data of Prototype Race Cars
Abstract
1. Introduction
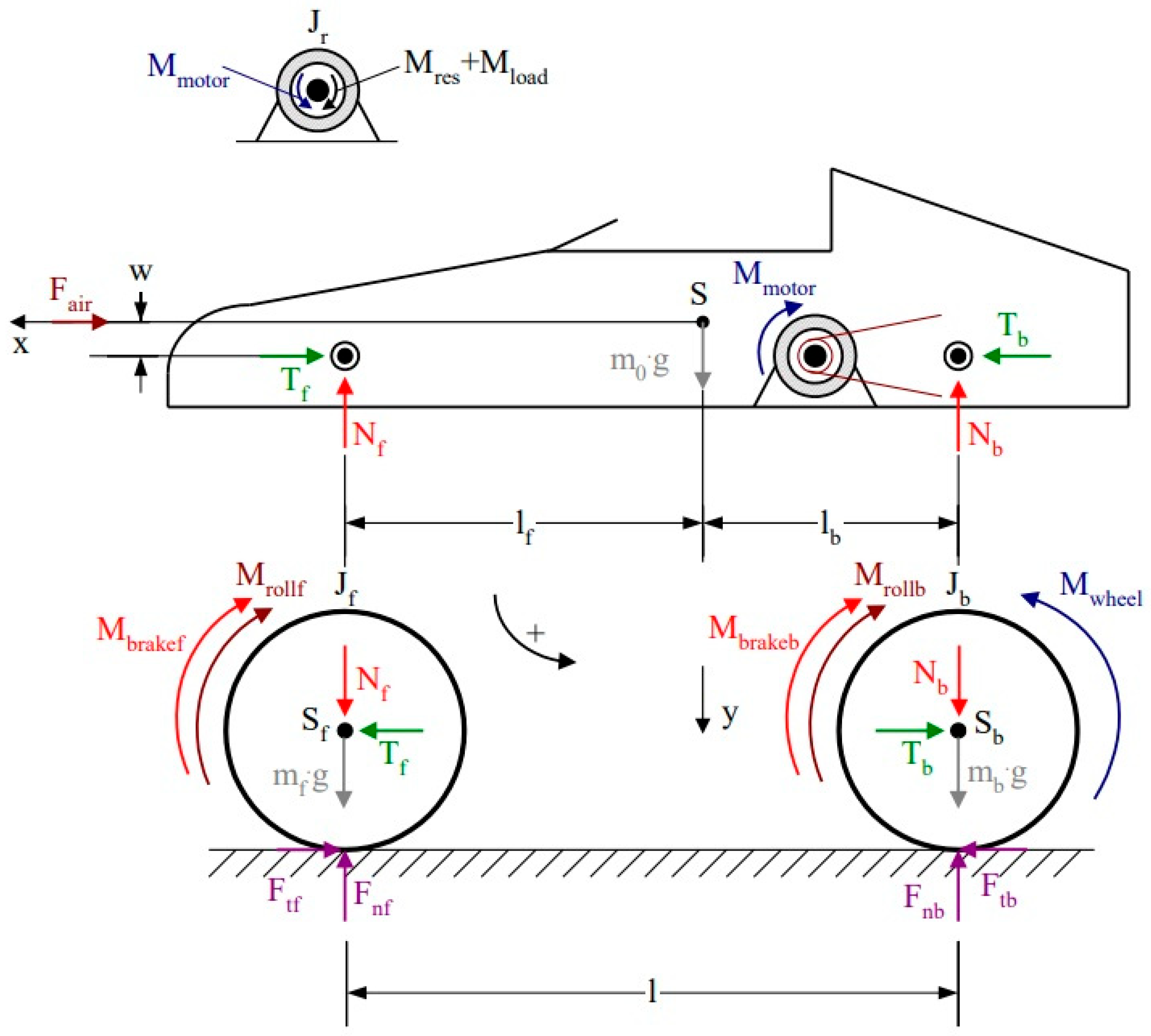
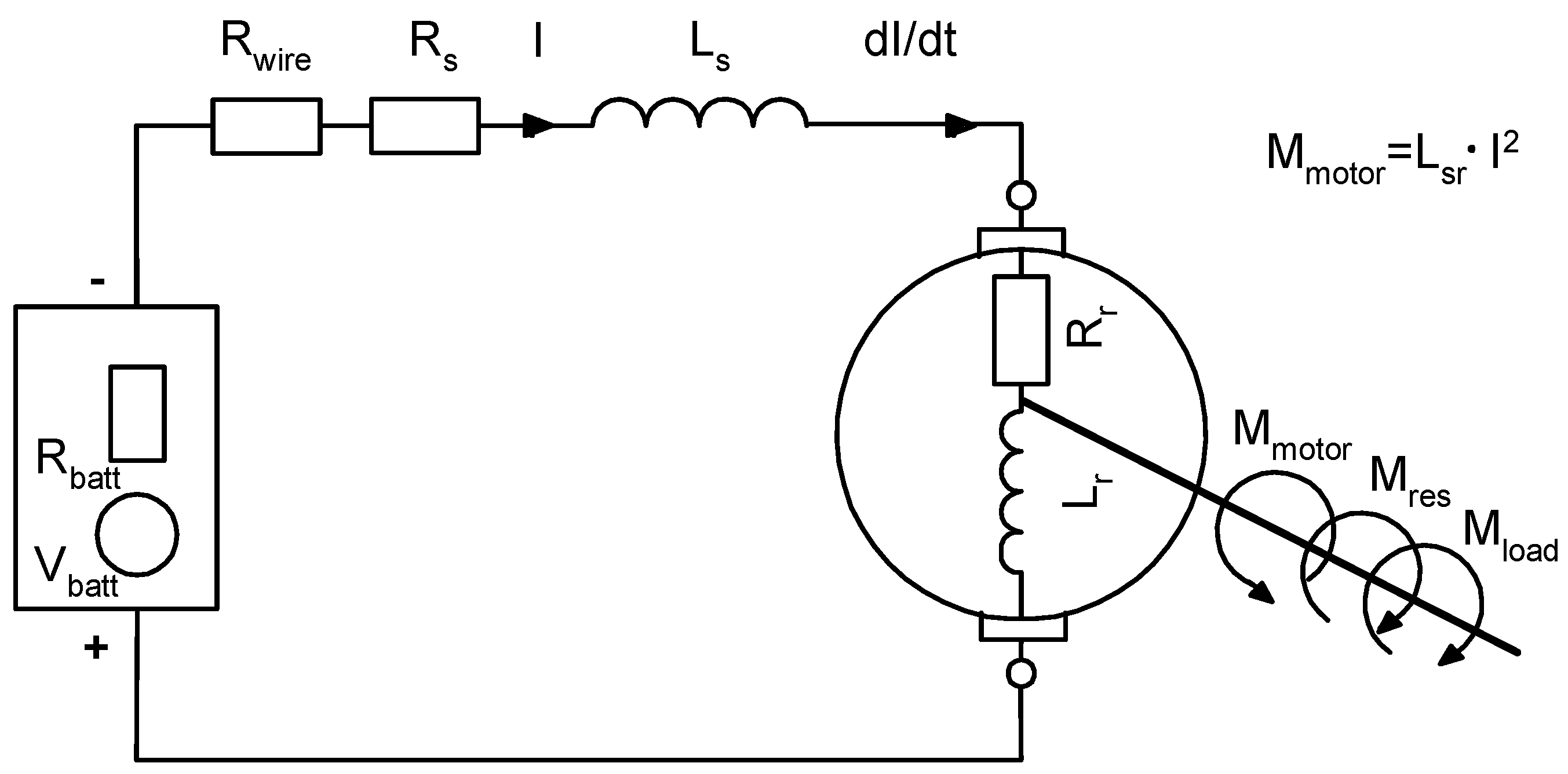
2. Brief Description of the Applied Vehicle Dynamics Model and Simulation Program
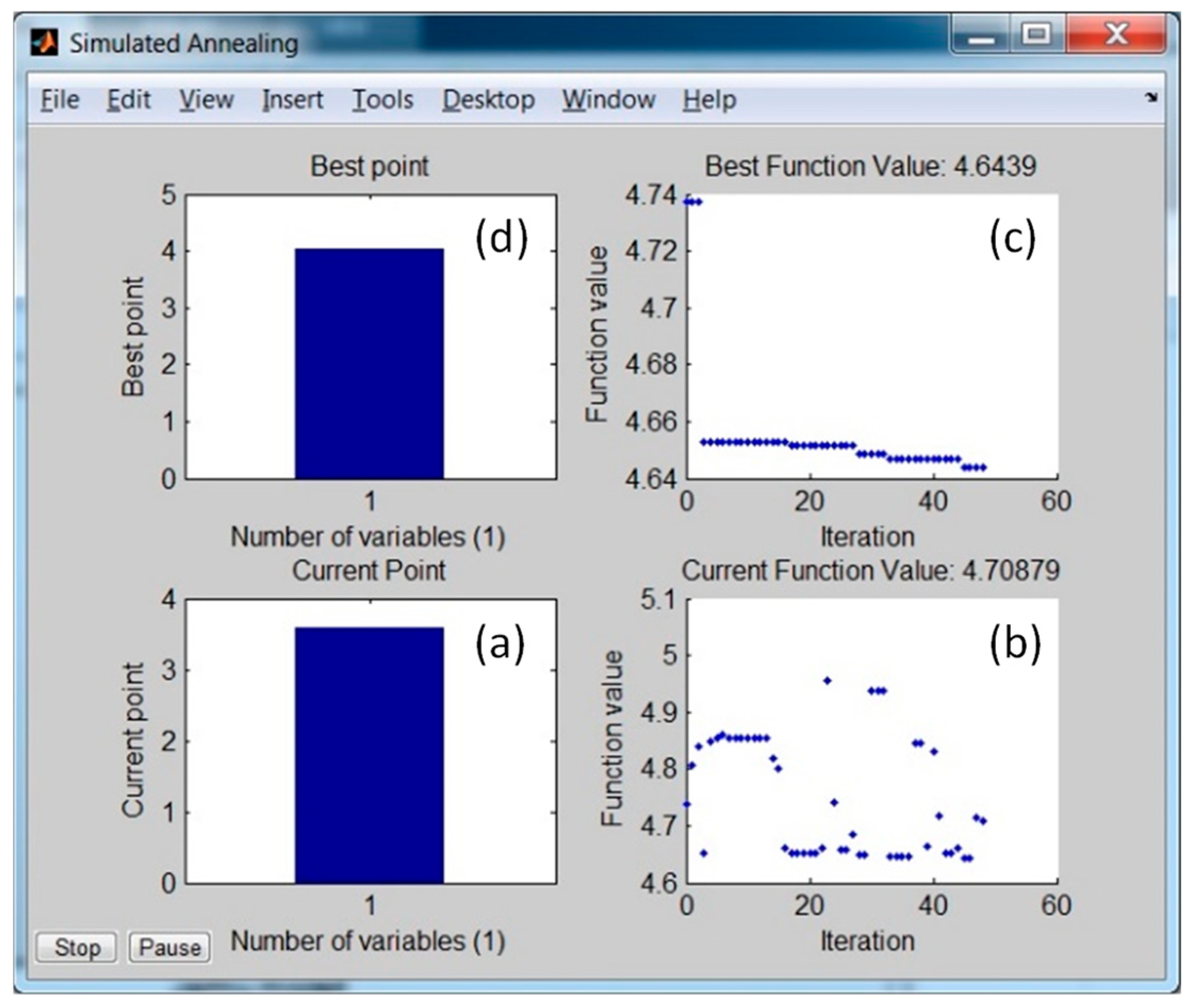
3. Brief Description of the Applied Optimization Method
4. Description of the Filtering Process
4.1. Determination of the Uncertainties of the Simulated Values
4.2. The Filtering Process
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Input parameters and characteristics of the simulation program | ||
| Notation | Description | Source of input data |
| the braking torques on the front and rear (back) wheels | - | |
| the efficiency of the chain drive | literature data [10] | |
| the number of teeth on the driver and driven sprockets | - | |
| drag coefficient of the vehicle | estimated data [10] | |
| maximum normal surface area of the vehicle | own measurement [10] | |
| the density of air | literature data [10] | |
| the distance between the front and rear (back) shafts in the tangential direction | own measurement [10] | |
| the distance of the centre of mass of the vehicle from the front and rear (back) shaft in the tangential direction | own measurement [10] | |
| the distance of the centre of mass of the vehicle from the front and rear (back) shafts in the normal direction | own measurement [10] | |
| the mass of the vehicle body, including the driver | own measurement [10] | |
| the mass of the front and rear (back) wheels with the rotating machine parts connected to them | own measurement [10] | |
| the moment of inertia of the front and rear (back) wheels with the rotating machine parts connected to them | own measurement [10] | |
| the coefficients of rolling resistance for the front and rear (back) wheels | estimated data [10] | |
| the coefficients of bearing friction for the front and rear (back) wheel shafts | catalog data [10] | |
| diameter of the front and rear wheel shafts | own measurement [10] | |
| the effective wheel radius | own measurement [10] | |
| the factors characterizing wheel friction | estimated data [10] | |
| the internal electric resistance of the battery | own measurement [38] | |
| the electromotive force of the battery | own measurement [38] | |
| the resultant electric resistance of the wires connecting the battery to the motor | own measurement [38] | |
| the electric resistances of the rotor and stator windings | own measurement [38] | |
| the intensity of the current flowing through the motor | - | |
| the self-dynamic inductance of the stator winding | own measurement [38] | |
| the self-dynamic inductance of the rotor winding | own measurement [38] | |
| the mutual dynamic inductance | own measurement [38] | |
| the moment of inertia of the rotor of the motor | own measurement [39] | |
| the sum of the bearing and brush friction torques on the rotor of the motor | own measurement [39] | |
| Output vehicle dynamic functions generated by the simulation program | ||
| Notation | Description | |
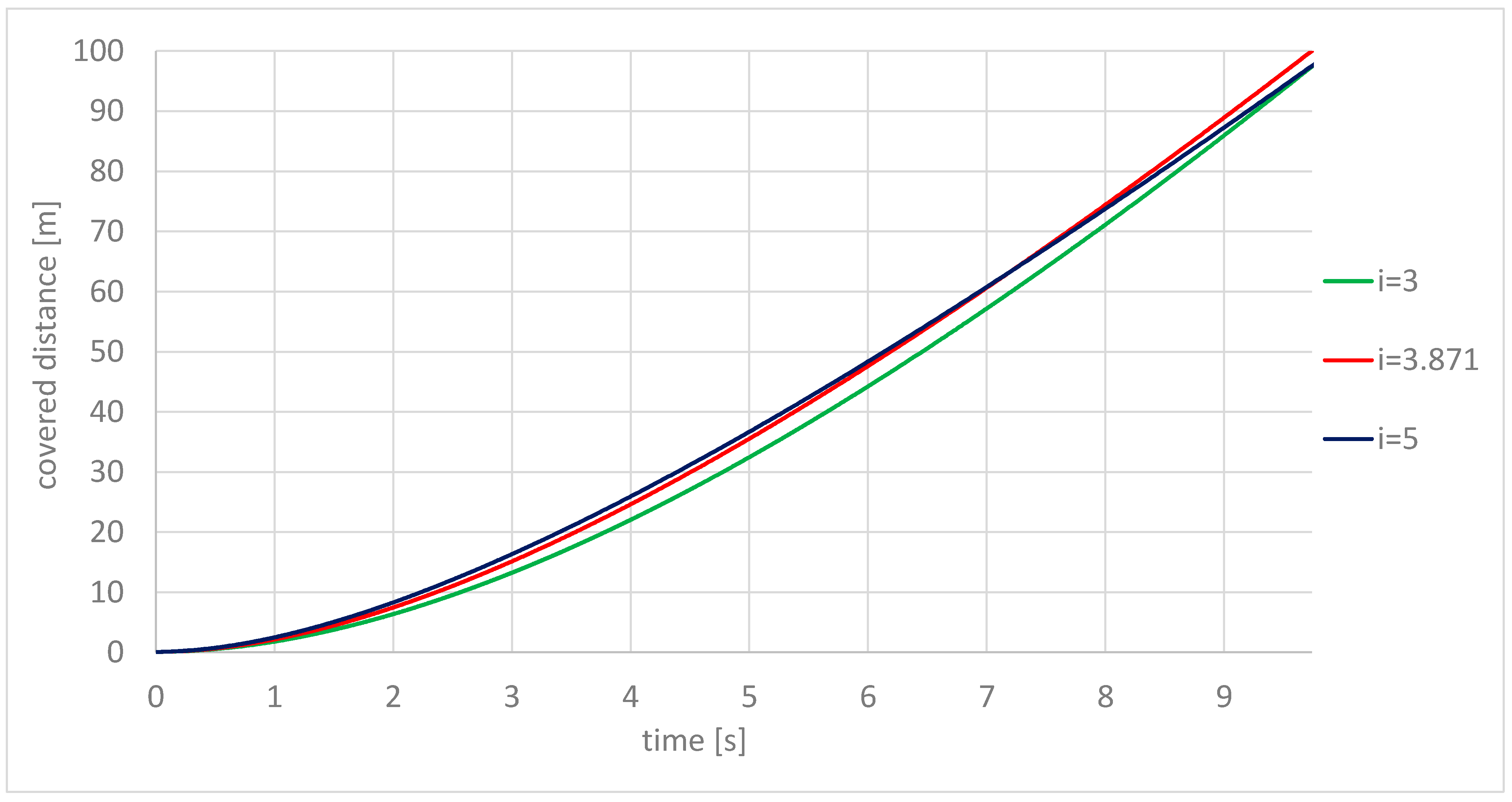
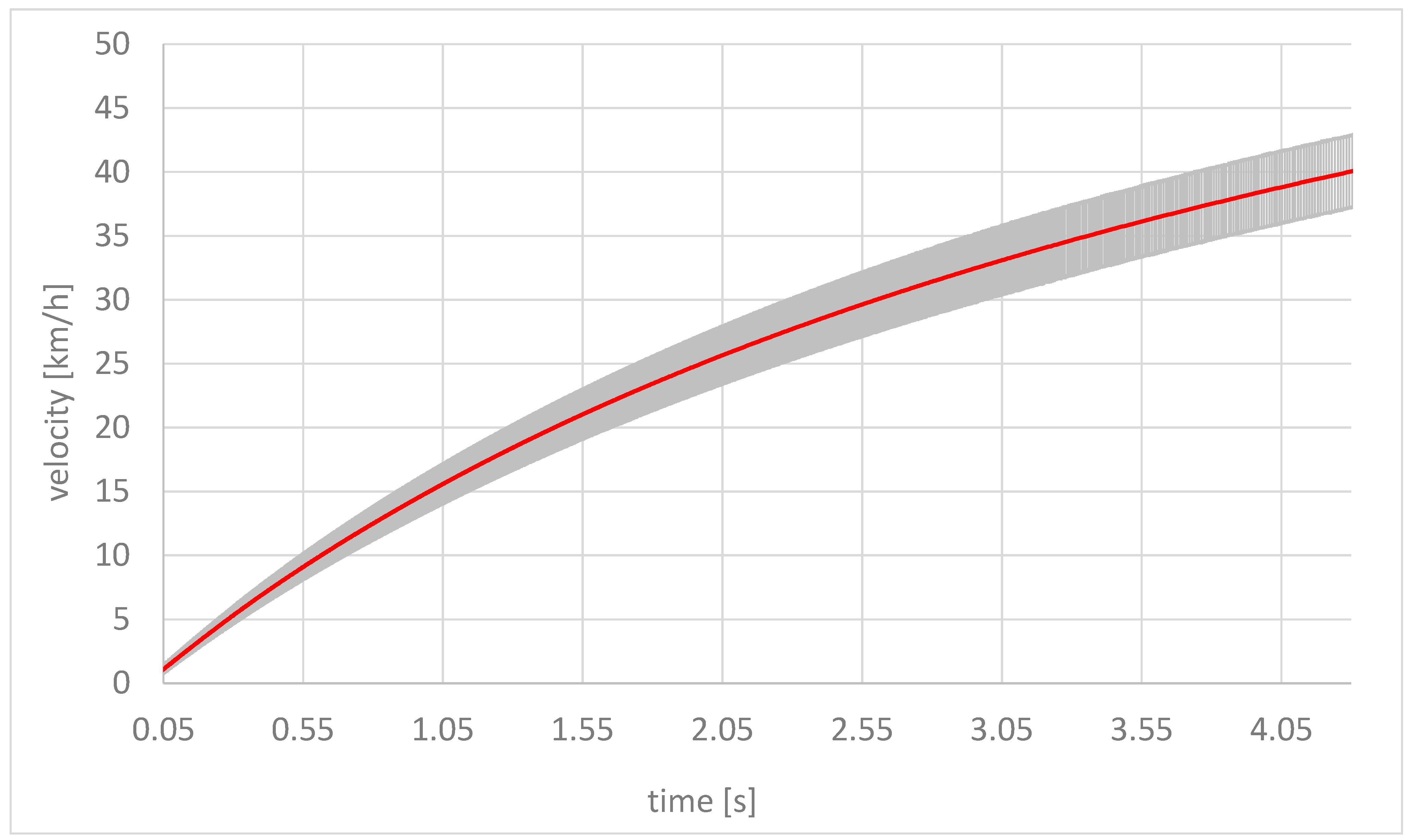
| the acceleration, velocity, and covered distance of the vehicle | ||
| the angular velocity and acceleration of the front and rear (back) wheels | ||
| the forces that the road exerts on the front and rear (back) tires in the tangential and normal directions | ||
| the front and rear (back) shafts’ loading in the tangential and normal directions | ||
| the rolling resistance torques | ||
| the tire slip | ||
| the air resistance force | ||
| the intensity of the current flowing through the motor | ||
| the torque and angular speed of the motor | ||
| the vehicle energy consumption | ||
| Other notations | ||
| Notation | Description | |
| the magnitude of the torque exerted by the chain drive on the back shaft | ||
| the magnitude of the torque exerted by the stator of the motor on its rotor | ||
| the magnitude of the rolling resistance torque on the front and rear (back) wheels | ||
| the resultant of air resistance force | ||
| the magnitude of the force exerted by the road on the front and rear (back) wheels in the tangential direction | ||
| the magnitude of the force exerted by the road on the front and rear (back) wheels in the normal direction | ||
| the load on the front and rear (back) shaft in the tangential direction | ||
| the load on the front and rear (back) shaft in the normal direction | ||
| the centre of gravity of the front and rear (back) wheels and the whole vehicle | ||
| the gear ratio in the chain drive | ||
| the loading torque on the rotor of the motor | ||
Appendix A

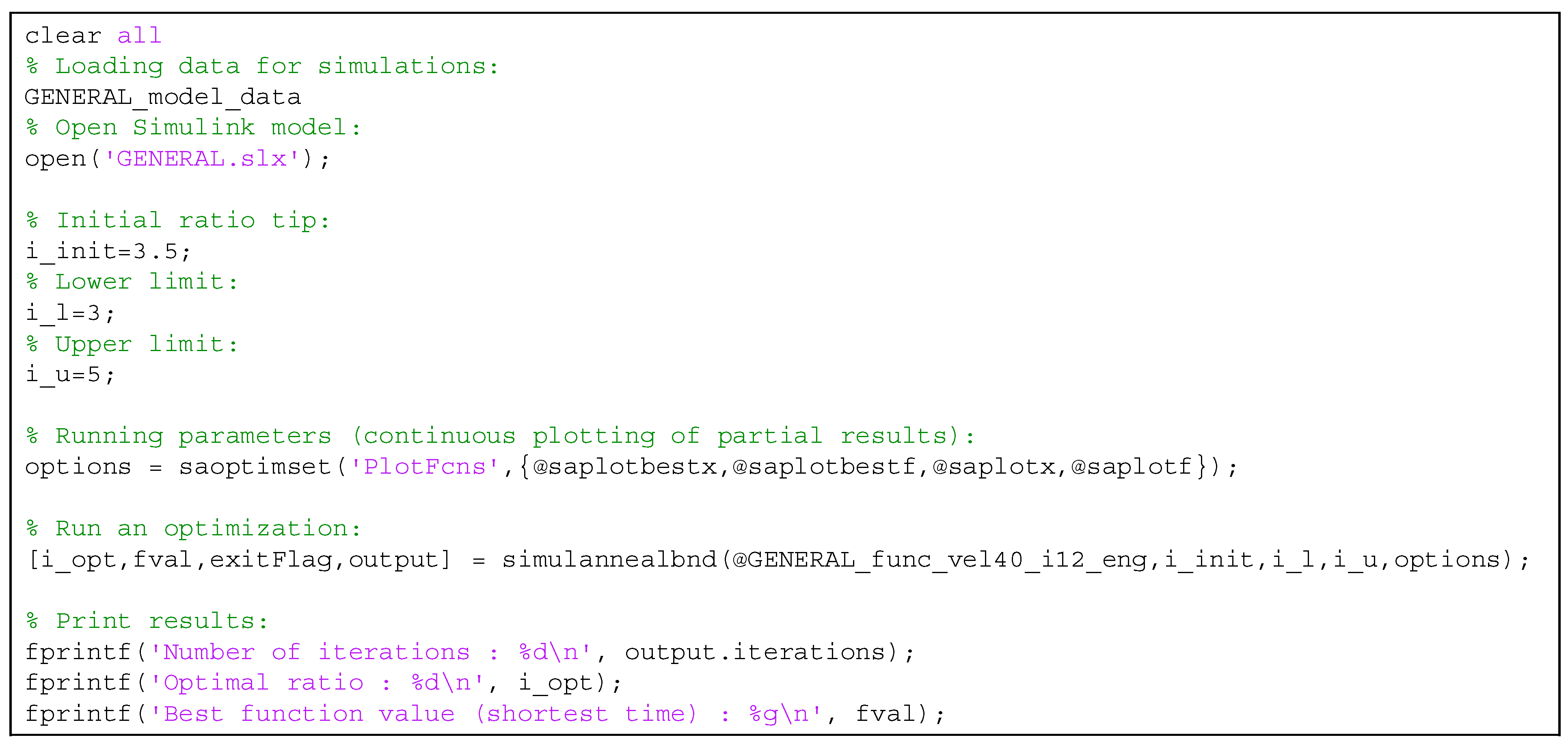
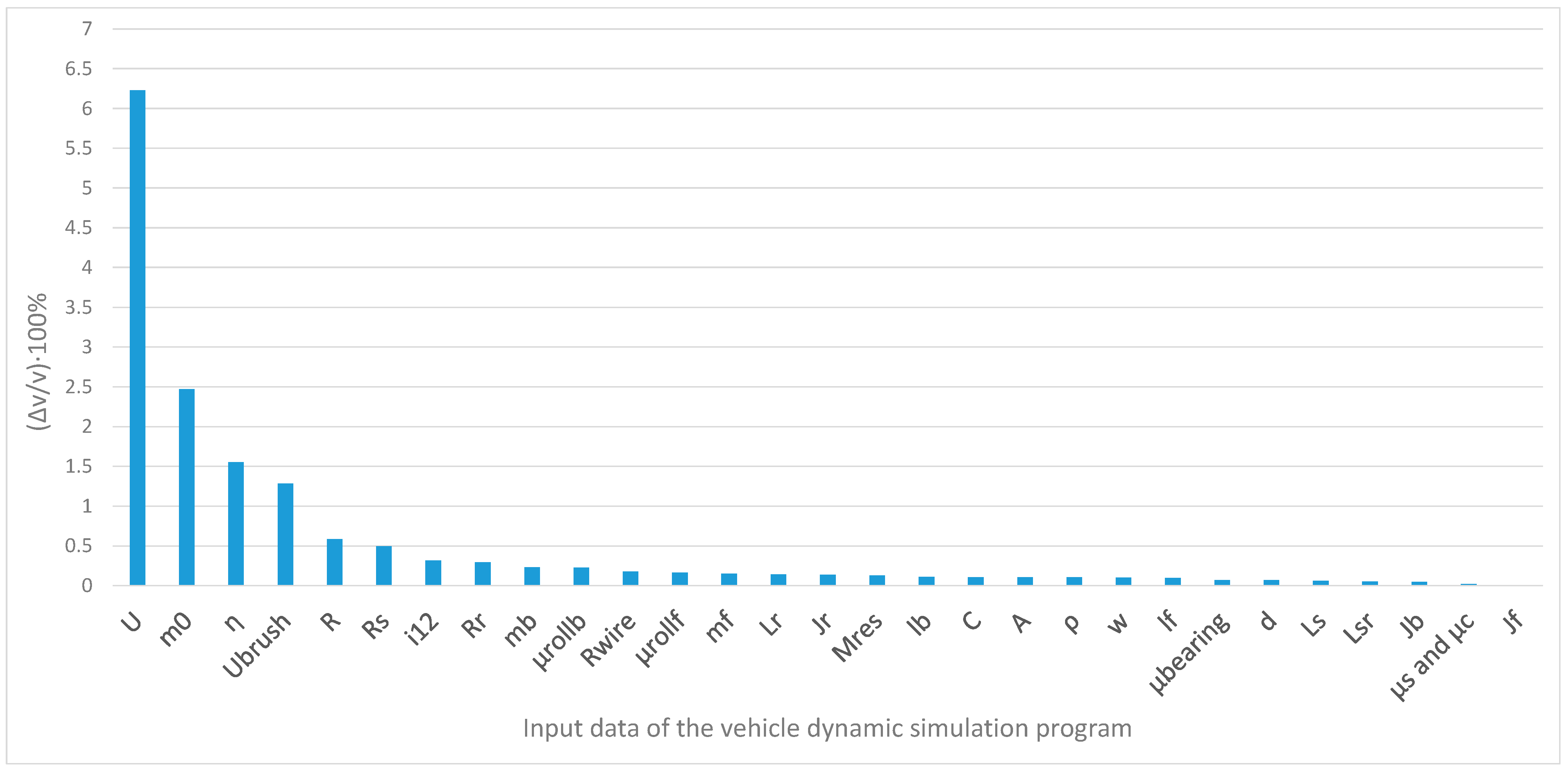
| U | m0 | η | Ubrush | R | Rs | i12 | Rr | mb | µrollb | |
| (Δv/v)·100% | 6.2301 | 2.4704 | 1.551279 | 1.2817 | 0.5853 | 0.4972 | 0.3157 | 0.294016 | 0.2319 | 0.2295 |
| Rwire | µrollf | mf | Lr | Jr | Mres | lb | C | A | ρ | |
| (Δv/v)·100% | 0.1774 | 0.1629 | 0.149842 | 0.138 | 0.1369 | 0.1283 | 0.1114 | 0.103202 | 0.1032 | 0.1032 |
| w | lf | µbearing | d | Ls | Lsr | Jb | µs and µc | Jf | ||
| (Δv/v)·100% | 0.0984 | 0.0962 | 0.068368 | 0.0684 | 0.0585 | 0.0512 | 0.0464 | 0.020672 | 0.0036 |
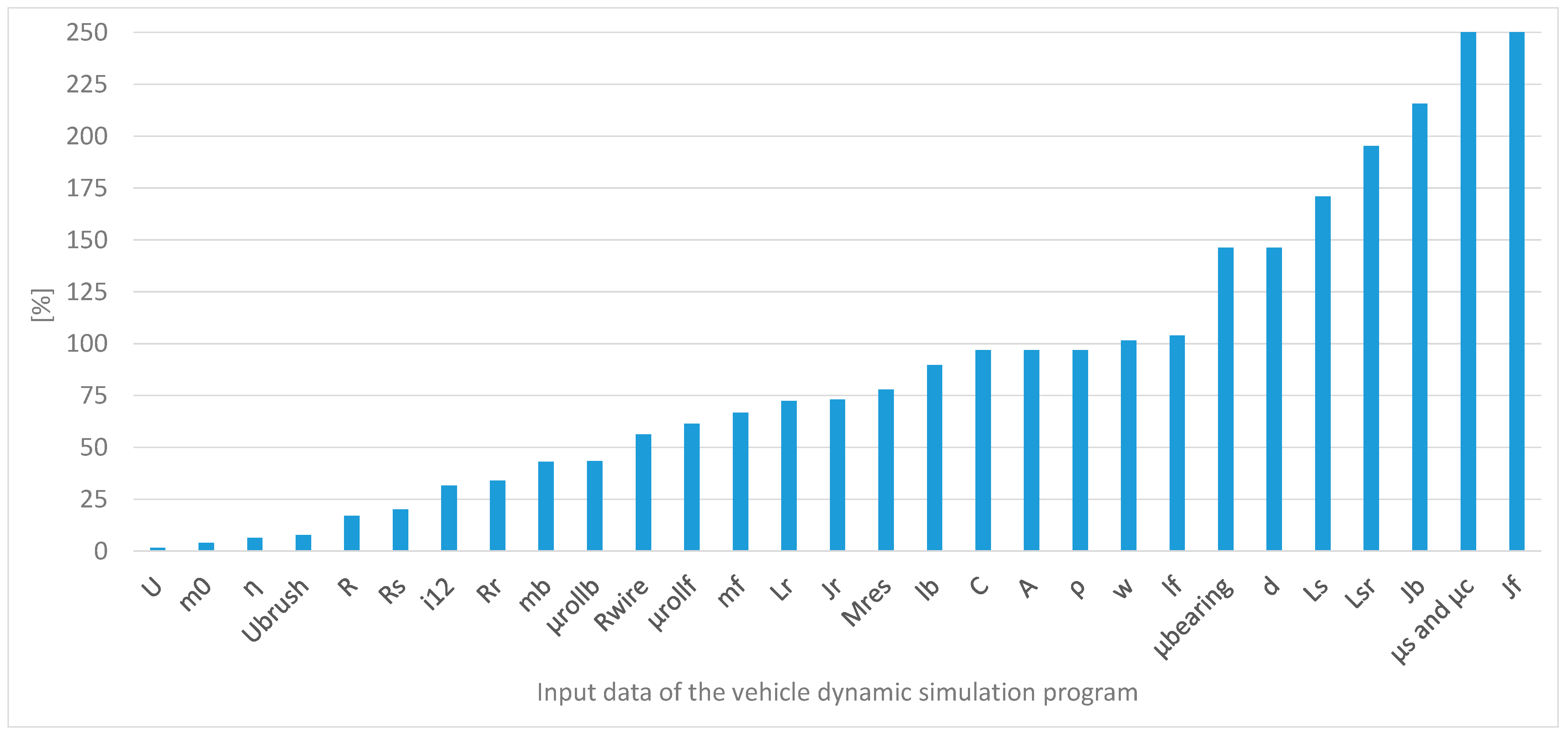
| U | m0 | η | Ubrush | R | Rs | i12 | Rr | mb | µrollb | |
| % | 1.6051 | 4.048 | 6.446293 | 7.8022 | 17.086 | 20.113 | 31.678 | 34.01172 | 43.125 | 43.573 |
| Rwire | µrollf | mf | Lr | Jr | Mres | lb | C | A | ρ | |
| % | 56.355 | 61.371 | 66.73718 | 72.459 | 73.061 | 77.949 | 89.771 | 96.89778 | 96.898 | 96.898 |
| w | lf | µbearing | d | Ls | Lsr | Jb | µs and µc | Jf | ||
| % | 101.65 | 103.91 | 146.2675 | 146.27 | 171.05 | 195.35 | 215.67 | 483.7421 | 2796.4 |
References
- Juhász, G. A pneumobil versenyek és az oktatás—A felkészülés tanári szemmel. Debreceni Műszaki közlemények 2011, 1, 35–40, ISSN: 1587-9801. [Google Scholar]
- Gábora, A.; Sziki, G.Á.; Szántó, A.; Varga, T.A.; Magyari, A.; Balázs, D. Prototype battery electric car development for Shell-ECO-Marathon® competition. In Proceedings of the XXII International Conference of Young Engineers, Xi’an, China, 21–22 April 2017; pp. 167–170. [Google Scholar]
- Available online: https://www.shellecomarathon.com/ (accessed on 6 March 2025).
- Available online: https://pneumobil.hu/ (accessed on 6 March 2025).
- Rill, G.; Castro, A.A. Road Vehicle Dynamics: Fundamentals and Modeling with MATLAB®; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Shakouri, P.; Ordys, A.; Askari, M.; Laila, D.S. Longitudinal vehicle dynamics using Simulink/Matlab. In Proceedings of the UKACC International Conference on Control 2010, Coventry, UK, 7–10 September 2010; IET: Stevenage, UK, 2010; pp. 955–960. [Google Scholar]
- Vairavel, M.; Girimurugan, R.; Shilaja, C.; Loganathan, G.B.; Kumaresan, J. Modeling, validation and simulation of electric vehicles using MATLAB. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2022; Volume 2452. [Google Scholar]
- Kıyaklı, A.O.; Solmaz, H. Modeling of an electric vehicle with MATLAB/Simulink. Int. J. Automot. Sci. Technol. 2019, 2, 9–15. [Google Scholar] [CrossRef]
- The MathWorks Inc. MATLAB Version: 9.13.0 (R2022b); The MathWorks Inc.: Natick, MA, USA, 2022; Available online: https://www.mathworks.com (accessed on 10 February 2025).
- Szántó, A.; Hajdu, S.; Sziki, G.Á. Dynamic simulation of a prototype race car driven by series wound DC motor in Matlab-Simulink. Acta Polytech. Hung 2020, 17, 103–122. [Google Scholar] [CrossRef]
- Szántó, A.; Hajdu, S.; Sziki, G.Á. Optimizing parameters for an electrical car employing vehicle dynamics simulation program. Appl. Sci. 2023, 13, 8897. [Google Scholar] [CrossRef]
- Li, P.; Löwe, K.; Arellano-Garcia, H.; Wozny, G. Integration of simulated annealing to a simulation tool for dynamic optimization of chemical processes. Chem. Eng. Process. 2000, 39, 357–363. [Google Scholar] [CrossRef]
- Vo, T.M.N. Centrifugal pump design: An optimization. Eurasia Proc. Sci. Technol. Eng. Math. 2022, 17, 136–151. [Google Scholar]
- Zadeh, L.A. Fuzzy logic. Computer 1988, 21, 83–93. [Google Scholar] [CrossRef]
- Adeli, H.; Sarma, K.C. Cost Optimization of Structures: Fuzzy Logic, Genetic Algorithms, and Parallel Computing; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Kim, J.; Kasabov, N. HyFIS: Adaptive neuro-fuzzy inference systems and their application to nonlinear dynamical systems. Neural Netw. 1999, 12, 1301–1319. [Google Scholar] [CrossRef]
- Elbaz, K.; Shen, S.L.; Zhou, A.; Yuan, D.J.; Xu, Y.S. Optimization of EPB shield performance with adaptive neuro-fuzzy inference system and genetic algorithm. Appl. Sci. 2019, 9, 780. [Google Scholar] [CrossRef]
- Karna, S.K.; Sahai, R. An overview on Taguchi method. Int. J. Eng. Math. Sci. 2012, 1, 1–7. [Google Scholar]
- Krishankant, J.T.; Bector, M.; Kumar, R. Application of Taguchi method for optimizing turning process by the effects of machining parameters. Int. J. Eng. Adv. Technol. 2012, 2, 263–274. [Google Scholar]
- Julong, D. Introduction to grey system theory. J. Grey system 1989, 1, 1–24. [Google Scholar]
- Li, Y.X.; Yang, J.G.; Gelvis, T.; Li, Y.Y. Optimization of measuring points for machine tool thermal error based on grey system theory. Int. J. Adv. Manuf. Technol. 2008, 35, 745–750. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–learning-based optimization: A novel method for con-strained mechanical design optimization problems. Comput.-Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Rao, R.V. Teaching-Learning-Based Optimization Algorithm; Springer International Publishing: Cham, Switzerland, 2016; pp. 9–39. [Google Scholar]
- Sivanandam, S.N.; Deepa, S.N.; Sivanandam, S.N.; Deepa, S.N. Genetic algorithm optimization problems. In Introduction to Genetic Algorithms; Springer International Publishing: Cham, Switzerland, 2008; pp. 165–209. [Google Scholar]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Glover, F.; Kelly, J.P.; Laguna, M. Genetic algorithms and tabu search: Hybrids for optimization. Comput. Oper. Res. 1995, 22, 111–134. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Kirkpatrick, S. Optimization by simulated annealing: Quantitative studies. J. Stat. Phys. 1984, 34, 975–986. [Google Scholar] [CrossRef]
- Faber, R.; Jockenhövel, T.; Tsatsaronis, G. Dynamic optimization with simulated annealing. Comput. Chem. Eng. 2005, 29, 273–290. [Google Scholar] [CrossRef]
- Ingber, L. Adaptive simulated annealing (ASA): Lessons learned. Invit. Pap. A Spec. Issue Pol. J. Control Cybern. Simulated Annealing Appl. Comb. Optim. 1995, 25, 33–54. [Google Scholar]
- Eckert, J.J.; Santiciolli, F.M.; Silva, L.C.; Dedini, F.G. Vehicle drivetrain design multi-objective optimization. Mech. Mach. Theory 2021, 156, 104123. [Google Scholar] [CrossRef]
- Eckert, J.J.; Silva, L.C.; Costa, E.S.; Santiciolli, F.M.; Dedini, F.G.; Corrêa, F.C. Electric vehicle drivetrain optimisation. IET Electr. Syst. Transp. 2017, 7, 32–40. [Google Scholar] [CrossRef]
- Salvan, L.; Brüll, M.; Hollstein, A.; Medina, R.; Wilkins, S.; Avramis, N. Electric Drivetrain Optimization for 48V Urban Vehicles. In Proceedings of the 35th Electric Vehicle Symposium (EVS35), Oslo, Norway, 11–15 June 2022; pp. 1–13. [Google Scholar]
- Lu, M.; Domingues-Olavarría, G.; Márquez-Fernández, F.J.; Fyhr, P.; Alaküla, M. Electric drivetrain optimization for a commercial fleet with different degrees of electrical machine commonality. Energies 2021, 14, 2989. [Google Scholar] [CrossRef]
- Zhang, P.; Chen, Y.; Lin, M.; Ma, B. Optimum matching of electric vehicle powertrain. Energy Procedia 2016, 88, 894–900. [Google Scholar] [CrossRef]
- Li, C.; Cong, Z.; Zhang, B.; Jing, H. A Simulated Annealing algorithm based optimization for vehicle Powertrain Mounting System. In Proceedings of the 2015 5th International Conference on Information Science and Technology (ICIST), Changsha, China, 24–26 April 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 10–13. [Google Scholar]
- Genc, M.O.; Kaya, N. Vibration Damping Optimization using Simulated Annealing Algorithm for Vehicle Powertrain System. Eng. Technol. Appl. Sci. Res. 2020, 10, 5164–5167. [Google Scholar] [CrossRef]
- Sziki, G.Á.; Sarvajcz, K.; Kiss, J.; Gál, T.; Szántó, A.; Gábora, A.; Husi, G. Experimental investigation of a series wound dc motor for modeling purpose in electric vehicles and mechatronics systems. Measurement 2017, 109, 111–118. [Google Scholar] [CrossRef]
- Szántó, A.; Kiss, J.; Mankovits, T.; Szíki, G.Á. Dynamic Test Measurements and Simulation on a Series Wound DC Motor. Appl. Sci. 2021, 11, 4542. [Google Scholar] [CrossRef]
- Pálinkás, S. Influence of Speed to Rolling Resistance Factor in Case of Autobus. In Vehicle and Automotive Engineering 4: Select Proceedings of the 4th VAE2022, Miskolc, Hungary; Springer International Publishing: Cham, Switzerland, 2022; pp. 157–164. [Google Scholar]
- Pálinkás, S.; Tóth, Á. Development of a measurement method to determine rolling resistance. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2022; Volume 1237, p. 012013. [Google Scholar]
- Szíki, G.Á.; Szántó, A.; Mankovits, T. Dynamic modeling and simulation of a prototype race car in MATLAB/Simulink applying different types of electric motors. Int. Rev. Appl. Sci. Eng. 2021, 12, 57–63. [Google Scholar]
- Szántó, A.; Szántó, A.; Sziki, G.Á. Review of the modeling methods of series wound DC motors. Műszaki Tudományos Közlemények 2020, 13, 166–169. [Google Scholar]
- Szántó, A.; Ádámkó, É.; Juhász, G.; Sziki, G.Á. Simultaneous measurement of the moment of inertia and braking torque of electric motors applying additional inertia. Measurement 2022, 204, 112135. [Google Scholar] [CrossRef]
- Hadžiselimović, M.; Blaznik, M.; Štumberger, B.; Zagradišnik, I. Magnetically nonlinear dynamic model of a series wound DC motor. Przegląd Elektrotechniczny 2011, 87, 60–64. [Google Scholar]
- Sziki, G.Á.; Szántó, A.; Kiss, J.; Juhász, G.; Ádámkó, É. Measurement system for the experimental study and testing of electric motors at the faculty of engineering, University of Debrecen. Appl. Sci. 2022, 12, 10095. [Google Scholar] [CrossRef]
- Error Propagation Calculator. Available online: http://julianibus.de/ (accessed on 12 April 2025).
- Saldaña, G.; San Martín, J.I.; Zamora, I.; Asensio, F.J.; Oñederra, O. Analysis of the current electric battery models for electric vehicle simulation. Energies 2019, 12, 2750. [Google Scholar] [CrossRef]
- Tremblay, O.; Dessaint, L.A. Experimental validation of a battery dynamic model for EV applications. World Electr. Veh. J. 2009, 3, 289–298. [Google Scholar] [CrossRef]
- Pattantyús, Á.G. Gépész és Villamosmérnökök Kézikönyve 2; Műszaki Könyvkiadó: Budapest, Hungary, 1961. [Google Scholar]

| |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szántó, A.; Ádámkó, É.; Sziki, G.Á. Filtering Process to Optimize the Technical Data of Prototype Race Cars. Appl. Sci. 2025, 15, 6889. https://doi.org/10.3390/app15126889
Szántó A, Ádámkó É, Sziki GÁ. Filtering Process to Optimize the Technical Data of Prototype Race Cars. Applied Sciences. 2025; 15(12):6889. https://doi.org/10.3390/app15126889
Chicago/Turabian StyleSzántó, Attila, Éva Ádámkó, and Gusztáv Áron Sziki. 2025. "Filtering Process to Optimize the Technical Data of Prototype Race Cars" Applied Sciences 15, no. 12: 6889. https://doi.org/10.3390/app15126889
APA StyleSzántó, A., Ádámkó, É., & Sziki, G. Á. (2025). Filtering Process to Optimize the Technical Data of Prototype Race Cars. Applied Sciences, 15(12), 6889. https://doi.org/10.3390/app15126889






