Series Arc Fault Detection Based on Improved Artificial Hummingbird Algorithm Optimizer Optimized XGBoost

Abstract

Based on the wide variety of electrical appliances, it is difficult to detect similar current waveforms when different appliances experience arc faults due to insufficient extraction of fault arc characteristics and low detection accuracy. To address these issues, a series arc fault detection method combining artificial hummingbird algorithm (AHA) and XGboost has been proposed. According to GB14287.4—2014, an experimental platform for fault arcs was designed and built to collect fault arc signals. By leveraging the global search capability and dynamic adaptive mechanism of AHA, key feature subsets sensitive to arcs are selected from high-dimensional time–frequency domain features. Combining the parallel computing advantages and regularization strategies of XGBoost, a low-complexity, highly interpretable fault classification model is constructed. The hyperparameters of XGBoost are simultaneously optimized by AHA. Experimental results show that the proposed method achieves a fault arc detection accuracy rate of 98.098%, effectively identifying series arc faults.

1. Introduction

As the proportion of renewable energy integration and the large-scale application of power electronic devices increase, the fault arc issues in low-voltage distribution systems have become increasingly complex. Series fault arcs, due to their low current amplitude and strong coupling with load dynamic behavior, can easily lead to the failure of traditional overcurrent protection devices, becoming one of the primary causes of electrical fires [1]. Studies show that more than 30% of hidden electrical fires are directly related to undetected series arc faults [2]. Although existing detection technologies (such as high-frequency noise analysis [3], time–frequency domain threshold method [4]) have achieved some success, they still face bottlenecks such as redundant feature extraction and insufficient model generalization capability in modern distribution systems dominated by nonlinear loads [5].

Traditional optimization algorithms often fall into local optima, and deep learning models face issues such as high computational complexity and heavy reliance on massive annotated data [6], making it challenging to meet the dual requirements of real-time performance and lightweight design in low-voltage distribution systems. In recent years, the integration of machine learning and optimization algorithms has provided new approaches for arc fault detection. For example, a support vector machine (SVM) model optimized using genetic algorithms (GAs) improves detection efficiency through feature reduction [7], while the combination of deep learning and attention mechanisms enhances robustness under complex operating conditions [8]. Ref. [9] uses raw current signals as input to construct a one-dimensional convolutional neural network (ArcNet) and verifies the algorithm’s real-time performance and accuracy on Raspberry Pi. Ref. [10] proposes an arc fault detection model based on a lightweight one-dimensional convolutional neural network, which is improved by using deep separable convolution. The GADF-CNN model proposed in Ref. [11] effectively extracts and classifies fault features. Ref. [12] introduces a domain adaptation framework based on multi-scale hybrid domain features (DA-MMDF) for cross-domain intelligent fault diagnosis under variable operating conditions. Ref. [13] employs a method of deep supervision without anchors and task alignment to encourage the model to make accurate and consistent predictions, significantly enhancing overall detection performance. Ref. [14] proposes a hybrid model framework of knowledge distillation convolutional neural networks–deep forest (KDCNNs-DF), which significantly improves classification accuracy.

The patterns of arc changes are complex, and traditional diagnostic models, such as SVM, often suffer from issues like insufficient accuracy, overfitting, and high data requirements [15]. XGBoost, with its simplified calculations and high classification and computational efficiency, has gained widespread application. However, the determination of hyperparameters heavily relies on expert prior knowledge. To enhance the classification performance of XGBoost, some scholars have employed various optimization algorithms to refine the parameters of XGBoost. Nevertheless, common optimization algorithms still face challenges such as weak local search capabilities, average global search capabilities, and a tendency towards premature convergence [16,17].

In response to the aforementioned challenges, this paper proposes a series arc fault detection method that integrates the artificial hummingbird algorithm (AHA) with XGBoost. By analyzing a large amount of arc fault data and selecting appropriate feature values based on the characteristics of the faults, the global search capability and dynamic adaptive mechanism of AHA are utilized to screen out key feature subsets sensitive to arcs from high-dimensional time–frequency domain features. Combining the parallel computing advantages and regularization strategies of XGBoost, a low-complexity, high-explanatory fault classification model is constructed. The hyperparameters of XGBoost are optimized synchronously by AHA, and the model is trained for series arc fault diagnosis.

2. Collection of Arc Fault Data in Series

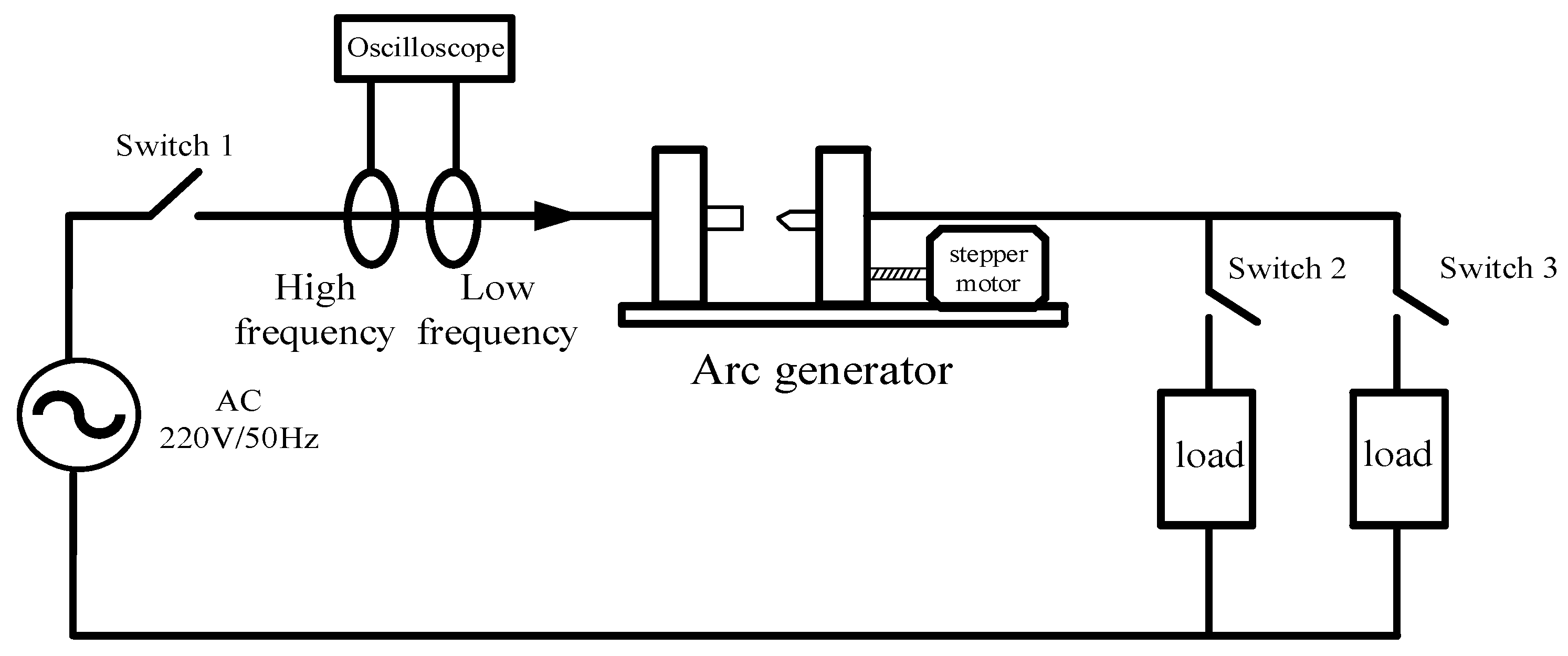
2.1. Arc Occurrence Platform Construction and Current Signal Collection

According to GB/T31143—2014 “Arc Fault Protection Appliances (General Requirements for AFDD),” [18] an independently designed and constructed AC arc fault signal acquisition platform suitable for 220 V has been established. The arc fault device consists of a fixed electrode and a moving electrode controlled by a stepper motor. The material of the fixed electrode is a stone grinding rod, while the moving electrode is a copper rod. The experimental platform mainly includes an experimental circuit and measuring equipment. The experimental circuit primarily comprises a 220 V/50 Hz AC power supply, an arc fault simulator, and a load in series. Among these, the arc fault simulator is connected to the load and oscilloscope, generating arcs when the electrical appliance operates; the oscilloscope is used to collect the load current signal; and high-frequency current transformers (cut-off frequency: 10 KHz) and low-frequency current transformers (cut-off frequency: 5 KHz) connected to the oscilloscope are linked to the live wire of the load, obtaining the operating current of the load. The torque of the stepper motor is 0.55 N.m and the step angle is 1.8. The experimental platform is shown in Figure 1.

Common household low-voltage AC appliances are used as experimental loads. At the start of the experiment, normal operating signals are collected. The two electrodes are in contact, and switch 1 is closed to form a circuit. Then, the distance between the two electrodes is controlled by a stepper motor. When a certain distance is reached, a sustained arc will be generated. During the experiment, first, the current signal when the load is operating normally is collected; then, the current signal under the arc generation state of the arc generator is collected, and finally, signal processing and analysis are performed. AC fault arc protection is mainly applied in homes or office settings, so different household appliances are selected as experimental loads. The load parameters used in the experiment are shown in

Table 1. Representative test loads and their main parameters.

Load Category	Load	Rated Electrical Parameters
Linear load	Electric kettle	220 V/1600 W
	Halogen lamp	220 V/600 W
	Hair dryer	220 V/1000 W
	Vacuum cleaner	220 V/1300 W
Nonlinear load	Voltage regulating circuit	220 V/800 W
	Computer	220 V/100 W
	Electric fan	220 V/60 W
Mixed load	Hair dryer + electric kettle	220 V/1000 W + 220 V/1600 W
	Hair dryer + computer	220 V/1000 W + 220 V/100 W
	Electromagnetic oven + voltage regulating circuit	220 V/1300 W + 220 V/800 W

.

2.2. Analysis of Arc Current Characteristics of Failure

Periodic sampling of normal working and fault arc current signals is performed. Waveforms of normal and fault load currents are shown in Figure 2, Figure 3, Figure 4 and Figure 5.

Under normal conditions (subfigure (a) in each figure), the time–domain waveforms of currents under different loads show significant differences. Some are sinusoidal waves, such as Figure 5a; some approach triangular waves, like Figure 2a and Figure 3a; and some exhibit zero-crossing lags, as seen in Figure 4a. These variations reflect the impedance characteristics of different loads and demonstrate how load diversity affects the series current. At the same time, the current waveforms under a specific load are stable over cycles, with consistent repetition before and after each cycle.

In the arc state (subfigure (b) in Figure 2, Figure 3, Figure 4 and Figure 5), the current amplitude under most loads does not significantly increase compared to its normal state; under resistive loads, the current amplitude even slightly decreases. The differences in the time–domain waveform of currents under different loads remain significant. Besides the impact of impedance differences, random spikes, waveform gaps, and zero-crossings caused by the arc introduce strong diversity and randomness to the arc current waveform. The waveform varies between cycles under a certain load, and the waveform is not fixed before and after each cycle.

3. Current Signal Processing and Feature Extraction

3.1. Characteristic Processing of High-Frequency Current Signal

The time domain characteristics of arc current are mainly manifested as the “flat shoulder” of the current waveform at zero crossing, the high-frequency components of arc current being rich, and the current waveform being asymmetric. In view of the above characteristics, the maximum rise rate and skewness of the current are selected as the time domain characteristics of arc current.

3.1.1. Maximum Rate of Current Rise

During an arc fault, the amplitude of the current undergoes a sudden change, leading to a sudden change in the maximum rate of increase of the current at zero crossing. The difference between the current signal sampling values of two adjacent discrete points within a cycle is selected, and the maximum absolute value represents the maximum rate of increase of the current. The calculation formula is as follows:

$$V_{\max }=(\left|I_2-I_1\right|,\left|I_3-I_2\right|,\dots ,\left|I_N-I_{N-1}\right|{)}_{\max }$$

(1)

In the formula, I is the instantaneous value of current, and N is the number of sampling points.

3.1.2. Peak Value

The peak index $C_f$ is defined as the ratio of signal peak to root mean square value, and the calculation formula is:

$$C_f={\displaystyle \frac{x_{\max }}{x_{rms}}}={\displaystyle \frac{\max \left[x_{\tau }(\tau )\right]}{\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N{x}_i^2}}}}$$

(2)

In the formula, x_max is the signal peak, x_rms is the signal root mean square value, x_i is the amplitude of the i discrete signal, and x_τ is the processed discrete signal sequence.

3.1.3. Pulse Indicators

The pulse index $I_f$ is defined as the ratio of signal peak to absolute mean, and the calculation formula is:

$$I_f={\displaystyle \frac{x_{\max }}{\left|\overline{x}\right|}}={\displaystyle \frac{\max \left[x_{\tau }(\tau )\right]}{\frac{1}{N}\sqrt{{\displaystyle \sum _{i=1}^N\left|x_i\right|}}}}$$

(3)

In the formula, $\left|\overline{x}\right|$ is the signal absolute mean.

3.1.4. Margin Indicators

The margin index $L_f$ is defined as the ratio of signal peak to root mean square amplitude, and the calculation formula is:

$$L_f={\displaystyle \frac{x_{\max }}{x_{\tau }}}={\displaystyle \frac{\max \left[x_{\tau }(\tau )\right]}{(\frac{1}{N}{\displaystyle \sum _{i=1}^N\sqrt{\left|x_i\right|}{)}^2}}}$$

(4)

In the formula, $x_{\tau }$ is the root amplitude of the signal.

3.1.5. Total Harmonic Distortion Rate

After FFT transformation of the time domain signal, it is found that the current waveform has different degrees of distortion in the fault state. The total harmonic distortion rate e_THD is used to characterize the distortion degree of the fault signal, and the calculation formula is as follows:

$$e_{THD}=\sqrt{{\displaystyle \sum _{k=2}^H(\frac{I_k}{I_1}{)}^2}}=\sqrt{{\displaystyle \sum _{k=2}^H(\frac{D_k}{D_1}{)}^2}}$$

(5)

In the formula, I₁ is the effective value of the fundamental wave of the current signal, I_k is the effective value of the k-th harmonic of the current signal, D₁ is the amplitude of the fundamental wave, D_k is the amplitude of the k-th harmonic, and H is the specified order.

3.2. Feature Extraction of Low-Frequency Current Signal

The low-frequency current signal is denoted as LF(n), where n = 1, 2, …, N, and N is the length of the signal, which is 4000 here.

A signal can be defined as:

$$I=\{\left.I_{wave}(e)\right|e=1,2,\cdots ,E\}$$

(6)

The number of sampling points for each full wave content is:

$$Q=0.02f_{s2}$$

(7)

The average AC current IMean(e) in the e-th full wave is:

$$IMean(e)={\displaystyle \frac{1}{Q}}{\displaystyle \sum _{q=1}^Q{\left.\left|LF(e,q)\right.\right|}^2}$$

(8)

In the formula, LF(e, q) is the q sampling points of the e-th full wave.

The amplitude symmetry factor of the e-th full wave is defined as:

$$AmpSymIndex(e)={\displaystyle \frac{\left|\underset{q=1,2,\cdots ,Q}{\max }LF(e,q)-DC\right|}{\left|DC-\underset{q=1,2,\cdots ,Q}{\min }LF(e,q)\right|}}$$

(9)

In the formula, DC is the DC component of the current signal.

The phase symmetry factor of the e-th full wave is defined as:

$$PhaseSymIndex(e)={\displaystyle \frac{\left|MaxLoc\_LF(e,q)-MinLoc\_LF(e,q)\right|}{Q/2}}$$

(10)

In the formula, MaxLoc_LF(e,q) and MinLoc_LF(e,q) are the positions of the maximum and minimum values in the e-th full wave, respectively.

(1)

The mean value of the average current of E full waves IMean_Mean is:

$$IMean\_Mean={\displaystyle \frac{1}{E}}{\displaystyle \sum _{e=1}^E\frac{1}{Q}{\displaystyle \sum _{q=1}^Q{\left.\left|LF(e,q)\right.\right|}^2}}$$

(11)

(2)

The instantaneous current IIN of E full waves is:

$$IIN=IMean(E)$$

(12)

(3)

The peak value of E full wave average current IMean_Max is:

$$IMean\_Max=\underset{e=1,2,\cdots ,E}{\max }[{\displaystyle \frac{1}{Q}}{\displaystyle \sum _{q=1}^Q{\left.\left|LF(e,q)\right.\right|}^2}]$$

(13)

4. Artificial Hummingbird Algorithm (AHA) and XGBoost

4.1. Artificial Hummingbird Algorithm (AHA)

The artificial hummingbird algorithm (AHA) represents an emerging heuristic approach [10], distinguished by its unique biological inspiration. AHA meticulously models three characteristic hummingbird flight maneuvers—axial, diagonal, and omnidirectional—alongside their intelligent foraging strategies, encompassing guided, regional, and migratory patterns. This formulation yields an artificial intelligence foraging model adept at tackling high-dimensional optimization problems, offering benefits like computational simplicity and high solution accuracy. Nevertheless, similar to many heuristic methods, AHA is not without limitations, exhibiting a tendency to converge prematurely on local optima and experiencing slower convergence speeds.

4.1.1. Initialize

Given n food sources at random, the artificial hummingbird population is randomly initialized:

$$x_i=Lb+rand(0,1)\cdot (\mathrm{Ub}-\mathrm{Lb}),\mathrm{i}=1,2,\dots ,\mathrm{n}$$

(14)

The algorithm employs Lb and Ub as the respective lower and upper bounds defining the search domain. A vector rand(0,1) provides randomness, with each element sampled uniformly between 0 and 1. Each candidate solution x_i (for i = 1, 2, …, N) is generated using the assignment. Subsequently, the access table undergoes initial setup according to:

$$V{T}_{i,j}=\left\{\begin{array}{c}0,i\ne j\\ null,i=j\end{array}\right.i=1,2,\dots ,n;j=1,2,\dots ,n$$

(15)

The entities modeled by Form (15) comprise the j-th physical source along with a distinct physical source that the i-th hummingbird visits.

4.1.2. Guide Foraging

The AHA algorithm can simulate three specific flight skills of hummingbirds (axial, diagonal, and omnidirectional). The expression for axial flight is as follows:

$$D^{\mathrm{i}}=\left\{\begin{array}{l}1,i=randi(\left[1,d\right])\\ 0, \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}else\end{array}\right.i=1,2,\dots ,d$$

(16)

In the formula, randi([1,d]) represents a random integer on [1,d]. The mathematical model of diagonal flight is as follows:

$$D^{\mathrm{i}}=\left\{\begin{array}{l} \hspace{1em}\hspace{1em}\hspace{1em}1,i=w(\mathrm{ii}),\mathrm{ii}\in \left[1,K\right],\\ w=randperm(\mathrm{K}),\mathrm{K}\in \left[2\cdot \left[R\cdot (\mathrm{d}-2)\right]+1\right]\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}0,else\end{array}\right.\begin{array}{cc}& i=1,2,\dots ,d\end{array}$$

(17)

Within this formulation, randperm(K) generates a random permutation of the integers from 1 to K. R denotes a uniformly distributed random scalar within the interval [0, 1]. Omnidirectional flight is characterized by any displacement vector whose projections onto the three Cartesian coordinate axes are governed by the following expression:

$$D^{\mathrm{i}}=1,i=1,2,\dots ,d$$

(18)

These flight adaptations enable hummingbirds to access designated nourishment locations, facilitating the identification of candidate sustenance sites. The formal characterization of the guiding foraging strategy and these provisional food sources is given by the following equations:

$$V{g}_i(\mathrm{t}+1)={\mathrm{x}}_{i\cdot \mathrm{target}}(\mathrm{t})+\mathrm{a}\cdot \mathrm{D}\cdot \left[{\mathrm{x}}_i(\mathrm{t})-{\mathrm{x}}_{i\cdot \mathrm{target}}(\mathrm{t})\right]\begin{array}{cc}& a~N(0,1)\end{array}$$

(19)

The position update for the i-th candidate solution, denoted as x_i(t), is given by the formula. This expression incorporates X_i·taregt(t), representing the position of the target candidate solution explored by the i-th hummingbird, and a, a regional foraging parameter drawn from a standard normal distribution.

$$x_i(\mathrm{t}+1)=\left\{\begin{array}{c}{x}_i(\mathrm{t}),f({\mathrm{x}}_i(\mathrm{t})\le f(\mathrm{V}{\mathrm{g}}_i(\mathrm{t}+1))\\ \mathrm{V}{g}_i(\mathrm{t}+1),f({\mathrm{x}}_i(\mathrm{t})>f(\mathrm{V}{\mathrm{g}}_i(\mathrm{t}+1))\end{array}\right.$$

(20)

In the formula, $f(\cdot )$ is the fitness value of the function. Equation (20) shows that if the nectar replenishment rate of the candidate physical source is higher than that of the current food source, the hummingbird will abandon the current food source.

4.1.3. Territory Foraging

Subsequent to identifying the target candidate solution, hummingbirds exhibit a probability-driven tendency to investigate alternative food sources, specifically avoiding the original one. This behavior promotes relocation to proximate zones for the purpose of acquiring alternative food intelligence, offering potential substitutes for the optimal solution. The mathematical representation of territorial foraging behavior and candidate food source positions is presented as follows:

$$V{t}_i(\mathrm{t}+1)=x_i(\mathrm{t})+\mathrm{b}\cdot \mathrm{D}\cdot x_i(\mathrm{t})\begin{array}{cc}& b~\mathrm{N}(0,1)\end{array}$$

(21)

where $b$ represents a regional foraging parameter adhering to the standard normal distribution. Formula (8) enables hummingbirds to pinpoint novel food source intelligence.

4.1.4. Migrate for Food

When food is scarce in frequently foraging areas, hummingbirds migrate to distant regions in search of food. Migration factors are predetermined in the AHA. Different behavioral effects will be produced based on these predetermined values. The specific migration expression is as follows:

$$x_{poor}=Lb+r\cdot (Ub-Lb),\mathrm{i}=1,2,\dots ,n$$

(22)

The variable $x_{poor}$ in the formula signifies the least optimal candidate solution. In configuring the AHA algorithm, the essential parameters of population size and maximum iterations are supplemented by a single unable parameter: the migration coefficient. This coefficient regulates the migration activation criterion. Its explicit formulation appears below:

$$M=2n$$

(23)

If candidate solutions are not fully replaced during guided or territorial foraging (each equally likely), a target solution can be revisited within 2^n iterations. Locking migration foraging addresses potential stagnation here by expanding the search space.

4.2. Extreme Gradient Boosting Tree (XGBoost)

XGBoost is an ensemble learning algorithm that improves upon the Gradient Boosting Decision Tree (GBDT) framework. By introducing regularization terms, parallelization, and second-order derivatives of loss functions, it achieves faster and more effective predictions. The algorithm optimizes iteratively by constructing new regression trees to fit the negative gradient (i.e., residuals) of the current model in each iteration, and achieves the final output by weighting and accumulating the predictions from all regression trees. This iterative optimization strategy not only enhances the prediction accuracy of the model but also effectively controls model complexity through regularization terms, thereby improving generalization capabilities. If there are M sub-trees, the model’s output result is:

$${\widehat{y}}_i={\displaystyle \sum _{m=1}^M{f}_m}({\mathrm{x}}_i)$$

(24)

In the formula, $y_i$ is the model output, $f_m$ is the m-th tree, and ${\mathrm{x}}_i$ is the i-th sample. The objective function to be minimized is:

$$L={\displaystyle \sum _{i=1}^{m}l(y_i,{\widehat{y}}_i)}+\mathsf{\Omega }(f_t)+\epsilon$$

(25)

$$\mathsf{\Omega }(f_t)=\gamma T+{\displaystyle \frac{1}{2}}\lambda {\displaystyle \sum _{i=1}^T{\omega }_j^2}$$

(26)

In the formula, $l$ is the loss function, $\epsilon$ is a constant, $T$ is the number of leaf nodes, $\omega$ is the weight of leaf nodes, and $\gamma$ and $\lambda$ are the regularization parameters that controls the complexity of the model. Compared with traditional GBDT, XGBoost introduces a regularization term to penalize the complexity of the model, making it less prone to overfitting when the regularization parameter increases [11]. The objective function in the t-th iteration can be expressed as:

$$\begin{array}{l}L(\mathrm{t})={\displaystyle \sum _{i=1}^{n}l({\mathrm{y}}_i,{\widehat{\mathrm{y}}}_i^{(\mathrm{t})})+\mathsf{\Omega }(f_t)}\\ \begin{array}{cc}& =\end{array}{\displaystyle \sum _{i=1}^{n}l({\mathrm{y}}_i,{\widehat{\mathrm{y}}}_i^{(\mathrm{t}-1)}+f_i({\mathrm{x}}_i))+\mathsf{\Omega }(f_t)}\end{array}$$

(27)

It can be obtained by performing a second-order Taylor expansion on $L(\mathrm{t})$ and deleting the constant term:

$$L(\mathrm{t})\approx {\displaystyle \sum _{i=1}^n\left[g_i{f}_i({\mathrm{x}}_i)+\frac{1}{2}{h}_i{f}_t^2({\mathrm{x}}_i)\right]}+\mathsf{\Omega }(f_t)$$

(28)

In the formula, $g_i$ and $h_i$ are the first and second gradients of the loss function, respectively. Let the sample number set of the j-th leaf node be $I_j=\left\{i\left|q({\mathrm{x}}_i)=\mathrm{j}\right.\right\}$, where $q({\mathrm{x}}_i)$ is the leaf label value corresponding to ${\mathrm{x}}_i$. Then, Equation (28) is rewritten as:

$$L(\mathrm{t})\approx {\displaystyle \sum _{j=1}^T\left[G_j{\omega }_j+\frac{1}{2}({\mathrm{H}}_j+\lambda ){\omega }_j^2\right]}+\gamma T$$

(29)

In the formula, $G_j$ and ${\mathrm{H}}_j$ are the sum of all g and h, respectively. Let the derivative of ${\omega }_j$ be 0, and get the leaf node score:

$${\omega }^{\ast }=-{\displaystyle \frac{G_j}{H_j+\lambda }}$$

(30)

The minimum value is obtained as follows:

$$L^{\ast }=-{\displaystyle \frac{1}{2}}{\displaystyle \sum _{j=1}^T\frac{G_j^2}{H_j+\lambda }}$$

(31)

The XGBoost algorithm performs well in structured data processing, with faster training speed and a lower required number of samples, so XGBoost is selected as the classifier [12].

4.3. AHA-XGBoost Arc Fault Detection Process

Step 1: Establish a series arc fault experimental platform to extract the features of the collected experimental data.

Step 2: Select 7 kinds of feature quantities as detection indicators, and carry out dimensionality reduction fusion of the features. Label samples according to the load type, and establish a data set.

Step 3: The training set and test set are randomly selected in the ratio of 8:2, and normalized processing is carried out.

Step 4: Use the AHA algorithm to optimize the five key parameters of XGBoost (number of trees, depth of trees, minimum weight sum of subnodes, learning rate, and sample ratio), and input the training set for training. Figure 6 shows the value of AHA fitness.

Step 5: Input the test set into the trained model, carry out fault diagnosis, and output the test results.

The AHA-XGBoost arc fault detection process is shown in Figure 7.

5. Identification of Fault Arc

5.1. Feature Importance and Interpretability via SHAP Analysis

In this study, the SHapley Additive ExPlanations (SHAP) framework was used to quantitatively analyze the contribution and influencing mechanism of the 11 selected features to the prediction results of the series arc fault detection model. As can be seen from Figure 8, all 11 features show a predictive influence that cannot be ignored, which jointly verifies their effectiveness for the detection task. Although there are significant differences in the influence of each feature, the SHAP value of any feature is consistently clustered around zero. This suggests that each feature provides unique and complementary information to the model. Crucially, the influence of the features associated with the mean value of the average current and amplitude symmetry factor is always at the forefront, which is highly consistent with the known physical properties of the tandem arc. The SHAP dependency diagram further illuminates the nature of these relationships, revealing both the expected monotonic tendencies and more complex nonlinear interactions between certain features and the predicted arc failure probability. This comprehensive SHAP analysis demonstrates the effectiveness of the selected feature set in capturing the discriminant features of series arc faults.

5.2. Parameter Configuration

According to the national standard GB14287.4—2014 “Electrical Fire Monitoring System-Part 4: Fault Arc Detector,” [19] the alarm performance indicators for fault arc detectors (arcfaultdetector, AFD) involve splitting each current sequence under different operating conditions into samples, with one cycle as a sample. Each sample contains 5000 current sampling points, forming a fault arc database. The data sets of each operating condition after splitting are divided into training and test sets according to random sampling principles, and they are divided in an 8:2 ratio, as shown in

Table 2. Database.

Data Mode	Database Set Type	Number	Total/Number
Normal (experimental label: 1)	Training set	13,368	15,456
	Test set	2088
Hitch (experimental label: 2)	Training set	13,248	15,462
	Test set	2214

. Under normal conditions, the training set has 15,456 samples, and the test set has 2088 samples. Under fault conditions, the training set has 15,462 samples, and the test set has 2214 samples.

5.3. Fault Arc Identification Results and Analysis

In this paper, six indexes are used to evaluate the performance of fault arc recognition model, namely sensitivity (Se), specificity (Sp), accuracy (Acc), precision (Precision), recall rate (Recall), and macro average F1 score (F1).

During the model training process, the prediction result curve of the test set is shown in Figure 9, and the accuracy rate of the verification set is 98.0983%. In the training process, there is no overfitting phenomenon, and the training results are good. Figure 10 shows the confusion matrix of the output model proposed in this paper. It can be seen that the recognition accuracy of samples in normal state of each type of load is high.

5.4. Comparison with Other Identification Methods

In order to verify the superiority of the proposed model in identifying fault arcs, the same data set collected by the experimental platform was used to train and test different models. The specific comparison models include BP neural network, extreme learning, random forest, and decision tree. In the random forest, the number of trees is 256, and the BP neural network has two hidden layers with three neurons each. The number of iterations is set to 3000, and the learning rate is 0.01.

Figure 11 shows the AUC curves for the five models: BP neural network with an AUC value of 0.9605, extreme learning with an AUC value of 0.9540, random forest with an AUC value of 0.9726, decision tree with an AUC value of 0.9582, and AHA-XGBoost with an AUC value of 0.9925. The AUC value of AHA-XGBoost is closest to 1, indicating that the fault detection method proposed in this paper can prioritize arc faults.

Table 3. Fault arc diagnosis results of different methods.

Model	Specificity (Sp)	Sensitivity (Se)	Accuracy (Acc)	Precision	Recall	F1
BP neural network	96.811	85.324	93.173	92.536	85.324	88.784
Extreme learning	96.904	75.607	90.16	91.882	75.607	82.954
Random forest	97.139	94.94	96.442	93.894	94.94	94.415
Decision tree	97.608	94.028	96.474	94.796	94.028	94.411
AHA-XGBoost	98.8743	95.648	98.098	97.523	95.648	96.576

lists the specific parameters of each model. Among them, compared with other models that have similar numbers of parameters, the accuracy of the designed model AHA-XGBoost is 98.098%, outperforming the other four models. The model proposed in this paper is slightly higher than the other four models in terms of specificity, sensitivity, precision, recall rate, and macro average F1 score. Additionally, this model significantly reduces the number of parameters and computational requirements, which to some extent reflects a simplification of the model complexity.

6. Conclusions

In response to the challenges of extracting characteristics from series arc faults and low accuracy in the fault world, this paper proposes a fault diagnosis method based on AHA-XGBoost. Through experimental analysis using an independently developed fault arc test platform, the superiority and effectiveness of this method have been verified. It can provide methodological support for subsequent series fault arc diagnosis and simultaneously improve accuracy. The main conclusions are as follows:

(1)

Feature selection optimization: Using the global search ability and dynamic adaptive mechanism of AHA, key feature subsets sensitive to arc are screened out from high-dimensional time–frequency domain features (such as wavelet packet entropy and high-frequency harmonic distortion rate) so as to overcome the local optimal defects of traditional filtering feature selection methods (such as the mutual information method).

(2)

Lightweight integrated modeling: Combining the parallel computing advantages of XGBoost and regularization strategies, a low-complexity and high-explanatory fault classification model is constructed. Through AHA synchronous optimization of XGBoost’s hyperparameters (such as learning rate and tree depth), the detection accuracy and real-time performance are significantly improved.

(3)

AHA optimizes XGBoost, which converges faster and has a better effect.

The analysis of the experimental conclusions shows that the series arc fault detection method based on AHA-XGBoost has significant advantages. By using the AHA algorithm to adaptively filter high-dimensional time–frequency domain features, it effectively addresses the challenge of insufficient extraction of arc-sensitive features, reducing the feature dimension to an optimal subset. Combining the XGBoost regularization model, it ensures a high detection accuracy of 97.523% while reducing model complexity, and its parallel computing characteristics enhance computational efficiency. Experiments verify that this method meets the requirements of GB14287.4—2014, with a feature dimension reduction of about 40% compared to traditional methods, and a misjudgment rate reduced to 1.9%, maintaining an identification accuracy of 98.098% even in low-current (<5 A) scenarios. This fusion algorithm provides a highly interpretable solution for multi-type electrical arc fault detection, offering practical engineering value for improving the reliability of electrical fire warning systems.

The core tasks in the future will focus on enhancing robustness in complex real-world environments (such as strong noise and diverse loads), achieving efficient integration and optimization of embedded systems, and ensuring continuous compliance with relevant safety and compatibility standards. This will be achieved by overcoming current limitations through methods such as collecting more comprehensive data, improving noise immunity, and model lightweighting, thereby facilitating the transition from laboratory achievements to large-scale practical applications.