Assessment of Uneven Wear of Freight Wagon Brake Pads

Abstract

This study deals with the problem of uneven wear of brake pads of wagons caused by a set of structural, dynamic, technological and operational factors. It has been found that an uneven distribution of the brake pad pressure force leads to higher maintenance costs and lower braking efficiency. The main causes of uneven wear are worn kinetostatic units, differences in the geometric parameters of pads, and imperfections in the lever transmission design. A method for optimizing the distribution of the pressure force using weight coefficients and the Lagrange function has been developed; it reduces the uneven wear of brake pads to 8–10% compared to that of a typical wagon bogie brake system, which is 20–35%. The experiments conducted have shown that for a mileage of 74,400 km and with the air distributor in empty mode, the wear of the pads is 19.6–28 mm, while in the loaded mode it amounts to 27.53–38.04 mm. The stress state of brake pads was determined with consideration of the weight coefficients. It was found that for abnormal wear of brake pads, their strength is not observed. The strength of the wheel when interacting with an abnormally worn pad has also been assessed. The resulting stresses are 1.5% higher than those that occur when the wheel interacts with the pad with nominal dimensions. The results of the research will contribute to the database of developments to be used for designing of modern structures of tribotechnical pairs of rolling stock and increasing the efficiency of railway transport.

1. Introduction

The efficiency of the wagon brake system is one of the key factors that determine the safety of railway traffic and its economic feasibility [1,2]. Particular attention is drawn to the problem of uneven wear of composite brake pads, which causes significant losses for railway transport and affects the country’s economy. When driving at speeds without braking, the brake pads remain inclined and rested with their upper ends on the rolling surface of the wheels, which creates harmful friction. This causes a number of negative consequences that significantly affect the operational efficiency of railway transport [3,4,5].

Firstly, the resistance to movement increases, and locomotives waste thousands of kWh of electricity and hundreds of tons of diesel fuel to overcome it. This entails significant financial costs, especially for large rail networks. Secondly, composite brake pads wear unevenly, which significantly reduces their service life. During braking, high-temperature damage to the rolling surfaces of the wheels occurs, which further increases the resistance to movement. As a result, the service life of wheel sets, which are one of the most expensive elements of rolling stock, is shortened, and the cost of railway track maintenance increases due to destructive dynamic loads (Figure 1).

The friction between pads and wheels significantly impairs the braking efficiency, thus increasing braking distances and reducing overall driving safety. This requires a decrease in the route speed of trains, which, in turn, reduces the performance of transportation and increases the excess costs for train traction. In addition, unevenly worn composite pads have to be replaced ahead of schedule, even with large residues of the working body. Such pads are removed to industrial landfills, which increases the volume of non-recyclable rubber-, soot-, and asbestos-containing waste and causes additional environmental damage to the natural environment.

Thus, the relevance of the study is caused to the need to solve the problem of uneven wear of composite brake pads, which negatively affects traffic safety, economic efficiency of railway transport and the environmental situation.

Experts and scientists from different countries have conducted a significant number of studies, the results of which have contributed to the development of a different brake lever transmission devices and mechanisms aimed at eliminating or slowing down the intense wear of pads, such as wedge-shaped wear. Reference [6] describes the development of a device for the parallel retraction of brake shoes in wagon bogies, which automatically adjusts the position of the brake pad relative to the rolling surface of the wheel. In theory, such a device can effectively solve these problems; however the use of it can significantly complicate the brake lever transmission design, which may cause a need for regular and time-consuming adjustments during operation. Therefore, there is a need to develop more optimized and easier-to-use solutions that would minimize maintenance cost without losing efficiency due to pad wear.

During the operation of the mechanical part of the wagon brake system, especially the articulated joints of the rods and levers, bushings significantly wear. This loosens connections and increases gaps, which negatively affects the operation of the automatic regulator and the efficiency of the brake lever transmission. According to [7], this problem is solved by applying innovative materials to manufacture bushings in hinged joints. In particular, the use of double pinned bushings for brake lever transmission elements and special protective brackets to replace traditional cotter pins in the brake beam reduces the impact of mechanical wear on the efficiency of the system, thereby increasing its reliability and durability.

In [8] the authors compare the efficiency of rolling stock brake pads made of different materials (gray cast iron, non-magnetic composite and magnetic composite) used in Indonesia. Methods of microhardness, X-ray energy dispersion analysis, microscopic analysis and finite element computational methods are used for the analysis. The results show that magnetic composite pads have the highest strength and wear resistance due to reinforcing fillers such as calcium carbonate and wollastonite. At the same time, non-magnetic composite and cast-iron pads are inferior in microhardness and wear resistance. It should be noted that there is a need for further research into uneven wear and the distribution of forces in brake pads because those affect the efficiency.

Scientific studies into the use of composite brake pads in rolling stock are related to traffic safety and environmental impact. Optimization of operating costs in the railway industry often leads to the situations where brake pads are considered as a product purchased at the lowest possible price, provided that they have satisfactory performance. However, this approach may not minimize long-term costs. The material for friction elements directly impacts the durability of wheel pairs; the cost of their replacement significantly exceeds the cost of replacement of other components of the wagon, as indicated in [9]. This highlights the need for an innovative approach to the selection of brake pad materials, thus assessing the overall operating costs and the lifespan of major rolling stock elements.

Reference [10] deals with the interaction of EU railway systems, in particular, the assessment of the brake characteristics of wagons manufactured both in Western European and post-Soviet countries. The main purpose of the research is to study the methods for calculating the braking mass and the pressure force from the brake pad to the wheel, as well as to assess the possibilities of implementing these methods within the EU single transportation system. Emphasis is placed on analyzing the compatibility of existing standards based on different approaches for assessing the braking characteristics of freight and passenger rolling stock. A disadvantage that significantly complicates the unification process is the uneven distribution of brake forces on the pad of bogies, which can lead to calculation errors.

The brake systems in road transportation are one of the key issues in ensuring road safety. Reference [11] focuses on the importance of the brake pad design, in particular, on the materials from which brake pads are made, and their interaction with other elements of the system. It is also emphasized that the wear of brake pads is accompanied by the occurrence of noise, which negatively affects human health. The study presents the analysis of how the pad design impacts the formation of noise; the authors also describe measures for its reduction. In particular, one of them is the use of insulators in the pad design and materials that reduce noise in the human environment. However, the study does not cover such an important problem as the uneven wear of pads, which is characteristic of both road and railway transport, for the correction of which the wedge dual ratio can be used.

Study [12] shows that the pressing force of brake pads largely depends on the dynamic processes in the lever transmission. As a result, the distribution of the pressing force between the pads may be uneven, which directly affects the wear intensity. Thus, there is an urgent need for developing new methods that take into account such factors and contribute to improving the operational efficiency of railway cars.

Study [13] proposes a regression model of the friction between pads and wheels of industrial transport locomotives, taking into account structural uncertainty and a significant number of input variables, including the friction coefficient. The author has successfully eliminated unstable solutions in the multiparameter model based on his own approach to solving the problem. However, when identifying models, a key parameter, i.e., wear in thickness, was not taken into account, which is critical when scheduling repairs and using certain brake pads for safety reasons.

Studies [14,15] present an analysis of typical block brakes, which are advisable to use for metro vehicles in China. Some of these brakes are characterized by operational flexibility, high reaction speed and compact design. In a number of countries, block brakes are used in the running gear of wagons to improve braking efficiency and ensure uniform wear of the pads. However, the introduction of such brake systems in wagons can increase their weight and air consumption during braking, as well as increase time spans for maintenance and repair of rail vehicles.

Based on the analysis of literature sources [6,7,8,9,10,11,12,13,14,15], it has been concluded that the issues of uneven wear of brake pads used for the rolling stock in Ukraine and other countries remain relevant and require additional research and improvement.

Therefore, the purpose of this study is to develop a modern approach to assessing the uneven wear of the brake pads of the wagon fleet.

To achieve this objective, the following tasks were set:

–

To optimize weight coefficient ki for uniform distribution of pressure force;

–

To conduct experimental studies on the uneven wear, evaluate the effectiveness of the proposed approach and build dependencies of the wear on the pressure force for each pad in the wagon bogie at different operating modes of the air distributor;

–

To investigate the stress states of the brake pad with abnormal wear and the wheel as well as the interaction between them.

2. Materials and Methods

This research was conducted using the 2TP-11 brake pad (Tribo, Bila Tserkva, Ukraine) as an example, since it is the most common type found in freight wagons with a gauge of 1520 mm.

The 2TP-11 brake pad is an important element of the wagon brake system due to its high resistance to wear and stability at elevated temperatures. However, the uneven distribution of the pressure force caused by the structural features of the brake system leads to different wear rates of the pad, which reduces its service life and increases maintenance costs.

The distribution of the pressure force between the brake pads in the wagon is a complex process, affected by structural, dynamic, operational, technological and external factors. Their combination leads to uneven force distribution, increased wear of pads, lower braking efficiency, and higher operating costs [16,17,18].

In order to eliminate the causes of unevenness, an integrated approach is needed; it will improve structural solutions, enhance the material properties, optimize operating conditions and introduce innovative regulation technologies.

Taking into account the above, a methodology based on a modern mathematical approach has been developed. It is based on the analysis of functional dependencies and integral calculations for accurate modeling of processes in the brake system of the wagon. This technique is presented as a tool to minimize uneven wear by optimizing the distribution of the pressure force between the pads.

The optimal distribution of the pressure force between the brake pads is one of the most important tasks in ensuring the efficiency and durability of the wagon brake systems. The distribution of the pressure force p on the i-th pad is defined as follows:

$$p_i=k_i\cdot K,$$

(1)

where $k_i$ is the weight coefficient of the pressure force distribution for i-th pad and K is the total pressure force on the pad, kN.

This equation takes into account that each pad receives a portion of the pressure force proportional to the weight coefficient k_i. To ensure physical correctness, the sum of all coefficients should be equal to one:

$${\displaystyle \sum _{i=1}^n{k}_i}=1.$$

(2)

where n is the number of brake pads involved in optimizing the distribution of the pressing force.

The wear rate $J_i$ is determined by the nonlinear dependence on the pressure force p_i:

$$J_i=\gamma \cdot {\phi }_k\cdot p_i^{\alpha },$$

(3)

where γ is a coefficient including the physical and mechanical properties of the pad material; φ_k is the friction coefficient; and α is the exponent characterizing the wear sensitivity to the pressure force of the pad, α > 1.

This formula can be used to model the actual dependence of wear on the pressure force and properties of the material of the pad.

The total wear of the brake pad is determined by integrating the wear rate:

$$H={\displaystyle \sum _{i=1}^n{H}_i}={\displaystyle \sum _{i=1}^n{\displaystyle \underset{0}{\overset{t}{\int }}{J}_{i}dt}},$$

(4)

where t is the operating time.

Substituting (3) into (4), the following can be obtained:

$$H={\displaystyle \sum _{i=1}^n\gamma {\phi }_k}{\displaystyle \underset{0}{\overset{t}{\int }}{\left(k_{i}K\right)}^{\alpha }dt}.$$

(5)

With constant pressure, the integral is simplified to the following:

$$H=\gamma {\phi }_{k}t{\displaystyle \sum _{i=1}^n{\left(k_{i}K\right)}^{\alpha }}.$$

(6)

This formula is the basis for estimating the total pad wear according to the known parameters of the pressure force and weight factors.

Optimization of pressure distribution.

Minimization of uneven wear is based on the deviation function, as follows:

$$f={\displaystyle \sum _{i=1}^n\left|H_i-\frac{H}{n}\right|},$$

(7)

where H_i is the wear of i-th pad and H/n is the average wear of pads.

This function can be used to evaluate the uneven wear of the pads and is the basis for optimization.

Lagrange function.

The Lagrange method was proposed in this research to find the optimal distribution of the pressure force between the brake pads of a freight wagon. This is due to the fact that the task is reduced to minimizing the unevenness of pad wear under the condition of fulfilling a physically justified restriction—the sum of the weight coefficients $k_i$, which determines the proportion of the pressure force, must be equal to one. The given weight coefficient can have a different meaning for each pad, taking into account the nonlinear nature of the dependence of wear on the pressure force, as well as the need to ensure a balanced load on all pads in real operating conditions.

To determine the optimal weight factors $k_i$, the Lagrange function is used as follows:

$$L\left(k_1,\dots ,k_n,\lambda \right)={\displaystyle \sum _{i=1}^n\left|H_i-\frac{H}{n}\right|}+\lambda \left({\displaystyle \sum _{i=1}^n{k}_i-1}\right).$$

(8)

Extremum conditions.

The extreme condition given in the Formula (9) allows us to determine such values of $k_i$ at which the wear deviation function reaches its minimum under the condition of normalizing the distribution of the pressure force. Setting this extreme ensures a uniform distribution of the braking force and an approximation of the individual wear of the pads to the average value, which, in turn, increases the efficiency and resource stability of the brake system.

Equations for optimal $k_i$ are as follows:

$${\displaystyle \frac{\partial L}{\partial k_i}}=\alpha \gamma {\phi }_k{K}^{\alpha }{k_i}^{\alpha -1}-\lambda =0,$$

(9)

$${\displaystyle \frac{\partial L}{\partial \lambda }}={\displaystyle \sum _{i=1}^n{k}_i-1}=0.$$

(10)

An uneven distribution of the pressure force can lead to the situation in which some pads will be more worn, and some pads will not fully utilize their resource. To solve this problem, weight coefficients are applied, which allow optimizing the pressure balance between all the pads of the wagon.

The weight coefficients take into account the design features of the brake lever transmission, operating conditions, and mechanical properties of the material of the pads. They can adapt the pressure force distribution model to actual conditions, which reduces the uneven wear.

Optimized weight coefficients can increase the accuracy of pressure force calculations for each pad, which is achieved by minimizing the difference between the actual and theoretically uniform force distribution. Therefore, the wear of each pad approaches the average value, which significantly increases the efficiency of all brake pads in the wagon.

One of the key advantages of using weight coefficients is the ability to model the uneven distribution of the pressure force in the system. For example, for the pads in a wagon bogie, the weight coefficients may have the following values:

$$k_1>k_2>k_3>k_4,$$

(11)

which corresponds to a greater pressure on the first pad compared to the others. This may be necessary in case of special operating conditions or asymmetry of the bogie brake lever transmission design.

The use of weight coefficient makes it possible to ensure a uniform or purposefully uneven distribution of the pressure force from the pads, which can achieve the following:

• Reduce uneven wear of brake pads;
• Increase the durability of pads due to more rational use of their resources;
• Ensure the stability of braking under different operating conditions of the rail vehicles.

Optimization of weight coefficients is carried out empirically on the basis of experimental data or using numerical methods. The use of models with weight coefficient makes it possible to integrate the influence of structural, mechanical and operational factors into a single system, which ensures the reliability and safety of the wagons as part of the train.

Weight coefficients are an important tool for simulating brake pad wear, as they improve prediction accuracy, adapt models to variable operating conditions and optimize resource utilization.

Optimal weight coefficients are defined as follows:

$$k_i={\left({\displaystyle \frac{\lambda }{\alpha \gamma {\phi }_k{K}^{\alpha }}}\right)}^{{\displaystyle \frac{1}{\alpha -1}}}.$$

(12)

The Lagrange function is an optimal distribution that ensures the same effective wear $k_i$·$J_i$ = const for all pads:

$$\lambda ={\displaystyle \frac{\alpha \gamma {\phi }_k{K}^{\alpha }}{n^{\alpha -1}}}.$$

(13)

Equation (13) is an analytical expression for finding the optimal weight coefficients $k_i$ obtained from the Lagrange function.

The following method can be used to determine the weight coefficients for each pad that ensure minimal uneven wear.

After determining the optimal weight coefficients $k_i$, they can be used to further calculate the wear rate $J_i$ and the total wear H. The results of these calculations can be used to assess the efficiency of optimization and reduce the cost of maintenance and repair of the brake systems of wagon bogies.

Optimal indicators, which are formed not only by the method of minimizing weight but also by the improvement of such individual characteristics of the systems are as follows:

• Structural asymmetry of important transmissions (β_i);
• Absorption of bearings and mechanical clearances;
• Proximity to the actual poor connection;
• Material and a geometry of the pad (through the coefficient δ_i).

Table 1. Comparison of a uniform and optimal distribution of the pressure force and wear of the brake pad.

No, of a Brake Pad	Pressure Force (Uniform)	Pressure Force (Optimal)	Wear at the Uniform Distribution Mode [mm]	Wear at the Optimal Distribution Mode [mm]
1	17.5	21.0	28,0	22.0
2	17.5	18.9	25.2	20.5
3	17.5	16.1	22.4	18.8
4	17.5	14.0	19.6	16.4

indicates the uniform distribution, which was checked for some galvanic pads depending on the operating mode in the uniform distribution mode and repeated measurement in accordance with the uniform and optimized options. As can be seen, it reaches critical values with a uniform and constant selection of pads, while they decrease by 3 to 6 mm and are aligned on all pads with optimization. This indicates the effectiveness of the approach to the adaptive use of resources using the method of reducing mass imbalance and increasing the resources of global elements of important supplies.

Table 2. Comparison of uneven brake pad wear before and after optimization.

Loading Mode	Maximal Wear Before Optimization [mm]	Maximal Wear After Optimization [mm]	Uneven Wear [%]
Empty	28	22	8
Medium	38.04	29	10

shows a comparative analysis of uneven brake pad wear before and after brake linkage optimization.

It can be concluded, by analyzing the obtained results, that the method of optimizing the distribution of the pressure force using weight coefficients and the Lagrangian function provides a reduction in the uneven wear of brake pads of 8 to 10% compared to the uniform pressure force.

The adequacy of the created model was checked using the F-criterion. In this case, the brake pad wear from the wagon’s run was used as a variational parameter (

Table 3. Comparison of experimental and simulated values of brake pad wear at different wagon mileages.

Wagon Mileage [thousand km]	Experimental Pad Wear [mm]	Simulated Pad Wear [mm]
7.2	1.10	2.32
14.4	5.33	6.21
26.4	12.00	12.69
36.0	18.00	17.85
42.3	22.00	21.24
48.0	25.00	24.30
54.6	28.00	27.84
62.4	32.00	32.01
68.3	35.00	35.17
74.4	38.04	38.42

).

The results of the calculations showed that the calculated value of the F-criterion is F_exp = 744.68. The tabulated critical value of the criterion is F_cr = 4.07.

Since F_exp > F_cr (744.68 > 4.07), the null hypothesis of the model’s inadequacy is rejected. This means that the mathematical model is statistically significant and adequate.

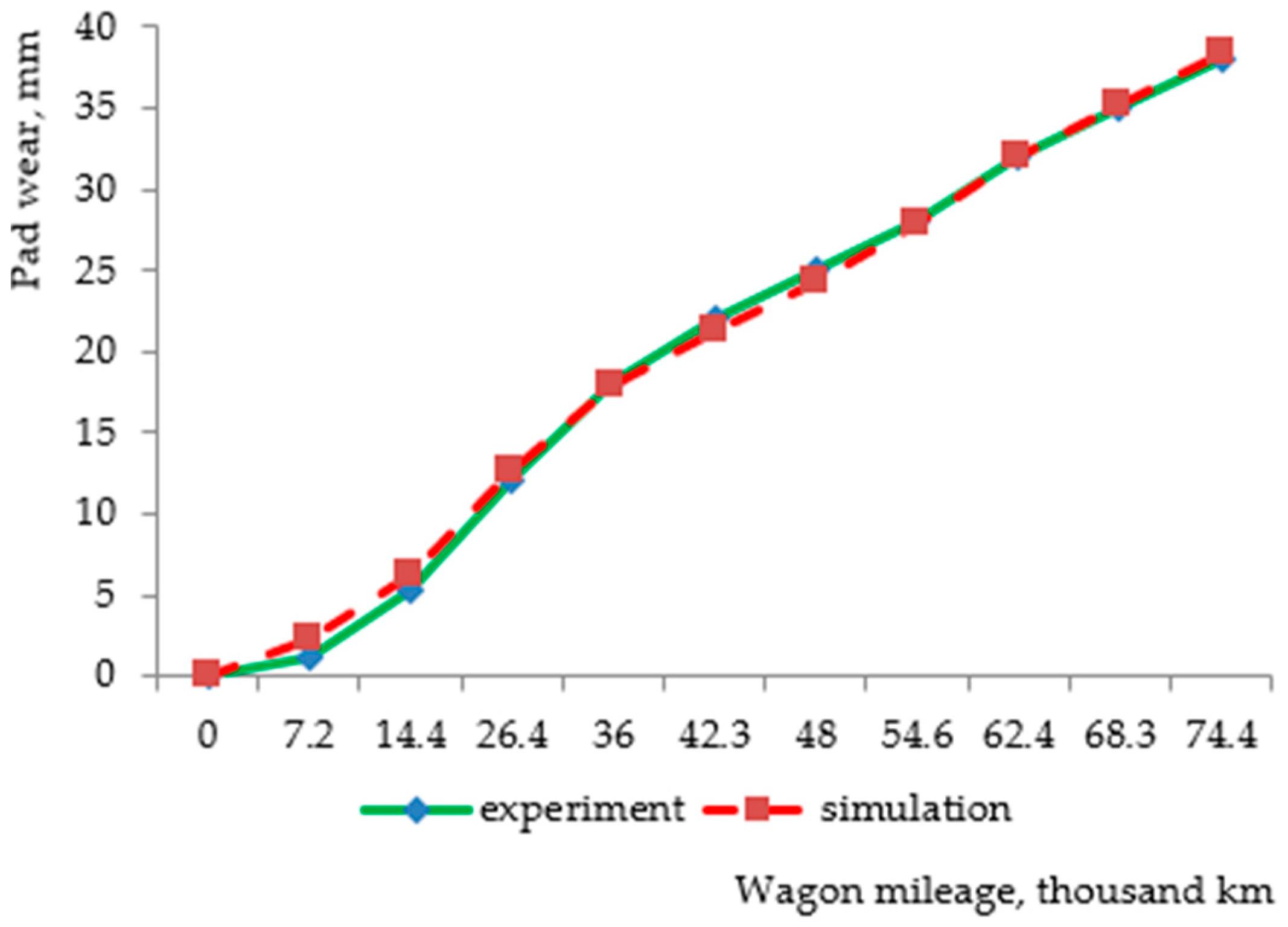
Figure 2 shows a graphical dependence of the pad wear on the mileage, which demonstrates the high correspondence of the model with the experimental data, in particular during the average and largest mileage of wagons.

The created model can be used for further calculations, optimization of technical condition parameters, and prediction of brake pad wear during the operation of rail vehicles.

The average relative error was determined to assess the accuracy of the constructed model:

$$\delta ={\displaystyle \frac{MAE}{{\overline{y}}_{exp}}}\cdot 100\%\approx {\displaystyle \frac{0.55}{20.4}}\cdot 100\%=2.7\%.$$

(14)

where MAE is the mean absolute error.

Thus, the average relative error is less than 3%, which is quite acceptable for technical tasks of predicting brake pad wear.

3. Results and Discussion

Field experiments were carried out to investigate the uneven wear of brake pads. The wagons that worked in different operating conditions (loaded and empty runs, technical condition and track profile, weather conditions, etc.) were observed.

Private fleet wagons (open wagons, box wagons and hopper wagons for the transportation of cement) were experimentally studied. They were separated from the state-owned fleet wagons and belonged to “Ivano-Frankivskcement”, a private joint-stock company (IFCEM). Unlike the wagons of Ukrainian Railways (Ukrzaliznytsia), the IFCEM wagons operated only along at a fixed 1173 km long route from the Yamnytsia station (the Lvivska Zaliznytsia regional branch) to the Osnova station (the Pivdenna Zaliznytsia regional branch), as was stipulated by the contracts for the supply of cement.

Production studies of a relatively small number of the IFCEM wagons were carried out in accordance with the developed “Program and techniques of production inspections of brake systems and wagon wheels”. The route under observation was not changed over the period of inspection, thus, the wagons worked in the same operating conditions. It should also be noted that in one direction, the wagons ran loaded, and in the other direction, they ran empty along the same tracks, thus the coefficient of empty mileage was 50%.

Experimental studies were carried out during the inspection of the brake systems of wagons at subdivisions of the wagon industry and at sorting stations. 2TE116 locomotives were used for the braking of the wagons under observation and they were changed within the guaranteed sections. The wagons under observation also included two box wagons with the air distributors No. 483 set to the empty mode. In accordance with the regulatory and technical documents, the load on the composite brake pad in the empty mode is 17.5 kN, and the its average value is 34.34 kN.

All inspections and measurements of the brake lever transmission elements of the wagons were carried out with tools, measuring instruments, and technological equipment, as stipulated by the appropriate regulatory and technical documents.

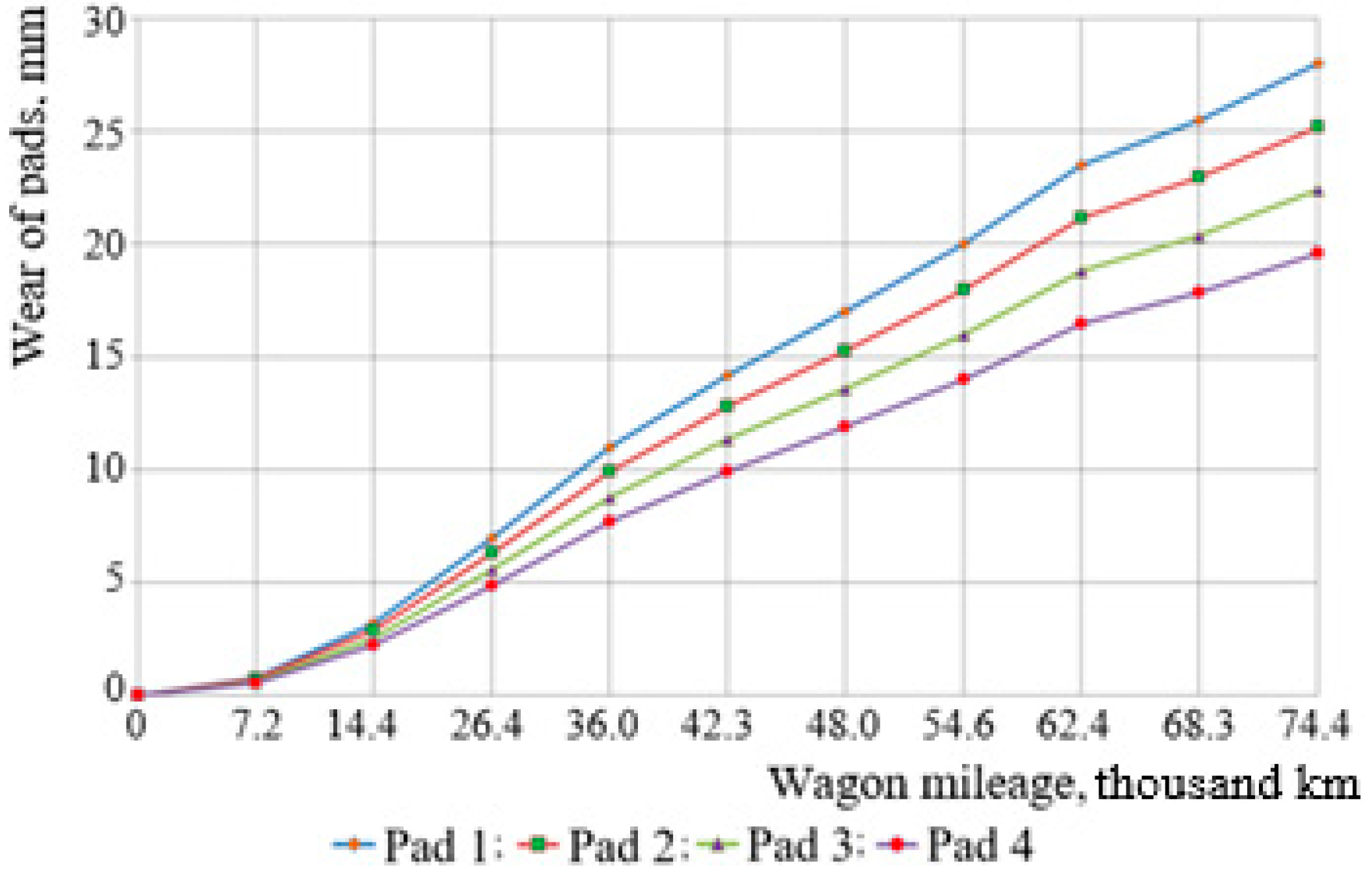
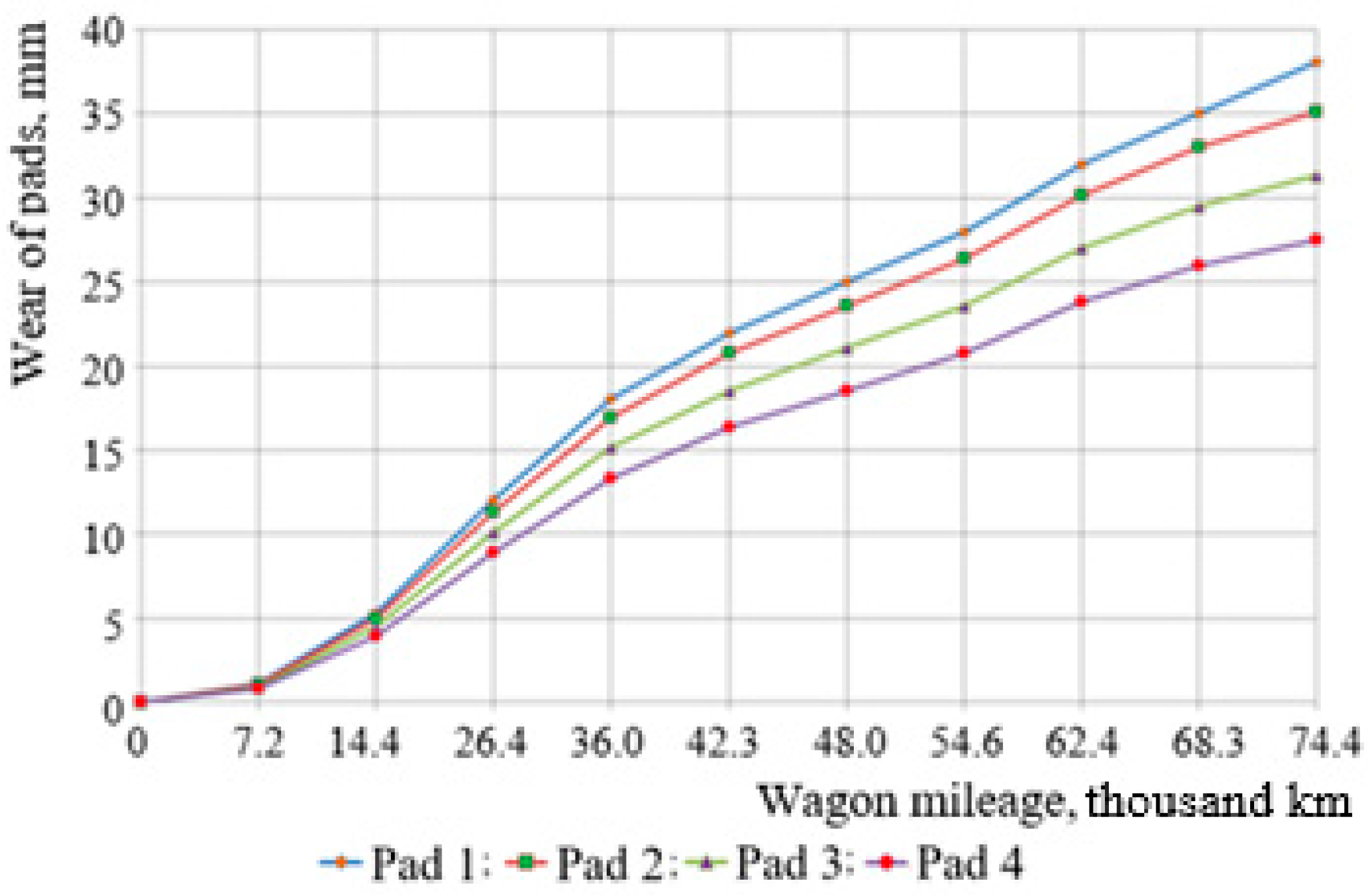
The obtained statistical data on thicknesses of composite brake pads at the control points of wagon bogies were processed. Based on the obtained data, graphical dependencies for the average wear value of the pads of wagon bogies were built (Figure 3 and Figure 4).

The results of calculations for loads of 35 kN and 17.5 kN showed a significant dependence of the wear of the pad on the pressure force value and the force distribution between the pads. Optimization of the weight coefficient k_i made it possible to consider the uneven distribution of the pressure force caused by the imperfection of the lever transmission design. For the load of 35 kN, the weight coefficients were as follows: $k_1$ = 0.28 (Pad 1), $k_2$ = 0.26 (Pad 2), $k_3$ = 0.24 (Pad 3), $k_4$ = 0.22 (Pad 4) (Figure 5).

For a load of 17.5 kN, the corresponding weight coefficients were as follows: k₁ = 0.3, k₂ = 0.27, k₃ = 0.23, k₄ = 0.2. The maximum wear of some pads was 38.04 mm for a pressure force of 35 kN and did not exceed 28 mm for 17.5 kN during a run of 74,400 km. The built dependencies demonstrate that the lower pressure force proportionally reduces the wear rate, which provides a longer service life of the pads, provided that the weight coefficients are correctly optimized.

Dependencies of the wear of the pads on the mileage, built on the basis of these weight coefficients, demonstrate a gradual increase in wear for each pad in accordance with its position in the bogie. This confirms that the correct distribution of forces can equalize the uneven wear, minimize material losses and increase the stability of the wagon brake system. In particular, for a greater load of 35 kN, a more noticeable increase in wear is observed; it indicates the need to take these parameters into account for optimization. The proposed approach of using weighting coefficients can not only accurately simulate dependencies, but also adapt the system for different operating modes.

Based on the analysis performed, it can be noted that uneven wear of the pads does not depend on the operating mode of the air distributor. This indicates that each pad is worn abnormally due to the uneven distribution of forces in the brake system of the wagon due to many factors. Among them are design defects of the lever transmission, wear of rollers and holes of kinetostatic units, improperly adjusted lever transmission, pads of different thicknesses, or pads previously used for other wagons. In addition, it should be noted that pads wear out faster in loaded wagons than in empty ones due to a number of factors, the major factor being increased pressure to the wheels.

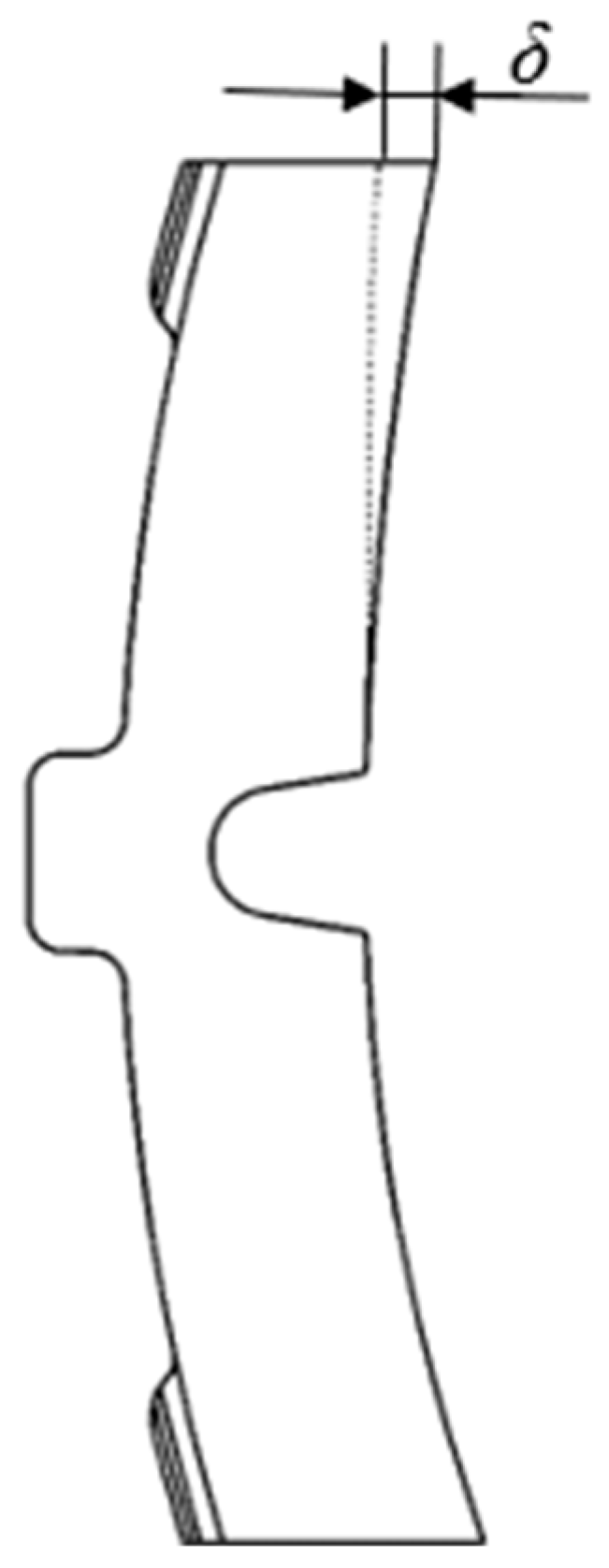
The weight coefficients obtained during the studies were taken into account when calculating the strength of the pad with uneven wear and load using a spatial model of the pad. The wear of the pad was determined on the basis of field studies (

Table 4. Wear value of pads.

Pad Number	Wear Value δ, mm
1	18
2	17
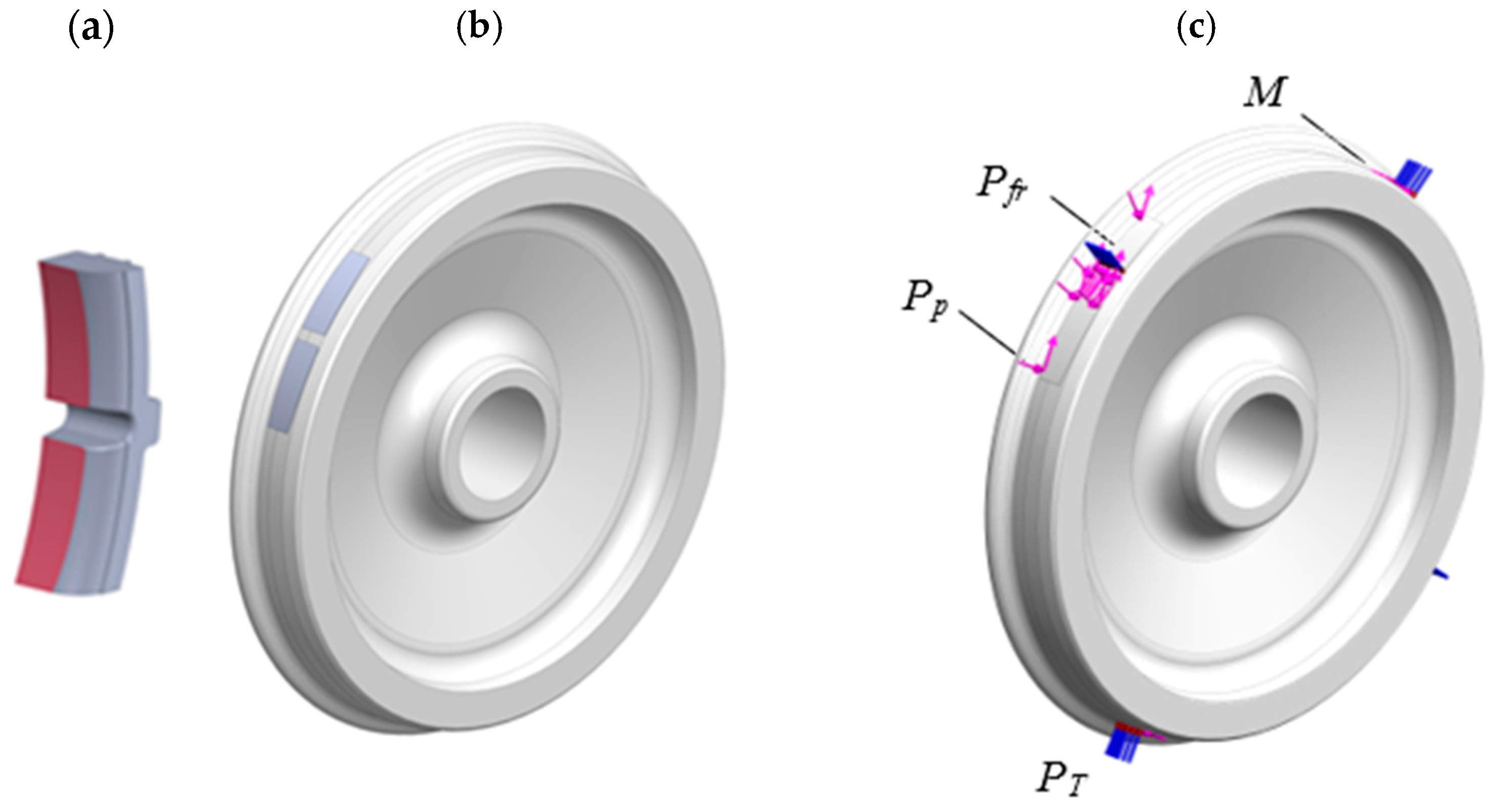
3	15
4	14

). The wear value was determined at the top of the pad (Figure 6). The study was conducted on the example of a box wagon, as one of the most common types in operation, which can transport goods that need protection from atmospheric precipitation.

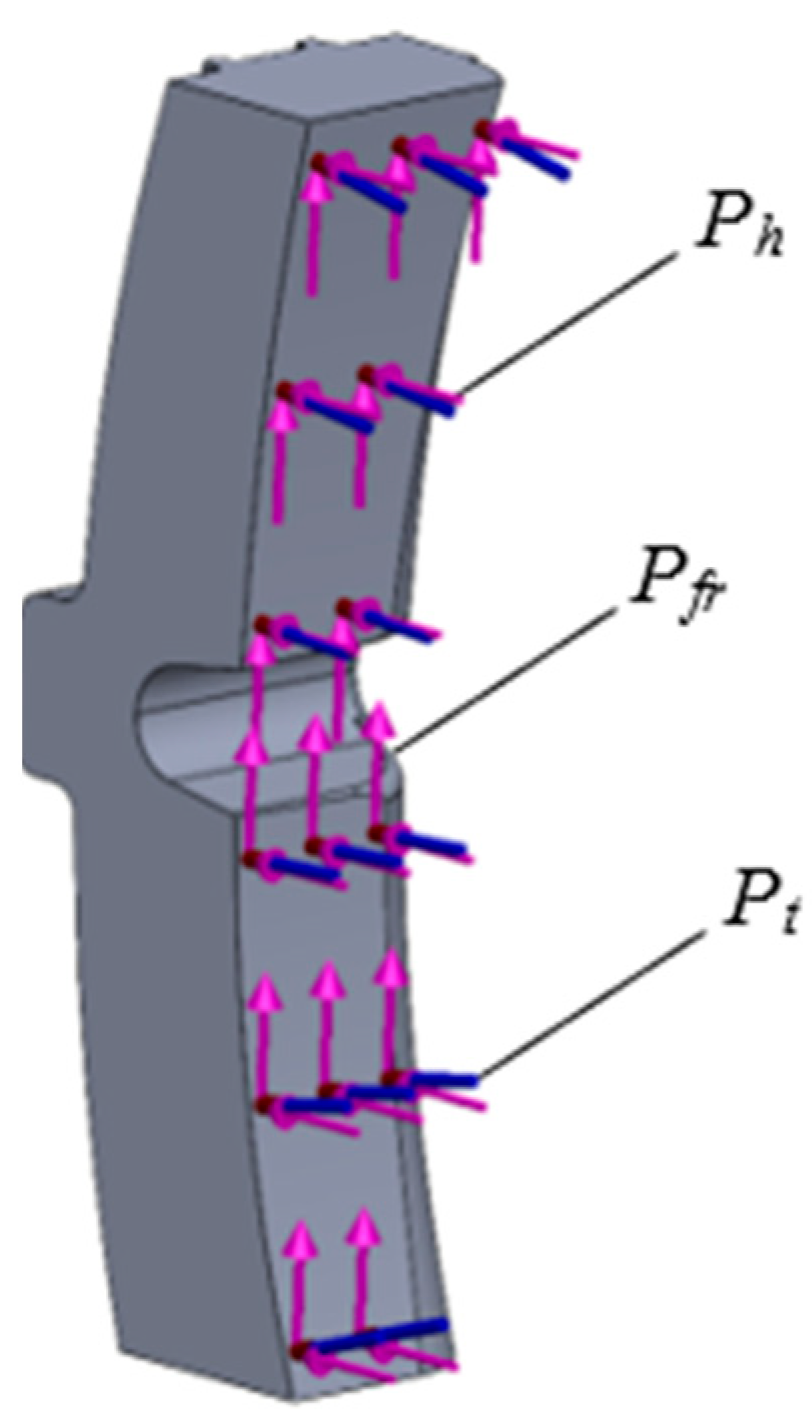
The calculation was carried out in SolidWorks Simulation (version 2024) using the finite element method [19,20,21,22]. When building the model, isoparametric tetrahedra were used [23,24,25,26]. The number of elements of the finite element model was determined using the graphical analytical method [27,28,29,30]. Their number was 21,177 with a maximum size of 15 mm and a minimum size of 3 mm. The model had 4750 nodes. The design diagram of the pad included the following loads: horizontal (pressure force from the pad to the wheel) P_h, vertical (friction force) P_fr and temperature P_t (Figure 7).

The pad was fixed by its back part, where it contacted with the shoe. The strength calculation was carried out using the Mohr–Coulomb criterion [31,32,33]. The material of the pad was composite. The main characteristics of the material are provided in

Table 5. Main characteristics of the material.

Name of Parameter	Value
Modulus of elasticity, Pa	5000
Poisson’s ratio	0.37
Mass density of the material, kg/m3	2200
Strength limit, MPa	15
Thermal expansion coefficient, deg−1	4.1 × 10−6
Thermal conductivity, W/m·deg	200

.

The input parameters used to calculate each pad are shown in

Table 6. Input parameters for calculation.

Pad Number	Pressure Force to the Wheel, kN	Friction Force, kN	Temperature °C
1	39.2	13.3	400
2	36.4	12.4
3	33.6	11.4
4	30.8	10.5

.

The calculation results are shown in

Table 7. Results of strength calculation of pads.

Pad Number	The 1st Principal Stress, MPa	The 2nd Principal Stress, MPa	The 3rd Principal Stress, MPa
1	12.5	9.2	16.5
2	8.1	9.0	16.3
3	5.8	6.4	11.8
4	5.9	6.5	11.8

.

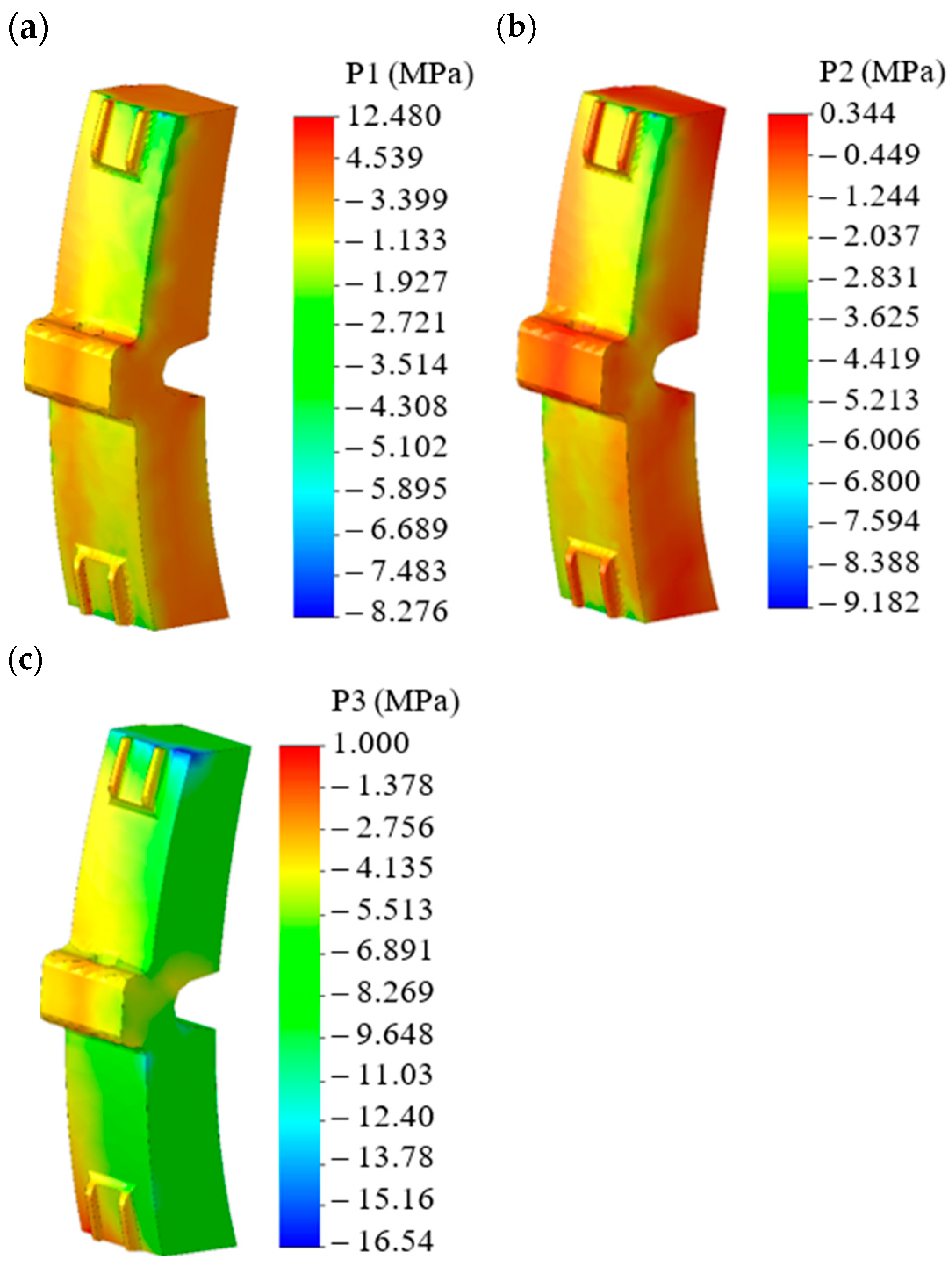
Table 4 shows that for pads 1 and 2, the 3rd principal stress exceeds the permissible value (15 MPa). The results obtained are illustrated in Figure 8, which shows the stressed state of pad 1. The maximum stresses were recorded in the upper part of the pad; the stresses in the pad were higher than permissible. Thus, the pad was susceptible to damage, thermal defects, cracks, etc.; consequently, the wheel can also be damaged.

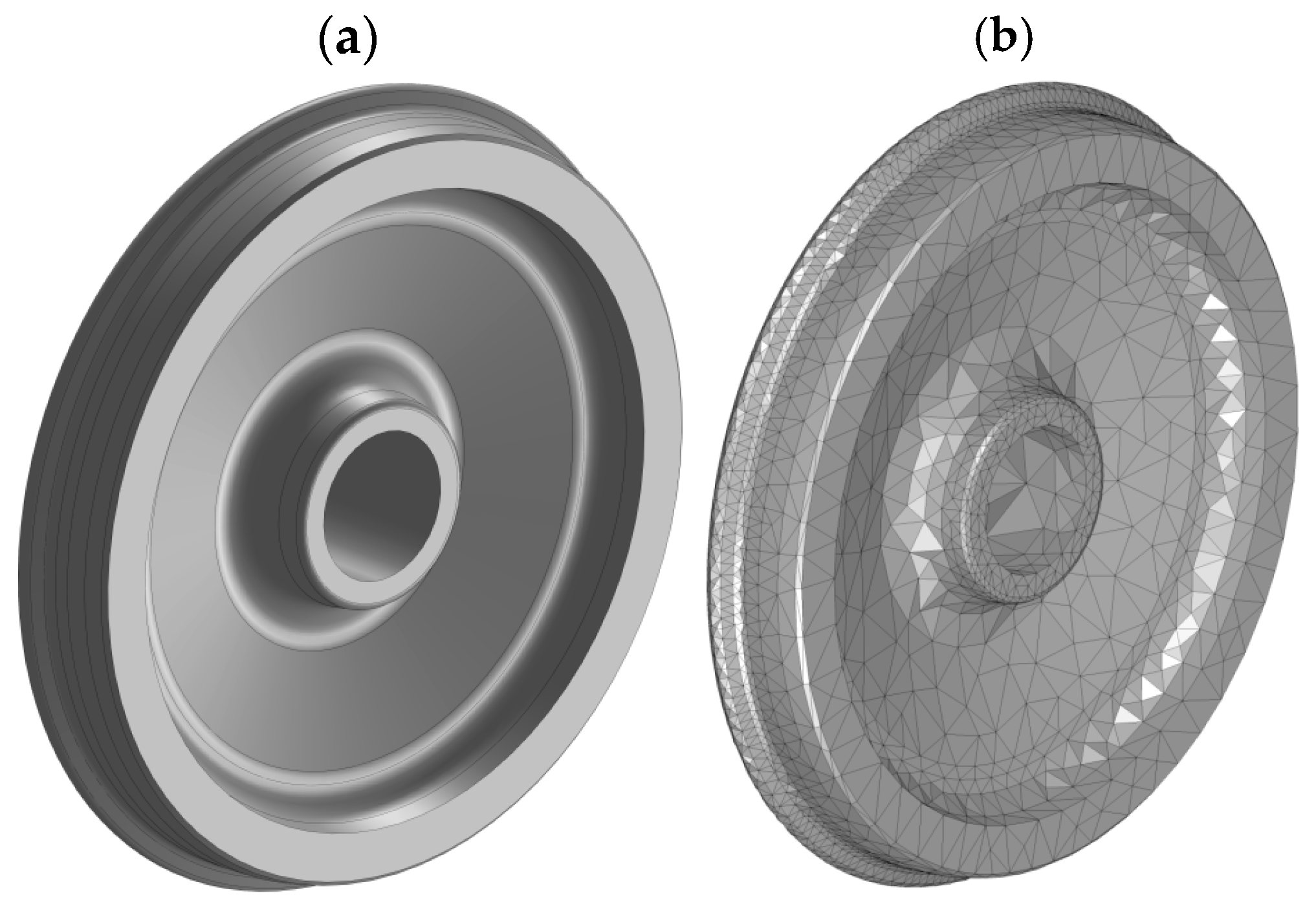
The load to the wheel from the composite pad was determined using the stressed state of the wheel. A spatial model of the wagon wheel was built (Figure 9a). Graphic works were carried out in SolidWorks.

The calculation was carried out by means of the finite element method in SolidWorks Simulation with the Mises criterion [34,35,36]. This criterion was chosen due to the fact that steel is an isotropic material, and the use of this criterion is inherent in the calculation of such materials. The finite-element model of the wheel was formed by spatial isoparametric tetrahedra with four Jacobian points (Figure 9b).

The optimal number of FEM elements was determined by the graphic analytical method [37,38,39]. The FEM of the wheel had 6342 nodes and 25,889 elements. The maximum element size was 75 mm and the minimum was 15 mm. The ratio of element size increase was 1.8. The number of elements in the circle was 1.6.

The material of the wheel was axle wagon steel with linear isotropic properties [40,41,42]. The main physical and mechanical properties of the solid-rolled wheel material are summarized in

Table 8. Basic physical and mechanical properties of the wheel material.

Parameter	Value
Modulus of elasticity, MPa	2.1 × 105
Poisson’s ratio	0.3
Mass density of the material, kg/m3	7850
Strength limit, MPa	900–1100
Yield strength, MPa	800
Thermal expansion coefficient, deg−1	11.9 × 10−6
Thermal conductivity, W/m·deg	43

[43].

When compiling the design model of the wheel, it was taken into account that it was loaded with the force from the composite brake pad, which corresponded to the average operating mode of the air distributor No. 483-000 and amounted to 35 kN. To simulate this load application to the wheel, linings were installed on it, the geometry of which was identical to the geometry of the working surface of a pad (Figure 10).

The design diagram of the wheel takes into account the following force factors: force from the pad P_p, friction force P_fr, torque M and temperature effect P_T (Figure 10c). The value of the temperature effect is taken as equal to 400 °C. The model does not include the force of adhesion of the wheel to the rail [44,45,46].

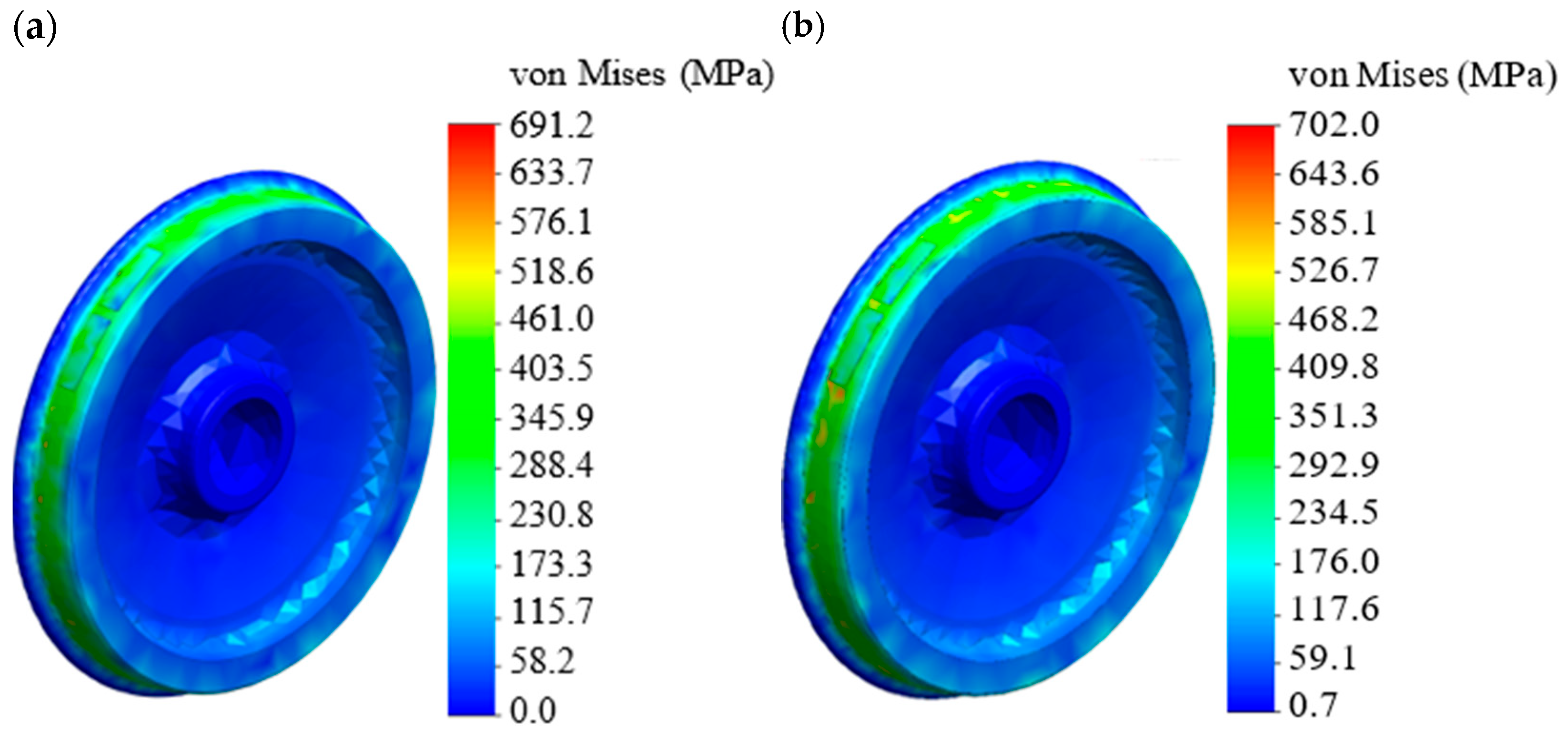
The model was fixed at the wheel hub assembly through a hard pinch [47,48,49,50]. The results are shown in Figure 11. The maximum stresses were recorded on the rolling surface of the wheel and amounted to 702.0 MPa, which is lower than the permissible values by 12%. The permissible stresses were assumed to be equal to the yield strength of the material, i.e., 800 MPa. Therefore, the strength of the wheel was ensured. However, the resulting stresses were 1.5% higher than those that occur in the wheel when it interacts with the pad with nominal dimensions.

The conducted studies will contribute to the development of recommendations for managing the temperature effect on the wheel, improving the safety of train traffic and reducing operating costs.

The paper presents an analytical model based on the generalized data on the dependence of pad wear on the pressing force, which is approximated by a power function. The model has an analytical form that allows to optimize calculations. At the same time, indeed, the paper does not provide the direct experimental data on the measured pad wear coefficients before and after the optimization. This limitation is recognized, and in further studies, it is planned to verify the model by testing bench samples and full-scale cars with a pad temperature profile control system as a wear indicator.

Within the framework of this paper, the main attention is focused on the analytical determination of the optimal weight coefficients $k_i$, which minimize the unevenness of brake pad wear. At the same time, their technical application involves the implementation of routine adjustments of the brake lever transmission in bogies by adjusting the lengths of the rods, positions of the adjustment levers or using elastic compensators that provide the necessary distribution of the pressure force in accordance with the found coefficients. This issue requires a separate engineering study and will be the subject in the further work devoted to algorithms of technical adjustment of the brake lever transmission based on optimization.

The limitation of this study is that the authors did not investigate the case of double-sided pressure of the brake pads on the wheel since most wagons use exactly this load diagram.

The disadvantage of this work is that it deals only with the box wagon and for the tank wagon, for example, the results may differ. But these issues will be considered in future research.

The results of the research will contribute to the database of developments to be used for designing modern structures of tribotechnical pairs of rolling stock and increasing the efficiency of railway transport operations.

4. Conclusions

1. It is found that the use of weight coefficients for simulating the distribution of the pressure force on the pads is the key approach to reduce their uneven wear, and to increase the efficiency of the wagon brake system. The application of a method using the Lagrange function is proposed, which provides an accurate assessment of the distribution of pressure force on the pads. The formulated extreme condition allows us to determine such values of $k_i$ at which the wear deviation function reaches its minimum under the condition of normalizing the distribution of the pressure force. It is proved that the integrated approach allows for minimizing the uneven wear, which can significantly extend the service life of 2TP-11 brake pads. This will help to reduce operating costs and increase the reliability of the entire brake system.

2. Experimental studies have confirmed that the uneven wear of brake pads depends on both the operating mode of the air distributor (empty or loaded) and the distribution of the pressure force on the pads. For a mileage of 74,400 km, when the air distributor was in the empty mode, the wear of the pads was 19.6–28 mm, and in the loaded mode it was 27.53–38.04 mm. It is also found that the uniform distribution of the pressure force ensures the stability and long service life of pads.

The dependencies built have confirmed that the use of weight coefficients provides new opportunities for improving the reliability of brake systems and reducing the cost of servicing the wagon fleet. It is estimated that the uneven wear without optimization is 20–35%, while after the optimization it amounts to 8–10%. Thus, the use of weight coefficients in optimizing the distribution of pressure force on pads is both reasonable and necessary in terms of higher efficiency, cost saving, and rail traffic safety.

3. The stress state of an abnormally worn brake pad when interacting with the wheel has also been investigated. The results of the calculations have shown that the maximum stresses occur at the top of the pad and are equal to 16.5 MPa. The resulting stresses exceed the permissible ones by 9%. The stresses in the pad are higher than the permissible ones; the pad is susceptible to damage, thermal defects, cracks, etc.

The strength calculation for the wheel when it interacts with an abnormally worn pad shows that the resulting stresses are 1.5% higher than those that occur in the wheel when it interacts with a pad with nominal dimensions.

The results of the research will contribute to the database of developments to be used for designing modern structures of tribotechnical pairs of rolling stock and increasing the efficiency of railway transport operation.