Vibration Localization in Cyclic Mistuned Structure and Its Application to Low-Frequency Broadband Vibration Control of Pipelines
Abstract
1. Introduction
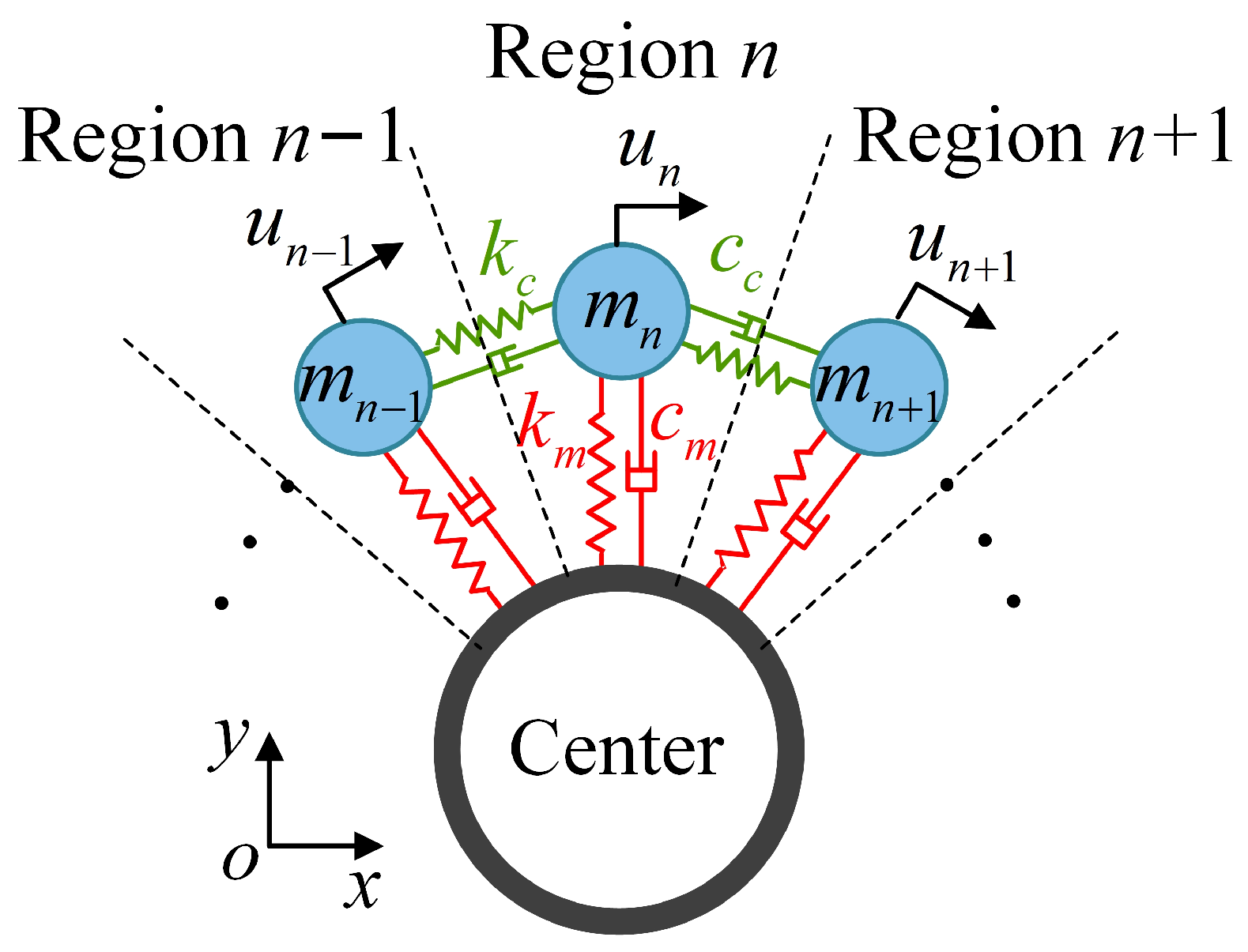
2. Perturbation Analysis of the CMS
3. Vibration Localization Characteristics and Their Influence Factors
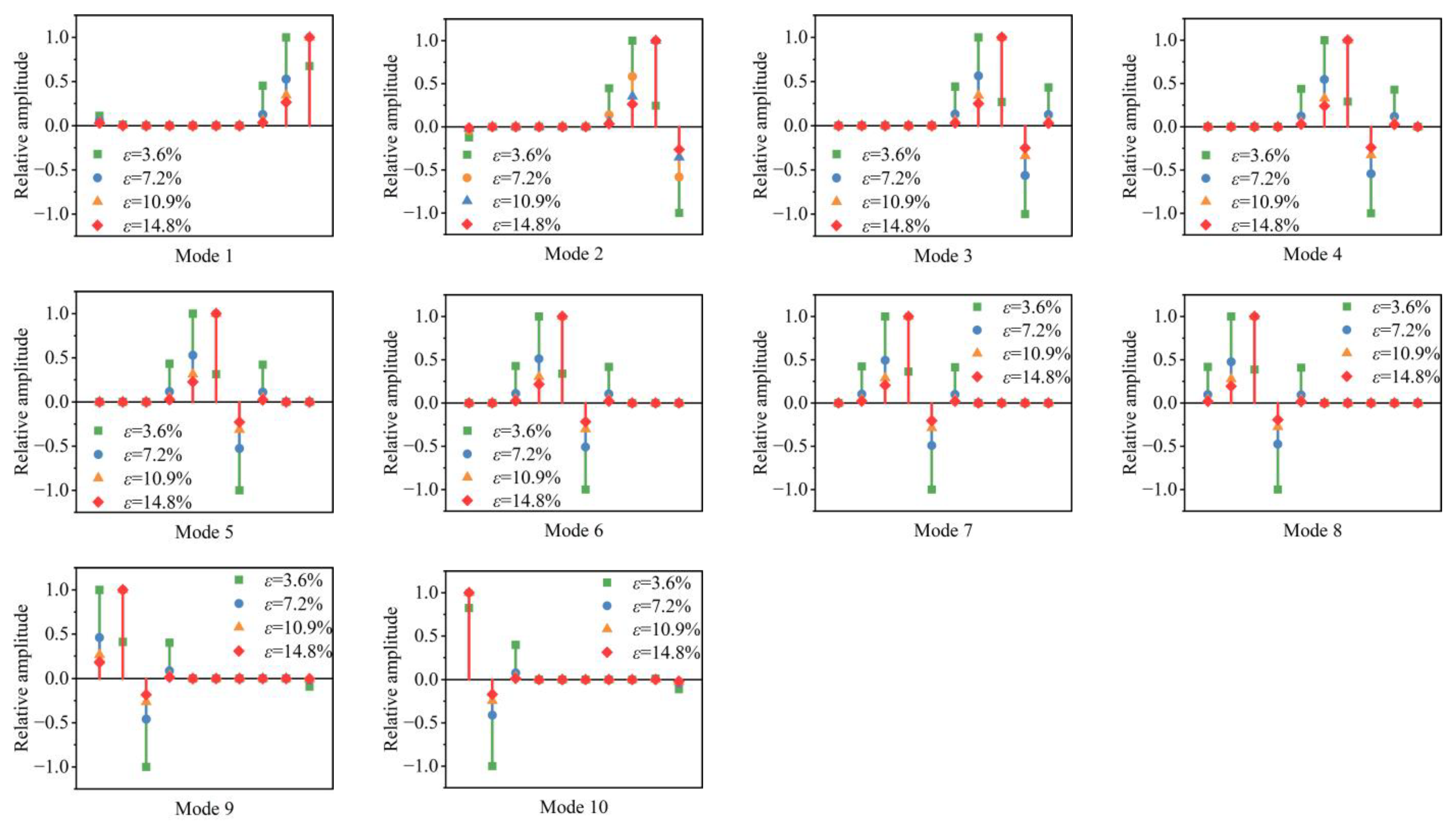
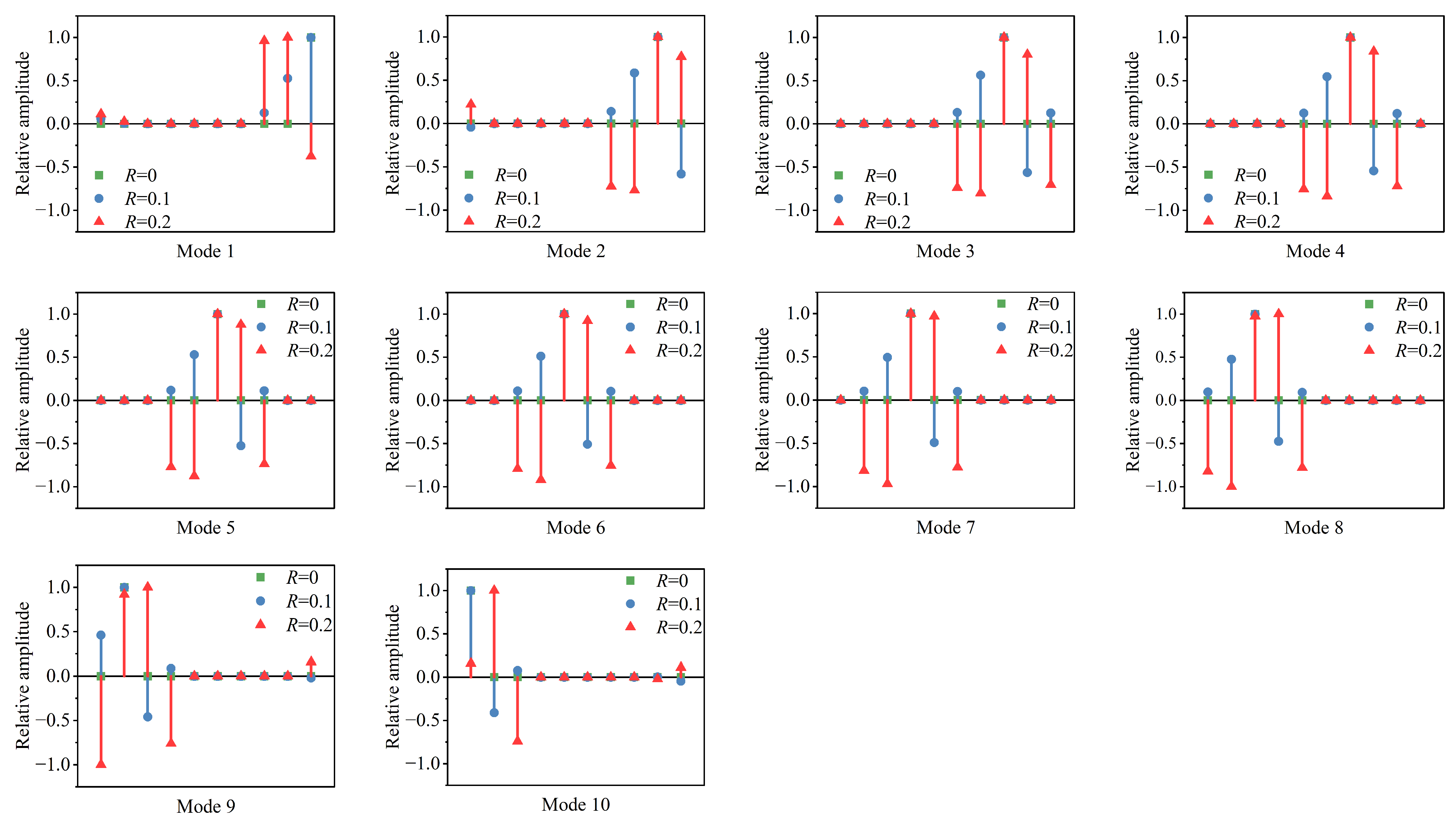
3.1. Mode Localization
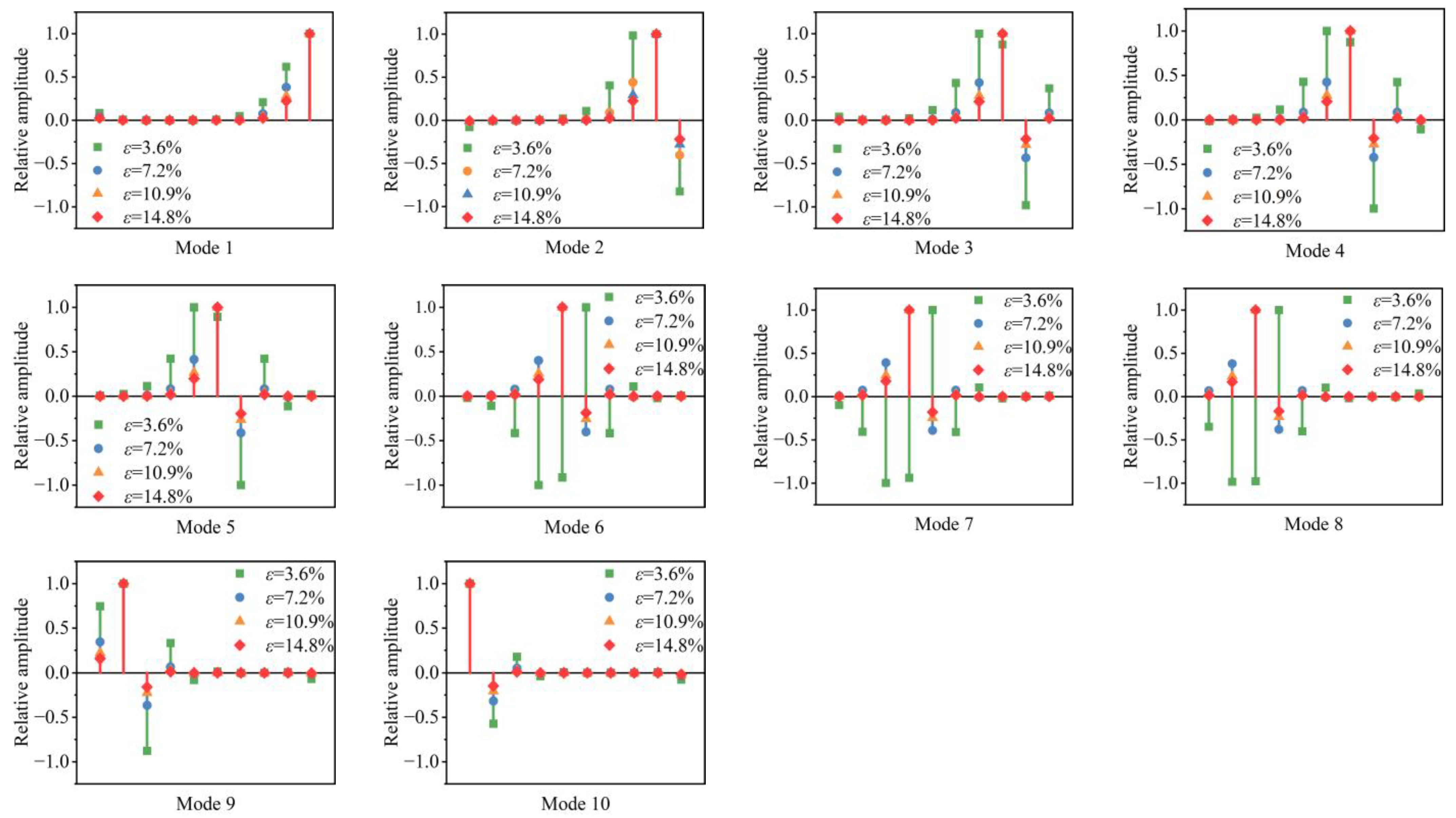
3.1.1. Mode Shapes Under Different Mistuning Strengths
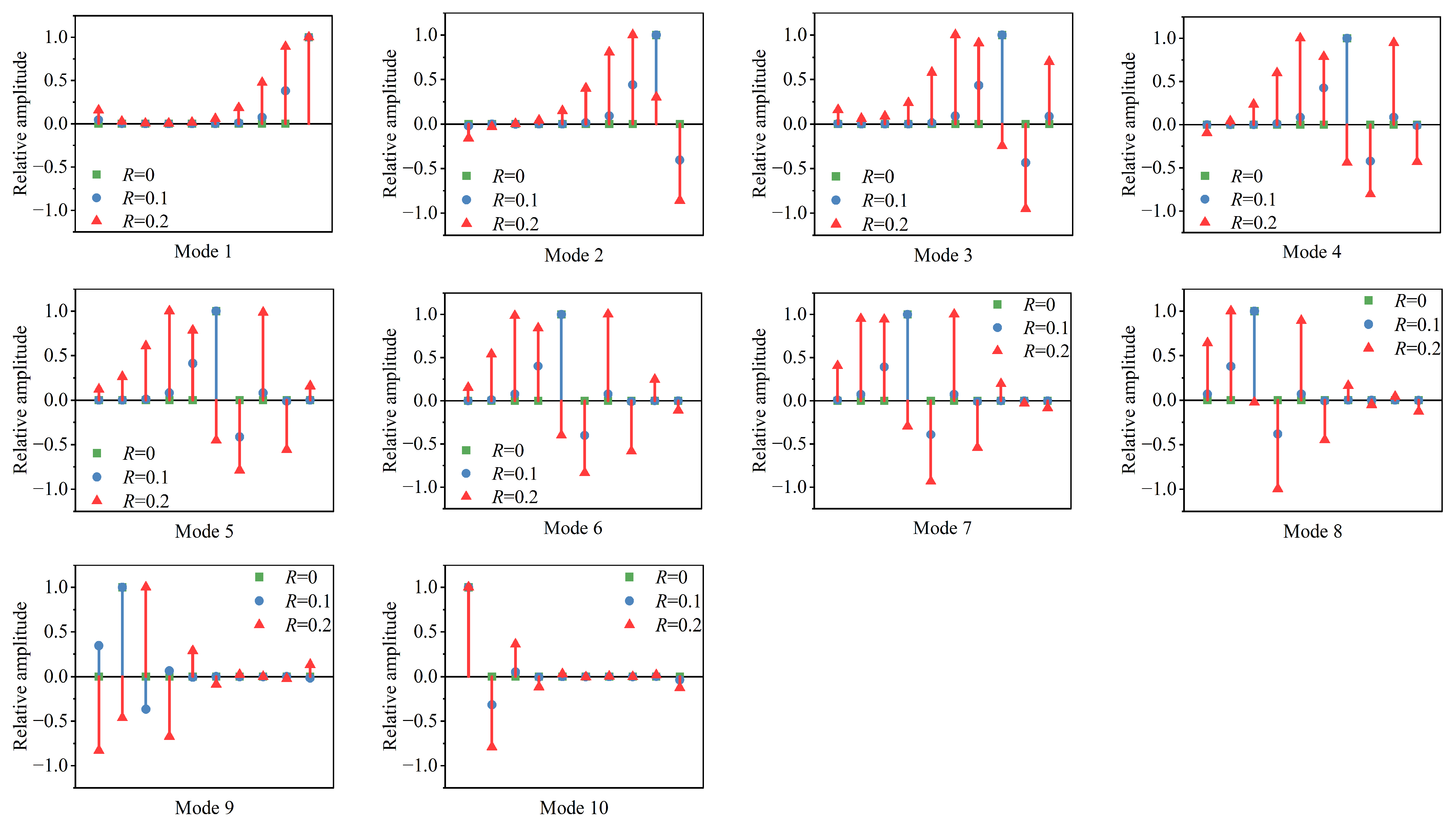
3.1.2. Modal Shapes Under Different Coupling Strengths
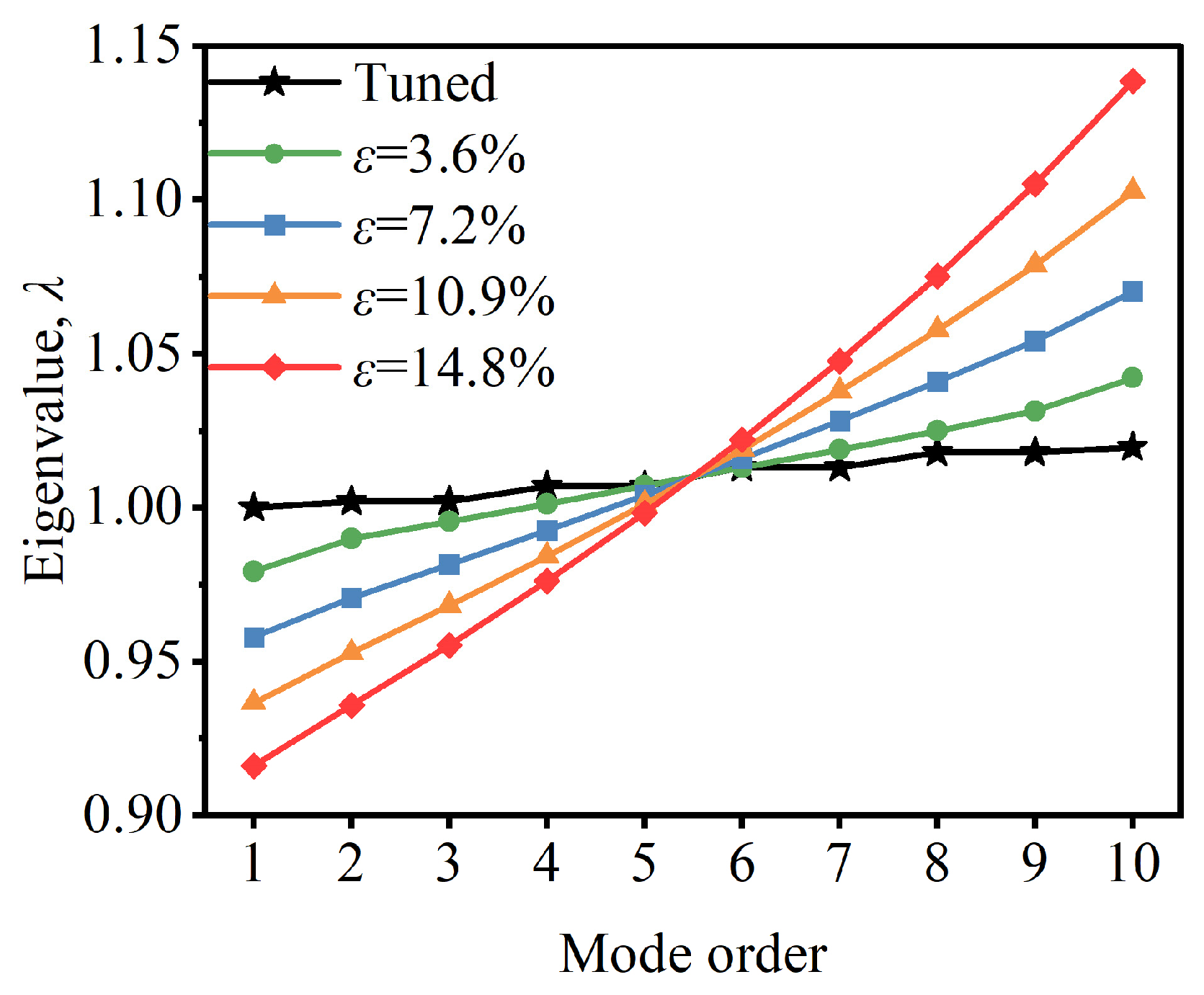
3.2. Eigenvalue Splitting
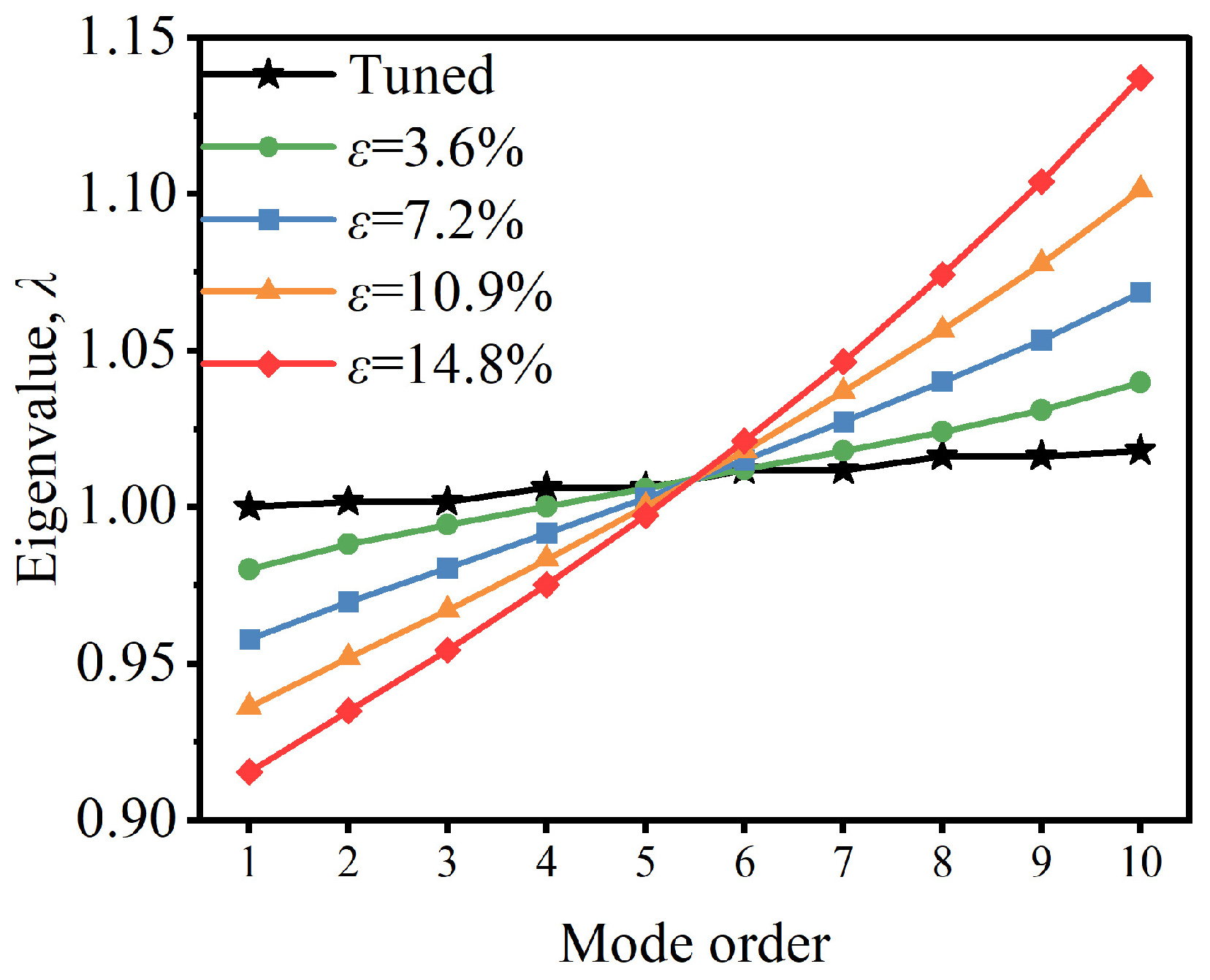
3.2.1. Eigenvalues Under Different Mistuning Strengths
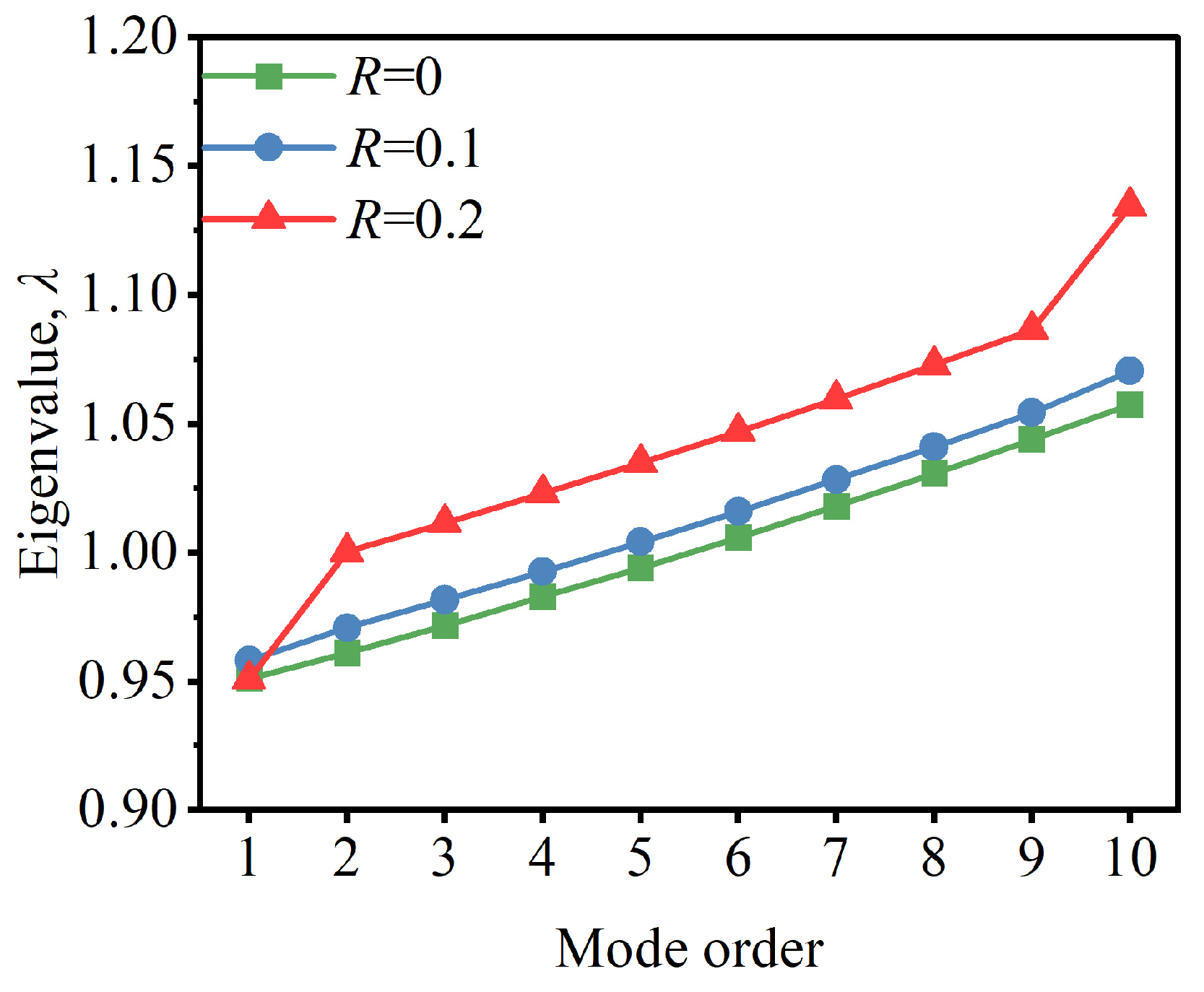
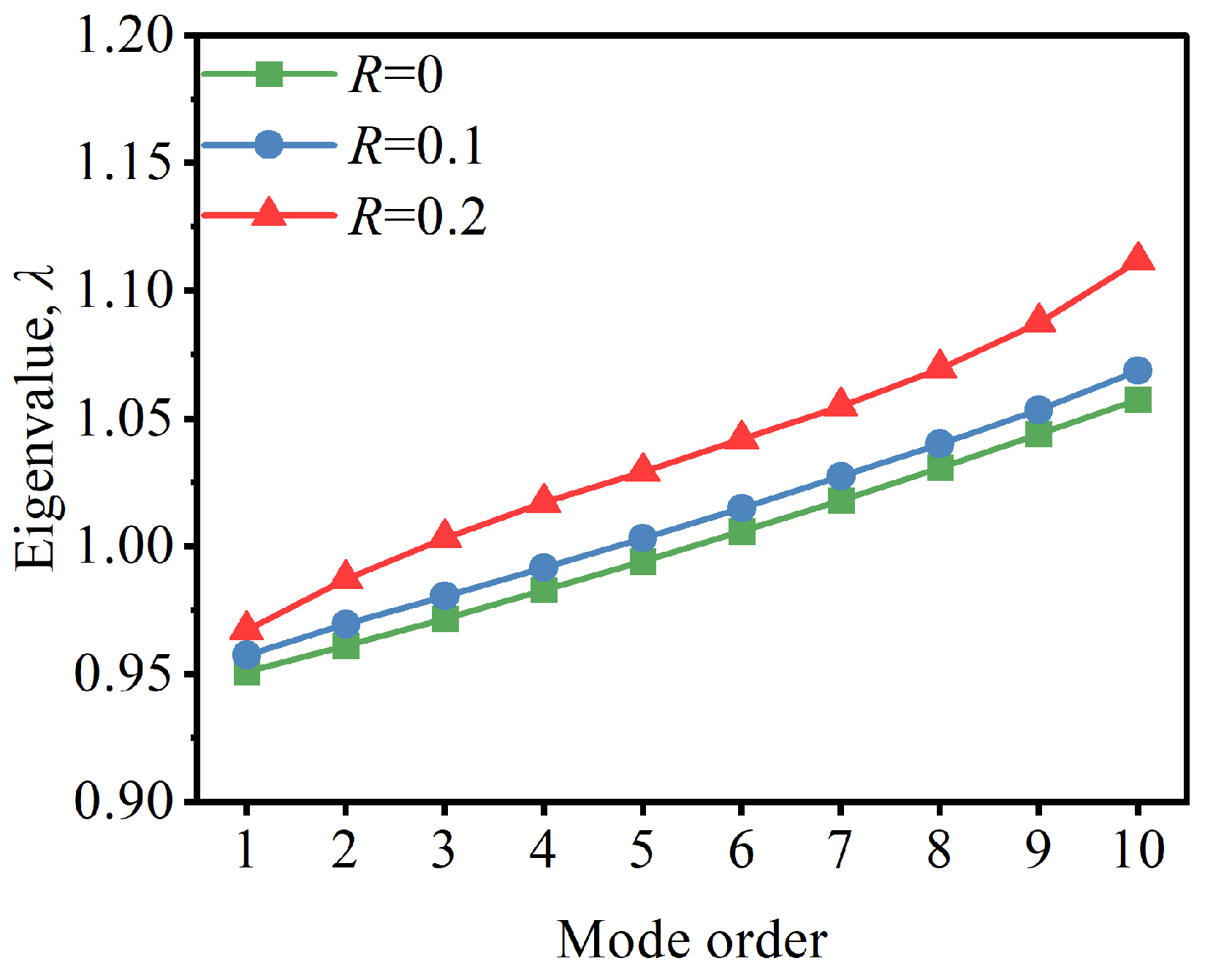
3.2.2. Eigenvalues Under Different Coupling Strengths
4. Numerical Analysis of Vibration Localization Characteristics
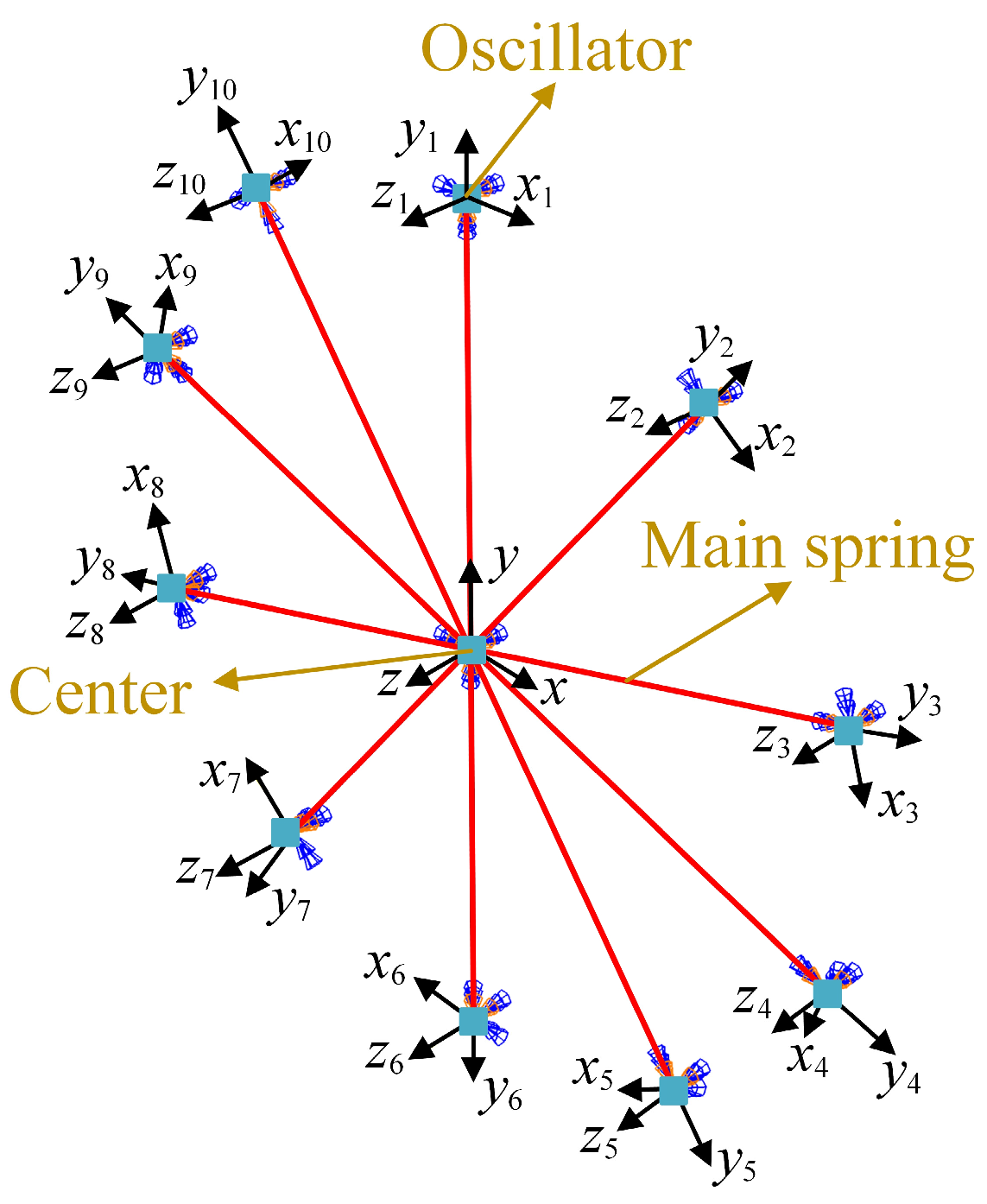
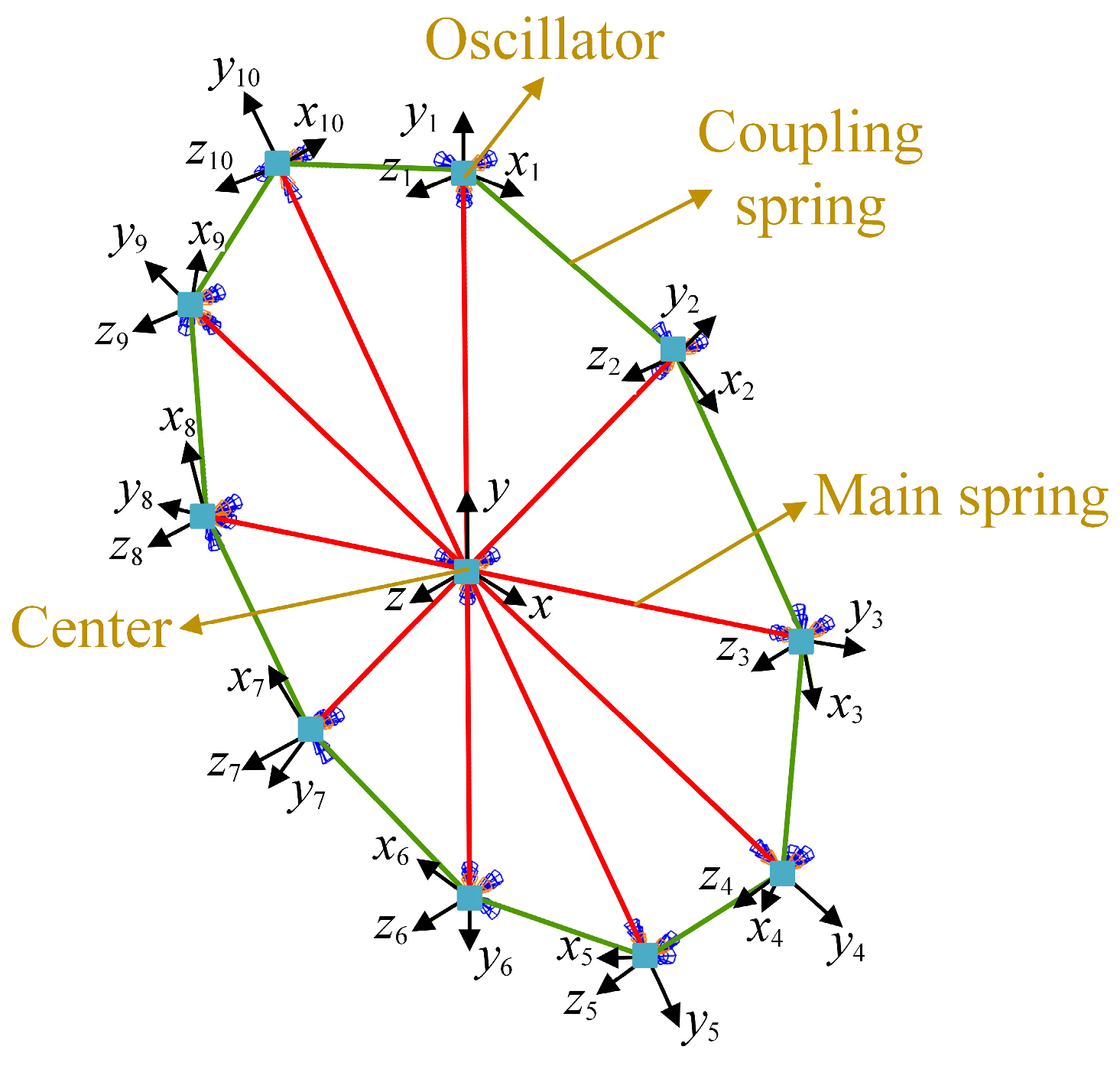
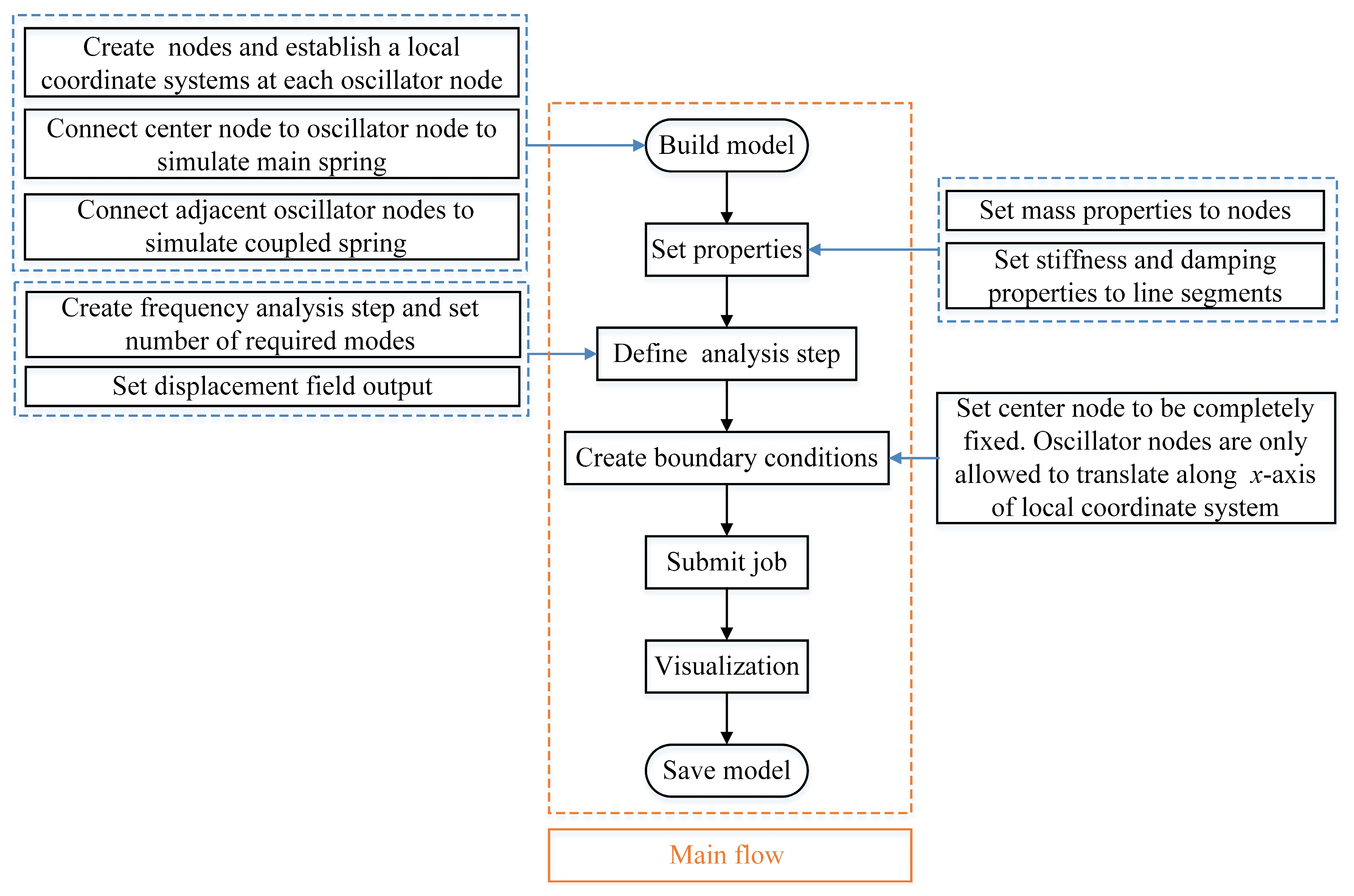
4.1. Numerical Model
4.2. Numerical Results
4.2.1. Validation of Mode Localization
4.2.2. Validation of Eigenvalue Splitting
5. Test Validation
5.1. Model of Pipeline-Oriented CMS
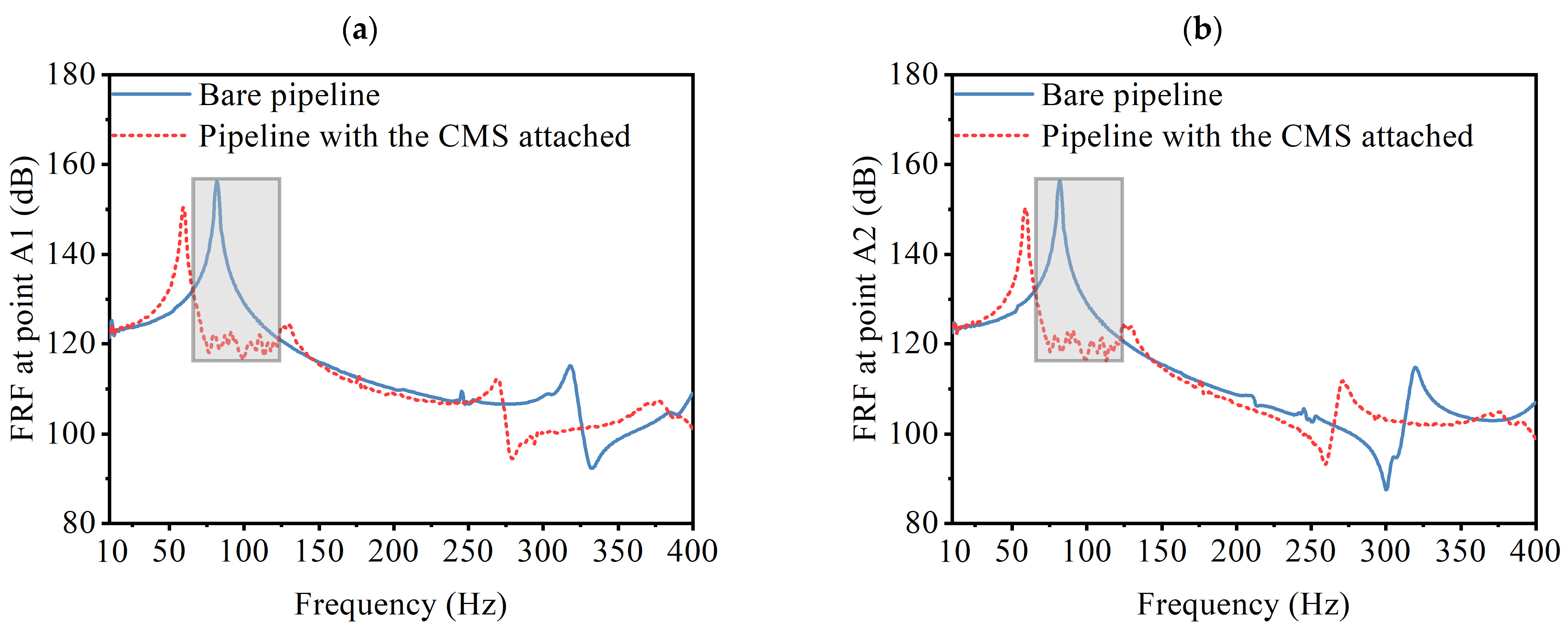
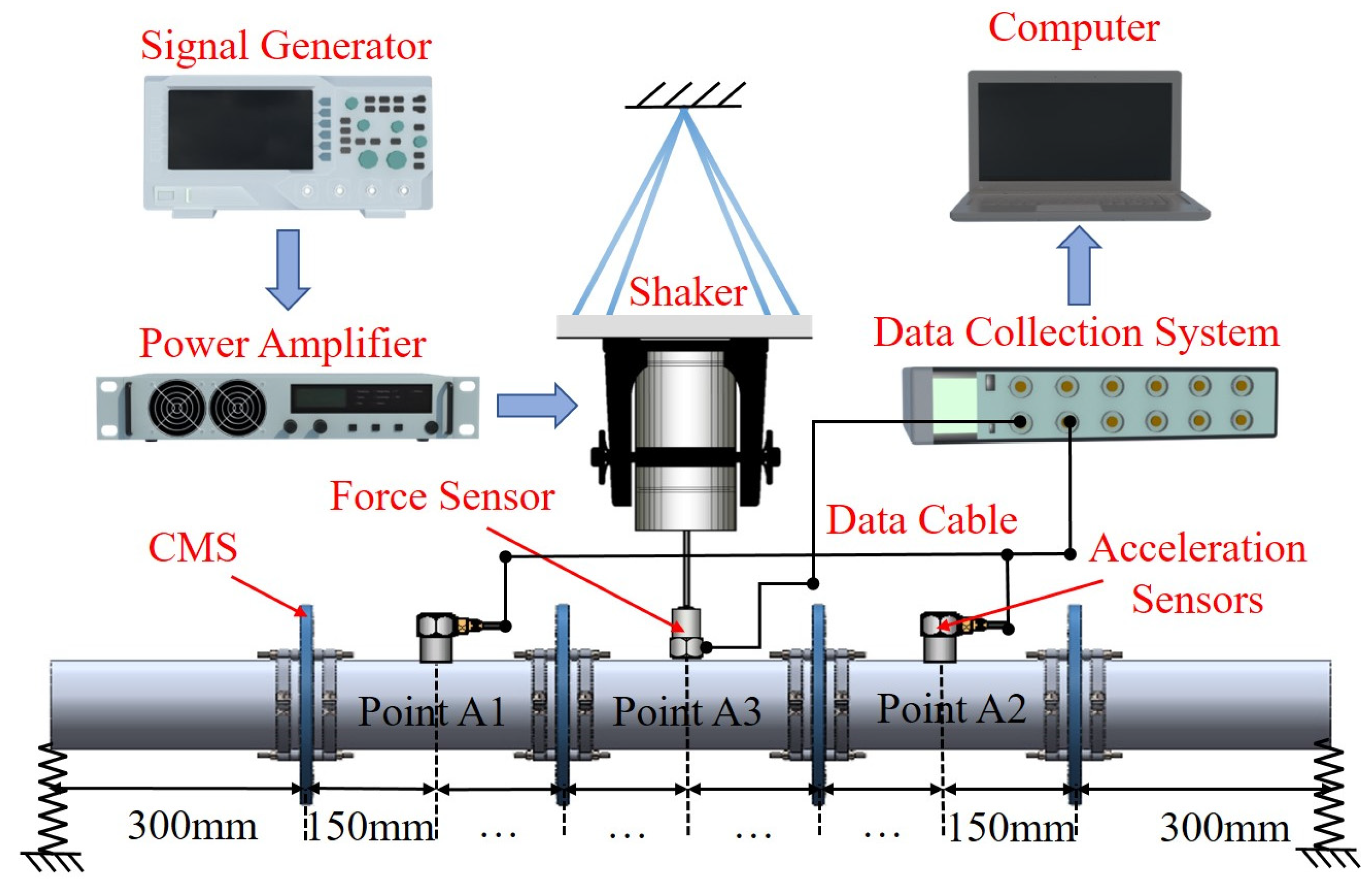
5.2. FRF Test of Pipeline
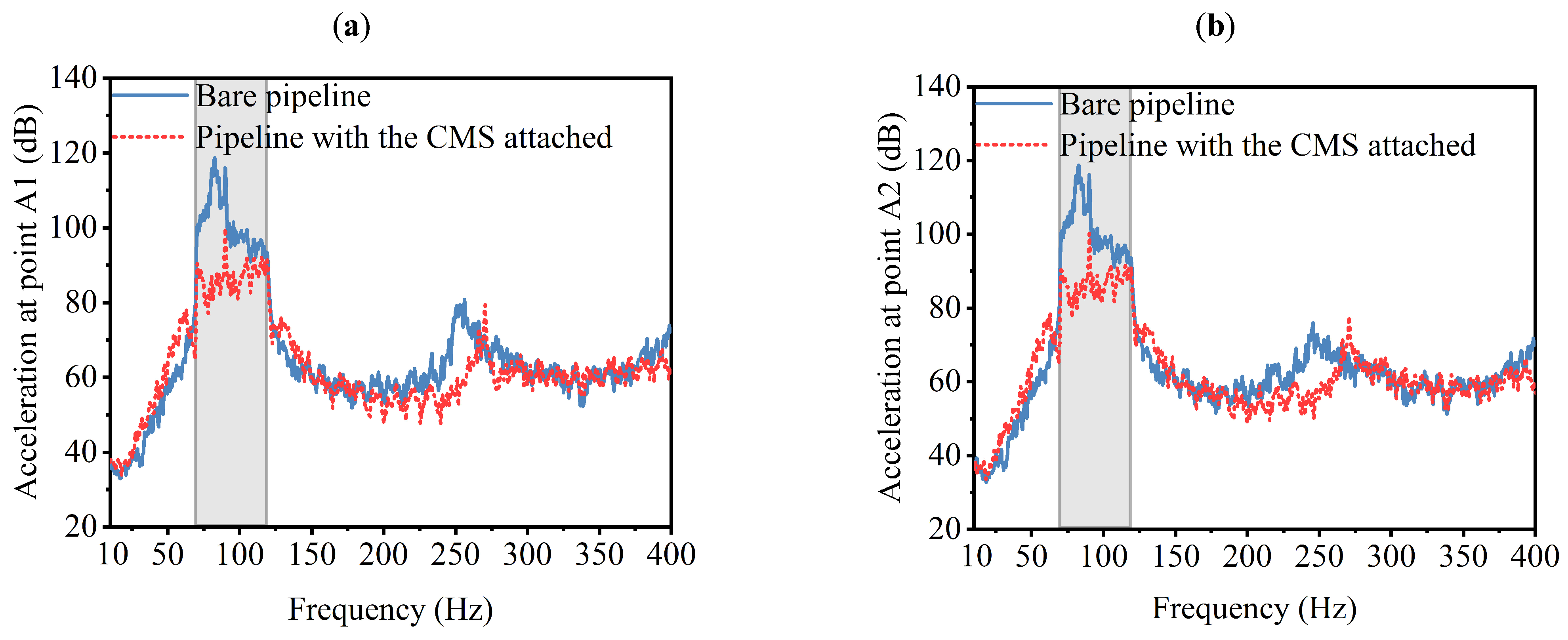
5.3. Excitation Test of Pipeline
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviation | Main frequency mistuning | ||
| CMS | Cyclic mistuned structure | Coupled frequency mistuning | |
| FRF | Frequency response function | Coupling strength | |
| MFCs | Macro-fiber composites | Frequency mistuning strength | |
| LQR | Linear-Quadratic Regulator | Average frequency mistuning | |
| PID | Proportional Integral Derivative | Circular frequency of the excitation | |
| DVA | Dynamic vibration absorber | Complex amplitude of the n-th resonant unit | |
| MDVAs | Multiple dynamic vibration absorbers | Dimensionless eigenvalue | |
| CTS | Cyclic tuned structure | I | Unit matrix |
| Main Symbol Explanation | Displacement vector | ||
| Stiffness of the main spring | A | Coefficient matrix | |
| Damping coefficient of the main spring | Base system matrix | ||
| Stiffness of the coupling spring | Perturbation matrix | ||
| Damping coefficient of the coupling spring | Eigenvector of the n-th resonant unit | ||
| N | Total number of the resonant units | Dimensionless eigenvalue of the n-th resonant unit | |
| n | Serial number of the resonant unit | Unperturbed eigenvector of the n-th resonant unit | |
| Displacement of the n-th resonant unit | Unperturbed eigenvalue of the n-th resonant unit | ||
| Main frequency of the n-th resonant unit when the structure is mistuned | First-order perturbation eigenvector of the n-th resonant unit | ||
| Coupled frequency of the n-th resonant unit when the structure is mistuned | First-order perturbation eigenvalue of the n-th resonant unit | ||
| Mass of the n-th resonant unit | Second-order perturbation eigenvector of the n-th resonant unit | ||
| Standard main frequency of the n-th resonant unit when the structure is tuned | Second-order perturbation eigenvalue of the n-th resonant unit | ||
| Standard coupled frequency of the n-th resonant unit when the structure is tuned | |||
References
- Liang, X.; Zha, X.; Jiang, X.; Wang, L.; Leng, J.; Cao, Z. Semi-analytical solution for dynamic behavior of a fluid-conveying pipe with different boundary conditions. Ocean Eng. 2018, 163, 183–190. [Google Scholar] [CrossRef]
- Païdoussis, M.P. Pipes conveying fluid: A fertile dynamics problem. J. Fluids Struct. 2022, 114, 103664. [Google Scholar] [CrossRef]
- Ding, H.; Ji, J.; Chen, L. Nonlinear vibration isolation for fluid-conveying pipes using quasi-zero stiffness characteristics. Mech. Syst. Signal. Process 2019, 121, 675–688. [Google Scholar] [CrossRef]
- Ji, W.; Sun, W.; Ma, H.; Li, J. Dynamic modeling and analysis of fluid-delivering cracked pipeline considering breathing effect. Int. J. Mech. Sci. 2024, 264, 108805. [Google Scholar] [CrossRef]
- Gao, P.; Li, J.; Zhai, J.; Tao, Y.; Han, Q. A novel optimization layout method for clamps in a pipeline system. Appl. Sci. 2020, 10, 390. [Google Scholar] [CrossRef]
- Cho, S.G.; Furuya, O.; Kurabayashi, H. Enhancement of seismic resilience of piping systems in nuclear power plants using steel coil damper. Nucl. Eng. Des. 2019, 350, 147–157. [Google Scholar] [CrossRef]
- Wang, B.; Wang, H.; He, Z.; Liu, D.; Pan, P. Test and analysis of multi-cavity particle damper for vertical vibration control of pipeline structures. Eng. Struct. 2023, 281, 115744. [Google Scholar] [CrossRef]
- Wen, Z.; Wang, J.; Yang, S.; Jiang, H.; Wang, J.; Chen, X.; Chen, K.; Zhu, W.; Wu, C. Study on the vibration characteristics of flexible dampers in finite single-coupled pipelines. Ocean Eng. 2025, 325, 120802. [Google Scholar] [CrossRef]
- Bi, K.; Hao, H. Numerical simulation on the effectiveness of using viscoelastic materials to mitigate seismic induced vibrations of above-ground pipelines. Eng. Struct. 2016, 123, 1–14. [Google Scholar] [CrossRef]
- Blocka, C.; Engelhardta, J.; Henkela, F.O. Active control of vibrations in piping systems. In Proceedings of the 20th International Conference on Structural Mechanics in Reactor Technology (SMiRT 20), Espoo, Finland, 9–14 August 2009. [Google Scholar]
- Zhang, Y.; Sun, W.; Zhang, H.; Du, D.; Xu, K. Active vibration control of fluid-conveying pipelines: Theoretical and experimental studies. Int. J. Mech. Sci. 2024, 270, 109106. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, L.; Zhang, X.; Zhou, Y.; Yang, Q. Active vibration control for ship pipeline system based on PI-LQR state feedback. Ocean Eng. 2024, 310, 118559. [Google Scholar] [CrossRef]
- Yang, F.; Esmailzadeh, E.; Sedaghati, R. Optimal vibration control of beam-type structures using multiple-tuned-mass-dampers. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2009, 224, 191–202. [Google Scholar] [CrossRef]
- Kwag, S.; Kwak, J.; Lee, H.; Oh, J.; Koo, G.-H. Enhancement in the Seismic Performance of a Nuclear Piping System using Multiple Tuned Mass Dampers. Energies 2019, 12, 2077. [Google Scholar] [CrossRef]
- Wang, X.; Pang, Y.; Wu, J.H.; Ma, F. A broadband metamaterial damper design based on synergetic coupling among multi-cells. Appl. Acoust. 2023, 206, 109303. [Google Scholar] [CrossRef]
- Huang, Y.; Li, J.; Chen, W.; Bao, R. Tunable bandgaps in soft phononic plates with spring-mass-like resonators. Int. J. Mech. Sci. 2019, 151, 300–313. [Google Scholar] [CrossRef]
- Jiang, W.; Yin, M.; Liao, Q.; Xie, L.; Yin, G. Three-dimensional single-phase elastic metamaterial for low-frequency and broadband vibration mitigation. Int. J. Mech. Sci. 2021, 190, 106023. [Google Scholar] [CrossRef]
- Shen, M.; Yang, J.; Yang, D.; Yang, X.; Qian, Y. Vibration control in bolted joints with locally resonant metamaterials. Int. J. Mech. Sci. 2025, 287, 109999. [Google Scholar] [CrossRef]
- Pires, F.A.; Boukadia, R.F.; Wandel, M.; Thomas, C.; Deckers, E.; Desmet, W.; Claeys, C. Novel resonator concept for improved performance of locally resonant based metamaterials. Thin-Walled Struct. 2025, 209, 112866. [Google Scholar] [CrossRef]
- Gomes, C.B.F.; dos Santos, M.C.P.; Araújo, B.C.C.; Pereira, F.N.; Nobrega, E.D.; Dos Santos, J.M.C.; Miranda, E.J.P., Jr.; Sinatora, A. Wave and vibration attenuation in graded elastic metamaterial beams with local resonators. Int. J. Mech. Sci. 2025, 293, 110125. [Google Scholar] [CrossRef]
- Poggetto, V.F.D.; Serpa, A.L. Elastic wave band gaps in a three-dimensional periodic metamaterial using the plane wave expansion method. Int. J. Mech. Sci. 2020, 184, 105841. [Google Scholar] [CrossRef]
- Nateghi, A.; Sangiuliano, L.; Claeys, C.; Deckers, E.; Pluymers, B.; Desmet, W. Design and experimental validation of a metamaterial solution for improved noise and vibration behavior of pipes. J. Sound Vib. 2019, 455, 96–117. [Google Scholar] [CrossRef]
- Wen, J.; Wang, G.; Wen, X.; Xiao, Y. Theoretical and experimental study of locally resonant and bragg band gaps in flexural beams carrying periodic arrays of beam-like resonators. J. Vib. Acoust. 2013, 135, 041006. [Google Scholar] [CrossRef]
- Yao, D.; Xiong, M.; Luo, J.; Yao, L. Flexural wave mitigation in metamaterial cylindrical curved shells with periodic graded arrays of multi-resonator. Mech. Syst. Signal Process. 2022, 168, 108721. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, W.; Gao, W.; Cheng, X. Advances of research on mode localization in mistuned cyclically periodic structures. Appl. Mech. Mater. 2013, 405–408, 3198–3203. [Google Scholar] [CrossRef]
- Wang, J.; Li, Q.; Zhu, Z. Vibratory localization of mistuned bladed disk assemblies—A review. Adv. Mech. 2000, 30, 517–528. [Google Scholar]
- Corral, R.; Khemiri, O.; Martel, C. Design of mistuning patterns to control the vibration amplitude of unstable rotor blades. Aerosp. Sci. Technol. 2018, 80, 20–28. [Google Scholar] [CrossRef]
- Bai, B.; Xiang, L.; Li, X. Probabilistic analysis-based vibration characteristics of intentionally mistuned blisk. Probabilistic Eng. Mech. 2022, 67, 103195. [Google Scholar] [CrossRef]
- Li, F.; Wang, Y. Study on wave localization in disordered periodic layered piezoelectric composite structures. Int. J. Solids Struct. 2005, 42, 6457–6474. [Google Scholar] [CrossRef]
- Zhao, T.; Yang, Z.; Xu, Y.; Tian, W. Mode localization in metastructure with T-type resonators for broadband vibration suppression. Eng. Struct. 2022, 268, 114775. [Google Scholar] [CrossRef]
- Wei, S.T.; Pierre, C. Localization phenomena in mistuned assemblies with cyclic symmetry part I: Free vibrations. J. Vib. Acoust. 1988, 110, 429–438. [Google Scholar] [CrossRef]
- Bendiksen, O.O. Mode localization phenomena in large space structures. AIAA J. 1987, 25, 1241–1248. [Google Scholar] [CrossRef]
- Pierre, C.; Dowell, E.H. Localization of vibrations by structural irregularity. J. Sound Vib. 1987, 114, 549–564. [Google Scholar] [CrossRef]
- Yin, L.; Xu, W.; Fu, J.; Cheng, G. Multi-directional broadband vibration control of marine pipe systems using mistuned cyclic symmetric structure as dynamic vibration absorbers. Ocean Eng. 2025, 320, 120272. [Google Scholar] [CrossRef]


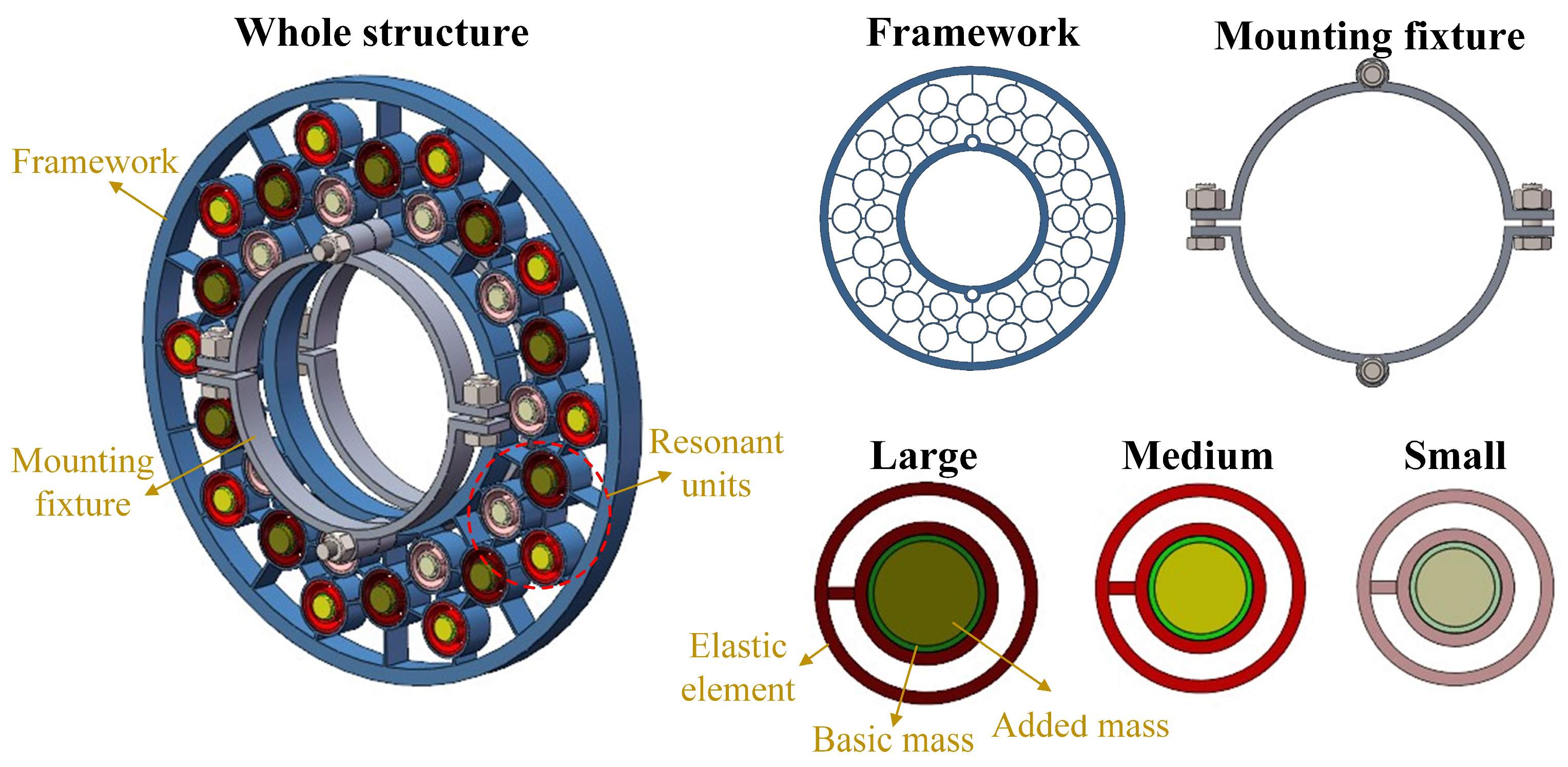

| Example | Range (g) | Interval (g) | Mistuning Strength (%) |
|---|---|---|---|
| E1 | 16.1~17.9 | 0.2 | 3.6 |
| E2 | 15.2~18.8 | 0.4 | 7.2 |
| E3 | 14.3~19.7 | 0.6 | 10.9 |
| E4 | 13.4~20.6 | 0.8 | 14.8 |
| Parameters | H | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Value (mm) | Large | 8.5 | 8.5 | 4.5 | 4.5 | 2 | 2.4 | 1 | 10 |
| Medium | 8 | 8 | 4 | 4 | 2 | 2 | 1 | 10 | |
| Small | 7.5 | 7.5 | 3.5 | 3.5 | 2 | 1.6 | 1 | 10 | |
| Type of Resonant Unit | Basic Mass (g) | Added Mass (g) |
|---|---|---|
| Large | 12.2 | 2.0 (3); 4.0 (3); 6.0 (2); 8.0 (2) |
| Medium | 9.7 | 0.6 (3); 1.8 (3); 3.0 (2); 4.2 (2) |
| Small | 7.4 | 0 (4); 0.88 (3); 1.76 (3) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, L.; Xu, W.; Zhou, J.; Liu, S.; Xiao, L. Vibration Localization in Cyclic Mistuned Structure and Its Application to Low-Frequency Broadband Vibration Control of Pipelines. Appl. Sci. 2025, 15, 6852. https://doi.org/10.3390/app15126852
Yin L, Xu W, Zhou J, Liu S, Xiao L. Vibration Localization in Cyclic Mistuned Structure and Its Application to Low-Frequency Broadband Vibration Control of Pipelines. Applied Sciences. 2025; 15(12):6852. https://doi.org/10.3390/app15126852
Chicago/Turabian StyleYin, Lihang, Wei Xu, Jian Zhou, Song Liu, and Liantao Xiao. 2025. "Vibration Localization in Cyclic Mistuned Structure and Its Application to Low-Frequency Broadband Vibration Control of Pipelines" Applied Sciences 15, no. 12: 6852. https://doi.org/10.3390/app15126852
APA StyleYin, L., Xu, W., Zhou, J., Liu, S., & Xiao, L. (2025). Vibration Localization in Cyclic Mistuned Structure and Its Application to Low-Frequency Broadband Vibration Control of Pipelines. Applied Sciences, 15(12), 6852. https://doi.org/10.3390/app15126852






