The Methods of Determining the Centre of Gravity of a Tilting Body on the Upper Ankle Joint and Weighing the Feet of a Living Human
Abstract
Featured Application
Abstract
1. Introduction
- The method of balancing the body (one-sided lever method) through placing horizontally on a special platform supported at one point at the level of the plantar side of the heel. The overall centre of gravity of the body measured in this way was first described by E. du Bois-Reymond in the 19th century [2].
- Segmental weighing method, in which the mass and position of the centre of gravity of individual body parts (head, torso, limbs) are determined based on special anthropometric tables. Mathematical formulas are then used to determine the centre of gravity of the entire body [6].
2. Materials and Methods
2.1. Description of the Measurement Station
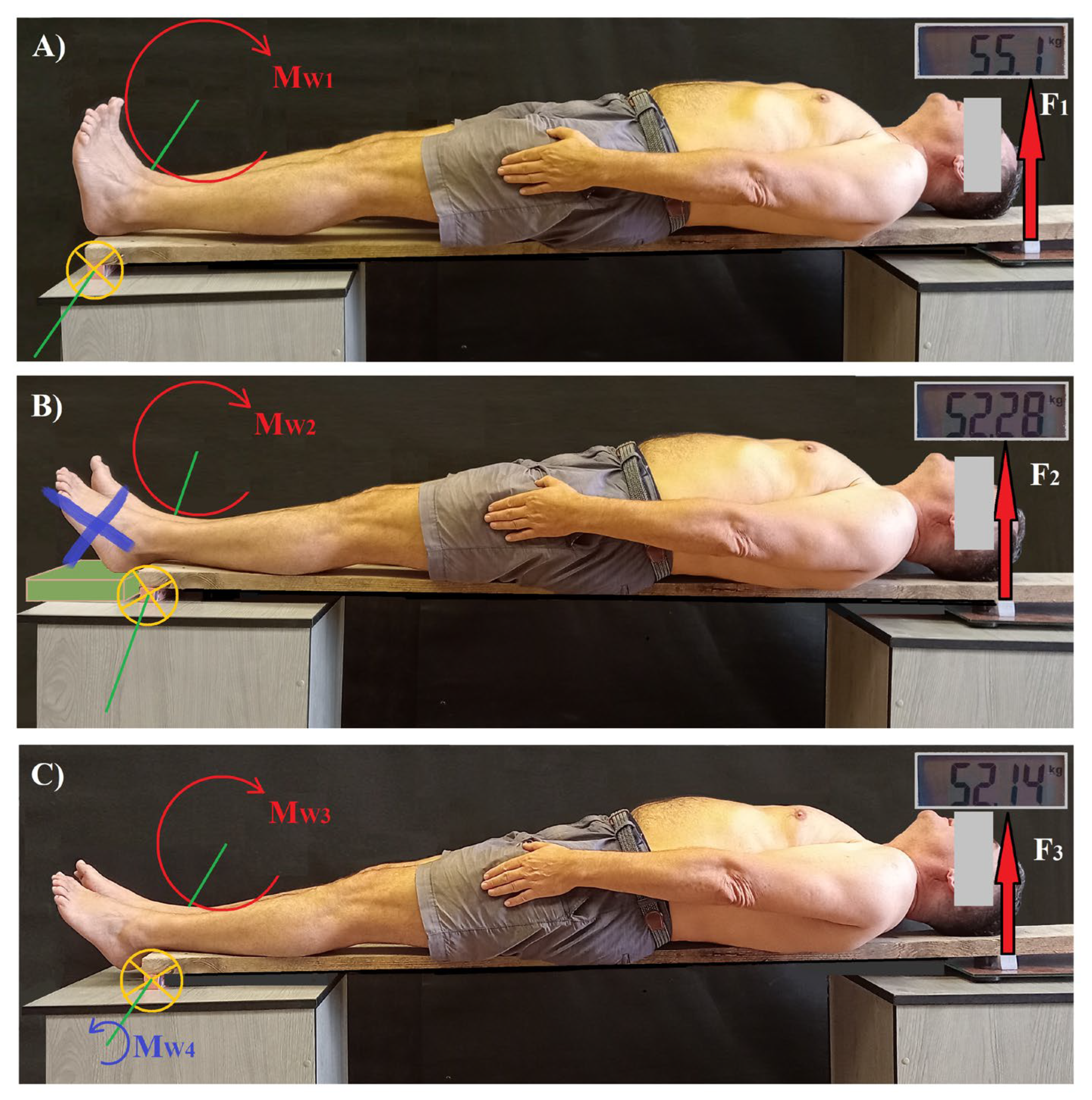
- (A)
- A human body placed on a board with the support point at the level of the tuberosity of the calcaneal bone on one side and, on the other, the reaction force (F1) was measured at the level of the top of the head using a scale. The feet were placed in the zero position (Figure 1A). In this way, the general centre of gravity of the body was determined.
- (B)
- The human body was placed on a board with the support point at the level of the axis of the upper ankle joint, while the weight of both feet was removed by independently supporting the feet at the level of the tuberosity of the calcaneal bone. The reaction force (F2) was measured at the level of the top of the head using a scale (Figure 1B). In this way, the centre of gravity of the leaning body part on the axis of the upper ankle joint (when the body was in upright position) was determined (method 1).
- (C)
- The human body was placed on a board with the support point at the level of the axis of the upper ankle joint, with the feet hanging freely on the edge of the board. The reaction force (F3) was measured at the level of the top of the head using a scale (Figure 1C). In this way, the centre of gravity of the leaning body part on the axis of the upper ankle joint (when the body was in upright position) was determined (method 2).
2.2. Weighing the Feet of Living People
2.3. Statistical Analysis
3. Results
3.1. Determining the Gravitational Arm of the Feet Concerning the Upper Ankle Joint
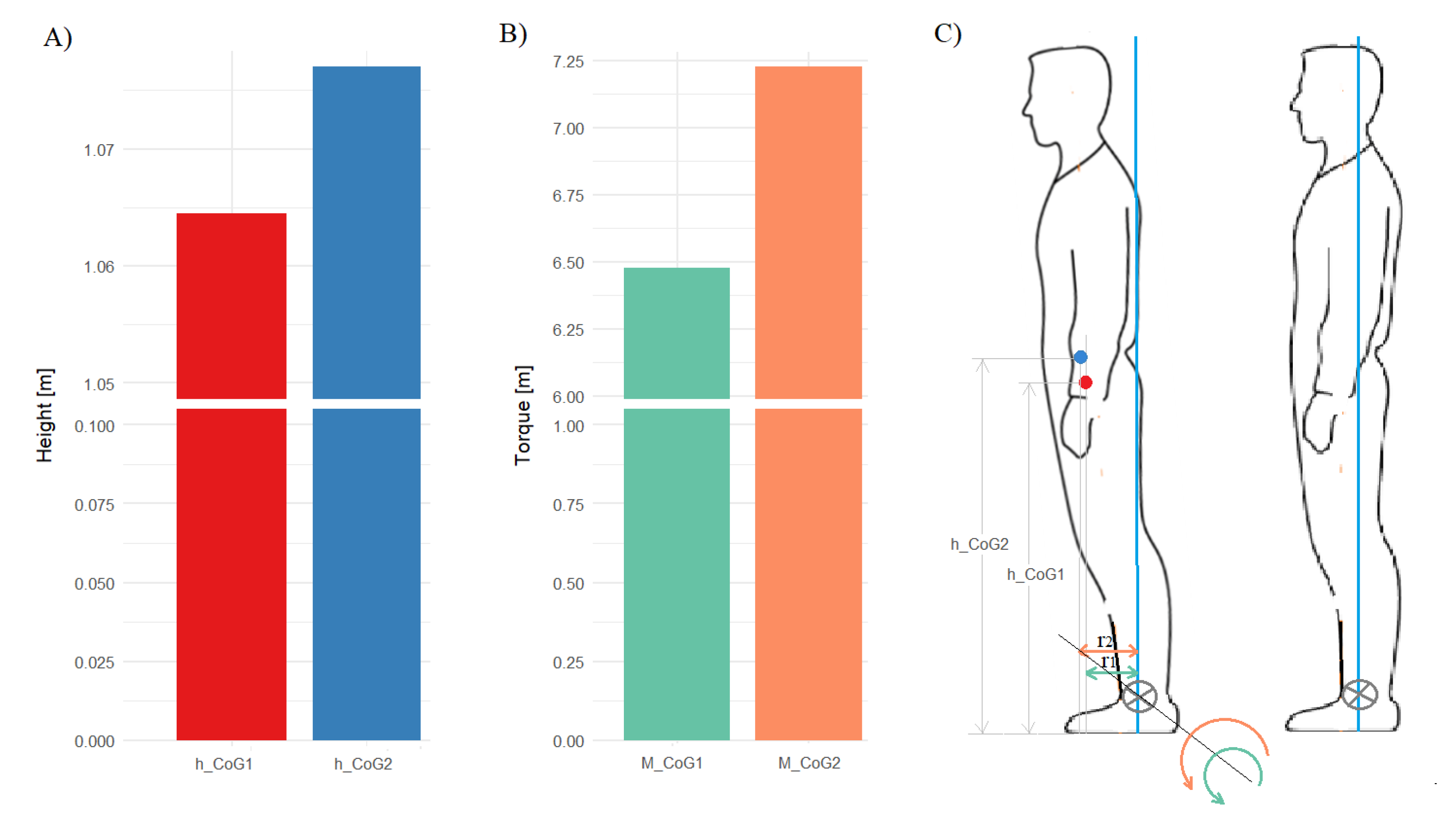
3.2. Determining the Position of the Centre of Gravity of the Body
3.2.1. Determining the Location of the General Centre of Gravity of the Human Body
3.2.2. Determining the Position of the Centre of Gravity of the Leaning Part of the Human Body on the Axis of the Upper Ankle Joint
- Excluding feet torques
- Taking into account the feet torques generated at the upper ankle joint—on one side by the feet and on the other by the rest of the body.
- Consequences of a different location of the centre of gravity
3.2.3. Determining the Weight of the Feet Using the Indirect Method
4. Discussion
5. Conclusions
- The overall centre of gravity of a human body considered as a rigid body is closer to the axis of the upper ankle joint than the centre of gravity of a tilting body segment.
- A higher-positioned centre of gravity in a leaning body places more strain on the upper ankle joint, which is due to the resultant force being a function of gravity and muscle force.
- Determining the position and value of the centre of gravity based on the assumption that the human body is rigid distorts the real loading conditions of the upper ankle joint by underestimating the values of muscle strength. This is due to the underestimation of the gravity arm, and therefore the gravitational moment, which is counteracted by the muscular moments with constant arm lengths of the muscle forces.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CoG | Centre of gravity |
| CoM | Centre of body mass |
References
- Ryan, D.M.; Emma, N.; Joshua, R. Woodman Olivia The Center of Mass. In Introductory Physics: Building Models to Describe Our World; Libretext: Davis, CA, USA, 2023. [Google Scholar]
- Wiktor, D. Orthopedics and Rehabilitation, 3rd ed.; Państwowy Zakład Wydawnictw Lekarskich: Warszawa, Poland, 1983. [Google Scholar]
- Liang, J.Y.; Chou, L.S. Center of Mass Acceleration during Walking: Comparison between IMU and Camera-Based Motion Capture Methodologies. Wearable Technol. 2024, 5, e16. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.; Noghani, M.A.; Bolívar-Nieto, E. Comparative Analysis of Whole-Body Center-of-Mass Estimation Methods in Dynamic and Static Activities Using Marker-Based Systems. arXiv 2024, arXiv:2411.18774. [Google Scholar]
- Hnat, S.K.; Audu, M.L.; Triolo, R.J.; Quinn, R.D. Estimating Center of Mass Kinematics during Perturbed Human Standing Using Accelerometers. J. Appl. Biomech. 2021, 37, 415–424. [Google Scholar] [CrossRef] [PubMed]
- Przeździak, B. Zaopatrzenie Rehabilitacyjne; Via Medica: PointeClaire, Quebec, 2003; ISBN 8389493810. [Google Scholar]
- Levine, D.; Richards, J.; Whittle, M.; Whittle, M. Whittle’s Gait Analysis, 5th ed.; Jim, R., David, L., Michael, W.W., Eds.; Churchill Livingstone Elsevier: London, UK, 2012; ISBN 978-0-7020-4265-2. [Google Scholar]
- Plagenhoef, F.G.E.S.; Abdelnour, T. Anatomical Data for Analyzing Human Motion. Res. Q. Exerc. Sport 1983, 54, 169–178. [Google Scholar] [CrossRef]
- Le Huec, J.C.; Saddiki, R.; Franke, J.; Rigal, J.; Aunoble, S. Equilibrium of the Human Body and the Gravity Line: The Basics. Eur. Spine J. Off. Publ. Eur. Spine Soc. Eur. Spinal Deform. Soc. Eur. Sect. Cerv. Spine Res. Soc. 2011, 20 (Suppl. S5), 558–563. [Google Scholar] [CrossRef] [PubMed]
- Roussouly, P.; Gollogly, S.; Noseda, O.; Berthonnaud, E.; Dimnet, J. The Vertical Projection of the Sum of the Ground Reactive Forces of a Standing Patient Is Not the Same as the C7 Plumb Line: A Radiographic Study of the Sagittal Alignment of 153 Asymptomatic Volunteers. Spine 2006, 31, E320–E325. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, T.; Takeda, H.; Izumi, T.; Ino, S.; Ifukube, T. Effects on the Location of the Centre of Gravity and the Foot Pressure Contribution to Standing Balance Associated with Ageing. Ergonomics 1999, 42, 997–1010. [Google Scholar] [CrossRef] [PubMed]
- Pawłowski, B.; Grabarczyk, M. Center of Body Mass and the Evolution of Female Body Shape. Am. J. Hum. Biol. Off. J. Hum. Biol. Counc. 2003, 15, 144–150. [Google Scholar] [CrossRef] [PubMed]
- Spathopoulos, V.M. An Introduction to the Physics of Sports; Gopublished: North Bergen, NJ, USA, 2013; ISBN 1483930076, 9781483930077. [Google Scholar]
- Kim, D.-H.; Park, J.-K.; Jeong, M.-K. Influences of Posterior-Located Center of Gravity on Lumbar Extension Strength, Balance, and Lumbar Lordosis in Chronic Low Back Pain. J. Back Musculoskelet. Rehabil. 2014, 27, 231–237. [Google Scholar] [CrossRef] [PubMed]
- de Leva, P. Adjustments to Zatsiorsky-Seluyanov’s Segment Inertia Parameters. J. Biomech. 1996, 29, 1223–1230. [Google Scholar] [CrossRef] [PubMed]
- Braune, W.; Fischer, O. On the Centre of Gravity of the Human Body as Related to the Equipment of the German Infantry Soldier, 1st ed.; Origina; Springer: Berlin/Heidelberg, Germany, 2012; ISBN 978-3-642-69611-4. [Google Scholar]
- Bober, T.; Zawadzki, J. Biomechanics of the Human Movement System. In Biomechanika Układu Ruchu Człowieka, 1st ed.; Bober, T., Zawadzki, J., Eds.; Wydawnictwo BK: Wrocław, Poland, 2001. [Google Scholar]
- Dygut, J.; Piwowar, M. Torques in the Human Upper Ankle Joint Level and Their Importance in Conservative and Surgical Treatment. Sci. Rep. 2024, 14, 7525. [Google Scholar] [CrossRef] [PubMed]
- Wu, G. Real-Time Feedback of Body Center of Gravity for Postural Training of Elderly Patients with Peripheral Neuropathy. IEEE Trans. Rehabil. Eng. 1997, 5, 399–402. [Google Scholar] [CrossRef] [PubMed]
- Burke, T.N.; França, F.J.R.; de Meneses, S.R.F.; Cardoso, V.I.; Pereira, R.M.R.; Danilevicius, C.F.; Marques, A.P. Postural Control among Elderly Women with and without Osteoporosis: Is There a Difference? Sao Paulo Med. J. 2010, 128, 219–224. [Google Scholar] [CrossRef]
- Lugade, V.; Lin, V.; Chou, L.S. Center of Mass and Base of Support Interaction during Gait. Gait Posture 2011, 33, 406–411. [Google Scholar] [CrossRef]
- Dusane, S.; Shafer, A.; Ochs, W.L.; Cornwell, T.; Henderson, H.; Kim, K.Y.A.; Gordon, K.E. Control of Center of Mass Motion during Walking Correlates with Gait and Balance in People with Incomplete Spinal Cord Injury. Front. Neurol. 2023, 14, 1146094. [Google Scholar] [CrossRef]


| F2 [kG] | F3 [kG] | l2 [m] | hCoG4 [m] | Body Mass [kG] | W4 [kG] | Foot Mass [% of Body Mass] | |
|---|---|---|---|---|---|---|---|
| P1 | 52.28 | 52.14 | 1.73 | 0.0832 | 94.2 | 2.91 | 3.09 |
| P2 | 56.65 | 56.49 | 1.75 | 0.0991 | 102.1 | 2.81 | 2.75 |
| P3 | 50.27 | 50.13 | 1.78 | 0.0879 | 89 | 2.95 | 3.32 |
| P4 | 52.37 | 52.21 | 1.74 | 0.0962 | 91.9 | 2.87 | 3.12 |
| P5 | 41.72 | 41.61 | 1.69 | 0.0791 | 75.2 | 2.48 | 3.31 |
| P6 | 45.70 | 45.59 | 1.71 | 0.088 | 80.9 | 2.03 | 2.51 |
| Mean (SD) | 49.83 (5.33) | 49.69 (5.31) | 1.73 (0.03) | 0.089 (0.007) | 88.88 (9.62) | 2.68 (0.36) | 3.02 (0.32) |
| 95% CI | [44.2, 55.4] | [44.1,55.2] | [1.7, 1.77] | [0.081, 0.097] | [78.7, 98.9] | [2.29, 3.051 | [2.678, 3.356] |
| Margin of_error_95CI | 5.59 | 5.57 | 0.03 | 0.007 | 10.09 | 0.37 | 0.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dygut, J.; Piwowar, M. The Methods of Determining the Centre of Gravity of a Tilting Body on the Upper Ankle Joint and Weighing the Feet of a Living Human. Appl. Sci. 2025, 15, 6812. https://doi.org/10.3390/app15126812
Dygut J, Piwowar M. The Methods of Determining the Centre of Gravity of a Tilting Body on the Upper Ankle Joint and Weighing the Feet of a Living Human. Applied Sciences. 2025; 15(12):6812. https://doi.org/10.3390/app15126812
Chicago/Turabian StyleDygut, Jacek, and Monika Piwowar. 2025. "The Methods of Determining the Centre of Gravity of a Tilting Body on the Upper Ankle Joint and Weighing the Feet of a Living Human" Applied Sciences 15, no. 12: 6812. https://doi.org/10.3390/app15126812
APA StyleDygut, J., & Piwowar, M. (2025). The Methods of Determining the Centre of Gravity of a Tilting Body on the Upper Ankle Joint and Weighing the Feet of a Living Human. Applied Sciences, 15(12), 6812. https://doi.org/10.3390/app15126812






