Identification of Torsional Fatigue Properties of Titanium Alloy Turned Surfaces and Their Distribution Characteristics

Abstract

The intricate and dynamic cutting behavior observed in titanium alloy turning leads to non-uniform surface and subsurface properties in the workpiece, impacting torsional strength and fatigue life. A transient pose model, founded on the configuration of a turning tool, is developed to elucidate the evolution of the transition surface during transient turning. Through finite element simulation, the plastic deformation, residual stress, and work hardening rate of the machined surface and subsurface of a titanium alloy are quantitatively examined. The torsional strength and fatigue life calculation method is developed based on initial performance parameters derived from the finite element model. This method enables the correlation identification between surface morphology characteristics, surface and subsurface performance parameters, and fatigue properties. Surface morphology, scanning electron microscopy (SEM), and energy-dispersive X-ray spectroscopy (EDS) are employed to quantitatively analyze the surface features and elemental composition of the titanium alloy turning surface, unveiling their influence on torsional fatigue properties. The findings demonstrate the efficacy of the proposed models and methodologies in identifying the torsional fatigue properties and their distribution patterns of titanium alloy turning surfaces.

1. Introduction

TC6 has emerged as a primary material for aero-engine hubs owing to its exceptional corrosion and fatigue resistance, high specific strength, and favorable ductility. The operational reliability, particularly the fatigue performance, of the hub is significantly impacted by the quality of the machined surface. During the high-efficiency turning of titanium alloys, the non-linear contact dynamics at the cutting interface, the intricate multi-field coupling in the cutting deformation zone, and the instantaneous state parameters of the machined surface layer undergo variations due to time-varying factors such as process system vibrations, tool degradation, and cutting load fluctuations induced by sawtooth chips. These variations contribute to the ambiguity and uncertainty in the distribution characteristics of the machined surface’s morphology, microstructure, residual stress layer, hardening layer, and plastic strain layer of titanium alloys. Detecting the uneven distribution and potential damage of the machined surface of titanium alloys poses challenges, directly impacting the assessment of the torsional fatigue resistance of the machined surface of titanium alloys.

Most of the research on titanium alloy turning surfaces focus on the influence of a single process parameter on a certain index of surface integrity or improving surface properties through a post-treatment process. However, there is still a lack of systematic research on the identification and regulation of the spatial heterogeneity of surface integrity parameters induced by dynamic factors and their potential damage. Most of the existing evaluation systems are based on a macro-average index, which makes it difficult to reveal the correlation between local parameter fluctuation and fatigue crack initiation and propagation. In addition, the existing models still have some limitations on the dynamic evolution of surface integrity parameter distribution under complex conditions such as variable parameter cutting. Zhou et al. [1] showed that radial vibration has a stronger degradation effect on surface morphology than axial and tangential vibration in the turning process because it directly changes the thickness of the cutting layer and the instantaneous cutting amount of the tool, resulting in increased surface waviness and periodic grooves. Wang et al. [2] found that cutting fluid penetration and lubricating film formation can reduce tool-workpiece interface friction and weaken the negative effect of vibration on surface morphology, but vibration can still induce subsurface microstructure evolution through periodic load fluctuations. Tepla T et al. [3] studied a machine learning-based selection method for medical biocompatible titanium alloys. This method can effectively reduce the time, material, and labor costs required for the study of titanium alloy properties and is suitable for material screening of biocompatible medical devices. Pimenov et al. [4] discuss advances in research to improve surface integrity in aluminum alloy machining by improving cutting parameters, tool materials, and coolant application. Singh [5] reveals the correlation between surface integrity and machining parameters in thin structure machining through experiments. Guo et al. [6] revealed the surface quality control mechanism of high-speed grinding aluminum/silicon carbide composites. Chen et al. [7] investigated the effects of cutting parameters and cooling strategies on the machined surface integrity of Ti-6Al-4V. Li et al. [8] further demonstrated the critical role of milling stability on surface integrity and fatigue properties.

In that aspect of the influence of cut parameters on the fatigue resistance of titanium alloy machined surface, Yang Shenliang, Li Xun et al. [9] took Ti-6Al-4V titanium alloy as experimental material, based on the single variable control strategy, and used the research method of combining the circumferential milling process with the durability evaluation of the specimen, systematically exploring the correlation mechanism between the multi-dimensional characteristics of machined surface and the fatigue resistance of materials by cutting parameter optimization. Shen Haolun et al. [10] studied the effect of feed rate on fatigue life in titanium alloy machining. By changing the feed rate, titanium alloy (Ti-6Al-4V) was machined with a single-factor Scheme, and the morphological characteristics of the machined surface under different feed rate conditions were observed. High-cycle fatigue tests were carried out for samples machined with different feed rates, and the effect of feed rates on high-cycle fatigue life was discussed. Zhao Wenshuo et al. [11] found that in FGH96 superalloy turning, the fatigue life of the tool wear VB ≤ 0.15 mm decreased slightly, and it decreased sharply after exceeding it, so it was necessary to control the wear amount. Jiang [12] pointed out that in turning, increasing the thickness of the TiAlN coating can reduce the surface tensile residual stress and improve the low-cycle fatigue life. The 3 μm coating can increase the life linearly by 15.6%. Comparing turning with grinding, Wan [13] found that the surface compressive residual stress, microhardness, and fatigue life of finish turning samples were higher than those of grinding samples. Lai et al. [14] study of TC17 titanium alloy shows that feed rate has the greatest effect on surface residual compressive stress and roughness, the former improves fatigue life, and the latter linearly decreases it. Dan [15] further reveals that feed has the most significant effect on fatigue life in TC17 turning, and cracks mostly originate from the surface, so it is necessary to optimize turning parameters to improve surface integrity. Wang [16] found that large tip radius, sharp cutting edge, and low feed speed can make polycrystalline copper amorphous and lattice transformation in diamond turning and obtain an ultra-smooth and ultra-hard surface. Imran [17] found that the surface quality of low carbon steel can be improved with the increase in cutting speed, deteriorated with the increase in feed rate and cutting depth, and the surface quality is the worst in the late stage of tool wear. Gaurav [18] pointed out that the tool flank wear and cutting speed increase will reduce the EN31 steel hard turning subsurface stress distribution compressibility, residual stress, and tool wear, where white layer thickness is highly correlated. Xia et al. [19,20] pointed out that residual stress is caused by surface thermal gradient or plastic deformation difference, which directly affects the service performance of materials. Liu et al. [21] found that the non-uniform distribution of surface integrity significantly accelerates stress corrosion cracking initiation. Yue et al. [22] further showed that the dynamic state parameters, such as residual stress and strain in the surface layer/subsurface layer, showed significant variability in multiple cutting strategies.

In essence, both national and international researchers have conducted comprehensive investigations on the surface integrity and fatigue characteristics of titanium alloy turning surfaces. These studies have focused on regulating processing parameters and examining the effects of vibration and interface conditions, thereby establishing a groundwork for assessing the fatigue properties of such surfaces. Nevertheless, ensuring the precise identification of fatigue properties for titanium alloy turning surfaces proves challenging due to intricate factors like surface morphology and the non-uniform distribution of subsurface property parameters. Hence, there is a critical need to explore the spatial distribution of surface integrity parameters and their impact on fatigue performance under dynamic circumstances.

This study presents a refined model of titanium alloy turning surface topography, which is developed through adjustments informed by experimental outcomes. Utilizing finite element simulation data, the spatial distribution of subsurface performance parameters is delineated. By integrating the revised machined surface morphology and the computed subsurface performance parameters, a torsional finite element model of a titanium alloy workpiece with initial performance parameters is constructed. This model aims to elucidate the torsional strength and fatigue life of the titanium alloy workpiece across various conditions. The investigation delves into the response characteristics and distribution profiles of torsional fatigue properties of the titanium alloy by manipulating cutting parameters, followed by experimental validation.

2. Characterization of Surface Structure and Properties of Titanium Alloy Turning Operations

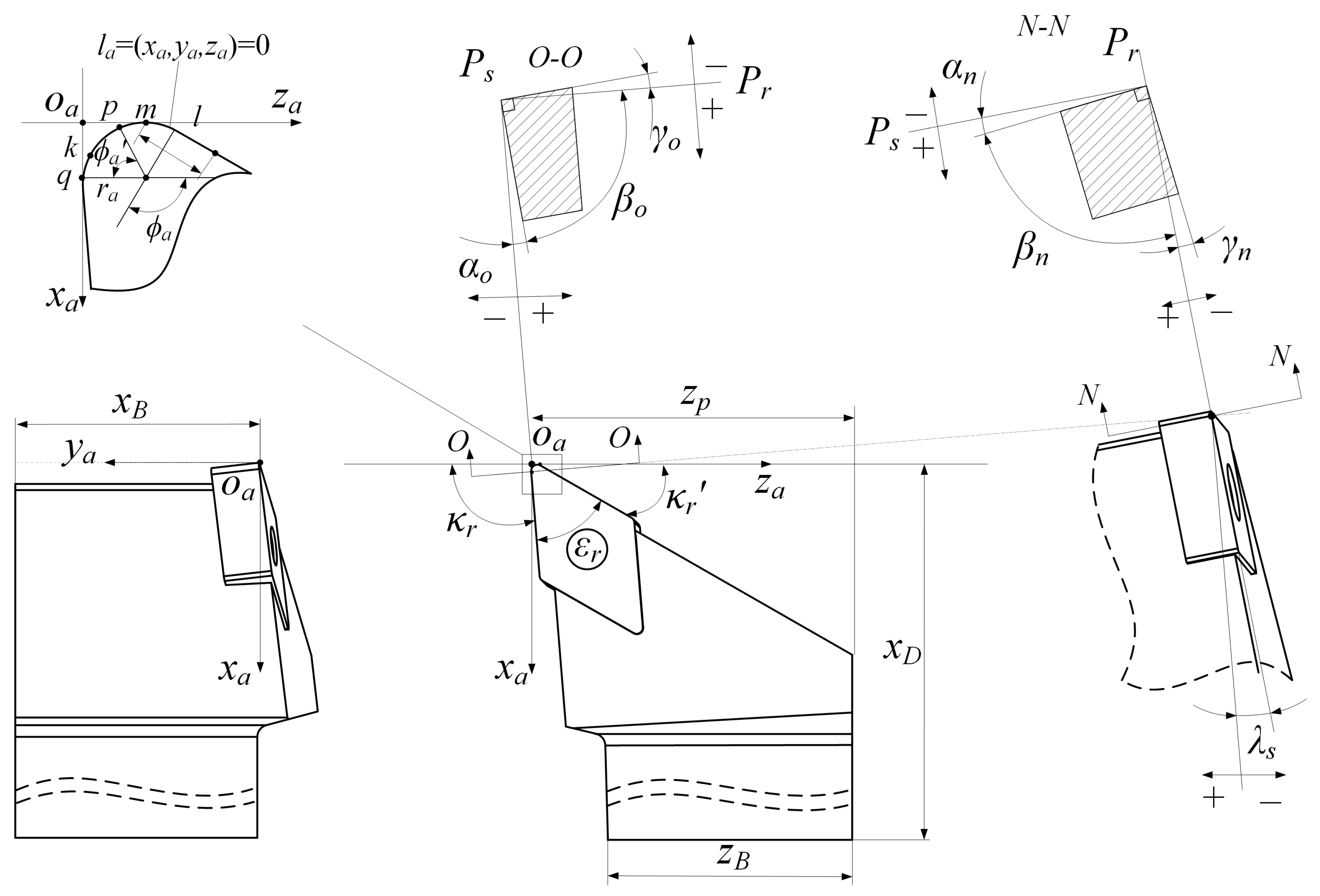
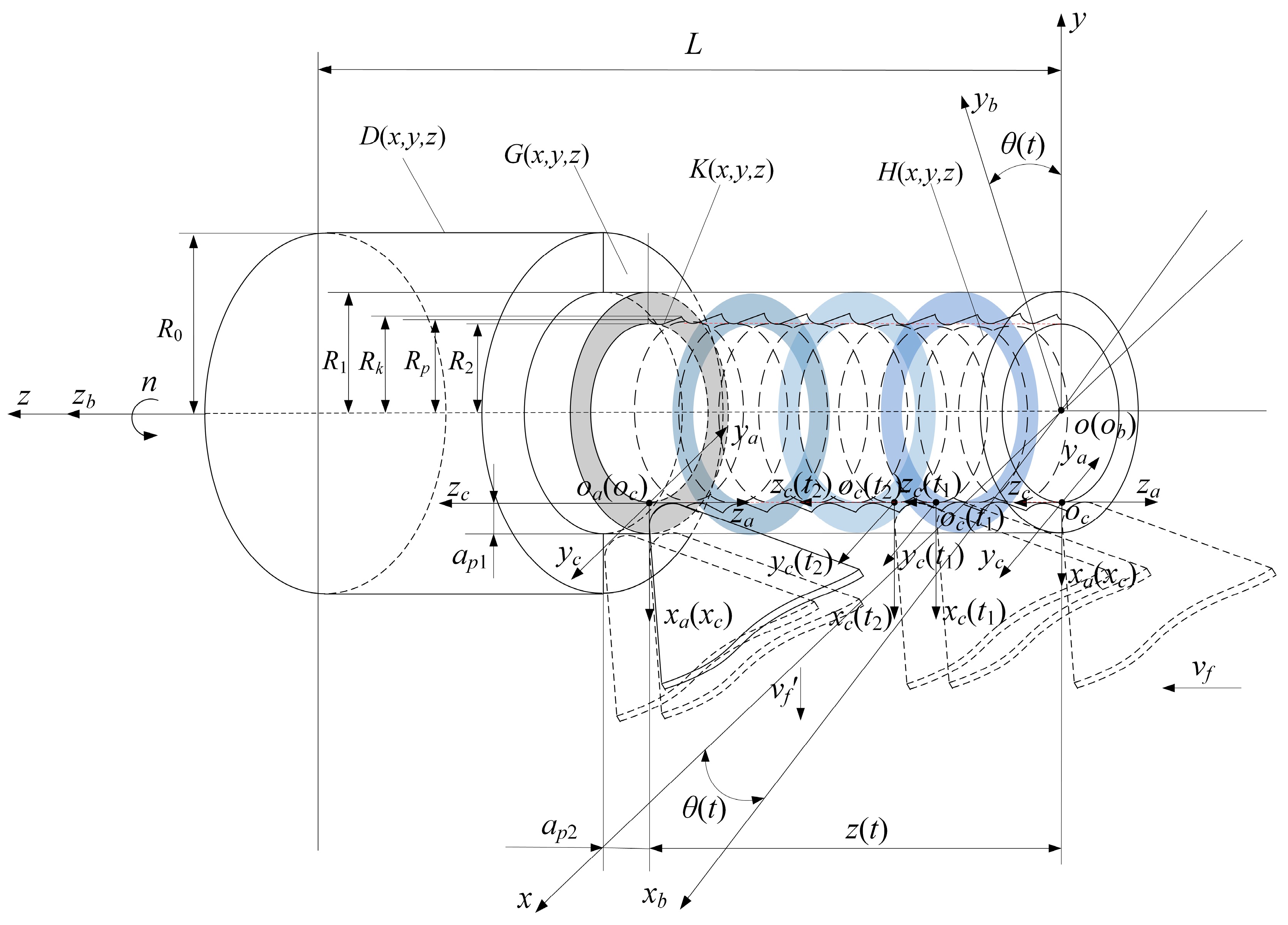
2.1. Turning Tool Structure and Instantaneous Cutting Position

In order to reveal the instantaneous dynamic characteristics of the cutting edge during the turning process, the structure of the turning tool and its cutting edge are characterized by geometric modeling, and the corresponding coordinate system is established, as shown in Figure 1.

The tool coordinate system, designated as o_a-x_ay_az_a in Figure 1, was established through the following geometric definitions: The origin o_a coincides with the intersection of the cutting edge’s apex plane and the radial maximum overhang projection. The z_a-axis extends along the line connecting o_a to the cutting edge apex, while the x_a-axis aligns with the radial overhang direction. The y_a-axis completes the right-handed Cartesian frame. Key geometric parameters include: q (cutting edge left boundary), m (upper boundary), p (arbitrary edge point), l (edge segment length), ϕ_a (transition arc angle), ϕ_a’ (angular offset from tool nose center), and l_a (edge profile equation). Dimensional parameters comprise z_B (shank length), x_D (tool height), x_B (shank width), and r_a (nose radius). The tool geometry is characterized by seven fundamental angles: principal cutting edge angle (κ_r), auxiliary cutting edge angle (κ_r’), tool included angle (ε_r), inclination angle (λ_s), radial components (rake γ_n, clearance α_n, wedge β_n), and axial components (rake γ₀, clearance α₀, wedge β₀).

As can be seen from Figure 1, the main cutting edge is solved by solving the equation in the lathe coordinate system, as follows:

$$L_{a1}(x_a,y_a,z_a)=\left\{\begin{array}{l}{x}_a=r_a+l\cdot \sin {\kappa }_r\\ y_a=\sin {\kappa }_r\cdot \left(r_a\cdot \left(1-\cos {\varphi }_a\right)+l\cdot \sin {\lambda }_s\right)\\ z_a=-l\cos {\kappa }_r\end{array}\right.$$

(1)

The tip arc of the transition section of the cutting edge is solved by solving the equation in the tool tooth coordinate system, as follows:

$$L_{a2}(x_a,y_a,z_a)=\left\{\begin{array}{l}{x}_a=r_a\cdot \left(1-\sin {{\varphi }_a}^{\prime }\right)\\ y_a=l\sin {\lambda }_s\\ z_a=r_a\cdot \left(1-\cos {{\varphi }_a}^{\prime }\right)\end{array}\right.$$

(2)

The sub-cutting edge is solved by solving the equations in the tool tooth coordinate system, as follows:

$$L_{a3}(x_a,y_a,z_a)=\left\{\begin{array}{l}{x}_a=r_a\cdot \left(1-\cos {{\kappa }_r}^{\prime }\right)+l\cdot \sin {{\kappa }_r}^{\prime }\\ y_a=\cos {{\kappa }_r}^{\prime }\cdot \left(r_a\cdot \left(1-\sin {\varphi }_a\right)+l\cdot \cos {\lambda }_s\right)\\ z_a=r_a\cdot \left(1+\sin {{\kappa }_r}^{\prime }\right)+l\cdot \cos {{\kappa }_r}^{\prime }\end{array}\right.$$

(3)

The cutting edge is solved by solving the equations in the tool tooth coordinate system, as follows:

$$L_a(x_a,y_a,z_a)=\left\{\begin{array}{l}{L}_{a1}(x_a,y_a,z_a)\\ L_{a2}(x_a,y_a,z_a)\\ L_{a3}(x_a,y_a,z_a)\end{array}\right.$$

(4)

In order to reveal the relative motion relationship between the workpiece and the tool and to control the formation process of the machined surface, the tool, the workpiece, and the relative motions of the tool coordinate system, the cutting coordinate system, the workpiece coordinate system, and the reference coordinate system are characterized as shown in Figure 2. The dynamic cutting process variables of the turning tool are explained as shown in

Table 1. TC6 material properties.

Material	Density (g/cm3)	Poisson Ratio	Hardness (N/mm2)	Yield Strength (MPa)	Tensile Strength (MPa)	Compressive Strength (MPa)	Elastic Modulus (GPa)
TC6	4.51	0.34	340	1231	1300	1687	109.8

.

In Figure 2, o-xyz is the reference coordinate system, which is a fixed coordinate system, o_b-x_by_bz_b is the workpiece coordinate system, the origin o_b of this coordinate system is the center point of the workpiece end face, x_b-axis is the direction of depth of cut, z_b-axis is the direction of feed rate, and y_b-axis is established according to the Cartesian coordinate system; o_c-x_cy_cz_c is cutting coordinate system, where the coordinate origin o_c is the intersection of the plane where the lowest point of the cutting tool tooth is located and the projection of the maximum radial extension point of the cutting tool tooth; the line between the coordinate origin and the lowest point of the cutting tool tooth is used as the direction of the z_c-axis, and the line between the coordinate origin and the maximum radial extension point of the cutting tool tooth is used as the direction of the x_c-axis. The y_c-axis was determined according to the principle of the Cartesian coordinate system; the origin o_c of the cutting coordinate system coincides with the origin o_a of the tool coordinate system, the x_c-axis coincides with the x_a-axis, the y_a-axis is in the opposite direction to the y_c-axis, and the z_a-axis is in the opposite direction to the z_c-axis; L is the length of the workpiece, R₀ is the radius of the big end of the workpiece, R₁ is the radius of the small end of the workpiece, R_k is the distance from the axis of the highest point of the machined surface, R_p is the distance of point p from the axis, R_m is the distance from the axis of the lowest point of the machined surface, v_f is the cylindrical turning tool feed rate, v_f’ is the face turning tool feed rate, a_p1 is the depth of cylindrical turning, a_p2 is the end face turning depth, n is the Spindle speed, θ(t) is the angle of rotation of the workpiece coordinate system relative to the initial position during cutting, z(t) is the feed distance of the turning tool in the direction of the feed rate during cutting, D(x,y,z) is the surface to be machined, and G(x,y,z) is the machining transition surfaces, K(x,y,z) is the machined surfaces.

According to Figure 2, the trajectory equation of the cutting coordinate system origin o_c in the machine coordinate system can be expressed as follows:

$$L_c(x_c(t),y_c(t),z_c(t))={\Phi }_0\cdot {\left[\begin{array}{cccc}0& 0& 0& 1\end{array}\right]}^T$$

(5)

where the transformation matrix Φ₀ is T₂T₁M₁. T₂ is the translation matrix of the tool to the reference coordinate system; T₁ is the rotation matrix of the tool coordinate system to the cutting coordinate system; M₁ is the rotation matrix of the workpiece coordinate system to the reference coordinate system.

The transient dynamic characteristics of the cutting edge in the turning process can be revealed by using the above lathe tool structure and transient cutting pose.

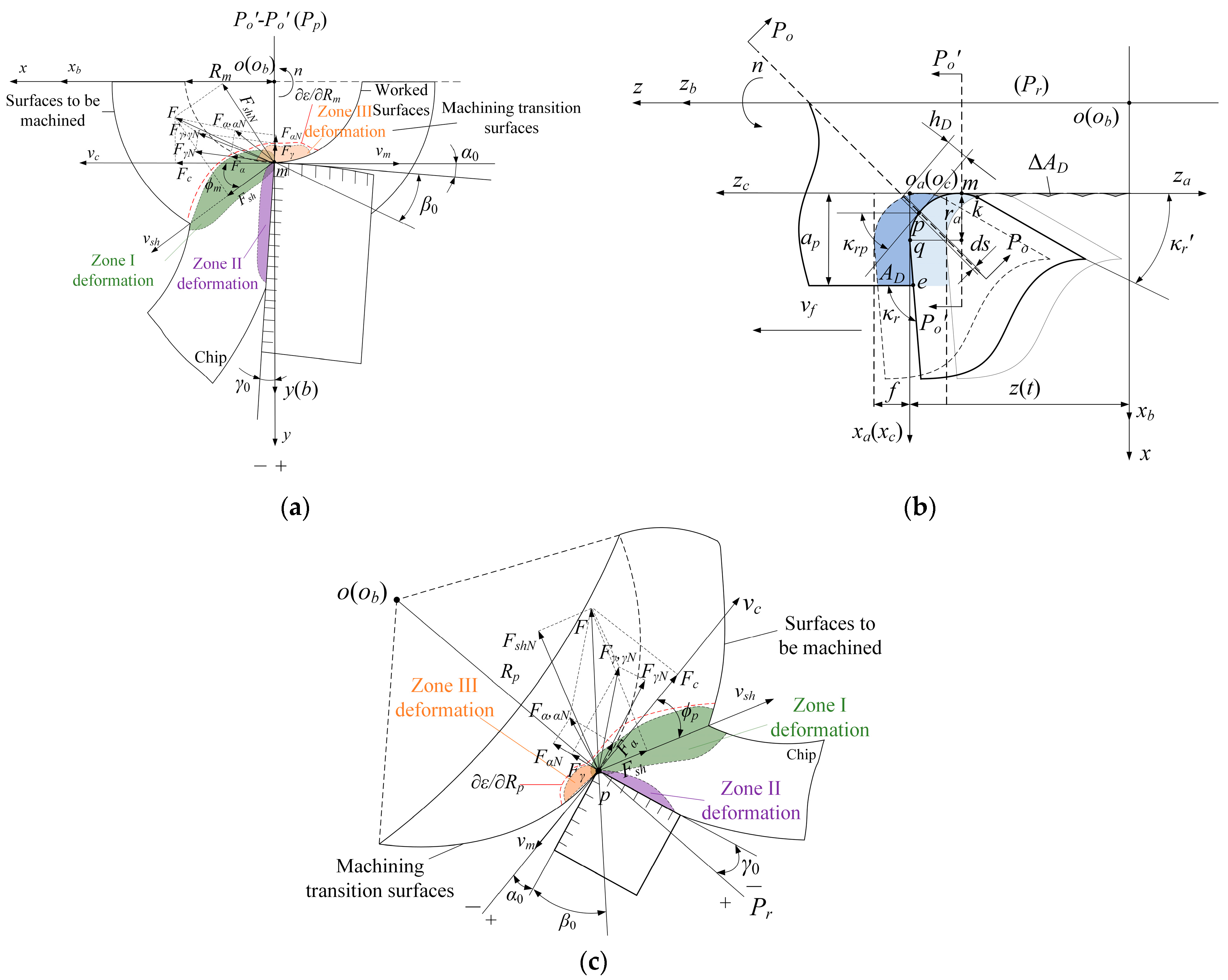
2.2. Transient Cutting Layer and Mechanical Behavior

To elucidate the cutting layer and its mechanical response during the turning of titanium alloy, we characterize the instantaneous force and cutting layer at the point where the lowest workpiece surface point and the tool’s transition arc segment make contact with the workpiece, as depicted in Figure 3.

In Figure 3, point m is the highest point on the cutting edge, point p is an arbitrary point on the transition arc of the cutting edge, γ₀ is the front angle of the tool, α₀ is the back angle of the tool, β₀ is the friction angle on the front face, ϕ_p is the shear angle of point p, f is the feed per revolution, κ_rp is the instantaneous main deflection angle of point p, h_D is the thickness of the cutting layer, ds is the instantaneous micrometer width of the cutting layer of point p, A_D is the actual cutting layer area, ΔA_D is the cutting residual area, R_m is the radius of gyration at point m, R_p is the radius of gyration at point p, v_c is the cutting speed, F_c is the main cutting force, v_m is the friction speed, F_γ is the friction force on the front blade surface, F_γN is the normal force of the friction force on the front blade surface, F_α is the friction force on the rear blade surface, F_αN is the normal force of the friction force on the rear blade surface, v_sh is the shear speed, F_sh is the shear force, F_shN is the shear force in the normal force, F is the combined force of front and rear tool face friction and its normal force, the combined force of shear force and its normal force, and the combined force of main cutting force and feed force.

The instantaneous cutting layer thickness solution for any point p is shown in Equation (6).

$$h_D=f\cdot \sin {\kappa }_{rp}\cdot \cos {\lambda }_s$$

(6)

The cutting layer area A_D solution is shown in Equation (7).

$$A_D={\displaystyle {\int }_e^m{h}_D(x,y,z)\cdot ds\cdot \cos {\lambda }_s}$$

(7)

From Figure 3, Equations (6) and (7), τ denotes the shear stress on the shear surface, and the solution of each force at point p is shown in Equations (8)–(11).

$$F_{sh}={\displaystyle \frac{\tau \cdot A_D}{\sin {\varphi }_p}}$$

(8)

$$F_{sh}=F\cdot \cos \left({\varphi }_p+{\beta }_0-{\gamma }_0\right)$$

(9)

$$F={\displaystyle \frac{F_{sh}}{\cos \left({\varphi }_p+{\beta }_0-{\gamma }_0\right)}}={\displaystyle \frac{\tau \cdot A_D}{\sin {\varphi }_p\cdot \cos \left({\varphi }_p+{\beta }_0-{\gamma }_0\right)}}$$

(10)

$$F_c=F\cdot \cos \left({\beta }_0-{\gamma }_0\right)={\displaystyle \frac{\tau \cdot A_D\cdot \cos \left({\beta }_0-{\gamma }_0\right)}{\sin {\varphi }_p\cdot \cos \left({\varphi }_p+{\beta }_0-{\gamma }_0\right)}}$$

(11)

According to the cutting layer and its mechanical behavior in the turning process, the instantaneous force on any point of the cutting edge and the instantaneous dynamic change characteristics of the cutting layer can be revealed.

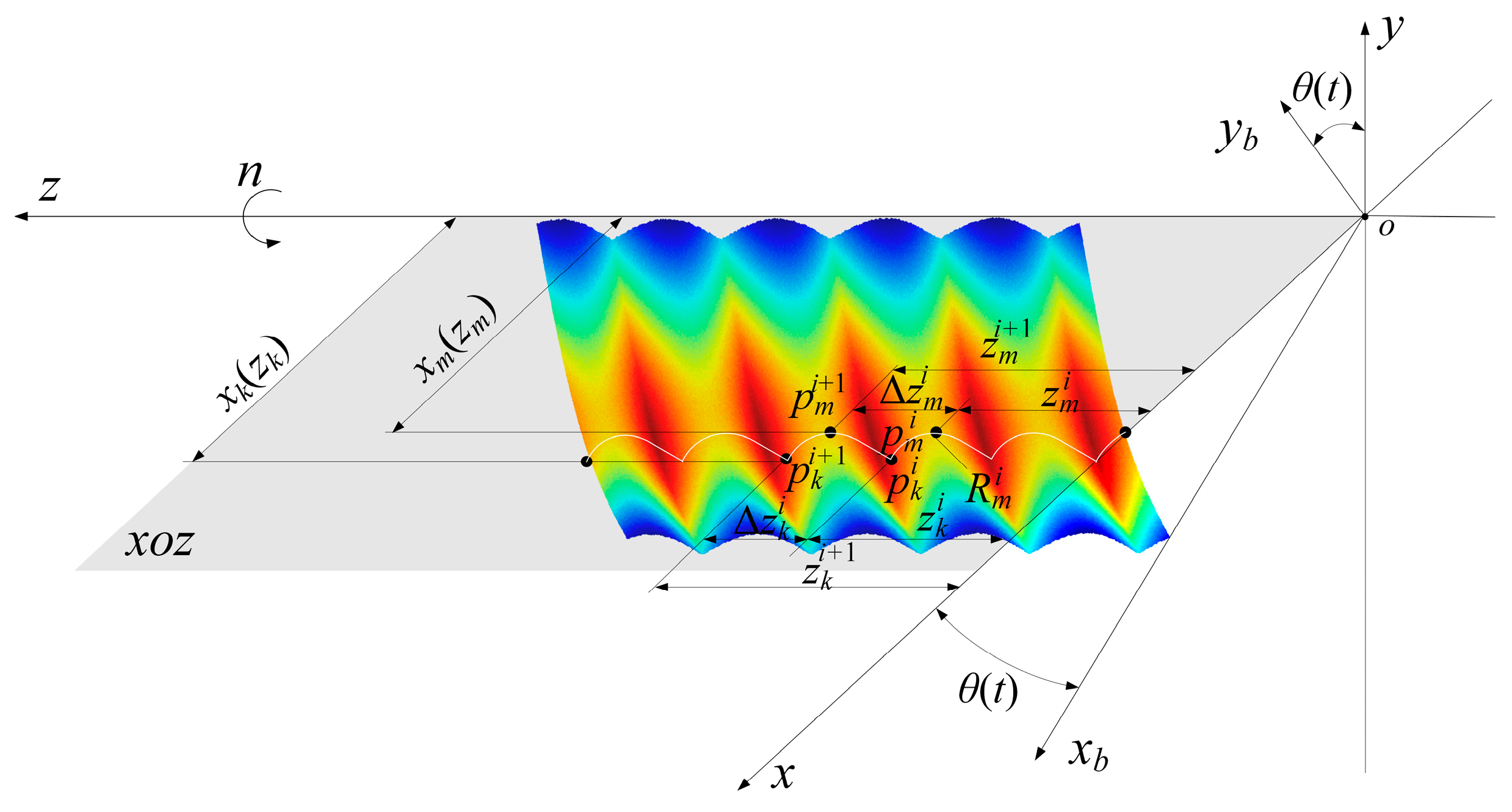
2.3. Surface Morphology Solution Method for Turning Machining

Without taking into account the cutting edge loss and the rear face of the machining of the transition surface of the extrusion effect of the premise, the final machined contour of the workpiece is essentially derived from the superimposed effect of the cutting edge trajectory of the two adjacent cutting cycles. The cutting edge in the previous cutting cycle generated the transition surface at the same time. The subsequent cycle will be partially eliminated through the material removal of the surface formed in the previous cycle and the formation of a new transition surface. The two cycles of the cutting edge trajectory intersection area constitute the cyclical height of the residual.

The turning machining transition surface solution is shown in Equations (12)–(15).

$$H\left(x,y,z\right)=\left\{\begin{array}{l}{H}_{a1}\left(x,y,z\right)\\ H_{a2}\left(x,y,z\right)\\ H_{a3}\left(x,y,z\right)\end{array}\right.$$

(12)

$$H_{a1}\left(x,y,z\right)=\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]={\Phi }_0\cdot L_{a1}=T_2\cdot T_1\cdot M_1\cdot \left[\begin{array}{c}{r}_a+l\sin {\kappa }_r\\ \sin {\kappa }_r\cdot \left(r_a\cdot \left(1-\cos {\varphi }_a\right)+l\cdot \sin {\lambda }_s\right)\\ -l\cos {\kappa }_r\\ 1\end{array}\right]$$

(13)

$$H_{a2}\left(x,y,z\right)=\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]={\Phi }_0\cdot L_{a2}=T_2\cdot T_1\cdot M_1\cdot \left[\begin{array}{c}{r}_t\cdot \left(1-\sin {{\varphi }_a}^{\prime }\right)\\ l\sin {\lambda }_s\\ r_a\cdot \left(1-\cos {{\varphi }_a}^{\prime }\right)\\ 1\end{array}\right]$$

(14)

$$H_{a3}\left(x,y,z\right)=\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]={\Phi }_0\cdot L_{a3}=T_2\cdot T_1\cdot M_1\cdot \left[\begin{array}{c}{r}_a\cdot \left(1-\cos {{\kappa }_r}^{\prime }\right)+l\cdot \sin {{\kappa }_r}^{\prime }\\ \cos {{\kappa }_r}^{\prime }\cdot \left(r_a\cdot \left(1-\sin {\varphi }_a\right)+l\cdot \cos {\lambda }_s\right)\\ r_a\cdot \left(1+\sin {{\kappa }_r}^{\prime }\right)+l\cdot \cos {{\kappa }_r}^{\prime }\\ 1\end{array}\right]$$

(15)

where H_a1 is the machining transition surface formed by the main cutting edge, H_a2 is the machining transition surface formed by the transition arc, and H_a3 is the machining transition surface formed by the secondary cutting edge.

t_s denotes the initial moment of cutting for each revolution of the workpiece, and t_e denotes the end moment of cutting for each revolution of the workpiece. The equation of the machined transition surface formed when the workpiece rotates i weeks is as follows:

$$G_i(x,y,z)=\left\{\begin{array}{l}H(x,y,z)={\left[\begin{array}{cccc}x(t^i)& y(t^i)& z(t^i)& 1\end{array}\right]}^T\\ t_s^i\le t^i\le t_e^i\end{array}\right.$$

(16)

The machined transition surface formed when the workpiece is rotated i + 1 weeks and intersects with the machined transition surface formed by the previous rotary turning is denoted as follows:

$$G_{i+1}(x,y,z)=\left\{\begin{array}{l}H(x,y,z)={\left[\begin{array}{cccc}x(t^{i+1})& y(t^{i+1})& z(t^{i+1})& 1\end{array}\right]}^T\\ G_i(x,y,z)\\ t_s^{i+1}\le t^{i+1}\le t_e^{i+1}\end{array}\right.$$

(17)

The machined transition surface formed when the workpiece is rotated i + 2 weeks and the machined transition surface formed with the previous turning forms the final turned surface can be expressed as follows:

$$G_{i+2}(x,y,z)=\left\{\begin{array}{l}H(x,y,z)={\left[\begin{array}{cccc}x(t^{i+2})& y(t^{i+2})& z(t^{i+2})& 1\end{array}\right]}^T\\ G_{i+1}(x,y,z)\\ t_s^{i+2}\le t^{i+2}\le t_e^{i+2}\end{array}\right.$$

(18)

Based on the above model, MATLAB 2022 software was used for simulation and calculation to simulate the surface morphology of the turning surface, resulting in the turning surface morphology shown in Figure 4.

Intercepting the intersection line between the current cutting position and the xoz plane, the characteristic points p_kⁱ and p_mⁱ are solved as shown in Equations (19) and (20):

$$p_k^i\left(x_k^i,y_k^i,z_k^i\right)=\left\{\begin{array}{c}{H}_{c2}\left(x\left(t^i\right)\right.,0,\left.z\left(t^i\right)\right)\\ H_{c3}\left(x\left(t^{i+1}\right)\right.,0,\left.z\left(t^{i+1}\right)\right)\\ K\left(x,y,z\right)=0\\ t=t^{i+1}\end{array}\right.$$

(19)

$$p_m^i\left(x_m^i,y_m^i,z_m^i\right)=\left\{\begin{array}{c}{H}_{c2}\left(x\left(t^{i+1}\right)\right.,0,\left.0\right)\\ K\left(x,y,z\right)=0\\ t=t^{i+1}\end{array}\right.$$

(20)

During the turning process, the property parameters of the subsurface layer of titanium alloys are constantly changing. During the machining process of turning titanium alloys, the characterization coefficients of the subsurface layer are important indicators for evaluating the material properties, which mainly include plastic strain, residual stress, and rate of work hardening. These three characteristic parameters not only characterize the deformation and stress state of the material during machining but also have a major influence on the fatigue life of the material. Plastic strain is the irreversible deformation of the material during the loading process. The plastic strain generated in titanium alloys during turning improves the fatigue resistance, but an excessively high level will lead to fatigue cracks and reduced fatigue life. Residual stresses are internal stresses due to uneven deformation that remains after the removal of external loads. Appropriate residual stresses improve fatigue strength, but uneven distribution causes stress gradients and reduces fatigue life. The rate of work hardening indicates the hardness of the material due to deformation, and a higher rate of work hardening helps to improve wear resistance and fatigue resistance.

The formula presents a set of characteristic parameters essential for evaluating the machined surface of titanium alloy. Here, D₁ represents the workpiece material attribute, D₂ denotes the tool material attribute, D₃ signifies the tool structure parameter, and D₄ reflects the turning process parameter.

$$D=\left\{D_1,D_2,D_3,D_4\right\}$$

(21)

$$D_3=\left\{{\kappa }_r,{{\kappa }_r}^{\prime },\gamma ,\beta ,r_a\right\}$$

(22)

$$D_4=\left\{a_p,n,f\right\}$$

(23)

Based on the above model, different surface morphology parameters can be obtained when the workpiece material properties, tool material properties, tool structure parameters, and process parameters are different.

3. Titanium Alloy Turning Process Morphology Correction Method

3.1. Workpiece Material and Tool Material

TC6 titanium alloy contains α-stabilizing element Al, eutectic β-stabilizing element Mo, and eutectoid β-stabilizing elements Cr and Fe, as well as neutral element Si. The β-stabilization coefficient Kp = 0.6. The D₁ set in Equation (21) in Section 2.3 is shown in Table 1.

The workpiece material is TC6, and the tool material is WC cemented carbide. The D₂ set in Section 2.3 Chinese (21) is shown in

Table 2. Parameters of WC materials.

Material	Density (g/cm3)	Elastic Modulus (GPa)	Poisson Ratio	Thermal Conductivity (W/m·°C)	Specific Heat Capacity (J/kg·°C)
WC	15.7	705	0.23	24	178

.

3.2. Experimental Conditions and Methods for Titanium Alloy Turning

During machining operations, the tool’s instantaneous pose exhibits dynamic fluctuations caused by factors such as vibration and precision deviations, resulting in stochastic changes in the microstructure of the machined surface. Experimental turning was conducted to measure the surface morphology of a titanium alloy. Data points from the sections were extracted and subjected to multi-Scheme regression analysis to refine the simulation model for the machining surface morphology of the titanium alloy.

A CNC lathe was utilized to machine a titanium alloy workpiece using a 55° cylindrical turning tool produced by Walter Company. The machining process involved cylindrical turning, with a main deviation angle of 93°. The radius of the tool tip arc was set at 0.4 mm. The tool holder model used was PDJNR2525M1506, and the insert model was DNMG150604. The selected cutting parameters are detailed in

Table 3. Turning experiment plan.

Plan	Turning Process Parameters
	ap (mm)	n (r/min)	f (mm)
1	0.1	590	0.1
2	0.15	590	0.1
3	0.2	590	0.1
4	0.25	590	0.1
5	0.2	491	0.1
6	0.2	786	0.1
7	0.2	1180	0.1
8	0.2	590	0.06
9	0.2	590	0.14
10	0.2	590	0.2

, and the cutting method employed was dry cutting. The materials for both the workpiece and the tool are specified in Table 1 and Table 2 in Section 2.1.

The three-dimensional surface topography of machined specimens was quantitatively characterized using a PZ-CS3500A super depth-of-field microscope produced by Beijing Pinzhichuangsi Precision Instruments Co., with the corresponding experimental setup illustrated in Figure 5.

3.3. Corrective Modeling of Surface Morphology for Turning of Titanium Alloys

The topographical parameters of titanium alloy machined surfaces exhibit stochastic variations across distinct sampling locations. These spatial-dependent characteristics were mathematically modeled through Equations(24)–(29), which establish functional relationships between surface parameters and sampling coordinates.

$$x_k^i\left(z_k^i,{\theta }_k^i\right)=\left\{x_k^1\left(z_k^1,{\theta }_k^1\right),x_k^2\left(z_k^2,{\theta }_k^2\right),x_k^3\left(z_k^3,{\theta }_k^3\right),\dots ,x_k^0\left(z_k^0,{\theta }_k^0\right)\right\}$$

(24)

$$x_m^i\left(z_m^i,{\theta }_m^i\right)=\left\{x_m^1\left(z_m^1,{\theta }_m^1\right),x_m^2\left(z_m^2,{\theta }_m^2\right),x_m^3\left(z_m^3,{\theta }_m^3\right),\dots ,x_m^0\left(z_m^0,{\theta }_m^0\right)\right\}$$

(25)

$$\Delta x_k^i\left(z_k^i,{\theta }_k^i\right)=\left\{\Delta x_k^1\left(z_k^1,{\theta }_k^1\right),\Delta x_k^2\left(z_k^2,{\theta }_k^2\right),\Delta x_k^3\left(z_k^3,{\theta }_k^3\right),\dots ,\Delta x_k^0\left(z_k^0,{\theta }_k^0\right)\right\}$$

(26)

$$\Delta x_m^i\left(z_m^i,{\theta }_m^i\right)=\left\{\Delta x_m^1\left(z_m^1,{\theta }_m^1\right),\Delta x_m^2\left(z_m^2,{\theta }_m^2\right),\Delta x_m^3\left(z_m^3,{\theta }_m^3\right),\dots ,\Delta x_m^0\left(z_m^0,{\theta }_m^0\right)\right\}$$

(27)

$$R_m^i\left(z_m^i,{\theta }_m^i\right)=\left\{R_m^1\left(z_m^1,{\theta }_m^1\right),R_m^2\left(z_m^2,{\theta }_m^2\right),R_m^3\left(z_m^3,{\theta }_m^3\right),\dots ,R_m^0\left(z_m^0,{\theta }_m^0\right)\right\}$$

(28)

$$R{a}^i\left(z_m^i,{\theta }_m^i\right)=\left\{R{a}^1\left(z_m^1,{\theta }_m^1\right),R{a}^2\left(z_m^2,{\theta }_m^2\right),R{a}^3\left(z_m^3,{\theta }_m^3\right),\dots ,R{a}^0\left(z_m^0,{\theta }_m^0\right)\right\}$$

(29)

Variations in machining parameters necessitate the identification of deterministic surface morphology variables in turning operations. Multivariate regression models through Equations (24)–(29) were developed to establish correlations between process parameters, sampling locations, and topographical descriptors of machined surfaces.

$$S_a=\left\{x_k\left(z_k,{\theta }_k\right),x_m\left(z_m,{\theta }_m\right),\Delta x_k\left(z_k,{\theta }_k\right),\Delta x_m\left(z_k,{\theta }_m\right),R_m\left(z_m,{\theta }_m\right),Ra\right\}$$

(30)

Let’s denote the characteristic covariates within the parameter set. The corresponding regression model is expressed by Equation (31), with its coefficients systematically summarized in

Table 4. Fitting coefficients of surface morphology characterizing coefficients for turning machining.

Characteristic Parameter: (sa)	Coefficients of the Fitted Equations
	β	α1	α2	α3	α4	α5
xk	0.0003	−0.0108	0.03	1.9188	0.0586	−0.0290
xm	0.0002	2.2266	−0.741	0.3109	0.0482	−0.0376
Δxk	6.9255 × 10−5	1.9741	−0.7651	0.8547	0.0076	0.0003
Δxm	3.7007 × 10−5	1.9987	−0.701	0.8742	0.0108	0.0092
Rm	3326.3511	−0.3473	0.196	−0.3868	0.012	0.0174
Ra	7.0221 × 10−8	4.4540	−1.6163	0.7695	−0.0015	−0.0008

.

$$s_a=\beta \cdot {a_p}^{{\alpha }_1}\cdot n^{{\alpha }_2}\cdot f^{{\alpha }_3}\cdot z^{{\alpha }_4}\cdot {\theta }^{{\alpha }_5}\cdot s_0$$

(31)

where β, α₁~α₅ are the coefficients of the fitted regression equation, and s₀ represents the value of each characteristic parameter corresponding to the ideal uniform surface. When the machined surface is ideal and uniform, β = 1, α₁~α₅ are all 0, meaning that s_a = s₀.

S₀ is related to tool parameters, process parameters, and other factors, with the set of variables shown in Equation(32).

$$s_0=\left\{D_1,D_2,D_3,D_4,L_c\right\}$$

(32)

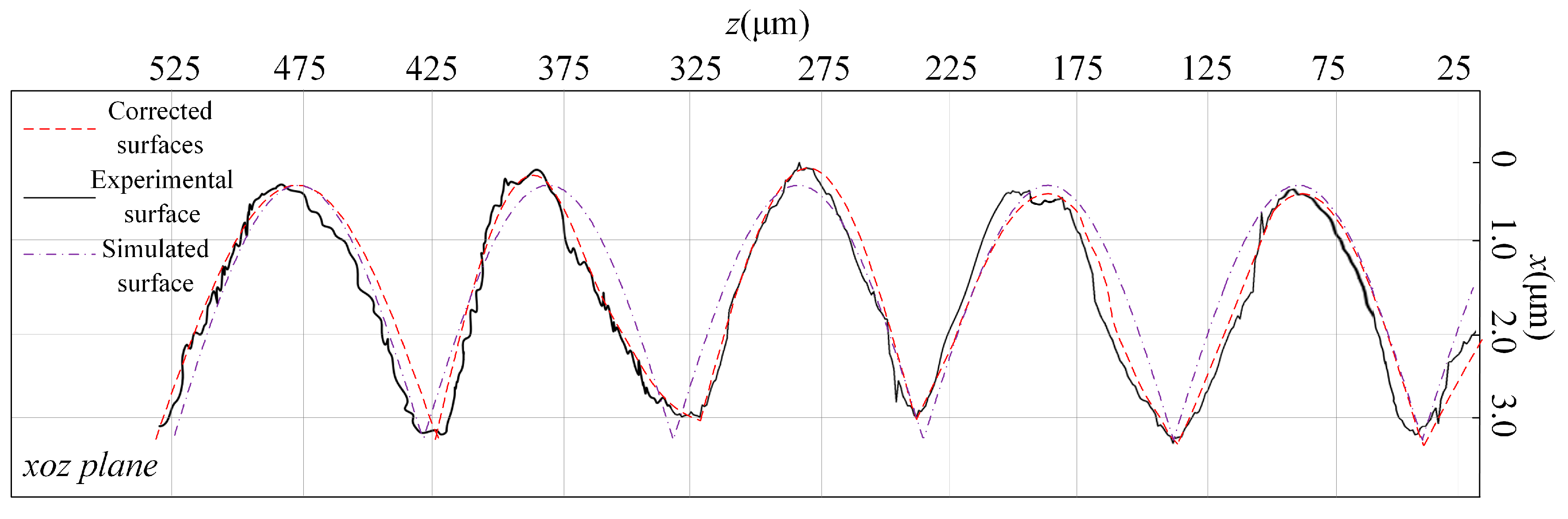
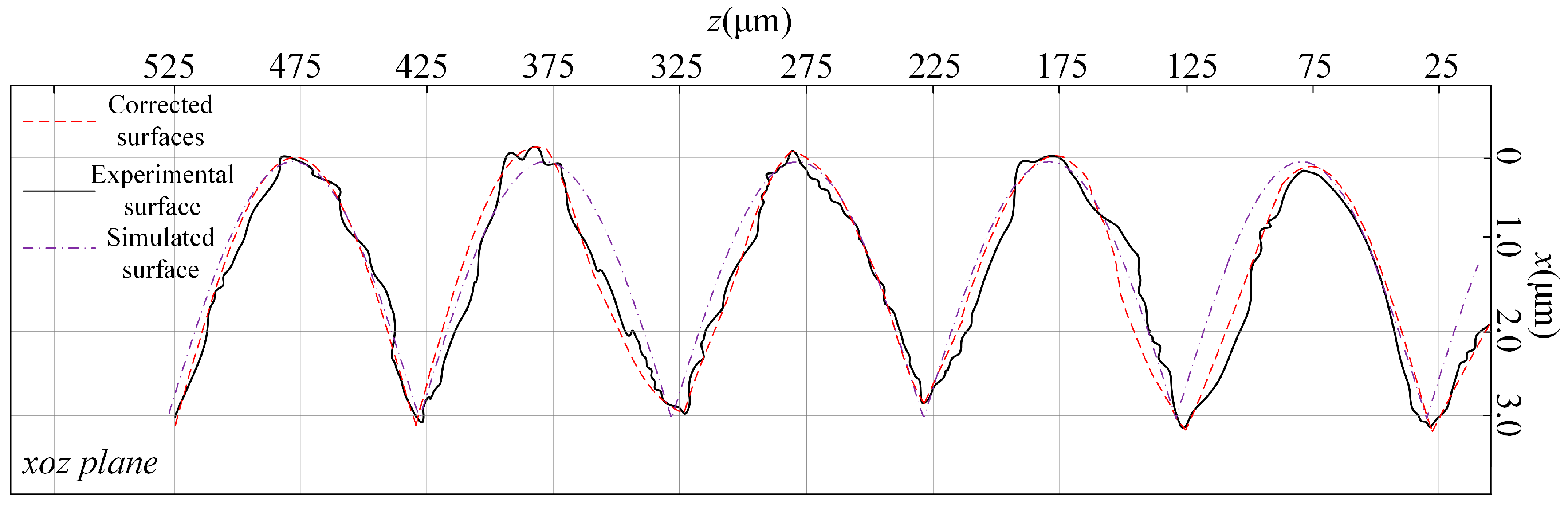
3.4. Comparison of Titanium Alloy Turning Surface Morphology Correction Results with Experimental Results

Based on the above-mentioned turning surface calculation correction model, MATLAB was used to calculate the turning morphology with the introduction of correction coefficients. In the turning process parameter set D₃, the feed rate f per revolution was 0.1 mm, the spindle speed n was 983 r/min, and the cutting depth a_p was 0.1 mm. This Scheme was defined as Scheme 1. The turning morphology was simulated again at the same position, and the feature point identification is shown in Figure 6.

Figure 7 compares the cross-sectional profiles of the machined surface topography with experimentally measured profiles, both before and after error correction. Gray correlation analysis reveals a correlation coefficient of 0.81 between the original simulated profile and the experimental measurements. After correction, this value increases to 0.93, indicating a strong correlation. These results validate the feasibility of applying fitted regression functions to enhance surface topography predictions in turning processes.

The location of different characteristic points of the surface topography of the turning process and the radius of curvature are solved, and the results are shown in

Table 5. Characteristic points of the machined surface morphology.

Group	Highest Point of Machined Surface Topography pk			Lowest Point of Machined Surface Topography pm
	xk (μm)	Δxk (μm)	Δzk (μm)	xm (μm)	Δxm (μm)	Δzm (μm)	Rm (μm)
1	0	0	0	0	0	0	∞
2	3	0	100	0	0	100	400
3	2.73~4.05	0~1.32	97.86~101.12	−0.75~1.08	0~1.83	98.76~102.11	383.54~415.24

. Group 1 is the ideal smooth surface, Group 2 is the simulated surface, and Group 3 is the modified surface.

Table 6. Position of the highest and lowest points of the machined surface profile and their errors.

		Direction	Highest Point of Surface Topography for Different Machining Cycles pki					Minimum Point of Surface Topography for Different Machining Cycles pmi
			i = 1	i = 2	i = 3	i = 4	i = 5	i = 1	i = 2	i = 3	i = 4	i = 5
Corrected surfaces		x (μm)	2.88	3.20	2.61	3.02	2.98	0.17	0.18	−0.29	−0.69	0.09
		z (μm)	28.89	127.05	227.17	312.76	424.25	79.84	179.57	275.84	380.56	478.57
		Δx (μm)	-	0.32	−0.59	0.41	−0.04	-	0.01	−0.47	−0.40	0.78
		Δz (μm)	-	98.16	100.12	85.59	111.49	-	99.73	96.27	104.72	98.01
Experimental surface		x (μm)	2.92	3.24	2.73	2.95	3.00	0.18	0.19	−0.26	−0.75	0.09
		z (μm)	29.17	127.03	227.12	313.68	424.14	80.32	181.14	276.33	379.97	480.18
		Δx (μm)	-	0.32	−0.51	0.22	0.05	-	0.01	−0.45	−0.49	0.66
		Δz (μm)	-	97.86	100.09	86.56	110.36	-	100.82	95.19	103.64	100.21
Absolute error		x (μm)	0.04	0.04	0.12	0.07	0.02	0.01	0.01	0.03	0.06	0
		z (μm)	0.28	0.02	0.05	0.92	0.11	0.48	1.57	0.49	0.59	1.61
		Δx (μm)	-	0	0.08	0.19	0.01	-	0	0.02	0.11	0.12
		Δz (μm)	-	0.30	0.03	0.97	4.13	-	1.09	1.08	1.08	2.2
Relative error		x (%)	1.37	1.23	4.40	2.37	0.67	5.56	5.26	11.54	8.00	0
		z (%)	6.71	0.99	2.36	8.13	12.79	9.02	25.57	36.84	11.87	31.08
		Δx (%)	-	0	15.69	53.66	20.00	-	0	4.44	22.45	18.18
		Δz (%)	-	0.31	0.01	1.12	3.74	-	1.08	1.13	1.04	2.20

presents the peak and valley positions in the machined surface topography, along with the absolute and relative errors between the corrected and experimental surfaces. The results indicate that after the correction of the machined surface topography, the relative errors for most positions and their corresponding distances in the feed and depth-of-cut directions are small. Specifically, 50.00% of the positions have relative errors between 0% and 5%, 16.67% fall between 5% and 10%, and 8.33% lie between 10% and 15%, totaling 75%. This suggests a high correlation between the characteristic coefficient positions and their respective measurements.

4. Method for Calculating the Distribution Characteristics of Surface and Subsurface Performance Parameters of Titanium Alloy Turned Parts

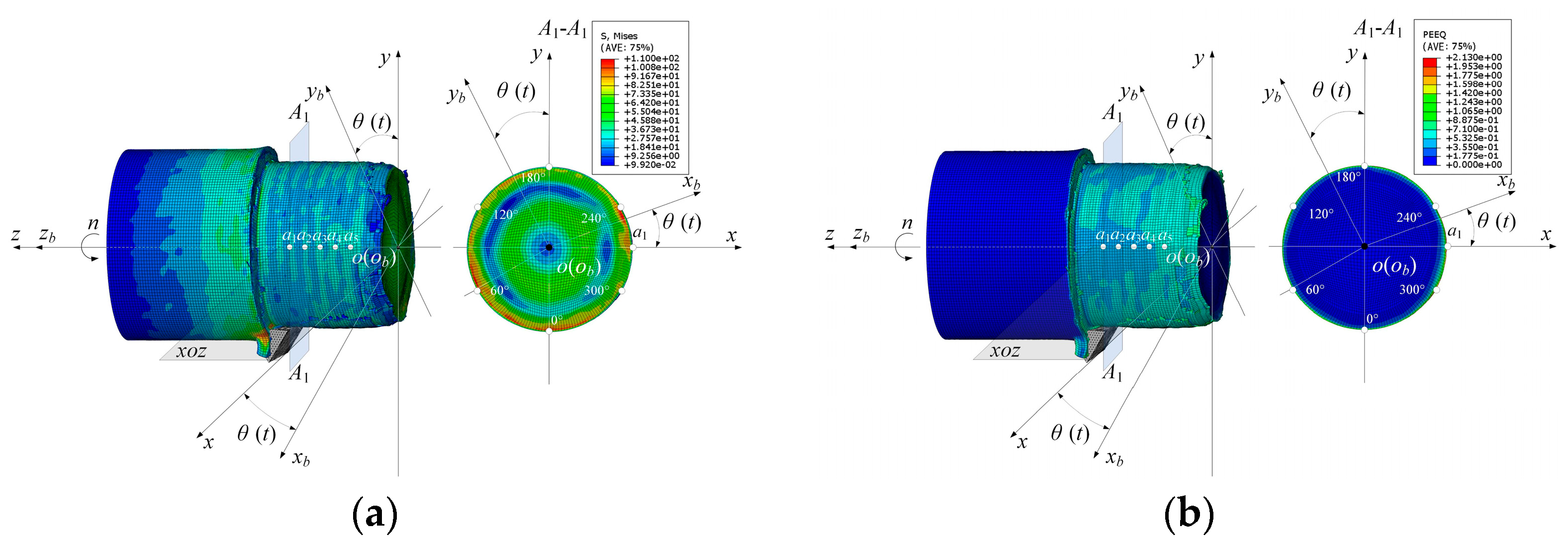
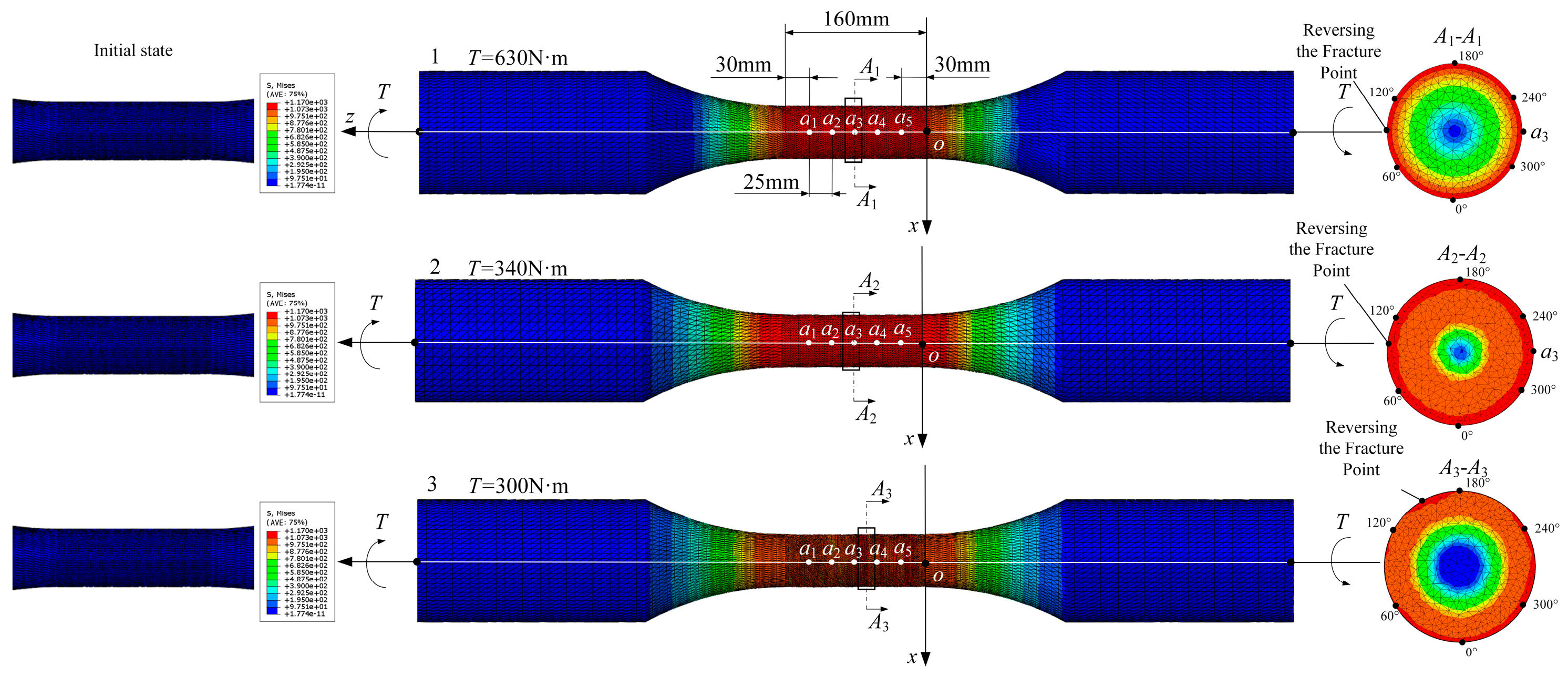
4.1. Finite Element Model Construction Method for Titanium Alloy Turning Process

Based on the properties of titanium alloys and tool materials presented in Table 1 and Table 2 of Section 3.1, it is evident that the elastic modulus of the tool material (705 GPa) is significantly higher than that of the workpiece material (109.8 GPa). As a result, the deformation of the tool during machining is minimal, allowing it to be treated as a rigid body in the modeling process. In the ABAQUS environment, a thermal-mechanical coupled field analysis model was developed for the external cylindrical turning of titanium alloy. Given the considerable heat generated by friction during the turning process, which impacts the material’s mechanical properties, the model underwent thermal-mechanical coupled field analysis. The boundary conditions of the model were established as follows: the bottom surface and both ends of the workpiece were fixed, while the tool moved relative to the workpiece at a predetermined feed rate and rotational speed, simulating actual turning conditions. Titanium alloys exhibit low thermal conductivity, which means that the heat generated by friction during machining can significantly influence their mechanical properties. During the machining of titanium alloy TC6, heat generated by plastic deformation cannot dissipate quickly within a short duration, thus allowing the machining process to be regarded as an adiabatic shearing process.

For this purpose, the Johnson–Cook dynamic response constitutive model was selected as the benchmark for material behavior analysis, as shown in Equation (33).

$$\sigma =(A+B{\epsilon }^n)(1+C\ln {\displaystyle \frac{\dot{\epsilon }}{{\dot{\epsilon }}_0}})[1-{({\displaystyle \frac{T-T_0}{T_{melt}-T_0}})}^m]$$

(33)

where plastic J–C stress is a function of strain, strain rate and temperature, A, B, n, C, and m are model constants. σ is the flow stress, ε is the equivalent plastic strain, is the strain rate, is the reference true strain, T is the operating temperature, T_melt is the melting temperature of the material, and T₀ is the ambient temperature.

In the context of mesh partitioning, the workpiece is modeled using linear reduced integration 8-node hexahedral elements, while the tool is represented by tetrahedral temperature-displacement coupled elements. The contact relationship between the tool and the workpiece is established as a master-slave contact pair, with the tool acting as the master surface and the workpiece serving as the slave surface. The tool-workpiece contact interface is characterized using a kinematic friction model, with a friction coefficient of μ = 0.1. The initial temperature of the workpiece is set to room temperature (20 °C). Using the developed finite element model, the turning process for the outer diameter of the titanium alloy is analyzed.

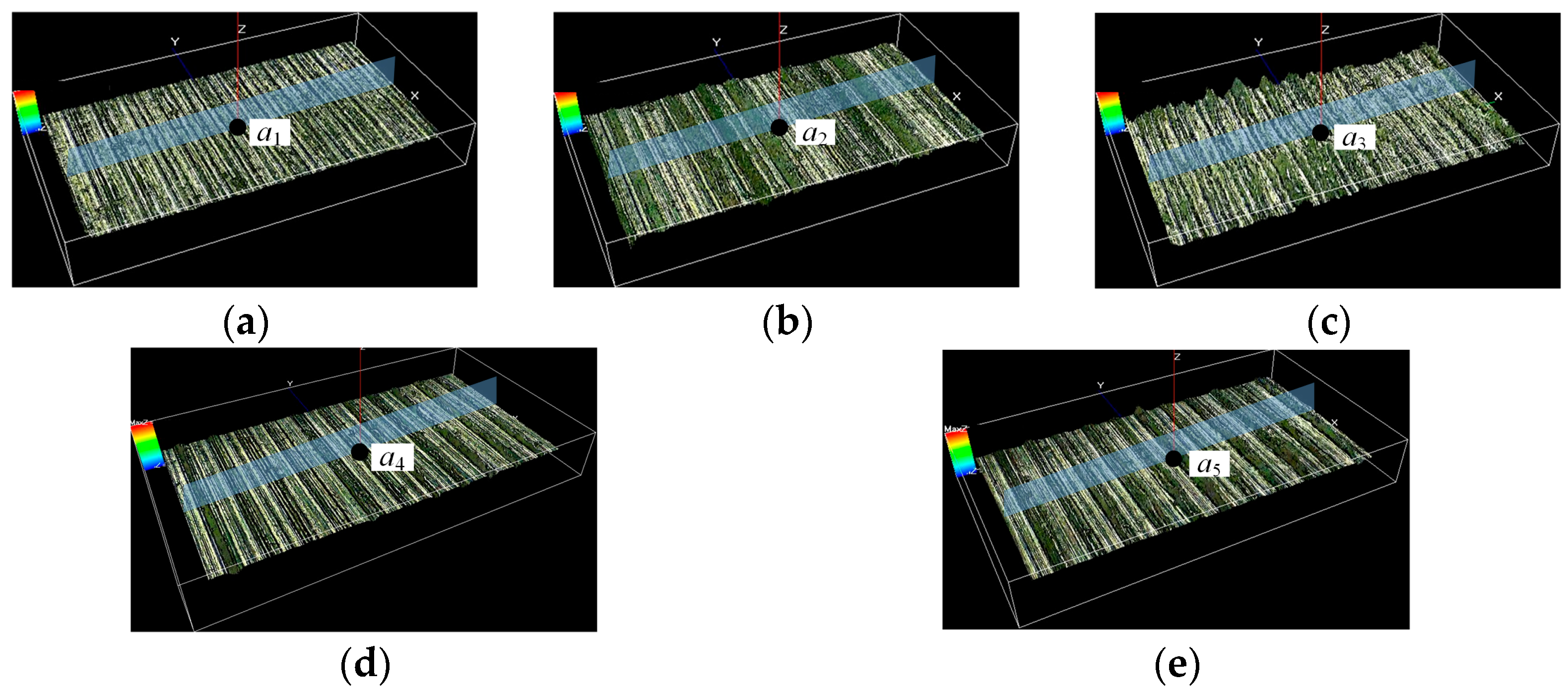
4.2. Method for Selecting Characteristic Points and Their Surface and Subsurface Performance Parameters

Five equidistant characteristic points (a₁–a₅) were analyzed along the xoz surface, spaced at 2.5 mm intervals over a 10 mm total length. As illustrated in Figure 8a,b, the stress and strain field distributions across section A₁-A₁ at point a₁ demonstrate typical cross-sectional behavior.

Utilizing the model and methodology delineated in Section 3.1, determine the dimensions and dispersion of the performance metrics pertaining to the specified characteristic points along both the axial orientation and the perimeter of the cross-section. This analysis is conducted under conditions where the feed rate per revolution (f) is 0.1 mm, the spindle speed (n) is 983 revolutions per minute, and the cutting depth (a_p) is 0.1 mm. Notably, the plastic strain and residual stress values can be directly extracted, while the work hardening rate necessitates derivation through the stress–strain relationship during the plastic strain phase of the stress–strain curve, as depicted in the provided formula.

$$\eta ={\displaystyle \frac{\partial \sigma }{\partial \epsilon }}$$

(34)

where σ and ε denote the stress and strain during plastic deformation, respectively.

Plastic strain denotes the permanent deformation of a material subjected to external forces, typically manifesting after the material’s yield point. Residual stress serves as a crucial metric for evaluating the surface quality of finished turning operations and plays a pivotal role in assessing the machinability of workpiece materials. The work hardening rate quantifies the extent of hardness augmentation in the material’s surface layer resulting from plastic deformation and thermodynamic influences during mechanical processing.

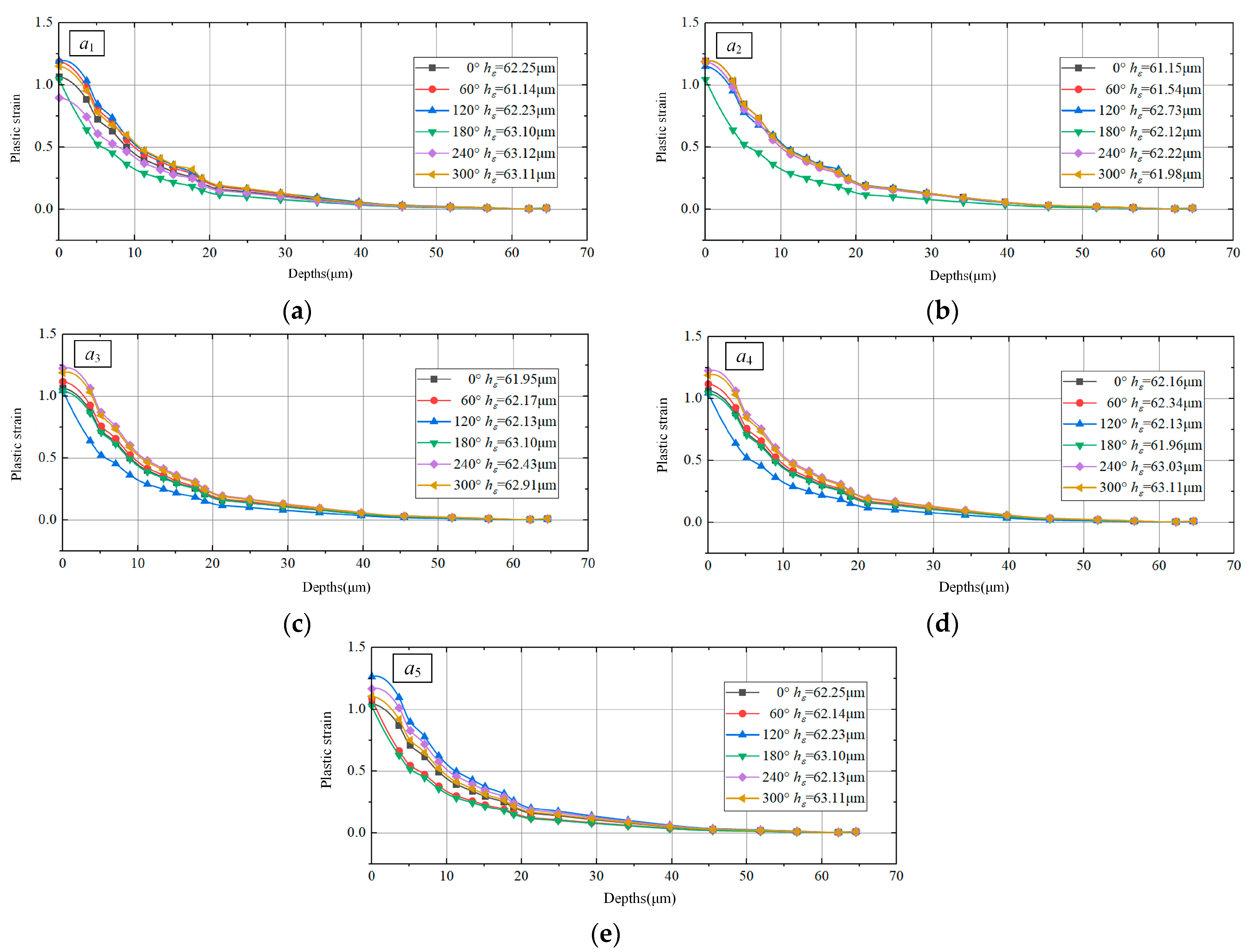
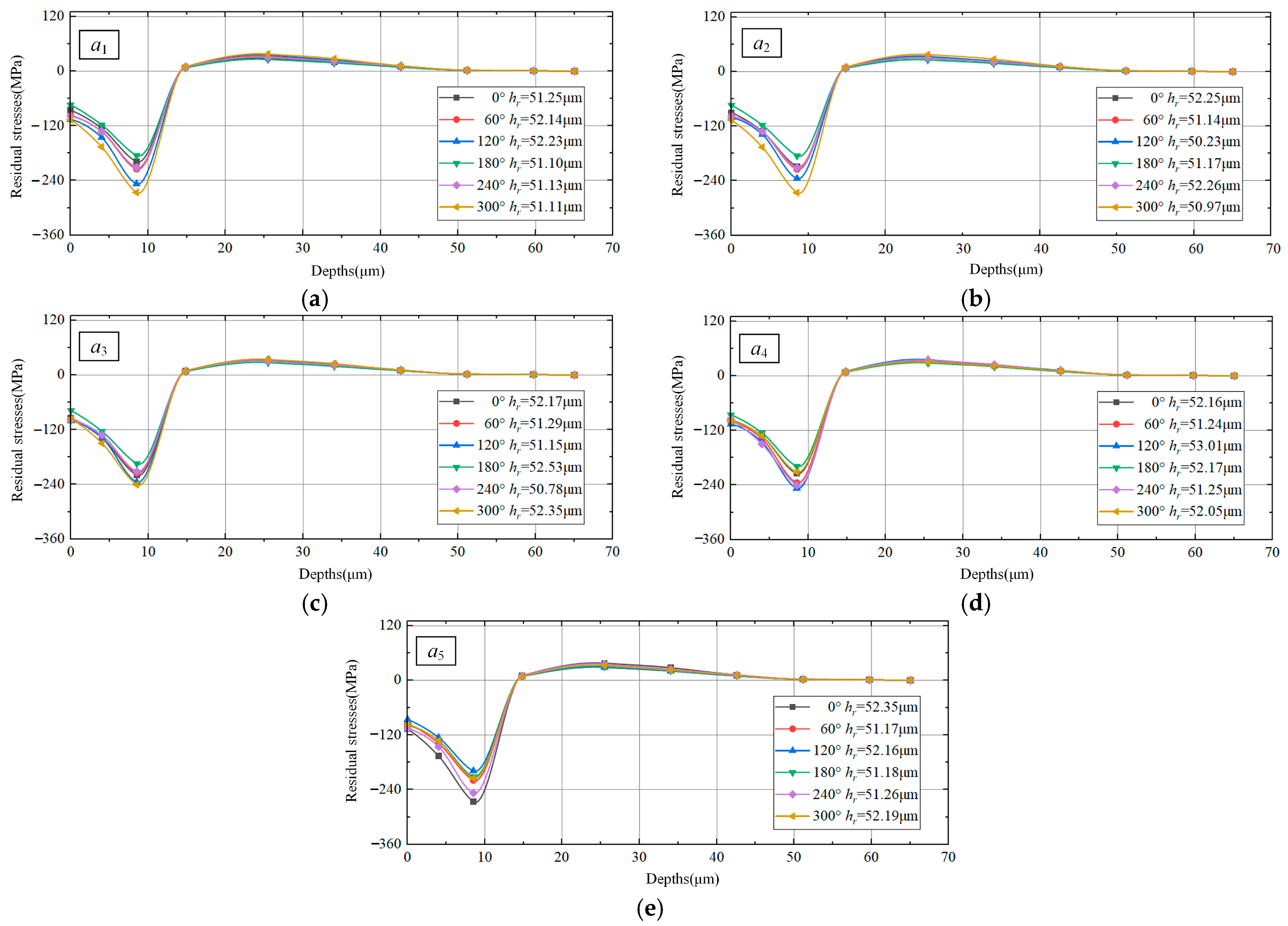
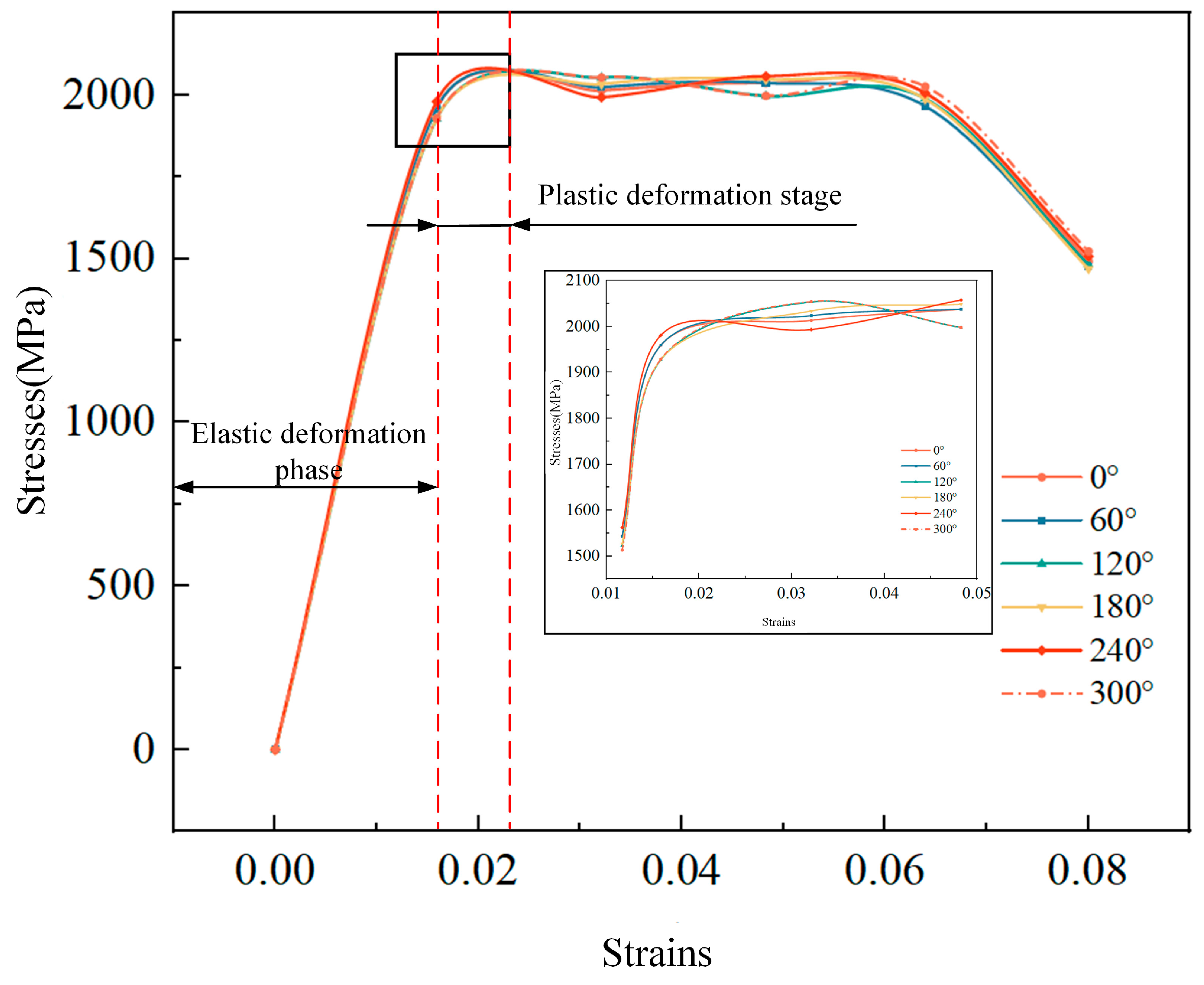
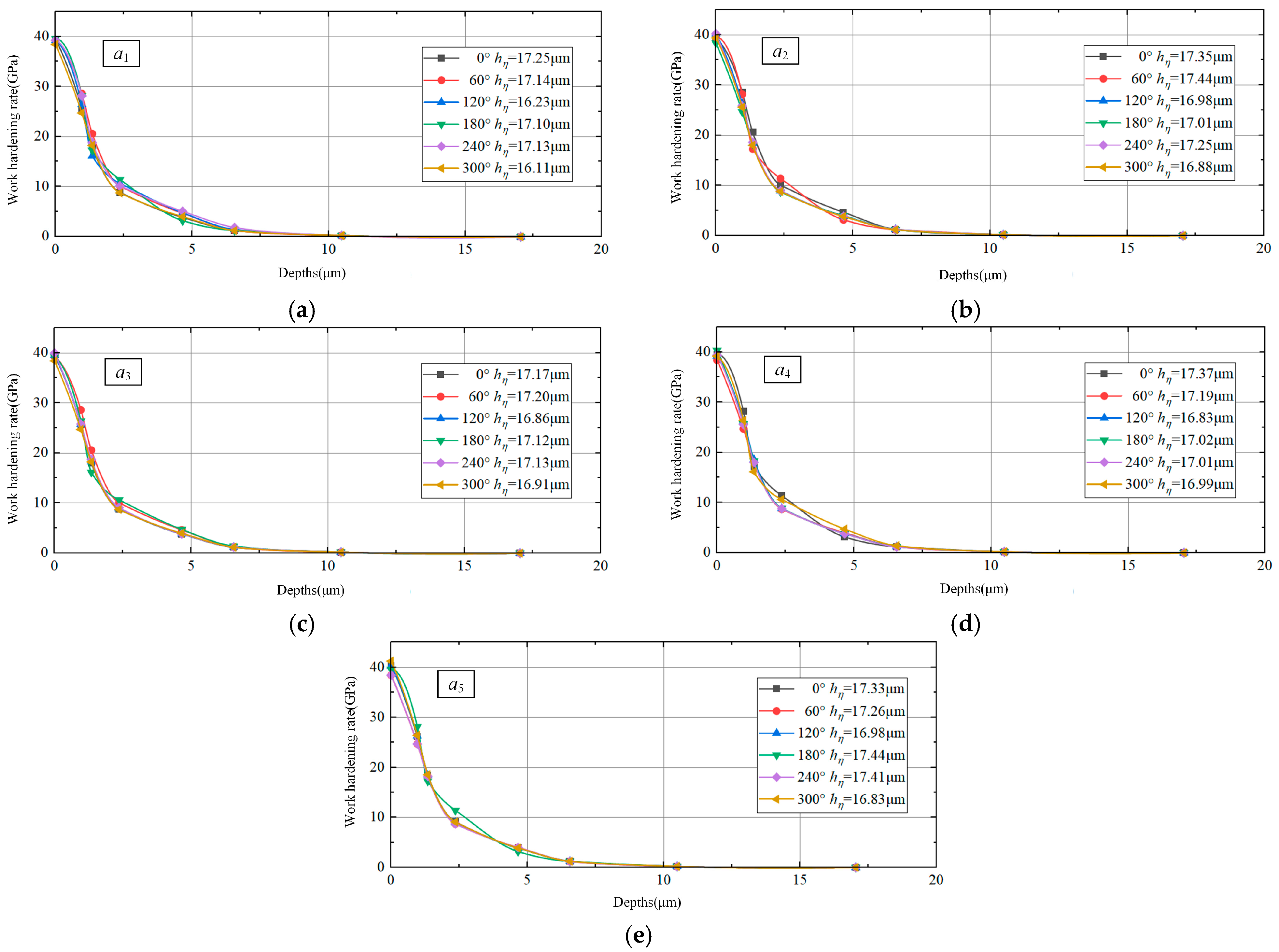
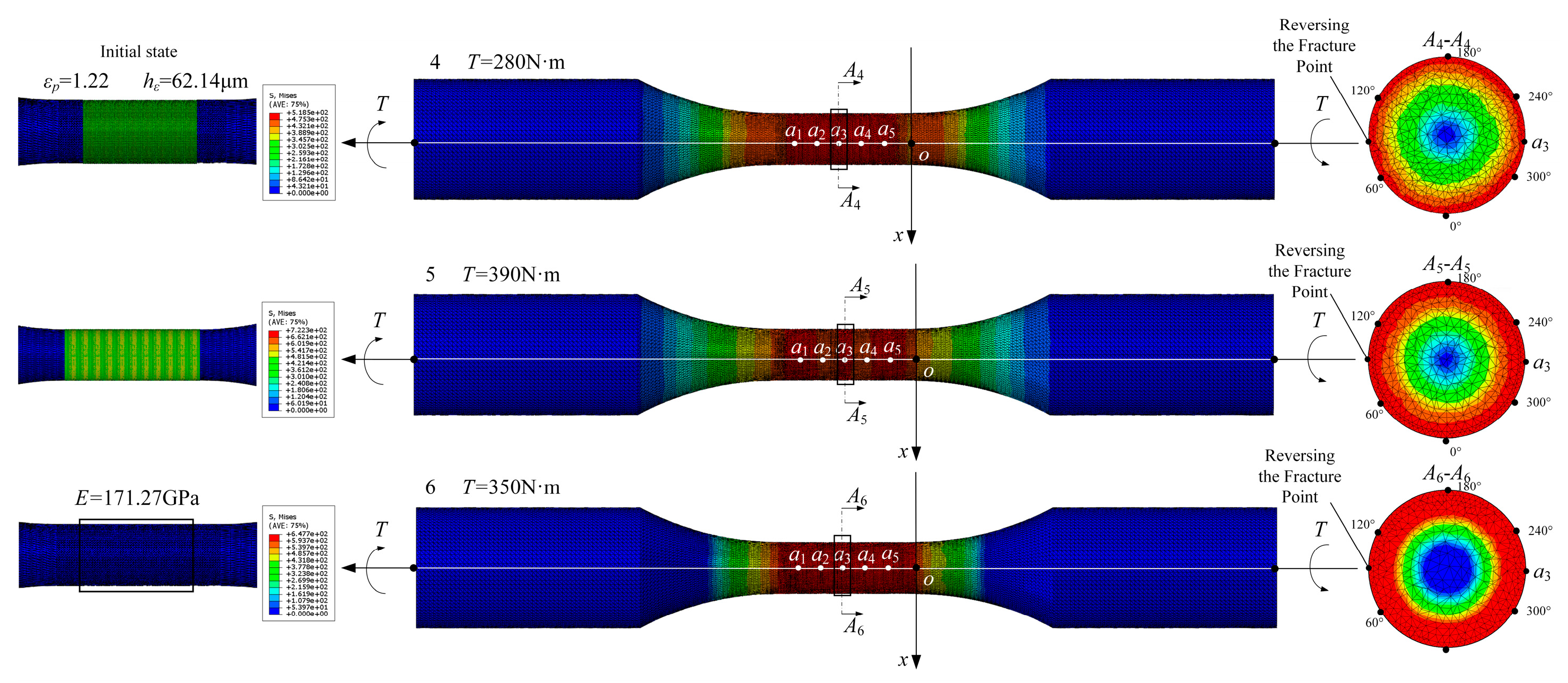
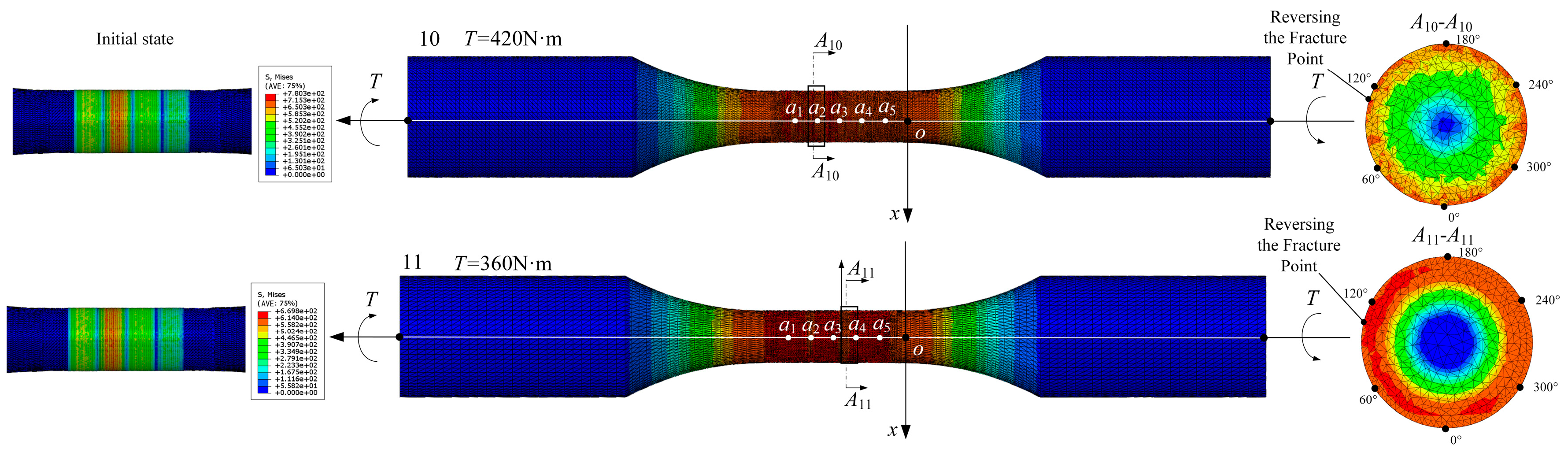
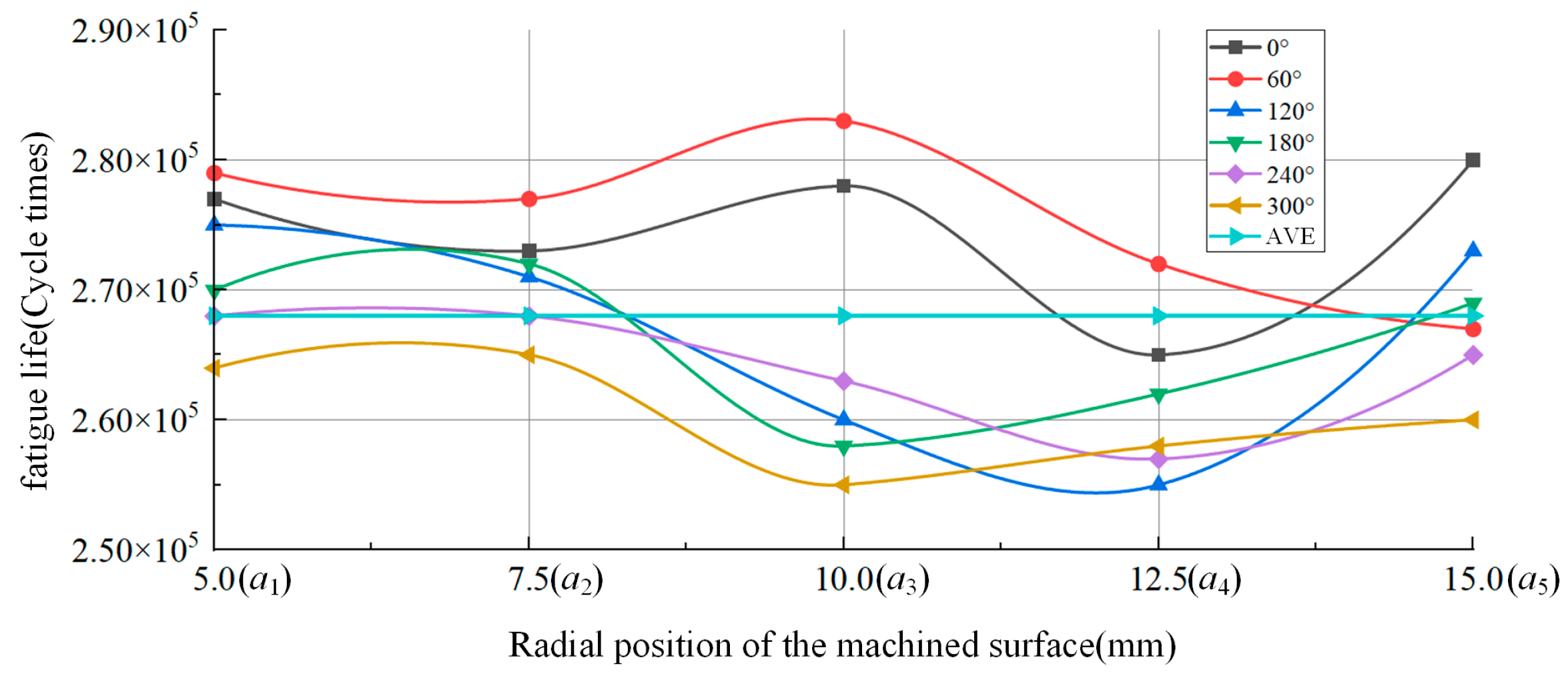
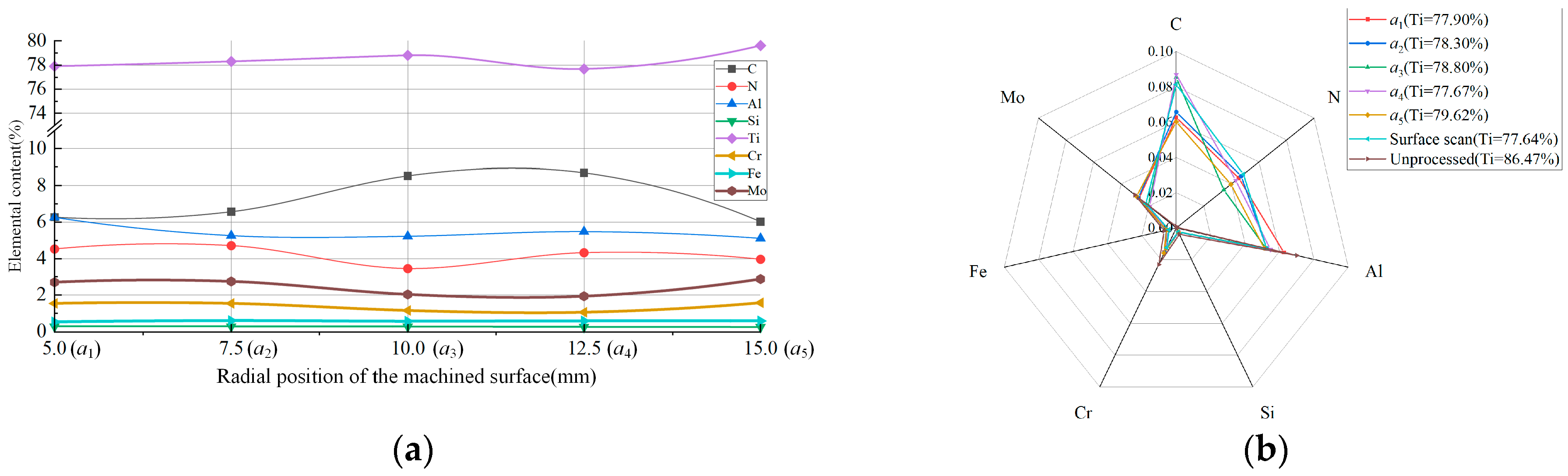
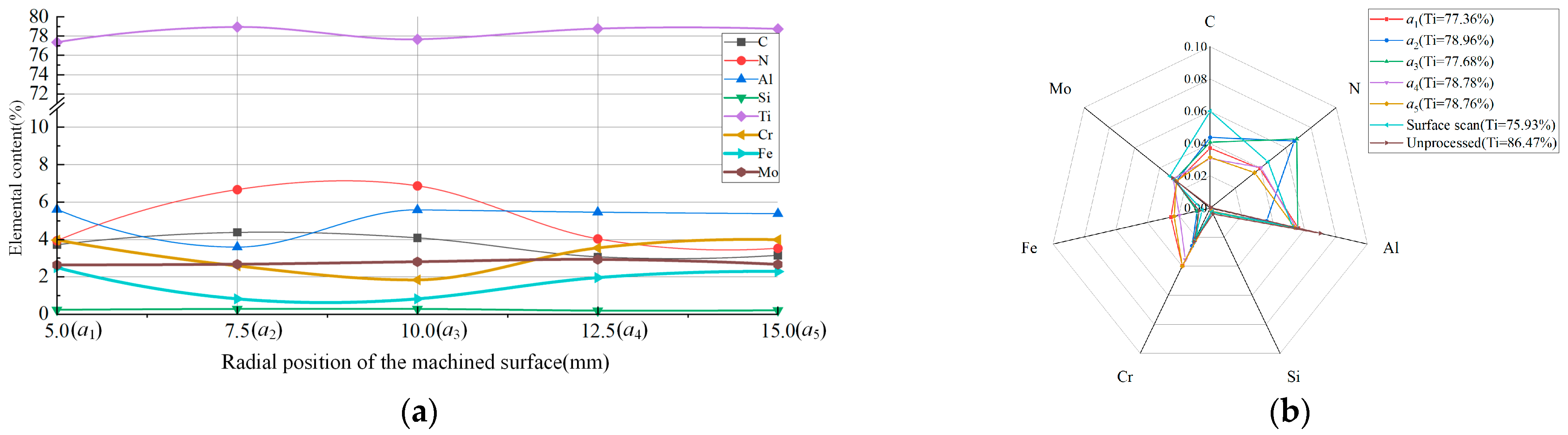
4.3. Surface and Subsurface Performance Parameter Calculation Results

Based on the characteristic points specified in Section 3.2 and the method for selecting surface and subsurface performance parameters, the characteristic points are selected, and the different surface and subsurface characteristic parameters in the axial and circumferential directions on their cross-sections are extracted. The plastic strain of the characteristic points on the cross-sections where a₁ to a₅ are located is shown in Figure 9, and the residual stress is shown in Figure 10. Taking a₁ as an example, its stress–strain curve is shown in Figure 11. By differentiating the stress–strain plastic deformation stage using the equation, the work hardening rate versus depth curve shown in Figure 12 is obtained.

As shown in Figure 9, Figure 10, Figure 11 and Figure 12, on the machined surface of titanium alloy, the variation characteristics of different surface and subsurface performance parameters along the axial and circumferential directions exhibit certain similarities, but their distribution still exhibits a certain degree of non-uniformity.

5. Calculation Method for Torsional Fatigue Life of Titanium Alloy Turning Surface

5.1. Construction Method of Torsional Strength and Fatigue Life Analysis Model of Titanium Alloys

In the titanium alloy machining surface performance assessment, its fatigue life is an important basis for assessment; the machining surface performance directly determines the fatigue life of the titanium alloy workpiece machining surface. Fatigue life not only reflects the endurance performance of the material under dynamic loading but also reveals the influence of surface properties on the long-term reliability of the material. Therefore, by combining surface properties and fatigue life research, the performance of titanium alloys in practical applications can be more accurately predicted and optimized to ensure their reliability and durability under high-stress and complex environments.

Using the results of processing surface morphology correction in Section 3.4 and Section 4.3 and the results of superficial sub-surface layer performance parameter solving and taking into account the non-uniformity of the distribution of each characteristic parameter on the machined surface of titanium alloys, the titanium alloy torsion model shown in Figure 13 is constructed by taking the cross-section where a4 is located as an example.

Figure 13 illustrates three key distribution functions along the depth direction: g₁ represents the plastic strain distribution, g₂ denotes the residual stress distribution, and g₃ characterizes the work-hardening rate distribution. Additionally, G₄(x,y,z) defines the mathematical formulation of the turning transition surface associated with characteristic point a₄.

Using ABAQUS, a torsional dynamics simulation is performed on the corrected surface under the conditions of applied initial performance parameters. The maximum stress of the frame before torsional fracture is extracted as 670 MPa, recorded as the torsional strength, and the corresponding maximum torque under the current conditions is 360 N m. When the workpiece undergoes torsion, the nominal shear stress it experiences is approximately 167.5 MPa (≈τ_max/4 [23]). When the nominal shear stress is 167.5 MPa, the torque T is approximately 90 N m. Therefore, in fatigue life analysis, a torque of 90 N m is uniformly selected for finite element simulation. Under the action of the maximum torque, the equivalent stress, plastic strain, and torsion process of the corrected surface are shown in Figure 14 and Figure 15, while the torsion process of the simulated surface of the titanium alloy under the maximum torque is shown in Figure 16.

Based on the results of the analysis of the torsion process, it is clear that the non-uniformity in the distribution of the machined surface morphology and the superficial sub-surface property parameters leads to significant differences in the location of the torsional fracture, which results in a deviation from the center of the workpiece.

5.2. Torsional Strength and Fatigue Life Analysis Program for Titanium Alloys

As evident from Figure 15 and Figure 16, the stress and strain distributions demonstrate pronounced non-uniformity during torsional plastic deformation of the titanium alloy workpiece. This heterogeneity stems from variations in both the initial characteristic surface parameters and their spatial distribution. Such non-uniform deformation induces localized stress concentrations, which may precipitate premature damage initiation or fatigue failure, ultimately compromising the material’s mechanical performance and fatigue life. This study systematically analyzes how machined surface topography parameters and surface/subsurface performance characteristics influence the torsional strength, maximum torque, fatigue life, and fracture location of titanium alloy workpieces. These effects are evaluated through different parametric definitions, with the specific performance parameter configurations detailed in

Table 7. Torsional finite element model surface parameters.

Group	Machined Surface Topography	Residual Stress Distribution			Hardening Rate Distribution		Plastic Strain Distribution		Elastic Modulus Distribution
		σr1 (MPa)	σr2 (MPa)	hr (μm)	η (GPa)	hη (μm)	εp	hε (μm)	E (GPa)	hE (μm)
1	1	0	0	0	0	0	0	0	109.80	0
2	2	0	0	0	0	0	0	0	109.80	0
3	3	0	0	0	0	0	0	0	109.80	0
4	2	0	0	0	0	0	1.22	62.14	109.80	0
5	2	−94.57	−221.95	53.01	0	0	0	0	109.80	0
6	2	0	0	0	39.41	17.05	0	0	171.27	17.05
7	2	−73.69	−184.87	51.10	38.40	16.11	0.89	63.12	168.85	16.11
8	2	−94.57	−221.95	53.01	39.41	17.05	1.22	62.14	171.27	17.05
9	2	−106.04	−247.01	52.23	41.21	16.83	1.26	62.23	175.77	16.83
10	2	−73.69 ~ −106.04	−184.87 ~ −247.01	51.1 ~ 52.23	38.4 ~ 41.21	16.11 ~ 16.83	0.89 ~ 1.26	51.1 ~ 52.23	168.85 ~ 175.77	16.11 ~ 16.83
11	3	−73.69 ~ −106.04	−184.87 ~ −247.01	51.1 ~ 52.23	38.4 ~ 41.21	16.11 ~ 16.83	0.89 ~ 1.26	51.1 ~ 52.23	168.85 ~ 175.77	16.11 ~ 16.83

.

5.3. Titanium Alloy Torsional Strength Solution Results

Groups 1–3 are simulation experiments with different machined surface topographies under the same surface and subsurface performance parameter conditions. Their initial states, torsional stress fields, and torsional fracture points are shown in Figure 17. When the machined surface topography is an ideal smooth surface and the surface/subsurface performance parameters are all zero, the torsional strength of the titanium alloy workpiece reaches a maximum of 1170 MPa, with the corresponding maximum torque being 630 N m, The torsional fracture position is any point on the central section where a₃ is located. When the machined surface topography is a surface with uniform wave crests, wave troughs, and their spacing, and the surface/subsurface performance parameters are all zero, the maximum torque of the titanium alloy workpiece decreases to 340 N m, with a large decline. The torsional fracture point is still any point on the central section where a₃ is located. When the machined surface topography is a modified surface and the surface/subsurface performance parameters are all zero, the maximum torque continues to decrease to 300 N m. However, the position of the torsional fracture point is between the sections corresponding to a₃ and a₄, and the fracture point is unique. It can be seen from the calculation results that when the machined surface topographies are different, the maximum torque, fatigue life, and fracture position of the titanium alloy workpieces are different.

Groups 4–6 are the simulation calculation results of single-factor analysis on the mean values of plastic strain, work hardening rate, and residual stress, as shown in Figure 18. The fracture positions are all arbitrary points on the central section where a₃ is located. When plastic strain acts alone, the maximum torque decreases compared to Group 3, indicating that plastic strain has a negative effect on the maximum torque; when residual stress acts alone, the maximum torque increases by 30.00% compared to Group 3, rising to 390 N m, showing a significant improvement; when the work hardening rate acts alone, the maximum torque increases by 16.67% compared to Group 3, rising to 350 N m, with the improvement range smaller than that of residual stress.

The maximum torque and fracture location corresponding to Groups 7–10 are shown in Figure 19. They are the results of solving the minimum, average, and maximum values of the three surface sub-surface performance parameters under the same machined surface morphology conditions and the inhomogeneous distribution, respectively. As can be seen from the figure, when the performance parameter increases from the minimum value to the maximum value, the maximum torque of Groups 7–9 increases continuously, which is 450 N m, 480 N m, and 560 N m, respectively, but there is no change in the location of the torsional fracture. Under the condition of Group 10, its maximum torque is smaller than 450 N m of Group 7, which is 420 N m. It shows that the load-carrying capacity and maximum torque decrease under the uneven distribution. From the solution results, it can be seen that when the machined surface topography is the same, applying the uniform surface sub-surface performance parameter has different effects on the maximum torque, but it has no effect on the location where the torsional fracture occurs. Among the three, the residual stress has the greatest positive effect on the maximum torque, the work-hardening rate is the second highest, and the plastic strain causes the maximum torque to decrease.

The maximum torque and torsional fracture locations for Groups 10 and 11 are shown in Figure 20. As can be seen from the figure, under the condition of the same initial performance parameters of the surface sub-surface layer, the maximum torque and torsional fracture point of titanium alloy workpieces are different with different surface morphology, which indicates that the surface morphology of the processed surface plays a decisive role in the torsional fracture location of titanium alloy workpieces. The maximum torque of the titanium alloy workpiece is higher than that of the modified titanium alloy workpiece when the surface morphology is more uniformly distributed, with the same subsurface property parameters.

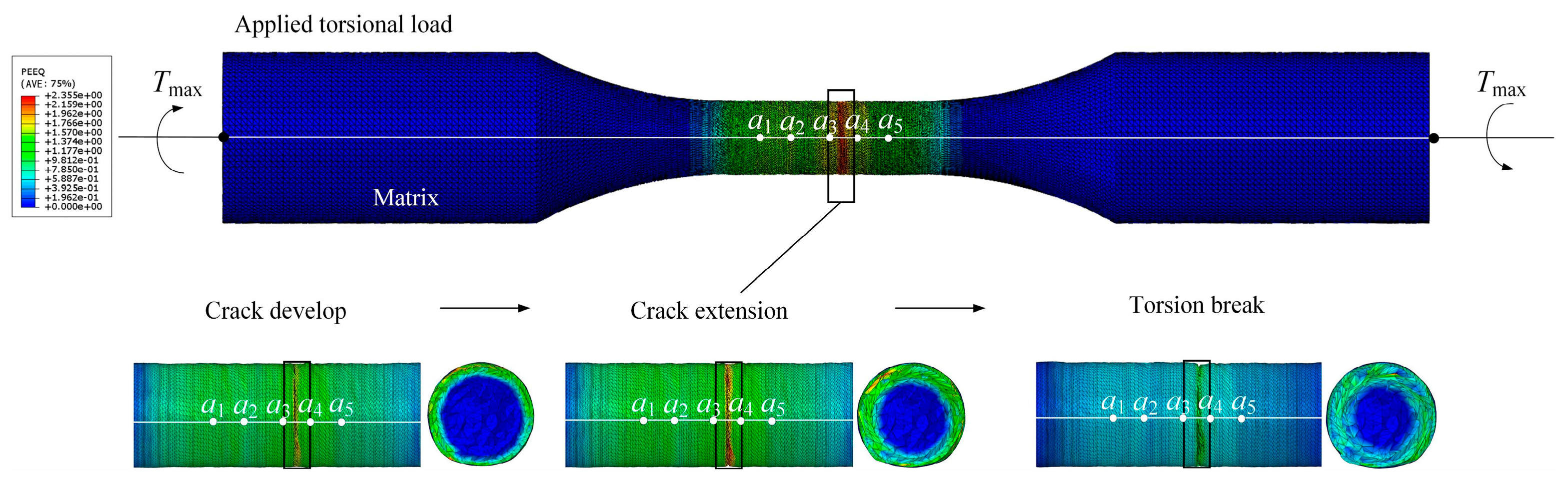
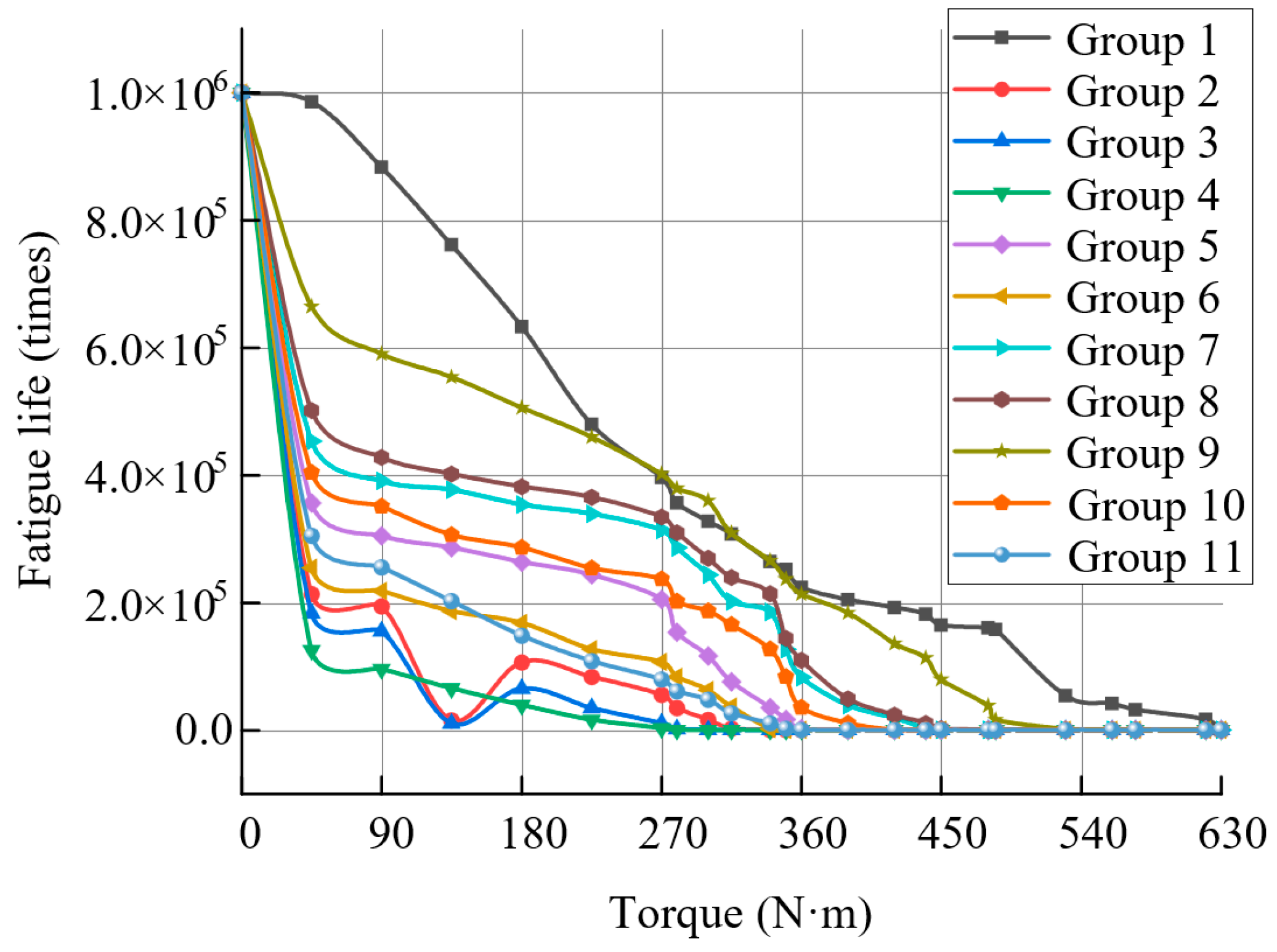
5.4. Titanium Alloys Fatigue Life Solution Results

This study establishes a torsional fatigue life analysis procedure for TC6 titanium alloy turned workpieces based on the fatigue life analysis function of FE-SAFE, with a detailed examination of its key components. The FE-SAFE fatigue analysis is conducted using ABAQUS simulation results as input data. Therefore, the initial modeling must be performed in ABAQUS to generate and export the necessary stress and strain parameters. In the subsequent FE-SAFE analysis, the Rainflow counting algorithm is applied at each nodal point to determine fatigue cycle counts and predict fatigue life.

During the FE-SAFE preprocessing phase, surface roughness and residual stress are incorporated as boundary conditions for the workpiece. The material constitutive model is calibrated using the Seeger algorithm, with key mechanical properties including elastic modulus and torsional strength being explicitly defined. A dedicated S-N curve is established to characterize the material’s fatigue behavior. Following the material property definition, the stress–strain results from the final torsional state are imported into FE-SAFE. The fatigue life assessment of TC6 titanium alloy turned workpieces is then performed using the S-N curve algorithm. The variation curves of fatigue life with torque for different surfaces are shown in Figure 21.

As can be seen from Figure 21, when the torque is 90 N m, the fatigue life of the ideal smooth surface titanium alloy specimens shows a significant decrease, and at this torque, the fatigue life of each group differs greatly, which is easier to analyze, verifying the validity of the selection of 90 N m torque as mentioned in the previous section.

The fatigue life of each point a₁–a₅ of the current turning surface is solved, and the results are shown in Figure 22.

Figure 22 presents the calculated maximum torque and fatigue life values at characteristic points a₁–a₅ on the machined turning surface. The results demonstrate substantial spatial variations in both mechanical properties across different axial positions of the titanium alloy workpiece. A clear correlation emerges between proximity to the fracture location and reduced performance metrics, with nearer points showing systematically lower maximum torque and fatigue life values. Although points a₁–a₅ display limited consistency under identical processing conditions, the overall variation remains considerable. Most significantly, point a₄ exhibits a markedly reduced fatigue life (approximately X% lower than the average of other points), indicating potential localized processing defects or non-uniform parameter distribution that warrant further investigation.

By analyzing the fatigue life of different characteristic points at corresponding angles, their degree of unevenness was obtained, as shown in Figure 22. The calculation results indicate that the fatigue lives of points a₃ and a₄ exhibit obvious fluctuations, suggesting poor distribution consistency.

It can be seen from the solution results that the fatigue life distribution of different feature points along the axial direction on the machined surface of titanium alloy is still quite different, and the fatigue life of the feature points close to the fracture position is lower. According to the results, although feature points a₁–a₅ show some consistency under the same process parameters, the overall consistency is not high, and the fatigue life of feature point a₄ is significantly lower than that of other points, which indicates potential processing problems and uneven distribution. The fatigue life at points a₃ and a₄ shows obvious fluctuations and poor distribution consistency, as shown by the solution results.

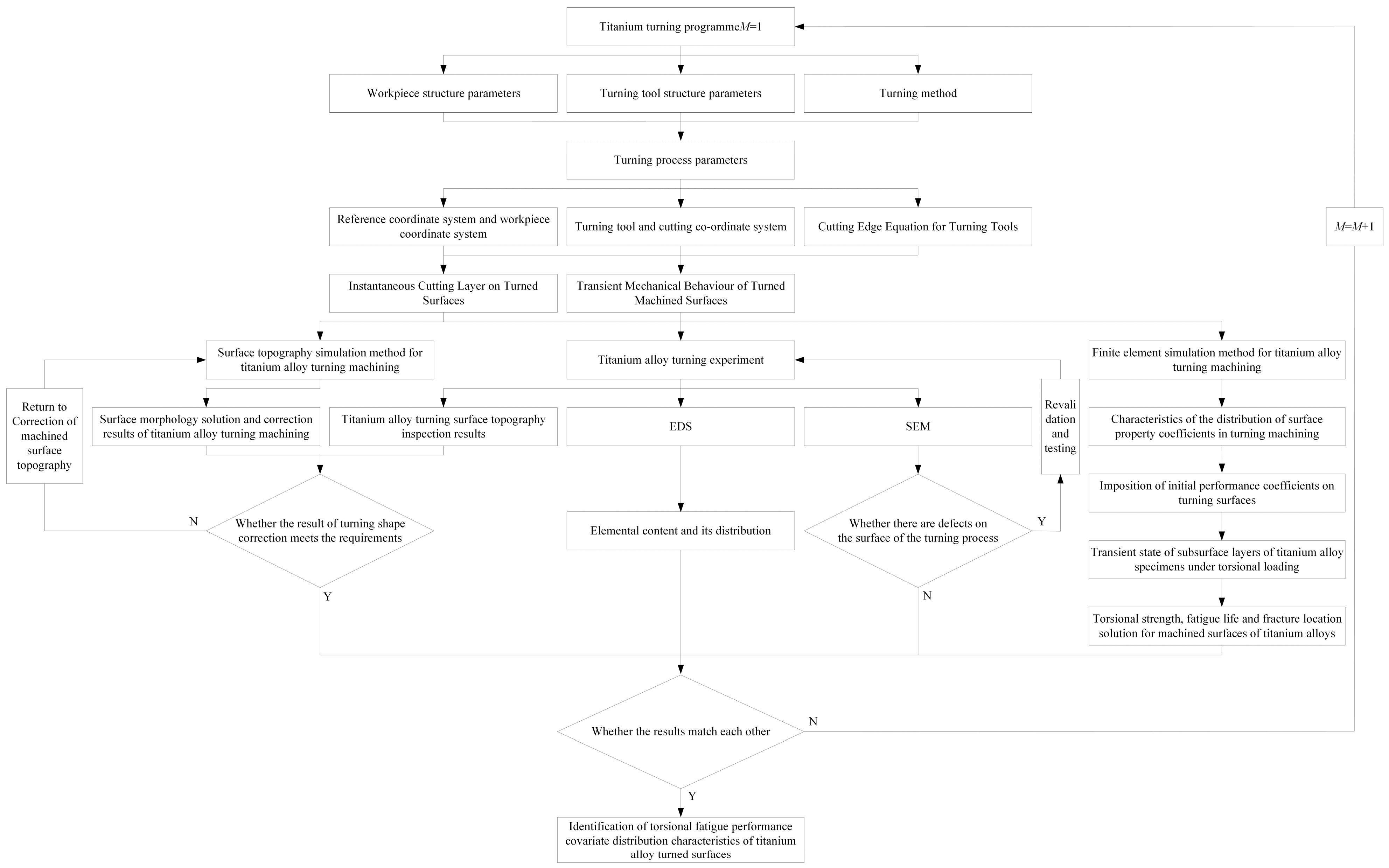
6. Torsional Fatigue Property and Distribution Characteristic Identification Method of Titanium Alloy Turning Surface

6.1. Identification Method for Torsion Fatigue Performance and Its Distribution Characteristics

The titanium alloy turning surface torsional fatigue performance parameter identification method is shown in Figure 23.

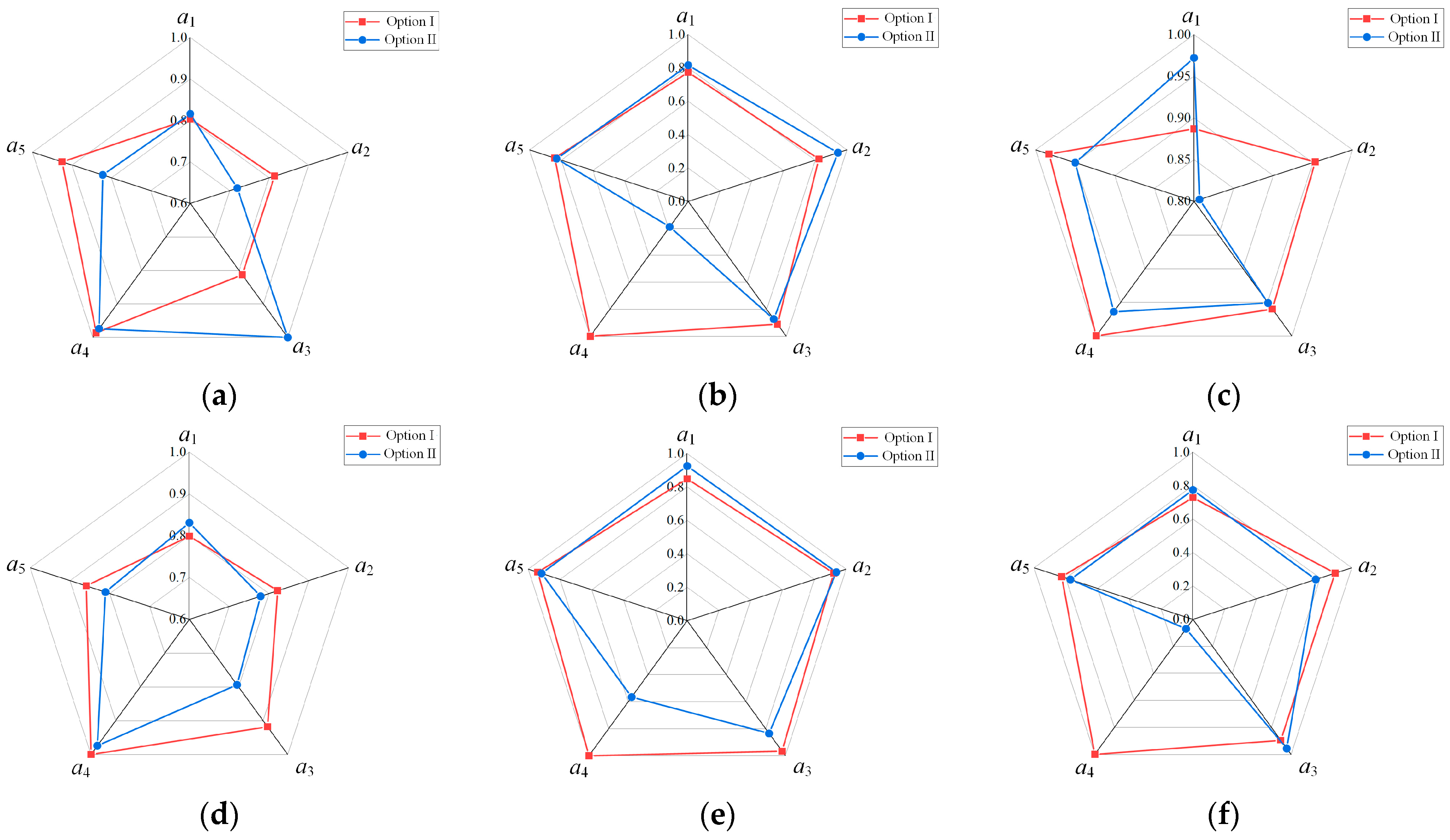
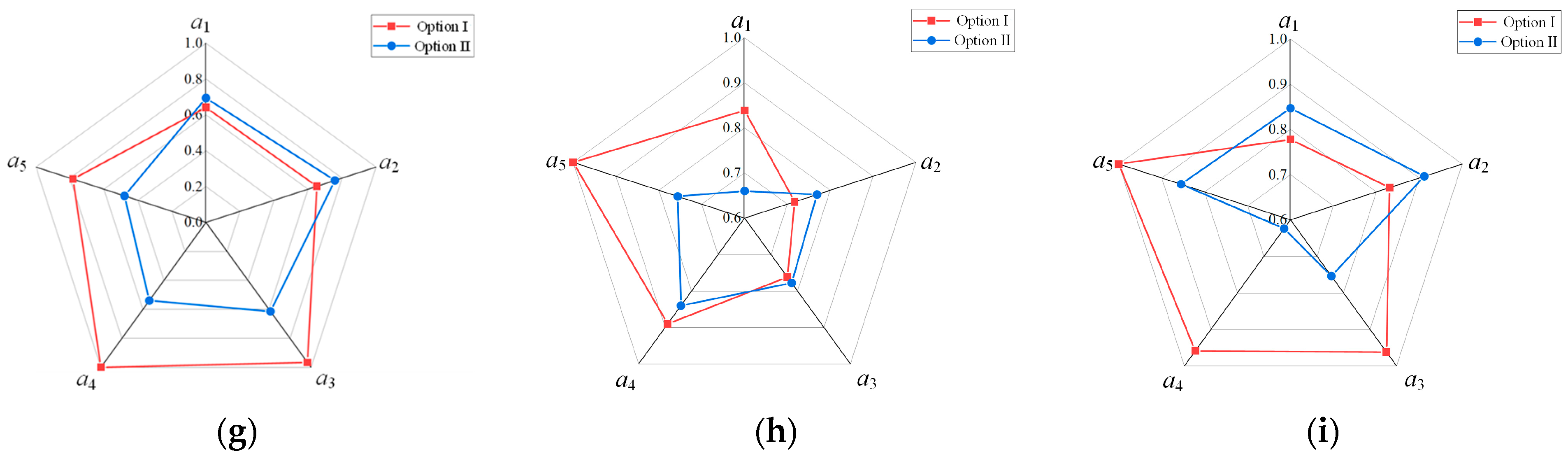
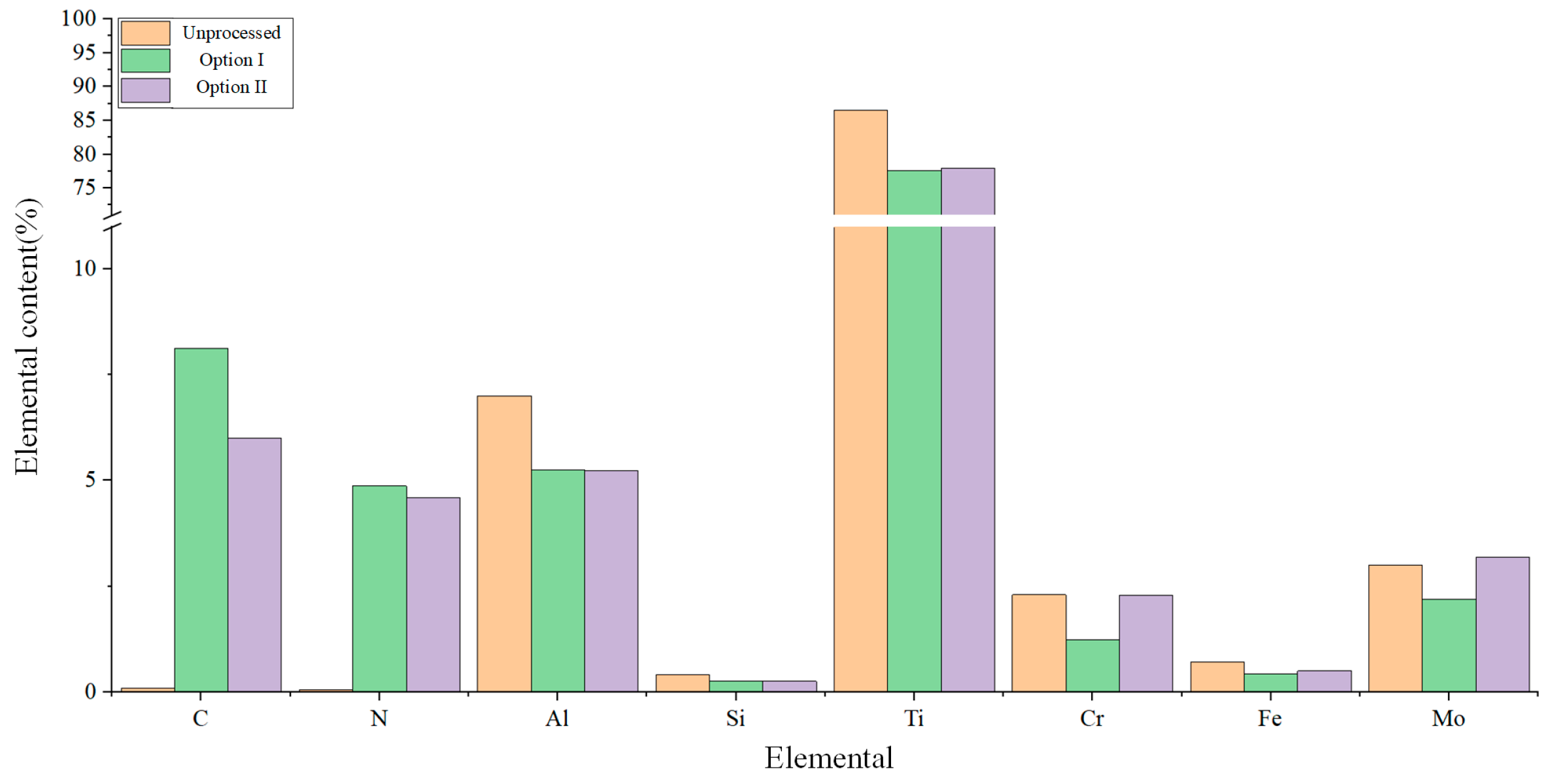
6.2. Comparison and Analysis of Calculation Results for Different Turning Process Solutions

To validate the effectiveness of the method for identifying surface torsional fatigue performance parameters in titanium alloy turning, turning simulations and experimental tests were conducted using the same cutting tool, workpiece, mounting method, cutting method, and testing method as in Section 3.4, Scheme 1. The feed rate per revolution f was 0.1 mm, the spindle speed n was 1081 r/min, and the cutting depth a_p was 0.1 mm.

The surface morphology of Scheme 2 was calculated and corrected for comparison, as shown in Figure 24.

Grey relational analysis was employed to evaluate the correlation between section profiles and experimental data. The pre-correction relational grade measured 0.88, increasing to 0.97 post-correction, demonstrating strong correlation characteristics. This optimized correlation significantly exceeds the performance observed in Scheme 1.

The titanium alloy turning process under the Scheme 2 parameters was simulated using ABAQUS finite element analysis. Five identical characteristic points corresponding to Scheme 1 were selected for comparative analysis. Material properties were initialized using the same definition methodology as Scheme 1, with consistent torsional loading application procedures. The resulting torsional response characteristics are depicted in Figure 25.

Finite element (FE) simulation results from the torsional fracture analysis were subsequently processed in FE-SAFE for fatigue life prediction. Scheme 2 demonstrates a fatigue life of 3.72 × 10⁵ cycles under cyclic loading conditions. Comparative performance metrics, including peak torque, fatigue life expectancy, and fracture locations for both experimental Schemes, are systematically presented in

Table 8. Maximum torque, fatigue life, and fracture location of Scheme 1 and Scheme 2.

Scheme	Maximum Torque Tmax (N m)	Fatigue Life Nf (×105)	Fracture Line
			z (mm)	θ (°)
1	360	2.55	68	282
2	430	3.72	83	31

.

Table 8 reveals that Scheme 2 exhibits a 19.44% increase in peak torque and a 45.88% enhancement in fatigue life compared to Scheme 1. Furthermore, the torsional fracture location demonstrates closer proximity to the titanium alloy specimen’s axial midpoint, suggesting improved uniformity in both material performance parameters and surface morphology characteristics.

Calculate the maximum torque and fatigue life of each point a₁~a₅ in Scheme 2, and the calculation results are shown in Figure 26. Compared with the first Scheme, the overall consistency of the second Scheme is improved after the optimization of process parameters. The radial maximum torque and fatigue life of the turning surface are more uniform, and the maximum torque and fatigue life of each feature point are improved.

By analyzing the fatigue life of different feature points corresponding to the angle to obtain their uneven degree, the results are shown in Figure 26. Through analysis, the error of characteristic point a₃ at all angles is relatively high, indicating that fatigue fracture is more likely to occur near a₃.

6.3. Comparison and Analysis of Experimental Methods and Measurement Results

The measurement method shown in Figure 5 of Section 2.2 was used to detect the five characteristic points of Scheme 1 and Scheme 2 separately. In surface morphology analysis, measurements were conducted within a 1 mm radius of the titanium alloy workpiece’s characteristic points. Figure 27 presents the test results for Scheme 1, revealing uniform and smooth surface morphology at positions a₁ and a₂. Figure 27 demonstrates that the characteristic parameters of surface morphology exhibit greater heterogeneity at positions a₃ and a₄ compared to other measurement points in Scheme 1. From a₃, surface roughness and irregular texture increase significantly, while surface defects become more pronounced at a₄, suggesting the presence of micro-defects or stress concentration zones. These material imperfections promote fatigue stress accumulation between a₃ and a₄, initiating crack propagation that ultimately leads to fracture in this region.

The results of Scheme 2 are shown in Figure 28. The surface morphology at points a₁ and a₂ is relatively smooth and regular, while the surface morphology at point a₃ exhibits more obvious roughness and an increase in microdefects. Due to pre-existing defects or stress concentration within the material, stress tends to accumulate and propagate cracks between points a₂ and a₃ during fatigue testing, resulting in fractures occurring in this region. The surface topography of the processed cross-sections at different characteristic points for Scheme 2 is shown as illustrated. The normalized comparison results of the characteristic parameter standard deviations between Scheme 1 and Scheme 2 are shown in Figure 29. As can be seen from the figure, Scheme 2 generally performs better than Scheme 1 under most parameters. In particular, the standardized values of parameters x and z are close to 1, indicating Scheme 2′s advantage in processing accuracy. In comparisons of spacing Δx and Δz in different directions, Scheme 2 also demonstrates significantly more consistent performance at most feature points.

The change in element content reflects the difference in surface characteristic parameters directly, which can effectively reveal the performance difference of the machined surface in different regions. Element composition and content ratio of the titanium alloy turning surface were obtained by SU5000 scanning electron microscope and energy spectrum analyzer, and element content of different machined surfaces and different positions of the same machined surface were analyzed and compared. The SEM scanning results of Scheme 1 and Scheme 2 and their area scanning element distributions are shown in Figure 30.

Figure 30 reveals that Scheme 1 exhibits inferior surface quality relative to Scheme 2, displaying increased surface defects, localized microcracks, and porosity. The results of scanning electron microscope testing show that there is obvious plastic deformation on the surface of the titanium alloy turned parts. These observations suggest localized stress concentration during machining. In contrast, Scheme 2 demonstrates a smooth, dense surface morphology, achieved through optimized machining parameters that enhance titanium alloy surface integrity. Figure 31 comparatively presents the elemental composition of machined surfaces from both Schemes.

As can be seen from Figure 31, after turning processing, the element content of α-phase elements C and N is significantly increased, and the element content of Al decreased by about 25%; The neutral element Si decreased from 0.40% to 0.25%, and the matrix element Ti decreased significantly. Compared with Scheme 1, the content of β-phase elements in Scheme 2 was higher, and the content of Cr, Fe, and Mo increased by 83.87%, 16.28%, and 45%, respectively. The content of α-phase elements in the three different surfaces was 7.13%, 18.25%, and 15.85%, respectively, and the content of β-phase elements was 6.00%, 3.87%, and 5.97%, respectively. The α-phase element content of the ideal titanium alloy workpiece without machining is low, and the β-phase element content is high, which makes it have better mechanical properties. However, after machining, the α-phase element content of Scheme 1 is higher than that of Scheme 2, and the β-phase element content is lower than that of Scheme 2, resulting in poor mechanical properties and low fatigue life.

Point scanning energy spectrum detection was performed on different characteristic points of the machined surface of Scheme 1, as shown in Figure 32. The detection results are shown in Figure 33.

The α-phase element ratios for a₁ to a₅ are 17.06%, 16.54%, 17.20%, 18.5%, and 15.09%, respectively, while the β-phase element ratios are 4.77%, 4.89%, 3.74%, 3.58%, and 5.04%. The α-phase element ratios for both a₃ and a₄ are higher than those of the other points, and the β-phase element ratios are lower than those of the other points, indicating that the brittleness increases between these two points, reducing ductility and toughness, leading to fatigue fracture first. The element content of the machining surface at different positions under the same process parameters shows obvious inhomogeneity. The uneven distribution of surface element content in this titanium alloy machining further affects the difference in its mechanical properties.

Scanning electron microscopy (SEM) analysis of the fracture surface reveals fine crack initiation sites and microstructural defects, including non-uniform particle distribution and micropores. These imperfections serve as stress concentration points. Pre-existing defects and localized stress concentrations predispose the material to accelerated crack propagation and fracture under subsequent torsional fatigue loading. This fracture mechanism primarily arises from cumulative micro-defect aggregation and localized stress intensification during cyclic loading.

In Scheme 2, point scanning spectroscopy was used to detect different characteristic points on the surface of turning. The test results are shown in Figure 34.

The α-phase element content of a₁~a₅ was 13.27%, 14.64%, 16.54%, 12.56%, and 12.06%, respectively, and the β-phase element content was 8.12%, 5.11%, 4.49%, 7.46%, and 7.96%, respectively. The α-phase element ratio of a₂ and a₃ is higher than that of other points, and the β-phase element ratio is lower than that of other points, resulting in the earliest fatigue fracture in the interval between two points. Compared with the fracture interval detection results of Scheme 1, there was no obvious non-uniform particle and hole formation on the surface of the titanium alloy workpiece of Scheme 2. Although dislocations and other phenomena still existed in some local areas, there were no obvious microcracks.

7. Conclusions

• To account for the influence of tool geometry parameters, cutting parameters, and cutting forces on tool-workpiece surface morphology, an instantaneous cutting behavior model was developed. Parametric equations describing the primary and secondary cutting edges, along with their transitional arc segments, were formulated. Solutions for machining transition surfaces across adjacent cutting cycles were derived. A methodology for characterizing instantaneous cutting layers and mechanical responses during titanium alloy machining was established. Furthermore, a simulation framework and surface morphology correction model were implemented to analyze machined titanium alloy surfaces.
• To address the non-uniform distribution of surface feature parameters in titanium alloy turning, the instantaneous subsurface state during machining was characterized. A finite element model and analytical framework were developed to investigate axial and radial distributions of surface feature parameters on machined titanium alloy surfaces. Results demonstrate positional variations in both axial and radial dimensions for the size and depth of machined surface features during titanium alloy processing.
• A torsional fatigue life prediction model for turned titanium alloys was developed, incorporating torque loading conditions and torsional strength variations induced by non-uniform initial load distributions. Fatigue life analysis of machined surfaces with heterogeneous parameter distributions was performed, accounting for surface feature parameter discrepancies across distinct regions. This investigation quantifies the influence of parameter heterogeneity on fatigue performance. Experimental results demonstrate significant variations in fatigue life distribution among titanium alloy workpieces under identical torque conditions, directly attributable to differences in surface feature parameters. Comparative analysis and experimental verification demonstrate that tool parameter optimization enables modification of titanium alloy turned surfaces’ performance parameters, elemental composition, and distribution characteristics. This adjustment enhances surface mechanical properties, effectively improving torsional strength and fatigue life in titanium alloy components.
• Comparative analysis and experimental verification results show that by adjusting the cutting tool process parameters to alter the performance parameters, element content, and distribution of the machined surface of titanium alloys, it is possible to improve the mechanical properties of the machined surface to a certain extent, thereby enhancing its torsional strength and fatigue life.