A Two-Layer User Energy Management Strategy for Virtual Power Plants Based on HG-Multi-Agent Reinforcement Learning
Abstract
1. Introduction
- (1)
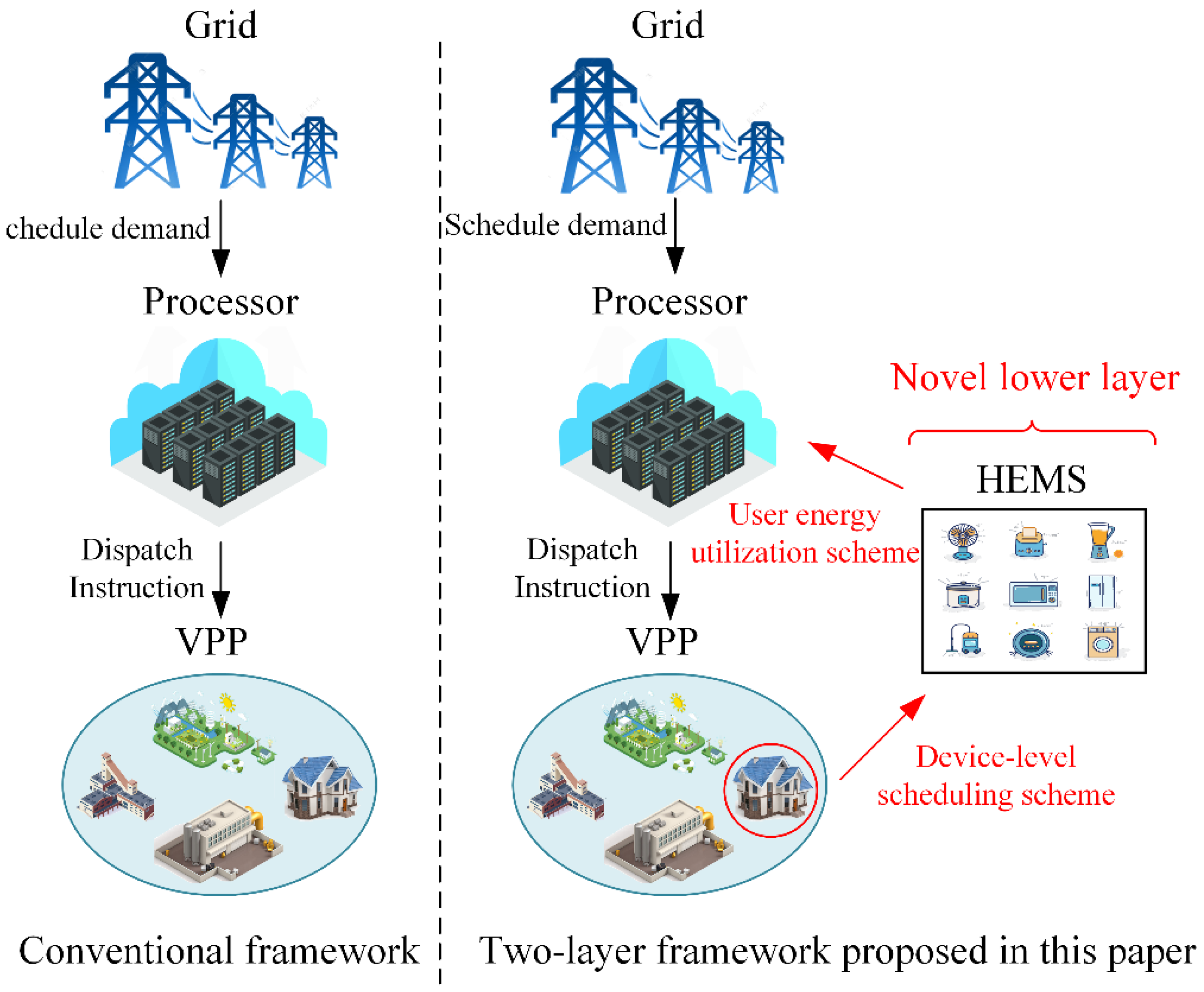
- A two-layer optimization framework for the VPP has been proposed, in which the upper layer coordinates the scheduling and benefit allocation among various stakeholders and the lower layer executes intelligent decision-making for users.
- (2)
- A detailed household power management model is proposed to generate predicted power demands and allocate power within each household user in the lower layer.
- (3)
- A HG-multi-agent reinforcement-based method is proposed, which reconstructs the objective functions of each stakeholder with the hierarchical game algorithm to simplify the solving process, utilizing the multi-agent Q-learning algorithm combined with upper-layer solution information to accelerate training and solving.
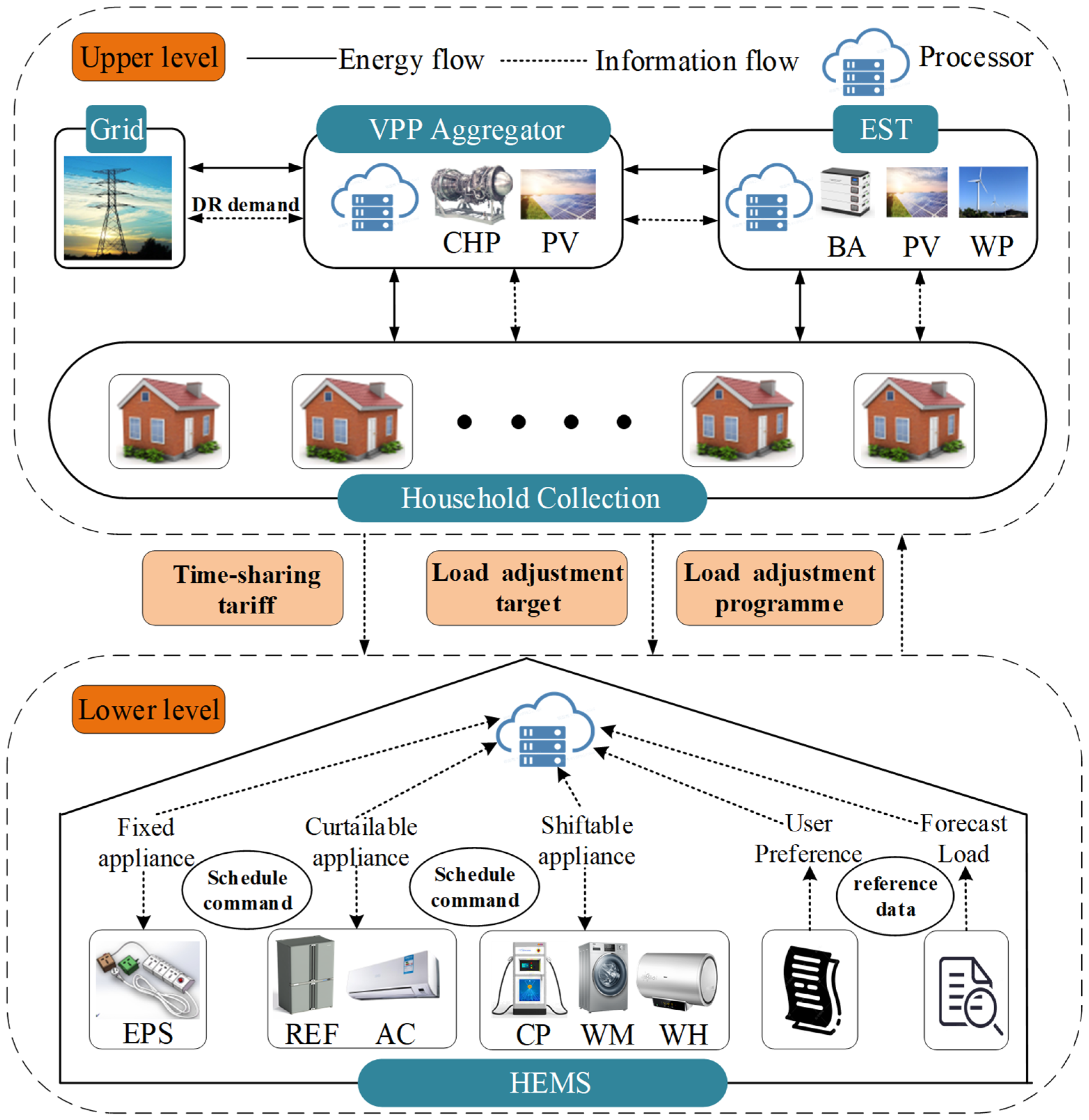
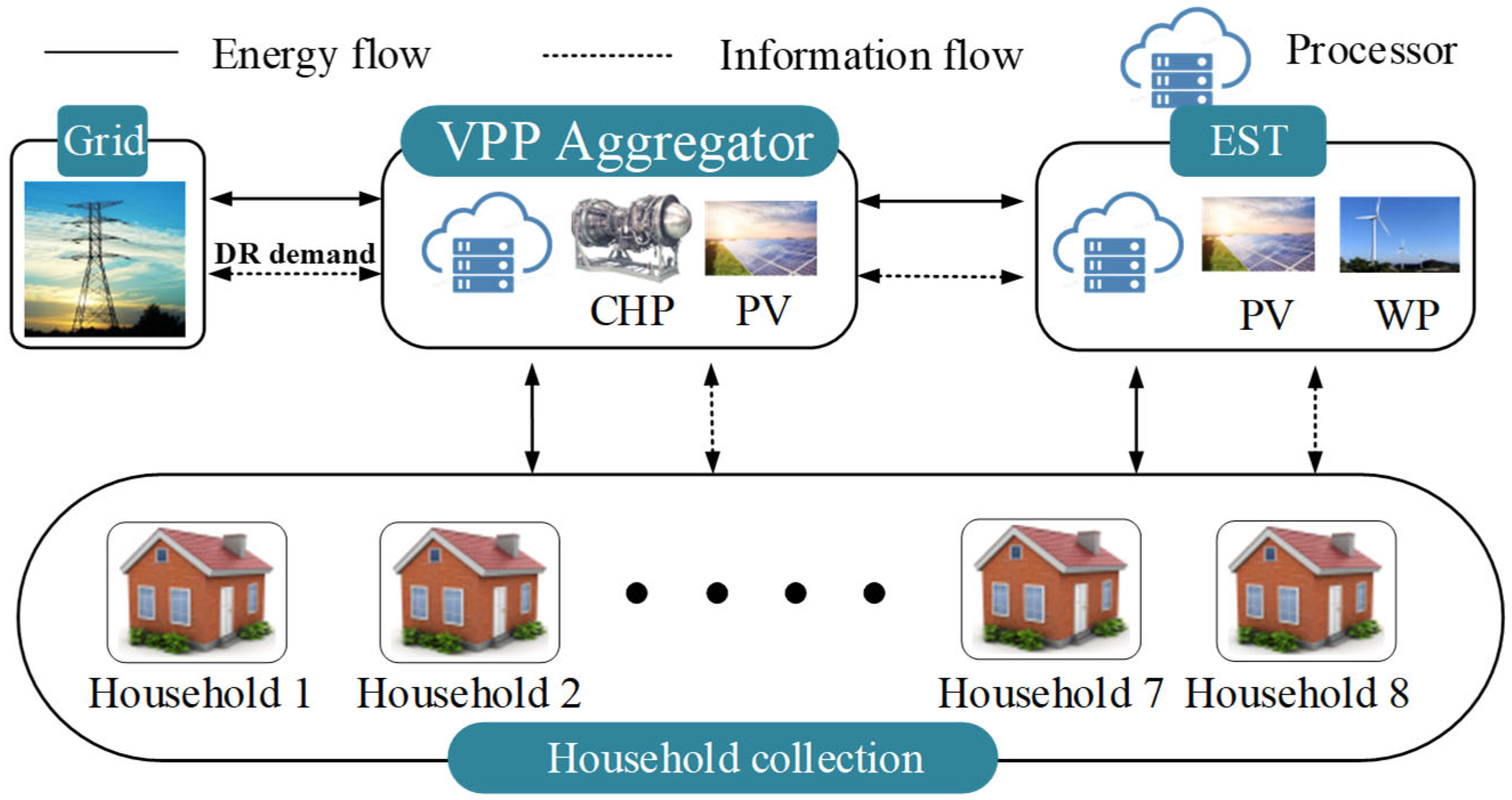
2. Two-Layer Optimization Framework for VPP
2.1. Operation Tasks of the Two-Layer Optimization Framework
- (1)
- Upper layer: Coordinate the scheduling and benefit allocation among stakeholders
- (2)
- Lower layer: Execute intelligent decision-making for users
2.2. Comparison of the Framework
3. Mathematical Model for the Proposed Framework
3.1. Mathematical Model for the Upper Layer
- (1)
- VPP aggregator model
- (2)
- EST model
- (3)
- Household collection model
- (4)
- Laddered DR mechanism
3.2. Mathematical Model for the Lower Layer
- (1)
- State
- (2)
- Action
- (3)
- Reward
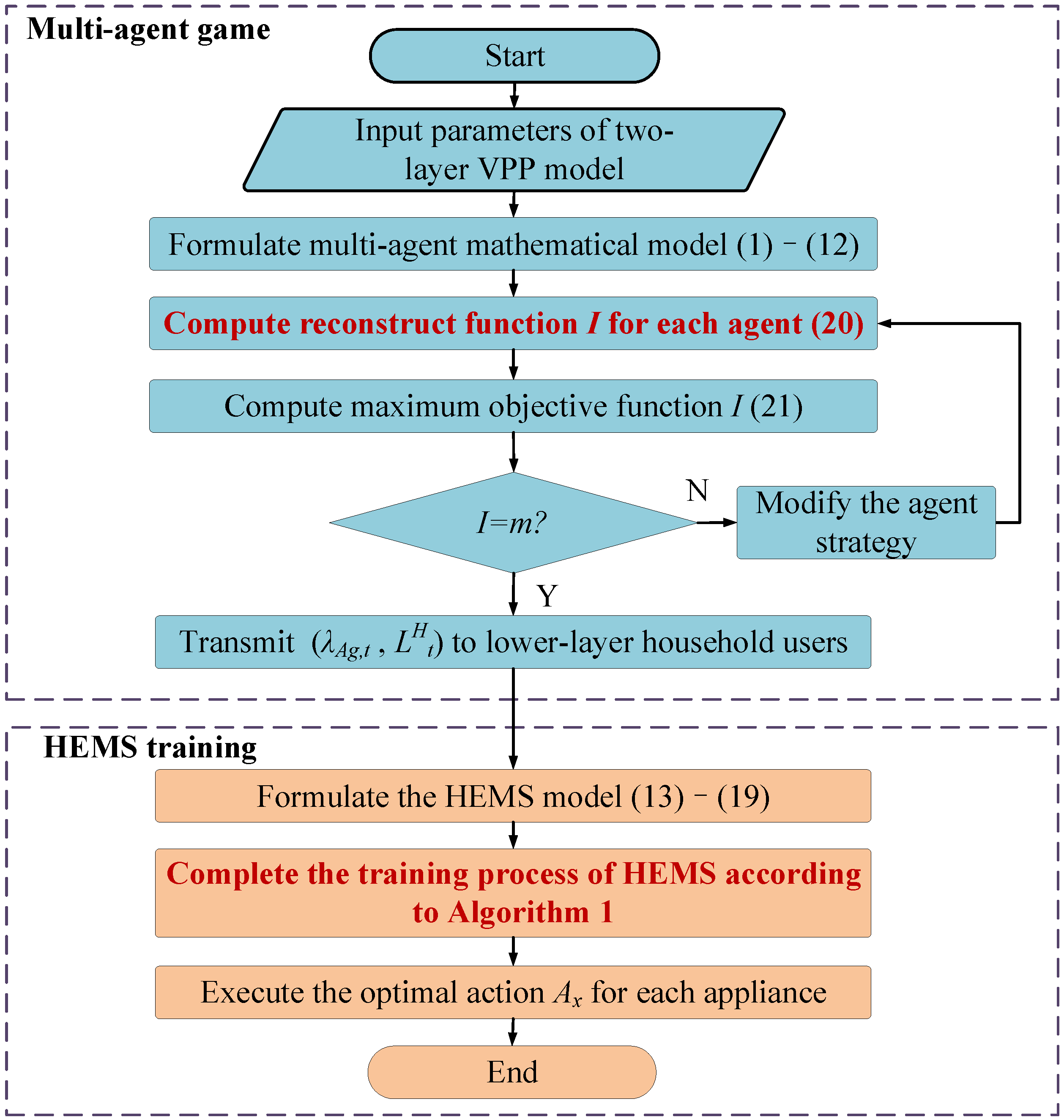
4. HG-Multi-Agent Reinforcement Learning
4.1. Flowchart of the Solving Method
4.2. Hierarchical Game Algorithm
4.3. Multi-Agent Q-Learning Algorithm
| Algorithm 1: Multi-Agent Q-learning Algorithm | |
| 1 | Initialization initialize Q-value |
| 2 | for episode = 1,2,…, max episode do |
| 3 | for t = 1,2,…, max time slot do |
| 4 | Initialize the state st |
| 5 | Choose the arbitrary action at of the device by (14)–(16) |
| 6 | Calculate the current reward r(st, at) and the next state st+1 by(17)–(19) |
| 7 | Update the Q-value Q(st, at) by(21) |
| 8 | Save st+1 |
| 9 | Calculate the absolute value diff between the Q values under two episodes |
| 10 | End until the diff is less than the set value ρ |
| 11 | Output the optimal policy |
5. Evaluation Results
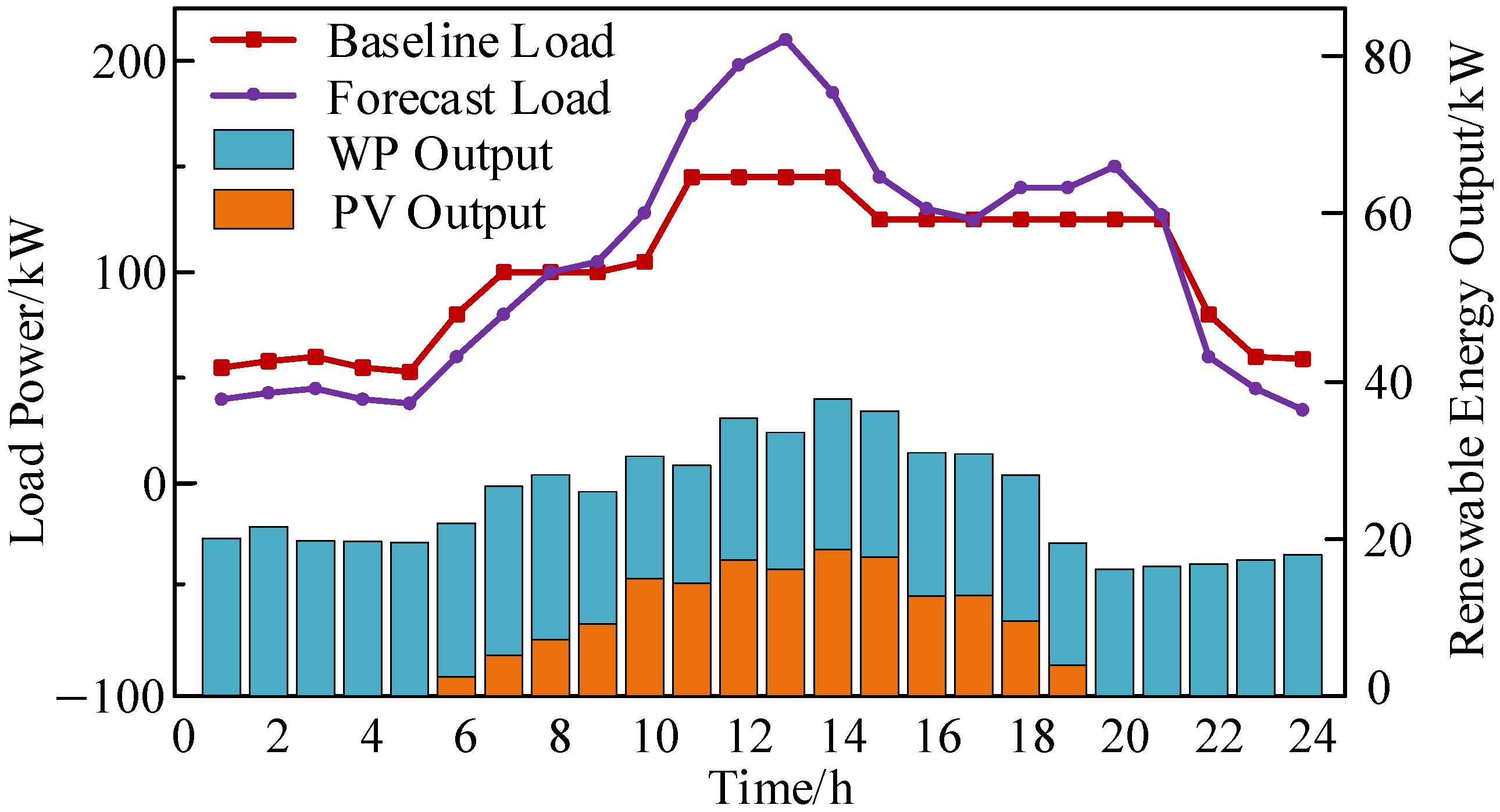
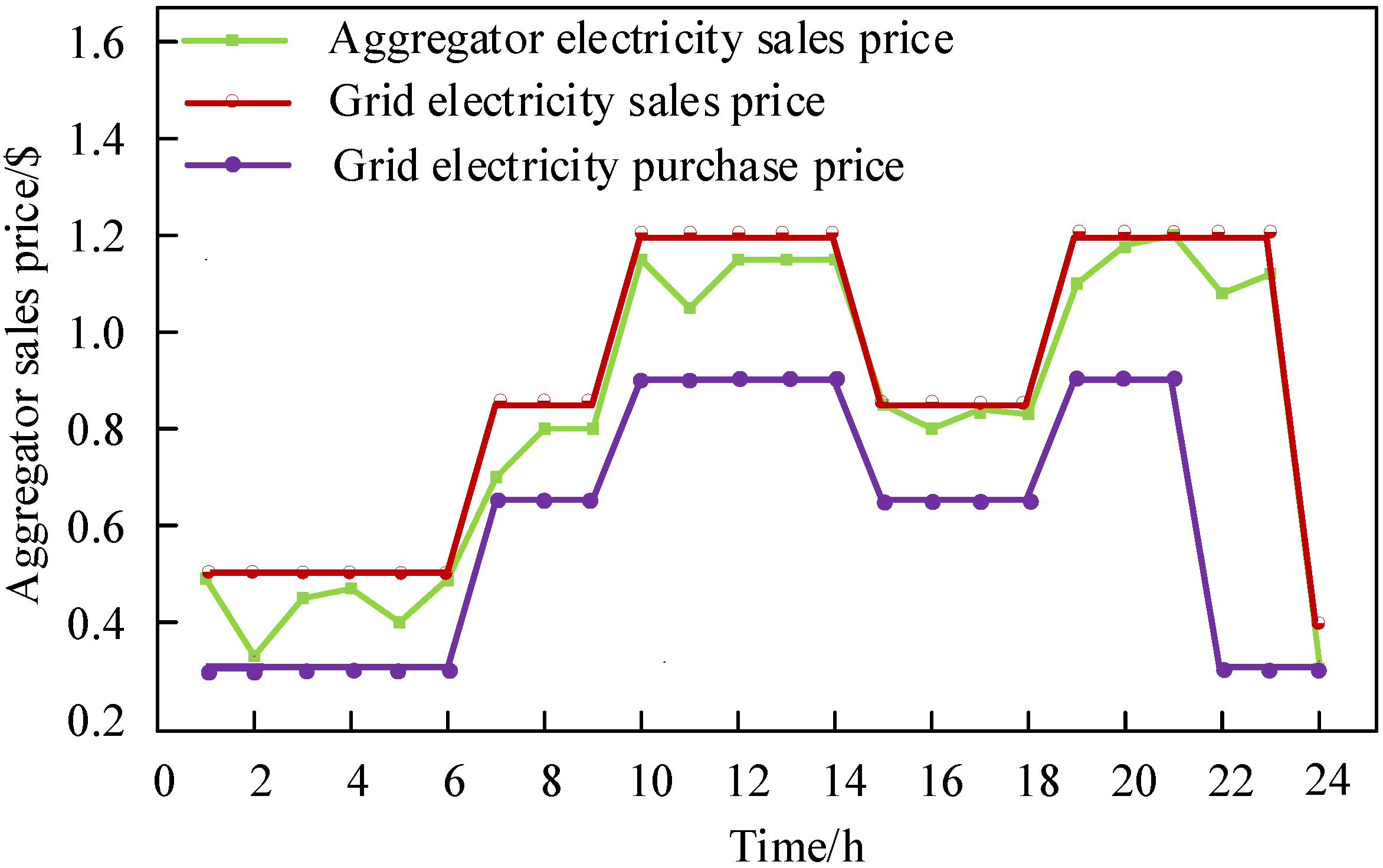
5.1. Case Study Setting
5.2. Analysis of Game Results
5.3. Comparative Analysis of the HG-Multi-Agent Reinforcement Learning Method
5.4. Convergence Analysis
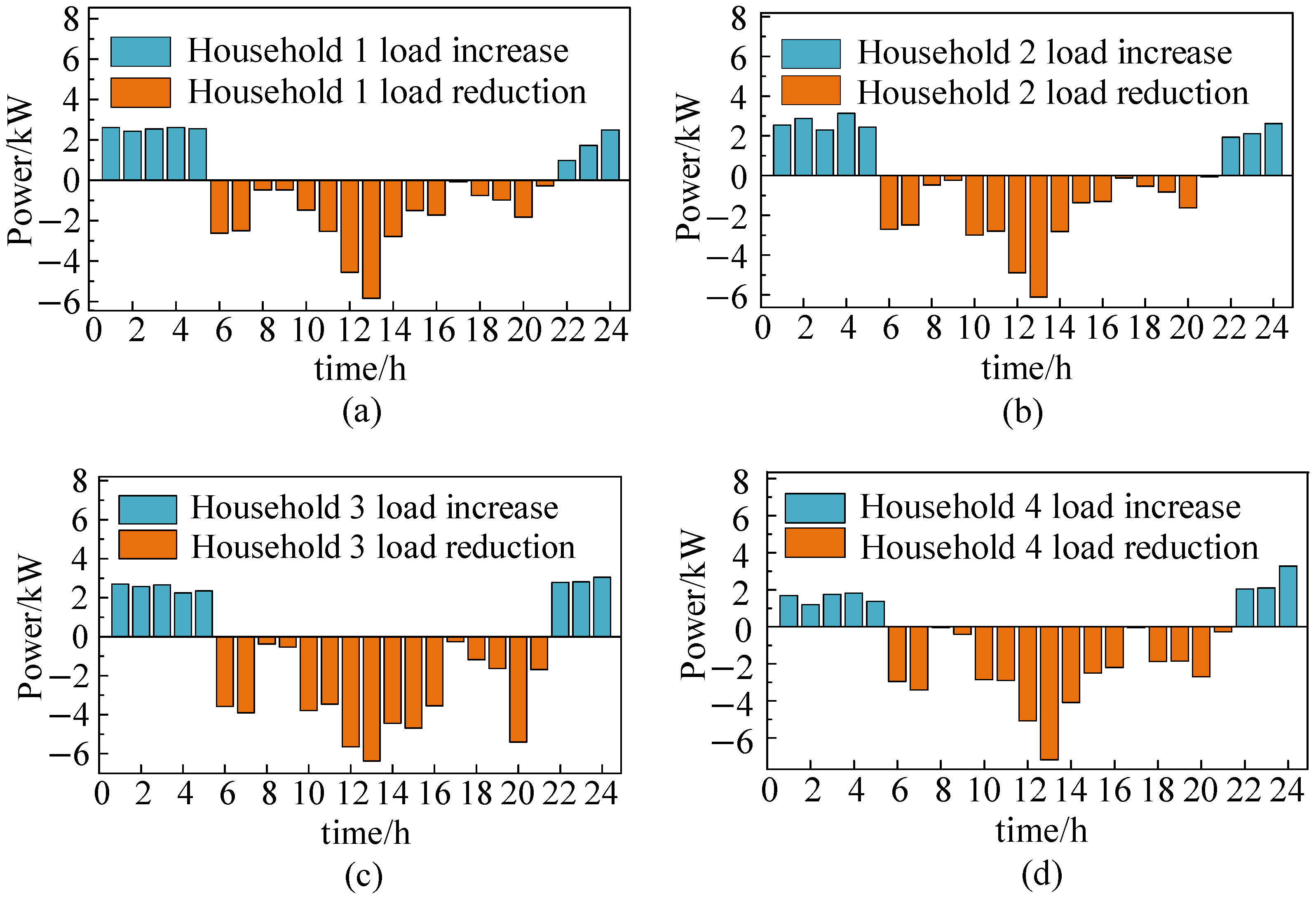
5.5. Analysis of Single-Household Load Adjustment
6. Conclusions
- (1)
- Compared to the conventional framework for optimized operation, the proposed framework and strategy can increase VPP aggregator benefit by over 56.2%, reduce user energy costs by over 12.9%, and increase ESS benefit by over 7.8%.
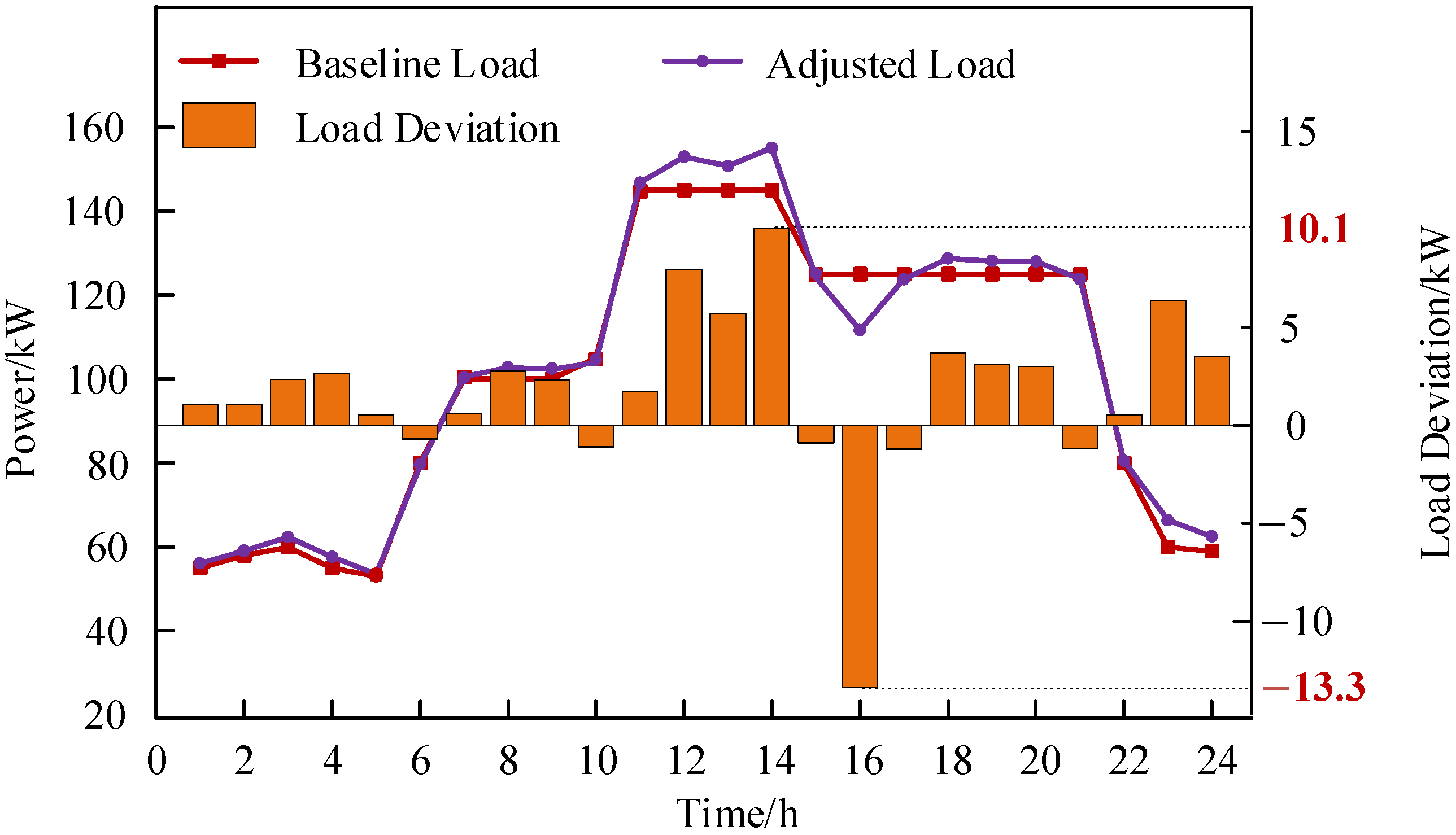
- (2)
- The proposed stepped DR mechanism helped the VPP reduce peak load by approximately 39.33%. Moreover, it safeguards users’ interests in cases of load adjustment deviations, increasing their willingness to respond to the power company’s policies actively.
- (3)
- Compared to conventional methods, the HG-multi-agent reinforcement learning method can reduce calculation time by over 23.8% and lower user costs after DR compensation by over 8.8%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pham, T.T.H.; Besanger, Y.; Hadjsaid, N. New challenges in power system restoration with large scale of dispersed generation insertion. IEEE Trans. Power Syst. 2009, 24, 398–406. [Google Scholar] [CrossRef]
- Baringo, A.; Baringo, L.; Arroyo, J.M. Day-ahead self-scheduling of a virtual power plant in energy and reserve electricity markets under uncertainty. IEEE Trans. Power Syst. 2019, 34, 1881–1894. [Google Scholar] [CrossRef]
- Tang, Y.; Zhai, Q.; Zhao, J. Multi-stage robust scheduling for community microgrid with energy storage. J. Mod. Power Syst. Clean Energy 2023, 11, 1923–1934. [Google Scholar] [CrossRef]
- Pudjianto, D.; Ramsay, C.; Strbac, G. Microgrids and virtual power plants: Concepts to support the integration of distributed energy resources. Proc. Inst. Mech. Eng. Part A J. Power Energy 2008, 222, 731–741. [Google Scholar] [CrossRef]
- Thavlov, A.; Bindner, H.W. Utilization of flexible demand in a virtual power plant set-up. IEEE Trans. Smart Grid 2015, 6, 640–647. [Google Scholar] [CrossRef]
- Xu, J.; Xiao, Q.; Jia, H.; Mu, Y.; Jin, Y.; Lu, W.; Ma, S. A simplified control parameter optimisation method of the hybrid modular multilevel converter in the medium-voltage DC distribution network for improved stability under a weak AC system. IET Energy Syst. Integr. 2024, 6, 512–524. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, J.; Wang, T.; Zhang, F.; Zheng, J.; Yin, L.; Ban, M. High-frequency resonance suppression based on cross-coupled filter and improved passive damper for MMC-HVDC system. IEEE Trans. Power Delivery 2024, 39, 1952–1962. [Google Scholar] [CrossRef]
- Kardakos, E.G.; Simoglou, C.K.; Bakirtzis, A.G. Optimal offering strategy of a virtual power plant: A stochastic bi-level approach. IEEE Trans. Smart Grid 2016, 7, 794–806. [Google Scholar] [CrossRef]
- Zhao, Y.; Lin, Z.; Wen, F.; Ding, Y.; Hou, J.; Yang, L. Risk-constrained day-ahead scheduling for concentrating solar power plants with demand response using info-gap theory. IEEE Trans. Ind. Inform. 2019, 15, 5475–5488. [Google Scholar] [CrossRef]
- Wen, L.; Zhou, K.; Feng, W.; Yang, S. Demand side management in smart grid: A dynamic-price-based demand response model. IEEE Trans. Eng. Manag. 2024, 71, 1439–1451. [Google Scholar] [CrossRef]
- Vahedipour-Dahraie, M.; Rashidizadeh-Kermani, H.; Parente, M.; Shafie-Khah, M.; Siano, P. Investigating the impact of external demand response flexibility on the market power of strategic virtual power plant. IEEE Access 2022, 10, 84960–84969. [Google Scholar] [CrossRef]
- Liang, H.; Ma, J. Data-driven resource planning for virtual power plant integrating demand response customer selection and storage. IEEE Trans. Ind. Inform. 2022, 18, 1833–1844. [Google Scholar] [CrossRef]
- Vahedipour-Dahraie, M.; Rashidizadeh-Kermani, H.; Shafie-Khah, M.; Catalão, J.P.S. Risk-averse optimal energy and reserve scheduling for virtual power plants incorporating demand response programs. IEEE Trans. Smart Grid 2021, 12, 1405–1415. [Google Scholar] [CrossRef]
- Gazijahani, F.S.; Salehi, J. IGDT-based complementarity approach for dealing with strategic decision making of price-maker VPP considering demand flexibility. IEEE Trans. Ind. Inform. 2020, 16, 2212–2220. [Google Scholar] [CrossRef]
- Chen, W.; Qiu, J.; Zhao, J.; Chai, Q.; Dong, Z.Y. Customized rebate pricing mechanism for virtual power plants using a hierarchical game and reinforcement learning approach. IEEE Trans. Smart Grid 2023, 14, 424–439. [Google Scholar] [CrossRef]
- Liu, X.; Li, S.; Zhu, J. Optimal coordination for multiple network-constrained VPPs via multi-agent deep reinforcement learning. IEEE Trans. Smart Grid 2023, 14, 3016–3031. [Google Scholar] [CrossRef]
- Bui, V.; Hussain, A.; Kim, H. Double deep Q-learning-based distributed operation of battery energy storage system considering uncertainties. IEEE Trans. Smart Grid 2020, 11, 457–469. [Google Scholar] [CrossRef]
- Wang, B.; Li, Y.; Ming, W.; Wang, S. Deep reinforcement learning method for demand response management of interruptible load. IEEE Trans. Smart Grid 2020, 11, 3146–3155. [Google Scholar] [CrossRef]
- Xu, Z.; Guo, Y.; Sun, H. Competitive pricing game of virtual power plants: Models, strategies, and equilibria. IEEE Trans. Smart Grid 2022, 13, 4583–4595. [Google Scholar] [CrossRef]
- Bahloul, M.; Breathnach, L.; Khadem, S. Residential Virtual power plant control: A novel hierarchical multi-objective optimization approach. IEEE Trans. Smart Grid 2025, 16, 1301–1313. [Google Scholar] [CrossRef]
- Li, X.; Li, C.; Liu, X.; Chen, G.; Dong, Z.Y. Two-stage community energy trading under end-edge-cloud orchestration. IEEE Internet Things J. 2023, 10, 1961–1972. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.; Du, X. Optimized operation of multi-virtual power plant for energy sharing based on nash multi-stage robust. IEEE Access 2024, 12, 169805–169823. [Google Scholar] [CrossRef]
- Wu, J.K.; Liu, Z.W.; Li, C.; Zhao, Y.; Chi, M. Coordinated operation strategy of virtual power plant based on two-layer game approach. IEEE Trans. Smart Grid 2025, 16, 554–567. [Google Scholar] [CrossRef]
- Feng, C.; Zheng, K.; Zhou, Y.; Palensky, P.; Chen, Q. Update scheduling for ADMM-based energy sharing in virtual power plants considering massive prosumer access. IEEE Trans. Smart Grid 2023, 14, 3961–3975. [Google Scholar] [CrossRef]
- Cappello, D.; Mylvaganam, T. Distributed differential games for control of multi-agent systems. IEEE Trans. Control Netw. Syst. 2022, 9, 635–646. [Google Scholar] [CrossRef]
- Zhang, T.; Li, Y.; Yan, R.; Siada, A.A.; Guo, Y.; Liu, J.; Huo, R. A master-slave game optimization model for electric power companies considering virtual power plant. IEEE Access 2022, 10, 21812–21820. [Google Scholar] [CrossRef]
- ElRahi, G.; Etesami, S.R.; Saad, W.; Mandayam, N.B.; Poor, H.V. Managing price uncertainty in prosumer-centric energy trading: A prospect-theoretic stackelberg game approach. IEEE Trans. Smart Grid 2019, 10, 702–713. [Google Scholar] [CrossRef]
- Chouikhi, S.; Merghem-Boulahia, L.; Esseghir, M.; Snoussi, H. A game-theoretic multi-level energy demand management for smart buildings. IEEE Trans. Smart Grid 2019, 10, 6768–6781. [Google Scholar] [CrossRef]
- Xu, X.; Jia, Y.; Xu, Y.; Xu, Z.; Chai, S.; Lai, C.S. A multi-agent reinforcement learning-based data-driven method for home energy management. IEEE Trans. Smart Grid 2020, 11, 3201–3211. [Google Scholar] [CrossRef]
- Wang, Y.; Ai, X.; Tan, Z.; Yan, L.; Liu, S. Interactive dispatch modes and bidding strategy of multiple virtual power plants based on demand response and game theory. IEEE Trans. Smart Grid 2016, 7, 510–519. [Google Scholar] [CrossRef]
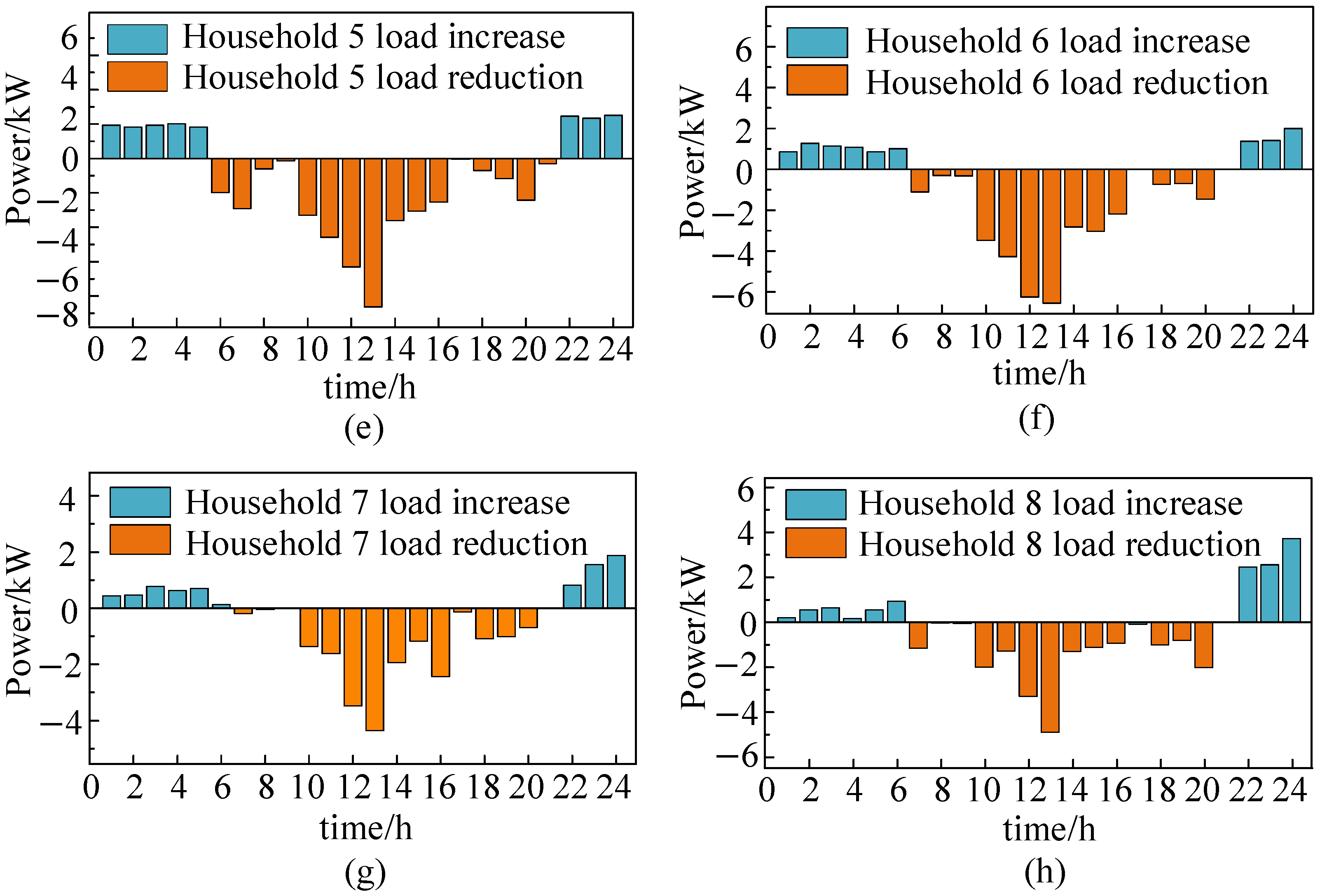
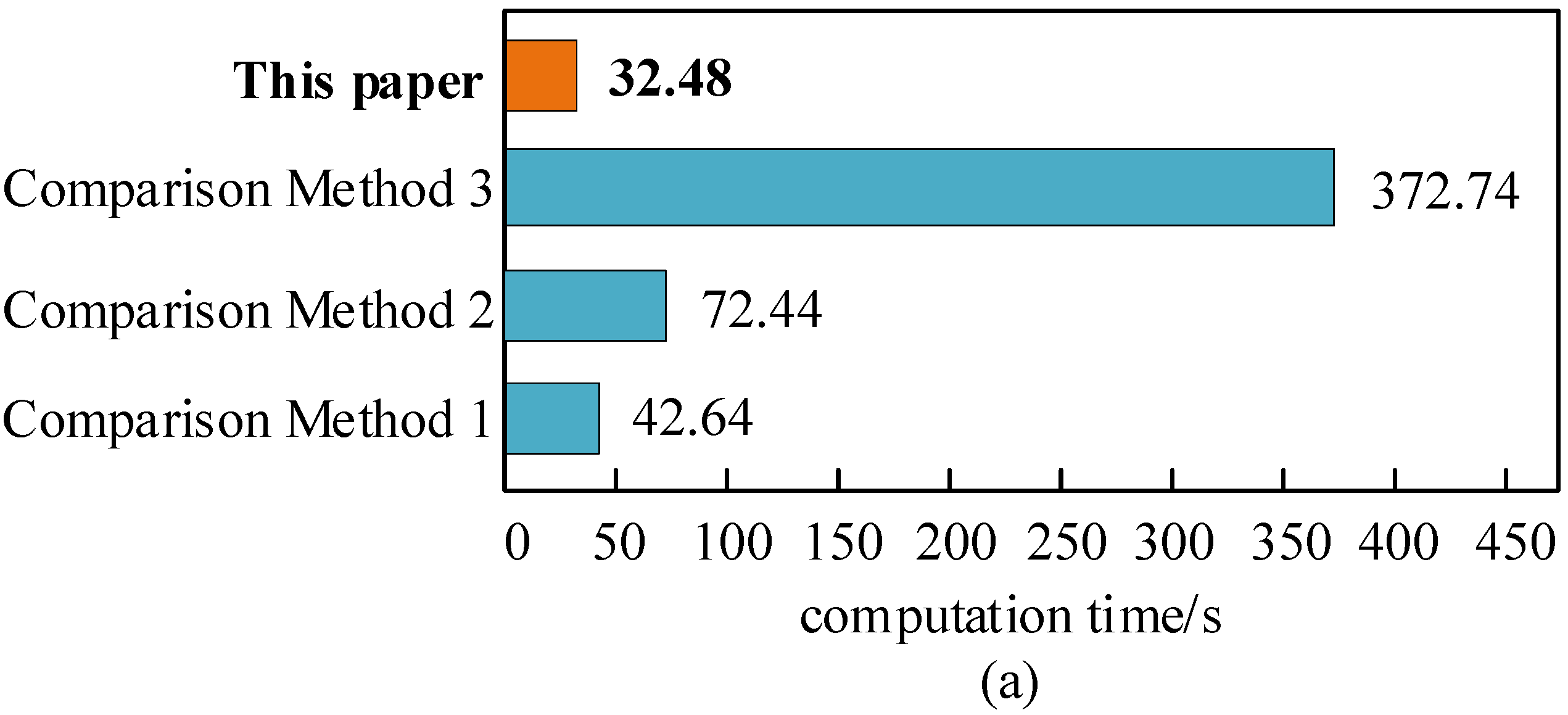
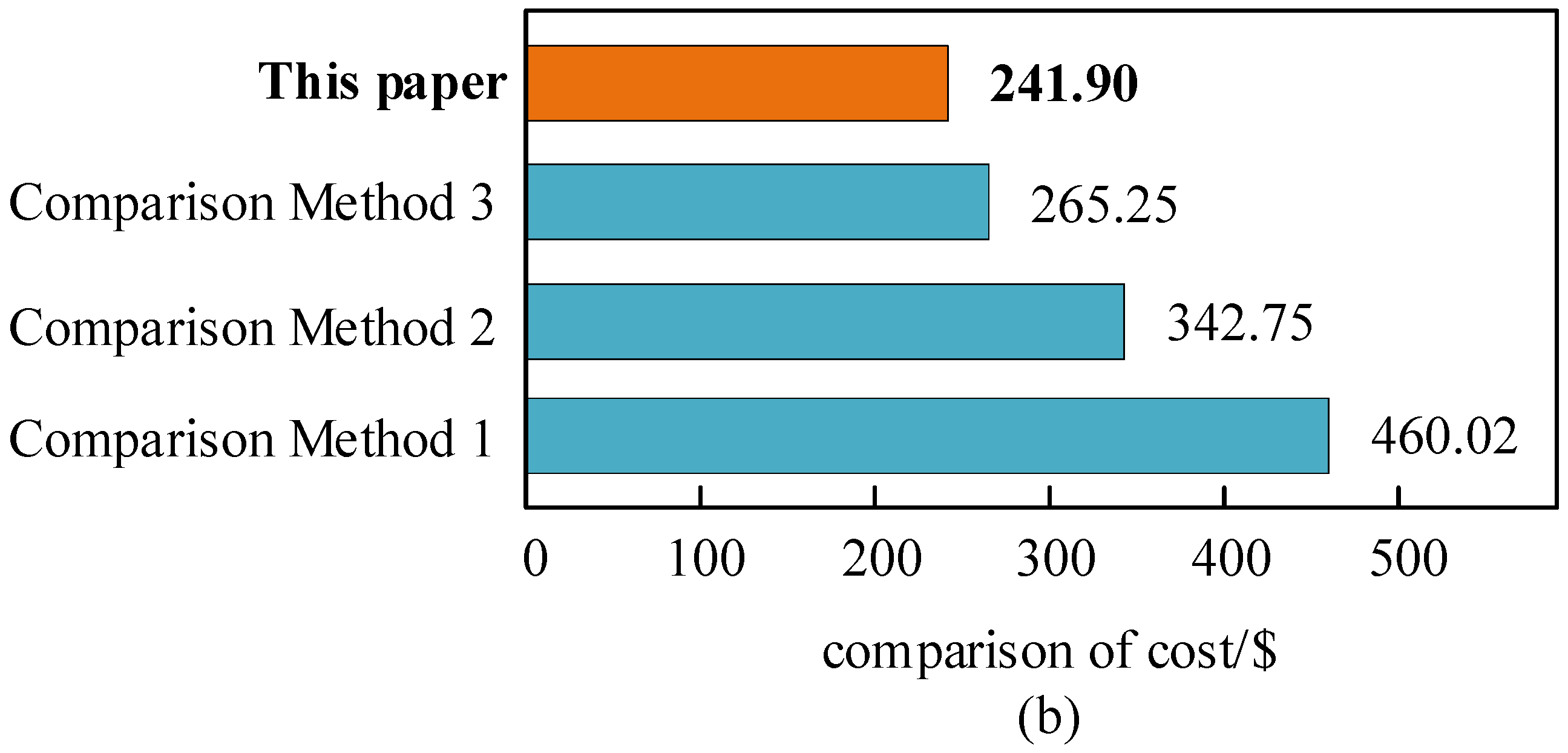

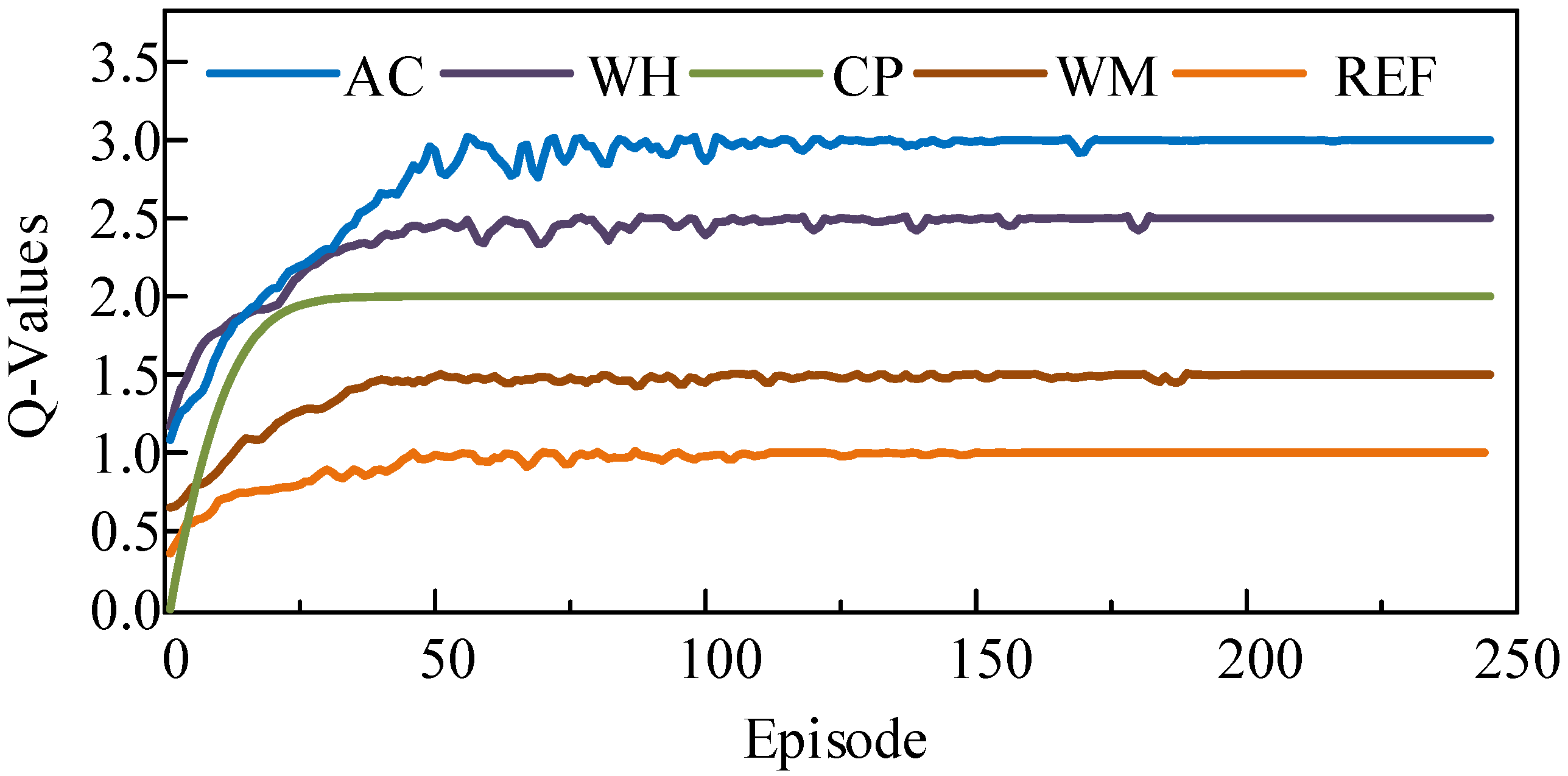
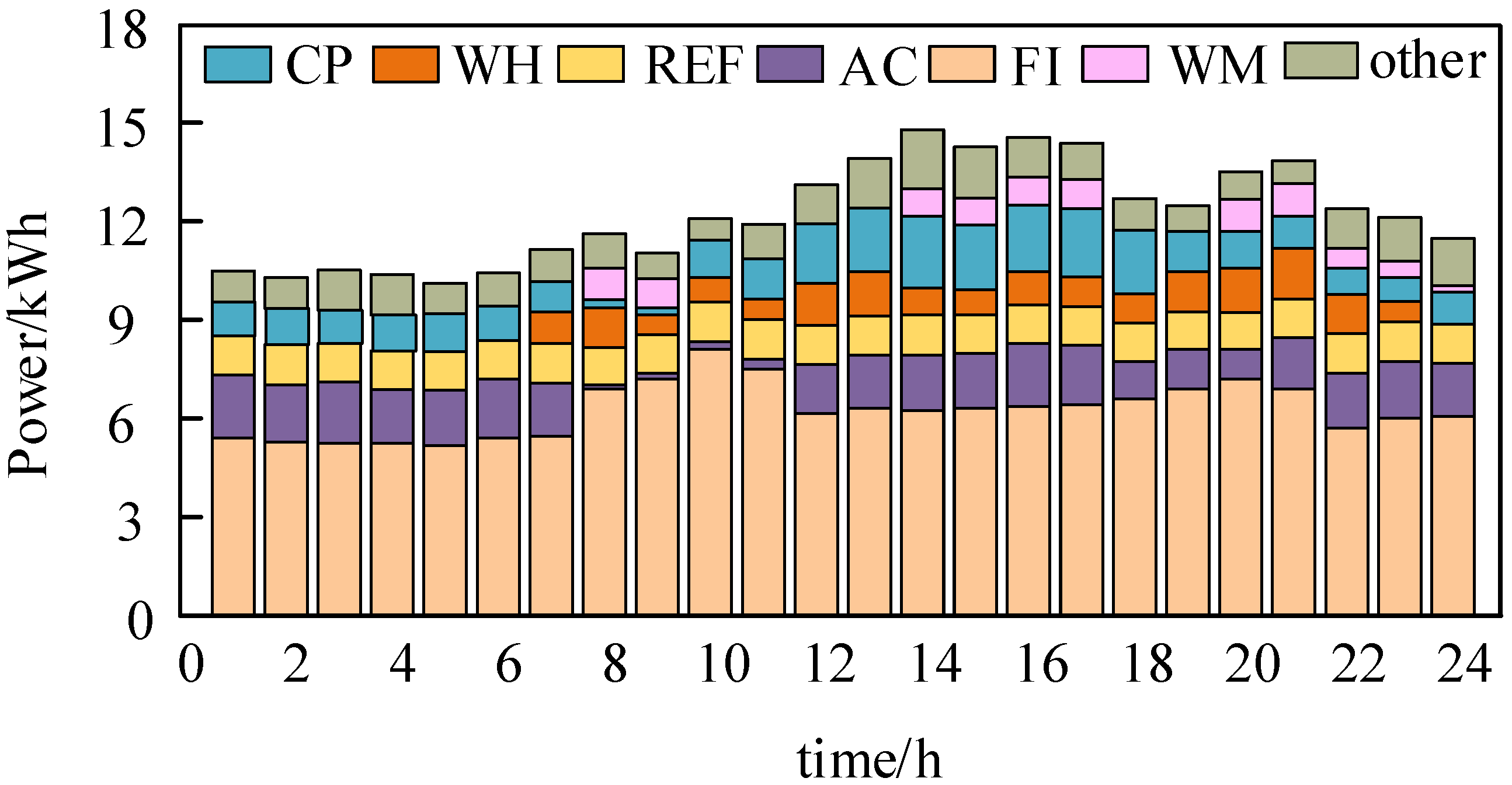

| Scene | Scene Description |
|---|---|
| 1 | No consideration of DR behaviors |
| 2 | Using conventional DR methods [30] |
| 3 | Using the proposed method, while EST is not involved in gaming |
| 4 | Using the proposed method in this paper |
| Scene | VPP Aggregator Benefit/USD | Household Benefit/USD | EST Benefit/USD | Total Benefit/USD |
|---|---|---|---|---|
| 1 | 85.06 | 513.74 | 143.97 | 229.03 |
| 2 | 174.14 | 334.75 | 113.76 | 287.90 |
| 3 | 237.47 | 302.42 | 87.92 | 325.39 |
| 4 | 272.06 | 291.73 | 122.67 | 394.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, S.; Xiao, Q.; Li, T.; Wang, Z.; Qiao, J.; Zhu, H.; Ji, W. A Two-Layer User Energy Management Strategy for Virtual Power Plants Based on HG-Multi-Agent Reinforcement Learning. Appl. Sci. 2025, 15, 6713. https://doi.org/10.3390/app15126713
Tian S, Xiao Q, Li T, Wang Z, Qiao J, Zhu H, Ji W. A Two-Layer User Energy Management Strategy for Virtual Power Plants Based on HG-Multi-Agent Reinforcement Learning. Applied Sciences. 2025; 15(12):6713. https://doi.org/10.3390/app15126713
Chicago/Turabian StyleTian, Sen, Qian Xiao, Tianxiang Li, Zibo Wang, Ji Qiao, Hong Zhu, and Wenlu Ji. 2025. "A Two-Layer User Energy Management Strategy for Virtual Power Plants Based on HG-Multi-Agent Reinforcement Learning" Applied Sciences 15, no. 12: 6713. https://doi.org/10.3390/app15126713
APA StyleTian, S., Xiao, Q., Li, T., Wang, Z., Qiao, J., Zhu, H., & Ji, W. (2025). A Two-Layer User Energy Management Strategy for Virtual Power Plants Based on HG-Multi-Agent Reinforcement Learning. Applied Sciences, 15(12), 6713. https://doi.org/10.3390/app15126713







