Experimental Investigation of Lateral Stresses and Bearing Capacity of Sandy Soil Under Shallow Foundation Loads
Abstract
1. Introduction
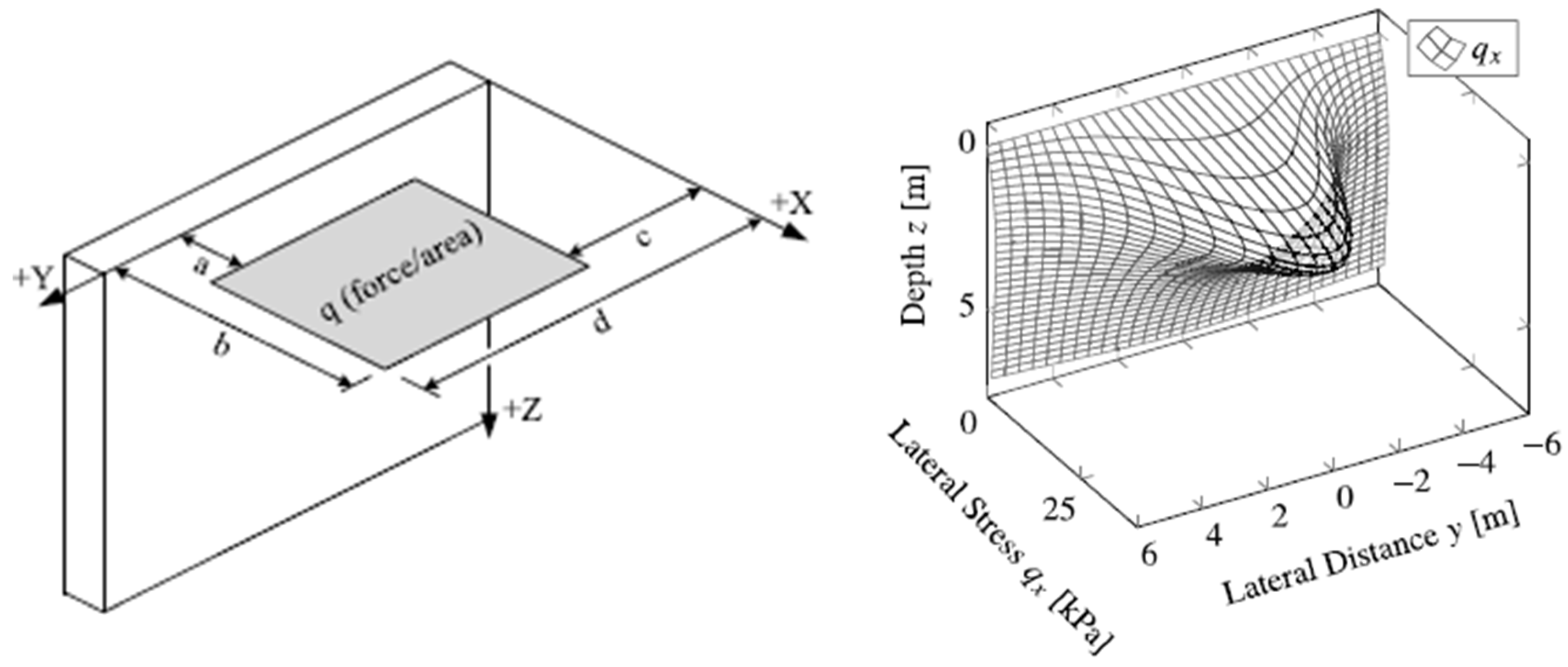
1.1. Lateral Stress Theories in Literature
1.2. Importance of the Study
2. Materials and Methods
2.1. Properties of Test Sand
2.2. Model Shallow Foundations
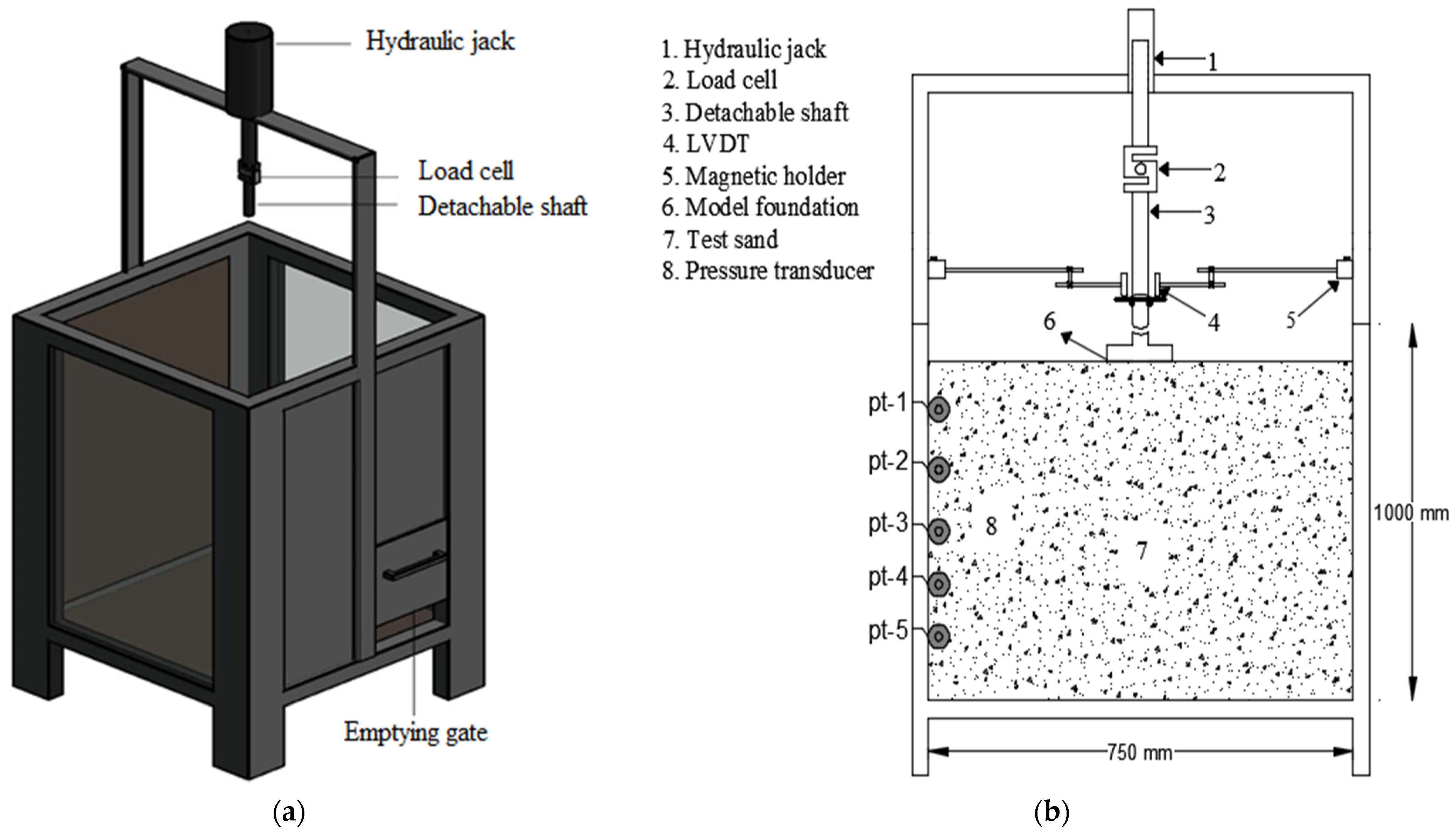
2.3. Experimental Setup and Test Program
3. Results and Discussion
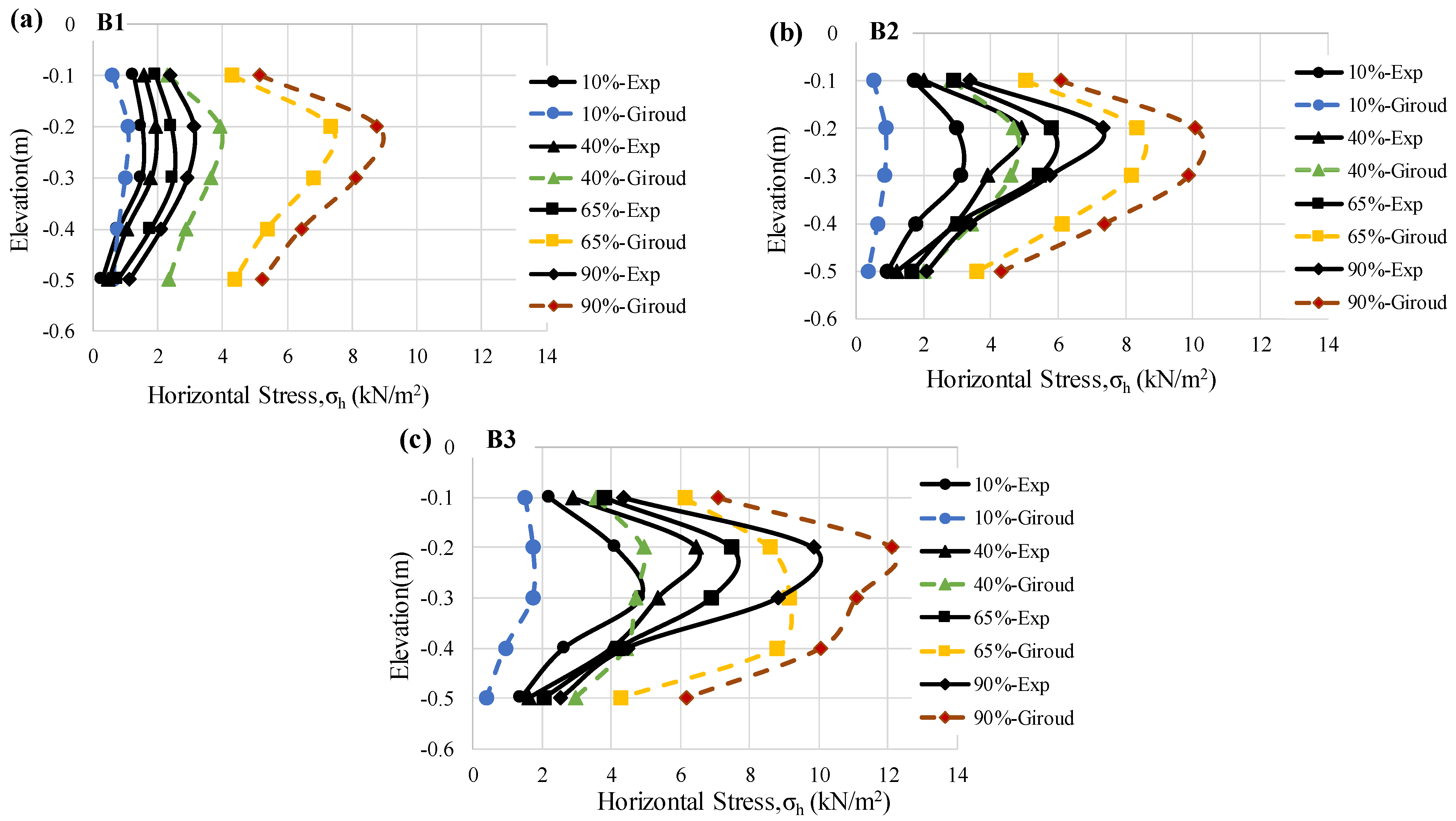
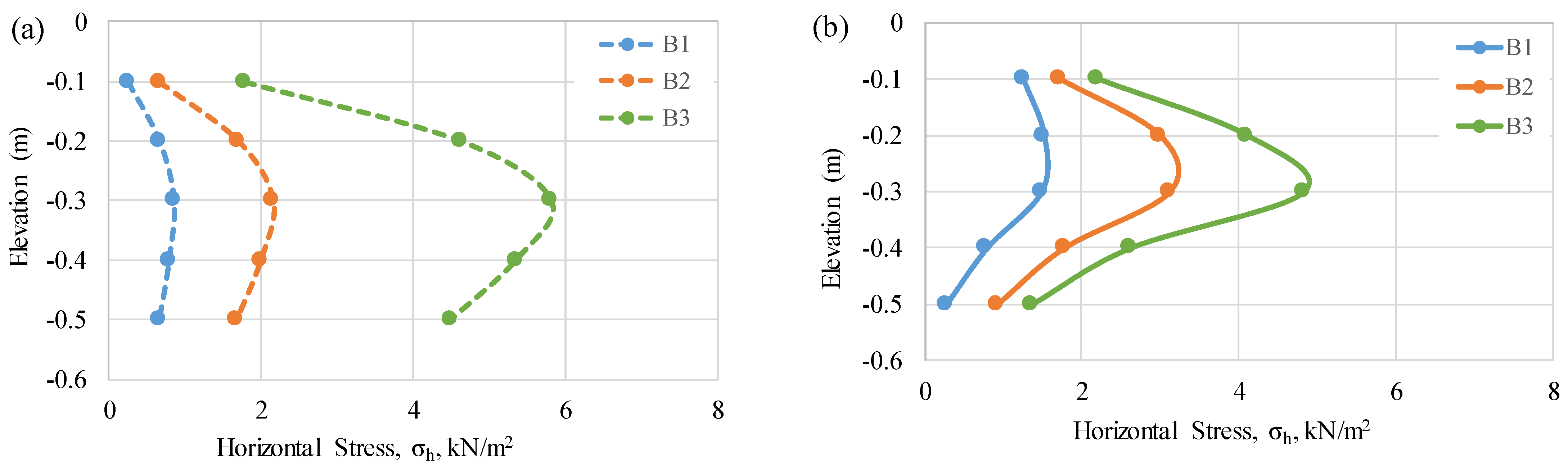
3.1. Evaluation of Lateral Stress Values
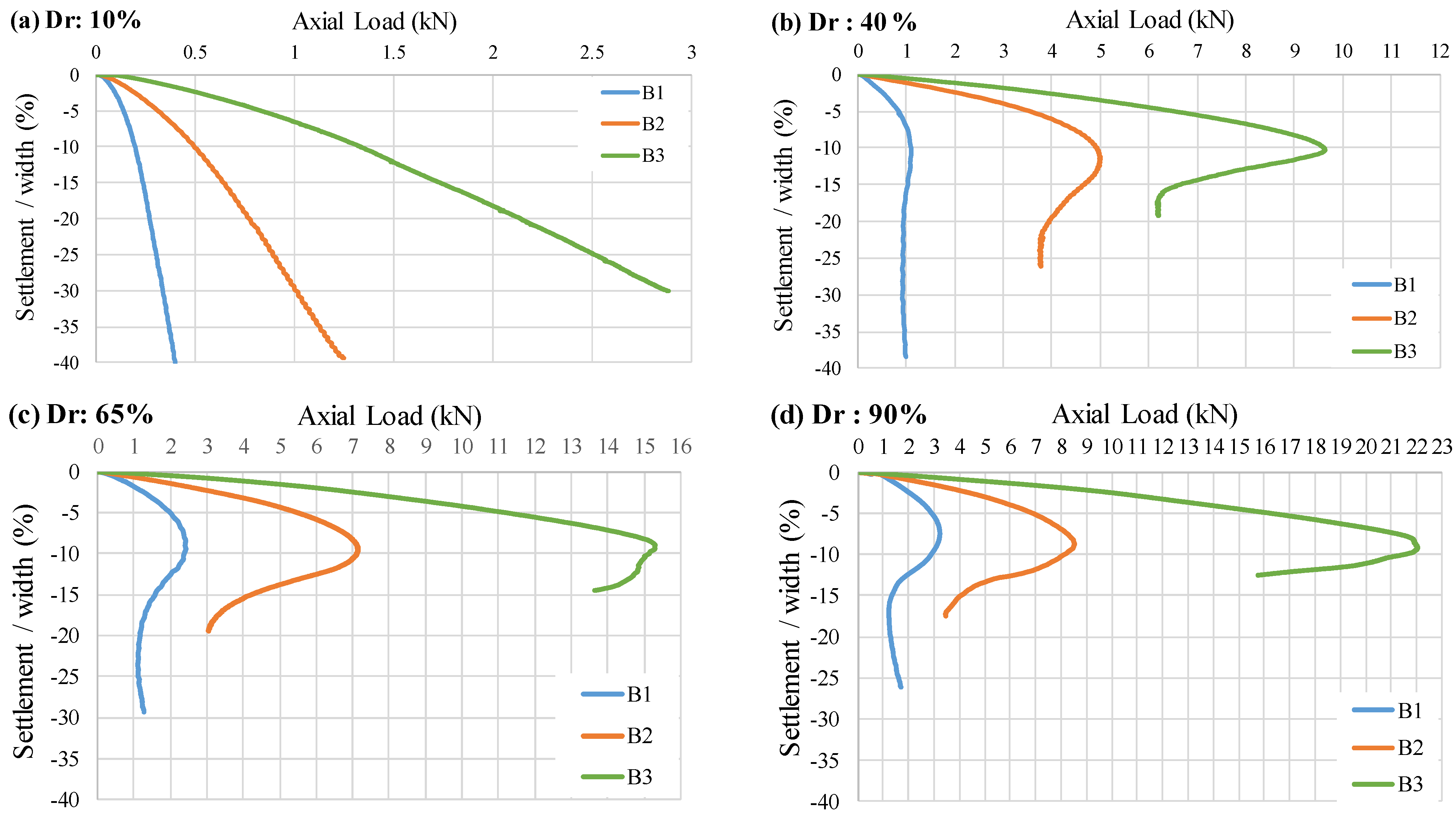
3.2. Load-Settlement Response
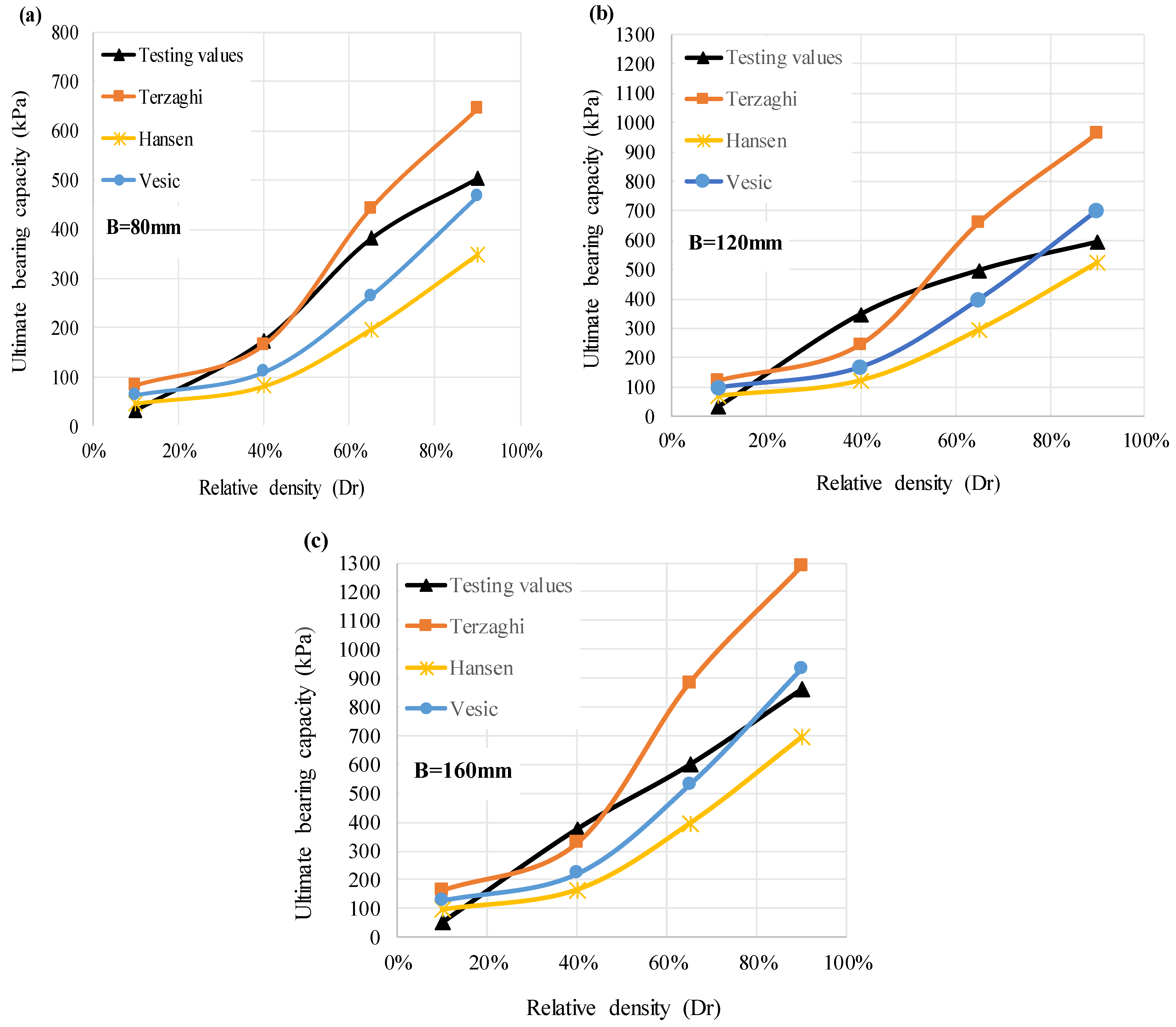
3.3. Comparison of Ultimate Bearing Capacity with Existing Theoretical Methods
3.4. Statistical Analysis
Validation of Statistical Analysis
4. Conclusions
- Lateral Stress Distribution Depending on Depth: The results of the model experiments showed that the measured lateral stresses changed systematically depending on both the relative density and foundation width. In particular, in the measurements made in the loosest case (Dr = 10%), the highest lateral stress value was σh = 4.10 kPa, and this value was measured at a depth of z = 3.75 B. In the same foundation size and very dense case (Dr = 90%), the maximum lateral stress value reached σh = 9.84 kPa, which was recorded at a depth of z = 2.5 B. While the maximum stresses in all foundation dimensions for Dr = 40%, 65%, and 90% are concentrated at the level of z = 2.5 B, these values are around z = 3.75 B in the case of Dr = 10%.
- Multivariate Regression for Lateral Stress Prediction: Multivariate regression analysis was performed to estimate the lateral pressure increases measured in the experiments. Considering the environmental geometric parameters and relative soil density, an equation was developed to determine the lateral stress increases under a square shallow foundation.
- Effect of Soil Density and Foundation Size: Its lateral stresses and ultimate bearing capacity increased significantly with increasing relative density and foundation size. At the largest foundation size (B3), when Dr is increased from 10% to 90%, there is an increase of 140% in lateral stress. Similarly, a more than 1500% increase in the bearing capacity was observed.
- Agreement with Theoretical Models: At high relative densities, the experimental results were in good agreement with Vesic’s theory. The ultimate bearing capacity values obtained from the model tests were compared with classical theoretical approaches, and the levels of agreement with different models were evaluated according to soil density. At Dr = 90% density, the experimental bearing capacity was calculated as 504.2 kPa for the B1 foundation size, while the Vesic bearing capacity was calculated as 466.7 kPa. The error rate was approximately 7.4%. In particular, the Vesic theory provides results that are very close to the experimental data in the experiments carried out on dense sands. At low densities, the Terzaghi and Hansen methods yield more realistic results. In contrast, Meyerhof’s method consistently overestimated the carrying capacity and did not agree with the experimental data.
- Load-Settlement Behavior: The load settlement curves exhibited nonlinear behavior with no obvious inflection points in the loose state (Dr = 10%). However, post-peak softening behavior was observed when the density increased steadily to 90%. Higher relative densities resulted in higher carrying capacity values at the same settlement level. However, the ultimate bearing capacity was reached at about 10% of the normalized settlement value when the settlement values were normalized with the foundation width.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bowles, J.E. Foundation Analysis and Design, 5th ed.; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Hoopes, O.; Hughes, J. In Situ Lateral Stress Measurement in Glaciolacustrine Seattle Clay Using the Pressuremeter. J. Geotech. Geoenviron. Eng. 2014, 140, 04013054. [Google Scholar] [CrossRef]
- Massarsch, K.R.; Wersäll, C.; Fellenius, B.H. Horizontal stress increase induced by deep vibratory compaction. Proc. Inst. Civ. Eng. Geotech. Eng. 2020, 173, 228–253. [Google Scholar] [CrossRef]
- Duncan, J.M.; Mokwa, R.L. Passive Earth Pressures: Theories and Tests. J. Geotech. Geoenviron. Eng. 2001, 127, 248–257. [Google Scholar] [CrossRef]
- Hanna, A.; Al Khoury, I. Passive Earth Pressure of Overconsolidated Cohesionless Backfill. J. Geotech. Geoenviron. Eng. 2005, 131, 978–986. [Google Scholar] [CrossRef]
- Roy, A.; Patra, N.R. Effect of arching on passive earth pressure for rigid retaining walls considering translation mode. In Structures Congress 2009: Don’t Mess with Structural Engineers: Expanding Our Role; American Society of Civil Engineers: Reston, VA, USA, 2009; pp. 2784–2793. [Google Scholar] [CrossRef]
- Yaghoubi, E.; Disfani, M.M.; Arulrajah, A.; Kodikara, J. Impact of compaction method on mechanical characteristics of unbound granular recycled materials. Road Mater. Pavement Des. 2018, 19, 912–934. [Google Scholar] [CrossRef]
- Terzaghi, K.V. Old earth pressure theories and new test results. Eng. News Rec. 1920, 85, 632–637. [Google Scholar]
- Jaky, J. Pressure in Silos. In Proceedings of the 2nd International Conference on Soil Mechanics and Foundation Engineering, Rotterdam, The Netherlands, 21–30 June 1948; pp. 103–107. [Google Scholar]
- Bishop, A.W. Test Requirements for Measuring proc. In Proceedings of the Test Requirements for Measuring Proc., Brussls, Belgium, 1958; pp. 2–14. [Google Scholar]
- Hendron, A. The Behavior of Sand in One Dimensional Compression; University of Illinois: Urbana, IL, USA, 1963. [Google Scholar]
- Brooker, E.W.; Ireland, H.O. Earth Pressures at Rest Related to Stress History. Can. Geotech. J. 1965, 2, 1–15. [Google Scholar] [CrossRef]
- Saglamer, A. Soil parameters affecting coefficient of earth pressure at rest of cohesionless soils. In Proceedings of the Istanbul Conference on Soil/Mechanics and Foundation Engineering, Istanbul, Turkey, 31 March–2 April 1975; pp. 9–16. [Google Scholar]
- Hanna, B.A.; Ghaly, A. Effects of K0 and overconsolidation on uplift capacity. J.Geotech. Eng. 1992, 118, 1449–1469. [Google Scholar] [CrossRef]
- Hanna, A.M.; Soliman-Saad, N. Effect of compaction duration on the induced stress levels in a laboratory prepared sand bed. Geotech. Test. J. 2001, 24, 430–438. [Google Scholar] [CrossRef]
- Bağrıaçık, B.; Laman, M. Investigation of the Size Effect at Different Geometries on Stress Distribution of Sandy Soils. In Proceedings of the International Balkans Conference on Challenges of Civil Engineering, Tirana, Albania, 19–21 May 2011; pp. 19–21. [Google Scholar]
- Talesnick, M.; Nachum, S.; Frydman, S. K0 determination using improved experimental technique. Geotechnique 2020, 71, 509–520. [Google Scholar] [CrossRef]
- Aksoy, H.S.; Küçükay, D.; Gör, M. KumZemïne Oturan Kare Temel Altinda Oluşan YanaGerïlmelerïn Deneysel VeTeorïÏncelemesï. Ömer Halisdemir Üniversitesi Mühendislik Bilim. Derg. 2019, 8, 912–921. [Google Scholar] [CrossRef]
- Das, B.M. Geotechnical Engineering Handbook; J. Ross Publishing: Plantation, FL, USA, 2010. [Google Scholar]
- Bilgen, G. Utilization of Powdered Glass as an Additive in Clayey Soils. Geotech. Geol. Eng. 2020, 38, 3163–3173. [Google Scholar] [CrossRef]
- Bilgen, G.; Altuntas, O.F. Sustainable re-use of waste glass, cement and lime treated dredged material as pavement material. Case Stud. Constr. Mater. 2023, 18, e01815. [Google Scholar] [CrossRef]
- Keskin, M.S.; Laman, M.; Baran, T. Experimental determination and numerical analysis of vertical stresses under square footings resting on sand. Tek. Dergi/Technical J. Turkish Chamb. Civ. Eng. 2008, 19, 1263–1279. [Google Scholar]
- Giroud, J.P. Settlement of a linearly loaded rectangular area. Civ. Eng. J. Soil Mech. ASCE 1968, 96, 813–831. [Google Scholar] [CrossRef]
- Li, L.; Dai, Z.; Liu, R.; Jian, F. Experimental Study on the Coefficient of Earth Pressure at Rest for Sand. Buildings 2023, 13, 1276. [Google Scholar] [CrossRef]
- Luo, Z.; Ding, X.; Zhang, X.; Ou, Q.; Yang, F.; Zhang, T.; Cao, G. Experimental and numerical investigation of the bearing capacity and deformation behavior of coral sand foundations under shallow footing loads. Ocean Eng. 2024, 310, 118601. [Google Scholar] [CrossRef]
- Lee, J.; Yun, T.S.; Lee, D.; Lee, J. Assessment of K0 correlation to strength for granular materials. Soils Found. 2013, 53, 584–595. [Google Scholar] [CrossRef]
- Li, Z.X.; Hou, G.Y.; Hu, T.; Zhou, T.C.; Xiao, H.L. Deformation behavior monitoring of a tunnel in its temporary shoring demolishing process using optical fiber sensing technology. Meas. J. Int. Meas. Confed. 2021, 176, 109170. [Google Scholar] [CrossRef]
- Moayedi, H.; Nazir, R.; Mosallanezhad, M.; Bin, R.; Noor, M. Lateral de fl ection of piles in a multilayer soil medium. Case study: The Terengganu seaside platform. Measurement 2018, 123, 185–192. [Google Scholar] [CrossRef]
- Liu, C.; Jiang, Z.; Yu, H. Safety analysis for bridge pier under nearby road construction and operation. Meas. J. Int. Meas. Confed. 2020, 151, 107169. [Google Scholar] [CrossRef]
- Xu, D.S.; Yin, J.H.; Cao, Z.Z.; Wang, Y.L.; Zhu, H.H.; Pei, H.F. A new flexible FBG sensing beam for measuring dynamic lateral displacements of soil in a shaking table test. Meas. J. Int. Meas. Confed. 2013, 46, 200–209. [Google Scholar] [CrossRef]
- Moayedi, H.; Nazir, R.; Gör, M.; Kassim, K.A.; Foong, L.K. A new real-time monitoring technique in calculation of the p-y curve of single thin steel piles considering the influence of driven energy and using strain gauge sensors. Measurement 2019, 153, 107365. [Google Scholar] [CrossRef]
- Boussinesq, J. et des pressions que produisent. In Proceedings of the Application des Potentiels à L’étude de L’équilibre et du Mouvement des Solides Élastiques: Principalement au Calcul des Déformations et des Pressions Que, Paris, France, 1885. [Google Scholar]
- Feld, J. Lateral Earth Pressure: The Accurate Experimental Determination of the Lateral Earth Pressure, Together with A Resume of Previous Experiments. Trans. Am. Soc. Civ. Eng. 1923, 86, 1448–1505. [Google Scholar] [CrossRef]
- Gerber, E. Untersuchungen über die Druckverteilung im Örtlich Belasteten Sand. Doctoral Dissertation, Eidgenössische Technische Hochschule Zürich (ETH Zurich), Zürich, Switzerland, 1929. [Google Scholar]
- Newmark, N.M. Simplified computation of vertical pressures in elastic foundations. Eng. Exp. Stn. Circ. 1935. [Google Scholar]
- Spangler, M.G. Horizontal Pressures on Retaining Walls Due to Concentrated Surface Loads; Iowa State College of Agriculture and Mechanic Arts: Ames, IA, USA, 1938. [Google Scholar]
- Heagler, J.B. Horizontal Pressures on Retaining Walls Due to Line Surface Loads. Master’s Thesis, Missouri University of Science and Technology, Rolla, MO, USA, 1954. [Google Scholar]
- James, R.W.; Brown, D.A. Wheel-load-induced earth pressures on box culverts. Transp. Res. Rec. 1987, 1129, 55–62. [Google Scholar]
- Rehnman, S.; Broms, B.B. Lateral pressures on basement wall. Results from full-scale tests. In Proceedings of the 5th European Conference on Soil Mechanics and Foundation Engineering, Madrid, Spain, 10–13 April 1972. [Google Scholar]
- Abdel-Karim, A.M.; Tadros, M.K.; Benak, J.V. Live load distribution on concrete box culverts. Transp. Res. Rec. 1990, 136–151. [Google Scholar]
- Poulos, H.G.; Davis, E.H. Elastic solutions for soil and rock mechanics. Textbook. Figs, Tabls, Refs. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1974, 11, A159. [Google Scholar] [CrossRef]
- Gray, H. Stress distribution in elastic solids. In Proceedings International Conference on Soil Mechanics and Foundation Engineering; ISSMGE: London, UK, 1936. [Google Scholar]
- AASHTO. LRFD Bridge Design Specifications, 8th ed.; AASHTO: Washington, DC, USA, 2017. [Google Scholar]
- Frazee, G.R. New Formulations of Boussinesq Solution for Vertical and Lateral Stresses in Soil. Pract. Period. Struct. Des. Constr. 2021, 26, 06021001. [Google Scholar] [CrossRef]
- Giroud, J.P. Stresses under linearly loaded rectangular area. J. Soil Mech. Found. Div. ASCE 1970, 96, 263–268. [Google Scholar] [CrossRef]
- Jardine, R.J.; Standing, J.R.; Chow, F.C. Some observations of the effects of time on the capacity of piles driven in sand. Geotechnique 2006, 56, 227–244. [Google Scholar] [CrossRef]
- Emirler, B.; Tolun, M.; Yildiz, A. Investigation on determining uplift capacity and failure mechanism of the pile groups in sand. Ocean Eng. 2020, 218, 108145. [Google Scholar] [CrossRef]
- ASTM-C1444-00; Standard Method for Measuring the Angle of Repose of Free-Flowing Mold Powders. American Society of Testing and Materials: Philadelphia, PA, USA, 2001; pp. 694–695.
- ASTM D422-63; Standard Test Method for Particle-Size Analysis of Soils. ASTM International: West Conshohocken PA, USA, 2007.
- ASTM D854-14; Standard Test Methods for Specific Gravity of Soil Solids by Water Pycnometer. ASTM International: West Conshohocken PA, USA, 2014.
- ASTM D4254; Standard Test Methods for Minimum Index Density and Unit Weight of Soils and Calculation of Relative Density. ASTM International: West Conshohocken, PA, USA, 2006.
- Holtz, R.D.; Kovacs, W.D.; Sheahan, T.C. An Introduction to Geotechnical Engineering, 2nd ed.; Pearson: London, UK, 2015. [Google Scholar]
- Chen, T.J.; Fang, Y.S. Earth pressure due to vibratory compaction. J. Geotech. Geoenviron. Eng. 2008, 134, 437–444. [Google Scholar] [CrossRef]
- Luo, Z.G.; Ding, X.M.; Ou, Q.; Fang, H.Q. Bearing capacity and deformation behavior of rigid strip footings on coral sand slopes. Ocean Eng. 2023, 267, 113317. [Google Scholar] [CrossRef]
- Wood, D.M. Geotechnical Modelling (Applied Geotechnics; v. 1); Taylor & Francis Group/Books: Boca Raton, FL, USA, 2004. [Google Scholar]
- Vesic, A.S. Analysis of ultimate loads of shallow foundations. J. Soil Mech. Found. Div. 1973, 99, 45–73. [Google Scholar] [CrossRef]
- Poulos, H.G.; Davis, E.H. Prediction of Downdrag Forces in End-Bearing Piles. J. Geotech. Eng. Div. 1975, 101, 189–204. [Google Scholar] [CrossRef]
- Meyerhof, G.G.; Hanna, A.M. Ultimate bearing capacity of foundations on layered soils under inclined load. Can. Geotech. J. 1978, 15, 565–572. [Google Scholar] [CrossRef]
- Terzaghi, A. Soil Management for Improvement of Soil Physical Characteristics Related to Erosion in Uruguay. Ph.D. Thesis, Wageningen University and Research, Wageningen, The Netherlands, 1996. [Google Scholar]
- Perkins, S.W.; Madson, C.R. Bearing capacity of shallow foundations on sand: A relative density approach. J. Geotech. Geoenviron. Eng. 2000, 126, 521–530. [Google Scholar] [CrossRef]
- Loukidis, D.; Salgado, R. Effect of relative density and stress level on the bearing capacity of footings on sand. Géotechnique 2011, 61, 107–119. [Google Scholar] [CrossRef]
- Lade, P.V.; Duncan, J.M. Elastoplastic stress-strain theory for cohesionless soil. J. Geotech. Eng. Div. 1975, 101, 1037–1053. [Google Scholar] [CrossRef]
- Terzaghi, K. Theoretical Soil Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 1943. [Google Scholar]
- Meyerhof, G.G. The ultimate bearing capacity of foudations. Geotechnique 1951, 2, 301–332. [Google Scholar] [CrossRef]
- Hansen, J.B. A Revised and Extended Formula for Bearing Capacity; Bull, 28; Danish Geotechnical Institute: Copenhagen, Denmark, 1970. [Google Scholar]
- Vesic, A.S. Bearing Capacity of Shallow Foundations. In Foundation Engineering Handbook; Winterkorn, F.S., Fand, H.Y., Eds.; Van Nostrand Reinhold: New York, NY, USA, 1975. [Google Scholar]
- Liu, G.; Liu, C. Derivation of the Ultimate Bearing Capacity Formula for Layered Foundations Based on Meyerhof’s Theory. Appl. Sci. 2024, 14, 5121. [Google Scholar] [CrossRef]
- Padmavathi, M.; Padmavathi, V.; Madhav, M.R. Foundation Subjected to Moment Loading: Re-evaluation of Meyerhof’s Approach. Indian Geotech. J. 2014, 44, 260–268. [Google Scholar] [CrossRef]
- Ravichandran, N.; Mahmoudabadi, V.; Shrestha, S. Analysis of the Bearing Capacity of Shallow Foundation in Unsaturated Soil Using Monte Carlo Simulation. Int. J. Geosci. 2017, 08, 1231–1250. [Google Scholar] [CrossRef]
- Bowles, J.E. Foundation Analysis and Design, 5th ed.; McGraw-Hill: Peoria, IL, USA, 2012. [Google Scholar]
- Ahmad, M.; Ahmad, F.; Wróblewski, P.; Al-Mansob, R.A.; Olczak, P.; Kamiński, P.; Safdar, M.; Rai, P. Prediction of ultimate bearing capacity of shallow foundations on cohesionless soils: A gaussian process regression approach. Appl. Sci. 2021, 11, 10317. [Google Scholar] [CrossRef]
- Shahnazari, H.; Tutunchian, M.A. Prediction of ultimate bearing capacity of shallow foundations on cohesionless soils: An evolutionary approach. KSCE J. Civ. Eng. 2012, 16, 950–957. [Google Scholar] [CrossRef]
- Tsai, H.C.; Tyan, Y.Y.; Wu, Y.W.; Lin, Y.H. Determining ultimate bearing capacity of shallow foundations using a genetic programming system. Neural Comput. Appl. 2013, 23, 2073–2084. [Google Scholar] [CrossRef]
- Kohestani, V.R.; Vosoughi, M.; Hassanlourad, M.; Fallahnia, M. Bearing Capacity of Shallow Foundations on Cohesionless Soils: A Random Forest Based Approach. Civ. Eng. Infrastructures J. 2017, 50, 35–49. [Google Scholar] [CrossRef]
- Zhang, L.; Shi, Z.; Cheng, M.M.; Liu, Y.; Bian, J.W.; Zhou, J.T.; Zheng, G.; Zeng, Z. Nonlinear Regression via Deep Negative Correlation Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 982–998. [Google Scholar] [CrossRef]


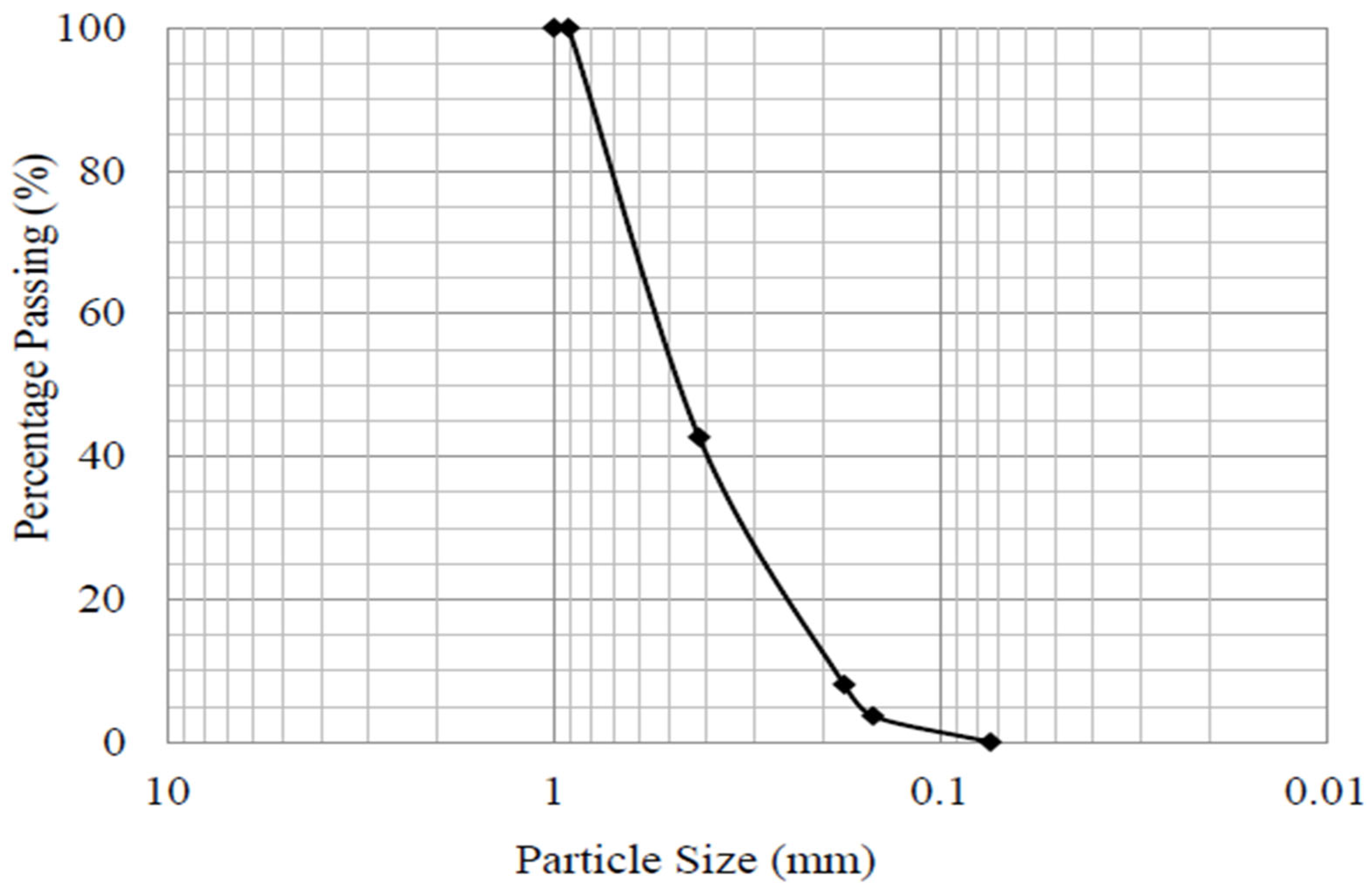





| Granulometry Parameters | Units | Values |
|---|---|---|
| Spesific gravity, Gs | - | 2.77 |
| D10 | mm | 0.18 |
| D50 | mm | 0.45 |
| Max − min particle size, Dmax − Dmin | mm | 1–0.074 |
| Max dry density | kN/m3 | 17.5 |
| Min dry density | kN/m3 | 14.3 |
| Max void ratio, emax | - | 0.903 |
| Min void ratio, emin | - | 0.553 |
| Soil class (USCS) | - | SP |
| Serial Number | Foundation Size (mm) | Dr (%) Relative Density | Loose-Dense Condition [52] |
|---|---|---|---|
| B1 = B | 80 | 10 | 10% ≤ very loose |
| 40 | 40% ≤ medium dense soil | ||
| 65 | dense | ||
| 90 | very dense | ||
| B2 = 1.5 B | 120 | 10 | 10% ≤ very loose |
| 40 | 40% ≤ medium dense soil | ||
| 65 | dense | ||
| 90 | very dense | ||
| B3 = 2 B | 160 | 10 | 10% ≤ very loose |
| 40 | 40% ≤ medium dense soil | ||
| 65 | dense | ||
| 90 | very dense |
| Relative Density (Dr, %) | Average Dry Unit Weight (γd), (kN/m3) | Void Ratio (e) | Pluviation and Compaction Process |
|---|---|---|---|
| 10 | 14.6 | 0.869 | Test sand was poured from a height of 10 to 15 cm until the model tank was filled to the needed depth. |
| 40 | 15.5 | 0.763 | The test sand was poured between 5 and 10 cm in height, and the tank was filled with layers every 10 cm. Each point (15 cm × 15 cm) was compacted for a brief period of time, less than a second. |
| 65 | 16.3 | 0.635 | The test sand was poured between 5 and 10 cm in height, and the tank was filled with layers every 10 cm. Each point (15 cm × 15 cm) was compacted for a brief period of time, less than a second. |
| 90 | 17.3 | 0.588 | The test sand was poured between 5 and 10 cm in height, and the tank was filled with layers every 5 cm. Each point (15 cm × 15 cm) was compacted for a brief period of time, less than a second. |
| Physical Parameters | Scaling Factor |
|---|---|
| Gravity (m/s2) | 1 |
| Length (m) | 1/n |
| Force (N) | 1/n3 |
| Displacement (m) | 1/n2−α |
| Area (m2) | 1/n2 |
| Strain | 1/n1−α |
| Stiffness (N) | 1/nα |
| Density (kg/m3) | 1 |
| Stress (kPa) | 1/n |
| α | 1 |
| Model Foundation | Dr (%) | This Study | Terzaghi [63] | Meyerhof [64] | Hansen [65] | Vesic [66] |
|---|---|---|---|---|---|---|
| B = B1 = 80 mm | 10 | 30.9 | 81.8 | 183.7 | 47.3 | 64.4 |
| 40 | 173.0 | 163.7 | 358.1 | 81.9 | 110.8 | |
| 65 | 380.6 | 440.1 | 1083.5 | 197.1 | 264.7 | |
| 90 | 504.2 | 642.8 | 2262.6 | 348.4 | 466.7 | |
| B2 | 10 | 34.5 | 122.8 | 275.6 | 71.0 | 96.6 |
| 40 | 347.2 | 245.5 | 537.1 | 122.9 | 166.2 | |
| 65 | 496.3 | 660.1 | 1625.3 | 295.7 | 397.0 | |
| 90 | 592.2 | 964.3 | 3393.8 | 522.6 | 700.0 | |
| B3 | 10 | 52.3 | 163.7 | 367.4 | 94.6 | 128.8 |
| 40 | 375.4 | 327.3 | 716.2 | 163.9 | 221.6 | |
| 65 | 597.9 | 880.2 | 2167.1 | 394.2 | 529.3 | |
| 90 | 859.5 | 1285.7 | 4525.1 | 696.8 | 933.4 |
| Δσ (kPa) | z (m) | B (m) | z/B | α | Dr (%) | |
|---|---|---|---|---|---|---|
| Average | 0.017 | 0.30 | 0.12 | 2.71 | 36.33 | 0.51 |
| Minimum | 0.023 | 0.10 | 0.08 | 0.63 | 14.93 | 0.10 |
| Maximum | 0.092 | 0.50 | 0.16 | 6.25 | 53.13 | 0.90 |
| Standard Deviation | 0.022 | 0.14 | 0.03 | 1.55 | 13.71 | 0.30 |
| Skewness | 2.3143 | 0 | 0 | 0.7005 | −0.3622 | −0.1064 |
| Kurtosis | 4.7189 | −1.3081 | −1.5259 | −0.1588 | −1.2081 | −1.3293 |
| Coefficient | T (1st) | V (2nd) | W (3rd) | X (4th) | Y (5th) | Z (6th) |
|---|---|---|---|---|---|---|
| Values | −14.21 | −112.33 | −48.60 | 2.69 | −40.94 | 140.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aksoy, H.S.; Küçükay Kayaalp, D. Experimental Investigation of Lateral Stresses and Bearing Capacity of Sandy Soil Under Shallow Foundation Loads. Appl. Sci. 2025, 15, 6699. https://doi.org/10.3390/app15126699
Aksoy HS, Küçükay Kayaalp D. Experimental Investigation of Lateral Stresses and Bearing Capacity of Sandy Soil Under Shallow Foundation Loads. Applied Sciences. 2025; 15(12):6699. https://doi.org/10.3390/app15126699
Chicago/Turabian StyleAksoy, Huseyin Suha, and Damla Küçükay Kayaalp. 2025. "Experimental Investigation of Lateral Stresses and Bearing Capacity of Sandy Soil Under Shallow Foundation Loads" Applied Sciences 15, no. 12: 6699. https://doi.org/10.3390/app15126699
APA StyleAksoy, H. S., & Küçükay Kayaalp, D. (2025). Experimental Investigation of Lateral Stresses and Bearing Capacity of Sandy Soil Under Shallow Foundation Loads. Applied Sciences, 15(12), 6699. https://doi.org/10.3390/app15126699






