A Comprehensive Review of Fused Filament Fabrication: Numerical Modeling Approaches and Emerging Trends
Abstract
1. Introduction
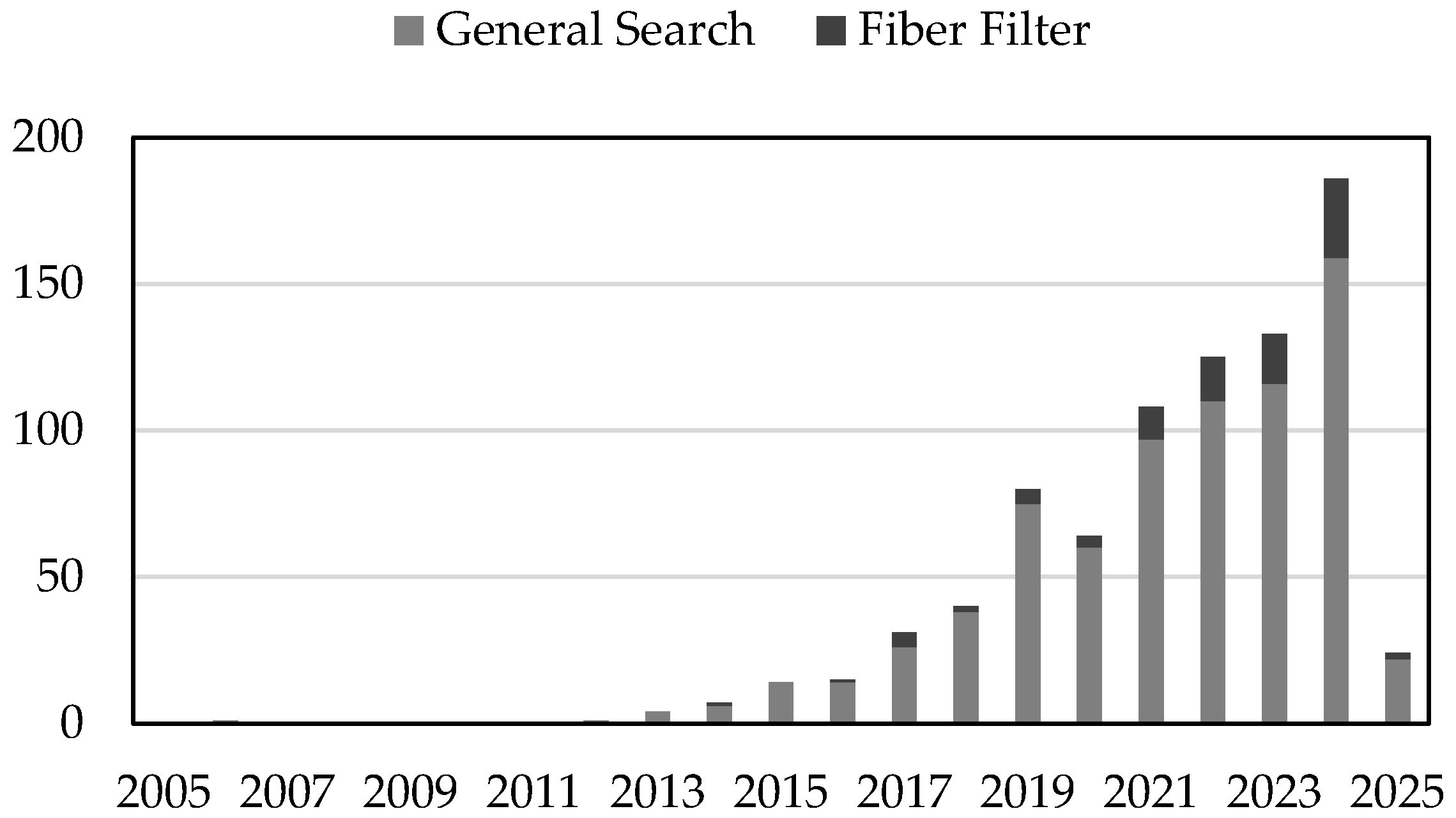
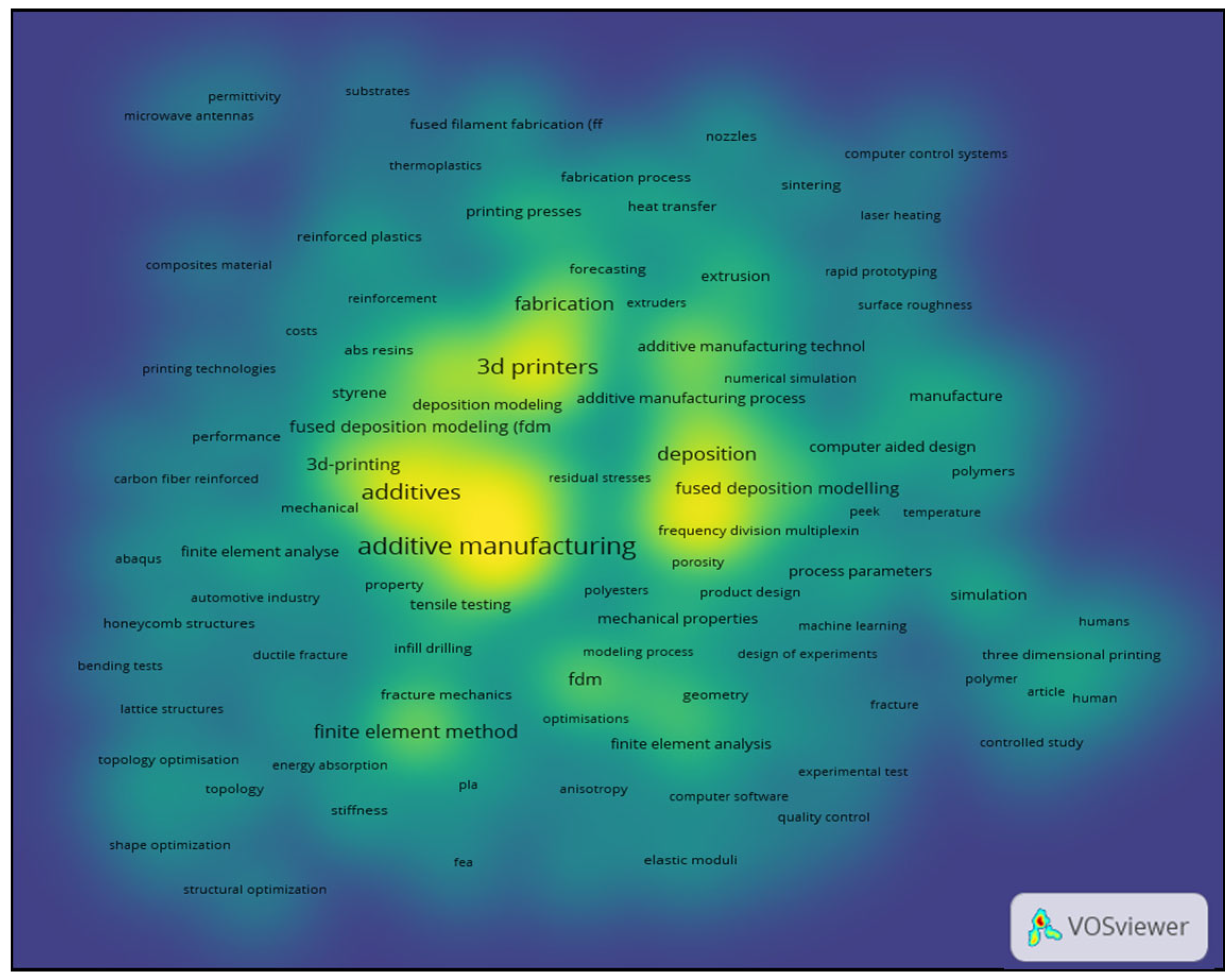
2. Meta-Analysis and Bibliometric Assessment
3. Fused Filament Fabrication
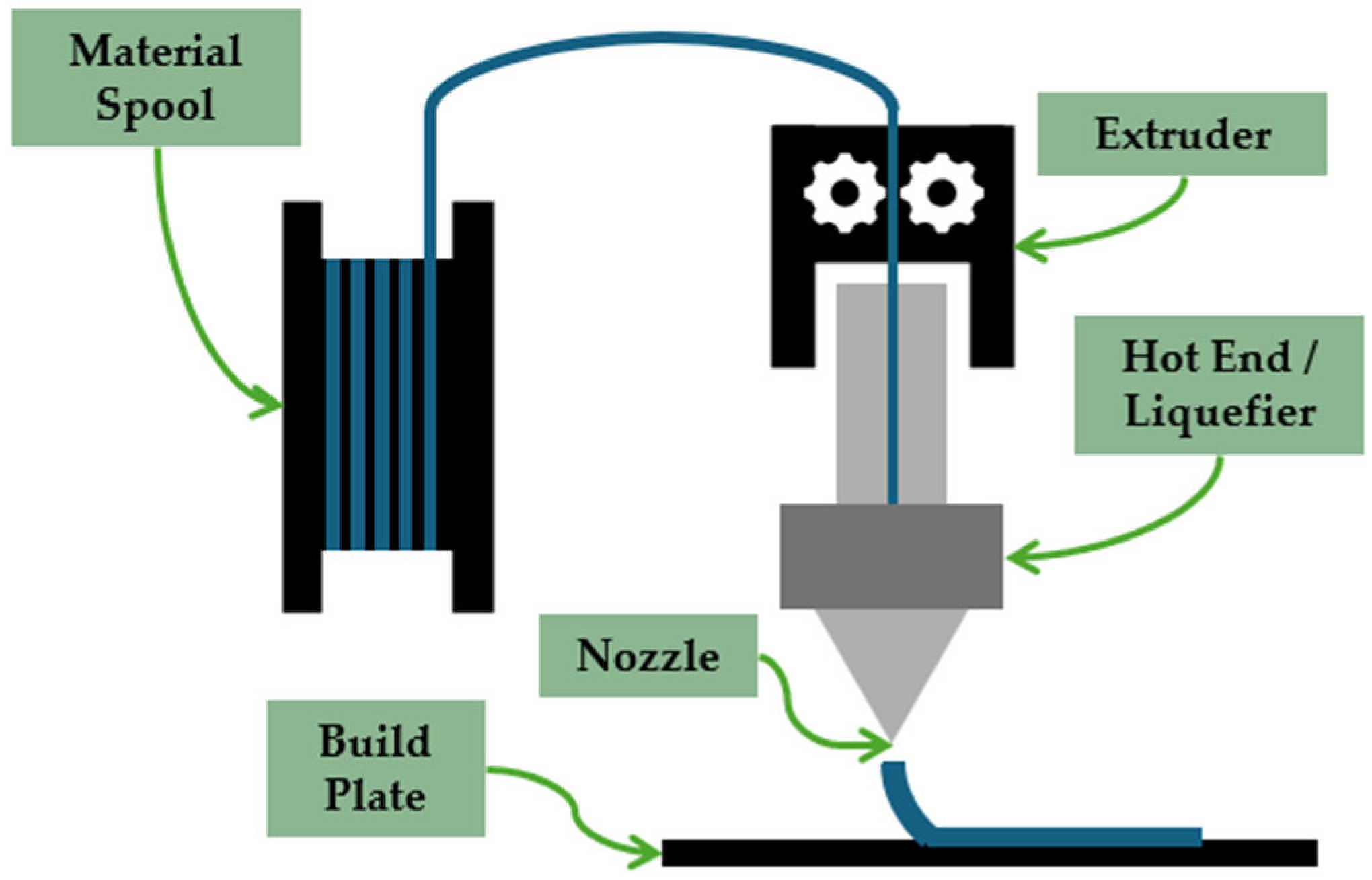
3.1. Overview of the FFF Process
3.2. Stages of Material Transformation in FFF
3.3. Rheological Behavior of Thermoplastics in FFF
4. Numerical Simulation Applied to the FFF Process
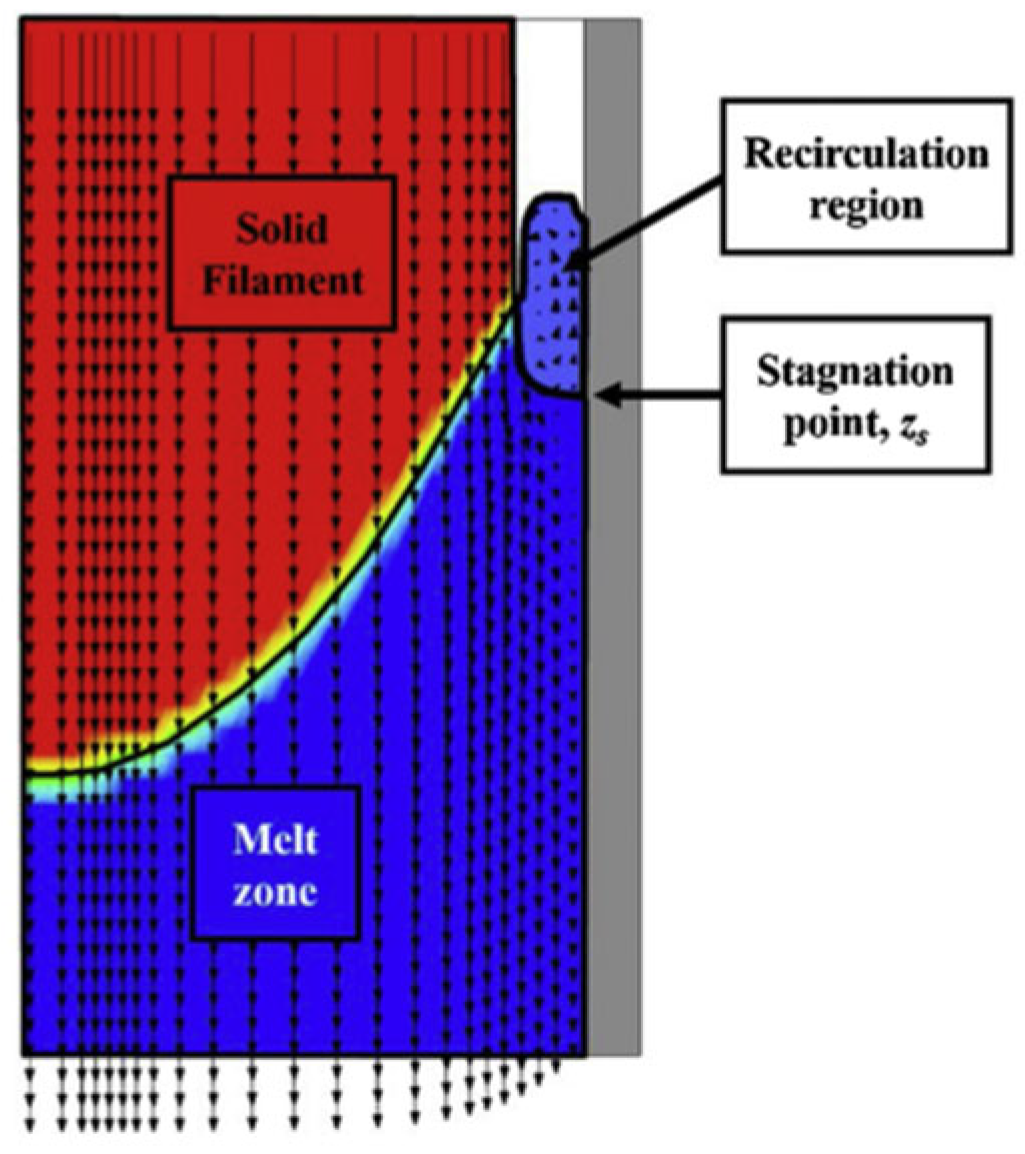
4.1. Melt Flow
4.2. Cooling and Solidification
4.3. Thermal–Mechanical
4.4. Material Property Characterization
5. Fiber-Reinforced Composites
6. Systematic Literature Review
6.1. General Trends in Simulation Approaches
6.2. Comparative Evaluation of Abaqus and Ansys
7. Discussion and Future Trends
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ABS | Acrylonitrile Butadiene Styrene |
| AFM | Atomic Force Microscopy |
| AI | Artificial Intelligence |
| AM | Additive Manufacturing |
| ANN | Artificial Neural Network |
| BAAM | Big Area Additive Manufacturing |
| CFF | Continuous Fiber Filament |
| CFD | Computational Fluid Dynamics |
| CF | Carbon Fiber |
| CFRC | Continuous Fiber-Reinforced Composite |
| CM | Computational Model |
| CMM | Coordinate Measuring Machine |
| CS | Cooling and Solidification |
| DEM | Discrete Element Method |
| DMA | Dynamic Mechanical Analysis |
| DSC | Differential Scanning Calorimetry |
| DOE | Design of Experiments |
| FEA | Finite Element Analysis |
| FDC | Fused Deposition of Ceramics |
| FFF | Fused Filament Fabrication |
| FRP | Fiber-Reinforced Polymer |
| FRC | Fiber-Reinforced Composites |
| IoT | Internet of Things |
| IR camera | Infrared Camera |
| LAAM | Large Area Additive Manufacturing |
| LSAM | Large-Scale Additive Manufacturing |
| ML | Machine Learning |
| MPC | Material Property Characterization |
| MEX | Material Extrusion |
| MF | Melt Flow |
| PA | Polyamide |
| PC | Polycarbonate |
| PEKK | Polyetherketoneketone |
| PETG | Polyethylene Terephthalate Glycol |
| PLA | Polylactic Acid |
| PP | Polypropylene |
| PPS | Polyphenylene Sulfide |
| ResNet | Residual Neural Network |
| RVE | Representative Volume Element |
| RW | Review |
| SEM | Scanning Electron Microscopy |
| SFRC | Short Fiber-Reinforced Composite |
| SPH | Smoothed Particle Hydrodynamics |
| TMB | Thermal–Mechanical Behavior |
| µCT | Micro-Computed Tomography |
References
- Gibson, I.; Rosen, D.; Stucker, B. Additive Manufacturing Technologies; Springer: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Rodríguez-Martín, M.; Domingo, R.; Ribeiro, J. Mapping and prospective of additive manufacturing in the context of Industry 4.0 and 5.0. Rapid Prototyp. J. 2024, 30, 1393–1410. [Google Scholar] [CrossRef]
- Behseresht, S.; Park, Y.H.; Love, A.; Pastrana, O.A.V. Application of Numerical Modeling and Finite Element Analysis in Fused Filament Fabrication: A Review. Materials 2024, 17, 4185. [Google Scholar] [CrossRef]
- Tuli, N.T.; Khatun, S.; Rashid, A.B. Unlocking the future of precision manufacturing: A comprehensive exploration of 3D printing with fiber-reinforced composites in aerospace, automotive, medical, and consumer industries. Heliyon 2024, 10, e27328. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Smith, D.E. Finite element modelling of fully-coupled flow/fiber-orientation effects in polymer composite deposition additive manufacturing nozzle-extrudate flow. Compos. B Eng. 2021, 219, 108811. [Google Scholar] [CrossRef]
- Xu, X.; Ren, H.; Chen, S.; Luo, X.; Zhao, F.; Xiong, Y. Review on melt flow simulations for thermoplastics and their fiber reinforced composites in fused deposition modeling. J. Manuf. Process. 2023, 92, 272–286. [Google Scholar] [CrossRef]
- Heller, B.P.; Smith, D.E.; Jack, D.A. Planar deposition flow modeling of fiber filled composites in large area additive manufacturing. Addit. Manuf. 2019, 25, 227–238. [Google Scholar] [CrossRef]
- Awenlimobor, A.; Smith, D.E.; Wang, Z. Simulation of fiber-induced melt pressure fluctuations within large scale polymer composite deposition beads. Addit. Manuf. 2024, 80, 103980. [Google Scholar] [CrossRef]
- Ribeiro, J.; Rodríguez-Martín, M.; Barreiro, J.; Fernández, A.-I.; García-Martín, R.; Rocha, J.; Martínez-Pellitero, S. New trends of additive manufacturing using materials based-on natural fibers and minerals: A systematic review. Heliyon 2025, 11, e41993. [Google Scholar] [CrossRef]
- Maqsood, N.; Rimašauskas, M.; Ghobakhloo, M.; Mordas, G.; Skotnicová, K. Additive manufacturing of continuous carbon fiber reinforced polymer composites using materials extrusion process. Mechanical properties, process parameters, fracture analysis, challenges, and future prospect. A review. Adv. Compos. Hybrid Mater. 2024, 7, 202. [Google Scholar] [CrossRef]
- Jin, Z.; Zhang, Z.; Gu, G.X. Automated Real-Time Detection and Prediction of Interlayer Imperfections in Additive Manufacturing Processes Using Artificial Intelligence. Adv. Intell. Syst. 2020, 2, 1900130. [Google Scholar] [CrossRef]
- Fu, Y.; Downey, A.R.J.; Yuan, L.; Huang, H.-T.; Ogunniyi, E.A. Simulation-in-the-loop additive manufacturing for real-time structural validation and digital twin development. Addit. Manuf. 2025, 98, 104631. [Google Scholar] [CrossRef]
- Rodríguez-Martín, M.; Fueyo, J.G.; Gonzalez-Aguilera, D.; Madruga, F.J.; García-Martín, R.; Muñóz, Á.L.; Pisonero, J. Predictive Models for the Characterization of Internal Defects in Additive Materials from Active Thermography Sequences Supported by Machine Learning Methods. Sensors 2020, 20, 3982. [Google Scholar] [CrossRef]
- Rodríguez-Martín, M.; Fueyo, J.G.; Pisonero, J.; López-Rebollo, J.; Gonzalez-Aguilera, D.; García-Martín, R.; Madruga, F. Step heating thermography supported by machine learning and simulation for internal defect size measurement in additive manufacturing. Measurement 2022, 205, 112140. [Google Scholar] [CrossRef]
- Lu, L.; Hou, J.; Yuan, S.; Yao, X.; Li, Y.; Zhu, J. Deep learning-assisted real-time defect detection and closed-loop adjustment for additive manufacturing of continuous fiber-reinforced polymer composites. Robot. Comput. Integr. Manuf. 2023, 79, 102431. [Google Scholar] [CrossRef]
- Zupic, I.; Čater, T. Bibliometric Methods in Management and Organization. Organ. Res. Methods 2015, 18, 429–472. [Google Scholar] [CrossRef]
- Altıparmak, S.C.; Yardley, V.A.; Shi, Z.; Lin, J. Extrusion-based additive manufacturing technologies: State of the art and future perspectives. J. Manuf. Process. 2022, 83, 607–636. [Google Scholar] [CrossRef]
- Jaganathan, S.; Kandasamy, R.; Venkatachalam, R.; Gunalan, M.; Dhairiyasamy, R. Advances in Optimizing Mechanical Performance of 3D-Printed Polymer Composites: A Microstructural and Processing Enhancements Review. Adv. Polym. Technol. 2024, 2024, 3168252. [Google Scholar] [CrossRef]
- Tao, Y.; Kong, F.; Li, Z.; Zhang, J.; Zhao, X.; Yin, Q.; Xing, D.; Li, P. A review on voids of 3D printed parts by fused filament fabrication. J. Mater. Res. Technol. 2021, 15, 4860–4879. [Google Scholar] [CrossRef]
- Chen, G.; Zhu, Z.; Lu, Z.; Wang, W.; Zhang, S.; He, P.; Wei, Y.; Han, R.; Peng, B.; Chen, N. Regulated the orientation of graphene nanoplatelets via flow field in material extrusion for enhancing thermal conductivity. Addit. Manuf. 2025, 101, 104718. [Google Scholar] [CrossRef]
- Das, A.; Riet, J.A.; Bortner, M.J.; McIlroy, C. Rheology, crystallization, and process conditions: The effect on interlayer properties in three-dimensional printing. Phys. Fluids 2022, 34, 123108. [Google Scholar] [CrossRef]
- Iandiorio, C.; Mattei, G.; Marotta, E.; Costanza, G.; Tata, M.E.; Salvini, P. Lost-PLAEffect of a TPMS-Based Fillet Shape on the Mechanical Strength of Metal Cubic Lattice Structures. Materials 2024, 17, 1553. [Google Scholar] [CrossRef] [PubMed]
- Ceci, A.; Cerini, C.; Costanza, G.; Tata, M.E. Production of Al Alloys with Kelvin Cells Using the Lost-PLA Technique and Their Mechanical Characterization via Compression Tests. Materials 2025, 18, 296. [Google Scholar] [CrossRef]
- Agarwala, M.K.; Jamalabad, V.R.; Langrana, N.A.; Safari, A.; Whalen, P.J.; Danforth, S.C. Structural quality of parts processed by fused deposition. Rapid Prototyp. J. 1996, 2, 4–19. [Google Scholar] [CrossRef]
- Venkataraman, N.; Rangarajan, S.; Matthewson, M.J.; Harper, B.; Safari, A.; Danforth, S.C.; Wu, G.; Langrana, N.; Guceri, S.; Yardimci, A. Feedstock material property—Process relationships in fused deposition of ceramics (FDC). Rapid Prototyp. J. 2000, 6, 244–253. [Google Scholar] [CrossRef]
- Turner, B.N.; Strong, R.; Gold, S.A. A review of melt extrusion additive manufacturing processes: I. Process design and modeling. Rapid Prototyp. J. 2014, 20, 192–204. [Google Scholar] [CrossRef]
- Schramm, G. A Practical Approach to Rheology and Rheometry; Haake: Karlsruhe, Germany, 1994. [Google Scholar]
- Manrich, S. Processamento de Termoplásticos: Rosca Única, Extrusão e Matrizes, Injeção e Moldes; Artliber Editora: São Paulo, Brazil, 2005. [Google Scholar]
- Phan, D.D.; Horner, J.S.; Swain, Z.R.; Beris, A.N.; Mackay, M.E. Computational fluid dynamics simulation of the melting process in the fused filament fabrication additive manufacturing technique. Addit. Manuf. 2020, 33, 101161. [Google Scholar] [CrossRef]
- Cheremisinoff, N.P. An Introduction to Polymer Rheology and Processing; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar]
- Bretas, R.E.S.; D’Ávila, M.A. Reologia de Polímeros Fundidos; EdUFSCar: São Carlos, Brazil, 2000. [Google Scholar]
- Poole, R.J. Inelastic and flow-type parameter models for non-Newtonian fluids. J. Non-Newton. Fluid Mech. 2023, 320, 105106. [Google Scholar] [CrossRef]
- Rosato, D.V. Rosato’s Plastics Encyclopedia and Dictionary; Hanser Publishers: Munich, Germany, 1993. [Google Scholar]
- Bradson, J.A. Flow Properties of Polymer Melts, 2nd ed.; George Godwin Ltd.: London, UK, 1981. [Google Scholar]
- Rauwendaal, C. Polymer Extrusion; Hanser Publishers: New York, NY, USA, 1990. [Google Scholar]
- Al Rashid, A.; Koç, M. Fused Filament Fabrication Process: A Review of Numerical Simulation Techniques. Polymers 2021, 13, 3534. [Google Scholar] [CrossRef]
- Yang, C.; Tian, X.; Li, D.; Cao, Y.; Zhao, F.; Shi, C. Influence of thermal processing conditions in 3D printing on the crystallinity and mechanical properties of PEEK material. J. Mater. Process. Technol. 2017, 248, 1–7. [Google Scholar] [CrossRef]
- Abhishek, C.; Raghukiran, N. Residual stresses in 4D printed structures: A review on causes, effects, measurements, mitigations and its applications. Forces Mech. 2025, 18, 100304. [Google Scholar] [CrossRef]
- Comminal, R.; Serdeczny, M.P.; Pedersen, D.B.; Spangenberg, J. Numerical modeling of the strand deposition flow in extrusion-based additive manufacturing. Addit. Manuf. 2018, 20, 68–76. [Google Scholar] [CrossRef]
- Serdeczny, M.P.; Comminal, R.; Mollah, M.T.; Pedersen, D.B.; Spangenberg, J. Viscoelastic simulation and optimisation of the polymer flow through the hot-end during filament-based material extrusion additive manufacturing. Virtual Phys. Prototyp. 2022, 17, 205–219. [Google Scholar] [CrossRef]
- Serdeczny, M.P.; Comminal, R.; Mollah, M.T.; Pedersen, D.B.; Spangenberg, J. Numerical modeling of the polymer flow through the hot-end in filament-based material extrusion additive manufacturing. Addit. Manuf. 2020, 36, 101454. [Google Scholar] [CrossRef]
- Jeong, D.-I.; Jain, A.; Oh, D.-W. Increasing perpendicular alignment in extruded filament by an orifice embedded 3D printing nozzle. Virtual Phys. Prototyp. 2022, 17, 1–18. [Google Scholar] [CrossRef]
- Schuller, T.; Jalaal, M.; Fanzio, P.; Galindo-Rosales, F.J. Optimal shape design of printing nozzles for extrusion-based additive manufacturing. Addit. Manuf. 2024, 84, 104130. [Google Scholar] [CrossRef]
- Liparoti, S.; Sofia, D.; Romano, A.; Marra, F.; Pantani, R. Fused Filament Deposition of PLA: The Role of Interlayer Adhesion in the Mechanical Performances. Polymers 2021, 13, 399. [Google Scholar] [CrossRef]
- Costa, S.F.; Duarte, F.M.; Covas, J.A. Thermal conditions affecting heat transfer in FDM/FFE: A contribution towards the numerical modelling of the process. Virtual Phys. Prototyp. 2015, 10, 35–46. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, X.Z.; Yu, W.W.; Deng, Y.H. Numerical investigation of the influence of process conditions on the temperature variation in fused deposition modeling. Mater. Des. 2017, 130, 59–68. [Google Scholar] [CrossRef]
- Zhou, Y.; Nyberg, T.; Xiong, G.; Liu, D. Temperature Analysis in the Fused Deposition Modeling Process. In Proceedings of the 2016 3rd International Conference on Information Science and Control Engineering (ICISCE), Beijing, China, 8–10 July 2016; pp. 678–682. [Google Scholar] [CrossRef]
- Coogan, T.J.; Kazmer, D.O. Healing simulation for bond strength prediction of FDM. Rapid Prototyp. J. 2017, 23, 551–561. [Google Scholar] [CrossRef]
- Lepoivre, A.; Boyard, N.; Levy, A.; Sobotka, V. Heat Transfer and Adhesion Study for the FFF Additive Manufacturing Process. Procedia Manuf. 2020, 47, 948–955. [Google Scholar] [CrossRef]
- Go, J.; Schiffres, S.N.; Stevens, A.G.; Hart, A.J. Rate limits of additive manufacturing by fused filament fabrication and guidelines for high-throughput system design. Addit. Manuf. 2017, 16, 1–11. [Google Scholar] [CrossRef]
- Xia, H.; Lu, J.; Tryggvason, G. Fully resolved numerical simulations of fused deposition modeling. Part II—Solidification, residual stresses and modeling of the nozzle. Rapid Prototyp. J. 2018, 24, 973–987. [Google Scholar] [CrossRef]
- Serdeczny, M.P. Numerical and Experimental Analysis of Filament-Based Material Extrusion Additive Manufacturing. Ph.D. Thesis, Technical University of Denmark, Kongens Lyngby, Denmark, 2020. [Google Scholar]
- Wang, T.-M.; Xi, J.-T.; Jin, Y. A model research for prototype warp deformation in the FDM process. Int. J. Adv. Manuf. Technol. 2007, 33, 1087–1096. [Google Scholar] [CrossRef]
- Bhandari, S.; Lopez-Anido, R.A. Discrete-Event Simulation Thermal Model for Extrusion-Based Additive Manufacturing of PLA and ABS. Materials 2020, 13, 4985. [Google Scholar] [CrossRef]
- Jiang, B. Thermal Simulations for Guiding 3D Printed Polymers and Composites Used in Fused Filament Fabrication. Ph.D. Thesis, The University of Sydney, Sydney, NSW, Australia, 2023. [Google Scholar]
- Morvayová, A.; Contuzzi, N.; Casalino, G. Defects and residual stresses finite element prediction of FDM 3D printed wood/PLA biocomposite. Int. J. Adv. Manuf. Technol. 2023, 129, 2281–2293. [Google Scholar] [CrossRef]
- Cattenone, A.; Morganti, S.; Alaimo, G.; Auricchio, F. Finite Element Analysis of Additive Manufacturing Based on Fused Deposition Modeling: Distortions Prediction and Comparison with Experimental Data. J. Manuf. Sci. Eng. 2019, 141, 011010. [Google Scholar] [CrossRef]
- El Moumen, A.; Tarfaoui, M.; Lafdi, K. Modelling of the temperature and residual stress fields during 3D printing of polymer composites. Int. J. Adv. Manuf. Technol. 2019, 104, 1661–1676. [Google Scholar] [CrossRef]
- Croccolo, D.; De Agostinis, M.; Olmi, G. Experimental characterization and analytical modelling of the mechanical behaviour of fused deposition processed parts made of ABS-M30. Comput. Mater. Sci. 2013, 79, 506–518. [Google Scholar] [CrossRef]
- Domingo-Espin, M.; Puigoriol-Forcada, J.M.; Garcia-Granada, A.-A.; Llumà, J.; Borros, S.; Reyes, G. Mechanical property characterization and simulation of fused deposition modeling Polycarbonate parts. Mater. Des. 2015, 83, 670–677. [Google Scholar] [CrossRef]
- Plaza, E.G.; López, P.N.; Torija, M.C.; Muñoz, J.C. Analysis of PLA Geometric Properties Processed by FFF Additive Manufacturing: Effects of Process Parameters and Plate-Extruder Precision Motion. Polymers 2019, 11, 1581. [Google Scholar] [CrossRef]
- Zouaoui, M.; Gardan, J.; Lafon, P.; Makke, A.; Labergere, C.; Recho, N. A Finite Element Method to Predict the Mechanical Behavior of a Pre-Structured Material Manufactured by Fused Filament Fabrication in 3D Printing. Appl. Sci. 2021, 11, 5075. [Google Scholar] [CrossRef]
- Kohutiar, M.; Pajtášová, M.; Janík, R.; Papučová, I.; Pagáčová, J.; Pecušová, B.; Labaj, I. Study of selected thermoplastics using dynamic mechanical analysis. MATEC Web Conf. 2018, 157, 07002. [Google Scholar] [CrossRef]
- Wikło, M.; Byczuk, B.H.; Skrzek, K. Mechanical Characterization of FDM 3D-Printed Components Using Advanced Measurement and Modeling Techniques. Materials 2025, 18, 1086. [Google Scholar] [CrossRef]
- Garg, A.; Bhattacharya, A. An insight to the failure of FDM parts under tensile loading: Finite element analysis and experimental study. Int. J. Mech. Sci. 2017, 120, 225–236. [Google Scholar] [CrossRef]
- Dai, S.; Zhu, K.; Wang, S.; Deng, Z. Additively manufactured materials: A critical review on their anisotropic mechanical properties and modeling methods. J. Manuf. Process. 2025, 141, 789–814. [Google Scholar] [CrossRef]
- Tekinalp, H.L.; Kunc, V.; Velez-Garcia, G.M.; Duty, C.E.; Love, L.J.; Naskar, A.K.; Blue, C.A.; Ozcan, S. Highly oriented carbon fiber–polymer composites via additive manufacturing. Compos. Sci. Technol. 2014, 105, 144–150. [Google Scholar] [CrossRef]
- Brenken, B.; Barocio, E.; Favaloro, A.; Kunc, V.; Pipes, R.B. Fused filament fabrication of fiber-reinforced polymers: A review. Addit. Manuf. 2018, 21, 1–16. [Google Scholar] [CrossRef]
- Yang, D.; Wu, K.; Wan, L.; Sheng, Y. A Particle Element Approach for Modelling the 3D Printing Process of Fibre Reinforced Polymer Composites. J. Manuf. Mater. Process. 2017, 1, 10. [Google Scholar] [CrossRef]
- Yang, Z.; Yang, Z.; Chen, H.; Yan, W. 3D printing of short fiber reinforced composites via material extrusion: Fiber breakage. Addit. Manuf. 2022, 58, 103067. [Google Scholar] [CrossRef]
- Yang, Z.; Fu, K.; Zhang, Z.; Zhang, J.; Li, Y. Topology optimization of 3D-printed continuous fiber-reinforced composites considering manufacturability. Compos. Sci. Technol. 2022, 230, 109727. [Google Scholar] [CrossRef]
- Yap, T.; He, Z.; Wang, Z.; Tamijani, A.; Tehrani, M. Experimental investigation and validation of strength-based topology and fiber path optimization in additively manufactured continuous fiber reinforced composites. Addit. Manuf. 2024, 89, 104274. [Google Scholar] [CrossRef]
- Brenken, B.; Barocio, E.; Favaloro, A.; Kunc, V.; Pipes, R.B. Development and validation of extrusion deposition additive manufacturing process simulations. Addit. Manuf. 2019, 25, 218–226. [Google Scholar] [CrossRef]
- Zhang, Z.; Hu, C.; Qin, Q.-H. The improvement of void and interface characteristics in fused filament fabrication-based polymers and continuous carbon fiber-reinforced polymer composites: A comprehensive review. Int. J. Adv. Manuf. Technol. 2025, 137, 1047–1087. [Google Scholar] [CrossRef]
- Plamadiala, I.; Croitoru, C.; Pop, M.A.; Roata, I.C. Enhancing Polylactic Acid (PLA) Performance: A Review of Additives in Fused Deposition Modelling (FDM) Filaments. Polymers 2025, 17, 191. [Google Scholar] [CrossRef] [PubMed]
- Somireddy, M.; Czekanski, A.; Atre, S.V. Modelling of Failure Behaviour of 3D-Printed Composite Parts. Appl. Sci. 2022, 12, 10724. [Google Scholar] [CrossRef]
- Ouyang, S.; Li, D.; Zhu, W.; Fu, L.; Zhang, Z.; Wang, N.; Zhi, Q. Process modeling and deformation prediction of 3D printed continuous fiber-reinforced composites based on in-situ micro-scale measuring. Compos. Sci. Technol. 2025, 267, 111209. [Google Scholar] [CrossRef]
- Ghane, E. Learning from Data and Physics for Multiscale Modeling of Woven Composites. Ph.D. Thesis, Univeristy of Gothenburg, Gothenburg, Sweden, 2025. [Google Scholar]
- Samy, A.A.; Golbang, A.; Harkin-Jones, E.; Archer, E.; McIlhagger, A. Prediction of part distortion in Fused Deposition Modelling (FDM) of semi-crystalline polymers via COMSOL: Effect of printing conditions. CIRP J. Manuf. Sci. Technol. 2021, 33, 443–453. [Google Scholar] [CrossRef]
- Wang, J.; Papadopoulos, P. Coupled thermomechanical analysis of fused deposition using the finite element method. Finite Elem. Anal. Des. 2021, 197, 103607. [Google Scholar] [CrossRef]
- Xia, Q.; Sun, G.; Kim, J.; Li, Y. Multi-scale modeling and simulation of additive manufacturing based on fused deposition technique. Phys. Fluids 2023, 35, 034116. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, S. Numerical simulation of temperature field and stress field in fused deposition modeling. J. Mech. Sci. Technol. 2018, 32, 3337–3344. [Google Scholar] [CrossRef]
- Favaloro, A.; Brenken, B.; Barocio, E.; Pipes, B. Simulation of Polymeric Composites Additive Manufacturing Using Abaqus. Sci. Age Exp. 2017, 103–114. [Google Scholar]
- Brenken, B.; Barocio, E.; Favaloro, A.J.; Pipes, B.R. Simulation of Semi-Crystalline Composites in the Extrusion Deposition Additive Manufacturing Process. Sci. Age Exp. 2017, 418, 90–102. [Google Scholar]
- Talagani, F.; DorMohammadi, S.; Dutton, R.; Godines, C.; Baid, H.; Abdi, F.; Kunc, V.; Compton, B.; Simunovic, S.; Duty, C.; et al. Numerical Simulation of Big Area Additive Manufacturing (3D Printing) of a Full Size Car. SAMPE J. 2015, 51, 27–36. [Google Scholar]
- Ravari, M.R.K.; Kadkhodaei, M.; Badrossamay, M.; Rezaei, R. Numerical investigation on mechanical properties of cellular lattice structures fabricated by fused deposition modeling. Int. J. Mech. Sci. 2014, 88, 154–161. [Google Scholar] [CrossRef]
- Alafaghani, A.; Qattawi, A.; Alrawi, B.; Guzman, A. Experimental Optimization of Fused Deposition Modelling Processing Parameters: A Design-for-Manufacturing Approach. Procedia Manuf. 2017, 10, 791–803. [Google Scholar] [CrossRef]
- Aldosari, F.; Khan, M.A.A.; Asad, M.; Djavanroodi, F. Finite Element Analysis of PolyLactic Acid (PLA) under Tensile and Compressive Loading. J. Phys. Conf. Ser. 2023, 2468, 012094. [Google Scholar] [CrossRef]
- Hachimi, T.; Majid, F.; Zekriti, N.; Rhanim, R.; Rhanim, H. Improvement of 3D printing polymer simulations considering converting G-code to Abaqus. Int. J. Adv. Manuf. Technol. 2024, 131, 5193–5208. [Google Scholar] [CrossRef]
- Ogaili, A.A.F.; Basem, A.; Kadhim, M.S.; Al-Sharify, Z.T.; Jaber, A.A.; Njim, E.K.; Al-Haddad, L.A.; Hamzah, M.N.; Al-Ameen, E.S. The Effect of Chopped Carbon Fibers on the Mechanical Properties and Fracture Toughness of 3D-Printed PLA Parts: An Experimental and Simulation Study. J. Compos. Sci. 2024, 8, 273. [Google Scholar] [CrossRef]
- Gebrehiwot, S.Z.; Leal, L.E.; Eickhoff, J.N.; Rechenberg, L. The influence of stiffener geometry on flexural properties of 3D printed polylactic acid (PLA) beams. Prog. Addit. Manuf. 2021, 6, 71–81. [Google Scholar] [CrossRef]
- Perez, D.B.; Celik, E.; Karkkainen, R.L. Investigation of Interlayer Interface Strength and Print Morphology Effects in Fused Deposition Modeling 3D-Printed PLA. 3D Print. Addit. Manuf. 2021, 8, 23–32. [Google Scholar] [CrossRef]
- Zhang, Y.; Chou, Y.K. Three-dimensional finite element analysis simulations of the fused deposition modelling process. Proc. Inst. Mech. Eng. B J. Eng. Manuf. 2006, 220, 1663–1671. [Google Scholar] [CrossRef]
- Zhang, Y.; Chou, K. A parametric study of part distortions in fused deposition modelling using three-dimensional finite element analysis. Proc. Inst. Mech. Eng. B J. Eng. Manuf. 2008, 222, 959–968. [Google Scholar] [CrossRef]
- Xu, X.; Qiu, W.; Wan, D.; Wu, J.; Zhao, F.; Xiong, Y. Numerical modelling of the viscoelastic polymer melt flow in material extrusion additive manufacturing. Virtual Phys. Prototyp. 2024, 19, e2300666. [Google Scholar] [CrossRef]
- Sukindar, N.A.; Ariffin, M.K.A.; Baharudin, B.T.H.T.; Jaafar, C.N.A.; Ismail, M.I.S. Analyzing the effect of nozzle diameter in fused deposition modeling for extruding polylactic acid using open source 3D Printing. J. Teknol. 2016, 78, 7–15. [Google Scholar] [CrossRef]
- Harshitha, V.; Rao, S.S. Design and analysis of ISO standard bolt and nut in FDM 3D printer using PLA and ABS materials. Mater. Today Proc. 2019, 19, 583–588. [Google Scholar] [CrossRef]
- Lei, M.; Wei, Q.; Li, M.; Zhang, J.; Yang, R.; Wang, Y. Numerical Simulation and Experimental Study the Effects of Process Parameters on Filament Morphology and Mechanical Properties of FDM 3D Printed PLA/GNPs Nanocomposite. Polymers 2022, 14, 3081. [Google Scholar] [CrossRef] [PubMed]
- Devender, B.; Kumar, P.K.; Lakshmi Kala, K.; Vemanaboina, H. Modeling and flow analysis of FDM based dual extruder. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Hou, H.; Yue, Y.; Liu, J.; Xi, D.; Liu, S. Numerical Simulation and Experimental Study of the Stress Formation Mechanism of FDM with Different Printing Paths. J. Renew. Mater. 2023, 11, 273–289. [Google Scholar] [CrossRef]
- Ganeshkumar, S.; Kumar, S.D.; Magarajan, U.; Rajkumar, S.; Arulmurugan, B.; Sharma, S.; Li, C.; Ilyas, R.A.; Badran, M.F. Investigation of Tensile Properties of Different Infill Pattern Structures of 3D-Printed PLA Polymers: Analysis and Validation Using Finite Element Analysis in ANSYS. Materials 2022, 15, 5142. [Google Scholar] [CrossRef]
- Dobos, J.; Hanon, M.M.; Oldal, I. Effect of infill density and pattern on the specific load capacity of FDM 3D-printed PLA multi-layer sandwich. J. Polym. Eng. 2022, 42, 118–128. [Google Scholar] [CrossRef]
- Popa, C.F.; Krausz, T.; Galatanu, S.-V.; Linul, E.; Marsavina, L. Numerical and experimental study for FDM printed specimens from PLA under IZOD impact tests. Mater. Today Proc. 2023, 78, 326–330. [Google Scholar] [CrossRef]






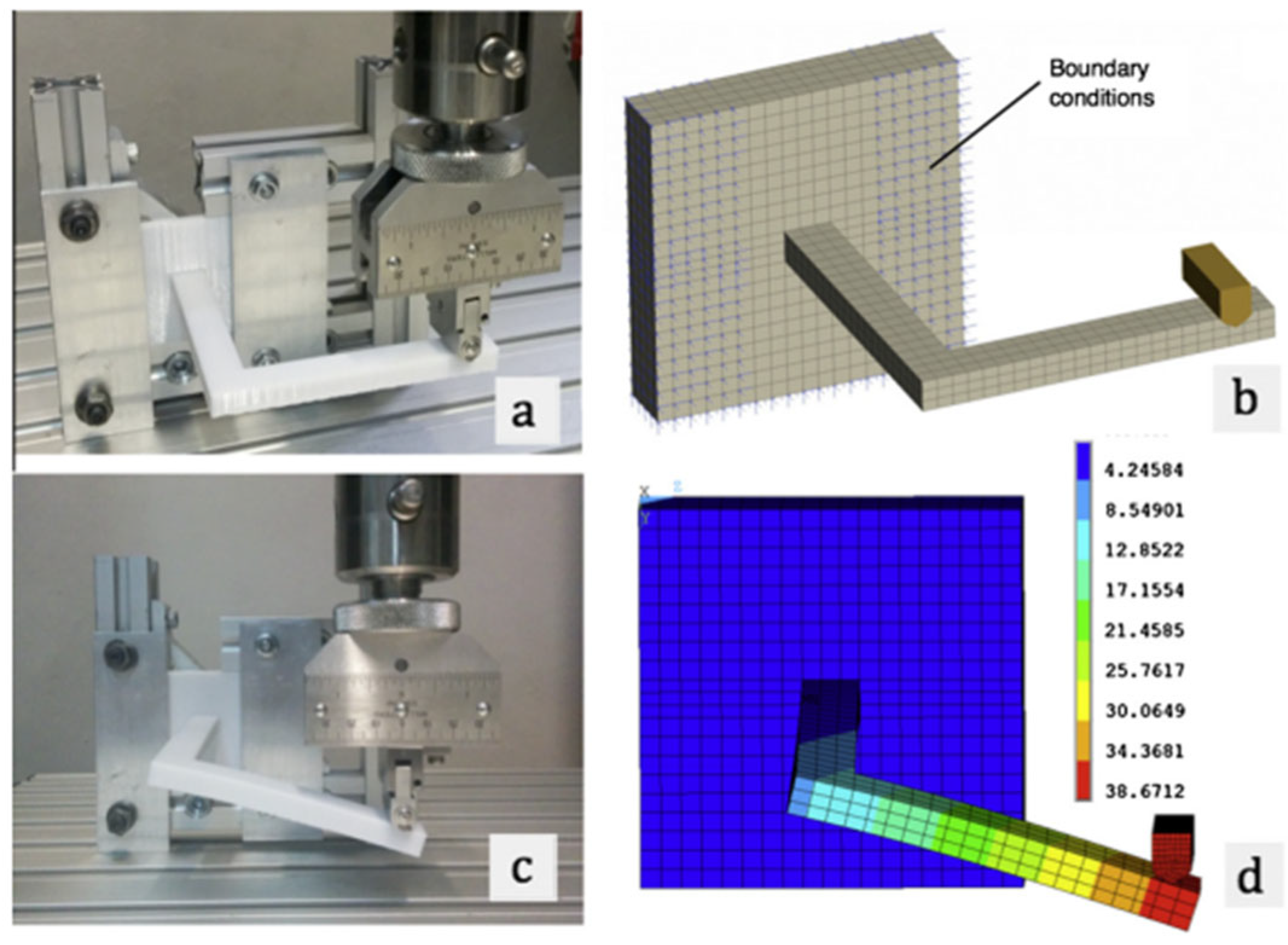


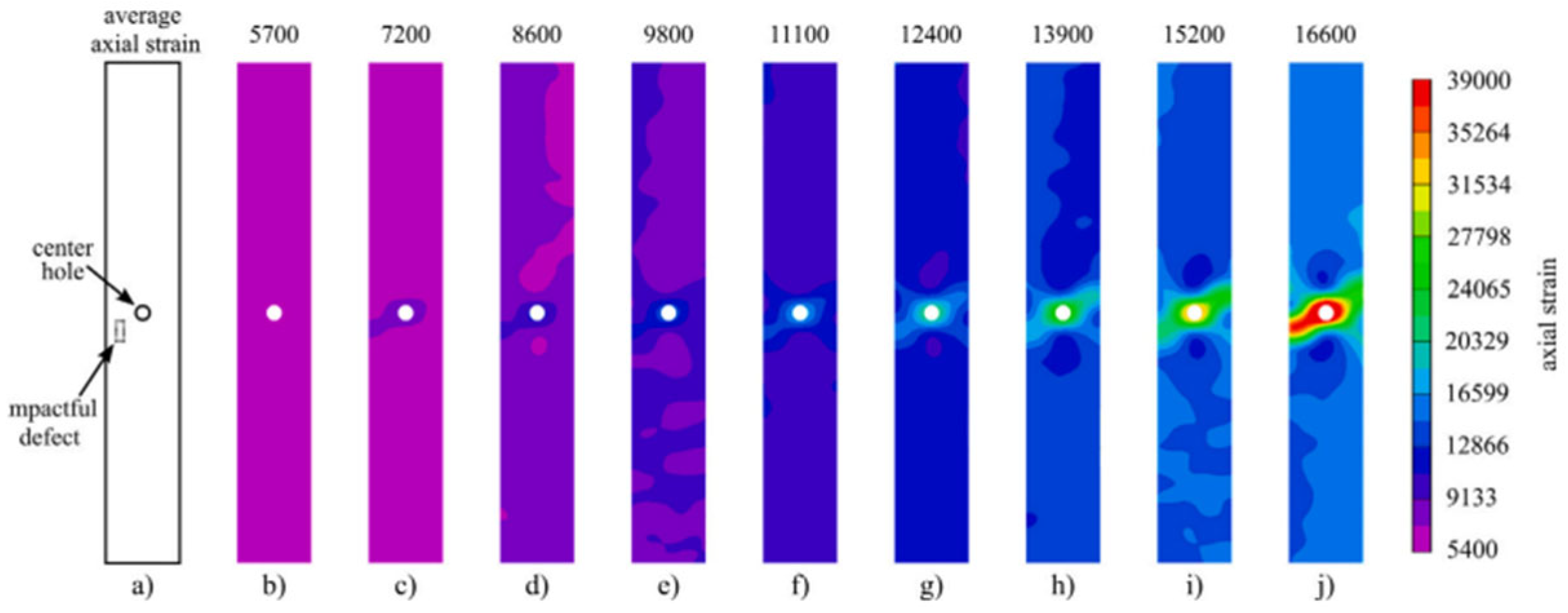

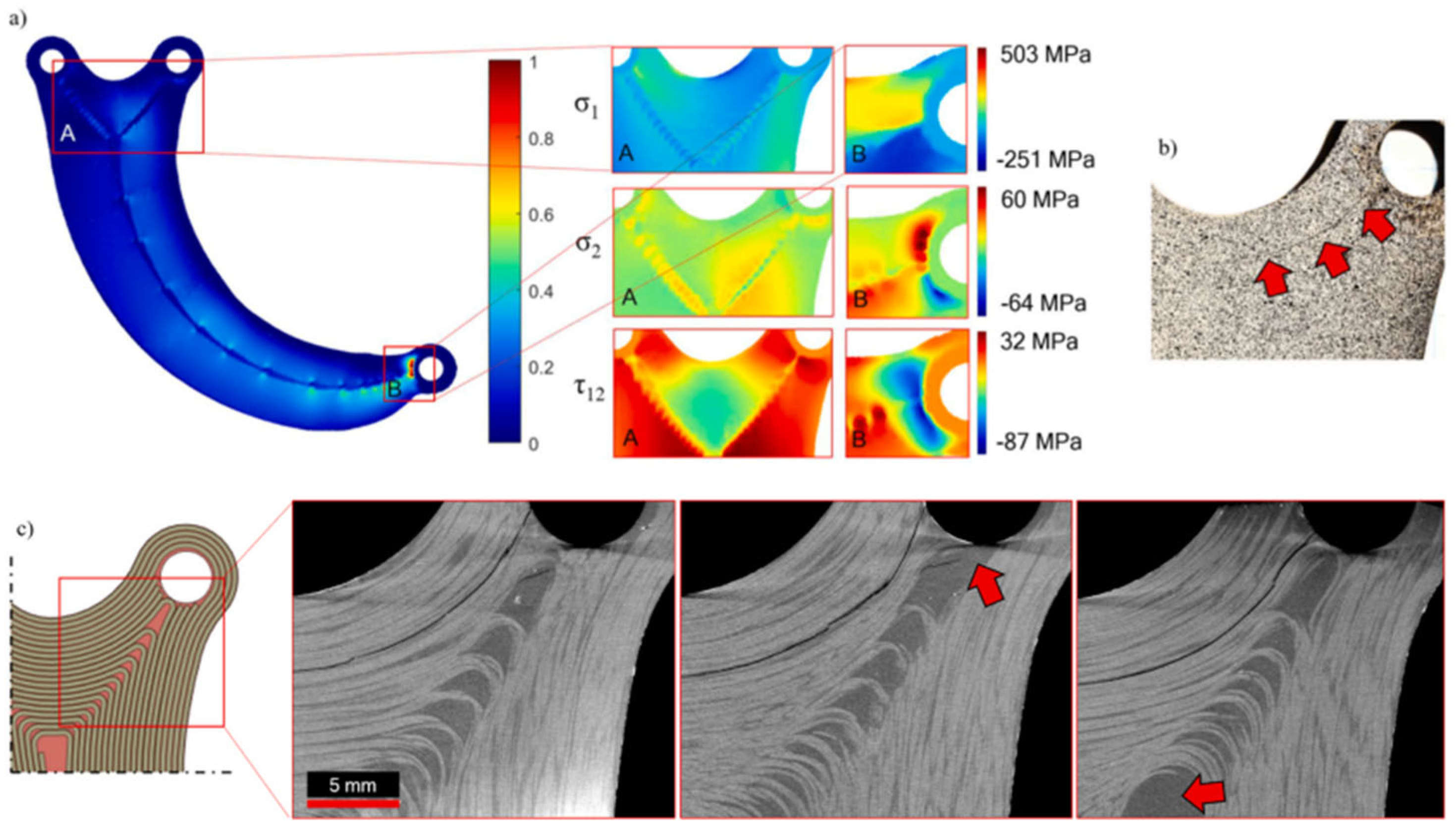

| REF | Analysis | Material Evaluated | Software | Parameters Analyzed | Results | Limitations and Gaps |
|---|---|---|---|---|---|---|
| [2] | RW | - | R (Bibliometrix), VOS viewer | Keywords, research trends, co-authorship, topic clusters. | Identifies growth in AM linked to Industry 4.0 (AI, IoT) and 5.0 (human-centric design). | Focused on Scopus data, lacks technical depth on AM process and integration. |
| [3] | RW | Polymers | Ansys, Abaqus, COMSOL, MATLAB | Melt flow, thermal behavior, mechanical properties. | Numerical models can predict process behavior but often rely on simplified assumptions. | Limited experimental validation and oversimplified material behavior. |
| [4] | RW | FRP | – | Applications, challenges, material systems, performance. | Reviews CFRP benefits in multiple sectors; emphasizes lightweighting and customizability. | Broad scope lacks deep technical analysis or modeling of fiber performance. |
| [9] | RW | Natural fibers and mineral composites | R (Bibliometrix), VOS viewer | Sustainability, biodegradability, fiber/matrix interaction. | Natural fillers offer eco-friendly AM options; fiber alignment and treatment improve properties. | Lacks standardization and process control; limited mineral-reinforced AM data. |
| [17] | RW | Thermoplastics | – | Material selection, design parameters, trends. | Covers extrusion methods, hybrid processes, and polymer categories. | Lacks coverage of real-time control, multi-materials, and long-term validation. |
| [19] | RW | Thermoplastics | – | Void types, formation causes, parameter effects. | Defines four main void types; parameter tuning and post-processing reduce defects. | No real-time detection methods: predictive modeling is still limited. |
| [32] | RW | - | – | Inelastic models, flow-type parameters, rheological equations. | Discusses flow-type parameter use in CFD to improve realism for non-Newtonian polymer melts. | No direct AM application serves as a foundational theory for future simulations. |
| [36] | RW | Polymers and Composites | Ansys, COMSOL, MATLAB | Melt flow, solidification, warpage, fiber orientation. | Models capture key process stages, including melt and solidification, but lack integration. | Few fully coupled models; limited experimental validation. |
| [38] | RW | Polymers and Composites | – | Material type, printing temperature, phase change, actuation behavior. | Residual stresses affect shape recovery and structural deformation; driven by thermal gradients and anisotropic effects. | Lack of quantitative models and experimental studies on stress evolution during actuation. |
| [66] | RW | Polymers and Composites | – | Multi-scale, data-driven, and hybrid modeling techniques. | Reviews challenges in capturing AM anisotropy; proposes hybrid models with higher fidelity. | Limited validation in complex shapes; no unified modeling framework. |
| [25] | MF | Ceramic-filled filaments (FDC) | – | Rheology, density, shrinkage, feed rate. | Establishes link between feedstock rheology and printing success in ceramic-FFF. | FDC-specific; outdated parameters and machine controls. |
| [26] | MF | ABS, PLA | – | Feed rate, heat transfer, pressure drop, bonding. | Models help to explain flow mechanics and bonding; support process improvement. | Lacks validation and real-time data; material property databases are limited. |
| [29] | MF | PLA | Ansys Fluent, Polyflow | Viscosity, pressure drop, temperature, flow patterns. | Identifies vortex formation and pressure concentration near nozzle tip affecting extrusion consistency. | Assumes Newtonian flow; neglects viscoelasticity and phase-change dynamics. |
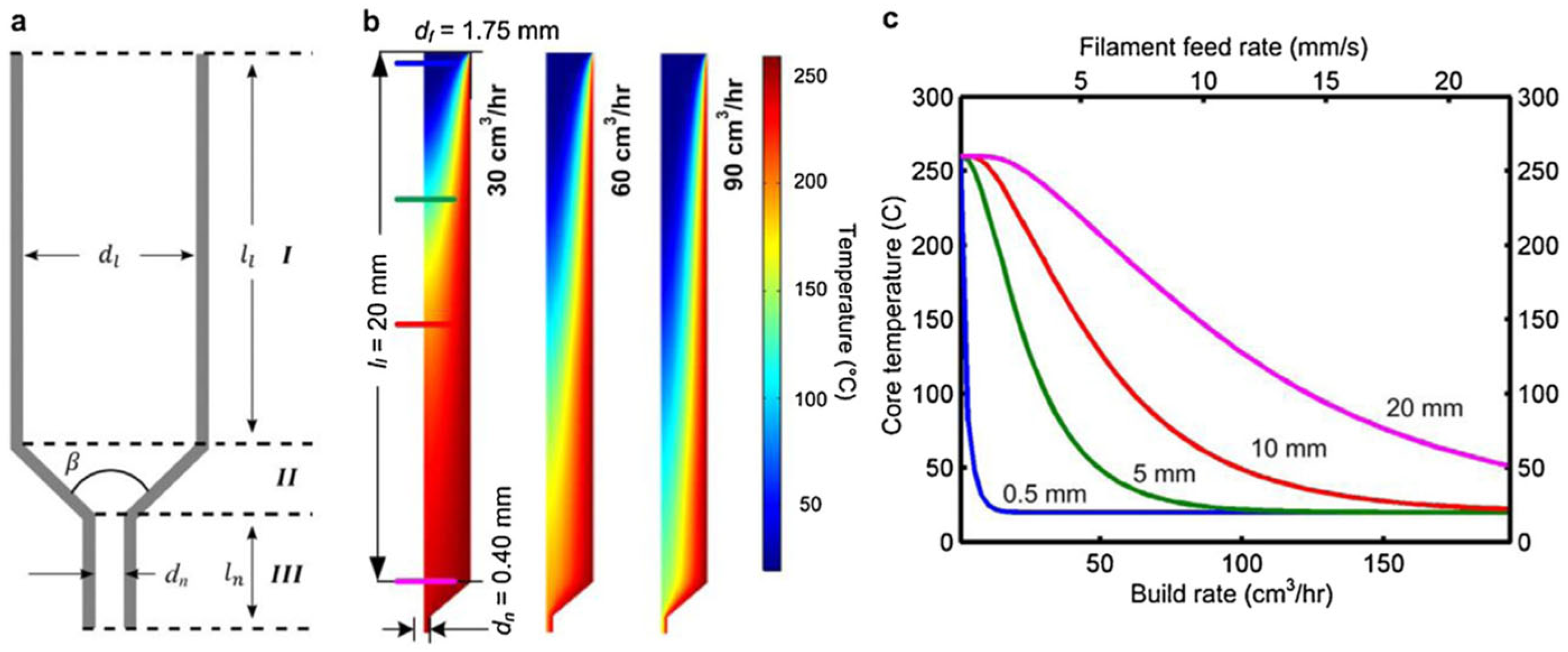
| [39] | MF | Thermoplastics | Ansys Fluent | Gap distance, velocity ratio, strand shape, flow rate. | Filament shape and contact area are strongly influenced by nozzle gap and speed ratio. | Neglects temperature effects and non-Newtonian material behavior. |
| [40] | MF | ABS | FLOW-3D, Open FOAM | Melt temperature, velocity, pressure, flow instability. | Viscoelastic model improves extrusion force prediction; design optimization reduces flow irregularities. | High computational cost; material-dependent parameters. |
| [41] | MF | ABS | FLOW-3D | Melt zone, pressure, recirculation, feed rate. | Models melt transition and pressure build-up; recirculation affects temperature and force. | Lacks viscoelasticity; requires calibration for different polymers. |
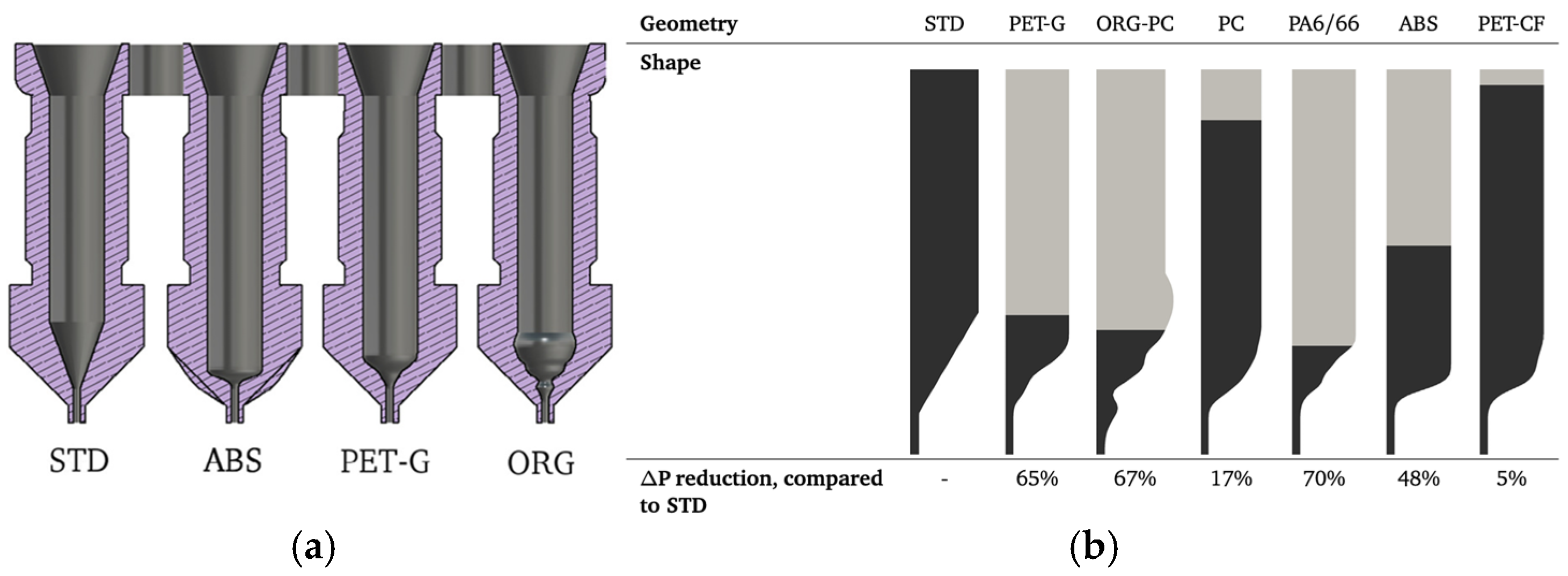
| [43] | MF | PET-G, PC, PA6/66, ABS, PET-CF | Open FOAM, DAKOTA | Pressure drop, flow type, extrusion force. | Optimized nozzle geometries reduce pressure drop and improve flow stability and control. | Complex implementation in practice; variations in material behavior not fully addressed. |
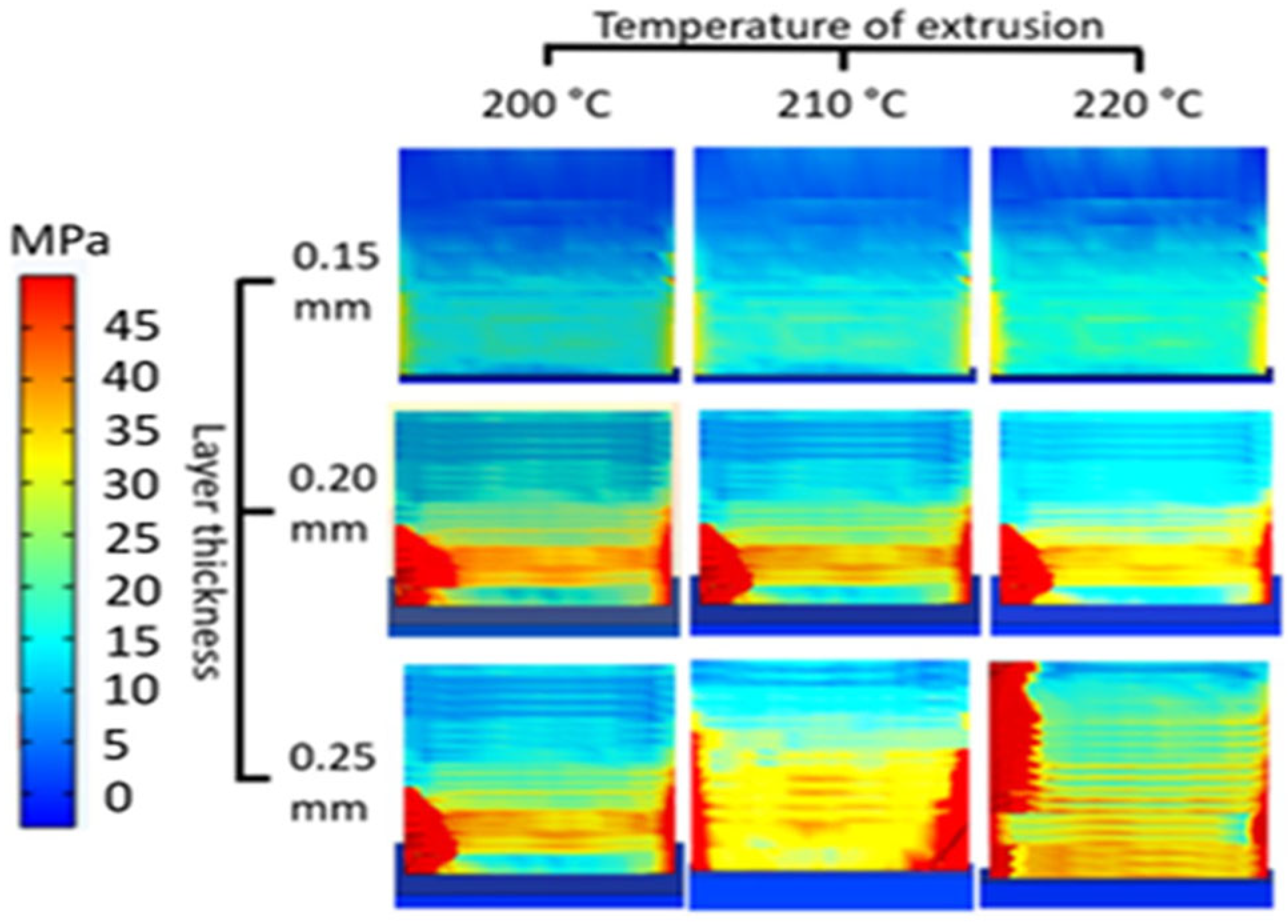
| [44] | CS | PLA | Custom (LabVIEW), DMA, DSC, AFM | Nozzle/bed temperature, cooling rate, crystallinity, modulus. | Improved adhesion with higher residence at 100–140 °C; mid-layers had higher modulus and compactness. | Upper layer bonding is limited by cooling rate; model excludes local defects and complex geometries. |
| [45] | CS | ABS | Abaqus | Conduction, convection, radiation, deformation. | Identifies conduction and convection as dominant heat transfer mechanisms. | Neglects 3D effects: minimal impact observed from radiation and air convection. |
| [46] | CS | PLA | – | Temperature field, cooling rate, reheating. | Shows reheating significantly impacts layer bonding quality. | Porosity and radiation not modeled; geometry simplifications limit accuracy. |
| [47] | CS | ABS | Ansys | Temperature, thermal conductivity, enthalpy. | Highlights the influence of latent heat on thermal gradients and solidification. | Simulates single-track only; complex geometries not included. |
| [48] | CS | ABS | – | Temperature, diffusion, wetting, bond strength. | Model predicts bond strength based on temperature-dependent healing dynamics. | Assumes ideal wetting; does not include geometric deformation. |
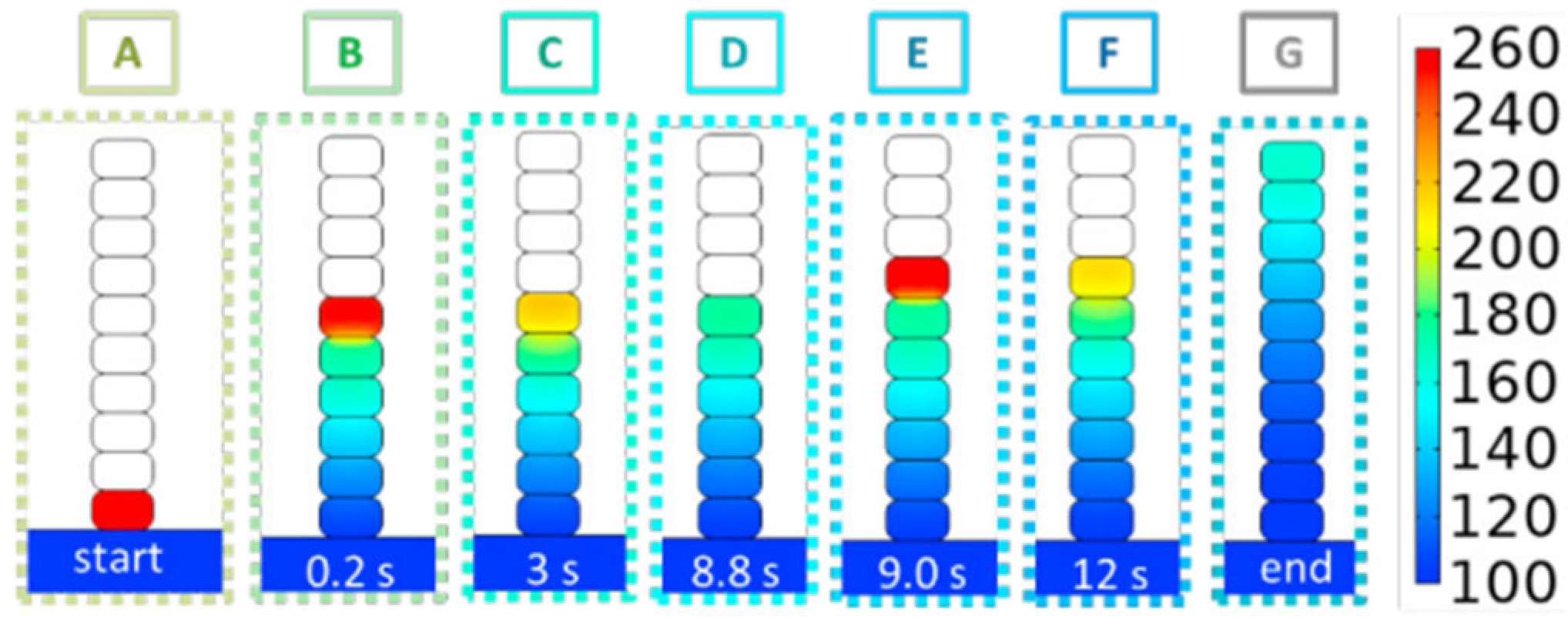
| [49] | CS | ABS, PEKK | COMSOL, IR camera | Temperature field, reptation degree, healing. | Demonstrates that thermal contact dominates bonding; validated with IR data. | Focuses only on early layer bonding; does not model long-term thermal behavior. |
| [50] | CS | ABS | COMSOL, MATLAB | Extrusion force, heating rate, gantry speed. | Heat transfer limitations restrict extrusion speed; system coordination is essential for performance gains. | Lacks real-time thermal feedback and uses simplified material assumptions. |
| [11] | CS | PLA | Python (ResNet), Arduino | Nozzle offset, strain, delamination, warping. | AI-based monitoring detects delamination early, enabling predictive quality control. | Model trained on limited data; generalizability across materials and setups is untested. |
| [51] | CS | PLA | Custom (in-house) | Shrinkage, stress, temperature, deformation. | Captures cooling-induced shrinkage and residual stress in detail. | High computational cost; does not account for viscoelastic material behavior. |
| [52] | CS | ABS, PLA | FLOW-3D, Open FOAM | Strand shape, temperature, pressure, feeding rate. | Simulates stable and unstable extrusion regimes based on pressure and flow patterns. | Viscoelastic effects and complex geometries underexplored. |
| [53] | TMB | ABS | – | Number of layers, section length, chamber temperature, shrinkage rate. | Model quantifies warping and highlights the influence of chamber temperature and print path length. | Assumes uniform material properties and constant speed; lacks validation for complex geometries. |
| [56] | TMB | PLA, Wood Biocomposite | FLOW-3D | Residual stress, temperature, distortion, defects. | Model accurately predicts defects and residual stress; results validated experimentally. | Assumes perfect bonding and uniform filler; coarse mesh limits defect resolution. |
| [57] | TMB | ABS | Abaqus | Distortion, residual stress, mesh and timestep effects. | Accurately predicts Z-direction distortion; results validated experimentally. | Does not model anisotropy or plasticity; simplistic detachment modeling. |
| [58] | TMB | PA12 | Digimat | Temperature gradient, residual stress, distortion. | Highlights stress accumulation in lower layers due to cooling and reheating cycles. | No experimental validation; simplified heat transfer and isotropic assumptions. |
| [62] | TMB | ABS | Abaqus, NCORR, Slic3r | Elastic modulus, yield strength, raster anisotropy. | Accurately models anisotropic mechanical response; results agree with experimental data. | Ignores bonding defects, filament-scale variations, and fracture mechanics. |
| [12] | TMB | Polymers | MATLAB, FEA | Strain, displacement, digital twin coupling. | Digital twin enables real-time AM validation; supports predictive modeling of defects. | Implementation complexity: integration with real-time feedback not yet streamlined. |
| [18] | MPC | PLA, ABS, PETG, Nylon, CF PLA and ABS | – | Infill density, print temperature, fiber reinforcement, tensile strength, modulus. | Fiber reinforcement and higher infill improve strength and stiffness; PLA–CF shows highest modulus (5.2 GPa). | No standardized testing; limited insight into fatigue, creep, and environmental effects. |
| [24] | MPC | ABS, FDC | – | Structural integrity, defects, shrinkage. | Highlights accuracy issues due to poor bonding and shrinkage in early FFF systems. | Limited by hardware/software of early systems; findings may not generalize. |
| [59] | MPC | ABS-M30 | Custom (in-house) | Ultimate strength, stiffness, build direction, contour number. | Model predicts tensile strength within ~4% of test data. | Study limited to flat tensile geometry; excludes fatigue and impact performance. |
| [60] | MPC | Polycarbonate | SolidWorks, Abaqus | Young’s modulus, shear modulus, Poisson’s ratio, stress distribution. | Orthotropic model closely matches experiments; building orientation significantly affects performance. | Plastic behavior is not captured; only linear elastic validation performed. |
| [61] | MPC | PLA | MATLAB, CMM, Talysurf | Dimensional accuracy, flatness, surface texture, roughness. | Layer thickness strongly influences geometric accuracy; ANN enables predictive tuning. | Study limited to a single material and printer type; generalizability is low. |
| [65] | MPC | ABS | ABAQUS | Stress–strain, fracture path, raster failure mode. | Model replicates failure patterns; thinner layers show higher elongation. | Assumes isotropy; excludes thermal effects and neck formation mechanics. |
| [73] | MPC | CF PPS | ABAQUS, Additive3D | Residual stress, crystallinity, shrinkage, thermal conductivity. | Model predicts deformation with <7% error; includes crystallization kinetics and anisotropy. | Requires extensive experimental input; does not address creep or fatigue. |
| [5] | FRC | CF Polymer | Custom (in-house) | Flow alignment, shear, swelling. | Coupling flow with orientation improves print accuracy and part quality. | Nozzle flow simplified; high computational demands. |
| [6] | FRC | FRP | – | Viscosity, temperature, fiber effects. | Summarizes key insights into melt flow and fiber orientation in composite FFF processes. | Most models are uncoupled; validation data is sparse. |
| [7] | FRC | CF ABS | Ansys Polyflow, MATLAB | Orientation, stiffness, nozzle effects. | Nozzle gap and path significantly affect fiber alignment and part stiffness. | Does not model fiber interaction; assumes Newtonian flow behavior. |
| [8] | FRC | CF ABS | Ansys Polyflow, MATLAB | Pressure, orientation, void risk. | Low-pressure regions form around fibers, potentially increasing void formation. | Only models single fiber; lacks full thermal coupling. |
| [37] | FRC | FRP | Custom (SPH-DEM) | Drag force, fiber deformation, flow. | Models fiber alignment during extrusion with good correlation. | Thermal effects excluded; limited to 2D simulation; lacks experimental validation. |
| [10] | FRC | CF Thermoplastics | – | Fiber alignment, interlayer bonding, voids, anisotropy. | Highlights design freedom and high strength potential of continuous CF composites. | Challenges include fiber placement accuracy, void control, and limited toolchain/software support. |
| [67] | FRC | CF ABS | – | Orientation, strength, modulus. | Fiber alignment increases strength by 115% over neat ABS. | Voids reduce toughness; print path has critical influence. |
| [68] | FRC | CF Thermoplastics | – | Strength, stiffness, alignment. | Fiber content enhances stiffness; anisotropy linked to print path. | Long-term mechanical behavior and standardization are lacking. |
| [69] | FRC | FRP | Custom (SPH-DEM) | Drag force, fiber deformation, flow. | Predicts fiber orientation and flow behavior with good correlation. | Excludes thermal effects; 2D model only; limited experimental validation. |
| [70] | FRC | CF PA66 | Amira, CFD | Fiber length, orientation, strength, modulus. | Nozzle size influences fiber breakage: fiber alignment improves with build height. | Neglects fiber interactions and complex geometries. |
| [71] | FRC | Continuous CF + PLA | Custom, FEA | Orientation, voids, stiffness. | Aligned paths reduce voids and increase stiffness by 30%. | The method is computationally intensive and demonstrated only on simple shapes. |
| [72] | FRC | Continuous CF + PEKK | Custom, μCT, FEA | Failure strength, fiber deviation. | Strength-based paths improve performance over stiffness-driven approaches. | High computational complexity; limited geometry scope. |
| [76] | FRC | Short CF + ABS | Altair Multi-scale Designer | Failure mode, stress, angle. | Model accurately predicts anisotropic failure behavior. | Requires calibration for each material-print setup. |
| Software/Criteria | Potentiality | Usability | Scalability | Accessibility |
|---|---|---|---|---|
| Abaqus | High | Very high | High | High |
| Ansys | Very high | High | Very high | High |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Enriconi, M.; Rodriguez, R.; Araújo, M.; Rocha, J.; García-Martín, R.; Ribeiro, J.; Pisonero, J.; Rodríguez-Martín, M. A Comprehensive Review of Fused Filament Fabrication: Numerical Modeling Approaches and Emerging Trends. Appl. Sci. 2025, 15, 6696. https://doi.org/10.3390/app15126696
Enriconi M, Rodriguez R, Araújo M, Rocha J, García-Martín R, Ribeiro J, Pisonero J, Rodríguez-Martín M. A Comprehensive Review of Fused Filament Fabrication: Numerical Modeling Approaches and Emerging Trends. Applied Sciences. 2025; 15(12):6696. https://doi.org/10.3390/app15126696
Chicago/Turabian StyleEnriconi, Maria, Rocío Rodriguez, Márcia Araújo, João Rocha, Roberto García-Martín, João Ribeiro, Javier Pisonero, and Manuel Rodríguez-Martín. 2025. "A Comprehensive Review of Fused Filament Fabrication: Numerical Modeling Approaches and Emerging Trends" Applied Sciences 15, no. 12: 6696. https://doi.org/10.3390/app15126696
APA StyleEnriconi, M., Rodriguez, R., Araújo, M., Rocha, J., García-Martín, R., Ribeiro, J., Pisonero, J., & Rodríguez-Martín, M. (2025). A Comprehensive Review of Fused Filament Fabrication: Numerical Modeling Approaches and Emerging Trends. Applied Sciences, 15(12), 6696. https://doi.org/10.3390/app15126696









