Abstract
Three-dimensional CAD reconstruction is a long-standing and important task in fields such as industrial manufacturing, architecture, medicine, film and television, research, and education. Reconstructing CAD models remains a persistent challenge in machine learning. There have been many studies on deep learning in the field of 3D reconstruction. In recent years, with the release of CAD datasets, there have been more and more studies on 3D CAD reconstruction using deep learning. With the continuous deepening of research, deep learning has significantly improved the performance of tasks in the field of CAD reconstruction. However, this task remains challenging due to data scarcity and labeling difficulties, model complexity, and lack of generality and adaptability. This paper reviews both classic and recent research results on 3D CAD reconstruction tasks based on deep learning. To the best of our knowledge, this is the first investigation focusing on the CAD reconstruction task in the field of deep learning. Since there are relatively few studies related to 3D CAD reconstruction, we also investigate the reconstruction and generation of 2D CAD sketches. According to the different input data, we divide all investigations into the following categories: point cloud input to 3D CAD models, sketch input to 3D CAD models, other input to 3D CAD models, reconstruction and generation of 2D sketches, characterization of CAD data, CAD datasets, and related evaluation indicators. Commonly used datasets are outlined in our taxonomy. We provide a brief overview of the current research background, challenges, and recent results. Finally, future research directions are discussed.
1. Introduction
CAD 3D modeling is widely used in various industries and has a profound impact on work efficiency and design accuracy. Three-dimensional CAD models form the core of modern design and manufacturing, playing a key role in product design, architectural planning, and medical equipment customization. Therefore, CAD 3D reconstruction tasks are crucial in many fields [1,2]. It has broad application prospects in manufacturing and industrial design, architecture, medicine, film and television, research and education, etc. [3,4,5,6]. CAD 3D reconstruction refers to the generation of 3D CAD models through the computer processing of given input data (such as point clouds or sketches). In the manufacturing industry, CAD 3D reconstruction can quickly generate manufacturable 3D models from sketches, shortening the product development cycle. In the field of architecture, it can help architects quickly transform design intent into visual 3D models. In the medical and film and television industries, it can be used for customized medical equipment and virtual model production, respectively. In the research and education fields, students and researchers can generate visual models to improve the efficiency of teaching and research, as shown in Figure 1. The emergence and application of mature CAD reconstruction technology will promote the efficiency and accuracy of various industries in the future, and foster innovation and progress in the industry.
Figure 1.
Real-world applications of CAD-related technologies: (a) automotive manufacturing; (b) education; (c) aerospace engineering; (d) the medical field; (e) robotics; (f) architectural design.
Traditional CAD 3D reconstruction methods rely on manual tool operations. Although these methods are effective in simple scenarios, they show obvious limitations when facing complex geometric structures. Manual tool operations often require experienced experts for adjustments and optimizations, have a low degree of automation, and cannot be adapted to large-scale industrial application needs.
With the emergence of large datasets of CAD representations in recent years, researchers in machine learning and deep learning have begun to study CAD data [7,8,9,10], as shown in Figure 2. Previous studies have used these datasets for many research applications, such as segmentation, classification, and assembly [11,12]. In order to solve the problems of traditional CAD 3D reconstruction, deep learning has been introduced into the field of CAD 3D reconstruction in recent years, which has greatly improved the degree of automation of reconstruction and the quality of model generation. With the deepening of the research, a series of deep learning methods has emerged for generating structured CAD data through 2D sketches or 3D models [13,14,15]. There is also research on B-rep (boundary representation), which is used to generate focused, unconstrained CAD models. B-rep is one form of CAD data [16,17]. Regarding the representation form of CAD, the research on 3D learning of the CSG (Constructive Solid Geometry) representation form has gradually increased [18,19,20], pursuing the universality, simplicity, and quality of learning models. As for boundary representation, neural networks were applied to its segmentation task in the 1990s [21,22,23,24], but, due to the lack of datasets and other factors, significant progress was not made until recent years [16,25]. Recent CAD generation models also use extrusion modeling operations to avoid the direct generation of B-rep [26,27,28]. The extrusion modeling operation is a common parametric modeling method that constructs three-dimensional geometry by extending a two-dimensional cross-section along a given direction. Compared with traditional manual tool operation methods, the emergence of these studies will not only reduce the dependence on professional knowledge for CAD 3D reconstruction, but also greatly speed up the reconstruction process.
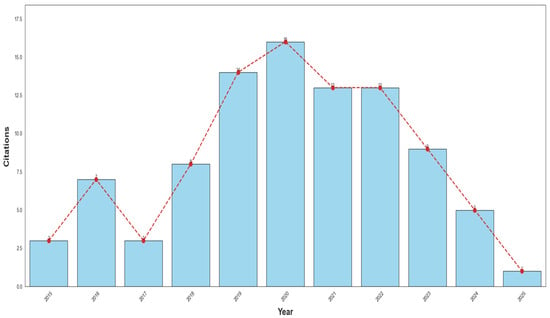
Figure 2.
This is the annual citation data of CAD papers.
The reconstruction of 3D CAD has always been a challenge in the field of deep learning. In the past two decades, with the continuous development of technology, the realization of 3D CAD reconstruction in this field has become increasingly feasible [29]. The research community has been committed to reconstructing 3D CAD models from point clouds, sketches, and other forms, and there have also been related studies on the generation of 2D CAD sketches [30,31,32].
In recent years, CAD 3D reconstruction has made remarkable progress, especially with the introduction of deep learning, which has led to more intelligent and automated reconstruction processes. Deep learning not only overcomes the limitations of traditional methods but also provides the technical foundations for large-scale industrial applications in the future. The aim of this survey is to comprehensively summarize the relevant work on deep learning in the field of 3D CAD reconstruction. The main contributions of this paper are summarized as follows:
- We briefly review the recent progress in deep learning-based 3D CAD reconstruction. In addition, recent research methods and research trends over the past years are also given.
- We summarize existing reconstruction approaches based on different input modalities, including point clouds, sketches, and other forms. We also summarize CAD sketch design generation based on deep learning.
- We introduce commonly used CAD data representation formats in deep learning frameworks, which helps improve our understanding of model structure and design consistency.
- We summarize the commonly used public CAD datasets.
- We discuss the main challenges, existing limitations, and potential directions for future research.
This paper is organized as follows: In Section 2, we present deep learning-based methods for reconstructing 3D CAD models from point cloud data. Section 3 introduces the reconstruction of 3D CAD models from sketches. Section 4 introduces the reconstruction of 3D CAD models from other forms. Section 5 discusses deep learning methods for CAD sketch generation, as shown in Figure 3. In Section 6, CAD data representation formats are introduced and explained. Section 7 reviews the commonly used CAD datasets. Section 8 introduces some evaluation metrics. Section 9 concludes the entire paper and looks forward to future research directions.
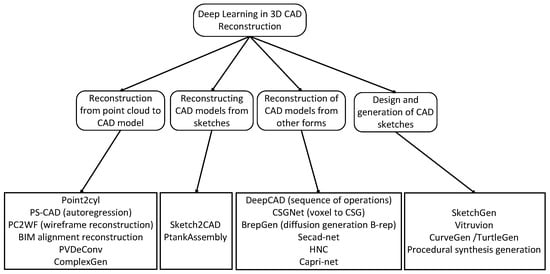
Figure 3.
A taxonomy of CAD model reconstruction methods.
2. Reconstruction from Point Cloud to CAD Model
The reverse engineering of original geometry to a CAD model a fundamental task [33]. The reconstruction from the point cloud to the CAD model is part of this process. The CAD model is in the form of a series of extruded columns, a 2D sketch plus an extruded axis and range, and their combination through Boolean operations [30]. Boolean operations are a type of geometric operation used to combine multiple entities through operations such as union, intersection, and difference [34]. To reconstruct a CAD model through point cloud reverse engineering, you first need to obtain the point cloud through a 3D sensor, then decompose it into primitives or surfaces, and then use some existing shape modelers for further analysis [35,36,37]. In recent years, a variety of analysis and modeling methods have been studied for the processing and geometric reconstruction of point clouds in complex scenes [38,39,40,41]. In the future, new ideas may be brought to reconstruction from point clouds to CAD models. From the perspective of CAD users, the entire modeling process usually starts with sketching. First, a two-dimensional sketch is drawn which is a closed curve. Then, it is stretched into a three-dimensional entity [10]. After that, these three-dimensional shapes can be combined through operations such as union, intersection, and difference.
For reverse engineering point clouds into primitives usable in CAD modeling [42,43], the traditional approach is to first convert the point cloud into a mesh, then generate a boundary representation [44] through a series of operations, and then infer that the input can generate the boundary representation in the CAD program [45].
DeepCAD [10] introduced a Transformer-based method to generate complete 3D CAD models, providing a technical direction for subsequent applications related to point cloud modeling. Uy et al. [30] proposed a supervised learning framework (point2cy) that can convert raw 3D point cloud data into a set of cylinders with extrusion parameters, making it possible to reconstruct CAD models from point clouds and supporting user edits of the reconstruction results. This method regards the modeling of extruded cylinders as a parameterized geometric unit, which is used to jointly express multiple sketch extrusion processes, and has demonstrated its applicability in CAD modeling and geometric representation [46,47]. Cherenkova et al. [48] proposed PVDeConv, a neural module for reconstructing structured CAD configurations from dense voxel or point cloud features. Yang et al. [49] proposed PS-CAD, which reconstructs CAD modeling sequences from point cloud data through an autoregressive model and uses local geometric information as guidance [50]. However, it lacks design rule constraints between different sketch extrusions. Guo et al. [13] proposed ComplexGen to reconstruct high-quality B-rep CAD models from input point clouds or implicit representations.
In recent research, Liu et al. [51] proposed a network architecture (PC2WF) that can directly map 3D point clouds to vector wireframes, which are composed of 3D junctions and the edges connecting them, representing the structural outline of the object [52]. The reconstructed wireframes can drive and help create 3D CAD models. Wireframes save storage space, are easy to edit in various operations in CAD software (e.g., AutoCAD 2024 or similar), and can be applied in many fields such as part design and manufacturing and CAD model creation [53,54]. For CAD reconstruction in specific applications, such as in piping systems and building facilities, some studies focused on reconstructing geometric CAD models from sparse or noisy point clouds [55,56]. For example, Yu et al. [57] used deep learning-based segmentation and BIM-driven alignment techniques to reconstruct pipeline structures from 3D point cloud data with poor scanning quality. BIM (Building Information Modeling) is a three-dimensional digital modeling method that integrates building geometry, physics, and functional information to support the management and collaboration of the entire life cycle of buildings [58,59].
In the task of reconstruction from a point cloud to a CAD model, although existing methods have made progress in parametric modeling, geometric structure expression, and reconstruction from low-quality point clouds in specific scenarios, they are still limited by factors such as high noise and uneven point cloud distribution, and the reconstruction accuracy is difficult to guarantee [60,61]. At the same time, the expressive power for complex structures and industrial parts is limited, and the integration of geometric constraint modeling with actual CAD systems is not yet mature [62,63]. In the future, it will be possible to integrate geometric priors, topological constraints, and multimodal information to build a more unified and interpretable reconstruction model to improve the robustness and industrial adaptability of the system.
3. Reconstructing CAD Models from Sketches
In the traditional method of converting a sketch to a CAD model, the designer first completes the sketch, and then converts the design sketch into a 3D CAD model through a high-precision and editable CAD tool. Due to the involvement of multiple professional skills, this process is often inefficient for design iterations and requires considerable time and resources [64]. Therefore, the research on generating CAD models through sketches is of great significance [65,66].
In recent research, Li et al. [67] proposed a sketch-based CAD modeling system, Sketch2CAD. By inferring CAD operations from sketch operations, an approximate sketch of man-made objects can be converted into a regular CAD model [68]. For users, the sketch strokes drawn by contextual users are mapped to regular CAD models, helping them to avoid browsing the complex CAD system interface [69]. However, there is also a limitation where this cannot achieve the same modeling level as modern CAD software, even though it can enable sketch designers to quickly generate CAD models. This study provides a reference for future research and promotes related research on converting sketches to CAD models.
If the process of automatically converting 2D CAD sketches into 3D CAD models can be achieved, it is expected to significantly improve the overall efficiency from design to practical application and greatly reduce costs [70]. Based on this demand, Hu et al. [31] proposed a system that uses vector line drawings as input to generate structured CAD models. This method uses three orthographic projections to reconstruct a complete 3D CAD model, and, especially when the input contains significant noise or missing information, it exhibits better performance than traditional methods [71,72]. This study effectively addresses a long-standing challenge in the CAD field: reconstructing 3D geometry from multiple orthographic views [73,74]. Researchers found that two key factors significantly improved the reconstruction effect: first, compared with directly establishing the mapping relationship between the two-dimensional and the three-dimensional, the introduction of an attention mechanism can enhance the model’s adaptability to incomplete inputs [75]; second, injecting professional domain knowledge into the generation framework can improve the output quality and enhance its practical value in subsequent tasks. This discovery provides strong theoretical support for subsequent related research. However, this method has not yet integrated the additional information commonly found in CAD drawings, such as layers, annotations, symbols, and text [76,77], which limits its practicality to some extent.
In recent years, research on the conversion process from a sketch to a CAD model has achieved some initial results in terms of robustness and generation quality. However, existing methods still have shortcomings in terms of multi-view information fusion, drawing semantics, and geometric structure consistency [78]. In the future, we can integrate layers, symbol semantics, and multimodal input to build a unified sketch-to-CAD framework, and introduce a user interaction mechanism to improve the system’s intelligent modeling capabilities and actual efficiency, which will promote the design process to develop towards intelligence.
4. Reconstruction of CAD Models from Other Forms
CAD modeling describe the process of users creating 3D shapes, which are very different from meshes and point clouds and are widely used in many industrial engineering design fields. With recent development, CAD models have been widely adopted as a standard means of shape description in most industrial manufacturing processes. The generation of 3D CAD models faces the challenges in the CAD operation sequence and irregular structure.
Wu et al. [10] proposed the first 3D generative model that describes shapes as a series of computer-aided design (CAD) operations. They found a representation of irregularities in coordinated CAD models. The deep generative model of CAD proposed by the authors is a series of operations used in CAD tools to construct 3D shapes. They can be directly converted to other shape formats such as point clouds [79] and polygonal meshes [80]. To improve the controllability and hierarchical expression ability of the generation process, Xu et al. [81] introduced a hierarchical neural encoder (HNC) architecture to achieve more refined and structured CAD model sequence generation. At the same time, Li et al. [26] designed an end-to-end method (SecAD-Net) that can automatically infer 2D sketches and their corresponding 3D extrusion parameters from the input original geometry, thereby realizing the reconstruction of CAD models. In addition, Yu et al. [82] proposed CAPRI-Net, which adaptively learns and assembles parametric geometries from 3D surface data to generate CAD models. This approach provides new insights into CAD model generation.
Geometry et al. [83] proposed CSGNet, which takes voxelized shapes as input and learns to generate a sequence of Constructive Solid Geometry (CSG) operations. In contrast, Wu et al. [10] designed an autoencoder architecture that outputs modeling results expressed as a sequence of CAD operations.
Xu et al. [84] proposed BrepGen, a diffusion-based generative framework [85] that directly generates CAD models in the form of boundary representations (B-reps). B-reps are more challenging to generate [86] than CSG or sketch representations, mainly because they contain a variety of parameterized surfaces and curves, and each type of geometric element has its own definition and parameter configuration. To form a closed solid, the topological relationship between all geometric shapes must remain correct. Therefore, the generation is very complicated. Other CAD generation models, therefore, use parametric modeling operations and extend two-dimensional cross-sections to operate without the need for generation through B-rep. The emergence of a system that can directly generate boundary representations will have a great impact, reducing a lot of manual labor for skilled designers, reducing the dependence of CAD on professional CAD software, and changing the overall CAD workflow. Therefore, the emergence of BrepGen will promote the goal of building an automatic system that can directly generate B-rep.
Generating CAD models from voxels and geometric shapes shows potential in operation sequence modeling and direct generation of B-rep models. However, there are still deficiencies in generalization and interpretability [82,87]. In the future, by introducing structural priors, multimodal fusion, and design rule constraints, the model’s ability to express complex shapes can be improved, and the connection with the CAD tool chain can be strengthened to promote the implementation of the model in actual engineering design.
5. Design and Generation of CAD Sketches
Since there are relatively few studies on 3D CAD reconstruction, we also investigated the reconstruction and generation of 2D CAD sketches.
In computer-aided design (CAD), a common method is to extrude and combine two-dimensional sketches to obtain complex three-dimensional models. The essence of a two-dimensional CAD model is a collection of primitives (such as lines and arcs) combined by a set of relationships (such as collinearity, parallelism, and tangents) [88,89]. A two-dimensional sketch is formed into a two-dimensional complex shape through a series of CAD operations.
When using training models to automatically generate CAD sketches, there are challenges in the complexity of the graph and the heterogeneity of the model [87,90]. Para et al. [91] proposed the SketchGen framework, which solved the problem of heterogeneity by designing a sequential language of primitives and constraints. The SketchGen framework is used for the automatic and complete generation of CAD sketches. It includes primitives and constraints. However, the SketchGen model has the defect of autoregressive characteristics that prevents error correction in the early part of the sequence.
In CAD models, two-dimensional sketches structured within three-dimensional structures are difficult to manufacture. Ganin et al. [92] proposed a machine learning model for automatic sketch generation. By combining general language modeling techniques with existing data serialization protocols, the generation of complex structured objects is achieved.
For parametric sketches, Seff et al. [93] proposed a method for modeling and synthesizing parametric CAD sketches. A generative model was used to synthesize CAD sketches using autoregressive sampling of geometric primitives and constraints. This model is expected to help mechanical design work by synthesizing realistic CAD sketches.
For engineering sketches, Willis et al. [32] proposed generative models for engineering sketches, CurveGen and TurtleGen. Both can generate curve primitives and generate realistic engineering sketches without using sketch constraint solvers. The generated model contains topological information to assist in the task of constraint and 3D CAD modeling.
Another potential approach in the generation of engineering sketches is program synthesis: using neural network and programming language technology to generate or infer programs representing geometric shapes [83].
In terms of CAD sketch generation, the existing research has improved its expressive capabilities through primitive modeling, constraint sequence, and program synthesis. However, due to the weak error correction ability of the model and insufficient modeling of constraint relationships, the accuracy and engineering usefulness of the generated sketches are still limited [94,95]. In the future, the combination of graph neural networks, constraint solving mechanisms, and language guidance can improve the controllability, structural integrity, and system integration of the generated model, increasing its practical value in engineering design scenarios.
6. CAD Representation
6.1. B-Rep (Boundary Representation)
In computer-aided design (CAD), parametric curves and surfaces constitute the core of modeling foundations [96]. B-rep (boundary representation) is a common CAD data structure used to encode geometry as parametric shapes and their topological relationships to achieve complex and accurate 3D modeling [97], as shown in Figure 4. It consists of faces, edges, and vertices, and supports surface expressions such as lines, arcs, cylinders, and non-uniform rational B-spline curves (NURBS). It can accurately describe complex models generated by CAD modeling operations [98]. CAD users can directly manipulate the geometric elements of B-rep for design and modification.
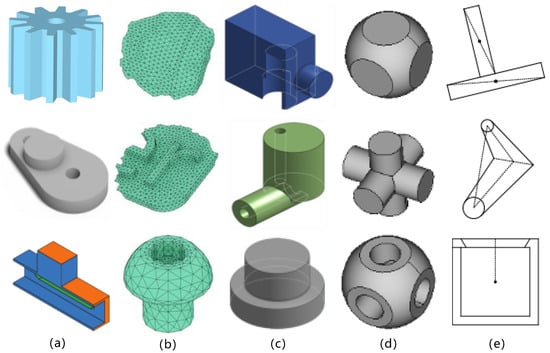
Figure 4.
Three-dimensional CAD model. (a) B-rep (boundary representation); (b) polygon mesh representation; (c) sequence representation; (d) CSG (Constructive Solid Geometry); (e) sketch.
B-rep (boundary representation) plays a bridging role between geometric modeling and solid modeling in CAD [99]. Geometric modeling focuses on using mathematical methods to describe the geometric features of objects, such as curves, surfaces, and their spatial distribution [100], while solid modeling further emphasizes the construction of three-dimensional models with closed volumes and topological integrity to meet the actual needs of manufacturing and engineering [101]. B-rep can accurately describe complex surfaces while ensuring the topological coherence and closure of the model. As a means of expression for geometric modeling and the basis for the implementation of solid modeling, it plays a key role in connecting the two in the CAD system.
Although B-rep data is widely used in the CAD field, its direct use in deep neural networks still faces many challenges [28]. B-rep consists of a variety of geometric and topological entities. The mapping between shapes and surface types is not one-to-one; its topological structure is complex, and the connection methods of each geometric unit need to be considered. In modern machine learning, algorithms such as BrepGen, BrepNet, and BRep-BERT are all based on B-rep [17,84,102]. However, due to the complex data structure, it remains a significant challenge. In order to apply the latest advances in deep neural networks to CAD software, Jayaraman et al. [16] proposed a unified representation of B-rep data which enables the network architecture UV-Net to effectively combine image and graph convolutional neural networks. However, B-rep still has the limitation of not being able to utilize other available information, such as edge convexity and curve type.
6.2. Polygon Mesh
In 3D CAD data, polygon mesh representation is a common method that can be used to represent complex 3D shapes [103]. Polygon mesh data consists of vertices (points in 3D space), edges (edges connect two vertices and represent the boundaries of geometric figures), and faces (faces are formed by a set of vertices connected in a specific order) [104]. Polygon mesh data in CAD software represents design details and complexity, with applications spanning 3D modeling, animation, and game development. The representation of polygon mesh combines geometric and topological information, and has the characteristic of being able to accurately describe complex 3D shapes.
Compared with B-rep, polygonal meshes differ fundamentally in their data structure. B-rep approximates the surface of an object through discrete triangles or polygonal patches and is mainly used in graphics rendering and visualization, such as in games and animations [105], while B-rep uses parameterized curves and surfaces to accurately represent geometric shapes and their topological relationships. It is widely employed in engineering design and manufacturing. In contrast, B-rep is better suited for structural modeling and geometric calculations, offering higher accuracy and more robust expression capabilities.
6.3. Sequence Representation
Sequence representation represents the generation or editing process of a CAD model as a series of sequential operations. Similar to text sequences in natural language processing, sequence representation records geometric operations, construction steps, and parameters as a time series, and the model can generate CAD models by learning these sequences [15,49,81]. Specifically, the construction process of CAD models usually involves various geometric operations, such as drawing straight lines, drawing arcs, rotating, extruding, etc. Each operation has its specific parameters, such as the starting point, end point, radius, angle, etc., of the operation. Sequence representation records these geometric operations in the order of execution to form a set of operation instructions. In this way, each instruction (or element in the sequence) represents a specific geometric operation and its corresponding parameters as seen, for example, in the recently proposed dataset DeepCAD [10] of large CAD command sequence models.
Similar to sequence representation are CAD procedural modeling and the macro parameter method (MPA). CAD procedural modeling automatically constructs geometric models through rules, scripts, or parameter instructions and is a model generation method. It emphasizes the automatic construction of models based on rules and parameters [106]. The macro parameter method (MPA) is a technical path to achieving semantic preservation and the exchange of CAD models, emphasizing the consistency of models across different platforms [107]. CAD procedural modeling is a modeling idea and method, whereas the MPA is an engineering solution for cross-platform semantic modeling conversion. In comparison, sequence representation is a form of data representation. It is a way to express the “construction history” of CAD models, which facilitates neural network learning and modeling, and is suitable for model generation and reconstruction tasks.
6.4. Constructive Solid Geometry (CSG)
Constructive Solid Geometry (CSG) is a classic 3D CAD expression form [108] which gradually builds complex 3D structures by applying Boolean operations (including union, intersection, and difference) to basic geometric bodies (such as cubes, spheres, cylinders, etc.) [109]. Among them, the difference operation is particularly important in the modeling process and is especially suitable for designing holes and protrusion structures. Unlike boundary representation (B-Rep), which directly records boundary information, CSG (Constructive Solid Geometry) constructs an expression tree through Boolean primitives and operations, only recording the construction process of the model without storing specific boundary geometry. Therefore, it is necessary to convert it into the final geometry through the Boolean evaluation process. CSG representation consists of Boolean primitives and Boolean operations.
CSG is usually modeled in a tree structure, with leaf nodes representing basic geometric bodies and intermediate nodes representing Boolean operations or geometric transformations. Among them, protrusion is a typical operation, which is often implemented by union. B-rep describes the boundaries of objects through vertices, edges, faces, and their topological relationships, and pays more attention to the detailed expression of the surface of the shape, which is suitable for scenes that require high-precision modeling. CSG focuses on the construction process, and B-rep emphasizes geometric expression. The two can complement each other.
CSG and sequence representation are essentially different. CSG combines basic geometric bodies through Boolean operations, focusing on the logical relationship between geometric bodies, and is usually represented by an operation tree. Sequence representation simulates the real design process through sketches and operation sequences, involving sketching, constraint setting, and modeling feature operations. It has stronger expressive ability and is more suitable for complex parametric modeling, which meets actual engineering needs.
CSG has a concise expression structure and is flexible to modify. It is widely used in many fields such as mechanical design and architectural modeling. Recently, Yu et al. [110] proposed the D2CSG model, which can learn compact CSG expressions in an unsupervised learning framework for representing three-dimensional CAD shapes.
6.5. Sketch Representation
Common sketch representations include vector graphics representation and graph structure representation.
Vector graphics is a common form of sketch representation which uses mathematical equations (such as line segments, circles, splines, etc.) to define the boundaries and shapes of graphics. Unlike pixel images, vector graphics do not distort when enlarged or reduced, and are suitable for high-precision geometric expressions in CAD. By directly using the vector graphics information in the CAD sketch, including geometric elements such as points, lines, and arcs, the geometric elements in the CAD sketch are converted into a series of feature vectors, each of which contains the type, coordinates, and other attributes of the geometric element. Vector graphics representation is often used to generate new CAD sketches or optimize existing designs using deep learning models. However, there are also challenges that require the processing of complex geometric and topological relationships, and model design and training are more complex.
A two-dimensional CAD sketch is represented as a graph structure where nodes represent geometric elements and edges represent the relationships between geometric elements. By constructing a graph, nodes represent geometric elements such as points, lines, and arcs, and edges represent the connection relationship or constraint relationship between geometric elements [111]. It can naturally represent the topological relationship between geometric elements, which is suitable for graph neural networks (GNNs) [112]. For example, in the SketchGraphs dataset [113], each CAD sketch can be represented as a graph structure, where nodes represent geometric elements (such as lines, circles, etc.) and edges represent constraints or relationships between these elements.
7. Datasets
This section systematically reviews the current mainstream open-source datasets in the CAD field. To deepen the understanding of data resources in this domain, the study presents the key characteristics of the relevant datasets in a structured format in Table 1, including core attributes such as release year, data size, and representation type. Additionally, the official download links provided in the original literature are included in Table 2, ensuring the traceability and reproducibility of the research data, and facilitating subsequent researchers in conducting comparative experiments and algorithm validation.

Table 1.
Dataset table. We collect the datasets used in related papers and explain some of their properties.

Table 2.
Datasets and download links. We provide the download links for the datasets used in the related papers.
7.1. ShapeNetCore Dataset
The ShapeNet dataset constructed by Chang et al. [7] collects a large number of 3D models, covering many common categories such as furniture, transportation, and electronic equipment. Although ShapeNet contains many CAD models, its original intention was not to serve CAD exclusively. ShapeNetCore is a subset of ShapeNet, focusing on models with relatively regular structures and CAD features. This subset provides rich data support for research in computer vision and machine learning, and can be applied to tasks such as object recognition, retrieval, and classification. Although ShapeNetCore was not built for industrial-grade CAD, its model resources still have significant practical value for many CAD-related topics.
In recent related research, Yi et al. [114] proposed an annotation tool that annotates a dataset to make it more than an order of magnitude larger than previously available datasets. The annotation tool was tested on ShapeNetCore, which significantly reduced the labor cost of the annotation work.
7.2. CSGNet Synthetic Dataset
Sharma et al. [11] proposed the CSGNet synthetic dataset. This dataset consists of 2D and 3D shapes automatically generated by CSG programs. The synthetic dataset is provided in the form of program expressions rather than rendered images.
7.3. ABC Dataset
Koch et al. [8] proposed the ABC dataset. Since a large number of datasets at that time were composed of acquired or synthesized point clouds or point grids, they did not meet the requirements of ground truth signals or parameter representation. Therefore, a new CAD model dataset, the ABC dataset, was proposed. It meets the requirements for a large size, ground truth signals, parameter representation, and scalability. It contains sufficient similar samples, diverse shapes, and high-quality ground truth values.
The ABC dataset [8] was created by collecting and creating Onshape, a large online collection of CAD models, and it can be used to study geometric deep learning methods and applications. The ABC dataset contains more than 1 million individual and high-quality CAD models. The parametric description of the sampled surfaces and curves in the models can generate data in different formats and resolutions so that various geometric learning algorithms can be compared fairly. Since the ABC dataset is a proprietary format provided by the Onshape CAD software, it has some additional building information; however, the missing information needs to be retrieved by querying the Onshape API (Onshape API version 2024).
7.4. CC3D Dataset
Cherenkova et al. [48] built a dataset called CC3D which contains more than 50,000 3D objects along with their corresponding CAD models and mesh data. This dataset covers a large number of real 3D scan samples and their associated CAD models, providing valuable resources for tasks such as 3D reconstruction and geometric analysis. The CC3D dataset contains models of unrestricted categories and complexities. The 3D CAD models collected by the CC3D dataset contain a total of 50k+ STEP format models with different categories and designs ranging from simple to complex.
7.5. CC3D-Ops Dataset
Dupont et al. [115] proposed the CC3D-ops dataset, which contains more than 37,000 CAD models and builds upon the previous CC3D dataset [48]. The CAD models in the CC3D dataset are annotated with detailed records of the construction process for each model, including the types and steps of operations, which were derived from the actual construction history of the model. Therefore, the B-rep data in the CC3D-ops dataset not only includes the corresponding geometric surface information but also provides detailed annotations of the operation types and steps.
Compared with other datasets, the CC3D-ops dataset has both B-reps and a clear construction history in a standard format. This advantage is only available in the CC3D-ops dataset and the Fusion360 dataset [9], but the CC3D-ops dataset’s complex model characteristics are closer to real-world industrial use than the Fusion360 dataset. The 50k+ industrial CAD models provided by the CC3D dataset [48] do not have construction steps and B-reps.
7.6. Fusion 360 Gallery Reconstruction Dataset
Willis et al. [9] proposed the Fusion 360 Gallery reconstruction dataset, which is the first artificial 3D CAD geometry dataset designed for machine learning. The dataset contains 8625 artificial design sequences (i.e., CAD programs), which are simple to operate and only involve sketching and extrusion modeling. Through basic CAD modeling operations and Boolean operations, various complex 3D designs can be created.
In contrast, many existing 3D CAD datasets focus on providing mesh geometry representations [7,116,117]. However, the standard format for parametric CAD is boundary representation (B-Rep), which provides richer surface and curve analysis. The Fusion 360 Gallery reconstruction dataset uses the B-Rep format, which not only facilitates fine control of 3D shapes but also records a clear design construction history, providing valuable information for analysis and modeling.
7.7. MFCAD++ Dataset
Colligan et al. [118] proposed a new processing feature dataset MFCAD++. The MFCAD++ dataset is based on the MFCAD dataset and contains 59,655 CAD models with planar and non-planar processing features. Each CAD model in the dataset contains 3 to 10 processing features and non-planar processing features, and the CAD models have very complex models. As for the MFCAD dataset [119], it consists of 15,488 CAD models, and each CAD model is generated from a stock cube and 16 planar processing feature classes. However, the MFCAD dataset has a limitation where each CAD model is relatively simple and lacks intersecting processing features.
7.8. DeepCAD Dataset
Wu et al. [10] proposed a new CAD command sequence dataset to train their proposed autoencoder. This dataset contains 178,238 CAD models and their CAD construction sequences. Each model in the dataset is represented as a CAD command sequence. Compared with other existing datasets of the same type, it is several orders of magnitude larger in size. Compared with the ABC dataset, the CADs in the ABC dataset are provided in B-rep format, and there is not enough information to recover how the CAD operations built the design. Compared with the Fusion 360 Gallery dataset, which only contains 8000 CADs, it is difficult for it to support the training of an effective generalized generative model. Therefore, the ABC dataset and the Fusion 360 Gallery dataset could not be used to train the proposed autoencoder model. However, the scale of the new dataset proposed was large enough and provided CAD command sequences, which made it sufficient to train their autoencoder network and it can be used for future research.
7.9. Fusion 360 Gallery Assembly Dataset
Willis et al. [120] proposed the Fusion 360 Gallery assembly dataset, which contains a large number of CAD assemblies and provides detailed information about joints, contacts, holes, and underlying assembly structures. The dataset is based on designs in Autodesk Fusion 360 and is divided into two parts: the assembly data, which includes 8251 assemblies and 154,468 parts, and the joint data, which contains 32,148 joints between 23,029 parts. The structure and representation of the data follow the Fusion 360 API specification. Compared with the ABC dataset, which also uses the B-Rep format, a significant advantage of the Fusion 360 Gallery assembly dataset is that it contains joint information about part connections and constraints, which is critical for understanding the relationships between parts. Other B-Rep datasets that only provide geometric part data lack such assembly information [9]. As a result, the Fusion 360 Gallery assembly dataset more realistically reflects the actual use of CAD components in the design process.
7.10. SketchGraphs Dataset
The word sketch is a term in the field of CAD that specifically refers to the 2D basis of a 3D CAD model which stores geometric primitives and imposed constraints. Seff et al. [113] proposed a dataset of 15 million sketches extracted from real-world CAD models: the SketchGraphs dataset. The SketchGraphs dataset is a CAD sketch dataset that focuses on the parametric CAD sketches underlying relational geometry. Each sketch in the dataset is accompanied by a real geometric constraint graph representing its configuration. The SketchGraphs dataset contains 15 million parametric CAD sketches extracted from parametric CAD models hosted on the cloud-based CAD platform Onshape. In existing CAD datasets that represent 3D geometry in voxels or meshes [7,116], the models are not modifiable in parametric design settings, so they cannot be directly used in most engineering workflows. The models in the SketchGraphs dataset are parametric CAD models that can support tasks such as patch segmentation and normal estimation.
7.11. Furniture Dataset
Xu et al. [84] proposed the Furniture B-rep dataset, which is the first dataset containing 3D CAD models designed by humans. They are represented in B-rep format. It contains 6171 B-rep CAD models of furniture in 10 common furniture categories. The dataset has standard category labels and 3D models containing free-form surfaces.
8. Metrics
In this section, we will introduce the evaluation indicators of different tasks in different papers. We will introduce them separately, covering conversion from point clouds, sketches, and other forms.
8.1. Reconstruction from a Point Cloud to a CAD Model
Point2Cyl, proposed by Uy et al. [30], converts an original 3D point cloud into a set of CAD models of extruded cylinders. The following evaluation metrics are used to evaluate different aspects of the algorithm. The specific parameter values are shown in Table 3.

Table 3.
Point2Cyl is compared with a strong geometric baseline jet fit (NJ), and H.V. is a simple hand-crafted baseline. ↑: the higher the better, ↓: the lower the better.
Segmentation IoU (Seg.): Uses the Hungarian algorithm to match the predicted extrusion segment with the actual extrusion segment. The segmentation result is compared with the true label. The total IoU loss (RloU loss) is defined as follows:
where represents the one-hot encoding.
Normal angle error (Norm.): Measures the angular consistency between the predicted normal and the true normal. The average error is calculated using the following definition formula:
Base/barrel classification accuracy (B.B.): Calculates the ratio of correctly predicted base and barrel labels. If the true label is consistent with the predicted label, it is counted. The formula is as follows:
Extrusion axis angle error (E.A.): Measures the angular error between the GT and the predicted axis. The formula is as follows:
Extrusion center error (E.C.): Measures the distance between the GT center and the predicted center:
Per-extrusion cylinder fitting loss (Fit Cyl.): A measure of how well each unrestricted extrusion cylinder parameter fits the GT extrusion cylinder segment:
where is the segment point after projecting the extrusion parameters.
Global fitting loss (Fit Glob.): A measure of whether at least one predicted unbound extrusion cylinder can explain each barrel point:
where .
The PS-CAD model proposed by Yang et al. [49] reconstructs CAD modeling sequences from point cloud data. The evaluation indicators shown in Table 4 were used to evaluate different aspects of the algorithm.

Table 4.
Quantitative comparisons of the geometric metrics (CD, HD, ECD, NC, and IR) of different methods on two different datasets. The scale of the CD, HD, and ECD is . ↑: the higher the better, ↓: the lower the better.
Chamfer distance (CD): By comparing the average distance from the randomly sampled points on the surface of two shapes to the nearest corresponding point, the geometric similarity is measured.
Hausdorff distance (HD): The farthest pair of distances among all pairs of randomly sampled points between two shapes is taken, reflecting the maximum geometric deviation between them.
Edge chamfer distance (ECD): Calculates the average nearest distance between the points on the edges of two CAD models to characterize the proximity of the contour structure.
Normal consistency (NC): Calculates the similarity between corresponding normal vectors, usually measured by cosine similarity.
Inefficiency (IR): The proportion of the statistically generated CAD operation sequence that cannot be executed indicates the effectiveness of the modeling process.
8.2. Reconstruction from Sketches to CAD Models
There are few studies on the conversion process from sketches to 3D CAD models, so we also investigated the generation and reconstruction of CAD sketches.
8.2.1. From Sketches to 3D CAD Models
Hu et al. [31] reconstructed a 3D CAD model by combining three orthogonal views. The quality of the 3D reconstruction results was evaluated using precision, recall, and F1 score. Hu et al. compared the results with the traditional 3D reconstruction method based on three orthogonal views. Since the implementation of the traditional pipeline is not public, the pipeline was reimplemented based on previous work [71,74]. The comparison only involved inputs with visible edges, as shown in Table 5.

Table 5.
Hu et al. method compared with the traditional 3D reconstruction method based on three orthographic views.
Precision: Refers to the proportion of model outputs predicted as positive that are actually positive.
Recall: Measures the proportion of all positive samples that the model correctly identifies as positive.
F1 score: The harmonic mean of precision and recall, combining the performance of both. The F1 score ranges from 0 to 1, where 1 indicates the best performance and 0 indicates the worst performance.
8.2.2. Generative Reconstruction of CAD Sketches
In the research on the generation and reconstruction of CAD sketches, Ganin et al. [92] proposed a machine learning model for automatically generating sketches. Following the standard evaluation method of autoregressive generative models (Nash et al, 2020 [72]), log-likelihood is used as the main quantitative indicator.
Log-likelihood: Measures the accuracy of the model’s predictions by calculating the log-likelihood of the observed data generated by the model. The higher the value, the more accurate the model is in predicting the data.
Seff et al. [93] proposed a method for modeling and synthesizing parametric CAD sketches. Quantitative evaluation was performed by measuring negative log-likelihood (NLL) and predictive accuracy on a stretched test set and through the distribution statistics of the generated sketches.
Negative Log-Likelihood (NLL): The negative value of the log-likelihood, which is often used to measure the deviation between model predictions and real observed data. The smaller the NLL value, the closer the model prediction is to the actual value.
Predictive Accuracy: Refers to the proportion of correct predictions made by the model on the test data, which is used to measure the overall prediction performance of the model. The higher the value, the better the model performance.
Willis et al. [32] proposed an engineering sketch generation model which provides a basis for subsequent parametric CAD model synthesis and combination. The quantitative evaluation indicators of the model are listed in Table 6.

Table 6.
Quantitative sketch generation results.
Bits per Vertex: The negative log-likelihood value of each test sample vertex is measured and expressed in bits. The lower the value, the better the performance.
Bits per Sketch: Refers to the average negative log-likelihood of each sketch, expressed in bits. The lower the value, the better the model performance. For CurveGen, we report the number of bits for vertex and curve models.
Unique: Measures how many of the generated sketches are unique as a proportion of all generated samples.
Valid: Measures how many of the generated sketches are valid as a proportion of all samples. Invalid sketches include those that fail to fit the curve, have more than four vertices, or have duplicate vertices.
Novel: Measures how many of the generated sketches are novel sketches that did not appear in the training set as a proportion of all generated samples.
Table 6 shows the comparative results of the generative models. Due to the difference between the sketch representation and the negative log-likelihood loss terminology, the bits per vertex and bits per sketch results are not directly comparable between models.
8.3. Reconstruction from Other Forms to CAD Models
8.3.1. Other Forms to B-Rep 3D CAD Model Reconstruction
For BrepGen, proposed by Xu et al. [84], the CAD model of the generated boundary representation (B-rep) is directly output, and the generation quality is quantitatively measured by distribution indicators and CAD indicators. Distribution indicators include Coverage (COV), the Minimum Matching Distance (MMD), and Jensen–Shannon Divergence (JSD). CAD indicators include Novel, Unique, and Valid, as shown in Table 7.

Table 7.
Quantitative evaluation of BrepGen and DeepCAD for unconditional generation comparison. ↑: the higher the better, ↓: the lower the better.
Coverage (COV): The proportion of generated data points that have at least one reference data point that matches after assigning each generated data point to its nearest reference data point (based on chamfer distance).
Minimum Matching Distance (MMD): Measures the average distance between each data point in the reference dataset and its closest neighbor in the generated data.
Jensen–Shannon Divergence (JSD): Calculates the distribution difference between the generated data and the reference data after converting the point cloud data into discrete voxels.
Novel: The percentage of generated data that did not appear in the training set.
Unique: The percentage of data that appeared once when generated.
Valid: The percentage of generated B-rep data that is a sealed solid.
8.3.2. Reconstruction of 3D CAD Models from Other Forms
Wu et al. [10] proposed the first method to model 3D shape generation as a sequence of CAD operations. The generative model uses chamfer distance (CD) as one of the evaluation metrics, which is widely used in many generative models based on discrete representations (such as point clouds) [122,123,124]. The accuracy of the command execution is evaluated by command accuracy (ACCcmd) and parameter accuracy (ACCparam), and the efficiency of the model is also taken into account. Due to the lack of similar CAD generative models at the time, the authors introduced multiple custom variants for comparative experiments to verify the effectiveness of their data encoding method and training method. These variants include the following: Alt-Rel, which is used to express the position of the curve relative to the position of the previous curve in the loop; Alt-Trans, which adds the position information of the loop initial position and the sketch plane origin in the stretch command; Alt-ArcMid, which uses the start, end, and middle points of the arc to define the arc curve; Alt-Regr, which directly regresses all CAD command parameters through the mean square error loss function; and DeepCAD + Aug, which introduces randomly combined CAD command sequences as a data augmentation strategy during the training phase. Specific experimental results are shown in Table 8.

Table 8.
Quantitative evaluation of DeepCAD autoencoder. ↑: the higher the better, ↓: the lower the better.
Chamfer Distance (CD): Calculates the distance metric between two sets of points. It is often used to evaluate the similarity between the generated point cloud and the real point cloud. The smaller the value, the closer the generated point cloud is to the real point cloud.
Command Accuracy (ACCcmd): Measures the proportion of each operation in the generated CAD operation sequence that is correctly executed. The higher the value, the more accurate the CAD operation generated by the model.
Parameter Accuracy (ACCparam): A measure of the closeness between the generated CAD operation parameters (such as size, position, etc.) and the real values. The higher the value, the closer the generated CAD model is to the real design target in terms of parameters.
Invalid Ratio: The proportion of the generated CAD model that cannot be successfully converted into a valid point cloud. It measures the effectiveness of model generation. The lower the value, the higher the quality of the generated CAD model.
9. Conclusions
In this paper, we presented a comprehensive overview of deep learning-based CAD reconstruction. We reviewed the reconstruction methods for CAD models developed over the past decade and classify them based on input type: point clouds, sketches, or others. We also summarized various CAD data representations and highlighted recent works to reflect current progress and research trends. Additionally, we introduced relevant public datasets to support reproducibility and benchmark comparisons.
This paper focused on key tasks such as point cloud reconstruction, sketch generation, and representation modeling. We conducted a systematic analysis of multiple dimensions, including input modalities, representation methods, modeling strategies, and evaluation metrics. By organizing the research landscape and identifying key findings, we constructed a multi-task knowledge framework that addresses the lack of a unified and comprehensive review in this domain.
In terms of data resources, we organized the mainstream public datasets and core evaluation metrics in a structured manner, facilitating better reproducibility and cross-method comparisons. While notable progress has been made in parametric modeling, structural representation, and task integration, challenges remain—such as the scarcity of well-annotated datasets, limited cross-modal modeling, and difficulties in handling complex constraints. To address these issues, we suggest future directions including multi-source data fusion, the incorporation of structural priors, and the enhancement of interactive modeling mechanisms.
Emerging technologies such as Transformer architectures, multimodal fusion, and structural prior learning show great promise for improving model controllability, interpretability, and practical applicability. We advocate for future research to focus on building unified frameworks for CAD reconstruction that enhance both system integration and industrial deployment. Overall, this paper not only summarizes the state-of-the-art advances and key challenges, but also provides a clear research roadmap and methodological guidance for advancing deep learning-based 3D CAD reconstruction towards intelligent design systems.
Author Contributions
Conceptualization, R.L.; methodology, R.L. and Y.J.; formal analysis, Y.J. and M.J.; data curation, W.D. and T.W.; visualization, Y.J.; writing—original draft, Y.J.; writing—review and editing, R.L. and Y.J.; supervision, Y.Z.; project administration, M.J.; funding acquisition, M.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Enterprise Commissioned Research Project (00852405) and the Fuzhou University Graduate Education and Teaching Reform Project (FYJG2023039).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article. The data presented in this study are available in [7,8,9,10,11,30,31,32,49,84,113,115,118,120].
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wu, J.; Zhang, C.; Xue, T.; Freeman, B.; Tenenbaum, J. Learning a probabilistic latent space of object shapes via 3D generative-adversarial modeling. Adv. Neural Inf. Process. Syst. 2016, 29, 82–90. [Google Scholar]
- Fan, H.; Su, H.; Guibas, L.J. A point set generation network for 3D object reconstruction from a single image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 605–613. [Google Scholar]
- Wohlers, T. 3D printing and additive manufacturing state of the industry. In Annual Worldwide Progress Report; Wohlers Associates: Fort Collins, CO, USA, 2014. [Google Scholar]
- Jamróz, W.; Szafraniec, J.; Kurek, M.; Jachowicz, R. 3D printing in pharmaceutical and medical applications–recent achievements and challenges. Pharm. Res. 2018, 35, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Prince, S. Digital Visual Effects in Cinema: The Seduction of Reality; Rutgers University Press: New Brunswick, NJ, USA, 2011. [Google Scholar]
- Galeazzi, F. Towards the definition of best 3D practices in archaeology: Assessing 3D documentation techniques for intra-site data recording. J. Cult. Herit. 2016, 17, 159–169. [Google Scholar] [CrossRef]
- Chang, A.X.; Funkhouser, T.; Guibas, L.; Hanrahan, P.; Huang, Q.; Li, Z.; Savarese, S.; Savva, M.; Song, S.; Su, H.; et al. ShapeNet: An information-rich 3D model repository. arXiv 2015, arXiv:1512.03012. [Google Scholar]
- Koch, S.; Matveev, A.; Jiang, Z.; Williams, F.; Artemov, A.; Burnaev, E.; Alexa, M.; Zorin, D.; Panozzo, D. ABC: A big CAD model dataset for geometric deep learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 9601–9611. [Google Scholar]
- Willis, K.D.; Pu, Y.; Luo, J.; Chu, H.; Du, T.; Lambourne, J.G.; Solar-Lezama, A.; Matusik, W. Fusion 360 gallery: A dataset and environment for programmatic CAD construction from human design sequences. ACM Trans. Graph. TOG 2021, 40, 1–24. [Google Scholar] [CrossRef]
- Wu, R.; Xiao, C.; Zheng, C. DeepCAD: A deep generative network for computer-aided design models. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 6772–6782. [Google Scholar]
- Sharma, G.; Goyal, R.; Liu, D.; Kalogerakis, E.; Maji, S. CSGNet: Neural shape parser for constructive solid geometry. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 5515–5523. [Google Scholar]
- Sharma, G.; Liu, D.; Maji, S.; Kalogerakis, E.; Chaudhuri, S.; Měch, R. ParSeNet: A parametric surface fitting network for 3D point clouds. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part VII 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 261–276. [Google Scholar]
- Guo, H.; Liu, S.; Pan, H.; Liu, Y.; Tong, X.; Guo, B. Complexgen: CAD reconstruction by B-rep chain complex generation. ACM Trans. Graph. TOG 2022, 41, 1–18. [Google Scholar] [CrossRef]
- Jayaraman, P.K.; Lambourne, J.G.; Desai, N.; Willis, K.D.; Sanghi, A.; Morris, N.J. SolidGen: An autoregressive model for direct B-rep synthesis. arXiv 2022, arXiv:2203.13944. [Google Scholar]
- Xu, X.; Willis, K.D.; Lambourne, J.G.; Cheng, C.Y.; Jayaraman, P.K.; Furukawa, Y. SkexGen: Autoregressive generation of CAD construction sequences with disentangled codebooks. arXiv 2022, arXiv:2207.04632. [Google Scholar]
- Jayaraman, P.K.; Sanghi, A.; Lambourne, J.G.; Willis, K.D.; Davies, T.; Shayani, H.; Morris, N. UV-Net: Learning from boundary representations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Virtual, USA, 19–25 June 2021; pp. 11703–11712. [Google Scholar]
- Lambourne, J.G.; Willis, K.D.; Jayaraman, P.K.; Sanghi, A.; Meltzer, P.; Shayani, H. BRepNet: A topological message passing system for solid models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Virtual, USA, 19–25 June 2021; pp. 12773–12782. [Google Scholar]
- Chen, Z.; Tagliasacchi, A.; Zhang, H. BSP-Net: Generating compact meshes via binary space partitioning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 45–54. [Google Scholar]
- Du, T.; Inala, J.P.; Pu, Y.; Spielberg, A.; Schulz, A.; Rus, D.; Solar-Lezama, A.; Matusik, W. InverseCSG: Automatic conversion of 3D models to CSG trees. ACM Trans. Graph. TOG 2018, 37, 1–16. [Google Scholar] [CrossRef]
- Kania, K.; Zieba, M.; Kajdanowicz, T. UCSG-NET-unsupervised discovering of constructive solid geometry tree. Adv. Neural Inf. Process. Syst. 2020, 33, 8776–8786. [Google Scholar]
- Chen, Y.; Lee, H. A neural network system feature recognition for two-dimensional. Int. J. Comput. Integr. Manuf. 1998, 11, 111–117. [Google Scholar] [CrossRef]
- Ding, L.; Yue, Y. Novel ANN-based feature recognition incorporating design by features. Comput. Ind. 2004, 55, 197–222. [Google Scholar] [CrossRef]
- Henderson, M.R.; Srinath, G.; Stage, R.; Walker, K.; Regli, W. Boundary representation-based feature identification. In Manufacturing Research and Technology; Elsevier: Amsterdam, The Netherlands, 1994; Volume 20, pp. 15–38. [Google Scholar]
- Marquez, M.; Gill, R.; White, A. Application of neural networks in feature recognition of mould reinforced plastic parts. Concurr. Eng. 1999, 7, 115–122. [Google Scholar] [CrossRef]
- Cao, W.; Robinson, T.; Hua, Y.; Boussuge, F.; Colligan, A.R.; Pan, W. Graph representation of 3D CAD models for machining feature recognition with deep learning. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Virtual, 17–19 August 2020. [Google Scholar]
- Li, P.; Guo, J.; Zhang, X.; Yan, D.M. SECAD-Net: Self-supervised CAD reconstruction by learning sketch-extrude operations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 18–22 June 2023; pp. 16816–16826. [Google Scholar]
- Ren, D.; Zheng, J.; Cai, J.; Li, J.; Zhang, J. ExtrudeNet: Unsupervised inverse sketch-and-extrude for shape parsing. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 482–498. [Google Scholar]
- Zhou, S.; Tang, T.; Zhou, B. CADParser: A learning approach of sequence modeling for B-rep CAD. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), Macau, China, 19–25 August 2023; International Joint Conferences on Artificial Intelligence Organization: Macau, China, 2023. [Google Scholar]
- Wang, X.; Xu, Y.; Xu, K.; Tagliasacchi, A.; Zhou, B.; Mahdavi-Amiri, A.; Zhang, H. PIE-NET: Parametric inference of point cloud edges. Adv. Neural Inf. Process. Syst. 2020, 33, 20167–20178. [Google Scholar]
- Uy, M.A.; Chang, Y.Y.; Sung, M.; Goel, P.; Lambourne, J.G.; Birdal, T.; Guibas, L.J. Point2Cyl: Reverse engineering 3D objects from point clouds to extrusion cylinders. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–24 June 2022; pp. 11850–11860. [Google Scholar]
- Hu, W.; Zheng, J.; Zhang, Z.; Yuan, X.; Yin, J.; Zhou, Z. PlankAssembly: Robust 3D Reconstruction from Three Orthographic Views with Learnt Shape Programs. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 2–6 October 2023; pp. 18495–18505. [Google Scholar]
- Willis, K.D.; Jayaraman, P.K.; Lambourne, J.G.; Chu, H.; Pu, Y. Engineering sketch generation for computer-aided design. In Proceedings of the IEEE/CVF conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 19–25 June 2021; pp. 2105–2114. [Google Scholar]
- Buonamici, F.; Carfagni, M.; Furferi, R.; Governi, L.; Lapini, A.; Volpe, Y. Reverse engineering modeling methods and tools: A survey. Comput.-Aided Des. Appl. 2018, 15, 443–464. [Google Scholar] [CrossRef]
- Masuda, H. Topological operators and Boolean operations for complex-based nonmanifold geometric models. Comput.-Aided Des. 1993, 25, 119–129. [Google Scholar] [CrossRef]
- Birdal, T.; Busam, B.; Navab, N.; Ilic, S.; Sturm, P. Generic primitive detection in point clouds using novel minimal quadric fits. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 1333–1347. [Google Scholar] [CrossRef]
- Li, L.; Sung, M.; Dubrovina, A.; Yi, L.; Guibas, L.J. Supervised fitting of geometric primitives to 3D point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 2652–2660. [Google Scholar]
- Sommer, C.; Sun, Y.; Bylow, E.; Cremers, D. PrimiTect: Fast continuous hough voting for primitive detection. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; IEEE: Paris, France, 2020; pp. 8404–8410. [Google Scholar]
- Dong, Y.; Xu, B.; Liao, T.; Yin, C.; Tan, Z. Application of local-feature-based 3-D point cloud stitching method of low-overlap point cloud to aero-engine blade measurement. IEEE Trans. Instrum. Meas. 2023, 72, 1–13. [Google Scholar] [CrossRef]
- Deng, J.; Liu, S.; Chen, H.; Chang, Y.; Yu, Y.; Ma, W.; Wang, Y.; Xie, H. A Precise Method for Identifying 3D Circles in Freeform Surface Point Clouds. IEEE Trans. Instrum. Meas. 2025. [Google Scholar] [CrossRef]
- Song, Y.; Huang, G.; Yin, J.; Wang, D. Three-dimensional reconstruction of bubble geometry from single-perspective images based on ray tracing algorithm. Meas. Sci. Technol. 2024, 36, 016010. [Google Scholar] [CrossRef]
- Xu, X.; Fu, X.; Zhao, H.; Liu, M.; Xu, A.; Ma, Y. Three-dimensional reconstruction and geometric morphology analysis of lunar small craters within the patrol range of the Yutu-2 Rover. Remote Sens. 2023, 15, 4251. [Google Scholar] [CrossRef]
- Birdal, T.; Busam, B.; Navab, N.; Ilic, S.; Sturm, P. A minimalist approach to type-agnostic detection of quadrics in point clouds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 3530–3540. [Google Scholar]
- Paschalidou, D.; Ulusoy, A.O.; Geiger, A. Superquadrics Revisited: Learning 3D Shape Parsing beyond Cuboids. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 10396–10405. [Google Scholar]
- Benko, P.; Várady, T. Segmentation methods for smooth point regions of conventional engineering objects. Comput.-Aided Des. 2004, 36, 511–523. [Google Scholar] [CrossRef]
- Xu, X.; Peng, W.; Cheng, C.Y.; Willis, K.D.; Ritchie, D. Inferring CAD modeling sequences using zone graphs. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 6062–6070. [Google Scholar]
- Atzmon, M.; Lipman, Y. SAL: Sign agnostic learning of shapes from raw data. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 2565–2574. [Google Scholar]
- Park, J.J.; Florence, P.; Straub, J.; Newcombe, R.; Lovegrove, S. DeepSDF: Learning continuous signed distance functions for shape representation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 165–174. [Google Scholar]
- Cherenkova, K.; Aouada, D.; Gusev, G. Pvdeconv: Point-voxel deconvolution for autoencoding CAD construction in 3D. In Proceedings of the 2020 IEEE International Conference on Image Processing (ICIP), Abu Dhabi, United Arab Emirates, 25–28 October 2020; IEEE: New York, NY, USA, 2020; pp. 2741–2745. [Google Scholar]
- Yang, B.; Jiang, H.; Pan, H.; Wonka, P.; Xiao, J.; Lin, G. PS-CAD: Local Geometry Guidance via Prompting and Selection for CAD Reconstruction. arXiv 2024, arXiv:2405.15188. [Google Scholar] [CrossRef]
- Kirillov, A.; Mintun, E.; Ravi, N.; Mao, H.; Rolland, C.; Gustafson, L.; Xiao, T.; Whitehead, S.; Berg, A.C.; Lo, W.Y.; et al. Segment anything. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 1–7 October 2023; pp. 4015–4026. [Google Scholar]
- Liu, Y.; D’Aronco, S.; Schindler, K.; Wegner, J.D. PC2WF: 3D wireframe reconstruction from raw point clouds. arXiv 2021, arXiv:2103.02766. [Google Scholar]
- Zhou, Y.; Qi, H.; Zhai, Y.; Sun, Q.; Chen, Z.; Wei, L.Y.; Ma, Y. Learning to reconstruct 3D manhattan wireframes from a single image. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 7698–7707. [Google Scholar]
- Zhou, Y.; Qi, H.; Ma, Y. End-to-end wireframe parsing. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 962–971. [Google Scholar]
- Xue, N.; Wu, T.; Bai, S.; Wang, F.; Xia, G.S.; Zhang, L.; Torr, P.H. Holistically-attracted wireframe parsing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 2788–2797. [Google Scholar]
- Wu, X.; Jiang, L.; Wang, P.S.; Liu, Z.; Liu, X.; Qiao, Y.; Ouyang, W.; He, T.; Zhao, H. Point transformer v3: Simpler faster stronger. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 18–22 June 2024; pp. 4840–4851. [Google Scholar]
- Yin, C.; Wang, B.; Gan, V.J.; Wang, M.; Cheng, J.C. Automated semantic segmentation of industrial point clouds using ResPointNet++. Autom. Constr. 2021, 130, 103874. [Google Scholar] [CrossRef]
- Yu, W.; Shu, J.; Yang, Z.; Ding, H.; Zeng, W.; Bai, Y. Deep learning-based pipe segmentation and geometric reconstruction from poorly scanned point clouds using BIM-driven data alignment. Autom. Constr. 2025, 173, 106071. [Google Scholar] [CrossRef]
- Volk, R.; Stengel, J.; Schultmann, F. Building Information Modeling (BIM) for existing buildings—Literature review and future needs. Autom. Constr. 2014, 38, 109–127. [Google Scholar] [CrossRef]
- Tang, S.; Li, X.; Zheng, X.; Wu, B.; Wang, W.; Zhang, Y. BIM generation from 3D point clouds by combining 3D deep learning and improved morphological approach. Autom. Constr. 2022, 141, 104422. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Kirkpatrick, D.; Seidel, R. On the shape of a set of points in the plane. IEEE Trans. Inf. Theory 1983, 29, 551–559. [Google Scholar] [CrossRef]
- Son, H.; Kim, C. Automatic segmentation and 3D modeling of pipelines into constituent parts from laser-scan data of the built environment. Autom. Constr. 2016, 68, 203–211. [Google Scholar] [CrossRef]
- Jung, J.; Hong, S.; Yoon, S.; Kim, J.; Heo, J. Automated 3D wireframe modeling of indoor structures from point clouds using constrained least-squares adjustment for as-built BIM. J. Comput. Civ. Eng. 2016, 30, 04015074. [Google Scholar] [CrossRef]
- Avetisyan, A.; Dahnert, M.; Dai, A.; Savva, M.; Chang, A.X.; Nießner, M. Scan2CAD: Learning CAD model alignment in rgb-d scans. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 2614–2623. [Google Scholar]
- Pu, J.; Lou, K.; Ramani, K. A 2D sketch-based user interface for 3D CAD model retrieval. Comput.-Aided Des. Appl. 2005, 2, 717–725. [Google Scholar] [CrossRef][Green Version]
- Bonnici, A.; Akman, A.; Calleja, G.; Camilleri, K.P.; Fehling, P.; Ferreira, A.; Hermuth, F.; Israel, J.H.; Landwehr, T.; Liu, J.; et al. Sketch-based interaction and modeling: Where do we stand? AI EDAM 2019, 33, 370–388. [Google Scholar] [CrossRef]
- Lun, Z.; Gadelha, M.; Kalogerakis, E.; Maji, S.; Wang, R. 3D shape reconstruction from sketches via multi-view convolutional networks. In Proceedings of the 2017 International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017; IEEE: New York, NY, USA, 2017; pp. 67–77. [Google Scholar]
- Li, C.; Pan, H.; Bousseau, A.; Mitra, N.J. Sketch2CAD: Sequential CAD modeling by sketching in context. ACM Trans. Graph. TOG 2020, 39, 1–14. [Google Scholar] [CrossRef]
- Huang, H.; Kalogerakis, E.; Yumer, E.; Mech, R. Shape synthesis from sketches via procedural models and convolutional networks. IEEE Trans. Vis. Comput. Graph. 2016, 23, 2003–2013. [Google Scholar] [CrossRef]
- Bae, S.H.; Balakrishnan, R.; Singh, K. ILoveSketch: As-natural-as-possible sketching system for creating 3d curve models. In Proceedings of the 21st Annual ACM Symposium on User Interface Software and Technology (UIST), Monterey, CA, USA, 19–22 October 2008; pp. 151–160. [Google Scholar]
- Han, W.; Xiang, S.; Liu, C.; Wang, R.; Feng, C. SPARE3D: A dataset for spatial reasoning on three-view line drawings. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 14690–14699. [Google Scholar]
- Shin, B.S.; Shin, Y.G. Fast 3D solid model reconstruction from orthographic views. Comput.-Aided Des. 1998, 30, 63–76. [Google Scholar] [CrossRef]
- Nash, C.; Ganin, Y.; Eslami, S.A.; Battaglia, P. PolyGen: An autoregressive generative model of 3D meshes. In Proceedings of the International Conference on Machine Learning (ICML), Washington, DC, USA, 13–18 July 2020; pp. 7220–7229. [Google Scholar]
- Wang, W.; Grinstein, G.G. A survey of 3D solid reconstruction from 2D projection line drawings. In Proceedings of the Computer Graphics Forum, Annaheim, CA, USA, 2–6 August 1993; Wiley Online Library: Hoboken, NJ, USA, 1993; Volume 12, pp. 137–158. [Google Scholar]
- Sakurai, H.; Gossard, D.C. Solid model input through orthographic views. ACM SIGGRAPH Comput. Graph. 1983, 17, 243–252. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st Advances in Neural Information Processing Systems (NeurIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Volume 30, pp. 5998–6008. [Google Scholar]
- Fan, Z.; Zhu, L.; Li, H.; Chen, X.; Zhu, S.; Tan, P. FloorPlanCAD: A large-scale CAD drawing dataset for panoptic symbol spotting. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Virtual Conference, 11–17 October 2021; pp. 10128–10137. [Google Scholar]
- Fan, Z.; Chen, T.; Wang, P.; Wang, Z. Cadtransformer: Panoptic symbol spotting transformer for CAD drawings. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 10986–10996. [Google Scholar]
- Shtof, A.; Agathos, A.; Gingold, Y.; Shamir, A.; Cohen-Or, D. Geosemantic snapping for sketch-based modeling. In Proceedings of the Computer Graphics Forum, Annaheim, CA, USA, 2–6 August 1993; Wiley Online Library: Hoboken, NJ, USA, 2013; Volume 32, pp. 245–253. [Google Scholar]
- Yang, G.; Huang, X.; Hao, Z.; Liu, M.Y.; Belongie, S.; Hariharan, B. PointFlow: 3D point cloud generation with continuous normalizing flows. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 4541–4550. [Google Scholar]
- Wang, N.; Zhang, Y.; Li, Z.; Fu, Y.; Liu, W.; Jiang, Y.G. Pixel2Mesh: Generating 3D mesh models from single rgb images. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 52–67. [Google Scholar]
- Xu, X.; Jayaraman, P.K.; Lambourne, J.G.; Willis, K.D.; Furukawa, Y. Hierarchical neural coding for controllable CAD model generation. arXiv 2023, arXiv:2307.00149. [Google Scholar]
- Yu, F.; Chen, Z.; Li, M.; Sanghi, A.; Shayani, H.; Mahdavi-Amiri, A.; Zhang, H. Capri-Net: Learning compact CAD shapes with adaptive primitive assembly. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 11768–11778. [Google Scholar]
- Geometry, C.S. Neural Shape Parsers for Constructive Solid Geometry. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 1234–1245. [Google Scholar]
- Xu, X.; Lambourne, J.G.; Jayaraman, P.K.; Wang, Z.; Willis, K.D.; Furukawa, Y. BrepGen: A B-rep Generative Diffusion Model with Structured Latent Geometry. arXiv 2024, arXiv:2401.15563. [Google Scholar] [CrossRef]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 2020, 33, 6840–6851. [Google Scholar]
- Jones, B.T.; Hu, M.; Kodnongbua, M.; Kim, V.G.; Schulz, A. Self-supervised representation learning for CAD. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–24 June 2023; pp. 21327–21336. [Google Scholar]
- Druc, S.; Balu, A.; Wooldridge, P.; Krishnamurthy, A.; Sarkar, S. Concept activation vectors for generating user-defined 3D shapes. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 2993–3000. [Google Scholar]
- Camba, J.D.; Contero, M.; Company, P. Parametric CAD modeling: An analysis of strategies for design reusability. Comput.-Aided Des. 2016, 74, 18–31. [Google Scholar] [CrossRef]
- Choi, G.H.; Mun, D.H.; Han, S.H. Exchange of CAD part models based on the macro-parametric approach. Int. J. CAD/CAM 2002, 2, 13–21. [Google Scholar]
- Yan, C.; Vanderhaeghe, D.; Gingold, Y. A benchmark for rough sketch cleanup. ACM Trans. Graph. TOG 2020, 39, 1–14. [Google Scholar] [CrossRef]
- Para, W.; Bhat, S.; Guerrero, P.; Kelly, T.; Mitra, N.; Guibas, L.J.; Wonka, P. SketchGen: Generating constrained CAD sketches. Adv. Neural Inf. Process. Syst. 2021, 34, 5077–5088. [Google Scholar]
- Ganin, Y.; Bartunov, S.; Li, Y.; Keller, E.; Saliceti, S. Computer-aided design as language. Adv. Neural Inf. Process. Syst. 2021, 34, 5885–5897. [Google Scholar]
- Seff, A.; Zhou, W.; Richardson, N.; Adams, R.P. Vitruvion: A generative model of parametric CAD sketches. arXiv 2021, arXiv:2109.14124. [Google Scholar]
- Xu, P.; Fu, H.; Zheng, Y.; Singh, K.; Huang, H.; Tai, C.L. Model-guided 3D sketching. IEEE Trans. Vis. Comput. Graph. 2018, 25, 2927–2939. [Google Scholar] [CrossRef]
- Karadeniz, A.S.; Mallis, D.; Mejri, N.; Cherenkova, K.; Kacem, A.; Aouada, D. DAVINCI: A Single-Stage Architecture for Constrained CAD Sketch Inference. arXiv 2024, arXiv:2410.22857. [Google Scholar]
- Sarcar, M.; Rao, K.M.; Narayan, K.L. Computer Aided Design and Manufacturing; PHI Learning Pvt. Ltd.: Delhi, India, 2008. [Google Scholar]
- Radhakrishnan, P.; Subramanyan, S.; Raju, V. Cad/Cam/Cim; New Age International: Delhi, India, 2008. [Google Scholar]
- Ansaldi, S.; De Floriani, L.; Falcidieno, B. Geometric modeling of solid objects by using a face adjacency graph representation. ACM SIGGRAPH Comput. Graph. 1985, 19, 131–139. [Google Scholar] [CrossRef]
- Ming, H.; Yanzhu, D.; Jianguang, Z.; Yong, Z. A topological enabled three-dimensional model based on constructive solid geometry and boundary representation. Clust. Comput. 2016, 19, 2027–2037. [Google Scholar] [CrossRef]
- Pottmann, H.; Leopoldseder, S.; Hofer, M.; Steiner, T.; Wang, W. Industrial geometry: Recent advances and applications in CAD. Comput.-Aided Des. 2005, 37, 751–766. [Google Scholar] [CrossRef]
- Stroud, I.; Nagy, H. Solid Modelling and CAD Systems: How to Survive a CAD System; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Lou, Y.; Li, X.; Chen, H.; Zhou, X. BRep-BERT: Pre-training boundary representation BERT with sub-graph node contrastive learning. In Proceedings of the 32nd ACM International Conference on Information and Knowledge Management, Birmingham, UK, 21–25 October 2023; pp. 1657–1666. [Google Scholar]
- Morovič, L.; Milde, J. CAD model created from polygon mesh. Appl. Mech. Mater. 2015, 808, 233–238. [Google Scholar] [CrossRef]
- Botsch, M.; Pauly, M.; Kobbelt, L.; Alliez, P.; Lévy, B.; Bischoff, S.; Röossl, C. Geometric Modeling Based on Polygonal Meshes. Technical Report, INRIA. 2007. Available online: https://hal.inria.fr/inria-00186820 (accessed on 30 March 2025).
- Guo, J.; Ding, F.; Jia, X.; Yan, D.M. Automatic and high-quality surface mesh generation for CAD models. Comput.-Aided Des. 2019, 109, 49–59. [Google Scholar] [CrossRef]
- Ebert, D.S.; Musgrave, F.K.; Peachey, D.; Perlin, K.; Worley, S. Texturing and Modeling: A Procedural Approach; Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Safdar, M.; Jauhar, T.A.; Kim, Y.; Lee, H.; Noh, C.; Kim, H.; Lee, I.; Kim, I.; Kwon, S.; Han, S. Feature-based translation of CAD models with macro-parametric approach: Issues of feature mapping, persistent naming, and constraint translation. J. Comput. Des. Eng. 2020, 7, 603–614. [Google Scholar] [CrossRef]
- Howard, E.; Musto, J. Introduction to Solid Modeling Using Solidworks; McGraw-Hill Inc.: New York, NY, USA, 2005. [Google Scholar]
- Shapiro, V.; Vossler, D.L. Construction and optimization of CSG representations. Comput.-Aided Des. 1991, 23, 4–20. [Google Scholar] [CrossRef]
- Yu, F.; Chen, Q.; Tanveer, M.; Mahdavi Amiri, A.; Zhang, H. D2CSG: Unsupervised learning of compact CSG trees with dual complements and dropouts. Adv. Neural Inf. Process. Syst. 2023, 36, 22807–22819. [Google Scholar]
- Gryaditskaya, Y.; Sypesteyn, M.; Hoftijzer, J.W.; Pont, S.C.; Durand, F.; Bousseau, A. OpenSketch: A richly-annotated dataset of product design sketches. ACM Trans. Graph. 2019, 38, 232-1. [Google Scholar] [CrossRef]
- Liao, R.; Li, Y.; Song, Y.; Wang, S.; Hamilton, W.; Duvenaud, D.K.; Urtasun, R.; Zemel, R. Efficient graph generation with graph recurrent attention networks. Adv. Neural Inf. Process. Syst. 2019, 32, 4257–4267. [Google Scholar]
- Seff, A.; Ovadia, Y.; Zhou, W.; Adams, R.P. Sketchgraphs: A large-scale dataset for modeling relational geometry in computer-aided design. arXiv 2020, arXiv:2007.08506. [Google Scholar]
- Yi, L.; Kim, V.G.; Ceylan, D.; Shen, I.C.; Yan, M.; Su, H.; Lu, C.; Huang, Q.; Sheffer, A.; Guibas, L. A scalable active framework for region annotation in 3D shape collections. ACM Trans. Graph. ToG 2016, 35, 1–12. [Google Scholar] [CrossRef]
- Dupont, E.; Cherenkova, K.; Kacem, A.; Ali, S.A.; Arzhannikov, I.; Gusev, G.; Aouada, D. Cadops-net: Jointly learning CAD operation types and steps from boundary-representations. In Proceedings of the 2022 International Conference on 3D Vision (3DV), Prague, Czech Republic, 12–15 September 2022; pp. 114–123. [Google Scholar]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3D shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1912–1920. [Google Scholar]
- Mo, K.; Zhu, S.; Chang, A.X.; Yi, L.; Tripathi, S.; Guibas, L.J.; Su, H. PartNet: A large-scale benchmark for fine-grained and hierarchical part-level 3D object understanding. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 909–918. [Google Scholar]
- Colligan, A.R.; Robinson, T.T.; Nolan, D.C.; Hua, Y.; Cao, W. Hierarchical CADNet: Learning from B-reps for machining feature recognition. Comput.-Aided Des. 2022, 147, 103226. [Google Scholar] [CrossRef]
- MFCAD: A Dataset of 3D CAD Models with Machining Feature Labels. 2021. Available online: https://github.com/hducg/MFCAD (accessed on 14 June 2021).
- Willis, K.D.; Jayaraman, P.K.; Chu, H.; Tian, Y.; Li, Y.; Grandi, D.; Sanghi, A.; Tran, L.; Lambourne, J.G.; Solar-Lezama, A.; et al. Joinable: Learning bottom-up assembly of parametric CAD joints. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–24 June 2022; pp. 15849–15860. [Google Scholar]
- Cazals, F.; Pouget, M. Estimating differential quantities using polynomial fitting of osculating jets. Comput. Aided Geom. Des. 2005, 22, 121–146. [Google Scholar] [CrossRef]
- Achlioptas, P.; Diamanti, O.; Mitliagkas, I.; Guibas, L. Learning representations and generative models for 3D point clouds. In Proceedings of the International Conference on Machine Learning (ICML), Stockholm, Sweden, 10–15 July 2018; pp. 40–49. [Google Scholar]
- Groueix, T.; Fisher, M.; Kim, V.G.; Russell, B.C.; Aubry, M. A papier-mâché approach to learning 3D surface generation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 216–224. [Google Scholar]
- Chen, Z.; Zhang, H. Learning implicit fields for generative shape modeling. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 5939–5948. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).