A Study on Denoising Autoencoder Noise Selection for Improving the Fault Diagnosis Rate of Vibration Time Series Data
Abstract
1. Introduction
1.1. Research Background and Motivation
1.2. Related Work
1.3. Research Objectives
2. Methodology
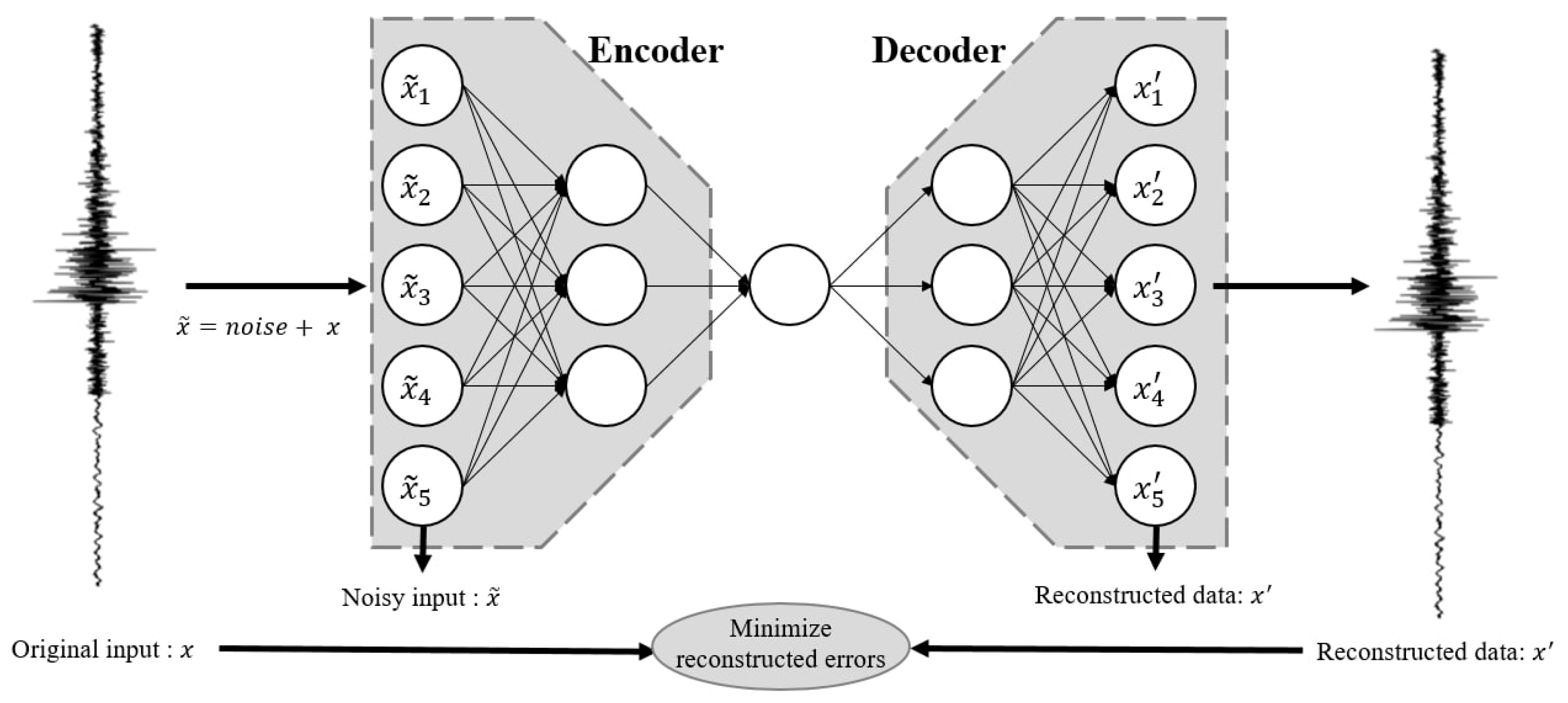
2.1. Denoising Autoencoder (DAE)
2.2. Feature Extraction
2.2.1. Mean
2.2.2. Root Mean Square (RMS)
2.2.3. Standard Deviation (STD)
2.2.4. Kurtosis
2.2.5. Skewness
2.3. One-Class Support Vector Machine
3. Preliminary Study
3.1. Dataset
3.2. Result of Noise Reduction
3.3. Result of Feature Extraction
3.4. Result of Classification
4. Case Study
4.1. Result of Noise Generation
4.2. Result of Noise Reduction (Highpass)
4.3. Result of Feature Extaction
4.4. Result of Classification (Highpass)
4.5. Final Comparative Analysis of Results
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tran, T.; Bader, S.; Lundgren, J. Denoising Induction Motor Sounds Using an Autoencoder. In Proceedings of the 2023 IEEE Sensors Applications Symposium (SAS), Ottawa, ON, Canada, 18–20 July 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Miranda-González, A.A.; Rosales-Silva, A.J.; Mújica-Vargas, D.; Escamilla-Ambrosio, P.J.; Gallegos-Funes, F.J.; Vianney-Kinani, J.M.; Velázquez-Lozada, E.; Pérez-Hernández, L.M.; Lozano-Vázquez, L.V. Denoising Vanilla Autoencoder for RGB and GS Images with Gaussian Noise. Entropy 2023, 25, 1467. [Google Scholar] [CrossRef] [PubMed]
- Rubin-Falcone, H.; Lee, J.M.; Wiens, J. Denoising Autoencoders for Learning from Noisy Patient-Reported Data. In Proceedings of the Conference on Health, Inference, and Learning, Cambridge, MA, USA, 22 June 2023; Volume 209, pp. 393–409. Available online: https://proceedings.mlr.press/v209/rubin-falcone23a.html (accessed on 16 April 2025).
- Zhou, S.; Zha, D.; Shen, X.; Huang, X.; Zhang, R.; Chung, K. Denoising-Aware Contrastive Learning for Noisy Time Series. In Proceedings of the 33rd International Joint Conference on Artificial Intelligence (IJCAI-24), Jeju, Republic of Korea, 3–9 August 2024; pp. 5644–5652. [Google Scholar] [CrossRef]
- Bakir, A.; Demircioğlu, U.; Yıldız, S. A Deep Learning-Based Approach for Image Denoising: Harnessing Autoencoders for Removing Gaussian and Salt-Pepper Noises. In Proceedings of the 4th International Artificial Intelligence and Data Science Congress, Izmir, Turkey, 14–15 March 2024. [Google Scholar]
- Kim, K.; Lee, J. Adaptive Scheme of Denoising Autoencoder for Estimating Indoor Localization Based on RSSI Analytics in BLE Environment. Sensors 2023, 23, 5544. [Google Scholar] [CrossRef] [PubMed]
- Alvarado, W.; Agrawal, V.; Li, W.S.; Dravid, V.P.; Backman, V.; de Pablo, J.J.; Ferguson, A.L. Denoising Autoencoder Trained on Simulation-Derived Structures for Noise Reduction in Chromatin Scanning Transmission Electron Microscopy. ACS Cent. Sci. 2023, 9, 1200–1212. [Google Scholar] [CrossRef] [PubMed]
- Fang, C.; Chen, Y.; Deng, X.; Lin, X.; Han, Y.; Zheng, J. Denoising Method of Machine Tool Vibration Signal Based on Variational Mode Decomposition and Whale-Tabu Optimization Algorithm. Sci. Rep. 2023, 13, 1505. [Google Scholar] [CrossRef]
- Shen, H.; George, D.; Huerta, E.A.; Zhao, Z. Denoising Gravitational Waves with Enhanced Deep Recurrent Denoising Auto-Encoders. In Proceedings of the 2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 3237–3241. [Google Scholar] [CrossRef]
- Mohanty, R.K.; Soni, V.; Pradhan, P. Environmental Noise Removal from Induction Motor Acoustic Signals Using Denoising Autoencoder. arXiv 2022, arXiv:2208.04462. [Google Scholar] [CrossRef]
- Chen, H.; Jin, C.; Xu, Y.; Liu, F. Adaptive Denoising Autoencoder for Distance-Dependent Noise Reduction in BLE RSSI Data. Sensors 2023, 23, 5631. [Google Scholar] [CrossRef]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P.A. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Erhan, D.; Courville, A.; Bengio, Y. Why does unsupervised pre-training help deep learning. J. Mach. Learn. Res. 2010, 11, 625–660. [Google Scholar]
- Jia, F.; Lei, Y.; Lin, J.; Zhou, X.; Lu, N. Deep neural networks: A promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data. Mech. Syst. Signal Process. 2016, 72–73, 303–315. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Jardine, A.K.S.; Lin, D.; Banjevic, D. A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mech. Syst. Signal Process. 2006, 20, 1483–1510. [Google Scholar] [CrossRef]
- Randall, R.B.; Antoni, J. Rolling element bearing diagnostics—A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Scholkopf, B.; Platt, J.C.; Shawe-Taylor, J.; Smola, A.J.; Williamson, R.C. Estimating the support of a high-dimensional distribution. Neural Comput. 2001, 13, 1443–1471. [Google Scholar] [CrossRef] [PubMed]
- Tax, D.M.; Duin, R.P. Support vector data description. Mach. Learn. 2004, 54, 45–66. [Google Scholar] [CrossRef]
- Ma, J.; Perkins, S. Time-series novelty detection using one-class support vector machines. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Portland, OR, USA, 20–24 July 2003; pp. 1741–1745. [Google Scholar] [CrossRef]
- Widodo, A.; Yang, B.S. Support vector machine in machine condition monitoring and fault diagnosis. Mech. Syst. Signal Process. 2007, 21, 2560–2574. [Google Scholar] [CrossRef]
- Jang, J.G.; Noh, C.M.; Kim, S.S.; Shin, S.C.; Lee, S.S.; Lee, J.C. Vibration data feature extraction and deep learning-based preprocessing method for highly accurate motor fault diagnosis. J. Comput. Des. Eng. 2023, 10, 204–220. [Google Scholar] [CrossRef]
- Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]











| Gaussian Noise | Actual Answer (Unit: Case) | Running Rate | Failure Rate | |||
|---|---|---|---|---|---|---|
| Normal | Failure | |||||
| Classification results by feature | Mean | Normal | 7303 | 497 | 93.63% | 100% |
| Failure | 0 | 7800 | ||||
| RMS | Normal | 7292 | 508 | 93.49% | 100% | |
| Failure | 0 | 7800 | ||||
| Standard Deviation | Normal | 7300 | 500 | 93.59% | 98.69% | |
| Failure | 102 | 7698 | ||||
| Skewness | Normal | 7313 | 487 | 93.76% | 95.77% | |
| Failure | 330 | 7470 | ||||
| Kurtosis | Normal | 7254 | 546 | 93% | 26.22% | |
| Failure | 5755 | 2045 | ||||
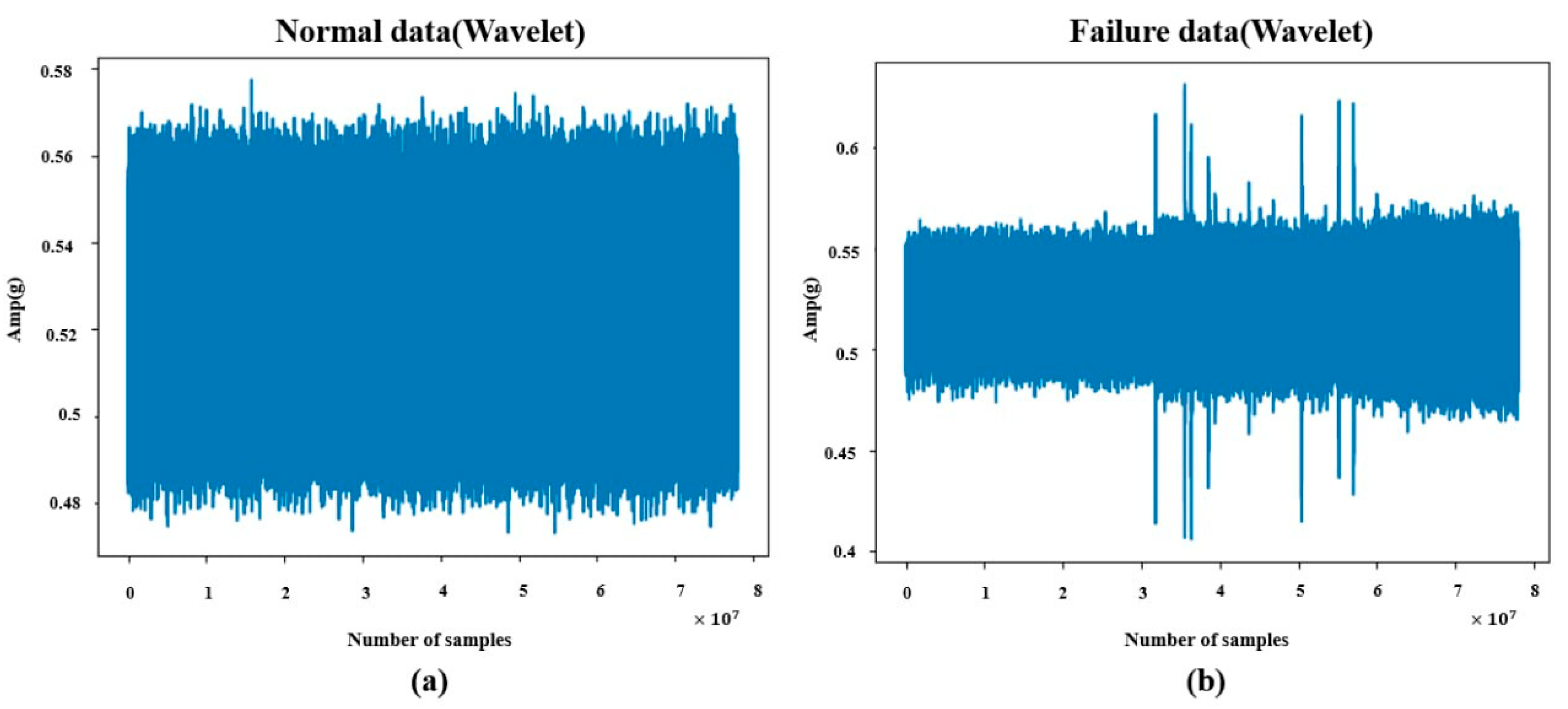
| Wavelet Transform | Actual Answer (Unit: Case) | Running Rate | Failure Rate | |||
|---|---|---|---|---|---|---|
| Normal | Failure | |||||
| Classification results by feature | Mean | Normal | 7565 | 235 | 96.99% | 1.41% |
| Failure | 7690 | 110 | ||||
| RMS | Normal | 7066 | 733 | 90.6% | 9.63% | |
| Failure | 7049 | 751 | ||||
| Standard Deviation | Normal | 7177 | 683 | 91.24% | 51.86% | |
| Failure | 3755 | 5045 | ||||
| Skewness | Normal | 7307 | 493 | 93.68% | 10.92% | |
| Failure | 6948 | 852 | ||||
| Kurtosis | Normal | 7323 | 477 | 93.88% | 11.63% | |
| Failure | 6893 | 907 | ||||
| High-Pass Noise | Actual Answer (Unit: Case) | Running Rate | Failure Rate | |||
|---|---|---|---|---|---|---|
| Normal | Failure | |||||
| Classification results by feature | Mean | Normal | 7331 | 469 | 94% | 100% |
| Failure | 0 | 7800 | ||||
| RMS | Normal | 7173 | 627 | 92% | 100% | |
| Failure | 0 | 7800 | ||||
| Standard Deviation | Normal | 7029 | 771 | 90.1% | 100% | |
| Failure | 0 | 7800 | ||||
| Skewness | Normal | 7331 | 469 | 94% | 68.6% | |
| Failure | 2453 | 5347 | ||||
| Kurtosis | Normal | 7411 | 389 | 95% | 99.5% | |
| Failure | 37 | 7763 | ||||
| Gaussian Noise | Precision | Recall | F1-Score | F1-Score Average | |
|---|---|---|---|---|---|
| Feature | Mean | 0.936 | 1 | 0.967 | 0.9074 |
| RMS | 0.935 | 1 | 0.966 | ||
| Standard Deviation | 0.936 | 0.986 | 0.96 | ||
| Skewness | 0.938 | 0.957 | 0.947 | ||
| Kurtosis | 0.93 | 0.558 | 0.697 | ||
| Wavelet Transform | Precision | Recall | F1-Score | F1-Score Average | |
|---|---|---|---|---|---|
| Feature | Mean | 0.986 | 0.496 | 0.66 | 0.6456 |
| RMS | 0.904 | 0.501 | 0.644 | ||
| Standard Deviation | 0.587 | 0.3657 | 0.62 | ||
| Skewness | 0.896 | 0.513 | 0.652 | ||
| Kurtosis | 0.89 | 0.515 | 0.652 | ||
| High-Pass Noise | Precision | Recall | F1-Score | F1-Score Average | |
|---|---|---|---|---|---|
| Feature | Mean | 0.94 | 1 | 0.97 | 0.9367 |
| RMS | 0.92 | 1 | 0.958 | ||
| Standard Deviation | 0.901 | 1 | 0.948 | ||
| Skewness | 0.94 | 0.749 | 0.834 | ||
| Kurtosis | 0.95 | 0.995 | 0.972 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jang, J.-g.; Lee, S.-s.; Hwang, S.-Y.; Lee, J.-c. A Study on Denoising Autoencoder Noise Selection for Improving the Fault Diagnosis Rate of Vibration Time Series Data. Appl. Sci. 2025, 15, 6523. https://doi.org/10.3390/app15126523
Jang J-g, Lee S-s, Hwang S-Y, Lee J-c. A Study on Denoising Autoencoder Noise Selection for Improving the Fault Diagnosis Rate of Vibration Time Series Data. Applied Sciences. 2025; 15(12):6523. https://doi.org/10.3390/app15126523
Chicago/Turabian StyleJang, Jun-gyo, Soon-sup Lee, Se-Yun Hwang, and Jae-chul Lee. 2025. "A Study on Denoising Autoencoder Noise Selection for Improving the Fault Diagnosis Rate of Vibration Time Series Data" Applied Sciences 15, no. 12: 6523. https://doi.org/10.3390/app15126523
APA StyleJang, J.-g., Lee, S.-s., Hwang, S.-Y., & Lee, J.-c. (2025). A Study on Denoising Autoencoder Noise Selection for Improving the Fault Diagnosis Rate of Vibration Time Series Data. Applied Sciences, 15(12), 6523. https://doi.org/10.3390/app15126523








