Synthesizing Time-Series Gene Expression Data to Enhance Network Inference Performance Using Autoencoder
Abstract
1. Introduction
2. Materials and Methods
2.1. Discretized Network Model
2.2. Network Inference Problem
2.3. Structural Performance Metrics
2.4. Network Inference Method
2.5. Autoencoder Model
3. Our Proposed Method
3.1. Synthesis of Gene Expression
3.2. Inference of GRN
4. Experimental Results
4.1. Experiment Setup
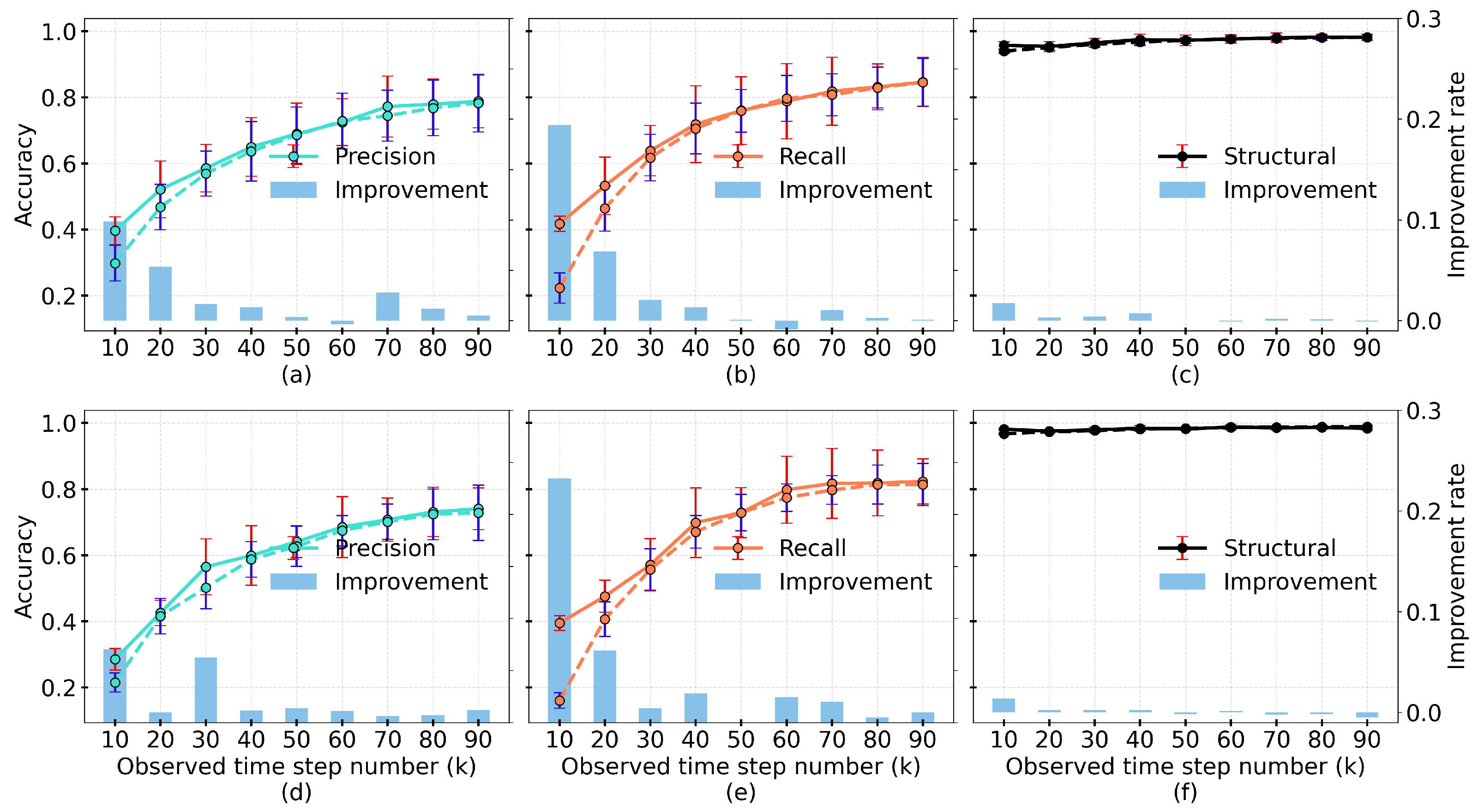
4.2. Results of Structural Performance
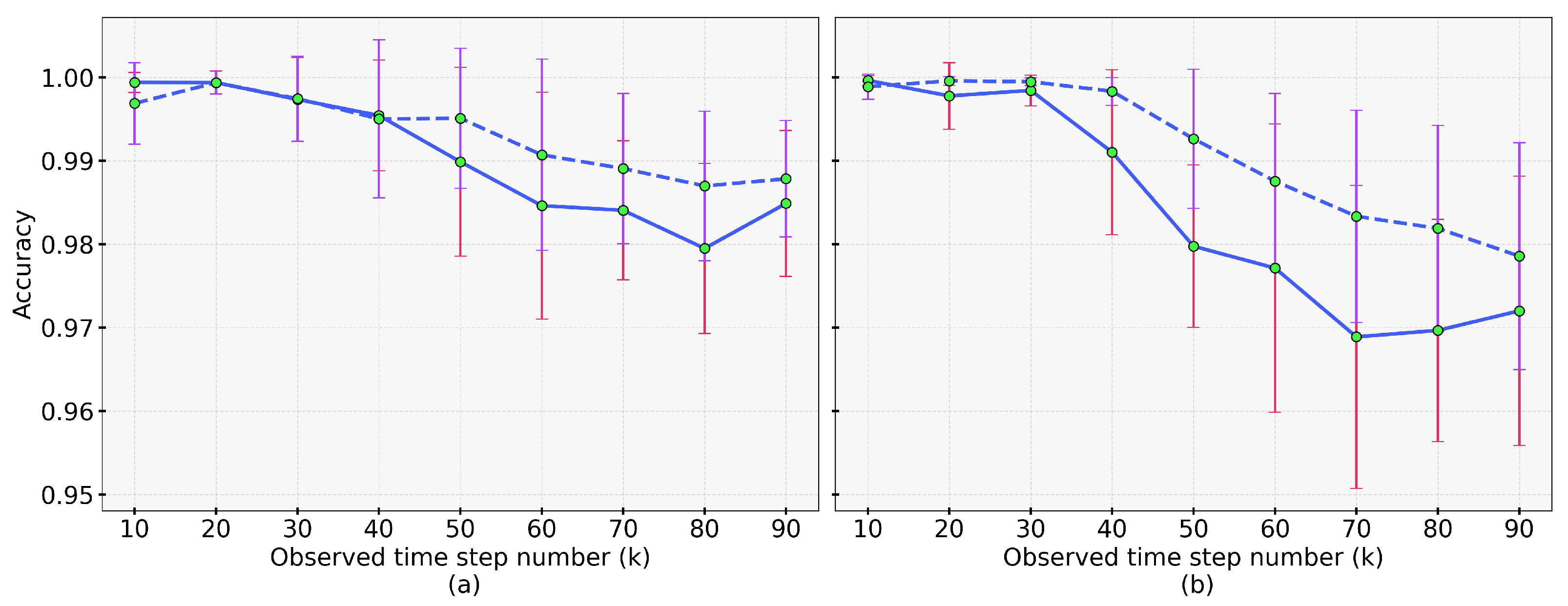
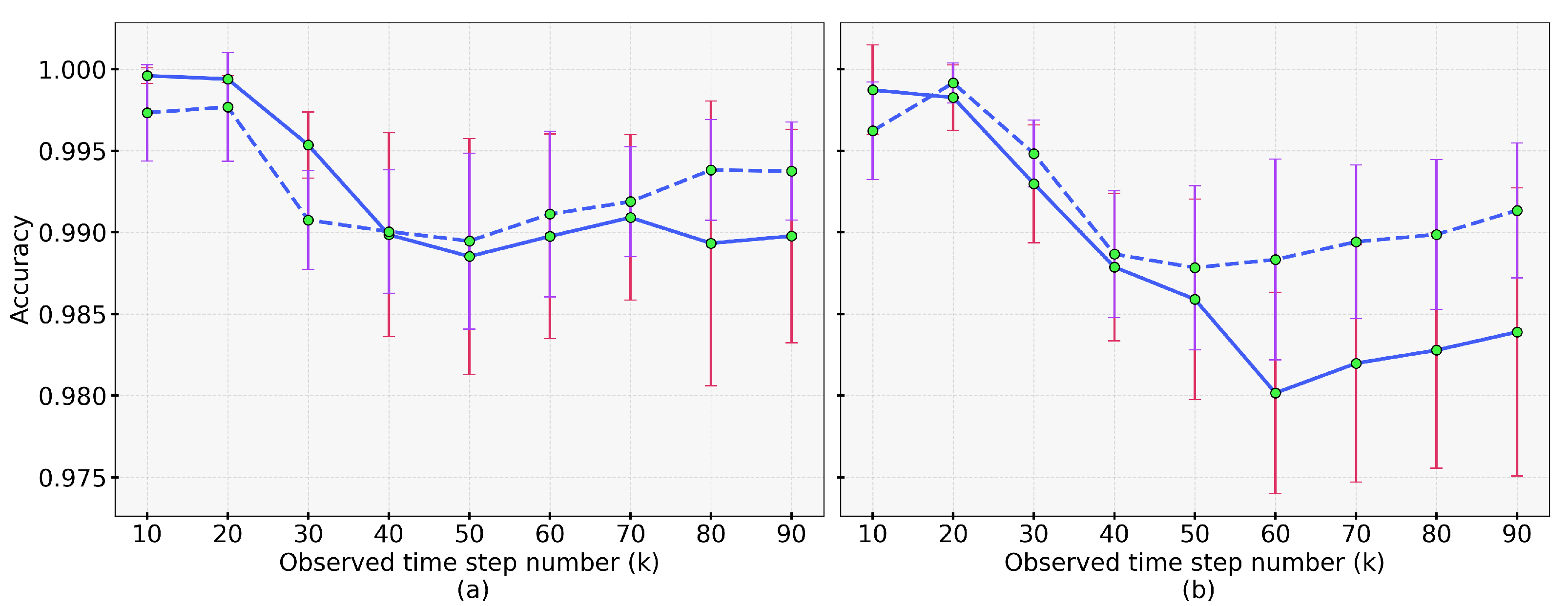
4.3. Results of Dynamic Accuracy
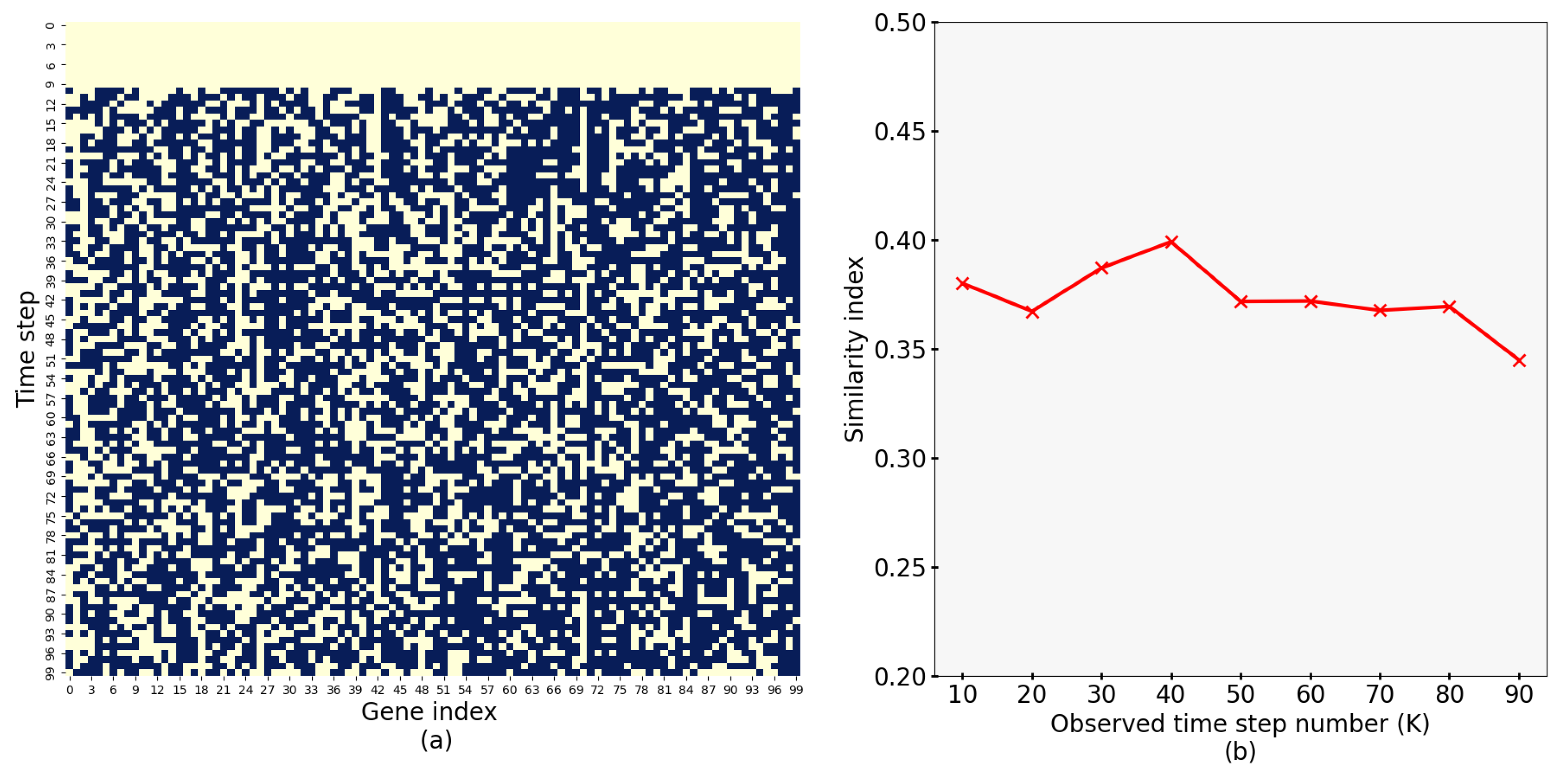
4.4. Results of Similarity of Synthesized Expressions
5. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Malvina, M.; Pancaldi, V. From time-series transcriptomics to gene regulatory networks: A review on inference methods. PLoS Comput. Biol. 2023, 19, e1011254. [Google Scholar]
- Margolin, A.A.; Nemenman, I.; Basso, K.; Wiggins, C.; Stolovitzky, G.; Favera, R.D.; Califano, A. ARACNE: An Algorithm for the Reconstruction of Gene Regulatory Networks in a Mammalian Cellular Context. BMC Bioinform. 2006, 7 (Suppl. 1), S7. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Xu, Y.; Maxwell, A.; Koh, W.; Gong, P.; Zhang, C. MICRAT: A novel algorithm for inferring gene regulatory networks using time series gene expression data. BMC Syst. Biol. 2018, 12, 19–29. [Google Scholar] [CrossRef]
- Liang, K.; Wang, X. Gene regulatory network reconstruction using conditional mutual information. EURASIP J. Bioinform. Syst. Biol. 2008, 2008, 253894. [Google Scholar] [CrossRef]
- Huynh-Thu, V.A.; Irrthum, A.; Wehenkel, L.; Geurts, P. Inferring regulatory networks from expression data using tree-based methods. PLoS ONE 2010, 5, e12776. [Google Scholar] [CrossRef]
- Petralia, F.; Wang, P.; Yang, J.; Tu, Z. Integrative random forest for gene regulatory network inference. Bioinformatics 2015, 31, i197–i205. [Google Scholar] [CrossRef]
- Park, S.; Kim, J.M.; Shin, W.; Han, S.W.; Jeon, M.; Jang, H.J.; Jang, I.S.; Kang, J. BTNET: Boosted tree-based gene regulatory network inference algorithm using time-course measurement data. BMC Syst. Biol. 2018, 12, 20. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Mundra, P.A.; Zhao, L.N.; Lin, F.; Zheng, J. Highly sensitive inference of time-delayed gene regulation by network deconvolution. BMC Syst. Biol. 2014, 8, S6. [Google Scholar] [CrossRef] [PubMed]
- Siegal-Gaskins, D.; Ash, J.N.; Crosson, S. Model-based deconvolution of cell cycle time-series data reveals gene expression details at high resolution. PLoS Comput. Biol. 2009, 5, e1000460. [Google Scholar] [CrossRef]
- Trinh, H.C.; Kwon, Y.K. A novel constrained genetic algorithm-based Boolean network inference method from steady-state gene expression data. Bioinformatics 2021, 37 (Suppl. 1), i383–i391. [Google Scholar] [CrossRef]
- Hickman, G.J.; Hodgman, T.C. Inference of gene regulatory networks using boolean-network inference methods. J. Bioinform. Comput. Biol. 2009, 7, 1013–1029. [Google Scholar] [CrossRef] [PubMed]
- Ma, B.; Fang, M.; Jiao, X. Inference of gene regulatory networks based on nonlinear ordinary differential equations. Bioinformatics 2020, 36, 4885–4893. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Li, P.; Krishnan, A.; Liu, J. Large-scale dynamic gene regulatory network inference combining differential equation models with local dynamic Bayesian network analysis. Bioinformatics 2011, 27, 2686–2691. [Google Scholar] [CrossRef] [PubMed]
- Aalto, A.; Viitasaari, L.; Ilmonen, P.; Mombaerts, L.; Gonçalves, J. Gene regulatory network inference from sparsely sampled noisy data. Nat. Commun. 2020, 11, 3493. [Google Scholar] [CrossRef]
- Bin, Y.; Chen, Y. Overview of gene regulatory network inference based on differential equation models. Curr. Protein Pept. Sci. 2020, 21, 1054–1059. [Google Scholar]
- Thorne, T. Approximate inference of gene regulatory network models from RNA-Seq time series data. BMC Bioinform. 2018, 19, 127. [Google Scholar] [CrossRef]
- Michailidis, G.; d’Alché-Buc, F. Autoregressive models for gene regulatory network inference: Sparsity, stability and causality issues. Math. Biosci. 2013, 246, 326–334. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Murphy, K.; Mian, S. Modelling Gene Expression Data Using Dynamic Bayesian Networks; Technical Report; Computer Science Division, University of California: Berkeley, CA, USA, 1999. [Google Scholar]
- Kim, S.Y.; Imoto, S.; Miyano, S. Inferring gene networks from time series microarray data using dynamic Bayesian networks. Brief. Bioinform. 2003, 4, 228–235. [Google Scholar] [CrossRef]
- Zou, M.; Conzen, S.D. A new dynamic Bayesian network (DBN) approach for identifying gene regulatory networks from time-course microarray data. Bioinformatics 2005, 21, 71–79. [Google Scholar] [CrossRef]
- Murphy, D. Gene expression studies using microarrays: Principles, problems, and prospects. Adv. Physiol. Educ. 2002, 26, 256–270. [Google Scholar] [CrossRef] [PubMed]
- Waqas, N.; Safie, S.I.; Kadir, K.A.; Khan, S.; Khel, M.H.K. DEEPFAKE Image Synthesis for Data Augmentation. IEEE Access 2022, 10, 80847–80857. [Google Scholar] [CrossRef]
- Frid-Adar, M.; Klang, E.; Amitai, M.; Goldberger, J.; Greenspan, H. Synthetic data augmentation using GAN for improved liver lesion classification. In Proceedings of the 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018), Washington, DC, USA, 4–7 April 2018; pp. 289–293. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Q.; Hu, B. MinimalGAN: Diverse medical image synthesis for data augmentation using minimal training data. Appl. Intell. 2023, 53, 3899–3916. [Google Scholar] [CrossRef]
- Shin, H.C.; Tenenholtz, N.A.; Rogers, J.K.; Schwarz, C.G.; Senjem, M.L.; Gunter, J.L.; Andriole, K.P.; Michalski, M. Medical Image Synthesis for Data Augmentation and Anonymization Using Generative Adversarial Networks. In Simulation and Synthesis in Medical Imaging; Gooya, A., Goksel, O., Oguz, I., Burgos, N., Eds.; SASHIMI 2018; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2018; Volume 11037. [Google Scholar] [CrossRef]
- Forestier, G.; Petitjean, F.; Dau, H.A.; Webb, G.I.; Keogh, E. Generating Synthetic Time Series to Augment Sparse Datasets. In Proceedings of the 2017 IEEE International Conference on Data Mining (ICDM), New Orleans, LA, USA, 9–12 December 2017; pp. 865–870. [Google Scholar] [CrossRef]
- Maweu, B.M.; Shamsuddin, R.; Dakshit, S.; Prabhakaran, B. Generating Healthcare Time Series Data for Improving Diagnostic Accuracy of Deep Neural Networks. IEEE Trans. Instrum. Meas. 2021, 70, 2508715. [Google Scholar] [CrossRef]
- Leznik, M.; Michalsky, P.; Willis, P.; Schanzel, B.; Östberg, P.O.; Domaschka, J. Multivariate Time Series Synthesis Using Generative Adversarial Networks. In Proceedings of the ACM/SPEC International Conference on Performance Engineering, ICPE ’21, New York, NY, USA, 19–23 April 2021; pp. 43–50. [Google Scholar] [CrossRef]
- Schaffter, T.; Marbach, D.; Floreano, D. GeneNetWeaver: In silico benchmark generation and performance profiling of network inference methods. Bioinformatics 2011, 27, 2263–2270. [Google Scholar] [CrossRef]
- DREAM. Dream: Dialogue for Reverse Engineering Assessments and Methods. 2009. Available online: https://gnw.sourceforge.net/dreamchallenge.html (accessed on 15 November 2010).
- Albert, I.; Thakar, J.; Li, S.; Zhang, R.; Albert, R. Boolean network simulations for life scientists. Source Code Biol. Med. 2008, 3, 16. [Google Scholar] [CrossRef]
- de Jong, H. Modeling and simulation of genetic regulatory systems: A literature review. J. Comput. Biol. 2002, 9, 67–103. [Google Scholar] [CrossRef]
- De Jong, H.; Geiselmann, J.; Hernandez, C.; Page, M. Genetic Network Analyzer: Qualitative simulation of genetic regulatory networks. Bioinformatics 2003, 19, 336–344. [Google Scholar] [CrossRef]
- Mendes, P.; Sha, W.; Ye, K. Artificial gene networks for objective comparison of analysis algorithms. Bioinformatics 2003, 19 (Suppl. 2), ii22–ii29. [Google Scholar] [CrossRef]
- Van den Bulcke, T.; Van Leemput, K.; Naudts, B.; van Remortel, P.; Ma, H.; Verschoren, A.; De Moor, B.; Marchal, K. SynTReN: A generator of synthetic gene expression data for design and analysis of structure learning algorithms. BMC Bioinform. 2006, 7, 43. [Google Scholar] [CrossRef]
- Martins Lopes, F.; Marcondes, R.M., Jr.; da Fontaura Costa, L. Gene expression complex networks: Synthesis, identification, and analysis. J. Comput. Biol. 2011, 18, 1353–1367. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Arjovsky, M.; Bottou, L. Towards Principled Methods for Training Generative Adversarial Networks. arXiv 2017, arXiv:1701.04862. [Google Scholar] [CrossRef]
- Salimans, T.; Goodfellow, I.; Zaremba, W.; Cheung, V.; Radford, A.; Chen, X. Improved Techniques for Training GANs. arXiv 2016, arXiv:1606.03498. [Google Scholar] [CrossRef]
- Tan, J.; Ung, M.; Cheng, C.; Greene, C.S. Unsupervised feature construction and knowledge extraction from genome-wide assays of breast cancer with denoising autoencoders. Pac. Symp. Biocomput. 2015, 20, 132–143. [Google Scholar] [PubMed] [PubMed Central]
- Chen, L.; Cai, C.; Chen, V.; Lu, X. Learning a hierarchical representation of the yeast transcriptomic machinery using an autoencoder model. BMC Bioinform. 2016, 17 (Suppl. 1), S9. [Google Scholar] [CrossRef]
- Anh, C.-T.; Kwon, Y.-K. Mutual Information Based on Multiple Level Discretization Network Inference from Time Series Gene Expression Profiles. Appl. Sci. 2023, 13, 11902. [Google Scholar] [CrossRef]
- Kauffman, S.A. Gene regulation networks: A theory for their structure and global behavior. In Current Topics in Developmental Biology 6; Moscana, A., Monroy, A., Eds.; Academic Press: New York, NY, USA, 1971; pp. 145–182. [Google Scholar] [CrossRef]
- Barman, S.; Kwon, Y.-K. A novel mutual information-based Boolean network inference method from time-series gene expression data. PLoS ONE 2017, 12, e0171097. [Google Scholar] [CrossRef]
- LeCun, Y. Connexionist Learning Models. Ph.D. Thesis, Sorbonne University—Pierre and Marie Curie Campus, Paris, France, 1987. [Google Scholar]
- Li, J.; Luong, M.; Jurafsky, D. A Hierarchical Neural Autoencoder for Paragraphs and Documents. arXiv 2015, arXiv:1506.01057. [Google Scholar] [CrossRef]
- Freitag, M.; Roy, S. Unsupervised Natural Language Generation with Denoising Autoencoders. arXiv 2018, arXiv:1804.07899. [Google Scholar] [CrossRef]
- Akram, M.W.; Salman, M.; Bashir, M.F.; Salman, S.M.S.; Gadekallu, T.R.; Javed, A.R. A novel deep auto-encoder based linguistics clustering model for social text. ACM Trans. Asian-Low-Resour. Lang. Inf. Process. 2022. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, X. Masked Autoencoders in Computer Vision: A Comprehensive Survey. IEEE Access 2023, 11, 113560–113579. [Google Scholar] [CrossRef]
- Parmar, G.; Li, D.; Lee, K.; Tu, Z. Dual contradistinctive generative autoencoder. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 823–832. [Google Scholar] [CrossRef]
- Cheng, Z.; Sun, H.; Takeuchi, M.; Katto, J. Deep convolutional autoencoder-based lossy image compression. In Proceedings of the 2018 Picture Coding Symposium (PCS), San Francisco, CA, USA, 24–27 June 2018; pp. 253–257. [Google Scholar] [CrossRef]
- Vachhani, B.; Bhat, C.; Das, B.; Kopparapu, S.K. Deep Autoencoder Based Speech Features for Improved Dysarthric Speech Recognition. In Interspeech; ISCA: Stockholm, Sweden, 2017; pp. 1854–1858. [Google Scholar]
- Karita, S.; Watanabe, S.; Iwata, T.; Delcroix, M.; Ogawa, A.; Nakatani, T. Semi-supervised end-to-end speech recognition using text-to-speech and autoencoders. In Proceedings of the ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 6166–6170. [Google Scholar] [CrossRef]
- Géron, A. Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow; O’Reilly Media; 2022; ISBN 9781098122478. Available online: https://books.google.co.kr/books?id=V5ySEAAAQBAJ (accessed on 4 October 2022).
- Song, Q.; Jin, H.; Hu, X. Automated Machine Learning in Action; Manning Publications; 2022; ISBN 9781617298059. Available online: https://www.manning.com/books/automated-machine-learning-in-action (accessed on 7 June 2022).
- Barabási, A.-L.; Albert, R. Emergence of Scaling in Random Networks. In The Structure and Dynamics of Networks; Princeton University Press: Princeton, NJ, USA, 2006; pp. 349–352. [Google Scholar] [CrossRef]
- Chen, F.; Wang, Y.-C.; Wang, B.; Kuo, C.-C.J. Graph representation learning: A survey. Apsipa Trans. Signal Inf. Process. 2020, 9, e15. [Google Scholar] [CrossRef]
- Li, G.; Zhao, B.; Su, X.; Yang, Y.; Hu, P.; Zhou, X.; Hu, L. Discovering Consensus Regions for Interpretable Identification of RNA N6-Methyladenosine Modification Sites via Graph Contrastive Clustering. IEEE J. Biomed. Health Inform. 2024, 28, 2362–2372. [Google Scholar] [CrossRef] [PubMed]


| Parameter’s Name | Value |
|---|---|
| Dimension of the input layer | N |
| Dimension of the output layer | N |
| Number of hidden layers | 3 |
| Number of neurons in the first hidden layer | |
| Number of neurons in the second hidden layer | 512 |
| Number of neurons in the third hidden layer | |
| Activation function in hidden layers | relu |
| Activation function in the output layer | linear |
| Parameter’s Name | Value |
|---|---|
| Model optimizer | Adam |
| Learning rate | 0.001–0.01 * |
| Loss function | mse |
| Number of epochs | 1000–10,000 * |
| Batch size | 32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anh, C.-T.; Kwon, Y.-K. Synthesizing Time-Series Gene Expression Data to Enhance Network Inference Performance Using Autoencoder. Appl. Sci. 2025, 15, 5768. https://doi.org/10.3390/app15105768
Anh C-T, Kwon Y-K. Synthesizing Time-Series Gene Expression Data to Enhance Network Inference Performance Using Autoencoder. Applied Sciences. 2025; 15(10):5768. https://doi.org/10.3390/app15105768
Chicago/Turabian StyleAnh, Cao-Tuan, and Yung-Keun Kwon. 2025. "Synthesizing Time-Series Gene Expression Data to Enhance Network Inference Performance Using Autoencoder" Applied Sciences 15, no. 10: 5768. https://doi.org/10.3390/app15105768
APA StyleAnh, C.-T., & Kwon, Y.-K. (2025). Synthesizing Time-Series Gene Expression Data to Enhance Network Inference Performance Using Autoencoder. Applied Sciences, 15(10), 5768. https://doi.org/10.3390/app15105768






