Application of Mathematical Models for Blood Flow in Aorta and Right Coronary Artery
Abstract
1. Introduction
2. Materials and Methods
2.1. Mathematical Models
- Newtonian Model: Assumes a constant viscosity irrespective of the shear rate. This model is suitable for large-caliber vessels like the aorta, where shear rates are high, and blood behaves nearly like a Newtonian fluid [2,3,4]. The Newtonian model simplifies calculations, making it computationally efficient but less accurate for small or highly deformable vessels.
- Non-Newtonian Shear-Thinning Models:
- Carreau Model: An empirical model that describes the decrease in viscosity with increasing shear rates. It captures the Newtonian plateaus at low and high shear rates and the intermediate pseudoplastic region. The Carreau model is expressed as follows:where : viscosity at infinite shear rate (in ), : viscosity at zero shear rate (in ), : relaxation time of the fluid (in seconds, ), : shear rate (in ), and n: power-law index (dimensionless), which determines the degree of shear-thinning behavior. For , the fluid behaves as a Newtonian fluid.The fluid behavior depends on the value of relative to :
- –
- If , the fluid behaves as a Newtonian fluid.
- –
- If , the fluid exhibits power-law fluid behavior.
The parameter values of the Carreau Model can be considered as follows (as reported in Fernandes et al. [6]): - Casson Model: Incorporates a yield stress () below which the fluid does not flow. It is particularly suited for blood, considering the aggregation of red blood cells at low shear rates. Additionally, it predicts viscosity changes due to hematocrit (Hct) variations.The model is described by the following equations:where : dynamic viscosity (in ), : yield stress, the minimum stress required for the fluid to flow (in ), : shear rate (in ), : a parameter related to viscosity changes due to hematocrit variations (dimensionless), : plasma viscosity, a constant property of the plasma (in ), and Hct: hematocrit, the volume fraction of red blood cells in the blood (dimensionless, typically expressed as a percentage).The parameter values for this model, as reported in Fernandes et al. [6], are as follows:Here, is linearly proportional to Hct and the Hct value is 40% of blood volume.This model effectively captures the non-Newtonian behavior of blood and accounts for the effects of both yield stress and hematocrit on viscosity.
- Viscoelastic Models [6]:
- Oldroyd-B Model: The model describes blood as a viscoelastic fluid, combining a Newtonian solvent with elastic polymer-like components. Despite its computational simplicity, it lacks precision in capturing shear-thinning effects. The governing equation is given as follows:where represents the stress tensor, is the relaxation time, is the retardation time, is the zero-shear viscosity, and denotes the shear rate. This model provides a basic framework for studying viscoelastic behaviors in complex fluids such as blood.
- Giesekus Model: A nonlinear extension of the Oldroyd-B model, the Giesekus model incorporates a mobility parameter () to account for shear-thinning and elastic behaviors, making it more realistic for describing blood flow in geometrically complex vessels. The governing equation is expressed as follows:where is the mobility parameter (), represents the velocity gradient, is the stress tensor, is the relaxation time, is the zero-shear viscosity, and denotes the shear rate.
- FENE-P Model (Finitely Extensible Nonlinear Elastic—Peterlin): Based on molecular theory, it describes the elasticity of long polymer chains while incorporating a finite extensibility factor. This makes it particularly suitable for modeling high-stress conditions, such as blood flow through stenosed arteries or within mechanical circulatory devices. The governing equation is expressed as follows:where f is the finite extensibility factor (set to 100), is the polymer viscosity, is the zero-shear viscosity (set to Pa·s), and is the relaxation time (set to s). The FENE-P model captures the nonlinear elastic behavior of polymers, making it highly effective for applications involving significant stress and deformation.
2.2. Geometric Models
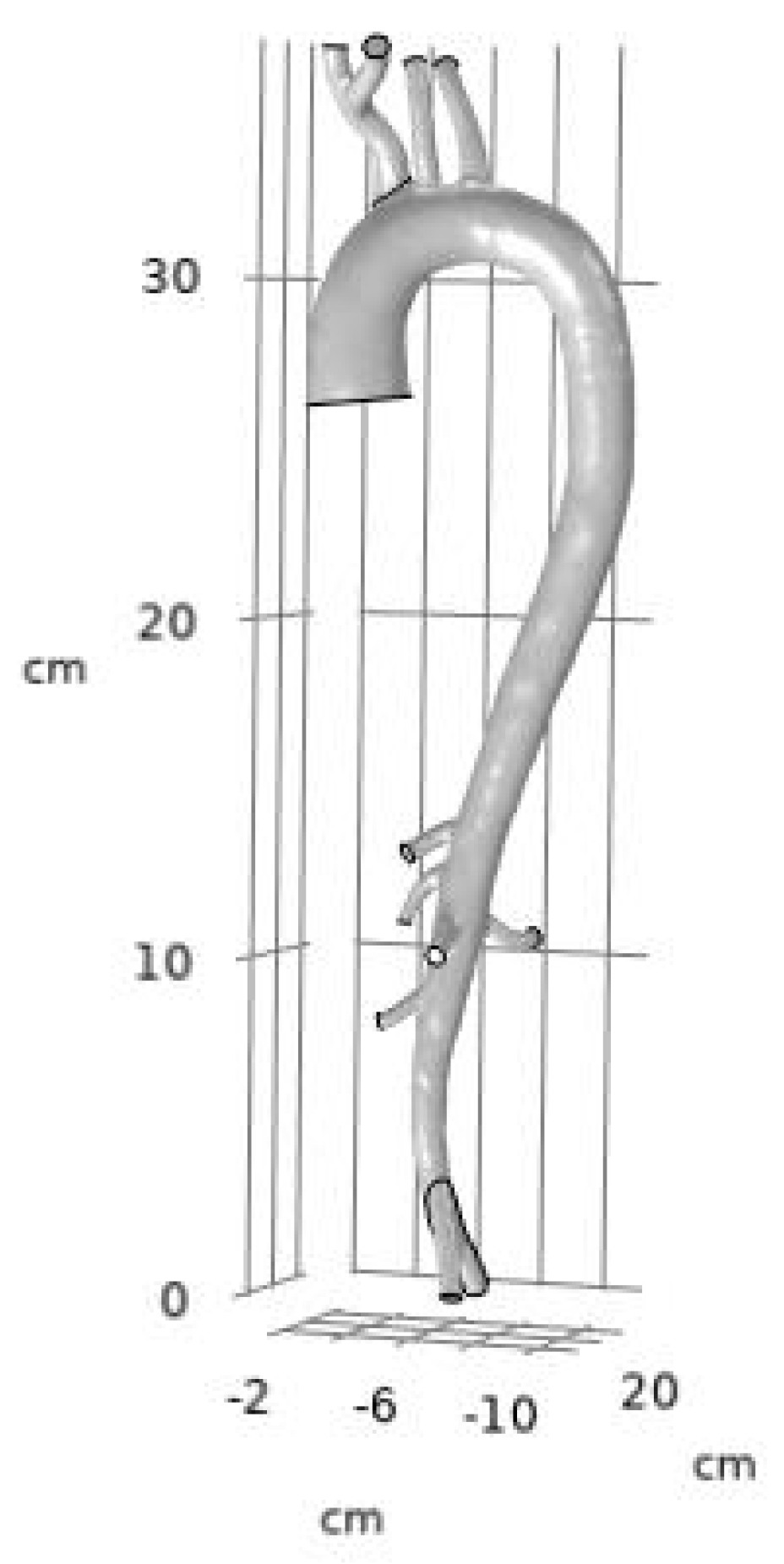
- Three-Dimensional Geometric Model of the Aorta:
- Three-Dimensional Geometric Model of the RCA:
2.3. Boundary Conditions
2.4. Simulation Details
2.5. Algorithm for Calculating the Error
3. Results
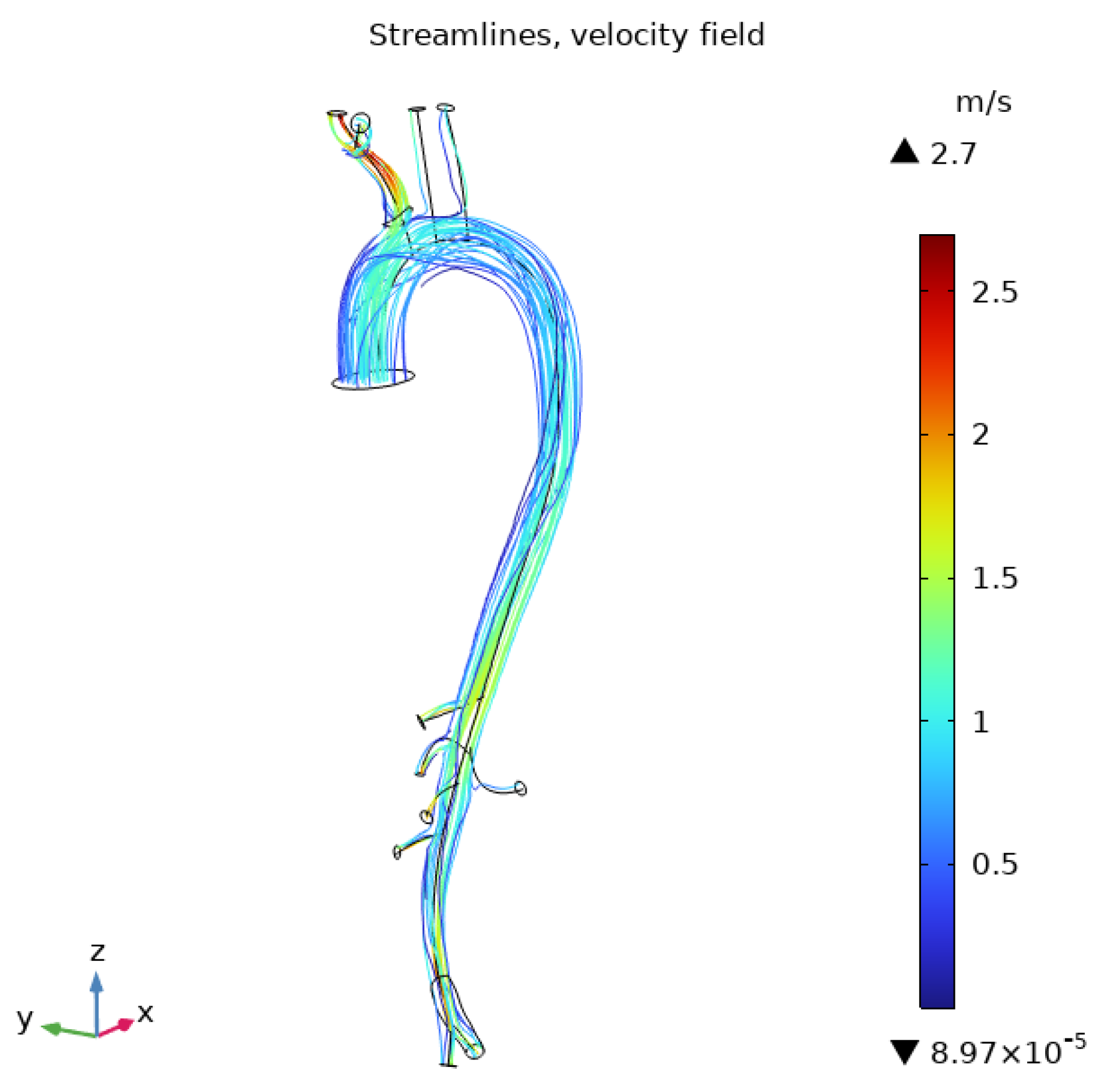
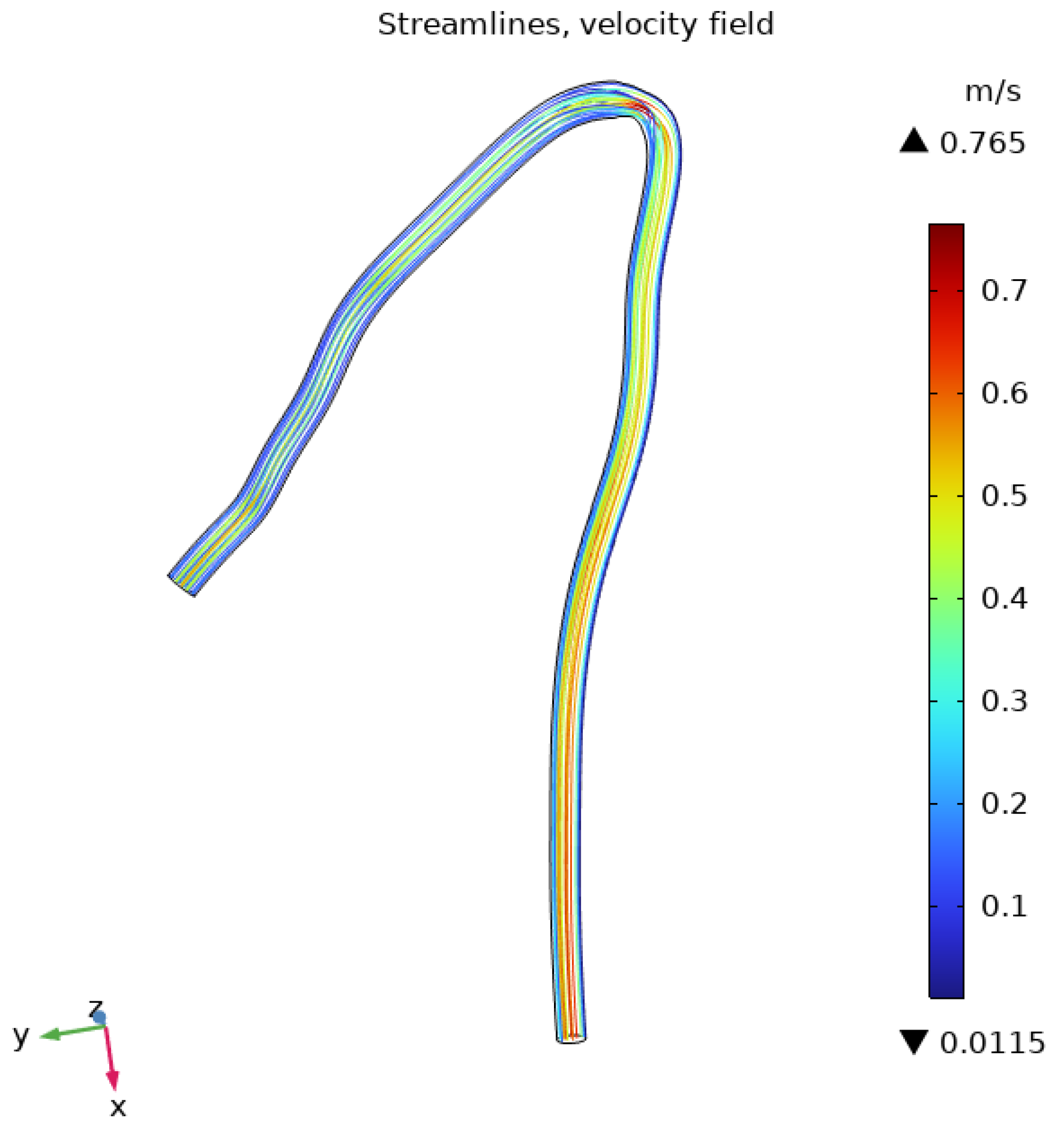
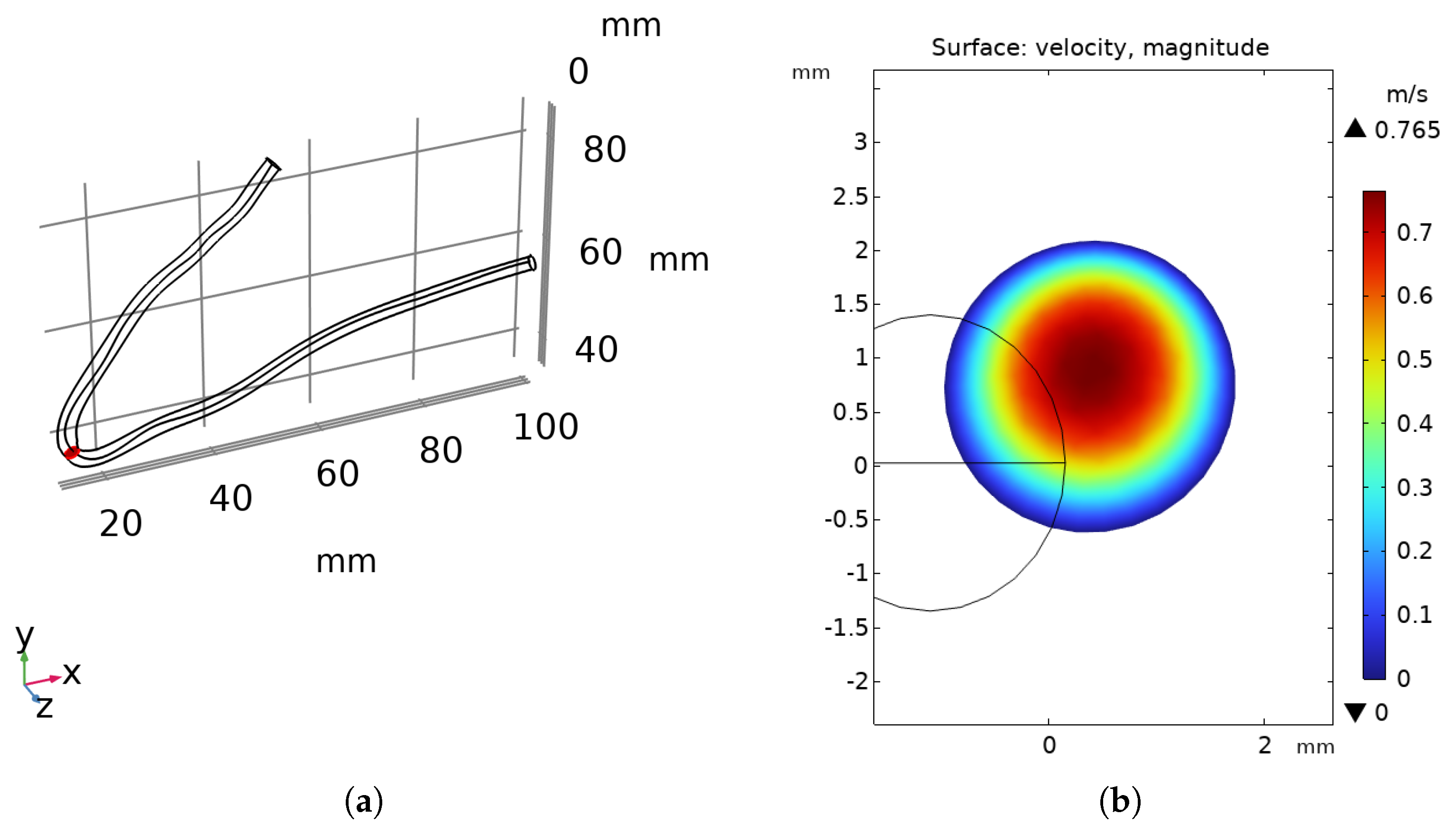
3.1. Flow Behavior in the Aorta
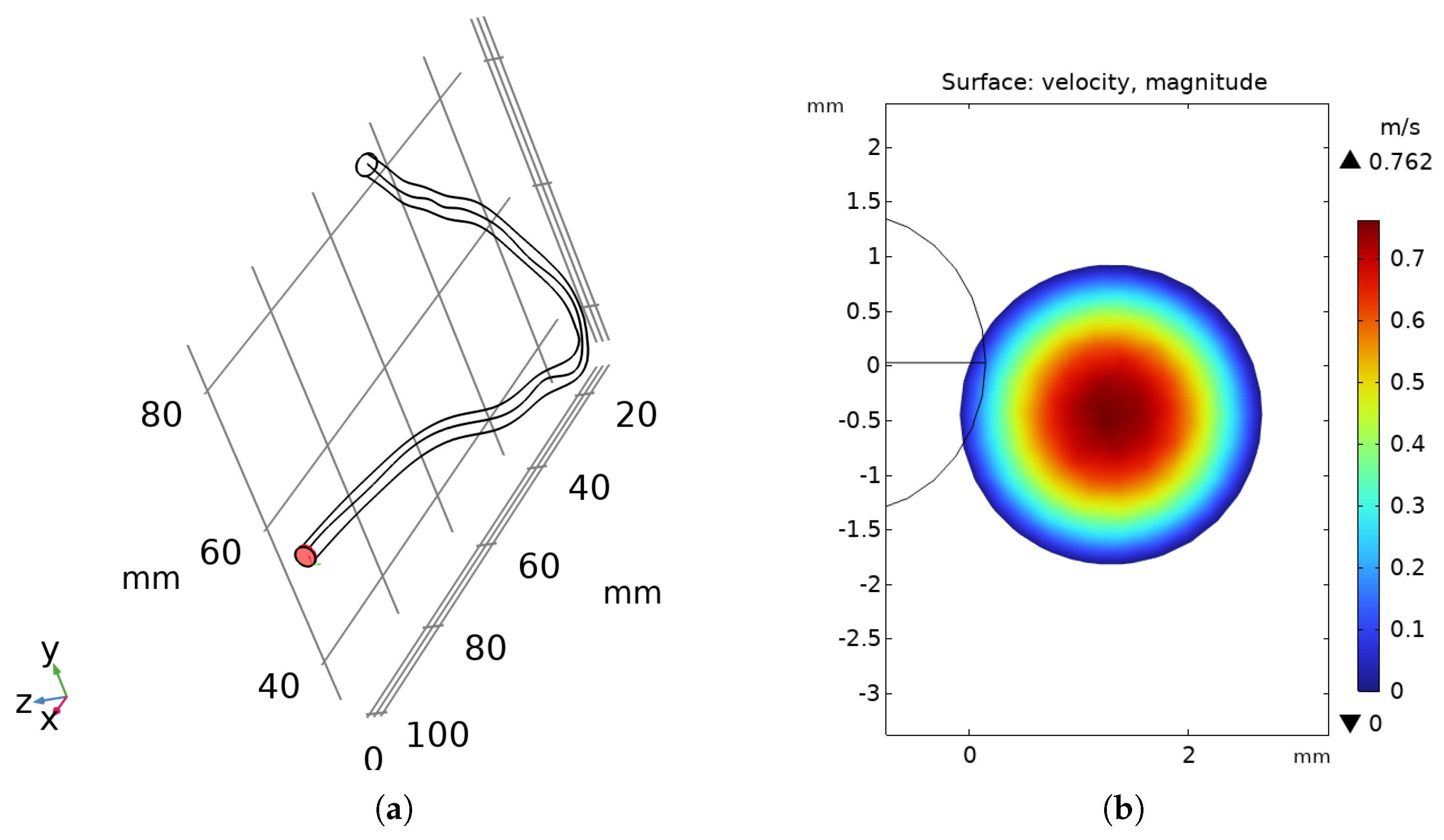
3.2. Flow Behavior in the RCA
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, Y.; Park, J.; Kim, M. Diagnostic approaches for inherited hemolytic anemia in the genetic era. Blood Res. 2017, 52, 84–94. [Google Scholar] [CrossRef] [PubMed]
- Formaggia, L.; Perktold, K.; Quarteroni, A. Basic mathematical models and motivations. In Cardiovascular Mathematics: Modeling and Simulation of the Circulatory System; Quarteroni, A., Formaggia, L., Veneziani, A., Eds.; Springer: Milan, Italy, 2009; pp. 47–75. [Google Scholar]
- Piatti, F.; Belkacemi, D.; Caimi, A.; Sturla, F.; Greiser, A.; Pluchinotta, F.; Redaelli, A. On the potential of 4D Flow in guiding CFD analyses: A case study of aortic coarctation. In Proceedings of the VII Meeting Italian Chapter of the European Society of Biomechanics (ESB-ITA 2017), Rome, Italy, 28–29 September 2017; pp. 28–29. [Google Scholar]
- Ramakrishnan, K.; Shailendhra, K. Hydromagnetic blood flow through a uniform channel with permeable walls covered by porous media of finite thickness. J. Appl. Fluid Mech. 2013, 6, 39–47. [Google Scholar]
- Hoque, K.E.; Ferdows, M.; Sawall, S.; Tzirtzilakis, E.E.; Xenos, M.A. The impact of hemodynamic factors in a coronary main artery to detect the atherosclerotic severity: Single and multiple sequential stenosis cases. Phys. Fluids 2021, 33, 31903. [Google Scholar] [CrossRef]
- Fernandes, M.; Sousa, L.C.; António, C.C.; Pinto, S.I.S. Accuracy and temporal analysis of non-Newtonian models of blood in the computational FFR—Numerical implementation. Int. J. Non-Linear Mech. 2024, 161, 104683. [Google Scholar] [CrossRef]
- Rafiei, A.; Saidi, M. Numerical evaluation on blood rheological behavior in a realistic model of aneurysmal coronary artery. Comput. Methods Biomech. Biomed. Eng. 2021, 6, 579–596. [Google Scholar]
- Yilmaz, F.; Gundogdu, M.Y. A Critical Review on Blood Flow in Large Arteries: Relevance to Blood Rheology, Viscosity Models, and Physiologic Conditions. Korea-Aust. Rheol. J. 2008, 20, 197–211. [Google Scholar]
- Campo-Deaño, L.; Dullens, R.; Aarts, D.G.; Pinho, F.T.; Oliveira, M.S. Viscoelasticity of blood and viscoelastic blood analogues for use in polydimethylsiloxane in vitro models of the circulatory system. Biomicrofluidics 2013, 7, 034102. [Google Scholar] [CrossRef]
- Fernandes, M.; Sousa, L.C.; António, C.A.C.; Pinto, S.I. Modeling the Five-Element Windkessel Model with simultaneous utilization of blood viscoelastic properties for FFR achievement: A proof-of-concept study. Mathematics 2023, 11, 4877. [Google Scholar] [CrossRef]
- Comsol. COMSOL-Software for Multiphysics Simulation. Available online: https://www.comsol.com/ (accessed on 10 February 2025).
- Caruso, M.V.; Renzulli, A.; Fragomeni, G. Influence of IABP-Induced Abdominal Occlusions on Aortic Hemodynamics: A Patient-Specific Computational Evaluation. ASAIO J. 2017, 63, 161–167. [Google Scholar] [CrossRef]
- Caruso, M.V.; De Rosa, S.; Indolfi, C.; Fragomeni, G. Computational analysis of stenosis geometry effects on right coronary hemodynamics. In Proceedings of the Engineering in Medicine and Biology Society (EMBC), 2015 37th Annual International Conference of the IEEE, Milan, Italy, 25–29 August 2015; pp. 981–984. [Google Scholar]
- Belkacemi, D.; Al-Rawi, M.; Abbes, M.T.; Laribi, B. Flow behaviour and wall shear stress derivatives in abdominal aortic aneurysm models: A detailed CFD analysis into asymmetry effect. CFD Lett. 2022, 14, 60–74. [Google Scholar] [CrossRef]
- Caruso, M.V.; Gramigna, V.; Fragomeni, G. A CFD investigation of intra-aortic balloon pump assist ratio effects on aortic hemodynamics. Biocybern. Biomed. Eng. 2019, 39, 224–233. [Google Scholar] [CrossRef]
- Perinajová, R.; Juffermans, J.F.; Westenberg, J.J.M.; van der Palen, R.L.; van den Boogaard, P.J.; Lamb, H.J.; Kenjereš, S. Geometrically induced wall shear stress variability in CFD-MRI coupled simulations of blood flow in the thoracic aortas. Comput. Biol. Med. 2021, 133, 104385. [Google Scholar] [CrossRef]
- Friedman, M.H.; Bargeron, C.B.; Duncan, D.D. Effects of arterial compliance and non-Newtonian rheology on correlations between intimal thickness and wall shear. J. Biomech. Eng. 1992, 114, 317. [Google Scholar] [CrossRef]
- Brown, A.G.; Shi, Y.; Marzo, A.; Staicu, C.; Valverde, I.; Beerbaum, P.; Lawford, P.V.; Hose, D.R. Accuracy vs computational time: Translating aortic simulations to the clinic. J. Biomech. 2012, 45, 516–523. [Google Scholar] [CrossRef]
- Suo, J.; Oshinski, J.; Giddens, D.P. Effects of wall motion and compliance on flow patterns in the ascending aorta. J. Biomech. Eng. 2003, 125, 347–354. [Google Scholar]
- Romarowski, R.M.; Lefieux, A.; Morganti, S.; Veneziani, A.; Auricchio, F. Patient-specific CFD modelling in the thoracic aorta with PC-MRI-based boundary conditions: A least-square three-element Windkessel approach. Int. J. Numer. Methods Biomed. Eng. 2018, 34, e3134. [Google Scholar] [CrossRef]
- Qiao, Y.; Mao, L.; Ding, Y.; Zhu, T.; Luo, K.; Fan, J. Fluid-structure interaction: Insights into biomechanical implications of endograft after thoracic endovascular aortic repair. Comput. Biol. Med. 2021, 138, 104882. [Google Scholar] [CrossRef]
- Xi, Y.; Li, Y.; Wang, H.; Sun, A.; Deng, X.; Chen, Z.; Fan, Y. The impact of ECMO lower limb cannulation on the aortic flow features under differential blood perfusion conditions. Med. Nov. Technol. Devices 2022, 16, 100183. [Google Scholar] [CrossRef]
- Hsiao, H.-M.; Lee, K.H.; Liao, Y.C.; Cheng, Y.C. Hemodynamic simulation of Intra-stent Blood Flow. Procedia Eng. 2012, 36, 128–136. [Google Scholar] [CrossRef]
- Hoque, K.E.; Wu, P.; Li, Z.; Zhao, X. The effect of hemodynamic parameters in patient-based coronary artery models with serial stenoses: Normal and hypertension cases. Comput. Methods Biomech. Biomed. Eng. 2020, 23, 1001–1008. [Google Scholar] [CrossRef]
- Gramigna, V.; Caruso, M.V.; Fragomeni, G. A computational fluid dynamics study to compare two types of arterial cannulae for cardiopulmonary bypass. Fluids 2023, 8, 302. [Google Scholar] [CrossRef]
- Wen, J.; Zhang, X.; Li, Y.; Sun, Q. A computational simulation of the effect of hybrid treatment for thoracoabdominal aortic aneurysm on the hemodynamics of the abdominal aorta. Sci. Rep. 2016, 6, 23801. [Google Scholar] [CrossRef] [PubMed]
- Buradi, A.; Mahalingam, A. Effect of stenosis severity on wall shear stress-based hemodynamic descriptors using multiphase mixture theory. J. Appl. Fluid Mech. 2018, 11, 1497–1509. [Google Scholar] [CrossRef]
- Miyazaki, S.; Itatani, K.; Furusawa, T.; Nishino, T.; Sugiyama, M.; Takehara, Y.; Yasukochi, S. Validation of numerical simulation methods in aortic arch using 4D Flow MRI. Heart Vessels. 2017, 32, 1032–1044. [Google Scholar] [CrossRef]
- Xie, X.; Li, N.; Yu, T.; Pu, W.; Lin, H.; Li, X.; Li, G.; Li, C.; Chen, Y.; Lian, K. Validation of a Novel Computational Fluid Dynamics Based Method for Assessing Intracoronary Flow: Combining Coronary Angiography and Fractional Flow Reserve. In Catheterization and Cardiovascular Interventions: Official Journal of the Society for Cardiac Angiography & Interventions; Wiley: New York, NY, USA, 2025. [Google Scholar]
- Caridi, G.C.A.; Torta, E.; Mazzi, V.; Chiastra, C.; Audenino, A.L.; Morbiducci, U.; Gallo, D. Smartphone-based particle image velocimetry for cardiovascular flows applications: A focus on coronary arteries. Front. Bioeng. Biotechnol. 2022, 10, 1011806. [Google Scholar] [CrossRef]

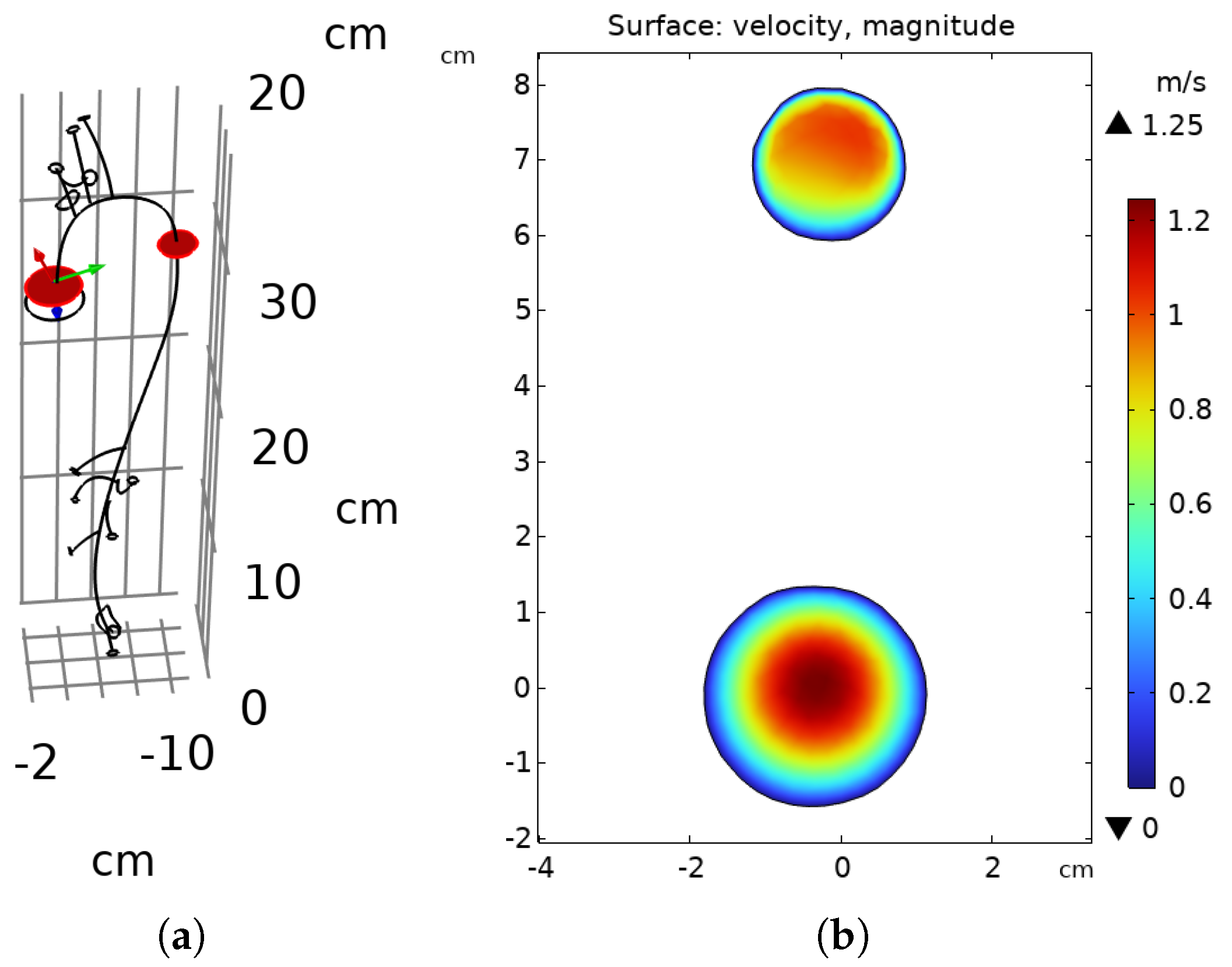


| Parameter | Value | Unit |
|---|---|---|
| vel (line average) | 1.25080 | m/s |
| volume-averaged velocity | 0.84300 | m/s |
| surface-averaged velocity (in) | 0.61699 | m/s |
| surface-averaged velocity (out) | 1.45420 | m/s |
| volume-averaged pressure | 12,679.00 | Pa |
| surface-averaged pressure (in) | 13,600.00 | Pa |
| surface-averaged pressure (out) | 9372.50 | Pa |
| Qin | 4.50 × | /s |
| Qout | 4.61 × | /s |
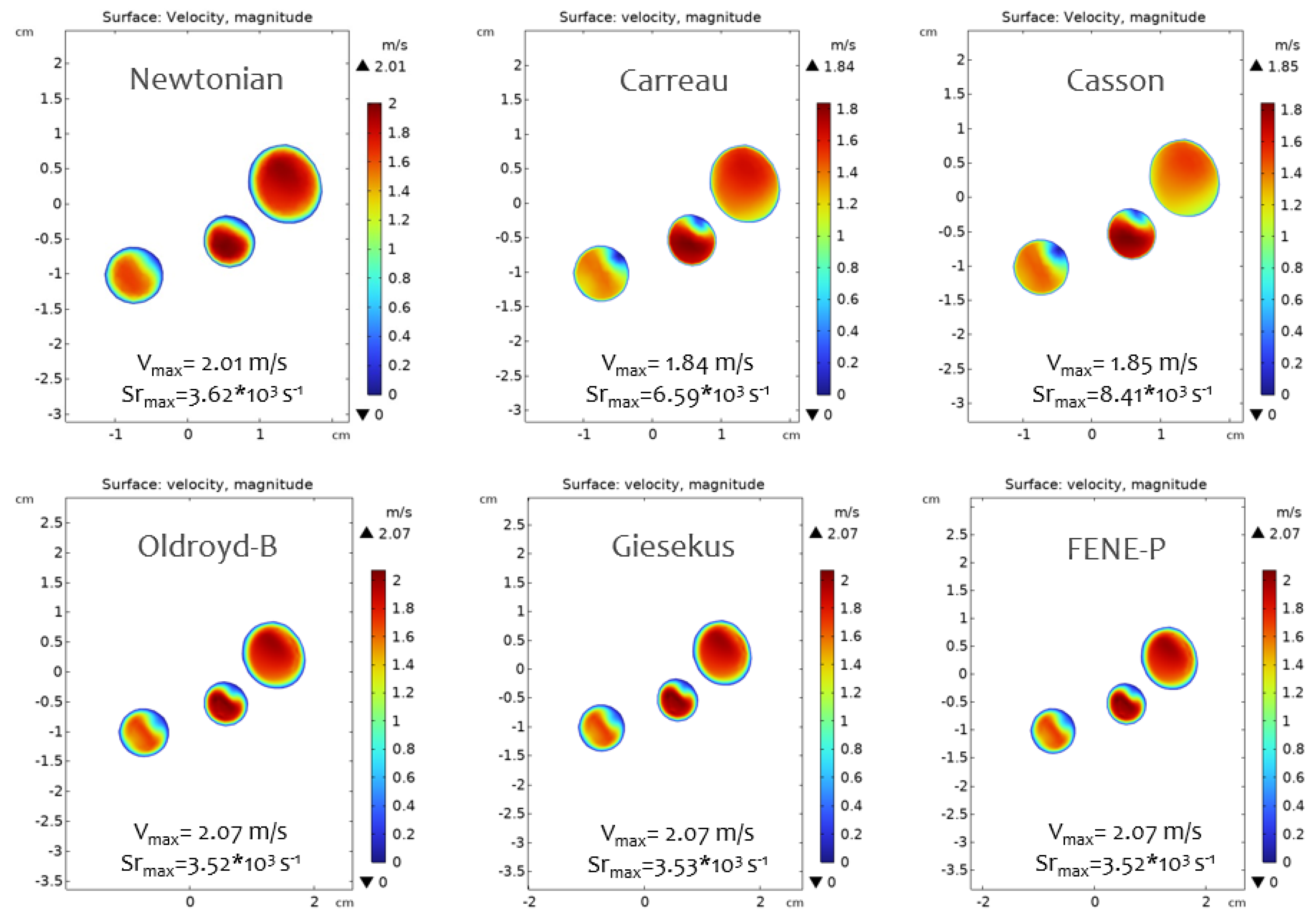
| Parameter | True Value | Newtonian | Carreau | Casson | Oldroyd-B | Giesekus | FENE-P |
|---|---|---|---|---|---|---|---|
| Average velocity on surface (in) | 0.617 m/s | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Average velocity on surface (out) | 1.417 m/s | 0.025 | 0.028 | 0.027 | 0.029 | 0.029 | 0.029 |
| Average pressure on surface (out) | 9332.54 Pa | 0.004 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 |
| Qin | 4.50 × /s | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Qout | 4.50 × /s | 0.025 | 0.028 | 0.026 | 0.042 | 0.029 | 0.042 |
| Avg Relative Error 1 | 0.011 | 0.012 | 0.011 | 0.015 | 0.012 | 0.015 |
| Parameter | True Value | Newtonian | Carreau | Casson | Oldroyd-B | Giesekus | FENE-P |
|---|---|---|---|---|---|---|---|
| Average velocity on volume | 0.34300 m/s | 0.118 | 0.110 | 0.109 | 0.110 | 0.110 | 0.108 |
| Average velocity on surface (in) | 0.29338 m/s | 0.008 | 0.012 | 0.014 | 0.008 | 0.008 | 0.012 |
| Average velocity on surface (out) | 0.39355 m/s | 0.023 | 0.028 | 0.035 | 0.022 | 0.022 | 0.021 |
| Average pressure on surface (out) | 17,731.83 Pa | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Qin | 2.25 × /s | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Qout | 2.25 × /s | 0.025 | 0.000 | 0.000 | 0.006 | 0.006 | 0.007 |
| Avg Relative Error 1 | 0.026 | 0.025 | 0.026 | 0.024 | 0.024 | 0.025 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minniti, M.; Gramigna, V.; Palumbo, A.; Fragomeni, G. Application of Mathematical Models for Blood Flow in Aorta and Right Coronary Artery. Appl. Sci. 2025, 15, 5748. https://doi.org/10.3390/app15105748
Minniti M, Gramigna V, Palumbo A, Fragomeni G. Application of Mathematical Models for Blood Flow in Aorta and Right Coronary Artery. Applied Sciences. 2025; 15(10):5748. https://doi.org/10.3390/app15105748
Chicago/Turabian StyleMinniti, Monica, Vera Gramigna, Arrigo Palumbo, and Gionata Fragomeni. 2025. "Application of Mathematical Models for Blood Flow in Aorta and Right Coronary Artery" Applied Sciences 15, no. 10: 5748. https://doi.org/10.3390/app15105748
APA StyleMinniti, M., Gramigna, V., Palumbo, A., & Fragomeni, G. (2025). Application of Mathematical Models for Blood Flow in Aorta and Right Coronary Artery. Applied Sciences, 15(10), 5748. https://doi.org/10.3390/app15105748








