Microscopic Pore–Throat Architecture and Fractal Heterogeneity in Tight Sandstone Reservoirs: Insights from the Denglouku Formation, Xujiaweizi Fault Depression
Abstract
1. Introduction
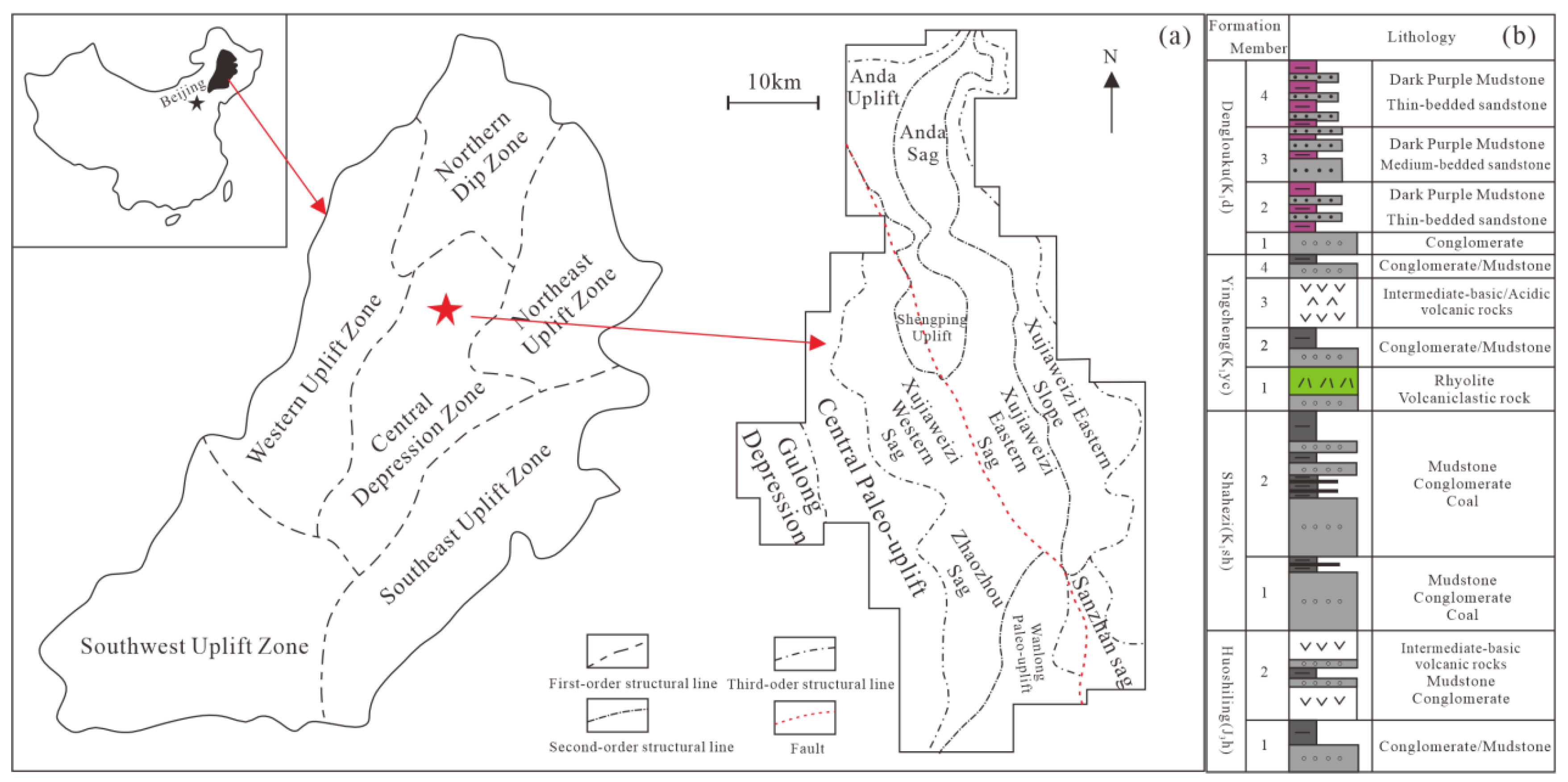
2. Geological Setting
3. Sample and Method
3.1. Cast Thin Section
3.2. High-Pressure Mercury Injection
3.3. Fractal Model
4. Results
4.1. Reservoir Physical Properties and Storage Space Characteristics
4.2. Microscopic Pore–Throat Structure Characteristics
4.3. Fractal Characteristics of Tight Sandstone Reservoirs
5. Discussion
5.1. The Relationship Between Fractal Dimension, Porosity, and Permeability
5.2. Fractal Dimension and Microscopic Pore–Throat Structure Characteristics
5.3. Reservoir Classification Based on Mercury Injection and Fractal Dimension
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zou, C.; Yang, Z.; He, D.; Wei, Y.; Li, J.; Jia, A.; Chen, J.; Zhao, Q.; Li, Y.; Li, J.; et al. Theory, technology and prospects of conventional and unconventional natural gas. Pet. Explor. Dev. 2018, 45, 575–587. [Google Scholar] [CrossRef]
- Bai, B.; Zhu, R.; Wu, S.; Cui, J.; Su, L.; Li, T. New micro-throat structural characterization techniques for unconventional tight hydrocarbon reservoir. China Pet. Explor. 2014, 19, 78–86. [Google Scholar]
- Zhu, X.M.; Pan, R.; Zhu, S.F.; Wei, W.; Ye, L. Research progress and core issues in tight reservoir exploration. Earth Sci. Front. 2018, 25, 141–146. [Google Scholar]
- Sun, L.D.; Zou, C.N.; Jia, A.L.; Wei, Y.; Zhu, R.; Wu, S.; Guo, Z. Development characteristics and orientation of tight oil and gas in China. Pet. Explor. Dev. 2019, 46, 1015–1026. [Google Scholar] [CrossRef]
- Lu, Z.; Liu, C.; Zang, Q.; Wu, Y.; Yang, X.; Yang, H.; Zeng, X.; Li, W. High-pressure mercury injection combined with fractal theory to analyze the pore structure of tight sandstone: A case study of the Heshui area in the Ordos Basin. Geol. Sci. Technol. Bull. 2023, 42, 264–273. [Google Scholar]
- Zou, C.; Yang, Z.; He, D.; Wei, Y.; Li, J.L.; Jia, A.; Chen, J.; Zhao, Q.; Li, Y.; Li, J.; et al. Theoretical technology and practice of unconventional oil and gas geology. Earth Sci. 2023, 48, 2376–2397. [Google Scholar]
- Zhu, R.; Wu, S.; Su, L.; Cui, J.; Mao, Z.; Zhang, X. Problems and Future Works of Porous Texture Characterization of Tight Reservoirs in China. Acta Pet. Sin. 2016, 37, 1323–1336. [Google Scholar]
- Yang, Y.; Zhang, H.R.; Yuan, W.; Yang, D.; Hu, D. Fractal Characteristids Comparison and Genesis Conventional Sandstone and Glutenite. Geoscience 2022, 36, 149–158. [Google Scholar]
- Lv, T.X.; Zhang, G.Y.; Yi, L.; Li, Z.C.; Song, P.; Li, S. Pore Structure Characteristicsand Fractal Characteristics of Low Permeability Reservoir. Spec. Oil Gas Reserv. 2022, 29, 59–65. [Google Scholar]
- Wu, H.; Zhang, C.; Ji, Y.; Liu, R.E.; Cao, S.; Chen, S.; Zhang, Y.; Wang, Y.; Du Wei, L.G. Pore-Throat Size Characterization of Tight Sandstone and Its Control on Reservoir Physical Properties: A Case Study of Yanchang Formation, Eastern Gansu, Ordos Basin. Acta Pet. Sin. 2017, 38, 876–887. [Google Scholar]
- Zhang, W.K.; Shi, Z.J.; Tian, Y.M. Characterization of Pore Throat Characteristics of Tight Sandstone by Combined High Pressure Mercury Injection and Constant Velocity Mercury Injection Experiments. Fault-Block Oil Gas Field 2021, 28, 14–20, 32. [Google Scholar]
- Chen, C.; Sun, Y. Fractional dimension of the pore-texture in sandstones and its application. Acta Sedimentol. Sin. 1996, 4, 109–114. [Google Scholar]
- Zhang, C.M.; Chen, Z.B.; Zhang, Z.S.; Li, J.; Linghu, S.; Sun, B.X. Based on NMR T2 study on pore fractal structure of reservoir rock based on spectrum distribution. J. Oil Gas Technol. 2007, 4, 80–86+166–167. [Google Scholar]
- Cheng, G.X.; Liu, Y.R.; Guo, N.; Wang, A.P.; Chang, H.Y.; Zhang, T.J. Fractal characterization of cast thin sections: A case study of Kunbei New Area, Qaidam Basin. Lithol. Reserv. 2016, 28, 72–76, 87. [Google Scholar]
- Han, X.J.; Shi, Z.J.; Li, Y.L. An improved algorithm for picking up the first arrival of seismic waves using fractal dimension. Pet. Geophys. Explor. 2002, 60–63, 98. [Google Scholar]
- Peng, J.; Han, H.D.; Xia, Q.S.; Li, B. Fractal characteristic of microscopic pore structure of tight sandstone reservoirs in Kalpintag Formation in Shuntuoguole area, Tarim Basin. Pet. Res. 2020, 5, 2096–2495. [Google Scholar] [CrossRef]
- Liu, Y.; Pang, X.Q.; Ding, C.; Chen, D.; Li, M. Pore structure and fractal characteristics of Yan 10 tight sandstone reservoir in Wuqi area. Sci. Technol. Eng. 2023, 23, 12474–12483. [Google Scholar]
- Wang, W.; Chen, C.B.; Xu, S.; Li, Y.; Zhu, Y.; Huang, X. Fractal characteristics of different scale pore throats and their controlling factors in Yanchang Formation tight sandstone, Ordos Basin. Pet. Exp. Geol. 2022, 44, 33–40. [Google Scholar]
- He, W.Z.; Zhong, F.; He, C. Research and application of fractal structure of reservoir rock pores. Nat. Gas Ind. 2000, 67–70, 43. [Google Scholar]
- Huang, J.L.; Dong, D.Z.; Li, J.; Hu, J.; Wang, Y. Reservoir fractal characteristies of continentalshale:An example from Triassie Xujiahe Formation shale, Sic huan Basin, China. Nat. Gas Geosci. 2016, 27, 1611–1618. [Google Scholar]
- Liu, K.; Shi, W.Z.; Wang, R.; Qin, S. Pore structure fractal characteristics its relationship with reservoir propertics of the first member of lower Shihezi Formation tight sandstone in Hangjinqi area, Ordos Basin. Bullentin Geol. Sci. Technol. 2021, 40, 57–68. [Google Scholar]
- Liu, Y.K.; Wang, Y.P.; Tang, H.M. Application of capillary pressure curve and fractal theory in reservoir classification. Lithol. Oil Gas Reserv. 2014, 26, 89–92, 100. [Google Scholar]
- Zhao, J.; Huang, Z.L.; Zhang, J.Y.; Deng, G.J.; Xu, M.G. Fractal and grading evaluation of pore structure in tight sandstone reservoirs taking the Huangliu Formation in Ledong District, Yinggehai Basin as an example. J. Sediment. 2024, 42, 295–308. [Google Scholar]
- Feng, Z.D.; Zhou, Y.; Wu, W.; Wang, G.X.; Liang, S.Y.; Yu, J. Fractal characteristics of mercury injection in heterogeneous sandstone reservoirs and reservoir evaluation. J. China Univ. Pet. (Nat. Sci. Ed.) 2021, 45, 25–34. [Google Scholar]
- Guo, R.L.; Xie, Q.C.; Qu, X.F.; Chu, M.J.; Li, S.T.; Ma, D.X.; Ma, X.F. Fractal characteristics of pore-throat structure and permeability estimation of tight sandstone reservoirs: A case study of Chang 7 of the Upper Triassic Yanchang Formation in Longdong area, Ordos Basin, China. J. Pet. Sci. Eng. 2020, 184, 0920–4105. [Google Scholar] [CrossRef]
- Song, Z.Z.; Lu, M.Y.; Zhao, L.B.; Zhang, Y.Q.; He, Y.Y.; Jiang, F.J.; Yang, Z.Z.; Chen, W.Y.; Huo, L.N.; Wang, R. Prediction model of tight sandstone permeability based on fractal theory. Acta Sedimentol. Sin. 2023, 41, 1847–1858. [Google Scholar]
- Zhang, J.H.; Fang, W.; Li, J.K.; Huo, Q.L. Deep gases and their genetic types of the Xujiaweizi fault depression zone, Songliao Basin and their contribution. Acta Geol. Sin. 2009, 83, 579–589. [Google Scholar]
- Bai, X.F.; Liang, J.P.; Zhang, W.J.; Fu, L.; Peng, J.; Xue, T.; Yang, L.; Liu, J. Geologic conditions, resource potential and exploratory direction of deep gas in the northern Songliao Basin. Nat. Gas Geosci. 2018, 29, 1443–1454. [Google Scholar]
- Shao, Z.; Wu, C.; Zhang, D.; Yang, B.Z. Reservoir characteristics and controlling factors of Shahezi Formation in Xujiaweizi Fault Depression, Songliao Basin. Oil Gas Geol. 2019, 40, 101–108. [Google Scholar]
- Sun, L.D.; Yang, L.; Li, X.M.; Zhou, X.; Hu, B.; Cai, Z.; Du, Y. Paleoenvironment and Main Controlling Factors of Source Rocks in the Shahezi Formation, Xujiaweizi Fault Depression. Acta Sedimentol. Sin. 2024, 42, 1753–1764. [Google Scholar]
- GB/T 17366-1998; National Microbeam Analysis Standardization Technical Committee. Methods of Mineral and Rock Specimen Preparation for EPMA. Standardization Administration of China: Beijing, China, 1988.
- Wu, Y.; Liu, C.; Ouyang, S.; Luo, B.; Zhao, D.; Sun, W.; Awan, R.S.; Lu, Z.; Li, G.; Zang, Q. Investigation of Pore-Throat Structure and Fractal Characteristics of Tight Sandstones Using HPMI, CRMI, and NMR Methods: A Case Study of the Lower Shihezi Formation in the Sulige Area, Ordos Basin. J. Pet. Sci. Eng. 2022, 210, 335–348. [Google Scholar] [CrossRef]
- Sing, K.S.W. Reporting Physisorption Data for Gas/Solid Systems with Special Reference to the Determination of Surface Area and Porosity (Recommendations 1984); Wiley VCH Verlag GmbH &. Co. KGaA: Hoboken, NJ, USA, 1990. [Google Scholar]
- Zhu, Y.Q.; Zhang, H.; Yao, Z.G.; Yin, S. Fractal characteristics and controlling factors of tight and stone reservoirs based on high-pressure mercury injection experiments. Sci. Technol. Eng. 2024, 24, 8419–8428. [Google Scholar]
- Li, H.Y.; Pang, Q.; Wei, K.Y.; Zeng, Y.; Cui, Y.; Zhu, Y. The Fractal Characteristics of Pore Structure in Tight Sandstone Reservoirs and Their Impact on Gas Water Permeability: A Case Study of Shanl Member in Tao2 Block, Southeastern Sulige Gas Field. Fault-Block Oil Gas Field 2023, 30, 177–185. [Google Scholar]
- Li, P.; Zheng, M.; Bi, H.; Wu, S.; Wang, X. Pore Throt Structure and Fractal Characteristics of Tight Oil Sandstone: A Case Study in the Ordos Basin, China. J. Pet. Sci. Eng. 2017, 149, 665–674. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; Freeman: New York, NY, USA, 1982; pp. 1–532. [Google Scholar]
- Wu, H.; Liu, R.E.; Ji, Y.L.; Zhang, C.; Chen, S.; Zhou, Y.; Du, W.; Zhang, Y.; Wang, Y. Pore throat fractal characteristics of tight gas reservoir and its relationship with seepage: Taking He 8 member of Lower Shihezi Formation in Ordos Basin as an example. Acta Sedimentol. Sin. 2017, 35, 151–162. [Google Scholar]
- Wang, W.; Song, Y.J.; Huang, J.; Li, Y.; Chen, Z.; Zhu, Y. Fractal characteristics of pore-throat structure in tight sandstones using high-pressure mercury intrusion porosimetry. Bull. Geol. Sci. Technol. 2021, 40, 22–30. [Google Scholar]
- Xu, Y.Q.; He, Y.H.; Bu, G.P.; Chen, L.; Liu, L.; Zhu, Y. Establishment of Classification and Evaluation Criteria for Tight Reservoirs Based on Characteristics of Microscopic Pore Throat Structure and Percolation: A Case Study of Chang 7 Reservoir in Longdong Area Ordos Basin. Pet. Geol. Exp. 2019, 41, 451–460. [Google Scholar]








| Sample Number | Formation | Depth /m | Sample Length /cm | Sample Diameter /cm | Porosity /% | Permeability /10−3 μm2 |
|---|---|---|---|---|---|---|
| S1 | Denglouku | 2889.8 | 3.283 | 2.513 | 4.4 | 0.018 |
| S2 | Denglouku | 2860.6 | 3.179 | 2.521 | 8.4 | 0.053 |
| S3 | Denglouku | 2914.7 | 3.375 | 2.514 | 9 | 0.070 |
| S4 | Denglouku | 3025.3 | 3.322 | 2.51 | 6.2 | 0.031 |
| S5 | Denglouku | 3075.3 | 3.319 | 2.464 | 3.7 | 0.010 |
| S6 | Denglouku | 3077.5 | 3.669 | 2.514 | 3.9 | 0.015 |
| S7 | Denglouku | 2874.2 | 3.06 | 2.513 | 5.9 | 0.094 |
| S8 | Denglouku | 3148.4 | 3.301 | 2.509 | 2.7 | 0.002 |
| S9 | Denglouku | 2958.5 | 3.255 | 2.465 | 3.6 | 0.017 |
| S10 | Denglouku | 2903.1 | 2.397 | 2.515 | 4.3 | 0.007 |
| S11 | Denglouku | 2898.6 | 3.459 | 2.513 | 3 | 0.023 |
| S12 | Denglouku | 2695 | 3.183 | 2.515 | 10.961 | 0.166 |
| S13 | Denglouku | 2725.3 | 3.202 | 2.507 | 9.8 | 0.072 |
| S14 | Denglouku | 2726.1 | 3.36 | 2.517 | 9.1 | 0.104 |
| S15 | Denglouku | 3055.5 | 3.115 | 2.52 | 5.628 | 0.004 |
| S16 | Denglouku | 3100.7 | 3.099 | 2.518 | 8.717 | 0.135 |
| S17 | Denglouku | 3021.2 | 3.687 | 2.513 | 7.1 | 0.048 |
| S18 | Denglouku | 2936.3 | 3.403 | 2.514 | 7.8 | 0.020 |
| Sample Number | Pore–Throat Radius Maximum /μm | Pore–Throat Radius Average /μm | Pore–Throat Radius Median /μm | Sorting Coefficient | Skewness | Maximum Mercury Injection Saturation/% | Withdrawal Efficience /% |
|---|---|---|---|---|---|---|---|
| S1 | 1.1 | 0.371 | 0.258 | 2.95 | 1.6 | 71.8 | 12.2 |
| S2 | 0.25 | 0.04 | 0.038 | 1.19 | 0.65 | 79.189 | 57.453 |
| S3 | 1.515 | 0.54 | 0.42 | 1.151 | 0.393 | 83.102 | 37.587 |
| S4 | 1.915 | 0.303 | 0.147 | 2.95 | −0.474 | 73.158 | 58.316 |
| S5 | 0.288 | 0.126 | 0.004 | 3.51 | −0.508 | 45.814 | 40.761 |
| S6 | 1.067 | 0.506 | 0.09 | 2.26 | −0.37 | 53.455 | 61.342 |
| S7 | 1.813 | 0.859 | 0.004 | 3.966 | −0.527 | 72.121 | 72.4 |
| S8 | 1.738 | 0.898 | 0.004 | 3.341 | −0.427 | 34.287 | 77.2 |
| S9 | 1.338 | 0.904 | 0.037 | 1.936 | −0.269 | 39.861 | 51.8 |
| S10 | 0.053 | 0.013 | 0.004 | 2.378 | −0.897 | 61.379 | 46.667 |
| S11 | 0.046 | 0.021 | 0.004 | 3.706 | −0.396 | 39 | 44.1 |
| S12 | 0.288 | 0.095 | 0.538 | 1.108 | 0.651 | 90.738 | 23.8 |
| S13 | 0.263 | 0.067 | 0.188 | 1.141 | 0.121 | 89.81 | 33.6 |
| S14 | 0.125 | 0.073 | 0.078 | 2.022 | 0.589 | 83.297 | 50.334 |
| S15 | 0.124 | 0.066 | 0.073 | 3.485 | 0.16 | 71.8 | 62.2 |
| S16 | 1.588 | 0.299 | 0.143 | 2.795 | 0.191 | 80.254 | 57.6 |
| S17 | 1.088 | 0.132 | 0.028 | 2.086 | 0.0267 | 73.431 | 34.404 |
| S18 | 1.458 | 0.479 | 0.104 | 2.221 | 0.152 | 75.348 | 46.903 |
| Max | 1.915 | 0.904 | 0.538 | 3.966 | 0.651 | 90.738 | 77.2 |
| Average | 0.880 | 0.319 | 0.112 | 2.427 | −0.055 | 67.414 | 50.380 |
| Min | 0.046 | 0.013 | 0.004 | 1.108 | −0.897 | 34.287 | 23.8 |
| Sample Number | Micropore | Mesopore | Macropore | D | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| D1 | R2 | φ1 | D2 | R2 | φ2 | D3 | R2 | φ3 | ||
| S1 | 2.3489 | 0.9928 | 0.11 | 2.6715 | 0.9565 | 3.69 | 2.9068 | 0.9961 | 0.60 | 2.6955 |
| S2 | 2.9986 | 0.9866 | 0.22 | 2.9583 | 0.9783 | 0.33 | 2.622 | 0.9247 | 3.15 | 2.6748 |
| S3 | 2.4228 | 0.9972 | 2.80 | 2.7626 | 0.9809 | 4.00 | 2.6347 | 0.9931 | 2.20 | 2.6256 |
| S4 | 2.9962 | 0.9695 | 1.03 | 2.9683 | 0.8636 | 4.65 | 2.3269 | 0.9926 | 0.52 | 2.9195 |
| S5 | 2.9951 | 0.9349 | 3.47 | 2.9934 | 0.9957 | 3.82 | 2.8759 | 0.9542 | 1.81 | 2.9707 |
| S6 | 2.9873 | 0.9951 | 0.52 | 2.989 | 0.9738 | 1.04 | 2.8043 | 0.992 | 2.34 | 2.8780 |
| S7 | 2.9669 | 0.869 | 1.06 | 2.993 | 0.9716 | 3.84 | 2.9045 | 0.8938 | 1.00 | 2.9733 |
| S8 | 2.9972 | 0.887 | 1.56 | 2.9923 | 0.9704 | 3.90 | 2.7746 | 0.993 | 2.34 | 2.9280 |
| S9 | 2.9921 | 0.8974 | 2.74 | 2.9897 | 0.9464 | 4.14 | 2.6939 | 0.9922 | 2.92 | 2.9023 |
| S10 | 2.9908 | 0.8776 | 0.42 | 2.9935 | 0.951 | 1.39 | 2.8085 | 0.8712 | 2.50 | 2.8858 |
| S11 | 2.9953 | 0.9516 | 0.75 | 2.9981 | 0.9303 | 0.75 | 2.9487 | 0.8646 | 1.50 | 2.9727 |
| S12 | 2.69 | 0.9321 | 0.17 | 2.3694 | 0.9944 | 0.84 | 2.5207 | 0.9948 | 1.69 | 2.4840 |
| S13 | 2.9968 | 0.9822 | 0.36 | 2.9805 | 0.9817 | 1.01 | 2.33 | 0.9192 | 2.23 | 2.5788 |
| S14 | 2.9967 | 0.9255 | 1.85 | 2.8665 | 0.9048 | 4.37 | 2.2113 | 0.9683 | 2.18 | 2.7248 |
| S15 | 2.9969 | 0.8689 | 1.70 | 2.9852 | 0.8944 | 3.76 | 2.8719 | 0.9754 | 1.63 | 2.9619 |
| S16 | 2.995 | 0.9901 | 0.48 | 2.6682 | 0.998 | 7.81 | 2.7824 | 0.9801 | 0.43 | 2.6919 |
| S17 | 2.9985 | 0.9359 | 0.05 | 2.7913 | 0.9888 | 4.70 | 2.6616 | 0.9964 | 0.88 | 2.7730 |
| S18 | 2.9953 | 0.9397 | 1.75 | 2.7598 | 0.9922 | 8.55 | 2.6855 | 0.9567 | 0.66 | 2.7930 |
| Average | 2.9089 | 0.9407 | 1.17 | 2.8739 | 0.9596 | 3.48 | 2.6869 | 0.9588 | 1.70 | 2.8019 |
| Pore Structure Classification | I | II | III |
|---|---|---|---|
| Pore Typology | Predominantly fine-to-medium intergranular pores with minor dissolution pores | Dominantly intragranular pores with subordinate intergranular pores | Primarily microporous networks with spatially limited dissolution voids |
| Throat Morphology | Narrow lamellar | Narrow lamellar | Tubular structures |
| Porosity (%) | 8.7~10.9 | 3.9~7.8 | 2.7~5.9 |
| Permeability (mD) | 0.07~0.17 | 0.004~0.05 | 0.002~0.09 |
| Median Pore–Throat Radius (μm) | 0.08~0.5 | 0.04~0.26 | 0.004~0.04 |
| Sorting Coefficient | 1.1~2.7 | 1.2~3.4 | 1.9~4.0 |
| Displacement Pressure (MPa) | 1.58~4.14 | 3.9~15.7 | 7.77~26.0 |
| Maximum Mercury Saturation (%) | >80 | 53.5~80 | 34.3~72.1 |
| Mercury Withdrawal Efficiency (%) | 23.8~57.6 | 34.4~62.2 | 40.8~77.2 |
| Fractal Dimension | 2.484~2.725 | 2.67~2.96 | 2.88~2.97 |
| Feci | >0 | −6~0 | −11.6~−6 |
| Sample ID | S3, S12, S13, S14, S16 | S1, S2, S4, S6, S7, S12, S15, S17, S18 | S5, S8, S9, S10, S11 |
| Fractal Fitting Characteristics of Representative Samples | 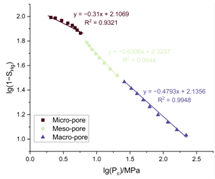 |  | 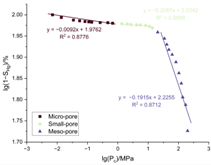 |
| Mercury Intrusion Signature of Representative Samples |  |  |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Zhang, Y.; Li, Y.; Yu, X.; Yuan, J.; Huang, B. Microscopic Pore–Throat Architecture and Fractal Heterogeneity in Tight Sandstone Reservoirs: Insights from the Denglouku Formation, Xujiaweizi Fault Depression. Appl. Sci. 2025, 15, 5730. https://doi.org/10.3390/app15105730
Wang Z, Zhang Y, Li Y, Yu X, Yuan J, Huang B. Microscopic Pore–Throat Architecture and Fractal Heterogeneity in Tight Sandstone Reservoirs: Insights from the Denglouku Formation, Xujiaweizi Fault Depression. Applied Sciences. 2025; 15(10):5730. https://doi.org/10.3390/app15105730
Chicago/Turabian StyleWang, Zeqiang, Yunfeng Zhang, Yilin Li, Xuntao Yu, Jiapeng Yuan, and Botao Huang. 2025. "Microscopic Pore–Throat Architecture and Fractal Heterogeneity in Tight Sandstone Reservoirs: Insights from the Denglouku Formation, Xujiaweizi Fault Depression" Applied Sciences 15, no. 10: 5730. https://doi.org/10.3390/app15105730
APA StyleWang, Z., Zhang, Y., Li, Y., Yu, X., Yuan, J., & Huang, B. (2025). Microscopic Pore–Throat Architecture and Fractal Heterogeneity in Tight Sandstone Reservoirs: Insights from the Denglouku Formation, Xujiaweizi Fault Depression. Applied Sciences, 15(10), 5730. https://doi.org/10.3390/app15105730





