Next Article in Journal
The Effect of Combined Extracts from By-Products, Seaweed, and Pure Phenolics on the Quality of Vacuum-Packed Fish Burgers
Previous Article in Journal
Interfacial Shear Properties of Red Clay and Polyurethane with Different Densities
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 15
Issue 10
10.3390/app15105509
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Springback Behavior of AA 7075-T6 Alloy in V-Shaped Bending

by
Çetin Karakaya
1 and
Seçil Ekşi
2,*
1
Independent Researcher, Hastings TN34 1EN, UK
2
Mechanical Engineering Department, Sakarya University, Sakarya 54100, Turkey
*
Author to whom correspondence should be addressed.
Appl. Sci. 2025, 15(10), 5509; https://doi.org/10.3390/app15105509
Submission received: 28 March 2025 / Revised: 19 April 2025 / Accepted: 2 May 2025 / Published: 14 May 2025
(This article belongs to the Section Mechanical Engineering)
Browse Figures
Versions Notes

Abstract

Springback is the most fundamental problem in all sheet metal-forming processes. Springback is affected by many process variables, and material properties are at the forefront of these variables. This study investigated the effects of the forming process at elevated temperature, bending radius, bending angle, and sheet metal thickness on the springback properties of AA 7075 aluminum alloy sheet metal with finite element analyses. The effects of process parameters on springback and maximum load are investigated using ANOVA analyses. The results show that the bending radius is the most effective on springback (45.2%). Metal thickness is the second critical parameter for springback (28.1%). The third most important factor is the process temperature (19.9%). Metal thickness (84.21%) is the most effective parameter on the maximum load. The bending angle is the second most important parameter (6.88%).

1. Introduction

Aluminum alloys are frequently preferred due to their low densities, high strength properties, low ductility values, and good corrosion resistance. Al7xxx series aluminum alloys are widely used in many vital areas of the industry due to their superior properties, such as automotive, defense, space, and aviation. However, various problems limit the shaping of these alloys using plastic forming methods. Low ductility and difficult formability at room temperature are among the factors that significantly restrict the formability of Al7075 material. To increase the forming capabilities of the Al7075 alloy, it is necessary to apply heat treatment before forming processes or to generate heat input during forming processes [1,2,3,4,5]. Sheet metal forming is a production method in many fields, such as the automotive, packaging, and home appliance industries. Bending is one of the most common processes among these production methods. The most significant problem in bending operations is springback. Springback can be defined as the elastic change in the form of a product when external loads are removed [6,7,8,9,10].
Numerous studies have focused on identifying the key factors influencing springback. These factors generally fall into two main categories: material characteristics and processing conditions. Material-related parameters include elastic modulus, yield strength, ultimate tensile strength, elongation capacity, strain hardening coefficient, plastic anisotropy, and sensitivity to strain rate. On the other hand, process-related variables encompass deformation speed, operating temperature, friction and lubrication levels, applied forming force, tool geometry and dimensions, and sheet thickness [11,12,13,14,15]. One particular study examined the influence of parameters like grain size, punch radius, and punching speed on springback behavior during micro-V-bending. The results indicated that springback tends to increase as the punch radius becomes larger. It was also noted that grain size and punch speed have a significant effect on minimizing springback [11]. In another investigation, Kim et al. analyzed how variations in temperature, blank holder force, frictional conditions, and forming rate gradients impact springback during warm forming of lightweight alloys. They observed a substantial reduction in springback when the forming temperature exceeded 200 °C, attributing this to the decreased strength of the material at elevated temperatures. Moreover, higher blank holder forces and increased friction levels contributed to minimizing springback. The study also concluded that reducing the forming rate further helps limit springback [15].
Researchers have employed various experimental methods, such as L-bending, V-bending, and U-bending, to examine and characterize springback, a crucial factor in achieving the desired geometry of bent sheet metal components. Alongside experimental approaches, numerical simulations have become widely adopted to explore the influence of tool geometry and process conditions on springback and to facilitate its prediction [16,17,18,19,20,21,22]. In a study by Lin et al., analytical solutions were proposed to evaluate springback behavior by dividing sheet metal into three segments and applying force using a rigid punch-in combination with an elastic die. The research highlighted the significant role of friction between the die and sheet during deformation. Using an elastic die helped reduce frictional effects, simplifying the shaping process with a rigid punch [23]. Carden et al. performed bending trials using three different types of automotive sheet materials. Their work analyzed variables such as the die gap-to-radius ratio, the coefficient of friction, and applied tensile forces. They also developed graphical models to analyze springback behavior and introduced these findings to the literature [24]. Mullan focused on estimating springback through a numerical algorithm that utilized two distinct bending theories. He validated his findings through corresponding experimental results [25]. Similarly, Özdemir et al. used the Minitab statistical analysis software to study how bending parameters impact springback, constructing both numerical and mathematical models to interpret their data [26,27]. Choudhury et al. explored the springback effects in V-bending operations using both experimental procedures and statistical analysis. Their findings indicated that variables such as punch dwell time, material type, and lubrication considerably impacted the springback behavior of aluminum sheets [27]. In another investigation, Panthi et al. studied how varying the die radius and sheet thickness influences the amount of springback, finding a good correlation between simulation and experimental outcomes [28]. Another researcher carried out an elastoplastic finite element analysis to predict springback, focusing on geometric factors and the mechanical properties of the material involved [29]. Liu et al. analyzed the springback behavior of 6063 aluminum profiles during the forming process, combining finite element simulations with experimental verification. Their study identified an optimal process route for manufacturing bent aluminum parts [30]. Enzhi et al. introduced a machine learning-based predictive model, supported by finite element simulations, to determine the springback angle of 7075-T6 high-strength aluminum alloy pipes. Their method provided a reliable and efficient means for estimating springback in large-diameter, thin-walled tubes and significantly enhanced the production quality of bent fittings [31].
This research focuses on analyzing the bending behavior of aluminum sheets at elevated temperatures through finite element simulations. The study explores the influence of key parameters including forming temperature, sheet thickness, bending angle, and bending radius on the V-shaped bending process. To achieve minimal springback, these parameters are optimized, and their individual and combined effects on springback are thoroughly examined. The findings are intended to serve as a reference for future applications and developments in industrial forming processes.

2. Simulation Study

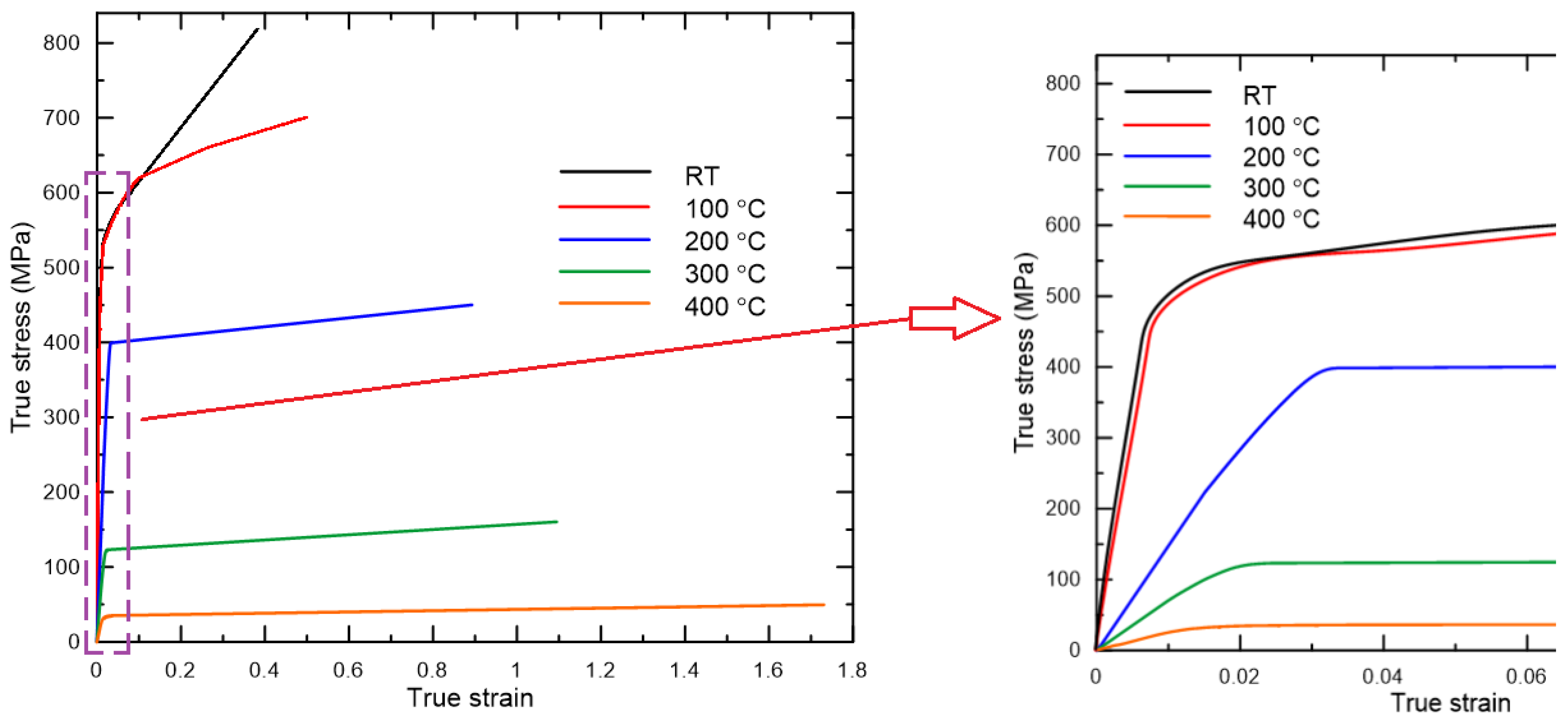
2.1. Material Properties

In this study, an AA 7075-T6 aluminum alloy was selected as the test material. The chemical composition of the alloy is presented in Table 1. Tensile tests were conducted at room and elevated temperatures to obtain the mechanical properties required for the finite element simulations. These tests were carried out at five different temperatures: room temperature (RT), 100 °C, 200 °C, 300 °C, and 400 °C, using a Zwick/Roell universal testing machine. The crosshead speed during testing was maintained at 1.0 mm/min. A visual representation of the testing setup is shown in Figure 1. All specimens were prepared and tested by EN ISO 6892-1 [32] and EN ISO 6892-2 [33] standards.
True stress–strain curves obtained from tensile test results are given in Figure 2. When the tensile tests performed at high temperatures were examined in the literature, it was seen that the results obtained were compatible with the literature [34,35,36]. Temperature-dependent material properties is given in Table 2.

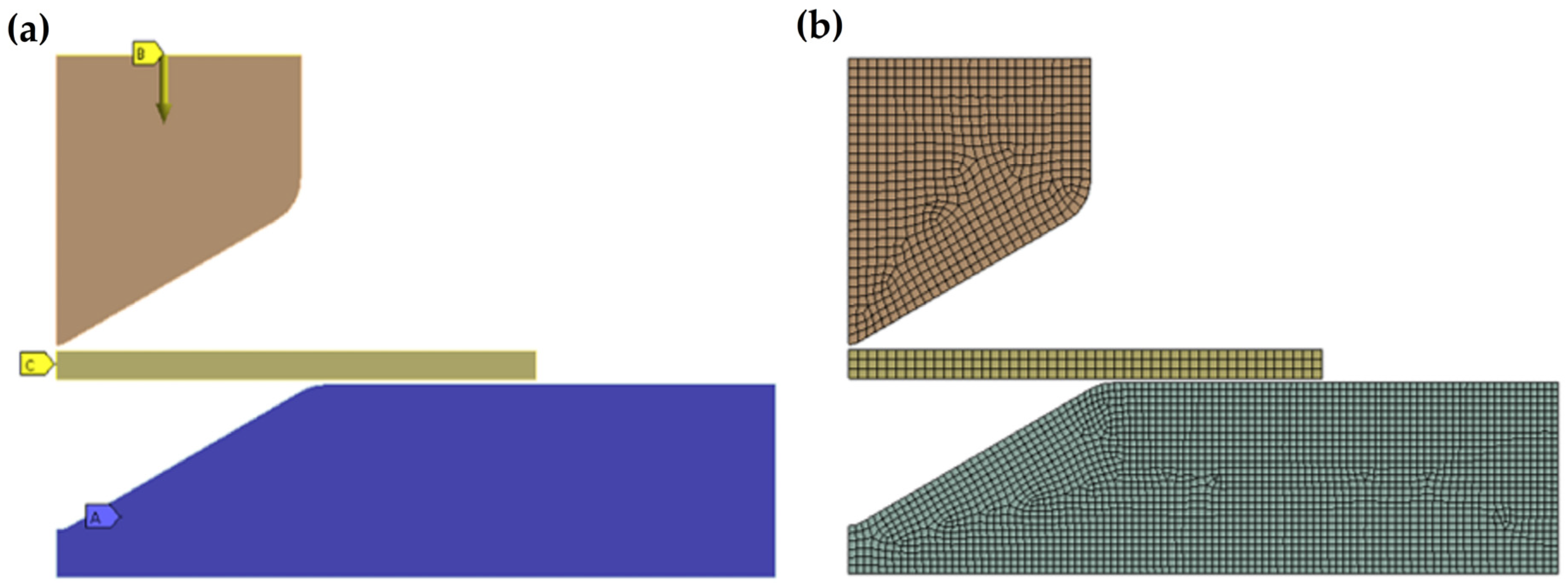
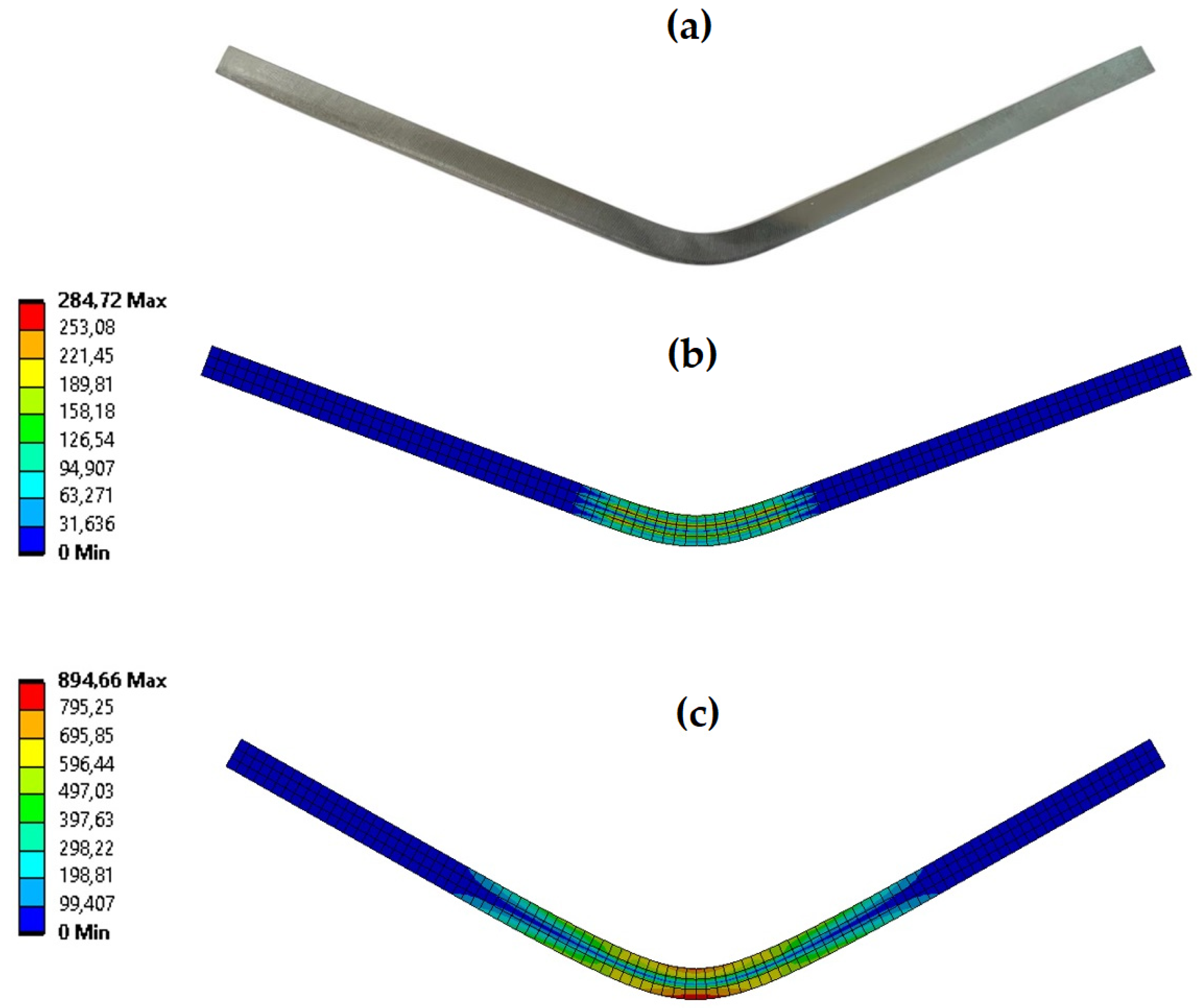
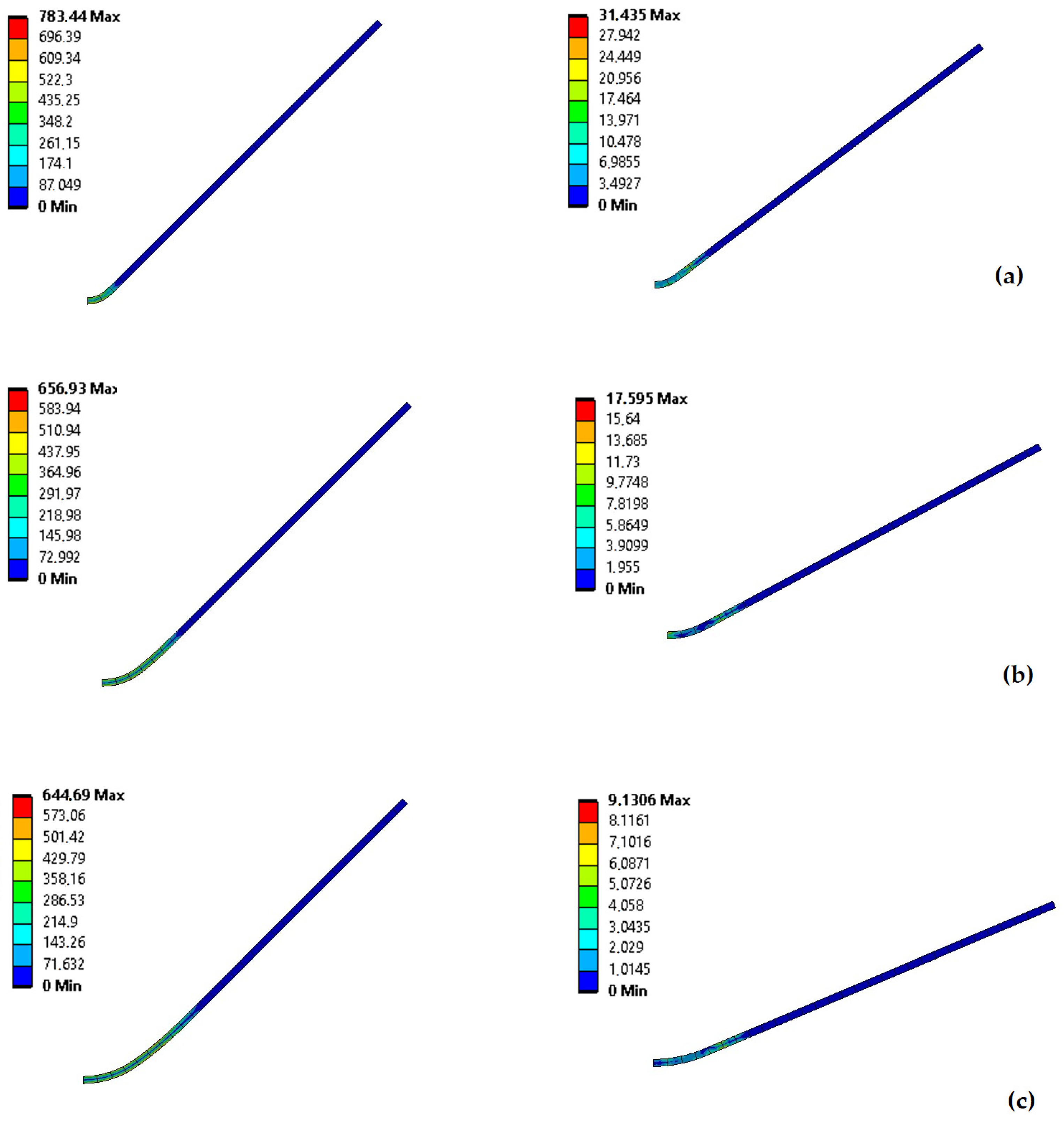
2.2. Validation of Finite Element Model

This section presents a validation study to compare the springback behavior of an AA 7075-T6 aluminum alloy at room temperature, using experimental testing and finite element simulations. The validation was performed through V-shaped bending tests utilizing 120° dies. The aluminum specimens used in the experiments had dimensions of 6 mm in thickness, 25 mm in width, and 200 mm in length. Testing was carried out on a DENER press machine with a capacity of 135 tons. All bending tests were conducted by the ASTM E290 standard, with a constant test speed of 1 mm/s. Each test was repeated three times to ensure repeatability. Following the bending process, the springback angles of the specimens were measured using a digital protractor. The experimental setup and sample geometry are illustrated in Figure 3. Finite element validation model of V-shaped bending is given Figure 4.
A finite element model was developed to replicate the experimental setup and validate the simulation methodology. The simulations were carried out using the ANSYS™ 2024 R1 software. A semi-symmetric model was constructed to enhance computational efficiency. The aluminum specimen and the die and punch components were modeled using 3062 PLANE183 elements and a total of 9619 nodes. Frictionless contact conditions were defined at the interfaces between the punch and sheet and between the sheet and die. Geometric nonlinearity was enabled in the analysis to accurately capture the large deformations occurring during the V-shaped bending process. The finite element validation model is shown in Figure 5. Additionally, Figure 5 includes the post-bending view of the aluminum specimen and the von Mises stress distribution in the model, both before and after the springback phase.
After the test, the springback value of the 6 mm thick sample was measured as 8.5°. From the finite element analysis, the springback value was obtained as 8°. The difference between the test and simulation is at an acceptable level. It was observed that the experimental and simulation images in Figure 5a,b are compatible. The comparison of springback values indicates a strong agreement between the experimental results and the finite element simulations, confirming the validity of the developed model and the simulation approach. Consequently, this modeling methodology can be confidently employed to investigate the V-shaped bending behavior of aluminum alloys under elevated temperature conditions.
A schematic view of the springback angle calculation is given in Figure 6.

2.3. Finite Element Analyses

This section investigated the V-shaped bending behavior of aluminum specimens at room and elevated temperatures with finite element simulations. The ANSYS program was used in FE analyses. True stress–strain values were used in multi-linear material properties in the ANSYS program. The finite element model of the aluminum specimen is 10 × 120 in dimensions. Sheet metal thickness (t) is 1, 2, and 3 mm. Bending angles (BA) are 60°, 90°, and 120°. Bending radius (BR) are 4 mm, 8 mm, and 12 mm in parametric analyses.
The simulation parameters to be used in the simulation studies are given in Table 3.

3. Results and Discussions

Springback refers to the partial recovery of a metal’s shape after the bending force is released. The sheet metal-forming process involves a comprehensive understanding of technical principles, manufacturing standards, and the interaction between process variables and material properties. Springback is a complex phenomenon that is challenging to predict accurately. Finite element analyses were conducted in this study to gain deeper insight into this behavior. This section will individually explore the effects of temperature, sheet metal thickness, bending radius, and bending angle on the springback behavior in V-shaped bending operations.

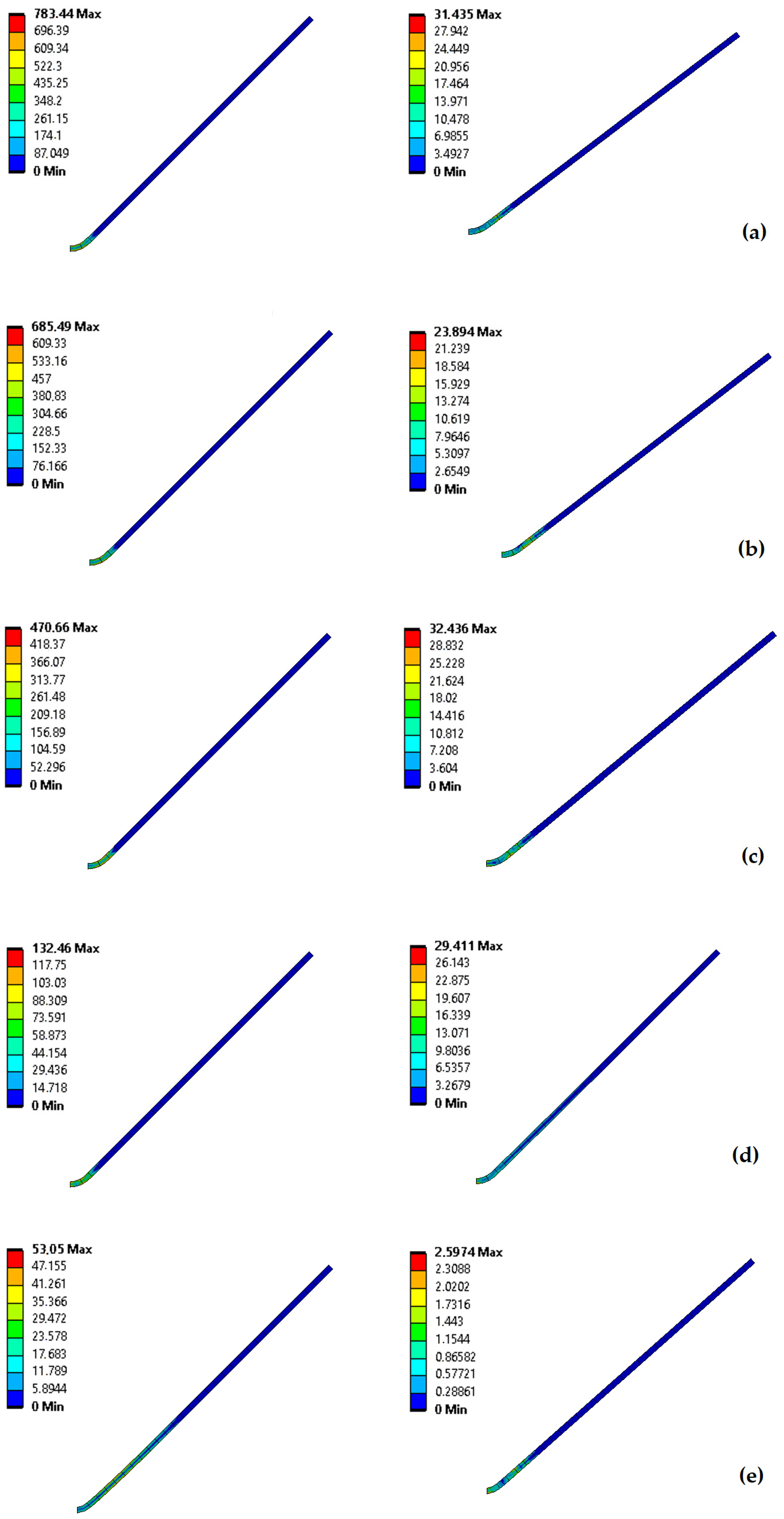
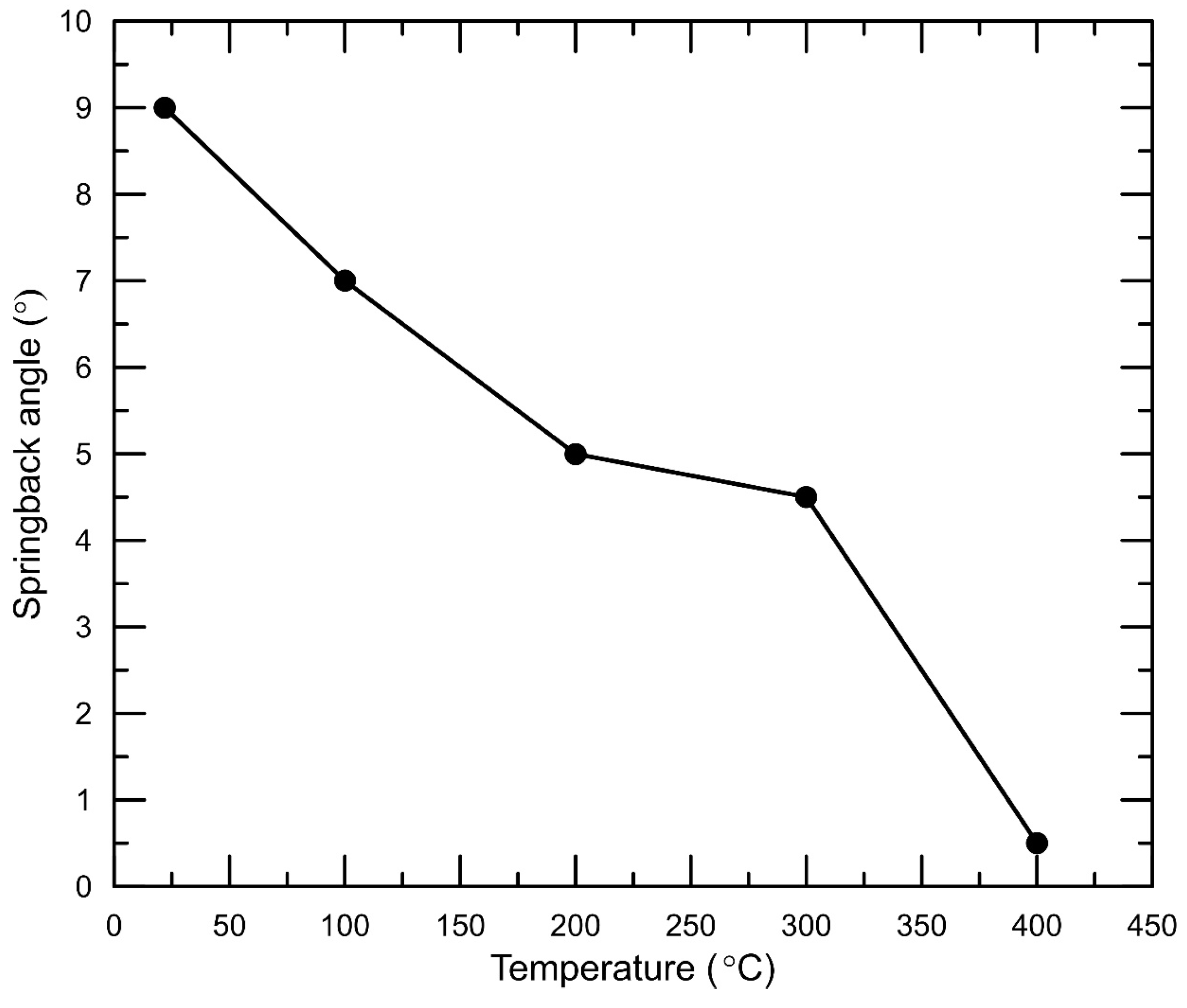
3.1. Effect of Temperature

Aluminum alloys are significantly affected by high temperatures. The mechanical properties of aluminum at elevated temperatures are reduced considerably. Temperature effects are significant for machine parts operating at high temperatures and deformation operations. In this section, the results of V-shaped bending analyses performed at room temperature, 100 °C, 200 °C, 300 °C, and 400 °C, will be presented. Von Mises stress distribution of sheet metal at RT, 100 °C, 200 °C, 300 °C, and 400 °C is given in Figure 7 obtained from FE analyses. It was observed that the maximum von Mises stress in the sheet metal decreased as the temperature increased (Figure 7). While a focus of 783.44 MPa occurred at room temperature, the stress decreased to 53.05 MPa at 400 °C. Maximum von Mises stress occurred at the middle section of V-shaped bending specimens. It is observed that the stress values decreased significantly after springback [17,37]. While 783.44 MPa stress occurred before springback at room temperature, this value decreased to 31.43 MPa after springback. At 400 °C, the values before and after springback were 53.05 MPa and 2.59 MPa, respectively.
The results obtained from the finite element analysis are presented in Table 4. As illustrated in Table 3, the springback angle was measured as 9° at room temperature and gradually decreased to 0.5° at 400 °C. This reduction highlights the significant influence of temperature on springback behavior. The forming characteristics of aluminum alloys at elevated temperatures have been extensively explored in the literature. Numerous studies report that when aluminum alloys are formed within the temperature range of 200–350 °C, formability parameters—such as drawability and elongation—can improve by approximately 200–300% [15,38,39]. While the springback value is higher at room temperature, the springback value decreases at higher temperatures [15]. Temperature appears to have an inverse effect on springback [9,40,41]. As the temperature increased, the bending load decreased, resulting in easier shaping. While 2318 N was required at room temperature, the bending load was reduced by 87% to 298 N at 400 °C. Figure 8 shows the variation in springback depending on the temperature.
As shown in Figure 8, springback decreases as temperature increases. It has been observed that the temperature dramatically influences the high-temperature deformation [41,42]. Researchers have shown that forming aluminum alloy sheets at high temperatures can increase formability and reduce springback [43,44,45].

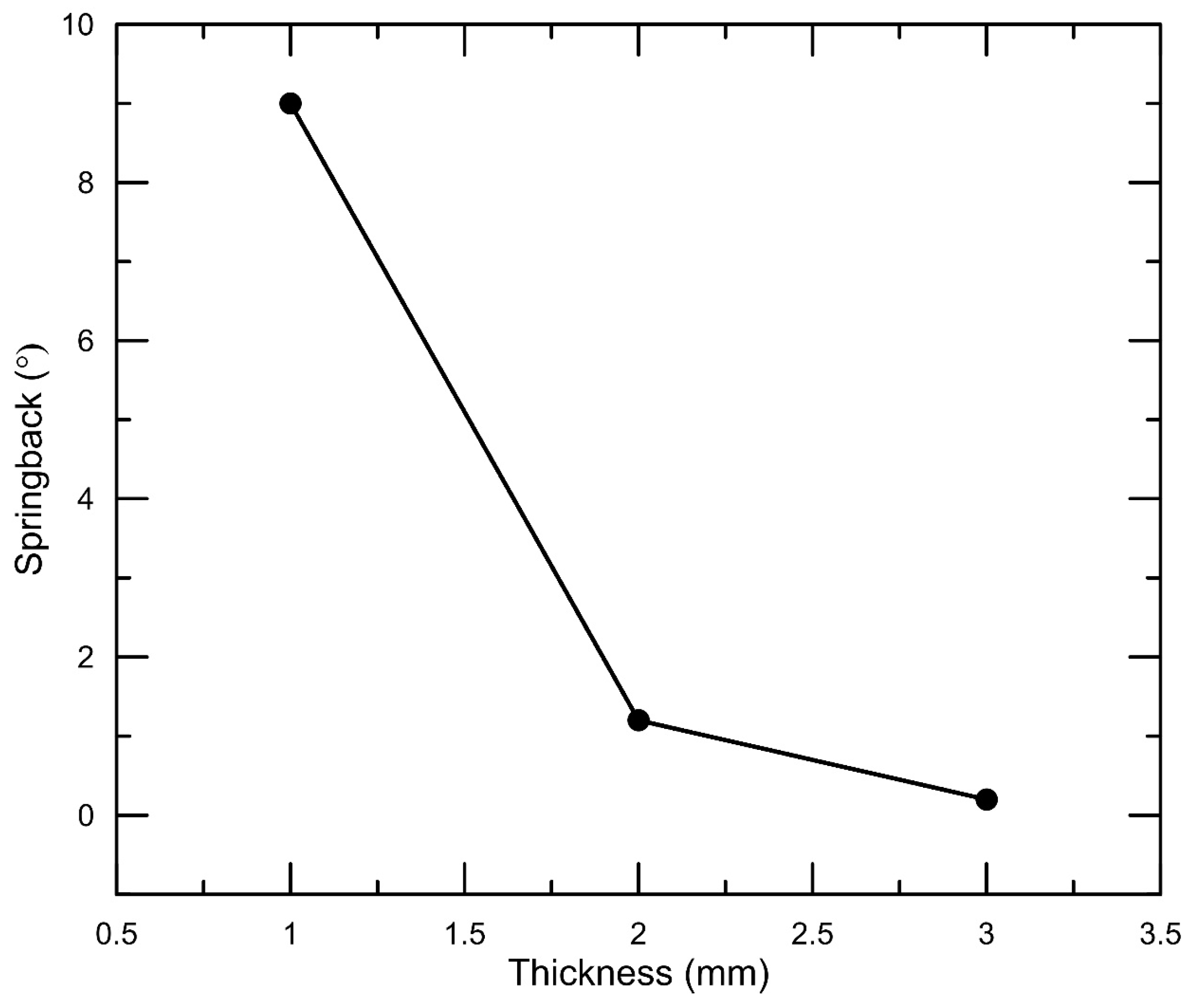
3.2. Effect of Sheet Metal Thickness

Von Mises stress distribution of sheet metal of different thicknesses is given in Figure 9. The simulations were performed at room temperature, at a constant bending radius (BR: 4 mm) and bending angle value (BA: 90°), and the springback behavior and bending load of sheet metals of different thicknesses were investigated. As the material thickness increases, the amount of elastic deformation and therefore the springback values decrease. It has been observed that the springback decreases when the sheet metal thickness increases [28]. The bending load increases while the springback decreases.
Simulation results of sheet metal at different thicknesses are given in Table 4. While the bending load was 2318 N in sheet metal with a thickness of 1 mm, the bending load increased 5.4 times to 12,556 N when the thickness increased to 3 mm. Springback decreased as the sheet thickness increased. While it was 8° in the 1 mm thick part, it decreased to 0.2 mm in the sheet metal with 3 mm thickness. Von Mises stress value also increased as the sheet thickness increased [46,47]. The highest stress was observed in the 3 mm thick sheet.
Variation in springback with sheet metal thickness is given in Figure 10.

3.3. Effect of Bending Angle

Figure 11 shows sheet metal’s von Mises stress distribution of different bending angles.
When the bending angle increased from 60° to 90°, the springback increased from 8° to 1° and increased to 9°. However, when the bending angle increased from 90° to 120°, the springback increased to 12°. It was observed that the bending load decreased as the bending angle increased. While the bending load at 60° is 4318 N, the bending load at the bending angle at 120° is 326 N.

3.4. Effect of Bending Radius

Figure 12 shows the sheet metal’s von Mises stress distribution of different bending radii. As the bending radius increases, the bending load becomes more accessible and decreases. It was observed that the degree of springback increased as the bending radius increased [45,48]. When V-shaped bending is performed with a bending radius of 4 mm, the maximum bending load is 2318 N, while when the bending radius is 12 mm, the bending load is reduced by 14% to 322 N. It has been reported in many studies in the literature that the springback angle increases linearly with the increase in the bending angle [30].
When the results are evaluated together, it is seen that, at constant material thickness (1 mm) and bending angle values (90°), nominal stresses decrease with increasing bending radius. This situation can be associated with the spreading of bending forces acting on the unit area to a wider area homogeneously with increasing bending radius and the distribution of stresses to the area rather than concentration. Accordingly, plastic deformation and deformation rates decrease. Thus, springback values increase with increasing bending radius.
In the finite element analyses performed at different bending radii, the value of the maximum stresses did not exceed the breaking stress of the aluminum material. In this case, it can be predicted that tearing will not occur in sheet metals.
The total view of simulation results obtained from finite element analyses is given in Table 4.

4. Analysis of Variance and Regression Analyses of Springback Angle and Maximum Load

Variance and regression analyses were performed using the MINITAB program. A variance analysis (ANOVA) is used to analyze the influence of parameters like temperature, sheet metal thickness, bending angle, bending radius on springback angle, and maximum load. The relationship of these parameters to the springback angle can be described by Equation (1) with a correlation coefficient (R2) of 0.96. ANOVA results are given in Table 5.
The regression equation is
Springback angle (°) = 2.33 − 0.0216 T − 5237 t + 0.0667 BA + 1.661 BR
Table 5 presents the results of the ANOVA conducted to evaluate the influence of key parameters—namely, forming temperature, sheet thickness, bending angle, and bending radius—on springback behavior. The total sum of squares was used to quantify the relative contribution of each factor, with higher values indicating a stronger influence on the response variable. These values were further utilized to calculate the percentage contribution of each parameter. As shown in Table 5, the bending radius emerges as the most dominant factor, accounting for 45.2% of the variation in springback angle. This is followed by sheet thickness, contributing 28.1%, and forming temperature, with a 19.9% influence. In contrast, the bending angle has a minimal effect on springback, contributing only 1.3%. The combined effect of these parameters on the maximum load can be described by a regression model, represented in Equation (2), which shows a strong correlation with an R2 value of 0.98, indicating excellent predictive accuracy.
Max. Load (N) = 4460 − 4.11 T + 5285 t − 66.5 BA − 310.2 BR
Table 6 shows the results of ANOVA Table 5 shows that sheet metal thickness (84.21%) is the most significant factor in maximum load, and the second factor is bending angle (6.88%). The influence of the bending radius is 4.65%. Temperature has a much lower impact among other bending parameters (2.12%).

5. Conclusions

This study investigates the springback behavior of aluminum sheet metal in V-shaped bending with finite element analyses. The effects of process temperature, metal thickness, bending radius, and bending angle on springback behavior were investigated with simulations and statistical analyses. As the bending temperature increased, the springback angle decreased. However, the maximum bending load also reduced as the temperature increased. It was observed that while the metal thickness increased, the springback decreased, while the maximum bending load increased. As the bending angle changed, the springback values in the sheet metal changed. When the bending angle was increased, the springback angle formed in the sheet metal increased. The effect of the bending radius was similar to the effect of the bending angle. The effects of process temperature, metal thickness, bending radius, and bending angle on springback and maximum load were found by analysis of variance (ANOVA). According to the variance analysis, the effective parameter on the springback was the bending radius of 45.2%. Metal thickness is the maximum load’s most influential parameter (84.21%).

Author Contributions

Ç.K.: conceptualization; methodology; software; validation; investigation; data curation; writing—original draft preparation; writing—review and editing; and visualization. S.E.: conceptualization; methodology; software; validation; writing—review and editing; visualization and project administration. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The original contributions presented in the study are included in the article. Further inquiries can be directed to the corresponding author.

Acknowledgments

This research was not funded by any institution.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Choi, Y.; Lee, J.; Panicker, S.S.; Jin, H.K.; Panda, S.K.; Lee, M.G. Mechanical Properties, Springback, and Formability of W-Temper and Peak Aged 7075 Aluminum Alloy Sheets: Experiments and Modeling. Int. J. Mech. Sci. 2020, 170, 105344. [Google Scholar] [CrossRef]
  2. Wang, H.; Yan, Z.; Xiao, A.; Yu, Z.; Chen, X.; Cui, X. Improvement of Flanging Accuracy with Small Springback and Service Performance of AA7075 Using High-Speed Forming. J. Manuf. Process. 2024, 119, 790–805. [Google Scholar] [CrossRef]
  3. Du, Z.; Han, Y.; Han, D.; Zhang, H.; Mao, X.; Zhang, Z.; Cui, X. Effect of Heat Treatment and Electromagnetic Forming on Springback and Related Properties of 7075 Aluminum Alloy Sheet. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 1–14. [Google Scholar] [CrossRef]
  4. Yan, Z.; Du, Z.; Cui, X.; Huang, C.; Meng, Y. Springback and Deformation Uniformity of High-Strength Aluminum Alloy Sheet Using Electromagnetic Forming. Int. J. Adv. Manuf. Technol. 2021, 114, 1293–1308. [Google Scholar] [CrossRef]
  5. Kim, H.K.; Kim, W.J. A Springback Prediction Model for Warm Forming of Aluminum Alloy Sheets Using Tangential Stresses on a Cross-Section of Sheet. Metals 2018, 8, 257. [Google Scholar] [CrossRef]
  6. Chen, C.; Jiang, C. Grain Size Effect in the Micro-V-Bending Process of Thin Metal Sheets. Mater. Manuf. Process. 2011, 6914, 78–83. [Google Scholar] [CrossRef]
  7. Mohammadtabar, N.; Bakhshi-Jooybari, M.; Gorji, H.; Jamaati, R.; Szpunar, J.A. Effect of Electric Current Pulse Type on Springback, Microstructure, Texture, and Mechanical Properties During V-Bending of AA2024 Aluminum Alloy. J. Manuf. Sci. Eng. 2021, 143, 011004. [Google Scholar] [CrossRef]
  8. Ozturk, F.; Ece, R.E.; Polat, N.; Koksal, A. Effect of Warm Temperature on Springback Compensation of Titanium Sheet Effect of Warm Temperature on Springback. Mater. Manuf. Process. 2010, 6914, 1021–1024. [Google Scholar] [CrossRef]
  9. Pornputsiri, N.; Kanlayasiri, K. Effect of Bending Temperatures on the Microstructure and Springback of a TRIP Steel Sheet. Def. Technol. 2020, 16, 980–987. [Google Scholar] [CrossRef]
  10. Yue, Z.; Qi, J.; Zhao, X.; Badreddine, H.; Gao, J.; Chu, X. Springback Prediction of Aluminum Alloy Sheet under Changing Loading Paths with Consideration of the Influence of Kinematic Hardening and Ductile Damage. Metals 2018, 8, 950. [Google Scholar] [CrossRef]
  11. Chen, C. Experimental Study on Punch Radius and Grain Size Effects in V-Bending Process. Mater. Manuf. Process. 2014, 29, 461–465. [Google Scholar] [CrossRef]
  12. Chen, Y.; Li, X.; Lang, L. Various Elastic Moduli of AA6016 and Their Application on Accurate Prediction of Springback. J. Chin. Inst. Eng. 2019, 42, 319–326. [Google Scholar] [CrossRef]
  13. Kagzi, S.A.; Gandhi, A.H.; Dave, H.K.; Raval, H.K. An Analytical Model for Bending and Springback of Bimetallic Sheets. Mech. Adv. Mater. Struct. 2016, 23, 80–88. [Google Scholar] [CrossRef]
  14. Kim, D.; Kim, J.H.; Lee, M.G.; Lee, Y.S.; Kang, S.H. Experimental Investigation into Effect of Annealing Treatment on Springback of Magnesium Alloy Sheets. Mater. Res. Innov. 2013, 15 (Suppl. 1), s183–s186. [Google Scholar] [CrossRef]
  15. Seok, H.; Koc, M. Numerical Investigations on Springback Characteristics of Aluminum Sheet Metal Alloys in Warm Forming Conditions. J. Mater. Process. Technol. 2007, 4, 370–383. [Google Scholar] [CrossRef]
  16. Asgari, S.A.; Pereira, M.; Rolfe, B.F.; Dingle, M.; Hodgson, P.D. Statistical Analysis of Finite Element Modeling in Sheet Metal Forming and Springback Analysis. J. Mater. Process. Technol. 2007, 3, 129–136. [Google Scholar] [CrossRef]
  17. Chatti, S. Effect of the Elasticity Formulation in Finite Strain on Springback Prediction. Comput. Struct. 2010, 88, 796–805. [Google Scholar] [CrossRef]
  18. Fu, Z.; Mo, J. Multiple-Step Incremental Air-Bending Forming of High-Strength Sheet Metal Based on Simulation Analysis. Mater. Manuf. Process. 2010, 25, 808–816. [Google Scholar] [CrossRef]
  19. Lee, S.W.; Yang, D.Y. An Assessment of Numerical Parameters Influencing Springback in Explicit Finite Element Analysis of Sheet Metal Forming Process. J. Mater. Process. Technol. 1998, 81, 60–67. [Google Scholar] [CrossRef]
  20. Li, X.; Yang, Y.; Wang, Y.; Bao, J.; Li, S. Effect of the Material-Hardening Mode on the Springback Simulation Accuracy of V-Free Bending. J. Mater. Process. Technol. 2002, 123, 209–211. [Google Scholar] [CrossRef]
  21. Nasrollahi, V.; Arezoo, B. Prediction of Springback in Sheet Metal Components with Holes on the Bending Area, Using Experiments, Finite Element and Neural Networks. Mater. Des. 2012, 36, 331–336. [Google Scholar] [CrossRef]
  22. Wasif, M.; Fatima, A.; Iqbal, S.A.; Tufail, M.; Karim, H. Analysis and Optimization of Springback during the V-Bending of Hot-Rolled High Strength Steels (JSH440). J. Eng. Res. 2022, 10, 298–314. [Google Scholar] [CrossRef]
  23. Zhang, L.C.; Lin, Z. An Analytical Solution to Springback of Sheet Metals Stamped by a Rigid Punch and an Elastic Die. J. Mater. Process Technol. 1997, 63, 49–54. [Google Scholar] [CrossRef]
  24. Carden, W.D.; Geng, L.M.; Matlock, D.K.; Wagoner, R.H. Measurement of Springback. Int. J. Mech. Sci. 2002, 44, 79–101. [Google Scholar] [CrossRef]
  25. Mullan, H.B. Improved Prediction of Springback on Final Formed Components. J. Mater. Process Technol. 2004, 153–154, 464–471. [Google Scholar] [CrossRef]
  26. Özdemir, M.; Dilipak, H.; Bostan, B. Numerically Modeling Spring Back and Spring Go Amounts and Bending Deformations of Cr-Mo Alloyed Sheet Material. Mater. Test. 2020, 62, 1265–1272. [Google Scholar] [CrossRef]
  27. Choudhury, I.A.; Ghomi, V. Springback Reduction of Aluminum Sheet in V-Bending Dies. Proc. Inst. Mech. Eng. B J. Eng. Manuf. 2014, 228, 917–926. [Google Scholar] [CrossRef]
  28. Panthi, S.K.; Ramakrishnan, N.; Pathak, K.K.; Chouhan, J.S. An Analysis of Springback in Sheet Metal Bending Using Finite Element Method (FEM). J. Mater. Process Technol. 2007, 186, 120–124. [Google Scholar] [CrossRef]
  29. Panthi, S.K.; Ramakrishnan, N.; Ahmed, M.; Singh, S.S.; Goel, M.D. Finite Element Analysis of Sheet Metal Bending Process to Predict the Springback. Mater. Des. 2010, 31, 657–662. [Google Scholar] [CrossRef]
  30. Liu, Z.; Li, L.; Wang, G.; Chen, J.; Yi, J. Springback Behaviors of Extruded 6063 Aluminum Profile in Subsequent Multi-Stage Manufacturing Processes. Int. J. Adv. Manuf. Technol. 2020, 109, 1–13. [Google Scholar] [CrossRef]
  31. Gao, E.; Xue, D.; Li, Y. Springback Angle Prediction for High-Strength Aluminum Alloy Bending via Multi-Stage Regression. Metals 2025, 15, 358. [Google Scholar] [CrossRef]
  32. ISO 6892-1: 2019; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature. International Organization for Standardization (ISO): Geneva, Switzerland, 2019.
  33. ISO 6892-2: 2018; Metallic Materials—Tensile Testing—Part 2: Method of Test at Elevated Temperature. International Organization for Standardization (ISO): Geneva, Switzerland, 2018.
  34. Pandya, K.S.; Roth, C.C.; Mohr, D. Strain Rate and Temperature Dependent Fracture of Aluminum Alloy 7075: Experiments and Neural Network Modeling. Int. J. Plast. 2020, 135, 102788. [Google Scholar] [CrossRef]
  35. Su, M.N.; Young, B. Material Properties of Normal and High Strength Aluminium Alloys at Elevated Temperatures. Thin-Walled Struct. 2019, 137, 463–471. [Google Scholar] [CrossRef]
  36. Zhang, H.; He, Y.; Li, L. Tensile Deformation and Fracture Behavior of Spray-Deposition 7075/15SiCp Aluminum Matrix Composite Sheet at Elevated Temperatures. Mater. Charact. 2008, 59, 1078–1082. [Google Scholar] [CrossRef]
  37. Hakimi, S.; Soualem, A. Evaluation of the sensitivity of springback to various process parameters of aluminum alloy sheet with different heat treatment conditions. Eng. Solid Mech. 2021, 9, 323–334. [Google Scholar] [CrossRef]
  38. Li, D.; Ghosh, A. Tensile Deformation Behavior of Aluminum Alloys at Warm Forming Temperatures. Mater. Sci. Eng. A 2003, 352, 279–286. [Google Scholar] [CrossRef]
  39. Finch, D.M.; Wilson, S.P.; Dorn, J.E. Deep-Drawing Aluminum Alloys at Elevated Temperatures. Trans. Am. Soc. Met. 1946, 36, 254–289. [Google Scholar]
  40. Öztürk, F.; Toros, S.; Kılıç, S.; Baş, M.H. Effects of Cold and Warm Temperatures on Springback of Aluminium—Magnesium Alloy 5083-H111. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2009, 223, 427–431. [Google Scholar] [CrossRef]
  41. Hou, H.; Zhao, G.; Yu, J.; Sun, Y.; Li, H. Experimental Studies and Modeling of Strain Rate- and Temperature-Dependent Springback Behavior of Hot-Deformed Aluminum Alloys. J. Mater. Process Technol. 2023, 318, 118029. [Google Scholar] [CrossRef]
  42. Grze, R.; Manach, P.Y.; Laurent, H.; Thuillier, S.; Menezes, L.F. Influence of the Temperature on Residual Stresses and Springback Effect in an Aluminium Alloy. Int. J. Mech. Sci. 2010, 52, 1094–1100. [Google Scholar] [CrossRef]
  43. Ma, W.P.; Wang, B.Y.; Xiao, W.C.; Yang, X.M.; Kang, Y. Springback Analysis of 6016 Aluminum Alloy Sheet in Hot V-Shape Stamping. J. Cent. South. Univ. 2019, 26, 524–535. [Google Scholar] [CrossRef]
  44. Daoming, L.; Ghosh, A.K. Effects of Temperature and Blank Holding Force on Biaxial Forming Behavior of Aluminum Sheet Alloys. J. Mater. Eng. Perform. 2004, 13, 348–360. [Google Scholar] [CrossRef]
  45. Zhang, J.X.; Fan, J.X.; Liu, Y.T.; Feng, W. Superplasticity of 6016 Aluminum Alloy at Elevated Temperatures. Rare Met. 2015, 34, 387–394. [Google Scholar] [CrossRef]
  46. Nikhare, C.P.; Kotkunde, N.; Singh, S.K. Effect of Material Discontinuity on Springback in Sheet Metal Bending. Adv. Mater. Process. Technol. 2021, 8, 1800–1819. [Google Scholar] [CrossRef]
  47. Tek, Z. An Experimental Study on the Examination of Springback of Sheet Metals with Several Thicknesses and Properties in Bending Dies. J. Mater. Process. Technol. 2004, 145, 109–117. [Google Scholar] [CrossRef]
  48. Sharma, P.K.; Gautam, V.; Agarwal, A. Effect of Punch Profile Radius and Sheet Setting on Springback in V-Bending of A 2-Ply Sheet. Adv. Mater. Process. Technol. 2023, 9, 416–424. [Google Scholar] [CrossRef]
Applsci 15 05509 g001
Figure 1. Tensile test machine.
Figure 1. Tensile test machine.
Applsci 15 05509 g001
Applsci 15 05509 g002
Figure 2. True stress–true strain curves of AA 7075-T6 at RT, 100 °C, 200 °C, 300 °C, 400 °C.
Figure 2. True stress–true strain curves of AA 7075-T6 at RT, 100 °C, 200 °C, 300 °C, 400 °C.
Applsci 15 05509 g002
Applsci 15 05509 g003
Figure 3. The experimental setup and test specimen; (a) Test machine; (b) Test specimen.
Figure 3. The experimental setup and test specimen; (a) Test machine; (b) Test specimen.
Applsci 15 05509 g003
Applsci 15 05509 g004
Figure 4. Finite element validation model of V-shaped bending. (a) Meshed model. (b) Boundary conditions of the model.
Figure 4. Finite element validation model of V-shaped bending. (a) Meshed model. (b) Boundary conditions of the model.
Applsci 15 05509 g004
Applsci 15 05509 g005
Figure 5. Test and simulation results. (a) Specimen view of the aluminum plate after the V-shaped bending test, (b) von Mises stress distribution of the FE model after the springback, (c) von Mises stress distribution of the FE model before the springback.
Figure 5. Test and simulation results. (a) Specimen view of the aluminum plate after the V-shaped bending test, (b) von Mises stress distribution of the FE model after the springback, (c) von Mises stress distribution of the FE model before the springback.
Applsci 15 05509 g005
Applsci 15 05509 g006
Figure 6. Schematic view of springback angle calculation.
Figure 6. Schematic view of springback angle calculation.
Applsci 15 05509 g006
Applsci 15 05509 g007
Figure 7. Von Mises stress distribution of sheet metal before and after springback (t = 1 mm) at (a) RT, (b) 100 °C, (c) 200 °C, (d) 300 °C, (e) 400 °C.
Figure 7. Von Mises stress distribution of sheet metal before and after springback (t = 1 mm) at (a) RT, (b) 100 °C, (c) 200 °C, (d) 300 °C, (e) 400 °C.
Applsci 15 05509 g007
Applsci 15 05509 g008
Figure 8. Variation in springback with temperature.
Figure 8. Variation in springback with temperature.
Applsci 15 05509 g008
Applsci 15 05509 g009
Figure 9. Von Mises stress distribution of sheet metal of different thicknesses before and after springback: (a) t = 1 mm, (b) t = 2 mm, (c) t = 3 mm.
Figure 9. Von Mises stress distribution of sheet metal of different thicknesses before and after springback: (a) t = 1 mm, (b) t = 2 mm, (c) t = 3 mm.
Applsci 15 05509 g009
Applsci 15 05509 g010
Figure 10. Variation in springback with sheet metal thickness.
Figure 10. Variation in springback with sheet metal thickness.
Applsci 15 05509 g010
Applsci 15 05509 g011
Figure 11. Von Mises stress distribution of sheet metal of different bending angles: (a) 60°, before and after springback (b) 90°, (c) 120°.
Figure 11. Von Mises stress distribution of sheet metal of different bending angles: (a) 60°, before and after springback (b) 90°, (c) 120°.
Applsci 15 05509 g011
Applsci 15 05509 g012
Figure 12. Von Mises stress distribution of sheet metal of different bending radii before and after springback: (a) r = 4 mm, (b) r = 8 mm, (c) r = 12.
Figure 12. Von Mises stress distribution of sheet metal of different bending radii before and after springback: (a) r = 4 mm, (b) r = 8 mm, (c) r = 12.
Applsci 15 05509 g012
Table 1. Chemical composition of aluminum AA 7075-T6.
Table 1. Chemical composition of aluminum AA 7075-T6.
ElementAlZnMgCuCrFeSiTi
Content (%)88.7763.081.520.240.230.10.03
Table 2. Temperature-dependent material properties.
Table 2. Temperature-dependent material properties.
Temperature
(°C)		Young’s Module (GPa)Yield Strength
(MPa)		Tensile Strength (MPa)Elongation at Break (%)
RT7054058220
1006852054523
2006540038524
3005912313026
40052354050
Table 3. Simulation parameters and levels.
Table 3. Simulation parameters and levels.
Bending ParametersLevels
Thickness, t (mm)1–2–3
Bending angle, BA, (°)60–90–120
Bending radius, BR, (mm)4–8–12
Temperature, T, (°C)RT–100–200–300–400
Table 4. Total view of simulation results.
Table 4. Total view of simulation results.
Temperature, T,
(°C)		Bending Angle, BA
(°)		Bending Radius, BR
(mm)		Thickness, t,
(mm)		Max. Load
(N)		Springback Angle
(°)
22904123189
100904120447
200904119485
300904119224.5
40090412980.5
22904123189
22904285901.2
22904312,5560.2
22604143188
22904123189
221204132612
22904123189
22908143017
229012132222
Table 5. ANOVA results.
Table 5. ANOVA results.
Variance SourceDFAdj SSAdj MSF-Valuep-ValueContribution Rate (%)
Temperature, T, (°C)167.88467.88421.970.00319.9
Thickness, t, (mm)195.82395.82331.010.00128.1
Bending angle, BA, (°)14.5004.5001.460.2731.3
Bending radius, BR, (°)1154.180154.18049.900.00045.2
Error618.5403.090 5.4
Total10340.927 100
Table 6. ANOVA results.
Table 6. ANOVA results.
Variance SourceDFAdj SSAdj MSF-Valuep-ValueContribution Rate (%)
Temperature, T, (°C)12.454.7062.454.7065.850.0522.12
Thickness (t)197.580.91197.580.911232.500.00084.21
Bending angle, BA, (°)17.968.0327.968.03218.980.0056.88
Bending radius, BR, (°)15.378.6605.378.66012.820.0124.65
Error62.518.261419.710 2.17
Total10115.900.570 100
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Karakaya, Ç.; Ekşi, S. Springback Behavior of AA 7075-T6 Alloy in V-Shaped Bending. Appl. Sci. 2025, 15, 5509. https://doi.org/10.3390/app15105509

AMA Style

Karakaya Ç, Ekşi S. Springback Behavior of AA 7075-T6 Alloy in V-Shaped Bending. Applied Sciences. 2025; 15(10):5509. https://doi.org/10.3390/app15105509

Chicago/Turabian Style

Karakaya, Çetin, and Seçil Ekşi. 2025. "Springback Behavior of AA 7075-T6 Alloy in V-Shaped Bending" Applied Sciences 15, no. 10: 5509. https://doi.org/10.3390/app15105509

APA Style

Karakaya, Ç., & Ekşi, S. (2025). Springback Behavior of AA 7075-T6 Alloy in V-Shaped Bending. Applied Sciences, 15(10), 5509. https://doi.org/10.3390/app15105509

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop