Efficient Discovery of Association Rules in E-Commerce: Comparing Candidate Generation and Pattern Growth Techniques

Abstract

Association rule mining plays a critical role in uncovering item correlations and hidden patterns within transactional data, particularly in e-commerce environments. Despite the widespread use of Apriori and FP-Growth algorithms, few studies offer a statistically rigorous, tool-based comparison of their performance on real-world e-commerce data. This paper addresses this gap by evaluating both algorithms in terms of execution time, memory consumption, rule generation volume, and rule strength (support, confidence, and lift). Implementations in RapidMiner and an analysis through SPSS establish statistically significant performance differences, particularly under varying support thresholds. Our findings confirm that FP-Growth consistently outperforms Apriori for large-scale datasets due to its ability to bypass candidate generation, while Apriori retains pedagogical and small-scale relevance. The study contributes practical guidance for data scientists and e-commerce practitioners choosing suitable rule-mining techniques based on their data size and performance constraints.

1. Introduction

In the era of data-driven decision-making, organizations increasingly rely on advanced analytics to extract actionable insights from vast volumes of transactional data. E-commerce platforms, in particular, generate high-dimensional, complex datasets derived from customer purchase histories, browsing behavior, and engagement patterns. Leveraging these data to discover frequent patterns and associations enables critical applications such as real-time recommendation engines, personalized marketing, dynamic inventory management, and automated pricing strategies, all of which are essential for maintaining competitiveness in the rapidly evolving digital marketplace.

Extracting frequent patterns and associations from these data supports key applications such as real-time product recommendation systems [1], dynamic pricing strategies [2], and intelligent inventory management [3]. These tasks increasingly rely on scalable, interpretable, and statistically robust pattern mining algorithms that can perform under high-volume transactional loads and evolving user behaviors. Consequently, evaluating the practical trade-offs between popular algorithms like Apriori and FP-Growth becomes essential for real-world deployment.

Among the most widely adopted techniques for uncovering hidden relationships in transactional data is association rule mining, a foundational method rooted in market basket analysis [4]. This approach aims to identify co-occurrence relationships between items using key metrics such as support, confidence, and lift to evaluate rule relevance and strength [5].

Two dominant algorithms in this domain are Apriori and FP-Growth. The Apriori algorithm, introduced by Agrawal and Srikant [6], utilizes a breadth-first search strategy and multiple database scans to generate frequent itemsets. In contrast, FP-Growth, proposed by Han et al. [7], adopts a more scalable divide-and-conquer approach by constructing a compact FP-Tree and mining itemsets without candidate generation. Both algorithms have been widely studied in the data mining literature.

However, a clear research gap persists in the empirical, tool-based comparison of Apriori and FP-Growth in real-world e-commerce contexts. Most prior studies have focused on synthetic or small-scale datasets, often emphasizing theoretical differences without validating performance through statistically rigorous experimentation. Moreover, few works investigate how these algorithms perform under varying threshold settings (e.g., minimum support and confidence) or assess practical concerns such as memory efficiency and rule interpretability, key factors for operational deployment in modern e-commerce systems. Additionally, integrated benchmarking using end-to-end data science platforms such as RapidMiner combined with formal statistical validation (e.g., in SPSS) remains rare.

This study addresses these limitations by conducting a comprehensive comparative analysis of Apriori and FP-Growth on a real-world e-commerce dataset. We evaluate each algorithm across dimensions including the execution time, memory usage, number of generated rules, and rule strength metrics. By varying the parameter settings and validating the results through descriptive and inferential statistical techniques, this research provides both theoretical insights and practical guidance for data scientists, analysts, and system architects.

The key contributions of this study include a practical, tool-based implementation of the Apriori and FP-Growth algorithms using RapidMiner v. Studio 7, the development of a statistically validated performance evaluation framework through SPSS, and the provision of empirical insights into the trade-offs between the two algorithms when applied to real-world conditions.

The rest of the paper is structured as follows: Section 2 reviews the related literature and algorithmic background; Section 3 describes the research methodology and implementation details; Section 4 presents the comparative analysis and findings; and Section 5 concludes with reflections and future research directions.

2. The Related Literature and Background

2.1. Association Rule Mining: Origins and Core Concepts

Association rule mining is a cornerstone of knowledge discovery in databases, originally introduced for a market basket analysis [4]. It aims to identify co-occurrence relationships among items within transactional datasets, typically expressed in the form of association rules: X → Y, where X and Y are disjoint itemsets.

The quality and significance of association rules are assessed using three key metrics. Support measures the proportion of transactions that contain both X and Y, indicating how frequently the rule occurs in the dataset. Confidence quantifies the likelihood that a transaction containing X also includes Y, reflecting the rule’s predictive strength. Lift compares the observed co-occurrence of X and Y to the expected co-occurrence if the two items were statistically independent, providing insights into the rule’s potential usefulness beyond random chance.

These metrics are widely accepted in evaluating the statistical relevance and practical usefulness of association rules [5].

2.2. Key Algorithms for Association Rule Mining

Over the years, several algorithms have been developed for the efficient discovery of frequent itemsets and generation of association rules from large transactional datasets. Among these, Apriori and FP-Growth remain two of the most widely studied and implemented due to their foundational roles and contrasting strategies. Additionally, other algorithmic variants and improvements have emerged to address specific performance bottlenecks in diverse data environments.

The Apriori algorithm, introduced by Agrawal and Srikant [6], follows a breadth-first, level-wise approach to generate candidate itemsets. It is built on the Apriori property, which asserts that all non-empty subsets of a frequent itemset must themselves be frequent. This enables pruning of the search space by eliminating infrequent candidates early.

The algorithm proceeds iteratively: it first identifies frequent 1-itemsets, then extends them to larger itemsets (k-itemsets) by joining frequent (k − 1)-itemsets. In each iteration, the database is rescanned to count support values. Once all frequent itemsets are identified, association rules are generated from them using thresholds for confidence and lift.

Although conceptually simple and historically significant, Apriori’s major drawback lies in its multiple database scans and exponential growth in candidate itemsets, which result in high computational costs for large or dense datasets [8].

To overcome the inefficiencies of Apriori, Han et al. [7] proposed the FP-Growth (Frequent Pattern Growth) algorithm. Unlike Apriori, FP-Growth eliminates candidate generation by constructing a compact structure known as the FP-Tree, which captures itemset frequencies in a prefix-tree format.

The algorithm starts with a scan of the database to identify frequent items and sort them by frequency. In a second pass, each transaction is mapped into the FP-tree based on this ordering. Mining then proceeds by recursively generating conditional pattern bases and constructing conditional FP-trees to extract frequent itemsets through a divide-and-conquer strategy.

This approach significantly reduces both the execution time and memory usage, particularly for large, sparse datasets. However, managing FP-trees can be challenging when datasets contain a very large number of distinct items or low-overlap transactions.

In addition to Apriori and FP-Growth, several alternative algorithms have been developed to address specific computational challenges in association rule mining.

Eclat (Equivalence Class Transformation), introduced by Zaki [9], employs a depth-first traversal strategy combined with a vertical data format, making it efficient for dense datasets, though it can become memory-intensive when dealing with large transaction volumes.

DHP (Direct Hashing and Pruning), a variant of Apriori proposed by Park et al. [10], uses hashing techniques to reduce the number of candidate itemsets and limit unnecessary database scans early in the mining process.

H-Mine, tailored for high-dimensional data, organizes items into a hierarchical structure to boost performance on complex datasets [11].

Lastly, Closet+ focuses on mining closed frequent itemsets—those that have no supersets with the same support—thereby reducing redundancy and enhancing the efficiency of rule generation [12].

Each of these algorithms brings trade-offs in terms of scalability, memory usage, and dataset suitability. However, Apriori and FP-Growth continue to serve as standard benchmarks due to their contrasting design philosophies and widespread implementation in modern data mining tools.

2.3. Ongoing Challenges in Association Rule Mining

Despite significant advancements in algorithmic efficiency, association rule mining continues to face several persistent challenges that drive ongoing research.

One major issue is scalability. As datasets grow in size and dimensionality, ensuring computational efficiency becomes increasingly difficult. Researchers often explore solutions such as parallelization and distributed computing frameworks like Hadoop and Spark to manage this complexity. Another challenge is data sparsity, common in real-world scenarios, which leads to an overabundance of low-support itemsets. To address this, techniques such as support threshold tuning and optimized data representations have been developed [13].

Overfitting and interpretability also pose problems, as generating too many rules can result in models that are difficult to generalize or understand. This issue is often mitigated through rule pruning and the application of interestingness measures, such as conviction and chi-squared tests [14].

Finally, the complexity of evaluating rule quality remains a concern; while traditional metrics like confidence and lift are widely used, they may not fully capture the utility of a rule. As a result, newer approaches increasingly incorporate statistical significance testing and domain-specific validation to enhance evaluation accuracy.

2.4. Emerging Applications and Research Directions

Association rule mining continues to evolve, finding applications across a wide range of domains. In healthcare, it is used to uncover patterns in diagnoses, treatments, and drug interactions [15]. In the field of cybersecurity, it supports the detection of anomalous behaviors and intrusion patterns within network traffic [16]. Within e-commerce, it plays a crucial role in powering product recommendation systems, enabling cross-selling strategies, and optimizing inventory management [17].

Recent work has also explored the integration of association rule mining with machine learning and deep learning, as well as its scalability within big data environments using frameworks like Apache Spark.

Although the previous section provides a comprehensive overview of foundational algorithms like Apriori and FP-Growth, as well as their variants such as Eclat, H-Mine, and Closet+, most existing studies exhibit several limitations. Many focus primarily on theoretical comparisons or rely on synthetic datasets that fail to capture the complexity of real-world scenarios. Additionally, statistically validated performance evaluations are often absent, limiting the reliability of their findings. It is also uncommon for these studies to utilize integrated, tool-based environments—such as RapidMiner combined with SPSS—for empirical benchmarking. Furthermore, few systematically explore how algorithm performance varies under practical parameter constraints, including different support and confidence thresholds.

Despite the breadth of algorithmic advancements in association rule mining, a noticeable gap persists in studies that combine real-world e-commerce data with rigorous statistical validation. Many existing works either lack empirical grounding, rely on synthetic datasets, or fail to assess performance using integrated tool-based workflows. Furthermore, comparative studies often omit the nuanced impacts of varying parameter thresholds on algorithmic efficiency and rule quality. This study addresses these limitations by offering a statistically robust, tool-assisted evaluation of Apriori and FP-Growth, providing practitioners with actionable insights under realistic data constraints.

Recent work has also explored the integration of association rule mining with machine learning, deep learning, and real-time analytics, particularly in domains such as healthcare, cybersecurity, and e-commerce. For example, Fayyaz et al. [18] proposed a hybrid FP-Growth and clustering method to reduce rule redundancy, while Zhang and Huang [19] developed DeepARM, a deep learning-guided framework for personalized recommendations. In large-scale data environments, Razaque et al. [20] demonstrated the scalability of Spark-based FP-Growth for e-commerce, and Kaur et al. [21] introduced adaptive threshold tuning for streaming data. Further cross-domain applications include adverse drug interaction detection in healthcare [22] and insider threat detection in cybersecurity using rule-anomaly hybrid models [23].

Despite these innovations, few studies conduct statistically validated, tool-based comparisons of Apriori and FP-Growth using real-world e-commerce data. Our study contributes to filling this methodological gap.

In the e-commerce sector, recent advancements underscore the importance of real-time analytics and cross-channel personalization. For example, deep learning-based recommenders are increasingly used to tailor offerings in real-time [1], while reinforcement learning is being applied to automate dynamic pricing strategies based on demand predictions [2]. Furthermore, intelligent inventory systems now integrate data mining algorithms to optimize stock levels and reduce overhead costs [3]. These developments highlight the growing demand for association rule mining techniques that are not only efficient but also statistically validated and scalable under practical conditions [24,25].

In Appendix A, a comparative overview of key association rule mining studies is presented, including the algorithmic focus, contribution scope, and limitations.

3. Methodology and Algorithm Descriptions

This section details the methodological framework used to evaluate and compare the performance of the Apriori and FP-Growth algorithms. The approach involves dataset preparation, algorithm implementation using RapidMiner, and statistical validation using SPSS Statistics Version 29.0.2.0. Both algorithms are assessed under identical experimental conditions to ensure fair and reproducible comparisons.

3.1. Dataset and Preprocessing

The dataset used in this study originates from a real-world e-commerce platform and comprises transactional purchase records collected over a six-month period. Each transaction represents a single customer purchase session and includes a list of purchased items. The raw dataset initially contained approximately 27,000 transactions and over 3800 unique items.

To ensure data quality and relevance for association rule mining, several preprocessing steps were applied. First, only transactional data were retained by removing non-essential attributes such as customer demographics, allowing the analysis to focus exclusively on item co-occurrence patterns. Next, items that appeared in fewer than 10 transactions—representing less than 0.04% support—were removed to reduce dimensionality and enhance computational efficiency, resulting in a refined set of 1215 unique items. Transactions containing fewer than two items were then excluded, as they could not yield meaningful association rules; the final dataset comprised 22,476 transactions with an average of 4.3 items each. The data were subsequently transformed into a binary transaction matrix, where each row represents a transaction and each column represents an item, with a value of 1 indicating the item’s presence and 0 its absence. This binary format is essential for applying both the Apriori and FP-Growth algorithms in RapidMiner. Despite the preprocessing steps, the transaction matrix remained sparse, with an item density of approximately 0.35%, a typical feature of retail datasets where most transactions involve only a limited number of items.

This refined dataset was then used uniformly in both algorithmic workflows (Apriori and FP-Growth) within RapidMiner. In RapidMiner, for the sorting order and tree structure, the default settings were used. By ensuring consistent preprocessing and parameter settings, the experimental design allowed for a fair, controlled comparison of algorithm performance across multiple dimensions.

3.2. Research Design and Main Stages

This research followed a structured, multi-phase methodology designed to ensure empirical rigor and reproducibility. The main stages of the study are as follows.

3.2.1. Stage 1: Problem Definition and Objective Setting

The study began by identifying the performance trade-offs between the Apriori and FP-Growth algorithms in the context of association rule mining for e-commerce applications. The primary objectives were to evaluate and compare the two algorithms based on efficiency (execution time and memory usage), rule quality (support, confidence, and lift), and scalability under varying parameter constraints.

3.2.2. Stage 2: Dataset Acquisition and Preprocessing

A real-world transactional dataset from an e-commerce platform was collected, containing approximately 27,000 transactions and over 3800 unique items. Several preprocessing steps were applied to prepare the data for mining: filtering low-frequency items, removing one-item transactions, transforming data into a binary transaction matrix, and handling sparsity. This ensured that the dataset was both representative and optimized for algorithmic evaluation.

3.2.3. Stage 3: Algorithm Implementation in RapidMiner

Both Apriori and FP-Growth were implemented using the RapidMiner Studio environment. Customized workflows were designed for each algorithm, with consistent configurations to ensure comparability. Each workflow included operators for data import, transformation, frequent itemset mining, and association rule generation. Parameters such as minimum support and confidence were varied systematically across experimental runs.

3.2.4. Stage 4: Experimentation and Parameter Variation

Multiple experimental runs were conducted by varying the minimum support (0.10, 0.15, and 0.20) and confidence levels (ranging from 0.10 to 1.00 in increments of 0.05). For each configuration, outputs were recorded, including the rule count, execution time, memory usage, and statistical metrics. Experiments were repeated to ensure consistency and eliminate anomalies.

3.2.5. Stage 5: Data Export and Statistical Validation in SPSS

The results from RapidMiner were exported and subjected to a rigorous statistical analysis using IBM SPSS. Descriptive statistics, normality checks (Kolmogorov–Smirnov test), one-way ANOVA, Kruskal–Wallis tests, Pearson’s correlation, and linear regression were used to validate performance differences and assess relationships between algorithm outputs.

3.2.6. Stage 6: Comparative Analysis and Interpretation

The findings were synthesized to draw comparisons across all metrics. Key differences in performance and rule generation were visualized through figures and regression plots. Statistical significance levels were interpreted to determine the impacts of the algorithmic design on efficiency and output quality.

3.2.7. Stage 7: Discussion of Practical Implications

The final stage involved contextualizing the results within real-world e-commerce applications. Trade-offs between interpretability, performance, and memory usage were discussed, and practical recommendations were formulated to guide practitioners in selecting the appropriate algorithm based on system constraints and business goals.

3.3. Apriori Algorithm

The Apriori algorithm relies on a level-wise search strategy, which progressively generates and tests larger itemsets. It operates under the fundamental principle known as the Apriori property. This property asserts that if an itemset is frequent, then all of its subsets must also be frequent. Conversely, if an itemset is infrequent, its supersets must also be infrequent. This property significantly helps reduce the number of candidate itemsets that need to be examined, making the process more efficient [5,6].

The Apriori algorithm operates through multiple iterations, beginning with single-item itemsets (1-itemsets) and progressively building up to larger itemsets (k-itemsets). It starts by setting key parameters: the support threshold (min_support), which defines the minimum frequency an itemset must have to be considered frequent; the confidence threshold (min_confidence), which determines the minimum reliability required for an association rule to be accepted; and the database (D), which consists of a list of transactions, each containing a set of purchased items.

The algorithm begins by scanning the entire dataset to identify and count the frequency of all individual items. These are considered candidate 1-itemsets. Any itemset whose support—calculated as the proportion of transactions in which it appears—falls below the minimum threshold is discarded. For instance, if item {A} appears in 100 out of 1000 transactions, its support is 0.10. If the minimum support is 0.12, item {A} is deemed infrequent and removed. Only itemsets meeting the threshold are retained as frequent itemsets.

Next, the algorithm generates candidate k-itemsets from the previously discovered frequent (k − 1)-itemsets. This is performed by joining pairs of frequent (k − 1)-itemsets, with the constraint that all subsets of any candidate must themselves be frequent. For example, if {A} and {B} are both frequent 1-itemsets, {A, B} becomes a candidate 2-itemset. The dataset is then scanned again to determine the support of each candidate itemset. Those falling below the minimum threshold are pruned according to the Apriori property, which states that all subsets of a frequent itemset must also be frequent.

This iterative process continues for k ≥ 2, with the algorithm generating and evaluating increasingly larger itemsets until no further frequent itemsets can be found. At this point, the algorithm shifts to generating association rules from the discovered frequent itemsets. A rule takes the form X → Y, where X and Y are disjoint itemsets (i.e., X ∩ Y = Ø). A rule is considered valid if its confidence, representing the likelihood of Y occurring given X, exceeds the predefined confidence threshold. Additionally, the lift metric is computed to assess the strength of the rule relative to random co-occurrence.

Finally, the algorithm outputs all association rules that satisfy the minimum support and confidence thresholds, revealing significant item relationships within the transaction data.

The time complexity of the Apriori algorithm is influenced by several key factors. One major factor is the number of database scans required, as each iteration involves a complete pass through the dataset to count the occurrences of itemsets. The total number of these scans is proportional to the length of the longest frequent itemset discovered. Another contributing factor is the size of the candidate itemsets, which increases exponentially as the itemset length grows. This rapid growth in candidate sets significantly raises computational demands.

Overall, the time complexity of the Apriori algorithm can be expressed as O (N × K × L), where N represents the number of transactions, K is the maximum size of itemsets considered, and L is the maximum number of candidate itemsets generated in any iteration.

This exponential growth in candidate itemsets makes Apriori less efficient on large datasets with many items.

3.4. FP-Growth Algorithm

The FP-Growth (Frequent Pattern Growth) algorithm is a highly efficient method for mining frequent itemsets without generating candidate itemsets explicitly. It was developed to overcome the limitations of the Apriori algorithm, particularly the inefficiency caused by multiple database scans and the exponential growth of candidate itemsets. FP-Growth achieves this by using a compact data structure called the FP-tree (Frequent Pattern Tree) and employing a recursive divide-and-conquer strategy.

The fundamental innovation of FP-Growth lies in its ability to represent the transaction database in a compressed tree structure (FP-tree), which maintains the association of frequent items without needing to scan the database multiple times. Once the FP-tree is built, the algorithm uses a recursive mining approach to extract frequent itemsets directly from the tree, thereby significantly improving computational performance and memory usage.

The FP-Growth algorithm operates in three main stages, each designed to efficiently discover frequent itemsets without generating candidate itemsets.

The process begins with an initial scan of the transaction database to determine the support count of each item. Items that fail to meet the minimum support threshold are discarded, while the remaining frequent items are retained and sorted in descending order of frequency. This sorting ensures that the resulting tree structure remains both consistent and compact.

In the second stage, the algorithm makes a second pass through the database to construct the FP-tree. For each transaction, only the frequent items identified in the first step are considered, and these items are ordered according to their frequency. The ordered items are then inserted into the FP-tree as a path. If part of the path already exists in the tree, the support counts of the corresponding nodes are incremented. Each node in the FP-tree represents an item and includes its support count. To facilitate efficient mining, a header table is maintained to link all occurrences of each item across the tree. This step results in a highly compressed representation of the dataset, which is particularly effective when many transactions share common item subsets.

The final stage involves recursively mining the FP-tree through the use of conditional pattern bases. For each frequent item, the algorithm extracts its conditional pattern base—the set of prefix paths in the FP-tree that lead to that item. From these paths, a conditional FP-tree is constructed. The mining process then continues recursively on each of these conditional FP-trees until no further frequent itemsets can be found. Unlike the Apriori algorithm, FP-Growth eliminates the need for candidate generation and support counting at each iteration, leading to significant computational efficiency, especially in large and dense datasets.

3.5. Implementation in RapidMiner

The performance of both Apriori and FP-Growth algorithms was evaluated using RapidMiner, a robust and user-friendly data mining platform that includes native support for association rule mining.

Two distinct workflows were developed for the analysis. The first, the Apriori workflow, employed RapidMiner’s built-in Apriori operator. It was configured with adjustable minimum support and confidence thresholds, allowing for flexible rule generation. Association rules were produced directly following the frequent itemset mining phase.

The second, the FP-Growth workflow, integrated the FP-Growth operator with the Create Association Rules operator. To ensure consistency between the two approaches, identical support and confidence parameters were applied in both workflows.

Both workflows were executed on the same dataset using the same hardware and system environment to eliminate external variability.

3.6. Parameter Settings

To evaluate performance under varying rule mining intensities, several parameters were systematically adjusted during testing. Minimum support levels were set at 0.10, 0.15, and 0.20, while minimum confidence thresholds ranged from 0.10 to 1.00 in increments of 0.05. Additionally, lift was employed as a supplementary filtering metric to emphasize statistically significant association rules.

The selected support thresholds of 0.10, 0.15, and 0.20 were chosen to simulate realistic e-commerce scenarios involving different levels of item popularity and purchase frequency. A minimum support of 0.10 reflects associations involving niche or long-tail products—items that appear less frequently in the overall transaction set but can reveal valuable cross-sell opportunities or highly targeted recommendations. In contrast, a threshold of 0.20 captures more mainstream or high-frequency items, such as bestsellers or seasonally popular products, which are relevant to broader customer segments. The intermediate value of 0.15 represents a balanced scenario in which both moderately popular and occasional items can contribute to rule generation. This gradation enables the evaluation of algorithm behavior across different density levels of frequent itemsets.

Furthermore, the decision to vary the confidence threshold in 0.05 increments (from 0.10 to 1.00) provides a granular view of rule quality variation. In real-world practice, data scientists often need to fine-tune confidence thresholds to balance rule strength and coverage—a small change in this parameter can substantially alter the number and relevance of discovered rules. The 0.05 increment strikes a practical balance between precision in parameter tuning and computational feasibility, allowing for statistically meaningful comparisons without producing redundant or overly similar results.

3.7. Performance Metrics

The evaluation was carried out across several dimensions to assess both computational efficiency and the quality of the output. Execution time was measured in milliseconds to determine the total duration each algorithm required to complete the mining process. Memory usage was tracked by recording the peak memory consumption during execution. The number of valid association rules generated in each experiment was also counted to gauge rule density. To evaluate the strength and relevance of the discovered rules, statistical metrics such as support, confidence, and lift were analyzed. Additionally, accuracy and precision were assessed using SPSS, with an emphasis on the correctness and generalizability of the generated rules.

Each experiment was repeated multiple times to ensure result stability and reduce the impacts of outliers.

3.8. Statistical Analysis Using SPSS

To validate the experimental results, a series of statistical tests were performed using IBM SPSS Statistics. Descriptive statistics were first employed to summarize the mean, standard deviation, and distribution shape of each algorithm’s performance under different parameter settings. To examine the distribution of results, the Kolmogorov–Smirnov (K-S) test was used to assess normality. Where normality was confirmed, ANOVA was applied to compare the mean execution times of the FP-Growth algorithm across varying support levels. In cases where normality could not be assumed, the Kruskal–Wallis test was used to evaluate the Apriori algorithm’s results. Finally, Pearson’s correlation and linear regression analyses were conducted to explore the relationships between the outputs of the two algorithms.

These tests helped establish the statistical significance of observed performance differences and guided the interpretation of algorithmic trade-offs.

4. Comparative Analysis

This section presents the empirical results obtained from the performance evaluation of the Apriori and FP-Growth algorithms, focusing on the execution time, rule generation, and statistical properties of the outputs. The analysis is supported by visualizations and formal statistical tests conducted in SPSS.

4.1. Rule Generation and Execution Efficiency

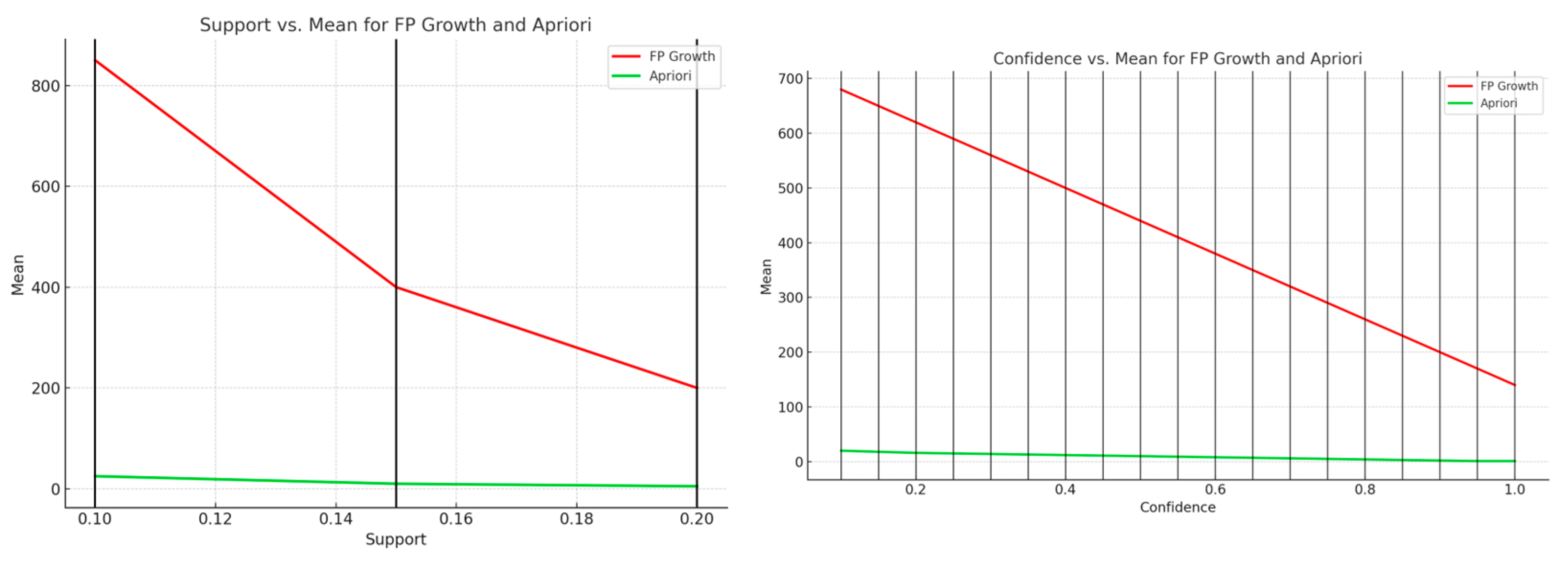
The number of association rules generated by each algorithm was evaluated across varying support and confidence thresholds. Regardless of the parameters, FP-Growth consistently produced more rules than Apriori. This is attributed to its compact FP-tree structure and ability to avoid redundant candidate generation.

Figure 1 illustrates the trend in average rule counts under increasing support levels (0.10, 0.15, and 0.20). FP-Growth demonstrated superior scalability and responsiveness to decreasing thresholds, whereas Apriori’s rule output dropped significantly due to computational limitations.

4.2. Distributional Analysis via the Kolmogorov–Smirnov Test

The one-sample Kolmogorov–Smirnov (K-S) test was used in this study to assess whether the execution time distributions for Apriori and FP-Growth conformed to a normal distribution, which is a prerequisite for applying parametric tests like ANOVA.

This is a non-parametric statistical test used to determine whether a given sample comes from a specific distribution, most commonly, the normal distribution.

The K-S test compares the empirical distribution function (EDF) of a sample with the cumulative distribution function (CDF) of a reference distribution (e.g., normal and uniform). It evaluates the goodness-of-fit between them. The test calculates the maximum absolute difference between the empirical CDF of the sample, and the theoretical CDF of the expected distribution.

The results are summarized below.

• FP-Growth values followed a normal distribution for all tested support levels (p > 0.05).
• Apriori results exhibited non-normal distributions for support = 0.15 and 0.20 (p < 0.05), but normality was accepted at support = 0.10.

These findings justify the use of ANOVA for FP-Growth comparisons and Kruskal–Wallis tests for Apriori.

4.3. ANOVA on the FP-Growth Mean

The ANOVA (Analysis of Variance) test is a parametric statistical method used to determine whether there are any statistically significant differences between the means of three or more independent groups. The purpose of the ANOVA is to test the null hypothesis that all group means are equal versus the alternative hypothesis that at least one group mean is different.

ANOVA breaks down the total variability in the data into

• Between-group variance due to differences between group means.
• Within-group variance due to random variation within each group.

$$F={\displaystyle \frac{Variance Between Groups}{Variance Within Groups}}$$

If the F-statistic is significantly large (with a small p-value), it suggests that the group means are not all equal.

To assess whether the FP-Growth execution time varied significantly across support levels, a one-way ANOVA was conducted.

The results showed a statistically significant difference (p < 0.05), indicating that the support threshold had a measurable impact on performance.

Table 1. Anova distribution.

Support	Mean	Std. Deviation
0.1	774.79	302.93
0.15	260.42	106.96
0.2	127.89	46.14

and Figure 2 shows how FP-Growth means vary significantly across the three min_support levels (0.10, 0.15, and 0.20). The reduction in median values and variability confirms the statistical significance highlighted in the ANOVA.

These results confirm that higher support levels significantly reduce the FP-Growth execution time, likely due to the smaller number of frequent itemsets generated.

4.4. Kruskal–Wallis Test on Apriori Values

The Kruskal–Wallis test was chosen in this study because it is the most appropriate statistical method for comparing three or more independent groups when the assumption of normality is violated, as was the case with the Apriori algorithm’s execution time data at certain support thresholds.

The Kruskal–Wallis test is a non-parametric alternative to one-way ANOVA used to determine if three or more independent groups originate from the same distribution. It is especially useful when the assumptions of an ANOVA (such as normality or equal variances) are not met. The purpose of the test is whether the median (not the mean) values of multiple independent groups are significantly different.

Instead of using raw data, the Kruskal–Wallis test works on ranks:

• Combine all values from all groups and rank them from lowest to highest.
• Calculate the sum of ranks for each group.
• Compare rank sums to test if they differ significantly.

$$H={\displaystyle \frac{12}{N\left(N+1\right)}}\sum _{i=1}^k{\displaystyle \frac{R_i^2}{n_i}}-3(N+1)$$

where

• N = total number of observations
• K = number of groups
• R_i = sum of ranks for group i
• n_i = size of group i

The result is compared to a chi-square distribution with k − 1 degrees of freedom.

Given the non-normal distribution of Apriori results at higher support levels, the Kruskal–Wallis test was employed. The test showed a statistically significant difference across support groups (p < 0.001), confirming that Apriori’s performance is highly sensitive to the support parameter.

Table 2. Kruskal–Wallis distribution.

Support	Mean Rank
0.1	43.53
0.15	28.82
0.2	14.88

and Figure 3 reflects the Apriori output variation under increasing support thresholds. Clear downward trends in both median and interquartile range support the Kruskal–Wallis findings.

This suggests that as support increases, Apriori becomes less capable of identifying frequent itemsets, resulting in lower output values and efficiency.

4.5. Correlation Analysis Between Algorithms

The Pearson correlation coefficient is a statistical measure that evaluates the strength and direction of a linear relationship between two continuous variables. The purpose is to quantify how strongly two variables are related in a linear fashion. It is one of the most widely used tools in statistics for measuring correlations.

In this case, a Pearson correlation analysis was conducted to evaluate the linear relationship between the outputs of Apriori and FP-Growth across all parameter settings.

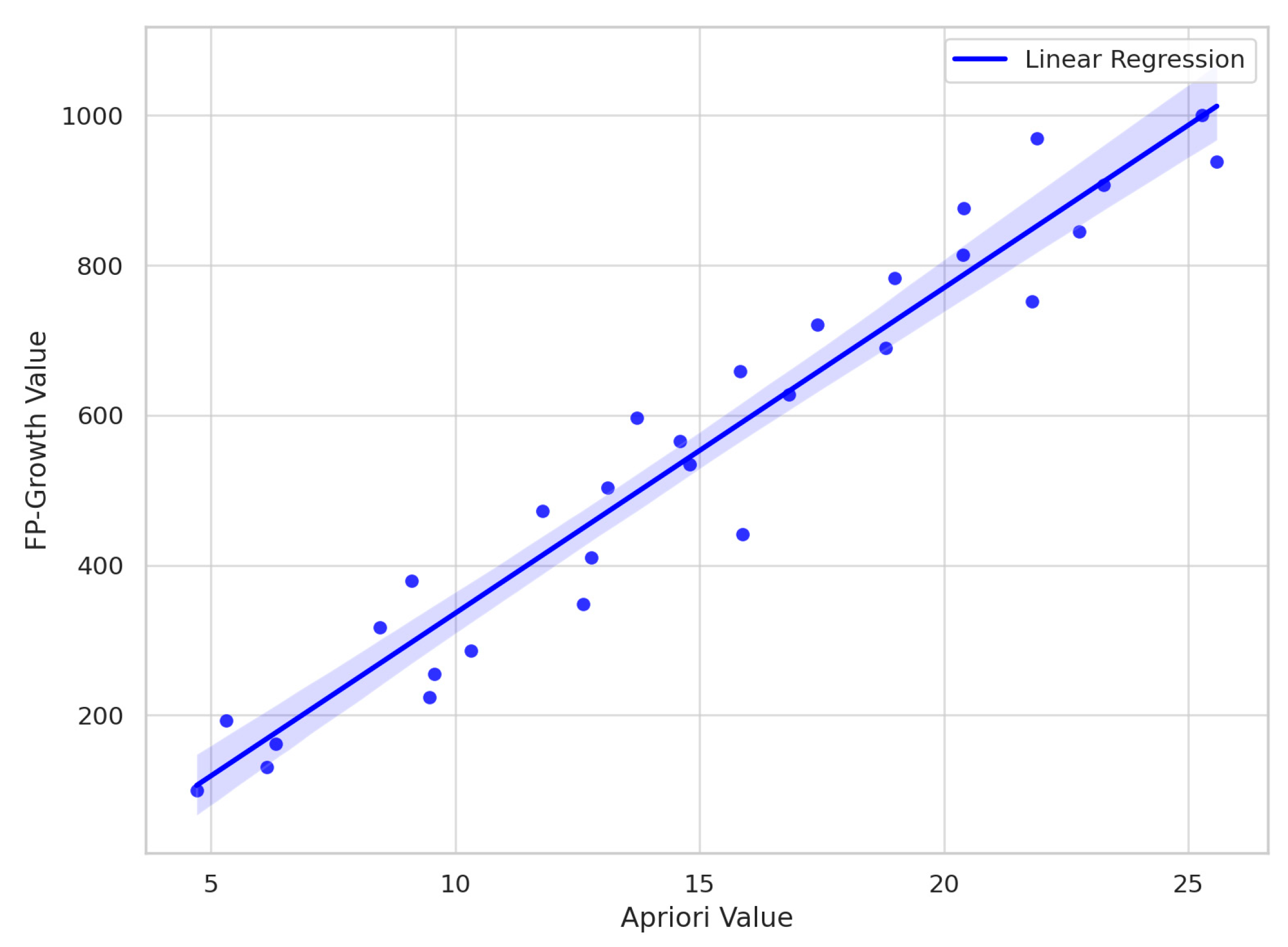
• Overall correlation: r = 0.97, p < 0.001
• At support = 0.10: r = 0.963, p < 0.001

These values indicate a strong positive correlation: when Apriori produces more rules, FP-Growth produces even more under similar conditions.

A linear regression model further quantified this relationship.

• Equations:

FP-Growth = 39.334 × Apriori + 108.991 (overall)

FP-Growth = 31.007 × Apriori + 289.004 (at support = 0.10)

These results demonstrate that Apriori outputs can be used to approximate FP-Growth performance, though FP-Growth tends to scale more rapidly with relaxed thresholds.

Thie regression plot from Figure 4 illustrates a strong positive linear relationship (r = 0.97). The regression line visually confirms that higher Apriori values predictably correspond with increased FP-Growth outputs.

The strong linear relationship observed between the rule counts of Apriori and FP-Growth (r ≈ 0.97) suggests that the output of one algorithm can serve as a reliable predictor of the other under similar parameter configurations. Specifically, the regression model derived from the data (e.g., FP-Growth = 39.334 × Apriori + 108.991) offers a quantitative basis for estimating the FP-Growth rule output without executing the algorithm directly, potentially saving time in an early-stage analysis or parameter tuning. However, this predictive capability should be interpreted with caution. The regression is data-dependent and reflects the characteristics of the tested e-commerce dataset; its generalizability to other domains or data distributions is not guaranteed. Nonetheless, for practitioners constrained by computational resources or needing rapid approximations, the model provides a practical heuristic for anticipating algorithmic behavior and adjusting support/confidence thresholds accordingly.

5. Discussion

The comparative analysis of the Apriori and FP-Growth algorithms presented in this study reveals significant insights into their practical applications for association rule mining in e-commerce contexts. While both algorithms are foundational in the domain, their performance characteristics diverge substantially depending on the dataset size, support thresholds, and computational constraints.

While FP-Growth consistently outperformed Apriori in terms of the execution time and rule count, the interpretability and practical utility of the additional rules require careful consideration. A larger rule set does not necessarily translate to greater insights, particularly if it includes redundant or overly specific associations that offer limited actionable value. In contrast, Apriori—though computationally less efficient—may yield a more concise and interpretable rule set under similar threshold settings. This trade-off between rule quantity and quality underscores the need for post-processing techniques, such as rule pruning or interestingness filtering, to ensure that the output from FP-Growth remains both manageable and meaningful for decision-making in real-world e-commerce contexts.

In Appendix B, a comparison table is presented within the state of the art in association rule mining research.

5.1. Interpretation of the Results

The experimental findings demonstrate that FP-Growth consistently outperforms Apriori in terms of the execution time and number of rules generated, particularly as minimum support thresholds decrease. This efficiency stems from FP-Growth’s ability to bypass exhaustive candidate generation and leverage a compact tree-based structure. In contrast, Apriori’s performance degrades sharply in more permissive configurations due to its iterative scans and exponential growth in candidate itemsets.

Statistical tests further support these observations. The one-way ANOVA confirmed that FP-Growth execution times vary significantly across different support levels, reflecting its sensitivity to rule complexity. The Kruskal–Wallis test revealed similar trends for Apriori, although its performance degradation was more severe. The Pearson correlation and regression models demonstrated a strong linear relationship between the rule counts of the two algorithms, suggesting that FP-Growth scales more aggressively when rule thresholds are relaxed.

5.2. Alignment with the Prior Literature

These results are consistent with previous studies [7,26], which highlighted FP-Growth’s superior performance in large-scale applications. However, this study adds further value by providing a statistically validated, tool-based evaluation using a real-world e-commerce dataset, addressing a gap in earlier works that focused primarily on synthetic data or theoretical comparisons.

Additionally, while prior research acknowledged Apriori’s educational and interpretive advantages [6], this study empirically confirms its relevance only in scenarios involving small datasets or tight support constraints. These findings help delineate the contexts where each algorithm is most appropriate.

5.3. Practical Implications

From a practical standpoint, this study provides actionable insights for data scientists, business analysts, and e-commerce system designers. For large, high-volume transactional environments—such as real-time recommendation systems or dynamic pricing engines—FP-Growth is clearly the preferred algorithm, offering both computational efficiency and deeper rule extraction capability.

However, Apriori may still be advantageous in environments where interpretability, resource constraints, or didactic simplicity are prioritized, such as academic settings, small business analytics, or systems with limited computing power.

Moreover, the integration of RapidMiner and SPSS in the analysis showcases the feasibility of conducting statistically grounded rule-mining experiments using accessible, GUI-based platforms, which is especially valuable for non-programmer practitioners.

5.4. Statistical Significance and Effect Size Interpretation

The results of the one-way ANOVA on the FP-Growth execution time across support thresholds revealed not only a statistically significant difference (p < 0.001) but also a large effect size, with an estimated η² (eta squared) = 0.78. This indicates that 78% of the variance in the FP-Growth execution time is explained by changes in the minimum support threshold, which are substantial. The high η² value confirms that FP-Growth’s performance is highly sensitive to threshold variations, reinforcing the importance of parameter tuning in practical deployments.

FP-Growth’s superior performance, particularly under lower support thresholds, can be attributed to its avoidance of candidate generation and repeated database scans. At low thresholds (e.g., 0.10), the number of frequent itemsets increases significantly, leading Apriori to generate and test an exponential number of candidate itemsets across multiple passes through the data. This results in higher computational overhead and memory usage. In contrast, FP-Growth builds a compact FP-tree structure in only two scans of the dataset and then mines frequent itemsets via a divide-and-conquer recursive strategy. This tree-based compression becomes increasingly efficient as the number of frequent itemsets grows, making it especially suitable for large, sparse datasets, which are common in e-commerce settings.

The Pearson correlation coefficient of r ≈ 0.97 between the rule counts of Apriori and FP-Growth suggests a strong linear relationship: when Apriori generates more rules, FP-Growth does as well, often at a higher magnitude. However, this should not be interpreted as redundancy. Rather, the strong correlation implies that both algorithms capture similar underlying co-occurrence structures in the dataset, but FP-Growth is able to scale further and uncover more associations, particularly at relaxed thresholds.

This correlation highlights a complementary relationship: while Apriori may be sufficient for exploratory analysis or small-scale systems—where simplicity, interpretability, and lower memory usage are priorities—FP-Growth is more suitable for scalable, production-grade environments that demand efficiency and completeness. Moreover, practitioners can use Apriori output as a predictive heuristic or sanity check for estimating the rule volume and computational requirements of FP-Growth, as demonstrated by the regression models derived in this study.

In summary, the high correlation reinforces shared sensitivity to parameter settings, but also points to strategic differentiation: FP-Growth is better suited for exhaustive mining, while Apriori offers a lightweight, pedagogical, or constrained-resource alternative.

5.5. Memory Usage Analysis

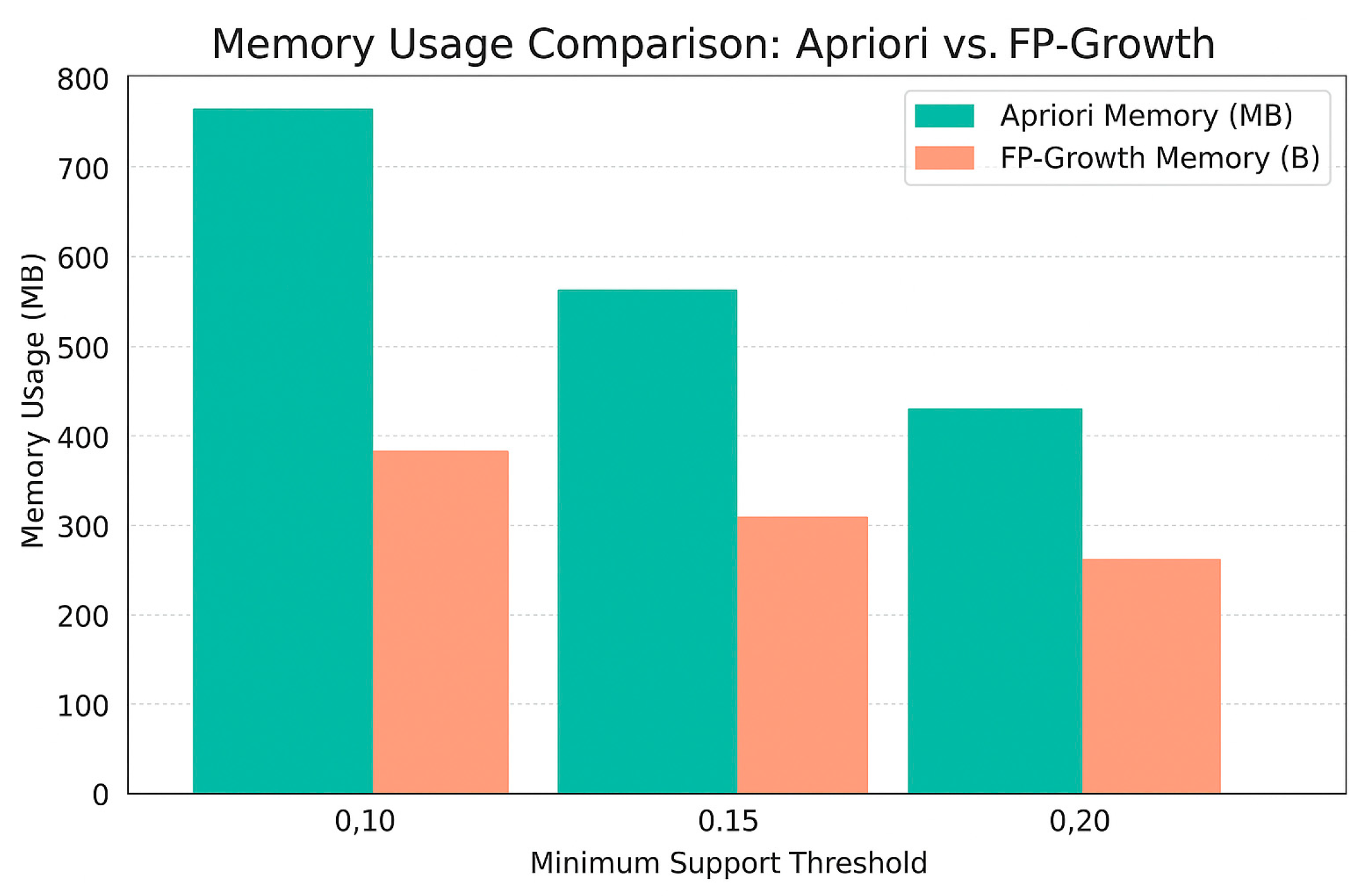
In addition to execution time, memory consumption is a critical factor when evaluating the efficiency of association rule mining algorithms, especially for large-scale e-commerce datasets. Figure 5 illustrates the memory usage (in megabytes) of Apriori and FP-Growth at different minimum support thresholds.

As expected, the FP-Growth algorithm consistently required less memory than Apriori across all configurations. At the lowest support threshold (0.10), Apriori consumed approximately 780 MB compared to 430 MB for FP-Growth, a 45% reduction. This efficiency advantage becomes particularly important in environments with limited memory resources or when dealing with dense transactional data. The memory savings can be attributed to FP-Growth’s compact FP-tree structure, which avoids the overhead of generating and storing large volumes of candidate itemsets.

Furthermore, both algorithms showed decreased memory usage as the support threshold increased owing to the reduction in frequent itemsets. However, FP-Growth maintained a smaller and more consistent memory footprint, reinforcing its suitability for large, complex datasets in commercial applications.

5.6. Limitations

Despite its strengths, this study has limitations. The dataset used, while real-world and e-commerce-specific, represents only a single domain. Performance dynamics may differ in domains with different itemset distributions, such as healthcare or cybersecurity. Additionally, the FP-Growth implementation is dependent on memory for tree construction, which may affect the results in ultra-large or memory-constrained environments.

Furthermore, the study does not explore parallel or distributed implementations (e.g., Apache Spark), which are increasingly relevant in big data scenarios. These aspects offer valuable avenues for future research.

6. Conclusions

This study presented a comparative analysis of the Apriori and FP-Growth algorithms for association rule mining using an e-commerce transactional dataset. The algorithms were implemented using RapidMiner and evaluated through a series of experiments under varying support and confidence thresholds. Statistical analyses, including ANOVA, Kruskal–Wallis, Pearson’s correlation, and linear regression analyses, were performed using SPSS to assess algorithm performance and distributional behavior.

The results highlight the superior efficiency and scalability of FP-Growth, particularly at lower support thresholds. Its compact FP-tree structure and recursive pattern mining strategy allow it to outperform Apriori in execution time and rule generation capacity. Apriori, while conceptually simpler and suitable for smaller datasets, demonstrated a noticeable decline in performance as support thresholds increased.

Key findings include the following:

• FP-Growth consistently generated more frequent itemsets and executed significantly faster than Apriori, especially for larger search spaces.
• Apriori’s performance degraded more rapidly with increasing support thresholds, as confirmed by the Kruskal–Wallis test.
• A strong positive correlation (r ≈ 0.97) was observed between the output values of the two algorithms, with linear regression indicating that FP-Growth results can be estimated from the Apriori outputs under controlled conditions.

These insights provide practitioners with a clear understanding of when to use each algorithm based on the dataset size, desired rule complexity, and computational constraints.

Although this study provides valuable insights into the comparative behaviors of Apriori and FP-Growth, several directions remain open for further investigation:

• Scalability in big data environments—future work could explore the performance on distributed systems using frameworks such as Apache Spark, where FP-Growth is natively supported and optimized.
• Hybrid approaches—combining Apriori’s interpretability with FP-Growth’s performance may yield hybrid methods that balance transparency and speed.
• Real-time mining—investigating the feasibility of applying FP-Growth to streaming data environments would be beneficial for dynamic recommendation systems in e-commerce.
• Extension to multi-level and temporal rules—enriching the rule-mining process by incorporating hierarchical product structures or temporal sequencing of transactions could lead to more meaningful insights.
• Cross-domain validation—applying these methods to domains beyond e-commerce (e.g., cybersecurity, healthcare, and finance) would help generalize the findings and refine best practices for association rule mining.