An Integrated Cellular Automata Model Improves the Accuracy of Secondary Fragmentation Prediction
Abstract
1. Introduction
2. Materials and Methods
2.1. Physical Experiment
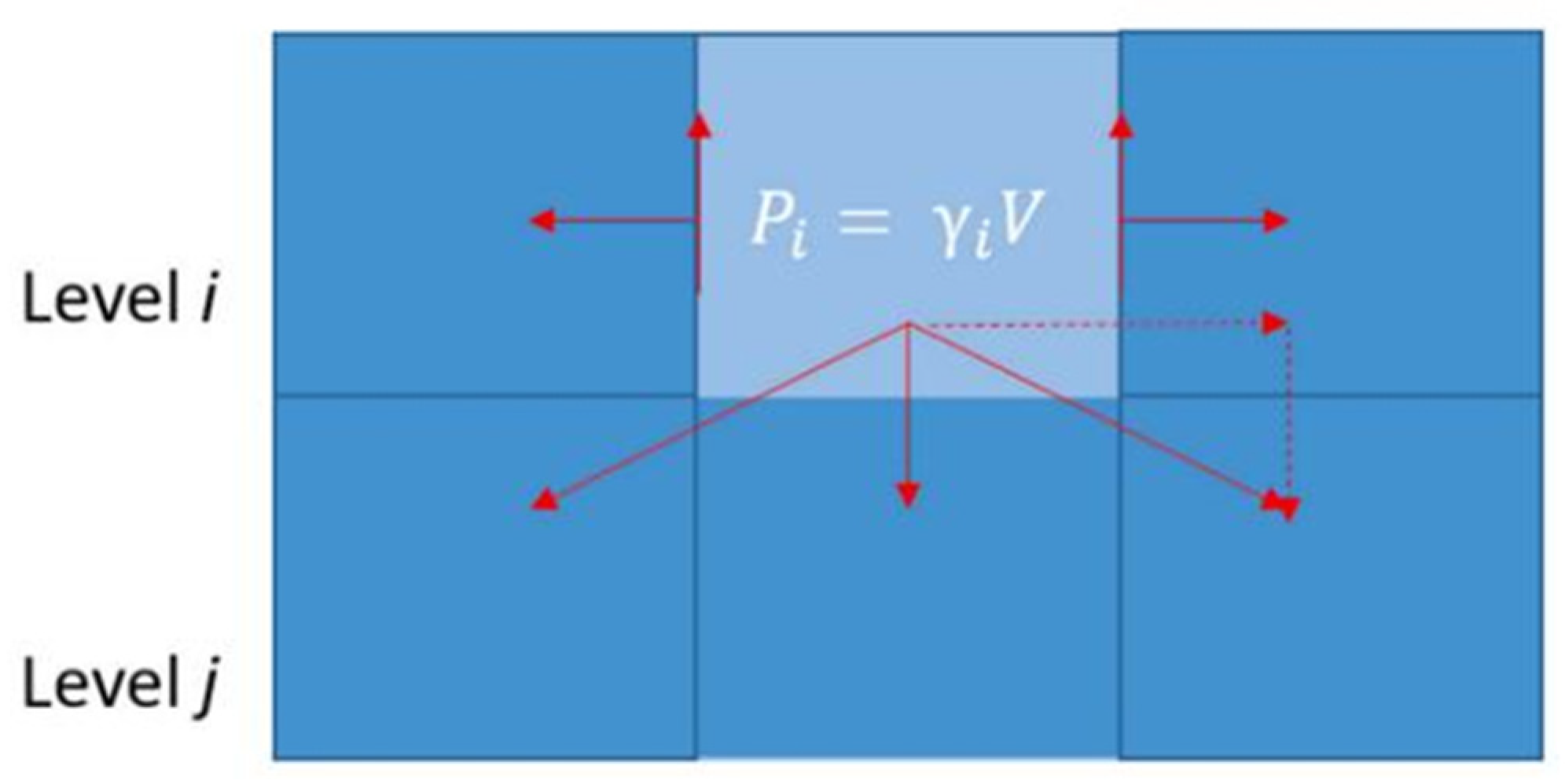
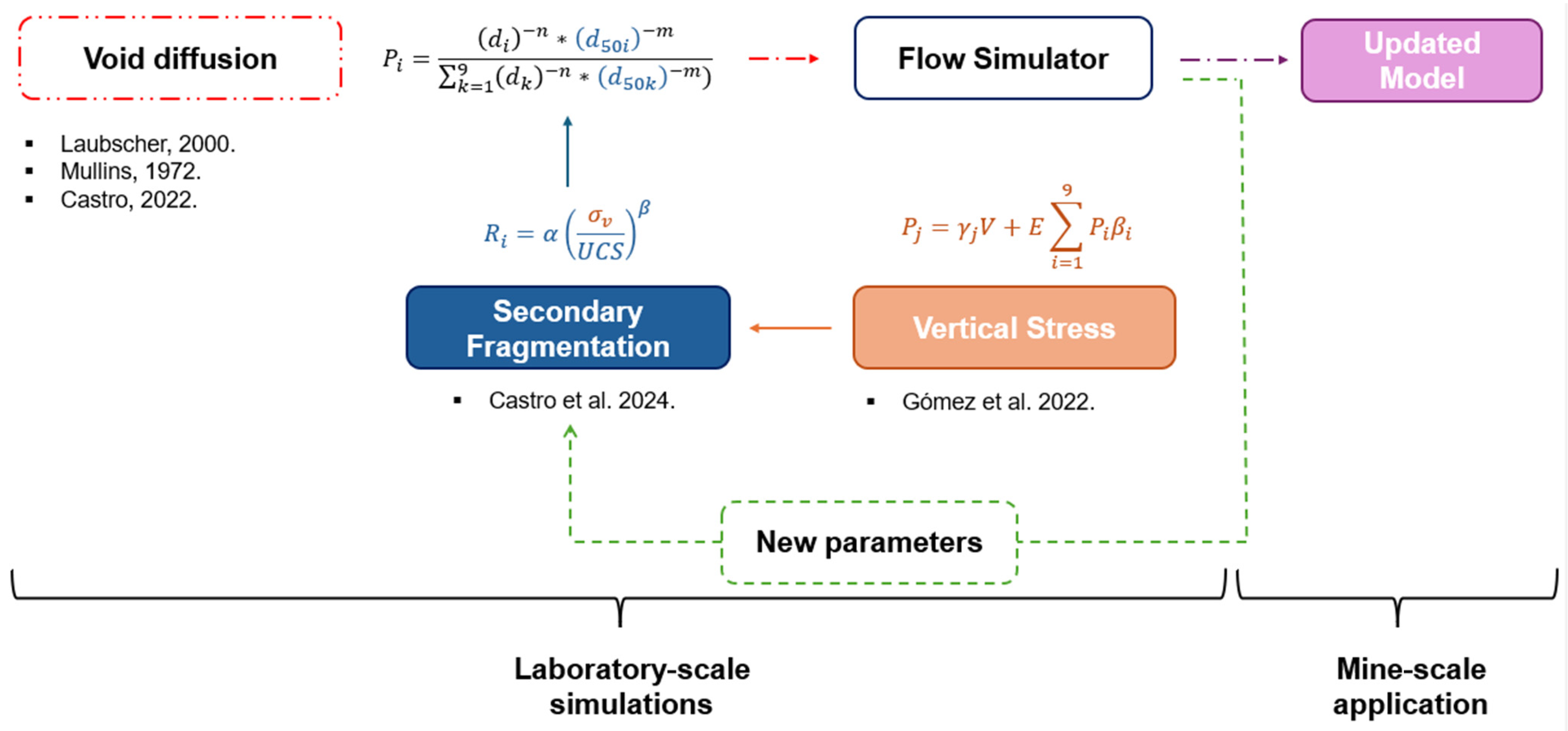
2.2. Stress Model
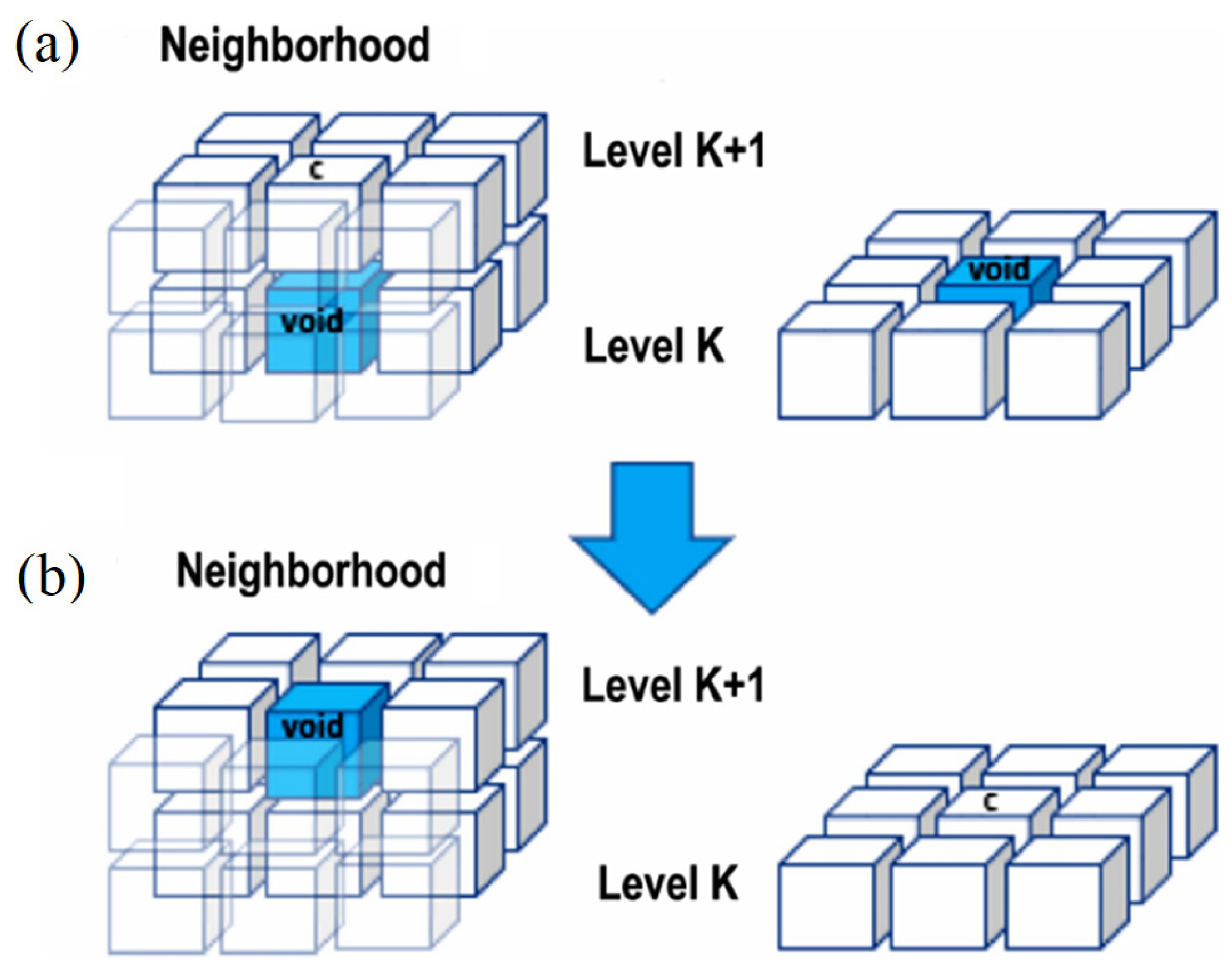
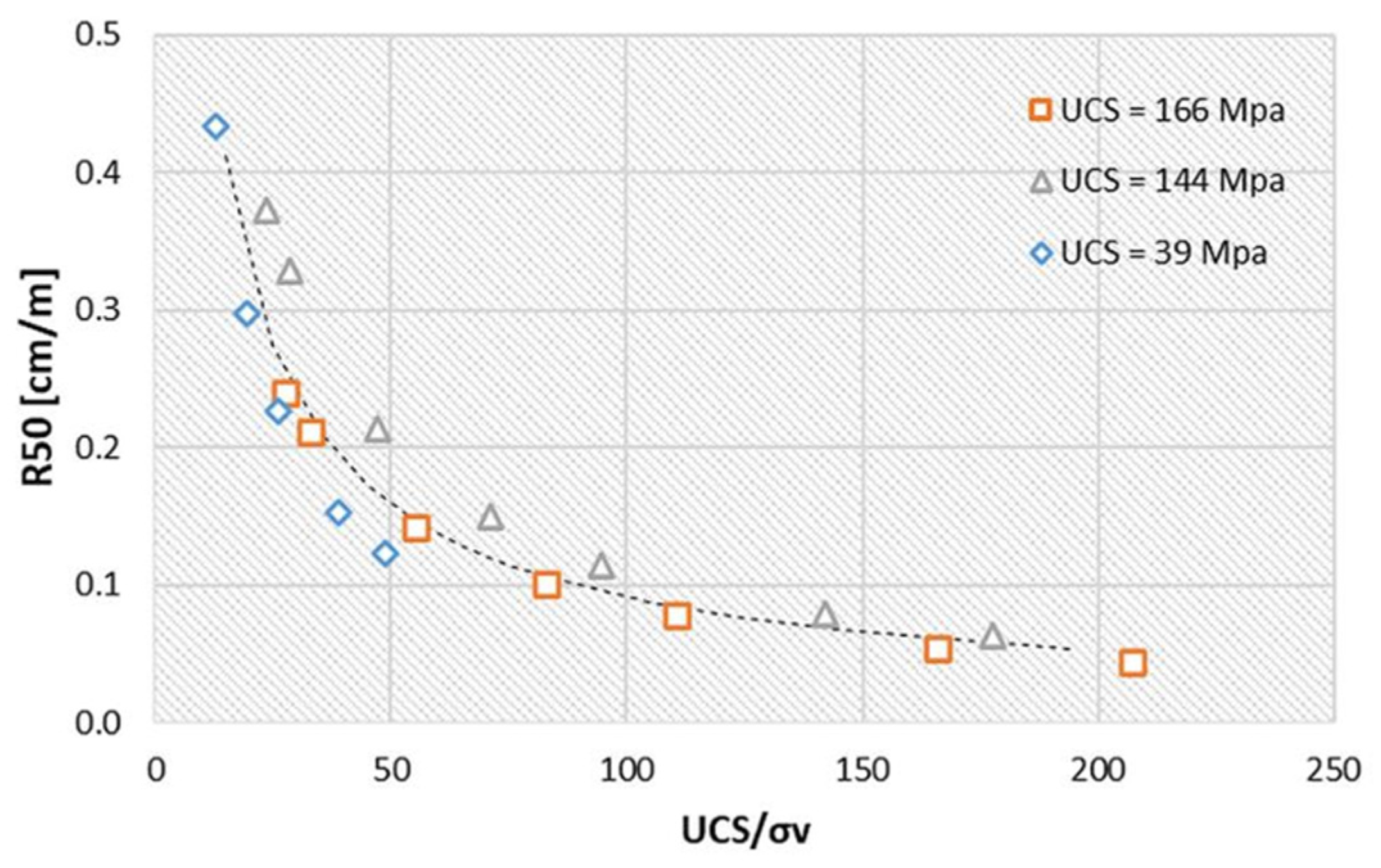
2.3. Fragmentation Model
2.4. Combining Models
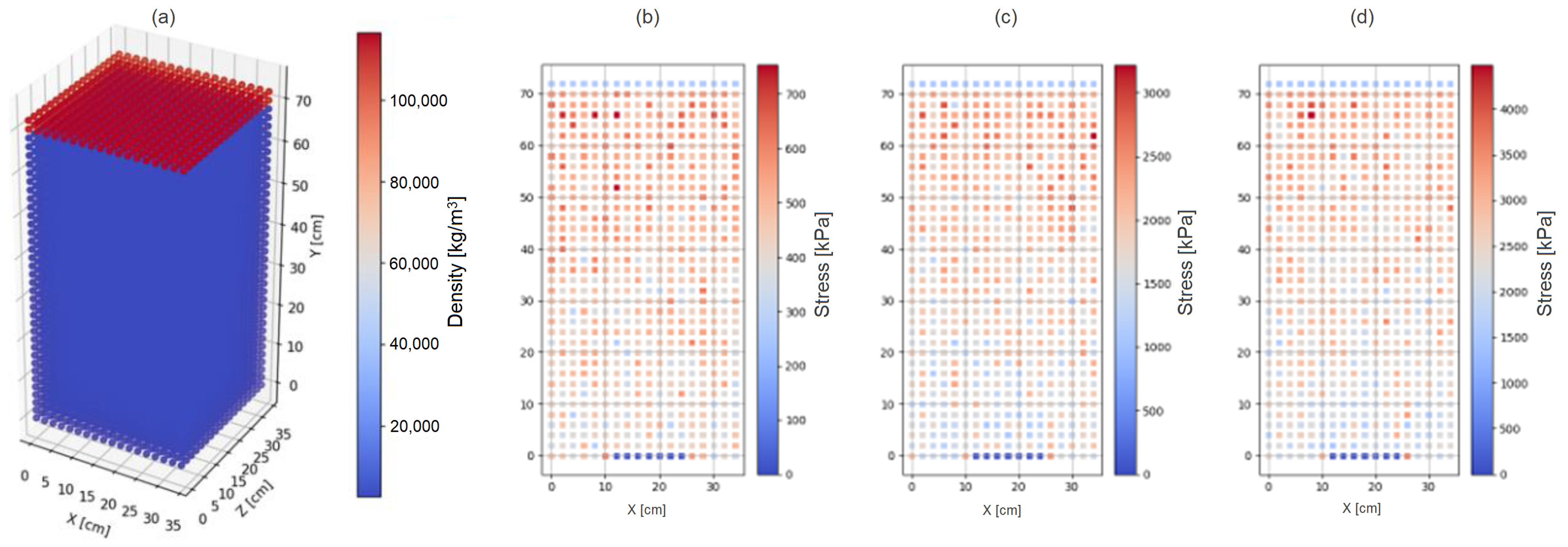
2.5. Numerical Model
3. Results
3.1. Original Model Results
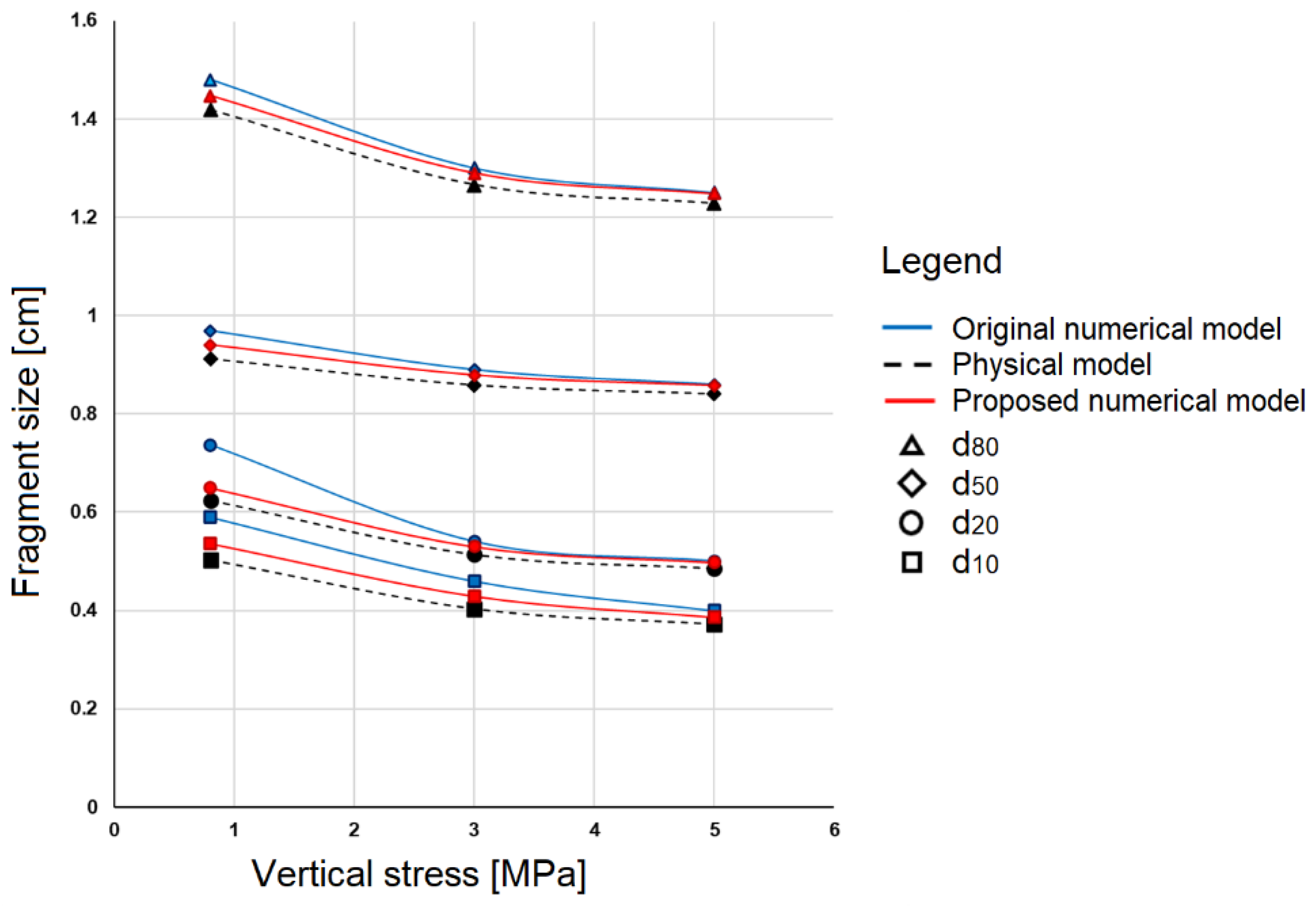
3.2. Fragmentation Model with Shear Effect
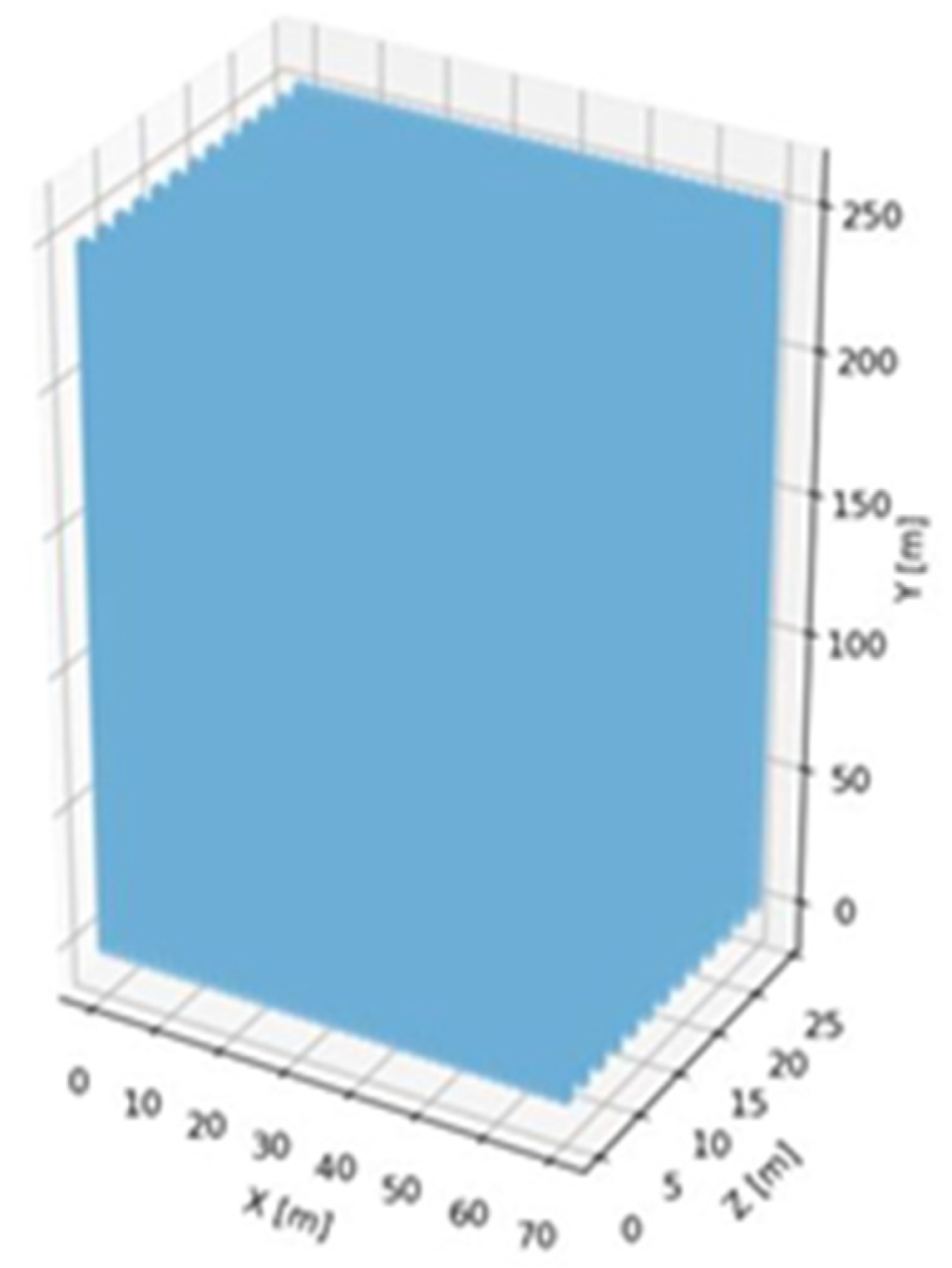
4. Mine-Scale Application
4.1. Input Data
4.2. Mine Scale Results
5. Conclusions
- With the inclusion of the shear strain effect, the results obtained with the new integrated model, which better represented the dynamics of the gravity flow and fragmentation of caved material, showed a notable improvement in fine granulometry, while for coarser sizes under conditions of high stresses, a slight improvement was also observed;
- Shear deformation influences smaller fragments due to secondary fragmentation more significantly, validating its integration into the proposed model and improving the model’s prediction accuracy.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chitombo, G. Importance of Geology in Cave Mining. SEG Discov. 2019, 119, 1–21. [Google Scholar] [CrossRef]
- Chacon, J.; Gopfert, H.; Ovalle, A. Thirty years evolution of block caving in Chile. In Proceedings of the MassMin 2004, Santiago, Chile, 22–25 August 2004; pp. 387–392. [Google Scholar]
- Laubscher, D.H. Cave mining-the state of the art. J. S. Afr. Inst. Min. Metall. 1994, 94, 279–293. [Google Scholar]
- Brown, E.T. Block Caving Geomechanics, 2nd ed.; Julius Kruttschnitt Mineral Research Centre: Indooroopilly, QLD, Australia, 2007. [Google Scholar]
- Dorador, L.; Eberhardt, E.; Elmo, D. Influence of rock mass veining and non-persistent joints on secondary fragmentation during block caving. In Fourth International Symposium on Block and Sublevel Caving, 2018; Potvin, Y., Jakubec, J., Eds.; ACG: Vancouver, BC, USA, 2018; pp. 271–282. [Google Scholar] [CrossRef]
- Pierce, M.; Weatherley, D.; Kojovic, T. A hybrid methodology for secondary fragmentation prediction in cave mines. In Second International Symposium on Block and Sublevel Caving; Potvin, Y., Ed.; ACG: Perth, WA, Australia, 2010; pp. 567–581. [Google Scholar] [CrossRef]
- Laubscher, D. Block Cave Manual; Julius Kruttschnitt Mineral Research Centre: Brisbane, QLD, Australia, 2000. [Google Scholar]
- Pretorius, D.; Ngidi, S. Cave management ensuring optimal life of mine at Palabora. In Proceedings of the 5th Conference and Exhibition on Mass Mining, Lulea, Sweden, 9–11 June 2008; pp. 63–71. [Google Scholar]
- Laubscher, D.H. Mud flow/Mud push and water inflow potential. In Block Cave Manual, International Caving Study (1997–2000); JKMRC and Itasca Consulting Group, Inc.: Brisbane, QLD, Australia, 2000; pp. 1–9. [Google Scholar]
- Pierce, M.E. A Model for Gravity Flow of Fragmented Rock in Block Caving Mines. Ph.D. Thesis, University of Queensland, Brisbane, QLD, Australia, 2009. [Google Scholar]
- Gómez, R.; Castro, R.L.; Casali, A.; Palma, S.; Hekmat, A. A Comminution Model for Secondary Fragmentation Assessment for Block Caving. Rock Mech. Rock Eng. 2017, 50, 3073–3084. [Google Scholar] [CrossRef]
- Gómez, R.; Castro, R.; Betancourt, F.; Moncada, M. Comparison of normalized and non-normalized block caving comminution models. J. S. Afr. Inst. Min. Metall. 2021, 121, 581–588. [Google Scholar] [CrossRef]
- Esterhuizen, G.S. BCF: A Program to Predict Block Cave Fragmentation (Version 3.05); [Computer Software]; Pittsburgh, PA, USA, 2005. [Google Scholar]
- Itasca. Massflow Tutorial. Itasca International Inc., 2024. Available online: https://docs.itascacg.com/itasca920/massflow/enginemassflow/doc/manual/massflow_manual/massflowhome.html (accessed on 21 March 2025).
- Hardin, B. Crushing of Soil Particles. J. Geotech. Eng. 1985, 111, 1177–1192. [Google Scholar] [CrossRef]
- Bridgwater, J.; Utsumi, R.; Zhang, Z.; Tuladhar, T. Particle attrition due to shearing-the effects of stress, strain and particle shape. Chem. Eng. Sci. 2003, 58, 4649–4665. [Google Scholar] [CrossRef]
- Pierce, M.; Fuenzalida, M. Application of a methodology for secondary fragmentation prediction in cave mines. In Proceedings of the 3rd International Symposium on Block and Sublevel Caving, Santiago, Chile, 5–6 June 2014; pp. 318–327. [Google Scholar]
- Golder. FracMan; FracMan Technology Group: Redmond, WA, USA, 2012. [Google Scholar]
- Rogers, S.; Elmo, D.; Webb, G.; Catalan, A. A discrete fracture network based approach to defining in situ, primary and secondary fragmentation distributions for the Cadia East panel cave. In Second International Symposium on Block and Sublevel Caving; Potvin, Y., Ed.; ACG: Perth, WA, Australia, 2010; pp. 425–440. [Google Scholar]
- Wang, P.; Ren, F.; Cai, M. Influence of joint geometry and roughness on the multiscale shear behaviour of fractured rock mass using particle flow code. Arab. J. Geosci. 2020, 13, 165. [Google Scholar] [CrossRef]
- Castro, R.; Gómez, R.; Castillo, J.J.; Jerez, O. Fragmentation model integrated in a gravity flow simulator for block caving planning. Granul. Matter 2024, 26, 20–22. [Google Scholar] [CrossRef]
- Gómez, R.; Castro, R. Stress modelling using cellular automata for block caving applications. Int. J. Rock Mech. Min. Sci. 2022, 154, 105124. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Andreotti, B.; Forterre, Y.; Pouliquen, O. Granular Media; Between Fluid and Solid, 55; Cambridge University Press: Cambridge, UK, 2013; Available online: https://books.google.cl/books?hl=es&lr=&id=2ekG3NYgpqsC&oi=fnd&pg=PR7&dq=granular+media+2013&ots=NZBBw_JSC1&sig=nRJYtYBABGO1pvK09hT75PhEou8&redir_esc=y#v=onepage&q=granular%20media%202013&f=false (accessed on 7 May 2025).
- Dorador, L.; Villalobos, F.A. Analysis of the geomechanical characterization of coarse granular materials using the parallel gradation method. Obras Proy. 2020, 27, 50–63. [Google Scholar] [CrossRef]
- Castro, R.; Gómez, R.; Pierce, M.; Canales, J. Experimental quantification of vertical stresses during gravity flow in block caving. Int. J. Rock Mech. Min. Sci. 2020, 127, 104237. [Google Scholar] [CrossRef]
- Pierce, M.E. Forecasting vulnerability of deep extraction level excavations to draw-induced cave loads. J. Rock Mech. Geotech. Eng. 2019, 11, 527–534. [Google Scholar] [CrossRef]
- Orellana, L.F. Evaluación de variables de Diseño del Sistema de Minería Continua a Partir de Experimentación en Laboratorio. Master’s Thesis, Universidad de Chile, Santiago, Chile, 2012. [Google Scholar]
- Laubscher, D. Dilution. In Block Cave Manual, International Caving Study (1997–2000); JKMRC and Itasca Consulting Group, Inc.: Brisbane, QLD, Australia, 2000. [Google Scholar]
- Hashim, M.; Hazizan, M.; Sharrock, G.; Saydam, S. A Review of Particle Percolation in Mining. In SHIRMS 2008; Potvin, Y., Carter, J., Dyskin, A., Jeffrey, R., Eds.; Australian Centre for Geomechanics: Perth, WA, Australia, 2008; pp. 273–284. [Google Scholar] [CrossRef]
- Castro, R.; Arancibia, L.; Gómez, R. Quantifying fines migration in block caving through 3D experiments. Int. J. Rock Mech. Min. Sci. 2022, 151, 8–10. [Google Scholar] [CrossRef]
- Aravena, M.; Palma, S.; Vivanco-Avaria, F.; Nelis, G. Quantification of fines migration in block caving mining through laboratory experiments. Results Eng. 2025, 25, 103576. [Google Scholar] [CrossRef]
- Castro, R.; Gómez, R.; Arancibia, L. Fine material migration modelled by cellular automata. Granul. Matter 2022, 24, 1–11. [Google Scholar] [CrossRef]
- Mullins, W.W. Stochastic theory of particle flow under gravity. J. Appl. Phys. 1972, 43, 665–678. [Google Scholar] [CrossRef]
- Dorador, L.; Heberhardt, E.; Elmo, D.; Norman, B.; Aguayo, A. Influence of secondary fragmentation and column height on block size distribution and fines migration reaching drawpoints. In Proceedings of the 3rd International Symposium on Block and Sublevel Caving, Santiago, Chile, 5–6 June 2014; pp. 128–137. [Google Scholar]
- Valderrama, M.M. Generacion de Material fino Inducido por Esfuerzo de Corte y su Aplicacion a la Fragmentacion Secundaria en Block Caving. Bachelor’s Thesis, Universidad de Concepción, Concepcion, Chile, 2024. [Google Scholar]
- Lapčević, V.; Torbica, S. Numerical investigation of caved rock mass friction and fragmentation change influence on gravity flow formation in sublevel caving. Minerals 2017, 7, 56. [Google Scholar] [CrossRef]
- Cardu, M.; Godio, A.; Oggeri, C.; Seccatore, J. The influence of rock mass fracturing on splitting and contour blasts. Geomech. Geoengin. 2022, 17, 822–833. [Google Scholar] [CrossRef]
- Brzovic, A.; Villaescusa, E. Rock mass characterization and assessment of block-forming geological discontinuities during caving of primary copper ore at the El Teniente mine, Chile. Int. J. Rock Mech. Min. Sci. 2007, 44, 565–583. [Google Scholar] [CrossRef]
- Pereira, J.; Divasto, C.; Barindelli, G. Evaluación Comparativa Metodologías Mapeo Presencial Granulométrico v/s Procesamiento Digital de Imágenes: Casos de Estudio Mina Subterránea. In SIMIN 2023; Universidad de Santiago de Chile: Santiago, Chile, 2023. [Google Scholar]
- Moss, A.; Russel, F.; Jones, C. Caving and Fragmentation at Palabora: Prediction to Production. In Proceeding of the Massmin 2004, Santiago, Chile, 22–25 August 2004; pp. 585–590. [Google Scholar]
- Kurniawan, C.; Setyoko, T.B. Impact of rock type variability on production rates and scheduling at the DOZ-ESZ block cave mine. In Proceedings of the 5th Conference and Exhibition on Mass Mining, Lulea, Sweden, 9–11 June 2008; pp. 291–302. [Google Scholar]
- Nadolski, S.; Munkhchuluun, M.; Klein, B.; Elmo, D.; Hart, C. Cave fragmentation in a cave-to-mill context at the New Afton Mine part I: Fragmentation and hang-up frequency prediction. Min. Technol. 2018, 127, 75–83. [Google Scholar] [CrossRef]




| Initial Size | Final Size | |||||||
|---|---|---|---|---|---|---|---|---|
| Stress [MPa] | d10 [mm] | d20 [mm] | d50 [mm] | d80 [mm] | d10 [mm] | d20 [mm] | d50 [mm] | d80 [mm] |
| 0.8 | 6.65 | 7.47 | 10.8 | 15.6 | 5.02 | 6.24 | 9.12 | 14.18 |
| 3 | 4.03 | 5.14 | 8.59 | 12.66 | ||||
| 5 | 3.72 | 4.86 | 8.41 | 12.28 | ||||
| Vertical Stress [MPa] | Upper Block Density [kg/m3] | Material Density [kg/m3] |
|---|---|---|
| 0.8 | 116,675.85 | 2620 |
| 3 | 437,027.03 | |
| 5 | 728,378.61 |
| Parameter | Value |
|---|---|
| Maximum extraction | 40 |
| N | 6 |
| Mv | 3 |
| d10 initial | 0.66 |
| d20 initial | 0.75 |
| d50 initial | 1.08 |
| d80 initial | 1.56 |
| Number of simulations per vertical stress | 5 |
| σv [MPa] | ε | |||
|---|---|---|---|---|
| R10 | R20 | R50 | R80 | |
| 0.8 | 0.540 | 0.916 | 0.345 | 0.437 |
| 3 | 0.218 | 0.111 | 0.140 | 0.067 |
| 5 | 0.096 | 0.054 | 0.079 | 0.066 |
| Reduction Ratios | α3 | |
|---|---|---|
| R10 | 0.79 | 1.03 |
| R20 | 1.58 | 2.10 |
| R50 | 0.74 | 0.53 |
| R80 | 1.25 | 1.15 |
| Parameter | Value | Unit |
|---|---|---|
| Density | 2600 | kg/m3 |
| d10 | 0.049 | m |
| d20 | 0.107 | m |
| d50 | 0.340 | m |
| d80 | 0.809 | m |
| UCS | 70.0 | MPa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gómez, R.; San Martin, C.; Castro, R. An Integrated Cellular Automata Model Improves the Accuracy of Secondary Fragmentation Prediction. Appl. Sci. 2025, 15, 5425. https://doi.org/10.3390/app15105425
Gómez R, San Martin C, Castro R. An Integrated Cellular Automata Model Improves the Accuracy of Secondary Fragmentation Prediction. Applied Sciences. 2025; 15(10):5425. https://doi.org/10.3390/app15105425
Chicago/Turabian StyleGómez, René, Camila San Martin, and Raúl Castro. 2025. "An Integrated Cellular Automata Model Improves the Accuracy of Secondary Fragmentation Prediction" Applied Sciences 15, no. 10: 5425. https://doi.org/10.3390/app15105425
APA StyleGómez, R., San Martin, C., & Castro, R. (2025). An Integrated Cellular Automata Model Improves the Accuracy of Secondary Fragmentation Prediction. Applied Sciences, 15(10), 5425. https://doi.org/10.3390/app15105425







