Investigation of Hybrid Tooth Profiles for Robotic Drives Based on IH Tooth Profiles and Cycloidal Curves
Abstract
1. Introduction
2. Tooth Profile Characteristics of Harmonic Reducer
3. HTP Tooth Profile Design Using IH Tooth Profile and Cycloidal Curve
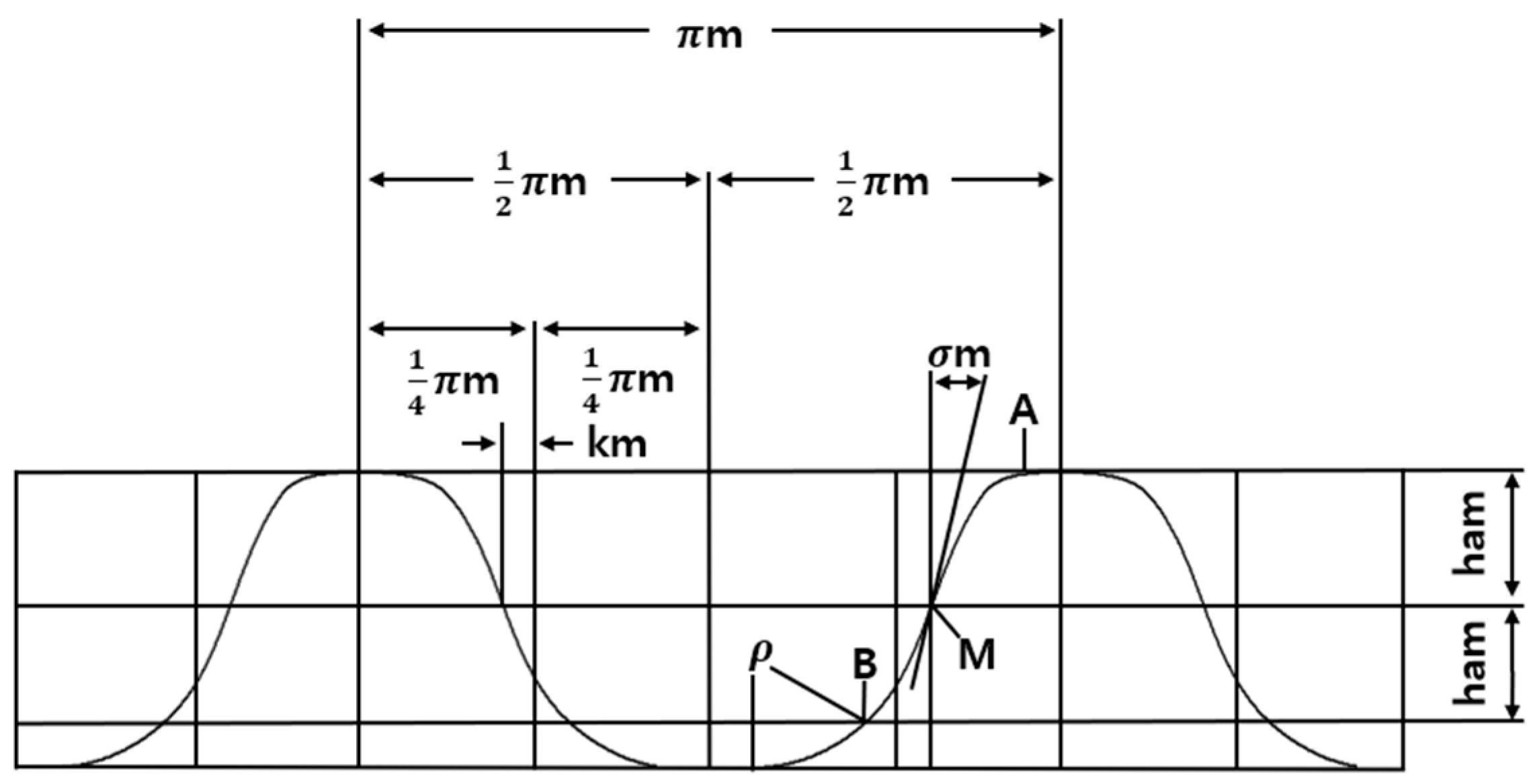
3.1. IH Tooth Profile Theory
3.2. Cycloid Curve Theory
3.3. HTP Tooth Profile Design Theory
3.4. Analysis of the HTP Tooth Profile and Conventional Tooth Profiles Through Schematic Comparison
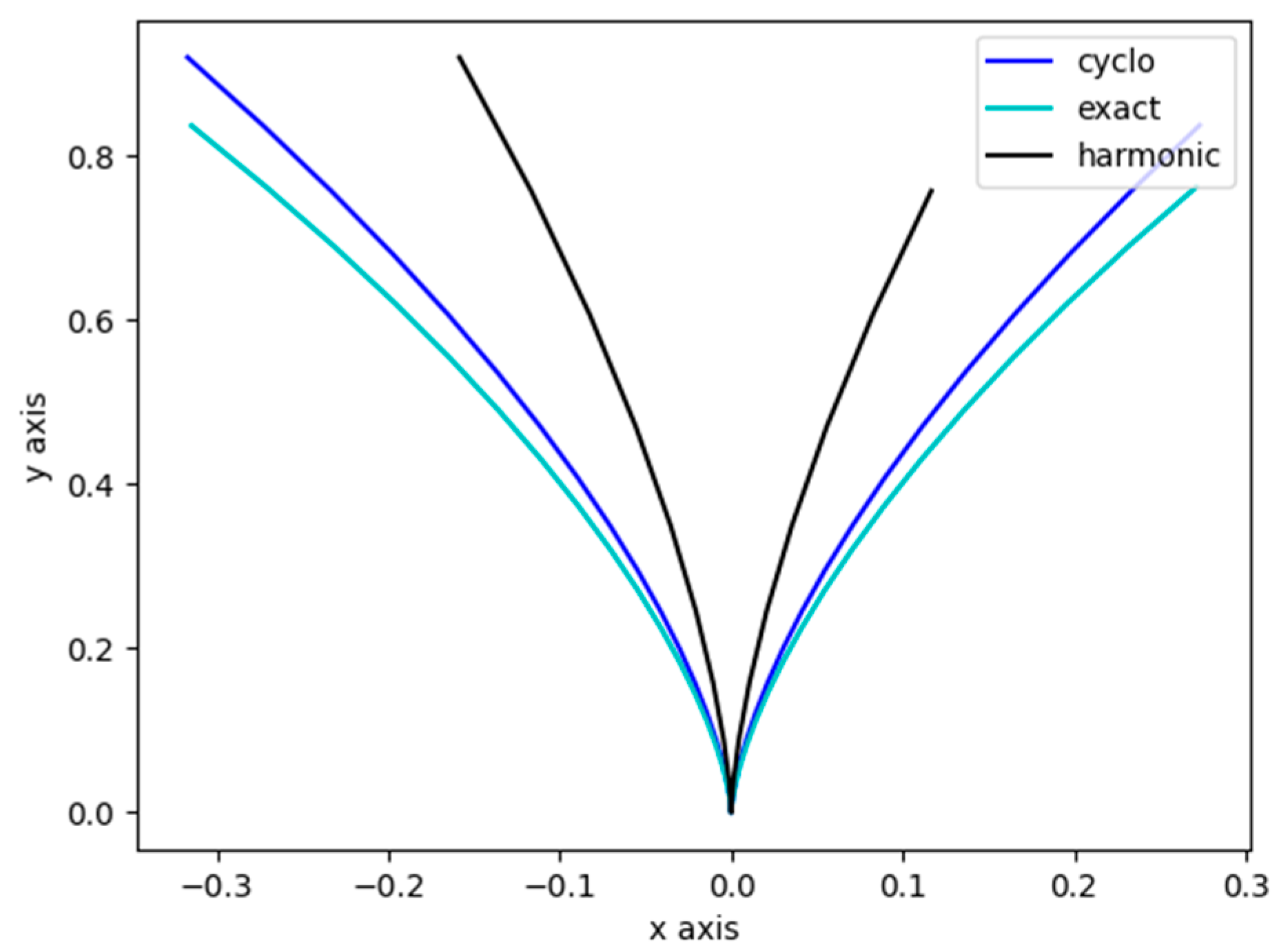
3.4.1. Comparison Among Cycloidal, Harmonic, and Exact Curves
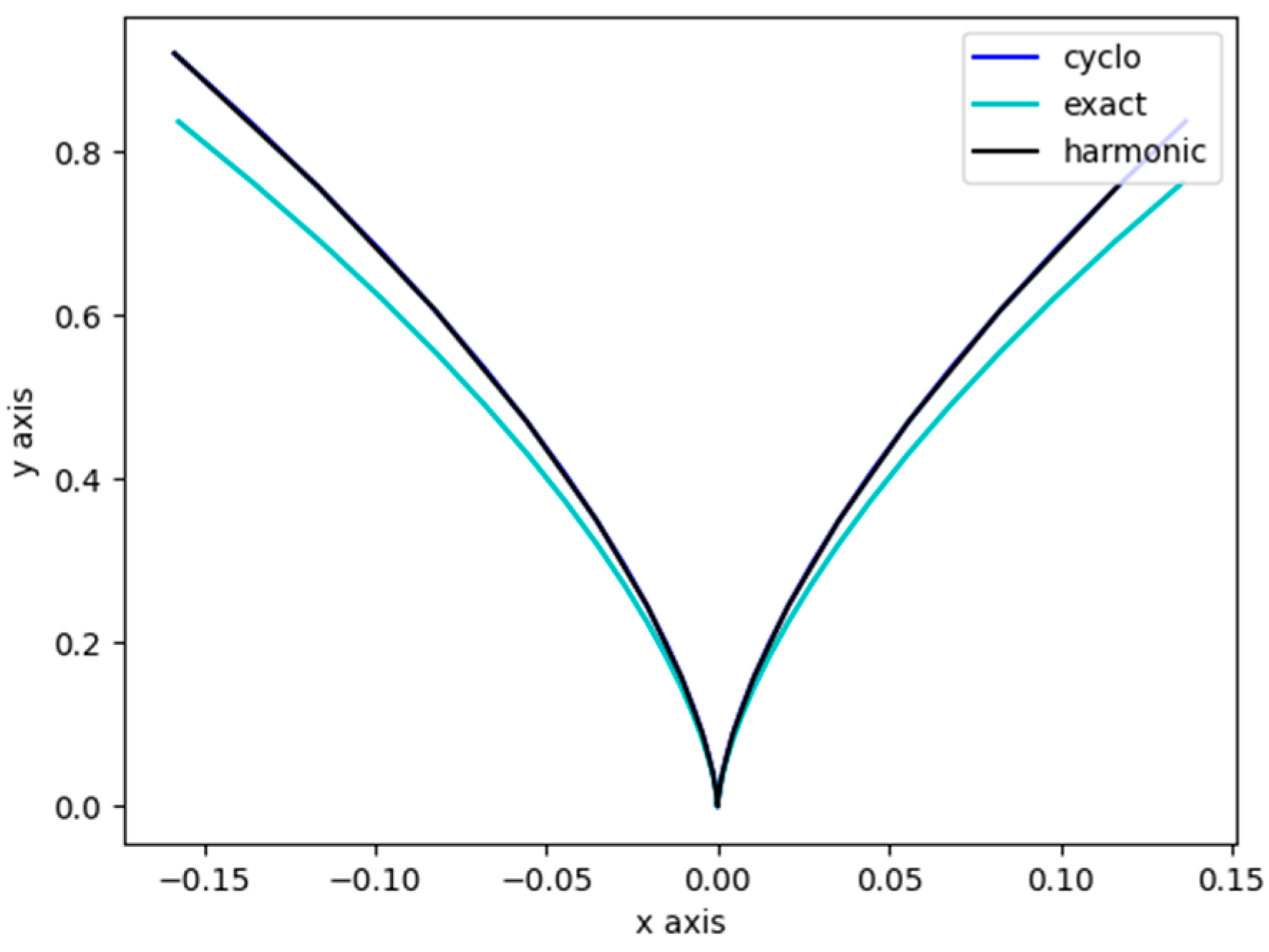
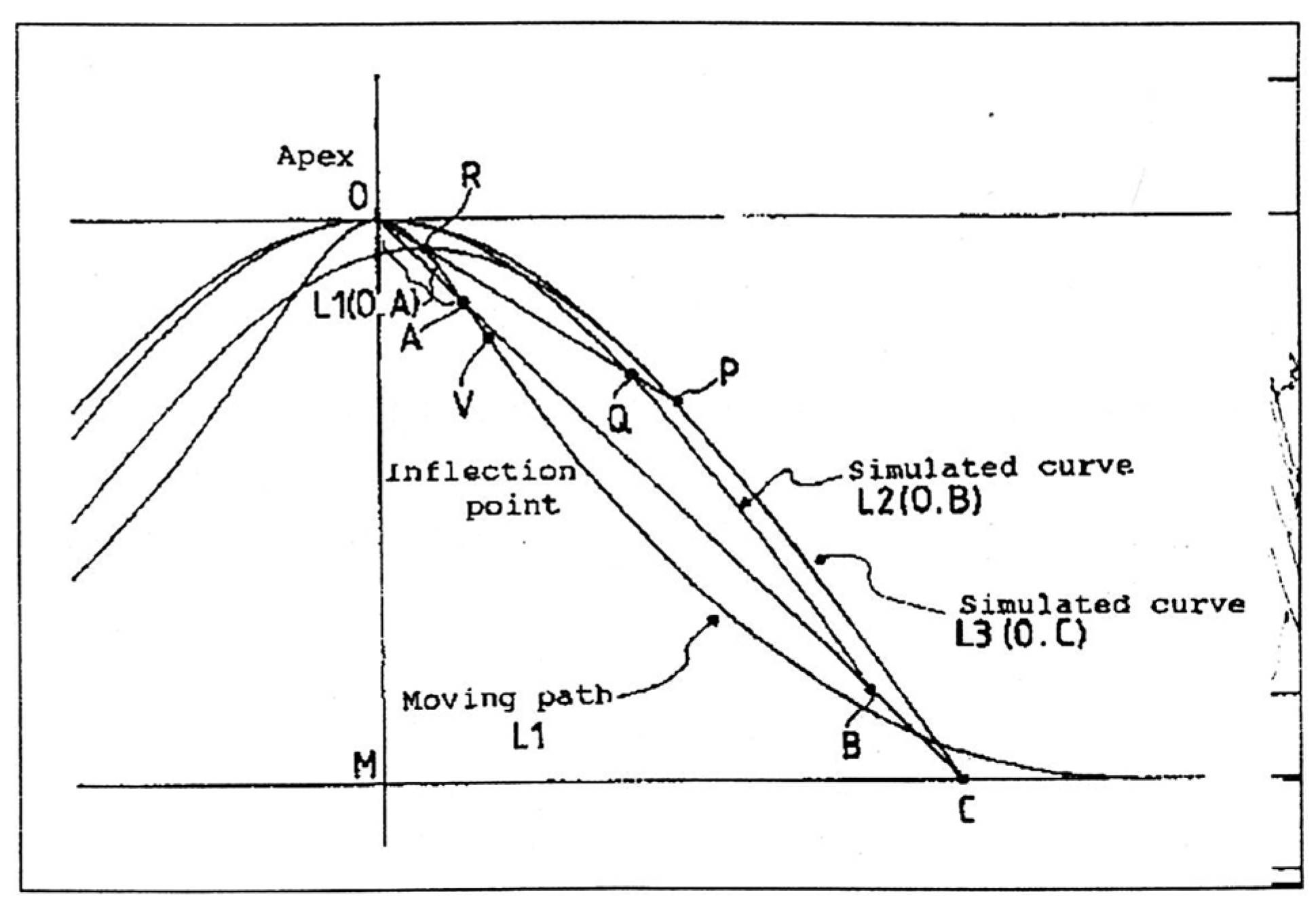
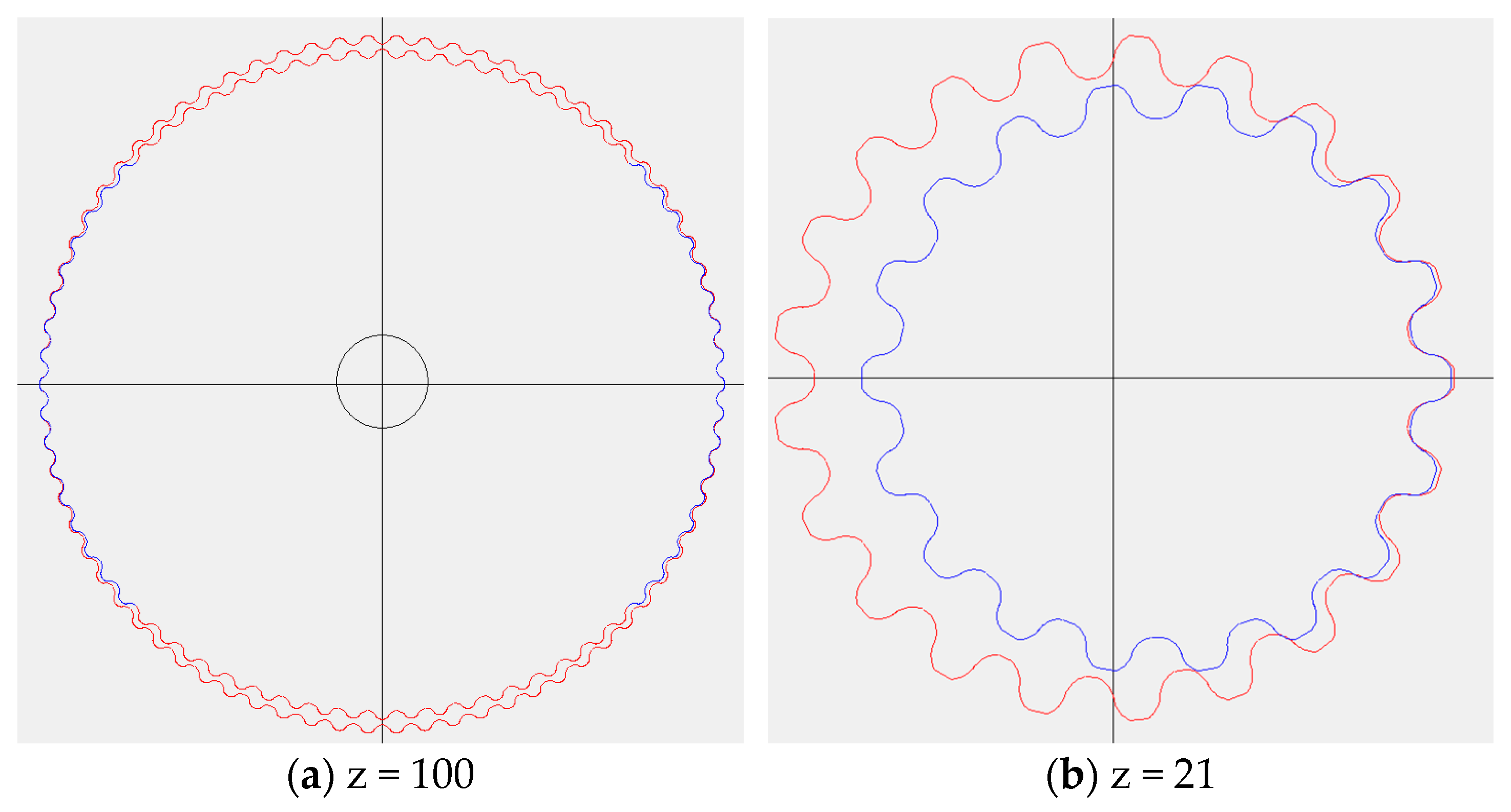
3.4.2. Comparison of Tooth Profile Curve Trajectories According to Tooth Number Change

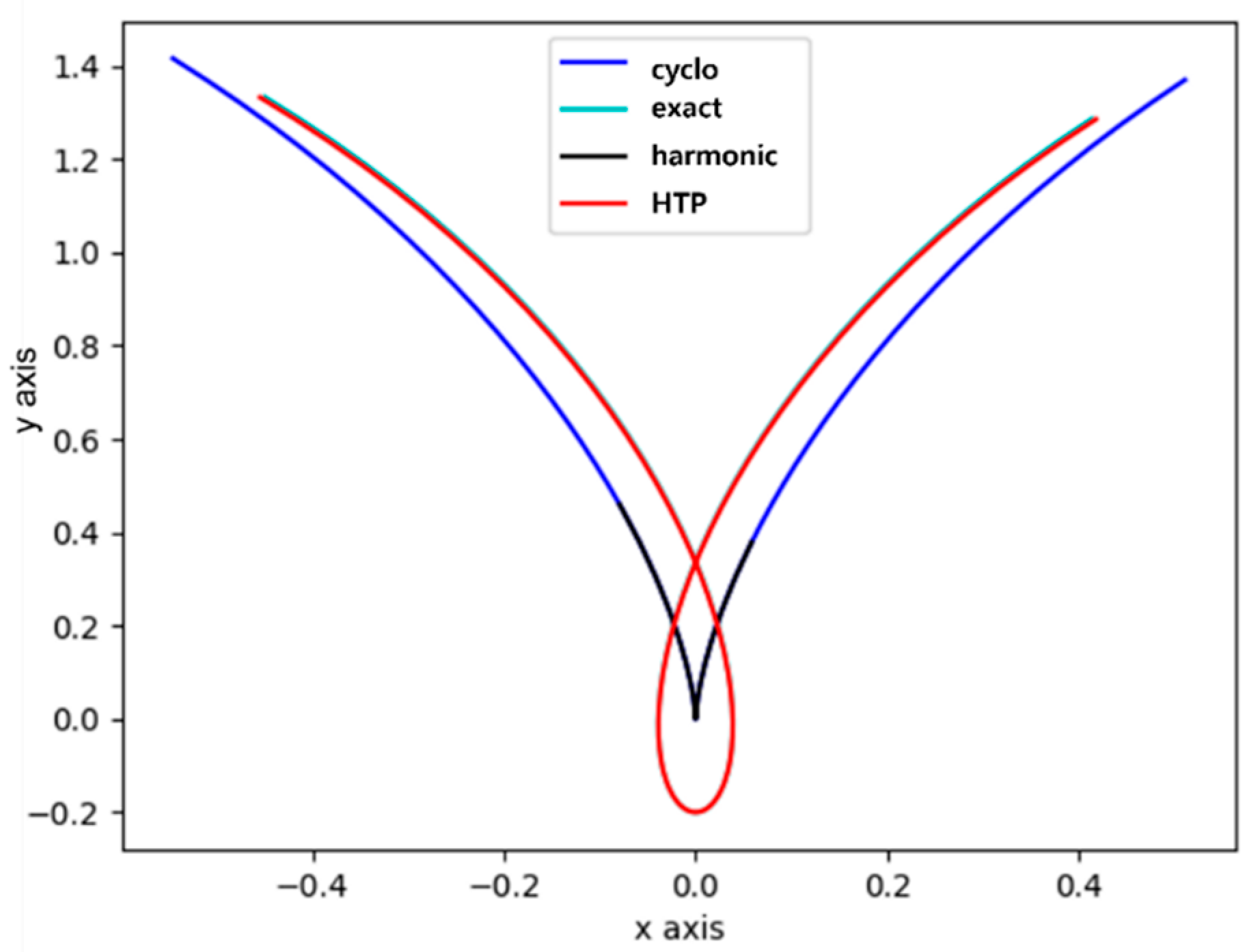
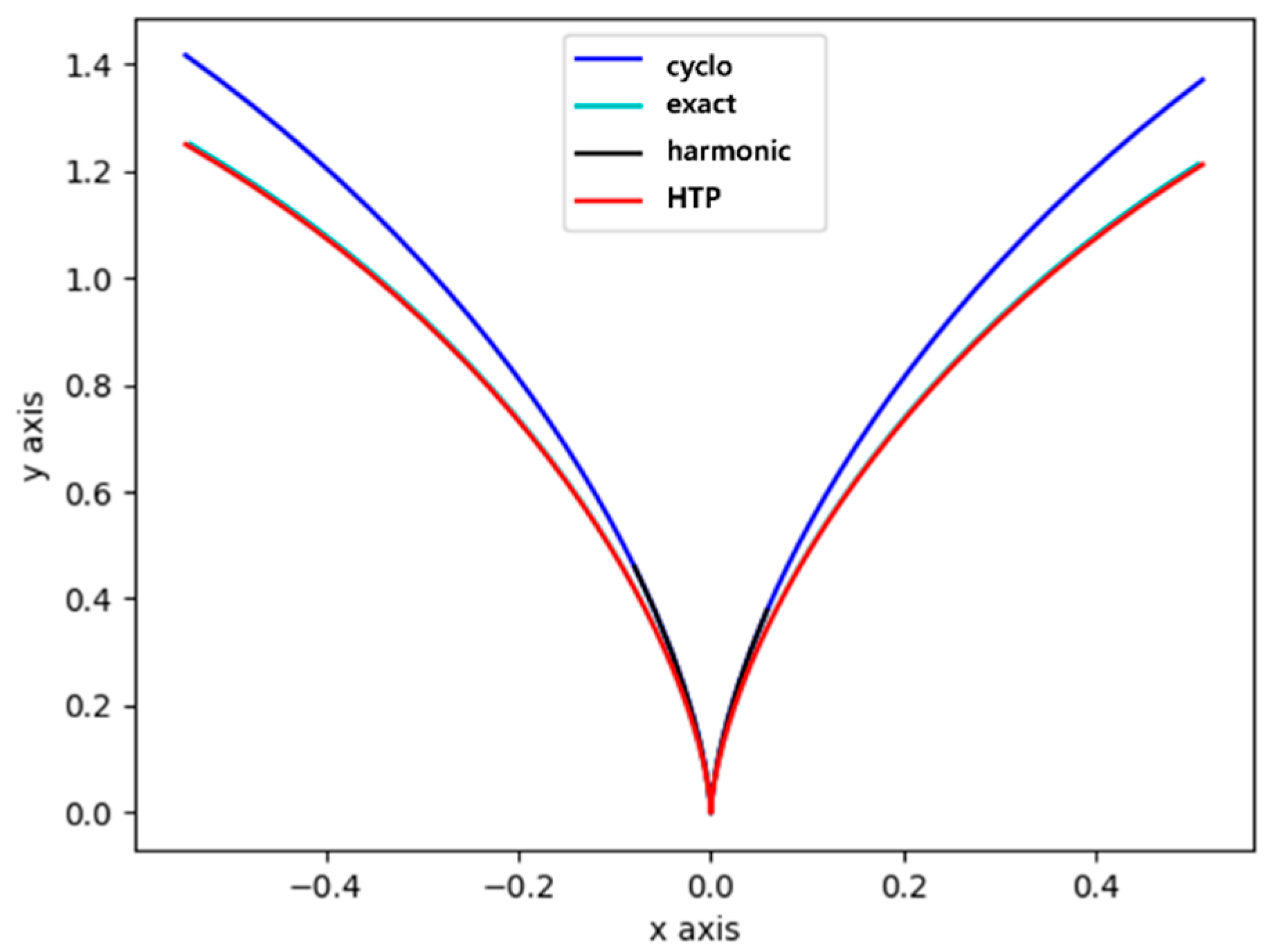
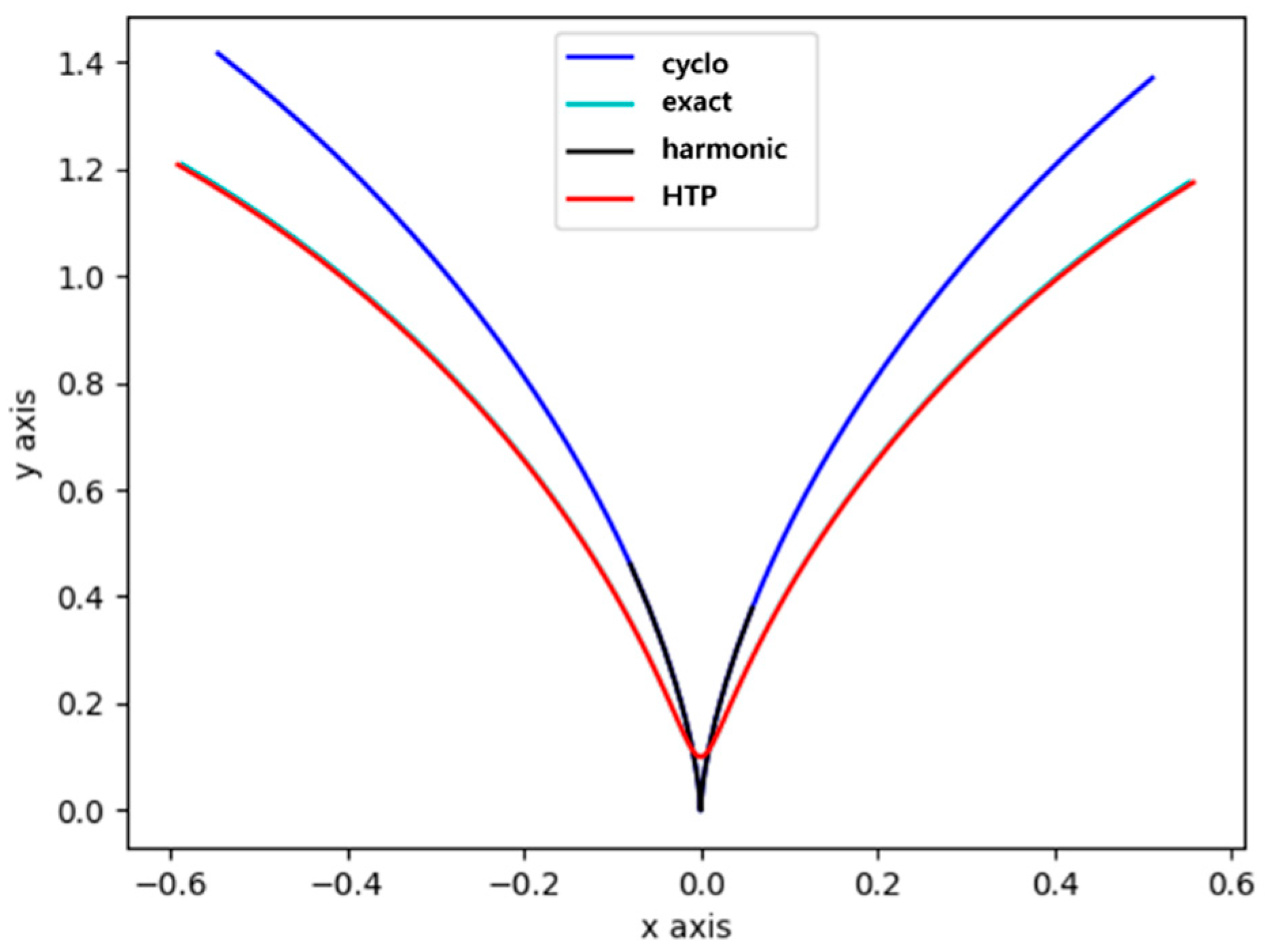
3.4.3. Analysis of Tooth Profile Meshing Geometry
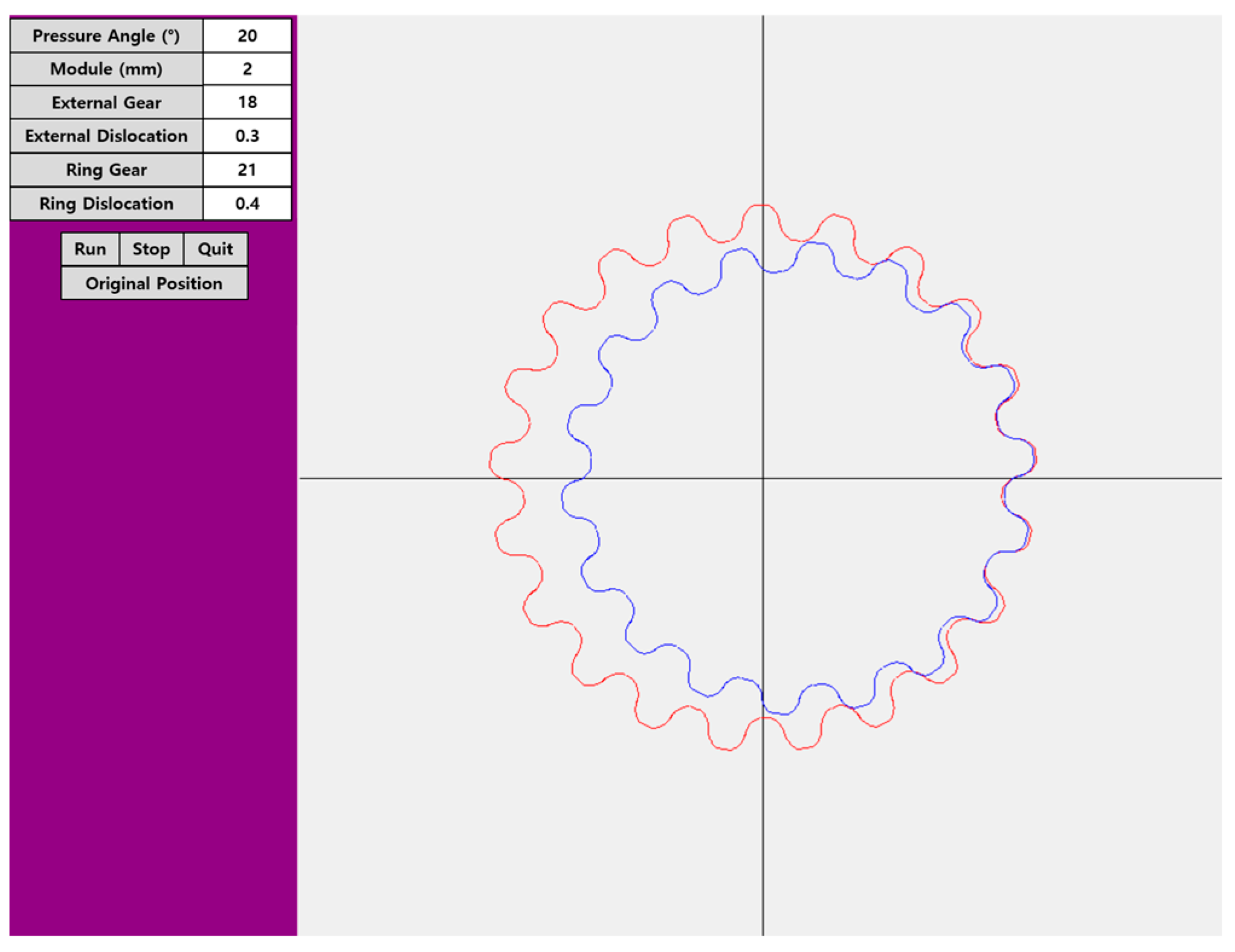
3.5. HTP Tooth Profile Design Software Using Python
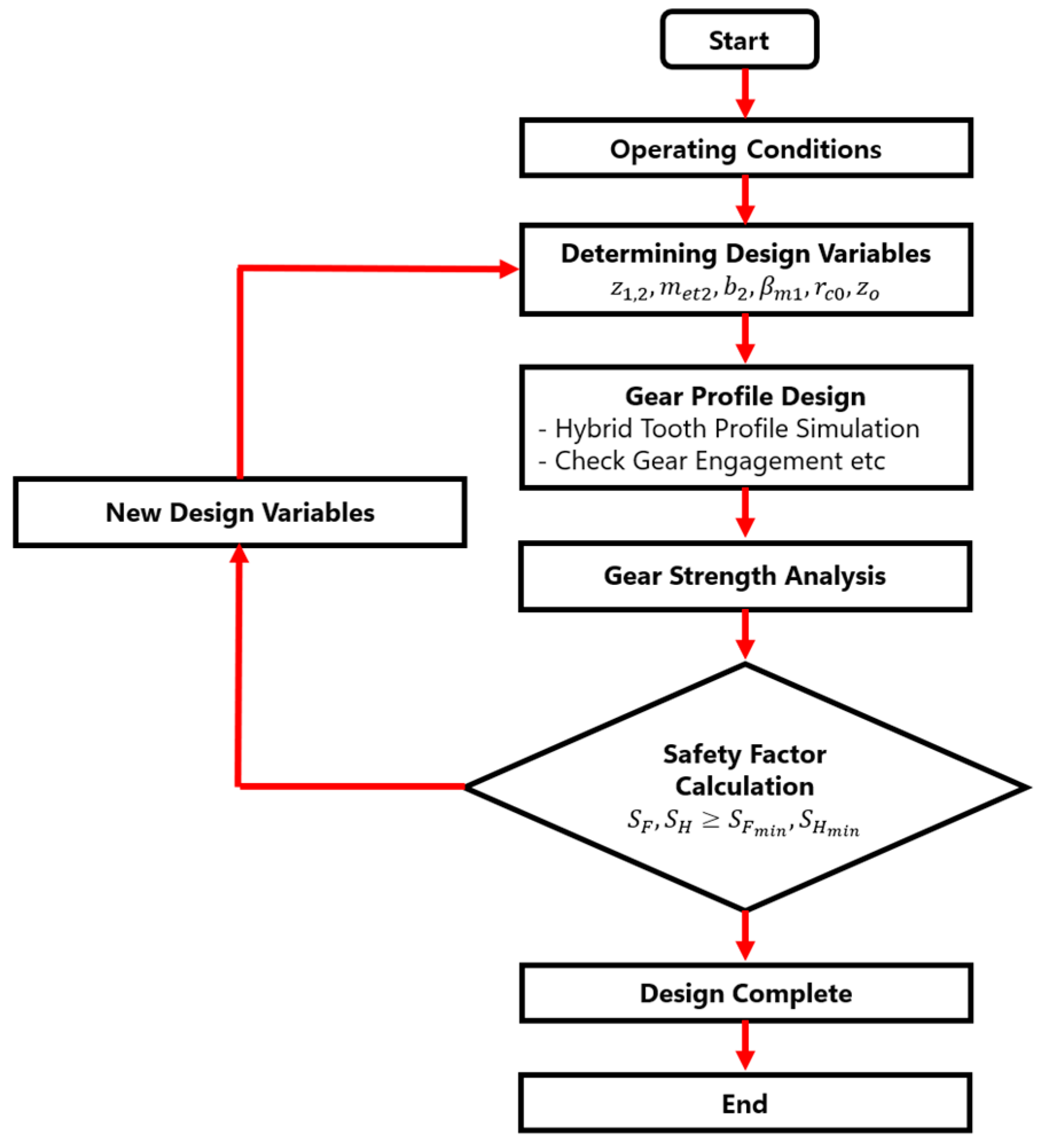
4. Design and Strength Analysis of an HTP Tooth Profile Reducer
4.1. Design of a Reducer with an HTP Tooth Profile Based on the IH Tooth Profile and Cycloidal Curves
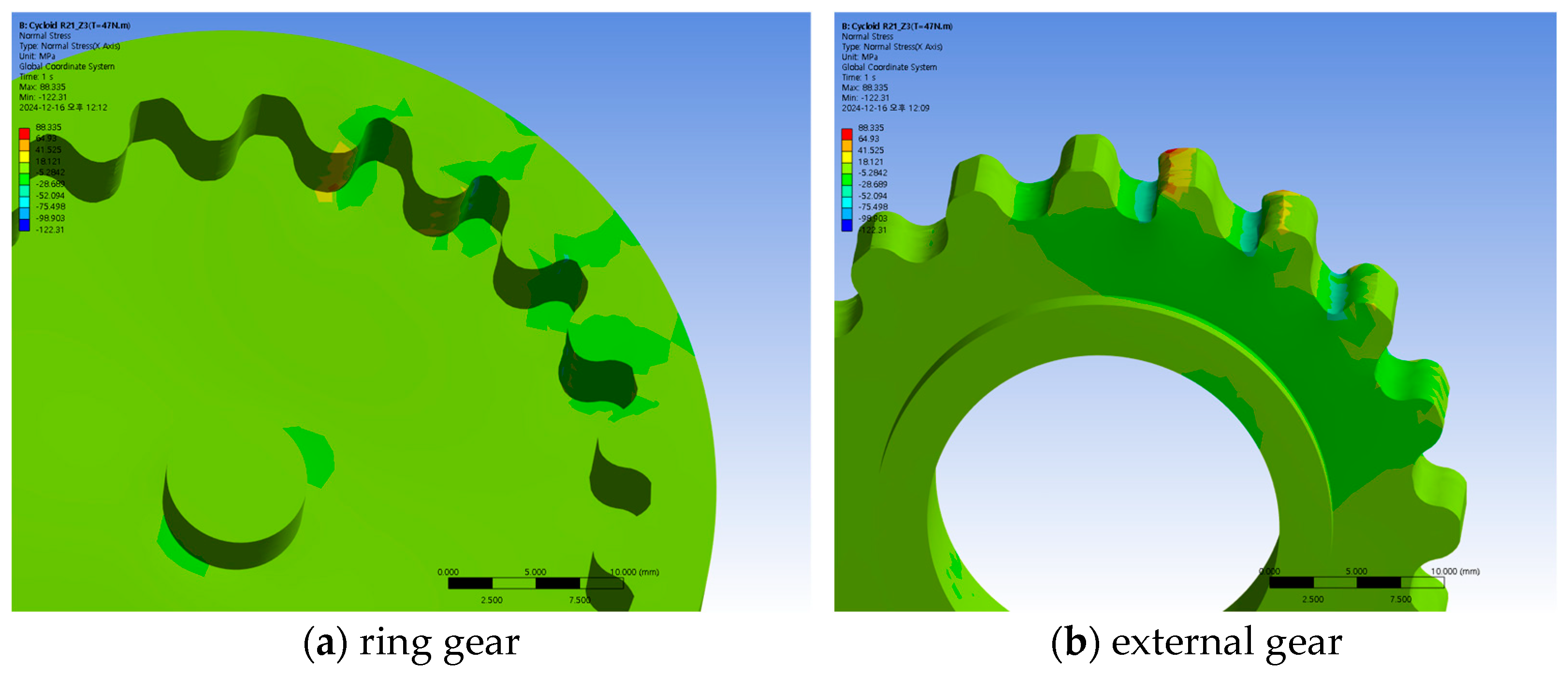
4.2. Strength Analysis of the Reducer
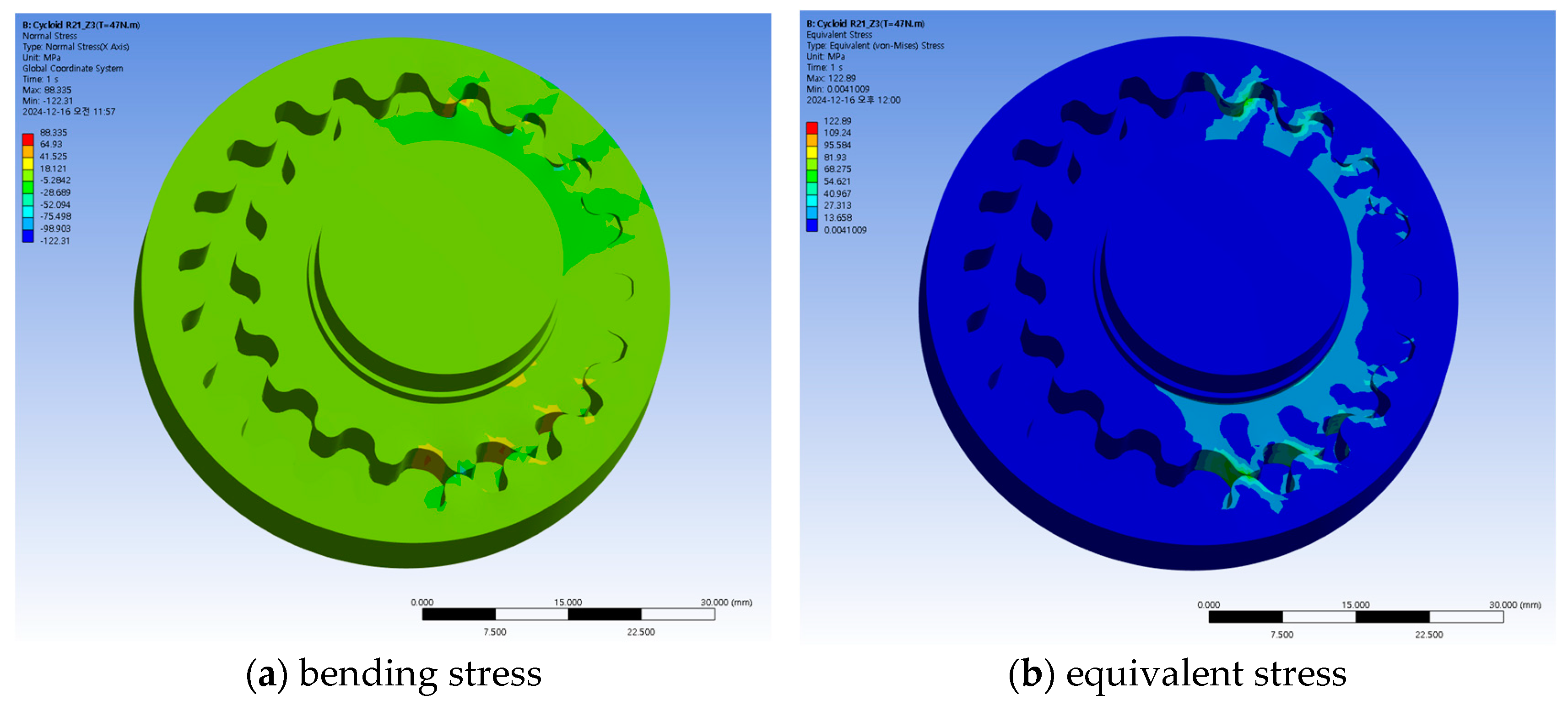
4.3. Prototype Fabrication of the Reducer
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nam, W.-K.; Oh, S.-H. A design of speed reducer with trapezoidal tooth profile for robot manipulator. J. Mech. Sci. Technol. 2011, 25, 171–176. [Google Scholar] [CrossRef]
- Ren, Z.Y.; Mao, S.M.; Guo, W.C.; Guo, Z. Tooth modification and dynamic performance of the cycloidal drive. Mech. Syst. Signal Process. 2017, 85, 857–866. [Google Scholar] [CrossRef]
- Jang, D.J.; Kim, Y.C.; Hong, E.P.; Kim, G.S. Geometry design and dynamic analysis of a modified cycloid reducer with epitrochoid tooth profile. Mech. Mach. Theory 2021, 164, 104399. [Google Scholar] [CrossRef]
- Li, T.; An, X.; Deng, X.; Li, J.; Li, Y. A new tooth profile modification method of cycloidal gears in precision reducers for robots. Appl. Sci. 2020, 10, 1266. [Google Scholar] [CrossRef]
- Thai, N.H.; Thom, P.V.; Trung, N.T. Experimental design and manufacture a pair of the internal non-circular gears with an improved cycloid profile. In Regional Conference in Mechanical Manufacturing Engineering; Springer: Singapore, 2021. [Google Scholar]
- Hsieh, C.-F. Traditional versus improved designs for cycloidal speed reducers with a small tooth difference: The effect on dynamics. Mech. Mach. Theory 2015, 86, 15–35. [Google Scholar] [CrossRef]
- Jia, H.; Li, J.; Xiang, G.; Wang, J.; Xiao, K.; Han, Y. Modeling and analysis of pure kinematic error in harmonic drive. Mech. Mach. Theory 2021, 155, 104122. [Google Scholar] [CrossRef]
- Kim, B.-S.; Jeong, S.-T.; Ahn, H.-J. The prediction of the angular transmission error of a harmonic drive by measuring noncontact tooth profile and considering three-dimensional tooth engagement. Int. J. Precis. Eng. Manuf. 2023, 24, 371–378. [Google Scholar] [CrossRef]
- Yang, C.; Ma, H.; Zhang, T.; Liu, Z.; Zhao, Y.; Hu, Q. Research on meshing characteristics of strain wave gearing with three different types of tooth profiles. Int. J. Precis. Eng. Manuf. 2021, 22, 1761–1775. [Google Scholar] [CrossRef]
- Tang, T.; Jia, H.; Li, J.; Wang, J.; Zeng, X. Modeling of transmission compliance and hysteresis considering degradation in a harmonic drive. Appl. Sci. 2021, 11, 665. [Google Scholar] [CrossRef]
- Wang, J.; Wan, Z.; Dong, Z.; Li, Z. Research on performance test system of space harmonic reducer in high vacuum and low temperature environment. Machines 2020, 9, 1. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, X.; Liu, Z.; Liu, J.; Zhang, J. Research on static and dynamic mechanical characteristics of flexible bearing in harmonic reducer. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420919953. [Google Scholar]
- Ishikawa, S. The gear geometry of tooth engagement in harmonic drive. In Proceedings of the JSME Semi-International Symposium, Tokyo, Japan, 4–8 September 1967. [Google Scholar]
- Ishikawa, S. Tooth Profile of Spline of Strain Wave Gearing. U.S. Patent No. 4,823,638, 25 April 1989. [Google Scholar]
- Kiyosawa, Y.; Sasahara, M.; Ishikawa, S. Performance of a strain wave gearing using a new tooth profile. In Proceedings of the 1989 International Power Transmission and Gearing Conference, Chicago, IL, USA, 25–28 April 1989; American Society of Mechanical Engineers: New York, NY, USA, 1989; Volume 2, pp. 607–612. [Google Scholar]
- Kondo, K.; Takada, J. Study on tooth profiles of the harmonic drive. J. Mech. Des. 1990, 112, 131–137. [Google Scholar] [CrossRef]
- Maiti, R. A novel harmonic drive with pure involute tooth gear pair. J. Mech. Des. 2004, 126, 178–182. [Google Scholar] [CrossRef]
- Cao, X.; Song, S.; Xie, H.; Wang, M. Design and analysis of double-arc tooth profile harmonic drive. In Recent Developments in Mechatronics and Intelligent Robotics: Proceedings of the International Conference on Mechatronics and Intelligent Robotics (ICMIR2017)–Volume 2; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 19–29. [Google Scholar]
- Yu, Z.; Ting, K.-L. Explicit dynamics analysis for harmonic drives. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, New York, NY, USA, 25–28 August 2014; American Society of Mechanical Engineers: New York, NY, USA, 2014; Volume 46285. [Google Scholar]
- Li, Y.; Zhang, N.; Zhang, Y.; Dai, B. New Design Method for Flexspline Tooth Profile of Harmonic Drive Considering Deformation. In Proceedings of the 2019 IEEE 6th International Conference on Industrial Engineering and Applications (ICIEA), Tokyo, Japan, 12–15 April 2019; IEEE: New York, NY, USA, 2019; pp. 111–115. [Google Scholar]
- Xie, R.; Yang, Y.; Zhou, G.; Gao, B.; Jiao, Y.; Yu, R. A novel harmonic drive with the full conjugate tooth profile. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024, 238, 9748–9760. [Google Scholar] [CrossRef]
- Huang, J.; Xu, J.; Qian, N. Investigation on high contact ratio harmonic two-dimensional tooth profile design based on mid-point meshing method. J. Mech. Sci. Technol. 2023, 37, 835–850. [Google Scholar] [CrossRef]
- Juvinall, R.C.; Marshek, K.M. Fundamentals of Machine Component Design, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1991; pp. 550–596. [Google Scholar]
- Jeon, H.-S. Study on the Flexspline for Harmonic Drive of Robots. Ph.D. Thesis, Chung-Ang University, Seoul, Republic of Korea, 1998. [Google Scholar]
- Ishikawa, S. Tertiary Negative-Deviation Flexing Contact Type Gear Drive of Non-Profile-Shifted Tooth Profile. U.S. Patent No. 5,458,756, 23 January 1996. [Google Scholar]
- Murayama, Y. Method for Designing Tooth Profile of Wave Gear Device. Korean Patent 10-2023-0147738, 23 October 2023. [Google Scholar]


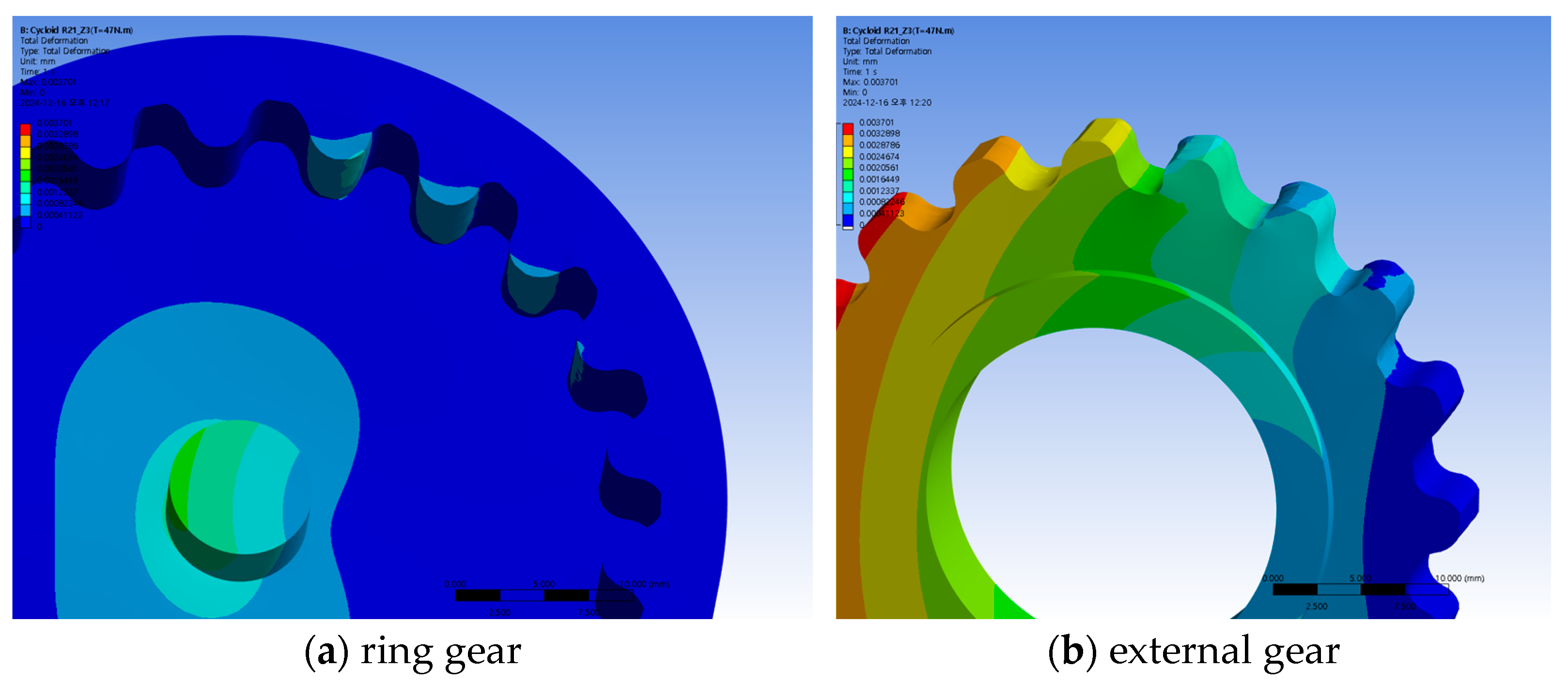
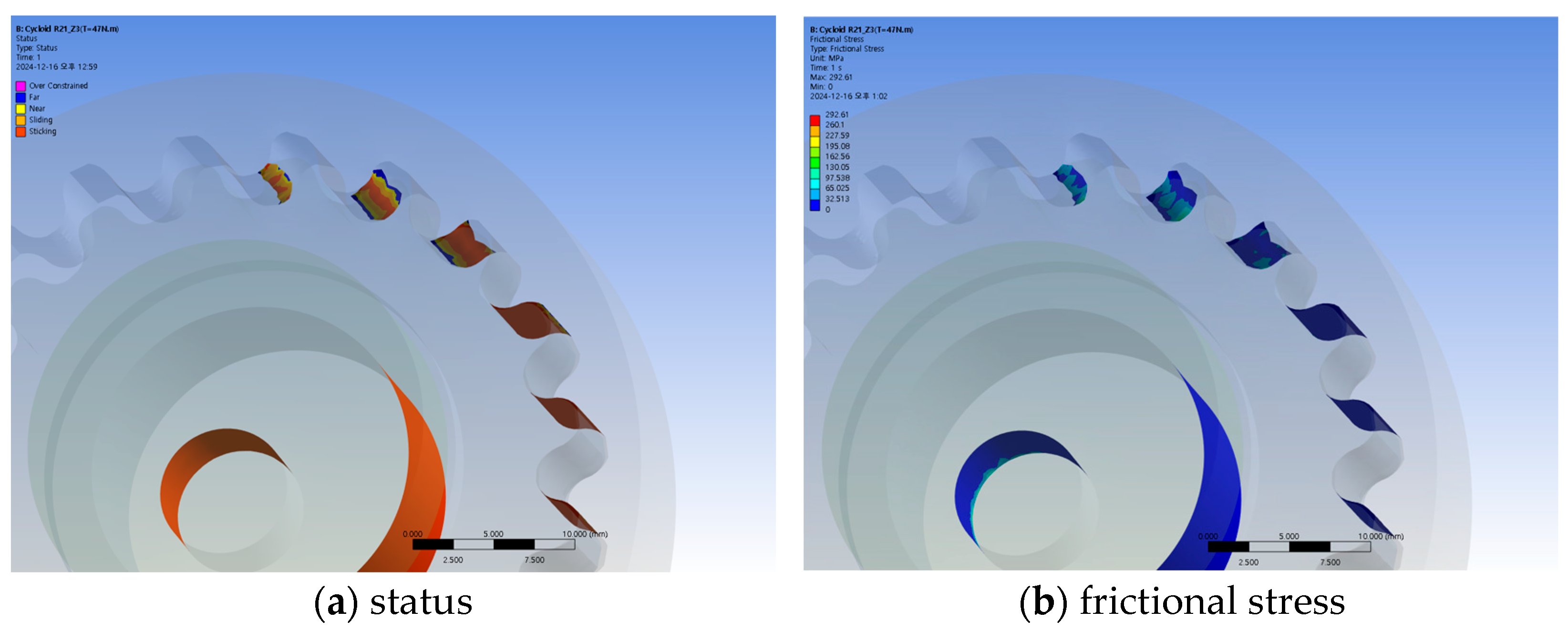
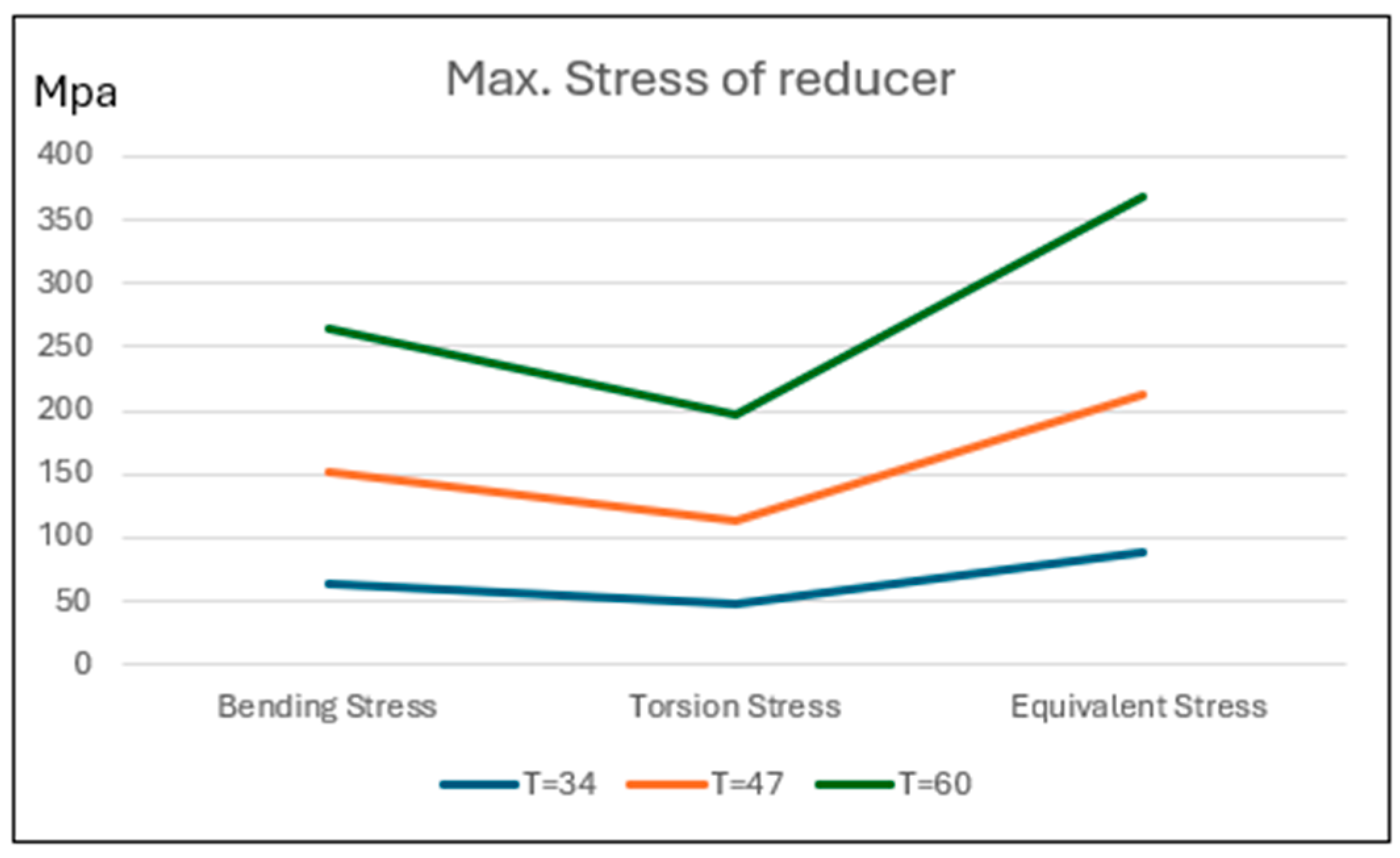

| Parameter | Involute Tooth Profile | Cycloid Tooth Profile | IH Tooth Profile |
|---|---|---|---|
| Tooth profile curve | Involute curve | Circular curve | Straight line and circular curve |
| Contact ratio | 15 | 30 | 30 |
| Efficiency (%) | 90 | 70–80 | 80 |
| Transmission error (arc min) | 1 | 2~3 | 1 |
| Tooth root stress | Reduction compared to involute tooth profile | ||
| Torque | Improvement compared to involute tooth profile | ||
| Meshing state | Instantaneous contact | Initial contact but separation in the intermediate stage | Not in contact for just a moment butremains in contact consistently |
| Parameter | (a) | (b) | ||
|---|---|---|---|---|
| External Gear | Ring Gear | External Gear | Ring Gear | |
| Module | 1.4 | 1.4 | 2 | 2 |
| Pressure angle (°) | 20 | 20 | 20 | 20 |
| Number of teeth | 97 | 100 | 18 | 21 |
| Profile shift coefficient | 0.65 | 0.6 | 0.3 | 0.4 |
| Pitch circle diameter (mm) | 135.8 | 140 | 36 | 42 |
| Center distance (mm) | 4.848 | - | 3.169 | - |
| Operating pressure angle (°) | 22.8 | - | 27.194 | - |
| Parameter | Design Value | |
|---|---|---|
| Module (mm) | 2.0 | |
| Number of teeth | Ring gear | 21 |
| External gear | 18 | |
| Tooth profiles | Hybrid tooth profile | |
| Reducer ratio | 1/6 | |
| Eccentricity (mm) | 3.0 | |
| Pressure angle (°) | 20 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, W.; Lee, M.; Oh, S.; Jeon, H.; Youm, K. Investigation of Hybrid Tooth Profiles for Robotic Drives Based on IH Tooth Profiles and Cycloidal Curves. Appl. Sci. 2025, 15, 5389. https://doi.org/10.3390/app15105389
Jeong W, Lee M, Oh S, Jeon H, Youm K. Investigation of Hybrid Tooth Profiles for Robotic Drives Based on IH Tooth Profiles and Cycloidal Curves. Applied Sciences. 2025; 15(10):5389. https://doi.org/10.3390/app15105389
Chicago/Turabian StyleJeong, Wonhyeong, Myungsung Lee, Sehoon Oh, Hansu Jeon, and Kwangouck Youm. 2025. "Investigation of Hybrid Tooth Profiles for Robotic Drives Based on IH Tooth Profiles and Cycloidal Curves" Applied Sciences 15, no. 10: 5389. https://doi.org/10.3390/app15105389
APA StyleJeong, W., Lee, M., Oh, S., Jeon, H., & Youm, K. (2025). Investigation of Hybrid Tooth Profiles for Robotic Drives Based on IH Tooth Profiles and Cycloidal Curves. Applied Sciences, 15(10), 5389. https://doi.org/10.3390/app15105389





