After the selection process and the implementation of the two methods of predictive maintenance have been described, the first results are presented and evaluated in this section. In the current development phase, each method is always applied to a completed measurement data set. This means that the evaluation takes place after each run. The results always show an entire endurance run, from the start to the point at which the device under test (DUT) could no longer be operated due to damage.
The statistical instrument of the empirical probability
is introduced to represent the results. The empirical probability
with respect to the event
A of a data sequence classified as abnormal is defined as the quotient of the absolute probability
and the number n of observed elements of a set. This indicates that, for
, each observed sequence n in the run N was classified as normal. Consequently, for
, each observed sequence is classified abnormal. On average, 215 data sequences with 2000 data points per run for the OSVM and 4300 data sequences with 100 data points per run for the LSTM were used to calculate the empirical probability. The empirical probability is a particularly good parameter to show the increase of abnormal data within many consecutive runs.
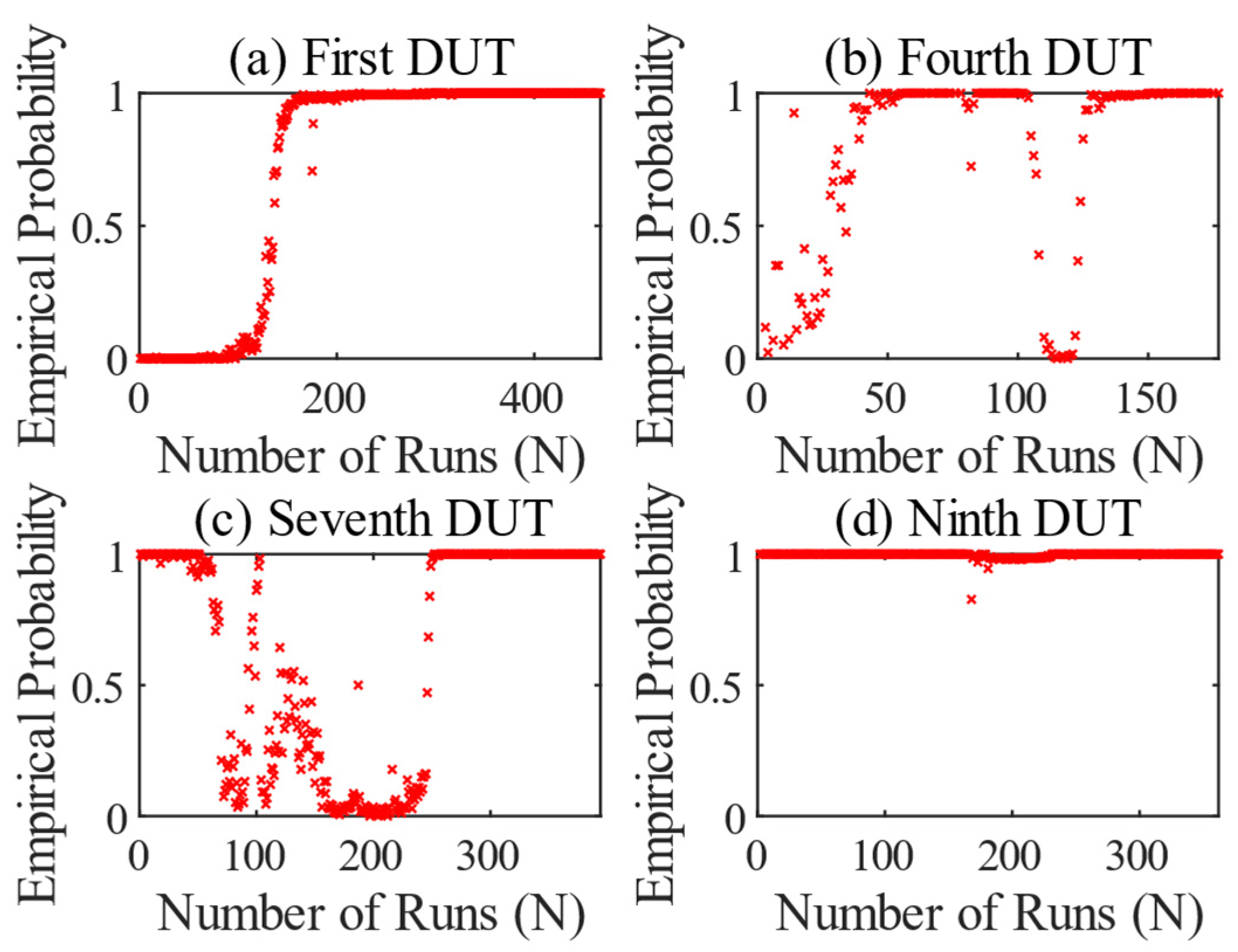
The results of the first, fourth, seventh, and ninth DUT are presented and compared from the test series. All other results are similar. The exact times at which, for example, a tooth broke are not known. The tests were each ended after a further operation was no longer possible due to excessive vibration or temperature values.
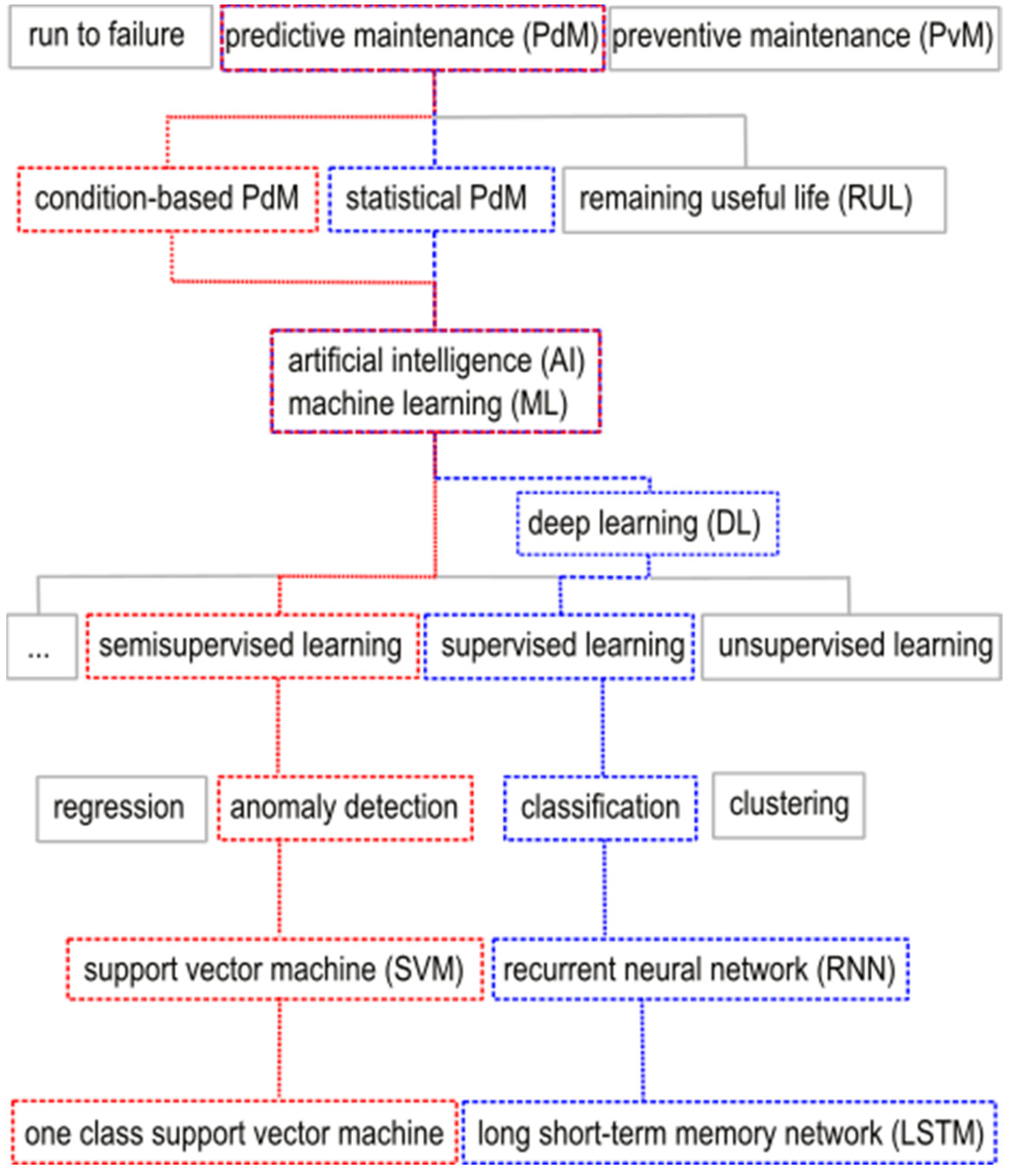
4.1. One-Class Support Vector Machine (ML)
The results of the OSVM presented are shown below. The empirical probability determined from Equation (17) is listed over the number N of runs of the target value profile driven. Runs 30–40 are used for training or for the specification of normally classified torque sequences. The basis for this is the check in
Figure 6. The first runs are not well suited, due to run-in processes. This was checked using runs 0–10, 10–20, and 20–30. Later runs (>40) should not be used, as otherwise the first signs of wear could be taught in.
In addition, a distinction was made in the anomaly detection of the OSVM between damage to a single tooth (local) and to all the teeth of the gear (circular). Furthermore, the trained models are also tested on other DUTs, i.e., the method is also used as a statistical PdM. The results of the inspection for circular tooth damage are shown below, followed by those for local tooth damage.
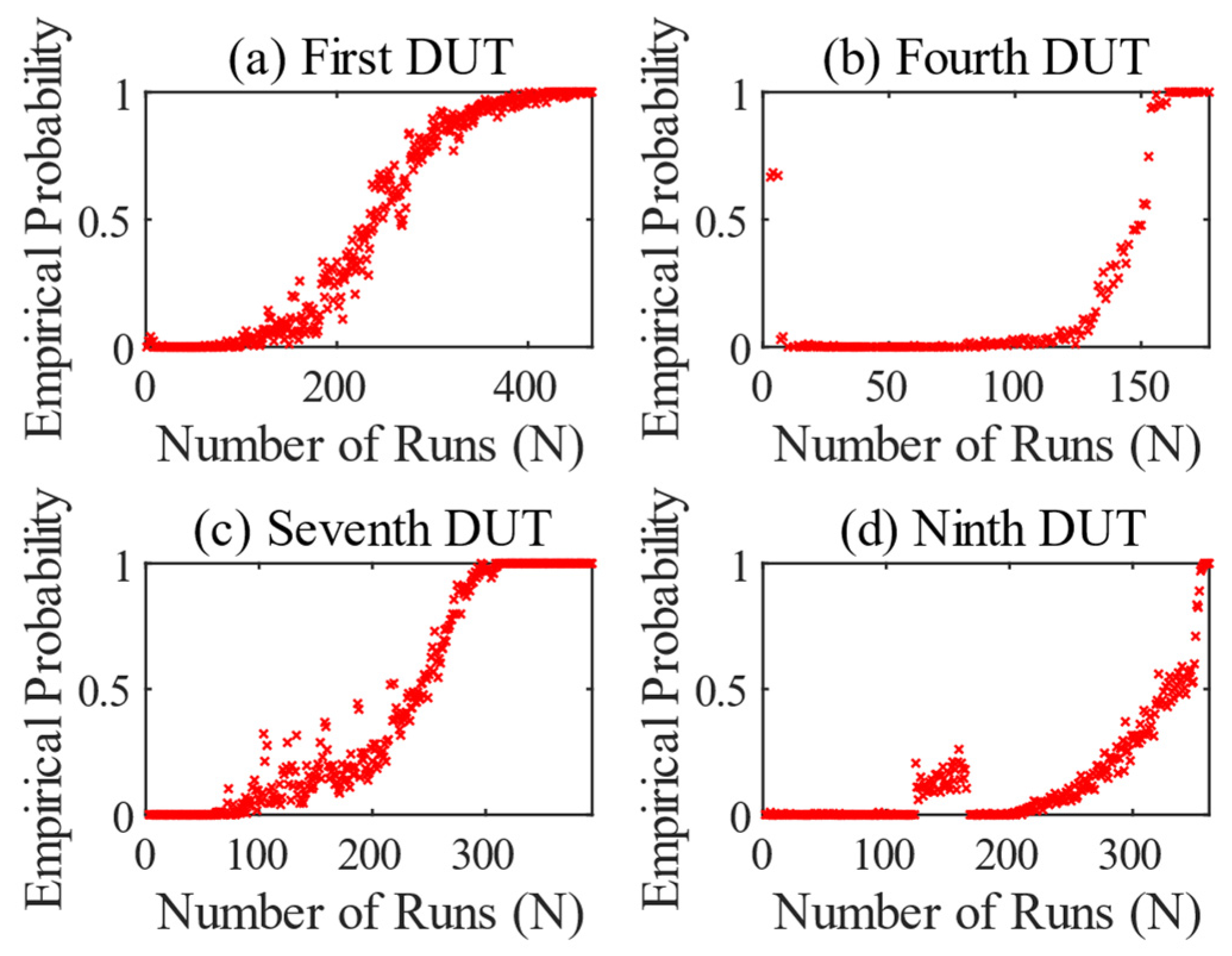
In
Figure 7, the OSVM results series shows that, for each test, a model for rotating gear damage, i.e., including all seven features, was trained and applied to the test in question. As already mentioned in
Section 2.2, there were several incidents during the tests that are explained in connection with the results.
The result of the first DUT is shown in
Figure 7a. The test ran normally and without any special incidents. From run 95 onwards, the OSVM begins to recognize an anomaly or a change in the specific features of the gearbox. From that point on, the empirical probability increases permanently. From run 215 onwards, the values are permanently 1, except for two outliers. However, the DUT did not fail until run number 465. This means that the method recognizes an anomaly at an early stage. Or, to put it another way, the anomaly that is recognized is an early sign of wear.
The test of the fourth DUT in
Figure 7b shows abnormal behavior at the beginning of the test, which quickly changes to a normal state. This may be due to changes in the gearbox caused by the running-in process. From run 50 onwards, the vibration values on the DUT increased. At this point, the side shafts of the differential had to be replaced due to abnormality. This meant that the empirical probability remained at 1 for the rest of the test. The test was terminated after the 177th run. The differential showed heavy pitting and bearing damage. The replacement of the side shafts led to a change in the monitored features, and thus to abnormal behavior, which caused the anomaly detection to fail.
Figure 7c shows the result for the seventh DUT, which behaves in a similar way to the first DUT. However, an anomaly appears in run 90, which initially disappears again. This can be seen from the steep increase in the empirical probability and the subsequent abrupt drop. From run 110 onwards, the value increases continuously and then remains at 1. In the context of the test procedure, the first anomaly detected is associated with impending breakage of a gearbox mounting of the DUT. To generate such a deflection, the resulting vibration must have been superimposed on the frequency of the gear-specific features. In run 103, this mounting was torn off and repaired. This resulted in elimination of the anomaly. Furthermore, wear in the differential is also identified as an anomaly here. The DUT failed from run 394.
The inspection of the ninth differential in
Figure 7d behaved similarly. From run 124, a kind of clustering occurs over 40 runs, after which the empirical probability breaks out and rises continuously until it stabilizes at 1 from run 185. Again, the wear was recognized as an anomaly. The DUT failed from run 362 and could no longer be operated. It is interesting to note in the context of the test that an abnormal bellows on the drive had to be replaced after run 165. After the replacement, the clustering ended. Here too, the PdM provided an indication of abnormal behavior of the test bench, which had a slight influence on the extracted features of the DUT.
Figure 8 shows the results of the OSVM when a model for circumferential gear damage was trained using the first test. This model is then applied to the data from the other tests. The results of the first test in
Figure 7a and
Figure 8a are therefore identical. No good results are generated for the other tests in
Figure 8b–d. Although the values are in the correct range towards the end of the tests, the behavior of the DUTs in the normal state appears to differ. This leads to anomalies being identified at the beginning. In some cases, these disappear again due to the factors mentioned, such as running-in processes or repairs of abnormal components on the test bench.
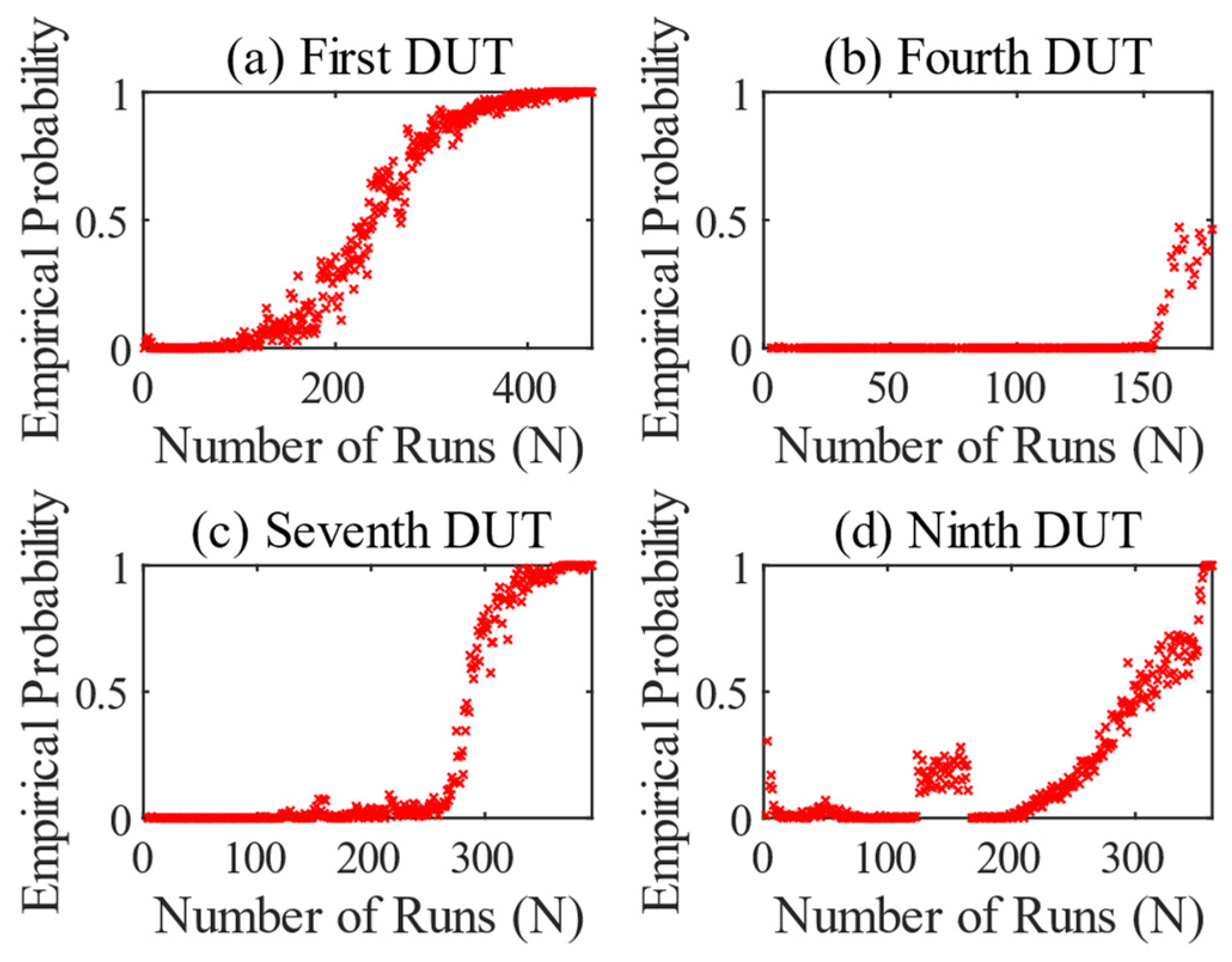
Figure 9 shows the results of the OSVM, where a model for local gear damage, i.e., in terms of the features
and
, was trained for each test and applied to the test in question. The results in
Figure 9 differ in principle from those of the circumferential tooth damage, as they only increase at a later stage. This is in line with the theory of tooth damage. The empirical probability in
Figure 9a increases gradually from run 150 onwards, as in the previous test, because wear can also affect the side bands, but not to the same extent as local damage. The value then increases steadily until it reaches 1 for the first time from run 405 onwards. After that, the empirical probability remains in this range until the end of the test.
The test of the fourth DUT in
Figure 9b again shows a strong run-in process, but then normal operating behavior for a long time. The change of the side shafts in run 50 has no influence on the monitored features of the local tooth damage. After 125 runs, the empirical probability then begins to rise and reaches a value of 1 after 25 more runs. The reason for the failure is not fully clear, but a combination of heavy pitting and bearing damage in the differential was observed. The result of the OSVM indicates abnormal behavior regarding the monitored features at the end of the test.
The result in
Figure 9c shows the same behavior as in
Figure 9a. It is noticeable that the anomaly described in
Figure 7c, where a mounting has come loose, is not recognizable. The external influences therefore had a greater effect on the tooth engagement frequency, which was not taken into account here. In contrast, examination of the data from the ninth test in
Figure 9d shows similar clustering, as previously described in
Figure 7d. An abnormal bellows stimulated the system in such a way that abnormal behavior was registered. In addition, the way in which the empirical probability develops towards the end is different. In comparison to the results of the first and seventh tests, which show a slowing increase, the progression here from run 350 onwards is more like exponential growth. Only the last eight runs have a value around 1.
The OSVM results in
Figure 10 show the use of the model trained on the first test run, in relation to the features
and
, which was applied to the other tests. The graphs in
Figure 9a and
Figure 10a are therefore identical. While the model trained on the fourth test in
Figure 9b already indicates an anomaly at run 150, the empirical probability in
Figure 10b is still 0 at run 150. The model trained on the first DUT obviously requires more strongly increasing amplitudes of the monitored frequencies for an increase in the empirical probability. Likewise, the increase only reaches a value of 0.5 towards the end of the test. With the knowledge that the differential failed with heavy pitting and without tooth breakage, this result is conclusive.
When looking at the results of the two seventh DUTs, it is noticeable that the foreign model used probably experienced higher feature values earlier. This delays the increase in the graph, but otherwise behaves the same.
Figure 10d only shows increased scatter at the beginning and around run 330 in comparison to
Figure 9d. Compared to the circumferential gear damage, a previously trained model can therefore be applied to further tests. This means that both condition-based and statistical PdM are possible with OSVM.
4.2. Recurrent Neural Network: Long Short-Term Memory (DL)
The results of the DL method of predictive maintenance are also presented by calculating the empirical probability from Equation (17).
Again, it is checked which runs are best suited for training normal data. For a classification task, it may be useful to use the same number of data sequences for both classes for training. For this reason, the last ten runs before the failure of the differential are used as abnormal data for the training process. Regarding the data of the abnormal class, this means that the LSTM network is trained on local tooth damage or heavy wear.
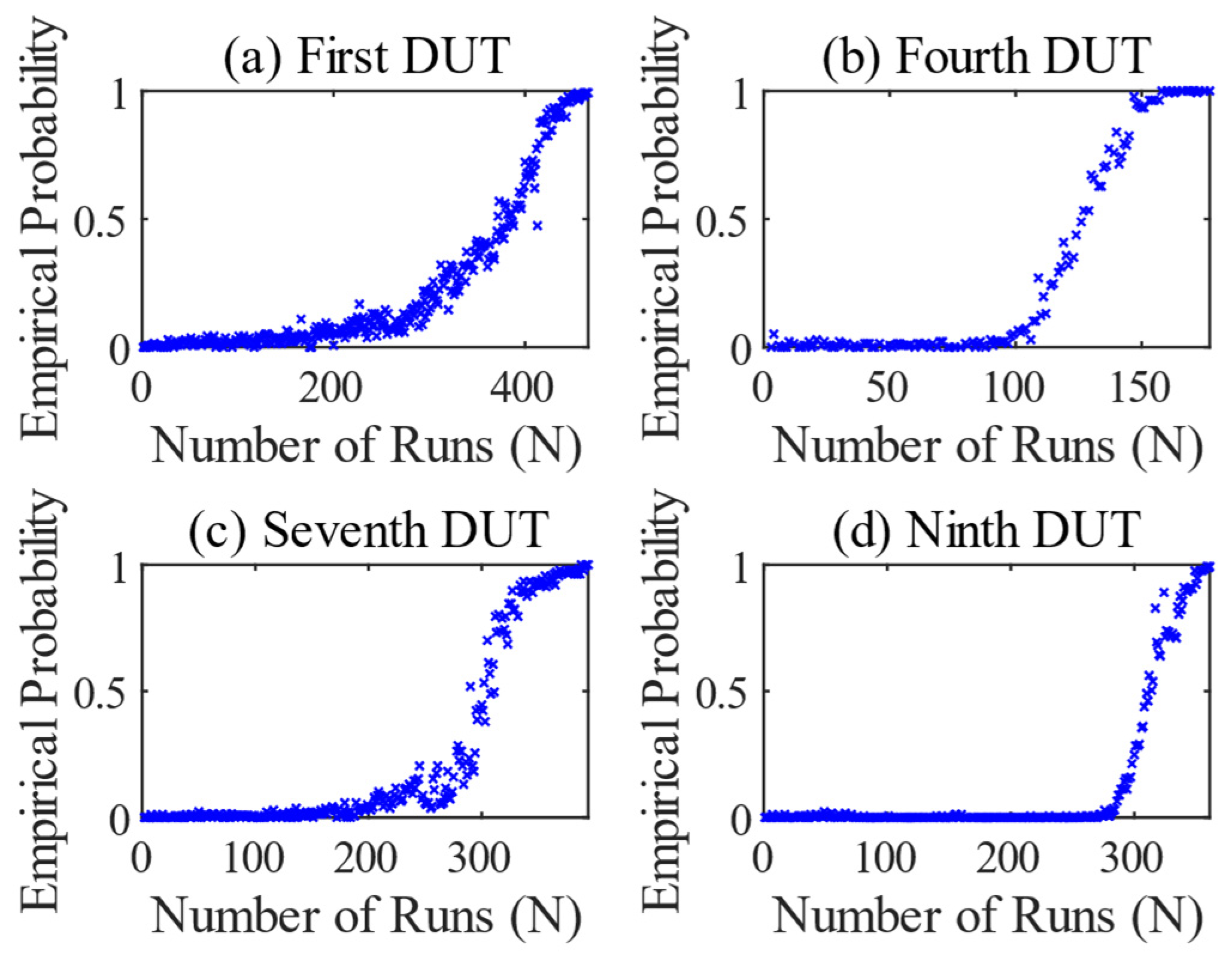
Figure 11 shows the results of the 1st DUT of the LSTM network. The runs used to train the network will have a slight influence on the result. Considering the running-in behavior and the occurrence of initial signs of wear, runs 30–40 are again selected for training.
Figure 12 shows the result series of the LSTM network classification, in which a model was trained for each DUT and applied to its own test. The result of the first DUT is shown in
Figure 12a. The empirical probability starts to increase from run 305 onwards, indicating a change in transmission. From there on, the torque sequences are no longer classified as normal. From run 450 on, the values are permanently in the range around 1. The method fulfills the classification task exactly as it was designed and recognizes the abnormal data sequences for the last runs. Early signs of wear are irrelevant to the LSTM network and are of little consequence. The results of the other tests are similarly good. In
Figure 12b–d, the values rise continuously towards the end and reach an empirical probability of 1 shortly before the DUTs fails. The LSTM network does not provide any indications of abnormal components on the test bench, as the OSVM does. Another special feature is that the fourth test in
Figure 12b was taught to recognize a combinatorial abnormality with damage to the gears and bearings. Here too, the LSTM network finds a good solution for the classification task of distinguishing the features in the measured values.
Figure 13 shows the results when a model trained on the first DUT is applied to the other tests, which follows the approach of statistical PdM. Graphs (a) and (c) in
Figure 12 and
Figure 13 show a high degree of correlation. The visible difference in (b) is because the model of the first DUT was trained on a missing tooth. When applied to the measurement data from the fourth test, in which no tooth was missing, the empirical probability in
Figure 13b does not reach a value of 1 at the end of the test. The result of the ninth test in
Figure 13d differs greatly from the condition-based PdM approach in
Figure 12d. Obviously, the data at the beginning are too different to use the model of the first DUT. The behavior of the graph only normalizes from run 165 onwards. This is where the abnormal bellows was replaced. After that, the values of the empirical probability slowly increase with an increased spread and reach values around 1 from run 300 on.
4.3. Comparison
The stated aim of this study is to find an approach that produces good results with a high degree of accuracy, even with highly varying test runs. Both methods have undeniable advantages for this purpose.
In addition to the results shown, the duration of the calculation is an important criterion for evaluating the PdM methods. For this purpose, a timer was integrated into the scripts for training and evaluation to output the calculation times.
Table 5 shows the calculation duration for the empirical probability of the OSVM of the respective tests. To better understand the influence on this, various factors are investigated. On the one hand, the effect of an already pretrained model is examined, which shows how long the evaluation, including the training process, takes. In addition, the weighting of the number of runs and features tested is also analyzed. To do this, the calculation for one run is shown, and the calculation time for all runs of the respective test is given in brackets. The table shows that, for the OSVM, a pretrained model reduces the calculation time slightly, especially when only a few runs are evaluated, as in this case, for example, which had only one run. There is almost no difference between the number of features used.
Equivalent to
Table 5, a runtime calculation was made for the DL method. As can be seen in
Table 6, the times for a single run and for all runs of a test are determined with and without a pretrained model. Despite the complexity of the RNN structure, the statement on the condition of the DUT of a single run is calculated in less than a second. In direct comparison, it is therefore significantly faster than the OSVM. When it comes to calculating the data for an entire test, evaluation with a pretrained LSTM network is up to twenty times faster.
It is difficult to determine the accuracy of OSVM in detecting anomalies, as it uses semi-supervised learning where no data are labeled as “abnormal” and therefore cannot be used to validate the results. The anomalies detected in the tests can be marked for subsequent evaluation.
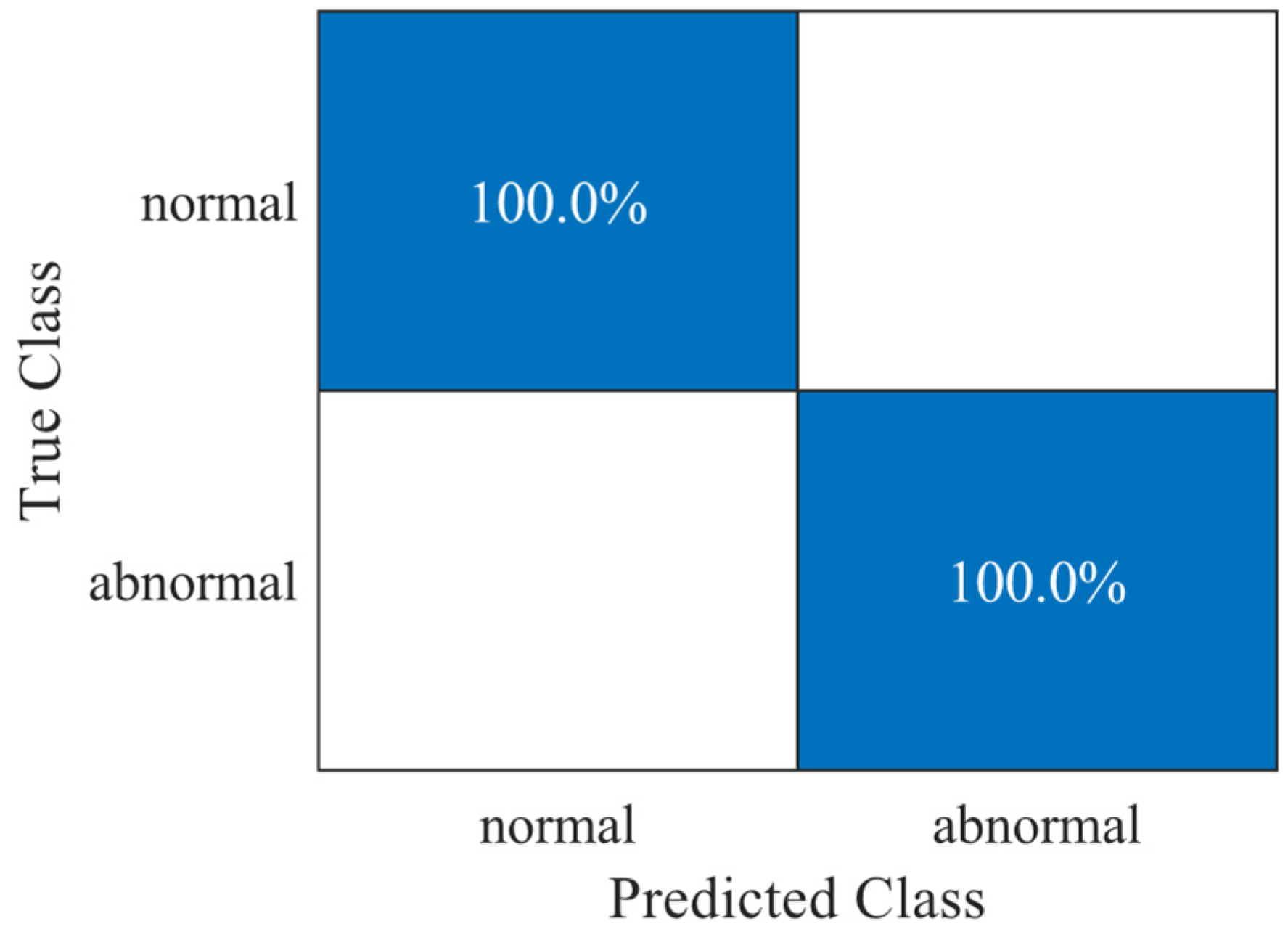
Figure 4 shows that normal data can be clearly distinguished from abnormal data. Other anomalies, such as damaged components of the test bench, also resulted in a detected anomaly. Of the nine test runs carried out, it can generally be said that no anomaly remained undetected.
The validation accuracy and the loss for the trained LSTM networks for the respective tests are determined in
Table 7. To calculate the accuracy, the trained model is applied to its own mixed data set, which contains a label of the actual class. The loss is formed by cross entropy of the predicted and the actual class and should be minimized in the training process. Both the high accuracy of over 99% and the low loss show that the trained models work with great precision.