Machine Learning Reveals Magmatic Fertility of Skarn-Type Tungsten Deposits

Abstract

The chemical composition of apatite has been utilized as an indicator of magmatic fertility related to tungsten mineralization in skarn systems. In this study, we compiled 5776 apatite trace element data from 374 intrusions, along with records indicating magmatic fertility. Then we trained and validated machine learning (ML) models, specifically support vector machine (SVM) and random forests (RF), to classify magmatic fertility based on apatite chemistry in igneous rocks. RF model achieved high classification accuracies (~93%) on the test dataset, demonstrating that employing ML approaches to distinguish apatite derived from fertile versus barren magmas is feasible and effective. Furthermore, we optimized classification thresholds to maximize the model’s predictive accuracy for identifying potentially fertile magmas. Feature-importance analysis of the machine learning classifier shows that elevated La, Yb, and Mn, together with depleted Sr, Y, Gd, and Tb, constitute the most diagnostic elemental signatures of magmatic fertility. As a case study, we applied our trained ML model to predict the magmatic fertility of apatite samples from the Nanling Range (southern China’s largest skarn-type tungsten mineralization province). Benefiting from the application of GAN-based techniques to address sample imbalance, our ML models can effectively identify tungsten-mineralized favorable skarn areas. Additionally, the visualization technique t-distributed stochastic neighbor embedding (t-SNE) was employed to validate and assess classification outcomes. Results showed clear separation between fertile and barren categories within the reduced 3D space. Our findings emphasize apatite as a sensitive indicator mineral for granite-related magmatic fertility and metallogenesis, underscoring its significant potential in mineral exploration. Finally, we provide a convenient prediction software for magmatic fertility based on a machine learning model utilizing apatite trace element compositions.

1. Introduction

Tungsten (W) is a rare refractory metal critical to industrial manufacturing, national security, and high-tech industries [1]. Skarn deposits constitute the primary global source of tungsten, accounting for approximately 50% of known tungsten reserves [2]. These deposits typically form within magmatic–hydrothermal systems and are spatially associated with deep-seated intermediate to felsic granitic intrusions [3]. The chemical composition of intrusive rocks and specific magmatic minerals, such as apatite [4] and zircon [5], have been widely used to evaluate the metallogenic potential of skarn-related tungsten deposits. Although the indicative roles of these minerals have been preliminarily recognized, systematically quantifying magmatic fertility based on their chemical signatures remains a significant research focus and challenge [6].

Apatite is a common accessory mineral in igneous rocks, characterized by the incorporation of trace elements such as Sr, Y, Mn, V, and rare earth elements (REEs) [7,8]. Due to its resistance to weathering and hydrothermal alteration [9], apatite is an ideal indicator mineral for tracing magmatic processes and sources, monitoring physicochemical conditions, and constraining magmatic crystallization ages [10,11,12,13,14]. Consequently, trace elements in apatite can effectively discriminate rock types [15], determine ore deposit genesis [4], and assess the metallogenic potential of host rocks [16,17]. Nevertheless, conventional analytical approaches for interpreting high-dimensional chemical data of apatite are often constrained by subjective interpretations and data complexity, limiting the accuracy and universality of assessments for ore-forming potential.

Machine learning (ML), the science of enabling computers to learn from data, has emerged as a powerful method for decoding hidden patterns within high-dimensional datasets. Recently, with improved computational capabilities and the accumulation of large datasets, ML techniques have become increasingly prominent in geological research, achieving notable successes in predicting crustal thickness [18], global climate reconstructions [19,20], tectonic settings [21], magmatic fertility [22,23,24,25], and multiscale mineral-prospectivity analysis. At the regional scale, three-dimensional convolutional neural networks applied to fused ASTER–Landsat imagery reduce false-positive Fe-skarn detections by >40% in eastern China [26]. District-level ensemble models—random forests and genetic-algorithm-optimized LightGBM—return F-scores of 0.96 when ranking cryptic Cu-polymetallic drill targets [27,28,29], whereas CNN, SVM, and LightGBM meta-analyses outperform logistic regression in tungsten-skarn prospectivity mapping across South China’s Nanling Belt [30]. Mineral-scale studies mirror these gains: partial least squares and deep classifiers trained on ~4000 magnetite LA-ICP-MS analyses now separate Fe–Sn, Fe–Zn, and W–Mo skarns with >90% accuracy [31,32], and random forest trace element fingerprints of grandite garnet reliably distinguish Au, Cu, and Zn skarn sub-types even within detrital sediments [33]. Beyond mineralogy, deposit-scale geochemical networks built on sphalerite trace element vectors achieve 94% precision when classifying skarn versus VMS, MVT, and SEDEX environments, underscoring the transferability of ML discriminants across ore systems [34].

Random forest (RF) ensembles excel on geochemical datasets because their bootstrap sampling and feature randomness mitigate over-fitting, handle high-dimensional, noisy or multicollinear element suites, and capture non-linear interactions among proxies such as trace element ratios and isotopes [35]. Because each tree votes independently, RF maintains robust accuracy even when classes are imbalanced or rare anomalies dominate, a common situation in regional mineral-prospectivity studies [36]. Support vector machine (SVM) perform strongly when sample sizes are limited yet predictor space is large, owing to their structural-risk minimization and kernel trick, which project complex geochemical boundaries into linearly separable hyperspaces [37]. SVM offers slightly sharper margins, whereas RF delivers greater interpretability, rendering the two algorithms complementary in exploration workflows [38].

In this study, we employed two widely used supervised learning algorithms—SVM and RF—to train models on global apatite trace element datasets to evaluate apatite-based magmatic fertility for skarn-type tungsten deposits (Figure 1). Cross-validation results demonstrated the efficiency of the trained models in accurately classifying apatite derived from fertile and barren magmas. After verifying the efficacy of the models, we applied them to the Nanling tungsten–tin skarn district in southern China, an extensively studied region hosting numerous known skarn-type deposits with well-constrained geological backgrounds, such as Weijia, Tongshanling, Xihuashan, Shuikoushan, Zhuxi, Dahutang, and Xintianling [39,40,41]. Through this investigation, we aimed to uncover fundamental relationships between apatite geochemistry and tungsten mineralization, providing robust scientific frameworks and efficient exploration methods for skarn-type tungsten deposits.

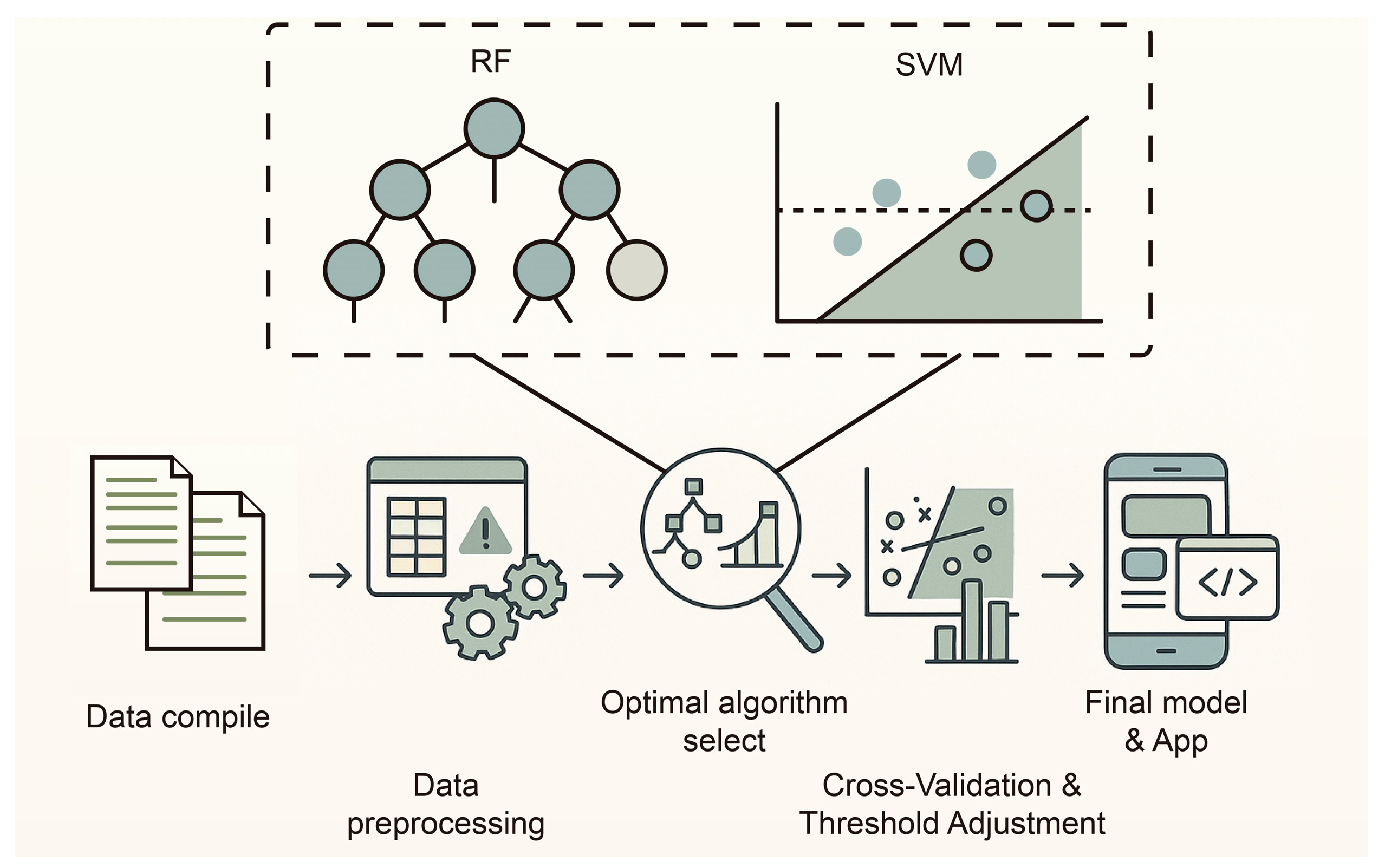
2. Dataset and Data Preprocessing

2.1. Dataset

In this study, fertile magmas are those that exhibit a spatial association with documented skarn-type tungsten deposits, whereas barren magmas represent the opposite condition. Apatite geochemical data related to skarn tungsten deposits were compiled from published literature (Supplementary SI). After data screening, a total of 1047 observations from intrusions related to skarn-type tungsten deposits (Supplementary SI) were labeled as “fertile apatite”, while 4729 observations from intermediate-felsic intrusions without mineralization or with other types of mineralization were labeled as “barren apatite”. The selected trace elements for modeling included Ce, Dy, Er, Eu, Gd, Ho, La, Lu, Mn, Nd, Pr, Sm, Sr, Tb, Tm, V, Y, and Yb. The rationale behind choosing these trace elements was based on three criteria: (1) significant compositional variation during petrogenetic processes, (2) proven effectiveness in discriminating skarn-type mineralization systems by prior studies, and (3) extensive documentation in the literature. We conducted an exploratory data analysis (EDA) and visualized the trace element profiles of apatite from fertile and barren intrusions using box plots (Figure 2). The results reveal pronounced contrasts in trace element concentrations between apatite derived from fertile versus barren intrusions. Moreover, the dataset was standardized prior to model training.

Besides the global apatite dataset, additional trace element data (204 samples) from apatite within the Nanling skarn W–Sn metallogenic province (Middle–Lower Yangtze River metallogenic belt, Supplementary SII) were used. These apatite samples were subjected to identical screening criteria applied to the global dataset and subsequently employed to validate the constructed ML models and for visualization analysis.

2.2. Data Preprocessing

• Outlier Detection and Processing

The Z-score method is a widely used statistical technique for identifying and handling outliers in datasets. The Z-score quantifies the number of standard deviations a data point deviates from the mean of the dataset. Its fundamental principle is that data points with Z-scores significantly higher or lower than the majority are considered outliers. Typically, data points exceeding an absolute Z-score threshold of 3 are regarded as anomalous [42]. In this study, data points with absolute Z-scores greater than 3 were treated as outliers. A total of 619 entries were identified as outliers and were consequently removed from the dataset.

b.

Missing Value Imputation

Appropriate treatment of missing values is critical for accurate modeling. Initially, entries with more than 50% missing variables were excluded [43]. Subsequently, we applied the K-nearest neighbor (KNN) method to impute the remaining missing values. The KNN imputation method has distinct advantages in handling missing data, especially when the underlying relationships among variables are nonlinear or complex. It preserves the intrinsic structure of the dataset by estimating missing values using information from neighboring observations. This method is particularly effective for datasets exhibiting local patterns, which might otherwise be ignored by simpler approaches such as mean or median imputation [44]. Selecting an optimal value of parameter k—the number of nearest neighbors considered—is critical for balancing variance and bias during the imputation process. A smaller k value tends to increase sensitivity to noise due to reliance on fewer neighbors, while a larger k can introduce bias by averaging across broader neighbor groups, thereby diluting local variability and potentially reducing imputation accuracy [45]. Therefore, choosing an optimal k is essential. Cross-validation was conducted to identify a k that minimized imputation error across subsets of the dataset. Sensitivity analysis further evaluated the robustness of imputation results across different k values, guiding parameter tuning to achieve optimal performance [46].

c.

Centered Log-Ratio (clr) Transformation

The centered log-ratio (clr) transformation is fundamental when analyzing compositional data. Compositional datasets inherently carry constant-sum constraints (e.g., concentrations summing up to a fixed constant, typically 100%), which introduce spurious correlations among elements, rendering traditional statistical analyses inappropriate on raw compositional data [47]. The clr transformation converts compositional data into a space free of these constraints, thereby mitigating distortions inherent to compositional data and ensuring subsequent analyses accurately represent true inter-element relationships.

d.

Data Augmentation Using Generative Adversarial Networks (GANs)

Due to class imbalance in the labeled dataset (“fertile” vs. “barren” apatite samples), we employed generative adversarial networks (GANs) to generate additional minority-class samples. GANs are powerful tools for addressing class imbalance, which arises when certain classes are significantly underrepresented, potentially biasing model performance toward the majority class. GAN-based augmentation alleviates this issue by generating synthetic data samples simulating the minority class, thereby enhancing its representation within the dataset rather than merely duplicating existing samples [48]. At its core, a GAN employs a game-theoretic framework involving two neural networks: a generator, which synthesizes new data samples by learning the underlying distribution of the training data, and a discriminator, which attempts to distinguish real samples from synthetic ones. Iterative training progressively improves the generator’s capacity to produce synthetic samples indistinguishable from real samples, thereby enhancing GANs’ efficacy in balancing class representation and improving model performance in classification tasks [49].

3. Method

3.1. Machine Learning Algorithms

Machine learning algorithms, such as RF, SVM, and artificial neural networks (ANN), are effective for binary classification tasks. However, considering the generally poorer performance of ANN with small, low-dimensional datasets [40], this study focused on the application of RF and SVM algorithms.

The RF algorithm is an ensemble learning approach, which involves constructing multiple decision trees during model training and predicting the classification outcome by aggregating the mode of outputs from individual trees. Mathematically, RF generates a large number of trees, each trained using bootstrapped subsets of the original dataset and random subsets of features. The final prediction is obtained by aggregating the predictions from individual trees, a procedure known as bagging. This ensemble strategy capitalizes on the Law of Large Numbers, enhancing both accuracy and stability of classification results [50,51]. In contrast, the SVM algorithm seeks to identify an optimal hyperplane that maximally separates two classes within the feature space. Mathematically, this involves solving an optimization problem to determine a hyperplane that maximizes the margin between classes. The optimal hyperplane is defined by the equation w⋅x + b = 0, where w represents the weight vector and b denotes the bias term. When data are not linearly separable, SVM employs kernel functions to map data into a higher-dimensional feature space, facilitating linear separability. This flexibility enables SVM to effectively manage complex classification scenarios [52,53].

3.2. Evaluation Metrics

Assessing the performance of classification models requires a multifaceted approach using various metrics to provide different perspectives on model behavior. Among these metrics, the receiver operating characteristic (ROC) curve, confusion matrix, F1 score, precision, and recall are commonly employed, each offering complementary insights into model performance.

The ROC curve graphically illustrates the trade-off between the true-positive rate (sensitivity) and the false positive rate (1-specificity; specificity means true negative rate) across different classification thresholds. The area under the ROC curve (AUC) serves as a summary measure, with higher AUC values indicating better model performance in distinguishing between classes. ROC curves are particularly suitable for comparing the effectiveness of different classifiers because they are independent of class distribution [54]. The confusion matrix provides a more detailed perspective, displaying counts of true positives, true negatives, false positives, and false negatives. From this matrix, additional performance metrics—such as precision and recall—can be derived. Precision is defined as the proportion of correctly classified positive instances among all predicted positive instances, whereas recall (or sensitivity) measures the proportion of actual positives accurately identified by the model. Recall is especially critical in scenarios where false negatives incur significant costs; for instance, in predicting metallogenic potential, a model failing to detect actual mineralization potential would have limited practical value. The F1 score, defined as the harmonic mean of precision and recall, provides a single measure balancing these two metrics and is particularly valuable when dealing with imbalanced class distributions [55]. Collectively, these metrics offer a comprehensive framework to evaluate the effectiveness of classification models across diverse contexts and applications.

3.3. Strategies

• Optimal Algorithm Selection

To effectively evaluate the generalization performance of RF and SVM algorithms while minimizing the influence of random error, we randomly selected 20% of the dataset (after GAN-based data augmentation) as the testing set, with the remaining 80% utilized for training. After performing 100 iterations, the classification performances of RF and SVM algorithms were compared to determine the optimal method.

b.

Cross-Validation

Upon identifying the most suitable algorithm for our dataset, we performed five-fold cross-validation to comprehensively evaluate model performance across the entire dataset (after GAN-based data augmentation). Specifically, the dataset was randomly partitioned into five subsets or “folds” of approximately equal size. Each fold sequentially served as the validation set once, while the remaining four folds were combined to form the training set. The model was trained using data from four folds and evaluated on the remaining fold. This procedure was repeated five times, ensuring that each fold was utilized once as the validation set.

c.

Threshold Adjustment

Threshold tuning represents a critical process for optimizing binary classification models, where the decision threshold defines how predicted probabilities map to class labels. Typically, a model outputs a probability score indicating the likelihood of an instance belonging to the positive class. A default threshold of 0.5 is commonly applied, meaning that instances with predicted probabilities above 0.5 are classified as positive, and those below as negative. However, this threshold is not always optimal, especially under conditions of class imbalance or when the costs of false positives and false negatives differ significantly [56]. The goal of threshold adjustment is to achieve an ideal balance between sensitivity (recall) and specificity (precision). In this study, aiming to maximize recall for the “fertile” class while maintaining classification accuracy, we adjusted the model’s decision output as follows: Output = P(fertile) − P(barren) + 0.2, where P(fertile) represents the probability of belonging to the fertile class and P(barren) denotes the probability of belonging to the barren class. Instances with an output greater than 0 were classified as fertile, whereas instances with values below 0 were classified as barren.

d.

t-SNE Discriminant

t-distributed stochastic neighbor embedding (t-SNE) is a robust dimensionality reduction technique particularly suitable for visualizing high-dimensional data [57]. When applied to classification problems, t-SNE projects complex data into a two- or three-dimensional embedding space, facilitating the visualization of patterns and clusters among different classes.

e.

Independent Case Validation

Since the training dataset included synthetic data generated by GANs, evaluating the model’s performance on entirely unseen data is essential. Therefore, we created an independent validation set comprising samples that were not involved in the model training process. Specifically, samples from four distinct intrusions within the Nanling Range were selected as an independent validation set to rigorously assess the generalization capability of the constructed model.

3.4. Feature Importances

SHapley Additive exPlanations (SHAP) is a powerful approach for interpreting machine learning models by offering clear and mathematically justified explanations of how predictions are derived from individual features. Rooted in cooperative game theory, particularly the concept of Shapley values, SHAP allocates a fair contribution to each feature by considering all possible combinations of feature contributions [58]. The core principle of SHAP is to decompose a model’s prediction into a summation of contributions from each feature, ensuring that the sum of these contributions precisely equals the difference between the model’s prediction for a specific instance and the average prediction across all instances. This approach provides a unified measure of feature importance that is both consistent and locally accurate.

4. Results

4.1. Optimal Algorithm

To determine the optimal algorithm, we performed 100 repeated experiments evaluating the performance of RF and SVM algorithms, focusing specifically on four key metrics: F1-score (mean: 0.93 and 0.73, n = 100), accuracy (mean: 0.93 and 0.68, n = 100), recall for barren apatite (mean: 0.91 and 0.49, n = 100), and recall for fertile apatite (mean: 0.95 and 0.87, n = 100). Results clearly indicated that the RF algorithm consistently outperformed the SVM algorithm across all evaluated metrics (Figure 3). The RF algorithm exhibited higher mean scores in F1-score, accuracy, barren recall, and fertile recall, demonstrating superior overall performance in terms of precision, true-positive rate, and general predictive accuracy. Furthermore, performance curve visualized via line plots (Figure 4) revealed that the RF algorithm not only had superior average performance compared to the SVM algorithm but also showed smaller variability across the 100 iterations. The narrower distribution observed for RF results indicates greater stability and reliability in predictions, whereas the broader distribution for SVM results highlights its comparative instability.

Prior to GAN data augmentation, 100 replicate trials yielded a mean F1-score of 0 for the SVM, an average accuracy of 0.82, and class-specific recall values of 1.00 (barren) and 0.00 (fertile). By contrast, the RF returned a mean F1-score of 0.67, an accuracy of 0.89, and recall values of 0.96 (barren) and 0.59 (fertile). After GAN-based data augmentation, the SVM’s mean F1-score rose to 0.73, with an accuracy of 0.68 and recall values of 0.49 (barren) and 0.87 (fertile), whereas the RF achieved a mean F1-score of 0.93, an accuracy of 0.93, and recall values of 0.91 (barren) and 0.95 (fertile). These results demonstrate that GAN augmentation markedly alleviates the bias introduced by class imbalance and substantially boosts overall model performance.

4.2. Cross-Validation

Five-fold cross-validation was conducted to evaluate the performance of the RF model across the entire dataset. ROC curves and PR curves demonstrated excellent performance of the RF model (Figure 5a,b; AUC = 0.98 for barren apatite, AUC = 0.98 for fertile apatite). Moreover, the confusion matrices (Figure 5c) indicated that the RF model effectively differentiated between barren and fertile categories. Specifically, recall for the barren class ranged from 0.90 to 0.91 (mean = 0.91, n = 5), while recall for the fertile class ranged from 0.89 to 0.91 (mean = 0.90, n = 5). The confusion matrix and ROC analysis collectively confirmed the robust capability of the RF model to discriminate barren and fertile samples.

In practical mineral exploration, failing to identify true-positive mineralized samples could result in potential economic losses. Thus, to enhance the probability of correctly predicting fertile samples without compromising overall accuracy, we adjusted the classification threshold of the RF model (Figure 5d–f). Following threshold adjustment, the overall model performance remained stable, with the F1-score ranging from 0.92 to 0.93 (mean = 0.93, n = 5). Importantly, recall for the fertile class was significantly improved, increasing to a range of 0.97 to 0.98 (mean = 0.97, n = 5).

Finally, we applied the t-SNE discriminant to reduce the dataset dimensionality from 18 to 3 dimensions. Based on predictions generated by the RF model, all data points were plotted in the three-dimensional embedding space. Each data point was color-coded according to the predicted classification of “barren” or “fertile”, allowing visualization of classification patterns and clear distinction between these categories within the reduced-dimensional space (Figure 6). Pink symbols denote the “barren” type and blue symbols the “fertile” type. Within the 3D embedding produced by dimensionality reduction, the two populations partition into two vertically stacked clusters.

4.3. Independent Case Validation

We applied the RF model to an independent validation dataset consisting of apatite samples collected from 10 rock bodies in the Nanling Range, which had not been involved in model training. The results demonstrate that the model maintains excellent generalization performance when applied to entirely unseen data, achieving a prediction accuracy of 90% across the 10 rock samples (

Table 1. Prediction of fertility of intrusions in Nanling Range by RF model.

No	Sample	Deposit Name	Fertile/Unfertile	Model Prediction
1	195	Weijia	Fertile	Fertile
2	602	Tongshanling	Unfertile	Unfertile
3	8S5	Tongshanling	Unfertile	Unfertile
4	XHS-5	Xihuashan	Fertile	Fertile
5	XHS-6	Xihuashan	Fertile	Fertile
6	XHS-18	Xihuashan	Fertile	Unfertile
7	XHS-21	Xihuashan	Fertile	Fertile
8	SKS-31	Shuikoushan	Unfertile	Unfertile
9	SKS-36	Shuikoushan	Unfertile	Unfertile
10	SKS-37	Shuikoushan	Unfertile	Unfertile

).

4.4. Feature Importances

The SHAP summary plot illustrates the relationship between elemental concentrations and model outputs, with elements ranked from top to bottom according to their importance (Figure 7). In the plot, point color denotes the concentration of each element, and the SHAP values displayed on the x-axis indicate the contribution to model classification decisions; larger SHAP values imply a greater likelihood that the model classifies samples as fertile. Specifically, higher concentrations of La, Mn, and Yb, as well as lower concentrations of Sr, Gd, Tb, and Y, were positively correlated with predictions of fertile magmas. In contrast, elements including V, Nd, Eu, Er, Ce, Lu, Pr, Dy, Sm, Tm, and Ho exhibited relatively limited influence on model predictions and showed no clear linear trend.

Notably, as not all elements are equally relevant to magmatic fertility, we systematically assessed the relationship between the number of input elements and model performance by incrementally adding elements in descending order of their importance. The results indicated that adding elements ranked lower than Eu did not further improve the model’s performance (Figure 8). Therefore, we selected a subset of ten elements (Sr, La, Mn, Gd, Yb, Tb, Y, V, Nd, and Eu) to construct the final model (which has been integrated into the software provided in Supplementary SIII).

5. Discussion

5.1. Limitations of Machine Learning Models

Although the RF and SVM algorithms performed well in classifying fertile and barren apatite samples, these machine learning models still exhibit certain limitations. First, model performance heavily depends on the quality and quantity of the training dataset. During mineral exploration, sample collection is often geographically constrained, and ore deposits tend to be unevenly distributed, potentially causing dataset imbalance and bias [59]. In particular, samples labeled as “fertile” are generally fewer than those labeled as “barren”, exacerbating the class imbalance [59]. Although employing generative adversarial networks (GANs) for data augmentation effectively generates additional minority-class samples, synthetic samples generated by GANs may not entirely capture geological complexities, potentially limiting the generalizability of the models [48]. Additionally, the sensitivity of these models to anomalous data merits careful consideration. Geological complexities and local anomalies in apatite geochemistry could negatively affect model predictions, further constraining model generalizability.

5.2. Reliability of Apatite as an Indicator of Magmatic Fertility

The results indicate that the RF model, based on concentrations of 18 trace elements in apatite, achieved high predictive performance, with F1-scores ranging from 0.92 to 0.93 and accuracies between 0.91 and 0.92. Furthermore, the ROC curves revealed outstanding model performance, achieving an AUC value of 0.98. The confusion matrix demonstrated stable recall rates of 0.91 and 0.92 for barren and fertile categories, respectively, and after threshold adjustment, recall for the fertile class increased to 0.98. These robust results strongly support apatite as a reliable indicator for evaluating magmatic fertility.

The source of tungsten-mineralized granites is typically derived from metamorphosed sedimentary rocks (e.g., S-type granites) or partially melted crustal material. These magmas generally exhibit relatively low oxygen fugacity (i.e., low oxidation states), creating favorable conditions for tungsten enrichment [60]. Tungsten-mineralized granites often demonstrate high degrees of magmatic differentiation [61,62], especially prominent in A-type granites characterized by elevated fluorine concentrations and higher zircon saturation temperatures [63]. Geochemically, these granitic bodies display distinctly negative εNd(t) values, suggesting derivation from older crustal components [64]. In tungsten-mineralized granites, apatite commonly exhibits low Eu/Eu* ratios accompanied by elevated Ga concentrations, indicative of strongly reduced magmatic environments [65]. Meanwhile, the tungsten-mineralized granites display steep light-REE enrichment (La/YbN > 100) with pronounced negative Sr anomalies, signatures of plagioclase-suppressed, highly oxidized differentiation that predisposes fluids to precipitate scheelite during late-stage exsolution [6,66]. Moreover, these granitic intrusions frequently coexist spatially with tin mineralization, particularly in the Nanling Range, where tungsten-mineralized intrusions are extensively distributed in the central and eastern segments and associated with granites originating from metamorphosed sedimentary rocks [67].

5.3. Geochemical Implications of Feature Importance Analysis

Feature importance analysis based on machine learning models of apatite trace element chemistry effectively discriminates apatite crystals derived from magmas of different origins, providing valuable insights into ore-genetic processes. In skarn-type tungsten deposits, apatite from fertile magmas exhibits distinct elemental concentration patterns compared to apatite from barren magmas. Specifically, fertile apatite is characterized by higher concentrations of La, Mn, and Yb, alongside lower concentrations of Sr, Gd, Tb, and Y. These differences likely reflect lower degrees of magmatic differentiation and higher aluminum saturation indices in the parent magma.

The concentrations of Sr and Y in apatite are critical proxies for evaluating magmatic differentiation processes [68]. Although feldspar is generally the primary host mineral for Sr, its crystallization has limited influence on the Sr concentrations in apatite. Previous studies indicate a relationship between Sr and Y concentrations in apatite and whole-rock SiO₂ content: apatite crystallizing during advanced differentiation stages typically shows decreased Sr concentrations relative to apatite crystallized in early magmatic stages [69]. Thus, the elevated Sr content observed in apatite from fertile magmas in skarn-type tungsten deposits likely indicates lower degrees of differentiation, consistent with the intermediate SiO₂ contents and moderately oxidized conditions typically associated with tungsten mineralization [16]. Experimental and natural data show that amphibole sequesters Y with partition coefficients an order of magnitude higher than those for most LREEs, especially in granitic to granodioritic melts where Y readily occupies the M2 site of hornblende [70]. As fractionation proceeds, titanite saturates and becomes an even stronger sink, that efficiently strips the residual melt of Y and coeval MREEs [71]. Consequently, late-crystallizing apatite inherits a pronounced Y trough relative to both LREEs and HREEs—an imprint of sequential amphibole–titanite fractionation followed by fluorine-enhanced melt evolution [72].

The systematic depletion of the MREEs Gd and Tb in apatite from W-bearing granites is best interpreted as the geochemical fingerprint of early MREE-scavenging by rock-forming mafic accessories during extreme, volatile-rich differentiation. Experimental partitioning data show that amphibole concentrates MREEs far more strongly than either LREEs or HREEs, progressively lowering the Gd–Tb budget of the residual melt as soon as hornblende saturation is achieved [73,74]. Titanite—which nucleates alongside amphibole in many peraluminous W granites—exhibits even higher partition coefficients for Gd and Tb, stripping the evolving magma of MREEs with each increment of crystallization and leaving late-stage apatite conspicuously MREE-poor [75]. Because the MREE sink phases crystallize before voluminous fluoride-rich volatile exsolution, the concomitant enrichment of F in the melt does little to replenish Gd and Tb yet enhances the solubility and transport of tungsten, thereby coupling MREE depletion in apatite to W fertility at the pluton scale [76,77]. The resulting concave-up “U-shaped” REE pattern in apatite is markedly low in Gd–Tb.

The pronounced Mn enrichment recorded by apatite from tungsten-fertile granites is a direct consequence of extreme, F-charged fractionation. Experiments show that the apatite–melt partition coefficient for Mn rises sharply—by more than an order of magnitude—as silicic melts evolve from metaluminous to highly polymerized peraluminous compositions, an effect controlled by melt structure rather than oxygen fugacity [13,78]. Global compilations confirm that apatite Mn scales positively with host-rock SiO₂ and aluminosity but is decoupled from redox state, indicating that Mn behaves as a “late compatible” cation whose uptake is dictated chiefly by the degree of differentiation [13,79]. In W-bearing granites, early depletion of Fe- and Mg-rich mafic silicates leaves Mn increasingly concentrated in the residual melt; continued crystallization of biotite, cordierite and tourmaline further elevates the Mn/Fe ratio until the liquid approaches spessartine saturation, at which point apatite captures Mn contents an order of magnitude above those in barren analogues [72,80]. On the other hand, the elevated La and Yb concentrations may reflect an increase in the melt’s F content, which dramatically raises the solubility of LaPO₄ and YbPO₄ [81].

5.4. Geological Implications of the Nanling Case

The independent validation performed on the Nanling Range demonstrated that the RF model achieved a high predictive accuracy (90%) for 10 rock samples encompassing 222 data entries. This confirms the robust applicability of the model within the Nanling Range, carrying significant regional geological implications. Firstly, Nanling represents one of the largest skarn-type tungsten metallogenic provinces worldwide, with tungsten mineralization closely associated with Yanshanian granitic intrusions [6,39,82]. SHAP analysis revealed linear relationships of trace elements such as Sr, Gd, and La, which strongly correspond with the highly differentiated and volatile-rich characteristics of Nanling granites. Specifically, relatively low concentrations of Gd and Tb, coupled with elevated La contents, likely indicate crustal contamination or partial melting processes. This geochemical signature aligns well with multi-stage magmatic activities under an intracontinental extensional regime in the Nanling Range [82].

Secondly, the model’s accuracy of 90% in predicting the dominant classification of rock samples indicates a systematic spatial distribution of fertile magmas in the Nanling Range, potentially concentrating near the contact zones between granite intrusions and carbonate rocks. This interpretation is further supported by the known locations of significant tungsten deposits, such as the Dayao Mountain and Huangshaping deposits [83]. After threshold adjustment, recall for fertile apatite increased to 0.98 (Figure 5f), underscoring the model’s effectiveness in identifying potential ore-bearing areas, thus significantly reducing the risk of missing exploration targets. This is especially crucial for exploration activities targeting concealed deposits located at the periphery or greater depths within the Nanling Range.

However, the reliability of apatite as an indicator of mineralization may be influenced by fluid metasomatic processes. Within the Nanling skarn mineralization systems, strong hydrothermal alteration could significantly modify apatite chemistry, thereby obscuring primary magmatic signals and reducing its efficacy as a standalone indicator [6]. Additionally, the misclassification of certain fertile samples as barren observed during independent validation may result from spatial heterogeneity of apatite chemistry. Samples proximal to mineralized zones commonly exhibit distinct geochemical enrichment signatures, whereas distal samples may lack such clear indicators. This heterogeneity highlights the necessity of incorporating comprehensive regional geological context and multi-indicator analysis to further enhance predictive accuracy when applying the model.

6. Conclusions

Significant geochemical differences exist between apatite crystals derived from fertile and barren magmas, with elements such as Sr, La, Mn, Gd, Yb, and Tb playing crucial roles in discriminating magmatic fertility. Machine learning approaches, particularly the random forest (RF) algorithm, have proven effective in predicting magmatic fertility by identifying key distinguishing features within complex chemical datasets, thus offering novel perspectives for mineral resource exploration. This study demonstrates that threshold optimization significantly enhances model classification performance, markedly improving prediction accuracy and effectively assessing mineralization potential in the Nanling tungsten–tin skarn metallogenic province. Furthermore, SHAP analysis highlights the contributions of trace elements in apatite to magmatic fertility, thereby advancing our understanding of magmatic genesis and mineralization mechanisms. Overall, this research provides valuable practical insights and practical applications for analyzing and predicting magmatic fertility in skarn-type tungsten deposits, underscoring the growing importance of machine learning methods in mineral exploration.