Explicit Time Integration Method Based on Uniform Trigonometric B-Spline Function for Transient Heat Conduction Analysis
Abstract
1. Introduction
2. The Proposed Method
3. Basic Properties
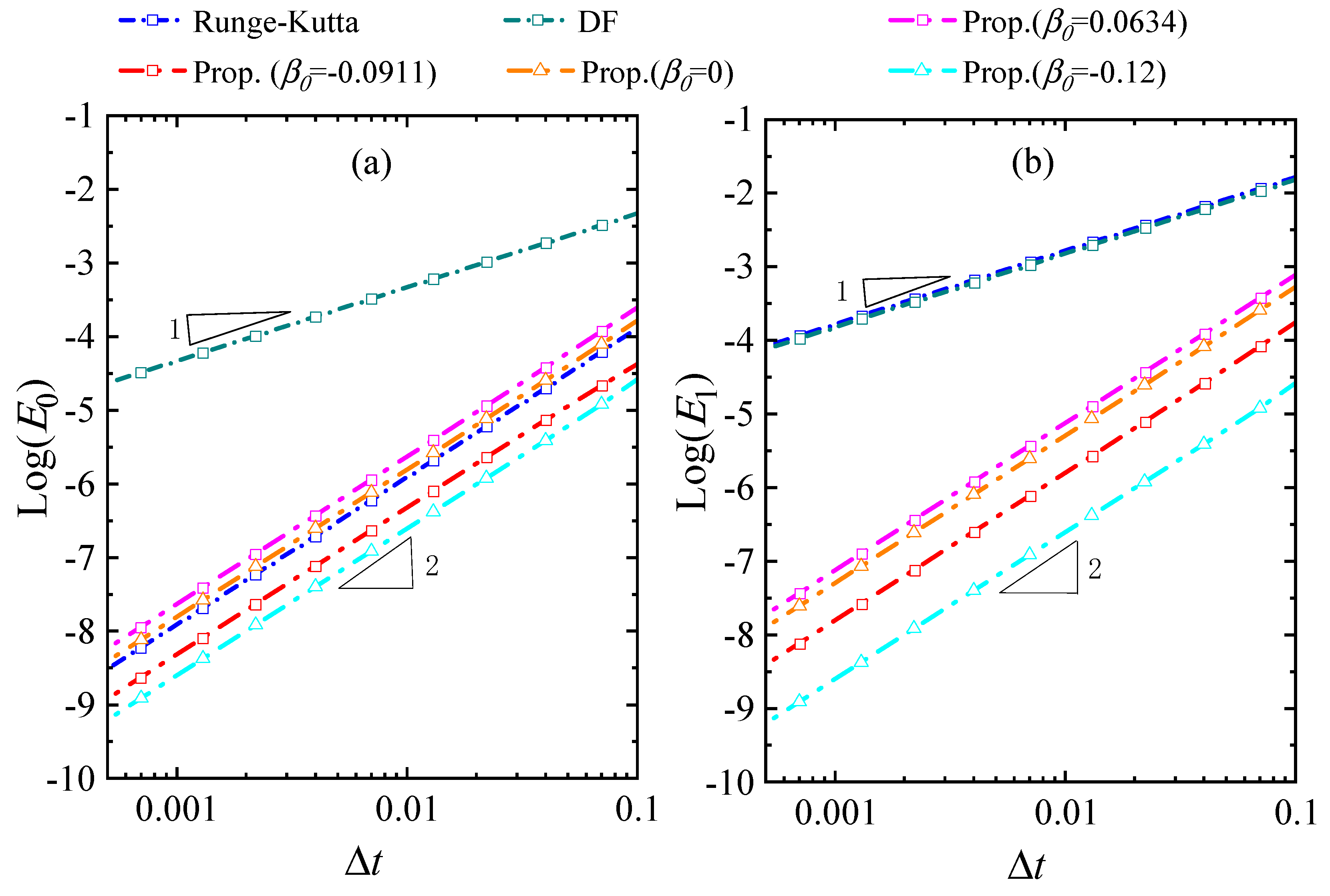
3.1. Accuracy Analysis
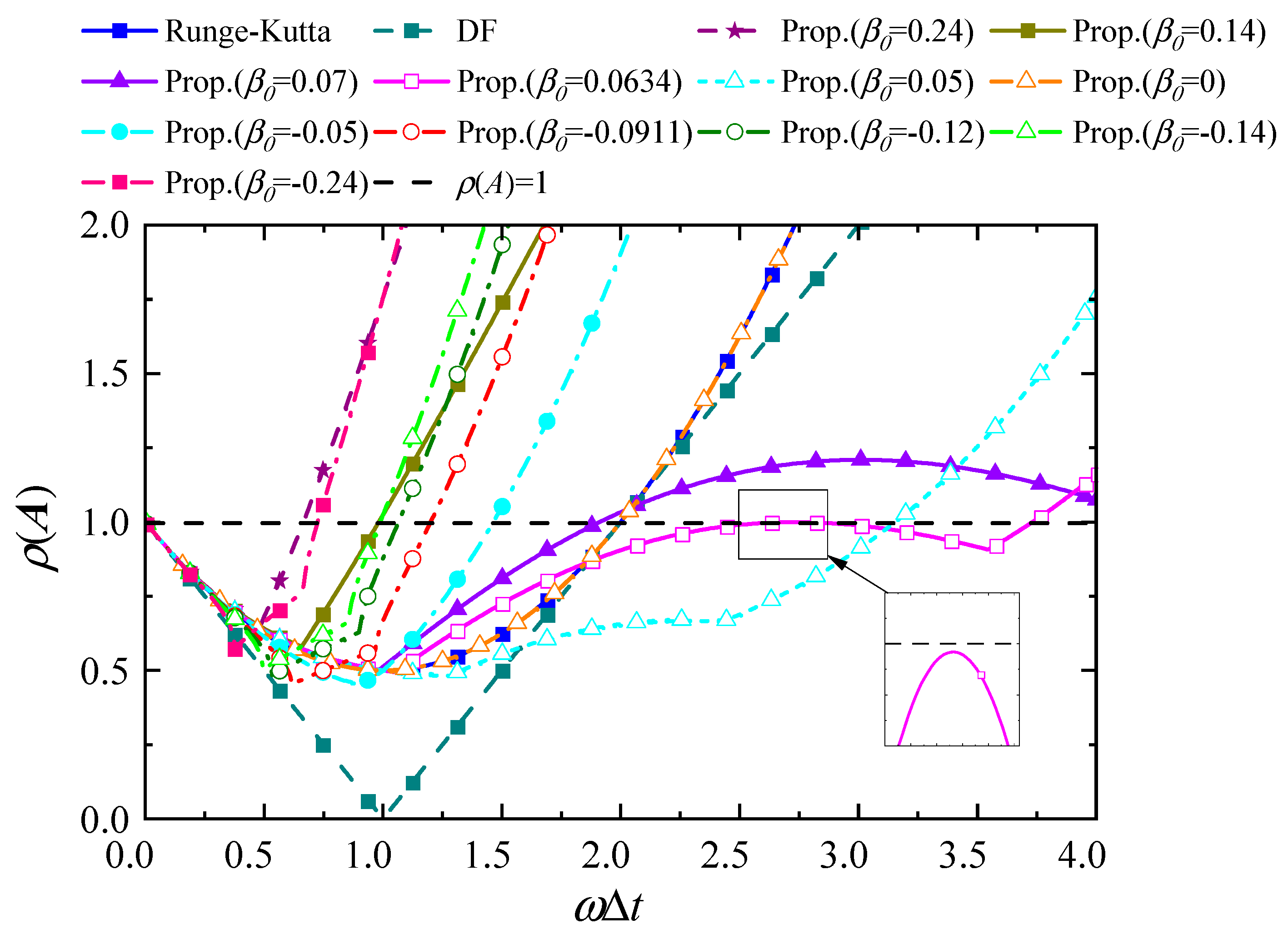
3.2. Spectral Stability
4. Illustrative Numerical Examples
4.1. A Linear SDOF System with Simple External Heat Source
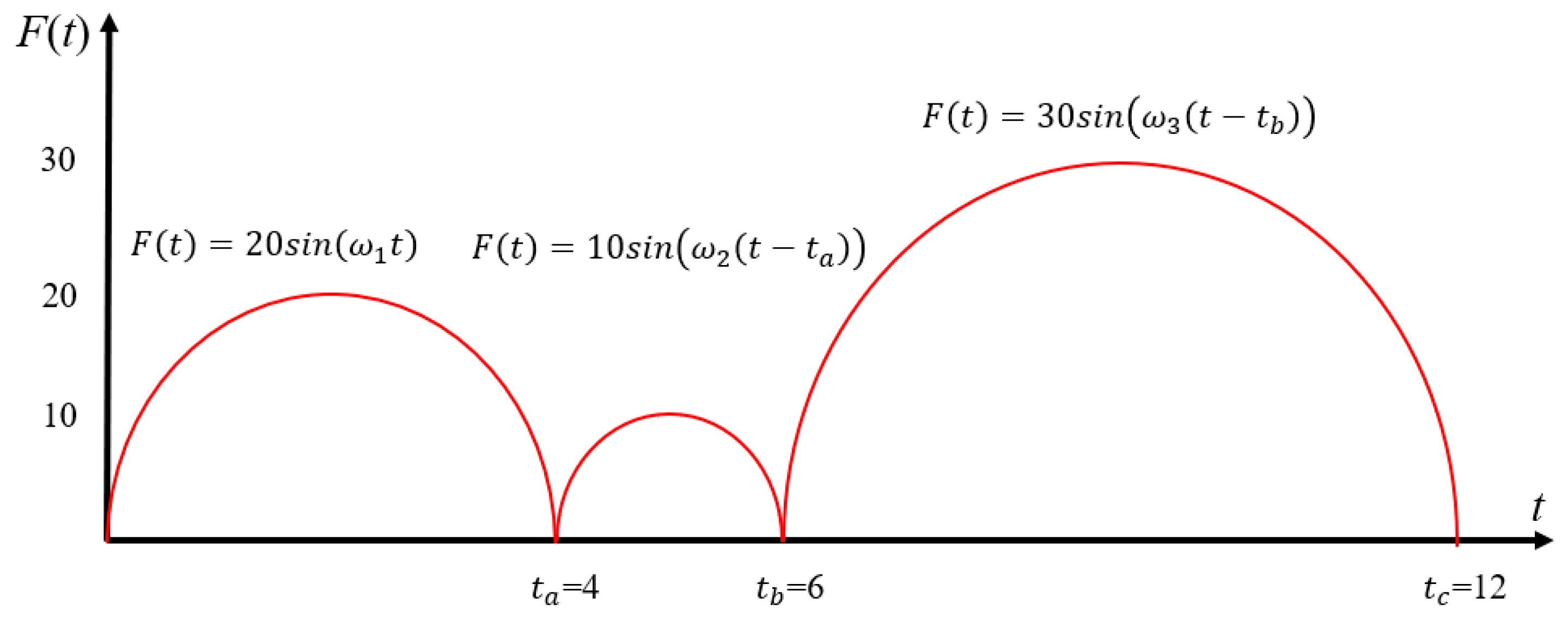
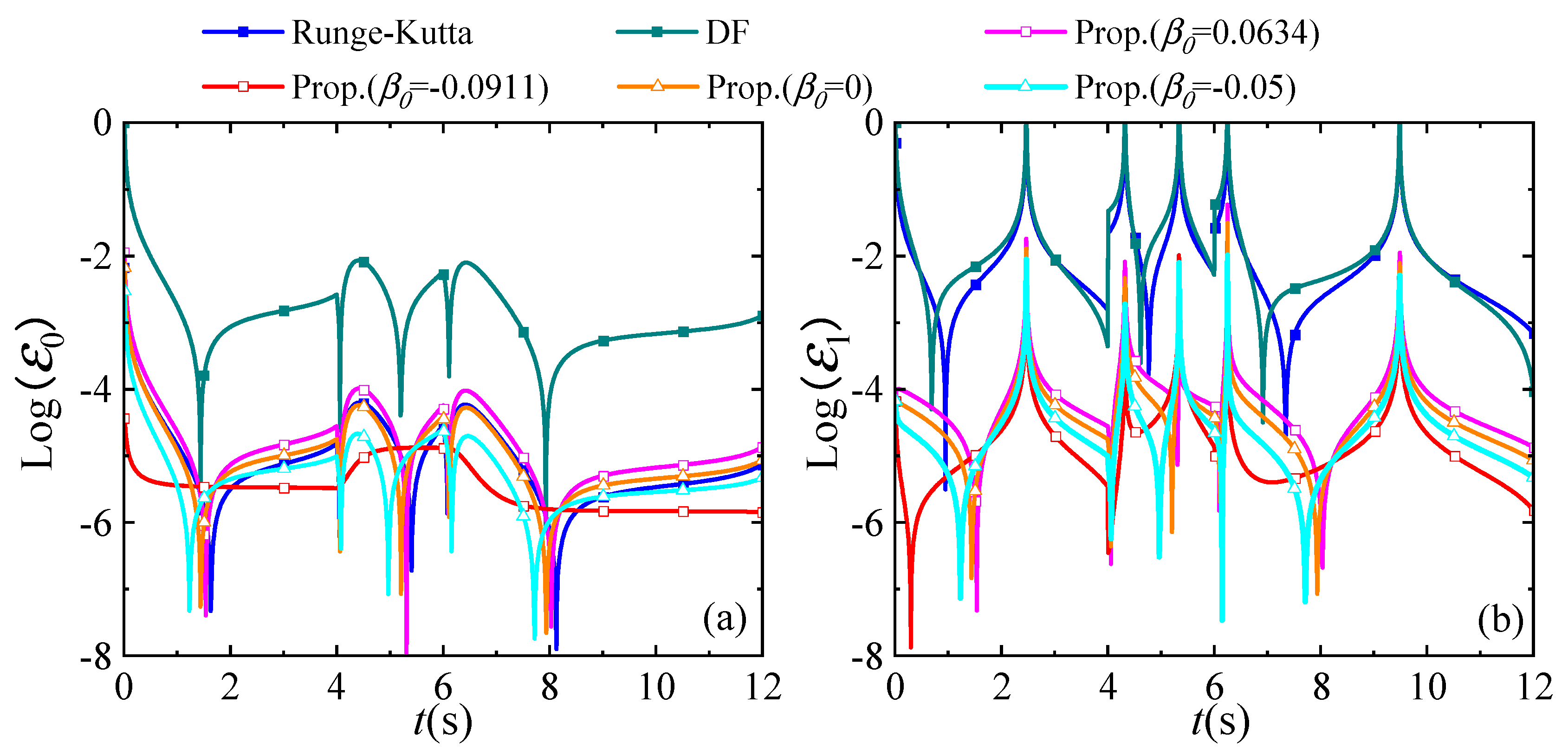
4.2. A Linear SDOF System with Complex External Heat Source
4.3. A Nonlinear SDOF System
4.4. A Linear MDOF System
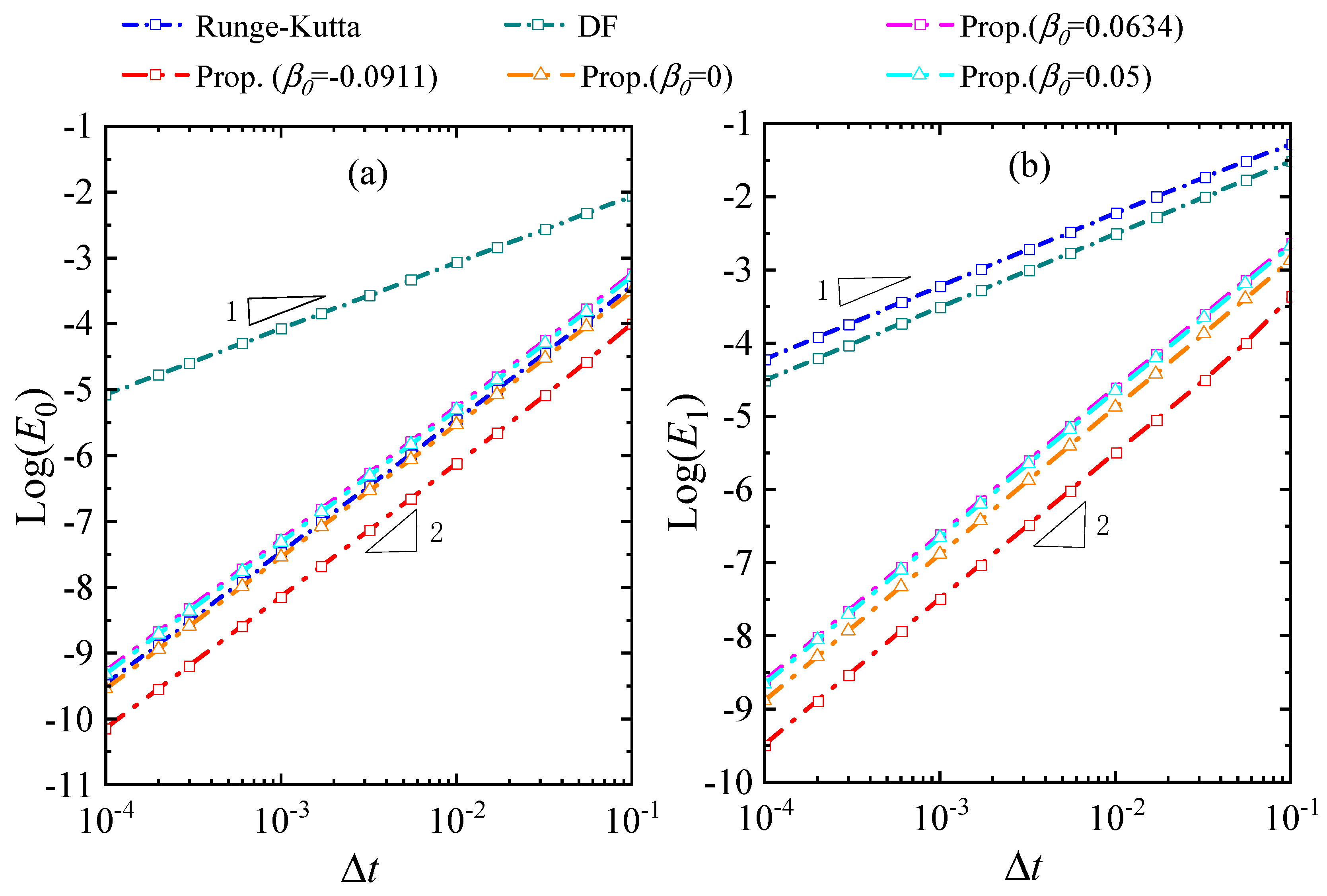
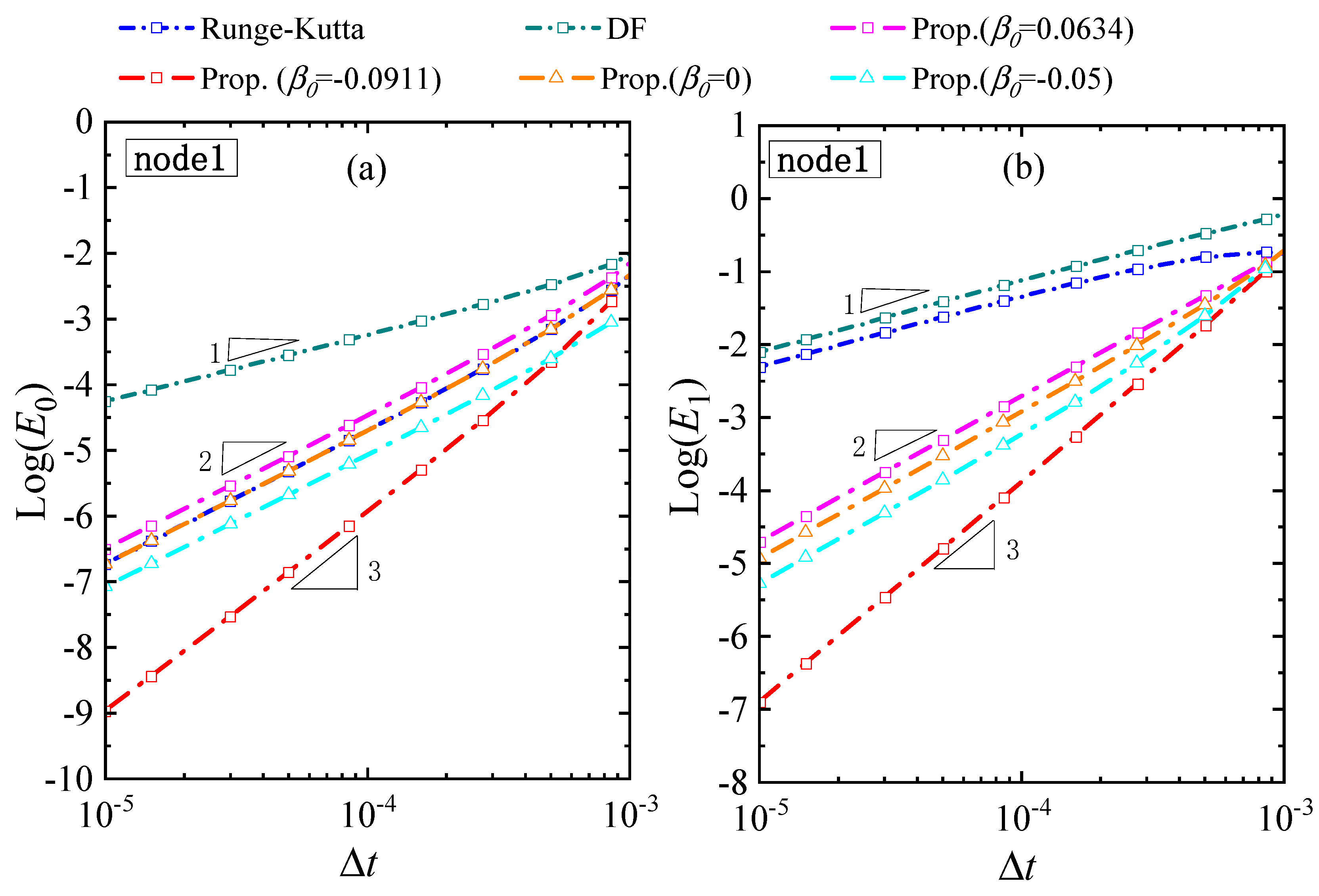
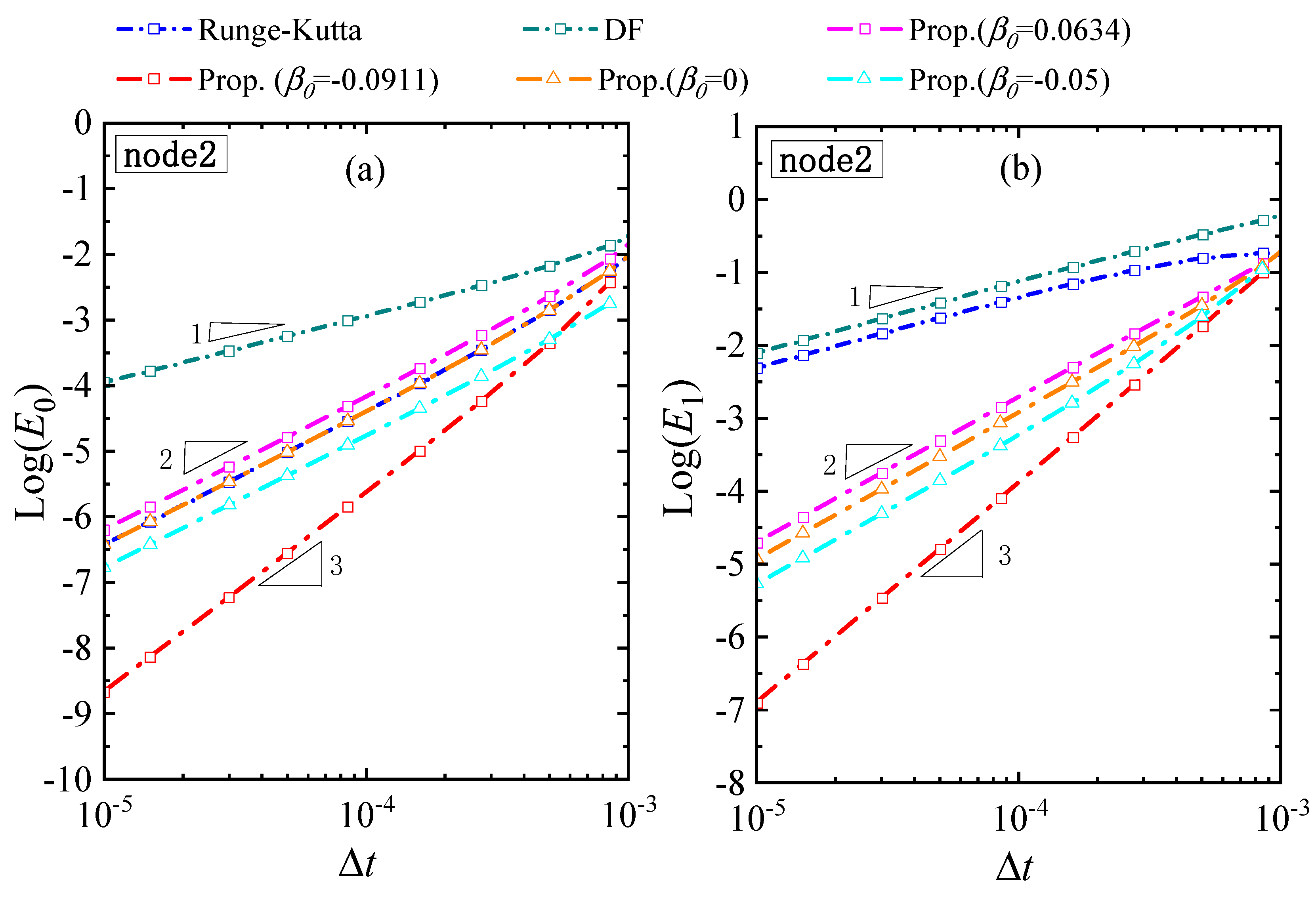
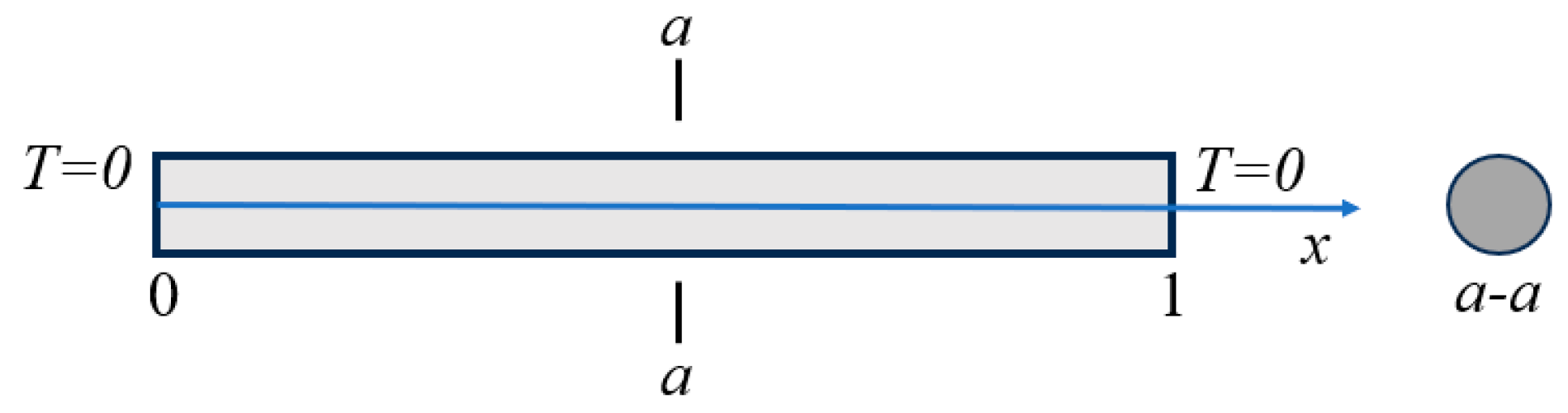
4.5. A Linear 1D System
4.6. A Nonlinear 1D System
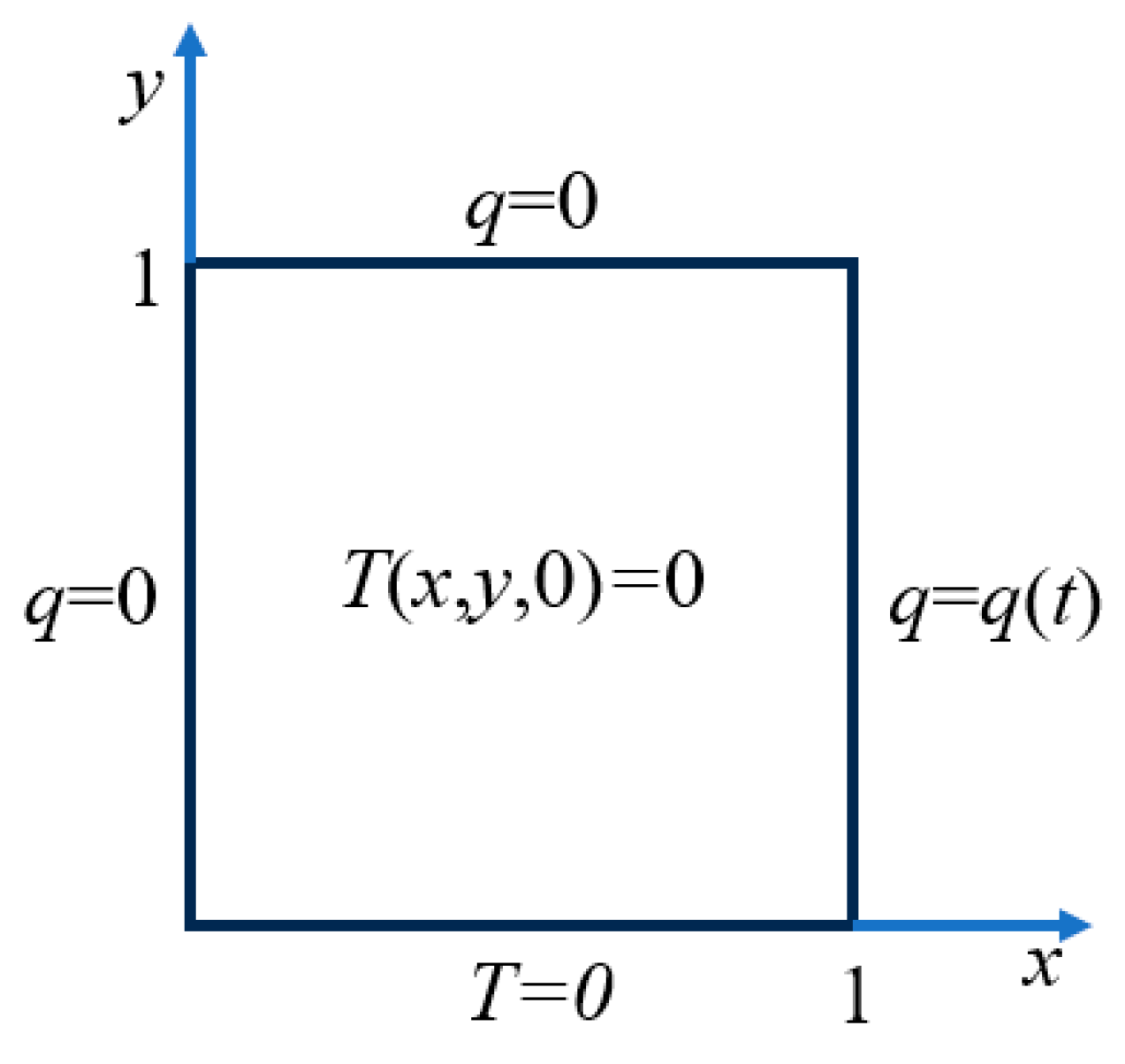
4.7. A 2D Square Plate
4.8. A 2D Air Fin Heat Dissipation Structure
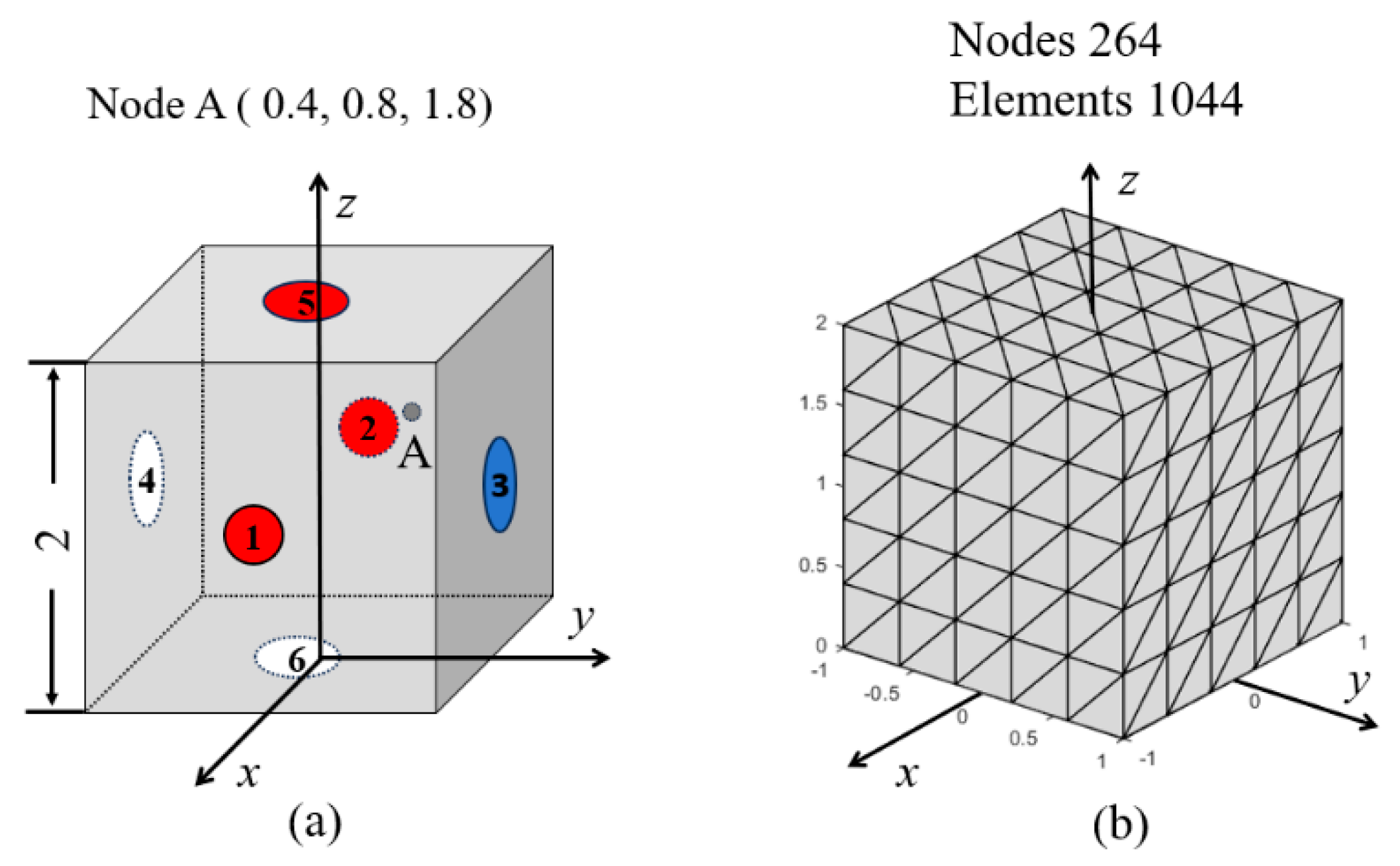
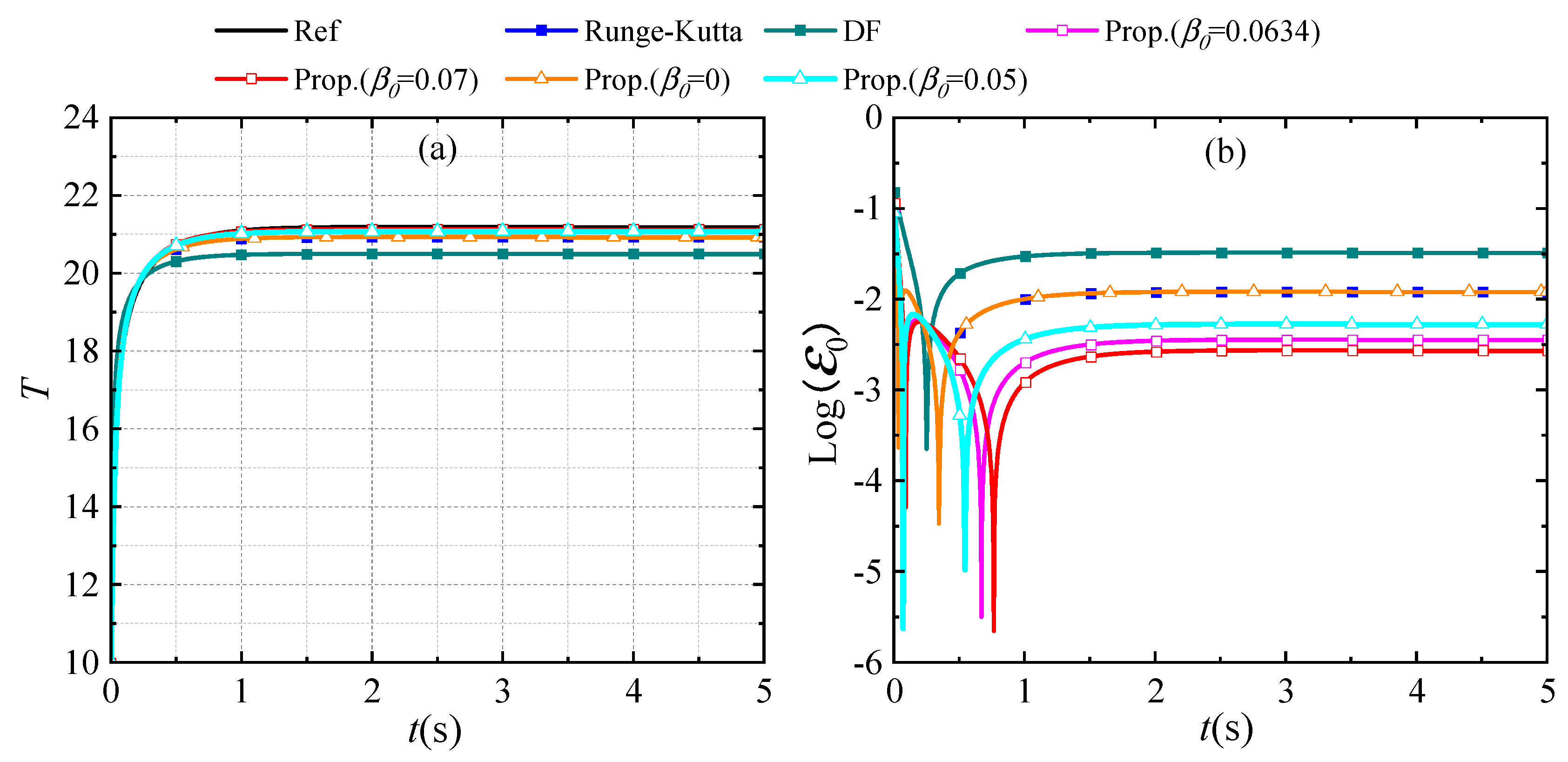
4.9. A 3D Cube Model
5. Conclusions
- (1)
- The proposed method has one free parameter () that can be used to control the basic algorithmic properties. With specific parameters, the proposed method demonstrates superior stability compared to those of the traditional methods.
- (2)
- Through numerical analyses, we recommend the case of the proposed method for large-scale systems. It allows for a large time step and can trade-off efficiency and accuracy. For uncoupled multi-degree-of-freedom problems, especially those without heat sources, the 0.0911 case is suggested, as it can significantly enhance accuracy.
- (3)
- Through theoretical analysis, the proposed method achieves at least second-order accuracy for temperature and its derivative. In some special cases, it can reach third-order accuracy for temperature.
- (4)
- For linear systems, the proposed method achieves desirable accuracy. As for nonlinear systems, the proposed method is effective and provides desirable solution accuracy.
- (5)
- In the proposed method, the integral weak form of the heat conduction equations is introduced to capture the variation in external heat source, which intrinsically improves the computation accuracy.
- (6)
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Lei, J.; Wang, Q.; Liu, X.; Gu, Y.; Fan, C.-M. A Novel Space-Time Generalized FDM for Transient Heat Conduction Problems. Eng. Anal. Bound. Elem. 2020, 119, 1–12. [Google Scholar] [CrossRef]
- Kubacka, E.; Ostrowski, P. Heat Conduction Issue in Biperiodic Composite Using Finite Difference Method. Compos. Struct. 2021, 261, 113310. [Google Scholar] [CrossRef]
- Zhang, J.; Chauhan, S. Fast Explicit Dynamics Finite Element Algorithm for Transient Heat Transfer. Int. J. Therm. Sci. 2019, 139, 160–175. [Google Scholar] [CrossRef]
- Suvin, V.; Ooi, E.T.; Song, C.; Natarajan, S. Temperature-Dependent Nonlinear Transient Heat Conduction Using the Scaled Boundary Finite Element Method. Int. J. Heat Mass Transf. 2025, 243, 126780. [Google Scholar] [CrossRef]
- Meng, Z.; Ma, Y.; Ma, L. A Fast Interpolating Meshless Method for 3D Heat Conduction Equations. Eng. Anal. Bound. Elem. 2022, 145, 352–362. [Google Scholar] [CrossRef]
- Noh, G.; Bathe, K.-J. An Explicit Time Integration Scheme for the Analysis of Wave Propagations. Comput. Struct. 2013, 129, 178–193. [Google Scholar] [CrossRef]
- Time Discretization of Equations of Motion: Overview and Conventional Practices. In Advances in Computational Dynamics of Particles, Materials and Structures; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2012; pp. 493–552. ISBN 978-1-119-96589-3.
- Crank, J.; Nicolson, P. A Practical Method for Numerical Evaluation of Solutions of Partial Differential Equations of the Heat-Conduction Type. Math. Proc. Camb. Phil. Soc. 1947, 43, 50–67. [Google Scholar] [CrossRef]
- Newmark, N.M. A Method of Computation for Structural Dynamics. J. Eng. Mech. Div. 1959, 85, 67–94. [Google Scholar] [CrossRef]
- Chung, J.; Hulbert, G.M. A Time Integration Algorithm for Structural Dynamics with Improved Numerical Dissipation: The Generalized-α Method. J. Appl. Mech. 1993, 60, 371–375. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Y.; Liu, D. Accuracy of a Composite Implicit Time Integration Scheme for Structural Dynamics. Int. J. Numer. Methods Eng. 2017, 109, 368–406. [Google Scholar] [CrossRef]
- Wen, W.; Wu, L.; Liu, T.; Deng, S.; Duan, S. A Novel Three Sub-Step Explicit Time Integration Method for Wave Propagation and Dynamic Problems. Int. J. Numer. Methods Eng. 2023, 124, 3299–3328. [Google Scholar] [CrossRef]
- Liu, T.; Wang, P.; Wen, W. An Improved Time-Marching Formulation Based on an Explicit Time Integration Method for Dynamic Analysis of Non-Viscous Damping Systems. Mech. Syst. Signal Process. 2023, 191, 110195. [Google Scholar] [CrossRef]
- Zhai, W.-M. Two Simple Fast Integration Methods for Large-Scale Dynamic Problems in Engineering. Int. J. Numer. Meth. Engng. 1996, 39, 4199–4214. [Google Scholar] [CrossRef]
- Hulbert, G.M.; Chung, J. Explicit Time Integration Algorithms for Structural Dynamics with Optimal Numerical Dissipation. Comput. Methods Appl. Mech. Eng. 1996, 137, 175–188. [Google Scholar] [CrossRef]
- Tchamwa, B.; Conway, T.; Wielgosz, C. An Accurate Explicit Direct Time Integration Method for Computational Structural Dynamics. In Proceedings of the Recent Advances in Solids and Structures, Nashville, TN, USA, 14 November 1999; American Society of Mechanical Engineers: Fairfield, NJ, USA, 1999; pp. 77–84. [Google Scholar]
- Soares, D. A Novel Time-Marching Formulation for Wave Propagation Analysis: The Adaptive Hybrid Explicit Method. Comput. Methods Appl. Mech. Eng. 2020, 366, 113095. [Google Scholar] [CrossRef]
- Malakiyeh, M.M.; Shojaee, S.; Hamzehei-Javaran, S.; Bathe, K.-J. The Explicit Β1/Β2-Bathe Time Integration Method. Comput. Struct. 2023, 286, 107092. [Google Scholar] [CrossRef]
- Kim, W.; Reddy, J.N. Novel Explicit Time Integration Schemes for Efficient Transient Analyses of Structural Problems. Int. J. Mech. Sci. 2020, 172, 105429. [Google Scholar] [CrossRef]
- Li, J.; Yu, K.; Zhao, R. Two Third-Order Explicit Integration Algorithms with Controllable Numerical Dissipation for Second-Order Nonlinear Dynamics. Comput. Methods Appl. Mech. Eng. 2022, 395, 114945. [Google Scholar] [CrossRef]
- Liu, T.; Huang, F.; Wen, W.; Deng, S.; Duan, S.; Fang, D. An Improved Higher-Order Explicit Time Integration Method with Momentum Corrector for Linear and Nonlinear Dynamics. Appl. Math. Model. 2021, 98, 287–308. [Google Scholar] [CrossRef]
- Wen, W.; Deng, S.; Duan, S.; Fang, D. A High-order Accurate Explicit Time Integration Method Based on Cubic B-spline Interpolation and Weighted Residual Technique for Structural Dynamics. Numer. Meth Eng. 2021, 122, 431–454. [Google Scholar] [CrossRef]
- Liu, T.; Wang, P.; Wen, W.; Feng, F. Improved Explicit Quartic B-Spline Time Integration Scheme for Dynamic Response Analysis of Viscoelastic Systems. Mech. Syst. Signal Process. 2024, 208, 110982. [Google Scholar] [CrossRef]
- Han, Y.; Liu, T.; Wen, W.; Liu, X. A New Family of B-Spline Based Explicit Time Integration Methods for Linear Structural Dynamic Analysis. Comput. Math. Appl. 2025, 185, 29–51. [Google Scholar] [CrossRef]
- Liu, T.; Wang, P.; Wen, W.; Feng, F. Formulation and Analysis of a Cubic B-Spline-Based Time Integration Procedure for Structural Seismic Response Analysis. Int. J. Struct. Stab. Dyn. 2023, 23, 2350180. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, J.; Chen, Z.; Li, X.; Zeng, X.-M. B-Spline Surface Fitting with Knot Position Optimization. Comput. Graph. 2016, 58, 73–83. [Google Scholar] [CrossRef]
- Park, H. B-Spline Surface Fitting Based on Adaptive Knot Placement Using Dominant Columns. Comput.-Aided Des. 2011, 43, 258–264. [Google Scholar] [CrossRef]
- Wen, W.-B.; Jian, K.-L.; Luo, S.-M. An Explicit Time Integration Method for Structural Dynamics Using Septuple B-Spline Functions. Int. J. Numer. Methods Eng. 2014, 97, 629–657. [Google Scholar] [CrossRef]
- Wen, W.; Li, H.; Liu, T.; Deng, S.; Duan, S. A Novel Hybrid Sub-Step Explicit Time Integration Method with Cubic B-Spline Interpolation and Momentum Corrector Technique for Linear and Nonlinear Dynamics. Nonlinear Dyn. 2022, 110, 2685–2714. [Google Scholar] [CrossRef]
- Nikolis, A. Numerical Solutions of Ordinary Differential Equations with Quadratic Trigonometric Splines. Appl. Math. E-Notes 2004, 4, 142–149. [Google Scholar]
- Liu, T.; Wang, P.; Wen, W. A Novel Single-Step Explicit Time Integration Method Based on Momentum Corrector Technique for Structural Dynamic Analysis. Appl. Math. Model. 2023, 124, 1–23. [Google Scholar] [CrossRef]
- Hughes, T.J.R. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis; Dover Publications: Mineola, NY, USA, 2000; ISBN 978-0-486-13502-1. [Google Scholar]
- Lü, Y.; Wang, G.; Yang, X. Uniform Trigonometric Polynomial B-Spline Curves. Sci. China Ser. F 2002, 45, 335–343. [Google Scholar] [CrossRef]
- Wang, Y.; Maxam, D.; Tamma, K.K.; Qin, G. Design/Analysis of GEGS4-1 Time Integration Framework with Improved Stability and Solution Accuracy for First-Order Transient Systems. J. Comput. Phys. 2020, 422, 109763. [Google Scholar] [CrossRef]
- Ji, Y.; Xing, Y. An Unconditionally Stable Method for Transient Heat Conduction. Lixue Xuebao/Chin. J. Theor. Appl. Mech. 2021, 53, 1951–1961. [Google Scholar] [CrossRef]
- Song, Z.; Lai, S.-K.; Wu, B. A New MIB-Based Time Integration Method for Transient Heat Conduction Analysis of Discrete and Continuous Systems. Int. J. Heat Mass Transf. 2024, 222, 125153. [Google Scholar] [CrossRef]
- Young, D.L.; Tsai, C.C.; Murugesan, K.; Fan, C.M.; Chen, C.W. Time-Dependent Fundamental Solutions for Homogeneous Diffusion Problems. Eng. Anal. Bound. Elem. 2004, 28, 1463–1473. [Google Scholar] [CrossRef]
- Chen, B.; Gu, Y.; Guan, Z.; Zhang, H. Nonlinear Transient Heat Conduction Analysis with Precise Time Integration Method. Numer. Heat Transf. Part B Fundam. 2001, 40, 325–341. [Google Scholar] [CrossRef]
- Li, Q.-H.; Chen, S.-S.; Kou, G.-X. Transient Heat Conduction Analysis Using the MLPG Method and Modified Precise Time Step Integration Method. J. Comput. Phys. 2011, 230, 2736–2750. [Google Scholar] [CrossRef]
- Yang, K.; Jiang, G.-H.; Li, H.-Y.; Zhang, Z.; Gao, X.-W. Element Differential Method for Solving Transient Heat Conduction Problems. Int. J. Heat Mass Transf. 2018, 127, 1189–1197. [Google Scholar] [CrossRef]
- Sun, W.; Qu, W.; Gu, Y.; Li, P.-W. An Arbitrary Order Numerical Framework for Transient Heat Conduction Problems. Int. J. Heat Mass Transf. 2024, 218, 124798. [Google Scholar] [CrossRef]
- Zhao, S.; Kong, H.; Zheng, H. The MLS Based Numerical Manifold Method for Bending Analysis of Thin Plates on Elastic Foundations. Eng. Anal. Bound. Elem. 2023, 153, 68–87. [Google Scholar] [CrossRef]
- Wang, P.; Han, X.; Wen, W.; Wang, B.; Liang, J. Galerkin-Based Quasi-Smooth Manifold Element(QSME)Method for Anisotropic Heat Conduction Problems in Composites with Complex Geometry. Appl. Math. Mech. (Engl. Ed.) 2024, 45, 137–154. [Google Scholar] [CrossRef]


| A. Initial calculation |
| A.1. Obtain capacity matrix C and conductivity matrix K |
| A.2. Give initial values , and calculate |
| A.3. Select , and determine and stable time step |
| B. For each time step |
| B.1. Calculate unknown B-spline coefficients vector by |
| B.2. Calculate the B-spline approximations of physical variable vectors as |
| B.3. Obtain the modified physical variable vectors as |
| B.4. Obtain the final physical variable vectors as |
| β0 | −0.24 | −0.14 | −0.12 | −0.0911 | −0.05 | 0 | 0.05 | 0.0634 | 0.07 | 0.14 | 0.24 |
| ωΔtc | 0.723 | 0.986 | 1.062 | 1.199 | 1.464 | 2 | 3.154 | 3.731 | 1.910 | 0.980 | 0.660 |
| Δt | Runge–Kutta | DF | Prop. | |||
|---|---|---|---|---|---|---|
| β0 = 0.0634 | β0 = −0.0911 | β0 = 0 | β0 = 0.05 | |||
| 0.001 | 0.02819 | 0.01735 | 0.06422 | 0.06313 | 0.06437 | 0.06566 |
| 0.0005 | 0.05590 | 0.03203 | 0.12570 | 0.12448 | 0.12256 | 0.12639 |
| 0.0001 | 0.25360 | 0.14495 | 0.59931 | 0.60162 | 0.59537 | 0.59457 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Hong, Y.; Wang, P.; Wen, W. Explicit Time Integration Method Based on Uniform Trigonometric B-Spline Function for Transient Heat Conduction Analysis. Appl. Sci. 2025, 15, 5227. https://doi.org/10.3390/app15105227
Li Z, Hong Y, Wang P, Wen W. Explicit Time Integration Method Based on Uniform Trigonometric B-Spline Function for Transient Heat Conduction Analysis. Applied Sciences. 2025; 15(10):5227. https://doi.org/10.3390/app15105227
Chicago/Turabian StyleLi, Zixu, Yongyu Hong, Pan Wang, and Weibin Wen. 2025. "Explicit Time Integration Method Based on Uniform Trigonometric B-Spline Function for Transient Heat Conduction Analysis" Applied Sciences 15, no. 10: 5227. https://doi.org/10.3390/app15105227
APA StyleLi, Z., Hong, Y., Wang, P., & Wen, W. (2025). Explicit Time Integration Method Based on Uniform Trigonometric B-Spline Function for Transient Heat Conduction Analysis. Applied Sciences, 15(10), 5227. https://doi.org/10.3390/app15105227







